1 Introduction

Entanglement, first described by Einstein et al. [1] and Schrödinger [2], is a quantum mechanical phenomenon that can be experimentally observed, representing a deviation of quantum from classical mechanics [3]. Entanglement has been in the focus of intense investigation due to its importance in quantum information processing [4], thus motivating protocols for its creation in different realistic platforms [5,6,7]. Among quantum entangled states, special attention is devoted to the ones having maximal amount of entanglement, since they differ the most from classical reality. In tripartite systems, there are two types of maximally entangled states: the W state [8, 9] and the Greenberger–Horne–Zeilinger (GHZ) state [10]. The entanglement present in the GHZ state disappears if one of the three qubits is traced over. On the other hand, W state has nonzero entanglement after bipartition.

Due to their diverse applications, finding simple and reliable resources to implement both types of states is of utmost importance. Heisenberg exchange interaction is the standard tool for manipulation with spins, and it is used in different aspects of quantum information [5, 11, 12]- and quantum computation [13,14,15,16,17,18,19]-related research. Since three-spin interaction affects all three spins at the same time, while the pairwise interactions are limited in the manipulation on the two spins only; in the context of tripartite entanglement, assumption that sophisticated three-spin terms can enhance entanglement naturally arises [20,21,22]. Up to now, variety of different types of effective three-spin interactions have been theoretically demonstrated in triple quantum dot [16,17,18,19], \({}^{13}C\) labeled Alanine [23], triangular optical lattice [24, 25], trapped ions [26] and cold polar molecules [27].

Here, we demonstrate that three-spin interaction can be used as an efficient resource to create maximally entangled states. We do not require set of gates to implement our scheme [11, 12]; rather, we focus on the natural entanglement [20,21,22, 28,29,30,31,32] of a system at thermal equilibrium and identify the parameter regime for which thermal entanglement reaches its maximum. Since main requirements needed to experimentally construct maximally entangled states are met in triple quantum dot and triangular optical lattice, obtained results are going to be illustrated on these systems.

The paper is organized as follows. In Sect. 2, we define entanglement measures going to be used in the analysis of the effects of different types of three-spin interactions. In Sect. 3, we discuss triple quantum dot system, while Sect. 4 is devoted to triangular optical lattice. In Sect. 5, we analyze the possibility to indirectly detect the presence of W type of entanglement by measuring magnetization in z direction. Finally, conclusions are given in Sect. 6.

2 Entanglement measures

To start with, we define a thermal state \(\rho \) of a system at thermal equilibrium as

$$\begin{aligned} \rho =\frac{\mathrm{e}^{-\beta H}}{Z}, \end{aligned}$$
(1)

where Hamiltonian H describes interactions present in the system, while \(Z=\mathrm{Tr}\,\mathrm{e}^{-\beta H}\) is the partition function (\(\beta =1/k_B T\), \(k_B\) is Boltzmann’s constant and T temperature). In order to identify the presence of thermal entanglement in the system, tripartite and bipartite entanglement measures will be introduced. Tripartite entanglement of the thermal state \(\rho \) will be analyzed using the tripartite negativity [33]

$$\begin{aligned} N_{123}=(N_{1-23}N_{2-13}N_{3-12})^{\frac{1}{3}}, \end{aligned}$$
(2)

equal to the geometric mean of bipartite negativities \(N_{1-23}\), \(N_{2-13}\) and \(N_{3-12}\) [34]. Bipartite negativity is defined as

$$\begin{aligned} N_{I-JK}=-2\sum _i\lambda _i\left( \rho ^{T}_{I}\right) , \end{aligned}$$
(3)

where \(\lambda _i(\rho ^{T}_{I})\) are negative eigenvalues of partially transposed statistical operator \(\rho ^{T}_I\) with respect to the subsystem I, (\(I-JK=\{1-23,2-13,3-12\}\)). The authors of [33] have shown that \(N_{123}\) reaches the value 1 for the GHZ state, while in the case of the W state tripartite negativity is approximately 0.94.

In order to distinguish between two types of entanglement, it is useful to study the concurrence [35,36,37], measuring the bipartite entanglement. First, we define three two-qubit states \(\rho _{JK}\), being equal to the partial traces over the third spin I, \(\rho _{JK}=\mathrm{Tr}_{I}\,\rho \). For a two-qubit state \(\rho _{JK}\), concurrence is defined as

$$\begin{aligned} C(\rho _{JK})=\mathrm{max}\left\{ 0,\sqrt{\beta _1}-\sqrt{\beta _2}-\sqrt{\beta _3}-\sqrt{\beta _4}\right\} , \end{aligned}$$
(4)

where \(\beta _i\) (\(i=1,2,3,4\)) represent eigenvalues of the operator

$$\begin{aligned} \rho _{JK}(\sigma _y\otimes \sigma _y)\rho _{JK}^*(\sigma _y\otimes \sigma _y), \end{aligned}$$
(5)

sorted in the descending order. In (5), conjugate of \(\rho _{JK}\) is employed, \(\rho _{JK}^*\), as well as Pauli \(\sigma _y\) matrix. Using the value \(C(\rho _{12})^2+C(\rho _{23})^2+C(\rho _{31})^2\), W and GHZ state can be distinguished. Namely, the GHZ state minimizes all three concurrences, \(C(\rho _{12})^2+C(\rho _{23})^2+C(\rho _{31})^2=0\), while for the W state this sum reaches 4 / 3. Putting the two conditions together, we will use two auxiliary functions

$$\begin{aligned} F_{W}(\rho )= & {} \frac{4}{3}-\sum _{JK} C(\rho _{JK})^2+N_{123}(W)-N_{123}(\rho ),\nonumber \\ F_{\mathrm{GHZ}}(\rho )= & {} \sum _{JK}C(\rho _{JK})^2+N_{123}(\mathrm{GHZ})-N_{123}(\rho ), \end{aligned}$$
(6)

which, if equal zero, confirm the presence of maximally entangled states. It should be further emphasized that \(F_{W}(\rho )\) and \(F_{\mathrm{GHZ}}(\rho )\) do not represent new measure, they are just combined constraint of tripartite negativity and concurrence.

Moreover, since there is no absolutely accepted measure of tripartite entanglement, it is plausible to use more than one measure and compare the obtained results. To assure the reader of the correctness of the results derived from \(F_{W}(\rho )\) and \(F_{\mathrm{GHZ}}(\rho )\), we will also calculate the distance of a given density matrix \(\rho \) to the target maximally entangled state \(| {\psi } \rangle \) through fidelity \(\langle {\psi } |\rho | {\psi } \rangle \), where the value 1 indicates that \(| {\psi } \rangle \) and \(\rho \) represent equivalent states. Finally, we note that minimization of \(F_{W}(\rho )\) and \(F_{\mathrm{GHZ}}(\rho )\) does not always give us exact W and GHZ states, respectively, but rather states that can be transformed into W/GHZ state using the local operations on each qubit. In what follows, we will identify each class of maximally entangled states [38] with their most prominent representatives, providing in each case concrete form of the calculated states.

3 Triple quantum dot

We start by performing a detailed analysis of the Hamiltonian describing the three-spin solid state qubit in an equilateral triangle geometry [16,17,18]

$$\begin{aligned} H=\sum _{i=1}^3 (J{\varvec{\sigma }}_i\cdot {\varvec{\sigma }}_{i+1}+b{\sigma }_i^z)+\alpha {\varvec{\sigma }}_1({\varvec{\sigma }}_2\times {\varvec{\sigma }}_3), \end{aligned}$$
(7)

where \({\varvec{\sigma }}_i=(\sigma _i^x,\sigma _i^y,\sigma _i^z)\) is the vector made of Pauli matrices, while \({\varvec{\sigma }}_4={\varvec{\sigma }}_1\). Exchange interaction has an isotropic form, with exchange interaction parameters equal for each pair of spins. Zeeman term is proportional to \(b=g\mu _B B\), where B is the external magnetic field in direction perpendicular to the system (z-axis), \(\mu _B\) is the Bohr magneton, while g factor depends on the material in which quantum dots are embedded. In addition to the exchange and Zeeman term, three-spin interaction in the box product form is present, usually called the chirality operator.

In what follows, we will represent matrix elements of the thermal state \(\rho \) in the eight-dimensional basis \(\mathcal {V}\),

$$\begin{aligned} \mathcal {V}= \{| {+++} \rangle ,| {++-} \rangle ,| {+-+} \rangle ,| {+--} \rangle ,| {-++} \rangle ,| {-+-} \rangle ,| {--+} \rangle ,| {---} \rangle \}, \end{aligned}$$
(8)

where \(| {+} \rangle \) is an eigenvector of Pauli z matrix \(\sigma _z\) for positive eigenvalue, i.e. spin-up state, while \(| {-} \rangle \) is an eigenvector of \(\sigma _z\) for negative eigenvalue (spin-down state). Nonzero matrix elements of \(\rho \) in the case of Hamiltonian (7) are the following (due to the fact that \(\rho \) is Hermitian operator, by knowing \(\rho _{ij}\), simply follows the relation \(\rho _{ji}=\rho _{ij}^{*}\))

$$\begin{aligned} \rho _{11}= & {} \frac{1}{(1+\mathrm {e}^{2\beta b})(1+\mathrm {e}^{4\beta b}+2\mathrm {e}^{2\beta (b+3J)}\cosh {2\sqrt{3}\beta \alpha })},\nonumber \\ \rho _{88}= & {} \frac{\mathrm {e}^{6\beta b}}{(1+\mathrm {e}^{2\beta b})(1+\mathrm {e}^{4\beta b}+2\mathrm {e}^{2\beta (b+3J)}\cosh {2\sqrt{3}\beta \alpha })},\nonumber \\ \rho _{22}= & {} \rho _{33}=\rho _{55}=\frac{1}{3(1+\mathrm {e}^{2\beta b}+\frac{\mathrm {e}^{-2\beta b}+\mathrm {e}^{4\beta b}}{1+2\mathrm {e}^{6\beta J}\cosh {2\sqrt{3}\beta \alpha }})},\nonumber \\ \rho _{44}= & {} \rho _{66}=\rho _{77}=\frac{1}{3(1+\mathrm {e}^{-2\beta b}+\frac{\mathrm {e}^{2\beta b}+\mathrm {e}^{-4\beta b}}{1+2\mathrm {e}^{6\beta J}\cosh {2\sqrt{3}\beta \alpha }})},\nonumber \\ \rho _{23}= & {} \rho _{52}=\rho _{35}=\mathrm {e}^{2\beta b}A,\nonumber \\ \rho _{47}= & {} \rho _{64}=\rho _{76}=\mathrm {e}^{4\beta b}A, \end{aligned}$$
(9)

where

$$\begin{aligned} A= -\frac{(1-\mathrm {i}\sqrt{3})\mathrm {e}^{6\beta J}-2\mathrm {e}^{2\sqrt{3}\beta \alpha }+(1+\mathrm {i}\sqrt{3})\mathrm {e}^{6\beta J+4\sqrt{3}\beta \alpha }}{6(1+\mathrm {e}^{2\beta b})(\mathrm {e}^{2\sqrt{3}\beta \alpha }(1+\mathrm {e}^{4\beta b})+\mathrm {e}^{2\beta (b+3J)}(1+\mathrm {e}^{4\sqrt{3}\beta \alpha }))}. \end{aligned}$$
(10)

By knowing \(\rho \), desired quantities \(F_{W}(\rho )\) and \(F_{\mathrm{GHZ}}(\rho )\) can be simply calculated. Due to the fact that analytical results are not very illustrative, dependencies of \(F_{W}(\rho )\) and \(F_{\mathrm{GHZ}}(\rho )\) on various parameters are going to be analyzed numerically.

Fig. 1
figure 1

Creation of the W state using the chirality operator. For fixed \(\beta |J|=10^1\), dependence of \(F_{W}(\rho )\) on the ratios \(b/J\in (-10,10)\) and \(\alpha /J\in (-10,10)\) in the antiferromagnetic (upper left panel) and ferromagnetic (upper right panel) regime is presented. Dependence of fidelity on the same parameters is given for the antiferromagnetic (lower left panel) and ferromagnetic (lower right panel) case

Full size image

We will discuss both antiferromagnetic (AF), \(J>0\), and ferromagnetic (F), \(J<0\), exchange interaction case and present the results in terms of the ratio of exchange interaction energy and thermal energy, \(\beta |J|\). First, independently of the value of model parameters and temperature, GHZ state is impossible to create. This is expected, since the interactions present in the system do not mix the subspaces with different z projections of total spin, being the essential requirement for the construction of the GHZ state. On the other hand, the W state belongs to the subspace with fixed z projection, making this type of entanglement more suitable for construction.

Neglecting the \(J=0\) situation, it turns out that \(\beta |J|\) needs to be larger or equal to \(10^1\) in order to enable the W state creation. In Fig. 1 (upper panels), we plot the dependency of \(F_{W}(\rho )\) on \(b/J\in (-10,10)\) and \(\alpha /J\in (-10,10)\) for the AF (upper left panel) and F (upper right panel) case, keeping the value \(\beta |J|\) fixed at \(10^1\). Results can be divided into three categories: The first category belongs to the maximal values (light blue); the second regime is intermediate (blue) and finally, the third category consists of minimal values (dark blue) of interest for us. Useful parameter regime in the AF/F case is limited by the value of Zeeman/chirality term from above/under. Additionally, rise of \(\beta |J|\) has a positive impact on the minimization of \(F_{W}(\rho )\) and can lead to the transition of intermediate values into the category of minimal values. As an example, 1.03 value of \(F_W(\rho )\) for \(\beta J=10^1\) and \(\alpha /J=b/J=10^{-1}\) can be lowered to \(1.21\times 10^{-4}\) and \(2.43\times 10^{-8}\) by increasing the value \(\beta J\) to \(10^2\) and \(10^3\), respectively, and keeping the other parameters fixed. Beside the fact that different phases of J have an impact on the parameter regime in which the W state can occur, exchange interaction plays no fundamental role in the creation of W type of entanglement. In the \(J=0\) case, we were able to find the parameters that create W state (\(|\alpha /b|\ge 0.6\), \(\beta b\ge 10^3\)), thus confirming the above statement. In all cases (\(J\ge <0\)), obtained states are solely dependent on the signs of b and \(\alpha \), being the eigenstates of the chirality operator, thus confirming its essential role.

Furthermore, we find the concrete form of the ideal \(| {W} \rangle \) states by assuming that fidelity \(\langle {W} |\rho | {W} \rangle \) should tend to 1 by appropriately adjusting the parameter regime. Dependence of the W state on b and \(\alpha \) is the following

$$\begin{aligned} | {W} \rangle _{b>0,\alpha>0}= & {} \frac{1}{\sqrt{3}}\left( | {+--} \rangle +\mathrm {e}^{\mathrm {i}\frac{4\pi }{3}}| {-+-} \rangle +\mathrm {e}^{\mathrm {i}\frac{2\pi }{3}}| {--+} \rangle \right) ,\nonumber \\ | {W} \rangle _{b>0,\alpha<0}= & {} \frac{1}{\sqrt{3}}\left( | {+--} \rangle +\mathrm {e}^{\mathrm {i}\frac{2\pi }{3}}| {-+-} \rangle +\mathrm {e}^{\mathrm {i}\frac{4\pi }{3}}| {--+} \rangle \right) ,\nonumber \\ | {W} \rangle _{b<0,\alpha >0}= & {} \frac{1}{\sqrt{3}}\left( | {++-} \rangle +\mathrm {e}^{\mathrm {i}\frac{2\pi }{3}}| {+-+} \rangle +\mathrm {e}^{\mathrm {i}\frac{4\pi }{3}}| {-++} \rangle \right) ,\nonumber \\ | {W} \rangle _{b<0,\alpha <0}= & {} \frac{1}{\sqrt{3}}\left( | {++-} \rangle +\mathrm {e}^{\mathrm {i}\frac{4\pi }{3}}| {+-+} \rangle +\mathrm {e}^{\mathrm {i}\frac{2\pi }{3}}| {-++} \rangle \right) . \end{aligned}$$
(11)

In Fig. 1 (lower panels), we plot the dependence of fidelity on b and \(\alpha \) in the same parameter regime as for \(F_W(\rho )\). (It is to be noted that in the case \(b=0\) (similar for \(\alpha =0\)), we have calculated fidelities \({}_{b>0,\alpha }\langle {W} |\rho | {W} \rangle _{b>0,\alpha }=\) \({}_{b<0,\alpha }\langle {W} |\rho | {W} \rangle _{b<0,\alpha }\).) As can be seen in Fig. 1, qualitatively both measures predict the same behavior of entanglement with respect to the given parameters, thus confirming the results acquired from \(F_W(\rho )\).

We discuss the obtained results in the context of GaAs triple quantum dot, being the standard solid state platform for implementation and manipulation with localized spins. AF regime is present in zero and low magnetic field, since only strong magnetic field can induce a sign change of J [19]. In order to minimize \(F_W(\rho )\), three-spin interaction does not have to be comparable in strength to the exchange interaction. This fact is convenient for us, since chirality is the weakest interaction present in the system. Assuming small three-spin term, \(\alpha /J=0.05\), at temperatures around \(\mathrm{mK}\) and \(J\approx 20\,\upmu \mathrm{eV}\) [11], we have found very low values \(F_W(\rho )\approx 10^{-8}\) for magnetic field \(b/J=0.2\), indicating the realizability of W state with high accuracy.

Finally, we address the effects of spin–orbit interaction, having the potential to interfere with the conclusions stated above. Effective spin–orbit Hamiltonian between two spins can be written as a sum of two terms, antisymmetric Dzyaloshinskii–Moriya (DM), and symmetric tensor term

$$\begin{aligned} H_{ij}^{SO}= & {} {\mathbf {d}}_{ij}({\varvec{\sigma }}_i\times {\varvec{\sigma }}_j)+\Gamma _{ij}({\mathbf {d}}_{ij}\cdot {\varvec{\sigma }}_i)({\mathbf {d}}_{ij}\cdot {\varvec{\sigma }}_j). \end{aligned}$$
(12)

In GaAs quantum dots, at low perpendicular magnetic fields, all DM vectors are in the plane in which quantum dots are embedded, say it to be the xy plane. Symmetric contribution is a second-order correction to the total spin–orbit interaction, and we will assume \(\Gamma _{ij}=J(\sqrt{1+|{\mathbf {d}}_{ij}|^2/J^2}-1)/|{\mathbf {d}}_{ij}|^2\) [39]. Furthermore, in the equilateral geometry, condition \({\mathbf {d}}_{12}+{\mathbf {d}}_{23}+{\mathbf {d}}_{31}=0\) is satisfied [19, 40] and, to a good level of approximation, all vectors have the same intensity. By setting the x-axis in \({\mathbf {d}}_{12}\) direction, vectors \({\mathbf {d}}_{23}\) and \({\mathbf {d}}_{31}\) are equal to \(R_{{\mathbf {e}}_z}(2\pi /3){\mathbf {d}}_{12}\) and \(R_{{\mathbf {e}}_z}(4\pi /3){\mathbf {d}}_{12}\), respectively, where \(R_{{\mathbf {e}}_z}(\varphi )\) is a rotational matrix around the z-axis for an angle \(\varphi \). Assuming reasonably small DM vector’s strength [19], \(|{\mathbf {d}}_{ij}|/|J|\le 10^{-2}\), it turns out that \(F_{W}(\rho )\) is not crucially affected by this interaction. In the parameter regime of interest (dark blue), maximal impact of spin–orbit interaction on \(F_{W}(\rho )\) is on the \(10^{-3}\) scale, making the triple quantum dot in GaAs an excellent platform for realization of the W state using the chirality operator.

4 Optical triangular lattice

In this section, we analyze the effective spin Hamiltonian in a triangular optical lattice [24, 25],

$$\begin{aligned} H= & {} \sum _{i=1}^3 \Big [{\mathbf {b}}\cdot {\varvec{\sigma }}_i+\lambda ^{(1)}\sigma _i^z\sigma _{i+1}^z+\lambda ^{(2)}\left( \sigma _i^x\sigma _{i+1}^x+\sigma _i^y\sigma _{i+1}^y\right) \nonumber \\&+\,\lambda ^{(3)}\sigma _1^z\sigma _2^z\sigma _3^z +\lambda ^{(4)}\left( \sigma _i^x\sigma _{i+1}^z\sigma _{i+2}^x+\sigma _i^{y}\sigma _{i+1}^z\sigma _{i+2}^y\right) \Big ], \end{aligned}$$
(13)

containing single spin, two-spin and two types of three-spin interaction. Magnetic field \({\mathbf {b}}\) can be arbitrarily tuned, as well as parameters \(\lambda ^{(i)}\), \(i=\{1,2,3,4\}\), being independent one on another.

First, we note that within this model it is possible to create approximate GHZ and exact W ground states [5] using the first three terms in (13) only. Alternatively, XZX + YZY type of three-spin interaction can be used for ever simpler creation of the W state. Using this term only, W state can be generated with highest precision. To obtain it, \(\beta |\lambda ^{(4)}|\) should be larger than \(10^{2}\). However, even for \(\beta |\lambda ^{(4)}|=10^1\) excellent value \(F_{W}(\rho )\approx 10^{-4}\) is achieved. Assuming \(|\lambda ^{(4)}|\approx 1\mathrm{kHz}\), \(\mathrm{nK}\) temperature mode is needed to implement this state.

Numerical results can be easily analytically confirmed by directly studying the statistical operator \(\rho \). If only interaction XZX + YZY is present, nonzero matrix elements of \(\rho \) are

$$\begin{aligned} \rho _{11}= & {} \rho _{88}=\frac{1}{8\cosh ^2{(\beta \lambda ^{(4)})}\cosh {(2\beta \lambda ^{(4)})}}, \nonumber \\ \rho _{22}= & {} \frac{1+3\mathrm {e}^{6\beta \lambda ^{(4)}}}{3(1+\mathrm {e}^{2\beta \lambda ^{(4)}})^2(1+\mathrm {e}^{4\beta \lambda ^{(4)}})},\nonumber \\ \rho _{33}= & {} \rho _{55}=\frac{2+3\mathrm {e}^{6\beta \lambda ^{(4)}}}{6(1+\mathrm {e}^{2\beta \lambda ^{(4)}})^2(1+\mathrm {e}^{4\beta \lambda ^{(4)}})},\nonumber \\ \rho _{44}= & {} \frac{\big (2\cosh {(3\beta \lambda ^{(4)})}-\sinh {(3\beta \lambda ^{(4)})}\big )\big (1+\tanh {(\beta \lambda ^{(4)})}\big )}{12\cosh {(\beta \lambda ^{(4)})}\cosh {(2\beta \lambda ^{(4)})}},\nonumber \\ \rho _{66}= & {} \rho _{77}=\frac{\big (5\cosh {(3\beta \lambda ^{(4)})}-\sinh {(3\beta \lambda ^{(4)})}\big ) \big (1+\tanh {(\beta \lambda ^{(4)})}\big )}{48\cosh {(\beta \lambda ^{(4)})}\cosh {(2\beta \lambda ^{(4)})}},\nonumber \\ \rho _{23}= & {} \rho _{25}=\frac{2-3\mathrm {e}^{6\beta \lambda ^{(4)}}}{6(1+\mathrm {e}^{2\beta \lambda ^{(4)}})^2(1+\mathrm {e}^{4\beta \lambda ^{(4)}})},\nonumber \\ \rho _{35}= & {} \frac{1}{3(1+\mathrm {e}^{2\beta \lambda ^{(4)}})^2(1+\mathrm {e}^{4\beta \lambda ^{(4)}})},\nonumber \\ \rho _{46}= & {} \rho _{47}=-\frac{\big (\cosh {(3\beta \lambda ^{(4)})}-5\sinh {(3\beta \lambda ^{(4)})}\big )\big (1+\tanh {(\beta \lambda ^{(4)})}\big )}{48\cosh {(\beta \lambda ^{(4)})}\cosh {(2\beta \lambda ^{(4)})}},\nonumber \\ \rho _{67}= & {} \frac{\mathrm {e}^{4\beta \lambda ^{(4)}}}{24\cosh ^2{(\beta \lambda ^{(4)})}\cosh {(2\beta \lambda ^{(4)})}}. \end{aligned}$$
(14)

In the regime of interest, when \(\beta |\lambda ^{(4)}|\gg 1\), depending on the sign of \(\lambda ^{(4)}\), there are two possible results. If \(\lambda ^{(4)}>0\), dominant nonzero matrix elements of \(\rho \) tend to 1/3

$$\begin{aligned} \rho _{44}=\rho _{66}=\rho _{77}=\rho _{46}=\rho _{64}=\rho _{47}=\rho _{74}=\rho _{67}=\rho _{76}=\frac{1}{3}, \end{aligned}$$
(15)

meaning that the resulting state is

$$\begin{aligned} | {W} \rangle _{\lambda ^{(4)}>0}=\frac{1}{\sqrt{3}}(| {--+} \rangle +| {-+-} \rangle +| {+--} \rangle ). \end{aligned}$$
(16)

In the opposite case, when \(\lambda ^{(4)}<0\), dominant nonzero \(\rho \) matrix elements approach the value 1/3

$$\begin{aligned} \rho _{22}=\rho _{33}=\rho _{55}=\rho _{23}=\rho _{32}=\rho _{25}=\rho _{52}=\rho _{35}=\rho _{53}=\frac{1}{3}, \end{aligned}$$
(17)

describing the state

$$\begin{aligned} | {W} \rangle _{\lambda ^{(4)}<0}=\frac{1}{\sqrt{3}}(| {++-} \rangle +| {+-+} \rangle +| {-++} \rangle ). \end{aligned}$$
(18)
Fig. 2
figure 2

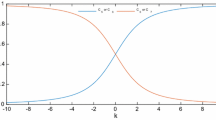
Creation of the W state using the XZX + YZY interaction. Dependence of \(F_W(\rho )\) and fidelity on the value \(\beta \lambda ^{(4)}\in (0,10)\) is plotted, where the values 1 of fidelity and 0 of \(F_W(\rho )\) indicate the presence of W type of entanglement. Both fidelity and \(F_{W}(\rho )\) are even to the sign change of \(\lambda ^{(4)}\)

Full size image

When the target state is identified, we can easily compare the results predicted from the \(F_{W}(\rho )\) and fidelity. In Fig. 2, we plot the dependence of \(F_{W}(\rho )\) and fidelity on \(\beta \lambda ^{(4)}\in (0,10)\). Plots clearly show that fidelity approaches the desired value faster than \(F_W(\rho )\), indicating that combination of tripartite negativity and concurrence in \(F_{W}(\rho )\) gives an upper bound on the presence of the W state.

We now turn to the another type of three-spin interaction present in optical lattice systems, the ZZZ term, which can be used to create both types of entanglement. To obtain the GHZ state, besides ZZZ term, magnetic field in the xy plane should be present. Resulting states are dependent on the sign of the \(\lambda ^{(3)}\) term, as well as of the magnetic field’s direction. If the resulting magnetic field \({\mathbf {b}}\) builds an angle \(\varphi \) with the x direction, thermal state \(\rho \) approaches the state

$$\begin{aligned} | {GHZ} \rangle _{\lambda ^{(3)}>0}= & {} \frac{1}{2}(| {++-} \rangle +| {+-+} \rangle +| {-++} \rangle +\mathrm {e}^{2\mathrm {i}\varphi }| {---} \rangle ),\nonumber \\ | {GHZ} \rangle _{\lambda ^{(3)}<0}= & {} \frac{1}{2}(\mathrm {e}^{-2\mathrm {i}\varphi }| {+++} \rangle +| {+--} \rangle +| {-+-} \rangle +| {--+} \rangle ). \end{aligned}$$
(19)

We also provide parameter regime needed to obtain the GHZ state. Since the only effect of the magnetic field is to induce a relative phase in the final state, see (19); for simplicity, we will discuss magnetic field in the x direction. In Fig. 3, we plot the dependence of \(F_{\mathrm{GHZ}}(\rho )\) and fidelity with respect to the ratio \(\lambda ^{(3)}/b_x\) for four different values of \(\beta b_x\): \(10^1\), \(10^{2}\), \(10^{3}\) and \(10^{4}\). The basic requirement to minimize \(F_{\mathrm{GHZ}}(\rho )\) and maximize fidelity is that ZZZ interaction needs to be the dominant source of interaction. However, depending on the value \(\beta b_x\), it is not always possible to precisely generate the GHZ state. For \(\beta b_x=10^1\), we do not reach the values below \(10^{-1}\) for \(F_{\mathrm{GHZ}}(\rho )\) and above 0.95 for fidelity. If we have \(\beta b_x=10^{2}\) minimal value of \(F_{\mathrm{GHZ}}(\rho )\) is around \(2.7\times 10^{-3}\) for \(\lambda ^{(3)}/b_x\approx 45\), while the maximal value of fidelity is close to 0.9985 for \(\lambda ^{(3)}/b_x\approx 43\). To conclude, \(\beta b_x\) governs the precision search of the GHZ state, automatically increasing the ratio \(\lambda ^{(3)}/b_x\) that minimizes \(F_{\mathrm{GHZ}}(\rho )\) and maximizes fidelity. Keeping the ZZZ term at fixed strength means that \(b_x\) should be correspondingly lowered to decrease \(F_{\mathrm{GHZ}}(\rho )\) and increase fidelity. However, this further lowers the optimal temperature. For \(T=10^{-1}\mathrm{nK}\) and \(\lambda ^{(3)}=1\mathrm{kHz}\), we were able to find \(F_W(\rho )\) only slightly below \(2\times 10^{-2}\). Further reduction requires stronger ZZZ term strength or lower temperatures.

Fig. 3
figure 3

Creation of the GHZ state using the ZZZ interaction. In the regime in which only magnetic field in x direction and \(\lambda ^{(3)}\) term are present, we plot the dependence of \(F_{\mathrm{GHZ}}(\rho )\) and fidelity on the ratio \(\lambda ^{(3)}/b_x\) in four cases: \(\beta b_x =10^1\), \(\beta b_x =10^{2}\), \(\beta b_x =10^{3}\) and \(\beta b_x =10^{4}\). Since \(F_{\mathrm{GHZ}}(\rho )\) and fidelity are even to the sign change of \(\lambda ^{(3)}\), we have presented the results only for positive \(\lambda ^{(3)}\)

Full size image
Fig. 4
figure 4

Creation of the W state using the ZZZ interaction. We analyze the regime in which beside ZZZ term, ferromagnetic XX interaction (\(\lambda ^{(2)}\) term) is present. Dependence of \(F_{W}(\rho )\) and fidelity on the ratio \(\lambda ^{(3)}/|\lambda ^{(2)}|\in (0,2)\) is given for three \(\beta |\lambda ^{(2)}|\) values: \(10^0\), \(10^1\) and \(10^2\). \(F_{W}(\rho )\) and fidelity are even to the sign change of \(\lambda ^{(3)}\)

Full size image

Finally, to obtain the W state, in addition to the ZZZ term, ferromagnetic XX coupling (\(\lambda ^{(2)}<0\) term) needs to be present. In Fig. 4, dependence of \(F_{W}(\rho )\) and fidelity on the ratio \(\lambda ^{(3)}/|\lambda ^{(2)}|\in (0,2)\) is presented for \(\beta |\lambda ^{(2)}|\) equal to \(10^0\), \(10^1\) and \(10^2\). In order to create the W state very precise, \(\beta |\lambda ^{(2)}|\ge 10^1\) limit should be used. For example, \(\beta |\lambda ^{(2)}|=10^1\) gives \(F_{W}(\rho )\approx 1.2\times 10^{-4}\) and excellent fidelity \(1-2\times 10^{-9}\). Again, there is a trade-off between precision, coupling strengths and the optimal temperature regime. Assuming that ZZZ and XX terms are of comparable strengths, \(\approx 1\mathrm{KHz}\), \(\beta |\lambda ^{(2)}|=10^1\) produces W state with \(10^{-8}\) precision, according to \(F_W(\rho )\), at temperature slightly above the \(\mathrm{nK}\) scale. Resulting state is equal to (18) if \(\lambda ^{(3)}>0\) and (16) if \(\lambda ^{(3)}<0\).

The benefits of potential realization of XXX and YYY terms are worth mentioning. Hamiltonian containing XXX and/or YYY term and magnetic field in z direction can be used to implement the GHZ state. In this case, the state

$$\begin{aligned} | {\mathrm{GHZ}} \rangle = \frac{1}{\sqrt{2}}(| {+++} \rangle +\mathrm {e}^{\mathrm {i}(\pi -\theta )}| {---} \rangle ) \end{aligned}$$
(20)

can be obtained, where \(\tan {\theta }\) describes the ratio of intensities of YYY and XXX terms.

5 Detection of the W state by measuring magnetization

In this section, we will discuss the possibility to indirectly detect [41, 42] W type of entanglement by measuring magnetization in z direction. Magnetization in z direction is defined as

$$\begin{aligned} M_z=\frac{1}{\beta Z}\frac{\partial Z}{\partial b_z}, \end{aligned}$$
(21)

where Z is the partition function, \(\beta =1/k_B T\) and \(b_z\) magnetic field in z direction.

In the previous section, we have shown that by using only XZX + YZY term of the Hamiltonian (13), W state can be realized. Using the different approach, we are able to achieve the same result if, additionally, magnetic field in z direction is present. In this case, partition function Z is equal to

$$\begin{aligned} Z=8\cosh ^2{\big (\beta (b_z+\lambda ^{(4)})\big )}\cosh {\big (\beta (2\lambda ^{(4)}-b_z)\big )} \end{aligned}$$
(22)

leading us to the magnetization

$$\begin{aligned} M_z=\frac{\sinh {\big (3\beta \lambda ^{(4)}\big )}-3\sinh {\big (\beta (\lambda ^{(4)}-2b_z)\big )}}{{\cosh {\big (3\beta \lambda ^{(4)}\big )}+\cosh {\big (\beta (\lambda ^{(4)}-2b_z)\big )}}}. \end{aligned}$$
(23)

On the other hand, nonzero matrix elements of \(\rho \) are

$$\begin{aligned} \rho _{11}= & {} \mathrm{e}^{-6\beta b_z} \rho _{88}=\frac{\mathrm {e}^{4\beta \lambda ^{(4)}}}{(\mathrm {e}^{2\beta b_{z}}+\mathrm {e}^{4\beta \lambda ^{(4)}})(1+\mathrm {e}^{2\beta (b_z+\lambda ^{(4)})})^2}, \nonumber \\ \rho _{22}= & {} -\frac{(2\cosh {(3\beta \lambda ^{(4)})}+\sinh {(3\beta \lambda ^{(4)})})(-1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{12\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{33}= & {} \rho _{55}=-\frac{(5\cosh {(3\beta \lambda ^{(4)})}+\sinh {(3\beta \lambda ^{(4)})} )(-1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{48\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{44}= & {} \frac{(2\cosh {(3\beta \lambda ^{(4)})}-\sinh {(3\beta \lambda ^{(4)})})(1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{12\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{66}= & {} \rho _{77}=\frac{(5\cosh {(3\beta \lambda ^{(4)})}-\sinh {(3\beta \lambda ^{(4)})})(1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{48\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{23}= & {} \rho _{25}=\frac{(\cosh {(3\beta \lambda ^{(4)})}+5\sinh {(3\beta \lambda ^{(4)})})(-1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{48\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{35}= & {} \frac{\mathrm {e}^{2\beta b_z}}{3(1+\mathrm {e}^{2\beta (b_z+\lambda ^{(4)})})^2(\mathrm {e}^{2\beta b_z}+\mathrm {e}^{4\beta \lambda ^{(4)}})},\nonumber \\ \rho _{46}= & {} \rho _{47}=-\frac{(\cosh {(3\beta \lambda ^{(4)})}-5\sinh {(3\beta \lambda ^{(4)})})(1+\tanh {(\beta (b_z+\lambda ^{(4)}))})}{48\cosh {(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}, \nonumber \\ \rho _{67}= & {} \frac{\mathrm {e}^{\beta (b_z+4\lambda ^{(4)})}}{24\cosh ^2{(\beta (b_z+\lambda ^{(4)}))}\cosh {(\beta (2\lambda ^{(4)}-b_z))}}. \end{aligned}$$
(24)

In Fig. 5, we plot the dependencies of \(F_{W}(\rho )\) and \(|M_z|\) on \(b_z/\lambda ^{(4)}\) for different \(\beta b_z\) values. By comparing these two functions, we see that appearance of magnetization plateaus is clearly a sign of creation of the W state, while the parameter regime of interest is placed on the \(|M_z|=1\) plateau. Ratio \(\beta b_z\) plays a deterministic role in the creation of maximal entanglement and appearance of magnetization plateaus. Roughly, values \(\beta b_z\ge 10^2\) provide the existence of W type of entanglement, while \(b_z/\lambda ^{(4)}\) is limited by the values − 1 and 2. Optimal temperature regime in this situation is on the same scale as in the case of XZX + YZY term only, providing that magnetic field and three-spin interaction are of comparable strengths.

Fig. 5
figure 5

Creation of the W state using the XZX + YZY interaction. We plot the dependencies of \(F_{W}(\rho )\) and absolute magnetization \(|M_z|\) on the ratio of magnetic field in z direction and XZX+YZY three-spin interaction, \(b_z/\lambda ^{(4)}\), in three different situations: \(\beta b_z =10^0\), \(\beta b_z =10^1\), \(\beta b_z =10^{2}\). Dip in absolute magnetization at \(b_z/\lambda ^{(4)}\approx -1\) represents a sign change of magnetic polarization

Full size image

Magnetization in systems described by the Hamiltonian (7), assuming that J and \(\alpha \) are independent on the strength of magnetic field, follows the same correlation behavior with \(F_{W}(\rho )\). Thus, magnetization can serve as an indicator of the presence of the W state, opening a way toward trustworthy entanglement detection. However, in the case of semiconductor quantum dots, exchange interaction J and three-spin term \(\alpha \) strongly depend on the magnetic field, indicating that a more elaborate analysis should be performed, including the details of the materials in which quantum dots are embedded. This is beyond the scope of the presented work.

6 Conclusions

We have investigated thermal entanglement in tripartite systems with different types of three-spin interactions present. Chiral and XZX+YZY terms are suitable for creation of the W state, while ZZZ term can be used to construct both types of maximally entangled states. Moreover, magnetization in z direction can be used to detect W type of entanglement. Potential experimental platforms for realization of maximally entangled states include triple quantum dot and triangular optical lattice.