Abstract
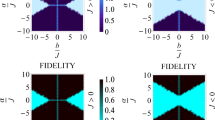
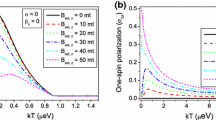
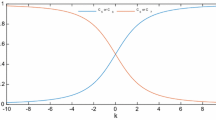
In this paper, thermal entanglement in three-qubit spin system has been addressed. The results show that spin-spin exchange interaction, the effective external magnetic field, next-nearest-neighbouring interaction have notable effects on the time evolution of the state and thermal entanglement So we can control thermal entanglement by changing the above parameters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum entangled plays a fundamental role in various fields of quantum computation and quantum information such as quantum cryptography and quantum teleportation [1–4]. Since the entanglement is very fragile, the question of how to create stable entanglement remains a main focus of recent studies in the field of quantum information processing. The quantum entanglement in solid state systems s is an important emerging field, spin chains are natural candidates for the realization of entanglement and has been researched [5–10].
In this paper, the eigenvalues, eigenstates of the Hamiltonian, thermal distribution function of the state and the density matrix and reduced density matrix in spin chain systems are addressed. The results show that spin-spin exchange interaction, the effective external magnetic field, next-nearest-neighbouring interaction have notable effects on the time evolution of the state, the density matrix, and thermal entanglement So we can control thermal entanglement by changing the above parameters.
2 Controlling Thermal Entanglement in Three-qubit Spin Systems
The Hamiltonian for a three-qubit anisotropic Heisenberg spin chain is
where
\({\sigma _{i}^{x}} ,{\sigma _{i}^{y}} ,{\sigma _{i}^{z}}\) are the Pauli operators. In the space of states
The Hamilton has the following form
According to \(H=\sum \nolimits E_{i} \left |\varphi _{i}\right \rangle \left \langle \varphi _{i}\right |\), the eigenvalue E i of Hamilton are:
The corresponding eigenstate \(\left |\varphi _{i}\right \rangle \) is:
Normalized \(\left |\varphi _{i} \right \rangle \) has the following form
Where \(\eta _{1} =\sqrt {4+\gamma \zeta _{2}}, \eta _{2} =\sqrt {4+\gamma \zeta _{1}}\)
For a system in equilibrium at temperature T, the density operator is
Entanglement of two qubits can be measured by the concurrence [11]
References
Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information. Cambridge University Press, Cambridge (2000)
Shan, C.-J., Liu, J.-B., Liu, T.-K., Huang, Y.-X., Li, H.: Int. J. Theor. Phys. 48, 1516 (2009)
Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Phys. Rev. Lett. 70, 1895 (1993)
Zheng, S.B.: Phys. Rev. A 69, 064302 (2004)
Wang, X.G.: Phys. Rev. A 64, 012313 (2001)
Zhou, L., Song, H.S., Guo, Y.Q., Li, C.: Phys. Rev. A 68, 024301 (2003)
Zhang, G.F.: Phys. Rev. A 72, 034302 (2005)
Shan, C.J., Chen, T., Liu, J.B., Cheng, W.W., Liu, T.K., Huang, Y.X., Li, H.: Int. J. Theor. Phys. 49, 717 (2010)
Zeng, H.F., Shao, B., Yang, L.G., Li, J., Zou, J.: Chin. Phys. B 18, 3265 (2009)
Shan, C.J., Cheng, W.W., Liu, T.K., Liu, J.B., Wei, H.: Chin. Phys. Lett. 25, 3115 (2008)
Wootters, W.K.: Phys. Rev. Lett. 80, 2245 (1998)
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No.61402099)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, J. Controlling Thermal Entanglement in a Three-qubit Spin System. Int J Theor Phys 55, 5344–5347 (2016). https://doi.org/10.1007/s10773-016-3154-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-016-3154-0