1 Introduction

Quantum entanglement is not only one of the most important features in quantum mechanics [1, 2], but also a key resource for testing quantum mechanics against local hidden theory [3]. Recently, the entangled states have attracted considerable attention because of their fundamental scientific significance [4] and have been applied in many fields in quantum information processing (QIP), such as quantum computing [5], quantum cryptography [6], quantum teleportation [7, 8] and quantum secret sharing [9]. These promising applications have greatly motivated the researches in the generation of entangled states.

It is worth noting that a typical entangled state so-called Greenberger–Horne–Zeilinger (GHZ) state \(|\hbox {GHZ}\rangle =\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )\), first proposed and named by Greenberger et al. [10], has raised much interest. Contrary to other entangled states, the GHZ state exhibits some special features, such as it is the maximally entangled state and can maximally violate the Bell inequalities [12]. In 2001, Zheng has proposed a scheme to test quantum mechanics against local hidden theory without the Bell’s inequalities by use of multiatom GHZ state [13]. Therefore, great interest has arisen regarding the significant role of GHZ state in the foundations of quantum mechanics measurement theory and quantum communication. At present, the first and main problem we face is how to fast and efficiently generate GHZ state by using current technologies. To our knowledge, in some experimental systems, such as trapped ions systems [14], photons systems [15, 16], and atoms systems [17], scientists have realized the generation of such GHZ state. Recently, a promising experimental instrument named cavity quantum electrodynamics (C-QED), which concerns the interaction between the atom and the quantized field within cavity [18], has aroused much attention. Based on C-QED, many theoretical schemes for generating GHZ state have been proposed. For example, Li et al. [19] have proposed a scheme to generate multiatom GHZ state under the resonant condition by Zeno dynamics, but the scheme is sensitive to the atomic spontaneous emission and fiber photonic leakage. Hao et al. [20] have proposed an efficient scheme to generate multiatom GHZ state under the resonant condition via adiabatic passage, but it takes too long time. Chen et al. have proposed a smart scheme to overcome the above drawbacks, but the scheme needs to trap three atoms in one cavity [21], such design is difficult to manipulate each atom in experiment and to construct a large-scale quantum network.

On the other hand, in modern quantum application field, an important method to manipulate the states of a quantum system, is adiabatic passage, included “rapid” adiabatic passage (RAP), stimulated Raman adiabatic passage (STIRAP), and their variants [22]. The adiabatic passage covers the shortage with respect to errors or fluctuations of the parameters compared with the resonant pulses, but its evolution speed is very slow, so it may be useless in some cases. In recent years, shortcuts to adiabatic passage (STAP), which accelerates a slow adiabatic quantum process via a non-adiabatic route, has aroused a great deal of attention. Many theoretical proposals have been presented to realize QIP, such as fast population transfer [23–26], fast entanglement generation [25, 27], and fast implementation of quantum phase gates [28, 29]. To our knowledge, the main methods to construct effective shortcuts have two forms: one is invariant-based inverse engineering-based Lewis–Riesenfeld invariant (IBLR) [30] and the other is transitionless quantum driving (TQD) [31], which is pointed out by Berry. The two methods are strongly related [32], but also have their own characteristics. For example, the former does not need to modify the original Hamiltonian \(H_0(t)\), but the algorithm is suitable for some special physical models. The latter needs to modify the original Hamiltonian \(H_0(t)\) to the “counter-diabatic driving” (CDD) Hamiltonian H(t) to speed up the quantum process. The fixed Hamiltonian H(t) can be obtained in theory, but it does not usually exist in real experiment.

In addition, the quantum Zeno effect (QZE), first understood by Neumann [33] and named by Misra and Sudarshan [34], exhibits a especially experimental phenomenon that transitions between quantum states can be hindered by frequent measurement. The system will evolve away from its initial state and remain in the so-called Zeno subspace defined by the measure due to frequently projecting onto a multidimensional subspace [35, 36]. This is so-called quantum Zeno dynamics (QZD). Without making using of projection operators and non-unitary, “a continuous coupling” can obtain the same quantum Zeno effect instead of discontinuous measurements [37, 38]. Now, we give a brief introduction of the quantum Zeno dynamics in the form of continuous coupling [38]. Suppose that the system and its continuously coupling external system are governed by the total Hamiltonian \(H_\mathrm{tot}=H_s+KH_e\), where \(H_s\) is the Hamiltonian of the quantum system to be investigated, \(H_e\) is an additional Hamiltonian caused by the interaction with the external system, K is the coupling constant. In the limit \(K\rightarrow \infty \), the evolution operator of system can be expressed as \(U(t)=\exp {[-it\sum _n(K\eta _nP_n+P_nH_sP_n)]}\), where \(P_n\) is the eigenprojection of \(H_e\) corresponding to the eigenvalue \(\eta _n\), i.e., \(H_eP_n=\eta _nP_n\) [39].

Inspired by the above useful works, we make use of Zeno dynamics and TQD to construct STAP to generate N-atom GHZ state in C-QED. Our scheme has the following advantages: (1) The atoms are trapped in different cavities so that the single-qubit manipulation is more available in experiment. (2) The fast quantum entangled state generation for multiparticle in spatially separated atoms can be achieved in one step. (3) Numerical results show that our scheme is not only fast, but also robust against variations in the experimental parameters and decoherence caused by atomic spontaneous emission and fiber photon leakage. In fact, further research shows that the total operation time for the scheme is irrelevant to the number N of qubits.

The paper is organized as follows. In Sect. 2, we give a brief introduction to the approach of TQD proposed by Berry. In Sect. 3, we introduce the physical modal and the systematic approximation by QZD. In Sect. 4, we propose the scheme to generate the three-atom GHZ state via TQD and adiabatic passage, respectively. The decoherence caused by various factors is discussed by the numerical simulation. In Sect. 5, we directly generalize the scheme in Sect. 4 to generate N-atom GHZ state in one step. At last, we discuss the experimental feasibility and make a conclusion about the scheme in Sect. 6.

2 Transitionless quantum driving

Suppose a system is dominated by a time-dependent Hamiltonian \(H_o(t)\) with instantaneous eigenvectors \(|\phi _n(t)\rangle \) and eigenvalues \(E_n(t)\),

$$\begin{aligned} H_o(t)|\phi _n(t)\rangle =E_n(t)|\phi _n(t)\rangle . \end{aligned}$$
(1)

When a slow change satisfying the adiabatic condition happens, the system governed by \(H_o(t)\) can be expressed at time t

$$\begin{aligned} |\psi (t)\rangle= & {} e^{i\xi _n(t)}|\phi _n(t)\rangle , \nonumber \\ \xi _n(t)= & {} -\frac{1}{h}\int _0^t\hbox {d}t^\prime E_n(t^\prime )+i\int _0^t\hbox {d}t^\prime \langle \phi _n(t^\prime )|\partial _{t^\prime }\phi _n(t^\prime )\rangle , \end{aligned}$$
(2)

where \(\partial _{t^\prime }=\frac{\partial }{\partial _{t^\prime }}\). Because the instantaneous eigenstates \(|\phi _n(t)\rangle \) do not meet the Schrödinger equation, i.e., \(i\hbar \partial _t|\phi _n(t)\rangle \ne H_0|\phi _n(t)\rangle \), a finite probability that the system is in the state \(|\phi _{m\ne n}(t)\rangle \) will occur during the whole evolution process even under the adiabatic condition.

To construct the Hamiltonian H(t) that drives the instantaneous eigenvector \(|\phi _n(t)\rangle \) exactly, i.e., there are no transitions between different eigenvectors during the whole evolution process, we define the unitary operator

$$\begin{aligned} U=\sum _n{e^{i\xi _n(t)}|\phi _n(t)\rangle \langle \phi _n(0)|}, \end{aligned}$$
(3)

we can formally solve the Schrödinger equation

$$\begin{aligned} H(t)=i\hbar (\partial _tU)U^\dag . \end{aligned}$$
(4)

Substituting Eq. (3) into Eq. (4), the Hamiltonian H(t) can be expressed

$$\begin{aligned} H(t)=i\hbar \sum _n{\Big (|\partial _t\phi _n\rangle \langle \phi _n|}-\hbar \sum _n{|\phi _n\rangle \dot{\xi _n}\langle \phi _n|\Big )}, \end{aligned}$$
(5)

the simplest choice is \(E_n=0\), for which the bare states \(|\phi _n(t)\rangle \), with no phase factors, are driven by

$$\begin{aligned} H(t)=i\hbar \sum _n{|\partial _t\phi _n\rangle \langle \phi _n|}. \end{aligned}$$
(6)

3 Physical modal and systematic approximation by QZD

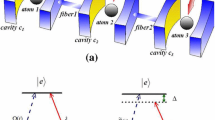
For the sake of the clearness, let us first consider the physical modal that three identical atoms \(a_1\), \(a_2\) and \(a_3\) are trapped in three linearly arranged optical cavities \(C_1\), \(C_2\) and \(C_3\), respectively. As shown in Fig. 1, each atom possesses one excited state \(|e\rangle \) and three ground states \(|g_l\rangle \), \(|g_o\rangle \) and \(|g_r\rangle \). The cavities \(C_1\) and \(C_3\) are single mode, and the cavity \(C_2\) is bi-mode. \(C_1\), \(C_2\) and \(C_3\) are connected by the optical fibers \(f_1\), \(f_2\), respectively. Assuming that the transition \(|e\rangle _{a_{1(3)}}\leftrightarrow |g_o\rangle _{a_{1(3)}}\) is resonantly driven by a external classical field with the time-dependent Rabi frequency \(\Omega _{1(3)}(t)\), while the transition \(|e\rangle _{1(2)}\leftrightarrow |g_l\rangle _{1(2)}(|e\rangle _{2(3)}\leftrightarrow |g_r\rangle _{2(3)})\) is resonantly coupled to the left-circularly (right-circularly) polarized cavity mode with the coupling constant \(g_{l(r)}\), respectively.

Fig. 1
figure 1

The structure of the experimental setup and atoms. Three identical atoms \(a_1\), \(a_2\) and \(a_3\) are trapped in three separated cavities \(C_1\), \(C_2\) and \(C_3\), which are linked by two fibers \(f_1\), \(f_2\)

Full size image

In the short-fiber limit, i.e., \((2L\bar{\nu })/(2\pi c)\ll 1\) (L is the length of the fibers, \(\bar{\nu }\) is the decay rate of the cavity fields into a continuum of fiber modes and c is the speed of light), only one resonant mode of the fiber interacts with the cavity mode [40]. In the rotating frame, the Hamiltonian of the whole system can be written as \((\hbar =1)\)

$$\begin{aligned} H_\mathrm{tot}= & {} H_l+H_c, \nonumber \\ H_l= & {} \sum _{o=1,3}\Omega _o(t)|e\rangle _{a_o}\langle g_0|+H.c., \nonumber \\ H_c= & {} g_{1l}a_{1l}|e\rangle _{a_1}\langle g_l|+g_{2l}a_{2l}|e\rangle _{a_2}\langle g_l|+g_{2r}a_{2r}|e\rangle _{a_2}\langle g_{r}|+g_{3r}a_{3r}|e\rangle _{a_3}\langle g_r|\nonumber \\&+\,v_1b_1^{\dag }(a_{1l}+a_{2l})+v_2b_2^{\dag }(a_{2r}+a_{3r})+H.c., \end{aligned}$$
(7)

where \(a_{kl}^{\dag }\ (a_{kr}^{\dag })\) and \(a_{kl}\ (a_{kr})\) denote the creation and annihilation operators for the left-circularly (right-circularly) polarized mode of cavities \(C_k\ (k=1,\ 2,\ 3)\), respectively; \(b_j^{\dag }\) and \(b_j\) denote the creation and annihilation operators associated with the resonant mode of fiber \(f_j\ (j=1,\ 2)\), respectively. For the sake of simplicity, we assume \(g_{1l}=g_{2l}=g_{2r}=g_{3r}=g\) and \(v_1=v_2=v\). If the initial state of the whole system is \(|g_og_lg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}\) (here \(|g_og_lg_r\rangle = |g_og_lg_r\rangle _{a_1 a_2 a_3}\)), the whole system evolves in the following subspaces

$$\begin{aligned} |\phi _1\rangle= & {} |g_og_lg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2},\quad ~|\phi _2\rangle =|eg_lg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}, \nonumber \\ |\phi _3\rangle= & {} |g_lg_lg_r\rangle |1\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2},\quad ~|\phi _4\rangle =|g_lg_lg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|1\rangle _{f_1}|0\rangle _{f_2}, \nonumber \\ |\phi _5\rangle= & {} |g_lg_lg_r\rangle |0\rangle _{C_1}|10\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2},\quad ~|\phi _6\rangle =|g_leg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}, \nonumber \\ |\phi _7\rangle= & {} |g_lg_rg_r\rangle |0\rangle _{C_1}|01\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2},\quad ~|\phi _8\rangle =|g_lg_rg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|1\rangle _{f_2}, \nonumber \\ |\phi _9\rangle= & {} |g_lg_rg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|1\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2},\quad ~|\phi _{10}\rangle =|g_lg_re\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}, \nonumber \\ |\phi _{11}\rangle= & {} |g_lg_rg_o\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}, \end{aligned}$$
(8)

where \(|ijk\rangle \ (i,\ j,\ k\in [e,\ g_l,\ g_o,\ g_r])\) denotes the state of the atoms in every cavity, \(|n\rangle _s\ (s=C_1,\ C_3,\ f_1,\ f_2)\) means that the quantum field state of system contains n photons. \(|n_1n_2\rangle _{C_2}\) means that the number of left-circularly photon is \(n_1\) and the number of right-circularly photon is \(n_2\) in the cavity \(C_2\).

Under the Zeno condition \(g,v\gg \Omega _1,\Omega _3\), the Hilbert subspace is split into nine invariant Zeno subspace

$$\begin{aligned} Z_1= & {} \{|\phi _1\rangle , |\psi _1\rangle , |\phi _{11}\rangle \},\quad Z_2=\{|\psi _2\rangle \}, \quad Z_3=\{|\psi _3\rangle \}\nonumber \\ Z_4= & {} \{|\psi _4\rangle \},\quad Z_5=\{|\psi _5\rangle \},\quad Z_6=\{|\psi _6\rangle \}, \nonumber \\ Z_7= & {} \{|\psi _7\rangle \},\quad Z_8=\{|\psi _8\rangle \},\quad Z_9=\{|\psi _9\rangle \}, \end{aligned}$$
(9)

where the eigenstates of \(H_c\) are

$$\begin{aligned} |\psi _1\rangle= & {} N_1(|\phi _2\rangle -\frac{g}{v}|\phi _4\rangle +|\phi _6\rangle -\frac{g}{v}|\phi _8\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _2\rangle= & {} N_2(-|\phi _2\rangle +\varepsilon _1|\phi _3\rangle -\eta _1|\phi _4\rangle -\chi _1|\phi _5\rangle + \chi _1|\phi _7\rangle +\eta _1|\phi _8\rangle -\epsilon _1|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _3\rangle= & {} N_3(-|\phi _2\rangle -\varepsilon _1|\phi _3\rangle -\eta _1|\phi _4\rangle +\chi _1|\phi _5\rangle - \chi _1|\phi _7\rangle +\eta _1|\phi _8\rangle +\epsilon _1|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _4\rangle= & {} N_4(|\phi _2\rangle -\mu _1|\phi _3\rangle -\zeta _1|\phi _4\rangle +\delta _1|\phi _5\rangle -\theta _1|\phi _6\rangle + \delta _1|\phi _7\rangle -\zeta _1|\phi _8\rangle -\mu _1|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _5\rangle= & {} N_5(|\phi _2\rangle +\mu _1|\phi _3\rangle -\zeta _1|\phi _4\rangle -\delta _1|\phi _5\rangle -\theta _1|\phi _6\rangle - \delta _1|\phi _7\rangle -\zeta _1|\phi _8\rangle +\mu _1|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _6\rangle= & {} N_6(-|\phi _2\rangle +\varepsilon _2|\phi _3\rangle -\eta _2|\psi _4\rangle +\chi _2|\phi _5\rangle -\chi _2|\phi _7\rangle + \eta _2|\phi _8\rangle -\epsilon _2|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _7\rangle= & {} N_7(-|\phi _2\rangle -\varepsilon _2|\phi _3\rangle -\eta _2|\psi _4\rangle -\chi _2|\phi _5\rangle +\chi _2|\phi _7\rangle + \eta _2|\phi _8\rangle +\epsilon _2|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _8\rangle= & {} N_8(|\phi _2\rangle -\mu _2|\phi _3\rangle +\zeta _2|\phi _4\rangle -\delta _2|\phi _5\rangle +\theta _2|\phi _6\rangle - \delta _2|\phi _7\rangle +\zeta _2|\phi _8\rangle -\mu _2|\phi _9\rangle +|\phi _{10}\rangle ), \nonumber \\ |\psi _9\rangle= & {} N_9(|\phi _2\rangle +\mu _2|\phi _3\rangle +\zeta _2|\phi _4\rangle +\delta _2|\phi _5\rangle +\theta _2|\phi _6\rangle + \delta _2|\phi _7\rangle +\zeta _2|\phi _8\rangle +\mu _2|\phi _9\rangle +|\phi _{10}\rangle ), \end{aligned}$$
(10)

with the corresponding eigenvalues

$$\begin{aligned} \lambda _1= & {} 0, \quad \lambda _2=-\sqrt{(g^2+2v^2-A)/2}, \quad \lambda _3=\sqrt{(g^2+2v^2-A)/2}, \nonumber \\ \lambda _4= & {} -\sqrt{(3g^2+2v^2-A)/2}, \quad \lambda _5=\sqrt{(3g^2+2v^2-A)/2}, \quad \lambda _6=-\sqrt{(g^2+2v^2+A)/2}, \nonumber \\ \lambda _7= & {} \sqrt{(g^2+2v^2+A)/2}, \quad \lambda _8=-\sqrt{(3g^2+2v^2+A)/2}, \quad \lambda _9=\sqrt{(3g^2+2v^2+A)/2}, \end{aligned}$$
(11)

where the parameters are

$$\begin{aligned} \epsilon _1= & {} \frac{\sqrt{g^2+2v^2-A}}{\sqrt{2}g},\quad \eta _1=\frac{-g^2+2v^2-A}{2gv},\quad \chi _1=\frac{\sqrt{g^2+2v^2-A}(g^2+A)}{2\sqrt{2}gv^2},\nonumber \\ \mu _1= & {} \frac{\sqrt{3g^2+2v^2-A}}{\sqrt{2}g},\quad \zeta _1=\frac{-g^2-2v^2+A}{2gv},\quad \delta _1=\frac{\sqrt{3g^2+2v^2-A}(-g^2+A)}{2\sqrt{2}gv^2},\nonumber \\ \theta _1= & {} \frac{-g^2+A}{v^2},\quad \epsilon _2=\frac{\sqrt{g^2+2v^2+A}}{\sqrt{2}g},\quad \eta _2=\frac{-g^2+2v^2+A}{2gv},\nonumber \\ \chi _2= & {} \frac{\sqrt{g^2+2v^2+A}(-g^2+A)}{2\sqrt{2}gv^2},\quad \mu _2=\frac{\sqrt{3g^2+2v^2+A}}{\sqrt{2}g},\quad \zeta _2=\frac{g^2+2v^2+A}{2gv},\nonumber \\ \delta _2= & {} \frac{\sqrt{3g^2+2v^2+A}(g^2+A)}{2\sqrt{2}gv^2},\quad \theta _2=\frac{g^2+A}{v^2}, \end{aligned}$$
(12)

in addition, \(A=\sqrt{g^4+4v^4}\) and \(N_w\) is the normalization factor of the eigenstate \(|\psi _w\rangle \ (w=1,2,\dots ,9)\).

The projector in the kth Zeno subspace \(Z_k\) is

$$\begin{aligned} P_k^\beta =|\beta \rangle \langle \beta |,\quad (|\beta \rangle \in Z_k). \end{aligned}$$
(13)

The Hamiltonian in Eq. (8) can be approximately given by

$$\begin{aligned} H_\mathrm{tot}\simeq & {} \sum _{k,\beta ,\gamma }{\lambda _kP_k^\beta +P_k^\beta H_lP_k^\gamma } \nonumber \\= & {} \sum _{k=2}^9{\lambda _k|\psi _k\rangle \langle \psi _k|+N_1(\Omega _1|\phi _1\rangle \langle \psi _1|+\Omega _3|\phi _{11}\rangle \langle \psi _1|+H.c.)}. \end{aligned}$$
(14)

If the initial state is \(|g_og_lg_r\rangle |0\rangle _{C_1}|00\rangle _{C_2}|0\rangle _{C_3}|0\rangle _{f_1}|0\rangle _{f_2}\), it reduces to

$$\begin{aligned} H_{eff}=N_1(\Omega _1|\phi _1\rangle \langle \psi _1|+\Omega _3|\phi _{11}\rangle \langle \psi _1|+H.c.), \end{aligned}$$
(15)

which can be treated as a simple three-level system with an excited state \(|\psi _1\rangle \) and two ground states \(|\phi _1\rangle \) and \(|\phi _{11}\rangle \). Then we obtain the eigenvectors and eigenvalues of the effective Hamiltonian \(H_\mathrm{eff}\) as

$$\begin{aligned} |\eta _o(t)\rangle =\left( \begin{array}{c} \cos \theta (t) \\ 0\\ -\sin \theta (t) \end{array} \right) , \quad |\eta _{\pm }(t)\rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} \sin \theta (t) \\ \pm 1\\ \cos \theta (t) \end{array} \right) , \end{aligned}$$
(16)

with the corresponding eigenvalues \(\eta _0=0\) and \(\eta _{\pm }=\pm N_1\Omega \), and \(\tan \theta =\frac{\Omega _1}{\Omega _3}\) and \(\Omega =\sqrt{\Omega _1^2+\Omega _3^2}\).

4 The generation of the three-atom GHZ state via transitionless quantum driving and adiabatic passage

4.1 Adiabatic passage method

For the sake of the clearness, we first briefly present how to generate the three-atom GHZ state via adiabatic passage. When the adiabatic condition \(|\langle n_0|\partial _tn_\pm \rangle |\ll |\lambda _{\pm }^\prime |\) is fulfilled well and the initial state is \(|\psi (0)\rangle =|\phi _1\rangle \), the state evolution will always follow \(|n_0(t)\rangle \) closely. To generate the three-atom GHZ state via the adiabatic passage and meet the boundary conditions of the fractional stimulated Raman adiabatic passage (STIRAP),

$$\begin{aligned} \lim _{t\rightarrow -\infty }{\frac{\Omega _1(t)}{\Omega _3(t)}}=0, \quad \lim _{t\rightarrow +\infty }{\frac{\Omega _3(t)}{\Omega _1(t)}}=\tan {\alpha }, \end{aligned}$$
(17)

we need properly to tailor the Rabi frequencies \(\Omega _1(t)\) and \(\Omega _3(t)\) in the original Hamiltonian \(H_\mathrm{tot}\)

$$\begin{aligned} \Omega _1(t)= & {} \sin {\alpha }\Omega _0\exp {\left[ \frac{-(t-t_0-t_f/2)^2}{t_c^2}\right] }, \nonumber \\ \Omega _3(t)= & {} \Omega _0\exp {\left[ \frac{-(t+t_0-t_f/2)^2}{t_c^2}\right] }+ \cos {\alpha }\Omega _0\exp {\left[ \frac{-(t-t_0-t_f/2)^2}{t_c^2}\right] }, \end{aligned}$$
(18)

where \(\Omega _0\) is the pulse amplitude and \(t_f\) is the operation time. \(t_c\) and \(t_0\) are some related parameters to be chosen for the best performance of the adiabatic passage process. In order to achieve better performance and meet the boundary conditions, we suitably chose the parameters that \(\tan {\alpha }=1\), \(t_0=0.14t_f\) and \(t_c=0.19t_f\). As shown in Fig. 2, the time-dependent \(\Omega _1(t)/\Omega _0\) and \(\Omega _3(t)/\Omega _0\) versus \(t/t_f\) are plotted with the fixed values \(t_0\) and \(t_c\). With the above parameters, we obtain our wanted three-atom GHZ state \(|\psi (t_f)\rangle =(|\phi _1\rangle -|\phi _{11}\rangle )/\sqrt{2}\) via the adiabatic passage. But this evolution process needs a relatively long time to satisfy the adiabatic condition. We will detail the reasons in the section of numerical simulations and analyses.

Fig. 2
figure 2

The laser pulses \(\Omega _1/\Omega _0\) and \(\Omega _3/\Omega _0\) versus \(t/t_f\)

Full size image

4.2 Transitionless quantum driving method

To reduce the evolution time and obtain the same state as the adiabatic passage, we use the approach of TQD to construct STAP. As introduced in the above, STAP speeds up a slow adiabatic passage via a non-adiabatic passage route to achieve a same outcome, and the TQD method is a important route to construct shortcuts. According to the ideas proposed by Berry [31], the instantaneous states in Eq. (16) do not meet the Schrödinger equation, i.e., \(i\partial _t|n_k\rangle \ne H_{eff}|n_k\rangle (k=0,\pm )\), so the situation that the system starts from the state \(|\psi _n(0)\rangle \) and ends up in the state \(|\psi _{m\ne n}(t)\rangle \) occurs in a finite probability even under the adiabatic condition. To drive the instantaneous states \(|n_k\rangle (k=0,\pm )\) exactly, we look for a Hamiltonian H(t) related to the original Hamiltonian \(H_{eff}\) according to Berry’s transitionless tracking algorithm [31]. From Sect. 2, we know the simplest Hamiltonian H(t) possessed the form,

$$\begin{aligned} H(t)=i\sum _{0,\pm }|\partial _tn_k(t)\rangle \langle n_k(t)|. \end{aligned}$$
(19)

Substituting Eq. (16) in Eq. (19), we obtain

$$\begin{aligned} H(t)=i\dot{\theta }|\phi _1\rangle \langle \phi _{11}|+H.c., \end{aligned}$$
(20)

where \(\dot{\theta }=[\dot{\Omega }_1(t)\Omega _3(t)-\Omega _1(t)\dot{\Omega }_3(t)]/\Omega ^2\). This is our wanted CCD Hamiltonian to construct STAP, and we will detail how to construct this Hamiltonian in experiment later.

Fig. 3
figure 3

The structure of the experimental setup and atoms for the APF Hamiltonian

Full size image

For the present system, the CDD Hamiltonian H(t) is given in Eq. (18), but it is irrealizable under current experimental condition. Inspired by Refs. [18, 20], we find an alternative physically feasible (APF) Hamiltonian whose effect is equivalent to H(t). The design is shown in Fig. 3; the atomic transitions are not resonantly coupled to the classical lasers and cavity modes with the detuning \(\Delta \). The Hamiltonian of the system reads \(H_\mathrm{tot}^\prime =H_c+H_l+H_d\), where \(H_d=\sum _{k=1}^3{\Delta |e\rangle _k\langle e|}\). Then, similar to the approximation by QZD in Sect. 3, we also obtain an effective Hamiltonian for the non-resonant system

$$\begin{aligned} H_\mathrm{eff}^\prime =N_1(\overline{\Omega }_1|\phi _1\rangle \langle \psi _1|+\overline{\Omega }_3|\phi _{11}\rangle \langle \psi _1|+H.c.) +3\Delta N_1^2|\psi _1\rangle \langle \psi _1|. \end{aligned}$$
(21)

When the large detuning condition \(3\Delta N_1\ge \overline{\Omega }_1,\ \overline{\Omega }_3\) is satisfied, we can adiabatically eliminate the state \(|\psi _1\rangle \) and obtain the final effective Hamiltonian

$$\begin{aligned} H_\mathrm{fe}=-\frac{\overline{\Omega }_1^2}{3\Delta }|\phi _1\rangle \langle \phi _1|-\frac{\overline{\Omega }_3^2}{3\Delta }|\phi _{11}\rangle \langle \phi _{11}| -\frac{\overline{\Omega }_1\overline{\Omega }_3}{3\Delta } (|\phi _1\rangle \langle \phi _{11}|+|\phi _{11}\rangle \langle \phi _1|). \end{aligned}$$
(22)

For simplicity, we set \(\overline{\Omega }_1=\overline{\Omega }_3=\overline{\Omega }(t)\). The front two terms caused by Stark shift can be removed and the Hamiltonian becomes

$$\begin{aligned} \overline{H}(t)=\Omega _x|\phi _1\rangle \langle \phi _{11}|+H.c., \end{aligned}$$
(23)

where \(\Omega _x=-\frac{\overline{\Omega }^2}{3\Delta }\). The equation has a similar form with Eq. (20), but the effective couplings between \(i\dot{\theta }\) and \(\Omega _x\) exist \(3\pi /2\)-dephased. To guarantee their consistency, we put a change that \(\Omega _3\rightarrow -i\Omega _3\). Then, the eigenstates of \(H_{eff}\) become

$$\begin{aligned} |\eta _o^\prime (t)\rangle =\left( \begin{array}{c} \cos \theta (t) \\ 0\\ i\sin \theta (t) \end{array} \right) , \quad |\eta _{\pm }^\prime (t)\rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} \sin \theta (t) \\ \pm 1\\ -i\cos \theta (t) \end{array} \right) , \end{aligned}$$
(24)

and the CDD Hamiltonian H(t) becomes

$$\begin{aligned} H(t)=-\dot{\theta }|\phi _1\rangle \langle \phi _{11}|-\dot{\theta }|\phi _{11}\rangle \langle \phi _1|. \end{aligned}$$
(25)

Compared Eq. (23) with Eq. (25), we can easily get the CDD Hamiltonian when the condition \(\Omega _x=-\dot{\theta }\) is satisfied.

$$\begin{aligned} \overline{\Omega }_1(t)=\overline{\Omega }_3(t)=\overline{\Omega }(t)=\sqrt{3\Delta \dot{\theta }}. \end{aligned}$$
(26)
Fig. 4
figure 4

The fidelity versus the laser pulses amplitude \(\Omega _0\) and the operation time \(t/t_f\)

Full size image
Fig. 5
figure 5

a The population \(P_\mathrm{target}\) of the target state \(|\psi _\mathrm{target}\rangle \) and the population \(P_0\) of the initial state \(|\psi (0)\rangle \) governed by the original Hamiltonian \(H_\mathrm{tot}\) via the adiabatic passage. b The population \(P_1(t)\) of the states \(|\phi _1\rangle \) and the population \(P_{11}(t)\) of the states \(|\phi _{11}\rangle \) governed by the original Hamiltonian \(H_\mathrm{tot}\) via adiabatic passage. The parameters are collectively with the fixed values \(\Omega _0=0.2g\), \(g=v\), \(t_0=0.14t_f\), \(t_c=0.19t_f\) and \(t_f=400/g\)

Full size image
Fig. 6
figure 6

The fidelity F of the target state \(|\psi (t_f)\rangle \) governed by \(H_\mathrm{tot}^\prime \) versus the interaction time \(gt_f\) and the detuning \(\Delta /g\)

Full size image

4.3 Numerical simulations and analyses

Next we will show that it takes less time to get the target state on the situation governed by the APF Hamiltonian \(H_\mathrm{tot}^\prime \) via TQD than by the original Hamiltonian \(H_\mathrm{tot}\) via adiabatic passage. The time-dependent population for any state \(|\psi \rangle \) is defined as \(P=|\langle \psi |\rho (t)|\psi \rangle |\), where \(\rho (t)\) is the corresponding time-dependent density operator. We present the fidelity versus the laser pulses amplitude \(\Omega _o\) and the operation time \(t/t_f\) via adiabatic passage in Fig. 4. As shown in Fig. 4, we can know that the bigger the laser pulse amplitude is, the less time that the system evolution to the target state needs. However, the value of the Rabi frequencies needs to meet some conditions. Firstly, we need to satisfy the Zeno conditions \(g,v\gg \Omega _1,\Omega _3\), so we set \(\Omega _0=0.2g\); Secondly, it has to ensure that the rotating wave approximation is effective; the last, it has to avoid to excite high-photon energy levels. In Fig. 5, we display the time-dependent populations of the states \(|\phi _1\rangle \), \(|\psi _\mathrm{target}\rangle \), and \(|\phi _{11}\rangle \) via adiabatic passage. As depicted in Figs. 4 and 5, the operation time needs \(t_f\ge 400/g\) to achieve an ideal result at least. It is awkward in some case.

Next we will detail the evolution governed by the APF Hamiltonian \(H_\mathrm{tot}^\prime \) via TQD. According to Eq. (24), we finally get a GHZ state \(|\psi (t_f)\rangle =\frac{1}{\sqrt{2}}(|\phi _1\rangle +i|\phi _{11}\rangle )\). In Fig. 6, we present the relationship between the fidelity of the three-atom GHZ state (governed by the APF Hamiltonian) and two parameters \(\Delta \) and \(t_f\) when \(\Omega _0=0.2g\) to satisfy the Zeno condition, where the fidelity of the three-atom GHZ state is defined as \(F=|\langle \hbox {GHZ}|\rho (t_f)|\hbox {GHZ}\rangle |\) (\(\rho (t_f)\) is the density operator of the whole system when \(t=t_f\)). We find that a wide range for parameters \(\Delta \) and \(t_f\) can obtain a high fidelity of the three-atom GHZ state, and the fidelity increases with the increasing of \(\Delta \) and the decreasing of \(t_f\). In order to satisfy the large detuning condition, we set \(\Delta =2.3g\). Figure 6 reveals that the operation time needs \(t_f\ge 72/g\) via TQD at least. In Fig. 7, we plot the operation time for the creation of the GHZ state governed by \(H_\mathrm{tot}^\prime \) and by \(H_\mathrm{tot}\) with the parameters that \(t_f=72/g\), \(\Omega _0=0.2g\), \(\Delta =2.3g\) and \(g=v\). Numerical results show that the APF Hamiltonian \(H_\mathrm{tot}^\prime \) can govern the evolution to a perfect GHZ state \(|\psi (t_f)\rangle \) from \(|\psi _1\rangle \) in a relatively short interaction time while the original Hamiltonian \(H_\mathrm{tot}\) cannot.

Fig. 7
figure 7

The population \(P_1(t)\) of the state \(|\phi _1\rangle \) and the population \(P_{11}(t)\) of the state \(|\phi _{11}\rangle \) governed by a the APF Hamiltonian \(H_\mathrm{tot}^\prime \) with \(\Delta =2.3g\). b The original Hamiltonian \(H_\mathrm{tot}\) collectively with the fixed values \(\Omega _0=0.2g\), \(g=v\), \(t_0=0.14t_f\), \(t_c=0.19t_f\), and \(t_f=72/g\)

Full size image

In above analysis, we do not consider the influence of decoherence caused by various factors, such as spontaneous emissions, cavity decays and fiber photon leakages. In fact, the decoherence is unavoidable during the evolution of the whole system in experiment. The master equation of the whole system is written as

$$\begin{aligned} \dot{\rho }= & {} -i [H_\mathrm{tot},\rho ] \nonumber \\&+\,\sum _{k=1}^3\frac{\gamma _k}{2}\left( 2\sigma _k^-\rho \sigma _k^+-\sigma _k^+\sigma _k^-\rho -\rho \sigma _k^+\sigma _k^-\right) \nonumber \\&+\,\sum _{k=1}^2\frac{\kappa _{c_k}}{2}\left( 2a_{l,k}\rho a_{l,k}^+-a_{l,k}^+a_{l,k}\rho -\rho a_{l,k}^+a_{l,k}\right) \nonumber \\&+\,\sum _{k=2}^3\frac{\kappa _{c_k}}{2}\left( 2a_{r,k}\rho a_{r,k}^+-a_{r,k}^+a_{r,k}\rho -\rho a_{r,k}^+a_{r,k}\right) \nonumber \\&+\,\sum _{k=1}^2\frac{\kappa _{f_k}}{2}\left( 2b_k\rho b_k^+-b_k^+b_k\rho -\rho b_k^+b_k\right) , \end{aligned}$$
(27)

where \(\gamma _k\) is the atomic spontaneous emission rate for the kth atom and \(\kappa _{c(f)}\) is the decay rate of the kth cavity (kth fiber), \(\sigma _k^-\) denotes the atomic transition from the ground states \(|m\rangle \ (m=g_0,\ g_l,\ g_r)\) to the excited state \(|e\rangle \). For the sake of simplicity, we assume that \(\gamma _1=\gamma _2=\gamma _3=\gamma \), \(\kappa _{c_1}=\kappa _{c_2}=\kappa _{c_3}=\kappa _c\) and \(\kappa _{f_1}=\kappa _{f_2}=\kappa _f\). As shown in Fig. 8, we plot the fidelity governed by the APF Hamiltonian \(H_\mathrm{tot}^\prime \) and by the original Hamiltonian \(H_\mathrm{tot}\) and the dimensionless parameters \(\gamma /g\), \(\kappa _c/g\) and \(\kappa _f/g\), respectively. We can draw a conclusion that the fidelities are almost unaffected by the fiber decay both via TQD and via adiabatic passage. We focus on the main decoherence factors included the cavity decay and the atomic spontaneous emission. As shown in Fig. 9, we plot the fidelity versus the cavity decay and the atomic spontaneous emission. We can know the most important decoherence factor is the cavity decay. This result can be understood from Ref. [19] that if the Zeno condition cannot be satisfied very well, the populations of the intermediate states including the cavity excited states cannot be suppressed ideally.

Fig. 8
figure 8

The fidelity of the target state \(|\psi (t_f)\rangle \) governed by a the APF Hamiltonian \(H_\mathrm{tot}^\prime \) with \(\Delta =2.3g\), \(t_f=72/g\) and \(\Omega _0=0.2g\). b The original Hamiltonian \(H_\mathrm{tot}\) with \(t_f=153/g\), and \(\Omega _0=0.5g\) collectively with the fixed values \(t_0=0.14t_f\), and \(t_c=0.19t_f\) versus the dimensionless parameters \(\gamma /g\), \(\kappa _c/g\), and \(\kappa _f/g\), respectively

Full size image
Fig. 9
figure 9

The fidelity of the target state \(|\psi (t_f)\rangle \) governed by a the APF Hamiltonian \(H_\mathrm{tot}^\prime \) with \(\Delta =2.3g\), \(t_f=72/g\), and \(\Omega _0=0.2g\). b The original Hamiltonian \(H_\mathrm{tot}\) with \(t_f=153/g\), and \(\Omega _0=0.5g\) collectively with the fixed values \(t_0=0.14t_f\), and \(t_c=0.19t_f\) versus the dimensionless parameters \(\gamma /g\) and \(\kappa _c/g\)

Full size image

From the above analyses, we can obviously know that the evolution time from the initial state to the target state via TQD is \(t_f=72/g\) when \(\Omega _0=0.2g\), \(\Delta =2.3g\), \(t_0=0.14t_f\), \(t_c=0.19t_f\) and \(g=v\), while the evolution time for the adiabatic passage is \(t_f=400/g\) when \(\Omega _0=0.2g\), \(t_0=0.14t_f\), \(t_c=0.19t_f\) and \(g=v\). So, the benefit of the TQD method is shown obviously that the speed via TQD method is faster than that via adiabatic passage. It is more worthy to note that the fidelity of the target state via TQD is almost equal to that via adiabatic passage. So our scheme has a huge advantage compared with the proposals via adiabatic passage. That means the present scheme via STAP method is not only fast but also robust.

As we all know, it is necessary for a good scheme to tolerate the deviations of the experimental parameters, because it is impossible to avoid the operational imperfection in experiment. Define that \(\delta x=x^{\prime }-x\) is the deviation of the ideal value x, \(x^{\prime }\) is the actual value. In Fig. 10, we plot the fidelity of the target state \(|\psi _\mathrm{target}\rangle \) versus the deviations of the experimental parameters g, v, \(\Omega _0\), and T (\(T=t_f\) denotes the operation time). Numerical results demonstrate that our scheme is robust against the fluctuation of the experimental parameters.

Fig. 10
figure 10

The fidelity of the target state \(|\psi _\mathrm{target}\rangle \) versus the deviations of a g and v, b T and \(\Omega _0\)

Full size image
Fig. 11
figure 11

The set-up diagram for the generation of N-atom GHZ states. The N-atoms are respectively trapped in N-cavities which are linked by \(N-1\) fibers

Full size image

5 The generation of the N-atom GHZ state via transitionless quantum driving

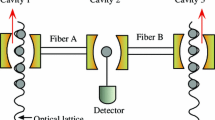
Next we briefly present the generalization of the scheme in Sect. 4 to generate N-atom GHZ state by the same principle. We consider the physical configuration shown in Fig. 11, where N atoms \(a_1,\ a_2, \ldots , a_N\) are trapped in N cavities \(C_1,\ C_2, \ldots , C_N\) connected by \(N-1\) fibers \(f_1,\ f_2, \dots , f_{N-1}\), respectively. The level configurations of the atoms between two ends are the same as that of the atom \(a_2\) in the three-atom case, and the level configurations of \(a_1\) and \(a_N\) are the same as those of \(a_1\) and \(a_3\) in the three-atom case, respectively. The Hamiltonian of the present system can be written as in the rotation framework

$$\begin{aligned} H_\mathrm{total}= & {} H_l^{\prime }+H_{c}^{\prime }, \nonumber \\ H_l^{\prime }= & {} \Omega _1^\prime |e\rangle _{a_1}\langle g_0| +\Omega _N^\prime |e\rangle _{a_N}\langle g_0|+H.c.,\nonumber \\ H_{c}^{\prime }= & {} \sum _{i=1}^{N-1}{g_{i,l}a_{i,l}|e\rangle _{a_i}\langle g_l|}+\sum _{j=2}^{N}{g_{j,r}a_{j,r}|e\rangle _{a_j}\langle g_r|} \nonumber \\&+\,\sum _{k=2}^{N-1}{[v_{k-1}b_{k-1}^{\dag }(a_{k-1,l}+a_{k,l})+v_{k}b_{k}^{\dag }(a_{k,r}+a_{k+1,r})]}+H.c.. \end{aligned}$$
(28)

Let us consider the situation where N is an odd number, i.e., \(N=2l+1,\ (l=1,\ 2,\ 3, \dots )\). Suppose that the initial state of the atoms is \(|g_0g_lg_rg_lg_r\ \dots \ g_r\rangle \) while all the cavities and fibers are vacuum, then the system can be expended in the following subspace

$$\begin{aligned}&|\phi _1^{\prime }\rangle =|g_0g_lg_r\ \dots \ g_r\rangle |0\rangle _\mathrm{all}, \quad |\phi _2^{\prime }\rangle =|eg_lg_r\ \dots \ g_r\rangle |0\rangle _\mathrm{all},\nonumber \\&|\phi _3^{\prime }\rangle =|g_lg_lg_r\ \dots \ g_r\rangle |1\rangle _{c_1}, \quad |\phi _4^{\prime }\rangle =|g_lg_lg_r\ \dots \ g_r\rangle |1\rangle _{f_1}, \nonumber \\&|\phi _5^{\prime }\rangle =|g_lg_lg_r\ \dots \ g_r\rangle |10\rangle _{c_2}, \quad |\phi _6^{\prime }\rangle =|g_leg_r\ \dots \ g_r\rangle |0\rangle _\mathrm{all}, \nonumber \\&|\phi _7^{\prime }\rangle =|g_lg_rg_r\ \dots \ g_r\rangle |01\rangle _{c_2}, \quad |\phi _8^{\prime }\rangle =|g_lg_rg_r\ \dots \ g_r\rangle |1\rangle _{f_2}, \nonumber \\&|\phi _9^{\prime }\rangle =|g_lg_rg_r\ \dots \ g_r\rangle |01\rangle _{c_3}, \quad |\phi _{10}^{\prime }\rangle =|g_lg_re\ \dots \ g_r\rangle |0\rangle _\mathrm{all}, \dots \nonumber \\&|\phi _{4N-1}^{\prime }\rangle =|g_lg_r\ \dots \ g_rg_0\rangle |0\rangle _\mathrm{all}, \end{aligned}$$
(29)

where \(|0\rangle _\mathrm{all}\) means that there is none photon in all boson modes, \(|n_1 n_2\rangle _{s_i}\ (s=C,\ f.\ i=1,\ 2, \dots , N)\) means that there are \(n_1\) left-circularly photon and \(n_2\) right-circularly photon in the corresponding cavity \(C_i\) or fiber \(f_i\).

Similar to the above procedure from Eq. (10) to Eq. (16), we get an effective Hamiltonian

$$\begin{aligned} H_{eff(N)}=N_1^{\prime }(\Omega _1^\prime |\phi _1^\prime \rangle \langle \psi _1^\prime |+ \Omega _N^\prime |\phi _{4N-1}^\prime \rangle \langle \psi _1^\prime |+H.c.), \end{aligned}$$
(30)

where

$$\begin{aligned} |\psi _1^\prime \rangle =N_1^\prime \left( \sum _{i=1}^N|\phi _{4i-2}^\prime \rangle - \sum _{i=1}^{N-1}\frac{g}{v}|\phi _{4i}^\prime \rangle \right) . \end{aligned}$$
(31)

In addition, the eigenstates and eigenvalues of the Hamiltonian in Eq. (30) can be written as

$$\begin{aligned} |\chi _o(t)\rangle =\left( \begin{array}{c} \cos \theta ^{\prime }(t) \\ 0\\ -\sin \theta ^{\prime }(t) \end{array} \right) , \quad |\chi _{\pm }(t)\rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} \sin \theta ^{\prime }(t) \\ \pm 1\\ \cos \theta ^{\prime }(t) \end{array} \right) , \end{aligned}$$
(32)

with the corresponding eigenvalues \(\chi _0^\prime =0\) and \(\chi _{\pm }^\prime =\pm N_1^{\prime }\Omega ^{\prime }\), where \(\tan \theta ^{\prime }=\frac{\Omega _1^{\prime }}{\Omega _N^{\prime }}\) and \(\Omega ^{\prime }=\sqrt{\Omega _1^{\prime 2}+\Omega _N^{\prime 2}}\). Substituting Eq. (32) in Eq. (19), we obtain

$$\begin{aligned} H^{\prime }(t)=i\dot{\theta }^{\prime }|\phi _1^{\prime }\rangle \langle \phi _{4N-1}^{\prime }|+H.c., \end{aligned}$$
(33)

where \(\dot{\theta }^{\prime }=[\dot{\Omega }_1^{\prime }(t)\Omega _N^{\prime }(t)-\Omega _1^{\prime }(t)\dot{\Omega }_N^{\prime }(t)]/\Omega ^{\prime 2}\).

Inspired by the above idea in Sect. 4, we make the system into a non-resonant system to construct the CDD Hamiltonian in Eq. (33). Therefore, the Hamiltonian of the present system reads \(H_\mathrm{total}^\prime =H_l^\prime +H_c^\prime +H_d^\prime \), where \(H_d^\prime =\sum _{i=1}^N\Delta |e\rangle \langle e|\). Similar to the above procedure from Eq. (22) to Eq. (23) in Sect. 4, we obtain the final effective Hamiltonian

$$\begin{aligned} H_{fe(N)}^{\prime }= & {} -\frac{\overline{\Omega }_1^{\prime 2}}{3\Delta }|\phi _1^{\prime }\rangle \langle \phi _1^{\prime }| -\frac{\overline{\Omega }_N^{\prime 2}}{3\Delta }|\phi _{4N-1}^{\prime }\rangle \langle \phi _{4N-1}^{\prime }|\nonumber \\&-\,\frac{\overline{\Omega }_1^\prime \overline{\Omega }_N^\prime }{3\Delta }\left( |\phi _1^{\prime }\rangle \langle \phi _{4N-1}^{\prime }| +|\phi _{4N-1}^{\prime }|\rangle \langle \phi _1^{\prime }|\right) . \end{aligned}$$
(34)

For simplicity, we set \(\overline{\Omega }_1^\prime =\overline{\Omega }_N^\prime =\overline{\Omega }^\prime \), the front two terms caused by Stark shift can be omitted and the Hamiltonian becomes

$$\begin{aligned} \overline{H}_N=\Omega _x^\prime (t)|\phi _1^\prime \rangle \langle \phi _{4N-1}^\prime |+H.c., \end{aligned}$$
(35)

where \(\Omega _x^\prime (t)=-\frac{\overline{\Omega }^{\prime 2}}{3\Delta }\). To guarantee their consistency, we put a change that \(\Omega _N\rightarrow -i\Omega _N\). Then the eigenstates of \(H_{\mathrm{eff}(N)}\) become

$$\begin{aligned} |\chi _o^\prime (t)\rangle =\left( \begin{array}{c} \cos \theta ^\prime (t) \\ 0\\ i\sin \theta ^\prime (t) \end{array} \right) , \quad |\chi _{\pm }^\prime (t)\rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} \sin \theta ^\prime (t) \\ \pm 1\\ -i\cos \theta ^\prime (t) \end{array} \right) , \end{aligned}$$
(36)

and the CDD Hamiltonian H(t) becomes

$$\begin{aligned} H^\prime (t)=-\dot{\theta }^\prime |\phi _1^\prime \rangle \langle \phi _{4N-1}^\prime |- \dot{\theta }^\prime |\phi _{4N-1}^\prime \rangle \langle \phi _1^\prime |. \end{aligned}$$
(37)

Compared Eq. (35) with Eq. (37), we can easily get the CDD Hamiltonian when the condition \(\Omega _x^\prime =-\dot{\theta }^\prime \) is satisfied.

$$\begin{aligned} \overline{\Omega }_1^\prime (t)=\overline{\Omega }_N^\prime (t) =\overline{\Omega }^\prime (t)=\sqrt{3\Delta \dot{\theta }^\prime }. \end{aligned}$$
(38)

6 Experimental feasibility and conclusions

Now experimental feasibility needs to be discussed. The configuration of \(^{87}\)Rb can be suitable for our proposals. Under current experimental condition, a set of CQED parameters \(g=2\pi \times 750\) MHz, \(\gamma =2\pi \times 2.62\) MHz, and \(\kappa _c=2\pi \times 3.5\) MHz is available with the wavelength in the region 630–850 nm [41]. By using fiber-taper coupling to high-Q silica microspheres, the efficiency of fiber–cavity coupling is higher than 99.9 % [42]. The optical fiber decay at a 852 nm wavelength is about 2.2 dB/km [43], which means the fiber decay rate is about \(\kappa _f=1.52\times 10^5\) Hz. With the above parameters, we obtain a relatively high fidelity about 97.15 %.

In conclusion, we have proposed an efficient scheme to fast deterministically generate N-atom GHZ state in separate coupled cavities via transitionless quantum driving (TQD) only by one-step manipulation. We apply a promising method to construct STAP by joint utilization of the Zeno dynamics and the approach of TQD in the cavities QED system. The method features are that we do not need to control the time exactly and the evolution process is fast. Because the atoms are trapped in separate coupled cavity, the single-qubit manipulation can be realized easily. When considering dissipation, we can see that the method is robust against the decoherences caused by the atomic spontaneous emission and fiber decay. The results show that the scheme has a high fidelity and may be possible to implement with the current experimental technology. So, the scheme is fast, robust and effective. We hope the scheme can be used to generate multiatom GHZ state in the future.