1 Introduction

Quantum-state engineering, i.e. active control over the coherent dynamics of suitable quantum-mechanical system to achieve a preselected state (e.g. entangled states) of the system, has become a fascinating prospect of modern physics. Fundamentally, entanglement is one of the most important traits in quantum mechanics. The many particle interaction creates the so called entangled states, which are interesting for fundamental studies of quantum mechanics, but also they have application in high precisely spectroscopy (Bollinger et al. 1996) and in quantum information theory (Nielsen and Chuang 2000). It has found different applications in quantum information processing, such as quantum cryptography (Ekert 1991), quantum teleportation (Bennett et al. 1993), quantum dense coding (Pan and Zeilinger 1998) and so on. Typical entangled states are Bell states (Bell 1964), Greenberger–Horne–Zeilinger (GHZ) (Greenberger et al. 1990), and W states (Dur et al. 2000; Amniat-Talab et al. 2010, 2012), which have been identified and can directly be utilized in quantum information processing. For decades, various quantum systems have been suggested as being possible candidates for performing quantum state preparation and quantum information processing and a large number of theoretical and experimental schemes were proposed for generating GHZ and W states of photons (Zou and Mathis 2005), atoms (Zheng 2001), ions (Bouwmeester et al. 1999; Ivanov et al. 2007; Ivanov and Vitanov 2008), etc. Among them, the cavity QED is one of the most popular systems to engineer quantum entanglement (Yang and Han 2004). It provides a promising avenue for achieving varieties of novel ideas, by utilizing the strong coupling between a high-Q optical cavity and atoms. Based on cavity QED, numerous schemes (Zheng 2009; Yin and Li 2007) have been proposed for deterministic generation of entanglement among atoms trapped in different cavities connected by optical fibers (Cirac et al. 1997; Enk et al. 1997; Bose et al. 1999).

The problem of controlling entanglement is directly connected to the problem of coherent control of population transfer in multilevel systems. A way to overcome such difficulties in state engineering is to force the systems initial state to evolve along a dark state, if any, by means of adiabatic passage. Such an evolution can be realized by the so-called technique of stimulated Raman adiabatic passage (STIRAP) (Kral et al. 2007; Vitanov et al. 2001; Gaubatz et al. 1990), which have been used by counterintuitive sequence of pulses (Stokes before pump) for complete population transfer in three state quantum systems. In the context of cavity QED, the STIRAP technique has been introduced by Parkins et al. (1993), where the Stokes pulse is replaced by a mode of a high-Q cavity. The advantage of STIRAP is the robustness of its control with respect to the precise pulse areas, pulse delay, pulse shapes and to the one photon detuning. Fractional STIRAP (F-STIRAP) is a variation of STIRAP which allows the creation of any preselected coherent superposition of the two degenerate ground states (Vitanov et al. 1999). The half-STIRAP process (F-STIRAP with final half population of two ground states) has also been studied in an optical cavity to prepare atom-photon and atom-atom entanglement (Amniat-Talab et al. 2005a, b).

There are several schemes discussing the preparation of atomic GHZ states (Li et al. 2010; Zheng and Liu 2011; Hao et al. 2013) in the atom-cavity-fiber system. In the scheme of Li et al. (2010) a system composed of three atom, two cavity and an optical fibre is used to create tripartite GHZ states by adiabatic passage. Another scheme to generate GHZ states of \(N\ge 3\) atoms trapped in spatially separated cavities connected by optical fibers, has been proposed in Hao et al. (2013). However in the schemes proposed in Li et al. (2010), Hao et al. (2013) the atomic qubits have been used as the asymetric coding, i.e qubits are encoded in the different states for each atom. In the scheme of Zheng and Liu (2011) N-atom GHZ states are generated in atom-cavity-fibre system consisting of \(N+1\) atoms trapped in \(N+1\) cavities connected with N fibres. However it requires stringent conditions of detuning which makes it difficult to implement in practice.

In this paper, we design a scheme to deterministically generate GHZ states of N atoms individually trapped in a linear array of optical cavities whose nearest neighbors are connected by \(N-1\) optical fibers. Two external lasers are needed to drive the two end atom-cavity subsystems. Our scheme is based on the adiabatic passage along a dark state, which is a specific eigenstate of the total atom-cavity-fiber system corresponding to the zero eigenvalue. The key idea is to choose suitable time-dependent Rabi frequencies of the driving lasers. We use STIRAP and F-STIRAP technique in multistate systems (Vitanov 1998) in which the populations of the intermediate states can be damped by large intermediate couplings. We obtain maximally entangled GHZ states of the form (\(\frac{1}{\sqrt{2}}(|a\rangle |a\rangle \cdots |a\rangle + |b\rangle |b\rangle \cdots |b\rangle )\)) where the qubits are encoded in the two levels \(|a\rangle\) and \(|b\rangle\) for all atoms \(1, 2, \ldots , N\).

The topics we are going to discuss in this paper are: The effective Hamiltonian of the system in the Sect. 2, the generation steps of GHZ state for three atoms and N atoms in atom-cavity-fiber system in the Sects. 3 and 4, and we discuss about decoherence effects of spontaneus emission and, fiber and cavity damping in Sect. 5. Finally, in Sect. 6, we briefly review the results.

Fig. 1
figure 1

Schematic diagram of atom-cavity-fiber system

Full size image

2 The system

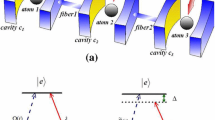
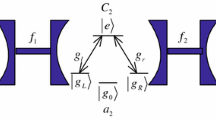
We consider the case of N five-level atoms in details. As shown in Fig. 1, N atoms \(a_1, a_2,\ldots , a_N\) are trapped in N distant linearly arranged optical cavities \(c_1, c_2,\ldots , c_N\) respectively. The single-mode cavities \(c_1, c_2,\ldots , c_N\) are connected by \(N-1\) short optical fibers \(f_1,\, f_2, \ldots , f_{N-1}\). The five-level atomic system has been presented in Fig. 2 (Goto and Ichimura 2004; Sangouard et al. 2005). The three ground states \(|a,0\rangle , |b,0\rangle\) and \(|g,1\rangle\) of five level atoms are coupled to the excited state \(|e,0\rangle\) respectively by two lasers (associated to the Rabi frequencies \(\varOmega _a\) and \(\varOmega _b\) ), and by a single mode cavity (associated to the Rabi frequency g). Furthermore, \(|a,0\rangle , |b,0\rangle\) and \(|g,0\rangle\) are coupled by three additional lasers (with Rabi frequencies \(\varOmega _a^{\prime \prime }, \varOmega _b^{\prime \prime }\) and \(\varOmega ^{\prime }\)) to the upper state \(|u,0\rangle\). Each atom (labeled by k) of the register is driven by a set of five pulsed laser fields \(\varOmega _a^{(k)}, \varOmega _b^{(k)}, \varOmega _a^{\text {''}(k)}, \varOmega _b^{\text {''}(k)}, \varOmega ^{\prime (k)}\) and by the cavity mode \(g^{(k)}\) which is time independent. The Rabi frequencies will be assumed to be real and each pair of which is on two-photon resonance and the upper states \(|e\rangle\) and \(|u\rangle\) are in single-photon resonance as shown in Fig. 2.

In the short-fiber limit, \((\frac{(L\varGamma )}{(2\pi c)}\ll 1)\) (Pellizzari 1997; Serafini et al. 2006) with L the fiber length, c the speed of light and \(\varGamma\) the decay rate of the cavity field into a continuum of fiber modes, only one resonant fiber mode interacts with the cavity mode. Then, in the interaction picture, the Hamiltonian of the total atom-cavity-fiber system in rotating wave approximation can be written as \((\hbar =1)\).

2.1 Hamiltonian

$$H= H_{ac}+H_{cf}+H_{al},$$
(1)
$$H_{ac}= \sum _{i=1}^{N} g_{i} a_{i}|e\rangle _{i}\langle g|+\text {H.c.},$$
(2)
$$H_{cf}= \nu _{1} b_{1}^{\dagger }(a_{1}+a_{2})+\nu _{2} b_{2}^{\dagger }(a_{2}+a_{3})+\cdots +\nu _{N-1}b_{N-1}^{\dagger }(a_{N-1}+a_{N})+H.c.,$$
(3)
$$\begin{aligned} H_{al}= & \sum _{i=1}^{N} \varOmega _a^{(i)}|e\rangle _{i}\langle a|_{i}+ \sum _{i=1}^{N} \varOmega _b^{(i)}|e\rangle _{i}\langle b|_{i}+ \sum _{i=1}^{N} \varOmega _a^{''(i)}|u\rangle _{i}\langle a|_{i} \nonumber \\ &+\sum _{i=1}^{N} \varOmega _b^{''(i)}|u\rangle _{i}\langle b|_{i}+\sum _{i=1}^{N} \varOmega ^{\prime (i)}|u\rangle _{i}\langle g|_{i}+H.c. \end{aligned}$$
(4)

where \(a^{\dagger }_i\) and \(a_i\) are the creation and annihilation operators for the mode of cavity \(c_i\), and \(b^{\dagger }_f (b_f)\) are the creation (annihilation) operators of the resonant mode of fiber \(f_f\). For simplicity, we assume equal atom-cavity and cavity-fiber coupling strength, i.e. \(g_{i}=\nu _{j}=\nu =g\).

Fig. 2
figure 2

Atom-field linkage pattern

Full size image

3 Generation of GHZ state for three atoms

3.1 General strategy

The initial state \(|\psi (t_{0})\rangle\) of atom-cavity-fiber system is defined as

$$\begin{aligned} |\psi (t_{0})\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}, \end{aligned}$$
(5)

where the labels m, n of the states of the form \(|m,n\rangle _{i}\) with \(i={1,2,3}\) denote respectively the atomic state and the number of photons in the mode of cavities and \(|s_{1},s_{2}\rangle _{f}\) represents number of photons in the mode of first and second fibers. Our goal is to transform the initial state of the system into a GHZ state as follows:

$$\begin{aligned} \vert \psi (t_{f})\rangle =\frac{1}{\sqrt{2}}[\vert a,0\rangle _{1} \vert a,0\rangle _{2} \vert a,0\rangle _{3} + \vert b,0\rangle _{1} \vert b,0\rangle _{2} \vert b,0\rangle _{3}] \vert 00\rangle _{f}. \end{aligned}$$
(6)

We use a simple interaction scheme to represent the proposed mechanism for the creation of a GHZ state (see Fig. 3). This mechanism is composed of three steps. We first transfer half of population of state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) into the state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) by F-STIRAP in multistate systems. In the second step we transfer the population of state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) into the state \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}] | 00\rangle _{f}\) by STIRAP in multistate systems. In this step the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) remains unchanged. In the final step the population of state \(\vert g,0\rangle _{1}\) is transferred into the state \(\vert b,0\rangle _{1}\) and the population of state \(\vert g,0\rangle _{3}\) is transferred into the state \(\vert a,0\rangle _{3}\) using three state STIRAP. In the next subsection, The details will be discussed proceedingly.

3.2 Description of the steps

The three steps summarized above can be explained as follows

Step (1)

In this step we use two laser pulses \(\varOmega _a^{(1)}, \varOmega _b^{(2)}\) and assume other laser pulses to be turned off. Considering the initial state of system (5), the system subspace in this step is spanned by the following seven states (Zheng 2009)

$$\begin{aligned} S_7^{(1)}=&\, \lbrace |a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f},|e ,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f} \nonumber \\&|g,1\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}, |g,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 10\rangle _{f} \nonumber \\&|g,0\rangle _{1}| g,1\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}, |g,0\rangle _{1}| e,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f} ,\nonumber \\&|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}\rbrace . \end{aligned}$$
(7)

The system Hamiltonian in its subspace:

$$\begin{aligned} H^{(1)}(t)=\left( \begin{array}{ccccccc} 0 &{}\quad \varOmega _a^{(1)}(t) &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \varOmega _a^{(1)}(t) &{}\quad 0 &{}\quad g &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad g &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad g &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad g &{}\quad 0 &{}\quad \varOmega _b^{(2)}(t)\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varOmega _b^{(2)}(t) &{}\quad 0\\ \end{array}\right) , \end{aligned}$$
(8)

Hamiltonian (44) has a zero eigenvalue, \(\lambda =0\). The corresponding eigenstate, which is called a dark state, is:

$$\begin{aligned} \vert D^{(1)}(t)\rangle =&\, C\left[ \varOmega _b^{(2)} (|a,0\rangle _{1} | g,0\rangle _{2} | b,0\rangle _{3} | 00\rangle ) - \frac{\varOmega _b^{(2)} \varOmega _a^{(1)}}{g}(| g,1\rangle _{1} | g,0\rangle _{2} | b,0\rangle _{3} \right. \nonumber \\&\left. -|g,0\rangle _{1} | g,1\rangle _{2} | b,0\rangle _{3}) | 00\rangle _{f} - \varOmega _a^{(1)} (| g,0\rangle _{1} | b,0\rangle _{2} | b,0\rangle _{3} | 00\rangle _{f}) \right] . \end{aligned}$$
(9)

where C is the normalization factor.

The half population transfer from state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) into the state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) is expected from the following behavior of the dark state:

$$\begin{aligned}&\lim _{t \rightarrow t_i}\left( \frac{\varOmega _a^{(1)}(t)}{\varOmega _b^{(2)}(t)}\right) =0,\quad |D^{(1)}(t_i)\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}, \end{aligned}$$
(10a)
$$\begin{aligned}&\lim _{t \rightarrow t_f}\left( \frac{\varOmega _a^{(1)}(t)}{\varOmega _b^{(2)}(t)}\right) =1, \end{aligned}$$
(10b)
$$\begin{aligned}&g, \nu \gg \varOmega _a^{(1)}(t), \varOmega _b^{(2)}(t). \end{aligned}$$
(10c)

Equations (10a), (10b) and (10c) are known as F-STIRAP conditions in multistate systems. As in three-state F-STIRAP, the laser pulse \(\varOmega _b^{(2)}(t)\) comes first and is followed after a certain time delay by the laser pulse \(\varOmega _a^{(1)}(t),\) but the two pulses vanish simultaneously. At the end of the interaction, the system evolves into the state

$$\begin{aligned} |\psi _{(1)}(t)\rangle =\frac{1}{\sqrt{2}} [|a,0\rangle _{1} | g,0\rangle _{2} | b,0\rangle _{3} - | g,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3}] |00\rangle _{f}. \end{aligned}$$
(11)
Fig. 3
figure 3

Schematic representation of the three steps GHZ state construction. For the first step, the initial state and the final state are represented by semifull circles which is corresponded to fractional population transfer into the final state. For the second and third steps, the initial state is represented by an empty circle whereas the final state is symbolised by a full black circle corresponding to complete population transfer into the final state

Full size image
Fig. 4
figure 4

Rabi frequencies of the laser fields satisfying the conditions of F-STIRAP in the first step (upper fram) and time evulation of populations (lower fram). The parameters used are \(g=\nu =100~T^{-1}, \varOmega _{0}=20~T^{-1}, \tau =0.7~T\)

Full size image

Figure 4 shows an example of such a superposition for atom-cavity-fiber system. We have used Gaussian pulses, to satisfy the conditions (10a) and (10b) as

$$\begin{aligned} \varOmega _b^{(2)}=&\, \varOmega _{0}\exp \left[ -(t-\tau )^{2}/T^2\right] + \frac{\varOmega _{0}}{\sqrt{2}} \exp \left[ -(t+\tau )^{2}/T^{2}\right] ,\end{aligned}$$
(12a)
$$\begin{aligned} \varOmega _a^{(1)}=&\, \frac{\varOmega _{0}}{\sqrt{2}}\exp \left[ -(t-\tau )^{2}/T^{2}\right] , \end{aligned}$$
(12b)

where \(\varOmega _0, 2\tau\) and T are, respectively, the peak Rabi frequency, the time delay between pulses, and the pulse duration.

Step (2):

In this step we use two laser pulses \(\varOmega _a^{(2)}, \varOmega _b^{(3)}\) and assume other laser pulses turned off. Considering the initial state of system as (11), the 15-dimensional Hilbert space \(S^{(2)}\) is composed of two orthogonal decoupled subspaces denoted \(S_7^{(2)}\) and \(S_8^{(2)}\), respectively spanned by the states

$$\begin{aligned} S_7^{(2)}=&\, \lbrace |a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}, |a,0\rangle _{1}| g,0\rangle _{2}| e,0\rangle _{3}| 00\rangle _{f} \nonumber \\&|a,0\rangle _{1}| g,0\rangle _{2}| g,1\rangle _{3}| 00\rangle _{f}, |g,0\rangle _{1}| g,0\rangle _{2}| g,0\rangle _{3}| 01\rangle _{f} \nonumber \\&|a,0\rangle _{1}| g,1\rangle _{2}| g,0\rangle _{3}| 00\rangle _{f}, |a,0\rangle _{1}| e,0\rangle _{2}| g,0\rangle _{3}| 00\rangle _{f} ,\nonumber \\&|a,0\rangle _{1}| a,0\rangle _{2}|g,0\rangle _{3}| 00\rangle _{f} \rbrace , \end{aligned}$$
(13)

and

$$\begin{aligned} S_8^{(2)}=&\, \lbrace |g,0\rangle _{0}| b,0\rangle _{2}|b,0\rangle _{3}| 00\rangle _{f},|g,0\rangle _{1}| b,0\rangle _{2}|e,0\rangle _{3}| 00\rangle _{f} ,\nonumber \\&|g,0\rangle _{0}| b,0\rangle _{2}|g,1\rangle _{3}| 00\rangle _{f} ,|g,0\rangle _{1}| b,0\rangle _{2}|g,0\rangle _{3}| 01\rangle _{f} ,\nonumber \\&|g,0\rangle _{0}| b,1\rangle _{2}|g,0\rangle _{3}| 00\rangle _{f} ,|g,0\rangle _{1}| b,0\rangle _{2}|g,0\rangle _{3}| 10\rangle _{f} , \nonumber \\&|g,1\rangle _{0}| b,0\rangle _{2}|g,0\rangle _{3}| 00\rangle _{f},|e,0\rangle _{1}| b,0\rangle _{2}|g,0\rangle _{3}| 00\rangle _{f}\rbrace . \end{aligned}$$
(14)

Hamiltonian \(H^{(2)}(t)\) is block-diagonal; two blocks connected to the initial state (11) have to be considered:

$$\begin{aligned} H^{(2)}(t)=\begin{pmatrix} H^{(2)}_7 (t) &{} O \\ O &{} H_8^{(2)}(t) \end{pmatrix} \end{aligned}$$
(15)

with

$$\begin{aligned} H_7^{(2)}(t)=\left( \begin{array}{ccccccc} 0 &{}\quad \varOmega _b^{(3)}(t) &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \varOmega _b^{(3)}(t) &{}\quad 0 &{}\quad g &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad g &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad g &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad g &{}\quad 0 &{}\quad \varOmega _a^{(2)}(t)\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varOmega _a^{(2)}(t) &{}\quad 0\\ \end{array} \right) , \end{aligned}$$
(16)

and

$$\begin{aligned} H_8^{(2)}(t)= \left( \begin{array}{cccccccc} 0 &{}\quad \varOmega _b^{(3)}(t) &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0&{}\quad 0 \\ \varOmega _b^{(3)}(t) &{}\quad 0 &{}\quad g &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad g &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 &{}\quad 0&{}\quad 0\\ 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad 0 &{}\quad \nu &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad 0&{}\quad g\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad g&{}\quad 0\\ \end{array} \right) . \end{aligned}$$
(17)

Hamiltonian (16) has a dark state as:

$$\begin{aligned} \vert D^{(2)}(t)\rangle=&\, C^{\prime }\left[ \varOmega _a^{(2)} (|a,0\rangle _{1} | g,0\rangle _{2} | b,0\rangle _{3} | 00\rangle ) - \frac{\varOmega _a^{(2)} \varOmega _b^{(3)}}{g} (| a,0\rangle _{1} | g,0\rangle _{2} | g,1\rangle _{3}\right. \nonumber \\&\left. -|a,0\rangle _{1} | g,1\rangle _{2} | g,0\rangle _{3}) | 00\rangle _{f} - \varOmega _b^{(3)} (| a,0\rangle _{1} | a,0\rangle _{2} | g,0\rangle _{3} | 00\rangle _{f})\right] . \end{aligned}$$
(18)

where \(C^{\prime }\) is the normalization factor.

Complete population transfer from the state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) into the state \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}] | 00\rangle _{f}\) is expected from the following behavior of the dark state:

$$\begin{aligned}&\lim _{t \rightarrow t_i}\left( \frac{\varOmega _b^{(3)}(t)}{\varOmega _a^{(2)}(t)}\right) =0, \quad |D^{(2)}(t_i)\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}, \end{aligned}$$
(19a)
$$\begin{aligned}&\lim _{t \rightarrow t_f}\left( \frac{\varOmega _a^{(2)}(t)}{\varOmega _b^{(3)}(t)}\right) =0, \quad |D^{(2)}(t_f)\rangle =[|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}] | 00\rangle _{f},\end{aligned}$$
(19b)
$$\begin{aligned}&g, \nu \gg \varOmega _a^{(2)}(t), \varOmega _b^{(3)}(t). \end{aligned}$$
(19c)

Equations (19a), (19b) and (19c) are known as STIRAP conditions in multistate systems. We initially turn on the Rabi frequency \(\varOmega _a^{(2)}(t)\), while the first Rabi frequency \(\varOmega _b^{(3)}(t)\) is turned off. In such condition, the initial state is initially connected to the dark state. Then we adiabatically increase \(\varOmega _b^{(3)}(t)\) and decrease \(\varOmega _a^{(2)}(t).\) At the end of the interaction the population of state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) transfers into the state \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}] | 00\rangle _{f}\) and the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) remains unchanged. As a result, at the end of this step the system will be in the state

$$\begin{aligned} |\psi _2(t)\rangle =-\frac{1}{\sqrt{2}}[|a,0\rangle _{1} | a,0\rangle _{2} |g,0\rangle _{3} + |g,0\rangle _{1} |b,0\rangle _{2} | b,0\rangle _{3}] |00\rangle _{f} \end{aligned}$$
(20)
Fig. 5
figure 5

Time dependence of the Rabi frequencies (upper fram) and time evulation of population of the first sublevel (lower fram). The parameters used are \(g=\nu =100T^{-1}, \varOmega _{0}=20T^{-1}, \tau =0.7T\)

Full size image

Figure 5 shows an example of such a superposition for the atom-cavity-fiber system. We have used Gaussian pulses, to satisfy the conditions (19a), (19b) and (19c) as

$$\begin{aligned} \varOmega _b^{(3)}= \varOmega _{0} \exp [-(t-\tau )^{2}/T^2], \end{aligned}$$
(21a)
$$\begin{aligned} \varOmega _a^{(2)}= \varOmega _{0} \exp [-(t+\tau )^{2}/T^{2}]. \end{aligned}$$
(21b)

Step (3):

In the final step we use four laser pulses \(\varOmega _b^{\prime \prime (1)}, \varOmega _a^{\prime \prime (3)}, \varOmega ^{'(1)}, \varOmega ^{'(3)}\) and assume other laser pulses turned off. Considering the initial state of the system as (20), the 6-dimensional Hilbert space \(S^{(3)}\) is composed of two orthogonal decoupled subspaces denoted by \(S^{'(3)}\) and \(S^{\text {''}(3)}\), as follows:

$$\begin{aligned} S^{'(3)}=\lbrace |g,0\rangle _{0}| b,0\rangle _{2}|b,0\rangle _{3}| 00\rangle _{f}, |u,0\rangle _{0}| b,0\rangle _{2}|b,0\rangle _{3}| 00\rangle _{f}, |b,0\rangle _{0}| b,0\rangle _{2}|b,0\rangle _{3}| 00\rangle _{f}\rbrace , \end{aligned}$$
(22)

and

$$\begin{aligned} S^{\prime \prime (3)}=\lbrace |a,0\rangle _{0}| a,0\rangle _{2}|g,0\rangle _{3}| 00\rangle _{f}, |a,0\rangle _{0}| a,0\rangle _{2}|u,0\rangle _{3}| 00\rangle _{f}, |a,0\rangle _{0}| a,0\rangle _{2}|a,0\rangle _{3}| 00\rangle _{f}\rbrace . \end{aligned}$$
(23)

Hamiltonian \(H^{(3)}(t)\) is block-diagonal; two blocks connected to the initial state (20) have to be considered:

$$\begin{aligned} H^{(3)}(t)=\left( \begin{array}{cc} H^{'(3)}(t) &{}\quad \text {O} \\ \text {O} &{}\quad H^{\prime \prime (3)}(t) \\ \end{array}\right) , \end{aligned}$$
(24)

with

$$\begin{aligned} H^{'(3)}(t) = \left( \begin{array}{ccc} 0 &{}\quad \varOmega _b^{\prime \prime (1)} &{}\quad 0\\ \varOmega _b^{\prime \prime (1)}&{}\quad 0 &{}\quad \varOmega ^{'(1)}\\ 0&{} \varOmega ^{'(1)}&{}0 \end{array} \right) , \qquad H^{\prime \prime (3)}(t)= \left( \begin{array}{ccc} 0 &{} \varOmega _a^{\prime \prime (3)} &{} 0\\ \varOmega _a^{\prime \prime (3)}&{} 0 &{} \varOmega ^{'(3)}\\ 0&{} \varOmega ^{'(3)}&{}0 \end{array} \right) . \end{aligned}$$
(25)

Hamiltonians \(H^{'(3)}(t)\) and \(H^{\prime \prime (3)}(t)\) have two dark states as:

$$\begin{aligned} |D^{'(3)}(t)\rangle =C_1[ \varOmega ^{'(1)} |g,0\rangle _{1} | b,0\rangle _{2} | b,0\rangle _{3} | 00\rangle - \varOmega _b^{\prime \prime (1)} | b,0\rangle _{1} | b,0\rangle _{2} | b,0\rangle _{3} | 00\rangle _{f}], \end{aligned}$$
(26a)
$$\begin{aligned} |D^{\text {''}(3)}(t)\rangle =C_2[ \varOmega ^{'(3)} |a,0\rangle _{1} | a,0\rangle _{2} | g,0\rangle _{3} | 00\rangle - \varOmega _a^{\prime \prime (3)} | a,0\rangle _{1} | a,0\rangle _{2} | a,0\rangle _{3} | 00\rangle _{f}] , \end{aligned}$$
(26b)

where \(C_1\) and \(C_2\) are normalization factors.

Complete population transfer from states \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) and \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}] | 00\rangle _{f}\) respectively into the states \([|b,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}] | 00\rangle _{f}\) and \([|a,0\rangle _{1}| a,0\rangle _{2}| a,0\rangle _{3}] | 00\rangle _{f}\) is expected from the following behavior of the dark states:

$$\begin{aligned}&\lim _{t \rightarrow t_i}\left( \frac{\varOmega ^{'(1)}(t)}{\varOmega _b^{''(1)}(t)}\right) =0, \quad \lim _{t \rightarrow t_i}\left( \frac{\varOmega ^{'(3)}(t)}{\varOmega _a^{''(3)}(t)}\right) =0, \end{aligned}$$
(27a)
$$\begin{aligned}&\lim _{t \rightarrow t_f}\left( \frac{\varOmega _b^{''(1)}(t)}{\varOmega ^{'(1)}(t)}\right) =0, \quad \lim _{t \rightarrow t_f}\left( \frac{\varOmega _a^{''(3)}(t)}{\varOmega ^{'(3)}(t)}\right) =0, \end{aligned}$$
(27b)

Equations (27a) and (27b) are known as STIRAP conditions in three-state systems. In three-state STIRAP, the Stokes pulses \(\varOmega _b^{\text {''}(1)}(t), \varOmega _b^{\text {''}(3)}(t)\) precedes the pump pulses \(\varOmega ^{'(1)}(t), \varOmega ^{'(3)}(t)\) which ensures complete population transfer from states \(|g,0\rangle _{1} | b,0\rangle _{2} | b,0\rangle _{3} | 00\rangle\) and \(|a,0\rangle _{1} | a,0\rangle _{2} | g,0\rangle _{3} | 00\rangle\) respectively to states \(| b,0\rangle _{1} | b,0\rangle _{2} | b,0\rangle _{3} | 00\rangle _{f}\) and \(| a,0\rangle _{1} | a,0\rangle _{2} | a,0\rangle _{3} | 00\rangle _{f}\) as

$$\begin{aligned} |\psi _3{(t)}\rangle =\frac{1}{\sqrt{2}} [|a,0\rangle _{1}| a,0\rangle _{2} |a,0\rangle _{3} + | b,0\rangle _{1} | b,0\rangle _{2} |b,0\rangle _{3}] |00\rangle _{f}, \end{aligned}$$
(28)

corresponding to the three-atom GHZ state.

4 Creation of GHZ state in N-atom systems

In this section we first give details of each step to create the GHZ state for four-atom and five-atom systems. Then we generalize this process to the creation of GHZ state for N-atom systems.

4.1 Creation of four-atom GHZ state

We assume the initial state \(|\psi (t_{0})\rangle\) of atom-cavity-fiber system as:

$$\begin{aligned} |\psi (t_{0})\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}] | 000\rangle _{f}. \end{aligned}$$
(29)

Our goal is to transform the initial state of the system into a GHZ state as follows:

$$\begin{aligned} \vert \psi (t_{f})\rangle =\frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} | a,0\rangle _{3}| a,0\rangle _{4} + |b,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |b,0\rangle _{4}] | 000\rangle _{f}). \end{aligned}$$
(30)

To reach this result, the required four steps can be explained as follows

Step (1):

In the first step we use two laser pulses \(\varOmega _a^{(1)}, \varOmega _b^{(2)}\) and assume other laser pulses turned off. Using F-STIRAP technique in multistate systems, the initial state (29) evolves into the following state:

$$\begin{aligned} |\psi (t_{1})\rangle =\frac{1}{\sqrt{2}}([|a,0\rangle _{1} |g,0\rangle _{2} | b,0\rangle _{3}| g,0\rangle _{4} + |g,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |g,0\rangle _{4}] | 000\rangle _{f}). \end{aligned}$$
(31)

Step (2):

In this step we use two laser pulses \(\varOmega _b^{(3)}, \varOmega _a^{(2)}\) and assume other laser pulses turned off. Using STIRAP technique in multistate systems, the population of state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}] | 000\rangle _{f}\) is transferred into the state \([|a,0\rangle _{1}| a,0\rangle _{2}|g,0\rangle _{3}| g,0\rangle _{4}] | 000\rangle _{f}\). In this step the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}|g,0\rangle _{4}] | 000\rangle _{f}\) remains unchanged. In such a way that state (31) becomes

$$\begin{aligned} |\psi (t_{2})\rangle =\frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} |g,0\rangle _{3}| g,0\rangle _{4} + |g,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |g,0\rangle _{4}] | 000\rangle _{f}). \end{aligned}$$
(32)

Step (3):

In this step we use two laser pulses \(\varOmega _b^{(2)}, \varOmega _b^{(4)}\) and assume other laser pulses to be turned off. Using STIRAP technique in multistate systems, the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}] | 000\rangle _{f}\) is transferred into the state \([|g,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| b,0\rangle _{4}] | 000\rangle _{f}\). In this step the population of state \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}|g,0\rangle _{4}] | 000\rangle _{f}\) remains unchanged. In such a way that the state (32) becomes:

$$\begin{aligned} |\psi (t_{3})\rangle =\frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} |g,0\rangle _{3}| g,0\rangle _{4} + |g,0\rangle _{1} |g,0\rangle _{2} |b,0\rangle _{3} |b,0\rangle _{4}] | 000\rangle _{f}). \end{aligned}$$
(33)

Step (4):

In this step we use eight laser pulses \(\varOmega _b^{\prime \prime (1)}, \varOmega _b^{\prime \prime (2)}, \varOmega _a^{\prime \prime (3)}, \varOmega _a^{\prime \prime (4)}, \varOmega ^{'(1)}, \varOmega ^{'(2)}, \varOmega ^{'(3)}, \varOmega ^{'(4)}\) and assume other laser pulses turned off. Using STIRAP technique in three-state systems state (33) becomes (30) corresponding to the four atom GHZ state.

4.2 Creation of five-atom GHZ state

Here we assume the initial state \(|\psi (t_{0})\rangle\) of atom-cavity-fiber system as:

$$\begin{aligned} |\psi (t_{0})\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] | 0000\rangle _{f}. \end{aligned}$$
(34)

Our goal is to transform the initial state of the system into a five-atom GHZ state as follows:

$$\begin{aligned} \vert \psi (t_{f})\rangle= & {} \frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} | a,0\rangle _{3}| a,0\rangle _{4}| a,0\rangle _{5} \nonumber \\&+ |b,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |b,0\rangle _{4}|b,0\rangle _{5}] | 0000\rangle _{f}). \end{aligned}$$
(35)

The five steps of evolution can be explained as:

Step (1):

In this step we use two laser pulses \(\varOmega _a^{(1)}, \varOmega _b^{(2)}\) and assume other laser pulses turned off. Using F-STIRAP technique in multistate systems the initial state (34) becomes:

$$\begin{aligned} |\psi (t_{1})\rangle= & {} \frac{1}{\sqrt{2}}([|a,0\rangle _{1} |g,0\rangle _{2} | b,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}\nonumber \\&+ |g,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |g,0\rangle _{4}| b,0\rangle _{5}] | 000\rangle _{f}). \end{aligned}$$
(36)

Step (2):

In this step we use two laser pulses \(\varOmega _b^{(3)}, \varOmega _a^{(2)}\) and assume other laser pulses turned off. Using STIRAP technique in multistate systems the population of the state \([|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] |0000\rangle _{f}\) is transferred into the state \([|a,0\rangle _{1}| a,0\rangle _{2}|g,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] | 0000\rangle _{f}\). In this step the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}|g,0\rangle _{4}|b,0\rangle _{5}] | 0000\rangle _{f}\) remains unchanged, In such a way that the state (36) becomes:

$$\begin{aligned} |\psi (t_{2})\rangle= & {} \frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} |g,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5} \nonumber \\&+ |g,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3} |g,0\rangle _{4}|b,0\rangle _{5}] | 0000\rangle _{f}). \end{aligned}$$
(37)

Step (3):

In this step we use two laser pulses \(\varOmega _b^{(2)}, \varOmega _b^{(4)}\) and assume other laser pulses turned off. Using STIRAP technique in multistate systems, the population of state \([|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] |0000\rangle _{f}\) is transferred into the state \([|g,0\rangle _{1}| g,0\rangle _{2}|b,0\rangle _{3}| b,0\rangle _{4}| b,0\rangle _{5}] | 0000\rangle _{f}\). In this step the population of state \([|a,0\rangle _{1}| a,0\rangle _{2}|g,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] | 0000\rangle _{f}\) remains unchanged. The state (37) becomes:

$$\begin{aligned} |\psi (t_{3})\rangle= & {} \frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} |g,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5} \nonumber \\&+ |g,0\rangle _{1} |g,0\rangle _{2} |b,0\rangle _{3} |b,0\rangle _{4}|b,0\rangle _{5}] | 0000\rangle _{f}). \end{aligned}$$
(38)

Step (4):

In this step we use two laser pulses \(\varOmega _b^{(5)}, \varOmega _a^{(3)}\) and that other laser pulses turned off. Using STIRAP technique in multistate systems the population of state \([|a,0\rangle _{1}| a,0\rangle _{2}| g,0\rangle _{3}| g,0\rangle _{4}| b,0\rangle _{5}] |0000\rangle _{f}\) is transferred into the state \([|a,0\rangle _{1}| a,0\rangle _{2}|a,0\rangle _{3}| g,0\rangle _{4}| g,0\rangle _{5}] | 0000\rangle _{f}\). In this step the population of state \([|g,0\rangle _{1}| g,0\rangle _{2}|b,0\rangle _{3}| b,0\rangle _{4}| b,0\rangle _{5}] | 0000\rangle _{f}\) remains unchanged. In such a way that the state (38) becomes:

$$\begin{aligned} |\psi (t_{4})\rangle= & {} \frac{1}{\sqrt{2}}([|a,0\rangle _{1} |a,0\rangle _{2} |a,0\rangle _{3}| g,0\rangle _{4}| g,0\rangle _{5}\nonumber \\&+|g,0\rangle _{1} |g,0\rangle _{2} |b,0\rangle _{3} |b,0\rangle _{4}|b,0\rangle _{5}] | 0000\rangle _{f}). \end{aligned}$$
(39)

Step (5):

In this step we use eight laser pulses \(\varOmega _a^{\prime \prime (4)}, \varOmega _a^{\prime \prime (5)}, \varOmega _b^{\prime \prime (1)}, \varOmega _b^{\prime \prime (2)}, \varOmega ^{'(1)}, \varOmega ^{'(2)}, \varOmega ^{'(4)}, \varOmega ^{'(5)}\) and assume other laser pulses turned off. Using STIRAP technique in three-state systems, the state (39) becomes (35) which is a five-atom GHZ state.

4.3 Generalization to N-atom GHZ state

We can generalize our scheme to generate a GHZ state for N-atom system. According to the pervious section, atoms are initially prepared in a seperable state as:

$$\begin{aligned} |\psi (t_{0})\rangle =[|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| g,0\rangle _{4}, \ldots ,| b,0\rangle _{2i-1}, | g,0\rangle _{2i}] | 00\ldots 0\rangle _{f}. \end{aligned}$$
(40)

Similar to previous subsections we use N steps to create N-atom GHZ state. The N steps of evolution can be explained as follows:

Step (1):

In the first step we use F-STIRAP technique in multistate system. We use two laser pulses \(\varOmega _a^{(1)}, \varOmega _b^{(2)}\) and assume other laser pulses turned off. Using F-STIRAP technique in multistate systems, the initial state (40) becomes:

$$\begin{aligned} |\psi (t_{1})\rangle= & {} \frac{1}{\sqrt{2}}(|a,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}\ldots | b,0\rangle _{2i-1} | g,0\rangle _{2i}\nonumber \\&+|g,0\rangle _{1}| b,0\rangle _{2}| b,0\rangle _{3}\ldots | b,0\rangle _{2i-1} | g,0\rangle _{2i}) | 00\ldots 0\rangle _{f}. \end{aligned}$$
(41)

Steps (\(2,...,N-1\)):

In the \(2^{nd},\ldots , (N-1)th\) steps, we use STIRAP technique in multistate system. Using \(N-2\) steps of STIRAP technique in multistate systems , the state (41) becomes:

$$\begin{aligned} |\psi (t_{(N-1)})\rangle= & {} \frac{1}{\sqrt{2}}(|a,0\rangle _{1}\ldots | a,0\rangle _{N/2}| g,0\rangle _{(N/2)+1}\ldots |g,0\rangle _{N}\nonumber \\&+ |g,0\rangle _{1}\ldots | g,0\rangle _{N/2}| b,0\rangle _{(N/2)+1}\ldots | b,0\rangle _{N}) |00\ldots 0\rangle _{f}. \end{aligned}$$
(42)

Step (N):

In the final step we use the three-state STIRAP simultaneously on N atoms, similar to the final steps in previous subsections. At the end of thid interaction, the state of system (42) evolves to:

$$\begin{aligned} |\psi (t_{(N)})\rangle= & {} \frac{1}{\sqrt{2}}(|a,0\rangle _{1} |a,0\rangle _{2} |a,0\rangle _{3}\ldots | a,0\rangle _{N} \nonumber \\&+|b,0\rangle _{1} |b,0\rangle _{2} |b,0\rangle _{3}\ldots |b,0\rangle _{N}) | 00\ldots 0\rangle _{f}. \end{aligned}$$
(43)

which is an N-atom GHZ state.

5 Decoherence effects

One issue that needs to be addressed in more detail, is the role of cavity-fiber damping and atomic spontaneous emission. The technique of adiabatic passage is expected to be robust against the effects of spontaneous emission and cavity-fiber damping as the excited atomic states and cavity-fiber modes are not populated in the adiabatic limit. In practice, as can be observed in Figures, a very small fraction of the population does reach the excited atomic state and cavity-fiber mode. As a case study, in the first step of our scheme, cavity and fiber damping results from the population of states \(|g,1\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}, |g,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 10\rangle _{f},|g,0\rangle _{1}| g,1\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}\) and atomic spontaneous emission results from the population of states \(|e ,0\rangle _{1}| g,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}, |g,0\rangle _{1}| e,0\rangle _{2}| b,0\rangle _{3}| 00\rangle _{f}\). In this case, the cavity decay rate \(\kappa _c\), the fiber decay rate \(\kappa _f\) and the atomic spontaneous emission rate \(\varGamma\) appear on the diagonal of the effective Hamiltonian as follows:

$$\begin{aligned} H^{(1)}(t)=\left( \begin{array}{ccccccc} 0 &{}\quad \varOmega _a^{(1)}(t) &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \varOmega _a^{(1)}(t) &{}\quad -i\varGamma &{}\quad g &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad g &{}\quad -i\kappa _c &{}\quad \nu &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \nu &{}\quad -i\kappa _f &{}\quad \nu &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \nu &{}\quad -i\kappa _c &{}\quad g &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad g &{}\quad -i\varGamma &{}\quad \varOmega _b^{(2)}(t)\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varOmega _b^{(2)}(t) &{}\quad 0\\ \end{array}\right) , \end{aligned}$$
(44)

Figure 6 shows that, as expected, the final fidelity \(|\langle \psi (t_f)|\psi _1 \rangle |^2\) of the desired state \(|\psi _1\rangle\) decreases for increasing \(\kappa _c=\kappa _f=\kappa\) and \(\varGamma\). However the final fidelity is not very sensitive to increase in \(\kappa\) and \(\varGamma\) when the adiabatic limit is well satisfied.

Fig. 6
figure 6

Final fidelity of the state \(|\psi _1\rangle\) as a function of \(\kappa\) and \(\varGamma\) with pulse parameters of Fig. 4. We observe that the effects of cavity-fiber decay and spontaneous emission are not very destructive in adiabatic limit

Full size image

6 Conclusion

In conclusion, we proposed a robust scheme for deterministic generation of GHZ states for any number of atoms individually trapped in spatially separated cavities connected with optical fibers via adiabatic passage by appropriately tailoring the external driving laser fields. Using a sequence of pulsed laser field, atom-cavity-fiber systems are always in the dark states. Losses due to the cavity decay are efficiently suppressed by employing STIRAP technique in multistate systems and appropriately designed atom-field couplings in which the populations of the intermediate states can be damped by large intermediate couplings. Moreover, it constitutes a decoherence-free method in the sense that the excited atomic states with short life times are not populated during the process. It was shown that this method can be used for any number of atoms in order to generate N-atom GHZ states \((N\ge 3)\) in N-steps. finally, we discuss the experimental feasibility and as a result, the present scheme is promising for generating an N-qubit GHZ state with the current techniques.