1 Introduction

Quantum entanglement is the soul of quantum mechanics. The manipulation of entangled states is not only the basic task for quantum information processing (QIP) [1, 2], but also fundamental for demonstrating quantum nonlocality [3, 4]. In general, entanglement of multi-qubit is more useful for QIP and shows more nonclassical effects. There are two main kinds of entangled states for three-qubit entanglement, the W state [5] and the Greenberger–Horne–Zeilinger (GHZ) state [4]. Among these two kinds of tripartite entanglement, the W state attracts much attention since it can retain bipartite entanglement when any one of the qubits is traced out, and it has the advantages in quantum teleportation [6]. Thus, many theoretical works have been devoted to the generation of W states via different techniques [7–26]. Among these techniques, the resonant interaction [16, 17] and the stimulated Raman scattering involving adiabatic passage (STIRAP) [18–21] have attracted attention in recent years. However, the schemes based on resonant interaction are very fast, but they depend on the exact knowledge of all parameters and require controlling the interaction time accurately. Although the schemes based on adiabatic passage are robust against experimental parameters and do not require controlling the interaction time accurately, the operation time required to get the goal is relatively long, which may lead to larger decoherence effects. In order to combine advantages of the resonant interaction and the adiabatic passage, a famous technique named “shortcuts to adiabatic passage” (STAP) [27–31], which can fast and robustly generate entangled states, has been extended in recent years.

The “transitionless quantum driving” (TQD) [31] is a well-known method to construct shortcuts to speed up adiabatic processes effectively. Generally speaking, the laser pulses are not strongly limited by using TQD to construct shortcuts, but a nonexistent Hamiltonian in real experiment is necessary by using this method. Apparently, if we take no account of that whether the constructed Hamiltonian in experiment is existent or not, TQD is an effective method to fast generate entangled states and implement quantum processing. Because for any time-dependent original Hamiltonian \(H_0(t)\), TQD provides a very effective method to construct a Hamiltonian H(t) which accurately derives the instantaneous eigenstates of \(H_0(t)\). Moreover, the transitions between them do not occur at all during the evolution of the whole system regardless of the rate of change. In other words, the instantaneous eigenstates of \(H_0(t)\) can be regarded as truly moving eigenstates of H(t). As we mentioned above, the outcome as the same as the adiabatic process can be obtained by using TQD in a shorter time. In view of the advantages of TQD, it is worth to finding ways to overcome the problem that the Hamiltonian H(t) designed by suing TQD does not exist in experiment. So far, lots of shortcut schemes have been proposed in theory and implemented in experiment [30–53].

It is worth noticing that Chen et al. [33] first constructed shortcuts to perform fast and noise-resistant populations transfer in multi-particle systems, by combining “Lewis–Riesenfeld invariants” with “quantum Zeno dynamics” (QZD). Soon after, a lot of schemes are rapidly proposed to perform fast and noise-resistant QIP [35–37, 54–56], by suing similar ideas with slightly breaking the Zeno condition down. However, most of the above shortcut schemes are based on a single cavity, which is still a challenge to manipulate a large number of qubits. This is due to the fact that the spatial separation between neighboring qubits decreases as the number of qubits increases, and thus, individual addressing becomes increasingly difficult. The coupled-cavity systems [57–64] are considered as a suitable candidate for the solution of the above deficiency. In view of that we wonder if it is possible to use TQD to construct shortcuts for generation of multi-atom entanglement, i.e., W states, in coupled cavities.

In this paper, we construct STAP to fast generate W states in spatially separated cavities by combining “TQD” with “QZD.” The scheme has the following advantages: (1) The interaction time required for the creation of the W state is much shorter than the adiabatic passage. (2) Numerical simulations show that the decoherence such as atomic spontaneous emission, cavity losses and the fiber photon leakages has little influence on this scheme. (3) Individual addressing becomes relatively easy in coupled cavities. (4) This scheme can be generalized to generation of N-atom W states as well.

This paper is structured as follows. In Sect. 2, we construct a theoretical model by using QZD. In Sect. 3, we construct a shortcut passage based on TQD and show how to use the constructed shortcut to fast generate W states. In Sect. 4, N-atom W states are generated in one step by the same principle. A discussion on experimental feasibility and a summary are given in Sect. 5.

2 Theoretical model

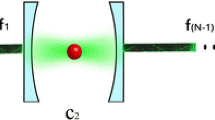
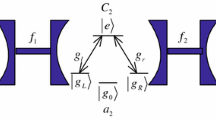
As shown in Fig. 1a, b, we consider that three identical \(\Lambda \)-type atoms are trapped in three spatially separated cavities \(C_1, C_2\) and \(C_3\), respectively. The cavities are linked by optical fibers \(f_1\) and \(f_2\). Each atom has an excited state \(|e\rangle \) and two ground states \(|f\rangle \) and \(|g\rangle \). The atomic transition \(|f\rangle \leftrightarrow |e\rangle \) is resonantly driven by classical field \(\varOmega (t)\), and the transition \(|g\rangle \leftrightarrow |e\rangle \) resonantly coupled to the cavity with coupling coefficient \(\lambda \). In the short-fiber limit, i.e., \(2L\nu /(2\pi c)\ll 1\) (where L denotes the fiber length, c denotes the speed of light, and \(\nu \) denotes the decay of the cavity field into a continuum of fiber mode), only one resonant fiber mode interacts with the cavity mode [65]. Under the rotating-wave approximation (RWA), the interaction Hamiltonian for this system can be written as \((\hbar =1)\)

$$\begin{aligned} H_{o}= & {} H_{al}+H_{ac},\nonumber \\ H_{al}= & {} \sum _{k=1}^3{\varOmega _k(t)|e\rangle _k\langle f|+H.c.},\nonumber \\ H_{ac}= & {} \sum _{k=1}^3{\lambda _ka_k|e\rangle _k\langle g|+\upsilon _1b_1^{\dag }(a_1+a_2)+\upsilon _2b_2^{\dag }(a_2+a_3)+H.c.}, \end{aligned}$$
(1)

where \(a_k^{\dag }\) and \(a_k\) denote creation and annihilation operators of the cavities \(C_k (k=1,2,3)\), respectively; \(b_j^{\dag }\) and \(b_j\) denote the creation and annihilation operators associated with the resonant mode of fiber \(f_j\) \((j=1,2)\), respectively. For the sake of simplicity, we assume \(\varOmega _2=\varOmega _x, \varOmega _1=\varOmega _3=\varOmega _y, \lambda _k=\lambda \) and \(\upsilon _j=\upsilon \). If we assume the initial state of the system is in \(|g,f,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}\), the whole system evolves in the subspace \(\forall \) spanned by:

$$\begin{aligned} |\psi _1\rangle= & {} |g,f,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2},\nonumber \\ |\psi _2\rangle= & {} |g,e,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}, \nonumber \\ |\psi _3\rangle= & {} |g,g,g\rangle _{1,2,3}|1,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2},\nonumber \\ |\psi _4\rangle= & {} |g,g,g\rangle _{1,2,3}|0,1,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}, \nonumber \\ |\psi _5\rangle= & {} |g,g,g\rangle _{1,2,3}|0,0,1\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2},\nonumber \\ |\psi _6\rangle= & {} |g,g,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|1,0\rangle _{f1,f2}, \nonumber \\ |\psi _7\rangle= & {} |g,g,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,1\rangle _{f1,f2},\nonumber \\ |\psi _8\rangle= & {} |g,g,e\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}. \nonumber \\ |\psi _9\rangle= & {} |g,g,f\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2},\nonumber \\ |\psi _{10}\rangle= & {} |e,g,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}, \nonumber \\ |\psi _{11}\rangle= & {} |f,g,g\rangle _{1,2,3}|0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}. \end{aligned}$$
(2)

Under the Zeno condition \(\varOmega _x, \varOmega _y\ll \sqrt{3}\lambda \), the Hilbert subspace \(\forall \) is split into seven Zeno subspaces according to the degeneracy of eigenvalues of \(H_{ac}\),

$$\begin{aligned} Z_0= & {} \{|\phi _1\rangle ,|\phi _2\rangle ,|\phi _3\rangle , |\phi _4\rangle ,|\phi _5\rangle \},\nonumber \\ Z_1= & {} \{|\phi _6\rangle \},\quad Z_2=\{|\phi _7\rangle \},\quad Z_3=\{|\phi _8\rangle \}, \nonumber \\ Z_4= & {} \{|\phi _9\rangle \},\quad Z_5=\{|\phi _{10}\rangle \},\quad Z_6=\{|\phi _{11}\rangle \}, \end{aligned}$$
(3)

where the eigenstates of \(H_{ac}\) are

$$\begin{aligned} |\phi _1\rangle= & {} |\psi _1\rangle ,\nonumber \\ |\phi _2\rangle= & {} \frac{\upsilon }{\sqrt{2\upsilon ^2+\lambda ^2}}\left[ |\psi _2\rangle +\frac{\lambda }{\upsilon }|\psi _7\rangle +|\psi _8\rangle \right] ,\nonumber \\ |\phi _3\rangle= & {} |\psi _9\rangle ,\nonumber \\ |\phi _4\rangle= & {} \frac{\upsilon }{\sqrt{2\upsilon ^2+\lambda ^2}}\left[ |\psi _2\rangle -\frac{\lambda }{\upsilon }|\psi _6\rangle +|\psi _{10}\rangle \right] , \nonumber \\ |\phi _5\rangle= & {} |\psi _{11}\rangle ,\nonumber \\ |\phi _6\rangle= & {} \frac{1}{\sqrt{6}}\left[ -|\psi _2\rangle +|\psi _3\rangle -|\psi _4\rangle -|\psi _5\rangle +|\psi _8\rangle +|\psi _{10}\rangle \right] , \nonumber \\ |\phi _7\rangle= & {} \frac{1}{\sqrt{6}}[-|\psi _2\rangle -|\psi _3\rangle +|\psi _4\rangle +|\psi _5\rangle +|\psi _8\rangle +|\psi _{10}\rangle ], \nonumber \\ |\phi _8\rangle= & {} \frac{\lambda }{2\sqrt{\upsilon ^2+\lambda ^2}}\left[ -\frac{\sqrt{\upsilon ^2+\lambda ^2}}{\lambda }|\psi _4\rangle +\frac{\sqrt{\upsilon ^2+\lambda ^2}}{\lambda }|\psi _5\rangle +\frac{\upsilon }{\lambda }|\psi _6\rangle \right. \nonumber \\&\left. -\,\frac{\upsilon }{\lambda }|\psi _7\rangle -|\psi _8\rangle +|\psi _{10}\rangle \right] , \nonumber \\ |\phi _9\rangle= & {} \frac{\lambda }{2\sqrt{\upsilon ^2+\lambda ^2}}\left[ \frac{\sqrt{\upsilon ^2-\lambda ^2}}{\lambda }|\psi _4\rangle -\frac{\sqrt{\upsilon ^2+\lambda ^2}}{\lambda }|\psi _5\rangle +\frac{\upsilon }{\lambda }|\psi _6\rangle \right. \nonumber \\&\left. -\,\frac{\upsilon }{\lambda }|\psi _7\rangle -|\psi _8\rangle +|\psi _{10}\rangle \right] , \nonumber \\ |\phi _{10}\rangle= & {} \frac{\lambda }{2\sqrt{3(3\upsilon ^2+\lambda ^2)}}\left[ 2|\psi _2\rangle -\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }|\psi _3\rangle -\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }|\psi _4\rangle \right. \nonumber \\&\left. -\,\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }|\psi _5\rangle +\frac{3\upsilon }{\lambda }|\psi _6\rangle +\frac{3\upsilon }{\lambda } |\psi _7\rangle +|\psi _8\rangle +|\psi _{10}\rangle \right] , \nonumber \\ |\phi _{11}\rangle= & {} \frac{\lambda }{2\sqrt{3(3\upsilon ^2+\lambda ^2)}} \left[ 2|\psi _2\rangle +\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }| \psi _3\rangle +\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }|\psi _4\rangle \right. \nonumber \\&\left. +\,\frac{2\sqrt{3\upsilon ^2+\lambda ^2}}{\lambda }|\psi _5\rangle +\frac{3\upsilon }{\lambda }|\psi _6\rangle + \frac{3\upsilon }{\lambda }|\psi _7\rangle +| \psi _8\rangle +|\psi _{10}\rangle \right] , \end{aligned}$$
(4)

and the corresponding eigenvalues are

$$\begin{aligned} \varsigma _0= & {} 0, \varsigma _1=-\lambda ,\quad \varsigma _2=\lambda ,\quad \varsigma _3=-\sqrt{\upsilon ^2+\lambda ^2},\quad \varsigma _4=\sqrt{\upsilon ^2+\lambda ^2}, \nonumber \\ \varsigma _5= & {} -\sqrt{3\upsilon ^2+\lambda ^2},\quad \varsigma _6=\sqrt{3\upsilon ^2+\lambda ^2}. \end{aligned}$$
(5)

Under the Zeno condition, we obtain the effective Hamiltonian governing the evolution

$$\begin{aligned} H_\mathrm{eff}=\delta \varOmega _x(|\phi _2\rangle +|\phi _4\rangle ) \langle \psi _1|+\delta \varOmega _y(|\phi _2\rangle \langle \psi _9| +|\phi _4\rangle \langle \psi _{11}|)+H.c., \end{aligned}$$
(6)

where \(\delta =\frac{\upsilon }{\sqrt{2\upsilon ^2+\lambda ^2}}\) is the normalization factors of the eigenstates \(|\phi _2\rangle \) and \(|\phi _4\rangle \). Then, we use four orthogonal vectors \(|\mu _+\rangle =\frac{1}{\sqrt{2}}(|\phi _2\rangle +|\phi _4\rangle ), |\mu _-\rangle =\frac{1}{\sqrt{2}}(|\phi _2\rangle -|\phi _4\rangle ), |\vartheta _+\rangle =\frac{1}{\sqrt{2}}(|\psi _9\rangle +|\psi _{11}\rangle )\) and \(|\vartheta _-\rangle =\frac{1}{\sqrt{2}}(|\psi _9\rangle -|\psi _{11}\rangle )\) to rewrite the Hamiltonian in Eq. (6) as

$$\begin{aligned} H_\mathrm{eff}^1=\sqrt{2}\delta \varOmega _x|\mu _+\rangle \langle \psi _1|+\delta \varOmega _y|\mu _+\rangle \langle \vartheta _+|+\delta \varOmega _y|\mu _-\rangle \langle \vartheta _-|+H.c.. \end{aligned}$$
(7)

It is obvious that when the initial state is \(|\psi _1\rangle \), the terms containing \(|\mu _-\rangle \) and \(|\vartheta _-\rangle \) are negligible because they are decoupled to the time evolution of initial state. Then, we can obtain the final effective Hamiltonian

$$\begin{aligned} H_\mathrm{fe}=\sqrt{2}\delta \varOmega _x|\mu _+\rangle \langle \psi _1|+\delta \varOmega _y|\mu _+\rangle \langle \vartheta _+|+H.c., \end{aligned}$$
(8)

which can be treated as a simple three-level system with an excited state \(|\mu _+\rangle \) and two ground states \(|\psi _1\rangle \) and \(|\vartheta _+\rangle \). Then, we obtain the instantaneous eigenstates of the final effective Hamiltonian \(H_\mathrm{fe}\)

$$\begin{aligned} |n_0(t)\rangle= & {} \cos \theta |\psi _1\rangle +\sin \theta |\vartheta _+\rangle ,\nonumber \\ |n_\pm (t)\rangle= & {} \frac{1}{\sqrt{2}}(\sin \theta |\psi _1\rangle \pm \sqrt{2}\beta |\mu _+\rangle -\cos \theta |\vartheta _+\rangle ), \end{aligned}$$
(9)

and corresponding eigenvalues \(\iota _0=0, \iota _\pm =\pm \delta \beta \), respectively. Here, \(\beta =\sqrt{2\varOmega _x^2+\varOmega _y^2}\) and \(\theta =\arctan -\frac{\sqrt{2}\varOmega _x}{\varOmega _y}\). It is obvious that the state \(|\psi _1\rangle =|n_0(0)\rangle \) would follow \(|n_0(t)\rangle \) closely, if the adiabatic condition \(|\left\langle n_0(t)|\partial _t n_\pm (t)\rangle \right| \ll |\iota _\pm |\) is fulfilled. However, it is undesirable to obtain the target state, because this process would take quite a long time.

Fig. 1
figure 1

Experimental setup and level configuration for each atom

Full size image

3 The shortcut scheme is proposed to generate W states based on TQD

3.1 Construct STAP by using TQD

As far as we know, the instantaneous states \(|n_k(t)\rangle \) \((k=0,\pm )\) we mentioned in Eq. (9) do not meet the Schrödinger equation \(i\partial _t|n_k(t)\rangle =H_\mathrm{fe}(t)|n_k(t)\rangle \). The key to solving the problem is to construct shortcuts for a system governed by \(H_0(t)\) with finding out a Hamiltonian H(t) which drives the instantaneous eigenstates \(|n_k(t)\rangle \) of \(H_0(t)\) exactly. According to the Berry’s transitionless tracking algorithm [31], the Hamiltonian H(t) can be reverse engineered from \(H_0(t)\). And disregarding the effect of phases, we obtain the simplest Hamiltonian H(t) in the form of

$$\begin{aligned} H(t)=i\sum _{k=0,\pm }|\partial _tn_k(t)\rangle \langle n_k(t)|. \end{aligned}$$
(10)

Then, we can use transitionless tracking algorithm to construct the Hamiltonian that exactly drives the eigenstates of \(H_\mathrm{fe}(t)\),

$$\begin{aligned} H_\mathrm{CCD}=i\dot{\theta }|\vartheta _+\rangle \langle \psi _1|+H.c., \end{aligned}$$
(11)

where \(\dot{\theta }=\sqrt{2}[\dot{\varOmega }_y(t) \varOmega _x(t)-\dot{\varOmega }_x(t)\varOmega _y(t)]/\beta ^2\). However, it is necessary to find out an alternative physically feasible (APF) system whose effective Hamiltonian is equivalent to \(H_\mathrm{CCD}\), because obtaining the CDD Hamiltonian H(t) is an outstanding challenge in present experimental condition. The model we used with three atoms trapped in coupled cavity is as the same as Fig. 1a. As shown in Fig. 1c, we make all the resonant atomic transitions into nonresonant atomic transitions with detuning \(\varDelta \). The interaction Hamiltonian for the present system reads

$$\begin{aligned} \tilde{H}_{o}= & {} \tilde{H}_{al}+\tilde{H}_{ac}+H_e,\nonumber \\ \tilde{H}_{al}= & {} \sum _{k=1}^3{\tilde{\varOmega }_k(t)|e\rangle _k\langle f|+H.c.},\\\tilde{H}_{ac}= & {} \sum _{k=1}^3{\lambda a_k|e\rangle _k\langle g|+\upsilon b_1^{\dag }(a_1+a_2)+\upsilon b_2^{\dag }(a_2+a_3)+H.c.},\nonumber \\ H_{e}= & {} \sum _{k=1}^3{|e\rangle _k\langle e|}. \end{aligned}$$
(12)

For the sake of simplicity, we set \(\tilde{\varOmega }_2=\tilde{\varOmega }_x, \tilde{\varOmega }_1=\tilde{\varOmega }_3=\tilde{\varOmega }_y, \tilde{\lambda }_k=\lambda \) and \(\tilde{\upsilon }_k=\upsilon \). Then, for the Hamiltonian in Eq. (12), performing similar processes from Eqs. (1)–(8), we can approximatively neglect the terms containing the high oscillating frequencies. Meanwhile, the terms that are decoupled to the time evolution of initial state can also be neglected. We obtain an effective Hamiltonian for present system

$$\begin{aligned} \tilde{H}_\mathrm{eff}=(\sqrt{2}\delta \tilde{\varOmega }_x| \mu _+\rangle \langle \psi _1|+\delta \tilde{\varOmega }_y| \mu _+\rangle \langle \vartheta _+|+H.c.)+3\varDelta \delta ^2|\mu _+\rangle \langle \mu _+|, \end{aligned}$$
(13)

where \(\delta =\frac{\upsilon }{\sqrt{2\upsilon ^2+\lambda ^2}}\). Then, we adiabatically eliminate the state \(|\mu _+\rangle \) by using second-order perturbation approximation. The effective Hamiltonian becomes

$$\begin{aligned} \tilde{H}_\mathrm{eff}^1=\frac{2|\tilde{\varOmega }_x|^2}{3\varDelta } |\psi _1\rangle \langle \psi _1|+ \frac{|\tilde{\varOmega }_y|^2}{3\varDelta }|\vartheta _+ \rangle \langle \vartheta _+| +\left( \frac{\sqrt{2}\tilde{\varOmega }_x \tilde{\varOmega }_y^*}{3\varDelta }|\vartheta _+ \rangle \langle \psi _1|+H.c.\right) .\nonumber \\ \end{aligned}$$
(14)

When we choose \(\tilde{\Omega }_x=\tilde{\Omega }_y^{*}=\Omega _{s}\), and \(\tilde{\varOmega }_x=\frac{i\varOmega _s}{\sqrt{2}}\), the front two terms caused by Stark shift being removed, the above Hamiltonian becomes

$$\begin{aligned} \tilde{H}_\mathrm{fe}=i\varOmega |\vartheta _+\rangle \langle \psi _1|+H.c., \end{aligned}$$
(15)

where \(\varOmega =\frac{\varOmega _s^2}{3\varDelta }\). If we set \(\varOmega =\dot{\theta }\), we can obtain \(\tilde{H}_\mathrm{fe}=H_\mathrm{CCD}\). That means, under condition \(\tilde{\varOmega }_x, \tilde{\varOmega }_y\) \(\ll \) \(\sqrt{3}\lambda , \sqrt{3}\varDelta \), the Hamiltonian for speeding up the adiabatic dark-state evolution governed by \(H_0\) has been constructed.

3.2 Generation of W states based on STAP

We will show that the generation of the W state based on STAP is much faster than the adiabatic passage. To generate a three-atom W state, we choose the Rabi frequencies as

$$\begin{aligned} \varOmega _x(t)= & {} \varOmega _0\sin \alpha \exp \left[ \frac{-(t-t_0-t_f/2)^{2}}{t_c^{2}}\right] , \nonumber \\ \varOmega _y(t)= & {} \varOmega _0\exp \left[ \frac{-(t+t_0-t_f/2)^{2}}{t_c^{2}}\right] +\varOmega _0\cos \alpha \exp \left[ \frac{-(t-t_0-t_f/2)^{2}}{t_c^{2}}\right] ,\nonumber \\ \end{aligned}$$
(16)

where \(\varOmega _0\) is the amplitude and \(\{t_0,t_c\}\) are related parameters. In order to meet the limited conditions, the time-dependent \(\varOmega _x(t)\) and \(\varOmega _y(t)\) are gotten as shown in Fig. 2 with parameters \(\tan \alpha =1, t_0=0.15t_f\) and \(t_c=0.2t_f\). As we mentioned above, the \(\varOmega _s\) is given

$$\begin{aligned} \varOmega _s=\sqrt{3\varDelta \dot{\theta }}= \sqrt{\frac{3\sqrt{2}\varDelta (\dot{\varOmega }_y \varOmega _x-\dot{\varOmega }_x\varOmega _y)}{\beta ^2}}. \end{aligned}$$
(17)

If we set two dimensionless parameters

$$\begin{aligned} \eta _1= & {} \frac{t't_f-t_0-0.5t_f}{t_c}, \nonumber \\ \eta _2= & {} \frac{t't_f+t_0-0.5t_f}{t_c}, \end{aligned}$$
(18)

where \(t'=\frac{t}{t_f}\). Then, putting Eqs. (16) and (18) into Eq. (17), we obtain

$$\begin{aligned} \varOmega _s=\sqrt{\frac{6\sqrt{2}\varDelta R^2}{t_f}}. \end{aligned}$$
(19)

where

$$\begin{aligned} R=\sqrt{\frac{\eta _1\varOmega _x\varOmega _y- \varOmega _x\varOmega _0(\eta _2e^{-\eta _2^2}+ \cos \alpha \eta _1e^{-\eta _1^2})}{2\varOmega _x^2+\varOmega _y^2}}. \end{aligned}$$
(20)

We find out the amplitude of \(\varOmega _s\) is mainly dominated by \(\chi =\sqrt{\frac{6\sqrt{2}\varDelta }{t_f}}\), since the amplitude of R is close to 1. Therefore, the limited conditions become

$$\begin{aligned} \sqrt{\frac{6\sqrt{2}\varDelta }{t_f}}\ll \sqrt{3}\lambda \Rightarrow t_f\gg \frac{2\sqrt{2}\varDelta }{\lambda ^2},\\\\\sqrt{\frac{6\sqrt{2}\varDelta }{t_f}}\ll \sqrt{3}\varDelta \Rightarrow t_f\gg \frac{2\sqrt{2}}{\varDelta }. \end{aligned}$$
(21)
Fig. 2
figure 2

Dependence on \(t/t_f\) of \(\varOmega _x/\varOmega _0\) and \(\varOmega _y/\varOmega _0\)

Full size image

In order to meet the Zeno condition, it is better to choose a smaller \(\varDelta \) if the interaction time \(t_f\) is short, when \(\lambda \) is a constant value. However, a larger \(\varDelta \) is still required due to need to meet the large detuning condition. This can be demonstrated in Fig. 3 which shows the fidelity of the W state versus parameters \(\lambda t_f\) and \(\varDelta /\lambda \). As shown in Fig. 3, a long operation time \(t_f\) is still required if \(\varDelta \) is too small or too large. The fidelity F of the state is defined as \(F=\left| \langle \psi |\rho (t_f)|\psi \rangle \right| \), where \(\rho (t_f)\) is the density operator of the given system when \(t=t_f\). Then, in order to verify the shortcut scheme effectively, we contrast the performances of population transfer from the initial state \(|\psi _1\rangle \). The time-dependent population for any state \(|\psi \rangle \) is given through relationship \(P=\left| \langle \psi |\rho (t)|\psi \rangle \right| \), where \(\rho (t)\) is the corresponding time-dependent density operator. Figure 4a shows that a perfect populations transfer can be achieved with suitable parameters \(\{\varDelta =3\lambda ,t_f=75/\lambda \}\). Unfortunately, slightly breaking the Zeno condition leads to a slight failure of the approximation during the stepped-up evolution. Wherefore, the parameter should be slightly corrected, i.e., a related parameter \((\tilde{\varOmega }_x\rightarrow 1.05\tilde{\varOmega }_x)\). We plot the time evolution of the populations in intermediate states \(|\tau \rangle =\frac{1}{\sqrt{3}}(|\psi _2\rangle +|\psi _8\rangle +|\psi _{10}\rangle ), |\tau _+\rangle =\frac{1}{\sqrt{3}}(|\psi _3\rangle +|\psi _4\rangle +|\psi _5\rangle )\) and \(|\tau _-\rangle =\frac{1}{\sqrt{2}}(|\psi _6\rangle +|\psi _7\rangle )\) in Fig. 4b to prove this. Figure 4b shows that the intermediate states can be effectively neglected, because the populations of the intermediate states are almost zero. In Fig. 5, we compare the fidelity between our scheme and adiabatic scheme. Generally speaking, the interaction time required for the creation of the W state via adiabatic passage becomes more and more shorter with increasing of \(\varOmega _0\), but the RWA is not longer effective for the system if \(\varOmega _0\) is relatively large. Figure 5 shows that the interaction time via adiabatic passage is still much longer than that via STAP, even if we choose \(\varOmega _0=0.5\lambda \). That means our scheme is much faster than the adiabatic passage. However, it is known to all that the fidelity of the W state is influenced with the mutative parameters. The fidelity of the W state versus the variation \(\delta \chi \) and \(\delta T\) is plotted in Fig. 6. Here, we define \(\delta x=x'-x\) as the deviation of any parameter x, where \(x'\) is the actual value and x is the ideal value. As shown in Fig. 6, the fidelity almost keeps unchanging with the variation \(\delta T (T=85/\lambda )\). Figure 6 also shows a deviation \(|\delta \chi /\chi |=5\,\%\) which means the variation in the amplitude of \(\varOmega _s\) only causes a reduction about 1.5 % in the fidelity. That is to say, our scheme is robust against variations in the experimental parameters.

Fig. 3
figure 3

Fidelity of the W state versus the interaction time \(\lambda t_f\) and the detuning \(\varDelta /\lambda \) in the shortcut scheme

Full size image
Fig. 4
figure 4

a Time evolution of the populations for the states \(|\psi _1\rangle , |\psi _9\rangle \) and \(|\psi _{11}\rangle \) with {\(t_f=75/\lambda \) and \(\varDelta =3\lambda \)}. b Time evolution of the populations for the intermediate states \(|\tau \rangle , |\tau _+\rangle \) and \(|\tau _-\rangle \) with {\(t_f=75/\lambda \) and \(\varDelta =3\lambda \)}

Full size image
Fig. 5
figure 5

Comparison between the fidelity of the W state via STIP and STIRAP

Full size image
Fig. 6
figure 6

Fidelity of the W state via STAP versus the variations of T and \(\chi \)

Full size image

Now, we will investigate the influence of various decoherence caused by the atomic spontaneous emission, cavity losses and the fiber photon leakages. The master equation of the whole system reads

$$\begin{aligned} \dot{\rho }= & {} -i[H_0,\rho ]+\Sigma _{k=1}^3\frac{\gamma _k}{2} \left( 2\sigma _k^-\rho \sigma _k^+-\sigma _k^+ \sigma _k^-\rho -\rho \sigma _k^+\sigma _k^-\right) \nonumber \\&+\,\Sigma _{k=1}^3\frac{\kappa _k}{2}\left( 2a_k^-\rho a_k^+-a_k^+a_k^-\rho -\rho a_k^+a_k^-\right) \nonumber \\&+\,\Sigma _{k=1}^2\frac{\beta _k}{2}\left( 2b_k^-\rho b_k^+-b_k^+b_k^-\rho -\rho b_k^+ b_k^-\right) , \end{aligned}$$
(22)

where \(\gamma _k\) denotes the atomic spontaneous decay rate of the kth atom; \(\kappa _k\) and \(\beta _k\) denote the decay rates of the kth cavity and fiber, respectively. For simplicity, we set \(\gamma _1=\gamma _2=\gamma _3=\gamma , \kappa _1=\kappa _2=\kappa _3=\kappa \) and \(\beta _1=\beta _2=\beta \). The master equation can be numerically solved in the subspace \(\tilde{\forall }\in \{\forall , |\psi _{12}\rangle =|g,g,g\rangle _{1,2,3} |0,0,0\rangle _{c1,c2,c3}|0,0\rangle _{f1,f2}\}\). Then, we plot the fidelity versus the dimensionless parameters \(\gamma /\lambda , \kappa /\lambda \) and \(\beta /\lambda \) in Fig. 7. We can see the fidelity is almost unaffected by the fiber loss rate \(\beta \), because the fiber length is very short. Thus, the cavity decay and the atomic spontaneous emission decay become the main sources of decoherence. It is necessary to focus on the influences of the atomic spontaneous emission rate \(\gamma \) and the cavity decay rate \(\kappa \). As shown in Fig. 8, the scheme is more sensitive to atomic spontaneous emissions than the cavity decay, since the Zeno condition is not satisfied faultlessly. Therefore, the populations of intermediate states (\(|\tau \rangle , |\tau _+\rangle \) and \(|\tau _-\rangle \)) cannot be completely suppressed. Fortunately, we still can create a three-atom W state with a high fidelity 96.27 %, even if we set \(\gamma =\kappa =0.01\lambda \). This means the scheme is robust since the fidelity decreases slowly.

Fig. 7
figure 7

Fidelity of the W state via STAP versus the decoherence parameters \(\gamma /\lambda , \kappa /\lambda \) and \(\beta /\lambda \) with \(t_f=75/\lambda \) and \(\varDelta =3\lambda \)

Full size image
Fig. 8
figure 8

Dependences on the decoherence parameters \(\gamma /\lambda \) and \(\kappa /\lambda \) of the fidelity of the W state via STAP with \(t_f=75/\lambda \) and \(\varDelta =3\lambda \)

Full size image

4 Generation of N-atom W states by STAP

In this section, we give a brief description about generation of N-atom \((N>3)\) W states in a similar system by the same principle. As shown in Fig. 9, we assume that N identical \(\Lambda \)-type atoms are trapped in N spatially separated cavities \(C_1, C_2, \ldots , C_N\), respectively. The cavities are linked by optical fibers \(f_1, f_2, \ldots , f_{N-1}\). The level configurations of the atoms are the same as we mentioned in Fig. 1b. Then, the Hamiltonian for the system in the interaction picture reads

$$\begin{aligned} \acute{H}_{o}= & {} \acute{H}_{al}+\acute{H}_{ac}+\acute{H}_{e}, \\\\\acute{H}_{al}= & {} \sum _{k=1}^N{\varOmega _k(t)|e\rangle _k\langle f|+H.c.},\nonumber \\ \acute{H}_{ac}= & {} \sum _{k=1}^N{\lambda _ka_k|e\rangle _k\langle g|}+\sum _{k=1}^{N-1}\upsilon _{k}b_{k}^{\dag }(a_1+a_{k+1})+H.c., \nonumber \\ \acute{H}_{e}= & {} \sum _{k=1}^N{|e\rangle _k\langle e|}. \end{aligned}$$
(23)

We assume the initial state is \(|f,g,\ldots ,g\rangle _{1,2,\ldots ,N} |0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N}|0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}\). The whole system evolves in the subspace spanned \(\acute{\forall }\) by

$$\begin{aligned} |\acute{\psi }_1\rangle= & {} |f,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\ |\acute{\psi }_2\rangle= & {} |e,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\ |\acute{\psi }_3\rangle= & {} |g,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|1,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\ |\acute{\psi }_4\rangle= & {} |g,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |1,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\ |\acute{\psi }_5\rangle= & {} |g,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,1,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}, \nonumber \\ |\acute{\psi }_6\rangle= & {} |g,e,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}, \nonumber \\ |\acute{\psi }_7\rangle= & {} |g,f,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}, \nonumber \\ |\acute{\psi }_8\rangle= & {} |g,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,1,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}, \nonumber \\ |\acute{\psi }_9\rangle= & {} |g,g,g,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,1,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}, \nonumber \\ |\acute{\psi }_{10}\rangle= & {} |g,g,e,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\ |\acute{\psi }_{11}\rangle= & {} |g,g,f,\ldots ,g\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}},\nonumber \\&\ldots \ldots \nonumber \\ |\acute{\psi }_{4N-1}\rangle= & {} |g,g,g,\ldots ,f\rangle _{1,2,\ldots ,N}|0,0,0,\ldots ,0\rangle _{c_1,c_2,\ldots ,c_N} |0,0,\ldots ,0\rangle _{f_1,f_2,\ldots ,f_{N-1}}.\nonumber \\ \end{aligned}$$
(24)
Fig. 9
figure 9

Experimental setup diagram for generation of N-atom W states

Full size image

The procedure is the same as we mentioned in Sect. 3, and we get an effective Hamiltonian (we set \(\acute{\varOmega }_2=\acute{\varOmega }_3= \cdots =\acute{\varOmega }_N=\acute{\varOmega }_y\))

$$\begin{aligned} \acute{H}_\mathrm{eff}= & {} \frac{(N-1)|\acute{\varOmega }_1|^2}{N\varDelta }|\acute{\psi }_1\rangle \langle \acute{\psi }_1|+\frac{|\acute{\varOmega }_y|^2}{N\varDelta }|\acute{\vartheta }_+\rangle \langle \acute{\vartheta }_+|\nonumber \\&+\,\left( \frac{\sqrt{N-1}\acute{\varOmega }_1\acute{\varOmega }_y^*}{N\varDelta }|\acute{\vartheta }_+\rangle \langle \acute{\psi }_1|+H.c.\right) . \end{aligned}$$
(25)

When we choose \(\acute{\varOmega }_y=\acute{\varOmega }_s\) and \(\acute{\varOmega }_1=\frac{i\acute{\varOmega }_s}{\sqrt{N-1}}\) (here \(\acute{\varOmega }_s\) is a real number), the above Hamiltonian becomes

$$\begin{aligned} \acute{H}_\mathrm{fe}=i\acute{\varOmega }|\acute{\vartheta }_+\rangle \langle \acute{\psi }_1|+H.c., \end{aligned}$$
(26)

where \(\acute{\varOmega }=\frac{|\acute{\varOmega _s}|^2}{N\varDelta }, |\acute{\vartheta }_+\rangle =\frac{1}{\sqrt{N-1}} (|\acute{\psi }_{7}\rangle +|\acute{\psi }_{11}\rangle +\cdots +|\acute{\psi }_{4N-1}\rangle )\) \((N=4,5,\ldots ,N)\). As long as \(\acute{\varOmega }=\dot{\theta }, \acute{H}_\mathrm{fe}=H_\mathrm{CCD}\), the Hamiltonian for speeding up the adiabatic dark-state evolution governed by \(\acute{H}_0\) has been constructed. Wherefore, we can obtain N-atom W states, i.e., \(|\acute{\psi }(t)\rangle =\frac{1}{\sqrt{2}}(|\acute{\psi }_{1}\rangle +|\acute{\vartheta }_+\rangle ) =\frac{1}{\sqrt{N}}(|\acute{\psi }_{1}\rangle +|\acute{\psi }_{7}\rangle +|\acute{\psi }_{11}\rangle +\cdots +|\acute{\psi }_{4N-1}\rangle )\).

5 Experimental feasibility and conclusions

Finally, let us consider the experimental feasibility of the proposed scheme. In experiment, this scheme can be realized in the strong-coupling regime [31, 66], if the cesium atoms can be cooled and trapped in coupled cavity. Furthermore, a set of cavity quantum electrodynamics (QED) parameters \((\lambda ,\gamma ,\kappa )/2\pi =(750,2.62,3.5)\) MHz is predicted to be available [67], with the cavity mode wavelength about 850 nm. In this condition, we can obtain a relatively high fidelity 98.42 % in the shortcut scheme.

In summary, we have proposed an efficient theoretical scheme to generate W states for three atoms trapped in coupled cavities linked by optical fibers based on STAP by combining “TQD” with “QZD.” The influences of the decoherence such as atomic spontaneous emission, cavity losses and the fiber photon leakages are numerically studied. Numerical simulations demonstrate that the shortcut scheme is faster and robust against the decoherence. Additionally, N-atom W states can also be generated when we set \(\acute{\varOmega }_1=\frac{i\acute{\varOmega }_s}{\sqrt{N-1}}\) and \(\acute{\varOmega }_2=\acute{\varOmega }_3=\cdots =\acute{\varOmega }_N=\acute{\varOmega }_s\). In fact, the shortcut is possible to be constructed with the same method presented in this scheme, so long as the quantum system whose Hamiltonian is possible to be simplified into a similar form in Eq. (8). That means the shortcut method is useful to realize fast and noise-resistant quantum information processing for multi-particle systems.