Language that researchers use to describe their assumptions about missing data tends to be imprecise. It is common to read that missing data were “handled using full-information maximum likelihood,” the implication being that maximum likelihood protects parameter estimates from bias as long as missing data are missing at random (MAR) conditional on observed data. However, such language underscores a small but fundamental misunderstanding about missing data that pervades social sciences. An intricacy that is lost in much of the discussion around missing data is that missing data assumptions apply to specific types of variables within specific models (Enders 2013; Graham 2009).

We define explicitly what the MAR assumption means when common approaches to handling missing data are used, and we show when this assumption has the potential to be problematic, focusing on a non-ignorable missing data mechanism that may arise when using multilevel models to analyze longitudinal data: random coefficient-dependent (RCD) missingness. We suggest that data conditions resulting in high determinacy of latent growth factors may minimize parameter bias that arises from violating missing data assumptions if multilevel multiple imputation models (MMIs) are used instead of single-level imputation models.

First, we briefly review our notation for multilevel growth models and then describe the RCD missingness mechanism. Next, we explain how RCD missingness might induce parameter bias when data are analyzed in a typical manner. We describe how the concept of growth factor score determinacy relates to RCD missingness and how MMIs might be leveraged to alleviate parameter bias without necessitating the formation of an explicit model for missing data. We test our hypotheses with a simulation design comparing parameter recovery when MMI is used with RCD missingness versus when a single-level imputation model is used to handle RCD missingness under a variety of data conditions that influence the level of growth factor determinacy.

Multilevel growth models follow the general form for person i: Y i  = X i b + Z i u i  + ε i , where Y i is an outcome vector of length T × 1 (T is the number of waves) and X i is a T × (K + 1) design matrix for the fixed effects in b, which is of dimension (K + 1) × 1. Typically, there are fixed effects for an intercept and K predictors, including time (and potentially higher-order functions of time), along with time-invariant and time-varying covariates. Z i is a T × M matrix usually containing a column of 1’s as well as subset of time-varying variables, such as time itself, from X i that have heterogeneous effects across subjects (i.e., random effects). u i is a M × 1 vector of latent subject-specific effects, which correspond to the columns of Z i , and are assumed to be distributed according to a multivariate normal distribution with unstructured covariance matrix T: (u i  ∼ MVN(0, T)). Finally, ε i is a T × 1 vector of normally distributed occasion-specific residuals (ε i  ∼ MVN(0, σ 2 I)) .

RCD missingness occurs when the probability that X ti or Y ti is missing for person, i, at wave, t, depends entirely or partially on the individual’s random coefficient values contained in the subject-specific, random effects, u i . The RCD mechanism results in a systematically skewed observation of X i and Y i , which in turn produce biased parameter estimates when fitting a standard multilevel growth model. The nature of the bias depends upon the precise selection pressures exerted by this MNAR mechanism. The extent of the bias depends upon the severity of the selection pressure and upon the reliability with which the random coefficients are determined by observed data (Gottfredson 2011). It is not possible to determine with certainty whether any MNAR mechanism is contributing to missing data, so the plausibility and potential consequences of the existence of such a mechanism must be considered (e.g., Enders 2011).

Strategies for Handling Missing Data with Multilevel Growth Models

Maximum likelihood (ML)-based estimators that make use of all available data (e.g., full ML, restricted ML, and quasi-ML) identify parameter values to optimize concordance between the outcome variable for an individual, i, Y i, and its expected value under the fitted model conditional on predictors, denoted by Ŷ i (Laird and Ware 1982; McCulloch 1997). Software used to estimate these regression models typically treat predictors (X i) as exogenous. Hence, no distributional assumptions are made about predictors in X i and mean and (co)variance parameters for predictors in X i are not estimated.

In contrast, software used to model longitudinal structural equation models tends to give the analyst the option of including the distribution of X i in the likelihood (i.e., making X i endogenous; Bollen 2014). This is not the default option in common SEM software (e.g. Mplus), nor is it always a desirable choice; however, to our knowledge, this option is not possible with conventional multilevel modeling software. Thus, when using multilevel modeling software, the commonly cited assumption that missing data are MAR only applies to missing outcome variables (Y i mis), and not to missing predictors in X i (X i mis). Rather, observations with missing predictors are entirely omitted (i.e., deleted listwise) from the model likelihood. This is a problem for longitudinal studies, especially those with time-varying predictors that may be missing on some occasions, because it requires missing values in X i mis to be missing completely at random (MCAR), a condition that would typically only occur if missing data are missing by design (Rubin 1976), or missing exclusively due to observed covariates (Little and Zhang 2011).

To avoid listwise deletion resulting from missing predictors, an analyst may choose to multiply impute missing predictors (and outcomes, if desired) prior to analysis. When missing data are imputed to form complete datasets, one need only assume that missing outcomes and predictors are MAR given all observed data in the imputation model. The analyst’s goal is to approach conditionally random missingness as closely as possible, reducing potential sources of bias to the fullest extent possible (Graham 2009). It is therefore essential to follow an inclusive imputation strategy by incorporating as many auxiliary variables and statistical interactions as can reasonably be accommodated into the imputation model (Collins et al. 2001).

Longitudinal data adds complexity in the multiple imputation procedure. Leaving the data in “long” format but using a single-level imputation approach and ignoring within-person correlation in the multiple imputation procedure is unprincipled; it results in over- or underestimation of the importance of covariates, underestimation of random effect variance, and conflation of within-person and between-person effects (Lüdtke et al. 2016; van Buuren 2011). However, because software options for imputing multilevel data have been limited historically, an analyst might be tempted to use the ad hoc approach of imputing missing data from a saturated imputation model using a “wide” (multivariate) data structure in a single-level multiple imputation program (e.g., SAS Proc MI) in order to incorporate autocorrelation of the within-person data. Such an approach is preferable to assuming independence of all observations within person, but it is still potentially problematic for a couple of reasons. First, the “wide” approach does not explicitly incorporate information about the timing of repeated measures. Second, the covariance structure in the saturated “wide” imputation model may not be sufficiently general to reflect the hypothesized model-implied covariance structure; for instance, covariance features involving random slopes of predictors with individual-specific values (such as X ti; Wu et al. 2009) may not be fully accounted for during imputation. Both of these limitations of the “wide” imputation approach may lead to substantial inefficiencies in the imputation model and may lead to biased variability estimates. All of the aforementioned, common methods for handling missing data require the MAR assumption, which is the limitation that we address in this manuscript.

Fortunately, software for conducting multiple imputation with multilevel data is advancing rapidly. Enders et al. (2016) summarized and compared two classes of multilevel multiple imputation (MMI) modeling approaches, and associated software, from which analysts may choose joint models (Asparouhov and Muthén 2010; Schafer and Yucel 2002) and chained equations (van Buuren 2011). Presently, categorical data can be accommodated in joint MMI modeling software, but not in software that uses chained equations. While we expect that technology will progress quickly, in this paper, we use the joint MMI modeling approach (specifically, the approach described in Schafer and Yucel 2002) due to this limitation of chained equations and its slower rate of convergence (the latter problem is a concern mainly for simulation studies such as ours).

Although MMI is slightly more complicated than traditional multiple imputation from the longitudinal analyst’s perspective, it may confer the unique benefit of mitigating bias in the presence of the non-ignorable RCD missing data mechanism, and it may do this without requiring explicit modeling of the missing data mechanism. MNAR models, including multilevel growth model allowing for RCD missingness (Albert and Follmann 2009; Gottfredson et al. 2014; Tsonaka et al. 2009; Vonesh et al. 2006), require untestable assumptions and are sensitive to misspecification (Little 1993; Roy 2003). When missing longitudinal data are imputed using a multilevel model, empirical Bayes estimates of the unobserved random effects in u i , are generated and imputed values are conditioned on these estimated latent values (Schafer and Yucel 2002). Thus, the MMI inherently accounts for missingness due to a RCD mechanism in proportion to the determinacy of the growth factors.

However, there is an important limitation to MMI’s potential for mitigating bias resulting from RCD missingness: MMI software cannot condition imputations on random coefficients corresponding to time-varying covariates with missing values (Enders et al. 2016; Grund et al. 2016). Consequently, MMI will be useful in reducing bias from non-ignorable RCD missingness only if the mechanism involves the random intercept, a random slope for time (because time is always known), or a random slope corresponding to a time-varying covariate that is completely observed. Unfortunately, the third situation may be unlikely in longitudinal designs because observations that are collected simultaneously on a given wave tend to be missing together. However, there are many exceptions (e.g., item-level missingness; when the source of outcome data differs from the source of predictor data; when predictors are lagged and the earlier time point is observed).

Study Overview

Under various realistic data scenarios, we conduct a simulation study to examine the performance of MMI relative to its most principled alternative: single-level, multivariate “wide” MI (SWMI). Simulation methodology is appropriate for addressing our research questions because the MMI model is not intended to handle MNAR missingness, so its performance under realistic conditions is unknown. First, we hypothesize that MMIs will mitigate bias that is due to non-ignorable, RCD missingness. Second, we hypothesize that conditions related to determinacy of the growth factors will affect how well the MMI approach is able to recover true parameter estimates. We do not expect the same to be true for SWMI because random effects are not incorporated into the imputation model. To test these hypotheses, we evaluate and compare performance of MMI and SWMI under varying degrees of determinacy (c.f. factor score determinacy; Grice 2001). In multilevel modeling, growth factor determinacy relates to the multiple correlations between the random coefficients and the repeated measures. We can therefore experimentally manipulate determinacy through the intraclass correlation (ICC) amongst repeated measures and number of repeated waves. We hypothesize that, when missing data are handled with MMI, bias resulting from a RCD missing data mechanism will be least severe when the ICC is relatively high and when there are more repeated measures. In a follow-up simulation, we evaluate how another factor related to growth factor determinacy, percentage of missing data, affects performance of MMI in the presence of an RCD mechanism.

Simulation Study

Data Generation

We generated 500 replicated datasets per experimental condition using R software (R Core Team 2015). There were 1000 clusters (i.e., level 2 units or “subjects”) in all conditions.

In the primary simulation study, two factors were crossed: the ICC (.25 and .75) and the number of waves (four and eight). ICC levels were chosen to reflect the range from modest, but non-negligible, nesting (.25) to high levels of nesting that would be observed in an intensive longitudinal study (.75; Bauer and Sterba 2011). Approximately 30% of data were missing across all conditions in the first part of the simulation. The two alternative numbers of waves were sampled from a realistic range that would be observed in most panel design studies or in short intensive longitudinal studies.

In the follow-up simulation, we held ICC constant at .5 and number of waves constant at 6 and we varied percent of missing data from fairly low but not negligible (20%), to moderately large (33%), and to extensive (50%) (Collins et al. 2001; Enders 2010).

Data were generated using the following multilevel model, where time was coded to start with 0 and increase one unit with each wave (0:3, 0:5, or 0:7 for four, six, and eight waves, respectively), and X ti followed a standard normal distribution:

$$ \begin{array}{c}{y}_{ti}={b}_0+{b}_1tim{e}_{ti}+{b}_2{X}_{ti}+{u}_{0i}+{u}_{1i}tim{e}_{ti}+{u}_{2i}{X}_{ti}+{\varepsilon}_{ti},\\ {}\\ {}\left[\begin{array}{c}\hfill {u}_{0i}\hfill \\ {}\hfill {u}_{1i}\hfill \\ {}\hfill {u}_{2i}\hfill \end{array}\right]\sim MVN\left(\left[\begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill {\tau}_{00}\hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill {\tau}_{10}\hfill & \hfill {\tau}_{11}\hfill & \hfill \hfill \\ {}\hfill {\tau}_{20}\hfill & \hfill {\tau}_{21}\hfill & \hfill {\tau}_{22}\hfill \end{array}\right]\right),\\ {}\\ {}{\varepsilon}_{ti}\sim N\left(0,{\sigma}^2\right).\end{array} $$
(1)

Parameters were chosen to optimize several criteria. First, ICCs had to equal to .25, .5, or .75 when time and X ti were equal to zero, and the ICCs were required to remain within reasonable bounds of these values at all levels of time and X ti :

$$ ICC\Big|{X}_{ti},tim{e}_{ti}=\frac{\tau_{00}+tim{e}_{ti}^2{\tau}_{11}+{X}_{ti}^2{\tau}_{22}+2tim{e}_{ti}{\tau}_{01}+2{X}_{ti}{\tau}_{02}+2tim{e}_{ti}{X}_{ti}{\tau}_{12}}{\tau_{00}+tim{e}_{ti}^2{\tau}_{11}+{X}_{ti}^2{\tau}_{22}+2tim{e}_{ti}{\tau}_{01}+2{X}_{ti}{\tau}_{02}+2tim{e}_{ti}{X}_{ti}{\tau}_{12}+{\sigma}^2}. $$
(2)

We aimed to have a \( {R}_{y_t}^2 \) of .5 to retain constancy across all conditions. Finally, we maintained proportionality for values in b and T across all conditions (e.g., the ratio of τ 10 to τ 00 was .06 regardless of ICC); also, each fixed effect explained the same proportion of variance in all conditions.

Waves of data were randomly selected to be missing based on a probabilistic RCD mechanism in which the log odds of missingness depended on subject-specific values of the random intercept (u 0i ) and the random slope for time (u 1i ). The intercept of the logit equation for missingness was varied to determine the total amount of missing information. Coefficients corresponding to the random effects varied by ICC condition; the correlation between the random effects and the missingness probability was approximately .15 across all conditions.

Data Analysis

We used the MplusAutomation package in R to analyze the simulated data using the MMI procedure (Hallquist and Wiley 2014). The Mplus input imputation script was modified from script presented in Enders et al.’s Appendix A (2016). X ti and time ti were listed as “within” variables. The imputation model included a random intercept and a random time coefficient, but it necessarily excluded the random coefficient for the effect of X ti because random coefficients are not permitted for covariates with missing values (as discussed previously; see also Grund et al. 2016). X ti and time were treated as endogenous in the imputation model to avoid listwise deletion of missing waves of data. Twenty complete-case datasets were imputed for each replication. For comparison, we used PROC MI in SAS version 9.4 to generate 20 imputations per replication with a SWMI model. The MCMC method imputed missing data to match mean and covariance data from the saturated model for all observed X i and Y i.

All imputed data were analyzed using the model shown in Eq. 1 with a maximum likelihood estimator. Results were aggregated according to Rubin’s (2004) pooling formulae to obtain parameter estimates and standard errors.

We combined information about the bias and efficiency of fixed effect parameter estimates by constructing the average 95% confidence interval for each parameter using the following equation, where k represents a given model parameter, θ k is the true value of a parameter, \( {\widehat{\theta}}_k \) is its estimate, and R represents the number of replicated datasets (500):

$$ {\displaystyle \sum_R{\widehat{\theta}}_k/R}\pm 1.96*{\displaystyle \sum_RSE\left({\widehat{\theta}}_k\right)/R}\ . $$
(3)

Generating parameters varied by condition, so we report percent relative bias (PRB) instead of average point estimates. PRB was obtained by subtracting true generating parameters from the average point estimates and dividing by the true parameter value, as shown in Eq. 4:

$$ PR{B}_k=100\times \frac{{\displaystyle {\sum}_{r=1}^R\left(\frac{{\widehat{\theta}}_{kr}-{\theta}_k}{{\widehat{\theta}}_{kr}}\right)}}{R}=100\times \frac{RB}{{\widehat{\theta}}_{kr}}\ . $$
(4)

PRB adjusts for scale differences when comparing bias across differently valued parameters so bias is interpreted relatively, as a percent discrepancy from the true value (as used in Maas and Hox 2005). The average 95% confidence intervals around point estimates from Eq. 3 were re-scaled into the PRB metric in order to combine information about parameter bias with efficiency of the estimates.

Because variance component estimates are bounded at zero, we used a log transformation to create asymmetric confidence intervals that could not go below zero, analogous to the procedure used in IBM SPSS MIXED. The 95% confidence intervals for variance components were calculated as follows:

$$ \ln \left({\displaystyle \sum_R{\widehat{\theta}}_k/R}\right)\pm 1.96*\raisebox{1ex}{${\displaystyle \sum_RSE\left({\widehat{\theta}}_k\right)/R}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum_R{\widehat{\theta}}_k/R}$}\right.\ . $$
(5)

The upper- and lower- confidence bounds were then back-transformed by exponentiation before they were re-scaled into the PRB matric.

We report results for all fixed effects and the random effect variance parameters. Results regarding random effect covariance parameters are available upon request.

Results

MMI Versus SWMI Performance Under RCD Mechanism

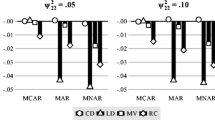
Figure 1 depicts the average 95% confidence intervals, re-scaled to PRB metric. The y-axes are scaled differently across parameters to accommodate different ranges. Dashed horizontal lines at ±10% indicate boundaries for what is sometimes considered an “acceptable” level of bias (e.g., Bollen et al. 2007). We note that although the RCD mechanism involved the random intercept (u 0i ) and random slope for time (u 1i ), bias was not isolated to b 0, b 1, τ 00, and τ 11, but instead propagated throughout the model (c.f., Kaplan 1988). Nevertheless, the parameters involved more directly in the RCD mechanism were the most affected.

Fig. 1
figure 1

Each pair of panels compares the percent relative bias (PRB) of estimates (solid shape) across data generating conditions (light shading: ICC = .75; dark shading: ICC = .25; circle: four waves; triangle: eight waves), as a function of the multiple imputation model. Error bars show the average lower and upper bounds of 95% confidence intervals for the parameters, re-scaled to the PRB metric. Solid horizontal line indicates zero bias. The area inside of the dashed horizontal lines at ±10% represents “acceptable” bias

Full size image

Fixed Effects

None of the re-scaled 95% confidence intervals for fixed effect estimates cover the true parameter value under the SWMI model (represented as PRB = 0). In contrast, almost all of the re-scaled 95% confidence intervals for the MMI models cover the true fixed effect generating values. The two exceptions are the fixed effect of time (b 1) when the ICC is low. Additionally, the re-scaled upper end of the 95% confidence interval for b 1 just reaches the true parameter value (PSB = 0) when the ICC is high but there are only four waves. Examining Fig. 1, we see that, with one exception, point estimates for fixed effects generated under MMI are within the “acceptable” range of PRB. The exception to this is for the fixed effect of time (b 1) when determinacy is lowest (ICC = .25 and four waves). In contrast, re-scaled 95% confidence intervals for fixed effects generated by the SWMI model never even overlap with acceptable levels of PRB. This is true even as confidence intervals are wider in the SWMI models.

Random Effect Variances

As is typical with maximum likelihood estimation, covariance parameters are not recovered as well as fixed effects and tend to be downwardly biased (Kenward and Roger 1997). The average point estimates generated under MMI are outside of the acceptable range for τ 11 when the ICC is low, and point estimates for τ 22 are outside of the acceptable range for all conditions. However, the re-scaled 95% confidence intervals always cover or nearly cover the true parameter value (PRB = 0). When compared with the SWMI results, the MMI model produces less biased and much more precise confidence intervals for random effect variances than the SWMI.

Effects of ICC and Number of Waves on Parameter Recovery: Comparison of MMI and SWMI Models

MMI Models

Fixed effect estimates were more efficient as the ICC decreased because each observation necessarily provided more independent information about the fixed effects. On the other hand, estimates for random effect variances were more efficient the ICC increased, and covariance parameter estimates were less biased with a higher ICC. As expected, fixed effect estimates were less biased as the number of repeated measures increased. As we noted previously, re-scaled confidence intervals covered the true fixed effect parameters (PRB = 0) in all cases except for the estimate of b 1 (the effect of time) when determinacy was low. Specifically, the true value of b 1 (PRB = 0) was not contained in the re-scaled 95% confidence interval when the ICC was low. The number of repeated measures did not have a strong influence on recovery of random effects when the ICC was high, but having more repeated measures resulted in more efficient estimates when the ICC was low.

SWMI Models

As expected, higher random coefficient determinacy did not result in systematically improved parameter estimates in the SWMI models. Having a higher ICC was worse for recovery of b 0 and b 2 and better for recovery of b 1. As with the MMI model, higher ICCs were associated with more efficient estimation of the random effects. Likewise, there was no discernable pattern of the effect of number of repeated measures on recovery of fixed or random effect parameters, except that confidence intervals for random effects were wider when there were fewer waves and the ICC was low.

Percent of Missing Data

As has been previously shown with non-randomly missing data more generally (Collins et al. 2001), we find that having RCD missing data is associated with biased estimates of generating parameters. Figure 2 shows re-scaled average 95% confidence intervals. These results illustrate that the MMI model cannot accommodate RCD missingness that occurs in extreme amounts (e.g., 50% with our generating model). Recovery of random coefficients is worst as missing data increases, both in terms of parameter bias and loss of efficiency. The effect of missing data on parameter bias is consistent with our hypothesis that MMI performance under RCD is a function of determinacy; if performance were unrelated to determinacy, then we would expect to see a loss of efficiency, but not increased bias, as the amount of missing data increased.

Fig. 2
figure 2

Each panels displays the percent relative bias (PRB) of estimates (solid shape) as a function of the percent of missing data when multilevel multiple imputation is used. Error bars show average lower and upper bounds of 95% confidence intervals for the parameters, re-scaled to the PRB metric. Solid horizontal line indicates zero bias. The area inside of the dashed horizontal lines at ±10% represents “acceptable” bias

Full size image

Discussion

Social scientists using longitudinal data have been cautioned repeatedly about the possibility that MNAR mechanisms may cause inferential errors that are impossible to detect empirically (Enders 2011; Muthén et al. 2011). Many different MNAR models are available for longitudinal analysts wishing to conduct sensitivity analyses (including shared parameter models: Albert and Follmann 2009; pattern mixture models: Little 1995; and seemingly countless extensions thereof). Unfortunately, none of these models is robust to misspecification, all require significant assumptions about the missing data mechanism(s), and there is no empirical method for evaluating fit of MNAR models.

Thus, in spite of the existence of a variety of MNAR models, many analysts prefer to use multiple imputation to handle missing data because, although multiple imputation requires the MAR assumption (unless imputing specifically from a MNAR model, Demirtas and Schafer 2003), it is considered to be robust and it is straightforward to implement in commonly used software packages. Given this tendency, it is fortunate that (under conditions of high-random coefficient determinacy) MMI methods lead to the benefit of reducing bias due to a non-ignorable missing data mechanism that may be common in longitudinal research: RCD missingness. However, our results also show that failing to account explicitly for the multilevel nesting structure during multiple imputation can have severe consequences.

Although researchers can never be sure of the extent to which an RCD mechanism might be causing missing data, they can have a good sense of the degree to which random coefficients are determined. Items with a higher communality (i.e., a higher ICC and less measurement error) lead to higher determinacy, and having more repeated measures and a higher proportion of observed data (i.e., less missing data) also increases determinacy. Thus, holding the severity of the RCD mechanism constant, a researcher with many repeated measures and a fairly stable, well-measured outcome has reason to be less concerned about parameter bias than a researcher with fewer repeated measures, measures that are less stable, and measures that are not as reliable. When data are more like the latter, we recommend evaluating parameter sensitivity using explicit MNAR models (e.g., Graham 2012; Sterba and Gottfredson 2015).

MMI software is under development and is being expanded fairly rapidly (Enders et al. 2016; Lüdtke et al. 2016). Presently, categorical variables can be accommodated only with a joint MMI model, although this feature may soon be available with software that uses chained equations. An important limitation to current MMI software is its inability to incorporate random slopes for predictors with missing values. Were this restriction lifted, we would expect to see more bias reduction under more RCD conditions.

Limitations

In addition to the aforementioned software limitations, our study was subject to the limitation common to all simulation studies: conclusions are restricted to the range of simulated conditions. We sought to maximize generalizability of our findings by considering a range of realistic data conditions, varying parameters that were the key for testing our hypothesis about random coefficient determinacy: ICC, number of waves, and percent of missing data. Parameters that were fixed across conditions were chosen to be moderate and representatives of a typical longitudinal study. One limitation of the simulation study is that we did not vary the response distribution of the repeated outcomes. We would expect to see the same pattern of results with non-normal data, whereby higher determinacy relates to less bias. However, because censored or binned items convey less information than continuous items, we would expect that reductions in bias might not be as dramatic with such variables. Second, because MMI models take much longer to converge with chained equations than with joint modeling, we did not evaluate parameter recovery using chained equations. Enders et al. (2016) compared parameter recovery under a MAR missing data mechanism and found that the joint model performed better for recovering fixed effects and chained equations were better for recovering the variance of random effects. Fixed effect estimates tend to be interpreted more frequently than variance parameters, so we suspect that most analysts choosing between joint models and chained equations would choose the former, all else equal.

Conclusion

Because of complexities inherent in longitudinal data collection, wave-level or item-level non-response is common. Multiple imputation is the modus operandi for handling longitudinal missing data because it protects against listwise deletion of cases. Until now, the ability of MMI to accommodate the RCD MNAR mechanism had not been understood, nor were the limitations of using SWMI to impute longitudinal data fully understood. By properly accounting for the multilevel structure of longitudinal data, analysts may take comfort in the fact that they will also be mitigating bias resulting from RCD mechanisms. We hope for continued development of MMI software, particularly the capability for inclusion of random slopes for predictors with missing values.