Measuring and enhancing the transferability of hidden Markov models for dynamic travel behavioral analysis

Abstract

As an emerging dynamic modeling method that incorporates time-dependent heterogeneity, hidden Markov models (HMM) are receiving increased research attention with regards to travel behavior modeling and travel demand forecasting. This paper focuses on the model transferability of HMM. Based on a series of transferability and goodness-of-fit measures, it finds that HMMs have a superior performance in predicting future transportation mode choice, compared to conventional choice models. Aimed at further enhancing its transferability, this paper proposes a Bayesian conditional recalibration approach that maps the model prediction directly to the context data. Compared to traditional model transferring methods, the proposed approach does not assume fixed parameterization and recalibrates the utilities and the prediction directly. A comparison between the proposed approach and the traditional transfer-scaling favors our approach, with higher goodness-of-fit. This paper fills the gap in understanding the transferability of HMM and proposes a practical method that enables potential applications of HMM.

Introduction

Background, research questions and objectives

Travel demand models are often tested and applied under different contexts (i.e., across spaces and time periods). How models, theories, or information developed in one context perform under other contexts is also known as the transferability problem (e.g., Gunn 2001; Rashidi and Mohammadian 2011; Sanko and Morikawa 2010). Beginning in the 1980s, a large body of literature has emerged with empirical evidence about the transferability of travel demand models. Methods that evaluate and enhance the model transferability may help modelers justify the applicability of the model and assess the accuracy of its prediction. It could also serve as a practical approach to the problem of applying the model to a future-year scenario or to an area where little data is available.

In an era of big data analytics and informatics, emerging transportation data sources are becoming readily available and encourage the development of more advanced modeling and demand forecasting methods. Greater research attention has been given to dynamic discrete choice analysis, activity-based models and agent-based simulation, which can reveal insightful individual-level activity and travel behavioral dynamics (Shepherd 2014; Allahviranloo et al. 2016; Djavadian and Chow 2016). More specifically, dynamic hidden Markov models (HMM) have recently attracted research attention for their capability in modeling short-term and long-term travel behavioral dynamics and capturing time-dependent heterogeneity (e.g. Ben-Akiva 2010; Vij 2013). Nevertheless, compared to traditional travel demand models, new methods such as HMM tend to have more complex model structure and higher dimensions of parameterization. How does HMM perform when applied to demand forecasting? Does it offer better prediction compared to traditional models? Are the conventional model-transferring techniques suitable to transfer an HMM model? These key research questions must be answered before we see more applications of HMM-based modeling methods.

Motivated by these research needs, the research objectives of this paper are three-fold:

• 1. to quantify the transferability of the HMM models using the widely-accepted measure-of-effectiveness for model transferability;

• 2. to apply conventional model-transferring techniques to HMM models and assess the performance of those techniques;

• 3. to propose and demonstrate a more flexible recalibration method to enhance the transferability of HMM models.

Literature review

Simply applying the original model to the application context often does not guarantee a satisfactory outcome because some model parameters may be less transferable or require updating. There are a number of studies in the field of transportation engineering that focused on evaluating the transferability and parameter-updating methods of transportation demand models. Two useful review papers summarized the current state of the practice. The National Cooperative Highway Research Program (NCHRP) Report 716 provided a comprehensive literature review in the context of four-step travel demand models (Cambridge Systematics et al. 2012). Karasmaa (2007) summarized and compared the parameter updating methods that are especially suitable for disaggregated travel demand models. Unfortunately, we are far from reaching consensus on how to recalibrate the models and make them more transferable. Existing parameter-updating methods include transfer scaling, Bayesian updating, combined transferring method, and joint context estimation. These methods are mostly applied to cross-sectional choice models. They must rely on strong assumptions and often focus on scenarios that have an inadequate number of data samples (Karasmaa 2007; Sanko 2014).

Existing methods can be summarized as a group of parameter-updating methods. They all focus on updating a number of model parameters by assuming different transferability of those parameters. For instance, the Bayesian updating method updates the original model parameters based on a classical Bayesian process using the application-context datasets. This method assumes that the estimation and application contexts have the same underlying set of parameters (Atherton and Ben-Akiva 1976; Abdelwahab 1991; Badoe and Miller 1995; Rashidi et al. 2013; Rossi et al. 2013). The transfer-scaling method only updates the utility function scales and alternative-specific constants in the application context. The remainder of the model parameters, including level-of-service and socio-economic parameters, are assumed to be completely transferable (e.g., Algers et al. 1994; Badoe and Miller 1995; Rossi et al. 2013). This method can mitigate the transfer bias (i.e., the difference in the true parameters between the estimated model and the application context) to some extent, especially for cases where the model is transferred from one location to another location and within the same temporal scope. It is likely that for the same time point, variables such as travel time and costs have the same effect on travel behavior. However, the assumptions about parameters may not hold; there is evidence that certain variables will generate time-varying impact and therefore should be incorporated when transferring the model to another time point. For example, level-of-service parameters have been found to evolve over time due to inflation, salary increase, and changes in congestion level (Börjesson 2014). The combined transferring and joint context estimation incorporates the aforementioned two methods and different data cross-sections (Badoe and Miller 1995; Ben-Akiva and Bolduc 1987; Ben-Akiva and Morikawa 1990; Bradley and Daly 1991). These assumptions about parameters (e.g., the scaling and constant parameters assumed in the transfer-scaling method) still remain a methodological issue for these parameter-updating methods.

Another fact about existing studies is that they evaluate transferability using static choice models and cross-sectional data. Due to data limitation, most existing travel demand models are based on cross-sectional observations. When applying these models for prediction at another time point, the transferability is almost always an issue. An increasing amount of research on travel behavior dynamics has become available recently (Walker 2001; Pendyala et al. 2005; Cirillo and Axhausen 2010; Ben-Akiva 2010; Vij 2013; Xiong et al. 2015; Xiong and Zhang 2017). Dynamic discrete choice methods have been developed. For instance, Cirillo and Axhausen (2010) studied car-ownership and mode dynamics by specifying dynamic variables in the systematic utility functions. The dynamics on entering the car-purchasing market have been formulated using dynamic programming and optimal stopping. As another line of dynamic formulation, hidden Markov models (HMM) have also drawn increased research attention. Vij (2013) demonstrated the use of the Markov process based on panel data from Santiago, Chile. Xiong et al. (2015) developed a HMM mode choice model using ten-wave travel panel survey data from the Puget Sound region. In HMM, hidden states are used to model travelers’ intrinsic behavioral status representing their action plans, modality styles, modal preferences, attitudes, etc. Dynamic discrete choice models and HMM models have improved goodness-of-fit in analyzing longitudinal data (Xiong et al. 2015, 2018). These dynamic models should be considered as useful modeling tools for future-year planning and prediction. Contrary to the increasing visibility of dynamic models, the transferability of these models largely remains untested. There are papers that discussed the use of multiple cross-sectional data to conduct joint estimation or parameter-based time series analysis in order to improve transferability of cross-sectional models (Sanko and Morikawa 2010; Sanko 2014). Again, how longitudinal models perform when transferred to future-year scenarios and how to calibrate them remain research gaps and need attention.

In summary, the HMM-based travel behavioral models take into account time-varying heterogeneity and are believed to have better model transferability than conventional choice models that are typically employed in the transportation planning process. In this paper, we will further quantify HMM models’ transferability by adopting various performance measures and compare with multinomial logit models in current state-of-the-practice. Then, an effort of enhancing the transferability of HMM models will be made. Existing parameter-updating methods will be applied as a benchmark. A Bayesian conditional recalibration approach will be developed to transfer the HMM model to different future-year time points. Compared to existing model-transferring methods, this approach is more flexible without the parameterization assumptions and focuses on recalibrating the prediction probabilities.

The remainder of the paper is organized as follows. The next section revisits the HMM model developed previously by the authors. Different transferability performance measures employed in the study are also presented. The benchmark model-transferring method and the proposed Bayesian conditional recalibration approach are described in detail. “Data” section presents the data source used in this study. “Analysis experiments and results” section reports estimation results and examines the performances of different methods. Concluding remarks and future research directions are discussed at the end of the paper.

Methodologies

Hidden Markov model

The following figure illustrates the structure of the hidden Markov model (HMM), using long-term travel mode choice as an example of analysis (Fig. 1).

Fig. 1

The modeling structure of the hidden Markov mode choice model

The travel mode choice dynamics are represented by a hierarchical framework. At the upper level, observed mode choices are governed by the hidden states, which represent different modality styles. At the lower level, the travel mode choice is state-dependent, and can be modeled as a typical multinomial logit or mixed logit model. This state-dependent choice can be easily extended to model other travel choices as well. By combining the hidden state transition probabilities with the state-dependent choice probabilities, a joint likelihood function can be derived and employed to estimate the HMM parameters. Xiong et al. (2015) has depicted two significant hidden states: habitual drivers (who innately prefer drive-alone mode) and time-sensitive multimodals (with higher value-of-time and use all different modes). Between time points, this behavioral predisposition may evolve. Individual and household-level attributes may influence this evolution. Over time, lifecycle changes such as marriage (divorce), an increase in family size, relocation, etc. certainly will influence the transition in hidden states. Graduating school and starting a commute to a central business district (CBD) is likely to switch a previous habitual driver to a time-sensitive transit taker. Relocating to a remote rural residential area, on the other hand, could possibly change an urban transit lover into an automobile veteran. This evolution is modeled as a Markov process, using a matrix to describe the transition between different states:

$${\mathbf{P}}_{it} = \left| {\begin{array}{*{20}c} {p_{it}^{{\text{(}h_{\text{1}} ,h_{\text{1}} \text{)}}} } & {p_{it}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} } \\ {p_{it}^{{\text{(}h_{2} ,h_{\text{1}} \text{)}}} } & {p_{it}^{{\text{(}h_{2} ,h_{2} \text{)}}} } \\ \end{array} } \right|$$

(1)

In this matrix, the transition probability $p^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}}$ denotes the likelihood that traveler i switches from hidden state h₁–h₂. It is associated with a number of personal and household-level factors that are changing over time, meaning that these factors can be strong enough to transition traveler i from one hidden preference state to another state. Xiong et al. has included two states and lifecycle stages as variables. This transition model is formulated as follows:

$$p_{it}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} = \frac{{\exp \left( {{\mathbf{Z}}_{it}^{\prime } {\varvec{\uplambda}}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} } \right)}}{{1 + \exp \left( {{\mathbf{Z}}_{it}^{\prime } {\varvec{\uplambda}}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} } \right)}}$$

(2)

Given the individual’s true state H_it in period t, the observed process of mode choices is conditionally independent of the hidden state of other time points. The state-dependent choice follows random utility maximization modeling form. The systematic utility function for alternative mode m is:

$$V_{{\left( {it\text{|}H_{it} } \right)}}^{m} = {\mathbf{Z}}_{it}^{\prime } {\varvec{\upbeta}}_{{\left( {m|H_{it} } \right)}} + {\mathbf{X}}_{m,t}^{\prime } {\varvec{\upgamma}}_{{\left( {m|H_{it} } \right)}} + \sigma_{{\left( {m|H_{it} } \right)}} \eta_{{\left( {im|H_{it} } \right)}} + \varepsilon_{{\left( {im|H_{it} } \right)}}$$

(3)

where Z_it is the vector of covariates measured at period t for individual i. X_it is the vector of covariates measured at period t for travel mode m. $\eta_{{\left( {im|H_{it} } \right)}}$ denotes the i.i.d. normally distributed error component across individual i, mode m, and hidden state H_it. ${\varvec{\upbeta}}_{{\left( {m|H_{it} } \right)}}$, ${\varvec{\upgamma}}_{{\left( {m|H_{it} } \right)}}$ and $\sigma_{{\left( {m|H_{it} } \right)}}$ are the corresponding regression coefficients for choosing mode m given hidden state H_it. One unique feature of this model is that it incorporates time-varying heterogeneity into the model formulation. When applied to a future-year prediction of modal split, the HMM model can better take into account the changing level-of-service and socio-demographic variables that are typically estimated by a regional transportation planning model. Different performance measures for transferability are introduced in the following section while results are summarized in “Analysis experiments and results” section.

Transferability performance measures

The first research objective is to quantify the transferability of the HMM models. To achieve the objective, various measures of effectiveness (MOEs) are established in this study to evaluate the transferability as well as the recalibration results. Three typical measures for goodness-of-fit are employed to assess the transferability effectiveness: hit ratio, log-loss (Good 1952) and mean squared error (Brier 1950). The hit ratio measures the prediction accuracy, applying the transferred model to the testing samples. Log-loss is employed when the model output is a numeric probability, which mainly performs as a gauge of prediction confidence. Log-loss measures the accuracy of a prediction and it can be considered as the cross entropy between the distribution of the true class and the prediction. Log-loss is calculated by Eq. (4):

$$\log loss = \sum\limits_{{C = \left\{ m \right\}}} {\delta \left( {C\left( E \right),C} \right)\log P\left( {C|E} \right)}$$

(4)

where δ denotes the Kronecker delta function, which is equal to 1 if the two arguments are identical and 0 otherwise and C(E) denotes the actual class of an empirical observation E. When the class of an observation is correctly predicted with a probability of 1, log-loss is 0. By minimizing the log-loss, one maximizes the accuracy of the model.

Mean squared error (MSE) describes the difference between the prediction and the observation. When the class of an observation is correctly predicted with a probability of 1, the associated MSE is 0. MSE is computed using Eq. (5):

$$MSE = \sum\limits_{{C = \left\{ m \right\}}} {\delta \left( {C\left( E \right),C} \right)\left( {1 - P\left( {C|E} \right)} \right)^{2} }$$

(5)

These MOEs will then be employed to evaluate the transferability performance of benchmark multinomial logit models, mixed logit models, and HMMs. Different recalibration methods described below, including the proposed Bayesian conditional recalibration, will also be evaluated using these metrics. Resulting statistics are summarized and presented in “Analysis experiments and results” section.

Benchmark recalibration model: transfer scaling

A benchmark methodology to transfer and recalibrate travel demand models is the parameter-updating method, which explicitly includes a pair of local parameters in the original utility functions. Assume that the systematic utility functions of the initial choice model are $V = \mu + \phi^{T} {\mathbf{X}}$. $\mu$ denotes the alternative specific constant. $\phi$ denotes the originally estimated parameters. If a subset of variables (denote by Z) of the original covariate vector X is transferred to another dataset, we can recalibrate the following representative utility:

$$V^{E} = \mu^{E} + \lambda^{E} \cdot \phi^{T} {\mathbf{Z}}^{E}$$

(6)

where $\mu^{E}$ and $\lambda^{E}$ are the parameters to be updated in this transferability problem. $\mu^{E}$ denotes the new constant. $\lambda^{E}$ denotes the scale of the transferred parameters $\phi^{\prime }$. To estimate the updated parameters, maximum log-likelihood estimation (MLE) can be adopted. When applying this benchmark method to HMM models, one needs to modify the parameterization for the Markovian transition matrix shown by Eq. (7):

$$\tilde{p}_{it}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} = \frac{{\exp \left( {\eta^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} + \varphi^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} \cdot {\mathbf{Z}}_{it}^{\prime } {\varvec{\uplambda}}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} } \right)}}{{1 + \exp \left( {\eta^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} + \varphi^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} \cdot {\mathbf{Z}}_{it}^{\prime } {\varvec{\uplambda}}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}} } \right)}}$$

(7)

where ${\varvec{\uplambda}}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}}$ is the vector of corresponding regression coefficients for the transition probability $p_{it}^{{\text{(}h_{\text{1}} ,h_{2} \text{)}}}$. Z denotes personal/household covariates. $\eta$ and $\varphi$ are the transferability parameters, i.e., the constant and the scale for the transition probability, respectively. Similarly, we adjust the parameterization for the state-dependent choice of alternative mode m as follows:

$$V_{{\left( {it\text{|}H_{it} } \right)}}^{m} = \eta_{{\left( {m\text{|}H_{it} } \right)}} + \varphi_{{\left( {m\text{|}H_{it} } \right)}} \left( {{\mathbf{Z}}_{it}^{\prime } {\varvec{\upbeta}}_{{\left( {m\text{|}H_{it} } \right)}} + {\mathbf{X}}_{mt} {\varvec{\upgamma}}_{{\left( {m\text{|}H_{it} } \right)}} } \right)$$

(8)

where ${\varvec{\upbeta}}$ and ${\varvec{\upgamma}}$ are the vectors of state-dependent fixed parameters for personal/household covariates Z and travel mode covariates X, respectively. Again, $\eta$ and $\varphi$ denote the transferability parameters.

A Bayesian conditional recalibration approach

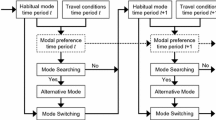
Aimed at developing a more flexible recalibration approach to transfer HMMs for application purposes, we propose a Bayesian conditional recalibration method that relaxes the rigidity of using scale/constant parameters. Instead, the proposed method directly recalibrates the systematic utilities and maps the prediction to enhanced accuracy. The modeling flowchart (using dynamic travel mode choice as an example) is illustrated in Fig. 2.

Fig. 2

A Bayesian conditional recalibration approach for travel demand model transfers

The estimated choice model predicts systematic utility functions based on a local or future-year dataset where the model is transferred to. Different utility values are converted into confidence scores for different travel modes (indicating the strength of the decision that the empirical observation chooses mode m). Note that the score may not necessarily match the local data well. Typically, this score is represented by log-odds defined using the following equation. This measurement transfers the original scale of choice probability (i.e. [0, 1]) to a space [− ∞, + ∞], where different continuous distributions are applicable.

$$s_{m} \left( E \right) = \log {\raise0.7ex\hbox{${p\left( m \right)}$} \!\mathord{\left/ {\vphantom {{p\left( m \right)} {\left( {1 - p\left( m \right)} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {1 - p\left( m \right)} \right)}$}}$$

(9)

The log-odd statistics and predicted probabilities may not match the observed probabilities. To transfer the choice model, it is necessary to perform a mapping of the model predictions to actual observations. This mapping is represented by a series of posterior calibration functions based on Bayes’ rule. Conditioned on each mode alternative, a probability density estimator f is produced.

$$p\left( {s|m} \right)\,\sim\,f\left( s \right)$$

(10)

Here, various distributions can be employed to approximate the distribution f. For enhancing the performance, asymmetric posterior functions can be adopted here to improve accuracy. For instance, an asymmetric Laplace distribution can be produced by mixing two exponentials:

$$p\left( {s|\theta ,\alpha ,\beta } \right) = \left\{ \begin{aligned} \frac{\alpha \beta }{\alpha + \beta }\exp \left[ { - \alpha \left( {\theta - s} \right)} \right]\;s \le \theta \hfill \\ \frac{\alpha \beta }{\alpha + \beta }\exp \left[ {\beta \left( {\theta - s} \right)} \right]\;s > \theta \hfill \\ \end{aligned} \right.$$

(11)

These functions map score s to the actual choice probabilities. In other words, the family of posterior calibration functions adjusts the utilities estimated by the HMM to approximate the unobserved distribution of utility values for the local/future year dataset. Then, Bayes’ rule and the choice priors are used to obtain the estimate:

$$p\left( {m|s} \right) = \frac{{p\left( m \right)p\left( {s|m} \right)}}{{\sum\nolimits_{{C \in \varvec{M}}} {p\left( C \right) \cdot p\left( {s|C} \right)} }}$$

(12)

Data

The longitudinal data used in this study came from the Puget Sound Transportation Panel (PSTP), which was conducted from 1989 to 2002 in the Puget Sound Region. Around 1700 households in the four-county metropolitan area participated in the 10-wave travel panel survey. The first wave of PSTP took place in the fall of 1989. Each wave includes socioeconomic information of the households and 2-day travel diaries. Approximately 20% of the samples left the panel between waves and were replaced by new households. The original model is estimated using the dataset that consists of the first six waves of travel behavior data. A total number of 336 individuals whose mode choices have been observed in each of the first six waves formed our panel dataset. Then, the next four waves are reserved to perform the transferability analysis. Descriptive statistics of the entire dataset are presented in Table 1.

Table 1 Descriptive statistics

As the first general-purpose travel panel survey in the US, PSTP data is rich in long-run travel behavior evolution. Figure 3 demonstrates the commute travel mode share change over time. Five alternative travel modes are identified in this study: drive-alone, carpool, transit, bike, and walk. We can observe a small expansion in the drive alone mode while transit and walk shares drop. The travel time and cost skims between each origin–destination pair for each transportation mode were provided by the Puget sound travel demand model.

Fig. 3

Travel mode share over the ten-wave time period (Xiong et al. 2015)

Analysis experiments and results

Transferability of hidden Markov model

This section focuses on evaluating the transferability of the HMM models. An HMM model estimated using the first six waves of data is applied to forecast individual mode choice for wave 7–10 data. Estimating HMM models would need at least two waves of data (i.e. base-year data and future-year data). For comparison purposes, a multinomial logit (MNL) model and a mixed logit (ML) model are estimated using exactly the same dataset and are applied to wave 7–10 data as well. The parameterization of the utility functions used in these three models follows a similar construct. The systematic utility functions for MNL/ML and for each HMM hidden state are given below:

$$\begin{aligned} & U_{drive} = \beta_{0,drive} + \beta_{1} \cdot t_{drive} + \beta_{4} \cdot c_{drive} + \beta_{5} \cdot income \cdot c_{drive} + \beta_{6} \cdot numveh/hhsize \\ & U_{carpool} = \beta_{0,carpool} + \beta_{1} \cdot t_{carpool} + \beta_{4} \cdot c_{carpool} + \beta_{5} \cdot income \cdot c_{carpool} + \beta_{7} \cdot numveh/hhsize \\ & U_{transit} = \beta_{0,transit} + \beta_{1} \cdot t_{transit} + \beta_{2} \cdot t_{access} + \beta_{4} \cdot c_{transit} + \beta_{10} \cdot buspass \\ & U_{walk} = \beta_{0,walk} + \beta_{2} \cdot t_{walk} + \beta_{8} \cdot male \\ & U_{bike} = \beta_{0,bike} + \beta_{3} \cdot t_{bike} + \beta_{9} \cdot male \\ \end{aligned}$$

(13)

where t and c denote different mode-specific travel times and costs, respectively; income is a dummy variable indicating individuals with higher household income level (higher than $50,000 per year); numveh denotes the number of vehicles owned by a household; hhsize is the household size; buspass is a dummy variable indicating the possession of a bus pass; male is a dummy indicating male travelers. $\beta$ denotes the coefficients to be estimated. Among them, the coefficients for in-vehicle travel time and travel costs are assumed to be lognormally distributed in the mixed logit (ML) model: $- \ln \beta \,\sim\,N\left( {\mu , \sigma } \right)$. The lognormal assumption is typically used for coefficients that are known to have the same signs, such as cost and travel time (Train 2009). The estimation results of the three models are summarized in Table 2.

Table 2 The estimation results of MNL, ML, and HMM models

The estimated coefficients have reasonable signs and statistical significance. In terms of the goodness-of-fit, the HMM model does outperform the MNL and ML models. A main advantage is the identification of two hidden states and the dynamic transition in between. State 1 can be labeled as a habitual driving state where the constant for drive alone mode is positive and has a dominating effect on utility. State 2 can be labeled as a time/cost-sensitive state where the coefficients for time and cost variables indicate a higher sensitivity. Moreover, the HMM transition model further depicts the dynamic movements between the two hidden states. Taking the $p^{{\left( {1,2} \right)}}$ model as an example, the negative coefficients for all variables indicate a behavioral inertia for travelers to move from state 1 to 2. This inertia for staying in state 1 (habitual driving) is stronger for individuals in life stage 2 (i.e. in a family with school-age kids) or life stage 3 (in a single-adult household). Readers interested in the details of the HMM travel behavior model can find the empirical explanations, value of travel time estimates, and model sensitivities in Xiong et al. (2015).

We have also measured the transferability of the MNL, ML, and HMM when applying them directly to the testing samples (wave 7, 8, 9, and 10). Different performance measures introduced in “Methodologies” section are used to quantitatively measure and compare the direct transferability, as shown in Table 3. Results for four waves are obtained. It is found that the HMM model has a consistently higher transferability when compared to its counterparts, MNL and ML models. When applied directly to the four waves of data, the HMM model has a higher predicting accuracy (hit-ratio) of 60–65%, while the hit-ratio of MNL remains around 57–63%. Comparing other performance measures, the HMM model has significantly more desirable performance for the four experiments with respect to mean squared errors and total squared error. HMM has less favorable log-loss measures, mainly due to the more complex modeling structure and parameterizations. We will show that the log-loss, among other performance measures, are greatly improved from the proposed Bayesian conditional recalibration approach.

Table 3 Transferability performance measures for MNL, ML, and HMM models

One reasonable explanation for the superiority of the HMM model is that it successfully incorporates the time-varying heterogeneity that influences travelers’ mode choice over time, while conventional travel demand models can only statistically cover cross-sectional factors. The results presented in this section provide quantitative evidence of temporal transferability for the family of HMM models and illustrate its capability in travel demand forecasting applications.

Transfer-scaling recalibration results

To further recalibrate the estimated model for enhanced transferability, the transfer-scaling method is applied to the dataset as a benchmark recalibration. The estimated constant and scaling parameters for transferring the model to wave 10 data are reported in Table 4. These variables represent the changes made based on wave 10 data, compared to the original estimates in Table 2. Results for the other waves are omitted but are available from the authors. The transfer-scaling method successfully adjusts the alternative specific constants and scales for the utility functions and the transition probability functions. It is found that habitual drivers (State 1) would be more likely to use drive-alone, carpool, and active modes in wave 10, because of their positive constants and reduced scales of disutility (i.e. the scale coefficients are less than one). Drive-alone has the lowest scale coefficient compared to carpool and walk. Lower scale coefficient leads to smaller disutility, especially for trips of longer distance. This indicates that drive-alone is still the most dominant travel mode in the future-year scenario (wave 10 data were collected in the year of 2002). For shorter-distance travels, on the other hand, the effect from the constant coefficient becomes more significant in the model, showing that habitual drivers are more willing to consider other alternative modes for shorter trips. Time/cost-sensitive travelers (State 2) have a higher propensity towards choosing carpool mode. This is based on the positive constant for carpool mode and negative constants for the other modes. In the meantime, they tend to have an increased utility scale for drive and carpool modes, indicating a decreased marginal probability of choosing drive-alone or carpool for trips with higher travel times and costs.

Table 4 Transfer scaling estimation results using the wave 10 data

The recalibration results for transition matrix are also obtained. Negative and significant constant coefficient is found for the probability function of transition from State 2 to 1. It depicts that in the future-year scenario, time/cost-sensitive travelers become more reluctant to switch their preference state. Other variables for the transition matrix are insignificant, which suggests that the transition parameters are already relatively more transferable between different time points. Judging by the findings obtained from “Transferability of hidden Markov model” and “Transfer-scaling recalibration results” sections, it is believed that the HMM method has higher transferability, when compared with cross-sectional MNL models. This dynamic modeling approach can and should be incorporated for any future-year prediction in planning/policy analysis.

Bayesian recalibration results

Two different continuous statistical distributions are applied in this paper as Bayesian recalibration functions: an asymmetric Gaussian mixture distribution and a Gaussian kernel density (GKD) distribution. The calibration is conducted on each alternative specific utility function to perform a mapping from model-predicted probabilities to actual observation. Log-odds are used to transfer the original scale of choice probability (i.e. [0, 1]) to a space of [− ∞, + ∞] in order to fit in different continuous distributions. Figure 4 illustrates the estimated posterior distributions for the calibration of probabilities for choosing the drive-alone mode. The estimated posteriors for other travel modes are available in the “Appendix”.

Fig. 4

Estimated drive-alone choice conditional log-odd densities versus the actual densities of the test data (wave 7, 8, 9, and 10)

In the subfigures, the curves of the test data represent the actual densities of log-odds for choosing the drive-alone mode. In general, log-odds distribute over the positive spectrum and skew toward the left side, indicating a higher propensity of choosing the drive-alone mode. The fits of the two statistical functions represent a qualitative comparison between using different distributions to approximate the conditional densities. Both the asymmetric distribution and the kernel density functions seem to fit the test data well.

As mentioned earlier, the recalibration approach maps the estimated log-odd scores to the actually observed choice probabilities. A concern is how to evaluate this proposed approach and compare it with existing approaches, such as transfer scaling. Measurements explained in “Transferability performance measures” section are employed here to assess the quality of the probability estimation. A better performance based on these measures can be termed improved “transferability”, while it actually indicates overall higher prediction accuracy. Performance measures are reported in Table 5.

Table 5 Performance measures for recalibrating the HMM model using transfer scaling, GEV-based Bayesian approach, and Gaussian-based Bayesian approach

Based on the performance measures, both the GKD and the Gaussian mixture calibration functions outperform the widely used transfer-scaling method. The average log-loss and total log-likelihood statistics are reduced greatly in all four experiments. The mean-squared error statistics are improved from near 0.40 to 0.29–0.34. It is worth noting that more favorable statistical distributions (e.g., compound distributions that mix two different types of distributions) can be further tested in order to enhance the goodness-of-fit.

This section demonstrated the transferability of the HMM model and quantitatively evaluated the performance of the proposed Bayesian recalibration approach. HMM enjoys more desirable performance measures when applied to demand forecasting in mode choice. This application context is temporally different and thus can be noted as a “temporal-transferring”. The results suggest that the HMM model has a higher temporal transferability. How it performs when transferred to a different location (i.e., spatial transferring) is another direction that is worth investigating in future research. Secondly, the proposed recalibration approach greatly enhances the model transferability. It improves the predicting accuracy by transforming the predicted probabilities to the actually observed probabilities. Without any presumptions on parameterization, the proposed approach is flexible enough and only lets the data dictates itself. It can be easily adapted and employed in any real-world policy and planning application.

Conclusions

In this paper, we aim at measuring and enhancing the transferability of an emerging dynamic travel behavioral analysis method, hidden Markov models (HMM). To the best of the authors’ knowledge, HMM has not yet been widely applied in transportation planning and policy analysis. Compared to standard modeling tools such as MNL and ML models, HMM successfully incorporates the time-dependent heterogeneity and has higher prediction accuracy in predicting the choices. Nevertheless, HMM has more complex modeling structure and require multiple years of data for model estimation (need two waves of behavioral data, at minimum). This may prevent a researcher or policy maker from developing its own HMM models for places with limited data, and thus has highlighted the research needs in transferring HMM models that are already developed for different application purposes, such as future-year scenarios, transferring to another study area, etc.

To achieve this, we employ ten rounds of panel survey data to test an estimated HMM model’s transferability and compare it with MNL and ML models. The first six waves of data are employed as the estimation dataset, while the latter four waves are reserved as the model transferring dataset. HMM’s transition matrix component takes into account the time-varying heterogeneity and thereby plays an important role in enhancing the transferability of this type of model. Our transferability analysis has verified that HMM models do have higher transferability in the analyzed scenarios, when compared with MNL and ML models.

Then, in order to further enhance the transferability of HMM, a more flexible recalibration approach is proposed and compared to traditional parameter-updating methods. Instead of recalibrating constants and scales for utility functions, our method focuses on gauging the utilities and prediction probabilities directly. The proposed method adjusts probabilities as posteriors by using data from the application context as a priori information. It is more flexible without making any assumptions about modeling parameters. A comparison between the proposed approach and transfer-scaling approach was conducted. Various goodness-of-fit measures were employed to assess the performance of the two approaches, including: hit ratio, log-likelihood, pseudo R-squared statistic, mean squared errors, and information loss. The results show that while both methods can significantly enhance the goodness-of-fit for the transferred model, the proposed approach outperforms the benchmark model for its superior performance.

The contributions of this paper are mainly three-fold. Firstly, the transferability of HMM models has been comprehensively analyzed. Literature on the transferability of dynamic travel demand models is limited. This paper successfully fills the gap and demonstrates the merits of HMM in dynamic travel behavioral analysis and travel demand forecasting. Second, this paper demonstrates how to improve the applicability of hard-to-estimate dynamic models by empirically testing the transfer scaling approach and our proposed Bayesian approach using a longitudinal dataset. Researchers and practitioners can use this paper as a useful reference when applying dynamic models in transportation planning practices. Finally, this paper has developed an alternative approach to calibrating and transferring travel demand models. Compared to the benchmark model that adjusts alternative-specific constants and scale parameters, the proposed Bayesian conditional recalibration enables us to fit local observations with much greater flexibility and with a similar number of parameters. The experiments comprehensively examine the performance of the proposed method on transfers to different time periods and have confirmed that the results and findings are stable and reliable.

Limitations of the study are fully acknowledged and future research shall address them. Compound distributions should be tested to further improve the goodness-of-fit of the proposed recalibration. This can be crucial for any data-driven statistical method. HMM models’ spatial transferability and the performance of our proposed method in different locations are worthwhile for exploration. Once again, we would like to emphasize the great potential of HMM models in travel demand forecasting and planning applications. Temporal and spatial applications can provide useful evidence for researchers and practitioners to move from static and cross-sectional analysis to dynamic modeling, which is visible when emerging data sources collected from global position system (GPS), smartphone applications, and social networks are readily available.

Appendix

See Figs. 5, 6, 7 and 8.

Fig. 5

Estimated carpool choice conditional log-odd densities versus the actual densities of the test data (wave 7, 8, 9, and 10)

Fig. 6

Estimated transit choice conditional log-odd densities versus the actual densities of the test data (wave 7, 8, 9, and 10)

Fig. 7

Estimated walk choice conditional log-odd densities versus the actual densities of the test data (wave 7, 8, 9, and 10)

Fig. 8

Estimated bike choice conditional log-odd densities versus the actual densities of the test data (wave 7, 8, 9, and 10)