Dynamical optical soliton solutions and behavior for the nonlinear Schrödinger equation with Kudryashov’s quintuple power law of refractive index together with the dual-form of nonlocal nonlinearity

Abstract

In this work, we use symbolic computation and ansatz function schemes, to investigate the soliton solutions for the nonlinear Schrödinger equation (NLSE) along with Kudryashov’s quintuple self-phase modulation system (KQSPMS) including dual-form of nonlocal nonlinearity (DFNLN). We initially determine the ordinary differential (OD) form for this model through a variable transformation. Then we introduce numerous new dynamical soliton types: the M-shaped rational soliton, the M-shaped interaction between one and two stripe solitons, the periodic cross-M-shaped rational (PCMR) soliton, the periodic cross-kink (PCK) soliton, multi-waves, and the homoclinic breather soliton. Secondly, we determine the partial differential (PD) form for this model through a variable transformation. Moreover, a lump soliton, a periodic wave, a rogue wave, a lump interaction with a periodic and kink wave, and three different types of breather soliton will obtain. We’ll demonstrate these solutions’ unique structure and extremely interesting interaction behavior. We’ll also use graphs (3-D and contour plots) to discuss the dynamics of the results after setting the parameters to the proper values.

1 Introduction

In the domains of mathematics and physical sciences, including chemistry, biology, and engineering, nonlinear partial differential equations (PDE) play a fundamental role in the resolution of numerous problems. Higher order NLSEs are the main nonlinear optics sectors in nonlinear PDEs that interpret the proliferation of nonlinear optics, particularly short pulses in optical fibers, and have significant applications in telecommunication systems and ultrafast signal routing, etc (Arora et al. 2022; Häger and Pfister 2018; Nandi et al. 2022; Aly 2015; Ma and Li 2018; Li and Ma 2018; Ma et al. 2023; Li et al. 2024). The proposed NLSE is the most realistic optical fiber theory that can explain the spread of ultra-short beats, unstable media, and time-unsettling impact in an imperceptibly steady manner. This model has numerous applications in the fields of medicine, media communication, material science, clinical research, and other branches of science. Nonlinear models in fluid mechanics, condensed matter physics, and optics are significantly impacted by the NLSE (Aly 2014; Inc et al. 2019; Ma 2019; Guan and Li 2020). There are many well-known NLSEs, including the derivative NLSE, the Fokas-Lenells equation (Aly 2016), the Biswas-Arshed (BA) equation (Iqbal et al. 2019; Safi-Ullah et al. 2022), the coupled NLSE (Jhangeer et al. 2021), and various others.

Soliton solutions exist for many precisely solvable models, such as the NLSE, coupled NLSE, and KdV equation (Rahman et al. 2021). There are various new methods for obtaining soliton solutions, including; generalized exponential rational function technique (Wang et al. 2023), $(\frac{G'}{G^2})$ -expansion scheme (Bilal et al. 2021), $\Phi ^6$ -model expansion technique (Seadawy et al. 2021), $\exp ((-\frac{\psi '}{\psi }) (\eta ) )$ -expansion method (Ghaffar et al. 2020), sub-ODE approach (Rizvi et al. 2020), Kudryashove scheme (Gaber et al. 2019), and many others.

Solitary waves can arise when the effects of dispersion and nonlinearity are precisely balanced. While nonlinearity tends to make the slope steeper, dispersion attempts to flatten it. The solitary wave emerges between these two dangerous, destructive forces. So, the balance between nonlinearity and dispersion is what causes solitary waves to exist (Ma 2019; Chen et al. 2022; Li 2020; Gai et al. 2019). As a result, the solitary waves are enormously strong. Solitons or solitary waves cannot be accurately described by linear equations. Solitons are single elevations, such as thickenings, which propagate as a singular entity with a specific speed, as opposed to ordinary waves, which represent a temporal periodical repetition of crests and troughs on a water surface and compressions of a density. Solitons have a unique history. Solitons can be categorized in a lot of different ways. As an example, here are topological and non-topological solitons (Seadawy et al. 2019; Aly 2024). By comparing their profiles, all solitons can be split into two groups: permanent and time-dependent, regardless of their topological nature. For example, all breathers have internal dynamics, even though they are static, but kink solitons have a permanent pattern. As a result, their shape changes over time. The third technique for categorizing solitons is to use nonlinear equations to explain their evolution (Ma and Li 2024a, b).

Many of the solitons are also classified on the basis of shapes like lump, kink, rogue, M-shaped, and breather solitons. Analytically, lump solitons are localized throughout all space. Lump wave applications are very wide, just like distant ghost waves that form and dissolve unpredictably and uncertainly. Rogue waves with an amplitude of more than 18 ms are powerful nonlinear waves capable of causing massive damage, even to giant ships. They are noticeably larger than regular sea waves. There is no consistency in how and when they appear (Olagnon 2017; Korpinar et al. 2020; Aly 2024; Jia et al. 2021; Guan and Li 2019; Aly 2020). Rogue wave solitons are extremely potent solutions that have been seen in a wide range of physical systems, from oceanography to optics. These rogue waves are very unpredictable because they appear suddenly and unexpectedly. As a result, when trying to solve nonlinear equations, researchers must pay particular attention to them. Kinky solitons, which are nonlinear waves with self-trapping characteristics, are also closely related to them. Bell-type solitons are another type of solitons, similar to rogue wave solitons but with lower energies or amplitudes. Bell-type solitons are typically employed in shallow water modeling and for research into how turbulence affects rogue wave solitons (Ma 2022; Feng and Zhang 2018; Belić et al. 2022). These different kinds of soliton are all interconnected and can be used to resolve a wide range of nonlinear equations. Researchers can better understand rogue waves, kinky solitons, and other physical phenomena by making use of the power of lump and breather solitons (Li and Guan 2021). In hybrid wave solutions, the interaction of a bell-type soliton and a rogue wave soliton produces bright and dark faces. Breather is characterized as a type of soliton that can occur and propagate periodically in a local and oscillating manner. For the sine-Gordon equation, the detailed breather solution was initially determined. The breather solution to the focused NLSE is another typical example. The generalized breather, the Kuznetsov-Ma breather, and the Akhmediev breather are the three different types of breathers (Guan and Li 2019; Kuznetsov 1977; Ma 1979; Li and Ma 2020; Ma 2020; Ali et al. 2024). Some soliton solutions of these kinds are studied in (Rizvi et al. 2022; Ashraf et al. 2022; Rizvi et al. 2020, 2022; Uthayakumar et al. 2024; Seadawy et al. 2021; Safi-ullah et al. 2020; Safi-Ullah et al. 2022; Rizvi et al. 2022, 2021, 2021; Ma et al. 2020; Younas et al. 2022; Seadawy et al. 2022, 2022; Bashir et al. 2022; Batool et al. 2022; Seadawy et al. 2022). By focusing on smooth and finite-valued solutions like solitons, breathers, rogue waves, periodic waves, etc., researchers can learn more about the system’s underlying dynamics and how various parameters affect the solutions. For instance, the interaction and energy transition between breathers and rogue waves in a generalized NLSEs with two higher-order dispersion operators is crucial because it can provide insight into how different nonlinearities interact in optical fibers (Li and Ma 2023; Meng and Guo 2022). By examining mixed structures of optical breathers and rogue waves in an inhomogeneous fiber system with a variable coefficient, it is also possible to comprehend the implications of various sorts of inhomogeneities on the solutions (Seadawy et al. 2022; Rizvi et al. 2022a, b, c; Uthayakumar et al. 2020). The dimensionless structure of NLSE having KQSPMS together with DFNLN studied in this paper is given by Ekici (2022),

$$\begin{aligned}{} & {} i \psi _t + b \psi _{xx} + \left[ c_1 |\psi |^{2m - 2n} + c_2 |\psi |^{2m - n} + c_3 |\psi |^{2m} +c_4 |\psi |^{2m + n} +c_5 |\psi |^{2m + 2n}\right. \nonumber \\{} & {} \left. \quad +c_6 (|\psi |^r)_{xx} + c_7 (|\psi |^{2r})_{xx} \right] \psi = 0. \end{aligned}$$

(1)

Here $\psi (x,t)$ is the complex-valued nonlinear wave function, and the independent variables x and t are, correspondingly, the spatial and temporal components. The first term denotes linear temporal evolution, with b expressing the coefficient of group velocity dispersion, while $c_j$, for $1 \le j \le 5$ is the self-phase modulation, suggested by Kudryashov (2021). The coefficients of two types of nonlocal nonlinearity are $c_6$ and $c_7$, respectively. m represents the order of the medium’s nonlinear response. It is usually a positive integer and relates to how strong the nonlinear effect is in the medium. The quintuple power law of the refractive index’s order is denoted by n. It is typically a positive integer as well. The nonlocal nonlinearity’s range is denoted by r. It is usually a positive real number and relates to the area over which the medium’s nonlinear response is averaged.

2 Mathematical analysis of the NLSE in OD form

Here, we’ll discuss the transformation of our model into an ordinary differential form. In order to begin with the solution to Eq. (1), the initial structural form is described as Biswas et al. (2017),

$$\begin{aligned} \psi (x,t) = u(\xi ) ~ e^{i \varphi (x, t)} \end{aligned}$$

(2)

where $u(\xi )$, is known as the wave envelope and describes the shape of the wave. The function of space and time, $\varphi (x, t)$, is known as the wave phase and describes the space and time dependence of the wave.

$$\begin{aligned} \xi = x - \nu t, \quad \quad \varphi (x, t) = -l x + p t + q. \end{aligned}$$

Here $\nu$ is the speed of soliton, l is the frequency, p is the wave number and q represents the phase constant. By using Eq. (2) into Eq. (1) we obtain real and imaginary parts. The real part gives;

$$\begin{aligned}{} & {} -(b l^2 + p) u^{2n + 2} + c_1 u^{2m + 2} + c_2 u^{2m + n + 2} + c_3 u^{2m + 2n + 2} + c_4 u^{2m + 3n + 2} + c_5 u^{2m + 4n + 2} + \nonumber \\{} & {} c_6 r(r-1) u^{2n + r} (u')^2 + 2 c_7 r(2r-1) u^{2n + 2r} (u')^2 + b u^{2n + 1} u'' + c_6 r u^{2n + r + 1} u''\nonumber \\{} & {} \quad + 2 c_7 r u^{2n + 2r + 1} u'' = 0, \end{aligned}$$

(3)

while the imaginary part leads the soliton’s velocity to rise as;

$$\begin{aligned} \nu = - 2 b l. \end{aligned}$$

(4)

Balancing $u^{2m + 4n + 2}$ with $u^{2n + 2r} (u')^2$ or $u^{2n + 2r + 1} u''$ leads to,

$$\begin{aligned} m N + n N = r N + 1. \end{aligned}$$

(5)

Suppose that $r = n$. Then Eq. (1) can be written as,

$$\begin{aligned}{} & {} i \psi _t + b \psi _{xx} + \left[ c_1 |\psi |^{2m - 2n} + c_2 |\psi |^{2m - n} + c_3 |\psi |^{2m} +c_4 |\psi |^{2m + n} +c_5 |\psi |^{2m + 2n}\right. \nonumber \\{} & {} \left. \quad +c_6 (|\psi |^n)_{xx} + c_7 (|\psi |^{2n})_{xx} \right] \psi = 0, \end{aligned}$$

(6)

and Eq. (3) shapes up,

$$\begin{aligned}&-(b l^2 + p) u^{2n + 2} + c_1 u^{2m + 2} + c_2 u^{2m + n + 2} + c_3 u^{2m + 2n + 2} + c_4 u^{2m + 3n + 2} + c_5 u^{2m + 4n + 2} + \nonumber \\&c_6 n(n-1) u^{3n} (u')^2 + 2 c_7 n(2n-1) u^{4n} (u')^2 + b u^{2n + 1} u'' + c_6 n u^{3n + 1} u'' + 2 c_7 n u^{4n + 1} u'' = 0. \end{aligned}$$

(7)

From Eq. (5) or by balance principle applied in Eq. (7), one reaches $N = 1/m$. Therefore the transformation is:

$$\begin{aligned} u = \phi ^{\frac{1}{m}}. \end{aligned}$$

(8)

By using this transformation, Eq. (7) turns into:

$$\begin{aligned}{} & {} c_1 m^2 \phi ^4 + c_2 m^2 \phi ^{\frac{n}{m}+4} - m^2 (b l^2 + p) \phi ^{\frac{2n}{m}+2} + c_3 m^2 \phi ^{\frac{2n}{m}+4} + c_4 m^2 \phi ^{\frac{3n}{m}+4} + c_5 m^2 \phi ^{\frac{4n}{m}+4} \nonumber \\{} & {} \quad - b(m-1) \phi ^{\frac{2n}{m}} (\phi ')^2 + c_6 n(n-m) \phi ^{\frac{3n}{m}} (\phi ')^2 - 2 c_7 n(m-2n) \phi ^{\frac{4n}{m}} (\phi ')^2 + b m \phi ^{\frac{2n}{m} + 1} \phi '' \nonumber \\{} & {} \quad + c_6 m n \phi ^{\frac{3n}{m} + 1} \phi '' + 2 c_7 m n \phi ^{\frac{4n}{m} + 1} \phi '' = 0. \end{aligned}$$

(9)

Now, choosing $n = \Im m$ for $\Im \ge 1$ in Eq. (9), the model under examination can recover from soliton and other solutions. Let’s say $n = 2 m$. In this scenario, Eq. (9) becomes,

$$\begin{aligned}{} & {} c_1 m^2 + c_4 m^2 \phi ^6 + c_5 m^2 \phi ^8 + (b - b m) (\phi ')^2 + m^2 \phi ^2 (c_2 - b l^2 - p + 2 c_6 (\phi ')^2) \nonumber \\{} & {} \quad +m^2 \phi ^4 (c_3 + 12 c_7 (\phi ')^2) + b m \phi \phi '' + 2 c_6 m^2 \phi ^3 \phi '' + 4 c_7 m^2 \phi ^5 \phi '' = 0. \end{aligned}$$

(10)

In the next sections, we’ll use symbolic computation and ansatz function schemes to evaluate the soliton solutions for our governing model.

2.1 M-shaped rational soliton

By using logarithmic transformation $\phi = 2 (\ln g)_{\xi }$, Eq. (10) transforms into the following form,

$$\begin{aligned}{} & {} c_1 m^2 g^8 + 256 (c_5 + 5 c_7) m^2 g_\xi ^8 -4 b (2 + m) g^5 g_\xi ^2 g_{\xi \xi } - 160 c_6 m^2 g^3 g_\xi ^4 g_{\xi \xi } - 2304 c_7 m^2 g g_\xi ^6 g_{\xi \xi } + \nonumber \\{} & {} 32 m^2 g^2 g_\xi ^4 \big ( (2 c_4 +3 c_6) g_\xi ^2 + 24 c_7 g_{\xi \xi }^2 + 8 c_7 g_{\xi } g_{\xi \xi \xi } \big ) + 4 g^6 \big ( m^2 (c_2 - b l^2 - p) g_{\xi }^2 - b (m - l) g_{\xi \xi }^2 + \nonumber \\{} & {} b m g_{\xi } g_{\xi \xi \xi } \big ) + 4 g^4 g_{\xi }^2 \big ( (b + b m + 4 c_3 m^2) g_{\xi }^2 + 8 c_6 m^2 g_{\xi \xi }^2 + 8 c_6 m^2 g_{\xi } g_{\xi \xi \xi } \big ) = 0. \end{aligned}$$

(11)

For M-shaped rational solution we choose a positive quadratic function g of the following type (Rizvi et al. 2022);

$$\begin{aligned} g(\xi ) = (a_1 \xi + a_2)^2 + (a_3 \xi + a_4)^2 + a_5, \end{aligned}$$

(12)

where $a_k (1 \le k \le 5)$ are all real parameters to be examined. Put g into Eq. (11) and compute the all powers of $\xi$ to get subsequent results on the following components:

$$\begin{aligned} a_3 = -\frac{a_1 a_2}{a_4}, \qquad b = \frac{a_4^2 c_1 - 2 a_1^2 p}{2 a_1^2 l^2}, \qquad a_5 = 0. \end{aligned}$$

(13)

Using these values in g, which implies the following solution in the form of $\phi$, we then use $u = \phi ^{\frac{1}{m}}$ and Eq. (2) to get the required solution.

$$\begin{aligned} \psi (x,t) = 4^{\frac{1}{m}} e^{i \big (q + p t - l x \big )} \bigg (\frac{a_1^2 l \big (a_4^2 c_1 t + a_1^2(l x - 2 p t) \big )}{a_4^4 c_1^2 t^2 + a_1^4 (l x - 2 p t)^2 +a_1^2 a_4^2 \big (l^2 -4 c_1 p t^2 +2 c_1 l t x \big )} \bigg )^\frac{1}{m}. \end{aligned}$$

(14)

Fig. 1

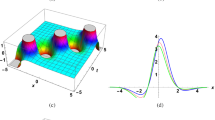
Plots of Eq. (14), at $m=1,~ l=0.5,~ p=-0.1,~ q=2,~ a_1=-3,~ a_4=-2,~ c_1=4$, respectively

2.2 Interaction of M-shaped rational soliton with one stripe soliton

To attain this solution we choose a positive quadratic function with an exponential function of the following type (Rizvi et al. 2022);

$$\begin{aligned} g(\xi ) = (a_1 \xi + a_2)^2 + (a_3 \xi + a_4)^2 + e^{a_5 \xi + a_6} + a_7, \end{aligned}$$

(15)

where $a_k (1 \le k \le 7)$ are all real parameters to be examined. Put g into Eq. (11) and compute the various powers of $\xi$ and exponential function, to get subsequent results on the following components:

$$\begin{aligned} a_2 = \frac{\sqrt{2 a_3^2 (-c_2 + p) - 5 a_4^2 c_1}}{\sqrt{c_1}}, \qquad c_1 = \frac{5 (c_2 - p)^2}{16 c_3}, \qquad b = - \frac{16 c_3 m^2}{1 + m}, \qquad a_1 = a_7 = 0. \end{aligned}$$

(16)

Using these values in g which implies the following solution,

$$\begin{aligned} \phi (\xi ) = \frac{2 \big (a_5 e^{a_6 + a_5 \xi } + 2 a_3 (a_4 + a_3 \xi ) \big )}{-4 a_4^2 + e^{a_6 + a_5 \xi } - \frac{32 a_3^2 c_3}{5 (c_2 - p)} + 2 a_3 a_4 \xi + a_3^2 \xi ^2 }. \end{aligned}$$

(17)

Using Eq. (17) into Eq. (8) and then in Eq. (2) to get the required solution.

$$\begin{aligned} \psi (x,t) = 2^\frac{1}{m} e^{i \big (q + p t - l x \big )} \bigg (\frac{a_5 e^{a_6 + a_5 (\Omega )} + 2 a_3 \big (a_4 + a_3 (\Omega ) \big )}{-4 a_4^2 + e^{a_6 + a_5 (\Omega )} - \frac{32 a_3^2 c_3}{5 (c_2 - p)} + 2 a_3 a_4 (\Omega ) + a_3^2 (\Omega )^2 } \bigg )^\frac{1}{m}, \end{aligned}$$

(18)

where $\Omega = - \frac{32 c_3 l m^2 t}{1 + m} + x$.

Fig. 2

Plots of interaction solution between M-shaped rational and one stripe soliton Eq. (18), at $m=5,~ l=1,~ p=-2,~ q=2,~ a_3=5,~ a_4=-3,~ a_5=3,~ a_6=-7,~ c_1=4,~ c_2=-0.08,~ c_3=0.06$, respectively

2.3 Interaction of an M-shaped rational soliton with two stripe solitons

To attain this solution we choose a positive quadratic function with two exponential functions as follows Rizvi et al. (2022);

$$\begin{aligned} g(\xi ) = (a_1 \xi + a_2)^2 + (a_3 \xi + a_4)^2 + e^{a_5 \xi + a_6} + e^{a_7 \xi + a_8} + a_9, \end{aligned}$$

(19)

where $a_k (1 \le k \le 9)$ are all real parameters to be measured. Put g into Eq. (11) and compute the various powers of $\xi$ and exponential functions, to get subsequent results on the following parameters:

$$\begin{aligned}{} & {} a_5 = \frac{a_1^2 + a_3^2}{3 a_3 a_4}, \quad a_7 = \frac{a_1^2 + a_3^2}{a_3 a_4}, \quad c_2 = b l^2 + p, \quad c_3 = - \frac{-9 b + 64 a_7^4 c_7 m}{144 m}, \quad \nonumber \\{} & {} c_4 = \frac{c_6}{4} + \frac{20 a_7^2 c_7}{9}, \quad c_5 = - \frac{3 \big (27 b + 36 a_7^2 c_6 m + 128 a_7^4 c_7 m \big )}{128 a_7^4 m}, \quad a_2 = a_9 = 0. \end{aligned}$$

(20)

Using these values in g which implies the following result,

$$\begin{aligned} \phi (\xi ) = \frac{2 \bigg (\frac{(a_1^2 + a_3^2) e^{a_6 + \frac{(a_1^2 + a_3^2) \xi }{3 a_3 a_4}}}{3 a_3 a_4} + \frac{(a_1^2 + a_3^2) e^{a_8 + \frac{(a_1^2 + a_3^2) \xi }{a_3 a_4}}}{a_3 a_4} + 2 a_1^2 \xi + 2 a_3 (a_4 + a_3 \xi ) \bigg ) }{e^{a_6 + \frac{(a_1^2 + a_3^2) \xi }{3 a_3 a_4}} + e^{a_8 + \frac{(a_1^2 + a_3^2) \xi }{a_3 a_4}} + a_1^2 \xi ^2 + (a_4 + a_3 \xi )^2 }. \end{aligned}$$

(21)

Using Eq. (21) into Eq. (8) and then in Eq. (2) to get the required solution.

$$\begin{aligned} \psi (x,t) = 2^{\frac{1}{m}} e^{i \big (q + p t - l x \big )} \bigg (\frac{\frac{(a_1^2 + a_3^2)}{3 a_3 a_4} e^{a_6 + \frac{\Delta }{3}} + \frac{(a_1^2 + a_3^2)}{a_3 a_4} e^{a_8 + \Delta } + 2 a_1^2 (2 b l t + x) + 2 a_3 \big (a_4 + a_3 (2 b l t + x) \big )}{e^{a_6 + \frac{\Delta }{3}} + e^{a_8 + \Delta } + a_1^2 (2 b l t + x)^2 + \big (a_4 + a_3(2 b l t + x) \big )^2 } \bigg )^\frac{1}{m}, \end{aligned}$$

(22)

where $\Delta = \frac{(a_1^2 + a_3^2)(2 b l t + x)}{a_3 a_4}$.

Fig. 3

Plots of interaction solution between M-shaped rational and two stripe soliton Eq. (22), at $m=5,~ p=0.05,~ l=-1,~ q=0.08,~ b=3,~ a_1=4,~ a_3=-5,~ a_4=3,~ a_6=4,~ a_8=-3$, respectively

2.4 PCMR soliton

To attain this solution we choose a positive quadratic function with cosine and hyperbolic cosine function as follows Rizvi et al. (2022);

$$\begin{aligned} g(\xi ) = (a_1 \xi + a_2)^2 + (a_3 \xi + a_4)^2 + z_1 \cos (a_5 \xi + a_6) + z_2 \cosh (a_7 \xi + a_8) + a_9, \end{aligned}$$

(23)

where $a_k (1 \le k \le 9)$ and $z_1, z_2$ are all real parameters to be measured. Put Eq. (23) into Eq. (11) and compute the various terms of $\xi$, $\cos$ and $\cosh$ functions, to get subsequent results on the following parameters:

$$\begin{aligned}{} & {} a_1 = - \sqrt{4 a_3 a_4 - a_3^2}, \quad a_5 = \frac{\sqrt{8 a_7^2 c_6 m^2 - b - b m - 4 c_3 m^2}}{2 \sqrt{c_6} m}, \quad a_2 = a_8 = 0, \nonumber \\{} & {} \quad a_7 = - \frac{\sqrt{3}\sqrt{2 c_4 + 3 c_6}}{14 \sqrt{c_7}}, \quad c_3 = \frac{637 c_6^2}{2500 c_7}, \quad c_4 = \frac{206}{75} c_6, \quad b = - \frac{4 c_3 m^2}{1 + m}. \end{aligned}$$

(24)

Using Eq. (24) into Eq. (23) which implies the following result;

$$\begin{aligned} \phi (\xi ) = 2 \bigg (\frac{2 a_1^2 \xi + 2 a_3 (a_4 + a_3 \xi ) - a_5 z_1 \sin (a_6 + a_5 \xi ) + a_7 z_2 \sinh (a_7 \xi )}{a_9 + a_1^2 \xi ^2 + (a_4 + a_3 \xi )^2 + z_1 \cos (a_6 + a_5 \xi ) + z_2 \cosh (a_7 \xi )} \bigg ), \end{aligned}$$

(25)

and the values of the parameters are mentioned in Eq. (23). Using Eq. (25) into Eq. (8) and then in Eq. (2) to get the required PCMR solution.

$$\begin{aligned}&\psi (x,t) = 625^{\frac{-1}{m}} e^{i (q + p t - l x)} \bigg ( \frac{\Omega - 125 \sqrt{26} c_7 \sqrt{\frac{c_6^2 m^2}{c_7}} (1 + m) z_1 \sin (\Delta _1) + 125 \sqrt{13 c_7} c_6 m (1 + m) z_2 \sinh (\Delta _2) }{\sqrt{c_6} c_7 m (1 + m) \big (a_9 - a_3 (a_3 - 4 a_4) \Delta ^2 + \big (a_4 + a_3 (\Delta ) \big )^2 + z_1 \cos (\Delta _1) + z_2 \cosh (\Delta _2) \big )} \bigg )^\frac{1}{m}, \end{aligned}$$

(26)

where $\Delta = x - \frac{1274 c_6^2\,l m^2 t}{625 c_7 (1 + m)}, \qquad \Delta _1 = a_6 + \frac{\sqrt{\frac{13 c_6^2\,m^2}{2 c_7}} (\Delta )}{5 \sqrt{c_6} m}, \qquad \Delta _2 = \frac{\sqrt{13 c_6} (\Delta )}{10 \sqrt{c_7}},$

and $\Omega = 4 a_3 a_4 \sqrt{c_6} m \big (-5096 c_6^2\,l m^2 t + 625 c_7 (1 + m) (1 + 4 x) \big ).$

Fig. 4

Plots of PCMR soliton solution Eq. (26), at $m=5,~ p=-1,~ l=2,~ q=-2,~ a_3=2,~ a_4=7,~ a_6=9,~ a_9=-3,~ c_6=6,~ c_7=8,~ z_1=-9,~ z_2=5$, successively

2.5 PCK soliton

We construct the following cosine and hyperbolic cosine function assumption with double exponential functions to seek this solution (Rizvi et al. 2022);

$$\begin{aligned} g(\xi ) = e^{-(a_1 \xi + a_2)} + z_0 e^{(a_1 \xi + a_2)} + z_1 \cos (a_3 \xi + a_4) + z_2 \cosh (a_5 \xi + a_6) + a_7, \end{aligned}$$

(27)

where $a_k (1 \le k \le 7)$, $z_0,$ $z_1,$ and $z_2$ all real parameters to be measured. Put Eq. (27) into Eq. (11) and compute the various terms of exp, $\cos$ and $\cosh$ functions, to get subsequent results on the following components:

$$\begin{aligned}{} & {} a_1 = \frac{\sqrt{-a_5^2 b - 2 c_2 m + 2 b l^2 m + 2 m p}}{\sqrt{3 b + 16 c_3 m + 8 a_5^2 c_6 m}}, \quad c_4 = - \frac{1}{4} c_6, \quad c_5 = - \frac{3}{8} c_7, \nonumber \\{} & {} \quad a_3 = \frac{\sqrt{-2 a_5^2 b - a_5^2 b m + 6 c_2 m^2 - 6 b l^2 m^2 - 6 m^2 p}}{\sqrt{-10 b + b m}}, \quad a_7 = 0. \end{aligned}$$

(28)

Using Eq. (28) into Eq. (27) which implies the following result;

$$\begin{aligned} \phi (\xi ) = 2 \bigg (\frac{-a_1 e^{-a_2 - a_1 \xi } + a_1 e^{a_2 + a_1 \xi } z_0 - a_3 z_1 \sin (a_4 + a_3 \xi ) + a_5 z_2 \sinh (a_6 + a_5 \xi )}{e^{-a_2 - a_1 \xi } + e^{a_2 + a_1 \xi } z_0 + z_1 \cos (a_4 + a_3 \xi ) + z_2 \cosh (a_6 + a_5 \xi )} \bigg ), \end{aligned}$$

(29)

and the values of the parameters are mentioned in Eq. (28). Using $\phi$ into Eq. (8) and then in Eq. (2) to get the required PCK solution.

$$\begin{aligned} \psi (x,t) =\, 2^{\frac{1}{m}} e^{i \big (q + p t - l x \big )} \bigg (\frac{\Delta _1 e^{- a_2 - \Delta _1 (2 b l t + x)} (e^{2(a_2 + \Delta _1 (2 b l t + x))} z_0 - 1) - \Delta _2 z_1 \sin (a_4 + \Delta _2 (2 b l t + x) ) + a_5 z_2 \sinh (\Omega )}{e^{- a_2 - \Delta _1 (2 b l t + x)} + e^{a_2 + \Delta _1 (2 b l t + x)} z_0 + z_1 \cos (a_4 + \Delta _2 (2 b l t + x) ) + z_2 \cosh (\Omega ) } \bigg )^\frac{1}{m}, \end{aligned}$$

(30)

where $\Delta _1 = \frac{\sqrt{-a_5^2 b + 2\,m \big (-c_2 + b l^2 + p \big )}}{\sqrt{3 b + 8 \big (2 c_3 + a_5^2 c_6 \big ) m}}$,   $\Delta _2 = \frac{\sqrt{-a_5^2 b (2 + m) + 6\,m^2 \big (c_2 - b l^2 - p \big )}}{\sqrt{b (-10 + m)}}$,   and   $\Omega = a_6 + a_5 (2 b l t + x)$.

Fig. 5

Plots of PCK soliton solution Eq. (30), at $m=3,~ p=0.4,~ l=-0.7,~ q=0.5,~ b=-2,~ a_2=8,~ a_4=3,~ a_5=-3,~ a_6=-1,~ c_2=-4,~ c_3=4,~ c_6=3,~ z_0=5,~ z_1=-2,~ z_2=2$, successively

2.6 Multi-waves soliton

To arrive at this solution, we construct the following double hyperbolic cosine relationship with a cosine function (Rizvi et al. 2022);

$$\begin{aligned} g(\xi ) = z_1 \cosh (a_1 \xi + a_2) + z_2 \cos (a_3 \xi + a_4) + z_3 \cosh (a_5 \xi + a_6), \end{aligned}$$

(31)

where $a_k (1 \le k \le 6)$, $z_1$, $z_2$ and $z_3$ all real parameters to be measured. Put g into Eq. (11) and compute the various terms of $\cos$ and $\cosh$ functions, to get subsequent results on the following components:

$$\begin{aligned}{} & {} a_1 = \frac{4 a_5^2 (m - 1)}{m^2}, \quad a_3 = - \sqrt{2 a_5^2 + \sqrt{3} \sqrt{2 a_1^4 + a_5^4}}, \quad c_2 = - \frac{9 c_3 c_7^2}{2 c_6^2}, \nonumber \\{} & {} b = - \frac{4 \big (c_3 - 8 a_5^2 c_6 + 48 a_5^4 c_7 \big ) m^2}{1 + m}. \end{aligned}$$

(32)

Using Eq. (32) into Eq. (31) which gives the following result;

$$\begin{aligned} \phi (\xi ) = 2 \bigg (\frac{-a_3 z_2 \sin (a_4 + a_3 \xi ) + a_1 z_1 \sinh (a_2 + a_1 \xi ) + a_5 z_3 \sinh (a_6 + a_5 \xi )}{z_2 \cos (a_4 + a_3 \xi ) + z_1 \cosh (a_2 + a_1 \xi ) + z_3 \cosh (a_6 + a_5 \xi )} \bigg ), \end{aligned}$$

(33)

and the values of the parameters are mentioned in Eq. (32). Using $\phi$ into Eq. (8) and then in Eq. (2) to get the required multi-waves solution.

$$\begin{aligned} \psi (x,t) = 2^{\frac{1}{m}} e^{i (p t - l x + q)} \bigg (\frac{\Delta _1 z_2 \sin (a_4 - \Delta _1 \Delta _2) + a_5 z_3 \sinh (a_6 + a_5 \Delta _2) + \frac{4 a_5^2 (m - 1) z_1 \sinh (a_2 + \frac{4 a_5^2 (m - 1)}{m^2} \Delta _2)}{m^2}}{z_2 \cos (a_4 - \Delta _1 \Delta _2) + z_3 \cosh (a_6 + a_5 \Delta _2) + z_1 \cosh (a_2 + \frac{4 a_5^2 (m - 1)}{m^2} \Delta _2) } \bigg )^{\frac{1}{m}}, \end{aligned}$$

(34)

where $\Delta _1 = \sqrt{2 a_5^2 + \sqrt{3} \sqrt{a_5^4 + \frac{512 a_5^8 (m - 1)^4}{m^8}}}$,   and   $\Delta _2 = \big (x - \frac{8 \big (c_3 - 8 a_5^2 c_6 + 48 a_5^4 c_7 \big ) l m^2 t}{1 + m} \big )$.

Fig. 6

Plots of multi-waves solution Eq. (34), at $p=-0.5,~ l=0.5,~ q=-1,~ m=5,~ a_2=-4,~ a_4=-2,~ a_5=0.2,~ a_6=-3,~ c_3=-2.4,~ c_6=4,~ c_7=-2.5,~ z_1=8,~ z_2=7,~ z_3=-6$, successively

2.7 Homoclinic breather

In order to find this solution, we build the following double exponential assumption with a cosine function (Rizvi et al. 2022);

$$\begin{aligned} g(\xi ) = e^{-\delta (a_1 \xi + a_2)} + z_0 e^{\delta (a_3 \xi + a_4)} + z_1 \cos \big (\lambda (a_5 \xi + a_6) \big ), \end{aligned}$$

(35)

where $a_k (1 \le k \le 6)$, $z_0$, $z_1$, $\delta$ and $\lambda$ are all real parameters to be investigated. Put g into Eq. (11) and compute the various terms of exp and $\cos$ functions, to get subsequent results on the following parameters:

$$\begin{aligned}{} & {} a_1 = (3 - 2 \sqrt{2}) a_3, \quad a_5 = \frac{\sqrt{\frac{55}{6}(3 - 2 \sqrt{2})} a_3 \delta }{\lambda }, \quad b = \frac{412 (2 \sqrt{2} -3) a_3^2 c_6 m^2 \delta ^2}{3 (5 + 7 m)}, \nonumber \\{} & {} c_3 = - \frac{13 (-239 + 266 m) (c_2 - p)}{72 (156 l^2 m^2 + a_5^2 (-67 + 58 m) \lambda ^2)}, \qquad a_2 = 0. \end{aligned}$$

(36)

Using Eq. (36) into Eq. (35) and then we use g into $\phi = 2 (\ln g)_{\xi }$ to get the following result;

$$\begin{aligned} \phi (\xi ) = 2 \bigg (\frac{a_3 \big ((2 \sqrt{2} -3) e^{(2 \sqrt{2} -3) a_3 \delta \xi } + e^{\delta (a_4 + a_3 \xi )} z_0 \big ) \delta - \sqrt{\frac{55}{6} (3 - 2 \sqrt{2})} a_3 z_1 \delta \sin (a_6 \lambda + \sqrt{\frac{55}{6} (3 - 2 \sqrt{2})} a_3 \delta \xi )}{e^{(2 \sqrt{2} -3) a_3 \delta \xi } + e^{\delta (a_4 + a_3 \xi )} z_0 + z_1 \cos (a_6 \lambda + \sqrt{\frac{55}{6} (3 - 2 \sqrt{2})} a_3 \delta \xi ) } \bigg ). \end{aligned}$$

(37)

Using $\phi$ into Eq. (8) and then in Eq. (2) to attain the required solution.

$$\begin{aligned} \psi (x,t) = 2^\frac{1}{m} e^{i (p t - l x + q)} \left( \frac{a_3 \big ((2 \sqrt{2} -3) e^{(2 \sqrt{2} -3) \Omega } + e^{a_4 \delta + \Omega } z_0 \big ) \delta - \sqrt{\frac{55}{6} (3 - 2 \sqrt{2})} a_3 z_1 \delta \sin (\sqrt{ \frac{55}{6} (3 - 2 \sqrt{2})} \Omega + a_6 \lambda )}{e^{(2 \sqrt{2} -3) \Omega } + e^{a_4 \delta + \Omega } z_0 + z_1 \cos (\sqrt{\frac{55}{6} (3 - 2 \sqrt{2})} \Omega + a_6 \lambda ) } \right) ^\frac{1}{m}, \end{aligned}$$

(38)

where $\Omega = a_3 \delta \big (x + \frac{824 (-3 + 2 \sqrt{2}) a_3^2 c_6 l m^2 t \delta ^2}{3 (5 + 7\,m)} \big )$.

Fig. 7

Plots of homoclinic breather solution Eq. (38), at $p=0.5,~ l=-1.5,~ q=-0.5,~ m=1,~ a_3=-0.3,~ a_4=2,~ a_6=-6,~ c_6=5,~ \delta =-2,~ \lambda =4,~ z_0=3,~ z_1=0.5$, successively

3 Mathematical analysis of the NLSE in PD form

In this section, we’ll discuss the transformation of our model into a partial differential form. In order to start with the solution to Eq. (1), the initial structural form is described as Taghizadeh et al. (2017),

$$\begin{aligned} \psi (x,t) = u(x,t) ~ e^{i \varphi (x,t)} \end{aligned}$$

(39)

where u(x, t) is the soliton’s amplitude component and the soliton’s phase is indicated by,

$$\begin{aligned} \varphi (x,t) = -l x + p t + q. \end{aligned}$$

Here l is the frequency, p is the wave number and q represents the phase constant. By using Eq. (39) into Eq. (1) we obtain real and imaginary parts;

$$\begin{aligned}&-\big (b l^2 + p \big ) u + b u_{xx} + c_1 u^{1 + 2m - 2n} + c_2 u^{1 + 2m - n} + c_3 u^{1 + 2m} + c_4 u^{1 + 2m + n} + c_5 u^{1 + 2m + 2n} - c_6 l^2 r \nonumber \\&\big (u^{2 + r} + r u^{3 + r} \big ) - 2 c_7 l^2 r \big (u^{2 + 2r} + 2 r u^{3 +2r} \big ) + c_6 r u^{1 + r} \big (r u_x^2 + u_{xx} \big ) + 2 c_7 r u^{1 + 2r} \big (2 r u_x^2 + u_{xx} \big ) = 0, \nonumber \\&u_t - 2 l \big (b + c_6 r u^{1 + r} + c_6 r^2 u^{2 + r} + 2 c_7 r u^{1 + 2r} + 4 c_7 r^2 u^{2 + 2r} \big ) u_x = 0. \end{aligned}$$

(40)

Using real part of Eq. (40) and suppose that $r = n$. Then Eq. (40) shapes up,

$$\begin{aligned}{} & -\big (b l^2 + p \big ) u + b u_{xx} + c_1 u^{1 + 2m - 2n} + c_2 u^{1 + 2m - n} + c_3 u^{1 + 2m} + c_4 u^{1 + 2m + n} + c_5 u^{1 + 2m + 2n} \nonumber \\{} &- c_6 l^2 n \big (u^{2 + n} \nonumber \\{} &+ n u^{3 + n} \big ) - 2 c_7 l^2 n \big (u^{2 + 2n} + 2 n u^{3 +2n} \big ) + c_6 n u^{1 + n} \big (n u_x^2 + u_{xx} \big ) \nonumber \\{} & + 2 c_7 n u^{1 + 2r} \big (2 n u_x^2 + u_{xx} \big ) = 0. \end{aligned}$$

(41)

By balance principle applied in Eq. (41), one reaches $N = 1/m$. Therefore the transformation is:

$$\begin{aligned} u = \phi ^{\frac{1}{m}}. \end{aligned}$$

(42)

Using this transformation, Eq. (41) turns into:

$$\begin{aligned}{} & {} m^2 \big ((c_1 - b l^2 - p) \phi ^2 + c_2 \phi ^3 + c_3 \phi ^4 + c_4 \phi ^5 + c_5 \phi ^6 - c_6 l^2 m^2 \phi ^{\frac{2}{m} +3} - 2 c_7 l^2 m \phi ^{\frac{1}{m} +4} \nonumber \\{} & {} \quad - 4 c_7 l^2 m^2 \phi ^{\frac{2}{m} +4} \big ) \nonumber \\{} & {} \quad - b (m -1) \phi _x^2 - c_6 (m -1) m \phi ^{\frac{1}{m} +1} \phi _x^2 + 4 c_7 m^2 \phi ^{\frac{2}{m} +2} \phi _x^2\nonumber \\{} & {} \quad + c_6 m^2 \phi ^{\frac{2}{m} +1} \phi _x^2 + b m \phi \phi _{xx} - m^2 \phi ^{\frac{1}{m} +3} \big (c_6 l^2 m \nonumber \\{} & {} \quad - 2 c_7 \phi _{xx} \big ) - m \phi ^{\frac{1}{m} +2} \big (2 c_7 (m -1) \phi _x^2 - c_6 m \phi _{xx} \big ) = 0. \end{aligned}$$

(43)

Now, choosing $n = \Im m$ for $\Im \ge 1$ in Eq. (43), the model under examination can recover from soliton and other solutions. Eq. (43) becomes,

$$\begin{aligned}{} & {} -m^2 (b l^2 + p) \phi ^2 + b \big (\phi _x^2 - m \phi _x^2 + m \phi \phi _{xx} \big ) + c_1 m^2 \phi ^2 + c_2 m^2 \phi ^3 + c_3 m^2 \phi ^4 + c_4 m^2 \phi ^5 + \nonumber \\{} & {} c_5 m^2 \phi ^6 - c_6 m \big (l^2 m^2 \phi ^2 + l^2 m^3 \phi ^3 - \phi _x^2 + m \phi _x^2 - m \phi \phi _x^2 - m \phi \phi _{xx} \big ) \phi ^2 - 2 c_7 m \big (l^2 m^2 \phi ^2 \nonumber \\{} & {} \quad + 2 l^2 m^3 \phi ^3 - \phi _x^2 + m \phi _x^2 - 2 m \phi \phi _x^2 - m \phi \phi _{xx} \big ) \phi ^3 = 0. \end{aligned}$$

(44)

In the next sections, we’ll use symbolic computation and ansatz function schemes to evaluate the lump soliton, periodic wave, rogue wave and different forms of breather solutions for our governing model.

3.1 Lump soliton

To obtain the solitary wave solutions we use the following travelling wave transformation as;

$$\begin{aligned} \phi = \frac{6}{\kappa } \big (\log f \big )_{x}, \end{aligned}$$

(45)

where $\kappa$ is a nonzero constant. Equation (45) transforms Eq. (44) into the following bilinear form;

$$\begin{aligned}{} & {} -5184 c_7 m^2 f_x^8 - 216 m f f_x^6 \big (\kappa (c_6 m + 2 c_7 + 2 c_7 m) f_x - 48 c_7 m f_{xx} \big ) \nonumber \\{} & {} + \kappa ^3 f^5 f_x^2 \big (-6 c_2 m^2 f_x + 2 b \kappa f_{xx} +b \kappa m f_{xx} \big ) - 36 m f^2 f_x^4 \bigg ( \big (c_6 \kappa ^2 + c_6 \kappa ^2 m + 36 m(c_5 - 4 c_7 l^2 m^2) \big ) f_x^2 \nonumber \\{} & {} - 12 \kappa \big (c_6 m + 2 c_7 + c_7 m) f_x f_{xx} +144 c_7 m f_{xx}^2 \bigg ) + \kappa ^4 f^6 \big (m^2 (b l^2 + p - c_1) f_x^2 + b(m -1) f_{xx}^2 - b m f_x f_{xxx} \big ) \nonumber \\{} & {} - \kappa ^2 f^4 f_x^2 \bigg ((b \kappa ^2 + b \kappa ^2 m +36 m^2 (c_3 - c_6 l^2 m)) f_x^2 - 36 c_6 (m -1) m f_{xx}^2 + 36 c_6 m^2 f_x f_{xxx} \bigg ) \nonumber \\{} & {} + 36 \kappa m f^3 f_x^3 \bigg ( \big (6 l^2 m^2(2 c_7 + c_6 m) -6 m c_4 \big ) f_x^2 - 6 (2 c_7(1 - m) + c_6 m) f_{xx}^2 + f_x \big (2 c_6 \kappa f_{xx} + c_6 \kappa m f_{xx} - 12 c_7 m f_{xxx} \big ) \bigg ) = 0. \end{aligned}$$

(46)

To seek the lump solution, we assume f as a polynomial function in the form Rizvi et al. (2022);

$$\begin{aligned} f = \mathfrak {B_1}^2 + \mathfrak {B_2}^2 + f_0, \end{aligned}$$

(47)

where

$$\begin{aligned} \mathfrak {B_1} = a_1 x + a_2 t + a_3, \qquad \mathfrak {B_2} = a_4 x + a_5 t + a_6, \end{aligned}$$

whereas $a_k (1 \le k \le 6)$ and $f_0$ are all real parameters to be examined. Put f into Eq. (46) and compute all coefficients of x and t to get subsequent results on the following components:

$$\begin{aligned}{} & {} a_1 = \sqrt{\frac{13}{3}} i a_4, \quad \kappa = m \sqrt{\frac{864 c_6 l^2 m - 864 c_3}{149 b m - 176 b}}, \quad p = -b l^2, \quad \nonumber \\{} & {} f_0 = \frac{8 a_4^2 b (149 m -176) \big (l^2 m (2 c_7 + c_6 m) -c_4 \big )}{45 c_2 m^2 (-c_3 + c_6 l^2 m)}, \quad a_2 = a_3 = 0. \end{aligned}$$

(48)

Using these parameters in f and f in Eq. (45), we then apply Eqs. (42) and (39) to obtain the following outcome,

$$\begin{aligned} \psi (x,t) = 2^{\frac{-1}{2 m}} 3^{\frac{-3}{2 m}} e^{i \big (q - l (b l t + x) \big )} \left( \frac{a_4 \big (3 a_6 + 3 a_5 t - 10 a_4 x \big )}{\Delta \bigg (\frac{8 a_4^2 b (149 m -176) \big (l^2 m (2 c_7 + c_6 m) -c_4 \big )}{45 c_2 m^2 (-c_3 + c_6 l^2 m)} - \frac{13 a_4^2 x^2}{3} + \big (a_6 + a_5 t + a_4 x \big )^2 \bigg )} \right) ^\frac{1}{m}, \end{aligned}$$

(49)

where $\Delta = m \sqrt{\frac{c_3 - c_6 l^2 m}{176 b - 149 b m}}$.

Fig. 8

Plots of lump soliton solution Eq. (49), at $b=2,~ q=3,~ l=-2,~ m=1,~ a_4=1,~ a_5=-5,~ a_6=-2,~ c_2=2,~ c_3=-2,~ c_4=-4,~ c_6=-8,~ c_7=5$, successively

3.2 Periodic waves

To seek the periodic wave solution, we assume f as a polynomial function with a cosine function as Rizvi et al. (2022);

$$\begin{aligned} f = \mathfrak {B_1}^2 + \mathfrak {B_2}^2 + d \cos (e_1 x + e_2 t) + f_0, \end{aligned}$$

(50)

where

$$\begin{aligned} \mathfrak {B_1} = a_1 x + a_2 t + a_3, \qquad \mathfrak {B_2} = a_4 x + a_5 t + a_6, \end{aligned}$$

whereas $a_k (1 \le k \le 6)$, d, $e_1$, $e_2$ and $f_0$ are all real parameters to be examined. Put f into Eq. (46) and compute all coefficients of x, t and $\cos$ function to get subsequent results on the following components:

$$\begin{aligned} a_3 = 2 a_4 \sqrt{\frac{c_7}{12 c_7 l^2 m^2 - 3 c_5}}, \quad e_1 = \frac{1}{2} \sqrt{12 l^2 m^2 - \frac{3 c_5}{c_7}}, \quad a_1 = a_6 = f_0 = 0. \end{aligned}$$

(51)

Using Eq. (51) into Eq. (50) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{6 \bigg (2 a_4 (a_5 t + a_4 x) - \frac{1}{2} \sqrt{-\frac{3 c_5}{c_7} + 12 l^2 m^2} d \sin (e_2 t + \frac{1}{2} \sqrt{-\frac{3 c_5}{c_7} + 12 l^2 m^2} x) \bigg )}{\kappa \bigg ((2 a_4 \sqrt{-\frac{c_7}{3 c_5 - 12 c_7 l^2 m^2}} + a_2 t)^2 + (a_5 t + a_4 x)^2 + d \cos (e_2 t + \frac{1}{2} \sqrt{-\frac{3 c_5}{c_7} + 12 l^2 m^2} x) \bigg )}. \end{aligned}$$

(52)

Using Eq. (52) into Eq. (42) then in Eq. (39) to attain the required periodic wave solution.

$$\begin{aligned} \psi (x,t) = 6^\frac{1}{m} e^{i (q + p t - l x)} \left( \frac{2 a_4 (a_5 t + a_4 x) - \frac{1}{2} \sqrt{-\frac{3 c_5}{c_7} + 12 l^2 m^2} d \sin (e_2 t + \frac{1}{2} \sqrt{-\frac{3 c_5}{c_7} + 12 l^2 m^2} x) }{\kappa \bigg ((2 a_4 \sqrt{\frac{c_7}{12 c_7 l^2 m^2 - 3 c_5}} + a_2 t)^2 + (a_5 t + a_4 x)^2 + d \cos (e_2 t + \frac{1}{2} \sqrt{12 l^2 m^2 -\frac{3 c_5}{c_7}} x) \bigg )} \right) ^\frac{1}{m}. \end{aligned}$$

(53)

Fig. 9

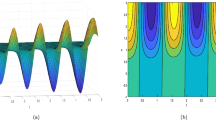
Plots of periodic waves solution Eq. (53), at $p=-0.5,~ l=0.8,~ q=-2,~ m=3,~ a_2=-5,~ a_4=-7,~ a_5=-5,~ e_2=3,~ c_5=-6,~ c_7=8,~ d=3,~ \kappa =5$, successively

3.3 Interaction between lump, periodic, and kink waves

For this solution, we suppose f as a polynomial function along with a cosine and exponential function as Rizvi et al. (2022);

$$\begin{aligned} f = \mathfrak {B_1}^2 + \mathfrak {B_2}^2 + z_1 \cos (e_1 x + e_2 t) + z_2 e^{e_3 x + e_4 t} + f_0, \end{aligned}$$

(54)

where

$$\begin{aligned} \mathfrak {B_1} = a_1 x + a_2 t + a_3, \qquad \mathfrak {B_2} = a_4 x + a_5 t + a_6, \end{aligned}$$

whereas $a_k (1 \le k \le 6)$, $e_k (1 \le k \le 4)$, $z_1$, $z_2$ and $f_0$ are all real parameters to be investigated. Put f into Eq. (46) and compute all coefficients of x, t, $\cos$ and exponential function to get subsequent results on the following parameters:

$$\begin{aligned} a_1 = - \frac{a_4 a_5}{a_2}, \quad e_3 = - \frac{\kappa \big (2 c_7 + c_6 m - 2 c_7 m \big )}{64 c_7 m}, \quad c_5 = \frac{5 c_3 c_4 (m + 2)}{3 c_2 (m + 1)}, \quad a_3 = a_6 = f_0 = 0. \end{aligned}$$

(55)

Using these parameters in Eq. (54) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{6 \bigg (2 a_4 (a_5 t + a_4 x) + \frac{2 a_4 a_5 (-a_2^2 t + a_4 a_5 x)}{a_2^2} + e_3 e^{e_4 t + e_3 x} - e_1 z_1 \sin (e_2 t + e_1 x) \bigg )}{\kappa \bigg ((a_5 t + a_4 x)^2 + (a_2 t - \frac{a_4 a_5 x}{a_2})^2 + e^{e_4 t + e_3 x} z_2 + z_1 \cos (e_2 t + e_1 x) \bigg )}. \end{aligned}$$

(56)

Using Eq. (56) into Eq. (42) then in Eq. (39) to attain the required interaction solution.

$$\begin{aligned} \psi (x,t) = 6^\frac{1}{m} e^{i \big (q + p t - l x \big )} \bigg (\frac{2 a_4 (a_5 t + a_4 x) + \frac{2 a_4 a_5 (-a_2^2 t + a_4 a_5 x)}{a_2^2} - \Omega - e_1 z_1 \sin (e_2 t + e_1 x)}{\kappa \big ((a_5 t + a_4 x)^2 + (a_2 t - \frac{a_4 a_5 x}{a_2})^2 + e^{e_4 t + \frac{\kappa \big (2 c_7 (m - 1) - c_6 m \big )}{64 c_7 m} x} z_2 + z_1 \cos (e_2 t + e_1 x) \big )} \bigg )^\frac{1}{m}, \end{aligned}$$

(57)

where $\Omega = \frac{e^{e_4 t + \frac{\kappa \big (2 c_7 (m - 1) - c_6 m \big )}{64 c_7 m} x} \kappa \big (-2 c_7 (m - 1) + c_6 m \big ) z_2}{64 c_7 m}$.

Fig. 10

Plots of interaction solution between lump periodic and kink wave Eq. (57), at $p=2,~ l=-3,~ q=-2,~ m=3,~ a_2=-5,~ a_4=5,~ a_5=-15,~ e_1=7,~ e_2=2,~ e_4=3,~ c_6=-2,~ c_7=8,~ z_1=6,~ z_2=-1,~ \kappa =5$, successively

3.4 Rogue wave

For this solution, we suppose f as a polynomial function along with a cosine hyperbolic function as Rizvi et al. (2022);

$$\begin{aligned} f = \mathfrak {B_1}^2 + \mathfrak {B_2}^2 + \cosh (e_1 x + e_2 t) + f_0, \end{aligned}$$

(58)

where

$$\begin{aligned} \mathfrak {B_1} = a_1 x + a_2 t + a_3, \qquad \mathfrak {B_2} = a_4 x + a_5 t + a_6, \end{aligned}$$

whereas $a_k (1 \le k \le 6)$, $e_1$, $e_2$, and $f_0$ are all real parameters to be measured. Put f into Eq. (46) and compute all coefficients of x, t and $\cosh$ to get the following subsequent parameters:

$$\begin{aligned}&a_1 = \sqrt{\frac{4 \sqrt{19} a_4^2}{5} - \frac{13 a_4^2}{5}}, \quad e_1 = \frac{\sqrt{3} m l}{\sqrt{m-1}}, \quad b = - \frac{216 c_6 l^2 m^3}{5 \kappa ^2 (2 + m)}, \quad a_2 = a_3 = 0. \end{aligned}$$

(59)

Using these parameters in Eq. (58) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{6 \big (2 a_1^2 x + 2 a_4 (a_6 + a_5 t + a_4 x) + e_1 \sinh (e_2 t + e_1 x) \big )}{\kappa \big (f_0 + a_1^2 x^2 + (a_6 + a_5 t + a_4 x)^2 + \cosh (e_2 t + e_1 x) \big )}, \end{aligned}$$

(60)

where the values of the parameters are mentioned in Eq. (59). Using Eq. (60) into Eq. (42) then in Eq. (39) to attain the required rogue wave solution.

$$\begin{aligned}&\psi (x,t) = 6^{\frac{1}{m}} e^{i (q + p t - l x)} \left( \frac{\frac{2}{5} a_4 \big (5 a_6 + 5 a_5 t + 4 (\sqrt{19} - 2) a_4 x \big ) + \frac{\sqrt{3} l m \sinh (e_2 t + \frac{\sqrt{3} l m}{\sqrt{m -1}} x)}{\sqrt{m - 1}} }{\kappa \big (f_0 + \frac{1}{5} (4 \sqrt{19} - 13) a_4^2 x^2 + (a_6 + a_5 t + a_4 x)^2 + \cosh (e_2 t + \frac{\sqrt{3} l m x}{\sqrt{m -1}}) \big )} \right) ^\frac{1}{m}. \end{aligned}$$

(61)

Fig. 11

Plots of rogue wave soliton Eq. (61), at $p=2,~ q=3,~ l=-5,~ m=3,~ f_0=8,~ a_4=1,~ a_5=-1,~ a_6=-3,~ e_2=5,~ \kappa =4$, successively

3.5 Generalized breather solution

To obtain this solution we choose the following hypothesis (Li and Ma 2020);

$$\begin{aligned} f = \frac{(1 - 4 e) \cosh (\alpha t) + \sqrt{2 e} \cos (\beta x) + i \alpha \sinh (\alpha t)}{\sqrt{2 e} \cos (\beta x) - \cosh (\alpha t)} e^{i t}, \end{aligned}$$

(62)

where $\alpha = \sqrt{8 e(1 - 2 e)}$, $\beta = 2 \sqrt{1 - 2 e}$, and e is the real-valued parameter. Put f into Eq. (46) and compute various coefficients of $\cos$, $\cosh$, $\sin$, $\sinh$ and exp functions, to get the following subsequent parameters:

$$\begin{aligned} e = \frac{2}{5}, \quad l = \frac{\sqrt{\frac{4 c_3 m}{c_6} + (2 - 3 m) \beta ^2}}{2 m}, \quad b = \frac{12 c_6 m^2 (c_1 - p)}{12 c_3 m + c_6 (2 + m) \beta ^2}, \quad c_7 = \frac{c_5 c_6}{4 c_3 m - c_6 (2 + 3 m) \beta ^2}. \end{aligned}$$

(63)

Using these parameters in Eq. (62) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{48 \sin (\frac{2 x}{\sqrt{5}}) \bigg (\cosh (\frac{4 t}{5}) + 2 i \sinh (\frac{4 t}{5}) \bigg )}{\kappa \bigg (2 \sqrt{5} \cos (\frac{2 x}{\sqrt{5}}) - 5 \cosh (\frac{4 t}{5}) \bigg ) \bigg (2 \sqrt{5} \cos (\frac{2 x}{\sqrt{5}}) - 3 \cosh (\frac{4 t}{5}) + 4 i \sinh (\frac{4 t}{5}) \bigg )}. \end{aligned}$$

(64)

The wave function $\phi (x,t)$ can have complex values. However, $|psi(x)|^2$, which is always a real, non-negative quantity, provides the probability of finding the particle in a specific position. In this case, instead of dealing with complex numbers, we can calculate physically significant quantities using the modulus.

$$\begin{aligned} |\phi (x,t)|^2 = \frac{2304 \sin (\frac{2 x}{\sqrt{5}})^2 \bigg (\cosh (\frac{4 t}{5})^2 + 4 \sinh (\frac{4 t}{5})^2 \bigg )}{\kappa ^2 \bigg (20 \cos (\frac{2 x}{\sqrt{5}})^2 - 25 \cosh (\frac{4 t}{5})^2 \bigg )^2 + 64 \kappa ^2 \sinh (\frac{4 t}{5})^2 \bigg (2 \sqrt{5} \cos (\frac{2 x}{\sqrt{5}}) - 3 \cosh (\frac{4 t}{5}) \bigg )}. \end{aligned}$$

(65)

Using this equation into Eq. (42) along with Eq. (39) to attain the required solution.

$$\begin{aligned} \psi (x,t) = 1152^{\frac{1}{m}} e^{i \big (q + p t - \frac{\sqrt{\frac{2}{5} - \frac{3 m}{5} + \frac{c_3 m}{c_6}} x}{m} \big )} \bigg (\frac{\sin (\frac{2 x}{\sqrt{5}})^2 \big (- 3 + 5 \cosh (\frac{8 t}{5}) \big )}{\kappa ^2 \bigg ( \big (20 \cos (\frac{2 x}{\sqrt{5}})^2 - 25 \cosh (\frac{4 t}{5})^2 \big )^2 + 64 \big (2 \sqrt{5} \cos (\frac{2 x}{\sqrt{5}}) - 3 \cosh (\frac{4 t}{5}) \big )^2 \sinh (\frac{4 t}{5})^2 \bigg )} \bigg )^\frac{1}{m}. \end{aligned}$$

(66)

Fig. 12

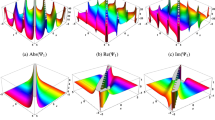
The interaction between the bright X-like soliton and rogue wave for Eq. (66), at $p=4,~ q=-2,~ m=3,~ c_3=5,~ c_6=15,~ \kappa =8$, successively

3.6 The Ma-breather and its corresponding rogue wave

To obtain this solution we choose the following hypothesis (Ma 2020);

$$\begin{aligned} f = 1 + \delta (e^{i a x} + e^{-i a x}) e^{\alpha t + \beta } + \gamma e^{2 (\alpha t + \beta )}, \end{aligned}$$

(67)

where $\alpha$, $\beta$, $\delta$, $\gamma$ are real valued parameters and a is complex number to be investigated. Put f into Eq. (46) and compute various coefficients of exponential functions, to get the following subsequent parameters:

$$\begin{aligned} a = 6 \sqrt{2} m \sqrt{\frac{c_3}{8 b + 3 b m}}, \quad l = \frac{a \sqrt{m-2}}{2 m}, \quad p = \frac{4 c_1 m^2 - a^2 b (2 + m)}{4 m^2}, \quad c_7 = 0. \end{aligned}$$

(68)

Using these parameters in Eq. (67) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{i a e^{t \alpha + \beta } (-1 + e^{2 i a x}) \delta }{\sqrt{2} m \sqrt{\frac{c_3}{8 b + 3 b m}} \bigg (e^{i a x} + e^{i a x + 2 t \alpha + 2 \beta } \gamma + e^{t \alpha + \beta } \delta + e^{2 i a x + t \alpha + \beta } \delta \bigg )}. \end{aligned}$$

(69)

Using this equation into Eq. (42) along with Eq. (39) to attain the required solution.

$$\begin{aligned}&\psi (x,t) = 2^{\frac{-1}{2 m}} e^{\frac{i \big (4 m^2 (q + c_1 t) - 2 a^2 b t - a m (a b t + 2 \sqrt{m -2} x) \big )}{4 m^2}} \left( \frac{i a e^{t \alpha + \beta } (-1 + e^{2 i a x}) \delta }{m \sqrt{\frac{c_3}{8 b + 3 b m}} \bigg (e^{i a x} + e^{i a x + 2 t \alpha + 2 \beta } \gamma + e^{t \alpha + \beta } \delta + e^{2 i a x + t \alpha + \beta } \delta \bigg )} \right) ^\frac{1}{m}. \end{aligned}$$

(70)

Fig. 13

Plots of Ma-breather and its corresponding rogue wave soliton Eq. (70), at $q=-3,~ a=-1,~ b=3,~ m=5,~ c_1=5,~ c_3=8,~ \alpha =3,~ \beta =-1,~ \delta =6$, successively

3.7 Kuznetsov-Ma breather, generalized breather, and their corresponding rogue waves

To attain this solution we choose f in the following form Ma (2020);

$$\begin{aligned} f = e^{-a_1 (x - \mu t)} + \delta _1 \cos \big (a(x + \nu t) \big ) + \delta _2 e^{a_1(x - \mu t)}, \end{aligned}$$

(71)

where $\delta _1$, $\delta _2$, $\mu$, $\nu$ are real and a, $a_1$ are complex parameters. To get the values of these parameters we Put f into Eq. (46) and compute various coefficients of $\cos$ and $\exp$ functions, to get the following subsequent results:

$$\begin{aligned}{} & {} a = \sqrt{\frac{15 l^2 m^2 + 4 a_1^2 (29 + 28 m)}{4 + 8 m}}, \quad \kappa = \frac{15 a_1 c_2}{4 c_1}, \quad c_3 = - \frac{25 a_1^2 b c_2^2 (m + 1)}{64 c_1^2 m^2}, \nonumber \\{} & {} \quad c_4 = \frac{25 c_2^3}{64 c_1^2}. \end{aligned}$$

(72)

Using these parameters in Eq. (71) and then we use f into Eq. (45) to get the following result;

$$\begin{aligned} \phi (x,t) = \frac{8 c_1 \bigg (-a_1 e^{-a_1 x + a_1 t \mu } + a_1 e^{a_1 (x - t \mu )} \delta _2 - a \delta _1 \sin (a (x + t \nu )) \bigg )}{5 a_1 c_2 \bigg (e^{-a_1 x + a_1 t \mu } + e^{a_1 (x - t \mu )} \delta _2 + \delta _1 \cos (a (x + t \nu )) \bigg ) }. \end{aligned}$$

(73)

Using this equation into Eq. (42) along with Eq. (39) to attain the required solution.

$$\begin{aligned} \psi (x,t) = (\frac{8}{5})^{\frac{1}{m}} e^{i (q + p t - l x)} \left( \frac{c_1 \big (a_1 e^{a_1 (x - t \mu )} \delta _2 -a_1 e^{a_1(t \mu - x)} - \sqrt{\frac{15 l^2 m^2 + 4 a_1^2 (28 m + 29)}{8 m + 4}} \delta _1 \sin (\sqrt{\frac{15 l^2 m^2 + 4 a_1^2 (28 m + 29)}{8 m + 4}} (x + t \nu )) \big )}{a_1 c_2 \big (e^{-a_1 x + a_1 t \mu } + e^{a_1 (x - t \mu )} \delta _2 + \delta _1 \cos (\sqrt{\frac{15 l^2 m^2 + 4 a_1^2 (29 + 28 m)}{8 m + 4}} (x + t \nu )) \big ) } \right) ^\frac{1}{m}. \end{aligned}$$

(74)

Fig. 14

Plots of Kuznetsov-Ma breather, generalized breather, and their corresponding rogue waves soliton Eq. (74), at $p=2,~ q=4,~ l=-2,~ m=5,~ c_1=-8,~ c_2=5,~ a_1=3,~ \mu =5,~ \nu =-0.1,~ \delta _1=25, \delta _2=10$, respectively

4 Result and discussions

The investigation of new imposed solutions for NLSE having KQSPMS together with DFNLN is extremely important among researchers. Much work has been done on our proposed model, like as Ekici studied bright, dark, singular and dark-singular solutions for NLSE with KQSPMS and two types of non-local law (Ekici 2022). Ozisik et al. investigated various analytic solutions for NLSE with Kudryashov’s sextic power-law nonlinearity (Ozisik et al. 2022). Zayed et al. studied dark, bright and singular optical solutions for NLSE along with Kudryashov’s sextic power-law nonlinearity (Zayed et al. 2022). Zayed et al investigated bright, singular optical solitons and their conserved quantities for cubic-quartic NLSE with Kudryashov’s sextic power-law (Zayed et al. 2020). Elsherbeny et al. obtained dark and singular soliton solutions for highly dispersive NLSE having Kudryashov’s arbitrary form along with generalized nonlocal and sextic-power law (Elsherbeny et al. 2021). Nofal et al. recovered dark, bright, singular and combo bright-singular solutions for perturbation NLSE having Kudryashov’s arbitrary form along with sextic-power law and generalized non-local nonlinearity (Nofal et al. 2022).

In this study, we designed our proposed model in OD and PD forms to generate several soliton solutions using Wolfram Mathematica and the suggested methodologies. We also gave figures to demonstrate the behavior of the solutions using proper parameter values. These figures show distinct acquired solutions in the form of 3D and contour plots. Fig. 1 presents M-shaped soliton solutions for Eq. (14). Figures 2 and  3 show the interaction of M-shaped soliton with kink waves in which dark and bright solitons appear respectively. Figure 4 presents the PCMR soliton solution for Eq. (26) in which two waves travel with constant speed while maintaining their permanent structures. Figure 5 show PCK soliton solution for Eq. (30). The multiwaves solution is presented in Fig. 6 that shows the interaction of two periodic waves. Figure 7 displays the homoclinic breather solution for $\psi$ in Eq. (38). Figure 8 displays the lump soliton solution in Eq. (49); these solitons appear in the form of dark and bright leaf petals. Figure 9 shows the periodic wave solution with dark and bright leaf-petals for Eq. (53). Figure 10 represents the interaction solution of three waves. Figure 11 presents the bell-type rogue wave solution. Figures 12, 13, and 14 show the degeneracies of first- and second-order hybrid waves. The interaction of the breather and rogue wave is seen in Fig. 12. We attained bell-type solitons with dark and bright leaf petals for different domains of x, and we can see the symmetry of hybrid waves along the t-axis. The projecting plots on the x, t plane are a and c. The breather transfers energy to the rogue wave. The hybrid solution produces the graphs. The interaction behavior between the breather and rogue wave is shown to be influenced by different time intervals, and these waves are symmetrical along the t-axis. In Fig. 13, solitons travel in a zig-zag pattern furthermore when we change the value of the $\gamma$ they follow an elliptical path, and correspondingly we can see the symmetry of these waves along t-axis. In Eq. (70), $\beta$ is the traveling wave parameter that allows soliton to move left or right along the x-axis. Figure 14 shows the hybrid first-order rogue and second-order breather solitons. Here we can see the interaction of two hybrid waves in different time intervals.

5 Conclusion

In this study, the soliton solutions for the NLSE with KQSPMS and the DFNLN were examined. The OD and PD forms of this model have been established through a variable transformation. We have introduced numerous new dynamical soliton types in addition to the previously known soliton types and have obtained various solutions for both the OD and PD forms. Using symbolic computation and ansatz function schemes, we have introduced a large number of new dynamical soliton types, including the M-shaped rational soliton, the M-shaped interaction between one and two-stripe solitons, the PCMR soliton, the PCK soliton, multi-waves, and the homoclinic breather soliton. Using the PD form, we have also formed a lump soliton, a periodic wave, a rogue wave, a lump interaction with a periodic and kink wave, and three different kinds of breather soliton. The unique structure and unusual interaction behavior of these solutions have been demonstrated using 3-D and contour plots.

Our findings greatly advance our understanding of the NLSE with KQSPMS, including the DFNLN, and provide insight into how solitons behave in these systems. Solitons play a significant part in optical fiber communication systems, which is one potential use in the area of optics. With the assistance of KQSPMS and the DFNLN, the soliton solutions obtained in this study can be used to study the behavior of solitons in optical fibers, which can aid in the development and improvement of optical fiber communication systems. Furthermore, to study the behavior of waves in materials, these soliton solutions can also be used in condensed matter physics. The results of this study can be used to design and improve materials with specific wave behavior by studying the act of waves in materials using the DFNLN and KQSPMS.