1 Introduction

In present era, multiple complex partial differential equations that are also known as nonlinear Schrödinger equations are studied by many researchers, which resulted in essential comprehensions to nonlinear pulses in optical fibers. These equations are a type of nonlinear PDEs and have been extensively investigated by researchers across a broad range of physical sciences. Partial differential equations known as nonlinear Schrödinger equations (NLSEs) appear in various areas of applied science as well as engineering, including but not limited to magneto static spin waves, optics, plasma physics, optical fibers, quantum mechanics, molecular biology, elastic media and fluid dynamics. These equations play a crucial role in modeling and understanding complex phenomena in these fields. For instance, new solitary solutions of complex Ginzburg–Landau model are studied in [1]. Multiple explicit exact solutions to the double-chain DNA dynamical system are reported in [2]. Different types of periodic solutions of new (3+ 1)-dimensional Boiti–Leon–Manna–Pempinelli equation are presented [3], Solving Local Time Fractional Telegraph Equations are demonstrated in [4].

Differential equations are very useful in describing the real-world phenomena including solitary waves solutions as well as fluid flow. Several researchers have worked in fluid mechanics, including ternary nanofluid, micropolar nanofluid, etc. For example new local and nonlocal solitary solutions of a nonlocal mKdV equation are observed in [5]. Resonance and fission/fusion solitons are presented in [6]. Besides these the numerical analysis of magneto-radiated annular fin natural convective heat transfer performance are reported in [7, 8]. Brownian motion and thermophoretic diffusion in bioconvective micropolar nanofluid flow are demonstrated in [9]. Numerical simulations of the temperature distribution of heat flow are presented in [10]. Heat transfer analysis of fractional model of couple stress Casson tri-hybrid nanofluid and conformable fluid mechanics model is studied in [11, 12]. Xu et al. studied bifurcation in a delayed chemostat model [13]. Further, predator–prey systems in fractional perspective is analyzed in [14, 15], chemical reaction models are studied in [16, 17] and bifurcations in fractional order BAM neural networks [18]. Similarly, SIR epidemic model is analyzed in [19], financial bubble mathematical model [20] and others [21].

Various researchers have delved into the study of NLS equations. As an illustration, efficient technique was employed by Biswas et al. for exploration of optical solitons in Schrödinger equation with nonlinear disturbance and resonance [22]. By the applications of fractional order singular as well as non-singular kernels the NLSE is studied in [23]. Hosseini et al. explored unstable NLSEs equations by Kudryashov method to obtain precise solutions in the form of traveling waves [24]. The extended tanh method was employed by Osman et al. to obtain soliton solutions for NLSE that incorporates time-dependent coefficients [25]. Soliton solutions for a nonlocal type NLSE were obtained by Kudryashov through the utilization of the simplest equation method [26]. Numerous scholars have directed their research efforts toward the domain of optical fiber communication systems. The study of solitons in fiber optics is a captivating and aesthetically pleasing area of research within the field of dynamical systems. Typically, the time-related aspects of these systems are emphasized and presented when they are analyzed or represented. These systems are examined with regard to their behavior and characteristics over time and analyzed through the transmission of the field at various frequencies. Dynamical systems, which are often in the form of complex nonlinear PDEs, have been extensively studied in this field /cite9,11,8. Fiber amplifiers, nonlinear optical effects, and optical solitons have drastically improved long-distance data transmission, including undersea cables, leading to significant progress in the field. Researchers have also linked discrete breathers with embedded solitons, demonstrating the interaction between these two essential solution classes for the nonlinear Schrödinger equation. These solutions have attracted widespread attention from scientists and can explain various complex nonlinear phenomena. Following the development of NLSEs, the quest for exact solutions has been a major focus, with intensive exploration in various forms and facets. To obtain traveling wave solutions in diverse forms, numerous effective and potent methods have been utilized. These include the rational expansion scheme [30], semi-inverse variational principle [31], similarity transformations method [32], F-expansion method [33], Darboux transformation [34], direct algebraic technique [35], Jacobi elliptic function technique [36], expansion method [38], simple equation method [39] and many more methods are introduced. The comprehensive third-order NLSE, that belongs to the class of NLSEs, has recently received considerable attention. Its mathematical representation is as follow:

$$\begin{aligned} \iota \left( \frac{\partial \mathfrak {V}}{\partial t}+\frac{\partial ^{3}\mathfrak {V}}{\partial x}\right) +\mathfrak {\left| V\right| }^{2}\left( \alpha _1\mathfrak {V}+\iota \alpha _2\frac{\partial \mathfrak {V}}{\partial x}\right) +\iota \alpha _3\frac{\mathfrak {\partial }\mathfrak {\left| V\right| }^{2}\mathfrak {V}}{\partial x}=0. \end{aligned}$$
(1)

The coefficients of nonlinear dispersions are represented by \(\alpha _j,~j=1,2,3\), and the coefficient \(\alpha _1\) corresponds to the cubic nonlinearity term in the equation. When \(\alpha _1\) and \(\alpha _3\) are equal to zero, the above model simplifies to the Hirota or modified KdV equation in complex form. This simplified equation can be solved using the inverse scattering transform. Several effective methods have been employed to solve the nonlinear model mentioned above, which is used for modeling ultra-short pulses. For example, Lu et al. utilized both the extended simple equation method and the exp(-f(\(\xi\)))-expansion method to demonstrate optical solitons in the model [40]. Using the generalized Riccati mapping method, Nasreen et al. identified different categories of soliton solutions for the model.

2 General analysis of the SSEM

In this section the steps of the suggested technique are presented. For the description of the method consider the following general nonlinear PDE:

$$\begin{aligned} \mathcal {Z}(\mathscr {B},\mathscr {B}_{t},\mathscr {B}_{x},\mathscr {B}_{tt},\mathscr {B}_{xx},\mathscr {B}_{t},\mathscr {B}_{tx},)=0. \end{aligned}$$
(2)

Further consider the following transformation

$$\begin{aligned} \mathscr {B}(x,t)= {\exp (\iota \varsigma )}\mathfrak{A}(\delta ),\;\delta =\kappa x+\mathscr {C}t,\varsigma =\Lambda x+\theta +\lambda t, \end{aligned}$$
(3)

in the above transformation \(\mathscr {C},\lambda ,\epsilon\) are real parameters, which are non-zero. Now to solve Eq.(2), the following are necessary to be followed:

Step I: Substitute Eq.(3) into Eq. 2, in order to convert the PDE to ODE and get the following form

$$\begin{aligned} \mathcal {Z}(\mathfrak {A}(\delta ),\mathfrak {A}^{\prime }(\delta ),\mathfrak {A}^{\prime \prime }(\delta ),\ldots )=0, \end{aligned}$$
(4)

in Eq.(4), the \mathcal{Z} is polynomial in \(\mathfrak {A}(\delta )\), where the superscripts (\(^{\prime }\)) represents ordinary derivatives of \(\mathfrak {A}(\delta )\).

Step II: Consider that the ODE in Eq.(4) has solution in the following form

$$\begin{aligned} \mathfrak {A}(\delta )=\sum _{l=0}^{{{\mathfrak {E}}}}\varrho _{l}\mathcal {C}(\delta )^{l},\quad \varrho _{\mathfrak {E}}\ne 0, \end{aligned}$$
(5)

where \(\mathcal {\varrho }_{0},\mathcal {\varrho }_{1},\varrho _{2},\ldots ,\varrho _{{{\mathfrak {E}}}}\)are real constants to be determined, \({{\mathfrak {E}}}\in \textrm{Z}^{+}\). One can determine \({{\mathfrak {E}}}\) by homogeneous balance principle by comparing highest power of nonlinearity and highest order of derivative. Further \(\mathcal {C}(\delta )\) satisfies the ODE presented below

$$\begin{aligned} \frac{d\mathcal {C}(\delta )}{d\delta }=\sqrt{{{\mathfrak {F}}}_{1}+{{\mathfrak {F}}}_{2}\mathcal {C}(\delta )^{2}+{{\mathfrak {F}}}_{3}\mathcal {C}(\delta )^{4}}. \end{aligned}$$
(6)

Equation (6) has the solutions presented below:

Case I: When \({{\mathfrak {F}}}_{2}>0\) and \({{\mathfrak {F}}}_{1}=0\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {C}_{1}^{\pm }(\delta ) &{} =\pm \sqrt{-\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\sec h_{\mathscr{J}\mathscr{K}}(\sqrt{{{{{\mathfrak {F}}}}}_{2}}\delta )\\ \mathcal {C}_{2}^{\pm }(\delta ) &{} =\pm \sqrt{\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\csc h_{\mathscr{J}\mathscr{K}}(\sqrt{{{{{\mathfrak {F}}}}}_{2}}\delta ) \end{array}, \end{aligned}$$
(7)

here

$$\begin{aligned} \sec h_{\mathscr{J}\mathscr{K}}(\delta )=\frac{2}{\mathscr {J}e^{\delta }+\mathscr {K}e^{-\delta }},\,\csc h_{\mathscr{J}\mathscr{K}}(\delta )=\frac{2}{\mathscr {J}e^{\delta }-\mathscr {K}e^{-\delta }}. \end{aligned}$$
(8)

Case II: When \({{\mathfrak {F}}}_{2}<0\) and \({{\mathfrak {F}}}_{1}=0\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {C}_{3}^{\pm }(\delta ) &{} =\pm \sqrt{-\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\sec _{\mathscr{J}\mathscr{K}}(\sqrt{-{{{{\mathfrak {F}}}}}_{2}}\delta )\\ \mathcal {C}_{4}^{\pm }(\delta ) &{} =\pm \sqrt{-\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\csc _{\mathscr{J}\mathscr{K}}(\sqrt{-{{{{\mathfrak {F}}}}}_{2}}\delta ) \end{array}, \end{aligned}$$
(9)

here

$$\begin{aligned} \sec _{\mathscr{J}\mathscr{K}}(\delta )=\frac{2}{\mathscr {J}e^{\iota \delta }+\upsilon e^{-\iota \delta }},\,\csc _{\mathscr{J}\mathscr{K}}(\delta )=\frac{2\iota }{\mathscr {J}e^{\iota \delta }-\upsilon e^{-\iota \delta }}. \end{aligned}$$
(10)

Case III: When \({{\mathfrak {F}}}_{2}<0\) and \({{\mathfrak {F}}}_{1}=\frac{\mathfrak {F}_{2}^{2}}{4}\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {C}_{5}^{\pm }(\delta ) &{} =\pm \sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\tanh _{\mathscr{J}\mathscr{K}}(\sqrt{-\frac{\mathfrak {F}_{2}}{2}}\delta )\\ \mathcal {C}_{6}^{\pm }(\delta ) &{} =\pm \sqrt{-\frac{\mathfrak {F}_{2}}{2}}\coth _{\mathscr{J}\mathscr{K}}(\sqrt{-\frac{\mathfrak {F}_{2}}{2}}\delta )\\ \mathcal {C}_{7}^{\pm }(\delta ) &{} =\pm \sqrt{-\frac{\mathfrak {F}_{2}}{2}}(\tanh _{\mathscr{J}\mathscr{K}}(\sqrt{-2{\mathfrak {F}}_{2}}\delta )+\iota \sqrt{-\mathscr{J}\mathscr{K}}\sec h_{\mathscr{J}\mathscr{K}}(\sqrt{-2{\mathfrak {F}}_{2}}\delta ))\\ \mathcal {C}_{8}^{\pm }(\delta ) &{} =\pm \sqrt{-\frac{\mathfrak {F}_{2}}{2}}(\coth _{\mathscr{J}\mathscr{K}}(\sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\delta )+\sqrt{-\mathscr{J}\mathscr{K}}\csc h_{\mathscr{J}\mathscr{K}}(\sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\delta ))\\ \mathcal {C}_{9}^{\pm }(\delta ) &{} =\pm \sqrt{-\frac{\mathfrak {F}_{2}}{2}}(\coth _{\mathscr{J}\mathscr{K}}(\sqrt{-\frac{\mathfrak {F}_{2}}{8}}\delta )+\iota \tanh _{\mathscr{J}\mathscr{K}}(\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\delta )), \end{array} \end{aligned}$$
(11)

here

$$\begin{aligned} \tanh _{\mathscr{J}\mathscr{K}}(\delta )=\frac{\mathscr {J}e^{\delta }-\mathscr {K}e^{-\delta }}{\mathscr {J}e^{\delta }+\mathscr {K}e^{-\delta }},\,\coth _{\mathscr{J}\mathscr{K}}(\delta )=\frac{\mathscr {J}e^{\delta }+\mathscr {K}e^{-\delta }}{\mathscr {J}e^{\delta }-\mathscr {K}e^{-\delta }}. \end{aligned}$$
(12)

Case IV: When \({{\mathfrak {F}}}_{2}>0\) and \({{\mathfrak {F}}}_{1}=\frac{\mathfrak {F}_{2}^{2}}{4}\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {C}_{10}^{\pm }(\delta ) &{} =\pm \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\tan _{\mathscr{J}\mathscr{K}}(\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\delta )\\ \mathcal {C}_{11}^{\pm }(\delta ) &{} =\pm \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\cot _{\mathscr{J}\mathscr{K}}(\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\delta )\\ \mathcal {C}_{12}^{\pm }(\delta ) &{} =\pm \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( \tan _{\mathscr{J}\mathscr{K}}(\sqrt{2{{{{\mathfrak {F}}}}}_{2}}\delta )+\sqrt{\mathscr{J}\mathscr{K}}\sec _{\mathscr{J}\mathscr{K}}(\sqrt{2{{{{\mathfrak {F}}}}}_{2}}\delta )\right) \\ \mathcal {C}_{13}^{\pm }(\delta ) &{} =\pm \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( \cot _{\mathscr{J}\mathscr{K}}(\sqrt{2{{{{\mathfrak {F}}}}}_{2}}\delta )+\sqrt{\mathscr{J}\mathscr{K}}\csc _{\mathscr{J}\mathscr{K}}(\sqrt{2{{{{\mathfrak {F}}}}}_{2}}\delta )\right) \\ \mathcal {C}_{14}^{\pm }(\delta ) &{} =\pm \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( \cot _{\mathscr{J}\mathscr{K}}(\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\delta )+\iota \tan _{\mathscr{J}\mathscr{K}}(\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\delta )\right) , \end{array} \end{aligned}$$
(13)

here

$$\begin{aligned} \tan _{\mathscr{J}\mathscr{K}}(\delta )=\frac{\mathscr {J}e^{\iota \delta }-\upsilon e^{-\iota \delta }}{\mathscr {J}e^{\iota \delta }+\upsilon e^{-\iota \delta }},\,\cot _{\mathscr{J}\mathscr{K}}(\delta )=\frac{\mathscr {J}e^{\iota \delta }+\upsilon e^{-\iota \delta }}{\mathscr {J}e^{\iota \delta }-\upsilon e^{-\iota \delta }}. \end{aligned}$$
(14)

3 Application of the SSEM

Here we apply the suggested scheme to the proposed model and acquire several novel solutions. For this we substitute the following transformations into Eq.(1)

$$\begin{aligned} \mathcal {\mathscr {U}}(x,t)= {\exp (\iota \varsigma )A}(\delta ),\;\delta =\kappa x+\mathscr {C}t,\varsigma =\Lambda x+\theta +\lambda t. \end{aligned}$$
(15)

The symbols \(\mathfrak {A}(\delta ),\delta\) and \(\mathscr {C}\) are used to denote the soliton pulse profile, frequency, wave number and soliton velocity respectively. On substituting Eq.(15) into Eq.(1), we obtained the real and imaginary parts as\(\alpha\)

$$\begin{aligned}{} & {} \left( \Lambda ^{3}-\lambda \right) \mathfrak {A}(\delta )-3\Lambda \kappa ^{2}\mathfrak {A}^{\prime \prime }(\delta )+\mathfrak {A}(\delta )^{3}(\alpha _{1}-\Lambda ({{\alpha _{2}}}+2{{\alpha _{3}}}))=0. \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \mathfrak {A^{\prime }}(\delta )\left( \gamma -3\Lambda ^{2}\kappa +\kappa ({{\alpha _{2}}}+2{{\alpha _{3}}})\mathfrak {A}(\delta )^{2}\right) +\kappa ^{3}\mathfrak {A^{\prime \prime \prime }}(\delta )=0. \end{aligned}$$
(17)

Now integrating Eq.(16) once and considering the integration constant as zero, we obtained

$$\begin{aligned} \mathfrak {A}(\delta )\left( \gamma -3\Lambda ^{2}\kappa \right) +\kappa ^{3}\mathfrak {A}^{\prime \prime }(\delta ))+\frac{1}{3}\kappa ({{\alpha _{2}}}+2{{\alpha _{3}}})\mathfrak {A}(\delta )^{3}=0, \end{aligned}$$
(18)

comparing Eq.(16) and Eq.(18), we obtained the following constraint conditions

$$\begin{aligned} {{\lambda }}=-\gamma +\Lambda ^{3}+3\Lambda ^{2}\kappa ;{{\alpha _{2}}} =\frac{3\alpha _{1}-6{{\alpha _{3}}}\Lambda -2{{\alpha _{3}}}\kappa }{3\Lambda +\kappa }; \end{aligned}$$

Using the homogeneous balance principle, we obtained the value of \({{\mathfrak {E}}}=1\), so from Eq.(5), we have

$$\begin{aligned} \mathfrak {A}(\delta )= {\varrho }_{0}+ {\varrho }_{1}\mathcal{C}(\delta ),\qquad {\varrho }_{1}\ne 0, \end{aligned}$$
(19)

where in Eq.(19), \(\mathcal {C}(\delta )\) satisfies the following ODE

$$\begin{aligned} \frac{d\mathcal {C}(\delta )}{d\delta }=\sqrt{{{\mathfrak {F}}}_{1}+{{\mathfrak {F}}}_{2}\mathcal {C}(\delta )^{2}+{{\mathfrak {F}}}_{3}\mathcal {C}(\delta )^{4}}. \end{aligned}$$
(20)

Further inserting Eq.(20) into Eq.(19) and then into Eq.(18), we get the algebraic system of equations which is as follows

$$\begin{aligned}{} & {} \mathcal {C}(\delta )^{0}:{{\varrho _{0}}}\left( \gamma -3\Lambda ^{2}\kappa +\frac{{{\alpha _{1}}}\kappa {{{{\varrho _{0}}}}}^{2}}{3\Lambda +\kappa }\right) = 0\\{} & {} \mathcal {C}(\delta )^{1}:\gamma -3\Lambda ^{2}\kappa -3\Lambda \kappa ^{2}{{\mathfrak {F}}}_{2}+\frac{3{{\alpha _{1}}}\kappa {{\varrho _{0}}}^{2}}{3\Lambda +\kappa } = 0\\{} & {} \mathcal {C}(\delta )^{2}:\frac{3{{\alpha _{1}}}\kappa {{\varrho _{0}}}{{\varrho _{1}}}^{2}}{3\Lambda +\kappa } = 0\\{} & {} \mathcal {C}(\delta )^{3}:\kappa {{\varrho _{1}}}\left( \frac{{{\alpha _{1}}}{{\varrho _{1}}}^{2}}{3\Lambda +\kappa }-6\Lambda \kappa {{{{\mathfrak {F}}}_{3}}}\right) =0. \end{aligned}$$

Solving the above system gives the following non-trivial values of parameters

$$\begin{aligned} {\varrho _{0}}=0,{{\varrho _{1}}} =\frac{\sqrt{6}\sqrt{3\Lambda ^{2}\kappa {{\mathfrak {F}}}_{3}+\Lambda \kappa ^{2}{{{{\mathfrak {F}}}_{3}}}}}{\sqrt{\alpha _{1}}}, {\mathfrak {F}}_{2}=\frac{\gamma -3\Lambda ^{2}\kappa }{3\Lambda \kappa ^{2}} \\ {{\varrho _{0}}}=0,{{\varrho _{1}}}=-\frac{\sqrt{6}\sqrt{3\Lambda ^{2}\kappa {{\mathfrak {F}}}_{3} +\Lambda \kappa ^{2}{\mathfrak {F}}_{3}}}{\sqrt{\alpha _{1}}},{{{{\mathfrak {F}}}_{2}}} =\frac{\gamma -3\Lambda ^{2}\kappa }{3\Lambda \kappa ^{2}} \end{aligned}.$$

On subtituting the above sets of parameter values into equations (7), (9), (11) and (13), we obtained the following exact solutions of the proposed perterbed NLSE

Case I: When \({{\mathfrak {F}}}_{2}>0\) and \({{\mathfrak {F}}}_{1}=0\), then

$$\begin{aligned} \mathcal {U}_{1}^{\pm }(x,t)=\pm \varrho _{1}\sqrt{-\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\exp (\iota \varsigma )\sec h_{\mathscr{J}\mathscr{K}}\left( \sqrt{{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) , \end{aligned}$$
(21)

where the existence condition for the above solution is \(\mathscr{J}\mathscr{K}<0.\)

$$\begin{aligned} \mathcal {U}_{2}^{\pm }(x,t)=\pm \varrho _{1}\sqrt{\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\exp (\iota \varsigma )\csc h_{\mathscr{J}\mathscr{K}}\left( \sqrt{{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) , \end{aligned}$$
(22)

where the existence condition for the above solution is \(\mathscr{J}\mathscr{K}>0.\)

Case II: When \({{\mathfrak {F}}}_{2}<0\) and \({{\mathfrak {F}}}_{1}=0\), then

$$\begin{aligned}{} & {} \mathcal {U}_{3}^{\pm }(x,t)=\pm \varrho _{1}\sqrt{-\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\exp (\iota \varsigma )\sec _{\mathscr{J}\mathscr{K}}\left( \sqrt{-{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) , \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \mathcal {U}_{4}^{\pm }(x,t)=\pm \varrho _{1}\sqrt{\mathscr{J}\mathscr{K}{{{{\mathfrak {F}}}}}_{2}}\exp (\iota \varsigma )\csc _{\mathscr{J}\mathscr{K}}\left( \sqrt{-{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) , \end{aligned}$$
(24)

where the existence condition for the above solutions is \(\mathscr{J}\mathscr{K}>0.\)

Case III: When \({{\mathfrak {F}}}_{2}<0\) and \({{\mathfrak {F}}}_{1}=\frac{\mathfrak {F}_{2}^{2}}{4}\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {U}_{5}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\tanh _{\mathscr{J}\mathscr{K}}\left( \sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right), \\ \mathcal {U}_{6}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\coth _{\mathscr{J}\mathscr{K}}\left( \sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right), \\ \mathcal {U}_{7}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \tanh _{\mathscr{J}\mathscr{K}}\left( \sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\iota \sqrt{\mathscr{J}\mathscr{K}}\sec h_{\mathscr{J}\mathscr{K}}\left( \sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right), \\ \mathcal {U}_{8}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \coth _{\mathscr{J}\mathscr{K}}\left( \sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\sqrt{\mathscr{J}\mathscr{K}}\csc h_{\mathscr{J}\mathscr{K}}\left( \sqrt{-2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right), \\ \mathcal {U}_{9}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \coth _{\mathscr{J}\mathscr{K}}\left( \sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\iota \tanh _{\mathscr{J}\mathscr{K}}\left( \sqrt{-\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right). \end{array} \end{aligned}$$
(25)

Case IV: When \({{\mathfrak {F}}}_{2}>0\) and \({{\mathfrak {F}}}_{1}=\frac{\mathfrak {F}_{2}^{2}}{4}\), then

$$\begin{aligned} \begin{array}{ll} \mathcal {U}_{10}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\tan _{\mathscr{J}\mathscr{K}}\left( \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right), \\ \mathcal {U}_{11}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\cot _{\mathscr{J}\mathscr{K}}\left( \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right), \\ \mathcal {U}_{12}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \tan _{\mathscr{J}\mathscr{K}}\left( \sqrt{2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\sqrt{\mathscr{J}\mathscr{K}}\sec _{\mathscr{J}\mathscr{K}}\left( \sqrt{2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right), \\ \mathcal {U}_{13}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \cot _{\mathscr{J}\mathscr{K}}\left( \sqrt{2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\sqrt{\mathscr{J}\mathscr{K}}\csc _{\mathscr{J}\mathscr{K}}\left( \sqrt{2{{{{\mathfrak {F}}}}}_{2}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right), \\ \mathcal {U}_{14}^{\pm }(x,t) &{} =\pm \varrho _{1}\sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{2}}\exp (\iota \varsigma )\left( \cot _{\mathscr{J}\mathscr{K}}\left( \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) +\iota \tan _{\mathscr{J}\mathscr{K}}\left( \sqrt{\frac{{{{{\mathfrak {F}}}}}_{2}}{8}}\left( {{\kappa x-\mathscr {C}t}}\right) \right) \right). \end{array} \end{aligned}$$
(26)

All of the above equations are checked and they satisfy the considered perterbed NLSE.

4 Simulations and discussions

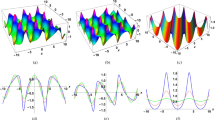
This goal of this section is to presents the numerical simulations of some of the exact solutions obtained with the suggested technique of Eq.(1), which are given in equations (21)-(26). The presented figures contains six sub-plots, where the sub-plots (a), (c), (e) depict the 3D dynamics while (b), (d), (f) show the 2D dynamics of some of the exact solutions with suitable parameter values. The sub-plots [(a),(b)] in all figures show the real parts, [(c),(d)] demonstrate imaginary parts and [(e),(f)] show the absolute values of the solutions. Figure 1 shows the physical dynamics of solution \(\mathcal {U}_{1}(x,t)\). The parameters in simulations of sub-figures [(a), (c), (e)] in Fig. 1 are considered as \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=-1,~\varrho _{3}=1,~\theta =1,~\lambda =1,~\mathscr {K}=1\). In sub-figures [(b), (d), (f)], the parameter \(\mathscr {K}\) is varied. The values are considered as for blue curve \(\mathscr {K}=1\), for pink curve \(\mathscr {K}=2\) and for green curve \(\mathscr {K}\) is used as \(\mathscr {K}=3\), where we see that increasing \(\mathscr {K}\) decreases amplitudes of the waves.

Figure 2 portrays the evolution of solution \(\mathcal {U}_{2}(x,t)\). The parameters during simulations of the sub-figures [(a), (c), (e)] in Fig. 2 are supposed to be \(\Lambda =1,~\kappa =-1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1,~\theta =1,~\lambda =-1,~\mathscr {K}=0.2\). In the sub-figures [(b), (d), (f)], \(\lambda\) is varied. The values are supposed as for the blue curve \(\lambda =1\), for pink curve \(\lambda =0.8\), for green curve \(\lambda\) is considered as \(\lambda =0.6\) and \(t=1\), where one can see that decreasing \(\lambda\) increases the singular soliton’s amplitude.

Fig. 1
figure 1

Visualization solution \(\mathcal {U}_{1}(x,t)\) with parameters used in the form \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=-1,~\varrho _{3}=1,~\theta =1,~\lambda =1,~\mathscr {K}=1\)

Full size image
Fig. 2
figure 2

Visualization solution \(\mathcal {U}_{2}(x,t)\) with parameters used in the form \(\Lambda =1,~\kappa =-1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1,~\theta =1,~\lambda =-1,~\mathscr {K}=0.2\)

Full size image
Fig. 3
figure 3

Visualization solution \(\mathcal {U}_{4}(x,t)\) with parameters used in the form \(\mathcal {U}_{4}(x,t)\) with parameters used in the form \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1,~\theta =1,~\lambda =3,~\mathscr {K}=1.1\)

Full size image

Figure 3 shows the physical demonstration of exact solution \(\mathcal {U}_{4}(x,t)\). The parameters are supposed in the sub-figures [(a), (c), (e)] in Fig. 3 as \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1,~\theta =1,~\lambda =3,~\mathscr {K}=1.1\). Similarly in the sub-figures [(b), (d), (f)], different values of \(\gamma _{3}\) are considered. These are supposed as for the blue curve \(\mathscr {K}=1.1\), for the pink curve \(\mathscr {K}=1.5\), for the green curve \(\mathscr {K}\) is used as \(\mathscr {K}=1.9\) and \(t=0\), where on can observe that increasing \(\mathscr {K}\) rapidly decreases the solitons’ amplitudes.

Fig. 4
figure 4

Visualization solution \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1.1,~\theta =1,~\lambda =0.9,~\mathscr {K}=1\)

Full size image

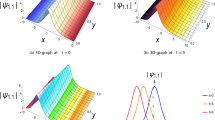
Figures 4 and 5 depict the dynamic evolution of the solutions \(\mathcal {U}{5}(x,t)\) and \(\mathcal {U}{6}(x,t)\), respectively. In the simulations of sub-figures [(a), (c), (e)] in Figs. 4 and 5, we consider the parameters as \(\Lambda =1,\kappa =1,\mathscr {C}=1,\alpha _{1}=1,\mathscr {J}=1,\varrho _{3}=1.1,\theta =1,\lambda =0.9,\mathscr {K}=1\) and \(\Lambda =1,\kappa =1,\mathscr {C}=1,\alpha _{1}=1,\mathscr {J}=1,\varrho _{3}=1.1,\theta =1,\lambda =0.9,\mathscr {K}=1\) for Figs. 4 and 5, respectively.

In sub-figures [(b), (d), (f)] of Fig. 4, we vary the parameter \(\varrho _{3}\). Specifically, the blue curve corresponds to \(\varrho _{3}=1\), the pink curve to \(\varrho _{3}=1.5\), and the green curve to \(\varrho _{3}=2\) at \(t=1\). Observations reveal that decreasing \(\varrho _{3}\) amplifies the amplitudes of a-periodic solitons.

Similarly, for the sub-figures [(b), (d), (f)] of Fig. 5, we vary the parameter \(\theta\). The values are set as follows: the blue curve represents \(\theta =1\), the pink curve \(\theta =2\), and the green curve \(\theta =3\) at \(t=1\). It is observed that increasing \(\theta\) results in an increase in the amplitudes of hybrid singular periodic solitons.

During the simulation of Fig. 6, the parameters are considered as \(\Lambda =1,\kappa =-1,\mathscr {C}=1,\alpha _{1}=-1,\mathscr {J}=5,\varrho _{3}=1.7,\theta =1.5,\lambda =3.5,\mathscr {K}=2.5\), illustrating the dynamics of solution \(\mathcal {U}_{7}(x,t)\). Furthermore, for the sub-figures [(b), (d), (f)] of Fig. 6, we vary the parameter \(\eta\): The blue curve represents \(\lambda =1.5\), the pink curve \(\lambda =2.5\), and the green curve \(\lambda =3.5\) at \(t=1\). It is observed that increasing \(\lambda\) displaces the locations of periodic solitons while maintaining constant amplitudes.

Fig. 5
figure 5

Visualization solution \(\mathcal {P}_{4}(x,t)\) with parameters used in the form \(\Lambda =1,~\kappa =1,~\mathscr {C}=1,~\alpha _{1}=1,~\mathscr {J}=1,~\varrho _{3}=1.1,~\theta =1,~\lambda =0.9,~\mathscr {K}=1\)

Full size image
Fig. 6
figure 6

Visualization solution \(\mathcal {P}_{4}(x,t)\) with parameters used in the form \(\Lambda =1,~\kappa =-1,~\mathscr {C}=1,~\alpha _{1}=-1,~\mathscr {J}=5,~\varrho _{3}=1.7,~\theta =1.5,~\lambda =3.5,~\mathscr {K}=2.5\)

Full size image

5 Conclusion

In summary, this study introduces an innovative approach to generate a diverse array of optical soliton solutions for the Nonlinear Schrödinger Equation (NLSE). The Sardar sub-equation (SSE) technique proves to be highly effective in obtaining precise analytical solutions for the NLSE. Initially, we applied a traveling wave transform to convert the NLSE into NLOD in both real and imaginary forms. Subsequently, through the expansion strategy of our proposed method, multiple soliton solutions are derived, including breather-like solitons, singular optical solitons, periodic solitons, the interaction of singular and periodic solitons, and a-periodic solitons. These solutions have significant implications across various applications.

Breather-like solitons, characterized by periodic oscillations, are valuable for robustly transmitting information over extended distances. Singular optical solitons, featuring infinite intensity at their center, find application in generating high-intensity laser pulses for precision cutting and welding. Periodic solitons, repeating at regular intervals, are pivotal in frequency combs for optical communication and metrology. The interplay between singular and periodic solitons can create complex light patterns for optical switches and other devices. Lastly, a-periodic solitons, lacking periodicity, have been utilized in creating nonlinear optical fibers for amplifying and manipulating light signals.

In conclusion, solitons encompass a broad spectrum of applications in optics, spanning from fundamental research to practical applications in telecommunications, sensing, and manufacturing.