1 Introduction

In recent years, Graphene has emerged as the foremost two-dimensional material (El-Shafai et al. 2023; Novoselov et al. 2005) thanks to its unique physical properties (Zhang et al. 2005; Gusynin and S.G. 2005; McCann and Falko 2006; Peres et al. 2006; Calogeracos and Dombey 1999; Itzykson and Zuber 2006). The electronic and optical properties of graphene multilayers differ significantly from those of conventional semiconductors, mainly due to the chiral nature of Dirac carriers in graphene (Park et al. 2008a, 2008b). However, its low conductivity, which is an important characteristic of electronic transport, poses a significant challenge in many technological applications, especially in the development of optoelectronic devices (El-Shafai et al. 2023; Novoselov et al. 2005; Zhang et al. 2005).

Another issue arises from the Klein-tunneling effect, whereby carriers incident at normal angles can be transmitted across potential barriers regardless of their width and height. This effect a substantial problem in confining of Dirac electrons. To address this limitation, the application of a magnetic field has been proposed (Martino et al. 2007a, 2007b). When a magnetic field is applied, it introduces additional confinement to the Dirac carriers through the Lorentz force, deflecting their trajectories. This magnetic field-induced confinement offers better control over electronic transmission across multibarrier graphene and facilitates control over conductance. The application of the magnetic field can be achieved using ferromagnetic stripes or strains (Ramezani Masir et al. 2009; Pereira and Castro Neto 2009).

Following the original results by Martino et al. (Martino et al. 2007a, 2007c), various theoretical and experimental studies on the impact of magnetic fields on electronic transport in graphene have been conducted (Ramezani Masir et al. 2008a, 2008b, 2011; Ghosh and Sharma 2009; Dell'Anna and De 2009, 2011; Tan et al. 2010; Xu et al. 2007; Park and Sim 2008; Kormanyos et al. 2008; Oroszlany et al. 2008; Ghosh et al. 2008; Bliokh et al. 2010; Wang and Jin 2009; Häusler et al. 2008; Myoung and Ihm 2009; Myoung et al. 2011). For instance, M. Ramezani Nasir demonstrated that single or bilayer graphene with multiple magnetic barriers could be utilized to realize wave-vector filters (Ramezani Masir et al. 2008a). Peeters et al. investigated the electronic transmission across magnetic barriers, such as magnetic steps and delta functions (Ramezani Masir et al. 2008b). Their results indicated that transmission primarily depends on the direction of incident electrons. Furthermore, they demonstrated that bound states are localized near the magnetic steps and the edges of magnetic barriers but not around the delta function barriers.

Many research papers have focused on periodic graphene systems and neglected aperiodic systems (Redouani and Jellal 2016; Biswas et al. 2017, 2010; Xu et al. 2019; Barbier et al. 2010; Reyes-Villagrana et al. 2017). However, in aperiodic systems, the symmetry of potential barriers is broken, leading to suppressed transmission of Dirac particles and the emergence of large gaps in the transmission coefficients. To the best of our knowledge, only a few works have addressed aperiodic systems in the presence of a magnetic field (Wei-Tao et al. 2013; Liu et al. 2013; Jonas 2015; Sun et al. 2010a, 2010b). For example, Wei-Tao Lu et al. investigated the transmission of Dirac electrons in Fibonacci and Thue-Morse magnetic superlattices (Wei-Tao et al. 2013). They demonstrated that the transmission coefficient exhibits a scaling property and fragmented behavior with self-similarity. In Thue-Morse systems, the transmission coefficients exhibit more pronounced resonant peaks, which arise from completely transparent states. Lifeng Sun et al. studied the transmission coefficients and conductance in fractal magnetic structures (Sun et al. 2010a). Their findings reveal that the transmission spectra can be considered distinctive fingerprints of the fractal structures, demonstrating the intricate relationship between magnetic structures and transport behaviors. R. Rodríguez-González et al. explored the transmission and conductance in Cantor graphene (Rodríguez-González 2017). They demonstrated that the magnetic field can be employed to control the transmission and conductance in graphene-based structures.

Despite the significant findings reported in the previous references, further investigation and explanation of the impact of electric and magnetic fields on electronic transport in graphene materials are needed to advance scientific understanding. In this study, we utilize the transfer matrix method (TMM) and the Landauer–Büttiker formalism to analyze the electronic transmission and conductance of magnetoelectric barriers deposited on top of a graphene layer. To incorporate the effects of these fields, we apply perpendicular electric and magnetic fields to a graphene monolayer in alternating regions, resulting in the creation of magnetic and electric barriers separated by well regions. Our objective is to explore the behavior of conductance and electronic transmission and observe how they are modified by varying structural parameters such as the number and sizes of barrier/well regions. The introduction of magnetoelectric barriers by applying electromagnetic fields in alternating regions represents a novel aspect of this study compared to previously published results. Moreover, this study considers a larger number of wells and barriers, providing more detailed insights into the formation of minigaps and minibands as influenced by the applied fields. This behavior was inadequately discussed in previous studies.

The remaining sections of this paper are organized as follows: In Sect. 2, we explain the theoretical model with appropriate approximations. Section 3 discusses the transmission coefficients and conductance for various system configurations. Finally, in Sect. 4, our conclusions and findings are presented.

2 Theory

The Dirac electrons motion under the effects of an electric and magnetic field can be described through the following equation (Sun et al. 2010a; Rodríguez-González 2017):

$$ \left[ {v_{F} \sigma \left( {p + eA} \right) + V\left( x \right)\sigma_{0} } \right]\varphi \left( {x,y} \right) = E\varphi \left( {x,y} \right) $$
(1)

where \({v}_{F}\) represents the Fermi velocity of Dirac particles, and \(p=({p}_{x},{p}_{y})\) is their momentum operator. Within Landau gauge, the vector potential is given by \(A=(0,{\mathrm{A}}_{\mathrm{y}},0)\). \({\sigma }_{0}\) denotes the unitary matrix and \(V\left(x\right)\) represents the scalar potential. In our problem, the vector potential is given by\(A\left(x\right)={A}_{y}\widehat{y}= {B}_{0}{l}_{B}\widehat{y}\). The intensity and length of the magnetic field are designed by \({B}_{0}\) and \(l_{B} = \sqrt {\hbar /eB_{0} }\), respectively. The electric field applied to each gate generates a difference of potential equal to \({V}_{0}\) in all barriers. The analytical resolution of Eq. (1) gives us the following dispersion relation:

$$ \left( {E - V_{0} } \right) = \pm \sqrt {v_{F}^{2} \left( {\hbar q_{y} + eA_{y} } \right)^{2} + \left( {\hbar v_{F} q_{x} } \right)^{2} } $$
(2)

\(+ (-)\) signs are devoted for electrons (holes), \({q}_{y}\) and \({q}_{x}\) represent the components of particle’s wavevector. The wavefunctions describing the motion of holes and electrons along the structure can be written in the barrier regions as (Sun et al. 2010a; Rodríguez-González 2017):

$$ \varphi_{ \pm } \left( {x,y} \right) = \frac{1}{\sqrt 2 }\left( {\begin{array}{*{20}c} 1 \\ {v_{ \pm } } \\ \end{array} } \right)e^{{ \pm iq_{x} x + iq_{y} y}} $$
(3)

with

$$ v_{ \pm } = \frac{{\hbar v_{F} \left( \pm q_{x} + i\left( {q_{y}+ \frac{e}{\hbar }A_{y} } \right)\right)}}{{(E - V_{0} )}} $$
(4)

In the well regions where the electric and magnetic fields are switched-off, the dispersion relation becomes:

$$ E = \pm \hbar v_{F} \sqrt {k_{x}^{2} + k_{y}^{2} } $$
(5)

Furthermore, the wavefunctions in well regions are formulated as following:

$$ \varphi_{ \pm } \left( {x,y} \right) = \frac{1}{\sqrt 2 }\left( {\begin{array}{*{20}c} 1 \\ {u_{ \pm } } \\ \end{array} } \right)e^{{ \pm ik_{x} x + ik_{y} y}} $$
(6)

with

$$ u_{ \pm } = \frac{{\hbar v_{F} ( \pm k_{x} + ik_{y} )}}{E} $$
(7)

The transmission coefficient \(T(E)\) is computed using the transfer matrix method (Yeh 2005; Markos and Soukoulis 2008; Rodríguez-González and Rodríguez-Vargas 2015). Using the conservation of the y component of the wavevector in well and barrier regions (\({k}_{y}={q}_{y})\) and the continuity of the wavefunctions at each interface, we can connect the amplitudes of the input and output wavefunctions by a transfer Matrix \(M\) via the following relation (Yeh 2005; Markos and Soukoulis 2008; Rodríguez-González and Rodríguez-Vargas 2015):

$$ \left( {\begin{array}{*{20}c} {A_{0} } \\ {B_{0} } \\ \end{array} } \right) = M\left( {\begin{array}{*{20}c} {A_{N + 1} } \\ 0 \\ \end{array} } \right) $$
(8)

where \(M\) represents the transfer matrix given by the following expression:

$$ M = D_{0}^{ - 1} \left( {\mathop \prod \limits_{j = 1}^{N} D_{j} P_{j} D_{j}^{ - 1} } \right)D_{0} $$
(9)

The propagation \({P}_{j}\) and dynamic \({D}_{j}\) matrices can be written as following:

$$ P_{j} = \left( {\begin{array}{ll} {e^{{ - iq_{x,j} d_{j} }} } & 0 \\ 0 & {e^{{ + iq_{x,j} d_{j} }} } \\ \end{array} } \right) $$
(10)
$$ D_{j} = \left( {\begin{array}{ll} 1 & 1 \\ {u_{ + ,j} } & {u_{ - ,j} } \\ \end{array} } \right) $$
(11)

The transmission coefficient \(T(E)\) is given by following expression (Myoung and Ihm 2009; Myoung et al. 2011)

$$ T\left( E \right) = \frac{1}{{\left| {M_{11} } \right|^{2} }} $$
(12)

With \({M}_{11}\) represents the first element of the matrix \(M\). Once the transmission coefficient is calculated, the conductance can be straightforwardly determined based on Landauer–Buttiker expression as (Wei-Tao et al. 2013)

$$ {\raise0.7ex\hbox{$G$} \!\mathord{\left/ {\vphantom {G {G_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${G_{0} }$}} = E_{F} \mathop \int \limits_{ - \pi /2}^{\pi /2} T\left( {E_{F} ,\theta } \right)\cos \left( \theta \right)d\theta $$
(13)

\({E}_{F}\) is the Fermi level and \({G}_{0}=2 {e}^{2}{L}_{y}{E}_{0}/{h}^{2}{v}_{F}\) represents the fundamental conductance factor. \({L}_{y}\) stands the width of the system in the transversal direction (y axis) and \(\theta \) is the angle of incidence.

3 Results and discussion

3.1 Electric field effects

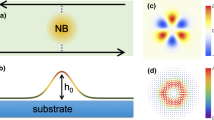
As mentioned above, the theoretical model was used to investigate the transmission coefficient and the conductance in multibarrier system under the effects of electric and magnetic fields. Figure 1 shows the studied structure. It consists of a graphene monolayer sitting above a non-interacting SiO2 substrate.

Fig. 1
figure 1

Schematic representation of graphene multibarrier under magnetic field. The top gates are used to apply magnetic and electric fields

Full size image

The graphene layer and SiO2 are sandwiched between back and top gates. The back gate (BG) is used to control the Fermi level; however, the top gates are used to select the desired electric and magnetic fields. For all numerical calculations, we adopt \({B}_{0}=0.1 T\) as the unit of magnetic field, for which the magnetic length is \(l_{B} = 811\) Å. The unit energy is equal to \({E}_{0}=7 meV.\)

At first the behavior of the transmission coefficient was analyzed as a function of the particle’s incident energy as shown in Fig. 2a–f. The number of barriers varies between \(N=2\) and 7. The structure is symmetric \({d}_{w}={d}_{B}={l}_{B}\) and the magnetic field is switched-off \(\left(B=0\right)\). In this only the effect of an electric field was considered. By examining these figures, it is clearly shown that the transmission coefficient demonstrated oscillations for all cases. These oscillations are multiplied when \(N\) increases and the resonant peaks become more pointed. For instance, by examining the case of two barriers \(\left(N=2\right),\) see Fig. 2a, we observe only three resonant states for positive energy \((E>0)\). However, for \(N>2\), These three resonant states are transformed into three energy minibands separated by minigaps. Each energy minibands present \((N-1)\) resonant states. The minigaps become well defined for higher values of \(N\) which represents an interesting result for technological applications especially in electronic filters. For negative energy (holes), it is demonstrated that the split of the resonant peaks into miniband gaps is less pronounced compared to that obtained in the case of electrons. Furthermore, the depth of the minigaps becomes deeper by increasing the number of barriers. In addition, it is found that all the minigaps in the transmission coefficient of the holes do not reach zero energy. It means that the Dirac electrons can be suppressed perfectly than the holes for higher values of \(N\).

Fig. 2
figure 2

Transmission coefficient as a function of incident energy for different number of barriers; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \(\theta = \pi /6\); \({d}_{w}={d}_{B}={l}_{B}\); V0 = 2 E0; B = 0 T

Full size image

To further analyze the behavior of the transmission coefficient and its dependence on the angle of incidence \(\theta \), the variation of \(T(E,\theta )\) for different values of \(N\) are plotted in Fig. 3a–f. It is clear that the number of minibands and minigaps increase with\(N\). The transmission is at its maximum for zero incidence, which confirms the Klein-Tunneling effect. For higher values of\(\theta \), the mingaps separating the minibands become larger for the electrons (\(E>0)\). In the case of the holes, the minigaps are less deep and large, which confirms the results observed in Fig. 2a–f obtained for\(\theta = \pi /6\). Furthermore, a regular increase of the number of resonant peaks around \(E=0\) with the number of barriers is obtained. For instance, the transmission has one peak for \(N=2;\) two peaks for\(N=3\); and so on. In general, there are \((N-1)\) peaks contained in the central miniband.

Fig. 3
figure 3

Contour plots of the transmission coefficients versus the angle of incidence and energy for different number of barriers a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \({ d}_{w}={d}_{B}={l}_{B}\); V0 = 2 E0; B = 0 T

Full size image

After discussing the behavior of the transmission coefficient, we evaluated the conductance in the absence of a magnetic field. We used the same physical parameters as before to calculate the conductance. Figure 4a–f illustrate the conductance as a function of the incident energy for different numbers of barriers. The conductance exhibits peaks and valleys. The number of peaks near the zero-energy region is proportional to the number of barriers. The conductance shows small oscillations in other energy regions (higher and lower values). The staircase-like variations observed for higher energies are attributed to additional resonant states that appear in the transmission coefficient as the energy increases. In fact, the conductance is a sum over energy and therefore exhibits more oscillations with an increasing number of resonant states.

Fig. 4
figure 4

Conductance as a function of energy for different barriers number; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \({d}_{w}={d}_{B}={l}_{B}\); V0 = 2 E0; B = 0 T

Full size image

3.1.1 Magnetic field effects

In this section, the electric field is switched-off, and a magnetic field is applied. Figure 5a–f display the variation of \(T(E)\) as a function of incident energy for different barrier number.

Fig. 5
figure 5

Transmission coefficient as a function of incident energy for different barriers number; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \(; {d}_{w}={d}_{B}={l}_{B} ; \theta = \pi /6\); V0 = 0; B = 0.1 T

Full size image

In this case, the magnetic field is equal to \(B=0.1 T\). In this case, the transmission coefficient exhibits some oscillations indicating the existence of resonant states within the minibands separated by minigaps. The behavior of the transmission coefficient in this case is different to that in absence of magnetic field (see Fig. 2a–f). The main observation is that the number of minibands in positive region of energy is reduced. In fact, when the magnetic field is applied, a shift of Dirac cones in the direction of wave-vector component \(( {q}_{y})\) occurs. In other words, the term (\({{v}_{F}^{2} \left(\hslash {q}_{y}+e{A}_{y}\right)}^{2}\) in the expression (2) will introduce a translation of resonant energy values. This energetic shift is responsible to the disappearance of the second miniband in positive energy region \((E>0)\) which was present in the absence of the magnetic field (Fig. 2a–f).

The contour plot of \(T(E,\theta )\) in the presence of magnetic field is given by Fig. 6a–f. By comparing these variations to those obtained in Fig. 3a–f, we observe that in the absence of magnetic field, the transmission coefficient is symmetric with respect to normal incidence \(\left(\theta =0\right)\).

Fig. 6
figure 6

Contour plots of the transmission coefficients as a function of both angle of incidence and energy for different number of barriers a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \({d}_{w}={d}_{B}={l}_{B}; \) V0 = 2 E0; B = 0.1 T

Full size image

This behavior becomes absent when the magnetic field is applied. Furthermore, additional minibands and minigaps are obtained in the region of positive incidence close to \(\theta = \pi /3\). This number of minibands increase with the number of barriers. The main observation is the relationship between resonant states of the central miniband around \(\left(E=0\right)\) and the number of barriers. This central miniband contains one resonant state for \(\left(N=2\right)\), two resonant states for \(\left(N=3\right)\), and so on. In general, we obtain \(\left(N-1\right)\) resonant states for a structure containing \(N\) barriers. In addition, it is clear from this figure that the resonant states are sharper at positive incidence \(\left(\theta >0\right)\) than those obtained at negative angles \(\left(\theta <0\right)\). This dissymmetry is caused by the application of the magnetic field.

The variation of the conductance under the impact of magnetic field is given by Fig. 7a–f. By examining the expression of the conductance given in Eq. (13), we see that it is obtained by summing over all the values of transmission channels and incident angles between \(-\pi /2\) and \(\pi /2\). This means that its behavior is closely related to that of the transmission coefficient. Mathematically, when a Fermi energy is selected and then an integration over all the possible angles between \(-\pi /2\) and \(\pi /2\) is done, the minibands and minigaps and the peaks of resonant states will be reflected in the conductance. Furthermore, the symmetric or asymmetric characteristics observed in the transmission coefficient is also repeated in the features of the conductance. By analyzing Fig. 7a, i.e. \((N=2)\), we remark the existence of two minibands. Each one contains one peak. However, for \((N=3\)), these minibands are split and then displayed two peaks. In general, there are \((N-1)\) peaks for \(N\) barriers. Furthermore, by increasing the number of barriers \(N\), the oscillatory characteristics observed in each miniband becomes less perceptible. All these behaviors reflect the features previously observed in the transmission coefficients variation.

Fig. 7
figure 7

Variation of conductance as a function of energy for different barriers number; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \({d}_{w}={d}_{B}={l}_{B}\); V0 = 2 E0; B = 0.1 T

Full size image

4 Quantum barrier and well widths effect

In the rest of this paper, the impacts of quantum size and magnetic fields on the transmission coefficients will be discussed. To do this, we have considered a width of barriers equal to the double of that of quantum wells \({({d}_{B}=2d}_{w})\). Figures 8a–f and 9a–f display the variation of the transmission coefficient without and with magnetic field, respectively. Without magnetic field, the figures show some minibands alternated by minigaps for electrons \(\left(E>0\right)\) and holes \(\left(E<0\right)\). The number of resonant states increases in each miniband by increasing the number of barriers. From these figures, it is clear that the central miniband located around zero energy contains the large number of resonant states. This central miniband becomes well defined and almost symmetric with respect to zero energy for higher number of barriers. By applying a magnetic field intensity (B = 0.1 T) (see Fig. 9a–f), the behavior of the transmission changes dramatically. In fact, the minibands and minigaps of holes transmission \(\left(E<0\right)\) still almost unchanged by applying B. However, the transmission of electrons \(\left(E>0\right)\) is considerably affected by the application of the magnetic field. In fact, the two minibands which were present without B are now suppressed. In other words, the magnetic field acts as a filter. It favorize the transmission of holes and suppress that of the electrons.

Fig. 8
figure 8

Transmission coefficient as a function of energy for different number of barriers; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \(\theta = \pi /6\); \({d}_{B}=2{d}_{w}=2{l}_{B}\); V0 = 2 E0; B = 0 T

Full size image
Fig. 9
figure 9

Transmission coefficient as a function of energy for different number of barriers; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7; \(\theta = \pi /6\); \({d}_{B}=2{d}_{w}=2{l}_{B}\); V0 = 2 E0; B = 0.1 T

Full size image

Finally, the effects of quantum wells width on the transmission coefficient with and without the presence of magnetic field are given in Figs. 10a–f and 11a–f, respectively. The quantum well width in these cases is twice of that of the barriers \({({d}_{w}=2d}_{B})\). It is clear from these figures that the number of resonant states is multiplied if compared to those appeared in the symmetric case \({({d}_{w}=d}_{B})\). The minibands and minigaps are well defined and the separations between different resonant states is almost constant. Furthermore, the transmission coefficient touches the unity for all particles (holes and electrons). When the magnetic field is applied, the number of resonant states in all minibands is reduced. As a result, the magnetic field suppress the transmission of electrons by doubling the barriers widths but keep small miniband regions by doubling the quantum well widths. This result is interesting to tune and select the desired transmission of carriers (holes and electrons) by selecting the suitable widths and applying an external magnetic field.

Fig. 10
figure 10

Transmission coefficient as a function of energy for different number of barriers; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7;\(\theta = \pi /6\); \({d}_{w}=2{d}_{B}=2{l}_{B}\); V0 = 2 E0; B = 0 T

Full size image
Fig. 11
figure 11

Transmission coefficient as a function of energy for different number of barriers; a N = 2, b N = 3, c N = 4, d N = 5, e N = 6, f N = 7;\(\theta = \pi /6\); \({d}_{w}=2{d}_{B}=2{l}_{B}\); V0 = 2 E0; B = 0.1 T

Full size image

5 Conclusion

In conclusion, the transmission and conductance of multibarrier graphene systems under the impact of quantum size, and electric, and magnetic fields were theoretically discussed. Their impacts on the behavior of the minibands and minigaps of the transmission coefficients and conductance are discussed in detail. Symmetric and asymmetric cases \(\left({d}_{w}={d}_{B}\right)\) and \(\left({d}_{w}\ne {d}_{B}\right)\) were considered. Our results showed that the transmission coefficients display some minibands sandwiched between minigaps. The number of resonant states in each miniband increases considerably with the number of barriers. For \(N\) barriers, we obtain \((N-1)\) resonant states. In addition, it was found that in the symmetric case \(\left({d}_{w}={d}_{B}\right)\), the application of magnetic field reduces the number of minibands and resonant states of electrons \(\left(E>0\right)\), but the holes are less affected. However, in the asymmetric case \(\left({{d}_{B}=2d}_{w}\right)\), the application of a magnetic field completely suppresses the minibands of electrons \(\left(E>0\right)\) for an odd number of barriers (\(\mathrm{N}=3, 5\mathrm{ and }7)\) and display one resonant state for even number of barriers (\(\mathrm{N}=2, 4\mathrm{ and }6)\). The variations of the transmission coefficient with the angle of incidence were discussed by plotting the contour plot \(T(E,\theta )\). The obtained results show that the transmission coefficient depends considerably on the angle of incidence. The total transmission at normal incidence \((\theta =0)\) known as Klein-Tunneling effect was demonstrated.