1 Introduction

Since the concept of semiconductor superlattices was proposed by Tsu and Esaki (1973), the electron resonant tunneling phenomena in semiconductor superlattices have attracted much attention from both theoretical and experimental scientists (Tsu and Esaki 1973; Yamamoto et al. 1992; Vezzetti and Cahay 1986; Liu and Stamp 1993, 1994; Esposito 2003; Pereyra and Castillo 2002; Kuiri et al. 2018; Kamal et al. 2018). By solving the electron’s Schrodinger equations with numerical calculations, Tsu and Esaki (1973) and Yamamoto et al. (1992) had shown that the electron resonance transmission peak through structures consisted of N-fold electric barriers and (N − 1)-fold wells splitted into (N − 1) peaks. This phenomenon was analytically proven by Vezzetti and Cahay (1986) and Liu and Stamp (1993, 1994), respectively, which has demonstrated that the (N − 1)-fold resonance splitting effect in one-dimensional periodic potentials structure with arbitrary profile is an inherent property of the semiconductor superlattices, and there is an explicit correlation between the resonance energies with the miniband structure of the corresponding infinite superlattice. Later, Zeng et al. (1999, 2001), Wang and Yan (2000), and Guo et al. (1998) theoretically investigated the resonant splitting of ballistic conductance peaks in magnetic superlattices, and found that there also exists a general (N − 1)-fold resonant peak splitting rule for ballistic conductance in magnetic superlattices with periodically arranged N-identical magnetic barriers. Therefore, it seems that one could depict the resonance splitting for electron tunneling through an electric superlattice and a magnetic superlattice in a unified way.

As both semiconductor and graphene superlattices are vastly promising to control the electron transport, the question arises as to whether the resonance splitting effect also exists in Dirac electrons transported through graphene superlattices. Recently, Lu et al. (2012a, b) numerically investigated the resonance splitting effect through Kronig–Penney, step and sinusoidal magnetic superlattices in graphene. They found that the transmission, the conductance and the shot noise presented (N − 1)-fold resonance splitting for the magnetic superlattices with N-barriers. Pham et al. (2015) also analytically and numerically investigated the resonant peak splitting in two graphene superlattices with periodic electrostatic potentials of rectangular barriers and δ-function magnetic potential. They demonstrated that the transmission probability spectra exhibited two types of resonance energies: the barrier-induced resonance energies were unchanged as N varies, while the well-induced resonance energies had undergone the (N − 1)-fold splitting as N increases. This phenomenon is similar to the Schrodinger electrons in semiconductor superlattices. Most recently, Xu et al. (2014) analytically and numerically investigated the resonant peak splitting in graphene superlattices with periodic electrostatic potentials of square barriers or sinusoidal barriers. They found that there were two resonance conditions for the graphene superlattices, and some of the resonance transmission peaks presented (N − 1)-fold resonance splitting for N-barriers, which was analogy of the (N − 1)-fold resonant splitting for transmission probability in N-barrier electric superlattice in semiconductor. However, the resonant splitting rule was not sensitive to the shape of the potential barrier, and there was no explicit rule for the conductance and shot noise, which was different from the magnetic case. Lately, Lu et al. (2015) found that there existed a (2N − 1)-fold resonance splitting for N-barriers superlattices with the realistic magnetic profile, and they attributed those differences to the different profiles between the realistic and the idealistic models used in their numerical calculations.

Previously, Huo et al. (2012a, b) investigated the transport properties through magnetic superlattices with double-barrier units, and they found that for an N-periodic asymmetric double-barrier unit, there was (N − 1)-fold resonance transmission peak splitting, but the splitting was (2N − 1)-fold for an N-periodic, symmetric double-barrier unit. Furthermore, Zeng et al. (2000) and Guo et al. (1998) found that for electron tunneling through the electric or magnetic superlattices made of two identical barriers or two different barriers, one resonant window of the former split into two subdomains, within each of which the resonance split into (N − 1)-fold, where N was the number of the renormalized building blocks consisting of two different barriers of the latter. They indicated that the resonant splitting was determined not only by the structure but also by the parameters of the building blocks. Guo et al. (1998) found that there was no explicit and general resonant peak splitting for transmission in magnetic superlattices, and the resonance splitting effect in magnetic barriers strongly depended on the tunneling momentum of electrons.

In this paper, the resonant splitting in superlattices with asymmetric double-barrier units in graphene will be analytically and numerically investigated. This work has discovered that there are two types of resonant peaks: (1) the resonant peak through a unit cell; and (2) the periodicity induced peak splitting of (N − 1)-fold. The splitting rule has been further confirmed by the conductance and noise versus the incident energy. The obtained results have contributed a great deal to the analysis and identification of the oscillatory characterization of transport in experiments, and the differentiation of the line-type resonance and the Fabry–Perot interference, especially when more complex resonant tunneling is involved. Furthermore, these discoveries will provide greatly superior advantages in the design and optimization of effective magneto resistance devices and filter devices.

2 Analytical derivation

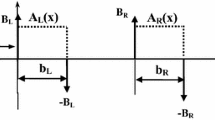
Figure 1 show the magnetic vector potential profiles of a unit cell with two barriers and two wells in one-dimensional finite superlattices. To simplify the calculations, the electric/magnetic fields are assumed as periodically arranged in the x-direction, and the potential A(x), defined on 0 < x < L, is of an arbitrary shape and nature of electric/magnetic type. The superlattice potential AN(x) is defined to be the same potential A(x) periodically repeated N times, on the interval 0 < x < NL. The spatial period of the external potential is assumed much larger than the graphene lattice constant (~ 1.42 Ǻ), so the intervalley scattering in the theoretical derivation can be neglected. Thus, the Dirac-like Hamiltonian around the K point, in a long-wavelength approximation, could be expressed as (with \(\hbar = c = 1\)):

$${\text{H}} = \nu_{F} \vec{\sigma } \cdot \left( {\vec{P} + e\vec{A}\left( x \right)} \right) + eU \cdot I,$$
(1)

where \(v_{F} = 10^{6} {m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}\) is the Fermi velocity, e is the absolute value of the electron charge, \(\vec{A}\)(x) is the vector potential, \(\vec{\sigma } = \left( {\sigma_{x} ,\sigma_{y} } \right)\) is a 2 × 2 Pauli matrices vector and I is the 2 × 2 unit matrix.

Fig. 1
figure 1

The magnetic vector potential profiles of a unit cell with two-barriers and two-wells in finite periodic superlattices

Full size image

The state function \(\psi\) is denoted by \(\psi = \left[ {\psi_{A} \left( {x,y} \right) , \psi_{B} \left( {x,y} \right)} \right]^{T}\), where \(\psi_{A} \left( {x,y} \right) = \psi_{A} \left( x \right)e^{{ik_{y} y}}\) and \(\psi_{B} \left( {x,y} \right) = \psi_{B} \left( x \right)e^{{ik_{y} y}}\) are the wave functions for two sublattices in graphene, ky is the wave vector along the y coordinate. By solving the Dirac equation in each region and by matching the wave function at the boundaries, the transmission probability through a unit cell can be simulated by the transfer matrix method below (Wang et al. 2014; Lin et al. 2011)

$$\left( {\begin{array}{*{20}c} 1 \\ {{\text{r}}_{1} } \\ \end{array} } \right) = {\text{M}}\left( {\begin{array}{*{20}c} {{\text{t}}_{1} } \\ 0 \\ \end{array} } \right),$$
(2)
$$T_{1} = \left| {t_{1} } \right|^{2} = 1/\left| {M_{11} } \right|^{2} ,$$
(3)

Here

$${\text{M}} = S_{L} S_{AL} S_{wL} S_{AR} S_{wR} S_{R} ,$$
(4)
$$S_{L} = \frac{{E}}{{2k_{w} }}\left( {\begin{array}{*{20}c} {\frac{{k_{w} - ik_{y} }}{E}} & {1.0} \\ {\frac{{k_{w} - ik_{y} }}{E}} & { - 1.0} \\ \end{array} } \right),$$
(5)
$$S_{R} = \left( {\begin{array}{*{20}c} {1.0} & {1.0} \\ {\frac{{k_{w} + ik_{y} }}{E}} & { - \frac{{k_{w} - ik_{y} }}{E}} \\ \end{array} } \right),$$
(6)
$$S_{{w_{j} }} = \left( {\begin{array}{*{20}c} {Cos\left( {k_{w} w_{j} } \right) - \frac{{k_{y} }}{{k_{w} }}Sin\left( {k_{w} w_{j} } \right)} & { - i\frac{{E}}{{k_{w} }}Sin\left( {k_{w} w_{j} } \right)} \\ { - i\frac{{E}}{{k_{w} }}Sin\left( {k_{w} w_{j} } \right)} & {Cos\left( {k_{w} w_{j} } \right) + \frac{{k_{y} }}{{k_{w} }}Sin\left( {k_{w} w_{j} } \right)} \\ \end{array} } \right),$$
(7)
$$S_{{A_{j} }} = \left( {\begin{array}{*{20}c} {Cos\left( {k_{{A_{j} }} d_{j} } \right) - Sin\left( {k_{A_{j}} d_{j} } \right)} & { - i\frac{{E}}{{k_{{A_{j} }} }}Sin\left( {k_{{A_{j} }} d_{j} } \right)} \\ { - i\frac{{E}}{{k_{{A_{j} }} }}Sin\left( {k_{{A_{j} }} d_{j} } \right)} & {Cos\left( {k_{{A_{j} }} d_{j} } \right) + \frac{{\left( {k_{y} + A_{j} } \right)}}{{k_{{A_{j} }} }}Sin\left( {k_{{A_{j} }} d_{j} } \right)} \\ \end{array} } \right).$$
(8)

with

$$k_{w} = \sqrt {\left( {E^{2} - k_{y}^{2} } \right)} ,\;\; k_{{A_{j} }} = \sqrt {\left[ {E^{2} - \left( {k_{y} + A_{j} } \right)^{2} } \right]} ,{\text{ j}} = {\text{R}},{\text{L}}.$$
(9)

For convenience, all quantities are expressed in dimensionless units, i.e. \(l \to l_{0} l\), \(k \to k_{0} k\), \(E \to E_{0} E\), \(A \to B_{0} l_{0} A\), where \(k_{0} = 1/l_{0}\), \(E_{0} = \hbar v_{F} /l_{0}\), \(B_{0} = \hbar /el_{0}^{2}\). For a realistic value B0 = 0.1 T, lB0 = 811 Å and E0 = 7.0 meV are used.

For the N-periods superlattice of potential AN(x), the transfer matrix is required to be applied N times to map an arbitrary solution from x = 0 to NL. There is an easy way to construct the transfer matrix once the single unit cell transmission problem is solved.

$${\text{M}} = \left( {\begin{array}{*{20}c} {\frac{{1}}{{{\text{t}}_{1} }}} & {\frac{{{\text{r}}_{1}^{ *} }}{{{\text{t}}_{1}^{ *} }}} \\ {\frac{{{\text{r}}_{1} }}{{{\text{t}}_{1} }}} & {\frac{{1}}{{{\text{t}}_{1}^{ *} }}} \\ \end{array} } \right),$$
(10)

The solution for the problem of N-periodic superlattice follows up the solution for the single unit cell case as:

$$\left( {\begin{array}{*{20}c} 1 \\ {{\text{r}}_{\rm{N}} } \\ \end{array} } \right) = {\text{M}}^{\text{N}} \left( {\begin{array}{*{20}c} {{\text{t}}_{\rm{N}} } \\ 0 \\ \end{array} } \right),$$
(11)

By using the Cayley–Hamilton theorem and after some derivations, obtains

$${\text{M}}^{\text{N}} = \frac{{1}}{\sin \emptyset }\left[ {{\text{M}}\sin {\text{N}}\emptyset - {\text{I}}\sin \left( {{\text{N}} - 1} \right)\emptyset } \right],$$
(12)

Finally, the transmission probability through an N-period superlattice is derived as:

$${\text{T}}_{\rm{N}} = \left\{ {1 + \frac{{\sin^{2} {\text{N}}\emptyset }}{{\sin^{2} \emptyset }}\left( {\frac{{1}}{{{\text{T}}_{1} }} - 1} \right)} \right\}^{ - 1} ,$$
(13)

Here \(\cos \emptyset = {\text{ReM}}_{11} = {\text{Re}}\left( {1/{\text{t}}_{1} } \right)\). In fact, \(\emptyset\) is the Bloch phase associated with the infinite periodic potential whose unit is cell A(x) (Lin et al. 2011; Barbier et al. 2010).

Equation (13) is expressed with transmission probability T1 of unit cell and the Bloch phase \(\emptyset\), which is the general transmission probability for all types of finite superlattice. It is evident that the resonant peaks appear whenever \({\text{T}}_{1} = 1\), in addition, there are (N − 1) peaks when \({\text{N}}\emptyset = {\text{m}}\pi\), m = 1, 2, … (N − 1) in each allowed band, where the increment of \(\emptyset\) is π. It is worthwhile to indicate that the resonance splitting rule is a universal rule, which is also applicable to the one-dimensional, finite, N-periodic semiconductor electrostatic superlattice, the magnetic superlattice and the alike one realized in modulation two-dimensional electron gas structure, as long as the superlattice is of N-periodicity.

Here, the analytical expression of transmission probability will be derived for several model superlattices frequently investigated in previous publications.

  1. (1)

    A magnetic vector potential Kronig–Penney superlattice: (Lu et al. 2012a, b; Wu et al. 2008) its unit cell consists of a square magnetic barrier of vector potential A of width dB and a well of vector potential zero of width w. The transmission probability of the unit cell is expressed as:

    $${\text{T}}_{1} = \left\{ {1 + \sin^{2} \left( {{\text{k}}_{\rm{A}} {\text{d}}_{\rm{B}} } \right)\left[ {\frac{{\text{EA}}}{{{\text{k}}_{\rm{A}} {\text{k}}_{\rm{W}} }}} \right]^{2} } \right\}^{ - 1} ,$$
    (14)

    with \({\text{k}}_{\rm{w}} = \sqrt {{\text{E}}^{2} - {\text{k}}_{\rm{y}}^{2} } ,\;\;{\text{k}}_{\rm{A}} = \sqrt {{\text{E}}^{2} - \left( {{\text{k}}_{\rm{y}} + {\text{A}}} \right)^{2} }\). The kBdB = 0 corresponds to the Fabry–Perot resonance of the single magnetic barrier, which was observed by Lu et al. (2012a, b), the result in Lu et al. (2012a, b) can be regard as only a specific case of the results presented in this paper.

  1. (2)

    An asymmetrical two-magnetic barrier superlattice: (Huo et al. 2012a, b) its unit cell consists of an asymmetrical two magnetic barrier of rectangular magnetic vector potential of AL, AR with widths of dL, dR, and two wells of zero vector potential of width of wL and wR, respectively. The unit cell transmission probability is given as follows: (Xu et al. 2017)

$${\text{T}} = \frac{{{\text{T}}_{\rm{M}} }}{{1 + \left[ {{\text{D}}_{\rm{s}} { \cos }\left( {\varPhi /2} \right)} \right]^{2} }},$$
(15)
$${\text{T}}_{\rm{M}} = \frac{{{\text{T}}_{\rm{L}} {\text{T}}_{\rm{R}} }}{{\left[ {1 - \sqrt {1 - {\text{T}}_{\rm{L}} } \sqrt {1 - {\text{T}}_{\rm{R}} } } \right]^{2} }},$$
(16)

where

$${\text{D}}_{\rm{S}} = \frac{{2\sqrt[4]{{1 - {\text{T}}_{\rm{L}} }}\sqrt[4]{{1 - {\text{T}}_{\rm{R}} }}}}{{1 - \sqrt {1 - {\text{T}}_{\rm{L}} } \sqrt {1 - {\text{T}}_{\rm{R}} } }},$$
(17)
$${\text{T}}_{{{\text{L}},{\text{R}}}} = \left\{ {1 + \sin^{2} \left( {{\text{k}}_{{{\text{L}},{\text{R}}}} {\text{d}}_{{{\text{L}},{\text{R}}}} } \right)\left( {\frac{{{\text{EA}}_{{{\text{L}},{\text{R}}}} }}{{{\text{k}}_{0} {\text{k}}_{{{\text{L}},{\text{R}}}} }}} \right)^{2} } \right\}^{ - 1},$$
(18)

and

$$\varPhi = \phi_{\rm{L}} + \phi_{\rm{R}} + 2{\text{k}}_{\rm{w}} {\text{w}}_{\rm{L}},$$
(19)
$$\phi_{{{\text{L}},{\text{R}}}} = {\text{Arctan}}\left( {\frac{{{\text{k}}_{\rm{L}}^{2} + {\text{k}}_{\rm{R}}^{2} + {\text{B}}_{{{\text{L}},{\text{R}}}}^{2} }}{{2{\text{k}}_{{{\text{L}},{\text{R}}}} {\text{k}}_{\rm{w}} }}{ \tan }\left( {{\text{k}}_{{{\text{L}},{\text{R}}}} {\text{d}}_{{{\text{L}},{\text{R}}}} } \right)} \right),$$
(20)

Here \(\phi_{{{\text{L}},{\text{R}}}}\) is the characteristic phase difference. When both the PDCR and the MCPV are satisfied simultaneously, the complete transmission (T1 = 1) will occur in an asymmetrical two-magnetic-barrier structure (Xu et al. 2017). Otherwise, the resonant transmission peak becomes less than unity (i.e., T1 < 1). When AL = AR, dL = dR, and wL ≠ wR, it reduces to the biperiodic superlattice case. For a general asymmetric two magnetic barriers structure as illustrated frequently in literature (Huo et al. 2012a, b), AL ≠ AR, dL ≠ dR, and wL ≠ wR, it most likely leads to TL ≠ TR, so the unit cell related resonant peak can only be observed in a few of the superlattices.

It should be pointed out that in Kronig–Penney type of superlattice, the unit cell consists of one barrier and one well, and the well layer is often assumed to be the same as the contact layer, it leads the transmission probability of N-fold barriers superlattice with N barriers and (N − 1) wells to coincide with that of the N period one with N barriers and N wells. As adding a well layer to the N barriers and (N − 1) wells superlattice only brings in a phase difference in its transmission amplitude. The phase difference has no effect on the transmission probability, as the transmission probability is given by square of the module of transmission amplitude. As a result, people were frequently misled to believe that the resonant peak splitting is correlated with the number of barriers, rather than the period number of a finite superlattice. It always arises confusions on understanding of the resonance peaks splitting in superlattices with complex unit, especially when different type of barriers are added one by one. For example, The authors of Zeng and Zhang (2000) and Guo et al. (1998) had investigated the superlattices periodically juxtaposed with two different barriers, they observed smaller number of resonance peaks in each resonant subdomain, and the total number of peaks is not always equal to N − 1 for N barrier tunneling. Moreover, the resonance splitting occurred each time when two new barriers are added to the exiting ones. Here, one could easily found out that the barriers are of odd numbers in the former situations, then the corresponding superlattices are no longer periodic ones. While in the later the barrier are of even numbers, and the new superlattices are still periodic ones. To clear up the confusions in the literatures, some numerical calculations will be carried out and presented below.

3 Results and discussions

Figure 2a shows the transmission probability versus the incident energy for biperiodic magnetic superlattices with different periods, wL = 0.5 and wR = 0.4. Other structural parameters in the numerical calculations are taken as BL = BR = 3.0, dL = dR = 0.5, respectively. It is clear that the periodicity induced resonant peaks split into (N − 1)-folds as N increases, while the resonant peak through a unit cell remains unchanged as N varies. Furthermore, the width of every peaks and the separation between them become narrower as N increases. Figure 2b shows the transmission probability versus the incident energy for 5-periods biperiodic magnetic superlattices with different righthand well width while fixed wL = 0.5. As the righthand well width becomes wider, the whole transmission spectra shift to lower energy, and each peak width and the separation between peaks becomes narrower. When wR < wL, the resonant peak through a unit cell appears as the highest energy one in the lower domain, while wR > wL, it becomes the lowest energy peak in the higher domain. When wR=wL, it appears to be the middle peak. Compared with the results of Peeters and Vasilopoulos (1989) and Vasilopoulos et al. (1990), one could easily find that the domain versus the asymmetry of the unit cell represents exactly the energy band splitting, and the transmission peaks in each subband contain (N − 1)-folds peaks, as described by Eq. (13).

Fig. 2
figure 2

a Transmission probability versus incident energy for biperiodic superlattices with different periods N; b Transmission probability versus incident energy in 5-periods superlattices with different right well width wR. Here, BL = BR = 3.0, dL = dR = 0.5 and wL = 0.5

Full size image

Figure 3 shows the transmission probability versus the incident energy for two superlattices of different periods with BL = 3.0, i.e., (a) BR = 2.4; (b) BR = 1.8. Other structural parameters in the numerical calculations are taken as dL = dR = 0.5 and wL = wR = 0.5. It is clear that the periodicity-related resonant peaks split into (N − 1)-folds of unity transmission probability in each subband while increasing the period number N. However, the number of the periods for observing the unit cell related imperfect resonant peaks depends on the asymmetry of the unit cell. The greater the asymmetry of the two magnetic barriers is, the smaller the number of the periods is for observing the unit cell related peak. Here, it is 6 periods with BR = 2.4 in Figs. 3a and 3 periods with BR = 1.8 in Fig. 3b. When the righthand barrier becomes asymmetrical to the lefthand barrier of the unit cell, the resonant transmission peak of the unit cell becomes less than unity (T1 < 1). Meanwhile, the greater the asymmetry of the unit cell is (i.e. the righthand barrier’s height or width is away from that of the lefthand’s barrier), the quicker the transmission probability of the unit cell related transmission peak approaches to zero (Xu et al. 2017). The unit cell related resonant transmission peak of the N-periods superlattice could be proximately expressed as (T1)N, thus it decreases much quicker when (T1 < 1). Finally, it becomes unobservable when the righthand barrier potential’s BR is lower than 2.4.

Fig. 3
figure 3

Transmission probability versus incident energy for two series of superlattices of different periods N. Here, a BR = 2.4 and b BR = 1.8, with BL = 3.0, dL = dR = 0.5 and wL = wR = 0.5

Full size image

Figure 4a shows the transmission probability for 5-periods superlattices with righthand barrier potential height BR of 3.0, 2.7, 2.4, 2.1, and 1.8, respectively. Other parameters in the numerical calculations are taken as BL = 3.0, dL = dR = 0.5, wL = wR = 0.5. When BR = BL, the superlattice is reduced to a magnetic Kronig-Penney superlattice of 10 periods with unit cell consisting of barrier BL and well wL, the resonant peaks split into 9-fold with the peak transmission probability of unity, and the Fabry–Perot resonant peak (kBdB = 0) from unit cell does not appear in the given energy region. Similar phenomena have been observed by Lu et al. (2012) and Pham et al. (2015), respectively. The degenerate 9 energy levels of the independent 9 identical wells become nondegenerate and split due to the coupling between the wells via tunneling through the barriers, thus the number of splits is equal to that of the case with 9 wells.

Fig. 4
figure 4

Transmission probability versus incident energy in 5-periods superlattices a with BR of 3.0, 2.7, 2.4, 2.1, and 1.8, here, BL = 3.0, dL = dR = 0.5; b with dR of 0.7, 0.6, 0.5, 0.4, and 0.3, here BL = BR = 3.0, dL = 0.5; and wL = wR = 0.5

Full size image

As the righthand barrier’s height BR is decreased gradually from 3.0 to 2.4, the unit cell becomes an asymmetrical two-magnetic barrier structure, the periodicity-related resonant peaks of N-periods superlattice split into (N − 1)-fold, and all the resonant peaks transmission probabilities are still of unity. However, the transmission probability of the unit cell-related resonant peak, corresponding to the middle one, becomes less than unity (T1 < 1). As the righthand barrier’s height BR is further decreased from 2.4 to 1.8, the unit cell related resonant peak becomes unobservable. As the righthand barrier’s height is decreased from 3.0 to 0, the domain on the lefthand of T1 peak shifts to lower energy, but the domain on the righthand of T1 peak shifts to higher energy. The width of peaks and the separations between them become wider, both domain width and the energy gap between these two domains are enlarged. Similar phenomena can also be observed when the righthand magnetic barrier’s width becomes asymmetrical to the lefthand barrier’s width dL, as shown in Fig. 4b. Here the righthand barrier’s width dR is of 0.7, 0.6, 0.5, 0.4, and 0.3, respectively, when the other parameters are taken as BL = BR = 3.0, dL = 0.5, wL = wR = 0.5.

The similar splitting features of the transmission probability are also reflected in the conductance. According to the Laudauer and Buttiker formula, the conductance G of the system at zero temperature is given as: (Büttiker 1986)

$${\text{G}} = {\text{G}}_{0} \mathop \int \limits_{ - \pi /2}^{\pi /2} {\text{T}}_{\rm{N}} { \cos }\theta_{0} {\text{d}}\theta_{0} ,$$
(21)

Here \(\theta_{0}\) is the angle of the incidence relative to the x-direction, TN is the transmission probability of the N-periods superlattice, and \({\text{G}}_{0} = 2{\text{e}}^{2} {\text{EL}}_{\rm{y}} /\left( {\pi \hbar } \right)\) is taken as the conductance unit and Ly is the sample’s width along the y-direction.

Figures 5 and 6 show the conductance as a function of incident energy for superlattices described in Figs. 3 and 4. The conductance spectra show (2N − 1) fold peaks for the superlattices with 2.4 \(\le\) BR\(\le\) 3.0 or width of 0.4 \(\le\) dR\(\le\) 0.6, while there are two domains of each with (N − 1)-fold resonant conductance peaks for superlattices when BR\(< 2.4\), or dR\(< 0.4\) or dR\(> 0.6\), and the resonant domain’s width and the gap between these two domains are enlarged. The zero-conductance region widens as the values of BR and dR increase. The higher the degree of asymmetry of the unit cell structure is, the more drastic the deduction of the unit cell related conductance peak turns out,and the wider the gap between these two domains becomes. The domain gap in the actual device structure can bring about various graphene based electronic devices.

Fig. 5
figure 5

Conductance versus Fermi energy for superlattices described in Fig. 3

Full size image
Fig. 6
figure 6

Conductance versus Fermi energy for superlattices described in Fig. 4

Full size image

Finally, the shot noise during the transmission will be investigated. The shot noise is a consequence of the quantization of charge, which is useful to reveal information on transmission beyond that contained in the conductance. Many researchers work on shot noise in graphene recently, and a convenient measure of shot nose is the Fano factor and it is given as follows: (Tworzydlo et al. 2006)

$${\text{F}} = \frac{{\mathop \smallint \nolimits_{ - \pi /2}^{\pi /2} {\text{T}}_{\rm{N}} \left( {1 - {\text{T}}_{\rm{N}} } \right){ \cos }\theta_{0} {\text{d}}\theta_{0} }}{{\mathop \smallint \nolimits_{ - \pi /2}^{\pi /2} {\text{T}}_{\rm{N}} { \cos }\theta_{0} {\text{d}}\theta_{0} }},$$
(22)

According to Eq. (22), the Fano factor F = 0 is the perfect transmission case while F = 1 corresponds to the case when transmission is blocked.

Figures 7 and 8 show the Fano factor as a function of incident energy for 2 series of superlattices described in Figs. 3, and 4. It is found that the valleys in the Fano factor are associated with the peak in the conductance. There are (N − 1)-fold valleys in the Fano factor spectra for N-period superlattices, corresponding to the (N − 1)-fold peaks in conductance, while a striking Poisson value plateaus of the Fano factor is formed in the lower energy region due to the conductance blockage. With a decrease in the righthand barrier’s height or width, the Poisson plateaus are broadened towards higher energy.

Fig. 7
figure 7

Fano factor versus Fermi energy for superlattices described in Fig. 3

Full size image
Fig. 8
figure 8

Fano factor versus Fermi energy for superlattices described in Fig. 4

Full size image

It is worth pointing out that the Eq. (13) is generic for all kinds of superlattices with unit of any combination of barriers and wells, including structures with two magnetic barriers/wells, or with two electric barriers, or with electric/magnetic composite double-barriers. For an electrostatic potential Kronig-Penney superlattice: (Pham and Nguyen 2015; Xu et al. 2014) its unit cell consists of a square electrostatic barrier of potential U with width dB and a well of potential zero with width w. The transmission probability of unit cell is obtained as:

$${\text{T}}_{1} = \left\{ {1 + \sin^{2} \left( {k_{U} {\text{d}}_{\rm{B}} } \right)\left[ {\frac{{{\text{k}}_{\rm{y}} {\text{U}}}}{{k_{U} {\text{k}}_{\rm{W}} }}} \right]^{2} } \right\}^{ - 1} ,$$
(23)

with \({\text{k}}_{\rm{w}} = \sqrt {{\text{E}}^{2} - {\text{k}}_{\rm{y}}^{2} }\), \(k_{U} = \sqrt {\left( {{\text{E}} - {\text{U}}} \right)^{2} - {\text{k}}_{\rm{y}}^{2} }\). It can be seen that the resonance occurs at ky = 0 for normal incidence, which corresponds to the Klein tunneling, or kBdB = 0 from T1 = 1 for oblique incidence, corresponding to the Fabry–Perot resonance of a single electrostatic barrier. The similar results have been obtained by Pham and Nguyen (2015) and Xu et al. (2014), respectively. Due to the Fabry–Perot resonant peak appearing frequently at the energy of allowed band, such a coexistence of both types of resonant peaks always leads to a confusion of the generic (N − 1)-fold resonance splitting effect.

For a biperiodic electric superlattice: (Sprung et al. 2008) its unit cell consists of two identical rectangular electric-barriers of potential height U of width dB and two wells of potential zero of different widths, wL and wR, (wL ≠ wR). The transmission probability of the unit cell is obtained as:

$${\text{T}}_{1} = \left\{ {1 + \sin^{2} \left( {{\text{k}}_{\rm{U}} {\text{d}}_{\rm{B}} } \right){\text{H}}^{2} } \right\}^{ - 1} ,$$
(24)

with

$${\text{H}} = \cos \left( {{\text{k}}_{\rm{U}} {\text{d}}_{\rm{B}} } \right)\cos \left( {{\text{k}}_{\rm{w}} {\text{w}}_{\rm{L}} } \right) - \frac{{k_{U}^{2} + k_{w}^{2} - U^{2} }}{{2{\text{k}}_{\rm{U}} {\text{k}}_{\rm{W}} }}\sin \left( {{\text{k}}_{\rm{U}} {\text{d}}_{\rm{B}} } \right){ \sin }\left( {{\text{k}}_{\rm{w}} {\text{w}}_{\rm{L}} } \right),$$
(25)

with \({\text{k}}_{\rm{w}} = \sqrt {{\text{E}}^{2} - {\text{k}}_{\rm{y}}^{2} } ,\;\; {\text{k}}_{\rm{U}} = \sqrt {\left( {{\text{E}} - {\text{U}}} \right)^{2} - {\text{k}}_{\rm{y}}^{2} }\).

The unit cell’s length of the biperiodic superlattice is dB + wL + dB + wR, while the transmission probability of unit cell at resonance T1 = 1 is determined by the symmetric double-barrier structure (UL + 0+UR). It does not change by varying the righthand well’s width. When wR = wL, the biperiodic superlattice is reduced to a 2N-periods electric Kronig-Penney superlattice, while the unit cell consists of (UL + 0) with the widths of (dB + wL). As well’s widths wL or wR increases, all the periodicity related resonant peaks shift to the lower energy, and the peaks’ separation and the subband domain width become narrower accordingly. As the two well’s widths diverge from each other, the separation between these two domains becomes enlarged, which is in a good agreement with the energy band variation obtained in Peeters and Vasilopoulos (1989) and Vasilopoulos et al. (1990)

4 Conclusion

In summary, the resonance splitting effect of transmission through a one-dimensional finite N-periods superlattice with a unit of two barriers and two wells in graphene has been studied analytically and numerically in this paper. It is shown that there are two types of resonant peaks: (1) the periodicity induced resonant peaks splitting of (N − 1)-fold as N increases; and (2) the resonant peak through a unit cell remains unchanged as N varies. As these two barriers in a unit cell become asymmetrical, the resonance transmission probability of the unit cell becomes imperfect (T1 < 1), and drops quickly as the its asymmetry increases. Therefore, the unit related resonant peak could only be observed in superlattices with less unit asymmetry, of a few period numbers. As the number of periods increase, the unit related resonant peak disappears and only periodicity induced (N − 1)-fold splitting remains.

Although the conclusion of this work is deduced based on an assumption of the Dirac electron, the (N − 1)-folds resonant peak splitting rule is guaranteed by the repeatability, and it is confirmed by peak splitting of ballistic conductance and shot noise. The analytical findings are generic and applicable to various kinds of finite graphene superlattices regardless of electron nature, Schrodinger or Dirac electron, their potential types (electric or magnetic) and potential barrier shapes, single barrier or multiple barriers in a unit cell, even though electron tunneling in an electric superlattice is a one-dimensional process and that in a magnetic superlattice is inherently two-dimensional. It is believed that these phenomena will be useful for the design of graphene based nanoelectronic devices, such as the multichannel electron wave filter.