1 Introduction

In recent years, the propagation properties of laser beam passing through atmospheric turbulence have been studied. The deployment of these beams has increased significantly in the atmospheric optics researchers, enabling their applications use in laser radar, remote sensing, free space optical communication and laser imaging systems (Andrews and Phillips 2005; Baykal 2004; Eyyuboglu 2005; Zhang and Yi 2009; Cai et al 2008; Wang et al 2015). During the past few years, several researches have been appeared to study the influence of atmospheric turbulence on the propagation properties of laser beams with various excitations (Zhu et al 2016; Khannous et al 2016; Saad et al 2017; Boufalah et al 2018; Elmabruk and Eyyubolu 2019; Nossir et al 2021). In this context, Casperson and Tovar (1998) have introduced a general laser beam named Hermite–sinusoidal-Gaussian (HsG) as exact solutions of the equation of paraxail wave. Many related studies of atmospheric turbulence have been published as special cases of HsG beam. For instance, the propagation properties of cosh-Gaussian beams through in turbulent atmosphere have been studied (Eyyuboğlu and Baykal 2004, 2005, 2007; Chu et al. 2007; Chu 2007). A detaild investigation of Hermite cosh-Gaussian beam passing through in turbulent atmosphere has been presented (Eyyuboğlu 2005). Another study by Zhou (2011) has focused on the higher order cosh-Gaussian beams propagating through turbulent atmosphere. In addition, the effect of atmospheric turbulence on the partially coherent generalized flattened Hermite cosh-Gaussian beam has been examined (Chib et al 2020). Recently, two further studies (Hricha et al 2021a, b) were presented about the propagation features of vortex cosh-Gaussian and vortex Hermite cosh-Gaussian beams through in atmospheric turbulence. The hollow higher order cosh-Gaussian beam defined as a superposition of cosh-Gaussian beams has been introduced and examined by our research group (Saad and Belafhal 2021; Saad et al 2022; Ebrahim et al 2022). More recently, two general models of vortex cosh-Gaussian beam, defined as vortex Hermite cosh-Gaussian and vortex Higher-order cosh-Gaussian beams and their propagation in the turbulent atmosphere have been investigated (Hricha et al 2022; Ebrahim et al 2023).

In addition, a new beam model of generalized Hermite cosh-Gaussian beam (GHCGB) as a general expression for the hollow higher order cosh-Gaussian beam has proposed by Saad and Belafhal (2023) about the properties of the beam upon propagating in free space and through a fractional Fourier transform (FRFT) system. In the present paper, our aim of interest is on the GHCGB propagating in the turbulent atmosphere optical system. The analytical expression of the beam in the considered optical system is obtained based on the extended Huygens-Fresnel integral diffraction and Rytov method. The intensity distribution of the GHCGB travailing in atmospheric turbulence is illustrated numerically by studying the effects of the structure constant of the turbulent atmosphere and the parameters of the beam. The remaining sections of this paper are organized: in the second Sect. 2, we present the definition form of the incident GHCGB and the theoretical calculations to develop an analytical expression for the GHCGB intensity distribution propagating in atmospheric turbulence. The intensity distribution evolution is performed and discussed by a numerical example in Sect. 3. We conclude our main results by a conclusion part in Sect. 4.

2 The GHCGB propagating in turbulent atmospheric

In the rectangular coordinates system, the GHCGB at the source plane z = 0, in the x- and y- directions, can be defined as follows (Saad and Belafhal 2023)

$$ E_{m,N}^{l,n} \left( {x_{0} ,y_{0} ,z = 0} \right) = A_{0} \left( {\frac{{x_{0} }}{{\omega_{0} }}} \right)^{l} \left( {\frac{{y_{0} }}{{\omega_{0} }}} \right)^{l} \cosh^{n} \left( {\Omega x_{0} } \right)\cosh^{n} \left( {\Omega y_{0} } \right)H_{m} \left( {\sqrt {2\,} \frac{{x_{0} }}{{\omega_{0} }}} \right)H_{N} \left( {\sqrt 2 \frac{{y_{0} }}{{\omega_{0} }}} \right)e^{{ - {{\left( {x_{0}^{2} + y_{0}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{0}^{2} + y_{0}^{2} } \right)} {\omega_{0}^{2} }}} \right. \kern-0pt} {\omega_{0}^{2} }}}} , $$
(1)

where \(A_{0}\) is the amplitude of the input beam, \(\left( {x_{0} ,y_{0} } \right)\) denoting the Cartesian coordinates at the source plane,\(\omega_{0}\) is the Gaussian waist width, \(l\,\) is the hollowness parameter and \(\left( {n,\Omega } \right)\) are the beam order and the decentered parameter associated to the cosh part. \(H_{m} \left( . \right)\,\) and \(H_{N} \left( . \right)\) denote the Hermite polynomials in the x- and y- directions, with mode indexes \(m\) and \(N\), respectively. By using the following identity (Gradshteyn and Ryzhik 1994)

$$ e^{{ - x^{2} /w_{0}^{2} }} \cosh^{n} \left( {\Omega x} \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\frac{n!}{{s!\left( {n - s} \right)!}}} \,e^{{a_{s}^{2} \delta }} e^{{ - (\frac{x}{{\omega_{0} }} - a_{s} \sqrt \delta )^{2} }} , $$
(2)

with \(a_{s} = \left( {s - \frac{n}{2}} \right)\,\,{\text{and}}\,\,\delta = \omega_{0}^{2\,} \Omega^{2}\), Eq. (1) can be expressed in the Cartesian coordinates as a superposition \(\left( {n + 1} \right)\) of decentered cosh part with the same waist in following alternative form

$$ \begin{gathered} E_{m,N}^{l,n} \left( {x_{0} ,y_{0} ,z = 0} \right) = \frac{{A_{0} \,}}{{2^{2n} }}\left( {\frac{{x_{0} }}{{\omega_{0} }}} \right)^{l} \,\left( {\frac{{y_{0} }}{{\omega_{0} }}} \right)^{l} \,\,H_{m} \left( {\sqrt {2\,} \frac{{x_{0} }}{{\omega_{0} }}} \right)\,H_{N} \left( {\sqrt {2\,} \frac{{y_{0} }}{{\omega_{0} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad \times \sum\limits_{s = 0}^{n} {\sum\limits_{u = 0}^{n} {\left( {_{s}^{n} } \right)} } \left( {_{u}^{n} } \right)\exp \left[ {\left( {a_{s}^{2} \delta + a_{u}^{2} \delta } \right)} \right]\exp \left[ { - \left( {\frac{{x_{0} }}{{\omega_{0} }} - a_{s} \sqrt \delta } \right)^{2} } \right]\exp \left[ { - \left( {\frac{{y_{0} }}{{\omega_{0} }} - a_{u} \sqrt \delta } \right)^{2} } \right]. \hfill \\ \end{gathered} $$
(3)

The propagation of a laser beam passing through in turbulent atmospheric at the output plane z can be described based on the extended Huygens–Fresnel diffraction integral as follows (Andrews and Phillips 2005; Born and Wolf 1999)

$$ \begin{gathered} E_{m,N}^{l,n} \left( {x,y,z} \right) = - \frac{ik}{{2\pi z}}\exp \left( {ikz} \right)\int\limits_{ - \infty }^{\infty } {\,\int\limits_{ - \infty }^{\infty } \, } E_{m,N}^{l,n} \left( {x_{0} ,y_{0} ,0} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \frac{ik}{{2z}}\left[ {\left( {x_{0}^{2} + y_{0}^{2} } \right) - 2\left( {xx_{0} + yy_{0} } \right) + \psi \left( {x_{0} ,y_{0} ,x,y} \right)} \right]} \right\}dx_{0} dy_{0} , \hfill \\ \end{gathered} $$
(4)

Here, \(k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) indicate wavenumber with \(\lambda\) being the optical wavelength, \(\left( {x,y} \right)\) refer to receiver plane coordinates, and \(\psi \left( {x_{0} ,y_{0} ,x,y} \right)\) represents the random part of the complex phase that defines the solution to the Rytov method. The average intensity of the GHCGB passing through the turbulent atmosphere at the receiver plane is given by

$$ \begin{aligned} \left\langle {I_{m,N}^{l,n} \left( {x,y,z} \right)} \right\rangle = & \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{m,N}^{l,n} \left( {x_{01} ,y_{01} ,0} \right)E_{m,N}^{ * l,n} \left( {x_{02} ,y_{02} ,0} \right)} } } } \\ & \; \times \exp \left[ { - \frac{ik}{{2z}}\left( {x_{01}^{2} - x_{02}^{2} + y_{01}^{2} - y_{02}^{2} } \right) - 2x\left( {x_{01} - x_{02} } \right) - 2y\left( {y_{01} - y_{02} } \right)} \right] \\ & \; \times \left\langle {\exp \left[ {\psi \left( {x_{01} ,y_{01} ,x,y} \right) + \psi^{*} \left( {x_{02} ,y_{02} ,x,y} \right)} \right]} \right\rangle dx_{01} dx_{02} dy_{01} dy_{02} , \\ \end{aligned} $$
(5)

where \(\langle {} \rangle\) represents the ensemble average over the medium statistics and * refer to complex conjugate. The ensemble average term is expressed as (Andrews and Phillips 2005)

$$ \left\langle {\exp \left[ {\psi \left( {x_{01} ,y_{01} ,x,y} \right) + \psi^{*} \left( {x_{02} ,y_{02} ,x,y} \right)} \right]\,} \right\rangle \,\, = \exp \left\{ { - \frac{1}{{\rho_{0}^{2} }}\left[ {\left( {x_{01} - x_{02} } \right)^{2} + \left( {y_{01} - y_{02} } \right)^{2} } \right]} \right\}, $$
(6)

where \(\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}} ,\) denotes the coherence radius of a spherical wave propagating in the turbulent medium with \(C_{n}^{2}\) is the constant of refractive index structure. From Eq. (3), the term \(E_{m,N}^{l,n} \left( {x_{01} ,y_{01} ,0} \right)E_{m.N}^{*l,n} \left( {x_{02} ,y_{02} ,0} \right)\) in Eq. (5) can be found as

$$ \begin{aligned} E_{m,N}^{l,n} \left( {x_{01} ,y_{01} ,0} \right)E_{m,N}^{ * l,n} \left( {x_{02} ,y_{02} ,0} \right) = & \frac{{A_{0}^{2} }}{{2^{4n} \left( {\omega_{0} } \right)^{4l} }}\sum\limits_{s = 0}^{n} {\sum\limits_{u = 0}^{n} {\left( {_{s}^{n} } \right)} } \left( {_{u}^{n} } \right)\sum\limits_{{s^{\prime} = 0}}^{n} {\sum\limits_{{u^{\prime} = 0}}^{n} {\left( {_{{s^{\prime } }}^{n} } \right)} } \left( {_{{u^{\prime } }}^{n} } \right) \\ & \; \times \exp \left( { - \frac{{x_{01}^{2} }}{{\omega_{0}^{2} }} + \frac{{2a_{s} \sqrt \delta }}{{\omega_{0} }}x_{01} } \right)\exp \left( { - \frac{{x_{02}^{2} }}{{\omega_{0}^{2} }} + \frac{{2a_{{s^{\prime } }} \sqrt \delta }}{{\omega_{0} }}x_{02} } \right)\left( {x_{01} } \right)^{l} \left( {x_{02} } \right)^{l} H_{m} \left( {\sqrt 2 \frac{{x_{01} }}{{\omega_{0} }}} \right)H_{m} \left( {\sqrt 2 \frac{{x_{02} }}{{\omega_{0} }}} \right) \\ & \; \times \exp \left( { - \frac{{y_{01}^{2} }}{{\omega_{0}^{2} }} + \frac{{2a_{u} \sqrt \delta }}{{\omega_{0} }}y_{01} } \right)\exp \left( { - \frac{{y_{02}^{2} }}{{\omega_{0}^{2} }} + \frac{{2a_{{u^{\prime } }} \sqrt \delta }}{{\omega_{0} }}y_{02} } \right)\left( {y_{01} } \right)^{l} \left( {y_{02} } \right)^{l} H_{N} \left( {\sqrt {2\,} \frac{{y_{01} }}{{\omega_{0} }}} \right)H_{N} \left( {\sqrt 2 \frac{{y_{02} }}{{\omega_{0} }}} \right). \\ \end{aligned} $$
(7)

Substituting Eqs. (6) and (7) into Eq. (5), the average intensity of the GHCGB through the turbulent atmosphere at the receiver plane can be rewritten as

$$ \begin{aligned} \left\langle {I_{m,N}^{l,n} \left( {x,y,z} \right)} \right\rangle = & \frac{{A_{0}^{2} k^{2} }}{{4z^{2} 2^{4n} }}\sum\limits_{s = 0}^{n} {\sum\limits_{u = 0}^{n} {\sum\limits_{{s^{\prime } = 0}}^{n} {\sum\limits_{{u^{\prime } = 0}}^{n} {\left( {_{s}^{n} } \right)} } \left( {_{u}^{n} } \right)\left( {_{{s^{\prime } }}^{n} } \right)} } \left( {_{{u^{\prime } }}^{n} } \right) \\ & \; \times \sum\limits_{k = 0}^{{\left[ {m/2} \right]}} {\sum\limits_{{k^{\prime } = 0}}^{{\left[ {m/2} \right]}} {\sum\limits_{h = 0}^{{\left[ {N/2} \right]}} {\sum\limits_{{h^{\prime } = 0}}^{{\left[ {N/2} \right]}} {\frac{{\left( { - 1} \right)^{{^{{k + k^{\prime } + h + h^{\prime } }} }} \left( {m!} \right)^{2} \left( {N!} \right)^{2} }}{{k!k^{\prime } !h!h^{\prime } !\left( {m - 2k} \right)!\left( {m - 2k^{\prime } } \right)!\left( {N - 2h} \right)!\left( {N - 2h^{\prime } } \right)!}}} } } } \,\,\left( {\frac{2\sqrt 2 }{{\omega_{0} }}} \right)^{{2m - 2k - 2k^{\prime } }} \,\left( {\frac{2\sqrt 2 }{{\omega_{0} }}} \right)^{{2N - 2h - 2h^{\prime } }} \\ & \; \times \int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\left( {x_{01} } \right)^{l + m - 2k} \left( {x_{02} } \right)^{{l + m - 2k^{\prime } }} \exp \left[ { - \alpha_{1x} x_{01}^{2} + 2\left( {\beta_{1x} + \frac{{x_{02} }}{{\rho_{0}^{2} }}} \right)x_{01} } \right]\exp \left[ { - \left( {\frac{1}{{\omega_{0}^{2} }} - \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }}} \right)x_{02}^{2} + 2\left( {\frac{{a_{{s^{\prime } }} \sqrt \delta }}{{\omega_{0} }} - \frac{ikx}{{2z}}} \right)x_{02} } \right]} } dx_{01} dx_{02} \\ & \; \times \int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\left( {y_{01} } \right)^{l + N - 2h} \left( {y_{02} } \right)^{{l + N - 2h^{\prime } }} \exp \left[ { - \alpha_{1y} y_{01}^{2} + 2\left( {\beta_{1y} + \frac{{y_{02} }}{{\rho_{0}^{2} }}} \right)y_{01} } \right]\exp \left[ { - \left( {\frac{1}{{\omega_{0}^{2} }} - \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }}} \right)y_{02}^{2} + 2\left( {\frac{{a_{{u^{\prime } }} \sqrt \delta }}{{\omega_{0} }} - \frac{ikx}{{2z}}} \right)y_{02} } \right]} } dy_{01} dy_{02} , \\ \end{aligned} $$
(8)

where

$$ \alpha_{1x} = \frac{1}{{\omega_{0}^{2} }} + \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }}, $$
(9a)
$$ \alpha_{1y} = \frac{1}{{\omega_{0}^{2} }} + \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }}, $$
(9b)
$$ \beta_{1x} = \frac{{a_{s} \sqrt \delta }}{{\omega_{0} }} + \frac{ikx}{{2z}}, $$
(9c)

and

$$ \beta_{1y} = \frac{{a_{u} \sqrt \delta }}{{\omega_{0} }} + \frac{iky}{{2z}}. $$
(9d)

Recalling these integrals and expansion formulae (Belafhal et al 2020; Erdelyi et al 1954; Abramowitz and Stegun 1970)

$$ \int\limits_{ - \infty }^{\infty } {x^{n} \,e^{{ - px^{2} + 2qx}} dx} = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),\, $$
(10a)
$$ \int\limits_{ - \infty }^{\infty } {x^{l} \,H_{m} \left( {ax} \right)\,e^{{ - px^{2} + 2qx}} dx} = \frac{1}{{2^{l} }}\sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\sum\limits_{k = 0}^{{\left[ {m/2} \right]}} {\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} \left( {\frac{\alpha }{i\sqrt p }} \right)^{m + l - 2k} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right),\, $$
(10b)

with \({\text{Re}} \left( p \right) > 0,\)

$$ H_{n} \left( {x + y} \right) = \frac{1}{{2^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} }}\sum\limits_{k = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)H_{k} \left( {\sqrt 2 x} \right)} H_{n - k} \left( {\sqrt 2 y} \right), $$
(11)

and

$$ H_{n} \left( x \right) = \sum\limits_{r = 0}^{{\left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right]}} {\left( { - 1} \right)^{r} \frac{n!}{{r!\left( {n - 2r} \right)!}}\left( {2x} \right)^{n - 2r} } , $$
(12)

and, after integration over \(x_{01} ,x_{02} ,y_{01}\) and \(y_{02}\), Eq. (8) becomes

$$ \begin{aligned} \left\langle {I_{m,N}^{l,n} \left( {x,y,z} \right)} \right\rangle = & \frac{{A_{0}^{2} k^{2} }}{{4z^{2} 2^{4n + 5l} \left( {\omega_{0} } \right)^{4l} }}\frac{1}{{\sqrt {\alpha_{1x} \alpha_{2x} \alpha_{1y} \alpha_{2y} } }} \\ & \; \times \sum\limits_{s = 0}^{n} {\sum\limits_{{s^{\prime } = 0}}^{n} {\sum\limits_{u = 0}^{n} {\sum\limits_{{u^{\prime } = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {s^{\prime } } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ u \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {u^{\prime } } \\ \end{array} } \right)} } } } G_{{_{{s,s^{\prime}}} }}^{m,k} \left( {x,z} \right)G_{{_{{u,u^{\prime}}} }}^{N,h} \left( {y,z} \right), \\ \end{aligned} $$
(13)

where

$$ \begin{aligned} G_{{_{{s,s^{\prime } }} }}^{m,k} \left( {x,z} \right) = & \exp \left( {\frac{{\beta_{1x}^{2} }}{{\alpha_{1x} }} + \frac{{\beta_{2x}^{2} }}{{\alpha_{2x} }}} \right)\sum\limits_{k = 0}^{{\left[ {m/2} \right]}} {\sum\limits_{{k^{\prime} = 0}}^{{\left[ {m/2} \right]}} {\frac{{\left( { - 1} \right)^{{k + k^{\prime } }} \left( {m!} \right)^{2} }}{{2^{{\left( {{{3m - 2k - 4k^{\prime } } \mathord{\left/ {\vphantom {{3m - 2k - 4k^{\prime } } 2}} \right. \kern-0pt} 2}} \right)}} k!k^{\prime } !\left( {m - 2k} \right)!\left( {m - 2k^{\prime } } \right)!}}\left( {\frac{1}{{2i\sqrt {\alpha_{1x} } }}} \right)^{l + m - 2k} } } \\ & \; \times \left( {\frac{2\sqrt 2 }{{\omega_{0} }}} \right)^{{2m - 2k - 2k^{\prime } }} \sum\limits_{\mu = 0}^{l + m - 2k} {\left( {\begin{array}{*{20}c} {l + m - 2k} \\ \mu \\ \end{array} } \right)} \sum\limits_{{c_{1} }}^{{\left[ {l + m - 2k - \mu } \right]/2}} {\frac{{\left( { - 1} \right)^{{c_{1} }} \left( {l + m - 2k - \mu } \right)!}}{{c_{1} !\left( {l + m - 2k - \mu - 2c{}_{1}} \right)!}}} \\ & \; \times \left( {\frac{\sqrt 2 }{{\sqrt {\alpha_{1x} \alpha_{2x} } \rho_{0}^{2} }}} \right)^{{2l + 2m - 2k - \mu - 2k^{\prime } - 2c_{1} }} H_{\mu } \left( {\frac{{\sqrt 2 i\beta_{1x} }}{{\sqrt {\alpha_{1x} } }}} \right)H_{{2l + 2m - 2k - \mu - 2k^{\prime } - 2c_{1} }} \left( {\frac{{i\beta_{2x} }}{{\sqrt {\alpha_{2x} } }}} \right), \\ \end{aligned} $$
(14a)

and

$$ \begin{aligned} G_{{u,u^{\prime } }}^{N,h} (y,z) = & \exp \left( {\frac{{\beta_{1y}^{2} }}{{\alpha_{1y} }} + \frac{{\beta_{2y}^{2} }}{{\alpha_{2y} }}} \right)\sum\limits_{h = 0}^{{\left[ {N/2} \right]}} {\sum\limits_{{h^{\prime } = 0}}^{{\left[ {N/2} \right]}} {\frac{{\left( { - 1} \right)^{{h + h^{\prime } }} \left( {N!} \right)^{2} }}{{2^{{\left( {{{3N - 2h - 4h^{\prime } } \mathord{\left/ {\vphantom {{3N - 2h - 4h^{\prime } } 2}} \right. \kern-0pt} 2}} \right)}} h!h^{\prime}!\left( {N - 2h} \right)!\left( {N - 2h^{\prime } } \right)!}}} } \left( {\frac{1}{{2i\sqrt {\alpha_{1y} } }}} \right)^{l + N - 2h} \\ & \; \times \left( {\frac{2\sqrt 2 }{{\omega_{0} }}} \right)^{{2N - 2h - 2h^{\prime } }} \sum\limits_{\sigma = 0}^{l + N - 2h} {\left( {\begin{array}{*{20}c} {l + N - 2h} \\ \sigma \\ \end{array} } \right)} \sum\limits_{{c_{2} }}^{{\left[ {l + N - 2h - \sigma } \right]/2}} {\frac{{\left( { - 1} \right)^{{c_{2} }} \left( {l + N - 2h - \sigma } \right)!}}{{c_{2} !\left( {l + N - 2h - \sigma - 2c{}_{2}} \right)!}}} \\ & \; \times \left( {\frac{\sqrt 2 }{{\sqrt {\alpha_{1y} \alpha_{2y} } \rho_{0}^{2} }}} \right)^{{2l + 2N - 2h - \sigma - 2h^{\prime } - 2c_{2} }} H_{\sigma } \left( {\frac{{\sqrt 2 i\beta_{1y} }}{{\sqrt {\alpha_{1y} } }}} \right)H_{{2l + 2N - 2h - \sigma - 2h^{\prime } - 2c_{2} }} \left( {\frac{{i\beta_{2y} }}{{\sqrt {\alpha_{2y} } }}} \right), \\ \end{aligned} $$
(14b)

with

$$ \alpha_{2x} = \frac{1}{{\omega_{0}^{2} }} - \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }} - \frac{1}{{\alpha_{1x} \rho_{0}^{2} }}, $$
(14c)
$$ \alpha_{2y} = \frac{1}{{\omega_{0}^{2} }} - \frac{ik}{{2z}} + \frac{1}{{\rho_{0}^{2} }} - \frac{1}{{\alpha_{1y} \rho_{0}^{2} }}, $$
(14d)
$$ \beta_{2x} = \frac{{a_{{s^{\prime } }} \sqrt \delta }}{{\omega_{0} }} - \frac{ikx}{{2z}} + \frac{{\beta_{1x} }}{{\alpha_{1x} \rho_{0}^{2} }}, $$
(14e)

and

$$ \beta_{2y} = \frac{{a_{{u^{\prime } }} \sqrt \delta }}{{\omega_{0} }} - \frac{iky}{{2z}} + \frac{{\beta_{1y} }}{{\alpha_{1y} \rho_{0}^{2} }}. $$
(14f)

Equation (13) represents the main mathematical result of the average intensity of the GHCGB propagating in turbulent atmosphere.

3 Numerical results and discussion

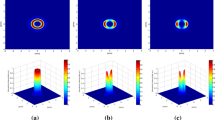
Based on the main mathematical formula of Eq. (13), we illustrate in this Section the numerical results of the turbulent atmosphere effects on the propagation of the GHCGB with paying the proper values of the structure constant of turbulent atmosphere and the incident beam parameters. Figure 1 illustrates the transverse intensity distribution of the GHCGB propagating in atmospheric turbulence for three values of the structure constant of turbulent atmosphere with different propagation distances z. The other parameters are set as: \(\omega_{0} = 0.02\;{\text{m}}\), \(n = 2\), \(\left( {m = N} \right) = 1,\,\,l = 1\), \(\Omega = 100\;{\text{m}}^{ - 1}\) and \(\lambda = 0.8\) μm. From Fig. 1, one can observe that the received beam takes a profile with four-petal and remains unchanged within a small distance range. Then, when the propagation distance z increases, the beam evolution is affected by the structure constant of atmospheric turbulence \(C_{n}^{2}\). When this latter is weaker (Fig. 1b–d), the beam profile interfere as four symmetrical bright lobes (see Fig. 1b), and the beam shape gradually becomes like a rhombic crystal at larger propagation distance (Fig. 1c, d). When \(C_{n}^{2}\) is stronger (Fig. 1f–l)), the beam will lose its bright lobes gradually with increasing the propagation distance z and eventually evolves into Gaussian-like beams. However, from Fig. 1, we can clearly see that, the GHCGB spreads more rapidly in turbulent atmosphere for the lager structure constant of refractive index.

Fig. 1
figure 1

Transverse intensity distribution of GHCGB, propagating in a turbulent atmosphere for different values of the parameter \(C_{n}^{2} = :\) a–d \(5 \times 10^{ - 16} m^{ - 2/3} ,\,\,{\mathbf{e}} - {\mathbf{h}}\,\,10^{ - 15} {\text{m}}^{ - 2/3}\) and i–l \(10^{ - 14} {\text{m}}^{ - 2/3}\). The other parameters are: \(\omega_{0} = 0.02\;{\text{m}}\), \(n = 2\), \(\left( {m = N} \right) = 1,\,\,l = 1\), \(\Omega \,\, = \,\,100\,\,{\text{m}}^{ - 1} \,\) and \(\lambda = 0.8\) μm

Full size image

Similarly, Fig. 2 depicts the normalized intensity distribution of GHCGB in x-direction propagating in the turbulent atmosphere for two values of the decentered cosh parameter.

Fig. 2
figure 2

Normalized intensity distribution of the GHCGB propagating in a turbulent atmosphere for different values of the parameter \(C_{n}^{2}\) and a–c \(\Omega \,\, = \,\,30\,{\text{m}}^{ - 1}\) and d–f \(\Omega \,\, = \,\,80\,\,{\text{m}}^{ - 1}\). The other parameters are: \(\omega_{0} = 0.02\;{\text{m}}\), \(n = 2\), \(m = 1,\,\,l = 1\), and \(\lambda = 0.8\) μm

Full size image

For each value of the decentered cosh parameter three figures are plotted for the structure constant \(C_{n}^{2}\) at various propagation distance z. From the results in Fig. 2, the intensity profile of the GHCGB with small propagation range remains unchanged. Also, the curves gradients in this figure denote that the GHCGB intensity profile spreads faster in turbulent atmosphere when the decentered cosh parameter is smaller and the structure constant is larger, especially in the far field, but the rising speed of the central peak of the GHCGB intensity is slower as the decentered cosh parameter is larger.

Figure 3 illustrates the effect of the atmospheric turbulent on the intensity profile of the GHCGB for various values of the beam orders l and m.

Fig. 3
figure 3

Normalized intensity distribution of the GHCGB propagating in a turbulent atmosphere for various values of the beam orders: \({\mathbf{a}}\,\,m = 0,\,\,l = 0,\,\,\,\,{\mathbf{b}}\,\,m = 1,\,\,l = 1,\,\,\,\,\,{\mathbf{c}}\,\,m = 2,\,\,l = 2\) and \({\mathbf{d}}\,\,m = 4,\,l = 4\). The other parameters are: \(z = 3\;{\text{km}}\),\(n = 2\), \(\Omega = 60\;{\text{m}}^{ - 1}\), \(\omega_{0} = 0.02\;{\text{m}}\) and \(\lambda = 0.8\) μm

Full size image

For each beam orders, three curves are plotted for the structure constant of the turbulent atmosphere \(C_{n}^{2}\) in the reference plane at z = 3 km. The other parameters are set as: \(n = 2\), \(\Omega = 60\;{\text{m}}^{ - 1}\), \(\omega_{0} = 0.02\;{\text{m}}\) and \(\lambda = 0.8\) μm. The graph indicates that the intensity profile of the beam propagating through turbulent atmosphere has the central peak with the zero beam orders l and m.

Figure 4 shows the influence of the decentered cosh parameter \(\Omega\) on the normalized intensity profile of the GHCGB travailing in the turbulent atmosphere with some values of l and m.

Fig. 4
figure 4

Normalized intensity distribution of the GHCGB propagating in a turbulent atmosphere for various values of the beam orders: \({\mathbf{a}}\,\,m = 0,\,\,\,l = 0,\,\,\,\,{\mathbf{b}}\,\,m = 1,\,\,l = 1,\,\,\,\,\,{\mathbf{c}}\,\,m = 2,\,\,l = 2\) and \({\mathbf{d}}\,\,m = 4,\,\,l = 4\). The other parameters are:\(z = 1\;{\text{km}}\), \(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{{ - }{{2} \mathord{\left/ {\vphantom {{2} {3}}} \right. \kern-0pt} {3}}}}\), \(\omega_{0} = 0.02\;{\text{m}}\), \(n = 2\) and \(\lambda = 0.8\) μm

Full size image

As seen in Fig. 4a, the GHCGB profiles through atmospheric turbulence, with the both orders l and m are zero, will take three distributions: first the Gaussian-like, then the flattened and finally the dark hollow, as the same results obtained by Zhou in Ref. (Zhou 2011) which be regarded as a special case of the present work.

These different distributions change its profiles gradually to the dark hollow with the beam orders l and m are increased (see Fig. 4b and c). The central dark region becomes lager with further increases of the beam orders l and m (see Fig. 4d).

The similar illustrations for the atmospheric turbulence effect on the normalized intensity of the GHCGB are shown in Fig. 5, with varying the cosh beam order n. For zero orders l and m, the curves plotted in Fig. 5a present on different central intensities. Then, when both orders l and m increase to one, all the curves evolve on central dark distribution with different area. From the results present in Fig. 5b–d, it can be seen that when n is larger, the central dark distribution appears and becomes wider with increasing orders l and m.

Fig. 5
figure 5

Normalized intensity distribution of the GHCGB propagating in a turbulent atmosphere for different values of the beam orders: \({\mathbf{a}}\,\,m = 0,\,\,l = 0,\,\,\,\,{\mathbf{b}}\,\,m = 1,\,\,l = 1,\,\,\,\,\,{\mathbf{c}}\,\,m = 2,\,\,l = 2\) and \({\mathbf{d}}\,\,m = 4,\,\,l = 4\). The other parameters are: \(z = 1\;{\text{km}}\), \(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{{ - }{{2} \mathord{\left/ {\vphantom {{2} {3}}} \right. \kern-0pt} {3}}}}\), \(\Omega = 60\;{\text{m}}^{ - 1}\), \(\omega_{0} = 0.02\;{\text{m}}\) and \(\lambda = 0.8\) μm

Full size image

In Fig. 6, the effect of the beam waist width \(\omega_{0}\) on the normalized intensity distribution of the GHCGB passing through the turbulent atmosphere is shown with various values of both orders l and m. When \(\omega_{0}\) is larger, the beam intensity has a zero central intensity as a dark hollow spot which be increased as the orders l and m are larger.

Fig. 6
figure 6

Normalized intensity distribution of GHCGB propagating in a turbulent atmosphere for different values of the beam orders: \({\mathbf{a}}\,\,m = 0,\,l = 0,\,\,\,\,{\mathbf{b}}\,\,m = 1,\,\,l = 1,\,\,\,\,\,{\mathbf{c}}\,\,m = 2,\,\,l = 2\) and \({\mathbf{d}}\,\,m = 4,\,l = 4\). The other parameters are:\(z = 1\;{\text{km}}\),\(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{{ - }{{2} \mathord{\left/ {\vphantom {{2} {3}}} \right. \kern-0pt} {3}}}}\), \(\Omega = 60\;{\text{m}}^{ - 1}\), \(n = 2\) and \(\lambda = 0.8\) μm

Full size image

So, it can be concluded that for the GHCGB beams propagating through atmospheric turbulence spreads more rapidly on the Gaussian-like distribution for a stronger turbulence and the smaller values of incident beam parameters, but the reverse phenomenon occurs and it will undergo on the dark hollow distribution when the incident beam parameters are large.

4 Conclusion

The current work presents an investigation into the spreading features of a GHCGB when it propagates through a turbulent atmosphere media. To study the beam properties, we have derived an analytical formula for the considered beam in atmospheric turbulence using the extended Huygens-Fresnel integral diffraction and Rytov method. Then, some numerical simulations have performed to confirm the mathematical formula under different parameters conditions. The results show that the propagated GHCGB spreads more rapidly on a Gaussian-like beam for a stronger turbulence and the smaller values of incident beam parameters, but the reverse pattern will undergo a dark hollow beam as the larger incident beam parameters. The results of the present study have potential applications of the GHCGB in remote sensing and free-space optical communications.