Nonparaxial solitons and the dynamics of solitary waves for the coupled nonlinear Helmholtz systems

Abstract

In this paper, the nonparaxial solitons in a dimensionless coupled nonlinear Schrödinger system with cross-phase modulation, which enables the propagation of ultra-broad nonparaxial pulses in a birefringent optical waveguide are studied. By noticing that the system is a non-integrable one, and also diverse forms of solitary wave solutions by using the Hirota’s bilinear scheme are reached. The binary bell polynomials and bilinear transformation and also the related theorem for getting to the bilinear form of nonlinear system are noticed. In particular, five forms of function solution including soliton, bright soliton, singular soliton, periodic wave and singular form of solutions are investigated. To achieve this, an illustrative example of the coupled nonlinear Helmholtz systems is provided to demonstrate the feasibility and reliability of the procedure is used in this study. The effect of the free parameters on the behavior of acquired figures of a few obtained solutions for two nonlinear rational exact cases was also discussed. We believe that our results would pave a way for future research generating optical memories based on the nonparaxial solitons.

1 Introduction

In this paper, the generation of non-slowly varying electric fields is concerned in a physical setting of liquid crystals or birefringent optical fibers to the coupled nonlinear Helmholtz systems. The following dimensionless coupled equations can be utilized to specify the propagation of incoherently coupled and orthogonally polarized waveguide modes in a Kerr medium (Tamilselvan et al. 2016) as follows

$$\begin{aligned} i\Sigma _{l,z}+\Lambda \Sigma _{l,zz}+\frac{\alpha }{2}\Sigma _{l,tt}+\delta (|\Sigma _{l}|^2+|\Sigma _{3-l}|^2)\Sigma _{l}=0,\quad \ l=1,2,\hspace{4cm} \end{aligned}$$

(1.1)

where $\Sigma _{l}, (l = 1, 2)$ symbolize the orthogonally polarized components of the optical modes and the variables z, and t, respectively, represent longitudinal and transverse co-ordinates. The second expression $\Lambda$ in Eq. (1.1) is the non-paraxial parameter (NP) and correspond to $1/2k_0L$ (Tamilselvan et al. 2016). The group-velocity dispersion (GVD) is stated by the parameter $\alpha$ and in this study, it is apportioned to be operating in the anomalous dispersion regime. Nonlinearity and its coupling parameters are denoted by using the terms $\delta$ and $\alpha$, respectively, which are attributed by the symmetry properties of third-order susceptibility tensor.

The evolution of broad optical beams in Kerr like nonlinear media can be well stated by the coupled nonlinear Helmholtz (CNLH) type equations. Equation (1.1) has been studied in Christian et al. (2006)) and bright and dark soliton solutions have been reported for focusing and defocusing nonlinearities respectively. Collision investigations of solitons in CNLH system revealed the fact that the interaction angle between two solitons is changed by altering the nonparaxial parameter (Chamorro-Posada and McDonald 2006). In Tamilselvan et al. (2016), the authors obtained a class of elliptic wave solutions of CNLH equations describing nonparaxial ultra-broad beam propagation in nonlinear Kerr-like media, in terms of the Jacobi elliptic functions and also discussed their limiting forms. Song et al. (2020) discussed a quartic eigenvalue problem of CNLH system arising in the context of an optical waveguiding problem involving atomically thick 2D materials. Also, the exact solutions of CNHE equations via the exp($-\Phi (\varepsilon )$)expansion method have been obtained (Singh et al. 2020).

Due to the unique physical properties of interaction between multiple coherent optical fields, a number of practical applications in optical transmission systems have been put forward such as switching, and modulators (Kivshar and Agrawal 2003). Also, the dynamics of optical modes traversing by way of the birefringent fiber can be mathematically governed by a system of coupled nonlinear Schrödinger equations, which results in a shape-preserving solution due to their multiple component natures. The vector soliton is produced when the nonlinearity of the fiber causes coupling between diverse optical modes during the propagation in the multimode optical fiber, which vector soliton provides an efficient way to a variety of practical applications such as channel wavelength division-multiplexing, pulse generation, and high-speed optical switching (Hansryd et al. 2002). Soliton interactions can be divided into two types: coherent interactions and incoherent interactions (Ku et al. 2005).

In the last decades, researchers have developed numerous methods such as, the generalized rational $\tan (\phi /2)$-expansion technique (Liu et al. 2023), k-lump and k-kink solutions (Gu et al. 2022), the extended sinh-Gordon equation expansion method (Ali et al. 2023), the multiple Exp-function method (Liu et al. 2018), the seismic wave attenuation (Bouchaala et al. 2022), the compressional seismic wave attenuation (Bouchaala et al. 2019), the Hirota’s bilinear method (Manafian and Lakestani 2020), the stress and dynamic analysis of truck ladder chassis (Mahmoodi-k et al. 2014), dual unscented kalman filter algorithm method (Davoodabadi et al. 2014), the quantum-mechanical method (Della Volpe and Siboni 2022), multiple soliton solutions and fusion interaction phenomena (Wen and Xu 2013), the truncated Painlevé series (Ren et al. 2019), single-lap adhesive joints method (Ghasemvand et al. 2023), truss optimization with metaheuristic algorithms method (Aslanova 2020), the modified Pfaffian technique (Liu et al. 2021), linear spectral dynamic analysis method (Madina and Gumilyov 2020), a carver matrix and providing solutions (Zahedi and Golivari 2022), a random decrement signature and artificial neural network algorithm techniques (Mojtahedi et al. 2022), logistic damping effect in chemotaxis models (Lyu and Wang 2023), the one-dimensional attraction-repulsion Keller–Segel model (Jin and Wang 2015), fracture analysis of fluid-structure interactions (Dai et al. 2023), energy relaxation of hot electrons (Du et al. 2023), variable weighted iterative learning (Xu et al. 2023), the dynamics analysis of Gompertz virus disease model (Wang et al. 2023), a novel data generation and quantitative characterization method (Sun et al. 2023), nonlinear energy recharging and consumption (Xiao et al. 2021), the renewable energy sources (Jiang et al. 2022), a hybrid convolutional neural network (Erfeng and Ghadimi 2022; Han and Ghadimi 2022), a hybrid robust-stochastic approach (Cai et al. 2019; Yu et al. 2020), a optimal chiller loading (Saeedi et al. 2019), the distributed series reactor (Yuan et al. 2020), an intelligent algorithm (Mir et al. 2020), the deep learning method (Zhang et al. 2022), the power systems (Chen et al. 2022), dual-form of generalized nonlocal nonlinearity (Li et al. 2023), high-order uncertain nonlinear systems (Guo and Hu 2023; Meng et al. 2023; Guo et al. 2023, 2023), nonlinear networked control systems (Zhong et al. 2022), and so forth (Bai et al. 2022; Xiang et al. 2023; Moghadam and Ebrahimi 2021; Brown and Mazumder 2021).

In the context of water wave theory, the complete study on the related physical systems were executed by exploring several integrable as well as non-integrable evolution equations in one and higher dimensions (Lakshmanan and Rajasekar 2003). Integrability is a fascinating property to characterize any dynamical models in addition to existence of Lax pair and infinitely many conserved quantities. The ancillary techniques containing direct algebraic techniques, auxiliary equation method, Kudryashov expansion method, Riccati-Bernoulli sub-ODE method, sinh-Gordon expansion method, cosh-tanh method, simplest equation method, and so on are utilized widely to get different classes of travelling wave solutions (Wazwaz 2009). Especially, these methodologies provide a variety of exotic wave patterns, including solitons, breathers, lumps, dromions, rogue waves, and elliptic waves. On the advantageous part, the Hirota bilinear method is an intermediate tool which can be utilized to extract the localized nonlinear wave solution to most of the integrable as well as a few class of non-integrable soliton models and it becomes a widely used tool to obtain several localized nonlinear wave solutions (Zhou et al. 2021; Manafian et al. 2020; Alimirzaluo et al. 2021; Pourghanbar et al. 2020; Dawod et al. 2023; Mehrpooya et al. 2021).

The general form of the fractional reduced differential transform method to (N+1)-dimensional fractional order partial differential equations were studied (Arshad et al. 2017). The unstable non-linear Shrödinger dynamical models has been investigated analytically by utilizing the tow variable (G’/G)-expansion approach (Shehzad et al. 2023). The weakly nonlinear wave propagation theory in the occurrence of magnetic fields in fluids of superposed was studied. Also, soliton and other kinds solutions of (2+1)-dimensional elliptic nonlinear Schrödinger equation were constructed (Seadawy et al. 2020).

In this paper, some solutions including soliton, bright soliton, singular soliton, periodic wave and singular form of solutions by Hirota bilinear method are also obtained.

Inspired by the previous work, the aim of the paper is to investigate the nonparaxial solitons and other form of solutions. The outline of the paper is as follows. In Sect. 2, the bilinear equations through Hirota operator for the CNLH system are obtained. Furthermore, in Sect. 3, different forms of solitary wave solutions are established. Finally, the conclusions are provided in Sect. 3.5.3.

2 Binary Bell polynomials and bilinear transformation

By way of Ma (2013) and $A= A(x_1, x_2,...,x_n)$ we have

$$\begin{aligned} & B_{n_1x_1,...,n_jx_j}(A)\equiv B_{n_1,...,n_j}(A_{d_1x_1,...,d_jx_j})\nonumber \\ & \quad =e^{-A}\partial _{x_1}^{n_1}...\partial _{x_j}^{n_j}e^{A}, \end{aligned}$$

(2.1)

with the multi-D Bell polynomials as

$$\begin{aligned} & A_{d_1x_1,...,d_jx_j}=\partial _{x_1}^{d_1}...\partial _{x_j}^{d_j}A, \ \ A_{0x_i}\\ & \quad \equiv A, \ d_1=0,...,n_1;...;d_j=0,...,n_j, \end{aligned}$$

and we get

$$\begin{aligned} & B_1(A)=A_x,\ \ B_2(A)=A_{2x}+A_x^2,\ \ B_3(A)=A_{3x}+3A_xA_{2x}+A_x^3,..._,\ \ \ A=A(x,t),\nonumber \\ & B_{x,t}(A)=A_{x,t}+A_xA_t,\ \ B_{2x,t}(A)=A_{2x,t}+A_{2x}A_{t}+2A_{x,t}A_{x}+A_x^2A_t,..._. \end{aligned}$$

(2.2)

The multi-dimensional binary Bell polynomials can be stated as

$$\begin{aligned} C_{n_1x_1,...,n_jx_j}(\mu _1,\mu _2)=\left. B_{n_1,...,n_j}(A)\right| _{{A_{d_1x_1,...,d_jx_j}}= \left\{ \begin{array}{ll} {\mu _1}_{d_1x_1,...,d_jx_j}, & d_1+d_2+...+d_j, \hbox { is odd} \\ {\mu _2}_{d_1x_1,...,d_jx_j}, & d_1+d_2+...+d_j, \hbox { is even.} \end{array} \right. } \end{aligned}$$

(2.3)

The following properties are as

$$\begin{aligned} C_{x}(\mu _1)={\mu _1}_{x},\ \ C_{2x}(\mu _1,\mu _2)={\mu _2}_{2x}+{\mu _1}_{x}^2,\ \ C_{x,t}(\mu _1,\mu _2)={\mu _2}_{x,t}+{\mu _1}_{x}{\mu _1}_{t},..._. \end{aligned}$$

(2.4)

Proposition 2.1

Let $\mu _1=\ln (\Omega _1/\Omega _2),\ \ \mu _2=\ln (\Omega _1\Omega _2),$ then the relations between binary Bell polynomials and Hirota D-operator reads

$$\begin{aligned} \left. C_{n_1x_1,...,n_jx_j}(\mu _1,\mu _2)\right| _{\mu _1=\ln (\Omega _1/\Omega _2),\ \ \mu _2=\ln (\Omega _1\Omega _2)}=(\Omega _1\Omega _2)^{-1}D_{x_1}^{n_1}...D_{x_j}^{n_j}\Omega _1\Omega _2, \end{aligned}$$

(2.5)

with Hirota operator

$$\begin{aligned} \prod _{i=1}^{j}D_{x_i}^{n_i}g.\ \eta =\left. \prod _{i=1}^{j}\left( \frac{\partial }{\partial x_i}-\frac{\partial }{\partial x_i'}\right) ^{n_i}\Omega _1(x_1,...,x_j)\Omega _2(x_1',...,x_j')\right| _{x_1=x_1',...,x_j=x_j'}. \end{aligned}$$

(2.6)

Proposition 2.2

Take $\Xi (\gamma )=\sum _{i} \delta _i\mathfrak {P}_{d_1x_1,...,d_jx_j}=0$ and $\mu _1=\ln (\Omega _1/\Omega _2),\ \ \mu _1=\ln (\Omega _1\Omega _2),$ we have

$$\begin{aligned} \left\{ \begin{array}{ll} \sum _{i} \delta _{1i}B_{n_1x_1,...,n_jx_j}(\mu _1,\mu _2)=0, \\ \sum _{i} \delta _{1i}B_{d_1x_1,...,d_jx_j}(\mu _1,\mu _2)=0, \end{array} \right. \end{aligned}$$

(2.7)

which need to satisfy

$$\begin{aligned} \mathfrak {R}(\gamma ',\gamma )=\mathfrak {R}(\gamma ')-\mathfrak {R}(\gamma )=\mathfrak {R}(\mu _2+\mu _1)-\mathfrak {R}(\mu _2-\mu _1)=0. \end{aligned}$$

(2.8)

The generalized Bell polynomials $\Upsilon _{n_1x_1,...,n_jx_j}(\xi )$ is as

$$\begin{aligned} & (\Omega _1\Omega _2)^{-1}D_{x_1}^{n_1}...D_{x_j}^{n_j}\Omega _1\Omega _2= \left. C_{n_1x_1,...,n_jx_j}(\mu _1,\mu _2)\right| _{\mu _1=\ln (\Omega _1/\Omega _2),\ \ \mu _2=\ln (\Omega _1\Omega _2)} \end{aligned}$$

(2.9)

$$\begin{aligned} & \quad =\left. C_{n_1x_1,...,n_jx_j}(\mu _1,\mu _1+\gamma )\right| _{\mu _1=\ln (\Omega _1/\Omega _2),\ \ \gamma =\ln (\Omega _1\Omega _2)}\nonumber \\ & \quad =\sum _{k_1}^{n_1}...\sum _{k_j}^{n_j}\prod _{i=1}^{j}\left( \begin{array}{c} n_i \\ k_i \end{array}\right) \mathfrak {P}_{k_1x_1,...,k_jx_j}(\gamma )B_{(n_1-k_1)x_1,...,(n_j-k_j)x_j}(\mu _1). \end{aligned}$$

(2.10)

The Cole–Hopf relation is as follows

$$\begin{aligned} & B_{k_1x_1,...,k_jx_j}(\mu _1=\ln (\varphi ))=\frac{\varphi _{n_1x_1,...,n_jx_j}}{\varphi }, \hspace{6cm} \end{aligned}$$

(2.11)

$$\begin{aligned} & \left. (\Omega _1\Omega _2)^{-1}D_{x_1}^{n_1}...D_{x_j}^{n_j}\Omega _1\Omega _2 \right| _{\Omega _2=\exp (\gamma /2),\ \ \Omega _1/\Omega _2=\varphi }\hspace{6cm}\nonumber \\ & \quad =\varphi ^{-1}\sum _{k_1}^{n_1}...\sum _{k_j}^{n_j}\prod _{l=1}^{j}\left( \begin{array}{c} n_l \\ k_l \end{array}\right) \mathfrak {P}_{k_1x_1,...,k_lx_l}(\gamma )\varphi _{(n_1-k_1)x_1,...,(n_d-k_l)x_l}, \end{aligned}$$

(2.12)

with

$$\begin{aligned} B_{t}(\mu _1)=\frac{\varphi _t}{\varphi },\ \ \ B_{2x}(\mu _1, \beta )=\gamma _{2x}+\frac{\varphi _{2x}}{\varphi },\ \ \ B_{2x,y}(\mu _1,\mu _2)=\frac{\gamma _{2x}\varphi _y}{\varphi }+ \frac{2\gamma _{x,y}\varphi _x}{\varphi }+\frac{\varphi _{2x,y}}{\varphi }. \end{aligned}$$

(2.13)

By taking $\Sigma _l(z,t)=\frac{g_l(z,t)}{f(z,t)},\ \ l=1,2$ and inserting it into Eq. (1.1), one obtains bilinear form. According to above process, the below Theorem will be considered.

Theorem 2.3

By the below issues, one gets

$$\begin{aligned} \Sigma _l(z,t)=\frac{g_l(z,t)}{f(z,t)},\ \ l=1,2, \end{aligned}$$

(2.14)

where $g_l, l=1,2$ are the complex functions and f is a real function. Plugging the above solution (2.14) into Eq. (1.1), we arrive at the bilinear equations as below

$$\begin{aligned} & \left( iD_z+\Lambda D_z^2+\frac{1}{2}D_t^2\right) (g_l.f)=0,\nonumber \\ & \quad \left( \Lambda D_z^2+\frac{1}{2}D_t^2\right) (f.f)=\delta \sum _{l=1}^{2}g_lg_l^{*}, \end{aligned}$$

(2.15)

where $*$ shows the complex conjugate and D denotes the Hirota’s bilinear operator which manages with respect to the functions of z and t. The bilinear definitions for operator are

$$\begin{aligned} & D_z(g_l.f)=\frac{\partial g_1}{\partial z}f-g_1\frac{\partial f}{\partial z},\nonumber \\ & \quad D_z^2(g_l.f)=\frac{\partial ^2 g_1}{\partial z^2}f-2\frac{\partial g_1}{\partial z}\frac{\partial f}{\partial z}+g_1\frac{\partial ^2 f}{\partial z^2},\nonumber \\ & \quad D_t^2(g_l.f)=\frac{\partial ^2 g_1}{\partial t^2}f-2\frac{\partial g_1}{\partial t}\frac{\partial f}{\partial t}+g_1\frac{\partial ^2 f}{\partial t^2}, \nonumber \\ & \quad D_z^2(f.f)=2f\frac{\partial ^2 f}{\partial z^2}-2(\frac{\partial f}{\partial z})^2, \nonumber \\ & \quad D_t^2(f.f)=2f\frac{\partial ^2 f}{\partial t^2}-2(\frac{\partial f}{\partial t})^2. \end{aligned}$$

(2.16)

3 Solitary wave solutions

In this section according to the rational transformation (2.14) the following cases will be analyzed as:

3.1 Nonparaxial soliton solutions

By supposing the below function

$$\begin{aligned} & f(z,t)=h_1\sin (b_1\zeta _1)\exp (b_2\zeta _2),\ \ g_l(z,t)=m_l\exp (ic_l\zeta _{l+2}),\ \ l=1,2,\nonumber \\ & \quad \zeta _l=\lambda _lz+\mu _l(t)+\xi _l, \ \ \ l=1,2,3,4. \end{aligned}$$

(3.1)

Afterwards, inserting $\Sigma _l=g_l(z,t)/f(z,t),\ l=l,2$ Eq. (2.15) and using relations (2.16) and taking the coefficients of the nonlinear expressions to zero, yield a system of algebraic equations including below:

$$\begin{aligned} & 4\,i\Lambda \,b_{{1}}c_{{1}}\lambda _{{1}}\lambda _{{3}}-4\,\Lambda \,b_{{ 1}}b_{{2}}\lambda _{{1}}\lambda _{{2}}\\ & \qquad +2\,ib_{{1}}c_{{1}}\mu _{{1}}\mu _{{ 3}}-2\,b_{{1}}\mu _{{1}}b_{{2}}\mu _{{2}}+2\,ib_{{1}}\lambda _{{1}}=0, \\ & \quad 4\,i\Lambda \,b_{{2}}c_{{1}}\lambda _{{2}}\lambda _{{3}}+2\,\Lambda \,{b_{ {1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{b_{{2}}}^{2}{\lambda _{{2}}}^ {2}\\ & \qquad +2\,\Lambda \,{c_{{1}}}^{2}{\lambda _{{3}}}^{2}+2\,ib_{{2}}c_{{1}}\mu _{{2}}\mu _{{3}}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{b_{{2}}}^{2}{\mu _{{2}}}^ {2}\\ & \qquad +{c_{{1}}}^{2}{\mu _{{3}}}^{2}+2\,ib_{{2}}\lambda _{{2}}+2\,c_{{1}} \lambda _{{3}}=0, \\ & \quad 4\,i\Lambda \,n_{{1}}b_{{1}}c_{{2}}\lambda _{{1}}\lambda _{{4}}-4\, \Lambda \,b_{{1}}b_{{2}}\lambda _{{1}}\lambda _{{2}}n_{{1}}\\ & \qquad +2\,in_{{1}}b_ {{1}}c_{{2}}\mu _{{1}}\mu _{{4}}-2\,b_{{1}}\mu _{{1}}b_{{2}}\mu _{{2}}n_{{ 1}}+2\,ib_{{1}}\lambda _{{1}}n_{{1}}=0, \\ & \quad 4\,i\Lambda \,b_{{2}}c_{{2}}\lambda _{{2}}\lambda _{{4}}+2\,\Lambda \,{b_{ {1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{b_{{2}}}^{2}{\lambda _{{2}}}^ {2}\\ & \qquad +2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{4}}}^{2}+2\,ib_{{2}}c_{{2}}\mu _{{2}}\mu _{{4}}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{b_{{2}}}^{2}{\mu _{{2}}}^ {2}+{c_{{2}}}^{2}{\mu _{{4}}}^{2}+2\,ib_{{2}}\lambda _{{2}}+2\,c_{{2}} \lambda _{{4}}=0, \\ & \quad 4\,i\Lambda \,b_{{2}}c_{{2}}\lambda _{{2}}\lambda _{{4}}n_{{2}}+2\, \Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}n_{{2}}\\ & \qquad -2\,\Lambda \,{b_{{2}}} ^{2}{\lambda _{{2}}}^{2}n_{{2}}+2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{4}} }^{2}n_{{2}}+2\,ib_{{2}}c_{{2}}\mu _{{2}}\mu _{{4}}n_{{2}}\\ & \qquad +{b_{{1}}}^{2} {\mu _{{1}}}^{2}n_{{2}}-{b_{{2}}}^{2}{\mu _{{2}}}^{2}n_{{2}}+{c_{{2}}}^{ 2}{\mu _{{4}}}^{2}n_{{2}}+ \\ & \quad 2\,ib_{{2}}\lambda _{{2}}n_{{2}}+2\,c_{{2}} \lambda _{{4}}n_{{2}}+4\,i\Lambda \,n_{{1}}b_{{1}}c_{{2}}\lambda _{{1}} \lambda _{{4}}-4\,\Lambda \,b_{{1}}b_{{2}}\lambda _{{1}}\lambda _{{2}}n_{{ 1}}+2\,in_{{1}}b_{{1}}c_{{2}}\mu _{{1}}\mu _{{4}}\\ & \qquad -2\,b_{{1}}\mu _{{1}}b_{ {2}}\mu _{{2}}n_{{1}}+2\,ib_{{1}}\lambda _{{1}}n_{{1}} =0. \end{aligned}$$

By solving the above equations get the following results:

3.1.1 Set I solutions

$$\begin{aligned} & b_{{1}}={\frac{ \sqrt{2\, \left( 2\, \left( i\Lambda \,\lambda _{{4}}c_ {{2}}-\Lambda \,b_{{2}}\lambda _{{2}}+i \right) {\lambda _{{1}}}^{2}+ \left( ic_{{2}}\lambda _{{4}}-b_{{2}}\lambda _{{2}} \right) {\mu _{{1}}} ^{2} \right) \Lambda \, \left( ic_{{2}}\lambda _{{4}}-b_{{2}}\lambda _{{2 }} \right) +2\,i \left( ic_{{2}}\lambda _{{4}}-b_{{2}}\lambda _{{2}} \right) {\mu _{{1}}}^{2}-{\lambda _{{1}}}^{2}}}{\mu _{{1}} \sqrt{2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2}}}} , \nonumber \\ & \quad \lambda _{{3}}={\frac{i \left( i\Lambda \,\lambda _{{4}}c_{{2}}-2\, \Lambda \,b_{{2}}\lambda _{{2}}+i \right) }{\Lambda \,c_{{1}}}},\ \ \mu _{{3}}={\frac{-i \left( 2\,i\Lambda \,\lambda _{{1}}\lambda _{{4}}c_{ {2}}-2\,\Lambda \,b_{{2}}\lambda _{{1}}\lambda _{{2}}+b_{{2}}\mu _{{1}}\mu _{{2}}+i\lambda _{{1}} \right) }{\mu _{{1}}c_{{1}}}}, \nonumber \\ & \quad \mu _{{4}}={\frac{i \left( 2\,i\Lambda \,\lambda _{{1}}\lambda _{{4}}c_{{ 2}}-2\,\Lambda \,b_{{2}}\lambda _{{1}}\lambda _{{2}}-b_{{2}}\mu _{{1}}\mu _ {{2}}+i\lambda _{{1}} \right) }{\mu _{{1}}c_{{2}}}}. \end{aligned}$$

(3.2)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l\exp (ic_l\zeta _{l+2})}{h_1\sin (b_1\zeta _1)\exp (b_2\zeta _2)},\ \ l=1,2,\nonumber \\ & \quad \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3,4. \end{aligned}$$

(3.3)

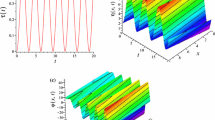
Further, the following analysis can be extended to explore multiple soliton dynamics on arbitrary backgrounds in a straightforward manner. Figure 1 depicts the impact of treatment of singular soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following chosen values

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1,\nonumber \\ & \quad \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1,\nonumber \\ & \quad \mu _1 = 1, m_1 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.4)

$$\begin{aligned} & \Sigma _1=2\,{\frac{{\mathrm{e}^{- 0.005000000000\,t+ 1.004000000\,it+ 2.500000000 \,z- 1002.0\,iz- 2.500000000+ 2.500000000\,i}}}{\sin \left( \left( 1.021552097- 2.457045519\,i \right) \left( t+z+1 \right) \right) }}, \end{aligned}$$

(3.5)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1,\nonumber \\ & \quad \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1, \nonumber \\ & \mu _1 = 1, m_2 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _4 = 2.5, \end{aligned}$$

(3.6)

$$\begin{aligned} & \Sigma _2=2\,{\frac{{\mathrm{e}^{ 0.0050\,t- 1.004\,it+2\,iz- 2.5+ 5.0\,i- 2.5\,z} }}{\sin \left( \left( 1.021552097- 2.457045519\,i \right) \left( t+ z+1 \right) \right) }}, \end{aligned}$$

(3.7)

in Eq. (3.3). We investigate the dynamics of general nonparaxial solitons received from the Hirota bilinear technique, which is presented in Fig. 1. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 1.

Fig. 1

Plot of soliton solution (3.3) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.1.2 Set II solutions

$$\begin{aligned} & b_{{1}}={\frac{\sqrt{2\, \left( 2\,i\Lambda \,{\lambda _{{1}}}^{2} \lambda _{{4}}c_{{2}}-2\,\Lambda \,b_{{2}}{\lambda _{{1}}}^{2}\lambda _{{2 }}+ic_{{2}}\lambda _{{4}}{\mu _{{1}}}^{2}-b_{{2}}\lambda _{{2}}{\mu _{{1}} }^{2}+2\,i{\lambda _{{1}}}^{2} \right) \Lambda \, \left( ic_{{2}}\lambda _{{4}}-b_{{2}}\lambda _{{2}} \right) -2\,ib_{{2}}\lambda _{{2}}{\mu _{{1} }}^{2}-2\,c_{{2}}\lambda _{{4}}{\mu _{{1}}}^{2}-{\lambda _{{1}}}^{2}}}{ \sqrt{2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2}}\mu _{{1}}}},\nonumber \\ & \lambda _{{3}}={\frac{c_{{2}}\lambda _{{4}}}{c_{{1}}}},\ \ \mu _{{3}}={\frac{i \left( 2\,i\Lambda \,\lambda _{{1}}\lambda _{{4}}c_{{ 2}}-2\,\Lambda \,b_{{2}}\lambda _{{1}}\lambda _{{2}}-b_{{2}}\mu _{{1}}\mu _ {{2}}+i\lambda _{{1}} \right) }{\mu _{{1}}c_{{1}}}} , \ \ \mu _{{4}}={\frac{i \left( 2\,i\Lambda \,\lambda _{{1}}\lambda _{{4}}c_{{ 2}}-2\,\Lambda \,b_{{2}}\lambda _{{1}}\lambda _{{2}}-b_{{2}}\mu _{{1}}\mu _ {{2}}+i\lambda _{{1}} \right) }{\mu _{{1}}c_{{2}}}} . \end{aligned}$$

(3.8)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l\exp (ic_l\zeta _{l+2})}{h_1\sin (b_1\zeta _1)\exp (b_2\zeta _2)},\ \ l=1,2, \nonumber \\ & \quad \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3,4. \end{aligned}$$

(3.9)

Figure 2 depicts the impact of treatment of singular soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1, \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1, \nonumber \\ & \quad \mu _1 = 1, m_1 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.10)

$$\begin{aligned} & \Sigma _1=2\,{\frac{{\mathrm{e}^{ 0.0050\,t- 1.004\,it+2\,iz- 2.5+ 2.5\,i- 2.5\,z} }}{\sin \left( \left( 1.021552097- 2.457045519\,i \right) \left( t+ z+1 \right) \right) }} , \end{aligned}$$

(3.11)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1, \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1, \nonumber \\ & \quad \mu _1 = 1, m_2 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _4 = 2.5, \end{aligned}$$

(3.12)

$$\begin{aligned} & \Sigma _2=2\,{\frac{{\mathrm{e}^{ 0.0050\,t- 1.004\,it+2\,iz- 2.5+ 5.0\,i- 2.5\,z} }}{\sin \left( \left( 1.021552097- 2.457045519\,i \right) \left( t+ z+1 \right) \right) }} , \end{aligned}$$

(3.13)

in Eq. (3.8). We investigate the dynamics of general nonparaxial solitons received from the Hirota bilinear technique, which is presented in Fig. 2. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 2.

Fig. 2

Plot of soliton solution (3.8) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.1.3 Set III solutions

$$\begin{aligned} & \Sigma _{1}=\frac{m_{{1}}{\mathrm{e}^{-1/2\,{\frac{-2\,\Lambda \,tb_{{2}}\mu _{{2}}+2\,i \Lambda \,tc_{{2}}\mu _{{4}}-2\,i\Lambda \,c_{{1}}\xi _{{3}}+2\,b_{{2}}\xi _{{2}}\Lambda +iz}{\Lambda }}}} }{h_{{1}}\sin \left( 1/2\,{\frac{ \sqrt{1-4\,ib_{{2}}c_{{2}}\mu _{{2}} \mu _{{4}}\Lambda +2\,{b_{{2}}}^{2}{\mu _{{2}}}^{2}\Lambda -2\,{c_{{2}}}^{ 2}{\mu _{{4}}}^{2}\Lambda } \left( z\lambda _{{1}}+\xi _{{1}} \right) }{ \lambda _{{1}}\Lambda }} \right) }, \end{aligned}$$

(3.14)

$$\begin{aligned} & \Sigma _{2}=\frac{m_{{2}}{\mathrm{e}^{1/2\,{\frac{2\,i\Lambda \,tc_{{2}}\mu _{{4}}+2\,i \Lambda \,c_{{2}}\xi _{{4}}-2\,\Lambda \,tb_{{2}}\mu _{{2}}-2\,b_{{2}}\xi _ {{2}}\Lambda -iz}{\Lambda }}}} }{h_{{1}}\sin \left( 1/2\,{\frac{ \sqrt{1-4\,ib_{{2}}c_{{2}}\mu _{{2}} \mu _{{4}}\Lambda +2\,{b_{{2}}}^{2}{\mu _{{2}}}^{2}\Lambda -2\,{c_{{2}}}^{ 2}{\mu _{{4}}}^{2}\Lambda } \left( z\lambda _{{1}}+\xi _{{1}} \right) }{ \lambda _{{1}}\Lambda }} \right) }. \end{aligned}$$

(3.15)

3.2 Singular soliton solutions

Supposing the below function

$$\begin{aligned} & f(z,t)=h_1\sinh (b_1\zeta _1),\ \ g_l(z,t)=m_l\exp (ic_l\zeta _{l+1}),\ \ l=1,2,\nonumber \\ & \quad \zeta _l=\lambda _lz+\mu _l(t)+\xi _l, \ \ \ l=1,2,3. \end{aligned}$$

(3.16)

Afterwards, inserting $\Sigma _l=g_l(z,t)/f(z,t),\ l=l,2$ Eq. (2.15) and using relations (2.16) and taking the coefficients of the nonlinear expressions to zero, yield a system of algebraic equations including below:

$$\begin{aligned} & -4\,i\Lambda \,c_{{1}}\lambda _{{2}}b_{{1}}\lambda _{{1}}-2\,ic_{{1}}\mu _ {{2}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{c_{{1}}}^{2} {\lambda _{{2}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{c_{{1}}}^{2}{\mu _{{2 }}}^{2}-2\,c_{{1}}\lambda _{{2}} =0, \\ & \qquad -4\,i\Lambda \,c_{{2}}\lambda _{{3}}b_{{1}}\lambda _{{1}}-2\,ic_{{2}}\mu _ {{3}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{c_{{2}}}^{2} {\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{c_{{2}}}^{2}{\mu _{{3 }}}^{2}-2\,c_{{2}}\lambda _{{3}} =0. \end{aligned}$$

Also, by solving $-2\,\Lambda \,{b_{{1}}}^{2}{h_{{1}}}^{2}{\lambda _{{1}}}^{2}-{h_{{1}}}^{ 2}{b_{{1}}}^{2}{\mu _{{1}}}^{2}- \left( \left| m_{{1}} \right| \right) ^{2}\delta - \left( \left| m_{{2}} \right| \right) ^{2} \delta =0$ we can get to the amplitude of solitary wave as below

$$\begin{aligned} h_{{1}}=\pm {\frac{ \sqrt{- \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2 } \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}}. \end{aligned}$$

(3.17)

By solving the above equations get the following results:

3.2.1 Set I solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} -2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} , \nonumber \\ & \quad \lambda _{{2}}={\frac{c_{{2}}\lambda _{{3}}}{c_{{1}}}},\ \ \mu _{{2}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.18)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, csch(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.19)

Figure 3 depicts the impact of analysis of singular soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1, c_1 = 1, c_2 = 2, b_1 \nonumber \\ & \quad = \frac{2}{3}, m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.20)

$$\begin{aligned} & \Sigma _1=0.6643035869\,{\frac{{\mathrm{e}^{i \left( - 1.888571085\,it+2\,z+1 \right) }}}{ \sqrt{ \left( \left| 1 \right| \right) ^{2}+ \left( \left| 2 \right| \right) ^{2}}\sinh \left( 2/3\,t+ 1.254031265\,iz+2 /3 \right) }} , \end{aligned}$$

(3.21)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 1, c_2 = 2, b_1 = \frac{2}{3}, m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.22)

$$\begin{aligned} & \Sigma _2=1.328607174\,{\frac{{\mathrm{e}^{2\,i \left( - 0.9442855426\,it+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 1 \right| \right) ^{2}+ \left( \left| 2 \right| \right) ^{2}}\sinh \left( 2/3\,t+ 1.254031265\,iz+2 /3 \right) }} , \end{aligned}$$

(3.23)

in Eq. (3.19). We investigate the dynamics of general nonparaxial solitons received from the Hirota bilinear technique, which is presented in Fig. 3. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 3.

Fig. 3

Plot of soliton solution (3.19) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.2.2 Set II solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} -2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} ,\nonumber \\ & \quad \lambda _{{2}}=-{\frac{\Lambda \,c_{{2}}\lambda _{{3}}+1}{\Lambda \,c_{{1 }}}} ,\ \ \mu _{{2}}={\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.24)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, csch(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.25)

Figure 4 depicts the impact of analysis of singular soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following chosen parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1, c_1 = 1, c_2 = 2, b_1 \nonumber \\ & \quad = \frac{4}{3}, m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.26)

$$\begin{aligned} & \Sigma _1=1.330369615\,{\frac{{\mathrm{e}^{i \left( 1.496033653\,it- 1002.0\,z+1 \right) }}}{ \sqrt{ \left( \left| 1 \right| \right) ^{2}+ \left( \left| 2 \right| \right) ^{2}}\sinh \left( 4/3\,t+ 1.986764478\,iz+4 /3 \right) }} , \end{aligned}$$

(3.27)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1, c_1 = 1, c_2 = 2, b_1 = \frac{4}{3}, \nonumber \\ & \quad m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.28)

$$\begin{aligned} & \Sigma _2=2.660739229\,{\frac{{\mathrm{e}^{2\,i \left( - 0.7480168264\,it+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 1 \right| \right) ^{2}+ \left( \left| 2 \right| \right) ^{2}}\sinh \left( 4/3\,t+ 1.986764478\,iz+4 /3 \right) }} , \end{aligned}$$

(3.29)

in Eq. (3.24). We investigate the dynamics of general nonparaxial solitons received from the Hirota bilinear technique, which is presented in Fig. 4. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 4.

Fig. 4

Plot of soliton solution (3.24) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.2.3 Set III solutions

$$\begin{aligned} & \Sigma _{{1}}=\frac{m_{{1}}{\mathrm{e}^{ic_{{1}} \left( {\frac{t\mu _{{3}}c_{{2}}}{c_{{1}}}}- 1/2\,{\frac{z}{c_{{1}}\Lambda }}+\xi _{{2}} \right) }} \sqrt{2} \sqrt{ \Lambda \,{\lambda _{{1}}}^{2}}b_{{1}} }{\sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\sinh \left( b_ {{1}} \left( 1/2\,{\frac{z \sqrt{2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}} ^{2}-1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.30)

$$\begin{aligned} & \Sigma _{{2}}=\frac{m_{{2}}{\mathrm{e}^{ic_{{2}} \left( t\mu _{{3}}-1/2\,{\frac{z}{c_{{2}} \Lambda }}+\xi _{{3}} \right) }} \sqrt{2} \sqrt{\Lambda \,{\lambda _{{1}}} ^{2}}b_{{1}} }{\sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\sinh \left( b_ {{1}} \left( 1/2\,{\frac{z \sqrt{2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}} ^{2}-1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }. \end{aligned}$$

(3.31)

3.3 Bright soliton solutions

Supposing bright soliton solutions as the below function

$$\begin{aligned} & f(z,t)=h_1\cosh (b_1\zeta _1),\ \ g_l(z,t)=m_l\exp (ic_l\zeta _{l+1}),\nonumber \\ & \quad l=1,2,\ \ \ \zeta _l=\lambda _lz+\mu _l(t)+\xi _l, \ \ \ l=1,2,3. \end{aligned}$$

(3.32)

By putting $\Sigma _l=g_l(z,t)/f(z,t),\ l=l,2$ Eq. (2.15) and using relations (2.16) and taking the coefficients of the nonlinear expressions to zero, yield a system of algebraic equations including below:

$$\begin{aligned} & 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{c_{{1}}}^{2} {\lambda _{{2}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{c_{{1}}}^{2}{\mu _{{2 }}}^{2}-2\,c_{{1}}\lambda _{{2}} =0, \\ & \qquad -4\,i\Lambda \,c_{{1}}\lambda _{{2}}b_{{1}}\lambda _{{1}}-2\,ic_{{1}}\mu _ {{2}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-2\,\Lambda \,{c_{{2}}}^{2} {\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}-{c_{{2}}}^{2}{\mu _{{3 }}}^{2}-2\,c_{{2}}\lambda _{{3}} =0, \\ & \qquad -4\,i\Lambda \,c_{{2}}\lambda _{{3}}b_{{1}}\lambda _{{1}}-2\,ic_{{2}}\mu _ {{3}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0. \end{aligned}$$

Also, by solving $2\,\Lambda \,{b_{{1}}}^{2}{h_{{1}}}^{2}{\lambda _{{1}}}^{2}+{h_{{1}}}^{2 }{b_{{1}}}^{2}{\mu _{{1}}}^{2}- \left( \left| m_{{1}} \right| \right) ^{2}\delta - \left( \left| m_{{2}} \right| \right) ^{2} \delta =0$ we can get to the amplitude of solitary wave as below

$$\begin{aligned} h_{{1}}=\pm {\frac{ \sqrt{ \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2} + \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}} . \end{aligned}$$

(3.33)

Therefore, the form of solutions is as below

$$\begin{aligned} \Sigma _{{l}}=\pm {\frac{ m_l\left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}{ \sqrt{ \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2} + \left( \left| m_{{2}} \right| \right) ^{2} \right) }}} \exp (ic_l\zeta _{l+1}) { sech}(b_1\zeta _1), \ \ l=1,2. \end{aligned}$$

(3.34)

By solving the above equations get the following results:

3.3.1 Set I solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} -2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} , \nonumber \\ & \quad \lambda _{{2}}={\frac{c_{{2}}\lambda _{{3}}}{c_{{1}}}},\ \ \mu _{{2}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.35)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { sech}(b_1\zeta _1),\ \ l=1,2,\ \nonumber \\ & \quad \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.36)

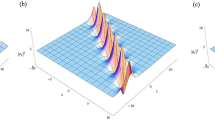
Figure 5 depicts the impact of analysis bright soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following values

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = \frac{5}{4}, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.37)

$$\begin{aligned} & \Sigma _1=5.001160405\,{\frac{{\mathrm{e}^{2\,i \left( - 0.2423331108\,t+3/2\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cosh \left( 5/2\,t+ 1.204438920\,z+5/ 4 \right) }} , \end{aligned}$$

(3.38)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 \nonumber \\ & \quad = \frac{5}{4}, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.39)

$$\begin{aligned} & \Sigma _2=7.501740608\,{\frac{{\mathrm{e}^{3\,i \left( - 0.1615554072\,t+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cosh \left( 5/2\,t+ 1.204438920\,z+5/ 4 \right) }} , \end{aligned}$$

(3.40)

in Eq. (3.36). We investigate the dynamics of general bright solitons received from the Hirota bilinear technique, which is presented in Fig. 5. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 5.

Fig. 5

Plot of bright soliton solution (3.36) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.3.2 Set II solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} -2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} , \nonumber \\ & \quad \lambda _{{2}}=-{\frac{\Lambda \,c_{{2}}\lambda _{{3}}+1}{\Lambda \,c_{{1 }}}} ,\ \ \mu _{{2}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}-{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}-2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.41)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { sech}(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.42)

Figure 5 depicts the impact of analysis of singular soliton solution where graphs of $\Sigma _l, l=1,2$ are given with the following chosen parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 2, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.43)

$$\begin{aligned} & \Sigma _1=8.081071928\,{\frac{{\mathrm{e}^{2\,i \left( - 1.605298328\,t- 501.5000000\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cosh \left( 4\, t+ 12.76579187\,z+2 \right) }} , \end{aligned}$$

(3.44)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 2, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.45)

$$\begin{aligned} & \Sigma _2=12.12160789\,{\frac{{\mathrm{e}^{3\,i \left( - 1.070198885\,t+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cosh \left( 4\,t+ 12.76579187\,z+2 \right) }} , \end{aligned}$$

(3.46)

in Eq. (3.42). We investigate the dynamics of general bright solitons received from the Hirota bilinear technique, which is presented in Fig. 6. From the figure, it is apparent that the bright solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 6.

Fig. 6

Plot of soliton solution (3.42) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.3.3 Set III solutions

$$\begin{aligned} & \Sigma _{{1}}=\frac{m_{{1}}{\mathrm{e}^{ic_{{1}} \left( {\frac{t\mu _{{3}}c_{{2}}}{c_{{1}}}}- 1/2\,{\frac{z}{c_{{1}}\Lambda }}+\xi _{{2}} \right) }} \sqrt{2} \sqrt{{ \frac{2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}}^{2}-1}{\Lambda \,{b_{{1}}}^ {2}}}}b_{{1}} }{2\, \sqrt{\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\cosh \left( b_{{1}} \left( 1/2\,{\frac{z \sqrt{2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3} }}^{2}-1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.47)

$$\begin{aligned} & \Sigma _{{2}}=\frac{m_{{2}}{\mathrm{e}^{ic_{{2}} \left( t\mu _{{3}}-1/2\,{\frac{z}{c_{{2}} \Lambda }}+\xi _{{3}} \right) }} \sqrt{2} \sqrt{{\frac{2\,\Lambda \,{c_{ {2}}}^{2}{\mu _{{3}}}^{2}-1}{\Lambda \,{b_{{1}}}^{2}}}}b_{{1}} }{2\, \sqrt{\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\cosh \left( b_{{1}} \left( 1/2\,{\frac{z \sqrt{2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3} }}^{2}-1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.48)

such that $\Lambda \, \left( b_{{1}}\right) ^{2} \left( 2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}}^{ 2}-1 \right) >0$.

3.4 Periodic solutions

Supposing periodic wave solutions as the below function

$$\begin{aligned} & f(z,t)=h_1\cos (b_1\zeta _1),\ \ g_l(z,t)=m_l\exp (ic_l\zeta _{l+1}),\ \ l=1,2,\nonumber \\ & \quad \zeta _l=\lambda _lz+\mu _l(t)+\xi _l, \ \ \ l=1,2,3. \end{aligned}$$

(3.49)

By putting $\Sigma _l=g_l(z,t)/f(z,t),\ l=l,2$ Eq. (2.15) and using relations (2.16) and taking the coefficients of the nonlinear expressions to zero, yield a system of algebraic equations including below:

$$\begin{aligned} & 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}+2\,\Lambda \,{c_{{1}}}^{2} {\lambda _{{2}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+{c_{{1}}}^{2}{\mu _{{2 }}}^{2}+2\,c_{{1}}\lambda _{{2}} =0, \\ & \qquad -4\,i\Lambda \,c_{{1}}\lambda _{{2}}b_{{1}}\lambda _{{1}}-2\,ic_{{1}}\mu _ {{2}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}+2\,\Lambda \,{c_{{2}}}^{2} {\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+{c_{{2}}}^{2}{\mu _{{3 }}}^{2}+2\,c_{{2}}\lambda _{{3}} =0, \\ & \qquad -4\,i\Lambda \,c_{{2}}\lambda _{{3}}b_{{1}}\lambda _{{1}}-2\,ic_{{2}}\mu _ {{3}}b_{{1}}\mu _{{1}}-2\,ib_{{1}}\lambda _{{1}} =0. \end{aligned}$$

Also, by solving $-2\,\Lambda \,{b_{{1}}}^{2}{h_{{1}}}^{2}{\lambda _{{1}}}^{2}-{h_{{1}}}^{ 2}{b_{{1}}}^{2}{\mu _{{1}}}^{2}- \left( \left| m_{{1}} \right| \right) ^{2}\delta - \left( \left| m_{{2}} \right| \right) ^{2} \delta =0$ we can get to the amplitude of solitary wave as below

$$\begin{aligned} h_{{1}}=\pm {\frac{ \sqrt{ \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2} + \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}} . \end{aligned}$$

(3.50)

Therefore, the form of solutions is as below

$$\begin{aligned} \Sigma _{{l}}=\pm {\frac{ \sqrt{- \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2 } \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}}\exp (ic_l\zeta _{l+1}) { sec}(b_1\zeta _1), \ \ l=1,2. \end{aligned}$$

(3.51)

By solving the above equations get the following results:

3.4.1 Set I solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} +2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} ,\nonumber \\ & \quad \lambda _{{2}}={\frac{c_{{2}}\lambda _{{3}}}{c_{{1}}}},\ \ \mu _{{2}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.52)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { sec}(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.53)

Figure 7 depicts the impact of analysis periodic wave solution where graphs of $\Sigma _l, l=1,2$ are given with the following chosen parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.54)

$$\begin{aligned} & \Sigma _1=3.960520280\,{\frac{{\mathrm{e}^{2\,i \left( - 1.576343096\,it+3/2\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cos \left( 2\,t+ 6.267765789\,iz+1 \right) }} , \end{aligned}$$

(3.55)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.56)

$$\begin{aligned} & \Sigma _2=5.940780420\,{\frac{{\mathrm{e}^{3\,i \left( - 1.050895397\,it+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cos \left( 2\,t+ 6.267765789\,iz+1 \right) }} , \end{aligned}$$

(3.57)

in Eq. (3.53). We investigate the dynamics of general periodic wave received from the Hirota bilinear technique, which is presented in Fig. 7. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 7.

Fig. 7

Plot of periodic wave solution (3.53) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.4.2 Set II solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} +2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} ,\nonumber \\ & \quad \lambda _{{2}}={\frac{c_{{2}}\lambda _{{3}}}{c_{{1}}}},\ \ \mu _{{2}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{\sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} . \end{aligned}$$

(3.58)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { sec}(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.59)

Figure 8 depicts the impact of analysis periodic wave solution where graphs of $\Sigma _l, l=1,2$ are given with the following parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.60)

$$\begin{aligned} & \Sigma _1=3.960520280\,{\frac{{\mathrm{e}^{2\,i \left( - 1.576343096\,it- 501.5000000\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cos \left( 2\,t + 6.267765789\,iz+1 \right) }} , \end{aligned}$$

(3.61)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1,\nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.62)

$$\begin{aligned} & \Sigma _2=5.940780420\,{\frac{{\mathrm{e}^{3\,i \left( - 1.050895397\,it+z+ 2.5 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\cos \left( 2\,t+ 6.267765789\,iz+1 \right) }} , \end{aligned}$$

(3.63)

in Eq. (3.59). We investigate the dynamics of general periodic wave received from the Hirota bilinear technique, which is presented in Fig. 8. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 8.

Fig. 8

Plot of soliton solution (3.59) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.4.3 Set III solutions

$$\begin{aligned} & \Sigma _{{1}}=\frac{m_{{1}}{\mathrm{e}^{ic_{{1}} \left( -{\frac{t\mu _{{3}}c_{{2}}}{c_{{1}}}} -1/2\,{\frac{z}{\Lambda \,c_{{1}}}}+\xi _{{2}} \right) }} \sqrt{2} \sqrt{{\frac{-2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}}^{2}+1}{\Lambda \,{ b_{{1}}}^{2}}}}b_{{1}} }{2\, \sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{ 2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\cos \left( b_{{1}} \left( 1/2\,{\frac{z \sqrt{-2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3 }}}^{2}+1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.64)

$$\begin{aligned} & \Sigma _{{2}}=\frac{m_{{2}}{\mathrm{e}^{ic_{{2}} \left( t\mu _{{3}}-1/2\,{\frac{z}{\Lambda \,c _{{2}}}}+\xi _{{3}} \right) }} \sqrt{2} \sqrt{{\frac{-2\,\Lambda \,{c_{ {2}}}^{2}{\mu _{{3}}}^{2}+1}{\Lambda \,{b_{{1}}}^{2}}}}b_{{1}} }{2\, \sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{ 2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }\cos \left( b_{{1}} \left( 1/2\,{\frac{z \sqrt{-2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3 }}}^{2}+1}}{b_{{1}}\Lambda }}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.65)

such that $\left( 2\,\Lambda \,{c_{{2}}}^{2}{\mu _{{3}}}^{ 2}-1 \right) <0$.

3.5 Singular form of solutions

Supposing singular form of solution as the below function

$$\begin{aligned} & f(z,t)=h_1\sin (b_1\zeta _1),\ \ g_l(z,t)=m_l\exp (ic_l\zeta _{l+1}),\ \ l=1,2,\nonumber \\ & \quad \zeta _l=\lambda _lz+\mu _l(t)+\xi _l, \ \ \ l=1,2,3. \end{aligned}$$

(3.66)

By putting $\Sigma _l=g_l(z,t)/f(z,t),\ l=l,2$ Eq. (2.15) and using relations (2.16) and taking the coefficients of the nonlinear expressions to zero, yield a system of algebraic equations including below:

$$\begin{aligned} & 4\,i\Lambda \,c_{{1}}\lambda _{{2}}b_{{1}}\lambda _{{1}}+2\,ic_{{1}}\mu _{ {2}}b_{{1}}\mu _{{1}}+2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}+2\,\Lambda \,{c_{{1}}}^{2} {\lambda _{{2}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+{c_{{1}}}^{2}{\mu _{{2 }}}^{2}+2\,c_{{1}}\lambda _{{2}} =0, \\ & \quad 4\,i\Lambda \,c_{{2}}\lambda _{{3}}b_{{1}}\lambda _{{1}}+2\,ic_{{2}}\mu _{ {3}}b_{{1}}\mu _{{1}}+2\,ib_{{1}}\lambda _{{1}} =0, \\ & \quad 2\,\Lambda \,{b_{{1}}}^{2}{\lambda _{{1}}}^{2}+2\,\Lambda \,{c_{{2}}}^{2} {\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+{c_{{2}}}^{2}{\mu _{{3 }}}^{2}+2\,c_{{2}}\lambda _{{3}} =0. \end{aligned}$$

Also, by solving $-2\,\Lambda \,{b_{{1}}}^{2}{h_{{1}}}^{2}{\lambda _{{1}}}^{2}-{h_{{1}}}^{ 2}{b_{{1}}}^{2}{\mu _{{1}}}^{2}-\delta \, \left( \left| m_{{1}} \right| \right) ^{2}-\delta \, \left( \left| m_{{2}} \right| \right) ^{2} =0$ we can get to the amplitude of solitary wave as below

$$\begin{aligned} h_{{1}}={\frac{ \sqrt{- \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2 } \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}} . \end{aligned}$$

(3.67)

Therefore, the form of solutions is as below

$$\begin{aligned} \Sigma _{{l}}=\pm {\frac{ \sqrt{- \left( 2\,\Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2 } \right) \delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2 }+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{ \left( 2\, \Lambda \,{\lambda _{{1}}}^{2}+{\mu _{{1}}}^{2} \right) b_{{1}}}}\exp (ic_l\zeta _{l+1}) { csc}(b_1\zeta _1), \ \ l=1,2. \end{aligned}$$

(3.68)

By solving the above equations get the following results:

3.5.1 Set I solutions

$$\begin{aligned} & h_{{1}}=1/2\,{\frac{ \sqrt{-2\,\Lambda \,{\lambda _{{1}}}^{2}\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) }}{\Lambda \,{\lambda _{{1}}}^{2}b _{{1}}}} ,\ \ c_{{1}}=1/2\,{\frac{ \sqrt{-2\,\Lambda \, \left( 4\,{\Lambda }^{2}{b_{{ 1}}}^{2}{\lambda _{{1}}}^{2}-1 \right) }}{\Lambda \,\mu _{{2}}}},\ \ \mu _1=0, \nonumber \\ & \quad c_{{2}}=1/2\,{\frac{ \sqrt{-2\,\Lambda \, \left( 4\,{\Lambda }^{2}{b_{{ 1}}}^{2}{\lambda _{{1}}}^{2}-1 \right) }}{\Lambda \,\mu _{{3}}}} ,\ \ \lambda _{{2}}=-{\frac{\mu _{{2}}}{ \sqrt{-2\,\Lambda \, \left( 4\,{ \Lambda }^{2}{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-1 \right) }}} ,\ \ \lambda _{{3}}=-{\frac{\mu _{{3}}}{ \sqrt{-2\,\Lambda \, \left( 4\,{ \Lambda }^{2}{b_{{1}}}^{2}{\lambda _{{1}}}^{2}-1 \right) }}}. \end{aligned}$$

(3.69)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { csc}(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.70)

Figure 9 depicts the impact of analysis singular wave solution where graphs of $\Sigma _l, l=1,2$ are given with the following parameters

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _1 = 2, b_1 = 1, m_1 = 2, m_2 = 3,\nonumber \\ & \quad \mu _2 = 2, \mu _3 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.71)

$$\begin{aligned} & \Sigma _1=0.016\,{\frac{{\mathrm{e}^{ 11.18025044\,i \left( 2\,t- 44.72171732\,z+ 1 \right) }}}{ \sqrt{ 0.008\, \left( \left| 2 \right| \right) ^{2}+ 0.008\, \left( \left| 3 \right| \right) ^{2}}\sin \left( 2\,z+1 \right) }} , \end{aligned}$$

(3.72)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _1 = 2, b_1 = 1, m_1 = 2, m_2 = 3,\nonumber \\ & \quad \mu _2 = 2, \mu _3 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5, \end{aligned}$$

(3.73)

$$\begin{aligned} & \Sigma _2=0.024\,{\frac{{\mathrm{e}^{ 7.453500295\,i \left( 3\,t- 67.08257598\,z+ 2.5 \right) }}}{ \sqrt{ 0.008\, \left( \left| 2 \right| \right) ^{2 }+ 0.008\, \left( \left| 3 \right| \right) ^{2}}\sin \left( 2\,z+1 \right) }} , \end{aligned}$$

(3.74)

in Eq. (3.69). We investigate the dynamics of general singular soliton received from the Hirota bilinear technique, which is presented in Fig. 9. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 9.

Fig. 9

Plot of singular solution (3.69) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.5.2 Set II solutions

$$\begin{aligned} & \lambda _{{1}}={\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) }\mu _{{1}}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2} +2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{ {3}}+1}} , \nonumber \\ & \quad \lambda _{{2}}={\frac{c_{{2}}\lambda _{{3}}}{c_{{1}}}},\ \ \mu _{{2}}=-{\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{1}}}} ,\nonumber \\ & \quad \mu _{{3}}=-{\frac{ \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{ \lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3} } \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{ b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) c_{{2}}}} ,\nonumber \\ & \quad h_1=\frac{ \sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) } }{\sqrt{-2\,{\frac{\Lambda \, \left( 2\,\Lambda \,{c_{{2}}}^{2}{\lambda _ {{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3}} \right) {\mu _{{1}}}^{2}}{4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}} ^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}} \lambda _{{3}}+1}}+{\mu _{{1}}}^{2}}b_{{1}} }. \end{aligned}$$

(3.75)

Then, the solution is

$$\begin{aligned} & \Sigma _l(z,t)=\frac{m_l}{h_1}\exp (ic_l\zeta _{l+1})\, { csc}(b_1\zeta _1),\nonumber \\ & \quad l=1,2,\ \ \zeta _k=\lambda _kz+\mu _k(t)+\xi _k, \ \ \ k=1,2,3. \end{aligned}$$

(3.76)

Figure 10 depicts the impact of analysis treatment of singular solution where graphs of $\Sigma _l, l=1,2$ are given with the following values

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 2, c_1 = 2, c_2 = 3, b_1 = 1, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 1, \end{aligned}$$

(3.77)

$$\begin{aligned} & \Sigma _1=7.784458700\,{\frac{{\mathrm{e}^{2\,i \left( - 2.608708939\,it+3\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\sin \left( 4\,t+ 20.62220506\,iz+2 \right) }} , \end{aligned}$$

(3.78)

$$\begin{aligned} & \Lambda = 0.1e-2, \delta = -1, \lambda _3 = 2, c_1 = 2, c_2 = 3, b_1 = 1, \nonumber \\ & \quad m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 1, \end{aligned}$$

(3.79)

$$\begin{aligned} & \Sigma _2=5.905832211\,{\frac{{\mathrm{e}^{3\,i \left( - 1.331141041\,it+2\,z+1 \right) }}}{ \sqrt{ \left( \left| 2 \right| \right) ^{2}+ \left( \left| 3 \right| \right) ^{2}}\sin \left( 2\,t+ 7.892140556\,iz+1 \right) }} , \end{aligned}$$

(3.80)

in Eq. (3.76). We investigate the dynamics of general singular solution received from the Hirota bilinear technique, which is presented in Fig. 10. From the figure, it is apparent that the solitons exhibit a stable propagation in both components of CNLH system as shown in Figs. 10.

Fig. 10

Plot of singular solution (3.76) ($|\Sigma _l|^2$) such as left graphs $|\Sigma _1|^2$ and right graphs $|\Sigma _2|^2$

3.5.3 Set III solutions

$$\begin{aligned} & \Sigma _{{1}}=\frac{m_{{1}}{\mathrm{e}^{ic_{{1}} \left( {\frac{t \sqrt{- \left( 4\,{\Lambda } ^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1 }}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{ {2}}\lambda _{{3}} \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2 \,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3 }}+1 \right) c_{{1}}}}-{\frac{z \left( \Lambda \,c_{{2}}\lambda _{{3}}+ 1 \right) }{\Lambda \,c_{{1}}}}+\xi _{{2}} \right) }} }{h_{{1}}\sin \left( b_{{1}} \left( t\mu _{{1}}+{\frac{z \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}} ^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3}} \right) }\mu _{{1}}}{4\,{\Lambda }^{ 2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}} }^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1}}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.81)

$$\begin{aligned} & \Sigma _{{2}}=\frac{m_{{2}}{\mathrm{e}^{ic_{{2}} \left( -{\frac{t \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{ 1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{ {2}}\lambda _{{3}} \right) } \left( 2\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) }{ \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2 \,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3 }}+1 \right) c_{{2}}}}+z\lambda _{{3}}+\xi _{{3}} \right) }} }{h_{{1}}\sin \left( b_{{1}} \left( t\mu _{{1}}+{\frac{z \sqrt{- \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}} ^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1 \right) \left( 2\,\Lambda \,{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+{b_{{1}}}^{2}{\mu _{{1}}}^{2}+2\,c_{{2}}\lambda _{{3}} \right) }\mu _{{1}}}{4\,{\Lambda }^{ 2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\,\Lambda \,{b_{{1}}}^{2}{\mu _{{1}} }^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}}+1}}+\xi _{{1}} \right) \right) }, \end{aligned}$$

(3.82)

such that $h_{{1}}={\frac{ \sqrt{-\delta \, \left( \left( \left| m_{{1}} \right| \right) ^{2}+ \left( \left| m_{{2}} \right| \right) ^{2} \right) \left( 4\,{\Lambda }^{2}{c_{{2}}}^{2}{\lambda _{{3}}}^{2}+2\, \Lambda \,{b_{{1}}}^{2}{\mu _{{1}}}^{2}+4\,\Lambda \,c_{{2}}\lambda _{{3}} +1 \right) }}{\mu _{{1}}b_{{1}}}}$.

4 Physical interpretation of solutions

The (1+1)-dimensional coupled nonlinear Helmholtz systems has been examined by using Hirota’s bilinear scheme. Three exact solutions to soliton, bright soliton, singular soliton, periodic wave and singular form of solutions have been obtained for Eq. (1.1). All the solutions depicted solitary wave solutions in the form of rational wave solutions. The physical phenomena of the solution graphs of (1+1)-dimensional coupled nonlinear Helmholtz systems is given as follows: Fig. 1 represents the singular soliton behaviour of Eqs. (3.5) and (3.7) for the parametric values $\Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1, \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1, \mu _1 = 1, m_1 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$. However, Fig. 2 depicts the singular soliton behaviour of Eqs. (3.11) and (3.13) for the parametric values $\Lambda = 0.1e-2, \delta = 1, \lambda _1 = 1, \lambda _2 = 1, \lambda _4 = 1, c_1 = 1, c_2 = 2, b_1 = 1, b_2 = 2.5, h_1 = 1, \mu _1 = 1, m_1 = 2, \mu _2 = 2, \mu _4 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$. Figure 3 represents the soliton behaviour of Eqs. (3.21) and (3.23) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1, c_1 = 1, c_2 = 2, b_1 = \frac{2}{3}, m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$. Figure 4 shows the soliton behaviour of Eqs. (3.27) and (3.29) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1, c_1 = 1, c_2 = 2, b_1 = \frac{4}{3}, m_1 = 2, \mu _2 = 2,\mu _1 = 1, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$. While, the bright soliton behaviour of Eqs. (3.38) and (3.40) for the parametric values $\Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = \frac{5}{4}, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$ has been seen in Fig. 5. And the bright soliton behaviour of Eqs. (3.44) and (3.46) for the parametric values $\Lambda = 0.1e-2, \delta = 1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 2, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$ has been seen in Fig. 6. Also, the periodic wave behaviour of Eqs. (3.55) and (3.57) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$ has been seen in Fig. 7. Moreover, the periodic wave behaviour of Eqs. (3.61) and (3.63) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _3 = 1,, c_1 = 2, c_2 = 3, b_1 = 1, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$ has been shown in Fig. 8. While, Fig. 9 displays the singular wave behaviour of Eqs. (3.72) and (3.74) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _1 = 2, b_1 = 1, m_1 = 2, m_2 = 3,\mu _2 = 2, \mu _3 = 3, \xi _1 = 1, \xi _2 = 1, \xi _3 = 2.5$. Finally, the singular wave behaviour of Eqs. (3.78) and (3.80) for the parametric values $\Lambda = 0.1e-2, \delta = -1, \lambda _3 = 2, c_1 = 2, c_2 = 3, b_1 = 1, m_1 = 2, m_2 = 3,\mu _1 = 2, \xi _1 = 1, \xi _2 = 1, \xi _3 = 1$ has been displayed in Fig. 10.

5 Comparison and novelty

Here, some concrete instances of our research findings and critically evaluate their originality are offered. Plenty of computational and approximate solutions to the issue at hand have been devised utilizing five modern analytical and numerical schemes. These solutions have been presented in a number of various ways employing numerical plots (1-10), displaying phenomena like singular soliton, soliton, bright soliton, periodic wave, and singular wave solutions in three-dimensional and density approaches. When presenting our findings, we compared them to those that had already been published (Christian et al. 2006; Chamorro-Posada and McDonald 2006; Song et al. 2020) to highlight the uniqueness of our findings. It is clear that our results are not consistent with those found in these publications.

6 Conclusion

To conclude, the nonparaxial solitary wave by using the Hirota’s bilinear scheme were analytically constructed. We noticed that the systems was non-integrable. The impact of nonparaxiality on the physical parameters such as speed and amplitudes of solitary waves were emphasized. The binary bell polynomials and bilinear transformation to the nonlinear system were studied. In particular, five forms of function solution including soliton, bright soliton, singular soliton, periodic wave and singular form of solutions were studied. To achieve this, an illustrative example of the coupled nonlinear Helmholtz systems was provided to demonstrate the feasibility and reliability of the procedure used in this study. The effect of the free parameters on the behavior of acquired figures to a few obtained solutions for two nonlinear rational exact cases was also discussed. For a better understanding on the resulting dynamics, a categorical discussion and clear graphical demonstration for solitons and periodic wave on both constant and spatially-varying backgrounds were provided. Further, the periodic and hyperbolic solutions with arbitrary spatial backgrounds for the considered model (1.1) through bilinear transformation were obtained. The obtained results will be an important addition along the context of nonlinear wave manipulation in higher-dimensional models due to controllable backgrounds. The present investigation shall also be extended to several other solitonic models towards improved understanding on the dynamical characteristics of respective nonlinear waves