1 Introduction

The nonlinear Schröinger (NLS) equation is a key model describing wave processes in plasma physics [1], Bose–Einstein condensates (BEC), nonlinear optics [2]. In general, the cubic nonlinearity is considered in the NLS equation. However, when the intensity of the incident light field becomes stronger to produce ultrashort optical pulses, the higher-order effects such as the third-order dispersion (TOD), self-steepening and self-frequency shift must be added to that equation [3], and non-Kerr nonlinearity must also be considered.

Nonlinear interactions are usually of a cubic nature, there are systems which engender cubic and quintic (CQ) nonlinearities, and the intensity of the optical pulse propagating inside a nonlinear medium exceeds a certain value or the two and three-body interactions in BEC. Optical solitons (bright and dark) in a fibers, which are created by a balance of group-velocity dispersion (GVD) and self-phase modulation (SPM), are governed by the NLS equation under idealized conditions and are inherently stable. There are many work for the NLS equation with (time, space)-modulated potential and nonlinearity [4–9]. Some pioneering works on multidimensional ground states of NLS-like equations have been considered; the analytical treatments of multi-dimensional singular NLS equation solutions with parabolic inhomogeneity were presented [11], which lens influence shortens the focal time of the wave. Berge and co-workers studied the propagation of intense optical beams in layered Kerr media [12] and analyzed the shape and stability of localized states in nonlinear cubic media with space-dependent potentials modeling an inhomogeneity [13]. Especially, Towers and Malomed presented a most essential result of optical beams in layered Kerr media in Ref. [14]. They introduced a model of an optical medium consisting of alternating layers with positive and negative Kerr nonlinearity, which demonstrates that stable quasi-stationary (2 + 1)-dimensional soliton beams exist in these media. The influence of higher-order optical nonlinearities on the self-guiding of femtosecond pulses in the atmosphere was investigated theoretically in Ref. [15]. The cubic–quintic nonlinear Schrödinger (CQNLS) equation with Raman effect i.e., the Kundu Eckhaus (KE) equation has been derived in Refs. [16, 17], the KE equation can be used to describe the propagation of the ultrashort optical pulses in optical fibers [18].

On the other hand, in inhomogeneous systems, the characteristic parameters of the optical fiber are not constant but variable coefficients [19]. Thus, the generalized coupled cubic–quintic nonlinear Schrödinger (GCCQNLS) equation with variable coefficients should be considered [20, 21]. Recently, there has been an increased interest in the CQNLS equation with variable coefficients because of the possibility of the soliton management and control through modulating nonlinearities in real experiments [22].

Recently, some new and important scientific studies of the optical solitons with Kerr law, power law nonlinearity and spatiotemporal dispersion are derived in nonlinear Schrödinger–Hirota equation and dense wavelength division multiplexed (DWDM) model [23–32]. Zhou and Guzman et al. consider the bright, dark optical solitons with nonlocal nonlinearity in parabolic law medium and spatiotemporal dispersion and reveal many specific features of optical solitons in [33–38]. Optical soliton in birefringent fibers with spatiotemporal dispersion is introduced in [39], and three types of solitons are obtained: bright, dark and singular solitons. Bhrawy and Abdelkawy study the propagation of optical solitons through nonlinear optical fibers in (1 + 1) and (2 + 1) dimensions [40]. Furthermore, they construct the numerical solution for the time fractional Schrödinger equations subject to initial boundary by the Jacobi Gauss–Lobatto quadrature rule [41].

The soliton solutions of the CQNLS equation with variable coefficients can maintain their overall shapes, but allow their widths, amplitudes and the pulse center to change according to the management of the system’s parameters. Because of their special properties, a lot of influential works have been performed to construct exact analytical solutions of the CQNLS equation with variable coefficients. The study of soliton solutions for the CQNLS equation with variable coefficients began with the pioneering work of Serkin et al. [42]. By assuming an ansatz solution, Hao et al. [43] constructed the exact quasi-soliton of the CQNLS equation with variable coefficients. He et al. [44] presented the exact bright, dark and gray self-similar solitarywave solutions. Tang et al. [45] gave some analytical soliton solutions of the spatially inhomogeneous CQNLS equation with an external potential. Yang and Zhang [46] derived bright, dark and kink quasi-soliton solutions under certain parametric conditions. However, most of the studies only considered the higher-order nonlinearity, i.e., the quintic nonlinearity, the inhomogeneous CQNLS equation with Raman effect, have not been reported up to now.

However, as far as we know, until recently no work has been reported on a general method used for solving the high-order dispersive GCCQNLS equation with time-modulated potential and nonlinearity. In this work, extending the ideas of Refs. [8, 9, 47, 48], we use the similarity transformation to reduce the variable coefficients GCCQNLS equation to the coupled CQNLS equation. Furthermore, we obtain two kinds of nonautonomous analytical matter-wave solitons. Then, the exact soliton solutions can be obtained with proper choices for the relevant parameters. At last, the interactions between the different-type bright two solitons have been asymptotically analyzed and presented, including the interactions between the linear-, parabolic- and periodic-type bright two solitons. There are many possibilities for managing these solitons, strongly justifying a quest for further analytical solutions. We present the general approach can provide many possibilities to manipulate soliton waves experimentally and consider the potential applications for the applications of optical fiber.

The paper is organized as follows. In Sect. 2, the similarity transformations for the variables coefficients GCCQNLS equation are obtained. In Sect. 3, we consider nonautonomous one-bright wave solution of GCCQNLS equation and present the general approach to manipulate soliton wave propagation. In Sect. 4, we present the nonautonomous bi-bright solutions of the GCCQNLS equation and manipulate the interactions of nonautonomous wave solution through manipulating nonlinear and gain/loss functions. In Sect. 5, we consider the trapping potential for both components is composed of a harmonic and a periodic potential in BEC. In Sect. 6, the numerical simulations of interaction properties between solitons are performed. The outcomes are summarized in the conclusion.

2 Similarity reduction in the variable coefficients GCCQNLS equation

We consider a GCCQNLS equation with variable coefficients and more arbitrary values, which describes the effects of quintic nonlinearity for the ultrashort optical pulse propagation in a non-Kerr medium, or in the twin-core nonlinear optical fiber or waveguide:

$$\begin{aligned}&i \Psi _{1t}+r(t) \Psi _{1xx}+m(t)(|\Psi _1|^2+|\Psi _2|^2)\Psi _1\nonumber \\&\quad +\,v_1(x,t)\Psi _{1}+n(t)(p_1|\Psi _1|^2+p_2|\Psi _2|^2)^2\Psi _1\nonumber \\&\quad +\,h(t)((\tau _1-p_1)|\Psi _1|^2+(\tau _2-p_2)|\Psi _2|^2)|\Psi _2|^2\Psi _1\nonumber \\&\quad -\,ip(t)[(p_1|\Psi _1|^2+p_2|\Psi _2|^2)\Psi _1]_x\nonumber \\&\quad +\,is(t)(p_1\Psi _1^*\Psi _{1x}+p_2\Psi _2^*\Psi _{2x})\Psi _1 +\,i\gamma (t)\Psi _1=0,\nonumber \\&i \Psi _{2t}+y(t) \Psi _{2xx}+k(t)(|\Psi _1|^2+|\Psi _2|^2)\Psi _2\nonumber \\&\quad +\,v_2(x,t)\Psi _{2}+w(t)(\tau _1|\Psi _1|^2+\tau _2|\Psi _2|^2)^2\Psi _2\nonumber \\&\quad +\,g(t)((p_1-\tau _1)|\Psi _1|^2+(p_2-\tau _2)|\Psi _2|^2)|\Psi _1|^2\Psi _2\nonumber \\&\quad -\,ia(t)[(\tau _1|\Psi _1|^2+\tau _2|\Psi _2|^2)\Psi _2]_x\nonumber \\&\quad +\,ib(t)(\tau _1\Psi _1^*\Psi _{1x}+\tau _2\Psi _2^*\Psi _{2x})\Psi _2 +\,i\gamma (t)\Psi _2=0,\nonumber \\ \end{aligned}$$
(1)

where \(p_1, p_2, \tau _1\) and \(\tau _2\) are real free parameters, \(\Psi _1=\Psi _1(x,t)\) and \(\Psi _2=\Psi _2(x,t)\) denote the two components of the electromagnetic fields, \(v_i(x,t)\) is the trapping potential, the subscripts x and t, respectively, represent the partial derivatives with respect to the normalized distance along the direction of the propagation and local time, r(t) and y(t) describe the group-velocity dispersions, m(t) and k(t) are the nonlinearity parameters, n(t), w(t), h(t) and g(t) are the saturations of the nonlinear refractive indexes, p(t) and a(t) are the self-steepening, s(t) and b(t) present the delayed nonlinear response effects, and the gain/loss coefficient \(\gamma (t)\) is real-valued function of time.

In fact, this nonlinear model (1) contains many special models. It is evident that with a symmetric reduction \(p_1=p_2=\tau _1=\tau _2\) we can recover coupled CQNLS equation from (1), while a different reduction with \(\Psi _1=q, \Psi _2=0\) and \(\gamma (t)=0\) (or \(\Psi _1=0\) and \(\Psi _2=q\)) yields the integrable KE equation with variable coefficients [49]

$$\begin{aligned}&i q_{t}+r(t) q_{xx}+m(t)|q|^2 q+n(t)|q|^4q\nonumber \\&\quad -\,ip(t)(|q|^2q)_x +is(t)|q|^2q_{x}=0, \end{aligned}$$
(2)

We search for a similar transformation connecting solutions of Eq. (1) with the constant coefficients coupled CQNLS Eq. [49], i.e.,

$$\begin{aligned} \begin{aligned}&i\Phi _{1T} +\Phi _{1 \eta \eta }+\,2(|\Phi _1|^2+|\Phi _2|^2)\Phi _1\\&\quad +\,(p_1|\Phi _1|^2+p_2|\Phi _2|^2)^2\Phi _1\\&\quad +\,2p_2[(\tau _1-p_1)|\Phi _1|^2+(\tau _2-p_2)|\Phi _2|^2]|\Phi _2|^2\Phi _1\\&\quad -\,2i[(p_1|\Phi _1|^2+p_2|\Phi _2|^2) \Phi _1]_\eta \\&\quad +\,2i (p_1\Phi _1^*\Phi _{1\eta }+p_2\Phi _2^*\Phi _{2\eta })\Phi _1=0,\\&i\Phi _{2T} +\,\Phi _{2 \eta \eta }+2(|\Phi _1|^2+|\Phi _2|^2)\Phi _2\\&\quad +\,(\tau _1|\Phi _1|^2+\tau _2|\Phi _2|^2)^2\Phi _2\\&\quad +\,2\tau _2[(p_1-\tau _1)|\Phi _1|^2+(p_2-\tau _2)|\Phi _2|^2]|\Phi _1|^2\Phi _2\\&\quad -\,2i[(\tau _1|\Phi _1|^2+\tau _2|\Phi _2|^2) \Phi _2]_\eta \\&\quad +\,2i (\tau _1\Phi _1^*\Phi _{1\eta }+\tau _2\Phi _2^*\Phi _{2\eta })\Phi _1=0. \end{aligned} \end{aligned}$$
(3)

The physical fields \(\Phi _i=\Phi _i(\eta ,T)\,(i=1,2)\) are a function of two variables \(\eta =\eta (x,t)\) and \(T=T(t)\), which are to be determined. The boundary conditions satisfy the following constraints \( \eta \longrightarrow 0 ~~{\text {at}}~~ x\longrightarrow 0 ~~{\text {and}}~~ \eta \longrightarrow \infty ~~{\text {at}}~~ x\longrightarrow \infty \) [50].

Let a Lax pair \(\mathbf U \) and \(\mathbf V \) is presented as follows

$$\begin{aligned} \mathbf U =\left( \begin{array}{cccccccc} -i \lambda &{}\quad \Phi _1 &{}\quad \Phi _2 \\ -\Phi _1^* &{}\quad -i\theta _{1\eta }+i\lambda &{}\quad 0 \\ -\Phi _2^* &{}\quad 0 &{}\quad -i\theta _{2\eta }+i\lambda \end{array}\right) \end{aligned}$$
(4)

and

$$\begin{aligned} M=4\left( \begin{array}{cccccccc} M_{11} &{}\quad 2\lambda \Phi _1+i\Phi _{1\eta }+\theta _{1\eta }\Phi _1 &{}\quad M_{13} \\ M_{21} &{}\quad 2i\lambda ^2-i|\Phi _1|^2-i\theta _{1\tau } &{}\quad M_{23} \\ M_{31} &{}\quad -i\Phi _1\Phi _2^* &{}\quad M_{33} \end{array}\right) , \end{aligned}$$

where the \(M_{11},M_{21},M_{31},M_{13},M_{23}, M_{33}, \theta _1\) and \(\theta _2\) are given in “Appendix 1”. \(\mathbf R \) is a column matrix \( \mathbf R =\left( \begin{array}{cccccccc}r\\ s \end{array}\right) , \) the dependent variables \(r=r(\eta , \tau )\) and \(s=s(\eta , \tau )\). Considering a linear system as following:

$$\begin{aligned} \mathbf R _\eta =\mathbf UR ,~~~~ \mathbf R _\tau =\mathbf VR , \end{aligned}$$
(5)

from the system (5) and the condition of compatibility

$$\begin{aligned} \mathbf R _{\eta \tau }=\mathbf R _{\tau \eta }, \end{aligned}$$

we get the coupled CQNLS Eq. (3).

Take using the Ansatz method [8–10], we search for the solutions of the physical fields \(\Psi _1(x,t), \Psi _2(x,t)\),

$$\begin{aligned}&\Psi _1(x,t)=\rho (t)e^{i \varphi (x,t)}\Phi _1(\eta (x,t),\tau (t)),\nonumber \\&\quad \Psi _2(x,t)=\rho (t)e^{i \varphi (x,t)}\Phi _2(\eta (x,t),\tau (t)), \end{aligned}$$
(6)

with \(\rho (t)\) and \(\varphi (x,t)\) being the real-value functions of the indicated variables. The Ansatz (6) can construct the relations between Eqs. (1) and (3). And, we substitute the transformation (6) into Eq. (1) and get the following system:

$$\begin{aligned} \begin{aligned}&\eta _{xx}=0,\\ {}&v_i(x,t)-\varphi _{t}-r(t)\varphi _{x}^2=0(i=1,2),\\ {}&\rho \gamma (t)+r(t)\rho \varphi _{xx}+\rho _t=0,\\ {}&\eta _{{{ t}}}+2r(t)\varphi _{{x}}\eta _{{x}}=0, \\ {}&r(t)\eta _{{x}}^2-\tau _t=0. \end{aligned} \end{aligned}$$
(7)

According to Eq. (7) and integrable condition, we obtain the functions \(\rho (t), r(t), m(t), n(t), h(t), p(t), a(t), s(t), b(t)\) in the following forms

$$\begin{aligned}&r(t)=y(t), \quad m(t)=k(t), \quad n(t)=w(t),\nonumber \\&\tau _2h(t)=p_2g(t), \quad p(t)=a(t)=s(t)=b(t),\nonumber \\&r(t)\eta _x^2=n(t)\rho ^4, \quad m(t)=2n(t)\rho ^2, \nonumber \\&h(t)=2p_2n(t), \quad p(t)\eta _x=2n(t)\rho ^2. \end{aligned}$$
(8)

We solve \(\eta _{xx}=0\) and \(\varphi _{xx}=0\) and obtain the functions \(\eta (x, t), \tau (t), \rho (t)\). If the function r(t) is given, the functions \(n(t),m(t), h(t), p(t), k(t), w(t), g(t), a(t), b(t) , s(t)\) and \(\varphi (x,t)\) can be expressed. Thus, we can establish a correspondence between selected solutions of Eqs. (1) and (3). In particular, we can obtain the nonautonomous wave solutions of Eq. (1).

Solving Eq. (7), we get the similarity variables \(\eta (x,t), \tau (t)\) and the phase \(\varphi (x,t)\) in the forms (case A):

$$\begin{aligned} \begin{aligned}&\eta (x,t)=Ax+c_0-2AC\int _0^tr(s)\mathrm{d}s,\\ {}&\tau (t)=A^2\int _0^tr(s)\mathrm{d}s,\\ {}&\varphi (x,t)=Cx+c_1-2C^2\int _0^tr(s)\mathrm{d}s,\\ {}&\rho (t)=\rho _0e^{-\int _0^t\gamma (s)\mathrm{d}s},\\ {}&v_i(x,t)=-C^2r(t), \end{aligned} \end{aligned}$$
(9)

we can also get the similarity variables \(\eta (x,t), \tau (t)\) and the phase \(\varphi (x,t)\) in the forms (case B):

$$\begin{aligned}&\eta (x,t)=A(t)x+c_0+B(t),\nonumber \\&\tau (t)=\int _0^tr(s)A^2(s)\mathrm{d}s,\nonumber \\&\varphi (x,t)=-\frac{\dot{A}(t)}{4A(t)r(t)}x^2-\frac{\dot{B}(t)}{2A(t)r(t)}x+c_1,\nonumber \\&\rho (t)=\rho _0e^{-\int _0^t(\gamma (s)-\frac{\dot{A}(s)}{A(s)})\mathrm{d}s},\nonumber \\&v_i(x,t)=\omega (t) x^2+\epsilon (t) x+\frac{\dot{B}^2(t)}{4A^2(t)r(t)}, \end{aligned}$$
(10)

and \(\omega (t)=\frac{\dot{A}^2(t)}{4A^2(t)r(t)}-(\frac{\dot{A}(t)}{4A(t)r(t)})^{'}, \epsilon (t)=-\frac{\dot{A}(t)\dot{B}(t)}{2A^2(t)r(t)}-(\frac{\dot{B}(t)}{2A(t)r(t)})^{'}\), where the fourth-order dispersion parameter r(t) influences the phase and effective propagation distance; the \(c_0\) and \(c_1\) are constants. We choose the free parameters and r(t); Fig. 1 depicts the profiles of the potential \(\eta (x,t), \tau (t)\) and the phase \(\varphi (x,t)\).

Fig. 1
figure 1

(Color online) a is the \(\tau (t)\) of (9) with \(r(t)=0.5{\text {sin}}(2t), A=1\), b is the \(\eta (x,t)\) of (9) with \(r(t)={\text {sin}}(2t), A=0.2,C=-10\), c is \(\varphi (x,t)\) of (9) with \(r(t)=cn(0.8t, 0.5)\), and \(C=1\), respectively

Full size image

3 Nonautonomous one-bright soliton solution and propagation manipulation

Although many people have investigated the GCCQNLS equation, but few people have studied the soliton dynamics of controllable propagation with free functions. Different from those work in the previous studies, we will aim to analyze the soliton dynamics of Eq. (1) with the management effects of r(t) and \(\gamma (t)\). The results have some guiding significance for controllable management of soliton and can provide some theoretical analysis for carrying out optical soliton communication experiments.

Fig. 2
figure 2

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) of (11) with \(r(t)=0.5 t\) and \(\kappa =1,\upsilon =0.3,\delta =1\). b \(|\Psi _2|^2\) of (11) with \(r(t)=0.5 t\) and \(\kappa =0.5,\upsilon =0.2,\delta =0.1\). And \(\gamma (t)=0.1 {\text {cos}}(4t) \rho _0=1,A=-3,C=8/3,\alpha =1,\beta =1\)

Full size image
Fig. 3
figure 3

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) of (11) with \(r(t)=t^2\) and \(\kappa =0.4,\upsilon =0.2,\delta =2\). b \(|\Psi _1|^2\) of (11) with \(r(t)={\text {cos}} t\) and \(\kappa =0.4,\upsilon =1,\delta =1\). And \(\gamma (t)=0.1 {\text {sin}}(2t) \rho _0=1,A=-1,C=-0.6,\alpha =1,\beta =1\)

Full size image

In Ref. [49], the one-bright soliton solutions are obtained via the Hirota bilinear method for a coupled Eq. (3). Based on the similarity transformation (7) and the bright soliton solutions of the Eq. (3), we present the nonautonomous one-bright soliton solution of Eq. (1) in the form

$$\begin{aligned} \begin{aligned}&\Psi _1(x,t)=\alpha \rho _{0}{\text {sec}}h(\upsilon (\eta -v\tau +\delta )) e^{-\int _0^t\gamma (s)\mathrm{d}s}\\ {}&\quad e^{i(\delta _1 {\text {tan}}h(\upsilon (\eta -v\tau +\delta ))+\varphi (x,t))} e^{i(\kappa \eta +\omega T)},\\ {}&\Psi _2(x,t)=\beta \rho _{0}{\text {sec}}h(\upsilon (\eta -v\tau +\delta )) e^{-\int _0^t\gamma (s)\mathrm{d}s}\\ {}&\quad e^{i\delta _2 {\text {tan}}h(\upsilon (\eta -v\tau +\delta ))+\varphi (x,t))} e^{i(\kappa \eta +\omega T)}, \end{aligned} \end{aligned}$$
(11)

where \(\eta (x,t)=Ax+c_0-2AC\int _0^tr(s)\mathrm{d}s, \tau (t)=A^2\int _0^tr(s)\mathrm{d}s, \varphi (x,t)=Cx+c_1-C^2\int _0^tr(s)\mathrm{d}s,\) the different parameters of the solution are related to the spectral parameter \(\lambda =\upsilon +i\kappa \) and the parameters of the model as \(v=2\kappa ,w=\upsilon ^2-\kappa ^2,\delta _1=\frac{1}{\upsilon }(p_1|\alpha |^2+p_2|\beta |^2), \delta _2=\frac{1}{\upsilon }(\tau _1|\alpha |^2+\tau _2|\beta |^2)\) and the phase \(\delta \) is a constant.

Fig. 4
figure 4

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) of (12) with \(\alpha =1\) and \(\kappa =1,\upsilon =0.3,\delta =1\). b \(|\Psi _1|^2\) of (12) with \(\beta =2\) and \(\kappa =1,\upsilon =0.3,\delta =1\). And \(\rho _0=A=r(s)=1,c_0=c_1=C=\gamma (s)=0\)

Full size image

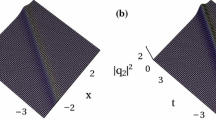
To illustrate the wave propagation of the obtained nonautonomous one-bright soliton solution (11), we can choose these free parameters in the form \(\upsilon ,\kappa ,\rho _0,\delta \). The evolution of the intensity distribution for the one-bright soliton solution given by Eq. (11) is illustrated in Fig. 2a, b with functions \(r(t)=0.5t\); such a structure of the soliton is known as “Parabola-like.” Moreover, it follows from Fig. 2 that the amplitude of the one-bright soliton solution is invariant as time increases. It can be observed that with the increasing distance, the amplitude and the width of the soliton remain the same. However, we can shown that the opening direction of the parabola in \(\Psi _1(x,t)\) and \(\Psi _2(x,t)\) is opposite, when we choose the different parameters \(\upsilon , \kappa \).

In particular, we consider the properties of \(r(t)=t^2\) in \(\Psi _1(x,t)\), the evolution of the intensity distribution for the one-bright soliton solution given by Eq. (11) is illustrated in Fig. 3a, and such a structure of the soliton is known as “S-like.” The evolution of the one-bright soliton solution \(\Psi _1(x,t)\) given by Eq. (11) is illustrated in Fig. 3b with functions \(r(t)={\text {cos}} t\); such a structure of the soliton is known as “Snaking-like.” Hence, we can control the soliton propagation through the different functions r(t) in Figs. 2 and 3.

If \(\rho _0=A=r(s)=1,c_0=c_1=C=\gamma (s)=0\) in Eq. (11), this means that \(\varphi _(x,t)\) is a constant. In this case, the obtained one-bright soliton solutions \(\Psi _1(x,t)\) and \(\Psi _2(x,t)\) in the following form

$$\begin{aligned} \Psi _1(x,t)= & {} \alpha e^{i\delta _1 {\text {tan}}h(\upsilon (x-vt+\delta ))} {\text {sec}}h(\upsilon (x-vt+\delta ))\nonumber \\&e^{i(\kappa x+\omega t)},\nonumber \\ \Psi _2(x,t)= & {} \beta e^{i\delta _2 {\text {tan}}h(\upsilon (x-vt+\delta ))} {\text {sec}}h(\upsilon (x-vt+\delta ))\nonumber \\&e^{i(\kappa x+\omega t)}, \end{aligned}$$
(12)

Figure 4 is plotted to describe the one-soliton solutions (12). Figure 4a shows that, when \(r={\text {constant}}\), neither the soliton amplitude nor velocity changes during the propagation. From the comparison between Fig. 4a, b, we can see that the amplitudes of the soliton become invariant during the propagation, which are the propagation of linear type with \(r(t)=1\) in Fig. 4.

Figures 2, 3 and 4 are plotted to describe the wave propagation of nonautonomous bright one-soliton solutions. From the comparison between Figs. 2, 3 and 4, we can see that the amplitudes of the soliton are invariant during the propagation with different function r(t), but the wave propagations of solitons depend on function r(t). As we can see in Fig. 4, the soliton is linear type, while in Fig. 2 it is parabolic type, and in Fig. 3 it is periodic type, which means that r(t) can control the wave propagation in the inhomogeneous optical fibers influencing the soliton type.

4 Nonautonomous two bright soliton solutions and interaction managements

Although Eq. (1) with constant coefficients has been investigated in such aspects as the conservation laws, Lax pair and multi-soliton solutions, few people have studied the soliton dynamics of controllable interactions with free functions. Different from those work in the previous studies, we will aim to analyze the soliton dynamics of Eq. (1) with the management effects of r(t) and \(\gamma (t)\), based on the two bright soliton solutions.

Fig. 5
figure 5

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) of (13) with \(r(t)=0.5t^2\) and \(\alpha _1=1,\alpha _2=(39-80i)/89,\beta _1=1,\beta _2=1,k_1=1.5+0.5i,k_2=2-0.7i,A=-0.2,C=0.3\). b \(|\Psi _2|^2\) of (13) with \(r(t)=t\) and \(\alpha _1=5i,\alpha _2=(39-80i)/89,\beta _1=10i,\beta _2=2-2i,k_1=1.5+0.5i,k_2=2-0.7i,A=-3,C=-0.33\). And \(\gamma (t)=0, \rho _0=1,\alpha =1,\beta =1\)

Full size image
Fig. 6
figure 6

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) of (13) with \(r(t)=2sn(5t,0.8)\) and \(\alpha _1=1,\alpha _2=(39-80i)/89,\beta _1=1,\beta _2=1,k_1=1.5+0.5i,k_2=2-0.7i,A=1,C=0.001\). b \(|\Psi _2|^2\) of (13) with \(r(t)=2sn(5t,0.8)\) and \(\alpha _1=5i,\alpha _2=(39+80i)/89,\beta _1=10i,\beta _2=2+2i,k_1=1.5+0.5i,k_2=2-0.7i,A=0.2,C=0.1\). And \(\gamma (t)=0.1{\text {cos}}(t), \rho _0=1,\alpha =1,\beta =1\)

Full size image

We consider the analysis of functions r(t) and \(\gamma (t)\) to control the soliton interactions. The results have some guiding significance for controllable management of soliton and can provide some theoretical analysis for carrying out optical soliton communication experiments. Based on the two bright soliton solutions of Eq. (3) and the similarity transformation (7), we obtain the nonautonomous two bright soliton solutions of Eq. (1) in the following form

$$\begin{aligned} \Psi _1(x,t)= & {} \alpha \rho _{0} e^{-\int _0^t\gamma (s)\mathrm{d}s} e^{i \varphi (x,t)} \Phi _{1M}\nonumber \\&e^{i\int (p_1|\Phi _{1M}|^2+p_2|\Phi _{2M}|^2))\mathrm{d}x} ,\nonumber \\ \Psi _2(x,t)= & {} \beta \rho _{0} e^{-\int _0^t\gamma (s)\mathrm{d}s} e^{i \varphi (x,t)}\Phi _{2M}\nonumber \\&e^{i\int (\tau _1|\Phi _{1M}|^2+\tau _2|\Phi _{2M}|^2))\mathrm{d}x} , \end{aligned}$$
(13)

with

$$\begin{aligned} \Phi _{1M}= & {} \frac{\alpha _{{1}}{\mathrm{e}^{\eta _{{1}}}}+\alpha _{{2}}{\mathrm{e}^{\eta _{{2}}}}+ {\mathrm{e}^{\delta _{{1}}+\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}}}+{ \mathrm{e}^{\delta _{{2}}+\eta _{{1}}+\eta _{{2}}+\eta _{{2}}^*}} }{1+{\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+{ R1}}}+{\mathrm{e}^{\eta _ {{1}}+ \eta _{{2}}^*+\delta _{{0}}}}+{\mathrm{e}^{ \eta _{{1}}^*+\eta _{{2}}+ \delta _{{0}}^*}}+{\mathrm{e}^{ \eta _{{2}}+ \eta _{{2}}^*+{ R2}}}+R },\nonumber \\ \\\Phi _{2M}= & {} \frac{\beta _{{1}}{\mathrm{e}^{\eta _{{1}}}}+\beta _{{2}}{\mathrm{e}^{\eta _{{2}}}}+ {\mathrm{e}^{\delta _{{1}}^{'}+\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}}}+{ \mathrm{e}^{\delta _{{2}}^{'}+\eta _{{1}}+\eta _{{2}}+\eta _{{2}}^*}} }{1+{\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+{ R1}}}+{\mathrm{e}^{\eta _ {{1}}+ \eta _{{2}}^*+\delta _{{0}}}}+{\mathrm{e}^{ \eta _{{1}}^*+\eta _{{2}}+ \delta _{{0}}^*}}+{\mathrm{e}^{ \eta _{{2}}+ \eta _{{2}}^*+{ R2}}}+R },\nonumber \\ \end{aligned}$$
(14)

In the above equations, \(\eta _1=k_1(\eta +ik_1\tau ),\eta _2=k_2(\eta +ik_2\tau ), R={\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}+\eta _{{2}}^*+{ R3}}}\) and the detailed expressions for other quantities can be obtained from the “Appendix 2”.

To illustrate the interaction between the obtained nonautonomous two bright soliton solutions, we can choose these free functions in the form r(t) and \(\gamma (t)\). Figure 5 shows the interaction between the two parabolic-type bright solitons propagating with the identical direction (Fig. 5a) and opposite direction (Fig. 5b). Seen on the x–t plane, the two bright solitons propagate along the same direction, before and after the interaction in Fig. 5a. Seen on the x–t planes, the two bright solitons propagate toward each other before the interaction, while they bounce back after the interaction in Fig. 5b.

Figure 6 illustrates the interaction between the two periodic-type bright solitons. As seen in Fig. 6a, the two bright solitons propagating on x–t planes share the same period. There exists a phase shift for the two solitons at each interaction region, but the velocity and amplitude of each soliton remain unchanged after the interaction, implying that the interaction is elastic. Meanwhile, the periodical interaction of the two solitons is observed in Fig. 6b. It can be seen that the central positions of the two solitons oscillate periodically, but the separation of the two solitons remains constant along the optical fiber. And it can also be seen that the single soliton has the same shape as “Snake-like.” Moreover, the amplitudes of solitons depend on parameters \(\alpha _1,\alpha _2,\beta _1\) and \(\beta _2\) in Fig. 6. The two solitons will be parallel with each other as Fig. 6b shows, which may be undistinguishable under equal amplitudes condition. Through the parameters \(\alpha _1,\alpha _2,\beta _1\) and \(\beta _2\), we can also change state from the parallel state to the bound state, as Fig. 6a. In conclusion, different states of two solitons can exist in two sides, which will be a benefit for state transition control and decrease soliton interactions.

In particular, \(\rho _0=A=r(s)=1,c_0=c_1=C=\gamma (s)=0\) in Eq. (13), this means that \(\varphi (x,t)\) is a constant. In this case, the obtained nonautonomous two bright soliton solutions \(\Psi _1(x,t),\Psi _2(x,t)\) are in the following forms

$$\begin{aligned} \Psi _1(x,t)= & {} \Phi _{1M} e^{i\int (p_1|\Phi _{1M}|^2+p_2|\Phi _{2M}|^2))\mathrm{d}x},\nonumber \\ \Psi _2(x,t)= & {} \Phi _{2M} e^{i\int (\tau _1|\Phi _{1M}|^2+\tau _2|\Phi _{2M}|^2))\mathrm{d}x}, \end{aligned}$$
(15)

and

$$\begin{aligned} \Phi _{1M}= & {} \frac{\alpha _{{1}}{\mathrm{e}^{\eta _{{1}}}}+\alpha _{{2}}{\mathrm{e}^{\eta _{{2}}}}+ {\mathrm{e}^{\delta _{{1}}+\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}}}+{ \mathrm{e}^{\delta _{{2}}+\eta _{{1}}+\eta _{{2}}+\eta _{{2}}^*}} }{1+{\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+{ R1}}}+{\mathrm{e}^{\eta _ {{1}}+ \eta _{{2}}^*+\delta _{{0}}}}+{\mathrm{e}^{ \eta _{{1}}^*+\eta _{{2}}+ \delta _{{0}}^*}}+{\mathrm{e}^{ \eta _{{2}}+ \eta _{{2}}^*+{ R2}}}+R },\nonumber \\ \Phi _{2M}= & {} \frac{\beta _{{1}}{\mathrm{e}^{\eta _{{1}}}}+\beta _{{2}}{\mathrm{e}^{\eta _{{2}}}}+ {\mathrm{e}^{\delta _{{1}}^{'}+\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}}}+{ \mathrm{e}^{\delta _{{2}}^{'}+\eta _{{1}}+\eta _{{2}}+\eta _{{2}}^*}} }{1+{\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+{ R1}}}+{\mathrm{e}^{\eta _ {{1}}+ \eta _{{2}}^*+\delta _{{0}}}}+{\mathrm{e}^{ \eta _{{1}}^*+\eta _{{2}}+ \delta _{{0}}^*}}+{\mathrm{e}^{ \eta _{{2}}+ \eta _{{2}}^*+{ R2}}}+R },\nonumber \\ \end{aligned}$$
(16)

where \(\eta _1=k_1(x+ik_1 t),\eta _2=k_2(x+ik_2 t), R={\mathrm{e}^{\eta _{{1}}+ \eta _{{1}}^*+\eta _{{2}}+\eta _{{2}}^*+{ R3}}}\).

Fig. 7
figure 7

(Color online). Color-coded plot of wave intensity a \(|\Psi _1|^2\) with \(\beta _1=1,\beta _2=1,k_1=1.5+0.5i,k_2=2-0.7i\) in (15) . b \(|\Psi _1|^2\) with \(\beta _1=1,\beta _2=1,k_1=2+2i,k_2=2-i\) in (15). c \(|\Psi _1|^2\) with \(\beta _1=2-2i,\beta _2=2+2i,k_1=2+2i,k_2=2-i\) in (15). And \(\alpha _1=10i,\alpha _2=(39+80i)/89,\beta =1,\alpha =1\). d \(|\Psi _1|^2\) with \(\beta _1=10i,\beta _2=2+2i,k_1=1.5+0.5i,k_2=2-0.7i,\alpha _1=5i,\alpha _2=(39+80i)/89,\beta =1,\alpha =1\) in (15)

Full size image

When r(t) is taken as a constant, interaction between the linear-type bright two solitons has been given and the bright two soliton velocities may decrease as r(t) decreases, as seen in Fig. 7. Fig. 7 shows the process of the interaction managements between two solitons with different controllable parameters. In Fig. 7a–c, when two solitons encounter with each other, they join together. After the interactions, two solitons separate from each other and revert to their original states, whose shapes keep invariant except for some phase shifts. Moreover, two solitons encounter with each other; they have not the phenomena of interactions in Fig. 7d.

Compared to Fig. 7, these free parameters \(k_1,k_2 \) effect on the angle of interaction between the linear-type bright two solitons. Figure 7a, b shows that the modulus value \(k_1,k_2\) is increased, while the angles of interaction are decreased. And the free parameters \(\beta _1,\beta _2 \) have not affect the angle of interaction between the linear-type bright two solitons through comparing the Fig. 7a, d and b, c.

Figures 5, 6 and 7 show the process of the interaction managements between two solitons with different controllable functions \(r(t),\gamma (t)\). In Figs. 6a and 7, when two solitons encounter with each other, they join together. After the interactions, two solitons separate from each other and revert to their original states, whose shapes keep invariant except for some phase shifts. Moreover, two solitons encounter with each other; they have not the phenomena of interactions in Fig. 6b.

It can be seen that the central positions of two solitons oscillate periodically, but the separation of two solitons remains constant along the optical fiber. And it can also be seen that the single soliton has the same shape as “Snake-like.” In this work, the parallels between nonlinear guided wave phenomena in optics and nonlinear guided wave phenomena in Bose condensates can be clearly demonstrated by considering optical and matter-wave soliton dynamics in the framework of nonautonomous evolution equations.

To observe nonautonomous soliton conveniently, all following discussions are made with the condition. It is meaningful to manipulate nonautonomous soliton to understand their fundamental character or even mechanism. We will study the evolution of nonautonomous soliton with exponential increasing and periodic changing nonlinearity in the following, to show possibilities to manipulate them in nonautonomous nonlinear optics and BEC systems.

Fig. 8
figure 8

(Color online) \(v_i(x,t)\) with \( \nu _2=1,\nu _1=0.8,A_0=0.5\) and \(q=0.5\), respectively

Full size image

5 BEC with two internal states (case B)

When the two coupled nonautonomous GCCQNLS models in BEC with two different internal states, we consider \(n(t)=A^{-2}(t)\) and \(\rho (t)=A(t)\). With this choice, we have \(r(t)=y(t)=1\) (constant mass) and \(\gamma (t)=0\) (conservative system). We consider the conditions

$$\begin{aligned}&B^{''}(t)=0, \quad A(t)=1+ \nu _2 sn(\nu _1 t,A_0),\end{aligned}$$
(17)
$$\begin{aligned}&\varphi (x,t)=-1/4\,{\frac{{ \nu _1}\,{ \nu _2}\,{ Cn} \left( { \nu _2}\,t,{ A_0} \right) { Dn} \left( { \nu _2}\,t,{ A_0} \right) }{ \left( 1+{ \nu _1}\,{ Sn} \left( { \nu _2}\,t,{ A_0} \right) \right) ^{2}}} x^2\nonumber \\&\qquad \qquad \quad - \frac{ sn^2(\xi |q)}{2( 1+ \nu _2 sn(\nu _1 t,A_0))} x, \end{aligned}$$
(18)

such that the trapping potential for both components is composed of a harmonic potential and a periodic potential as following

$$\begin{aligned} v_i(x,t)=\omega (t) x^2+ \frac{sn^2(\xi |q)}{4 ( 1+ \nu _2 sn(\nu _1 t,A_0))^2}, \quad i=1,2.\nonumber \\ \end{aligned}$$
(19)

The external potential functions \(v_1(x,t)\) and \(v_2(x,t)\) include a magnetic trap and an optical lattice, which are important ingredients of experimental BEC setups [51–53] (Fig. 8 shows this trapping potential). The \(sn(\xi |q)\) is the Jacobi elliptic function defined by \(sn(\xi |q)={\text {sin}}\theta \), with respect to the integral \(\xi =\int _0^{\theta }d\alpha /(1-q {\text {sin}}^2 \alpha )^{1/2}\) , where \(\theta \) is called the amplitude and \( q (0\le q\le 1)\) is the elliptic parameter.

And, the choice of A(t) implies that the nonlinearities n(t), m(t), h(t), p(t), s(t), k(t), w(t), g(t), a(t) and b(t) are periodic functions in time, which is a desirable feature for the coefficients that describe the strength management of the interaction between two atoms [m(t)], [k(t)] and three atoms \([n(t)], [h(t)] [w(t)], [g(t)]\).

6 The numerical simulation of collision

In these numerical simulations, a pseudo-spectral method in the time domain and a Runge–Kutta scheme with an adaptive step-size control in the spatial domain are employed. The initial conditions for the fiber are given by

$$\begin{aligned} \Psi _1(x,0)= & {} \alpha [1+0.01R(X)] e^{i\delta _1 {\text {tan}}h(\upsilon (x+\delta ))}\nonumber \\&{\text {sec}}h(\upsilon (x+\delta ))e^{i(\kappa x)},\nonumber \\ \Psi _2(x,0)= & {} \beta [1+0.01R(X)] e^{i\delta _2 {\text {tan}}h(\upsilon (x+\delta ))}\nonumber \\&{\text {sec}}h(\upsilon (x+\delta ))e^{i(\kappa x)}, \end{aligned}$$
(20)

where R(X) is a random number between 0 and 1.

Running this code, we get Fig. 9, which shows that the collision is a position shift. In Fig. 9a, b, when two solitons encounter with each other, they join together. After the interactions, two solitons separate from each other and revert to their original states, whose shapes keep invariant except for some phase shifts.

We next present our simulation results regarding the interaction between two solitary wave solutions. To reveal and understand the collision properties of solitons, the initial condition in this code is taken as two solitons of (15), which are moving toward each other. The initial conditions of a two soliton solution are given as following

$$\begin{aligned} \Psi _1(x,0)= & {} \Phi _{1M} e^{i\int (p_1|\Phi _{1M}|^2+p_2|\Phi _{2M}|^2))\mathrm{d}x},\nonumber \\ \Psi _2(x,0)= & {} \Phi _{2M} e^{i\int (\tau _1|\Phi _{1M}|^2+\tau _2|\Phi _{2M}|^2))\mathrm{d}x}. \end{aligned}$$
(21)
Fig. 9
figure 9

(Color online). Evolution of the amplitude a for the interaction between two solutions \(|\Psi _1(x,t)|\) with \(\alpha =1.2\) in Eq. (20). Evolution of the amplitude b for the interaction between two solutions \(|\Psi _2(x,t)|\) with \(\beta =1.5\) in Eq. (20). And \(\delta _1=\delta _2=1,\nu =1,\delta =20\)

Full size image
Fig. 10
figure 10

(Color online). Evolution of the amplitude a the solution \(|\Psi _1|\) with the same parameters as those given in Fig. 6b. Evolution of the amplitude b for the interaction between two solutions \(|\Psi _2|\) with the same parameters as those given in Fig. 7b

Full size image

It can be seen that the central positions of the two solitons oscillate periodically, but the intensity of solitons has no change in this case, which means that energy transfer and energy loss do not exist during the collision in Fig. 10a. This is the ideal situation of large-capacity, multi-channel soliton transmission systems. Through the expressions in Fig. 10b, we find that the amplitudes after collision of two soliton solution can be related to those before collision, which means that the intensities of solitons keep the same after collision. This implies that the collision between two solitons in system (1) is elastic.

7 Conclusions

In this paper, we used similarity reductions in the variable coefficients GCCQNLS equation to the coupled CQNLS equation. Furthermore, we can also obtain the nonautonomous bright one and two wave solutions of Eq. (1). It is reported that there are possibilities to manipulate the interactions of nonautonomous wave solution through manipulating nonlinear and gain/loss functions. Interactions between the different-type bright two solitons have been asymptotically analyzed and presented. The interactions between the linear-, parabolic- and periodic-type bright two solitons are elastic. And, the two parabolic-type dark solitons propagating with the opposite directions both change their directions after the interaction. In order to better understand the interaction properties between solitons, we perform the numerical simulation for Eq. (1). We present the general approach can provide many possibilities to manipulate soliton waves experimentally and consider the potential applications in non-Kerr media and BEC.