1 Introduction

In classical physics, Newton’s second law of motion is used to describe the motion and behavior of macroscopic particles. However, the behavior of microscopic particles cannot be estimated accurately through the classical force equation. The Schrödinger equation is the basic model used to demonstrate the behavior of microscopic particles like, electron, photon, neutron, and others. The nonlinear Schrödinger equation (NLSE) is a remarkable area of research due to its inherently nonlinear nature and its ability to accurately describe a wide range of natural phenomena. It was first introduced by Chiao et al. (1964) in their work on superconductivity. Nowadays, the NLSE is used to model a diverse range of physical phenomena, including optical fiber communication, plasma physics, quantum mechanics, bio-engineering, fluid mechanics, and many others (Rizvi et al. 2023a, 2023b). Optical fibers are of paramount importance in modern technology and have revolutionized the way we communicate and transmit information. Unlike copper wire, optical fibers are impervious to electromagnetic interference, which can degrade signal quality and cause data loss. Additionally, optical fibers can transmit data in long distances with minimal signal loss. This makes them ideal for application in undersea communications, telecommunication in data center, development medical instruments that use radio active lights, and so on. Even though optical fiber communication has its roots in the 1960s, it was not until the early 1970s that the use of optical fibers become practical, with the reduction of fiber losses to below 20 dB/Km. Subsequent advancements in optical fibers enabled a loss of only 0.2 dB/Km. The field of optical fibers advancements have been boosted by the optical soliton solutions of the nonlinear models used in optics and quantum physics. Soliton solutions are resulted from the balancing between the highest order linear and nonlinear terms, and cause a minimal energy loss of wave packets that enables the wave to maintain their shape during long-distanced propagation. Although the history of solitons can be traced back to the observation made by Russel in 1834 (Russel 1845), but their mathematical theory was not developed until the 1960s. Korteweg and de Vries (1895) introduced an equation, known as Korteweg de–Vries (KdV) equation, including solitary wave in 1895. However, in 1965, the soliton behavior was first demonstrated by Zabusky and Kruskal (1965), while investigating KdV equation via finite difference method. They found that under certain conditions, the nonlinear interaction between waves could lead to the formation of solitons.

Over the past decades, nonlinear evolution equations (NLEEs) and their soliton solutions have played significant roles in the study of nonlinear systems. Many academics have devoted their efforts to finding new approaches to explain these models. As a result, several analytical and numerical approaches have been introduced to unravel the NLEEs. For instance, the improved \(\tan ((\phi \left( \xi \right)/2)\)-expansion method (Raza et al. 2020), the sine–Gordon expansion scheme (Kundu et al. 2021; Fahim et al. 2022), the Hirota’s bilinear method (Alsallami et al. 2023), the ansatz transformation technique (Batool et al. 2023; Seadawy et al. 2023), the finite difference method (Saqib et al. 2023), the sine–cosine method (Liang et al. 2022), the modified simple equation approach (Rasheed et al. 2021), the improved F-expansion scheme (Islam et al. 2017), the modified fractional homotopy analysis (Wang and Liu 2016), the extended rational sinh-cosh process (Mahak and Akram 2019), the homotopy analysis Elzaki technique (Pankaj 2022), the mapping method (Biswas et al. 2019), the fractional sub-equation procedure (Martìnez and Aguilar 2019), the generalized Kudryashov procedure (Akbar et al. 2022), the \(\left( {G^{\prime}/G} \right)\)-expansion method (Al-Askar et al. 2022), the improved \(\left( {G^{\prime}/G} \right)\)-expansion method (Sahoo et al. 2020), the \((G^{\prime}/G\),\(1/G)\)-expansion scheme (Akbar et al. 2023a, 2023b; Khatun and Akbar 2023), etc. are some well-established techniques to resolve NLEEs.

1.1 Governing equation

The well-established NLSE can be stated mathematically in the following form (Zakharov and Manakov 1974):

$$i\frac{\partial u}{{\partial t}} + (1/2)\frac{{\partial^{2} u}}{{\partial x^{2} }} + b|u|^{2} u = 0,$$
(1)

where \(u = u\left( {x,t} \right)\) is a complex valued wave function of \(x\) (spatial variable), and \(t\) (temporal variable). The first term describes the temporal evolution, while the second and third terms respectively imply the group velocity dispersion and nonlinear term.

The perturbed nonlinear Schrödinger equation (pNLSE) is a generalization of the NLSE that includes an additional perturbation term to account for external influences on the system. This article focuses on the space–time beta fractional perturbed NLSE, which can be mathematically represented as follows (Akbar et al. 2023c):

$$iD_{t}^{\beta } u + aD_{xx}^{2\beta } u + bF\left| u \right|^{2} u = i[cD_{x}^{\beta } u + dD_{x}^{\beta } \left( {\left| u \right|^{2n} u} \right) + lD_{x}^{\beta } \left( {\left| u \right|^{2n} } \right)u,$$
(2)

wherein the right side of Eq. (2), perturbation terms are introduced by considering \(c\), \(d\), and \(l\) as the inter model dispersion, self-steeping, and nonlinear dispersion coefficients, respectively. In Eq. (2), \(0 < \beta \le 1\) (order of fractional derivative), \(F\left( u \right)\) is a complex valued function of \(u = u\left( {x,t} \right)\), and \(n\) is a parameter that characterizes the nonlinearity of the equation. Setting \(n = 1\) and \(F\left( u \right) = u\), the equation experiences Kerr-law nonlinearity. Kerr-law nonlinearity is the term that describes the interaction between a wave and a medium with a nonlinear response. Therefore, the space–time beta fractional perturbed NLSE with Kerr-law nonlinearity takes the form (Akbar et al. 2023c):

$$iD_{t}^{\beta } u + aD_{xx}^{2\beta } u + b\left| u \right|^{2} u = i[cD_{x}^{\beta } u + dD_{x}^{\beta } \left( {\left| u \right|^{2} u} \right) + lD_{x}^{\beta } \left( {\left| u \right|^{2} } \right)u,$$
(3)

The Eq. (3) has a wide-range of application in real-life. This equation is used to simulate the dynamics of ultra-short pulses in mode-locked lasers, which are important in spectroscopy and metrology applications. It is also useful for the investigation of the behavior of solitons in nonlinear optical fiber communications and signal processing. As the optical solitons described by this equation have a wide-range of application in technological advancements, many researchers have conducted studies to ascertain soliton solutions of the asserted perturbed NLSE. Wang (2021), Khater et al. (2021), Yépez-Martínez et al. (2022), Osman et al. (2022), Savaissou et al. (2020), Sulaiman et al. (2020), and some others recently investigated the perturbed NLSE.

Though the well-behaved \((G^{\prime}/G\),\(1/G)\)-expansion and the \(F\)-expansion approaches provide admissible optical soliton solutions, to the optimum of our knowledge these approaches have not yet been implemented to the erstwhile model. Thus, the aim of this research is to utilize these two approaches to derive analytical soliton solutions to the space–time fractional perturbed NLSE (3) with Kerr-law nonlinearity. The fractional derivative is referred to as the beta fractional derivative. Furthermore, we briefly discuss the applicability of the obtained soliton solutions in relevant disciplines such as optical and plasma physics.

2 Beta fractional derivative

The fractional derivative (FD) is a generalization of the concept of the derivative of integer order, extending the concept to non-integer orders. Fractional calculus has revolutionized the study of differential equations and many scientific fields. Several academics have tried their best to formulate a universal definition of fractional derivative. Consequently, some well-known definitions like the Caputo FD, the Riemann–Liouville FD, the conformable FD, the modified Riemann–Liouville FD, the beta FD, etc. The beta FD is a newly introduced definition, proposed by Atangana and Baleanu (2016). This definition is consistent with all the principles of integer-ordered derivative. The rest of the definitions have some drawbacks to satiate the elementary principles of differentiation. The beta FD is defined as follows. For any function \(q\left( x \right)\), the beta derivative of the function is (Atangana and Baleanu 2016):

$$D_{x}^{\beta } q\left( x \right) = \mathop {\lim }\limits_{\kappa \to 0} \frac{{q\left( {x + \kappa \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{1 - \beta } } \right) - q\left( x \right)}}{\kappa },$$

where \(0 < \beta \le 1\).

3 Methodology

We present the key techniques of the approaches for investigating the fractional nonlinear evolution equations (FNLEEs) in this section. Consider the following FNLEE:

$$P\left( {u,u_{{x_{1} }} ,u_{t} ,u_{{x_{2} }} ,u_{{tx_{1} }} , \ldots ,D_{t}^{\beta } u,D_{{x_{1} }}^{\beta } u, \ldots } \right) = 0,\quad 0 < \beta < 1,$$
(4)

where \(P\) is the polynomial of the unknown function \(u\left( {t,x_{1} ,x_{2} , \ldots } \right)\), \(t\) is the temporal variable, \(x_{1} ,x_{2} , \ldots\), represent spatial variables, and \(\beta\) stands for the order of fractional derivative. The unknown wave function \(u\left( {t,x_{1} ,x_{2} , \ldots } \right)\) is transformed to a function of single variable through a wave transformation. The wave transformation is

$$u\left( {t,x_{1} ,x_{2} , \ldots } \right) = V\left( \zeta \right),\quad \zeta = \frac{{k_{1} }}{\beta }\left( {x_{1} + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \frac{{k_{2} }}{\beta }\left( {x_{2} + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \ldots \pm \frac{v}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } .$$
(5)

Here \(V\left( \zeta \right)\) represents the amplitude of the new wave function, \(v\) and \(k_{i}\) correspond to the wave velocity and wave number, respectively. The application of the transformation (5) to the Eq. (4) yields the ensuing differential equation in \(V\left( \zeta \right)\):

$$L\left( {V,V^{\prime},V^{\prime\prime},V^{\prime\prime\prime}, \ldots } \right) = 0,$$
(6)

where the prime implies the ordinary differentiation of \(V\left( \zeta \right)\) with respect to \(\zeta\).

The different steps are to be followed depending on the approach taken, outlined below:

3.1 The \(({G^{\prime}}/{{G}}\), \(1/{{G}})\)-expansion strategy

  • Step 1: According to this method, the soliton solutions of Eq. (6) can be stated as:

    $$V\left( \zeta \right) = \mathop \sum \limits_{j = 0}^{N} m_{j} \left( {G^{\prime}/G} \right)^{j} + \mathop \sum \limits_{j = 1}^{N} n_{j} \left( {G^{\prime}/G} \right)^{j - 1} (1/G).$$
    (7)

    The value of \(j\) in Eq. (7) must be a positive integer, which is to be estimated through the homogeneous principle of balance. The constants \(m_{j}\), \(n_{j}\) are arbitrary, and \(G = G\left( \zeta \right)\) is the general solution of the second ordered differential equation:

    $$G^{\prime\prime}\left( \zeta \right) + \lambda G\left( \zeta \right) = \mu ,$$
    (8)

    with \({\Upsilon }\left( \zeta \right) = G^{\prime}/G\), \({\Theta }\left( \zeta \right) = 1/G\), and \(\lambda\), \(\mu\) are arbitrary parameters. Subsequently, the following relations can be derived

    $${\text{Y}}^{\prime} = - {\text{Y}}^{2} + \mu \Theta - \lambda ,\quad \Theta^{\prime} = - {\text{Y}}\Theta .$$
    (9)

    There arise three cases for the general solution of Eq. (8) which have been discussed in the following context.

    Case 1. When \(\lambda > 0\), the solution of (8) includes trigonometric functions as follows:

    $$G\left( \zeta \right) = \alpha_{1} \sin \left( {\sqrt \lambda \zeta } \right) + \alpha_{2} \cos \left( {\sqrt \lambda \zeta } \right) + \frac{\mu }{\lambda },$$
    (10)

    along with \({\Theta }^{2} = \frac{{\lambda \left( {{\Upsilon }^{2} - 2\mu {\Theta } + \lambda } \right)}}{{\lambda^{2} {\uprho } - {\upmu }^{2} }}\), \(\rho = \alpha_{1}^{2} + \alpha_{2}^{2}\), and \(\alpha_{1}\), \(\alpha_{2}\) are arbitrary parameters.

    Case 2. When \(\lambda < 0\), the general solution of (8) is constructed in terms of hyperbolic functions of the form:

    $$G\left( \zeta \right) = \alpha_{1} \sinh \left( {\sqrt { - \lambda } \zeta } \right) + \alpha_{2} \cosh \left( {\sqrt { - \lambda } \zeta } \right) + \frac{\mu }{\lambda },$$
    (11)

    together with \({\Theta }^{2} = - \frac{{\lambda \left( {{\Upsilon }^{2} - 2\mu {\Theta } + \lambda } \right)}}{{\lambda^{2} \rho + {\upmu }^{2} }}\), \(\rho = \alpha_{1}^{2} - \alpha_{2}^{2}\), and \(\alpha_{1}\), \(\alpha_{2}\) are arbitrary parameters.

    Case 3. When \(\lambda = 0\), the general solution of Eq. (8) involves rational algebraic functions and holds the form:

    $$G\left( \zeta \right) = \frac{\mu }{2}\zeta^{2} + \alpha_{1} \zeta + \alpha_{2} ,$$
    (12)

    along with \({\Theta }^{2} = \frac{1}{{\alpha_{1}^{2} - 2\mu \alpha_{2} }}\left( {{\Upsilon }^{2} - 2\mu {\Theta }} \right)\), \(\alpha_{1} ,\alpha_{2} =\) arbitrary parameters.

  • Step 2: Putting the values of \(V\left( \zeta \right)\) and its derivatives in Eq. (6), an equation is derived that includes \({\Upsilon }^{{\text{j}}} \left( \zeta \right)\), \({\Theta }^{{\text{j}}} \left( \zeta \right)\), and their derivatives. Now, substituting the values of their derivatives and \({\Theta }^{2} \left( \zeta \right)\), the derivatives and higher order of \({\Theta }\left( \zeta \right)\) are extinguished from the obtained equation.

  • Step 3: Equating the coefficients of \({\Upsilon }^{j} {\Theta }^{i}\) \(\left( {j = 0,1, \ldots N;i = 0,1} \right)\) on both sides of the obtained equation, an algebraic system of equations is attained. Finally, solving these equations, a variety of solutions to the ordinary differential Eq. (6) are attained. Subsequently, by utilizing the wave transformation Eq. (5), our desired exact traveling wave solutions of FNLEE (4) are extracted.

3.2 The strategies of the improved F-expansion method

  • Step 1: In consistent with this method, the solution of Eq. (6) can be expressed in the form:

    $$V\left( \zeta \right) = \mathop \sum \limits_{j = 0}^{N} h_{j} \left( {m + F\left( \zeta \right)} \right)^{j} + \mathop \sum \limits_{j = 1}^{N} r_{j} \left( {m + F\left( \zeta \right)} \right)^{ - j} ,$$
    (13)

    here \(m\), \(h_{j}\), \(r_{j}\) are arbitrary parameters, and \(j\) must be a positive integer, which is to be computed via homogeneous principle of balance. In Eq. (13), \(h_{N}\), and \(r_{N}\) may be individually zero, but they cannot be zero at a time. \(F\left( \zeta \right)\) is the general solution of the Riccati equation:

    $$F^{\prime}\left( \zeta \right) = \sigma + F^{2} \left( \zeta \right).$$
    (14)

    There arise three cases of general solution depending on the values of \(\sigma\). These solutions may be stated as follows:

    $$F\left( \zeta \right) = \left\{ {\begin{array}{*{20}c} { - \sqrt { - \sigma } \tanh \left( {\sqrt { - \sigma } \zeta } \right),\quad \sigma < 0} \\ { - \sqrt { - \sigma } \coth \left( {\sqrt { - \sigma } \zeta } \right),\quad \sigma < 0} \\ {\sqrt \sigma \tan \left( {\sqrt \sigma \zeta } \right), \quad \sigma > 0} \\ { - \sqrt \sigma , \quad \cot \left( {\sqrt \sigma \zeta } \right),\quad \sigma > 0} \\ { - (1/\zeta ), \quad \sigma = 0} \\ \end{array} } \right..$$
    (15)

  • Step 2: Setting the values of \(V\left( \zeta \right)\) and its derivatives in Eq. (6), an equation is derived that contains \(F^{j} \left( \zeta \right)\) and its derivatives. By substituting the value of its derivative from Eq. (14) to the obtained equation, the derivatives are eliminated from the equation. An algebraic system of equations is derived from the computation of the coefficients of \(F^{j} \left( \zeta \right)\) to zero.

  • Step 3: At last the desired analytical solitary wave solutions to Eq. (6) are resulted from the computation of the algebraic system of equations. The solutions of perceived FNLEE are generated by setting these solutions in the wave transformation Eq. (5).

4 Extraction of solutions

This module describes how to apply the previously described methods to the space–time fractional perturbed NLSE. To transform Eq. (3) into a differential equation, we utilize the wave transformation

$$u\left( {x,t} \right) = V\left( \zeta \right)e^{{i\delta \left( {x,t} \right)}} ,$$
(16)

along with \(\zeta = \frac{k}{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{v}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), and \(\delta \left( {x,t} \right) = - \frac{\omega }{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \frac{\eta }{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\).

Thus, the extracted nonlinear equation is

$$\begin{aligned} & - \left( {\eta + \omega \left( {c + a\omega } \right)} \right)V\left( \zeta \right) - \left( { - b + d\omega } \right)V\left( \zeta \right)^{3} - i\left( {ck + v + 2ak\omega } \right)V^{\prime}\left( \zeta \right) \\ \quad - ik\left( {3d + 2l} \right)V\left( \zeta \right)^{2} V^{\prime}\left( \zeta \right) + ak^{2} V^{\prime\prime}\left( \zeta \right) = 0. \\ \end{aligned}$$
(17)

Setting the real and imaginary part of (17) to zero, the following two equations are obtained:

$$\left( { - \eta - c\omega - a\omega^{2} } \right)V\left( \zeta \right) + \left( {b - d\omega } \right){\text{V}}\left( {\upzeta } \right)^{3} + ak^{2} V^{\prime\prime}\left( \zeta \right) = 0.$$
(18)
$$- \left( {ck + v + 2ak\omega + k\left( {3d + 2l} \right)V\left( \zeta \right)^{2} } \right)V^{\prime}\left( \zeta \right) = 0.$$
(19)

From Eq. (19), it can be computed

$$v = - k\left( {c + 2a\omega } \right),\quad d = - (2/3)l.$$
(20)

There remains the real part of the equation, which is to be examined. From the homogeneous balance principle, the obtained result is \(N = 1\). Therefore, the subsequent solutions to the considered equation have been ascertained by utilizing the stated couple of approaches.

4.1 Solutions: Through the \(({G^{\prime}}/{{G}}\),\(1/{\boldsymbol{G}})\)-expansion method

In conformity with this method, the trail solution of (18) can be formulated as:

$$V\left( \zeta \right) = m_{0} + m_{1} {\Upsilon }\left( \zeta \right) + n_{1} {\Theta }\left( \zeta \right),$$
(21)

here \({\Upsilon }\left( \zeta \right) = G^{\prime}/G\), \({\Theta }\left( \zeta \right) = 1/G\), and \(m_{0}\), \(m_{1}\), \(n_{1}\) are arbitrary parameters. Now, following the steps outlined in methodology chapter, we have obtained three sets of solutions for each individual case. The obtained solutions have been discussed as follows:

Category 1. When \(\lambda < 0\), the delivered solutions for this case are:

  • Family 1: \(m_{0} = 0\), \(m_{1} = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt { - \lambda } \sqrt {b - d\omega } }}\), \(n_{1} = \pm \frac{{\sqrt {\mu^{2} + \lambda^{2} \rho } \sqrt {\eta + c\omega + a\omega^{2} } }}{{\lambda \sqrt {b - d\omega } }}\), \(k = \pm \frac{{\sqrt 2 \sqrt { - \left( {\eta + c\omega + a\omega^{2} } \right)} }}{{\sqrt a \sqrt { - \lambda } }}\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 2: \(m_{0} = n_{1} = \mu = 0\), \(m_{1} = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt { - \lambda } \sqrt {b - d\omega } }}\), \(k = \pm \frac{{\sqrt { - \left( {\eta + c\omega + a\omega^{2} } \right)} }}{{\sqrt {2a} { }\sqrt { - \lambda } }}\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 3: \(m_{0} = m_{1} = \mu = 0\), \(n_{1} = \pm \frac{{\sqrt {2\rho } \sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt { - b + d\omega } }}\), \(k = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt a \sqrt { - \lambda } }}\), \(v = - k\left( {c + 2a\omega } \right)\).

Category 2. When \(\lambda > 0\), the obtained solutions are as follows:

  • Family 1: \(m_{0} = 0\), \(m_{1} = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt \lambda \sqrt { - b + d\omega } }}\), \(n_{1} = \pm \frac{{\sqrt { - \mu^{2} + \lambda^{2} \rho } \sqrt {\eta + c\omega + a\omega^{2} } }}{{\lambda \sqrt { - b + d\omega } }}\), \(k = \pm \frac{{\sqrt 2 \sqrt {\eta + c\omega + a\omega^{2} } }}{\sqrt a \sqrt \lambda }\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 2: \(m_{0} = 0\), \(m_{1} = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt \lambda \sqrt { - b + d\omega } }}\), \(n_{1} = 0\), \(\mu = 0\), \(k = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt {2a} \sqrt \lambda }}\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 3: \(m_{0} = 0\), \(m_{1} = 0\), \(n_{1} = \pm \frac{{\sqrt 2 \sqrt \rho \sqrt { - \eta - c\omega - a\omega^{2} } }}{{\sqrt { - b + d\omega } }}\), \(\mu = 0\), \(k = \pm \frac{{\sqrt { - \eta - c\omega - a\omega^{2} } }}{\sqrt a \sqrt \lambda }\), \(v = - k\left( {c + 2a\omega } \right)\).

Category 3. When \(\lambda = 0\), the obtained solutions are:

  • Family 1: \(m_{0} = 0\), \(m_{1} = \pm \frac{{n_{1} }}{{\sqrt {\alpha_{1}^{2} - 2\mu \alpha_{2} } }}\), \(k = \pm \frac{{\sqrt 2 \sqrt { - b + d\omega } n_{1} }}{{\sqrt {a\alpha_{1}^{2} - 2a\mu \alpha_{2} } }}\), \(\eta = - c\omega - a\omega^{2}\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 2: \(m_{0} = 0\), \(m_{1} = 0\), \(n_{1} = n_{1}\), \(k = \pm \frac{{\sqrt { - bn_{1}^{2} + d\omega n_{1}^{2} } }}{{\sqrt 2 \sqrt a \alpha_{1} }}\), \(\eta = - c\omega - a\omega^{2}\), \(\mu = 0\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 3: \(m_{0} = 0\), \(n_{1} = 0\), \(m_{1} = m_{1}\), \(k = \pm \frac{{\sqrt { - bm_{1}^{2} + d\omega m_{1}^{2} } }}{\sqrt 2 \sqrt a }\), \(\eta = - c\omega - a\omega^{2}\), \(\mu = 0\), \(v = - k\left( {c + 2a\omega } \right)\).

Introducing the above assessed values of parameters in (21) and (16), the soliton solutions of the Eq. (3) are derived as:

$$\begin{gathered} u_{11} = \pm \frac{{e^{{i\delta \left( {x,t} \right)}} \sqrt {\eta + c\omega + a\omega^{2} } }}{{\lambda \sqrt {b - d\omega } \left( {\frac{\mu }{\lambda } + \sinh \left( {\zeta \sqrt { - \lambda } } \right)\alpha_{1} + \cosh \left( {\zeta \sqrt { - \lambda } } \right)\alpha_{2} } \right)}} \hfill \\ \left\{ {\sqrt {\mu^{2} + \lambda^{2} \rho } + \lambda \left( {{\text{cosh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{1} + {\text{sinh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{2} } \right)} \right\}, \hfill \\ \end{gathered}$$
(22)

together with \(\zeta = \pm \frac{{\sqrt 2 \sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt { - a} \beta \sqrt { - \lambda } }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and

$$\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }$$
(23)

Here \(\alpha_{1}\), \(\alpha_{2}\), \(\mu\), \(\lambda\) are free parameters, and \(\rho = \alpha_{1}^{2} - \alpha_{2}^{2}\). The subscripts of the solution correspond the category and family numbers, respectively. For instance, to obtain the solution \(u_{11}\), we have utilized the solutions belonging to the category 1 and family 1. Analogously, the rest of the solutions can be formulated as follows:

$$u_{12} \left( {x,t} \right) = \pm e^{{i\delta \left( {x,t} \right)}} \frac{{\sqrt {\eta + c\omega + a\omega^{2} } \left( {{\text{cosh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{1} + {\text{sinh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{2} } \right)}}{{\sqrt {b - d\omega } \left( {{\text{sinh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{1} + {\text{cosh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{2} } \right)}},$$
(24)

with \(\zeta = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt 2 \sqrt { - a} \beta \sqrt { - \lambda } }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{13} \left( {x,t} \right) = \pm \frac{{e^{{i\delta \left( {x,t} \right)}} \sqrt 2 \sqrt \rho \sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt { - b + d\omega } \left( {{\text{sinh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{1} + {\text{cosh}}\left( {\zeta \sqrt { - \lambda } } \right)\alpha_{2} } \right)}},$$
(25)

including \(\zeta = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{{\sqrt a \beta \sqrt { - \lambda } }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{21} = \pm \frac{{e^{i\delta } \sqrt {\eta + c\omega + a\omega^{2} } }}{{\lambda \sqrt { - b + d\omega } \left( {\frac{\mu }{\lambda } + {\text{sin}}\left( {\zeta \sqrt \lambda } \right)\alpha_{1} + {\text{cos}}\left( {\zeta \sqrt \lambda } \right)\alpha_{2} } \right)}}\left\{ {\sqrt { - \mu^{2} + \lambda^{2} \rho } + \lambda \left( {{\text{cos}}\left( {\zeta \sqrt \lambda } \right)\alpha_{1} - {\text{sin}}\left( {\zeta \sqrt \lambda } \right)\alpha_{2} } \right)} \right\},$$
(26)

here \(\zeta = \pm \frac{{\sqrt 2 \sqrt {\eta + c\omega + a\omega^{2} } }}{\sqrt a \beta \sqrt \lambda }\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), \(\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{22} \left( {x,t} \right) = \pm e^{{i\delta \left( {x,t} \right)}} \frac{{\sqrt {\eta + c\omega + a\omega^{2} } \left( {{\text{cos}}\left( {\zeta \sqrt \lambda } \right)\alpha_{1} - {\text{sin}}\left( {\zeta \sqrt \lambda } \right)\alpha_{2} } \right)}}{{\sqrt { - b + d\omega } \left( {{\text{sin}}\left( {\zeta \sqrt \lambda } \right)\alpha_{1} + {\text{cos}}\left( {\zeta \sqrt \lambda } \right)\alpha_{2} } \right)}},$$
(27)

including \(\zeta = \pm \frac{{\sqrt {\eta + c\omega + a\omega^{2} } }}{\sqrt 2 \sqrt a \beta \sqrt \lambda }\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{23} \left( {x,t} \right) = \pm \frac{{e^{{i\delta \left( {x,t} \right)}} \sqrt 2 \sqrt \rho \sqrt { - \eta - c\omega - a\omega^{2} } }}{{\sqrt { - b + d\omega } \left( {{\text{sin}}\left( {\zeta \sqrt \lambda } \right)\alpha_{1} + {\text{cos}}\left( {\zeta \sqrt \lambda } \right)\alpha_{2} } \right)}},$$
(28)

with \(\zeta = \pm \frac{{\sqrt { - \eta - c\omega - a\omega^{2} } }}{\sqrt a \beta \sqrt \lambda }\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\eta \left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{31} \left( {x,t} \right) = \frac{{e^{{i\delta \left( {x,t} \right)}} n_{1} }}{{\frac{{\zeta^{2} \mu }}{2} + \zeta \alpha_{1} + \alpha_{2} }}\left\{ {1 \pm \frac{{\left( {\zeta \mu + \alpha_{1} } \right)}}{{\sqrt {\alpha_{1}^{2} - 2\mu \alpha_{2} } }}} \right\},$$
(29)

together with \(\zeta = \pm \frac{{\sqrt 2 \sqrt { - b + d\omega } n_{1} }}{{\beta \sqrt {a\alpha_{1}^{2} - 2a\mu \alpha_{2} } }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\omega \left( { - c - a\omega } \right)}}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{32} \left( {x,t} \right) = \frac{{e^{{i\delta \left( {x,t} \right)}} n_{1} }}{{\zeta \alpha_{1} + \alpha_{2} }},$$
(30)

with \(\zeta = \pm \frac{{\sqrt { - b + d\omega } n_{1} }}{{\sqrt 2 \sqrt a \alpha_{1} \beta }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\omega \left( { - c - a\omega } \right)}}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

$$u_{33} \left( {x,t} \right) = \frac{{e^{{i\delta \left( {x,t} \right)}} \alpha_{1} m_{1} }}{{\zeta \alpha_{1} + \alpha_{2} }},$$
(31)

here \(\zeta = \pm \frac{{\sqrt { - b + d\omega } n_{1} }}{{\sqrt 2 \sqrt a \alpha_{1} \beta }}\left\{ {\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \left( {c + 2a\omega } \right)\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } } \right\}\), and \(\delta = \frac{{\omega \left( { - c - a\omega } \right)}}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{{\omega \left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } }}{\beta }\).

4.2 Solutions: through the improved F-expansion method

According to this method the solution of the Eq. (18) can be stated as

$$V\left( \zeta \right) = h_{0} + h_{1} \left( {m + F\left( \zeta \right)} \right) + r_{1} \left( {m + F\left( \zeta \right)} \right)^{ - 1} .$$
(32)

Now, applying the strategies narrated in the methodology, the following solution sets have been obtained for different cases of the values of \(\sigma\).

Category 1. When \(\sigma \ne 0\), the following values of parameters are delivered via this method,

  • Family 1: \(h_{0} = - mh_{1}\), \(h_{1} = h_{1}\), \(r_{1} = 0\), \(k = \pm \frac{{h_{1} \sqrt { - b + d\omega } }}{\sqrt 2 \sqrt a }\), \(\eta = - c\omega - a\omega^{2} - h_{1}^{2} \left( {b\sigma - d\sigma \omega } \right)\), \(\omega = \omega\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 2: \(h_{1} = 0\), \(r_{1} = \frac{{ - m^{2} h_{0} - \sigma h_{0} }}{m}\), \(k = \pm \frac{{\sqrt \sigma \sqrt {m^{2} + \sigma } \sqrt { - b + d\omega } h_{0} }}{{m\sqrt {2am^{2} \sigma + 2a\sigma^{2} } }}\), \(\omega = \omega\), \(v = - k\left( {c + 2a\omega } \right)\).

    $$\eta = - \omega \left( {c + a\omega } \right) - \frac{{\sigma \left( {3b + 2l\omega } \right)h_{0}^{2} }}{{3m^{2} }}.$$

  • Family 3: \(m = 0\), \(h_{0} = 0\), \(r_{1} = \pm \sigma h_{1}\), \(h_{1} = h_{1}\), \(k = \pm \frac{{\sqrt { - bh_{1}^{2} + d\omega h_{1}^{2} } }}{\sqrt 2 \sqrt a }\), \(v = - k\left( {c + 2a\omega } \right)\),

    \(\eta = - c\omega - a\omega^{2} - 4b\sigma h_{1}^{2} + 4d\sigma \omega h_{1}^{2}\), \(\omega = \omega\).

  • Family 4: \(m = 0\), \(h_{0} = 0\), \(h_{1} = 0\), \(r_{1} = r_{1}\), \(k = \pm \frac{{\sqrt { - br_{1}^{2} + d\omega r_{1}^{2} } }}{\sqrt 2 \sqrt a \sigma }\), \(\eta = \frac{{ - c\sigma \omega - a\sigma \omega^{2} - br_{1}^{2} + d\omega r_{1}^{2} }}{\sigma }\), \(\omega = \omega\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 5: \(m = \pm \sqrt { - \sigma }\), \(h_{1} = 0\), \(r_{1} = \pm 2\sqrt { - \sigma } h_{0}\), \(\eta = \frac{{ - ab^{2} - bcd - 4ad^{2} k^{2} \sigma }}{{d^{2} }}\), \(\omega = \frac{b}{d}\), \(k = k\), \(h_{0} = h_{0}\), \(v = - k\left( {c + 2a\omega } \right)\).

Category 2. When \(\sigma = 0\), the following sets of solutions are obtained via the proposed method.

  • Family 1: \(m = 0\), \(h_{0} = h_{0}\), \(h_{1} = 0\), \(r_{1} = r_{1}\), \(k = k\), \(\eta = \frac{{ - ab^{2} - bcd}}{{d^{2} }}\), \(\omega = \frac{b}{d}\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 2: \(m = m\), \(h_{0} = - mh_{1}\), \(h_{1} = h_{1}\), \(r_{1} = 0\), \(k = \pm \frac{{\sqrt { - bh_{1}^{2} + d\omega h_{1}^{2} } }}{\sqrt 2 \sqrt a }\), \(\eta = - c\omega - a\omega^{2}\), \(\omega = \omega\), \(v = - k\left( {c + 2a\omega } \right)\).

  • Family 3: \(m = m\), \(h_{0} = h_{0}\), \(h_{1} = 0\), \(r_{1} = - mh_{0}\), \(k = \pm \frac{{\sqrt { - bh_{0}^{2} + d\omega h_{0}^{2} } }}{\sqrt 2 \sqrt a m}\), \(\eta = - c\omega - a\omega^{2}\), \(\omega = \omega\), \(v = - k\left( {c + 2a\omega } \right)\).

Exerting the above-estimated values of parameters in Eqs. (32) and (16), the desired analytical exact traveling solutions have been derived, which are thoroughly discussed below.

Solution set 1: For \(\sigma < 0\), the application of the estimated values of parameters in Eq. (32) and (16) have provided the following solutions:

$$u_{11,1} \left( {x,t} \right) = e^{i\delta } \left\{ { - mh_{1} + h_{1} \left( {m - \sqrt { - \sigma } \tanh \left( {\zeta \sqrt { - \sigma } } \right)} \right)} \right\}.$$
(33)
$$u_{11,1} \left( {x,t} \right) = e^{i\delta } \left\{ { - mh_{1} + h_{1} \left( {m - \sqrt { - \sigma } \coth \left( {\zeta \sqrt { - \sigma } } \right)} \right)} \right\}.$$
(34)
$$u_{12,1} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{ - m^{2} h_{0} - \sigma h_{0} }}{{m\left( {m - \sqrt { - \sigma } \tanh \left( {\zeta \sqrt { - \sigma } } \right)} \right)}}} \right\}.$$
(35)
$$u_{12,1} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{ - m^{2} h_{0} - \sigma h_{0} }}{{m\left( {m - \sqrt { - \sigma } \coth \left( {\zeta \sqrt { - \sigma } } \right)} \right)}}} \right\}.$$
(36)
$$u_{13,1} \left( {x,t} \right) = e^{i\delta } \left\{ { \pm \frac{{\sigma \coth \left( {\zeta \sqrt { - \sigma } } \right)h_{1} }}{{\sqrt { - \sigma } }} - \sqrt { - \sigma } h_{1} \tanh \left( {\zeta \sqrt { - \sigma } } \right)} \right\}.$$
(37)
$$u_{13,1} \left( {x,t} \right) = e^{i\delta } \left\{ { - \sqrt { - \sigma } \coth \left( {\zeta \sqrt { - \sigma } } \right)h_{1} \pm \frac{{\sigma h_{1} \tanh \left( {\zeta \sqrt { - \sigma } } \right)}}{{\sqrt { - \sigma } }}} \right\}.$$
(38)
$$u_{14,1} \left( {x,t} \right) = e^{i\delta } \left\{ { - \frac{{{\text{coth}}(\zeta \sqrt { - \sigma } r_{1} }}{{\sqrt { - \sigma } }}} \right\}.$$
(39)
$$u_{14,1} \left( {x,t} \right) = e^{i\delta } \left\{ { - \frac{{{\text{tanh}}(\zeta \sqrt { - \sigma } r_{1} }}{{\sqrt { - \sigma } }}} \right\}.$$
(40)
$$u_{15,1} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{2\sqrt { - \sigma } h_{0} }}{{\sqrt { - \sigma } \pm \sqrt { - \sigma } \tanh \left( {\zeta \sqrt { - \sigma } } \right)}}} \right\}.$$
(41)
$$u_{15,1} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{2\sqrt { - \sigma } h_{0} }}{{\sqrt { - \sigma } \pm \sqrt { - \sigma } \coth \left( {\zeta \sqrt { - \sigma } } \right)}}} \right\}.$$
(42)

Here \(\zeta = \frac{k}{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{v}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), \(\delta = - \frac{\omega }{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \frac{\eta }{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), and the subscripts of the solutions represent the category, family and solution set numbers, respectively.

Solution set 2. For \(\sigma > 0\), the execution of the derived values as asserted in the category 1 in Eqs. (32) and (16) have yielded the following solutions:

$$u_{11,2} \left( {x,t} \right) = e^{i\delta } \{ - mh_{1} + h_{1} \left( {m + \sqrt \sigma {\text{tan}}\left( {\zeta \sqrt \sigma } \right)} \right),$$
(43)
$$u_{11,2} \left( {x,t} \right) = e^{i\delta } \left\{ { - mh_{1} + \left( {m - \sqrt \sigma \cot \left( {\zeta \sqrt \sigma } \right)} \right)h_{1} } \right\},$$
(44)
$$u_{12,2} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{ - m^{2} h_{0} - \sigma h_{0} }}{{m\left( {m + \sqrt \sigma {\text{tan}}\left( {\zeta \sqrt \sigma } \right)} \right)}}} \right\}.$$
(45)
$$u_{12,2} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} + \frac{{ - m^{2} h_{0} - \sigma h_{0} }}{{m\left( {m - \sqrt \sigma \cot \left( {\zeta \sqrt \sigma } \right)} \right)}}} \right\}.$$
(46)
$$u_{13,2} \left( {x,t} \right) = e^{i\delta } \left\{ { - \sqrt \sigma \cot \left( {\zeta \sqrt \sigma } \right)h_{1} \pm \sqrt \sigma h_{1} \tan \left( {\zeta \sqrt \sigma } \right)} \right\}.$$
(47)
$$u_{14,2} \left( {x,t} \right) = e^{i\delta } \left\{ { - \frac{{r_{1} \tan \left( {\zeta \sqrt \sigma } \right)}}{\sqrt \sigma }} \right\}.$$
(48)
$$u_{14,2} \left( {x,t} \right) = e^{i\delta } \left\{ {\frac{{r_{1} \cot \left( {\zeta \sqrt \sigma } \right)}}{\sqrt \sigma }} \right\}.$$
(49)

Here \(\zeta = \frac{k}{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{v}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), \(\delta = - \frac{\omega }{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \frac{\eta }{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), and the subscripts of the solutions represent the category, family and solution number, respectively.

Solution set 3. For \(\sigma = 0\), the application of the estimated values of parameters asserted in category 2 in Eqs. (32) and (16) have provided the following solutions:

$$u_{21,3} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} - \zeta r_{1} } \right\}.$$
(50)
$$u_{22,3} \left( {x,t} \right) = e^{i\delta } \left\{ { - mh_{1} + \left( {m - \frac{1}{\zeta }} \right)h_{1} } \right\}.$$
(51)
$$u_{23,3} \left( {x,t} \right) = e^{i\delta } \left\{ {h_{0} - \frac{{mh_{0} }}{{m - \frac{1}{\zeta }}}} \right\}.$$
(52)

Here \(\zeta = \frac{k}{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } - \frac{v}{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), \(\delta = - \frac{\omega }{\beta }\left( {x + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta } + \frac{\eta }{\beta }\left( {t + \frac{1}{{{\Gamma }\beta }}} \right)^{\beta }\), and the subscripts of the solutions represent the category, family and solution number respectively.

5 Comparison of the results

In this section, the derived results in this article are compared to the results of previous literature to confirm the originality of the obtained solutions. The comparison is provided in the Tables 1 and 2 given below:

Table 1 Comparison of the obtained results with the former results reported in Sulaiman et al. (2020)
Full size table
Table 2 Comparison of the obtained results with the former results reported in Wang (2021)
Full size table

From the above tables, it can be observed that some of the attained solutions may be resemble existing solutions from previous research, depending on the selection of appropriate parameter values. However, the governing structures of obtained solutions are novel. Additionally, several of the solutions obtained in this article do not match the results of any previous studies for any choice of parameter values. Therefore, it can be concluded that we have obtained several novel soliton solutions for the concerned equation that have not been reported any prior articles.

6 Graphical representations

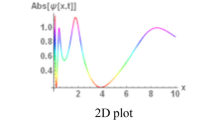
This section represents the graphical structures of the obtained solutions. The three- and two-dimensional graphs, contour plots of the solutions have been sketched for the range \(0 \le x \le 10\) and \(0 \le t \le 10\). The two-dimensional plot is drawn for the different values of \(\beta\) (fractional order) to comprehend the influence of the fractional derivative.

6.1 Plots of the solutions obtained through \(\left( {G^{\prime}/G,1/G} \right)\)-expansion method.

See Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.

Fig. 1
figure 1

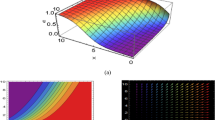
Plot of modulus of solution (23)

Full size image
Fig. 2
figure 2

Plot of modulus of solution (24)

Full size image
Fig. 3
figure 3

Plot of real part of solution (24)

Full size image
Fig. 4
figure 4

Plot of imaginary part of solution (24)

Full size image
Fig. 5
figure 5

Plot of modulus of solution (25)

Full size image
Fig. 6
figure 6

Plot of imaginary part of solution (25)

Full size image
Fig. 7
figure 7

Plot of modulus of solution (26)

Full size image
Fig. 8
figure 8

Plot of modulus of solution (27)

Full size image
Fig. 9
figure 9

Plot of modulus of solution (29)

Full size image
Fig. 10
figure 10

Plot of modulus of solution (30)

Full size image

6.2 Plots of the solutions obtained through improved \({{F}}\)-expansion method

See Figs. 11, 12 and 13.

Fig. 11
figure 11

Plot of modulus of solution (33)

Full size image
Fig. 12
figure 12

Plot of modulus of solution (35)

Full size image
Fig. 13
figure 13

Plot of modulus of solution (46)

Full size image

7 Results and discussion

This section contains the discussion of the properties, usefulness, and applications of the obtained results in this article. The modulus of solution (23) includes first degree hyperbolic functions and represents a periodic soliton for the apt values of parameters \(\eta = - 2.81\), \(c = - 8.38\), \(\omega = - 0.34\), \(a = - 4.02\), \(b = 2.34\), \(n_{1} = - 1.47\), \(\lambda = - 5\), \(\mu = - 5\), \(\alpha_{1} = - 7.3\), \(\alpha_{2} = 5.6\), \(l = 15\). Periodic soliton is a robust and effective soliton in communication engineering, fluid dynamics and many other fields. It is a self-reinforcing solitary wave that is characterized by their stable, long-lasted, and periodic structures. In optical fiber communication, it is used in high-speed telecommunications to transmit data over long distances without distortion, to control the propagation of light in photonic crystal, to control signal processing system, and many others. It is a highly nonlinear solitons, which means that its properties depend on amplitude. As we can see from Fig. 1 that the amplitude of the wave is broadened proportionally with the decreasing value of \(\beta\) (order of fractional derivative), and finally lost its stability. Therefore, fractional derivative has an effective influence on the characteristics of soliton solutions. Figure 2 contains the diagram of the modulus of solution (24) which is drawn for the values \(\eta = - 0.26\), \(c = - 3.6\), \(\omega = - 0.18\), \(a = - 4.36\), \(b = - 10\), \(n_{1} = 0.96\), \(\lambda = - 4.86\), \(\alpha_{1} = - 7.45\), \(\alpha_{2} = - 7.8\), \(l = 13.2\). The modulus of solution (23) exhibits an anti-peakon soliton for \(\beta = 0.99\), and turns to a flat-kink soliton for \(\beta = 0.1\). Unlike peakon solitons, anti-peakon solitons have a sharp trough rather than crest. Although these solitons have discontinuous first derivatives at the negative peak, they are analytical functions. Anti-peakon solitons are particularly used for modeling waves in shallow water, traffic flow, and certain types of data analysis. In optics, this type of solitons is used for manipulating optical signals in nonlinear optical medium, generating high-speed optical pulses, and compensating dispersion effect. Figure 3 is plotted to represent the real part of solution (23), whereas Fig. 4 is drawn to illustrate the imaginary part of solution (23). The real part is drawn for the values \(\eta = 1.92\), \(c = - 2.76\), \(\omega = - 1.18\), \(a = - 0.72\), \(b = - 2.76\), \(n_{1} = - 0.88\), \(\lambda = - 4.24\), \(\alpha_{1} = 7.15\), \(\alpha_{2} = 8.62\), \(l = - 12.05\). In the meanwhile, the imaginary part is drawn for the values \(\eta = - 2.18\), \(c = - 1.6\), \(\omega = - 1.68\), \(a = - 0.09\), \(b = 2.5\), \(n_{1} = 2.46\), \(\lambda = - 2.595\), \(\alpha_{1} = - 10.95\), \(\alpha_{2} = 0.32\), \(l = 0.1\). From these figures we can observe that both of the real and imaginary parts of solution (23) present periodic solitons with some different properties. The real part exhibits a periodic soliton, whereas the imaginary part shows a singular periodic soliton. The modulus of solution (25) presents a periodic-peakon soliton as shown in Fig. 5, which is drawn for the values \(\eta = - 0.51\), \(c = - 0.84\), \(\omega = - 3.7\), \(a = - 0.17\), \(b = 5.94\), \(n_{1} = - 3.18\), \(\lambda = - 3.18\), \(\alpha_{1} = 5.65\), \(\alpha_{2} = - 0.84\), \(l = 9.75\). Figure 6 portrays the graphical features of the imaginary part of solution (25), that is plotted for \(\eta = 1.8\), \(c = 0.66\), \(\omega = - 0.34\), \(a = 2.17\), \(b = - 0.26\), \(n_{1} = - 3.27\), \(\lambda = - 1.57\), \(\alpha_{1} = - 9.45\), \(\alpha_{2} = - 10\), \(l = - 15\). The imaginary part of solution (25) presents a breather soliton. Breather solitons are time-periodic solutions with a well-defined period in non-linear system. This type of soliton has potential applications in real life problems such as data transmission over long distances through optical fibers, the study of the properties of high-temperature superconductors, the development of new types of biosensors, the control of the behavior of nanoscale devices, the development of new types of energy efficient devices, and many others. They are typically characterized by a single peak or hump in their amplitude, which travels through the medium without spreading out or changing shape as shown in two-dimensional diagram of the Fig. 6. Figure 7 is drawn to illustrate the modulus of solution (26). As we can observe that the modulus of solution (26) exhibits a singular bell-shaped soliton for the values \(\eta = 1.38\), \(c = 1.66\), \(\omega = 1.66\), \(a = - 0.8\), \(b = 3.42\), \(n_{1} = 4.72\), \(\lambda = 0.1\), \(\mu = - 1\), \(\alpha_{1} = 15\), \(\alpha_{2} = - 8.12\), \(l = 1.1\), and \(\beta = 0.99\). But it turns to a bell-shaped soliton for \(\beta = 0.5\), and becomes irregular at \(\beta = 0.1\). Singular solution has narrow scope to apply in any physical problems. Therefore, the solution is not applicable in real life problems for the value \(\beta = 0.99\) under the certain values of parameters as stated above. Figure 8 is drawn for the values \(\eta = 0.21\), \(c = 0.1\), \(\omega = 0.42\), \(a = - 1.13\), \(b = 3.84\), \(n_{1} = - 1.09\), \(\lambda = 5.98\), \(\alpha_{1} = - 15\), \(\alpha_{2} = - 10\), \(l = 11.55\) to demonstrate the graphical feature of the modulus solution (27), and Fig. 9 is drawn for the values \(\eta = - 0.92\), \(c = 2.5\), \(\omega = 0.92\), \(a = - 1.93\), \(b = 4\), \(n_{1} = - 5\), \(\mu = - 5\), \(\alpha_{1} = 7.4\), \(\alpha_{2} = - 3.78\), \(l = - 15\) to demonstrate the physical characteristics of the modulus of solution (29). The modulus of these solutions represents anti-bell-shaped and bell-shaped solitons, respectively. Bell-shaped solitons have a Gaussian profile that means the amplitude of the wave is highest at the center and decrease gradually towards the edges. In contrast, anti-bell-shaped soliton has minimum amplitude at the center and increase gradually towards edges. Bell-shaped soliton is used in optics to transmit data in long distance without the need for signal regeneration due to its properties of maintaining shape and velocity over long distance. Beside it has applications fluid dynamics, quantum optics, plasma physics, and many other fields. Figure 10 contains the diagram of modulus of the solution (30) which is drawn for the values \(\eta = - 3.9\), \(c = 6.78\), \(\omega = - 0.84\), \(a = 4.68\), \(b = 5.68\), \(n_{1} = 1.13\), \(\alpha_{1} = - 11.8\), \(\alpha_{2} = - 3.7\), \(l = 8.15\). The modulus of the solution (30) describes a compacton, which is a soliton with compact support and finite energy. It is well-stable solution that means small perturbations to the solution do not cause it to break apart. It has significant applications in optical fiber communications, plasma physics, fluid dynamics, tsunami wave’s studies, and others.

Figure 11 is drawn for the values \(m = 10\), \(c = - 1.94\), \(\omega = 1.16\), \(a = 0.41\), \(b = - 3.02\), \(h_{1} = 0.04\), \(\rho = - 4.84\), \(l = - 6.05\), which portrays physical properties the modulus of solution (33). From this figure, it is observed that the solution exhibits a V-shaped soliton for the chosen values of parameters. V-shaped soliton has a sharp trough as like peakons. It is a well-stable soliton, and retrains its shape and velocity after the collision with other solitons. V-shaped soliton has significant applications in the study of wave behavior of microscopic particles in plasma physics and optics. Additionally, this type of soliton is observed in fluid dynamics. Figure 12 includes the graphs of the modulus of solution (35), which is drawn for the values \(m = - 5.3\). \(c = - 0.76\), \(\omega = - 0.1\), \(a = - 0.55\), \(b = - 0.1\), \(h_{0} = - 2.47\), \(\rho = - 7.24\), \(l = 5.4\). The modulus of solution (46) is attached to the Fig. 13,which is drawn for the values \(m = 15\), \(c = - 10\), \(\omega = - 1.94\), \(a = - 2.31\), \(b = 9.44\), \(h_{0} = 1.25\), \(\rho = 0.1\), \(l = 11.8\). This solution exhibits a bell-shaped soliton. Bell-shaped soliton provides a constant value as \(t \to \infty\), and goes under a smooth amplitude peak at the center. Therefore, bell-shaped soliton is used to transfer data over long distance without any need of signal amplifier.

8 Conclusion

In this study, we construct assorted optical soliton solutions to the space–time fractional nonlinear perturbed Schrödinger equation exploiting a pair of efficient approaches, namely the \((G^{\prime}/G,1/G)\)-expansion and the improved \(F\)-expansion methods. The solutions contains subjective parameters, and for apposite values of these parameters, certain characteristic solitons, including compacton, periodic soliton, bell-shaped soliton, anti-bell-shaped soliton, V-shaped soliton, kink, complex periodic, and some others, are established. The Tables demonstrated that some of the obtained results are fresh that were not reported in previous literatures. It is established that the fractional derivative has a vital role in the shape, amplitude, velocity, and width of the solitons. The soliton solutions derived in this article have applications in optics, plasma physics, fluid dynamics, and some other scientific fields. The present research highlights the effectiveness and reliability of the adopted approaches and can be put forward to other space–time fractional nonlinear equations important in nonlinear optical fiber communication, signal processing, etc.