1 Introduction

The importance of the nonlinear phenomena has grown in a number of newly established categories, including fiber optic interactions and ionised physics. A particular kind of nonlinear partial differential equations that deal with optical soliton fields are nonlinear Schrödinger equations (NLSE). These include transmission of optical solitons, ultrashort waves, and light waves in fibre optics. The transmission of optical soliton is significantly impacted by the high dispersion. Many scientific disciplines, including biological assessment, plasma, life sciences, image processing, power technology, and electrical transmission, can benefit from the implementation of the dynamical model. The fractional Schrödinger–Hirota equation (FSHE) is an extension of the well-known NLSE that arises in the study of integrable systems and mathematical physics which describes the behavior of quantum mechanical systems (Jaradat and Alquran 2020, 2022; Ali et al. 2022; Ala 2022; Ala and Shaikhova 2022). The FSHE exhibits several key properties and characteristics that distinguish it from the standard Schrödinger equation. One of the most notable features is the presence of fractional derivatives, which introduce memory effects and long-range interactions into the system dynamics. These non-local effects play a crucial role in describing phenomena such as anomalous diffusion and sub-diffusion, which are prevalent in complex physical systems. Additionally, the nonlinear nature of the governing model gives rise to rich dynamical behavior, including soliton solutions and other coherent structures. The inclusion of fractional derivatives enables us a more accurate description of wave propagation in complex media with memory effects. Furthermore, the equation has implications for understanding anomalous diffusion processes in classical and quantum systems, offering insights into phenomena such as sub-diffusion and super-diffusion (Ozdemir et al. 2022; Alquran 2022; Alhami and Alquran 2022).

In literature, different approaches can be apply on this model such as finite differences method (Li and Zeng 2012), the improved tanh function method (Zhang and Xia 2008), the improved complex tanh-function method (Abdusalam 2005), the simplified Hirota’s method (Wazwaz and El-Tantawy 2017), the unified transform method (Fokas 1997), the Jacobi elliptic function expansion method (Zhang 2007), the Adomian Pade technique (Dehghan et al. 2007), the \((G' /G)\)-expansion method (Kudryashov 2010) and many others.

This paper contributes to advancing our understanding of nonlinear wave equations and their applications in various scientific disciplines. Its findings have implications for both theoretical developments in mathematical physics and practical applications in fields such as quantum mechanics, optics, and fluid dynamics. The study provides insights into the dynamics and solutions of this nonlinear equation, shedding light on its unique characteristics and implications for physical systems. In comparing the effectiveness of applied strategies to the governing model, it is evident that both approaches offer valuable tools for obtaining analytical solutions and understanding the behavior of complex physical systems. The Sardar sub-equation method (Alsharidi and Bekir 2023; Rezazadeh et al. 2020) excels in transforming fractional differential equations into manageable systems of ordinary differential equations, while the \(exp(-\psi (\zeta ))\)-expansion method (Hassan et al. 2022; Ferdous et al. 2019) provides a systematic framework for obtaining explicit solutions through algebraic manipulation. According to the authors, these approaches have not yet been implemented in the governing model in literature up to their limited knowledge.

We arrange the article as follows: In the Sect. 2, the governing model is introduced while in Sect. 3, the conformable fractional derivative is defined whereas the detail about the applied strategies are elaborated in Sect. 4. The Sect. 5, deals with the application of analytical techniques while in Sect. 6, the graphical description of solutions is discussed. The conclusions have been drawn at the end.

2 The governing model

The fractional Schrödinger Hirota equation (Du et al. 2023) is given by:

$$\begin{aligned} i\mathcal {O}_t^{\gamma }+\frac{1}{2}\mathcal {O}_{xx}+|\mathcal {O}|^2\mathcal {O}+i\beta \mathcal {O}_{xxx},~~t{\ge }0,~0<\gamma \le 1= & {} 0, \end{aligned}$$
(1)

where \(\mathcal {O}(x,t)\) is the complex envelope of the optical field, \(\beta \) is a real parameter representing the nonlinearity strength, and and denote the partial derivatives with respect to time t and space x, respectively. The fractional derivative term accounts for the dispersive effects in the system (Akram et al. 2023).

The FSHE can be derived from the standard nonlinear Schrödinger equation by considering higher-order dispersion effects which provides a more accurate description of the dynamics of dispersive optical solitons in certain physical systems where higher-order dispersion terms become significant. The study of dispersive optical solitons of the fractional Schrödinger–Hirota equation involves investigating their existence, stability, and propagation characteristics. One important aspect of dispersive optical solitons is their ability to exhibit different types of behavior depending on the value of the nonlinearity parameter \(\beta \). For \(\beta > 0\), bright solitons can exist, which are characterized by a localized intensity peak surrounded by a background field. These solitons can propagate without changing their shape due to a balance between self-focusing nonlinearity and dispersive effects. On the other hand, for \(\beta < 0\), dark solitons can exist, which are characterized by a localized intensity dip surrounded by a higher-intensity background. These solitons can also propagate without changing their shape due to a balance between self-defocusing nonlinearity and dispersive effects (Hirota 2004; Sulaiman et al. 2019).

3 The conformable fractional derivative

Traditional fractional differential equations often require specialized numerical methods that can be computationally expensive and prone to instability. Conformable fractional derivatives, being defined in a more consistent and well-behaved manner, can be discretized using standard numerical techniques, such as finite difference or finite element methods, leading to more efficient and stable algorithms in dealing many complex dynamical models (Machado et al. 2011; Zhao and Luo 2017; Balcı et al. 2019; Gao and Chi 2020). In literature, a variety of fractional derivatives are devised to characterize many crucial physical phenomena, For instance, the modified Riemann–Liouville derivative of Jumarie, for Riemann–Liouville derivative (Podlubny 1999), the conformable derivative of Atangana (Wu et al. 2020), their Caputo derivative (Almeida 2017) or the Beta-derivative (Gurefe 2020), have been used in many applications in different fields of contemporary science and engineering; fractional-order derivatives provide a more suitable illustration (Bekir et al. 2021). Let \(\mathcal {O}\): \([0,\infty )\rightarrow R\), The conformable derivative fractional \(\mathcal {O}\) of an order \(\zeta \) is defined

$$\begin{aligned} \mathcal {O}_{x }^{\zeta }(x)=\displaystyle \lim _{\varepsilon \rightarrow 0} \frac{ \mathcal {O} \left( {\varepsilon x}^{1-\zeta }+x\right) - \mathcal {O} (x)}{\varepsilon }, \end{aligned}$$

for each \(x> 0\) and \(\zeta \in (0,1)\). Additionally, a few characteristics of conformable fractional derivatives are provided

$$\begin{aligned}{} & {} \mathcal {O}_x^{\zeta }(x^{\gamma }) ={\lambda x }^{\gamma -\zeta }, ~~~ \forall \gamma \in R,\\{} & {} \mathcal {O}_x^{\zeta }(\mu (x)+\upsilon (x))= \mathcal {O}_x^{\zeta }\mu (x)+ \mathcal {O}_x^{\zeta }\upsilon (x),\\{} & {} \mathcal {O}_x^{\zeta }(\mu o \upsilon )(x)= x^{1-\zeta }\upsilon (x^{\zeta -1})\upsilon '(t) \mathcal {O}_x^{\zeta }(\mu (x))|_{x=\mu (x)}. \end{aligned}$$

4 Methodology

In this section, a couple of analytical techniques namely the Sardar sub-equation method and the \(\exp (-\psi (\zeta ))\)-expansion method are introduced. One of the key advantages of the Sardar sub-equation method is its ability to handle a wide range of nonlinear fractional differential equations, including the governing model efficiently. By converting the original equation into a system of ordinary differential equations, it becomes feasible to obtain exact analytical solutions or approximate solutions with high accuracy.

4.1 The \(exp(-\psi (\zeta ))\)-expansion method

Consider we have a solution

$$\begin{aligned} \mathcal {V}(\zeta )= & {} \sum _{i=0}^{N}B_i(\exp (-\psi (\zeta )))^i, \end{aligned}$$
(2)

in this equation, \(\psi (\zeta )\) satisfies the given given ordinary differential equation

$$\begin{aligned} \psi '(\zeta )= & {} e^{-\psi (\zeta )}+\hbar e^{\psi (\zeta )}+\varrho , \end{aligned}$$
(3)

where \(\hbar \) and \(\varrho \) are constants. Following cases are applying on Eq. (2)

Case 1 When \(\hbar \ne 0\) and \(\varrho ^2-4\hbar >0\), then

$$\begin{aligned} \psi (\zeta )= & {} \ln \left( -\frac{\sqrt{\varrho ^2-4\hbar }\tanh \left( \frac{\sqrt{\varrho ^2-4\hbar }}{2}(F+\zeta )\right) +\varrho }{2\hbar }\right) , \end{aligned}$$
(4)

Case 2 When \(\hbar \ne 0\) and \(\varrho ^2-4\hbar <0\), then

$$\begin{aligned} \psi (\zeta )= & {} \ln \left( \frac{\sqrt{4\hbar -\varrho ^2}\tan \left( \frac{\sqrt{4\hbar -\varrho ^2}}{2}(F+\zeta )\right) -\varrho }{2\hbar }\right) , \end{aligned}$$
(5)

Case 3 When \(\hbar =0\), \(\varrho \ne 0\) and \(\varrho ^2-4\hbar >0\), then

$$\begin{aligned} \psi (\zeta )= & {} -\ln \left( \frac{\varrho }{\cosh (\varrho (F+\zeta ))+\sinh (\varrho (F+\zeta ))-1}\right) , \end{aligned}$$
(6)

Case 4 When \(\hbar \ne 0\), \(\varrho \ne 0\) and \(\varrho ^2-4\hbar =0\), then

$$\begin{aligned} \psi (\zeta )= & {} \ln \left( -\frac{-2(\varrho (F+\zeta )+2)}{\varrho ^2(F+\zeta )}\right) , \end{aligned}$$
(7)

Case 5 When \(\hbar =0\), \(\varrho =0\) and \(\varrho ^2-4\hbar =0\), then

$$\begin{aligned} \psi (\zeta )= & {} \ln (F+\zeta ), \end{aligned}$$
(8)

where F is a constant of integration.

4.2 The Sardar sub-equation method

Let us consider the solution

$$\begin{aligned} \mathcal {V}(\zeta )= & {} \sum _{i=0}^{N}B_i\psi (\zeta )^i,~~B_n\ne 0, \end{aligned}$$
(9)

in this above equation \(B_0, B_1,\ldots ,B_n\) are real parameters. Also \(\psi (\zeta )\) satisfied the ordinary differential equation, which is

$$\begin{aligned} \psi '(\zeta )^2= & {} \varrho _1+\varrho _2 \psi (\zeta )^2+\varrho _3 \psi (\zeta )^4, \end{aligned}$$
(10)

from the Eq. (10), we obtained the following results:

Case 1 When \(\varrho _2>0\) and \(\varrho _1=0\),

$$\begin{aligned} \begin{matrix} \psi _1^{\pm } (\zeta )&{}=&{}\pm \,\sqrt{-fg\varrho _2}\sec h_{fg}(\sqrt{\varrho _2}\zeta ),\\ \psi _2^{\pm } (\zeta )&{}=&{}\pm \,\sqrt{fg\varrho _2}\csc h_{fg}(\sqrt{\varrho _2}\zeta ), \end{matrix} \end{aligned}$$
(11)

Case 2 When \(\varrho _2<0\) and \(\varrho _1=0\),

$$\begin{aligned} \begin{matrix} \psi _3^{\pm } (\zeta )&{}=&{}\pm \,\sqrt{-fg\varrho _2}\sec _{fg}(\sqrt{-\varrho _2}\zeta ),\\ \psi _4^{\pm } (\zeta )&{}=&{}\pm \,\sqrt{-fg\varrho _2}\csc _{fg}(\sqrt{-\varrho _2}\zeta ), \end{matrix} \end{aligned}$$
(12)

Case 3 When \(\varrho _2<0\) and \(\varrho _1=\frac{\varrho _2^2}{4}\),

$$\begin{aligned} \psi _5^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{-\varrho _2}{2}}\tan h_{fg}\left( \sqrt{\frac{-\varrho _2}{2}}\zeta \right) , \nonumber \\ \psi _6^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{-\varrho _2}{2}}\cot h_{fg}\left( \sqrt{\frac{-\varrho _2}{2}}\zeta \right) , \nonumber \\ \psi _7^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{-\varrho _2}{2}}\left( \tan h_{fg}(\sqrt{-2\varrho _2}\zeta )+i\sqrt{ef}\sec h_{fg}(\sqrt{-2\varrho _2}) \right) , \nonumber \\ \psi _8^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{-\varrho _2}{2}}\left( \cot h_{fg}(\sqrt{-2\varrho _2}\zeta )+\sqrt{ef}\csc h_{fg}(\sqrt{-2\varrho _2}) \right) , \nonumber \\ \psi _9^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{-\varrho _2}{8}}\left( \cot h_{fg}\left( \sqrt{\frac{-\varrho _2}{8}}\zeta \right) +\tan h_{fg}\left( \sqrt{\frac{-\varrho _2}{8}}\zeta \right) \right) , \end{aligned}$$
(13)

Case 4 When \(\varrho _2>0\) and \(\varrho _1=\frac{\varrho _2^2}{4}\),

$$\begin{aligned} \psi _{10}^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{\varrho _2}{2}}\tan _{fg}\left( \frac{\varrho _2}{2}\zeta \right) , \nonumber \\ \psi _{11}^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{\varrho _2}{2}}\cot _{fg}\left( \frac{\varrho _2}{2}\zeta \right) , \nonumber \\ \psi _{12}^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{\varrho _2}{2}}\left( \tan _{fg}\left( \sqrt{2\varrho _2\zeta }\right) +\sqrt{fg}\sec h_{fg}\left( \sqrt{2\varrho _2\zeta }\right) \right) , \nonumber \\ \psi _{13}^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{\varrho _2}{2}}\left( \cot _{fg}\left( \sqrt{2\varrho _2\zeta }\right) +\sqrt{fg}\csc h_{fg}\left( \sqrt{2\varrho _2\zeta }\right) \right) , \nonumber \\ \psi _{14}^{\pm } (\zeta )= & {} \pm \,\sqrt{\frac{\varrho _2}{2}}\left( \tan _{fg}\left( \sqrt{\frac{\varrho _2}{8}}\zeta \right) +\cot _{fg}\left( \sqrt{\frac{\varrho _2}{8}}\zeta \right) \right) , \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{matrix} \sec h_{fg}&{}=&{}\frac{2}{fe^{\zeta }+ge^{-\zeta }},~~ \csc h_{fg}=\frac{2}{fe^{\zeta }-ge^{-\zeta }}, \\ \sec _{fg}&{}=&{}\frac{2}{fe^{i\zeta }+ge^{-i\zeta }},~~ \csc _{fg}=\frac{2i}{fe^{i\zeta }-ge^{-i\zeta }}, \\ \tan h_{fg}&{}=&{}\frac{fe^{\zeta }-ge^{-\zeta }}{fe^{\zeta }+ge^{-\zeta }},~~ \cot h_{fg}=\frac{fe^{\zeta }+ge^{-\zeta }}{fe^{\zeta }-ge^{-\zeta }}, \\ \tan _{fg}&{}=&{}-i\frac{fe^{i\zeta }-ge^{-i\zeta }}{fe^{i\zeta }+ge^{-i\zeta }},~~ \cot _{fg}=\frac{fe^{i\zeta }+ge^{-i\zeta }}{fe^{i\zeta }-ge^{-i\zeta }}. \end{matrix} \end{aligned}$$

in these above equations f and g are real constant.

5 Soliton development

Consider the wave transformation

$$\begin{aligned} \mathcal {O}(x,t)=\mathcal {V}(\zeta )e^{-i \lambda },~~~\zeta =x-\frac{2 n }{\gamma }t^{\gamma },~~~\lambda =n x+\frac{K }{\gamma }t^{\gamma }, \end{aligned}$$
(15)

by putting Eq. (15) in Eq. (1) then we obtained the ordinary differential equation

$$\begin{aligned} \frac{3}{2}\mathcal {V}''(\zeta )+\mathcal {V}(\zeta )^3-\left( K+\frac{5}{54 \beta }\right) \mathcal {V}(\zeta )= & {} 0, \end{aligned}$$
(16)

5.1 Applications of the \(exp(-\psi (\zeta ))\)-expansion method

Step 1 By the help of balancing principle, we attained the homogenous balance \(N=1\), Eq. (2) reduces to

$$\begin{aligned} \mathcal {V}(\zeta )=B_0+B_1 e^{\psi (\zeta )}. \end{aligned}$$
(17)

Step 2 Plugging Eq. (17) along Eq. (3) in Eq. (16) and then expand. After expanding, we collect the coefficient of similar power and skip the \(e^{i\psi (\zeta )}\).

Step 3 We gained the system of algebraic equations, which are

$$\begin{aligned}{} & {} -\frac{5 B_0}{54 \beta }-B_0 K+\frac{3}{2} B_1 \varrho \hbar +B_0^3=0,\\{} & {} -\frac{5 B_1}{54 \beta }-B_1 K+\frac{3 B_1 \varrho ^2}{2}+3 B_1 \hbar +3 B_0^2 B_1=0,\\{} & {} \frac{9 B_1 \varrho }{2}+3 B_0 B_1^2=0, \end{aligned}$$

Step 4 To solve these system of algebraic equations with Mathematica, and attained the values of unknowns.

$$\begin{aligned} \begin{matrix} B_1= i \sqrt{3},~~\varrho = -\frac{2 i B_0}{\sqrt{3}},~~\hbar = \frac{-54 \beta B_0^2+54 \beta K+5}{162 \beta }, \end{matrix} \end{aligned}$$

putting these unknowns along Eq. (15) in Eq. (17) then

Case 1 When \(\hbar \ne 0\) and \(\varrho ^2-4\hbar >0\), then for reducing lengthy equation, we use

$$\begin{aligned}{} & {} \theta _1=\sqrt{-\frac{2 \left( -54 \beta B_0^2+54 \beta K+5\right) }{81 \beta }-\frac{1}{3} 4 B_0^2}, \nonumber \\{} & {} \mathcal {O}_1(x,t)=e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( B_0-\frac{i \left( -54 \beta B_0^2+54 \beta K+5\right) }{27 \sqrt{3} \beta \left( \theta _1 \tanh \left( \frac{1}{2} \theta _1 \left( -\frac{2 n t^{\gamma }}{\gamma }+S+x\right) \right) -\frac{2 i B_0}{\sqrt{3}}\right) }\right) , \end{aligned}$$
(18)

by using here

$$\begin{aligned} \begin{matrix}\theta _2=\sqrt{-\frac{\left( -54 \beta B_0^2+54 \beta K+5\right) {}^2}{26244 \beta ^2}-\frac{8 i B_0}{\sqrt{3}}},~\theta _3= \frac{\left( -54 \beta B_0^2+54 \beta K+5\right) \left( -\frac{2 n t^{\gamma }}{\gamma }+S+x\right) }{162 \beta },\end{matrix} \end{aligned}$$

Case 2 When \(\hbar \ne 0\) and \(\varrho ^2-4\hbar <0\), then

$$\begin{aligned} \mathcal {O}_2(x,t)= & {} e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( B_0+\frac{4 B_0}{-\frac{-54 \beta B_0^2+54 \beta K+5}{162 \beta }+ \theta _2 \tan \left( \frac{1}{2} \theta _2 \left( -\frac{2 n t^{\gamma }}{\gamma }+S+x\right) \right) }\right) , \end{aligned}$$
(19)

Case 3 When \(\hbar =0\), \(\varrho \ne 0\) and \(\varrho ^2-4\hbar >0\), then

$$\begin{aligned} \mathcal {O}_3(x,t)= & {} e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( B_0+\frac{162 i \sqrt{3} \beta \left( \sinh \left( \theta _3\right) +\cosh \left( \theta _3\right) -1\right) }{-54 \beta B_0^2+54 \beta K+5}\right) , \end{aligned}$$
(20)

Case 4 When \(\hbar \ne 0\), \(\varrho \ne 0\) and \(\varrho ^2-4\hbar =0\), then

$$\begin{aligned} \mathcal {O}_4(x,t)= & {} e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( B_0-\frac{i \left( -54 \beta B_0^2+54 \beta K+5\right) {}^2 \left( -\frac{2 n t^{\gamma }}{\gamma }+S+x\right) }{17496 \sqrt{3} \beta ^2 \left( \theta _3+2\right) }\right) , \end{aligned}$$
(21)

Case 5 When \(\hbar =0\), \(\varrho =0\) and \(\varrho ^2-4\hbar =0\), then

$$\begin{aligned} \mathcal {O}_5(x,t)= & {} e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( B_0+\frac{i \sqrt{3}}{-\frac{2 n t^{\gamma }}{\gamma }+S+x}\right) . \end{aligned}$$
(22)

5.2 Applications of the Sardar sub-equation method

Step 1 We find the homogenous balance which is \(N=1\) and put in Eq. (9) then we gained

$$\begin{aligned}{} & {} \mathcal {V}(\zeta ) = B_0+B_1\psi (\zeta ), \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \psi '(\zeta )^2 = \varrho _1+\varrho _2 \psi (\zeta )^2+\varrho _3 \psi (\zeta )^4, \end{aligned}$$
(24)

putting Eq. (23) along Eq. (24) in Eq. (16).

Step 2 We collect the expanding terms with power of \(\psi ^i (\zeta )\) the we get system of algebraic equations.

$$\begin{aligned}{} & {} -\frac{5 B_0}{54 \beta }-B_0 K+B_0^3 = 0,\\{} & {} -\frac{5 B_1}{54 \beta }-B_1 K+\frac{3 B_1 \varrho _2}{2}+3 B_1 B_0^2 = 0,\\{} & {} 3 B_1 \varrho _3+B_1^3 = 0, \end{aligned}$$

Step 3 By the Mathematica software, we solve these equations and got the values of unknowns.

$$\begin{aligned} \begin{matrix} B_0= \frac{i \sqrt{-54 \beta K-5}}{3 \sqrt{6} \sqrt{\beta }},~B_1= i \sqrt{3} \sqrt{\varrho _3},~\varrho _2= -\frac{2 (54 \beta K+5)}{81 \beta }, \end{matrix} \end{aligned}$$

putting these unknowns along Eq. (15) in Eq. (23) then

Case 1 When \(\varrho _2>0\) and \(\varrho _1=0\), substituting

$$\begin{aligned}{} & {} \tau _1 = e^{\frac{1}{9} \sqrt{2} \sqrt{-\frac{54 \beta K+5}{\beta }} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) }, \nonumber \\{} & {} \mathcal {O}_6(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{2 i \sqrt{\frac{2}{3}} \sqrt{\varrho _3} \sqrt{-\frac{f g (54 \alpha K+5)}{\alpha }}}{3 \left( f e^{\tau _1}+g e^{-\tau _1}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \mathcal {O}_7(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{4 i \sqrt{\varrho _3}\left( -\frac{54 \alpha K+5}{\alpha }\right) \sqrt{fg} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) }{27 \sqrt{3} \left( f e^{\tau _1}-g e^{-\tau _1}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) . \end{aligned}$$
(26)

Case 2 When \(\varrho _2<0\) and \(\varrho _1=0\),

$$\begin{aligned}{} & {} \tau _2 = \frac{1}{9} i \sqrt{2} \sqrt{\frac{54 \beta K+5}{\beta }} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) , \nonumber \\{} & {} \mathcal {O}_8(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{2 i \sqrt{\frac{2}{3}} \sqrt{\varrho _3} \sqrt{\frac{f g (54 \alpha K+5)}{\alpha }}}{3 \left( f e^{\tau _2}+g e^{-\tau _2}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \mathcal {O}_9(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}-\frac{2 \sqrt{\frac{2}{3}} \sqrt{\varrho _3} \sqrt{\frac{f g (54 \alpha K+5)}{\alpha }}}{3 \left( f e^{\tau _2}-g e^{-\tau _2}\right) }\right) . \end{aligned}$$
(28)

Case 3 When \(\varrho _2<0\) and \(\varrho _1=\frac{\varrho _2^2}{4}\),

$$\begin{aligned}{} & {} \tau _3 = \frac{\sqrt{\frac{54 \beta K+5}{\beta }} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) }{9 \sqrt{2}},~\tau _4=\frac{2}{9} \sqrt{\frac{54 \beta K+5}{\beta }} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) , \nonumber \\{} & {} \mathcal {O}_{10}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{\frac{54 \alpha K+5}{\alpha }} \left( f e^{\tau _3}-g e^{-\tau _3}\right) }{3 \sqrt{6} \left( f e^{\tau _3}+g e^{-\tau _3}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \mathcal {O}_{11}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{\frac{54 \alpha K+5}{\alpha }} \left( f e^{\tau _3}+g e^{-\tau _3}\right) }{3 \sqrt{6} \left( f e^{\tau _3}-g e^{-\tau _3}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \mathcal {O}_{12}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{\frac{54 \alpha K+5}{\alpha }} \left( \frac{f e^{\tau _4}-g e^{-\tau _4}}{f e^{\tau _4}+g e^{-\tau _4}}+\frac{2 i \sqrt{f g}}{f e^{\tau _4}+g e^{-\tau _4}}\right) }{3 \sqrt{6}}+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \mathcal {O}_{13}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{\frac{54 \alpha K+5}{\alpha }} \left( \frac{f e^{\tau _4}+g e^{-\tau _4}}{f e^{\tau _4}-g e^{-\tau _4}}+\frac{2 i \sqrt{f g}}{f e^{\tau _4}-g e^{-\tau _4}}\right) }{3 \sqrt{6}}+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \mathcal {O}_{14}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \sqrt{\frac{54 \alpha K+5}{\alpha }}\left( \frac{i \sqrt{\varrho _3} \left( \frac{f e^{\frac{1}{4}}+g e^{-\frac{1}{4}}}{f e^{\frac{1}{4}}-g e^{-\frac{1}{4}}}+\frac{i \sqrt{f g} \left( f e^{\frac{1}{4}}-g e^{-\frac{1}{4}}\right) }{f e^{\frac{1}{4}}+g e^{-\frac{1}{4}}}\right) }{6 \sqrt{3}}-\frac{1}{3 \sqrt{6} }\right) . \end{aligned}$$
(33)

Case 4 When \(\varrho _2>0\) and \(\varrho _1=\frac{\varrho _2^2}{4}\),

$$\begin{aligned}{} & {} \tau _5 = \frac{1}{9} i \sqrt{-\frac{54 \beta K+5}{\beta }} \left( x-\frac{2 n t^{\gamma }}{\gamma }\right) , \nonumber \\{} & {} \mathcal {O}_{15}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{-\frac{54 \alpha K+5}{\alpha }} \left( f e^{\tau _5}-g e^{-\tau _5}\right) }{3 \sqrt{3} \left( f e^{\tau _5}+g e^{-\tau _5}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(34)
$$\begin{aligned}{} & {} \mathcal {O}_{16}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } \left( \frac{i \sqrt{\varrho _3} \sqrt{-\frac{54 \alpha K+5}{\alpha }} \left( f e^{\tau _5}+g e^{-\tau _5}\right) }{3 \sqrt{3} \left( f e^{\tau _5}-g e^{-\tau _5}\right) }+\frac{i \sqrt{-54 \alpha K-5}}{3 \sqrt{6} \sqrt{\alpha }}\right) , \end{aligned}$$
(35)
$$\begin{aligned}{} & {} \mathcal {O}_{17}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) }i\sqrt{-\frac{54 \alpha K+5}{\alpha }} \left( \frac{i \sqrt{\varrho _3} \left( \frac{f e^{2\tau _5}-g e^{-2\tau _5}}{g e^{-2\tau _5}+f e^{2\tau _5}}+\frac{2 \sqrt{f g}}{g e^{-2\tau _5}+f e^{2\tau _5}}\right) }{3 \sqrt{3}}+\frac{1}{3 \sqrt{6} }\right) , \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \mathcal {O}_{18}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) }i\sqrt{-\frac{54 \alpha K+5}{\alpha }} \left( \frac{i \sqrt{\varrho _3} \left( \frac{g e^{-2\tau _5}+f e^{2\tau _5}}{f e^{2\tau _5}-g e^{-2\tau _5}}+\frac{2 i \sqrt{f g}}{f e^{2\tau _5}-g e^{-2\tau _5}}\right) }{3 \sqrt{3}}+\frac{1}{3 \sqrt{6} }\right) , \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \mathcal {O}_{19}(x,t) = e^{-i \left( \frac{K t^{\gamma }}{\gamma }+n x\right) } i\sqrt{-\frac{54 \alpha K+5}{\alpha }}\left( \frac{i \sqrt{\varrho _3} \left( \frac{f e^{\frac{1}{2}\tau _5}+g e^{-\frac{1}{2}\tau _5}}{f e^{\frac{1}{2}\tau _5}-g e^{-\frac{1}{2}\tau _5}}-\frac{f e^{\frac{1}{2}\tau _5}-g e^{-\frac{1}{2}\tau _5}}{f e^{\frac{1}{2}\tau _5}+g e^{-\frac{1}{2}\tau _5}}\right) }{6 \sqrt{3}}+\frac{1}{3 \sqrt{6} }\right) .\nonumber \\ \end{aligned}$$
(38)

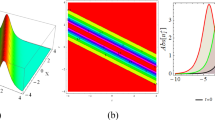
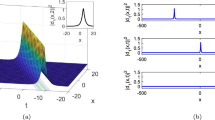
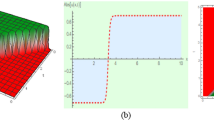
6 Discussion and results

By applying the Sardar sub-equation method and the \(exp(-\psi (\zeta ))\)-expansion method to the fractional Schrödinger–Hirota equation, researchers have obtained valuable insights into the behavior of the system. By employing these mathematical techniques, exact solutions can be derived, shedding light on the dynamics and properties of the underlying physical phenomena. The resulting solutions provide a deeper understanding of the interplay between nonlinearity, fractional derivatives, and other relevant parameters in the equation. Furthermore, the application of these methods allows for the identification of specific regimes or parameter ranges where interesting phenomena such as solitons, periodic waves, or other nonlinear structures emerge. This contributes to the broader theoretical framework for studying complex wave dynamics in physical systems governed by fractional Schrödinger–Hirota equations. The physics of the fractional Schrödinger–Hirota equation encompasses concepts from fractional calculus, nonlinear dynamics, soliton theory, dispersion phenomena, and quantum mechanics. Understanding these aspects provides valuable insights into the behavior of physical systems described by this mathematical model.

Fig. 1
figure 1

The behaviour of singular periodic solution \(|\mathcal {O}_{1}(x,t)|\) for \(\gamma =1,\beta =0.3,K=0.9,S=0.8,B_0=0.1,n=0.1\)

Full size image
Fig. 2
figure 2

The behaviour of bell-shaped singular soliton \(|\mathcal {O}_{2}(x,t)|\) for \(\gamma =1,\beta =0.3,K=0.9,S=0.8,n=0.1,B_0=0.5\)

Full size image
Fig. 3
figure 3

The behaviour of solitary wave structure \(|\mathcal {O}_{6}(x,t)|\) for \( \gamma =1,\beta =0.3,K=0.9,S=0.8,n=0.1,f=0.2,g=0.7,\varrho _3=0.8\)

Full size image
Fig. 4
figure 4

The behaviour of solitary wave structure \(|\mathcal {O}_{7}(x,t)|\) for \(\gamma =1,\beta =0.3,K=0.9,S=0.8,n=0.1,f=0.2,g=0.7,\varrho _3=0.8\)

Full size image
Fig. 5
figure 5

The behaviour of w-shaped periodic wave solution \(|\mathcal {O}_{9}(x,t)|\) for \(\gamma =1,\beta =1,K=0.9,S=0.8,n=0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image
Fig. 6
figure 6

The behaviour of dark wave solution \(|\mathcal {O}_{10}(x,t)|\) for \(\gamma =1,\beta =1,K=0.9,S=0.8,0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image
Fig. 7
figure 7

The behaviour of smooth bright soliton \(|\mathcal {O}_{12}(x,t)|\) for \(\gamma =1,\beta =0.4,K=0.9,S=0.8,n=0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image
Fig. 8
figure 8

The behaviour of anti-kink singular soliton \(|\mathcal {O}_{13}(x,t)|\) for \(\gamma =1,\beta =1,K=0.9,S=0.8,n=0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image
Fig. 9
figure 9

The behaviour of bright soliton \(|\mathcal {O}_{15}(x,t)|\) for \(\gamma =1,\beta =1,K=0.9,S=0.8,n=0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image
Fig. 10
figure 10

The behaviour of anti kink soliton \(|\mathcal {O}_{17}(x,t)|\) for \(\gamma =1,\beta =1,K=0.9,S=0.8,n=0.1,f=0.8,g=0.03,\varrho _3=0.1\)

Full size image

7 Concluding remarks

In this study, we investigated the fractional Schrödinger–Hirota equation analytically which is a nonlinear partial differential equation that combines the fractional Schrödinger equation and the Hirota bilinear form. It provides a generalized framework for studying quantum particles with nonlocal effects and memory effects. The equation supports various soliton solutions, including bright solitons, dark solitons, and rogue waves. Its integrability properties have also been extensively investigated, revealing an infinite number of conservation laws and exact solutions. By utilising the most recent computational strategies, these results are confirmed. The obtained solitons are also explored graphically by using 3D, 2D, and contour plots, for details see Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. Finally, it is proposed that the strategies employed are extremely beneficial, credible, and simple to deal with many other nonlinear dynamical models of recent times. The progress in the supplementary analysis of such models may lead to excel in many emerging fields of research such as telecommunications industry, plasma physics, quantum electronics, fluid dynamics, photonics, fiber optics and other relevant wave guides. The fractional model presents a rich landscape for future research encompassing theoretical developments, numerical analysis, physical applications, and interdisciplinary connections with other fields such as quantum mechanics and nonlinear optics. Exploring these avenues has the potential to deepen our understanding of fundamental wave phenomena and contribute to practical advancements across various scientific and engineering domains.