1 Introduction

One of the featured concepts that was introduced during 2019 is highly dispersive (HD) optical solitons. This happens when in addition to chromatic dispersion (CD), the effects of inter-modal dispersion (IMD), third-order dispersion (3OD), fourth order dispersion (4OD), fifth order dispersion (5OD) and sixth-order dispersion (6OD) effects are all included. This leads to solitons to the governing nonlinear Schrödinger’s equation. There are only four forms of nonlinear refractive index that leads to the retrieval of closed form of a soliton solution (Alshaery et al. 2014; Biswas et al. 2019a, b, c, d, e, f, 2020; Kara et al. 2018; Kohl et al. 2019a, 2020a, b; Kudryashov 2020a, b, c, d; Vega-Guzman et al. 2014; Yanan et al. 2013; Yildirim et al. 2020). These are Kerr law, quadratic-cubic law, non-local law and polynomial law. Today’s paper will study HD solitons, with nonlocal nonlinear form, in polarization-preserving optical fibers.

In this context, it must be noted that with the effect of higher order dispersions, one will naturally encounter the effect of soliton radiation that will lead to the shedding of energy. However, these effects have been discarded and the solitons only in the discrete regime with bound states have been studied. Our numerical scheme is the Laplace-Adomian algorithm that studies bright optical solitons and the accuracy of the scheme is depicted in the error plots are exhibited with impressive measure. After a quick revisitation of the governing model and the algorithmic scheme, the results are enumerated and displayed.

2 Governing equation

The nonlinear Schrödinger’s equation (NLSE) for highly dispersive optical solitons in the presence of a non-local nonlinearity is given by Biswas et al. (2019g, h, i, j), Rehman et al. (2019) and Kohl et al. (2019b):

$$\begin{aligned} iq_{t}+ia_{1}q_{x}+a_{2}q_{xx}+ia_{3}q_{xxx}+a_{4}q_{xxxx}+ia_{5}q_{xxxxx}+a_{6}q_{xxxxxx}+b(\vert q\vert ^{2})_{xx}q=0, \end{aligned}$$
(1)

where \(q=q(x,t)\) is a complex-valued function of x (space) and t (time). In Eq. (1), the first term stands for linear temporal evolution with \(i=\sqrt{-1}\). The next six terms are dispersion terms that make the solitons highly dispersive. These are given by the coefficients of \(a_k\) for \(1\le k\le 6\) which are inter-modal dispersion (IMD), group velocity dispersion (GVD), third-order dispersion (3OD), fourth-order dispersion (4OD), fifth-order dispersion (5OD) and sixth-order dispersion (6OD) respectively. Finally, b is the coefficient of non-local nonlinearity.

2.1 Bright highly dispersive optical solitons

The bright highly dispersive optical soliton solution to (1) was recently reported in Biswas et al. (2019g), using the extended Jacobi’s elliptic function scheme the authors obtain

$$\begin{aligned} q(x,t)=A \text { sech}^2[(x-\nu t)] \times \exp \{i[-\kappa x+\omega t+\theta _0 ]\}. \end{aligned}$$
(2)

In Eq. (2), where \(\nu\) is the speed of the wave, \(\omega\) is its wave number, \(\kappa\) is the soliton frequency and \(\theta _0\) is the phase center constant.

In Biswas et al. (2019g, h), the parameters and constraints for the highly dispersive optical soliton are given by:

  1. (a)

    The relationship between the system parameters are:

    $$\begin{aligned}&\omega =\frac{1260a_{1}\kappa +b\beta _{2}^{2}(25\kappa ^{6}-336\kappa ^{4}+560\kappa ^{2}+768m^{3}+80(7\kappa ^{2}+36)m^{2}-16ml_{1}+768)}{1260}, \end{aligned}$$
    (3)
    $$\begin{aligned}&a_{4}=-\frac{b\beta _{2}^{2}(-75\kappa ^{2}+112(m+1))}{1260}, \qquad \nu =a_{1}-2\kappa (a_{2}+4a_{4}\kappa ^{2}+8a_{5}\kappa ^{3}),\quad A=\beta _{2}m, \end{aligned}$$
    (4)
    $$\begin{aligned}&a_{2}=-\frac{b\beta _{2}^{2}(75\kappa ^{4}-672\kappa ^{2}+560m^{2}-112(6\kappa ^{2}+35)m)+560)}{1260}, \end{aligned}$$
    (5)

    where

    $$\begin{aligned} \beta _{2}^{2}=-\frac{252a_6}{b},\qquad l_{1}=21\kappa ^{4}+245\kappa ^{2}-180, \end{aligned}$$

    and m is any parameter that satisfies the Eqs. (3), (4) and (5).

  2. (b)

    The constraint condition are

    $$\begin{aligned} a_{5}=6a_{6}\kappa ,\qquad a_{3}=\frac{4}{3}\kappa (3a_{4}+5a_{5}\kappa )\qquad \text{ and }\qquad a_{6}b< 0. \end{aligned}$$
    (6)

3 Description of the method applied

The aim of this section is to discuss the use of the Laplace-Adomian decomposition method (LADM) and its algorithm to solve the NLSE (1). The present method was first proposed in Adomian (1994) and Khuri (2001).

Let us look for soliton solutions of Eq. (1) in the form \(q(x,t)=u(x,t)+iv(x,t)\). Then we can decompose the Eq. (1) in its real and imaginary parts, respectively as

$$\begin{aligned}&u_t=-a_{1}u_{x}-a_{2}v_{xx}-a_{3}u_{xxx}-a_{4}v_{xxxx}-a_{5}u_{xxxxx}-a_{6}v_{xxxxxx}-2bv(uu_{xx} +vv_{xx}) \end{aligned}$$
(7)
$$\begin{aligned}&v_t=-a_{1}v_{x}+a_{2}u_{xx}-a_{3}v_{xxx}+a_{4}u_{xxxx}-a_{5}v_{xxxxx}+a_{6}u_{xxxxxx}+2bu(uu_{xx} +vv_{xx}) \end{aligned}$$
(8)

In order to find analytical approximate solutions for Eq. (1) using LADM, we first rewrite the Eqs. (7) and (8) in the following operator form

$$\begin{aligned}&D_{t}u=-a_{1}D^{1}_{x}u-a_{2}D^{2}_{x}v-a_{3}D^{3}_{x}u-a_{4}D^{4}_{x}v-a_{5}D^{5}_{x}u-a_{6}D^{6}_{x}v+N_{1}(u,v) \end{aligned}$$
(9)
$$\begin{aligned}&D_{t}v=-a_{1}D^{1}_{x}v+a_{2}D^{2}_{x}u-a_{3}D^{3}_{x}v+a_{4}D^{4}_{x}u-a_{5}D^{5}_{x}v+a_{6}D^{6}_{x}u+N_{2}(u,v) \end{aligned}$$
(10)

with initial conditions \(u(x,0)=\mathfrak {R}e (q(x,0))\) and \(v(x,0)=\mathfrak {I}m (q(x,0))\).

In the equations system (9)–(10) the operator \(D_{t}\) denotes derivative with respect to t, whereas that \(D^{j}_{x}\) is the \(j-\)th order linear differential operator \(\frac{\partial ^{j}}{\partial x^j}\) and \(N_k\) represents nonlinear differential operators for \(k=1,2\).

The method consists of first applying the Laplace transform \({\mathscr {L}}\) to both sides of equations in system (9)–(10) and then by using initial conditions, we have

$$\begin{aligned}&u(x,s)=\frac{u(x,0)}{s}+\frac{1}{s}{\mathscr {L}}\{-a_{1}D^{1}_{x}u-a_{2}D^{2}_{x}v-a_{3}D^{3}_{x}u-a_{4}D^{4}_{x}v-a_{5}D^{5}_{x}u-a_{6}D^{6}_{x}v+N_{1}(u,v)\} \end{aligned}$$
(11)
$$\begin{aligned}&v(x,s)=\frac{v(x,0)}{s}+\frac{1}{s}{\mathscr {L}}\{-a_{1}D^{1}_{x}v+a_{2}D^{2}_{x}u-a_{3}D^{3}_{x}v+a_{4}D^{4}_{x}u-a_{5}D^{5}_{x}v+a_{6}D^{6}_{x}u+N_{2}(u,v)\} \end{aligned}$$
(12)

Now, applying inverse Laplace transform \({\mathscr {L}}^{-1}\) and initial conditions to system (11) and (12), we get

$$\begin{aligned}&u(x,t)=u(x,0)+{\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-a_{1}D^{1}_{x}u-a_{2}D^{2}_{x}v-a_{3}D^{3}_{x}u-a_{4}D^{4}_{x}v-a_{5}D^{5}_{x}u-a_{6}D^{6}_{x}v+N_{1}(u,v)\}\Big ] \end{aligned}$$
(13)
$$\begin{aligned}&v(x,t)=v(x,0)+{\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-a_{1}D^{1}_{x}v+a_{2}D^{2}_{x}u-a_{3}D^{3}_{x}v+a_{4}D^{4}_{x}u-a_{5}D^{5}_{x}v+a_{6}D^{6}_{x}u+N_{2}(u,v)\}\Big ] \end{aligned}$$
(14)

Now we represent the unknown functions u and v by an infinite series of the form

$$\begin{aligned} u(x,t)=\sum _{n=0}^{\infty }u_{n}(x,t),\qquad v(x,t)=\sum _{n=0}^{\infty }v_{n}(x,t) \end{aligned}$$
(15)

In addition, the nonlinear terms can be written as

$$\begin{aligned} N_{1}(u, v)=-2bv(uu_{xx} +vv_{xx})=-2b\sum _{n=0}^{\infty }A_{n}(u_{0}, u_{1},\ldots ,u_{n};v_{0}, v_{1},\ldots ,v_{n}) \end{aligned}$$
(16)

and

$$\begin{aligned} N_{2}(u, v)= 2bu(uu_{xx} +vv_{xx})=2b\sum _{n=0}^{\infty }B_{n}(u_{0}, u_{1},\ldots ,u_{n};v_{0}, v_{1},\ldots ,v_{n}) \end{aligned}$$
(17)

where \(A_n\) and \(B_n\) are the Adomian’s polynomials (Rach 1984; Wazwaz 2000), which are defined by

$$\begin{aligned}&A_{n}(u_{0},\ldots ,u_{n};v_{0},\ldots ,v_{n})=\frac{1}{n!}\frac{d^{n}}{d\lambda ^{n}}\Big [N_{1}\Big (\sum _{i=1}^{\infty }\lambda ^{i}u_{i};\sum _{i=1}^{\infty }\lambda ^{i}v_{i}\Big ) \Big ]_{\lambda =0},\quad n=0,1,2,\ldots \end{aligned}$$
(18)
$$\begin{aligned}&B_{n}(u_{0},\ldots ,u_{n};v_{0},\ldots ,v_{n})=\frac{1}{n!}\frac{d^{n}}{d\lambda ^{n}}\Big [N_{2}\Big (\sum _{i=1}^{\infty }\lambda ^{i}u_{i};\sum _{i=1}^{\infty }\lambda ^{i}v_{i}\Big ) \Big ]_{\lambda =0},\quad n=0,1,2,\ldots \end{aligned}$$
(19)

On making the substitution of Eqs. (15) and (16) into Eqs. (13) and (14), we can arrive at

$$\begin{aligned}&\sum _{n=0}^{\infty }u_{n}=u(x,0)+{\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})\sum _{n=0}^{\infty }u_{n}-(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})\sum _{n=0}^{\infty }v_{n}-2b\sum _{n=0}^{\infty }A_{n} \}\Big ] \end{aligned}$$
(20)
$$\begin{aligned}&\sum _{n=0}^{\infty }v_{n}=v(x,0)+{\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})\sum _{n=0}^{\infty }v_{n}+(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})\sum _{n=0}^{\infty }u_{n}+2b\sum _{n=0}^{\infty }B_{n}\}\Big ] \end{aligned}$$
(21)

In general, the recursive relations are given by

$$\begin{aligned}&\left\{ \begin{array}{ll} u_{0}(x,t)=\mathfrak {R}e (q(x,0)),\\ u_{n+1}(x,t)={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})u_{n}-(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})v_{n}-2bA_{n} \}\Big ],\;\; n\ge 0, \end{array} \right. \end{aligned}$$
(22)
$$\begin{aligned}&\left\{ \begin{array}{ll} v_{0}(x,t)=\mathfrak {I}m (q(x,0)),\\ v_{n+1}(x,t)={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})v_{n}+(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})u_{n}+2bB_{n}\}\Big ],\;\; n\ge 0. \end{array} \right. \end{aligned}$$
(23)

With the help of the above procedure first few terms of Adomian polynomials \(A_n\) and \(B_n\) can be obtained as

$$\begin{aligned} \begin{aligned} A_{0}&= v_{0xx} v_0^2+u_0 u_{0xx} v_0,\\ A_{1}&= v_{1xx}v_0^2+u_1 u_{0xx} v_0+u_0 u_{1xx} v_0+2 v_1 v_{0xx}v_0+u_0 u_{0xx} v_1,\\ A_{2}&=v_{2xx}v_0^2+u_2 u_{0xx} v_0++u_1 u_{1xx}v_0+u_0 u_{2xx} v_0+2 v_2 v_{0xx} v_0+2 v_1 v_{1xx} v_0+u_{1}u_{0xx}v_{1}+u_{0}u_{1xx}v_{1}\\&\quad +u_{0}u_{0xx}v_{2}+v_{1}^{2}v_{0xx}, \\ A_{3}&=v_{3xx}v_{0}^{2}+u_{3}u_{0xx}v_{0}+u_{2}u_{1xx}v_{0}+u_{1}u_{2xx}v_{0}+u_{0}u_{3xx}v_{0}+2v_{3}v_{0xx}v_{0}+2v_{2}v_{1xx}v_{0}+2v_{1}v_{2xx}v_{0}\\&\quad +u_{2}u_{0xx}v_{1}+u_{1}u_{1xx}v_{1}+u_{0}u_{2xx}v_{1}+u_{1}u_{0xx}v_{2}+u_{0}u_{1xx}v_{2}+u_{0}u_{0xx}v_{3}+2v_{1}v_{0xx}v_{2}+v_{1}^{2}v_{1xx},\\ A_{4}&=v_{4xx}v_{0}^{2}+u_{4}u_{0xx}v_{0}+u_{3}u_{1xx}v_{0}+u_{2}u_{2xx}v_{0}+u_{1}u_{3xx}v_{0}+u_{0}u_{4xx}v_{0}+2v_{4}v_{0xx}v_{0}+2v_{3}v_{1xx}v_{0}\\&\quad +2v_{2}v_{2xx}v_{0}+2v_{1}v_{3xx}v_{0}+u_{3}u_{0xx}v_{1}+u_{2}u_{1xx}v_{1}+u_{1}u_{2xx}v_{1}+u_{0}u_{3xx}v_{1}+u_{2}u_{0xx}v_{2}+u_{1}u_{1xx}v_{2}\\&\quad +u_{0}u_{2xx}v_{2}+u_{1}u_{0xx}v_{3}+u_{0}u_{1xx}v_{3}+u_{0}u_{0xx}v_{4}+2v_{1}v_{0xx}v_{2}+2v_{1}v_{1xx}v_{2}+v_{1}^{2}v_{2xx}+v_{2}^{2}v_{0xx},\\ A_{5}&=v_{5xx}v_{0}^{2}+u_{5}u_{0xx}v_{0}+u_{4}u_{1xx}v_{0}+u_{3}u_{2xx}v_{0}+u_{2}u_{3xx}v_{0}+u_{1}u_{4xx}v_{0}+u_{0}u_{5xx}v_{0}+2v_{5}v_{0xx}v_{0}\\&\quad +2v_{4}v_{1xx}v_{0}+2v_{3}v_{2xx}v_{0}+2v_{2}v_{3xx}v_{0}+2v_{1}v_{4xx}v_{0}+u_{4}u_{0xx}v_{1}+u_{3}u_{1xx}v_{1}+u_{2}u_{2xx}v_{1}+u_{1}u_{3xx}v_{1}\\&\quad +u_{0}u_{4xx}v_{1}+u_{3}u_{0xx}v_{2}+u_{2}u_{1xx}v_{2}+u_{1}u_{2xx}v_{2}+u_{0}u_{3xx}v_{2}+u_{2}u_{0xx}v_{3}+u_{1}u_{1xx}v_{3}+u_{0}u_{2xx}v_{3} +u_{1}u_{0xx}v_{4}\\&\quad +u_{0}u_{1xx}v_{4}+u_{0}u_{0xx}v_{5}+2v_{2}v_{0xx}v_{3}+2v_{1}v_{0xx}v_{4}+2v_{1}v_{1xx}v_{3}+2v_{1}v_{2xx}v_{2}+v_{1}^{2}v_{3xx}+v_{2}^{2}v_{1xx}. \end{aligned} \end{aligned}$$
(24)

and

$$\begin{aligned} \begin{aligned} B_{0}&= u_{0xx} u_0^2+u_0 v_{0xx} v_0,\\ B_{1}&= u_{1xx}u_0^2+u_1 v_{0xx} v_0+u_0 v_{1xx} v_0+2 u_1 u_{0xx}u_0+u_0 v_{0xx} v_1,\\ B_{2}&=u_{2xx}u_0^2+u_2 v_{0xx} v_0+u_1 v_{1xx}v_0+u_0 v_{2xx} v_0+2 u_2 u_{0xx} u_0+2 u_1 u_{1xx} u_0+u_{1}v_{0xx}v_{1}+u_{0}v_{1xx}v_{1}\\&\quad +u_{0}v_{0xx}v_{2}+u_{1}^{2}u_{0xx}, \\ B_{3}&=u_{3xx}u_{0}^{2}+u_{3}v_{0xx}v_{0}+u_{2}v_{1xx}v_{0}+u_{1}v_{2xx}v_{0}+u_{0}v_{3xx}v_{0}+2u_{3}u_{0xx}u_{0}+2u_{2}u_{1xx}u_{0}+2u_{1}u_{2xx}u_{0}\\&\quad +u_{2}v_{0xx}v_{1}+u_{1}v_{1xx}v_{1}+u_{0}v_{2xx}v_{1}+u_{1}v_{0xx}v_{2}+u_{0}v_{1xx}v_{2}+u_{0}v_{0xx}v_{3}+2u_{1}u_{0xx}u_{2}+u_{1}^{2}u_{1xx},\\ B_{4}&=u_{4xx}u_{0}^{2}+u_{4}v_{0xx}v_{0}+u_{3}v_{1xx}v_{0}+u_{2}v_{2xx}v_{0}+u_{1}v_{3xx}v_{0}+u_{0}v_{4xx}v_{0}+2u_{4}u_{0xx}u_{0}+2u_{3}u_{1xx}u_{0}\\&\quad +2u_{2}u_{2xx}u_{0}+2u_{1}u_{3xx}u_{0}+u_{3}v_{0xx}v_{1}+u_{2}v_{1xx}v_{1}+u_{1}v_{2xx}v_{1}+u_{0}v_{3xx}v_{1}+u_{2}v_{0xx}v_{2}+u_{1}v_{1xx}v_{2}\\ &\quad +u_{0}v_{2xx}v_{2}+u_{1}v_{0xx}v_{3}+u_{0}v_{1xx}v_{3}+u_{0}v_{0xx}v_{4}+2u_{1}u_{0xx}u_{2}+2u_{1}u_{1xx}u_{2}+u_{1}^{2}u_{2xx}+u_{2}^{2}u_{0xx},\\ B_{5}&=u_{5xx}u_{0}^{2}+u_{5}v_{0xx}v_{0}+u_{4}v_{1xx}v_{0}+u_{3}v_{2xx}v_{0}+u_{2}v_{3xx}v_{0}+u_{1}v_{4xx}v_{0}+u_{0}v_{5xx}v_{0}+2u_{5}u_{0xx}u_{0}\\&\quad +2u_{4}u_{1xx}u_{0}+2u_{3}u_{2xx}u_{0}+2u_{2}u_{3xx}u_{0}+2u_{1}u_{4xx}u_{0}+u_{4}v_{0xx}v_{1}+u_{3}v_{1xx}v_{1}+u_{2}v_{2xx}v_{1}+u_{1}v_{3xx}v_{1}\\&\quad +u_{0}v_{4xx}v_{1}+u_{3}v_{0xx}v_{2}+u_{2}v_{1xx}v_{2}+u_{1}v_{2xx}v_{2}+u_{0}v_{3xx}v_{2}+u_{2}v_{0xx}v_{3}+u_{1}v_{1xx}v_{3}+u_{0}v_{2xx}v_{3} +u_{1}v_{0xx}v_{4}\\ &\quad +u_{0}v_{1xx}v_{4}+u_{0}v_{0xx}v_{5}+2u_{2}u_{0xx}u_{3}+2u_{1}u_{0xx}u_{4}+2u_{1}u_{1xx}u_{3}+2u_{1}u_{2xx}u_{2}+u_{1}^{2}u_{3xx}+u_{2}^{2}u_{1xx}. \end{aligned} \end{aligned}$$
(25)

Using Eqs. (22) and (23) through the LADM method, we obtain the next recursive algorithm for the real and imaginary part of solution q(x, t), respectively.

$$\begin{aligned} u_{0}(x,t)&=\mathfrak {R}e (q(x,0)),\\ v_{0}(x,t)&=\mathfrak {I}m (q(x,0)),\\ u_{1}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})u_{0}-(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})v_{0}-2bA_{0} \}\Big ], \\ v_{1}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})v_{0}+(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})u_{0}+2bB_{0}\}\Big ],\\ u_{2}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})u_{1}-(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})v_{1}-2bA_{1} \}\Big ], \\ v_{2}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})v_{1}+(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})u_{1}+2bB_{1}\}\Big ],\\ \vdots \\ u_{n}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})u_{n-1}-(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})v_{n-{^\mathrm{o}}}-2bA_{n-1} \}\Big ],\\ v_{n}(x,t)&={\mathscr {L}}^{-1}\Big [\frac{1}{s}{\mathscr {L}}\{-(a_{1}D^{1}_{x}+a_{3}D^{3}_{x}+a_{3}D^{5}_{x})v_{n-1}+(a_{2}D^{2}_{x}+a_{4}D^{4}_{x}+a_{6}D^{6}_{x})u_{n-1}+2bB_{n-1}\}\Big ]. \end{aligned}$$

The approach introduced above will illustrated through examples in the following section. All our computations are performed by MATHEMATICA software package (Mangano 2010).

4 Numerical simulations

To illustrate the ability, reliability and the accuracy of the proposed method for find solutions of Eq. (1) in the case of bright highly dispersive optical solitons in the presence of a non-local nonlinearity, some examples are provided. The results reveal that the method is very simple to use and highly efficient.

We now consider the initial condition at \(t=0\) from Eq. (2)

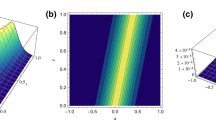
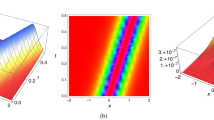
$$\begin{aligned} q(x,0)=A \text { sech}^{2}(x) \times \exp \{i[-\kappa x+\theta _0 ]\}=u_{0}(x,t)+iv_{0}(x,t). \end{aligned}$$
(26)

We now perform the simulation of the four cases listed in Table 1 and the results obtained as well as the absolute errors are shown in Figs. 1, 2, 3 and 4.

Table 1 Coefficients of Eq. (1) for bright highly dispersive optical solitons
Full size table
Fig. 1
figure 1

Numerically computed bright highly dispersive optical soliton (a), corresponding density plot (b) and absolute error (c) for case I

Full size image
Fig. 2
figure 2

Numerically computed bright highly dispersive optical soliton (a), corresponding density plot (b) and absolute error (c) for case II

Full size image
Fig. 3
figure 3

Numerically computed bright highly dispersive optical soliton (a), corresponding density plot (b) and absolute error (c) for case III

Full size image
Fig. 4
figure 4

Numerically computed bright highly dispersive optical soliton (a), corresponding density plot (b) and absolute error (c) for case IV

Full size image

5 Conclusions

Today’s paper retrieved HD bright optical solitons by the aid of LADM. The numerical scheme also yielded the error estimates of the approximations. These error measures stand very impressive. The simulations with bright solitons are exhibited for nonlocal form of nonlinearity. These results will now be extended to birefringent fibers with nonlocal law of nonlinearity where LADM will be implemented to demonstrate the numerics in it. In future, the mode will also be studied with additional forms of nonlinear media in the context of birefringent fibers and these would include Kerr law, quadratic-cubic law and polynomial law. The results of those research activities would be reported with time.