Introduction

Optical solitons have left a lasting impression in the field of telecommunications. There are a variety of concepts that stem from soliton studies that are currently studied. A few of them are dispersion-managed solitons, Bragg gratings, pure–cubic solitons, pure–quartic solitons, cubic–quartic solitons, highly dispersive (HD) solitons, quasi-linear pulses and several others. One of the concepts that have been recently proposed and have gained a lot of attention is HD solitons. This kind of solitons has been extensively studied with a variety of forms of nonlinear refractive index [1,2,3,4,5,6,7,8,9,10,11,12]. This study has also been extended to the case of birefringent fibers [13,14,15,16,17,18,19,20,21,22,23,24]. The conservation laws have been reported for HD solitons. Moreover, perturbed HD soliton solutions have been studied by the semi-inverse variational principle [25, 26]. The current paper will address HD optical solitons by the aid of variational iteration method (VIM). The governing equation is the nonlinear Schrodingers equation with intermodal dispersion (IMD), chromatic dispersion (CD), third-order dispersion (3OD), fourth-order dispersion (4OD), fifth-order dispersion (5OD) and sixth-order dispersion (6OD). The law of nonlinear refractive index is quadratic–cubic (QC) type. The numerical scheme is exhibited in the subsequent section along with an impressive error measure which exposes the efficiency and accuracy of the numerical scheme. Both bright and dark soliton solutions are studied today.

Model description

The nonlinear Schrödinger’s equation (NLSE) for highly dispersive optical solitons in polarization-preserving fibers with the quadratic–cubic law is given by [4, 11, 27,28,29]:

$$\begin{aligned}&iq_{t}+ia_{1}q_{x}+a_{2}q_{xx}+ia_{3}q_{xxx}+a_{4}q_{xxxx}+ia_{5}q_{xxxxx}\nonumber \\&\quad +a_{6}q_{xxxxxx}+(b_1\vert q\vert +b_2\vert q\vert ^{2})q=0, \end{aligned}$$
(1)

where \(q=q(x,t)\) is a complex-valued function of x (space) and t (time). In Eq. (1), the first term stands for linear temporal evolution with \(i=\sqrt{-1}\). The next six terms are dispersion terms that make the solitons highly dispersive. These are given by the coefficients of \(a_k\) for \(1\le k\le 6\) which are IMD, CD, 3OD, 4OD, 5OD and 6OD, respectively. Finally, the constants \(b_1\) and \(b_2\) are coefficients of the quadratic and cubic terms, respectively.

It must be noted that the model equ. (1) produces substantial radiation that will shed the energy of the soliton as it propagates down the fiber. However, soliton radiation is not considered in this paper. These can be studied by the aid of “variational principle” or “beyond all-order asymptotics” or by the implementing the “theory of unfoldings,” and they can be independently addressed in a different research publication. Another aspect that has been excluded from this study is the issue of collision-induced timing jitter of intra-channel collision that can be controlled by quasi-particle theory. Today’s paper stays focused on the core of the soliton in a polarization-preserving fiber.

Summary of variational iteration method (VIM)

The variational iteration method transforms the differential equation to a recurrence sequence of functions, and the limit of the sequence, if exists, is considered as the solution of the differential equation. Consider the following nonlinear partial differential equation:

$$\begin{aligned} \left\{ \begin{array}{ll} L w(x,t)+Rw(x,t)+Nw(x,t)=h(x,t),\\ w(x,0)=w_{0}(x). \end{array} \right. \end{aligned}$$
(2)

where \(L=\frac{\partial }{\partial t}\), R and N are linear and nonlinear operators, respectively, and h(x, t) is an inhomogeneous term (or source). The variational iteration method admits the use of the correction functional for Eq. (2) which can be written as

$$\begin{aligned} w_{n+1}(x,t)= & {} w_{n}(x,t) +\int _{0}^{t}\lambda (\xi )\big (Lw_{n}(x,\xi )\nonumber \\&+R{\tilde{w}}_{n}(x,\xi )+N{\tilde{w}}_{n}(x,\xi )\nonumber \\&-h(x,\xi )\big )\text {d}\xi ,\quad n\ge 0. \end{aligned}$$
(3)

where \(\lambda (\xi )\) is a general Lagrange multiplier, which can be identified optimally via the variational theory [30,31,32,33] and \({\tilde{w}}_{n}\) is considered as a restricted variation, i.e., \(\delta {\tilde{w}}_{n}=0.\)

According to the variational iteration method, the terms of a sequence \(\{w_n\}\) are constructed such that this sequence converges to the exact solution. The successive approximations \(w_{n+1}\), \(n\ge 0\), of the solution w will be readily obtained by suitable choice of trial function \(w_0\). Consequently, the solution is given as

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }w_{n}(x,t)=w(x,t). \end{aligned}$$
(4)

The VIM was proved by many to be very effective and can be used in a direct manner without any need to linearization of the nonlinear terms that may change the physical feature of the problem. As we have said before, we will use the VIM to determine bright and dark optical solitons for the NLSE with the quadratic–cubic law (1) for a variety of given initial conditions.

Implementation of the proposed method to the model (1)

Substituting \(q(x, t) = u(x, t) + iv(x, t)\), where u(x, t) and v(x, t) are real functions of x and t, in Eq. (1), results in the following coupled system of partial differential equations

$$\begin{aligned} \left\{ \begin{array}{ll} u_t+a_{1}^{1}u_{x}+a_{2}^{1}v_{xx}+a_{3}^{1}u_{xxx}+a_{4}^{1}v_{xxxx}+a_{5}^{1}u_{xxxxx}+a_{6}^{1}v_{xxxxxx}+v[b_{2}^{1}(u^2+v^2)+b_{1}^{1}\sqrt{u^2+v^2}]=0,\\ v_t+a_{1}^{2}v_{x}-a_{2}^{2}u_{xx}+a_{3}^{2}v_{xxx}-a_{4}^{2}u_{xxxx}+a_{5}^{2}v_{xxxxx}-a_{6}^{2}u_{xxxxxx}-u[b_{2}^{2}(u^2+v^2)+b_{1}^{2}\sqrt{u^2+v^2}]=0, \end{array} \right. \end{aligned}$$
(5)

with the following initial conditions

$$\begin{aligned} u(x,0)=f(x), \qquad v(x,0)=g(x). \end{aligned}$$
(6)

According to Eq. (3), the variational iteration algorithm for the problem (5) with the following initial conditions (6) has the form

$$\begin{aligned} \begin{aligned} u_{n+1}(x,t)&=u_{n}(x,t)+\int _{0}^{t}\lambda _{1}(\tau )\Big (u_{n\tau }\\&\quad +a_{1}{\hat{u}}_{nx}+a_{2}{\hat{v}}_{nxx}+a_{3}{\hat{u}}_{nxxx}\\&\quad +a_{4}{\hat{v}}_{nxxxx}+a_{5}{\hat{u}}_{nxxxxx}+a_{6}{\hat{v}}_{nxxxxxx}\\&\quad +{\hat{v}}_{n}\big [b_{2}^{1}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})+b_{1}^{1}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau ,\\ v_{n+1}(x,t)&=v_{n}(x,t) +\int _{0}^{t}\lambda _{2}(\tau )\Big (v_{n\tau }\\&\quad +a_{1}^{2}{\hat{v}}_{nx}-a_{2}^{2}{\hat{u}}_{nxx}+a_{3}^{2}{\hat{v}}_{nxxx}\\&\quad -a_{4}^{2}{\hat{u}}_{nxxxx}+a_{5}^{2}{\hat{v}}_{nxxxxx}-a_{6}^{2}{\hat{u}}_{nxxxxxx}\\&\quad -{\hat{u}}_{n}\big [b_{2}^{2}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})+b_{1}^{2}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau , \end{aligned} \end{aligned}$$
(7)

where \(\lambda _{1}(\tau )\) and \(\lambda _{2}(\tau )\) are general Lagrange multipliers. Moreover,

$$\begin{aligned}{\hat{u}}_{n},\quad {\hat{u}}_{nx},\quad {\hat{u}}_{nxx},\quad {\hat{u}}_{nxxx},\quad {\hat{u}}_{nxxxx},\quad {\hat{u}}_{nxxxxx},\quad {\hat{u}}_{nxxxxxx}\end{aligned}$$

and

$$\begin{aligned} {\hat{v}}_{n},\quad {\hat{v}}_{nx},\quad {\hat{v}}_{nxx},\quad {\hat{v}}_{nxxx},\quad {\hat{v}}_{nxxxx},\quad {\hat{v}}_{nxxxxx},\quad {\hat{v}}_{nxxxxxx}\end{aligned}$$

denote restricted variations, i.e.

$$\begin{aligned} \delta {\hat{u}}_{n}= & {} \delta {\hat{u}}_{nx}=\delta {\hat{u}}_{nxx}=\delta {\hat{u}}_{nxxx}\\= & {} \delta {\hat{u}}_{nxxxx}= \delta {\hat{u}}_{nxxxxx}=\delta {\hat{u}}_{nxxxxxx}=0\end{aligned}$$

and

$$\begin{aligned} \delta {\hat{v}}_{n}= & {} \delta {\hat{v}}_{nx}=\delta {\hat{v}}_{nxx}=\delta {\hat{v}}_{nxxx}\\= & {} \delta {\hat{v}}_{nxxxx}= \delta {\hat{v}}_{nxxxxx}=\delta {\hat{v}}_{nxxxxxx}=0.\end{aligned}$$

Making the above correction functionals stationary, we obtain the following stationary conditions:

$$\begin{aligned} \left\{ \begin{array}{lll} 1+\lambda _{1}'(\tau )|_{\tau =t}=0,\quad \lambda _{1}'(\tau )|_{\tau =t}=0,\\ 1+\lambda _{2}'(\tau )|_{\tau =t}=0,\quad \lambda _{2}'(\tau )|_{\tau =t}=0,\\ \end{array} \right. \end{aligned}$$
(8)

Therefore, the Lagrange multipliers can be identified as \(\lambda _{1}(\tau )=\lambda _{2}(\tau )=-1\). Substituting this value of the Lagrangian multiplier into functional Eq. (7) gives the iterative formulas

$$\begin{aligned} \begin{aligned} u_{n+1}(x,t)&=u_{n}(x,t)-\int _{0}^{t}\Big (u_{n\tau }+a_{1}^{1}{\hat{u}}_{nx}\\&\quad +a_{2}^{1}{\hat{v}}_{nxx}+a_{3}^{1}{\hat{u}}_{nxxx}\\&\quad +a_{4}^{1}{\hat{v}}_{nxxxx}+a_{5}^{1}{\hat{u}}_{nxxxxx}+a_{6}^{1}{\hat{v}}_{nxxxxxx}\\&\quad +{\hat{v}}_{n}\big [b_{2}^{1}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})\\&\quad +b_{1}^{1}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau ,\\ v_{n+1}(x,t)&=v_{n}(x,t) -\int _{0}^{t}\Big (v_{n\tau }+a_{1}^{2}{\hat{v}}_{nx}-a_{2}^{2}{\hat{u}}_{nxx}\\&\quad +a_{3}^{2}{\hat{v}}_{nxxx}\\&\quad -a_{4}^{2}{\hat{u}}_{nxxxx}+a_{5}^{2}{\hat{v}}_{nxxxxx}-a_{6}^{2}{\hat{u}}_{nxxxxxx}\\&\quad -{\hat{u}}_{n}\big [b_{2}^{2}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})+b_{1}^{2}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau , \end{aligned} \end{aligned}$$
(9)

where \(n\ge 0\) and \(u_{0}(x,t)=u(x,0)\), \(v_{0}(x,t)= v(x,0).\) The VIM solutions u(x, t) and v(x, t) can be expressed as

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }u_{n}(x,t)=u(x,t) \quad \text{ and }\quad \lim \limits _{n\rightarrow \infty }v_{n}(x,t)=v(x,t), \end{aligned}$$
(10)

where \(u_n\) and \(v_n\) will be determined recursively.

Application to bright highly dispersive solitions

We first consider the nonlinear Schrödinger Eq. (1) with the initial condition

$$\begin{aligned} u(x,0)= & {} \Big (\alpha _1+\beta _1 {\text {sech}}(x)+\gamma _1 {\text {sech}}^3(x)\Big )e^{i(-\kappa x+\theta _0)} \end{aligned}$$
(11)
$$\begin{aligned} v(x,0)= & {} \Big (\alpha _2+\beta _2 {\text {sech}}(x)+\gamma _2 {\text {sech}}^3(x)\Big )e^{i(-\kappa x+\theta _0)}. \end{aligned}$$
(12)

Here we will use the initial condition as derived in [13] and \(\alpha _j\), \(\beta _j\) and \(\gamma _j\) are constants related to system coefficients (5) for every \(j=1,2\).

The correction functionals for (5) are given as in Eq. (9). Consequently, we obtain the successive approximations as follows:

$$\begin{aligned} u_{0}(x,t)&=\Big (\alpha _1+\beta _1 {\text {sech}}(x)+\gamma _1 {\text {sech}}^3(x)\Big )e^{i(-\kappa x+\theta _0)},\\ v_{0}(x,t)&=\Big (\alpha _2+\beta _2 {\text {sech}}(x)\\&\quad +\gamma _2 {\text {sech}}^3(x)\Big )e^{i(-\kappa x+\theta _0)},\\ u_{1}(x,t)&=u_{0}(x,t)-\int _{0}^{t}\Big (u_{0\tau }+a_{1}^{1}{\hat{u}}_{0x}\\&\quad +a_{2}^{1}{\hat{v}}_{0xx}+a_{3}^{1}{\hat{u}}_{0xxx}\\&\quad +a_{4}^{1}{\hat{v}}_{0xxxx}+a_{5}^{1}{\hat{u}}_{0xxxxx}\\&\quad +a_{6}^{1}{\hat{v}}_{0xxxxxx}\\&\quad +{\hat{v}}_{0}\big [b_{2}^{1}({\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0})+b_{1}^{1}\sqrt{{\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0}}\big ]\Big )\text {d}\tau , \\ v_{1}(x,t)&=v_{0}(x,t)-\int _{0}^{t}\Big (v_{0\tau }+a_{1}^{2}{\hat{v}}_{0x}\\&\quad -a_{2}^{2}{\hat{u}}_{0xx}+a_{3}^{2}{\hat{v}}_{0xxx}\\&\quad -a_{4}^{2}{\hat{u}}_{0xxxx}+a_{5}^{2}{\hat{v}}_{0xxxxx}-a_{6}^{2}{\hat{u}}_{0xxxxxx}\\&\quad -{\hat{u}}_{0}\big [b_{2}^{2}({\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0})\\&\quad +b_{1}^{2}\sqrt{{\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0}}\big ]\Big )\text {d}\tau ,\\ u_{2}(x,t)&=u_{1}(x,t)-\int _{0}^{t}\Big (u_{1\tau }+a_{1}^{1}{\hat{u}}_{1x}\\&\quad +a_{2}^{1}{\hat{v}}_{1xx}+a_{3}^{1}{\hat{u}}_{1xxx}\\&\quad +a_{4}^{1}{\hat{v}}_{1xxxx}+a_{5}^{1}{\hat{u}}_{1xxxxx}\\&\quad +a_{6}^{1}{\hat{v}}_{1xxxxxx}\\&\quad +{\hat{v}}_{1}\big [b_{2}^{1}({\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1})\\&\quad +b_{1}^{1}\sqrt{{\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1}}\big ]\Big )\text {d}\tau , \\ v_{2}(x,t)&=v_{1}(x,t)-\int _{0}^{t}\Big (v_{1\tau }+a_{1}^{2}{\hat{v}}_{1x}\\&\quad -a_{2}^{2}{\hat{u}}_{1xx}+a_{3}^{2}{\hat{v}}_{1xxx}-a_{4}^{2}{\hat{u}}_{1xxxx}\\&\quad +a_{5}^{2}{\hat{v}}_{1xxxxx}-a_{6}^{2}{\hat{u}}_{1xxxxxx}\\&\quad -{\hat{u}}_{1}\big [b_{2}^{2}({\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1})\\&\quad +b_{1}^{2}\sqrt{{\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1}}\big ]\Big )\text {d}\tau ,\\&\quad \vdots \\ u_{n+1}(x,t)&=u_{n}(x,t)-\int _{0}^{t}\Big (u_{n\tau }+a_{1}^{1}{\hat{u}}_{nx}\\&\quad +a_{2}^{1}{\hat{v}}_{nxx}+a_{3}^{1}{\hat{u}}_{nxxx}\\&\quad +a_{4}^{1}{\hat{v}}_{nxxxx}+a_{5}^{1}{\hat{u}}_{nxxxxx}+a_{6}^{1}{\hat{v}}_{nxxxxxx}\\&\quad +{\hat{v}}_{n}\big [b_{2}^{1}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})\\&\quad +b_{1}^{1}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau ,\\ v_{n+1}(x,t)&=v_{n}(x,t)-\int _{0}^{t}\Big (v_{n\tau }+a_{1}^{2}{\hat{v}}_{nx}\\&\quad -a_{2}^{2}{\hat{u}}_{nxx}+a_{3}^{2}{\hat{v}}_{nxxx}-a_{4}^{2}{\hat{u}}_{nxxxx}+a_{5}^{2}{\hat{v}}_{nxxxxx}-a_{6}^{2}{\hat{u}}_{nxxxxxx}\\&-{\hat{u}}_{n}\big [b_{2}^{2}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})\\&\quad +b_{1}^{2}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau . \end{aligned}$$

Application to dark highly dispersive solitions

We first consider the nonlinear Schrödinger Eq. (1) with the initial condition

$$\begin{aligned} u(x,0)= & {} \Big (\alpha _1+\beta _1 {\text {tanh}}(x)+\gamma _1 {\text {tanh}}^3(x)\Big )e^{i(-\kappa x+\theta _0)} \end{aligned}$$
(13)
$$\begin{aligned} v(x,0)= & {} \Big (\alpha _2+\beta _2 {\text {tanh}}(x)+\gamma _2 {\text {tanh}}^3(x)\Big )e^{i(-\kappa x+\theta _0)}. \end{aligned}$$
(14)

Here we will use the initial condition as derived in [13] and \(\alpha _j\), \(\beta _j\) and \(\gamma _j\) are constants related to system coefficients (5) for every \(j=1,2\).

The correction functionals for (5) are given as in Eqs. ((9)). Consequently, we obtain the successive approximations as follows:

$$\begin{aligned} u_{0}(x,t)&=\Big (\alpha _1+\beta _1 {\text {tanh}}(x)\\&\quad +\gamma _1 {\text {tanh}}^3(x)\Big )e^{i(-\kappa x+\theta _0)},\\ v_{0}(x,t)&=\Big (\alpha _2+\beta _2 {\text {tanh}}(x)\\&\quad +\gamma _2 {\text {tanh}}^3(x)\Big )e^{i(-\kappa x+\theta _0)},\\ u_{1}(x,t)&=u_{0}(x,t)-\int _{0}^{t}\Big (u_{0\tau }+a_{1}^{1}{\hat{u}}_{0x}\\&\quad +a_{2}^{1}{\hat{v}}_{0xx}+a_{3}^{1}{\hat{u}}_{0xxx}\\&\quad +a_{4}^{1}{\hat{v}}_{0xxxx}+a_{5}^{1}{\hat{u}}_{0xxxxx}+a_{6}^{1}{\hat{v}}_{0xxxxxx}\\&\quad +{\hat{v}}_{0}\big [b_{2}^{1}({\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0})+b_{1}^{1}\sqrt{{\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0}}\big ]\Big )\text {d}\tau , \\ v_{1}(x,t)&=v_{0}(x,t)-\int _{0}^{t}\Big (v_{0\tau }+a_{1}^{2}{\hat{v}}_{0x}\\&\quad -a_{2}^{2}{\hat{u}}_{0xx}+a_{3}^{2}{\hat{v}}_{0xxx}\\&\quad -a_{4}^{2}{\hat{u}}_{0xxxx}+a_{5}^{2}{\hat{v}}_{0xxxxx}-a_{6}^{2}{\hat{u}}_{0xxxxxx}\\&\quad -{\hat{u}}_{0}\big [b_{2}^{2}({\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0})+b_{1}^{2}\sqrt{{\hat{u}}^{2}_{0}+{\hat{v}}^{2}_{0}}\big ]\Big )\text {d}\tau ,\\ u_{2}(x,t)&=u_{1}(x,t)-\int _{0}^{t}\Big (u_{1\tau }+a_{1}^{1}{\hat{u}}_{1x}\\&\quad +a_{2}^{1}{\hat{v}}_{1xx}+a_{3}^{1}{\hat{u}}_{1xxx}+a_{4}^{1}{\hat{v}}_{1xxxx}+a_{5}^{1}{\hat{u}}_{1xxxxx}+a_{6}^{1}{\hat{v}}_{1xxxxxx}\\&\quad +{\hat{v}}_{1}\big [b_{2}^{1}({\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1})+b_{1}^{1}\sqrt{{\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1}}\big ]\Big )\text {d}\tau , \\ v_{2}(x,t)&=v_{1}(x,t)-\int _{0}^{t}\Big (v_{1\tau }+a_{1}^{2}{\hat{v}}_{1x}\\&\quad -a_{2}^{2}{\hat{u}}_{1xx}+a_{3}^{2}{\hat{v}}_{1xxx}-a_{4}^{2}{\hat{u}}_{1xxxx}\\&\quad +a_{5}^{2}{\hat{v}}_{1xxxxx}-a_{6}^{2}{\hat{u}}_{1xxxxxx}\\&\quad -{\hat{u}}_{1}\big [b_{2}^{2}({\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1})+b_{1}^{2}\sqrt{{\hat{u}}^{2}_{1}+{\hat{v}}^{2}_{1}}\big ]\Big )\text {d}\tau ,\\&\quad \vdots \\ u_{n+1}(x,t)&=u_{n}(x,t)-\int _{0}^{t}\Big (u_{n\tau }+a_{1}^{1}{\hat{u}}_{nx}\\&\quad +a_{2}^{1}{\hat{v}}_{nxx}+a_{3}^{1}{\hat{u}}_{nxxx}\\&\quad +a_{4}^{1}{\hat{v}}_{nxxxx}+a_{5}^{1}{\hat{u}}_{nxxxxx}\\&\quad +a_{6}^{1}{\hat{v}}_{nxxxxxx}\\&\quad +{\hat{v}}_{n}\big [b_{2}^{1}({\hat{u}}^{2}_{n}\\&\quad +{\hat{v}}^{2}_{n})+b_{1}^{1}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau ,\\ v_{n+1}(x,t)&=v_{n}(x,t)-\int _{0}^{t}\Big (v_{n\tau }+a_{1}^{2}{\hat{v}}_{nx}\\&\quad -a_{2}^{2}{\hat{u}}_{nxx}+a_{3}^{2}{\hat{v}}_{nxxx}-a_{4}^{2}{\hat{u}}_{nxxxx}\\&\quad +a_{5}^{2}{\hat{v}}_{nxxxxx}-a_{6}^{2}{\hat{u}}_{nxxxxxx}\\&\quad -{\hat{u}}_{n}\big [b_{2}^{2}({\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n})\\&\quad +b_{1}^{2}\sqrt{{\hat{u}}^{2}_{n}+{\hat{v}}^{2}_{n}}\big ]\Big )\text {d}\tau . \end{aligned}$$

The approach introduced above will illustrated through examples in the following section.

Numerical experiments and graphical results

In this section, we consider some different cases for the nonlinear Schrödinger equation with the quadratic–cubic law given in (1) to illustrate the application of the VIM scheme we presented in the above section. The numerical solutions will be obtained, and the results will be graphically illustrated. In all these examples, software MATHEMATICA version 11 has been used for calculations and graphs.

Bright highly dispersive solitons

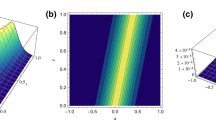
The result and the profile of two cases are graphically illustrated in Table 1 and in Figs. 1, 2, and 3.

Table 1 Coefficients of Eq. (1) for bright highly dispersive solitons
Full size table

Dark highly dispersive solitons

The result and the profile of two cases are graphically illustrated in Table 2 and in Figs. 4, 5, and 6.

Table 2 Coefficients of Eq. (1) for dark highly dispersive solitons
Full size table
Fig. 1
figure 1

Numerically computed bright highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case B-1

Full size image
Fig. 2
figure 2

Numerically computed bright highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case B-2

Full size image
Fig. 3
figure 3

Numerically computed bright highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case B-3

Full size image
Fig. 4
figure 4

Numerically computed dark highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case D-1

Full size image
Fig. 5
figure 5

Numerically computed dark highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case D-2

Full size image
Fig. 6
figure 6

Numerically computed dark highly dispersive soliton (a), corresponding density plot (b) and absolute error (c) for case D-3

Full size image

Conclusions

This paper studied HD optical solitons by VIM where the nonlinear refractive index is of QC type. The adopted numerical scheme displayed surface plots and the error graphs that are of the order of \(10^{-9}\). The error measure stands impressively small. The results of this manuscript are therefore strongly encouraging to look at HD solitons that appear with additional forms of refractive index. Later, HD solitons will be addressed in birefringent fibers for a variety of nonlinear refractive index. These results are currently awaited and will be disseminated across a variety of journals. In future, several additional models that describe soliton dynamics will also be addressed numerically. These include Kudryashovs equation, Chen–Lee–Liu equation, Kaup–Newell equation, Gerdjikov–Ivanov equation, Lakshmanan–Porsezian–Daniel model and several others. These are all in the bucket list for now.