Solitary and traveling wave solutions for the Davey–Stewartson equation using the Jacobi elliptic function expansion method

Abstract

In our paper we modify the Jacobi elliptic function expansion method to obtain solutions to the Davey–Stewartson system of equations. Two categories of nonsingular solutions are obtained for both traveling and solitary waves and both with and without chirp. In both cases there is an arbitrary term in the mean flow field, meaning one can obtain solutions for arbitrary forms of the mean flow field.

1 Introduction

The Davey–Stewartson (DS) system of nonlinear partial differential equations, henceforth abbreviated as the DS system, was first introduced in fluid dynamics for the study of the evolution of three-dimensional wave packets in water of finite depth (Davey and Stewartson 1974). It has since found application in numerous areas of physics, most notably nonlinear-optics (Newell and Moloney 1992) as well as related fields such as the study of Bose–Einstein condensates (Huang 2005) and the study of electro-magnetic (EM) waves in ferromagnets (Leblond 1999). A surprising property of the DS system is that it is one of the few multidimensional systems whose inverse scattering transform is known (Sung 1994a, b, c, 1995). Of considerable interest is also the fact that rogue waves have been shown to exist in DS systems (Ohta and Yang 2012, 2013).

Various techniques have been put forth to obtain solutions to the DS system. The earliest attempt was given in Anker and Freeman (1978) where the Zakharov–Shabat scheme (1974) was used to obtain one- and two-soliton solutions, as well as model some basic properties of interaction of multiple solitons. In Hieraninta and Hirota (1990) the Hirota method (Hieraninta 1997) was used to construct a multi-dromion solution. Various other methods have been used to find new solutions to the DS system: the variable separation method (Lou and Lu 1996; Lou 2002; Wang and Huang 2010), the $G'/G$ method (Ebadi and Biswas 2011), the first integral method (Jafari 2012) as well as many others (Deng and Qin 2006; Wazwaz 2008; Tian and Gao 1997; Yildirm 2012). Of particular interest for this paper is the work done by Yan (2003) in which Jacobi elliptic functions (JEFs) were used to construct solutions to a system of equations resembling the DS system. In the paper, a basic expansion of the solution in terms of the twelve JEFs was used and solutions were obtained in the form of the first order polynomial (of the JEFs) for the basic wave, while the two auxiliary waves were represented with a second order polynomial.

Recently, work was done to find solutions using the JEF expansion method for various forms of the Nonlinear Schrödinger Equation (NLSE) (Zhong 2008; Belić 2008; Petrović 2009) and the Gross–Pitaevskii equation (GPE) (2010, 2011). These forms use distributed coefficients which allow the use of dispersion (Eiermann 2003) and diffraction management (Eisenberg 2000). The solutions obtained in Zhong (2008), Belić (2008) and Petrović (2009, 2010, 2011) were found to have either absolute modulational stability or modulational stability under diffraction/dispersion management (Petrović 2015, 2011).

The form of the solutions of JEF expansion method is well suited when all the nonlinearity in the problem is solely dependant on amplitude. In the DS system we have two fields: the wave-amplitude field which is complex and the mean-field which is real. As will be shown, it emerges from the DS system that for the matching conditions to work it is natural to consider the mean-flow field to be second order with respect to the wave-amplitude field. Therefore the DS system is highly suitable for the JEF expansion method. In this paper we will apply the JEF expansion method and the ideas developed in Belić (2008) to solving the DS system.

2 Method

The Davey–Stewartson (DS) system of equations has the following general form:

$$\begin{aligned}&i u_t + \frac{\beta (t)}{2}(r u_{xx}+s u_{yy})+ \chi (t)|u|^{2} u+ \alpha (t) u n= 0,\end{aligned}$$

(1)

$$\begin{aligned}&n_{xx}+q n_{yy}+\delta \left( \left| u\right| ^2\right) _{xx}=0, \end{aligned}$$

(2)

where u is the wave-amplitude field (WAF), n is the mean-flow field (MFF), t is time, x and y are transverse variables, indices are partial derivatives, $\beta (t)$ is the diffraction coefficient, $\chi (t)$ is the strength of nonlinearity, $\alpha (t)$ is the coupling function and r, s, q and $\delta$ are non-zero real parameters. As in Belić (2008), we propose the following solution for the WAF:

$$\begin{aligned} u=A e^{iB}, \end{aligned}$$

(3)

where A and B are real functions of x, y and t denoting the amplitude and the phase of the solution. Following Belić (2008) and Petrović (2009) we assume the following forms for A and B:

$$\begin{aligned} A= & {} f_1(t)F(\theta )+f_0(t)+f_{-1}(t)F(\theta )^{-1},\end{aligned}$$

(4)

$$\begin{aligned} \theta= & {} k(t)x + l(t) y +\omega (t), \end{aligned}$$

(5)

$$\begin{aligned} B= & {} a(t)(x^2/r+y^2/s)+ b(t) (x + y) + e(t), \end{aligned}$$

(6)

where F is a JEF satisfying the differential equation:

$$\begin{aligned} \left( \frac{d F}{d\theta }\right) ^2=c_0+c_2 F^2+c_4 F^4. \end{aligned}$$

(7)

Here, $c_0$, $c_2$ and $c_4$ are coefficients which depend on the choice of the JEF and M, the parameter of the JEF. We will assume that at most one of $c_0$, $c_2$ and $c_4$ is 0. For the MFF we take the following form to ensure matching conditions for the top-order terms with respect to F:

$$\begin{aligned} n=g_2(t)F(\theta )^2+g_1(t)F(\theta )+g_0(t)+g_{-1}(t)F(\theta )^{-1}+g_{-2}(t)F(\theta )^{-2}. \end{aligned}$$

(8)

We cannot have all of $g_2,\,g_1,\,g_{-1},\,g_{-2}$ be zero as n would have no dependence on the transverse spatial coordinates and Eq. (2) would be trivially satisfied.

Plugging in Eqs. (4)–(8) into Eqs. (1)–(2) we obtain the following equations for parameters k, l, $f_i$ ($i=1,0,-1$), a, b and $\omega$:

$$\begin{aligned}&f_{it}+2a\beta f_i=0,\;i=1,0,-1,\end{aligned}$$

(9)

$$\begin{aligned}&k_t+2a\beta k=0,\end{aligned}$$

(10)

$$\begin{aligned}&l_t+2a\beta l=0,\end{aligned}$$

(11)

$$\begin{aligned}&\omega _t+\beta b(rk+ls)=0,\end{aligned}$$

(12)

$$\begin{aligned}&a_t+2a^2\beta =0,\end{aligned}$$

(13)

$$\begin{aligned}&b_t+2a\beta b=0. \end{aligned}$$

(14)

We also obtain the following set of integrability conditions:

$$\begin{aligned}&k^2(2 \delta f_0f_i+g_i)+ g_i l^2 q=0,\;i=\pm 1,\end{aligned}$$

(15)

$$\begin{aligned}&k^2(\delta f_i^2+g_{2i})+g_{2i} l^2 q=0,\;i=\pm 1,\end{aligned}$$

(16)

$$\begin{aligned}&3\chi f_i^2f_0+\alpha f_ig_i+\alpha f_0g_{2i}=0,\;i=\pm 1,\end{aligned}$$

(17)

$$\begin{aligned}&\chi f_i^3+\alpha f_ig_{2i}+\beta c_{2+2i}(rk^2+sl^2)=0,\;i=\pm 1. \end{aligned}$$

(18)

and the following equations for parameter e:

$$\begin{aligned}&f_0\left( -e_t-\frac{b^2\beta }{2}(1+s)+\chi f_0^2+6\chi f_1f_{-1}\right) +\alpha (f_0g_0+f_1g_{-1}+f_{-1}g_1)=0,\end{aligned}$$

(19)

$$\begin{aligned}&f_i\left( -e_t-\frac{b^2\beta }{2}(1+s)+3\chi f_0^2+3\chi f_1f_{-1}+\frac{\beta c_{2}}{2}(k^2r+l^2s)\right) +\alpha (f_ig_0+f_0g_i+f_{-i}g_{2i})=0,\;i=\pm 1. \end{aligned}$$

(20)

We note that while the general set-up is similar to that of Belić (2008), there are several key differences. First, due to the presence of the MFF, we obtain four pairs of integrability conditions instead of one, albeit with several new parameters to work with. Note that the function $g_0$ only appears in the equations for e. Second, the presence of the MFF in Eq. (1) affects Eqs. (19)–(20). In particular, one can no longer trivially discard Eq. (19) by assuming $f_0=0$. We shall see that the obtained constraints on the parameters are quite different from those in Belić (2008).

3 Results

We now proceed to solve Eqs. (9)–(20). Solving Eqs. (9)–(14) we obtain:

$$\begin{aligned}&f_{i}=f_{i0}p,\;i=1,0,-1,\end{aligned}$$

(21)

$$\begin{aligned}&k=k_0p,\end{aligned}$$

(22)

$$\begin{aligned}&l=l_0p,\end{aligned}$$

(23)

$$\begin{aligned}&a=a_0p,\end{aligned}$$

(24)

$$\begin{aligned}&b=b_0p,\end{aligned}$$

(25)

$$\begin{aligned}&\omega =\omega _0-b(k_0+l_0s)p\int _0^t\beta (t)dt, \end{aligned}$$

(26)

Where p is the chirp function given by:

$$\begin{aligned} p=\frac{1}{1+2a_0\int _0^t\beta (t)dt}. \end{aligned}$$

(27)

We now distinguish between two cases: $f_0\ne 0$ and $f_0=0$.

3.1 Case $f_0\ne 0$

We first cover the most general case, i.e. the case when $f_0$ is non-zero. First we assume that $f_1$ and $f_{-1}$ are also non-zero. We also assume $k_0^2+ql_0^2\ne 0$, as from assuming otherwise it quickly follows that $f_1,\,f_{-1}=0$. Solving Eqs. (15)–(16), we obtain the following equations:

$$\begin{aligned}&g_{i}=2\epsilon f_0f_i,\;i=\pm 1,\end{aligned}$$

(28)

$$\begin{aligned}&g_{2i}=\epsilon f_i^2,\;i=\pm 1, \end{aligned}$$

(29)

where the parameter $\epsilon$ is given by the formula:

$$\begin{aligned} \epsilon =-\frac{\delta k_0^2}{k_0^2+ql_0^2}. \end{aligned}$$

(30)

Equations (28)–(29) coincide with Eq. (14) in Ebadi and Biswas (2011) for $n=2$ in the special case of $f_0=f_{-1}=0$. Plugging the results in Eqs. (17) we obtain a matching condition:

$$\begin{aligned} \chi =-\epsilon \alpha . \end{aligned}$$

(31)

Finally, plugging in this condition into Eqs. (18), one obtains the constraint:

$$\begin{aligned} rk_0^2+sl_0^2=0. \end{aligned}$$

(32)

This constraint doesn’t occur in the previous systems studied in Belić (2008) and Petrović (2010). Given these conditions one obtains that Eqs. (19)–(20) are automatically matched with each other, i.e. equivalent. A surprising result emerges in that there are no constraints on function $g_0(t)$. In other words, for every form of $g_0(t)$ one can find a form for the free term of the phase e(t) for which give us a solution to the DS system. Thus, we truly obtain a wide range of solutions and the ability to study many different forms of the DS system of equations. It is also worth noting that unlike in Belić (2008) the nonlinearity $\chi$ as an integrability condition no longer has to follow the form of f and that there is no longer any imposed relationship between $f_{10}$ and $f_{-10}$. Additionally, since $\chi$ is free to be of arbitrary form, there is no longer a simple formula for e, but e is highly dependent on the choice of $\chi$ and $g_0$.

Assuming $f_{-1}=0$ and $f_{1}\ne 0$ one obtains:

$$\begin{aligned}&g_{1}=2\epsilon f_0f_1,\;i=\pm 1,\end{aligned}$$

(33)

$$\begin{aligned}&g_{2}=\epsilon f_1^2,\;i=\pm 1,\end{aligned}$$

(34)

$$\begin{aligned}&g_{-1}=g_{-2}=0,\end{aligned}$$

(35)

$$\begin{aligned}&c_4(rk_0^2+sl_0^2)=0. \end{aligned}$$

(36)

Similarly, assuming $f_{1}=0$ and $f_{-1}\ne 0$ one obtains:

$$\begin{aligned}&g_{-1}=2\epsilon f_0f_{-1},\;i=\pm 1,\end{aligned}$$

(37)

$$\begin{aligned}&g_{-2}=\epsilon f_{-1}^2,\;i=\pm 1,\end{aligned}$$

(38)

$$\begin{aligned}&g_{1}=g_{2}=0,\end{aligned}$$

(39)

$$\begin{aligned}&c_0(rk_0^2+sl_0^2)=0. \end{aligned}$$

(40)

In both cases, Eq. (31) holds and $g_0(t)$ is arbitrary.

3.2 Case $f_0=0$

We now assume $f_0=0$ and, without loss of generality, $f_1\ne 0$. As in the previous section $k_0^2+ql_0^2\ne 0$. From Eqs. (15)–(16), we obtain:

$$\begin{aligned}&g_{i}=0,\;i=\pm 1,\end{aligned}$$

(41)

$$\begin{aligned}&g_{2i}=\epsilon f_i^2,\;i=\pm 1. \end{aligned}$$

(42)

It follows that Eqs. (17) are automatically satisfied. In order for Eqs. (18) to be satisfied we must either have Eqs. (31)–(32) or:

$$\begin{aligned}&f_{-1}=\eta \sqrt{\frac{c_0}{c_4}}f_1,\;\eta =0,\pm 1,\end{aligned}$$

(43)

$$\begin{aligned}&\chi =-\alpha \epsilon -\frac{\beta c_4(k^2+l^2s)}{f_1^2}. \end{aligned}$$

(44)

We note that for the special case of $\alpha =0$, coinciding with the system in Belić (2008), we obtain the matching condition from Belić (2008). Finally, given these conditions, Eq. (19) is trivially satisfied, while Eq. (20) are automatically matched with each other. In this case, we no longer have the constraint given in Eq. (32).

Fig. 1

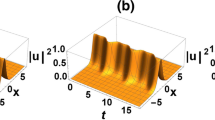
(Color online) Solitary and traveling wave solutions for $F=\text{ dn }$ as functions of time. Intensity $|u|^2$ for $a_0=0$ (a–c) and $a_0=0.2$ (d–f) are presented as a function of $k_0x+l_0y$ and t for $p=-3$, $\beta (z)=\beta _0 \cos \Omega t$ and a, d$M=0.97$, $l_0=1$b, e$M=0.97$, $l_0=-1$ and c, f$M=1$, $l_0=-1$. Coefficients: $b_0=0$, $e_0=0$, $k_0=1$, $\omega _0=0$, $\beta _0=1$, $f_{10}=1$, $f_{00}=f_{-10}=0$, $r=1$, $s=-1$, $q=1$ and $\delta =-1$

4 Solutions

We now analyze the obtained solutions. We note that the condition (32) largely restricts us to r and s being the opposite sign. By default we take $F=\text{ dn }$ which is the most convenient function as both it and its inverse are free from singularities, though one can obtain similar solutions in many cases with other choices for F. We note that for all cases where $g_0=0$ we have that n is qualitatively similar to $|u|^2$ and therefore only $|u|^2$ will be shown.

We take $M=0.97$, describing so-called traveling wave solutions. In Fig. 1a we see the most basic form of the solution for $|u|^2$. Since k and l are of equal sign they cancel out in 12 leading to no time dependence in $\theta$ in the absence of chirp. In Fig. 1b we see the results when $k_0$ and $l_0$ are of opposite sign. For $M=1$, a solitary wave solutions is obtained as shown in Fig. 1c. In Fig. 1d–f we see the effects of chirp on our solutions. We note the loss of periodicity in the traveling wave solutions and the stretching effect present in Fig. 1d away from the center, whereas in Fig. 1e this pattern is shifted away from the center. We also note the oscillation in amplitude in all three cases, especially in Fig. 1f, where the solution corresponds to a breather solitary wave.

Fig. 2

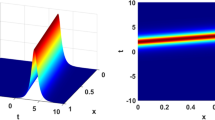
(Color online) Traveling wave solutions as functions of time. The parameters are the same as in Fig. 1b except $a_0=0.2$ in (d–f) and a, d$f_{10}=f_{-10}=1$, $f_{00}=0$b, e$f_{10}=f_{00}=1$, $f_{-10}=0$ and c, f$f_{10}=f_{-10}=f_{00}=1$

In Fig. 2 we see the effects of combining several terms in the solution. We see the inverse function dominate in Fig. 2a with respect to Fig. 1a. The presence of $f_{00}=1$ shifts the function upward in the regime without chirp.

Fig. 3

(Color online) Traveling wave solutions as functions of time for Case 2. The parameters are the same as in Fig. 1b except s = 1, $a_0=0.2$ in (d–f) and a, d$\eta =0$, b, e$\eta =1$ and c, f$\eta =0$ and $F=\text{ sn }$

Finally in Fig. 3 we only cover cases not applicable under Case 1, i.e. we see the solutions for $r=s=1$ which was inadmissable under Case 1. In Fig. 3a we take $\eta =0$, in Fig. 3b $\eta =1$, while in Fig. 3c we look at dark soliton solutions by taking $F=\text{ sn }$.

In all of these solutions, the novelty comes from the presence of chirp. The previous papers dealing with solutions using expansion methods or related methods, such as Refs. Ebadi and Biswas (2011), Jafari (2012), Yildirm (2012) and Yan (2003) all utilize a linear dependence of the phase on the transverse variables. In addition, we have demonstrated that any function satisfying Eq. (7) can be used to construct solutions to the DS system of equations.

In all these solutions we’ve set $g_0=0$. However, you can add an arbitrary function of time to $g_0$ and as a consequence to n. The only restriction is that there is no dependence on the transverse variable. Thus, a large range of possible forms for n is possible.

5 Conclusion

To sum up, we analyzed the Davey–Stewartson system and obtained large new classes of solitary and traveling wave solutions using the JEF expansion method. We obtained large classes of new solutions, both solitary and traveling wave solutions and both with and without chirp. Since the DS system appears in many areas of physics, there is a good possibility of practical application for these solutions.