Keywords

1 Introduction

Progressing of soliton formation and its application in differential systems has been remarkable in recent years. Disputing modes of solitary energy propagating on behalf of a chain of other biological molecules has pulled forward interesting. New attainment of topological, nontopological solitons as well as transformation phenomena in polyacetylene chains with the action of an electrical field [1]. The physical phenomena of nonlinear partial differential equations (NLPDEs) are involved in many fields of physics, for example, plasma physics, optical fibers, nonlinear optics, fluid mechanics, chemistry, biology, geochemistry as well as engineering sciences [2].

Researchers have been reported an assorted numerical and analytical techniques to seek solutions of NLPDEs for example a homotopy analysis method [3, 4], a finite forward difference method [5, 6], homotopy perturbation method [7, 8], spectral methods [9], Adomian decomposition method [10, 11], Adams-Bashforth scheme [12], Adams-Bashforth-Moulton scheme [13], shooting scheme [14,15,16,17], the sine-Gordon expansion method [18, 19], the inverse scattering method [20], functional variable method [21], the Bernoulli sub-ODE function method [22, 23], the modified auxiliary expansion method [24], the modified \(\exp \left( -\varphi \left( \xi \right) \right) \)-expansion function method [25,26,27], the tan\(\left( \phi \left( \xi \right) /2 \right) \)-expansion method [28, 29], \({{{G}'}}/{G}\)-expansion method [30, 31], the decomposition-Sumudu-like-integral-transform method [32], the extended sinh-Gordon expansion method [33, 34] and the generalized exponential rational function method [35, 36].

Scholars have been used different methods to find some kind of solution like exact, analytical, numerical and semi-analytic solutions of Davey-Stewartson equations for instance, the \({{{G}'}}/{G}\) method [37], the improved tan\(\left( \phi \left( \xi \right) /2 \right) \)-expansion method with generalized \({{{G}'}}/{G}\)-expansion method [32], the rational expansion method [38], time splitting spectral method [39], the Gram-type determinant solution and Casorati-type determinant solution [40]. Also, different analytical approaches such as, the method of multiple scales combined with a quasi discreteness approximation [41], sine-Gordon expansion method [42], the new generalized \({{{G}'}}/{G}\)-expansion method [43], the extended Weierstrass transformation method [44], the sine-cosine, tanh-coth and exp-function methods [45] and the extended mapping method technique [46] have been developed to investigate analytical solutions for the different types of NLPDEs.

In this study, some novel soliton solution of Davey and Stewartson equations by using the Bernoulli sub-equation is investigated. The variable approach of the traveling wave changes the NLPDEs into nonlinear ordinary differential equations and it is solved for different physical nonzero parameters. Outcomes cases are present in 2D and 3D-dimensions.

2 Structures of Bernoulli Sub-equation Function Method

The mainly modified steps of this technique are [47, 48]:

Let we have a nonlinear partial differential equation:

$$\begin{aligned} P\left( {{u}_{x}},{{u}_{t}},{{u}_{xt}},{{u}_{xx}},... \right) =0, \end{aligned}$$
(1)

and defining the traveling wave transformation

$$\begin{aligned} u(x,t)=q(\eta ),\eta =x+\gamma t, \end{aligned}$$
(2)

where \(\gamma \ne 0\). Applying Eq. (4) on Eq. (3) as a result, we get a nonlinear ordinary differential equation:

$$\begin{aligned} N(q,{{q}^{'}},{{q}^{''}},...)=0. \end{aligned}$$
(3)

Using a trial equation of solution as follows:

$$\begin{aligned} q\left( \eta \right) =\sum \limits _{i=0}^{n}{{{a}_{i}}{{F}^{i}}={{a}_{0}}+{{a}_{1}}F+{{a}_{2}}{{F}^{2}}+...+{{a}_{n}}{{F}^{n}},} \end{aligned}$$
(4)

and

$$\begin{aligned} F^{'}=b F+d F^{M}, b\ne 0, d\ne 0, M\in R-\{0,1,2\}. \end{aligned}$$
(5)

here \(F\left( \eta \right) \) is Bernoulli differential polynomial. Inserting Eq. (6) into Eq. (5) as well as using Eq. (7) produces:

$$\begin{aligned} \varOmega (F(\eta ))={{b}_{k}}F{{(\eta )}^{s}}+\cdots +{{b }_{1}}F(\eta )+{{b }_{0}}=0, \end{aligned}$$
(6)

via the balance principle, the connection of n and M will be evaluate.

By taking all the coefficients of \(\varOmega (F(\eta ))\) to be zero, we get an algebraic equations system:

$$\begin{aligned} b_{i}=0,\,\,\,i=0,\cdots ,k, \end{aligned}$$
(7)

solving Eq. (9), we will find the values of \({{a}_{0}},{{a}_{1}},...,{{a}_{n}}.\)

Step 4. Solving Bernoulli Eq. (7), two cases are observed depending on the values of b and d:

$$\begin{aligned} F(\eta )={{\left[ \frac{-d}{b}+\frac{E}{{{e}^{b(M-1)\eta }}} \right] }^{\frac{1}{1-M}}},b\ne d, \end{aligned}$$
(8)
$$\begin{aligned} F(\eta )={{\left[ \frac{(E-1)+(E+1)\tanh \left( \frac{b(1-M)\eta }{2} \right) }{1-\tanh \left( \frac{b(1-M)\eta }{2} \right) } \right] }^{\frac{1}{1-M}}},b=d,E\in R. \end{aligned}$$
(9)

Where E is the non-zero constant of integration, with the help of Mathematical packages, we gain the solutions to Eq. (5), using a complete polynomial discrimination system. Also, all the solutions gained in this method are plotted and the suitable parameter values on (1+1)-dimensional surfaces of solutions are taken into account.

3 The (2+1)-Dimensional Davey-Stewartson Equations

In this article, the Davey-Stewartson equations in dimensional [49, 50] are considered

$$\begin{aligned} i{{\phi }_{t}}+\frac{1}{2}{{\sigma }^{2}}\left( {{\phi }_{xx}}+{{\sigma }^{2}}{{\phi }_{yy}} \right) +\text { }\!\!\lambda \!\!\text { }\!\!~\!\!\text { }{{\left| \phi \right| }^{2}}\phi -\phi \,{{\psi }_{x}}=0, \end{aligned}$$
(10)
$$\begin{aligned} {{\psi }_{xx}}-{{\sigma }^{2}}{{\psi }_{yy}}-2\text { }\!\!\lambda \!\!\text { }{{\left( \text { }\!\!~\!\!\text { }{{\left| \phi \right| }^{2}} \right) }_{x}}=0, \end{aligned}$$
(11)

here \(\phi \left( x,y,t \right) \) and \(\psi \left( x,y,t \right) \) represents the dependent variables while, x and y are the independent variables axes as well as is represent a time-independent variable. Also, \(\sigma \) and \(\lambda \) represent constant coefficients. First of all we convert the (2+1)-dimensional imaginary Davey-Stewartson equations into a system of nonlinear ODE to study and analyze its exact solutions.

Using the following transformation:

$$\begin{aligned} \phi \left( x,y,t \right) ={{e}^{i\theta }}u\left( \xi \right) ,\,\,\psi \left( x,y,t \right) =v\left( \xi \right) ,\,\xi =\mu \left( x+y-\eta t \right) ,\,\theta =\kappa x+\lambda y+\beta t. \end{aligned}$$
(12)

where \(\mu ,\eta ,\kappa ,\lambda \) and \(\beta \) are real constants. Applying Eq. (12), the (2+1)-dimensional Davey-Stewartson equations are changed to

$$\begin{aligned} {{\mu }^{2}}\left( 1-{{\sigma }^{2}}-2{{\sigma }^{4}} \right) {u}''-\left( \beta +{{\kappa }^{2}}{{\sigma }^{2}}+{{\lambda }^{2}} \right) u-uv+\kappa {{u}^{3}}=0, \end{aligned}$$
(13)
$$\begin{aligned} \mu \left( \eta -2\kappa {{\sigma }^{2}}-2\lambda \right) i\,{u}'=0, \end{aligned}$$
(14)
$$\begin{aligned} -{{\mu }^{2}}\left( 1-{{\sigma }^{2}} \right) {{v}^{''}}+4\kappa {{\mu }^{2}}\left( u{{u}^{''}}+{{u}^{{{'}^{2}}}} \right) =0. \end{aligned}$$
(15)

Integrating Eq. (15) twice with respect to \(\xi \) and taking the constant of integration to be zero, one gets

$$\begin{aligned} v=\frac{2\kappa }{1-{{\sigma }^{2}}}{{u}^{2}}\,. \end{aligned}$$
(16)

Finding the close solution, we find from Eq. (14) that

$$\begin{aligned} \eta =2\kappa {{\sigma }^{2}}+2\lambda . \end{aligned}$$
(17)

Now substituting Eq. (16) into Eq. (13), we get

$$\begin{aligned} {{\mu }^{2}}\left( 1-{{\sigma }^{2}} \right) \left( 1-{{\sigma }^{2}}-2{{\sigma }^{4}} \right) {{u}^{''}}-\left( 1-{{\sigma }^{2}} \right) \left( \beta +{{\kappa }^{2}}{{\sigma }^{2}}+{{\lambda }^{2}} \right) u-\kappa \left( 1+{{\sigma }^{2}} \right) {{u}^{3}}=0. \end{aligned}$$
(18)

Now to evaluate the balances between and, the relationship between and can written

$$\begin{aligned} M=n+1. \end{aligned}$$
(19)

Case 1. Using \(n=2\), \(M=3\) and then substituting them into Eq. (4) with using Eq. (5), the following equations are obtained:

$$\begin{aligned} u={{a}_{0}}+{{a}_{1}}F+{{a}_{2}}{{F}^{2}}, \end{aligned}$$
(20)
$$\begin{aligned} {{u}^{'}}={{a}_{1}}bF+{{a}_{1}}d{{F}^{3}}+2{{a}_{2}}b{{F}^{2}}+2{{a}_{2}}d{{F}^{4}}, \end{aligned}$$
(21)
$$\begin{aligned} {u}''={{a}_{1}}{{b}^{2}}F+4{{a}_{2}}{{b}^{2}}{{F}^{2}}+4{{a}_{1}}bd{{F}^{3}}+12{{a}_{2}}bd{{F}^{4}}+3{{a}_{1}}{{d}^{2}}{{F}^{5}}+8{{a}_{2}}{{d}^{2}}{{F}^{6}}, \end{aligned}$$
(22)

where \({{a}_{2}}\ne 0,\,b\ne 0,\,d\ne 0.\) Substituting Eqs. (20–22) into Eq. (18), a system of algebraic equations are found. Inserting Eqs. (8) or (9) into a system of algebraic equations, we can investigate the following solutions:

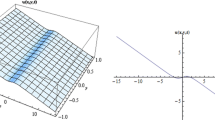
Case 1a. For \({{a}_{0}}=\frac{b\mu \sqrt{2-6{{\sigma }^{2}}+4{{\sigma }^{4}}}}{\sqrt{\kappa }}\), \({{a}_{1}}=0,{{a}_{2}}=\frac{2d\mu \sqrt{2-6{{\sigma }^{2}}+4{{\sigma }^{4}}}}{\sqrt{\kappa }}\), \(\beta =-{{\lambda }^{2}}-{{\kappa }^{2}}{{\sigma }^{2}}+2{{b}^{2}}{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) \), we get (Fig. 1)

$$\begin{aligned} \phi \left( x,y,t \right) \text {=}\frac{b\mu \sqrt{2-6{{\sigma }^{2}}+4{{\sigma }^{4}}}{{\text {e}}^{\text {i}\left( \beta t+\kappa x+\lambda y \right) }}\left( d{{\text {e}}^{2b\mu \left( x+y-2\left( \lambda +\kappa {{\sigma }^{2}} \right) t \right) }}+bE \right) }{\sqrt{\kappa }\left( -d{{\text {e}}^{2b\mu \left( x+y-2\left( \lambda +\kappa {{\sigma }^{2}} \right) t \right) }}+bE \right) }, \end{aligned}$$
(23)
$$\begin{aligned} \psi \left( x,y,t \right) =-\frac{4{{b}^{2}}{{\mu }^{2}}\left( -1+2{{\sigma }^{2}} \right) {{\left( d{{\text {e}}^{2b\mu \left( x+y-2\left( \lambda +\kappa {{\sigma }^{2}} \right) t \right) }}+bE \right) }^{2}}}{{{\left( d{{\text {e}}^{2b\mu \left( x+y-2\left( \lambda +\kappa {{\sigma }^{2}} \right) t \right) }}-bE \right) }^{2}}}. \end{aligned}$$
(24)
Fig. 1.
figure 1

3D surfaces with its 2D figures of Eqs. (21) and (22) with values \(b=1,d=-1,E=1,\sigma =0.1,\kappa =0.1,t=0.5,\mu =0.1,\lambda =1\) and \(y=2\) for 2D surface.

Full size image

Case 1b. \(\lambda =\sqrt{-\alpha +{{\kappa }^{2}}}\), \(\sigma =i\), we get (Fig. 2)

$$\begin{aligned} \phi \left( x,y,t \right) \text {=}{{\text {e}}^{\text {i}\left( \beta t+\kappa x+\lambda y \right) }}\left( {{a}_{0}}+\frac{{{a}_{2}}}{-\frac{d}{b}+E{{\text {e}}^{-2b\xi }}}+\frac{{{a}_{1}}}{\sqrt{-\frac{d}{b}+E{{\text {e}}^{-2b\xi }}}} \right) , \end{aligned}$$
(25)
$$\begin{aligned} \psi \left( x,y,t \right) =\kappa {{\left( {{a}_{0}}+\frac{{{a}_{2}}}{-\frac{d}{b}+E{{\text {e}}^{-2b\xi }}}+\frac{{{a}_{1}}}{\sqrt{-\frac{d}{b}+E{{\text {e}}^{-2b\xi }}}} \right) }^{2}}. \end{aligned}$$
(26)
Fig. 2.
figure 2

3D surfaces with its 2D figures of Eqs. (23) and (24) with values \(b=1,d=-1,E=0.1,\kappa =2,{{a}_{0}}=0.1,{{a}_{2}}=0.1,{{a}_{1}}=0.2,t=0.5,\mu =0.1,\alpha =-0.5\) and \(y=2\) for 2D surface.

Full size image

Case 2. If taking \(n=3\) and \(M=4\) in Eq. (4) with using Eq. (5), the following equations are found:

$$\begin{aligned} u={{a}_{0}}+{{a}_{1}}F+{{a}_{2}}{{F}^{2}}+{{a}_{3}}{{F}^{3}}, \end{aligned}$$
(27)
$$\begin{aligned} {u}'={{a}_{1}}bF+2{{a}_{2}}b{{F}^{2}}+3{{a}_{3}}b{{F}^{3}}+{{a}_{1}}d{{F}^{4}}+2{{a}_{2}}d{{F}^{5}}+3{{a}_{3}}d{{F}^{6}}, \end{aligned}$$
(28)
$$\begin{aligned} \begin{aligned}&{u}''={{a}_{1}}{{b}^{2}}F+4{{a}_{2}}{{b}^{2}}{{F}^{2}}+9{{a}_{3}}{{b}^{2}}{{F}^{3}}+5{{a}_{1}}bd{{F}^{4}}+14{{a}_{2}}bd{{F}^{5}} \\&\,\,\,\,\,\,\,\,\,\,\,\,+\,27{{a}_{3}}bd{{F}^{6}}+4{{a}_{1}}{{d}^{2}}{{F}^{7}}+10{{a}_{2}}{{d}^{2}}{{F}^{8}}+18{{a}_{3}}{{d}^{2}}{{F}^{9}},\\ \end{aligned} \end{aligned}$$
(29)

where \({{a}_{3}}\ne 0,b\ne 0,d\ne 0.\) putting Eqs. (27–29) into Eq. (18), a system of algebraic equations is evaluated. Solving this system the following cases and solutions have resulted:

Case 2a. When \({{a}_{0}}=-\frac{\mu \sqrt{\beta +{{\lambda }^{2}}+{{\kappa }^{2}}{{\sigma }^{2}}}\sqrt{1-3{{\sigma }^{2}}+2{{\sigma }^{4}}}}{\sqrt{\kappa }\sqrt{{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) }}\), \({{a}_{1}}=0\), \({{a}_{2}}=0\), \({{a}_{3}}=-\frac{3d\mu \sqrt{2-6{{\sigma }^{2}}+4{{\sigma }^{4}}}}{\sqrt{\kappa }}\), \(b=\frac{\sqrt{2}\sqrt{\beta +{{\lambda }^{2}}+{{\kappa }^{2}}{{\sigma }^{2}}}}{3\sqrt{{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) }}\), we obtain (Fig. 3)

$$\begin{aligned} \phi \left( x,y,t \right) \text {=}{{\text {e}}^{\text {i}\left( \beta t+\kappa x+y\lambda \right) }}\frac{\mu \sqrt{B}}{\sqrt{\kappa }}\left( -\frac{3\sqrt{2}d}{-\frac{d}{b}+E{{\text {e}}^{-3b\xi }}}-\frac{\sqrt{A}}{\sqrt{{{\mu }^{2}}B}} \right) , \end{aligned}$$
(30)
$$\begin{aligned} \psi \left( x,y,t \right) =-\frac{2{{\left( bE\sqrt{A}-d{{\text {e}}^{3b\xi }}\left( \sqrt{A}-3\sqrt{2}b\sqrt{{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) } \right) \right) }^{2}}}{{{\left( d{{\text {e}}^{3b\xi }}-bE \right) }^{2}}\left( 1+{{\sigma }^{2}} \right) }, \end{aligned}$$
(31)

where \(A=\beta +{{\lambda }^{2}}+{{\kappa }^{2}}{{\sigma }^{2}}\) and \(B=1-3{{\sigma }^{2}}+2{{\sigma }^{4}}.\)

Fig. 3.
figure 3

3D surfaces with its 2D figures of Eqs. (30) and (31) with values \(d=-1,E=1,\sigma =2,\kappa =1,t=1/2,\mu =0.1,\alpha =0.5,\lambda =1\) and \(y=2\) for 2D surface.

Full size image

Case 2b. When \({{a}_{0}}=-\frac{\mu \sqrt{\beta +{{\lambda }^{2}}+{{\kappa }^{2}}{{\sigma }^{2}}}\sqrt{1-3{{\sigma }^{2}}+2{{\sigma }^{4}}}}{\sqrt{\kappa }\sqrt{{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) }}\), \({{a}_{1}}=0\), \({{a}_{2}}=0\), \({{a}_{3}}=-\frac{3d\mu \sqrt{2-6{{\sigma }^{2}}+4{{\sigma }^{4}}}}{\sqrt{\kappa }}\), \(b=\frac{\sqrt{2}\sqrt{\beta +{{\lambda }^{2}}+{{\kappa }^{2}}{{\sigma }^{2}}}}{3\sqrt{{{\mu }^{2}}\left( -1+{{\sigma }^{2}}+2{{\sigma }^{4}} \right) }}\), we obtain (Fig. 4)

$$\begin{aligned} \phi \left( x,y,t \right) \text {=}{{\text {e}}^{\text {i}\left( \beta t+\kappa x+\lambda y \right) }}\left( \begin{aligned}&{{a}_{0}}+\frac{{{a}_{3}}}{-\frac{d}{b}+E{{\text {e}}^{-3b\xi }}}+\frac{{{a}_{2}}}{{{\left( -\frac{d}{b}+E{{\text {e}}^{-3b\xi }} \right) }^{2/3}}}+ \\&\frac{{{a}_{1}}}{{{\left( -\frac{d}{b}+E{{\text {e}}^{-3b\xi }} \right) }^{1/3}}} \\ \end{aligned} \right) , \end{aligned}$$
(32)
$$\begin{aligned} \psi \left( x,y,t \right) =\kappa {{\left( {{a}_{0}}+\frac{{{a}_{3}}}{-\frac{d}{b}+E{{\text {e}}^{-3b\xi }}}+\frac{{{a}_{2}}}{{{\left( -\frac{d}{b}+E{{\text {e}}^{-3b\xi }} \right) }^{2/3}}}+\frac{{{a}_{1}}}{{{\left( -\frac{d}{b}+E{{\text {e}}^{-3b\xi }} \right) }^{1/3}}} \right) }^{2}}. \end{aligned}$$
(33)
Fig. 4.
figure 4

3D surfaces with its 2D figures of Eqs. (32) and (33) with values \(b=1,d=-1,{{a}_{0}}=0,{{a}_{1}}=0.4,{{a}_{2}}=0.1,{{a}_{3}}=0.1,E=1,t=0.5,\mu =0.1,\alpha =0.5,\lambda =2\) and \(y=2\) for 2D surface.

Full size image

4 Conclusion

In this researcher, the Bernoulli sub-equation is used to find some novel solutions of (2 + 1)-dimensional imaginary Davey-Stewartson equations with different physical parameters by utilizing the Wolfram Mathematica package. These methods with using computer-based symbolic computation utilized to construct broad classes of soliton solutions of nonlinear differential equations that arise in applied physics. Our resultant may appreciate and useful in some sciences like mathematical physics, applied physics, and engineering in terms of nonlinear science. Moreover, the method proposed in this paper, should be reliable, effective, provide more solutions as well. These methods may be applied to other nonlinear partial differential equations.