1 Introduction

In recent years, the study of traveling wave solutions of nonlinear evolution equations (NLEEs) of fractional order have attracted many mathematicians and physicists in exploring new research areas of nonlinear sciences such as nonlinear optics, plasma physics, relativity, solid state physics, biomechanics etc. For explaining the motion of isolated waves, the use of NLEEs is very important whose exact solutions reflect the structure of complex physical phenomena (Akter and Ali 2015). A good deal of methods have been formulated to tackle NLEEs such as homogeneous balance method (Wang 1995; Zayed et al. 2004), Jacobi elliptic function method (Ali 2011), tanh-function method (Malfliet 1992; Fan 2000; Abdou 2007), truncated painleve expansion method (Weiss et al. 1983), sine–cosine method (Bibi and Mohyud-Din 2014), homotopy perturbation method (Tauseef Mohyud-Din et al. 2011a, b) Hirota bilinear transformation method (Hirota and Satsuma 1981), F-expansion method (Wang and Li 2005), etc. In this work, we apply (G′/G)-expansion method, introduced by Wang et al. (2008) that was further modified in Zheng (2012) for solution of differential equations of fractional order. The method includes fractional complex transformation (He et al. 2012; Wang 2006; Li and He 2010), and modified Riemann–Liouville fractional differential operator (Jumarie 2006, 2009) to seek traveling wave solutions of two pivotal nonlinear problems, namely, the fractional Benny–Luke equation and the fractional Phi-4 equation (Akter and Ali 2015). The former describes an approximation of full water wave equations and is formally appropriate for portraying two-way water propagation in the presence of surface tension (Akter and Ali 2015), and the latter holds a considerable role in particle physics, related to the interaction between kink and antikink solitary waves (Doha et al. 2009).

2 The G′/G-expansion method

Consider nonlinear fractional partial differential equation containing higher order derivatives as well as nonlinear terms

$$P\left( {u,\frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }},\frac{{\partial^{\beta } u}}{{\partial x^{\beta } }},\frac{{\partial^{\gamma } u}}{{\partial y^{\gamma } }}, \ldots } \right) = 0,$$
(1)

u being a function to be known and P is a polynomial of u and its partial fractional operators.

  • Step 1 Using the fractional complex transformation (He et al. 2012; Wang 2006; Li and He 2010)

    $$u = \varvec{u}(\xi ),{\text{where}} = L\frac{{t^{\alpha } }}{\varGamma (\alpha + 1)} + K\frac{{x^{\beta } }}{\varGamma (\beta + 1)} + M\frac{{y^{\gamma } }}{\varGamma (\gamma + 1)},$$
    (2)

    We obtain the following ODE

    $$P(u,u^{\prime},u^{\prime\prime},u^{\prime\prime\prime}, \ldots ) = 0.$$
    (3)

    If possible, we integrate the above equation term by term once or more times.

  • Step 2 We assume that the solution of Eq. (1) can be expressed in the form as follows

    $$\varvec{u}(\xi ) = \sum\limits_{i = - m}^{m} {\alpha_{i} \left( {\frac{{G^{\prime}}}{G}} \right)^{i} } ,\alpha_{m} \ne 0,$$
    (4)

    where α i ’s are constants and G(ξ) satisfies the equation

    $$G^{\prime\prime}(\xi ) + \lambda G^{\prime}(\xi ) + \mu G(\xi ) = 0.$$
    (5)

  • Step 3 By using homogeneous balance principle, we determine the value of m by balancing the higher order derivatives and nonlinear terms that appear in (3), substitute Eq. (4) into Eq. (3) and using Eq. (5), collect all the terms with the same order of (G′/G) together. Then we equate each coefficient of the obtained polynomial to zero that will give us a system of algebraic equations that can be solved for the values of K, L, M, N, λ, μ, α i , \(i = 0, \pm 1, \pm 2, \pm 3, \ldots \pm m.\)

  • Step 4 After solving system of algebraic equations and using Eq. (5), different traveling wave solutions can be extracted by using generalized solutions of this equation:

    $$\frac{{G^{\prime}}}{G} = \left\{ {\begin{array}{*{20}l} {\frac{ - \lambda }{{\mathbf{2}}} + \sqrt {\frac{{\lambda^{2} - 4\mu }}{2}} \left( {\frac{{A\sinh \left( {\frac{\xi }{2}\sqrt {\lambda^{2} - 4\mu } } \right) + B\cosh \left( {\frac{\xi }{2}\sqrt {\lambda^{2} - 4\mu } } \right)}}{{A\cosh \left( {\frac{\xi }{2}\sqrt {\lambda^{2} - 4\mu } } \right) + B\sinh \left( {\frac{\xi }{2}\sqrt {\lambda^{2} - 4\mu } } \right)}}} \right),\quad \lambda^{2} - 4\mu > 0,} \hfill \\ {\frac{ - \lambda }{{\mathbf{2}}} + \sqrt {\frac{{4\mu - \lambda^{2} }}{2}} \left( {\frac{{A\sin \left( {\frac{\xi }{2}\sqrt {4\mu - \lambda^{2} } } \right) + B\cos \left( {\frac{\xi }{2}\sqrt {4\mu - \lambda^{2} } } \right)}}{{A\cos \left( {\frac{\xi }{2}\sqrt {4\mu - \lambda^{2} } } \right) + B\sin \left( {\frac{\xi }{2}\sqrt {4\mu - \lambda^{2} } } \right)}}} \right),\quad \lambda^{2} - 4\mu < 0,} \hfill \\ {\frac{ - \lambda }{{\mathbf{2}}} + \frac{B}{{A + B\xi^{\prime}}},\quad \lambda^{2} - 4\mu = 0,} \hfill \\ \end{array} } \right.$$
    (6)

    where A and B are arbitrary constants.

3 Applications of \(\left( {G^{\prime}/G} \right)\)-expansion method

3.1 The Benny–Luke equation

Consider the Benny–Luke equation of the form

$$u_{tt} - u_{xx} + \gamma u_{xxxx} - \delta u_{xxtt} + u_{t} u_{xx} + 2u_{x} u_{xt} = 0,$$
(7)

where \(\gamma\) and \(\delta\) are positive parameters, linked to the inverse bond number, whose characteristics is to capture the effects of surface tension and the gravity forces. Fractional version of this equation can be interpreted as

$$D_{tt}^{2\alpha } u - D_{xx}^{2\beta } u + \gamma D_{xxxx}^{4\beta } u - \delta D_{xxtt}^{2\alpha + 2\beta } u + D_{t}^{\alpha } uD_{xx}^{2\beta } u + 2D_{x}^{\beta } uD_{xt}^{\alpha + \beta } u = 0, \quad 0 < \alpha ,\beta \le 1,$$
(8)

We use following complex transformation

$$\varvec{u} = \varvec{u}\left( \xi \right), \xi = L\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + K\frac{{x^{\beta } }}{{\varGamma \left( {\beta + 1} \right)}} ,$$
(9)

along with Jumarie’s modified Riemann–Liouville derivative, to convert (8) into the ODE that is further integrated (neglecting constant of integration) to obtain

$$(L^{2} - K^{2} )\varvec{u^{\prime}} + K^{2} \left( {\gamma K^{2} - \delta L^{2} } \right)\varvec{u^{\prime\prime\prime}} + \frac{3}{2}LK^{2} \left( {u^{\prime}} \right)^{2} = 0,$$
(10)

after homogeneous balancing, we obtain \(m = 1\), so that our supposed solution is

$$\varvec{u}\left( \xi \right) = \alpha_{ - 1} \left( {\frac{{G^{\prime}}}{G}} \right)^{ - 1} + \alpha_{0} + \alpha_{1} \left( {\frac{{G^{\prime}}}{G}} \right),$$
(11)

where \(\alpha_{ - 1} ,\alpha_{0} ,\alpha_{1}\) are arbitrary constants. On substituting Eq. (11) into Eq. (10), and by using step no. 3 as described above, we obtain a system of equations and solve it for arbitrary constants \(\alpha_{ - 1} ,\alpha_{0} ,\alpha_{1} ,\lambda ,\mu ,L,K,\;{\text{and}}\;M\), yielding following cases yielding their respective traveling wave solutions.

  • Case 1

    $$\begin{aligned} & \alpha_{ - 1} = \frac{1}{4}\frac{{K^{2} - L^{2} }}{{K^{2} L}},\quad \alpha_{0} = \alpha_{0} ,\quad \alpha_{1} = \frac{{4K^{2} \left( {\gamma K^{2} - \delta L^{2} } \right)}}{L}, \quad \lambda = 0, \\ & \quad \mu = \frac{ - 1}{16}\frac{{K^{2} - L^{2} }}{{K^{2} \left( {\gamma K^{2} - \delta L^{2} } \right)}},\quad L = L, \quad K = K. \\ \end{aligned}$$
    (12)

    The traveling wave solutions for above case, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\begin{aligned} \varvec{u}_{{\mathbf{1}}} \left( \xi \right) & = \alpha_{0} + \frac{{\left( {K^{2} - L^{2} } \right)\left( {A\cosh \left( {\frac{1}{4}\xi\upkappa} \right) + B\sinh \left( {\frac{1}{4}\xi\upkappa} \right)} \right)}}{{K^{2} L\upkappa(A\sinh \left( {\frac{1}{4}\xi\upkappa} \right) + B\cosh \left( {\frac{1}{4}\xi\upkappa} \right) }} \\ & \quad + \,\frac{{\left( {K^{2} \gamma - L^{2} \delta } \right)\kappa \left( {A\sinh \left( {\frac{1}{4}\xi\upkappa} \right) + B\cosh \left( {\frac{1}{4}\xi \kappa } \right)} \right)}}{{L(\left( {A\cosh \left( {\frac{1}{4}\xi\upkappa} \right) + B\sinh \left( {\frac{1}{4}\xi \kappa } \right)} \right) }}, \\ \end{aligned}$$
    (13)

    where \(\kappa = \sqrt {\frac{{K^{2} - L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{2}}} \left( \xi \right) & = \alpha_{0} + \frac{{\left( {K^{2} - L^{2} } \right)\left( {A\cos \left( {\frac{1}{4}\xi \kappa } \right) + B\sin \left( {\frac{1}{4}\xi \kappa } \right)} \right)}}{{K^{2} L\kappa \left( { - A\sin \left( {\frac{1}{4}\xi \kappa } \right) + B\cos \left( {\frac{1}{4}\xi \kappa } \right)} \right)}} \\ & \quad + \,\frac{{\left( {K^{2} \gamma - L^{2} \delta } \right)\kappa \left( { - A\sin \left( {\frac{1}{4}\xi \kappa } \right) + B\cos \left( {\frac{1}{4}\xi\upkappa} \right)} \right)}}{{L\left( {A\cos \left( {\frac{1}{4}\xi \kappa } \right) + B\sin \left( {\frac{1}{4}\xi \kappa } \right)} \right)}}, \\ \end{aligned}$$
    (14)

    where \(\kappa = \sqrt {\frac{{L^{2} - K^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\varvec{u}_{{\mathbf{3}}} \left( \xi \right) = \alpha_{0} + \frac{1}{4}\frac{{\left( {K^{2} - L^{2} } \right)\left( {B\xi + A} \right)}}{{K^{2} LB}} + 4\frac{{\left( {K^{2} \gamma - L^{2} \delta } \right)B}}{{L\left( {B\xi + A} \right)}}.$$
    (15)

  • Case 2

    $$\begin{aligned} & \alpha_{ - 1} = 0,\quad \alpha_{0} = \alpha_{0} ,\quad \alpha_{1} = - 4\frac{{K\left( {\gamma - \delta } \right)}}{{K^{2} \delta \lambda^{2} - 1}}\left( {\sqrt {\frac{{K^{2} \gamma \lambda^{2} - 1}}{{K^{2} \delta \lambda^{2} - 1}}} } \right)^{ - 1} ,\quad \lambda = \lambda , \\ & \quad \mu = \mu ,\quad L = \sqrt {\frac{{K^{2} \gamma \lambda^{2} - 1}}{{K^{2} \delta \lambda^{2} - 1}}} K, \quad K = K. \\ \end{aligned}$$
    (16)

    The traveling wave solutions for above case, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\varvec{u}_{{\mathbf{4}}} \left( \xi \right) = \alpha_{0} - 4\frac{{K\left( {\gamma - \delta } \right)}}{{K^{2} \delta \lambda^{2} - 1}}\left( {\frac{1}{2}\frac{{\lambda \left( {A\sinh \left( {\frac{\lambda }{2}\xi } \right) + B\cosh \left( {\frac{\lambda }{2}\xi } \right)} \right)}}{{A\cosh \left( {\frac{\lambda }{2}\xi } \right) + B\sinh \left( {\frac{\lambda }{2}\xi } \right)}} - \frac{\lambda }{2}} \right)\left( {\sqrt {\frac{{K^{2} \gamma \lambda^{2} - 1}}{{K^{2} \delta \lambda^{2} - 1}}} } \right)^{ - 1} .$$
    (17)
    $$\varvec{u}_{{\mathbf{5}}} \left( \xi \right) = \alpha_{0} - 4\frac{{K\left( {\gamma - \delta } \right)}}{{K^{2} \delta \lambda^{2} - 1}}\left( {\frac{1}{2}\frac{{i\lambda \left( { - iA\sinh \left( {\frac{\lambda }{2}\xi } \right) + B\cosh \left( {\frac{\lambda }{2}\xi } \right)} \right)}}{{{\text{Acosh}}\left( {\frac{\lambda }{2}\xi } \right) + iB\sinh \left( {\frac{\lambda }{2}\xi } \right)}} - \frac{\lambda }{2}} \right)\left( {\sqrt {\frac{{K^{2} \gamma \lambda^{2} - 1}}{{K^{2} \delta \lambda^{2} - 1}}} } \right)^{ - 1} .$$
    (18)
    $$\varvec{u}_{{\mathbf{6}}} \left( \xi \right) = \alpha_{0} - 4\frac{{K\left( {\gamma - \delta } \right)}}{{K^{2} \delta \lambda^{2} - 1}}\left( { - \frac{\lambda }{2} + \frac{B}{B\xi + A}} \right)\left( {\sqrt {\frac{{K^{2} \gamma \lambda^{2} - 1}}{{K^{2} \delta \lambda^{2} - 1}}} } \right)^{ - 1} .$$
    (19)

  • Case 3

    $$\begin{aligned} \varvec{ } & \alpha_{ - 1} = 0, \quad \alpha_{0} = \alpha_{0} , \quad \alpha_{1} = 4\frac{{\left( {K^{2} \gamma - L^{2} } \right)}}{\text{L}}, \quad \lambda = \lambda , \quad L = L, \\ & \quad K = K,\quad \mu = \frac{1}{4}\frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}. \\ \end{aligned}$$
    (20)

    The traveling wave solutions for above case, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\varvec{u}_{{\mathbf{7}}} \left( \xi \right) = \alpha_{0} + \frac{4}{L}(K^{2} \gamma - L^{2} \delta )\left( {\frac{1}{2}\frac{{\kappa \left( {A\sinh \left( {\frac{1}{2}\xi \kappa } \right) + B\cosh \left( {\frac{1}{2}\xi\upkappa} \right)} \right) }}{{A\cosh \left( {\frac{1}{2}\xi \kappa } \right) + B\sinh \left( {\frac{1}{2}\xi \kappa } \right) }} - \frac{1}{2}\lambda } \right),$$
    (21)

    where \(\kappa = \sqrt {\lambda^{2} - \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\varvec{u}_{{\mathbf{8}}} \left( \xi \right) = \alpha_{0} + \frac{4}{L}(K^{2} \gamma - L^{2} \delta )\left( {\frac{1}{2}\frac{{\kappa \left( { - A\sin \left( {\frac{1}{2}\xi \kappa } \right) + B\cos \left( {\frac{1}{2}\xi\upkappa} \right)} \right) }}{{A\cos \left( {\frac{1}{2}\xi \kappa } \right) + B\sin \left( {\frac{1}{2}\xi \kappa } \right) }} - \frac{1}{2}\lambda } \right),$$
    (22)

    where \(\kappa = \sqrt { - \lambda^{2} + \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\varvec{u}_{{\mathbf{9}}} \left( \xi \right) = \alpha_{0} + 4\frac{{K^{2} \gamma - L^{2} \delta }}{L}\left( { - \frac{\lambda }{2} + \frac{B}{B\xi + A}} \right).$$
    (23)

  • Case 4

    $$\begin{aligned} & \alpha_{ - 1} = - \frac{{\left( {K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} } \right)}}{{K^{2} L}},\quad \mu = \frac{1}{4}\frac{{\left( {K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} } \right)}}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}, \\ & \quad \alpha_{0} = \alpha_{0} , \quad \alpha_{1} = 0, \quad \lambda = \lambda , \quad L = L, \quad K = K. \\ \end{aligned}$$
    (24)

    The traveling wave solutions for above case, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows (Fig. 1)

    $$\varvec{u}_{{{\mathbf{10}}}} \left( \xi \right) = \alpha_{0} - \frac{{\left( {K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} } \right)}}{{2K^{2} L}}\left( {\frac{{\kappa \left( {A\sinh \left( {\frac{1}{2}\xi \kappa } \right) + B\cosh \left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{{\text{Acosh}}\left( {\frac{1}{2}\xi \kappa } \right) + B\sinh \left( {\frac{1}{2}\xi \kappa } \right)}} - \frac{\lambda }{2}} \right)^{ - 1} ,$$
    (25)

    where \(\kappa = \sqrt {\lambda^{2} - \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\varvec{u}_{{{\mathbf{11}}}} \left( \xi \right) = \alpha_{0} - \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{2K^{2} L}} \left( {\frac{{\kappa \left( { - {\text{Asin}}\left( {\frac{1}{2}\xi \kappa } \right) + {\text{Bcos}}\left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{{\text{Acos}}\left( {\frac{1}{2}\xi \kappa } \right) + {\text{Bsin}}\left( {\frac{1}{2}\xi \kappa } \right)}} - \frac{\lambda }{2}} \right)^{ - 1} ,$$
    (26)

    where \(\kappa = \sqrt { - \lambda^{2} + \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} \left( {K^{2} \gamma - L^{2} \delta } \right)}}} .\)

    $$\varvec{u}_{{{\mathbf{12}}}} \left( \xi \right) = \alpha_{0} - \frac{{K^{4} \gamma \lambda^{2} - K^{2} L^{2} \delta \lambda^{2} - K^{2} + L^{2} }}{{K^{2} L}}\left( { - \frac{\lambda }{2} + \frac{B}{B\xi + A}} \right)^{ - 1} .$$
    (27)

    For all of the above solutions,\(\xi = L\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + K\frac{{x^{\beta } }}{{\varGamma \left( {\beta + 1} \right)}}\).

Fig. 1
figure 1

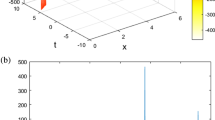
Graphical view of solitary wave solutions of Benny–Luke equation for α = β= 0.25, 0.5, 0.75, 0.85 and 1, depicted by gray, red, yellow, green and blue colors respectively. Case 1: a solution (13) for α 0 = 1, A = 1, B = 0, γ = 2, δ = 1, K = 4, L = 3, (0 < x < 10) and (0 < t < 10). b Solution (14) for α 0 = 1, A = − 1, B = 0, γ = 3, δ = 1, K = 3, L = 4, (0 < x < 10) and (0 < t < 10). c Solution (15) for α 0 = 1, A = − 1, B = 1, γ = 3, δ = 1, K = 4, L = 3, (0 < x < 10) and (0 < t < 10). Case 2: a solution (17) for α 0 = 1, A = − 1, B = 1, λ = 1, γ = 2, δ = 3, K = 2, (0 < x < 10) and (0 < t < 10). b Solution (18) for α 0 = 1, A = − 1, B = 1, λ = 1, γ = 2, δ = 3, K = 10, (0.5 < x < 5) and (0.5 < t < 5). c Solution (19) for α 0 = 1, A = − 8, B = 1, λ = 1, γ = 1, δ = 3, K = 2, (− 2 < x < 5) and (− 2 < t < 10). Case 3: a solution (21) for α 0 = 1, A = 1, B = 0, λ = 3, γ = 3, δ = 1, K = 4, L = 3, (0 < x < 10) and (0 < t < 10). b Solution (22) for α 0 = 1, A = 1, B = 0, λ = 1, γ = 2, δ = 1, K = 1, L = 2, (− 15 < x < 10) and (− 15 < t < 10). c Solution (23) for α 0 = 1, A = 0, B = − 1, λ = − 3, γ = 3, δ = 1, K = 1, L = 3, (0 < x < 25) and (0 < t < 25). Case 4: a solution (25) for α 0 = 1, A = 1, B = 0, λ = 3, γ = 3, δ = 1, K = 4, L = 3, (− 20 < x < 20) and (− 20 < t < 20). b Solution (26) for α 0 = 1, A = 1, B = 0, λ = 2, γ = 2, δ = 1, K = 3, L = 1, (− 20 < x < 20) and (− 20 < t < 20). c Solution (26) for α 0 = 1, A = 1, B = − 3, λ = 1, γ = 1, δ = 3, K = 1, L = 1, (− 20 < x < 20) and (− 20 < t < 20). (Color figure online)

Full size image

3.2 The Phi-4 equation

Consider the Phi-4 equation of the form

$$u_{tt} - u_{xx} + m^{2} u + \sigma u^{3} = 0,$$
(28)

\(m,\) and \(\sigma\) being real constants. Fractional version of this equation can be interpreted as

$$D_{tt}^{2\alpha } u - D_{xx}^{2\beta } u + m^{2} u + \sigma u^{3} = 0, \quad 0 < \alpha ,\beta \le 1,$$
(29)

We use following complex transformation

$$\varvec{u} = \varvec{u}\left( \xi \right), \;\xi = L\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + K\frac{{x^{\beta } }}{{\varGamma \left( {\beta + 1} \right)}} ,$$
(30)

along with Jumarie’s modified Riemann–Liouville derivative, to convert (29) the ODE that is further integrated (neglecting constant of integration) to obtain

$$(L^{2} - K^{2} )\varvec{u^{\prime\prime}} + m^{2} \varvec{u} + \sigma \varvec{u}^{3} = 0,$$
(31)

after homogeneous balancing, we obtain \(m = 1\), so that our supposed solution is of the form (11), yielding following solution cases with their respective traveling wave solutions

  • Case 1

    $$\begin{aligned} & \alpha_{ - 1} = 0,\quad \alpha_{0} = \frac{{K^{2} - L^{2} }}{\sigma }\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \sigma } \right)^{ - 1} \\ & \alpha_{1} = \sqrt {2\frac{{L^{2} - K^{2} }}{\sigma }} ,\quad \lambda = \sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} ,\quad \mu = \mu ,\quad L = L, \quad K = K. \\ \end{aligned}$$
    (32)

    The traveling wave solutions for above cases, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\begin{aligned} \varvec{u}_{{\mathbf{1}}} \left( \xi \right) & = \frac{{K^{2} - L^{2} }}{\sigma }\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \sigma } \right)^{ - 1} \\ & \quad + \,\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \left( {\frac{1}{2}\frac{{\kappa \left( {{\text{Asinh}}\left( {\frac{1}{2}\xi \kappa } \right) + {\text{Bcosh}}\left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{{\text{Acosh}}\left( {\frac{1}{2}\xi \kappa } \right) + {\text{Bsinh}}\left( {\frac{1}{2}\xi \kappa } \right)}} - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right), \\ \end{aligned}$$
    (33)

    where \(\kappa = \sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }} - 4\mu } .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{2}}} \left( \xi \right) & = \frac{{K^{2} - L^{2} }}{\sigma }\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \sigma } \right)^{ - 1} \\ & \quad + \,\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \left( {\frac{1}{2} \frac{{\kappa \left( { - A\sin \left( {\frac{1}{2}\xi \kappa } \right) + B\cos \left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{{\text{Acos}}\left( {\frac{1}{2}\xi \kappa } \right) + B\sin \left( {\frac{1}{2}\xi \kappa } \right)}} - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right), \\ \end{aligned}$$
    (34)

    where \(\kappa = \sqrt {\frac{{ - 4K^{2} \mu + 4L^{2} \mu + 2m^{2} }}{{K^{2} - L^{2} }} + 4\mu } .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{3}}} \left( \xi \right) & = \frac{{K^{2} - L^{2} }}{\sigma }\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \sigma } \right)^{ - 1} \\ & \quad + \,\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \left( { - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} + \frac{B}{B\xi + A}} \right), \\ \end{aligned}$$
    (35)

  • Case 2

    $$\begin{aligned} & a_{ - 1} = \frac{1}{{K^{2} - L^{2} }}\left( { - \left( {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} \right)^{{\frac{3}{2}}} \sigma - \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} m^{2} } \right) \\ & \left( {\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} ,\quad \alpha_{0} = \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} , \\ & \quad \alpha_{1} = 0,\quad \lambda = \sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \\ & \quad \mu = \mu , \quad L = L,\quad K = K. \\ \end{aligned}$$
    (36)

    The traveling wave solutions for above cases, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\begin{aligned} \varvec{u}_{{\mathbf{4}}} \left( \xi \right) & = \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} - \frac{1}{{K^{2} - L^{2} }}\left( { - \left( { - \frac{{ - 2K^{2} \mu + 2L^{2} \mu + m^{2} }}{\sigma }} \right)^{{\frac{3}{2}}} \sigma } \right) \\ & \quad - \,\sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} m^{2} \left( {\sqrt {\frac{{ + 4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} \sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} \\ & \quad \left( {\frac{1}{2}\kappa \frac{{\left( {A\sinh \left( {\frac{1}{2}\xi \kappa } \right) + B\cosh \left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{\left( {{\text{Acosh}}\left( {\frac{1}{2}\xi\upkappa} \right) + {\text{Bsinh}}\left( {\frac{1}{2}\xi \kappa } \right)} \right)}} - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} , \\ \end{aligned}$$
    (37)

    where \(\kappa = \sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }} - 4\mu } .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{5}}} \left( \xi \right) & = \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} - \frac{1}{{K^{2} - L^{2} }}\left( { - \left( {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} \right)^{{\frac{3}{2}}} \sigma } \right) \\ & \quad - \,\sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} m^{2} \left( {\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} \\ & \quad \left( {\frac{1}{2}\kappa \frac{{\left( { - A\sin \left( {\frac{1}{2}\xi \kappa } \right) + B\cos \left( {\frac{1}{2}\xi \kappa } \right)} \right)}}{{\left( {{\text{Acos}}\left( {\frac{1}{2}\xi \kappa } \right) + {\text{Bsin}}\left( {\frac{1}{2}\xi \kappa } \right)} \right)}} - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} , \\ \end{aligned}$$
    (38)

    where \(\kappa = \sqrt {\frac{{ - 4K^{2} \mu + 4L^{2} \mu + 2m^{2} }}{{K^{2} - L^{2} }} + 4\mu } .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{6}}} \left( \xi \right) & = \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} \\ & \quad + \,\frac{1}{{K^{2} - L^{2} }}\left( { - \left( {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} \right)^{{\frac{3}{2}}} \sigma - \sqrt {\frac{{2K^{2} \mu - 2L^{2} \mu - m^{2} }}{\sigma }} m^{2} } \right) \\ & \quad \left( {\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} } \right)^{ - 1} \left( { - \frac{1}{2}\sqrt {\frac{{4K^{2} \mu - 4L^{2} \mu - 2m^{2} }}{{K^{2} - L^{2} }}} + \frac{B}{B\xi + A}} \right)^{ - 1} , \\ \end{aligned}$$
    (39)

  • Case 3

    $$\begin{aligned} & a_{ - 1} = - \frac{1}{2\sigma }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} ,\quad a_{0} = 0, \\ & \quad \alpha_{1} = \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} , \quad \lambda = 0, \quad \mu = - \frac{{m^{2} }}{{4\left( {K^{2} - L^{2} } \right)}},\quad L = L,\quad K = K. \\ \end{aligned}$$
    (40)

    The traveling wave solutions for above cases, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\begin{aligned} \varvec{u}_{{\mathbf{7}}} \left( \xi \right) & = - \frac{1}{2\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \\ & \quad \left( {\frac{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi\upkappa} \right)}}{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi \kappa } \right)}}} \right) + \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \kappa \left( {\frac{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi \kappa } \right)}}{{A\cosh \left( {\xi \kappa } \right) + B\sinh \left( {\xi \kappa } \right)}}} \right), \\ \end{aligned}$$
    (41)

    where \(\kappa = \sqrt {\frac{{m^{2} }}{{4\left( {K^{2} - 4L^{2} } \right)}}} .\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{8}}} \left( \xi \right) & = - \frac{1}{2\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \\ & \quad \left( {\frac{{A\cos \left( {\xi \kappa } \right) + B\sin \left( {\xi \kappa } \right)}}{{ - A\sin \left( {\xi \kappa } \right) + B\cos \left( {\xi \kappa } \right)}}} \right) + \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \kappa \left( {\frac{{ - A\sin \left( {\xi \kappa } \right) + B\cos \left( {\xi \kappa } \right)}}{{A\cos \left( {\xi \kappa } \right) + B\sin \left( {\xi \kappa } \right)}}} \right), \\ \end{aligned}$$
    (42)

    where \(\kappa = \sqrt { - \frac{{m^{2} }}{{4\left( {K^{2} - L^{2} } \right)}}.}\)

    $$\begin{aligned} \varvec{u}_{{\mathbf{9}}} \left( \xi \right) & = - \frac{1}{2\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \left( {\frac{B\xi + A}{B}} \right) \\ & \quad + \,\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \left( {\frac{B}{B\xi + A}} \right), \\ \end{aligned}$$
    (43)

  • Case 4

    $$\begin{aligned} & \alpha_{ - 1} = \frac{5}{12\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} ,\quad a_{0} = 0, \\ & \quad \alpha_{1} = \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} , \quad \lambda = 0, \quad \mu = \frac{{m^{2} }}{{8K^{2} - 8L^{2} }}, \quad L = L,\quad K = K. \\ \end{aligned}$$
    (44)

    The traveling wave solutions for above cases, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows

    $$\begin{aligned} \varvec{u}_{{{\mathbf{10}}}} \left( \xi \right) & = \frac{5}{12\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \\ & \quad \frac{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi\upkappa} \right)}}{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi \kappa } \right)}} + \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \kappa \left( {\frac{{A\sinh \left( {\xi \kappa } \right) + B\cosh \left( {\xi \kappa } \right)}}{{A\cosh \left( {\xi \kappa } \right) + B\sinh \left( {\xi \kappa } \right)}}} \right), \\ \end{aligned}$$
    (45)

    where \(\kappa = \sqrt { - \frac{{m^{2} }}{{8\left( {K^{2} - L^{2} } \right)}}} .\)

    $$\begin{aligned} \varvec{u}_{{{\mathbf{11}}}} \left( \xi \right) & = \frac{5}{12\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \\ & \quad \left( {\frac{{A\cos \left( {\xi \kappa } \right) + B\sin \left( {\xi \kappa } \right)}}{{ - A\sin \left( {\xi \kappa } \right) + B\cos \left( {\xi \kappa } \right)}}} \right) + \sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \kappa \left( {\frac{{ - A\sin \left( {\xi \kappa } \right) + B\cos \left( {\xi \kappa } \right)}}{{A\cos \left( {\xi \kappa } \right) + B\sin \left( {\xi \kappa } \right)}}} \right), \\ \end{aligned}$$
    (46)

    where \(\kappa = \sqrt {\frac{{m^{2} }}{{8\left( {K^{2} - L^{2} } \right)}}} .\)

    $$\begin{aligned} \varvec{u}_{{{\mathbf{12}}}} \left( \xi \right) & = \frac{5}{12\sigma \kappa }m^{2} \left( {\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} } \right)^{ - 1} \left( {\frac{B\xi + A}{B}} \right) \\ & \quad + \,\sqrt {2\frac{{K^{2} - L^{2} }}{\sigma }} \left( {\frac{B}{B\xi + A}} \right), \\ \end{aligned}$$
    (47)

  • Case 5

    $$\begin{aligned} & \alpha_{ - 1} = \sqrt {\left( {2K^{2} \sigma - 2L^{2} \sigma } \right)^{ - 1} } m^{2} , \quad \alpha_{0} = 0, \quad \alpha_{1} = 0, \quad \lambda = 0, \quad \\ & \quad \mu = \frac{1}{2}\frac{{m^{2} }}{{K^{2} - L^{2} }},\quad L = L, \quad K = K. \\ \end{aligned}$$
    (48)

    The traveling wave solutions for above cases, when (I) \(\lambda^{2} - 4\mu > 0\), (II) \(\lambda^{2} - 4\mu < 0\), and (III) \(\lambda^{2} - 4\mu = 0\) are respectively as follows (Fig. 2)

    $$\varvec{u}_{{{\mathbf{13}}}} \left( \xi \right) = \sqrt {\frac{{m^{4} }}{{\kappa^{2} \sigma \left( {K^{2} - L^{2} } \right)}}} \left( {\frac{{A\cosh \left( {\frac{1}{2}\xi \kappa } \right) + B\sinh \left( {\frac{1}{2}\xi \kappa } \right)}}{{A\sinh \left( {\frac{1}{2}\xi \kappa } \right) + B\cosh \left( {\frac{1}{2}\xi \kappa } \right)}}} \right),$$
    (49)

    where \(\kappa = \sqrt { - \frac{{2m^{2} }}{{K^{2} - L^{2} }}.}\)

    $$\varvec{u}_{{{\mathbf{14}}}} \left( \xi \right) = \sqrt {\frac{{m^{4} }}{{\kappa^{2} \sigma \left( {K^{2} - L^{2} } \right)}}} \left( {\frac{{A\cos \left( {\frac{1}{2}\xi \kappa } \right) + B\sin \left( {\frac{1}{2}\xi \kappa } \right)}}{{ - A\sin \left( {\frac{1}{2}\xi \kappa } \right) + B\cos \left( {\frac{1}{2}\xi \kappa } \right)}}} \right),$$
    (50)

    where \(\kappa = \sqrt {\frac{{2m^{2} }}{{K^{2} - L^{2} }}} .\)

    $$\varvec{u}_{{{\mathbf{15}}}} \left( \xi \right) = \sqrt {\frac{{m^{4} }}{{2\sigma \left( {K^{2} - L^{2} } \right)}}} \frac{{\left( {B\xi + A} \right)}}{B},$$
    (51)

    For all of the above solutions, \(\xi = L\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + K\frac{{x^{\beta } }}{{\varGamma \left( {\beta + 1} \right)}}\).

Fig. 2
figure 2

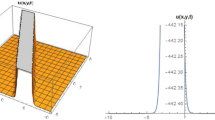
Graphical view of solitary wave solutions of Phi-4 equation for α = β= 0.25, 0.5, 0.75, 0.85 and 1, depicted by gray, red, yellow, green and blue colors respectively. Case 1: a solution (33) for A = 1, B = 0, m = 1, σ = 1, K = 2, L = 1, (− 10 < x < 10) and (− 10 < t < 10). b Solution (34) for A = − 3, B = 0, m = 1, σ = 1, K = 3, L = 2, (− 10 < x < 10) and (− 10 < t < 10). c Solution (35) for A = 1, B = − 3, m = 2, σ = 1, K = 2, L = 1, (− 10 < x < 10) and (− 10 < t < 10). Case 2: a solution (37) for A = 1, B = 0, m = 2, σ = 1, μ = 1, K = 2, L = 1, (0 < x < 10) and (0 < t < 10). b Solution (38) for A = − 3, B = 0, m = 2, σ = 1, μ = 1, K = 3, L = 2, (0 < x < 10) and (0 < t < 10). c Solution (39) for A = − 3, B = 5, m = 4, σ = 1, μ = 1, K = 6, L = 5, (− 10 < x < 10) and (− 10 < t < 10). Case 3: a solution (41) for A = 1, B = 3, m = 2, σ = 5, K = 9, L = 1, (− 2 < x < 5) and (0 < t < 5). b Solution (42) for A = 1, B = − 15, m = 1, σ = − 2, K = 1, L = 2, (− 5 < x < 10) and (0 < t < 5). c Solution (43) for A = 0, B = 5, m = 3, σ = − 1, K = 4, L = 1, (0 < x < 5) and (0 < t< 5). Case 4: a solution (45) for A = − 1, B = − 3, m = 1, σ = − 1, K = 2, L = 3, (0 < x < 5) and (0 < t < 5). b Solution (46) for A = 0, B = 1, m = 2, σ = 1, K = 2, L = 1, (0 < x < 5) and (0 < t < 5). c Solution (47) for A = − 3, B = 1, m = 3, σ = 2, K = 2, L = 1, (− 5 < x < 5) and (− 5 < t < 5). Case 5: a solution (49) for A = − 3, B = 0, m = 2, σ = 1, K = 2, L = 1, (0 < x < 5) and (0 < t < 5). b Solution (50) for A = − 5, B = 0, m = 1, σ = 1, K = 2, L = 1, (0 < x < 5) and (0 < t < 5). c Solution (51) for A = 1, B = 1, m = 7, σ = 1, K = 2, L = 1, (0 < x < 5) and (0 < t < 5). (Color figure online)

Full size image

4 Conclusion

We obtained several new solitary wave solutions of Benny–Luke equation and Phi-4 equation of fractional order by implementing \(\left( {G^{\prime}/G} \right)\)-expansion method and to the best of our knowledge, such a work has not been reported yet. Fractional complex transformation and modified Reimann-Liouville derivative are used to come upon these solutions. Graphical perspective of the obtained solutions for different values of \(\alpha ,\beta\) and the related physical parameters is represented that will be very much supportive in understanding the physical aspects of the incorporated problems. The results of our work clearly indicate the validity and proficiency of the proposed scheme for solving numerous other NLEEs of fractional order.