New solitary wave solutions of time-fractional coupled Jaulent–Miodek equation by using two reliable methods

Abstract

In the present article, we have developed new exact analytical solutions of a nonlinear evolution equation that appear in mathematical physics, specifically time-fractional coupled Jaulent–Miodek equation by tanh method and $(G'/G)$-expansion method by means of fractional complex transform. As a result, we acquire new exact analytical solutions of Jaulent–Miodek equation.

1 Introduction

Consider the nonlinear time-fractional-type coupled Jaulent–Miodek equation [1, 2]

$$\begin{aligned}&D_t^\alpha u+u_{xxx} +\frac{3}{2}vv_{xxx} +\frac{9}{2}v_x v_{xx}\nonumber \\&\quad -\,6uu_x -6uvv_x -\frac{3}{2}u_x v^{2}=0 \end{aligned}$$

(1.1)

and

$$\begin{aligned} D_t^\alpha v+v_{xxx} -6u_x v-6uv_x -\frac{15}{2}v_x v^{2}=0 \end{aligned}$$

(1.2)

where $0<\alpha \le 1$.

Jaulent and Miodek [3] introduced Jaulent–Miodek(JM) equation by using inverse scattering transform from the nonlinear evolution equation. Matsuno [4] linearized JM equation by hodograph transformation and relate it with Euler–Darboux equation. The JM spectral problem which associates with JM equation has been studied in [5, 6]. By utilizing lax pair of the JM spectral problem, Xu [7] constructed the exact solutions of Jaulent–Miodek equation. The symmetries of JM Hierarchy have been studied by Ruan and Lou [8].

Atangana and Baleanu [2] have studied nonlinear fractional Jaulent–Miodek equation and presented the series solution by using Sumudu transform homotopy method (STHPM). By three-dimensional solution graph, the nature of the solutions has also been presented by Atangana and Baleanu in their study. By using two-dimensional Hermite wavelet method, Gupta and Saha Ray [9] have studied the numerical approximation for time-fractional coupled Jaulent–Miodek equation. Fractional Jaulent–Miodek (JM) hierarchy and its super-Hamiltonian structure by using fractional supertrace identity have been studied by Wang and Xia [10].

In past few years, an excellent deal of attention has been intended by the researchers on the study of nonlinear evolution equations [11–14] that appeared in mathematical physics. Recent past varied analytical and numerical methods like tanh–coth and sech [15] method, extended tanh method [16], Adomian’s decomposition method [5], Homotopy analysis method  [17], $(G'/G)$-expansion method [18], exp function method [19, 20], Homotopy perturbation method [21] have been used for solving classical JM equation.

This present article is dedicated to study the fractional coupled Jaulent–Miodek equation. Hence, it emphasizes on the implementation of two reliable methods, viz tanh method [22, 23] and $(G'/G)$-expansion [24, 25] method to find the exact solutions of time-fractional coupled Jaulent–Miodek equation. With a view to exhibit the capabilities of the methods, we employ these methods to deal with fractional order coupled Jaulent–Miodek equations. The main objective of this paper is to ascertain additional new general exact solutions of time-fractional coupled Jaulent–Miodek equation by implementing two reliable strategies, viz tanh method and $(G'/G)$-expansion method. Some solutions given in this paper are new solutions which have not been reported yet.

The present article is organized as follows. Some definitions with properties of local fractional calculus [26–28] are provided in Sect. 2. The algorithm of tanh and $(G'/G)$-expansion methods for determining the solution of fractional coupled JM equation are presented in Sects. 3 and 4, respectively. The implementation of proposed method for establishing the exact solutions of Eqs. (1.1) and (1.2) are proposed in Sects. 5 and 6, respectively. The numerical simulation for proposed tanh method is presented in Sect. 7. In Sect. 8, brief conclusions of study are presented.

2 Preliminaries of local fractional calculus and proposed method

2.1 Local fractional continuity of a function

Definition 2.1

Suppose that f(x) is defined throughout some interval containing $x_0$ and all point near $x_0$, then f(x) is said to be local fractional continuous at $x=x_0$, denote by $\lim \nolimits _{x\rightarrow x_0 } f(x)=f(x_0 )$, if to each positive $\varepsilon$ and some positive constant k corresponds some positive $\delta$ such that [26–28]

$$\begin{aligned} \left| {f(x)-f(x_0 )} \right| <k\varepsilon ^{\alpha }, \quad 0<\alpha \le 1 \end{aligned}$$

(2.1)

whenever $\left| {x-x_0 } \right| <\delta$, $\varepsilon , \delta >0$ and $\varepsilon , \delta \in {\texttt {\textit{R}}}$. Consequently, the function f(x) is called local fractional continuous on the interval (a, b), denoted by

$$\begin{aligned} f(x)\in C_\alpha (a,b), \end{aligned}$$

(2.2)

where $\alpha$ is fractal dimension with $0<\alpha \le 1$.

Definition 2.2

A function $f(x):{\varvec{\mathsf{{ R}}}}\rightarrow$ -${\varvec{\mathsf{{ R}}}}$, $X\mapsto f(X)$ is called a non-differentiable function of exponent $\alpha$, $0<\alpha \le 1$, which satisfies Hölder function of exponent $\alpha$, then for $x,y\in X$, we have [26–28]

$$\begin{aligned} \left| {f(x)-f(y)} \right| \le C\left| {x-y} \right| ^{\alpha }. \end{aligned}$$

(2.3)

Definition 2.3

A function $f(x):{\varvec{\mathsf{{ R}}}}\rightarrow$ -${\varvec{\mathsf{{ R}}}}$, $X\mapsto f(X)$ is called to be local fractional continuous of order $\alpha$, $0<\alpha \le 1$, or shortly $\alpha -$local fractional continuous, when we have [26–28]

$$\begin{aligned} f(x)-f(x_0 )=O\left( {(x-x_0 )^{\alpha }} \right) . \end{aligned}$$

(2.4)

Remark 1

A function f(x) is said to be in the space $C_\alpha [a,b]$ if and only if it can be written as [26–28]

$$\begin{aligned} f(x)-f(x_0 )=O\left( {(x-x_0 )^{\alpha }} \right) \end{aligned}$$

with any $x_0 \in [a,b]$ and $0<\alpha \le 1$.

2.2 Local fractional derivative

Definition 2.4

Let $f(x)\in C_\alpha (a,b)$. Local fractional derivative of f(x) of order $\alpha$ at $x=x_0$ is defined as [26–28]

$$\begin{aligned} f^{(\alpha )}(x_0 )=\left. {\frac{\hbox {d}^{\alpha }f(x)}{\hbox {d}x^{\alpha }}} \right| _{x=x_0 } =\mathop {\lim }\limits _{x\rightarrow x_0 } \frac{\Delta ^{\alpha }(f(x)-f(x_0 ))}{(x-x_0 )^{\alpha }},\nonumber \\ \end{aligned}$$

(2.5)

where $\Delta ^{\alpha }(f(x)-f(x_0 ))\cong \Gamma (1+\alpha ) (f(x)-f(x_0 ))$ and $0<\alpha \le 1$.

Remark 2

The following rules are hold [28]

• (1) $\frac{\hbox {d}^{\alpha }x^{k\alpha }}{\hbox {d}x^{\alpha }}=\frac{\Gamma (1+k\alpha )}{\Gamma (1+(k-1)\alpha )}x^{(k-1)\alpha };$

• (2) $\frac{\hbox {d}^{\alpha }E_\alpha (kx^{\alpha })}{\hbox {d}x^{\alpha }}=kE_\alpha (kx^{\alpha }), k$ is a constant.

Remark 3

 [26–29] If $y(x)=(f\circ u)(x)$ where $u(x)=g(x)$, then we have

$$\begin{aligned} \frac{\hbox {d}^{\alpha }y(x)}{\hbox {d}x^{\alpha }}=f^{(\alpha )}\left( {g(x)} \right) \left( {g^{(1)}(x)} \right) ^{\alpha }, \end{aligned}$$

(2.6)

when $f^{(\alpha )}\left( {g(x)} \right)$ and $g^{(1)}(x)$ exist.

If $y(x)=(f\circ u)(x)$ where $u(x)=g(x)$, then we have

$$\begin{aligned} \frac{\hbox {d}^{\alpha }y(x)}{\hbox {d}x^{\alpha }}=f^{(1)}\left( {g(x)} \right) g^{(\alpha )}(x), \end{aligned}$$

(2.7)

when $f^{(1)}\left( {g(x)} \right)$ and $g^{(\alpha )}(x)$ exist.

The above property (2.7) plays an important role in the Tanh method and $(G'/G)$-expansion method via fractional complex transform.

3 Algorithm of the proposed Tanh method

In this part, we use tanh method [22, 23] to obtain the explicit solutions of Eqs. (1.1) and (1.2). The principle steps of the proposed method are portrayed as follows:

Step 1: Assume that the nonlinear FPDE in two independent variables x and t is given by

$$\begin{aligned} P(u,u_x ,u_{xx} ,u_{xxx} ,\ldots D_t^\alpha u,\ldots )=0, \quad 0<\alpha \le 1\nonumber \\ \end{aligned}$$

(3.1)

where u(x, t) is an unknown function, P is a function in u(x, t) and its various partial derivatives in which the highest order derivatives and nonlinear terms are included.

Step 2: Using the fractional complex transform  [30–34], we have

$$\begin{aligned} u(x,t)=\Phi (\xi ), \quad \xi =x-\frac{\nu t^{\alpha }}{\Gamma (\alpha +1)} \end{aligned}$$

(3.2)

where $\nu$ is a constant to be evaluated later.

By using the chain rule Eq. (2.7) [31, 34], we have

$$\begin{aligned} D_t^\alpha u= & {} \sigma _t \Phi _\xi D_t^\alpha \xi ,\\ D_x^\alpha u= & {} \sigma _x \Phi _\xi D_x^\alpha \xi , \end{aligned}$$

where $\sigma _t$ and $\sigma _x$ are the fractal indexes  [33, 34], without loss of generality we can take $\sigma _t =\sigma _x =\kappa$, where $\kappa$ is a constant.

The FPDE (3.1) is reduced to the following nonlinear ordinary differential equation (ODE) for $u(x,t)=\Phi (\xi )$:

$$\begin{aligned} P(\Phi ,{\Phi }',{\Phi }'',{\Phi }''',\ldots ,-\nu {\Phi }',\ldots )=0. \end{aligned}$$

(3.3)

Step 3: Presume that the solution of Eq. (3.3) can be written by a polynomial in Y given as follows:

$$\begin{aligned} \Phi (\xi )=a_0 +\sum _{i=1}^n {a_i Y^{i}} \end{aligned}$$

(3.4)

the integer n can be determined by balancing the highest order derivative term and nonlinear term appearing in Eq. (3.3).

Here $Y=\tanh (\xi )$ is a new independent variable. Then we can find the derivative with respect to $\xi$ as follows:

$$\begin{aligned} \frac{\hbox {d}\Phi }{\hbox {d}\xi }\rightarrow & {} \left( {1-Y^{2}} \right) \frac{\hbox {d}\Phi }{\hbox {d}Y},\nonumber \\ \frac{\hbox {d}^{2}\Phi }{\hbox {d}\xi ^{2}}\rightarrow & {} \left( {1-Y^{2}} \right) \left( {-2Y\frac{\hbox {d}\Phi }{\hbox {d}Y}+\left( {1-Y^{2}} \right) \frac{\hbox {d}^{2}\Phi }{\hbox {d}Y^{2}}} \right) ,\nonumber \\ \frac{\hbox {d}^{3}\Phi }{\hbox {d}\xi ^{3}}\rightarrow & {} \left( {1-Y^{2}} \right) ^{3}\frac{\hbox {d}^{3}\Phi }{\hbox {d}Y^{3}}-6Y\left( {1-Y^{2}} \right) ^{2}\frac{\hbox {d}^{2}\Phi }{\hbox {d}Y^{2}}\nonumber \\&+\,2Y\left( {1-Y^{2}} \right) \left( {3Y^{2}-1} \right) \frac{\hbox {d}\Phi }{\hbox {d}Y},\nonumber \\ \frac{\hbox {d}^{4}\Phi }{\hbox {d}\xi ^{4}}\rightarrow & {} -8Y\left( {1-Y^{2}} \right) \left( {3Y^{2}-2} \right) \frac{\hbox {d}\Phi }{dY}\nonumber \\&+\,4\left( {1-Y^{2}} \right) ^{2}\left( {9Y^{2}-2} \right) \frac{\hbox {d}^{2}\Phi }{\hbox {d}Y^{2}}\nonumber \\&-\,12Y\left( {1-Y^{2}} \right) ^{3}\frac{\hbox {d}^{3}\Phi }{\hbox {d}Y^{3}}+\left( {1-Y^{2}} \right) ^{4}\frac{\hbox {d}^{4}\Phi }{\hbox {d}Y^{4}},\nonumber \\ \end{aligned}$$

(3.5)

and other higher-order derivatives can be found accordingly.

Step 4: By replacing Eq. (3.4) in Eq. (3.3) and using Eq. (3.5) followed by bringing together all the like terms with the same degree of $Y^{i}(i=0,1,2,\ldots )$, Eq. (3.3) is changed into a polynomial in $Y^{i}(i=0,1,2,\ldots )$. Equating every coefficient of this polynomial to zero yields a set of algebraic equations for $a_i (i=0,1,2,\ldots ,n)$ and $\nu$.

Step 5: By solving the algebraic equations system obtained in Step 4 and substituting these constants $a_i (i=0,1,2,\ldots ,n),\nu$ in Eq. (3.4), we can obtain the explicit new solutions of Eq. (3.1) instantly.

4 Algorithm of $(G'/G)$-expansion method

In this part, we deal with the explicit solutions of Eqs. (1.1) and (1.2) obtained by using $(G'/G)$-expansion [24, 25] method. The principle procedures of this method are discussed as follows:

Step 1: Suppose that the nonlinear FPDE in two independent variables x and t is given by

$$\begin{aligned} P(u,u_x ,u_{xx} ,u_{xxx} ,\ldots D_t^\alpha u,\ldots )=0, \quad 0<\alpha \le 1\nonumber \\ \end{aligned}$$

(4.1)

where u(x, t) is an unknown function, P is a function in u(x, t) and its different partial derivatives in which the highest order derivatives and nonlinear terms are included.

Step 2: By applying the fractional complex transform  [30–34]:

$$\begin{aligned} u(x,t)=\Phi (\xi ), \quad \xi =kx+\frac{ct^{\alpha }}{\Gamma (\alpha +1)} \end{aligned}$$

(4.2)

where the constants k and c are to be evaluated later on.

By using the chain rule Eq. (2.7) [31, 34], we have

$$\begin{aligned} D_t^\alpha u= & {} \sigma _t u_\xi D_t^\alpha \xi ,\\ D_x^\alpha u= & {} \sigma _x u_\xi D_x^\alpha \xi ,\\ \end{aligned}$$

where $\sigma _t$ and $\sigma _x$ are the fractal indexes  [33, 34], without loss of generality we can take $\sigma _t =\sigma _x =\kappa$, where $\kappa$ is a constant.

The FPDE (4.1) is reduced to the following ODE for $u(x,t)=\Phi (\xi )$:

$$\begin{aligned} P(\Phi ,k{\Phi }',k^{2}{\Phi }'',k^{3}{\Phi }''',\ldots c{\Phi }',\ldots )=0 \end{aligned}$$

(4.3)

Step 3: By assuming the solution of Eq. (4.3) by a polynomial in $\left( {{{G}'}/G} \right)$, we can write it as in the following manner:

$$\begin{aligned} \Phi (\xi )=a_0 +\sum _{i=1}^n {a_i \left( {\frac{{G}'}{G}} \right) ^{i}} , \end{aligned}$$

(4.4)

where $G=G(\xi )$ satisfies the second-order ODE in the form

$$\begin{aligned} {G}''+\lambda {G}'+\mu G=0, \end{aligned}$$

(4.5)

the integer n can be determined by balancing the highest order derivative term and the nonlinear term appearing in Eq. (4.3). Further, Eq. (4.5) can be converted into

$$\begin{aligned} \frac{d}{d\xi }\left( {\frac{{G}'}{G}} \right) =-\left( {\frac{{G}'}{G}} \right) ^{2}-\lambda \left( {\frac{{G}'}{G}} \right) -\mu . \end{aligned}$$

(4.6)

By the generalized solutions of Eq. (4.5), we have

$$\begin{aligned} \left( {\frac{{G}'}{G}} \right) =\left\{ {\begin{array}{l} \frac{\sqrt{\lambda ^{2}-4\mu }}{2}\left( {\frac{C_1 \sinh \left( {\frac{\sqrt{\lambda ^{2}-4\mu }}{2}\xi } \right) +C_2 \cosh \left( {\frac{\sqrt{\lambda ^{2}-4\mu }}{2}\xi } \right) }{C_1 \cosh \left( {\frac{\sqrt{\lambda ^{2}-4\mu }}{2}\xi } \right) +C_2 \sinh \left( {\frac{\sqrt{\lambda ^{2}-4\mu }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}, \lambda ^{2}-4\mu >0 \\ \frac{\sqrt{-\lambda ^{2}+4\mu }}{2}\left( {\frac{-C_1 \sin \left( {\frac{\sqrt{-\lambda ^{2}+4\mu }}{2}\xi } \right) +C_2 \cos \left( {\frac{\sqrt{-\lambda ^{2}+4\mu }}{2}\xi } \right) }{C_1 \cos \left( {\frac{\sqrt{-\lambda ^{2}+4\mu }}{2}\xi } \right) +C_2 \sin \left( {\frac{\sqrt{-\lambda ^{2}+4\mu }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}, \lambda ^{2}-4\mu <0 \\ \left( {\frac{C_2 }{C_1 +C_2 \xi }} \right) -\frac{\lambda }{2}, \lambda ^{2}-4\mu =0 \\ \end{array}} \right. \end{aligned}$$

(4.7)

where $C_1$ and $C_2$ are arbitrary constants.

Step 4: After substituting Eq. (4.4) in Eq. (4.3) and using Eq. (4.6), followed by collecting all the like terms with the same degree of $(G'/G)$ into together, Eq. (4.3) can be written as an another polynomial in $(G'/G)$. By equating each of the coefficient of the obtained polynomial to zero, we can obtain a set of algebraic equations for $a_i (i=0,1,2,\ldots ,n),\lambda , k,c$ and $\mu$.

Step 5: Solving the algebraic equations system obtained in Step 4 and subsequently substituting these constants $a_i (i=0,1,2,\ldots ,n),\lambda , k,c$ and $\mu$, and also solutions of Eq. (4.6) in Eq. (4.4), we can obtain the explicit new exact solutions of Eq. (4.1) instantly.

5 Implementation of Tanh method for the exact solutions of time-fractional coupled Jaulent–Miodek

In this part, we implement the tanh method to determine the new exact solutions for time-fractional coupled Jaulent–Miodek equation (1.1) and (1.2).

By applying the fractional complex transform (3.2), Eqs. (1.1) and (1.2) can be reduced to the following nonlinear ODE:

$$\begin{aligned}&-\nu {\Phi }'(\xi )+{\Phi '''}(\xi )+\frac{3}{2}\Psi (\xi )\Psi '''(\xi ) +\,\frac{9}{2}{\Psi }'(\xi )\Psi ''(\xi )\nonumber \\&\quad -6\Phi (\xi ){\Phi }'(\xi )-6\Phi (\xi )\Psi (\xi ){\Psi }'(\xi )\nonumber \\&\quad -\frac{3}{2}{\Phi }'(\xi )\Psi ^{2}(\xi )=0 \end{aligned}$$

(5.1)

and

$$\begin{aligned}&-\nu {\Psi }'(\xi )+\Psi '''(\xi )-6{\Phi }'(\xi )\Psi (\xi )-\,6\Phi (\xi ){\Psi }'(\xi )\nonumber \\&\quad -\frac{15}{2}{\Psi }'(\xi )\Psi ^{2}(\xi )=0 \end{aligned}$$

(5.2)

Let

$$\begin{aligned} \Phi (\xi )=a_0 +\sum _{i=1}^{n_1 } {a_i Y^{i}} \hbox { and }\Psi (\xi )=b_0 +\sum _{i=1}^{n_2 } {b_i Y^{i}}\nonumber \\ \end{aligned}$$

(5.3)

By balancing the highest order derivative term and nonlinear term in Eqs. (5.1) and (5.2), the values of $n_1$ and $n_2$ can be determined, which are $n_1 =2$ and $n_2 =1$ in this problem.

Therefore by Eq. (5.3), we have the following ansatz:

$$\begin{aligned} \Phi (\xi )= & {} a_0 +a_1 Y+a_2 Y^{2}, \nonumber \\ \Psi (\xi )= & {} b_0 +b_1 Y \end{aligned}$$

(5.4)

According to Eq. (3.5), we have

$$\begin{aligned} \frac{\hbox {d}\Phi }{\hbox {d}\xi }\rightarrow & {} \left( {1-Y^{2}} \right) \left( {a_1 +2a_2 Y} \right) ,\nonumber \\ \frac{\hbox {d}^{2}\Phi }{\hbox {d}\xi ^{2}}\rightarrow & {} \left( {1-Y^{2}} \right) \left( {-2Y\left( {a_1 +2a_2 Y} \right) +2a_2 \left( {1-Y^{2}} \right) } \right) ,\nonumber \\ \frac{\hbox {d}^{3}\Phi }{\hbox {d}\xi ^{3}}\rightarrow & {} -6Y\left( {1-Y^{2}} \right) ^{2}2a_2 \nonumber \\&+2Y\left( {1-Y^{2}} \right) \left( {3Y^{2}-1} \right) \left( {a_1 +2a_2 Y} \right) ,\nonumber \\ \frac{\hbox {d}\Psi }{\hbox {d}\xi }\rightarrow & {} b_1 \left( {1-Y^{2}} \right) ,\nonumber \\ \frac{\hbox {d}^{2}\Psi }{\hbox {d}\xi ^{2}}\rightarrow & {} -2Yb_1 \left( {1-Y^{2}} \right) ,\nonumber \\ \frac{\hbox {d}^{3}\Psi }{\hbox {d}\xi ^{3}}\rightarrow & {} 2Yb_1 \left( {1-Y^{2}} \right) \left( {3Y^{2}-1} \right) , \end{aligned}$$

(5.5)

Putting these values of Eq. (5.5) together with Eq. (5.4) in Eq. (5.1), then collecting all the like terms with the same degree of $Y^{i}(i=0,1,2,\ldots )$, we can obtain a system of algebraic equations for $a_i (i=0,1,2,\ldots ,n)$, $b_i (i=0,1,2,\ldots ,n)$ and $\nu$ as follows:

$$\begin{aligned}&\hbox {Coefficient of }Y^{0}:-4a_1 -2\nu a_1 -12a_0 a_1 \nonumber \\&\quad -3a_1 b_0^2 -6b_0 b_1 -12a_0 b_0 b_1 =0,\nonumber \\&\hbox {Coefficient of }Y^{1}:-12a_1^2 -32a_2 -4\nu a_2 \nonumber \\&\quad -24a_0 a_2 -6a_2 b_0^2 -18a_1 b_0 b_1 -24b_1^2 \nonumber \\&-12a_0 b_1^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{2}:16a_1 +2\nu a_1 +12a_0 a_1\nonumber \\&\quad -36a_1 a_2 +3a_1 b_0^2 +24b_0 b_1 +12a_0 b_0 b_1 \nonumber \\&\quad -24a_2 b_0 b_1 -15a_1 b_1^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{3}:12a_1^2 +80a_2 +4\nu a_2 \nonumber \\&\quad +24a_0 a_2 -24a_2^2 +6a_2 b_0^2\nonumber \\&\quad +18a_1 b_0 b_1 +60b_1^2 +12a_0 b_1^2 -18a_2 b_1^2 =0,\nonumber \\&\hbox {Coefficient of } Y^{4}:12a_1 -36a_1 a_2 +18b_0 b_1 \nonumber \\&\quad -24a_2 b_0 b_1 -15a_1 b_1^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{5}:-48a_2 +24a_2^2 -36b_1^2\nonumber \\&\quad +18a_2 b_1^2 =0, \end{aligned}$$

(5.6)

Putting these values of Eq. (5.5) together with Eq. (5.4) in Eq. (5.2), then collecting all the like terms with the same degree of $Y^{i}(i=0,1,2,\ldots )$,

we can obtain another system of algebraic equations for $a_i (i=0,1,2,\ldots ,n)$, $b_i (i=0,1,2,\ldots ,n)$ and $\nu$ as follows:

$$\begin{aligned}&\hbox {Coefficient of }Y^{0}:-12a_1 b_0 -4b_1 \nonumber \\&\quad -2\nu b_1 -12a_0 b_1 -15b_1 b_0^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{1}:-24a_2 b_0 -24a_1 b_1 -30b_0 b_1^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{2}:12a_1 b_0 +16b_1 +2\nu b_1 \nonumber \\&\quad +12a_0 b_1 -36a_2 b_1 +15b_0^2 b_1 -15b_1^3 =0,\nonumber \\&\hbox {Coefficient of }Y^{3}:24a_2 b_0 +24a_1 b_1 +30b_0 b_1^2 =0,\nonumber \\&\hbox {Coefficient of }Y^{4}:-12b_1 +36a_2 b_1 +15b_1^3 =0.\nonumber \\ \end{aligned}$$

(5.7)

Solving the above algebraic Eqs. (5.6) and (5.7), we have the following sets of coefficients for the solutions of Eq. (5.4) as given below:

Case 1:

$$\begin{aligned}&\nu =\nu , \quad a_0 =\frac{1}{12}(-7+\nu ), a_1 =-\frac{i\sqrt{1-\nu }}{2\sqrt{3}},\\&a_2 =\frac{3}{4}, \quad b_0 =-\frac{\sqrt{1-\nu }}{\sqrt{3}}, \quad b_1 =-i \end{aligned}$$

For Case 1, we have the following solution

$$\begin{aligned} \Phi _{11}= & {} \frac{1}{12}(-7+\nu )-\frac{i\sqrt{1-\nu }}{2\sqrt{3}}\tanh (\xi )\nonumber \\&+\frac{3}{4}\tanh ^{2}(\xi ),\nonumber \\ \Psi _{11}= & {} -\frac{\sqrt{1-\nu }}{\sqrt{3}}-i\tanh (\xi ) \end{aligned}$$

(5.8)

where $\xi =x-\frac{\nu t^{\alpha }}{\Gamma (\alpha +1)}$.

Case 2:

$$\begin{aligned}&\nu = \nu , \quad a_0 =\frac{1}{12}(-7+\nu ), a_1 =\frac{i\sqrt{1-\nu }}{2\sqrt{3}},\\&a_2 =\frac{3}{4}, \quad b_0 =\frac{\sqrt{1-\nu }}{\sqrt{3}}, \quad b_1 =-i \end{aligned}$$

For Case 2, we have the following solution

$$\begin{aligned} \Phi _{21}= & {} \frac{1}{12}(-7+\nu )+\frac{i\sqrt{1-\nu }}{2\sqrt{3}}\tanh (\xi )\nonumber \\&+\frac{3}{4}\tanh ^{2}(\xi ),\nonumber \\ \Psi _{21}= & {} \frac{\sqrt{1-\nu }}{\sqrt{3}}-i\tanh (\xi ) \end{aligned}$$

(5.9)

where $\xi =x-\frac{\nu t^{\alpha }}{\Gamma (\alpha +1)}$.

Case 3:

$$\begin{aligned}&\nu = \nu , \quad a_0 =\frac{1}{12}(-7+\nu ), a_1 =\frac{i\sqrt{1-\nu }}{2\sqrt{3}},\nonumber \\&a_2 = \frac{3}{4}, \quad b_0 =-\frac{\sqrt{1-\nu }}{\sqrt{3}}, \quad b_1 =i\nonumber \\&\Phi _{31} = \frac{1}{12}(-7+\nu )+\frac{i\sqrt{1-\nu }}{2\sqrt{3}}\tanh (\xi )+\frac{3}{4}\tanh ^{2}(\xi ),\nonumber \\&\Psi _{31} = -\frac{\sqrt{1-\nu }}{\sqrt{3}}+i\tanh (\xi ) \end{aligned}$$

(5.10)

where $\xi =x-\frac{\nu t^{\alpha }}{\Gamma (\alpha +1)}$.

Case 4:

$$\begin{aligned}&\nu =\nu , \quad a_0 =\frac{1}{12}(-7+\nu ), a_1 =-\frac{i\sqrt{1-\nu }}{2\sqrt{3}},\nonumber \\&a_2 =\frac{3}{4}, \quad b_0 =\frac{\sqrt{1-\nu }}{\sqrt{3}}, \quad b_1 =i\nonumber \\&\Phi _{41} =\frac{1}{12}(-7+\nu )-\frac{i\sqrt{1-\nu }}{2\sqrt{3}}\tanh (\xi )+\frac{3}{4}\tanh ^{2}(\xi ),\nonumber \\&\Psi _{41} =\frac{\sqrt{1-\nu }}{\sqrt{3}}+i\tanh (\xi ) \end{aligned}$$

(5.11)

where $\xi =x-\frac{\nu t^{\alpha }}{\Gamma (\alpha +1)}$.

6 Implementation of $(G'/G)$-expansion method to the time-fractional coupled Jaulent–Miodek equation

In this part, we apply the $(G'/G)$-expansion method to determine the new exact solutions for time-fractional coupled Jaulent–Miodek equation (1.1) and (1.2).

By applying the fractional complex transform (4.2), Eqs. (1.1) and (1.2) can be reduced to the following nonlinear ODE:

$$\begin{aligned}&c{\Phi }'(\xi )+k^{3}\Phi '''(\xi )+\frac{3}{2}k^{3}\Psi (\xi )\Psi '''(\xi )\nonumber \\&\quad +\,\frac{9}{2}k^{3}{\Psi }'(\xi )\Psi ''(\xi ) -6k\Phi (\xi ){\Phi }'(\xi )\nonumber \\&\quad -\,6k\Phi (\xi )\Psi (\xi ){\Psi }'(\xi )-\frac{3}{2}k{\Phi }'(\xi )\Psi ^{2}(\xi )=0 \end{aligned}$$

(6.1)

and

$$\begin{aligned}&c{\Psi }'(\xi )+k^{3}\Psi '''(\xi )-6k{\Phi }'(\xi )\Psi (\xi )-6k\Phi (\xi ){\Psi }'(\xi )\nonumber \\&\quad -\frac{15}{2}k{\Psi }'(\xi )\Psi ^{2}(\xi )=0 \end{aligned}$$

(6.2)

$$\begin{aligned}&\hbox {Let }\Phi (\xi )=a_0 +\sum _{i=1}^{n_1 } {a_i \left( {\frac{{G}'}{G}} \right) ^{i}}\hbox { and } \nonumber \\&\quad \Psi (\xi )=b_0 +\sum _{i=1}^{n_2 } {b_i \left( {\frac{{G}'}{G}} \right) ^{i}} \end{aligned}$$

(6.3)

By balancing the highest order derivative term and the nonlinear term in Eqs. (6.1) and (6.2), the values of $n_1$ and $n_2$ can be determined, which are $n_1 =2$ and $n_2 =1$ in this problem.

Therefore by Eq. (6.3), we have the following ansatz:

$$\begin{aligned}&\Phi (\xi )=a_0 +a_1 \left( {\frac{{G}'}{G}} \right) +a_2 \left( {\frac{{G}'}{G}} \right) ^{2}\nonumber \\&\Psi (\xi )=b_0 +b_1 \left( {\frac{{G}'}{G}} \right) \end{aligned}$$

(6.4)

where G satisfies Eq. (4.5).

Substituting Eq. (6.4) along with Eq. (6.6) in Eq. (6.1), then equating each coefficients of $\left( {\frac{{G}'}{G}} \right) (i=0,1,2,\ldots )$ to zero, we can find a system of algebraic equations for $a_i (i=0,1,2,\ldots ,n),b_i (i=0,1,2,\ldots ,n),\lambda , k,c$ and $\mu$ as follows:

(6.5)

Substituting Eq. (6.4) along with Eq. (6.6) in Eq. (6.2), then equating each coefficients of $\left( {\frac{{G}'}{G}} \right) (i=0,1,2,\ldots )$ to zero, we can find another system of algebraic equations for $a_i(i=0,1,2,\ldots ,n),b_i (i=0,1,2,\ldots ,n),\lambda ,k$. c and $\mu$ as follows:

(6.6)

Solving the above algebraic Eqs. (6.5) and (6.6), we have the following sets of coefficients for the solutions of Eq. (6.4) as given below:

Case 1:

$$\begin{aligned}&c=c, \lambda =\lambda , k=k,\\&a_0 =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu +i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k},\\&a_1 =\frac{1}{12}\left( {9k^{2}\lambda +i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) ,\\&a_2 =\frac{3k^{2}}{4}, b_0 =-\frac{3ik^{2}\lambda -\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k},\\&b_1 =-ik. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=c, \lambda =\lambda , k=k,\\&a_0 =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu -i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k},\\&a_1 =\frac{1}{12}\left( {9k^{2}\lambda -i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) , a_2 =\frac{3k^{2}}{4},\\&b_0 =-\frac{3ik^{2}\lambda +\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k}, \quad b_1 =-ik. \end{aligned}$$

Case 3:

$$\begin{aligned}&c=c, \lambda =\lambda , k=k,\\&a_0 =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu -i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k},\\&a_1 =\frac{1}{12}\left( {9k^{2}\lambda -i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) ,\\&a_2 =\frac{3k^{2}}{4}, \quad b_0 =-\frac{3ik^{2}\lambda -\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k},\\&b_1 =ik. \end{aligned}$$

Case 4:

$$\begin{aligned}&c=c, \lambda =\lambda , k=k,\\&a_0 =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu +i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k},\\&a_1 =\frac{1}{12}\left( {9k^{2}\lambda +i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) ,\\&a_2 =\frac{3k^{2}}{4}, \quad b_0 =-\frac{3ik^{2}\lambda +\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k},\\&b_1 =ik. \end{aligned}$$

Substituting the above obtained results in Eq. (6.4) along with Eq. (6.7), we can find a series of exact solutions to Eq. (1.1) and (1.2).

From Case 1, we obtain the following exact solutions:

Fig. 1

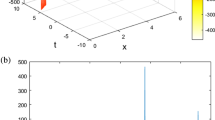
a The tanh method three-dimensional solitary wave solution for u(x, t) appears in Eq. (5.8) as $\Phi _{11}$ of Case 1, b corresponding two-dimensional solution graph for u(x, t) when $t=0$,$\nu =0.5$ and $\alpha =1$.

(i) When $\Delta =\lambda ^{2}-4\mu >0$, we obtain hyperbolic function solution as:

$$\begin{aligned}&\Phi _{11} = \frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu +i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k}\nonumber \\&\quad +\frac{1}{12}\left( {9k^{2}\lambda +i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) \nonumber \\&\left( {\frac{\sqrt{\Delta }}{2}\left( {\frac{C_1 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }{C_1 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) \nonumber \\&\quad +\frac{3k^{2}}{4}\left( {\frac{\sqrt{\Delta }}{2}\left( {\frac{C_1 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }{C_1 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) ^{2}, \end{aligned}$$

(6.7)

$$\begin{aligned}&\Psi _{11} =-\frac{3ik^{2}\lambda -\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k}\nonumber \\&\quad -ik\left( {\frac{\sqrt{\Delta }}{2}\left( {\frac{C_1 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }{C_1 \cosh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) +C_2 \sinh \left( {\frac{\sqrt{\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) .\nonumber \\ \end{aligned}$$

(6.8)

(ii) When $\Delta =\lambda ^{2}-4\mu <0$, we obtain trigonometric function solution as:

$$\begin{aligned}&\Phi _{12} =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu +i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k}\nonumber \\&\quad +\frac{1}{12}\left( {9k^{2}\lambda +i\sqrt{3}\sqrt{4ck+k^{4} \lambda ^{2}-4k^{4}\mu }} \right) \nonumber \\&\quad \left( {\frac{\sqrt{-\Delta }}{2}\left( {\frac{-C_1 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }{C_1 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) \nonumber \\&\quad +\frac{3k^{2}}{4}\left( {\frac{\sqrt{-\Delta }}{2}\left( {\frac{-C_1 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }{C_1 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) ^{2}, \end{aligned}$$

(6.9)

$$\begin{aligned}&\Psi _{12} =-\frac{3ik^{2}\lambda -\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{6k}\nonumber \\&\quad -ik\left( {\frac{\sqrt{-\Delta }}{2}\left( {\frac{-C_1 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }{C_1 \cos \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) +C_2 \sin \left( {\frac{\sqrt{-\Delta }}{2}\xi } \right) }} \right) -\frac{\lambda }{2}} \right) \nonumber \\ \end{aligned}$$

(6.10)

(iii) When $\Delta =\lambda ^{2}-4\mu =0$, we obtain the following solution as:

$$\begin{aligned}&\Phi _{13} =\frac{-2c+k^{3}\lambda ^{2}+14k^{3}\mu +i\sqrt{3}k\lambda \sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }}{24k}\nonumber \\&\quad +\frac{1}{12}\left( {9k^{2}\lambda +i\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2}-4k^{4}\mu }} \right) \nonumber \\&\quad \times \left( {\left( {\frac{C_2 }{C_1 +C_2 \xi }} \right) -\frac{\lambda }{2}} \right) +\frac{3k^{2}}{4}\left( {\left( {\frac{C_2 }{C_1 +C_2 \xi }} \right) -\frac{\lambda }{2}} \right) ^{2}, \end{aligned}$$

(6.11)

$$\begin{aligned}&\Psi _{13} =-\frac{3ik^{2}\lambda -\sqrt{3}\sqrt{4ck+k^{4}\lambda ^{2} -4k^{4}\mu }}{6k}\nonumber \\&\quad -ik\left( {\left( {\frac{C_2 }{C_1 +C_2 \xi }} \right) -\frac{\lambda }{2}} \right) . \end{aligned}$$

(6.12)

Similarly as the obtained solutions in Case 1, we can formulate corresponding new exact solutions to Eqs. (1.1) and (1.2) for Cases 2–4, which are omitted here.

7 The numerical simulations for solutions of time-fractional coupled Jaulent–Miodek equation using tanh method

In this present numerical experiment, the exact solutions for Eqs. (1.1) and (1.2) obtained by using tanh method presented in Eq. (5.8) have been used to draw the 3-D and 2-D solution graphs as shown in Figs. 1 and 2.

Fig. 2

a The tanh method three-dimensional solitary wave solution for v(x, t) appears in Eq. (5.8) as $\Psi _{11}$ of Case 1, b corresponding two-dimensional solution graph for u(x, t) when $t=0$, $\nu =0.5$ and $\alpha =1$.

In the present numerical simulation, we have presented the 3-D and 2-D solution graphs for coupled JM equation by proposed tanh method. We have concluded that the nature of the solution graph is solitary, which can be used to describe in many physical phenomenon. Due to the presence of many parameters and arbitrary constants in the solution of Eqs. (1.1) and (1.2) obtained by $(G'/G)$-expansion method, it is difficult to examine the nature of solution graphs.

8 Conclusion

In the present paper, we have presented the tanh and $(G'/G)$-expansion method to construct more general exact solutions of fractional coupled JM equation. With the successful implementation of proposed methods, we have found many new exact solutions, which may be useful for describing certain nonlinear physical phenomena in fluid. Here we have used fractional complex transform along with proposed methods, which can easily convert the fractional differential equation into its equivalent ordinary differential form. Since $(G'/G)$-expansion method yields many parameters and arbitrary constants, so in this case the degree of freedom of solution is high for which it is difficult to handle the solutions in practical purpose. On the other hand, in proposed tanh method the solution contains only one parameter. Hence, the degree of freedom of the solution obtained by tanh method is much less than that of other solutions obtained by $(G'/G)$-expansion method. Three-dimensional plots of some of the investigated solutions by tanh method have been also drawn to visualize the underlying dynamics of such results. Although the proposed tanh method renders solutions with physical phenomena, the suggested methods are very effective, powerful, standard, direct, and easily computerizable technique providing new exact solutions of partial differential equations.