1 Introduction

Fractional calculus was born from a letter written by L’Hospital to Leibniz (1695) asking him if nth order of derivative is \(\frac{1}{2}\), what would the result be (Diethelm 2010; Oldham and Spanier 1974; Podlubny 1999).

The nonlinear fractional equations plays a crucial role in a wide variety of physical problems arising in such as fluid mechanics (especially in the research work of viscoelastic flow), control systems, signal processing, biology systems, material diffusion including normal diffusion and anomalous diffusion. The availability of symbolic computation packages can be facilitate many powerful direct approaches to establish exact solutions to these equations (Metzler et al. 1999; Lohmann et al. 1996). Include exp-function method (Bekir et al. 2013), Kudryashov method (Eslami 2016; Hosseini et al. 2017; Pandir et al. 2016), first integral method (Eslami et al. 2014), trial equation method (Pandir et al. 2013; Demiray et al. 2015), the \((G^{\prime }/G\))-expansion method (Zheng 2012; Zayed and Gepreel 2009), simplest equation method (Taghizadeh et al. 2013; Akter and Akbar 2016) and so on (Iyiola et al. 2017).

The current work is arranged as follows: In Sect. 3, some basic properties of conformable fractional calculus are given. In Sect. 4, the main steps of the MSE method and exponential rational function method are provided. We construct the exact solutions of the nonlinear conformable time-fractional Boussinesq equation in Sect. 4.1. Also the graphical representation of the obtained solutions have given by taking parameters as special values. Some conclusions are shown in Sect. 4.2.

2 Conformable fractional calculus

There are several fractional derivatives including Grunwald–Letnikov, Caputo and Riemann–Liouville definition. All definitions satisfy the property that the fractional derivative is linear whereas they don’t satisfy the known formula of the derivative of the product of two functions (Khalil et al. 2014).

Recently, the authors Khalil et al. have given a new simple well-behaved definition of the fractional derivative called conformable fractional derivative. Unlike other definitions, this satisfies formulas of derivative of product and quotient of two functions and has a simpler the chain rule. In addition to conformable fractional derivative definition, the conformable fractional integral definition, Rolle theorem and Mean value theorem for conformable fractional differentiable functions was given (Abdeljawad 2015; Atangana et al. 2015; Cenesiz et al. 2017; Eslami and Rezazadeh 2016; Unal and Gokdogan 2017; Ekici et al. 2016).

Definition 1

Suppose \(f:\left[ 0,\infty \right) \rightarrow R\) be a function. Then, the conformable fractional derivative of f of order \(\alpha\) is defined as

$$\begin{aligned} (T_{\alpha }f)(t)=\lim _{\varepsilon \rightarrow 0}\frac{f(t+\varepsilon t^{1-\alpha })-f(t)}{\varepsilon } \end{aligned}$$
(1)

for all \(t>0\), \(\alpha \in \left( 0,1\right] .\) Some useful properties can be listed as follows

  • \(T_{\alpha }(af+bg)=a(T_{\alpha }f)+b(T_{\alpha }g)\), for all \(a,b\in R\)

  • \(T_{\alpha }(t^{p})=pt^{p-\alpha },\) for all \(p\in R\)

  • \(T_{\alpha }(\lambda )=0\), for all constant functions \(f(t)=\lambda\)

  • \(T_{\alpha }(fg)=fT_{\alpha }(g)+gT_{\alpha }(f)\)

  • \(T_{\alpha }(f/g)=\frac{g(T_{\alpha }f)-f(T_{\alpha }g)}{g^{2}}\)

Additively, if f is differentiable, then \(T_{\alpha }(f)(t)=t^{1-\alpha } \frac{df}{dt}(t).\)

Theorem

Let f \(:(0,\infty )\rightarrow R\) be a differentiable and α -differentiable function, g be a differentiable function defined in the range of f.

$$\begin{aligned} T_{\alpha }(f\circ g)(t)=t^{1-\alpha }g^{\prime }(t)f^{\prime }(g(t)). \end{aligned}$$
(2)

3 Methods of finding solutions

In the current section we present two algorithms. The main steps are as follows:

  1. 1.

    Assume that a nonlinear partial differential equation with conformable time-fractional derivative is given as follows

    $$\begin{aligned} F\left( u,\frac{\partial ^{\alpha }u}{\partial t^{\alpha }},\frac{\partial u}{ \partial x},\frac{\partial ^{2\alpha }u}{\partial t^{2\alpha }},\frac{ \partial ^{2}u}{\partial x^{2}},\ldots \right) =0, \end{aligned}$$
    (3)
  2. 2.

    To solve this equation, we take the traveling wave transformation:

    $$\begin{aligned} u(x,t)=u(\xi ), { \ }\xi =x-c\frac{t^{\alpha }}{\alpha }, \end{aligned}$$
    (4)

where c is the wave speed. By using this transformation Eq. (3) can be rewritten as an ordinary differential equation (ODE)

$$\begin{aligned} Q\left( u,u^{\prime },u^{\prime \prime },u^{\prime \prime \prime },\ldots \right) =0. \end{aligned}$$
(5)

We should integrate Eq. (5) term by term as soon as possible.

The MSE method is an useful method to find analytical solutions to fractional differential equations. It has been applied to conformable fractional differential equations (Kaplan et al. 2017).

Concerning the MSE method, we seek the solutions of Eq. (5) in terms of \(\frac{\Phi ^{^{\prime }}\left( \xi \right) }{\Phi \left( \xi \right) }\) as follows (Kaplan et al. 2015; Younis 2014; Jawad et al. 2010)

$$\begin{aligned} {u\left( \xi \right) =\sum \limits _{n=0}^{m}}a_{n}\left[ \frac{ \Phi ^{^{\prime }}\left( \xi \right) }{\Phi \left( \xi \right) }\right] ^{n},\quad { }a_{n}= {const.,}\,\,a_{m}\ne 0. \end{aligned}$$
(6)

Here \(\Phi \left( \xi \right)\) is a function to be determined \((\Phi ^{^{\prime }}\left( \xi \right) \ne 0)\).

Find the positive integer m in the formula Eq. (6) by equating the highest power of the nonlinear term(s) and the highest power of the highest order derivative of Eq. (5).

By substituting Eq. (6) into Eq. (5) , collecting all the coefficients \(\Phi ^{j}\left( \xi \right)\) \((j=0,-1,-2,\ldots)\) and set them to zero, to get a system of algebraic equations. Then we solve this system by using symbolic computation and substitute them into Eq. (6) to find the exact solutions of Eq. (3).

Concerning the exponential rational function method (Aksoy et al. 2016), the solutions can be expressed by

$$\begin{aligned} u\left( \xi \right) =\sum \limits _{n=0}^{m}\frac{a_{n}}{(1+e^{\xi })^{n}}, \end{aligned}$$
(7)

where \(a_{n}\) \(\left( a_{m}\ne 0\right)\) are constants to be determined later. The balancing number is determined previously.

Substituting Eq. (7) into Eq. (5) and collecting all terms with the same order of \(e^{i\xi }\) \((i=0,1,2,\ldots )\) together, the left-hand side of Eq. (5) is transformed into another polynomial in \(e^{i\xi }\). Equating each coefficient of this polynomial to zero yields a set of algebraic equations for \(a_{n}\) unknown parameters. Solving the equation system with the aid of Maple packet program, we can obtain the exact solutions of Eq. (3).

4 Application of the methods

We apply two different methods to the nonlinear conformable time-fractional Boussinesq equation. Recently Hosseini and Ansari have solved this equation analytically by using modified Kudryashov method [30].

4.1 Modified simple equation method

Firstly, we use the MSE method for solving the nonlinear conformable time-fractional Boussinesq equation (Demiray et al. 2014).

$$\begin{aligned} \frac{\partial ^{2\alpha }u(x,t)}{\partial t^{2\alpha }}-\frac{\partial ^{2}u(x,t)}{\partial x^{2}}-\frac{\partial ^{2}u^{2}(x,t)}{\partial x^{2\alpha }}+\frac{\partial ^{4}u(x,t)}{\partial x^{4}}=0, { }\quad 0<\alpha \le 1, \end{aligned}$$
(8)

which describes the surface water waves whose horizontal scale is much larger than the depth of the water. Equation (8) can be educed the following ODE by using the travelling wave transformation Eq. (4):

$$\begin{aligned} (c^{2}-1)u-(u^{2})^{\prime \prime }+u^{(4)}=0. \end{aligned}$$
(9)

Integrating this equation twice with respect to \(\xi\) and setting the integration constants as zero we find:

$$\begin{aligned} u^{\prime \prime }+(c-1)u-u^{2}=0. \end{aligned}$$
(10)

We get the balancing number as \(m=2.\) According to the MSE method, we seek the exact solution of Eq. (10) as:

$$\begin{aligned} u(\xi )=a_{0}+a_{1}\left( \frac{\Phi ^{^{\prime }}\left( \xi \right) }{\Phi \left( \xi \right) }\right) +a_{2}\left( \frac{\Phi ^{^{\prime }}\left( \xi \right) }{\Phi \left( \xi \right) }\right) ^{2}. \end{aligned}$$
(11)

Substitution of Eq. (11) the into Eq. (8) provides to obtain following algebraic equation system:

$$\begin{aligned}\Phi ^{0}\left( \xi \right) &: ca_{0}-a_{0}^{2}-a_{0}=0,\nonumber \\ \Phi ^{-1}\left( \xi \right) &: -a_{1}\Phi ^{^{\prime }}+a_{1}\Phi ^{\prime \prime \prime }-2a_{0}a_{1}\Phi ^{^{\prime }}+ca_{1}\Phi ^{^{\prime }}=0, \nonumber \\\Phi ^{-2}\left( \xi \right) &: 2a_{2}(\Phi ^{\prime \prime })^{2}-a_{2}(\Phi ^{^{\prime }})^{2}-2a_{0}a_{2}(\Phi ^{^{\prime }})^{2}-a_{1}^{2}(\Phi ^{^{\prime }})^{2} \nonumber \\&\quad -3a_{1}\Phi ^{\prime \prime }\Phi ^{^{\prime }}+2a_{2}\Phi ^{^{\prime }}\Phi ^{\prime \prime \prime }+ca_{2}(\Phi ^{^{\prime }})^{2}=0, \nonumber \\\Phi ^{-3}\left( \xi \right) &: -10a_{2}(\Phi ^{^{\prime }})^{2}\Phi ^{\prime \prime }-2a_{1}(\Phi ^{^{\prime }})^{3}a_{2}+2a_{1}(\Phi ^{^{\prime }})^{3}=0, \nonumber \\ \Phi ^{-4}\left( \xi \right) &: -a_{2}^{2}(\Phi ^{^{\prime }})^{4}+6a_{2}(\Phi ^{^{\prime }})^{4}=0. \end{aligned}$$
(12)

We find

$$\begin{aligned} a_{0}=0,\,c-1. \end{aligned}$$
(13)

from the first equation of Eq. (12) and

$$\begin{aligned} a_{2}=6. \end{aligned}$$
(14)

from the last equation of Eq. (12). Thereafter, we substitute these values into the remainder of the system. Let us deal with two cases arising out of different values of \(a_{0}.\)

Case 1

When \(a_{0}=0,\) Eq. (12) turns into:

$$\begin{aligned}\Phi ^{1}\left( \xi \right) &: -a_{1}\Phi ^{^{\prime }}+a_{1}\Phi ^{\prime \prime \prime }+ca_{1}\Phi ^{^{\prime }}=0, \nonumber \\ \Phi ^{2}\left( \xi \right) &: 12(\Phi ^{\prime \prime })^{2}-6(\Phi ^{^{\prime }})^{2}-a_{1}^{2}(\Phi ^{^{\prime }})^{2} \nonumber \\&\quad -3a_{1}\Phi ^{\prime \prime }\Phi ^{^{\prime }}+12\Phi ^{\prime }\Phi ^{\prime \prime \prime }+6c(\Phi ^{^{\prime }})^{2}=0, \nonumber \\ \Phi ^{3}\left( \xi \right)& : -60(\Phi ^{^{\prime }})^{2}\Phi ^{\prime \prime }-10a_{1}(\Phi ^{^{\prime }})^{3}=0. \end{aligned}$$
(15)

From Eq. (15), we find

$$\begin{aligned} a_{1}=\pm 6\sqrt{1-c} \end{aligned}$$
(16)

and

$$\begin{aligned} \Phi \left( \xi \right) =\mp \frac{c_{1}e^{-\sqrt{1-c}\xi }}{\sqrt{1-c}} +c_{2}, \end{aligned}$$
(17)

where \(c\ne 1.\) Therefore, we obtain

$$\begin{aligned}&u(\xi ) =\frac{6\sqrt{1-c}c_{1}\left(\cosh (\sqrt{1-c}\xi )-\sinh (\sqrt{1-c} \xi )\right)}{\mp \frac{c_{1}\left(\cosh (\sqrt{1-c}\xi )-\sinh (\sqrt{1-c}\xi )\right)}{ \sqrt{1-c}}+c_{2}} \end{aligned}$$
(18)
$$\begin{aligned}+\frac{6c_{1}^{2}\left(\cosh (\sqrt{1-c}\xi )-\sinh (\sqrt{1-c}\xi )\right)^{2}}{ \left( \mp \frac{c_{1}\left(\cosh (\sqrt{1-c}\xi )-\sinh (\sqrt{1-c}\xi )\right)}{\sqrt{ 1-c}}+c_{2}\right) ^{2}}, \end{aligned}$$
(19)

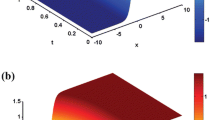
where \(\xi =x-c\frac{t^{\alpha }}{\alpha }\) (Fig. 1).

Fig. 1
figure 1

The traveling solution for u(x, t) obtained in Eq. (18) \(c_{1}=1,c_{2}=1;c=2\) when \(\alpha =0.1\) and 1 respectively

Full size image

Case 2

When \(a_{0}=c-1,\) Eq. (12) turns into:

$$\begin{aligned}\Phi ^{1}\left( \xi \right) &: -a_{1}\Phi ^{^{\prime }}+a_{1}\Phi ^{\prime \prime \prime }+ca_{1}\Phi ^{^{\prime }}+2(1-c)a_{1}\Phi ^{^{\prime }}=0, \nonumber \\ \Phi ^{2}\left( \xi \right) &: 12(\Phi ^{\prime \prime })^{2}-6(\Phi ^{^{\prime }})^{2}-a_{1}^{2}(\Phi ^{^{\prime }})^{2}-3a_{1}\Phi ^{\prime \prime }\Phi ^{^{\prime }} \nonumber \\&\quad+12\Phi ^{\prime }\Phi ^{\prime \prime \prime }+6c(\Phi ^{^{\prime }})^{2}-12(1-c)(\Phi ^{^{\prime }})^{2}=0, \nonumber \\ \Phi ^{3}\left( \xi \right) &: -60(\Phi ^{^{\prime }})^{2}\Phi ^{\prime \prime }-10a_{1}(\Phi ^{^{\prime }})^{3}=0. \end{aligned}$$
(20)

By solving the system above, we verify:

$$\begin{aligned} a_{1}= & {} \pm 6\sqrt{c-1} \end{aligned}$$
(21)
$$\begin{aligned} \Phi \left( \xi \right)= & {} \mp \frac{c_{1}e^{-\sqrt{c-1}\xi }}{\sqrt{c-1}} +c_{2}, \end{aligned}$$
(22)

where \(c\ne 1.\) Finally, substitution of the values into Eq. (11) completes the determination of the solution of nonlinear conformable time-fractional Boussinesq equation as

$$\begin{aligned}&u(\xi ) =c-1+\frac{6\sqrt{c-1}c_{1}(\cosh (\sqrt{c-1}\xi )-\sinh (\sqrt{c-1 }\xi ))}{\mp \frac{c_{1}(\cosh (\sqrt{c-1}\xi )-\sinh (\sqrt{c-1}\xi ))}{ \sqrt{1-c}}+c_{2}} \end{aligned}$$
(23)
$$\begin{aligned}&+\frac{6c_{1}^{2}(\cosh (\sqrt{c-1}\xi )-\sinh (\sqrt{c-1}\xi ))^{2}}{ \left( \mp \frac{c_{1}(\cosh (\sqrt{c-1}\xi )-\sinh (\sqrt{c-1}\xi ))}{\sqrt{ c-1}}+c_{2}\right) ^{2}}, \end{aligned}$$
(24)

where \(\xi =x-c\frac{t^{\alpha }}{\alpha }\) (Fig. 2).

Fig. 2
figure 2

The traveling solution for u(x, t) obtained in Eq. (23) \(c_{1}=1,c_{2}=1;c=2\) when \(\alpha =0.1\) and 1 respectively

Full size image

4.2 Exponential rational function method

According to the exponential rational function method, we seek the exact solution of Eq. (10) as:

$$\begin{aligned} u(\xi )=a_{0}+\frac{a_{1}}{1+e^{\xi }}+\frac{a_{2}}{(1+e^{\xi })^{2}}. \end{aligned}$$
(25)

Substituting Eq. (25) into Eq. (10) and collecting the coefficients of \(e^{n}\left( \xi \right) ,(n=0,1,2,3,4)\) and by equating each coefficient to zero, we find:

$$\begin{aligned}e^{0}\left( \xi \right) &: ca_{0}-a_{0}^{2}-2a_{0}a_{1}-2a_{0}a_{2}-2a_{1}a_{2}-a_{0} \nonumber \\&\quad -a_{1}-a_{2}+ca_{1}+ca_{2}-a_{2}^{2}-a_{1}^{2}=0, \nonumber \\e^{1}\left( \xi \right) &: 4ca_{0}-2a_{1}a_{2}-4a_{0}+3ca_{1}-6a_{0}a_{1} \nonumber \\&\quad-4a_{1}-2a_{1}^{2}-4a_{2}-4a_{0}a_{2}-4a_{0}^{2}+2ca_{2}=0, \nonumber \\e^{2}\left( \xi \right) &: 6ca_{0}+3a_{2}+3ca_{1}-3a_{1}-6a_{0}a_{1} \nonumber \\&\quad{0}-2a_{0}a_{2}-a_{1}^{2}-6a_{0}^{2}+ca_{2}=0, \nonumber \\e^{3}\left( \xi \right) &: 4ca_{0}+ca_{1}-4a_{0}-2a_{0}a_{1}-4a_{0}^{2}=0, \nonumber \\e^{4}\left( \xi \right) &: -a_{0}+ca_{0}-a_{0}^{2}=0. \end{aligned}$$
(26)

From the solutions of the system above , we obtain

$$\begin{aligned} a_{0}=1,a_{1}=-6,a_{2}=6,c=2. \end{aligned}$$
(27)

Finally, we substitute Eq. (27) into Eq. (25) to get:

$$\begin{aligned} u(\xi )=1-\frac{6}{1+\cosh \xi +\sinh \xi }+\frac{6}{(1+\cosh \xi +\sinh \xi )^{2}}. \end{aligned}$$
(28)

Here \(\xi =x-2\frac{t^{\alpha }}{\alpha }\) (Fig. 3).

Fig. 3
figure 3

The travelling wave solution for u(x, t) obtained in Eq. (27) when \(\alpha =0.1\) and 1 respectively

Full size image

5 Conclusions

In this article, we have constructed some exact travelling wave solutions for the nonlinear conformable time-fractional Boussinesq equation by using MSE and exponential rational function methods. The present methodologies are shown to provide a useful approaches to solve the nonlinear partial differential equations with conformable fractional derivative in mathematical physics. On comparing the results obtained in this paper, we conclude that the MSE method gives more solutions, but it is more complicated than exponential rational function method. Also by comparing the solutions with the existing solutions, it can be stated that these solutions are new [30]. Furthermore, the exact solutions obtained in this paper might be very useful in various areas of applied mathematics in interpreting some physical phenomena. Finally, mathematical software Maple is used to show that all solutions obtained in this paper satisfy the original equations.