1 Introduction

Fractional calculus have been one of the most intensively developing areas of mathematical analysis, including several definitions of fractional operators like Riemann-Liouville, Caputo, and Grünwald-Letnikov. It implies the calculus of the differentiation and integration whose order is given by a fractional number. The history of the fractional derivatives goes back to the seventeenth century Diethelm (2010), Oldham and Spanier (1974), Podlubny (1999).

Nonlinear fractional partial differential equations (NFDE) play an important role due to its application in various fields of science not only in physics, but also in engineering, optimal problem, finance, chemistry and biology. So obtaining solutions of these equations have become more important. Therefore, many new methods have been introduced. For example, sub equation method Sahoo and Saha Ray (2015), \((G^{\prime }/G)\)-expansion method Bekir et al. (2016), Kudryashov method Demiray et al. (2014), modified Kudryashov method Hosseini et al. (2017), Korkmaz (2017) trial equation method Gurefe et al. (2011), homotopy analysis method Pandir et al. (2014), first integral method Cenesiz et al. (2017), Eslami and Rezazadeh (2016) and so on Unal and Gokdogan (2017), Ekici et al. (2016), Guner et al. (2017a, b).

The text below is organized in the following way. In Sect. 2, brief of conformable fractional derivative is given. Then in Sect. 3, the modified simple equation method is presented. In Sect. 4, applications of the method are given. Finally we give some conclusions.

2 Brief of conformable fractional derivative

Recently, the authors Khalil et al. (2014) introduced a new simple well-behaved definition of the fractional derivative called conformable fractional derivative. In this section, we give the brief of conformable fractional derivative.

Definition 1

Suppose that \(f=f(t)\) be a function defined on the positive half space. Then, the conformable fractional derivative of f of order \(\alpha\) is defined as

$$\begin{aligned} \left( D_{t}^{\alpha }f\right) (t)=\lim _{\varepsilon \rightarrow 0}\frac{f(t+\varepsilon t^{1-\alpha })-f(t)}{\varepsilon } \end{aligned}$$
(1)

for all \(t>0\), \(\alpha \in \left( 0,1\right]\) and \(f:\left[ 0,\infty \right) \rightarrow\) Some useful properties can be listed as follows: \(\cdot D_{t}^{\alpha }(af+bg)=a(D_{t}^{\alpha }f)+b(D_{t}^{\alpha }g)\), for all \(a,b\in\)

  • \(\cdot D_{t}^{\alpha }(t^{p})=pt^{p-\alpha },\) for all \(p\in\)

  • \(\cdot D_{t}^{\alpha }(\lambda )=0\), for all constant functions \(f(t)=\lambda\)

  • \(\cdot D_{t}^{\alpha }(fg)=fD_{t}^{\alpha }(g)+gD_{t}^{\alpha }(f)\)

  • \(\cdot D_{t}^{\alpha }(f/g)=\frac{g(D_{t}^{\alpha }f)-f(D_{t}^{\alpha }g)}{ g^{2}}\)

Additively, if f is differentiable, then \(D_{t}^{\alpha }(f)(t)=t^{1-\alpha }\frac{df}{dt}(t)\).

Theorem

Let \(f:(0,\infty )\rightarrow\) be a differentiable and \(\alpha -\) conformable differerentiable function and also g be a differentiable function defined in the range of f. Then the following property holds

$$\begin{aligned} D_{t}^{\alpha }(f\circ g)(t)=t^{1-\alpha }g^{\prime }(t)f^{\prime }(g(t)). \end{aligned}$$
(2)

Here \(^{\prime }\) denotes the derivative with respect to \(\alpha\).

3 Method of finding solutions

In this section, we illustrate the main idea of the MSE method Kaplan et al. (2015). A NFDE in the sense of the conformable derivative is given as follows

$$\begin{aligned} F\left( u,D_{t}^{\alpha }u,D_{x}^{\alpha }u,D_{y}^{\alpha }u,...\right) =0. \end{aligned}$$
(3)

By making use of the following transformation

$$\begin{aligned} u(x,y,t)=u(\xi ),\xi =k\frac{x^{\alpha }}{\alpha }+h\frac{ y^{\alpha }}{\alpha }-l\frac{t^{\alpha }}{\alpha }, \end{aligned}$$
(4)

where k, h and l are nonzero arbitrary constants. Equation (3) can be reduced to an ordinary differential equation (ODE) as follows:

$$\begin{aligned} Q(u,u^{\prime },u^{\prime \prime },u^{\prime \prime \prime },...)=0. \end{aligned}$$
(5)

Determine the positive integer m in the formula Eq. (6) by equating the highest power of the nonlinear term(s) and the highest power of the highest order derivative of Eq. (5). We seek the solution in the form

$$\begin{aligned} u\left( \xi \right) =\sum \limits _{n=0}^{m}a_{n}\left[ \frac{ \vartheta ^{^{\prime }}\left( \xi \right) }{\vartheta \left( \xi \right) } \right] ^{n},a_{m}\ne 0. \end{aligned}$$
(6)

Here \(\vartheta \left( \xi \right)\) is an unknown function. Substituting Eq. (6) into Eq. (5) and setting the coefficients of \(\left[ \frac{\vartheta ^{^{\prime }}\left( \xi \right) }{ \vartheta \left( \xi \right) }\right] ^{n}\) to be zero, one obtains an over-determined nonlinear algebraic equation in \(a_{n}(n=0,1,\ldots ,m), \vartheta \left( \xi \right)\) and its derivatives, k and l. Finally substitution of these values into Eq. (6) completes the determination of exact solutions of Eq. (3).

Note: Here \(\vartheta \left( \xi \right)\) is the auxiliary function of the modified simple equation method. It is not a solution of any pre-defined or known function. Thus, the modified simple equation method gives more fresh solutions.

4 Applications of the method

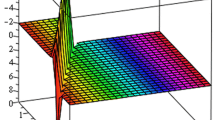
4.1 (2+1)-dimensional conformable time-fractional Zoomeron equation

Let us apply the above methodology to the (2+1)-dimensional conformable time-fractional Zoomeron equation Zhou et al. (2015)

$$\begin{aligned} D_{tt}^{2\alpha }\left( \frac{u_{xy}}{u}\right) -\left( \frac{u_{xy}}{u} \right) _{xx}+2D_{t}^{\alpha }(u^{2})_{x}=0,0<\alpha \le 1, \end{aligned}$$
(7)

which is a convenient model to display the novel phenomena associated with boomerons and trappons. We substitute the following transformation into Eq. (7)

$$\begin{aligned} u(x,y,t)=u(\xi ),\xi =k\frac{x^{\alpha }}{\alpha }+h\frac{y^{\alpha }}{ \alpha }-l\frac{t^{\alpha }}{\alpha } \end{aligned}$$
(8)

and then the following ODE is obtained.

$$\begin{aligned} khl^{2}\left( \frac{u^{\prime \prime }}{u}\right) ^{\prime \prime }-k^{3}h\left( \frac{u^{\prime \prime }}{u}\right) ^{\prime \prime }-2kl(u^{2})^{\prime \prime }=0 \end{aligned}$$
(9)

Integrating twice Eq. (9) with respect to \(\xi\) results the following equation

$$\begin{aligned} kh(l^{2}-k^{2})u^{\prime \prime }-2klu^{3}-au=0, \end{aligned}$$
(10)

where a is a non-zero integration constant. Here the balancing number is found as \(m=1\). Therefore, the solution of Eq. (10) is of the form:

$$\begin{aligned} u(\xi )=a_{0}+a_{1}\left( \frac{\vartheta ^{^{\prime }}\left( \xi \right) }{ \vartheta \left( \xi \right) }\right) , \end{aligned}$$
(11)

where \(a_{0}\) and \(a_{1}\) are constants to be determined and \(\vartheta \left( \xi \right)\) is an unknown function. Substituting Eq. (11) into Eq. (10), and vanishing all coefficients of each order of \(\vartheta \left( \xi \right) ,\) we obtain a set of over-determined algebraic equations as follows:

$$\begin{aligned}&\vartheta ^{0}\left( \xi \right) : -2kla_{0}^{3}-aa_{0}=0, \nonumber \\&\vartheta ^{1}\left( \xi \right) : -k^{3}ha_{1}\vartheta ^{\prime \prime \prime }-6kla_{0}^{2}a_{1}\vartheta ^{\prime }+khl^{2}a_{1}\vartheta ^{\prime \prime \prime }-aa_{1}\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{2}\left( \xi \right) : 3k^{3}ha_{1}\vartheta ^{\prime \prime }\vartheta ^{\prime }-6kla_{0}a_{1}^{2}\vartheta ^{\prime 2}-3khl^{2}a_{1}\vartheta ^{\prime \prime }\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{3}\left( \xi \right) : -2k^{3}ha_{1}\vartheta ^{\prime 3}+2khl^{2}a_{1}\vartheta ^{\prime 3}-2kla_{1}^{3}\vartheta ^{\prime 3}=0. \end{aligned}$$
(12)

Solving these algebraic equations with the help of computer algebra, we obtain

$$\begin{aligned} a_{0}=\pm \sqrt{-\frac{a}{2kl}},a_{1}=\pm \sqrt{\frac{h(l^{2}-k^{2})}{l}} ,(\left| k\right| \ne \left| l\right| ) \end{aligned}$$
(13)

and then we substitute Eq. (13) into the reminder of the system to find:

$$\begin{aligned} \vartheta (\xi )=c_{1}+c_{2}e^{\sqrt{\frac{2a}{kh(k^{2}-l^{2})}}\xi }. \end{aligned}$$
(14)

Then by substituting Eqs. (13) and (14), we get

$$\begin{aligned} u(\xi )=\sqrt{\frac{-2a}{kl}}\left( \frac{c_{1}+c_{2}\sinh \left( \frac{ 2a\xi }{kh(k^{2}-l^{2})}\right) -c_{2}\cosh \left( \frac{2a\xi }{ kh(k^{2}-l^{2})}\right) }{c_{1}+c_{2}\cosh \left( \frac{2a\xi }{ kh(k^{2}-l^{2})}\right) -c_{2}\sinh \left( \frac{2a\xi }{kh(k^{2}-l^{2})} \right) }\right) , \end{aligned}$$
(15)

where \(\xi =kx+hy-l\frac{t^{\alpha }}{\alpha }\).

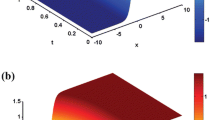
4.2 The conformable space-time fractional EW equation

The space-time fractional EW equation Korkmaz (2017)

$$\begin{aligned} D_{t}^{\alpha }u(x,t)+aD_{x}^{\alpha }u^{2}(x,t)-cD_{xxt}^{3\alpha }u(x,t)=0 \end{aligned}$$
(16)

where a and c are positive parameters. This equation is used to model nonlinear dispersive waves. The fractional EW is defined in the positive half space since conformal derivative is defined only in positive domains.

Employing the transformation Eq. (17),

$$\begin{aligned} u(x,t)=u(\xi ),\xi =k\frac{x^{\alpha }}{\alpha }-l\frac{t^{\alpha }}{\alpha }, \end{aligned}$$
(17)

Equation (16) can be reduced to an ODE. Then integrating this equation once with respect to \(\xi\) by taking the integration constant to zero gives the following equation

$$\begin{aligned} -lu+aku^{2}+clk^{2}u^{\prime \prime }=0 \end{aligned}$$
(18)

According to MSE method, the exact solution of the reduced equation can be taken as

$$\begin{aligned} u(\xi )=a_{0}+a_{1}\left( \frac{\vartheta ^{^{\prime }}\left( \xi \right) }{ \vartheta \left( \xi \right) }\right) +a_{2}\left( \frac{\vartheta ^{^{\prime }}\left( \xi \right) }{\vartheta \left( \xi \right) }\right) ^{2}. \end{aligned}$$
(19)

Substitution of Eq. (19) the into Eq. (18) provides to obtain following algebraic equation system:

$$\begin{aligned}&\vartheta ^{0}\left( \xi \right) : -la_{0}+aka_{0}^{2}=0, \nonumber \\&\vartheta ^{1}\left( \xi \right) : clk^{2}a_{1}\vartheta ^{\prime \prime \prime }+2aka_{0}a_{1}\vartheta ^{\prime }-la_{1}\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{2}\left( \xi \right) : 2clk^{2}a_{2}\vartheta ^{\prime }\vartheta ^{\prime \prime \prime }+2aka_{0}a_{2}(\vartheta ^{\prime })^{2}+aka_{1}^{2}(\vartheta ^{\prime })^{2} \nonumber \\&\qquad \quad +2clk^{2}a_{2}(\vartheta ^{\prime \prime })^{2}-3clk^{2}a_{1}\vartheta ^{\prime \prime }\vartheta ^{\prime }-la_{2}(\vartheta ^{\prime })^{2}=0, \nonumber \\&\vartheta ^{3}\left( \xi \right) : 2aka_{1}(\vartheta ^{\prime })^{3}a_{2}-10clk^{2}a_{2}(\vartheta ^{\prime })^{2}\vartheta ^{\prime \prime }+2clk^{2}a_{1}(\vartheta ^{\prime })^{3}=0, \nonumber \\&\vartheta ^{4}\left( \xi \right) : aka_{2}^{2}(\vartheta ^{\prime })^{4}+6clk^{2}a_{2}(\vartheta ^{\prime })^{4}=0. \end{aligned}$$
(20)

We find

$$\begin{aligned} a_{0}=0,\frac{l}{ak} \end{aligned}$$
(21)

from the first equation of Eq. (20) and

$$\begin{aligned} a_{2}=-\frac{6ckl}{a}, \end{aligned}$$
(22)

from the last equation of Eq. (20). Thereafter, we substitute these values into the reminder of the system. Let us deal with two cases arising out of different values of \(a_{0}\).

Case 1 When \(a_{0}=0\), equation system (20) is reduced to:

$$\begin{aligned}&\vartheta ^{1}\left( \xi \right) : clk^{2}a_{1}\vartheta ^{\prime \prime \prime }-la_{1}\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{2}\left( \xi \right) : -\frac{12c^{2}l^{2}k^{3}}{a}\vartheta ^{\prime }\vartheta ^{\prime \prime \prime }+aka_{1}^{2}(\vartheta ^{\prime })^{2}-\frac{12c^{2}l^{2}k^{3}}{a}(\vartheta ^{\prime \prime })^{2} \nonumber \\&\qquad \quad -3clk^{2}a_{1}\vartheta ^{\prime \prime }\vartheta ^{\prime }+\frac{ 6l^{2}ct}{a}(\vartheta ^{\prime })^{2}=0, \nonumber \\&\vartheta ^{3}\left( \xi \right) : -10clk^{2}a_{1}(\vartheta ^{\prime })^{3}+\frac{60c^{2}l^{2}k^{3}}{a}(\vartheta ^{\prime })^{2}\vartheta ^{\prime \prime }=0. \end{aligned}$$
(23)

When we solve this system we obtain

$$\begin{aligned} a_{1}=\pm \frac{6\sqrt{c}l}{a} \end{aligned}$$
(24)

and

$$\begin{aligned} \vartheta (\xi )=\pm c_{1}\sqrt{c}ke^{\pm \frac{\xi }{\sqrt{c}k}}+c_{2}. \end{aligned}$$
(25)

Finally by substituting these values into Eq. (19), we verify the exact solution of the conformable space-time fractional EW equation

$$\begin{aligned} u(\xi )= & {} \pm \frac{6\sqrt{c}lc_{1}\left( \cosh \left( \frac{\xi }{k\sqrt{c} }\right) \pm \sinh \left( \frac{\xi }{k\sqrt{c}}\right) \right) }{a\left( \pm k\sqrt{c}c_{1}\left( \cosh \left( \frac{\xi }{k\sqrt{c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{c}}\right) \right) +c_{2}\right) } \\&-\frac{6cklc_{1}^{2}\left( \cosh \left( \frac{\xi }{k\sqrt{c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{c}}\right) \right) ^{2}}{a\left( \pm k\sqrt{c }c_{1}\left( \cosh \left( \frac{\xi }{k\sqrt{c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{c}}\right) \right) +c_{2}\right) ^{2}}, \end{aligned}$$

where \(\xi =k\frac{x^{\alpha }}{\alpha }-l\frac{t^{\alpha }}{\alpha }\).

Case 2 Let us discuss the case \(a_{0}=\frac{l}{ ak}\). In this case equation system (23) takes the form:

$$\begin{aligned}&\vartheta ^{1}\left( \xi \right) : clk^{2}a_{1}\vartheta ^{\prime \prime \prime }+la_{1}\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{2}\left( \xi \right) : -\frac{12c^{2}l^{2}k^{3}}{a}\vartheta ^{\prime }\vartheta ^{\prime \prime \prime }-\frac{6l^{2}ct}{a}(\vartheta ^{\prime })^{2}+aka_{1}^{2}(\vartheta ^{\prime })^{2} \nonumber \\&\qquad \quad -\frac{12c^{2}l^{2}k^{3}}{a}(\vartheta ^{\prime \prime })^{2}-3clk^{2}a_{1}\vartheta ^{\prime \prime }\vartheta ^{\prime }=0, \nonumber \\&\vartheta ^{3}\left( \xi \right) : -10clk^{2}a_{1}(\vartheta ^{\prime })^{3}+\frac{60c^{2}l^{2}k^{3}}{a}(\vartheta ^{\prime })^{2}\vartheta ^{\prime \prime }=0. \end{aligned}$$
(26)

Then, we solve the system above to find

$$\begin{aligned} a_{1}=\pm \frac{6\sqrt{-c}l}{a} \end{aligned}$$
(27)

and

$$\begin{aligned} \vartheta (\xi )=\mp c_{1}\sqrt{-c}ke^{\pm \frac{\xi }{\sqrt{-c}k}}+c_{2}. \end{aligned}$$
(28)

Finally, we substitute the values of \(a_{0},a_{1},\) \(a_{2}\) and \(\vartheta (\xi )\) into Eq. (19) to obtain:

$$\begin{aligned} u(\xi )= & {} \frac{l}{ak}\pm \frac{6\sqrt{-c}lc_{1}\left( \cosh \left( \frac{ \xi }{k\sqrt{-c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{-c}}\right) \right) }{a\left( \mp k\sqrt{-c}c_{1}\left( \cosh \left( \frac{\xi }{k\sqrt{ -c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{-c}}\right) \right) +c_{2}\right) } \\&-\frac{6cklc_{1}^{2}\left( \cosh \left( \frac{\xi }{k\sqrt{-c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{-c}}\right) \right) ^{2}}{a\left( \mp k\sqrt{ -c}c_{1}\left( \cosh \left( \frac{\xi }{k\sqrt{-c}}\right) \pm \sinh \left( \frac{\xi }{k\sqrt{-c}}\right) \right) +c_{2}\right) ^{2}}, \end{aligned}$$

where \(\xi =k\frac{x^{\alpha }}{\alpha }-l\frac{t^{\alpha }}{\alpha }\).

5 Conclusions

In this work, we have discussed the new definition for traveling wave transformation and new conformable fractional derivative to converting the NFDEs into the ODEs and its applications to the (2+1)-dimensional conformable time-fractional Zoomeron equation and the conformable space-time fractional EW equation. In this paper, different cases of the balancing number are came up. The MSE method is applied to the model reveals soliton solutions. Since the technique is direct and powerful it can be used to handle a variety of FPDE’s which appears in applications in several branch of the nonlinear sciences. In additional to algorithms can be applied to obtain such soliton solutions so that a complete picture can be drawn.