Application of the ITEM for the modified dispersive water-wave system

Abstract

The aim of this paper is to introduce a novel study of obtaining an analytical solutions to the modified dispersive water-wave system. An analytical technique based on the improved $\tan (\phi /2)$-expansion method (ITEM) is extended to handle such a system. Description of the method is given and the obtained results reveal that the ITEM is a new significant method for exploring nonlinear partial differential models. By using this method, exact solutions including the hyperbolic function solution, traveling wave solution, soliton solution, rational function solution, and periodic wave solution of this system of equations have been obtained. Moreover, by using Matlab, some graphical simulations were done to see the behavior of these solutions.

1 Introduction

Partial differential equations (PDEs) find special applicability within many scientific and mathematical disciplines. Moreover, nonlinear partial differential equations (NPDEs) are widely used to describe complex phenomena in various fields of sciences. For this purpose, one way is using integration methods for finding the exact solutions. A large variety of physical, chemical, and biological phenomena are governed by nonlinear partial differential equations. One of the most exciting advances in the field of nonlinear science and theoretical physics is the development of methods to look for exact solutions of NPDEs. One of the most recent approaches is using semi-analytical methods (Dehghan and Manafian 2009; Dehghan et al. 2010a, b; Rashidi et al. 2013) or analytical methods (Biswas 2009; Dehghan et al. 2011a, b; Manafian 2015; Manafian and Lakestani 2015a, b, c, 2016a, b; Manafian et al. 2016; Baskonus et al. 2016; Demiray 2017). So instead of using current models of partial differential equations, we can transfer PDEs to ordinary differential equations. Hence there occurs a need to use solitary wave variable that would appropriately transforms PDEs to ODEs and solve them. In this paper, we apply the ITEM to solve the modified dispersive water-wave system. Many research papers dealing with analytical methods exists in open literatures and some of them are reviewed and cited here for better understanding of the physical problems. Dehghan et al. (2010a) have used the homotopy analysis method for solving nonlinear fractional PDEs. HAM has been used for finding appropriate solutions for the Zakharov–Kuznetsov equations with fully nonlinear dispersion (Nawaz et al. 2013). Hasseine et al. (2013), have developed analytical solutions of the particle breakage using the population balance equation in batch and continuous flow systems. Authors of Dehghan and Manafian (2009) and Dehghan et al. (2010b) have applied the homotopy perturbation method and variational iteration method for variable coefficients fourth-order PDEs and Fitzhugh–Nagumo equation respectively. Rashidi et al. (2013) have studied heat transfer in a second-grade fluid through a porous medium with the modified differential transform method. Exp-function method (EFM) was used to solve PDEs arising in biology and population genetics and mathematical physics (Dehghan et al. 2011a, b). Also, in Manafian and Lakestani (2015a) and Manafian (2015), EFM was utilized to Biswas–Milovic equation for Kerr, power, parabolic and dual parabolic law nonlinearities. The solitary wave ansatz was used to integrate the K(m, n) equation having time-dependent damping and dispersion coefficients by Biswas (2009). In Manafian and Lakestani (2015b), the (G′/G)-expansion method was studied for solving Burgers, Fisher, Huxley and combined forms of these equations. Authors of Manafian and Lakestani (2015c); Manafian et al. (2016); Manafian and Lakestani (2016a, b, c); Manafian (2016), have solved the generalized Fitzhugh–Nagumo equation with time-dependent coefficients, Biswas–Milovic equation for Kerr law nonlinearity, (2+1)-dimensional Zoomeron, the Duffing and the SRLW equations, Tzitzéica type nonlinear evolution equations, Schrödinger type nonlinear evolution equations and Kundu–Eckhaus equation respectively by $\tan (\phi /2)$-expansion method. Baskonus and Bulut (2016a) and Baskonus et al. (2016) have used the Bernoulli sub-equation function method for solving the for (2+1)-dimensional Boiti–Leon–Pempinelli systems and Zakharov–Kuznetsov equation with power law nonlinearity. Moreover, the improved Bernoulli sub-equation function method has been applied for the (2+1)-dimensional dispersive long water-wave system by Bulut and Baskonus (2016). Baskonus et al. (2016b) have obtained the exact solutions by the modified exp($-\Omega (\xi )$) expansion function method for structures of longitudinal wave equation in a magneto-electro-elastic circular rod. Finally, in Baskonus and Bulut (2016c) the sine-Gordon expansion method has been proposed for obtaining solutions of the system of equations for the ion sound and Langmuir waves. Based on the idea of the homogeneous balance method the exact solutions of nonlinear partial differential equations have been obtained by Fan and Zhang (1998). For constructing multiple travelling wave solutions of nonlinear partial differential equations has been used the extended tanh-function method by Fan (2000). Also, Fan (2000) used the extended tanh method to obtain more travelling wave solutions for two generalized Hirota–Satsuma coupled KdV systems.

In this paper, we consider the modified dispersive water-wave system as follows (Huang 2009; Wen and Xu 2013)

$$\begin{aligned} u_{yt}+u_{xxy}-2v_{xx}-(u^2)_{xy}=0, \quad v_t-v_{xx}-2(uv)_x=0. \end{aligned}$$

(1.1)

Huang (2009) has obtained a general solution with three arbitrary functions for system (1.1) by means of the WTC truncation method, special types of periodic folded waves are derived. Also, Wen and Xu (2013) have give multiple soliton solutions and fusion interaction phenomena for system (1.1) by means of Bäcklund transformation and the Hirota bilinear method. In Liu et al. (2008), method of bifurcation of planar dynamical systems and method of numerical simulation of differential equations are employed to investigate the modified dispersive water wave equation. System (1.1) can model nonlinear and dispersive long gravity waves traveling in two horizontal directions on shallow waters of uniform depth, it also can be derived from the well-known Kadomtsev–Petviashvili (KP) equation using the symmetry constraint (Lou and Hu 1997). Tang et al. (2002) and Tang and Lou (2003) have derived abundant propagating localized excitations with the help of Painlevé-Bäcklund transformation and a multilinear variable separation approach. Li and Zhang (2004) have derived many new types of non-traveling solutions have been obtained by a further generalized projective Riccati equation approach. Moreover, in Zheng et al. (2005), have obtained some nonpropagating and propagating solitons by means of the extended mapping approach. Ali et al. (2015) have described the propagation of surface water waves in a uniform channel by obtaining the solitary wave and topological soliton solutions. Meng et al. (2012) have modeled the propagation of the long weakly nonlinear and weakly dispersive surface waves of variable depth in shallow water by using of the generalized dispersive water-wave system. In Liu et al. (2008), the method of bifurcation of planar dynamical systems and method of numerical simulation of differential equations are employed to investigate the modified dispersive water wave equation. Ma (2002) presented a novel class of explicit exact solutions to the Korteweg-de Vries (KdV) equation in the bilinear form. Also, Ma and Maruno (2004) used a set of coupled conditions consisting of differential-difference equations to solve the Toda lattice equation. Authors of Ma and You (2004a) utilized the Wronskian determinant to solve the KdV equation in the bilinear form. Ma and Fuchssteiner (1996) presented two ansätze methods for obtaining explicit traveling wave solutions to a Kolmogorov–Petrovskii–Piskunov equation. Constructing rational solutions to the Toda lattice equation through the Casoratian formulation have been made by Ma and You (2004b). Moreover, Ma et al. (2007) introduced Frobenius integrable decompositions for partial differential equations. Explicit exact solution of a generalized KdV equation have been investigated by Ma and Zhou (1997). Mohyud-Din et al. (2012a) presented a numerical solution of a family of generalized fifth-order KdV equations using a meshless method of lines. Authors of Mohyud-Din et al. (2009a) applied the He’s polynomials to investigate propagating traveling solitary wave solutions of seventh order generalized KdV equations. Ensuring increased and sustainable biomass production is critical for European countries in Sabattia et al. (2014). The homotopy perturbation method is used for obtaining soliton solution of the Kaup–Kupershmidt equation by Mohyud-Din et al. (2011a). Also, authors of Mohyud-Din et al. (2011b) have used the homotopy perturbation method to obtain numerical soliton solution of the improved Boussinesq equation. Moreover, Mohyud-Din et al. (2012b) applied Exp-function method to construct generalized solitary and periodic solutions of Fitzhugh–Nagumo equation. Alam et al. (2014) constructed abundant traveling wave solutions involving parameters to the Boussinesq equation by means of the novel (G′/G)-expansion method. Also, Mohyud-Din et al. (2010a) have used the exp-function and variational iteration methods for re-formated partial differential equations. The exp-function method has been tested on the modified Zakharov–Kuznetsov and Zakharov–Kuznetsov-Modified-Equal-Width equations by Noor et al. (2010b). In Mohyud-Din et al. (2009b), HPM and VIM and in Noor et al. (2008) and Mohyud-Din et al. (2010c) Exp-function method have been applied for some partial differential equation. The paper is organized as follows: in Sect. 2, we describe the ITEM. In Sect. 3, we examine the modified dispersive water-wave system with method introduced in Sect. 2. Moreover, in Sect. 4, we give discussion and remark of the solutions. Also conclusion is given in Sect. 5.

2 Description of the ITEM

The ITEM is well-known analytical method which was first presented and developed in Manafian et al. (2016).

Step 1 We suppose that given nonlinear partial differential equation for $\mathrm {u(x, t)}$ to be in the form

$$\begin{aligned} \mathcal {N}(u, u_x, u_t, u_{xx}, u_{tt},...)=0, \end{aligned}$$

(2.1)

can be reduced to an ODE

$$\begin{aligned} \mathcal {Q}(u, u', -\mu u', u'', \mu ^2u'',...)=0, \end{aligned}$$

(2.2)

by the transformation $\xi =x-\mu t$ is the wave variable. Also, $\mu$ is constant to be determined later.

Step 2 Suppose the traveling wave solution of Eq. (2.2) can be expressed as follows:

$$\begin{aligned} u(\xi )=S(\phi )=\sum _{k=0}^{m}A_k\left[ p+\tan (\phi /2)\right] ^k+ \sum _{k=1}^{m}B_k\left[ p+\tan (\phi /2)\right] ^{-k}, \end{aligned}$$

(2.3)

where $A_k (0\le k \le m)$ and $B_k (1\le k \le m)$ are constants to be determined, such that $A_m\ne 0, B_m\ne 0$ and $\phi =\phi (\xi )$ satisfies the following ordinary differential equation:

$$\begin{aligned} \phi '(\xi )=a\sin (\phi (\xi ))+b\cos (\phi (\xi ))+c. \end{aligned}$$

(2.4)

We will consider the following special solutions of Eq. (2.4):

Family 1::

When $\Delta =a^2+b^2-c^2<0$ and $b-c\ne 0$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}-\frac{\sqrt{-\Delta }}{b-c}\tan \left( \frac{\sqrt{-\Delta }}{2}\overline{\xi }\right) \right] .$

Family 2::

When $\Delta =a^2+b^2-c^2>0$ and $b-c\ne 0$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}+\frac{\sqrt{\Delta }}{b-c}\tanh \left( \frac{\sqrt{\Delta }}{2}\overline{\xi }\right) \right] .$

Family 3::

When $\Delta =a^2+b^2-c^2>0$, $b\ne 0$ and $c=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b}+\frac{\sqrt{b^2+a^2}}{b}\tanh \left( \frac{\sqrt{b^2+a^2}}{2}\overline{\xi }\right) \right] .$

Family 4::

When $\Delta =a^2+b^2-c^2<0$, $c\ne 0$ and $b=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ -\frac{a}{c}+\frac{\sqrt{c^2-a^2}}{c}\tan \left( \frac{\sqrt{c^2-a^2}}{2}\overline{\xi }\right) \right] .$

Family 5::

When $\Delta =a^2+b^2-c^2>0$, $b-c\ne 0$ and $a=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ \sqrt{\frac{b+c}{b-c}}\tanh \left( \frac{\sqrt{b^2-c^2}}{2}\overline{\xi }\right) \right] .$

Family 6::

When $a=0$ and $\mathrm {c=0,}$ then $\phi (\xi )=\tan ^{-1}\left[ \frac{e^{2b\overline{\xi }}-1}{e^{2b\overline{\xi }}+1}, \ \frac{2e^{b\overline{\xi }}}{e^{2b\overline{\xi }}+1}\right] .$

Family 7::

When $b=0$ and $c=0,$ then $\phi (\xi )=\tan ^{-1}\left[ \frac{2e^{a\overline{\xi }}}{e^{2a\overline{\xi }}+1}, \ \frac{e^{2a\overline{\xi }}-1}{e^{2a\overline{\xi }}+1}\right] .$

Family 8::

When $a^2+b^2=c^2$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a\overline{\xi }+2}{(b-c)\overline{\xi }}\right] .$

Family 9::

When $a=b=c=ka$, then $\phi (\xi )=2\tan ^{-1}\left[ e^{ka\overline{\xi }}-1\right] .$

Family 10::

When $a=c=ka$ and $\mathrm {b=-ka}$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{e^{ka\overline{\xi }}}{-1+e^{ka\overline{\xi }}}\right] .$

Family 11::

When $c=a$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{(a+b)e^{b\overline{\xi }}-1}{(a-b)e^{b\overline{\xi }}-1}\right] .$

Family 12::

When $a=c$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{(b+c)e^{b\overline{\xi }}+1}{(b-c)e^{b\overline{\xi }}-1}\right] .$

Family 13::

When $c=-a$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{e^{b\overline{\xi }}+b-a}{e^{b\overline{\xi }}-b-a}\right] .$

Family 14::

When $b=-c$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{ae^{a\overline{\xi }}}{1-ce^{a\overline{\xi }}}\right] .$

Family 15::

When $b=0$ and $\mathrm {a=c}$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{c\overline{\xi }+2}{c\overline{\xi }}\right] .$

Family 16::

When $a=0$ and $b=c$, then $\phi (\xi )=2\tan ^{-1}\left[ c\overline{\xi }\right] .$

Family 17::

When $a=0$ and $b=-c$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{1}{c\overline{\xi }}\right] .$

Family 18::

When $a=0$ and $b=0$, then $\phi (\xi )=c\xi +C.$

Family 19::

When $b=c$ then $\phi (\xi )=2\tan ^{-1}\left[ \frac{e^{a\overline{\xi }}-c}{a}\right] ,$

where $\overline{\xi }=\xi +C, p, A_k, B_k (k=1,2,...,m), a, b$ and c are constants to be determined later.

Step 3 Determine m. This, usually, can be accomplished by balancing the linear term(s) of highest order with the highest-order nonlinear term(s) in Eq. (2.2). But, the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in Eq. (2.2). If $m = q/p$ (where $m = q/p$ be a fraction in the lowest terms), we let

$$\begin{aligned} u(\xi )=v^{q/p}(\xi ), \end{aligned}$$

(2.5)

then substitute Eq. (2.5) into Eq. (2.2) and then determine the value of m in new Eq. (2.2). If m be a negative integer, we let

$$\begin{aligned} u(\xi )=v^m(\xi ), \end{aligned}$$

(2.6)

then substitute Eq. (2.6) into Eq. (2.2). Then we determine the new value of m in obtained equation.

Step 4 Substituting (2.3) into Eq. (2.2) with the value of m obtained in Step 2. Collecting the coefficients of $\tan (\phi /2)^k$, $\cot (\phi /2)^k (k=0,1,2,...)$, then setting each coefficient to zero, we can get a set of over-determined equations for $A_0, A_k, B_k (k = 1, 2,..., m)$ a, b, c and p with the aid of symbolic computation Maple.

Step 5 Solving the algebraic equations in Step 3, then substituting $A_0, A_1, B_1, . . . , A_m, B_m, \mu , p$ in (2.3).

3 The modified dispersive water-wave system

We consider the (2+1)-dimensional modified dispersive water-wave system as follows

$$\begin{aligned} u_{yt}+u_{xxy}-2v_{xx}-(u^2)_{xy}=0,\quad \,\, v_t-v_{xx}-2(uv)_x=0. \end{aligned}$$

(3.1)

By make the transformation $\xi =kx+m(y)+nt$, Eq. (3.1) becomes

$$\begin{aligned} m'nu+k^2m'u'-2k^2v-km'u^2=0,\quad \,\,nv-k^2v'-2kuv=0, \end{aligned}$$

(3.2)

where obtained by twice integrating and neglecting the constant of integration and $u'=\frac{du}{d \xi }$, $v'=\frac{dv}{d \xi }$, $m'=\frac{dm}{dy}$. By considering the homogeneous balance principle between the highest order derivatives $u'$ and nonlinear terms $u^2$ and also $v'$ and uv, we obtain $M+1=2M$ and $N+1=M+N$, then $M=1$ and $N=2$. Therefore, by considering $p=0$ in (2.3), suppose that the solutions for Eq. (3.2) can be expressed in the following form

$$\begin{aligned} u(\xi )= & {} \sum _{k=0}^{1}A_k\tan ^k(\phi /2)+\sum _{k=1}^{1}B_k\cot ^k(\phi /2),\nonumber \\ v(\xi )= & {} \sum _{k=0}^{2}C_k\tan ^k(\phi /2)+\sum _{k=1}^{2}D_k\cot ^k(\phi /2). \end{aligned}$$

(3.3)

By substituting (3.3) into Eq. (3.2) and collecting all terms with the same order of $\tan (\phi /2)$ together, the left-hand side of (3.3) are converted into polynomial in $\tan (\phi /2)$. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for $a, b, c, k, m', n, A_0, A_1, B_1, C_0, C_1, C_2, D_1$, and $D_2$ as follows :

Coefficients of $Y=\tan (\phi /2)$:

$$\begin{aligned} \left\{ \begin{array}{ll} Y^0: &{} {-4k^2D_2-k^2m'cB_1-2km'B_1^2-k^2m'bB_1=0,} \\ Y^0: &{} {-4kB_1D_2+2k^2cD_2+2k^2bD_2=0,} \\ Y^1: &{} {2m'nB_1-4k^2D_1-2k^2m'aB_1-4km'A_0B_1=0,} \\ Y^1: &{} {-4kB_1D_1+k^2cD_1+k^2bD_1-4kA_0D_2+2nD_2+4k^2aD_2=0,} \\ Y^2: &{} {-2km'A_0^2+k^2m'cA_1-4k^2C_0+k^2m'bB_1+2m'nA_0-k^2m'cB_1-4km'A_1B_1+k^2m'bA_1=0,}\\ Y^2: &{} {2k^2aD_1+2k^2cD_2-2k^2bD_2-4kA_1D_2-4kA_0D_1-4kB_1C_0+2nD_1=0,}\\ Y^3: &{} {2k^2m'aA_1+2m'nA_1-4k^2C_1-4km'A_0A_1=0,}\\ Y^3: &{} {-k^2bD_1+k^2cD_1-k^2cC_1-4kA_1D_1-4kB_1C_1-k^2bC_1-4kA_0C_0+2nC_0=0,}\\ Y^4: &{} {k^2m'cA_1-2km'A_1^2-k^2m'bA_1-4k^2C_2=0,} \\ Y^4: &{} {-4kB_1C_2-4kA_1C_0-2k^2bC_2-2k^2aC_1-2k^2cC_2-4kA_0C_1+2nC_1=0,} \\ Y^5: &{} {k^2bC_1-4kA_1C_1-4k^2aC_2-k^2cC_1-4kA_0C_2+2nC_2=0,} \\ Y^6: &{} {-4kA_1C_2+2k^2bC_2-2k^2cC_2=0.} \end{array} \right. \end{aligned}$$

(3.4)

Solving the above algebraic equations (3.4), we have the following sets:

Set I We have the following:

$$\begin{aligned} a= & {} \frac{2kA_0-n}{k^2}, \,\,\,b=\frac{k(B_1^2-A_0^2)+nA_0}{k^2B_1},\,\,\,c =\frac{k(B_1^2+A_0^2)-nA_0}{k^2B_1},\,\,\,\Delta =a^2+b^2-c^2=\frac{n^2}{k^4},\,\,k = k,\,\,m'=m',\,\,n=n,\nonumber \\ A_0= & {} A_0,\,\,A_1=0,\,\,B_1=B_1,\,\, C_0=\frac{m'A_0(n-kA_0)}{k^2},\,\,C_1=0,\,\,C_2=0, \,D_1=\frac{m'B_1(n-2kA_0)}{k^2},\,\,D_2=-\frac{m'B_1^2}{k}. \end{aligned}$$

(3.5)

By using of Family 2, (3.3) become

$$\begin{aligned} u_1(x,y,t)\,=\, & {} A_0-2A_0(kA_0-n)\left[ 2kA_0-n+n \tanh \left( \frac{n}{2k^2}(kx+m(y)+nt+C)\right) \right] ^{-1},\nonumber \\ v_1(x,y,t)\,=\,& {} \frac{m'A_0(n-kA_0)}{k^2}-\frac{2m'A_0(kA_0-n)(n-2kA_0)}{k^2}\left[ 2kA_0-n+n \tanh \left( \frac{n}{2k^2}(kx+m(y)+nt+C)\right) \right] ^{-1}\nonumber \\&-\frac{4m'A_0^2(kA_0-n)^2}{k}\left[ 2kA_0-n+n \tanh \left( \frac{n}{2k^2}(kx+m(y)+nt+C)\right) \right] ^{-2}, \end{aligned}$$

(3.6)

where $A_0,k,m,n$ and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_2(x,y,t)\,=\, & {} A_0+A_0\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}-1}{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}+1}, \ \frac{2e^{\frac{2A_0}{k}(kx+m(y)+2kA_0t+C)}}{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}+1}\right] \right) ,\nonumber \\ v_2(x,y,t)= & {} \frac{m'A_0^2}{k}-\frac{m'A_0^2}{k}\cot ^2\left( \frac{1}{2} \arctan \left[ \frac{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}-1}{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}+1}, \ \frac{2e^{\frac{2A_0}{k}(kx+m(y)+2kA_0t+C)}}{e^{\frac{4A_0}{k}(kx+m(y)+2kA_0t+C)}+1}\right] \right) , \end{aligned}$$

(3.7)

where $A_0,k,$ and C are arbitrary constants. By using of Family 12, (3.3) become

Case 1: ($k=k,n=n,A_0=B_1,B_1=B_1$)

$$\begin{aligned} u_{3_1}(x,y,t)\,=\, & {} B_1+B_1 \left[ \frac{\frac{2n-2kB_1}{k^2}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}+1}\right] , \quad \,v_{3_1}(x,y,t)=\frac{m'B_1(n-kB_1)}{k^2}\nonumber \\&+\frac{m'B_1(n-2kB_1)}{k^2} \left[ \frac{\frac{2n-2kB_1}{k^2}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}+1}\right] -\frac{m'B_1^2}{k}\left[ \frac{\frac{2n-2kB_1}{k^2}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+nt+C)}+1}\right] ^2. \end{aligned}$$

(3.8)

Case 2: ($k=k,n=k(A_0-B_1),A_0=A_0,B_1=B_1$)

$$\begin{aligned} u_{3_2}(x,y,t)\,=\, & {} A_0+B_1 \left[ \frac{\frac{2n-2kB_1}{k^2}e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}+1}\right] , \quad \,v_{3_2}(x,y,t)=\frac{m'A_0(n-kA_0)}{k^2}\nonumber \\&+\frac{m'B_1(n-2kA_0)}{k^2} \left[ \frac{\frac{2n-2kB_1}{k^2}e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}+1}\right] -\frac{m'B_1^2}{k}\left[ \frac{\frac{2n-2kB_1}{k^2} e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}-1}{\frac{2B_1}{k}e^{\frac{n}{k^2}(kx+m(y)+k(A_0-B_1)t+C)}+1}\right] ^2, \end{aligned}$$

(3.9)

where $A_0,k,$ and C are arbitrary constants.

Fig. 1

The real values of $v_1$ are demonstrated at $A_0=n=0.5, k=2, C=2,$ and $m(y)=exp(-y),$ for a and b and $m(y)=\frac{1}{1+y^2},$ for c and d at different times $t=-16, 16$ respectively

Fig. 2

The real values of $v_1$ are demonstrated at $A_0=n=0.5, k=2, C=2$ and $m(y)=\tan (y),$ for a and b and $m(y)=\cot (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 3

The real values of $v_1$ are demonstrated at $A_0=n=0.5, k=2, C=2$ and $m(y)=\sin (y),$ for a and b and $m(y)=\cos (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 4

The real values of $v_2$ are demonstrated at $A_0=0.5, k=2, C=2$ and $m(y)=exp(-y),$ for a and b and $m(y)=\frac{1}{1+y^2},$ for c and d at different times $t=-16, 16$ respectively

Fig. 5

The real values of $v_2$ are demonstrated at $A_0=0.5, k=2, C=2$ and $m(y)=\tan (y),$ for a and b and $m(y)=\cot (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 6

The real values of $v_2$ are demonstrated at $A_0=0.5, k=2, C=2$ and $m(y)=\sin (y),$ for a and b and $m(y)=\cos (y),$ for c and d at different times $t=-16, 16$ respectively

Set II We have the following:

$$\begin{aligned} a\,=\, & {} a, \,\,\,b=-\frac{-16B_1^2A_0^2-8B_1^2kaA_0-B_1^2k^2a^2-4A_0^4+8kA_0^3a+4k^3a^3A_0-2k^2a^2A_0^2}{(4A_0+ka)^2B_1k}, \,\,k = k,\,\,m'=m',\nonumber \\ \Delta= & {} \frac{(ka-2A_0)^4}{k^2(4A_0+ka)^2},\,\,\,A_0=A_0,\,A_1=0,\,B_1=B_1, \,n=-\frac{2k(k^2a^2-kaA_0-2A_0^2)}{4A_0+ka}, \,\,C_1=0,\,\,C_2=0,\nonumber \\ c= & {} \frac{16B_1^2A_0^2+8B_1^2kaA_0+B_1^2k^2a^2-4A_0^4+8kA_0^3a+4k^3a^3A_0-2k^2a^2A_0^2}{(4A_0+ka)^2B_1k},\, D_2=-\frac{(3k^2a^2+4kaA_0+4A_0^2)m'B_1^2}{8k(2ka-A_0)A_0}, \nonumber \\ C_0= & {} -\frac{m'A_0(-4A_0^3+4kaA_0^2+5k^2a^2A_0+6k^3a^3)}{2k(4A_0+ka)^2},\, D_1=-\frac{m'B_1(3k^2a^2+4kaA_0+4A_0^2)}{2k(4A_0+ka)}. \end{aligned}$$

(3.10)

By using of Family 2, (3.3) become

$$\begin{aligned} u_4(\xi )\,=\, & {} A_0-\frac{4A_0(-2A_0^3+4kaA_0^2+2k^3a^3-A_0k^2a^2)}{(4A_0+ka)}\left[ ak(4A_0+ka)+(ka-2A_0)^2 \tanh \left( \frac{(ka-2A_0)^2}{2(4A_0+ka)k}(\xi +C)\right) \right] ^{-1},\nonumber \\ v_4(\xi )= & {} -\frac{m'A_0(-4A_0^3+4kaA_0^2+5k^2a^2A_0+6k^3a^3)}{2k(4A_0+ka)^2}\nonumber \\&+\frac{4m'A_0(-2A_0^3+4kaA_0^2+2k^3a^3-A_0k^2a^2)}{2k(4A_0+ka)^2(3k^2a^2+4kaA_0+4A_0^2)^{-1}}\left[ ak(4A_0+ka)+(ka-2A_0)^2 \tanh \left( \frac{(ka-2A_0)^2}{2(4A_0+ka)k}(\xi +C)\right) \right] ^{-1}\nonumber \\&-\frac{16m'A_0^2(-2A_0^3+4kaA_0^2+2k^3a^3-A_0k^2a^2)^2}{8kA_0(2ka-A_0)(4A_0+ka)^2(3k^2a^2+4kaA_0+4A_0^2)^{-1}}\left[ ak(4A_0+ka)+(ka-2A_0)^2 \tanh \left( \frac{(ka-2A_0)^2}{2(4A_0+ka)k}(\xi +C)\right) \right] ^{-2}, \end{aligned}$$

(3.11)

where $\xi =kx+m(y)-\frac{2k(k^2a^2-kaA_0-2A_0^2)}{4A_0+ka}t$, $A_0,k,a$ and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_5(x,y,t)\,=\, & {} 2B_1+B_1\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+my+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) ,\nonumber \\ v_5(x,y,t)= & {} \frac{m'A_0^2}{8k}-\frac{m'B_1^2}{k}\cot \left( \frac{1}{2} \arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) \nonumber \\&+\frac{m'B_1^2}{2k}\cot ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) , \end{aligned}$$

(3.12)

where $B_1,k,$ and C are arbitrary constants. By using of ($a=\frac{\sqrt{-2}A_0}{k}$) and Family 18, (3.3) become

$$\begin{aligned} u_{6}(x,y,t)\,=\, & {} A_0+B_1 \left[ \frac{\frac{\sqrt{-2}A_0}{k}}{\frac{\sqrt{-2}A_0}{k}e^{\frac{\sqrt{-2}A_0}{k}\left( kx+m(y)+ \frac{2k(4A_0^2+\sqrt{-2}A_0^2)}{4A_0+\sqrt{-2}A_0}t+C\right) }-\frac{14B_1^2A_0^2+8B_1^2\sqrt{-2}A_0^2}{k(4A_0+\sqrt{-2}A_0)^2B_1}}\right] ,\, v_{6}(x,y,t)=\frac{m'A_0(14A_0^3+8\sqrt{-2}A_0^3)}{2k(4A_0+\sqrt{-2}A_0)^2}\nonumber \\&-\frac{m'B_1(-2A_0^2+4\sqrt{-2}A_0^2)}{2k(4A_0+\sqrt{-2}A_0)} \left[ \frac{\frac{\sqrt{-2}A_0}{k}}{\frac{\sqrt{-2}A_0}{k}e^{\frac{\sqrt{-2}A_0}{k}\left( kx+m(y)+ \frac{2k(4A_0^2+\sqrt{-2}A_0^2)}{4A_0+\sqrt{-2}A_0}t+C\right) }-\frac{14B_1^2A_0^2+8B_1^2\sqrt{-2}A_0^2}{k(4A_0+\sqrt{-2}A_0)^2B_1}}\right] \nonumber \\&-\frac{(-2A_0^2+4\sqrt{-2}A_0^2)m'B_1^2}{8k(2\sqrt{-2}A_0-A_0)A_0} \left[ \frac{\frac{\sqrt{-2}A_0}{k}}{\frac{\sqrt{-2}A_0}{k}e^{\frac{\sqrt{-2}A_0}{k}\left( kx+m(y)+ \frac{2k(4A_0^2+\sqrt{-2}A_0^2)}{4A_0+\sqrt{-2}A_0}t+C\right) }-\frac{14B_1^2A_0^2+8B_1^2\sqrt{-2}A_0^2}{k(4A_0+\sqrt{-2}A_0)^2B_1}}\right] ^2, \end{aligned}$$

(3.13)

where $A_0,k,$ and C are arbitrary constants.

Set III We have the following:

$$\begin{aligned} a= & {} 0, \,\,\, b=\frac{n^2+4B_1^2k^2}{2k^3B_1},\,\,c=\frac{-n^2+4B_1^2k^2}{2k^3B_1}, \,\,k = k,\,\,m'=m',\,\,n=n,\,\,A_0=0,\,\,A_1=0,\,\,B_1=B_1,\nonumber \\ \Delta= & {} \frac{4n^2}{k^4},\,C_0=\frac{m'n^2}{4k^3},\,C_1=0,\,C_2=0, \,\,D_1=\frac{m'nB_1}{2k^2},\,\,D_2=0. \end{aligned}$$

(3.14)

By using of Family 5, (3.3) become

$$\begin{aligned} {u_7(x,y,t)=\frac{n}{2k}\coth \left[ \frac{n}{k^2}(kx+m(y)+nt+C)\right] ,}\quad {v_7(x,y,t)=\frac{mn^2}{4k^3}+\frac{m'n^2}{4k^3}\coth \left[ \frac{n}{k^2}(kx+m(y)+nt+C)\right] ,} \end{aligned}$$

(3.15)

where k, m, n and C are arbitrary constants. By using of Family 6, (3.3) becomes

$$\begin{aligned} u_8(x,y,t)= & {} B_1\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) ,\nonumber \\ v_8(x,y,t)= & {} \frac{m'B_1^2}{k}+\frac{m'B_1^2}{k}\cot \left( \frac{1}{2} \arctan \left[ \frac{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{8B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) , \end{aligned}$$

(3.16)

where $B_1,k,$ and C are arbitrary constants. By using of Family 11, (3.3) become

$$\begin{aligned} u_{9}(x,y,t)\,=\,B_1 \left[ \frac{\frac{4B_1}{k}e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}{\frac{4B_1}{k}e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}\right] , \,\,\,v_{9}(x,y,t)\,=\,\frac{m'B_1^2}{k}+\frac{m'B_1^2}{k} \left[ \frac{\frac{4B_1}{k}e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}{\frac{4B_1}{k}e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}\right] , \end{aligned}$$

(3.17)

where $B_1,k,$ and C are arbitrary constants.

Set IV We have the following:

$$\begin{aligned} a= & {} -\frac{nD_2^2}{m'^2B_1^4}, \,\,\,b=-\frac{D_2}{m'B_1},\,\,c=-\frac{D_2}{m'B_1}, \,\,k = -\frac{m'B_1^2}{D_2},\,\,m'=m',\,\,n=n,\,\,A_0=0,\,\,A_1=0,\,\,B_1=B_1,\nonumber \\ \Delta= & {} \frac{n^2D_2^4}{m'^4B_1^8},\,C_0=0,\,C_1=0,\,C_2=0, \,\,D_1=\frac{nD_2^2}{m'B_1^3},\,\,D_2=D_2. \end{aligned}$$

(3.18)

By using of Family 18, (3.3) become

$$\begin{aligned} u_{10}(x,y,t)= & {} \frac{-nD_2^2B_1}{-nD_2^2 e^{-\frac{nD_2^2}{m'^2B_1^4}\left( -\frac{m'B_1^2}{D_2}x+m(y)+nt+C\right) }+m'D_2B_1^3},\nonumber \\ v_{10}(x,y,t)= & {} \frac{-\frac{n^2D_2^4}{m'B_1^3}}{-nD_2^2 e^{-\frac{nD_2^2}{m'^2B_1^4}\left( -\frac{m'B_1^2}{D_2}x+m(y)+nt+C\right) }+m'D_2B_1^3}+D_2\left[ \frac{-nD_2^2}{-nD_2^2 e^{-\frac{nD_2^2}{m'^2B_1^4}\left( -\frac{m'B_1^2}{D_2}x+m(y)+nt+C\right) }+m'D_2B_1^3}\right] ^2, \end{aligned}$$

(3.19)

where $n, B_1, D_2$ and C are arbitrary constants.

Set V We have the following:

$$\begin{aligned} a\,=\, & {} -\frac{\sqrt{-2}A_0}{k}, \,\,\,b=\frac{B_1}{k},\,\,c=\frac{B_1}{k}, \,\,k = k,\,\,m'=m',\,\,n=2kA_0,\,\,A_0=A_0,\,\,A_1=0,\,\,B_1=B_1, \nonumber \\ C_0= & {} -\frac{2D_2A_0^2}{B_1^2},\,C_1=0,\,C_2=0, \,\,D_1=\frac{2\sqrt{-2}A_0D_2}{B_1},\,\,D_2=-\frac{B_1^2}{4k}m'. \end{aligned}$$

(3.20)

By using of Family 18, (3.3) become

$$\begin{aligned} u_{11}(x,y,t)\,=\, & {} A_0+\frac{\frac{\sqrt{-2}A_0B_1}{k}}{\frac{\sqrt{-2}A_0}{k}e^{-\frac{\sqrt{-2}A_0}{k} \left( kx+m(y)+2kA_0t+C\right) }+\frac{B_1}{k}},\nonumber \\ v_{11}(x,y,t)= & {} \frac{m'A_0^2}{2k}+\frac{A_0B_1^2m'}{k\sqrt{-2}A_0e^{-\frac{\sqrt{-2}A_0}{k} \left( kx+m(y)+2kA_0t+C\right) }+kB_1}-\frac{m'B_1^2}{4k}\left[ \frac{\frac{\sqrt{-2}A_0B_1}{k}}{\frac{\sqrt{-2}A_0}{k}e^{-\frac{\sqrt{-2}A_0}{k} \left( kx+m(y)+2kA_0t+C\right) }+\frac{B_1}{k}}\right] ^2, \end{aligned}$$

(3.21)

where $n,A_0, B_1, D_2$ and C are arbitrary constants.

Set VI We have the following:

$$\begin{aligned} a= & {} 0, \,\,\,b=\frac{n^2+4B_1^2k^2}{4k^3B_1},\,\,c=\frac{-n^2+4B_1^2k^2}{4k^3B_1}, \,\,k = k,\,\,m'=m',\,\,n=n,\,\,A_0=0,\,\,A_1=0,\,\,B_1=B_1, \nonumber \\ \Delta= & {} \frac{n^2}{k^4},\,C_0=\frac{m'n^2}{8k^3},\,C_1=0,\,C_2=0, \,\,D_1=\frac{m'nB_1}{2k^2},\,\,D_2=\frac{m'B_1^2}{2k}. \end{aligned}$$

(3.22)

By using of Family 5, (3.3) become

$$\begin{aligned} u_{12}(x,y,t)= & {} \frac{n}{2k}\coth \left[ \frac{n}{2k^2}(kx+m(y)+nt+C)\right] ,\nonumber \\ v_{12}(x,y,t)= & {} \frac{m'n^2}{8k^3}+\frac{m'n^2}{4k^3}\coth \left[ \frac{n}{2k^2}(kx+m(y)+nt+C)\right] + \frac{m'n^2}{8k^3}\coth ^2\left[ \frac{n}{2k^2}(kx+m(y)+nt+C)\right] , \end{aligned}$$

(3.23)

where k, n and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_{13}(x,y,t)= & {} B_1\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) ,\nonumber \\ v_{13}(x,y,t)= & {} \frac{m'B_1^2}{2k}+\frac{m'B_1^2}{k}\cot \left( \frac{1}{2} \arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right)\nonumber \\&+\frac{m'B_1^2}{2k}\cot ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kB_1t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kB_1t+C)}+1}\right] \right) , \end{aligned}$$

(3.24)

where $B_1,k,$ and C are arbitrary constants.

Fig. 7

The real values of $v_2$ are demonstrated at $A_0=B_1=0.5, k=2, C=2$ and $m(y)=exp(-y),$ for a and b and $m(y)=\frac{1}{1+y^2},$ for c and d at different times $t=-16, 16$ respectively

Fig. 8

The real values of $v_2$ are demonstrated at $A_0=0.5, B_1=0.5, k=2, C=2$ and $m(y)=\tan (y),$ for a and b and $m(y)=\cot (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 9

The real values of $v_2$ are demonstrated at $A_0=0.5, B_1=0.5, k=2, C=2$ and $m(y)=\sin (y),$ for a and b and $m(y)=\cos (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 10

The real values of $v_{23}$ are demonstrated at $b=1, c=A_0=A_1=D_2=0.5, k=2, C=2$ and $m(y)=exp(-y),$ for a and b and $m(y)=\frac{1}{1+y^2},$ for c and d at different times $t=-16, 16$ respectively

Fig. 11

The real values of $v_{23}$ are demonstrated at $b=1, c=A_0=A_1=D_2=0.5, k=2, C=2$ and $m(y)=\tan (y),$ for a and b and $m(y)=\cot (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 12

The real values of $v_{23}$ are demonstrated at $b=1, c=A_0=A_1=D_2=0.5, k=2, C=2$ and $m(y)=\sin (y),$ for a and b and $m(y)=\cos (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 13

The real values of $v_{23}$ are demonstrated at $a=A_0=0.5, k=2, C=2$ and $m(y)=exp(-y),$ for a and b and $m(y)=\frac{1}{1+y^2},$ for c and d at different times $t=-16, 16$ respectively

Fig. 14

The real values of $v_{23}$ are demonstrated at $a=A_0=0.5, k=2, C=2$ and $m(y)=\tan (y),$ for a and b and $m(y)=\cot (y),$ for c and d at different times $t=-16, 16$ respectively

Fig. 15

The real values of $v_{23}$ are demonstrated at $a=A_0=0.5, k=2, C=2$ and $m(y)=\sin (y),$ for a and b and $m(y)=\cos (y),$ for c and d at different times $t=-16, 16$ respectively

Set VII We have the following:

$$\begin{aligned} a= & {} 0, \,\,\,b=\frac{2B_1-kc}{k},\,\,c=c, \,\,k = k,\,\,m'=m',\,\,n=2kA_0,\,\,A_0=A_0,\,\,A_1=0,\,\,B_1=B_1,\nonumber \\ C_0= & {} -\frac{m'(kB_1c-A_0^2-B_1^2)}{2k},\,C_1=0,\,C_2=0, \,\,D_1=0,\,\,D_2=-\frac{m'B_1(kB_1c-A_0^2-B_1^2)}{2k(kc-B_1)}. \end{aligned}$$

(3.25)

By using of Family 5, (3.3) become

$$\begin{aligned} u_{14}(x,y,t)\,=\, & {} A_0+B_1\sqrt{\frac{2B_1-2ck}{2B_1}}\coth \left[ \frac{\sqrt{B_1^2-ckB_1}}{k}(kx+m(y)+2kA_0t+C)\right] ,\nonumber \\ v_{14}(x,y,t)= & {} -\frac{m'(kB_1c-A_0^2-B_1^2)}{2k}+\frac{m'(kB_1c-A_0^2-B_1^2)}{2k} \coth ^2\left[ \frac{\sqrt{B_1^2-ckB_1}}{k}(kx+m(y)+2kA_0t+C)\right] , \end{aligned}$$

(3.26)

where $k,n, A_0, B_1$ and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_{15}(x,y,t)\,=\, & {} A_0+B_1\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kA_0t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}+1}\right] \right) ,\nonumber \\ v_{15}(x,y,t)= & {} \frac{m'(A_0^2+B_1^2)}{2k}-\frac{m'(A_0^2+B_1^2)}{2k} \cot ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}-1}{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}+1}, \ \frac{2e^{\frac{2B_1}{k}(kx+m(y)+2kA_0t+C)}}{e^{\frac{4B_1}{k}(kx+m(y)+2kA_0t+C)}+1}\right] \right) , \end{aligned}$$

(3.27)

where $A_0, B_1,k,$ and C are arbitrary constants. By using of Family 11, (3.3) become

$$\begin{aligned} u_{16}(x,y,t)\,=\, & {} A_0+B_1\left[ \frac{\frac{2B_1}{k}e^{\frac{2B_1}{k} (kx+m(y)+2kA_0t+C)}+1}{\frac{2B_1}{k}e^{\frac{2B_1}{k}(kx+m(y)+2kA_0t+C)}-1}\right] ,\nonumber \\ v_{16}(x,y,t)= & {} \frac{m'(A_0^2+B_1^2)}{2k}-\frac{m'(A_0^2+B_1^2)}{2k} \left[ \frac{\frac{2B_1}{k}e^{\frac{2B_1}{k}(kx+m(y)+2kA_0t+C)}+1}{\frac{2B_1}{k}e^{\frac{2B_1}{k}(kx+m(y)+2kA_0t+C)}-1}\right] ^2, \end{aligned}$$

(3.28)

where $A_0, B_1,k,$ and C are arbitrary constants.

Set VIII We have the following:

$$\begin{aligned} a\,=\, & {} 0, \,\,\,b=b,\,\,c=c, \,\,k =\frac{\sqrt{-2}A_0}{\sqrt{b^2-c^2}},\,\,m'=m', \,\,n=\frac{2\sqrt{-2}A_0^2}{\sqrt{b^2-c^2}},\,\,A_0=A_0,\,\, A_1=\frac{\sqrt{-2}(b-c)A_0}{2\sqrt{b^2-c^2}},\nonumber \\ B_1= & {} \frac{\sqrt{b^2-c^2}A_0}{\sqrt{-2}(b-c)},\,\,C_0=0, \,C_1=0,\,C_2=-\frac{\sqrt{-2}m'(b-c)^2}{4\sqrt{b^2-c^2}}, \,\,D_1=0,\,\,D_2=0. \end{aligned}$$

(3.29)

By using of Family 5, (3.3) becomes

$$\begin{aligned} u_{17}(x,y,t)\,=\, & {} A_0+\frac{\sqrt{-2}A_0}{2}\tanh \left[ \frac{\sqrt{b^2-c^2}}{2} \left( \frac{\sqrt{-2}A_0}{\sqrt{b^2-c^2}}x+m(y)+\frac{2\sqrt{-2}A_0^2}{\sqrt{b^2-c^2}}t+C\right) \right] \nonumber \\&+\frac{A_0}{\sqrt{-2}}\coth \left[ \frac{\sqrt{b^2-c^2}}{2} \left( \frac{\sqrt{-2}A_0}{\sqrt{b^2-c^2}}x+m(y)+\frac{2\sqrt{-2}A_0^2}{\sqrt{b^2-c^2}}t+C\right) \right] ,\nonumber \\ v_{17}(x,y,t)= & {} -\frac{\sqrt{-2(b^2-c^2)}m'}{4}\tanh ^2\left[ \frac{\sqrt{b^2-c^2}}{2} \left( \frac{\sqrt{-2}A_0}{\sqrt{b^2-c^2}}x+m(y)+\frac{2\sqrt{-2}A_0^2}{\sqrt{b^2-c^2}}t+C\right) \right] , \end{aligned}$$

(3.30)

where $b,c, A_0$ and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_{18}(x,y,t)\,=\, & {} A_0+\frac{\sqrt{-2}A_0}{2}\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{2b \left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+my+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}, \ \frac{2e^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}\right] \right) \nonumber \\&+\frac{A_0}{\sqrt{-2}}\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}, \ \frac{2e^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}\right] \right) ,\nonumber \\ v_{18}(x,y,t)= & {} -\frac{\sqrt{-2}m'b}{4}\tan ^2\left( \frac{1}{2} \arctan \left[ \frac{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+my+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}, \ \frac{2e^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }}{e^{2b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}\right] \right) , \end{aligned}$$

(3.31)

where $b,c, A_0$ and C are arbitrary constants. By using of Family 11, (3.3) becomes

$$\begin{aligned} u_{19}(x,y,t)\,=\, & {} A_0+\frac{\sqrt{-2}A_0}{2}\left[ \frac{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}\right] +\frac{A_0}{\sqrt{-2}}\left[ \frac{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}\right] ,\nonumber \\ v_{19}(x,y,t)= & {} -\frac{\sqrt{-2}m'b}{4}\left[ \frac{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }-1}{be^{b\left( \frac{\sqrt{-2}A_0}{b}x+m(y)+\frac{2\sqrt{-2}A_0^2}{b}t+C\right) }+1}\right] ^2, \end{aligned}$$

(3.32)

where $b,c,A_0$ and C are arbitrary constants.

Set IX We have the following:

$$\begin{aligned} a\,=\, & {} 0, \,\,\,b=b,\,\,c=c, \,\,k =\frac{2A_0}{\sqrt{b^2-c^2}},\,\,m'=m', \,\,n=\frac{4A_0^2}{\sqrt{b^2-c^2}},\,\,A_0=A_0,\,\, A_1=\frac{(b-c)A_0}{\sqrt{b^2-c^2}},\nonumber \\ B_1= & {} 0,\,\,C_0=\frac{m'\sqrt{b^2-c^2}A_0}{2},\,C_1=0,\,C_2=-\frac{m'(b-c)^2A_0}{2\sqrt{b^2-c^2}}, \,\,D_1=0,\,\,D_2=0. \end{aligned}$$

(3.33)

By using of Family 5, (3.3) becomes

$$\begin{aligned} u_{20}(x,y,t)\,=\, & {} A_0+A_0\tanh \left[ \frac{\sqrt{b^2-c^2}}{2} \left( \frac{2A_0}{\sqrt{b^2-c^2}}x+m(y)+\frac{4A_0^2}{\sqrt{b^2-c^2}}t+C\right) \right] ,\nonumber \\ v_{20}(x,y,t)= & {} \frac{m'\sqrt{b^2-c^2}A_0}{2}-\frac{m'\sqrt{b^2-c^2}A_0}{2}\tanh ^2\left[ \frac{\sqrt{b^2-c^2}}{2} \left( \frac{2A_0}{\sqrt{b^2-c^2}}x+m(y)+\frac{4A_0^2}{\sqrt{b^2-c^2}}t+C\right) \right] , \end{aligned}$$

(3.34)

where $b,c, A_0$ and C are arbitrary constants. By using of Family 6, (3.3) becomes

$$\begin{aligned} u_{21}(x,y,t)\,=\, & {} A_0+A_0\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{2b \left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }-1}{e^{2b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}, \ \frac{2e^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }}{e^{2b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}\right] \right) ,\nonumber \\ v_{21}(x,y,t)= & {} \frac{m'bA_0}{2}-\frac{m'bA_0}{2}\tan ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{2b \left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }-1}{e^{2b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}, \ \frac{2e^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }}{e^{2b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}\right] \right) , \end{aligned}$$

(3.35)

where $b,c, A_0$ and C are arbitrary constants. By using of Family 11, (3.3) become

$$\begin{aligned} u_{22}(x,y,t)\,=\, & {} A_0+A_0\left[ \frac{be^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }-1}{be^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}\right] ,\nonumber \\ v_{22}(x,y,t)= & {} \frac{m'bA_0}{2}-\frac{m'bA_0}{2}\left[ \frac{be^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }-1}{be^{b\left( \frac{2A_0}{b}x+m(y)+\frac{4A_0^2}{b}t+C\right) }+1}\right] ^2, \end{aligned}$$

(3.36)

where $b,c, A_0$ and C are arbitrary constants.

Set X We have the following:

$$\begin{aligned} a\,=\, & {} 0, \,\,\,b=-\frac{4(4A_1^2+A_0^2)D_2A_1}{m'A_0^4},\,\,c=-\frac{4(A_0^2-4A_1^2)D_2A_1}{m'A_0^4}, \,\,k =-\frac{m'A_0^4}{16A_1^2D_2},\,\,m'=m', \,\,n=-\frac{m'A_0^5}{8A_1^2D_2},\,\,A_0=A_0,\nonumber \\ A_1= & {} A_1,\,\,B_1=\frac{A_0^2}{4A_1},\,\,C_0=-\frac{8A_1^2D_2}{A_0^2}, \,C_1=0,\,C_2=\frac{16D_2A_1^4}{A_0^4}, \,\,D_1=0,\,\,D_2=D_2. \end{aligned}$$

(3.37)

By using of Family 5, (3.3) becomes

$$\begin{aligned} u_{23}(x,y,t)\,=\, & {} A_0+\frac{A_0}{2}\tanh \left[ \frac{\sqrt{b^2-c^2}}{2} \left( -\frac{m'A_0^4}{16A_1^2D_2}x+m(y)-\frac{m'A_0^5}{8A_1^2D_2}t+C\right) \right] \nonumber \\&+\frac{A_0}{2}\coth \left[ \frac{\sqrt{b^2-c^2}}{2} \left( -\frac{m'A_0^4}{16A_1^2D_2}x+m(y)-\frac{m'A_0^5}{8A_1^2D_2}t+C\right) \right] ,\nonumber \\ v_{23}(x,y,t)= & {} -\frac{8A_1^2D_2}{A_0^2}+\frac{4D_2A_1^2}{A_0^2}\tanh ^2\left[ \frac{\sqrt{b^2-c^2}}{2} \left( -\frac{m'A_0^4}{16A_1^2D_2}x+m(y)-\frac{m'A_0^5}{8A_1^2D_2}t+C\right) \right] \nonumber \\&+\frac{4D_2A_1^2}{A_0^2}\coth ^2\left[ \frac{\sqrt{b^2-c^2}}{2} \left( -\frac{m'A_0^4}{16A_1^2D_2}x+m(y)-\frac{m'A_0^5}{8A_1^2D_2}t+C\right) \right] , \end{aligned}$$

(3.38)

where $b,c, A_0, D_2$ and C are arbitrary constants. By using of Family 6, (3.3) are given

$$\begin{aligned} u_{24}(x,y,t)\,=\, & {} 2A_1+A_1\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{-\frac{4D_2}{m'A_1} \left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{e^{-\frac{4D_2}{m'A_1} \left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}, \ \frac{2e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] \right) \nonumber \\&+\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{-\frac{4D_2}{m'A_1} \left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}, \ \frac{2e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] \right) ,\nonumber \\ v_{24}(x,y,t)= & {} -2D_2+D_2\tan ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{-\frac{4D_2}{m'A_1} \left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}, \ \frac{2e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] \right) \nonumber \\&+D_2\cot ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{-\frac{4D_2}{m'A_1} \left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}, \ \frac{2e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }}{e^{-\frac{4D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] \right) , \end{aligned}$$

(3.39)

where $A_1, D_2$ and C are arbitrary constants. By using of Family 11, (3.3) get

$$\begin{aligned} u_{25}(x,y,t)\,=\, & {} 2A_1+A_1\left[ \frac{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] + \left[ \frac{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1} \right] , \nonumber \\ v_{25}(x,y,t)= & {} -2D_2+D_2\left[ \frac{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1}{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}\right] ^2+D_2 \left[ \frac{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }+1}{-\frac{2D_2}{m'A_1}e^{-\frac{2D_2}{m'A_1}\left( \frac{-m'A_1^2}{D_2}x+m(y)-\frac{4A_1^3}{D_2}t+C\right) }-1} \right] ^2, \end{aligned}$$

(3.40)

where $A_1, D_2$ and C are arbitrary constants.

Set XI We have the following:

$$\begin{aligned} a\,=\, & {} a, \,\,\,b=\frac{A_1^2+kaA_0+A_0^2}{kA_1},\,\,c=\frac{-A_1^2+kaA_0+A_0^2}{kA_1}, \,\,k =k,\,\,m'=m', \,\,n=k(2A_0+ka),\,\,A_0=A_0,\nonumber \\ \Delta= & {} \left( \frac{ka+2A_0}{k}\right) ^2,\,\, A_1=A_1,\,\,B_1=0,\,\,C_0=\frac{m'A_0(ka+A_0)}{k}, \,C_1=m'aA_1,\,C_2=-\frac{m'A_1^2}{k}, \,\,D_1=0,\,\,D_2=0. \end{aligned}$$

(3.41)

By using of Family 1 and if ($ka+2A_0=\lambda i,\ i=\sqrt{-1}$), (3.3) are given

$$\begin{aligned} u_{26}(x,y,t)\,=\, & {} A_0+\frac{ka}{2}-\frac{\lambda }{2}\tan \left[ \frac{\lambda }{2k} \left( kx+m(y)+\lambda kit+C\right) \right] , \nonumber \\ v_{26}(x,y,t)= & {} \frac{m'A_0(ka+A_0)}{k}+\frac{m'ka^2}{2}-\frac{m'a\lambda }{2}\tan \left[ \frac{\lambda }{2k} \left( kx+m(y)+\lambda kit+C\right) \right] \nonumber \\&-\frac{m'}{k}\left[ \frac{ka}{2}-\frac{\lambda }{2}\tan \left( \frac{\lambda }{2k} \left( kx+m(y)+\lambda kit+C\right) \right) \right] ^2, \end{aligned}$$

(3.42)

where $b,c, A_0, D_2$ and C are arbitrary constants. By using of Family 2, (3.3) get

$$\begin{aligned} u_{27}(x,y,t)\,=\, & {} A_0+\frac{ka}{2}+\frac{ka+2A_0}{2}\tanh \left[ \frac{ka+2A_0}{2k} \left( kx+m(y)+k(ka+2A_0)t+C\right) \right] , \nonumber \\ v_{27}(x,y,t)= & {} \frac{m'A_0(ka+A_0)}{k}+\frac{m'ka^2}{2}+\frac{m'a(ka+2A_0)}{2}\tanh \left[ \frac{ka+2A_0}{2k} \left( kx+m(y)+k(ka+2A_0)t+C\right) \right] \nonumber \\&-\frac{m'}{k}\left[ \frac{ka}{2}+\frac{ka+2A_0}{2}\tanh \left( \frac{ka+2A_0}{2k} \left( kx+m(y)+k(ka+2A_0)t+C\right) \right) \right] ^2, \end{aligned}$$

(3.43)

where $k,a, A_0, D_2$ and C are arbitrary constants. By using of Family 6, (3.3) become

$$\begin{aligned} u_{28}(x,y,t)\,=\, & {} A_0+A_0\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4A_0}{k} \left( kx+m(y)+2kA_0t+C\right) }-1}{e^{\frac{4A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }+1}, \ \frac{2e^{\frac{2A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }}{e^{\frac{4A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }+1}\right] \right) ,\nonumber \\ v_{28}(x,y,t)= & {} \frac{m'A_0^2}{k}-\frac{m'A_0^2}{k}\tan ^2\left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{4A_0}{k} \left( kx+m(y)+2kA_0t+C\right) }-1}{e^{\frac{4A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }+1}, \ \frac{2e^{\frac{2A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }}{e^{\frac{4A_0}{k}\left( kx+m(y)+2kA_0t+C\right) }+1}\right] \right) , \end{aligned}$$

(3.44)

where $k, A_0$ and C are arbitrary constants.

$\bullet$ Note that All the obtained results have been checked with Maple 13 by putting them back into the original equation and found correct.

4 Discussion and Remark

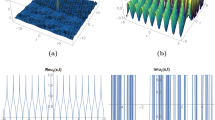
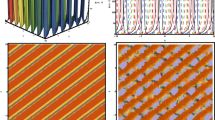
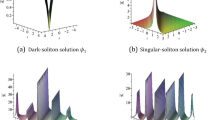
In this section, the numerical simulations of the modified dispersive water-wave system will be given. Now, we will discuss all possible physical significance for each parameter. In Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15, we plot three dimensional graphics of real values of $v_1, v_2, v_{16}, v_{23}$ and $v_{26}$, which denote the dynamics of solutions with appropriate parametric selections. We plot three dimensional graphics of Figs. 1–15, when $-10<x<10, -10<y<10$. At the different times the surface graphics of the exact solutions are plotted in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15, represent the exact traveling wave solutions of the modified dispersive water-wave system. The analytical solutions and figures obtained in this paper give us a different physical interpretation for the modified dispersive water-wave system. Solution $v_1$ of the modified dispersive water-wave system represent the soliton wave solution. Solitons are special kinds of solitary waves. Solitons have a remarkable property that keeps its identity upon interacting with other solitons. Soliton solutions have particle-like structures, for example, magnetic monopoles, and extended structures, like, domain walls and cosmic strings, that have implications in cosmology of the early universe. Solution $v_2, v_{23}$ and $v_{26}$ of the modified dispersive water-wave system represent the exact periodic wave solution. Periodic solutions are traveling wave solutions that are periodic. Solution $v_{16}$ of the modified dispersive water-wave system represent the singular kink-type traveling wave solutions. In $\xi =kx+m(y)+nt$, by considering m(y) in the forms of functions of trigonometric, hyperbolic, exponential and rational, properties of soliton, periodic, traveling and singular kink-type wave solutions have been depicted.

5 Conclusion

In this paper, a new analytical technique based on the improved $\tan (\phi /2)$-expansion method is proposed to obtain the exact solutions to the modified dispersive water-wave system. It has been found that the construction of this recent $\tan (\phi /2)$-expansion method possesses in general a variety of further solutions comparing with other analytical methods. The improved $\tan (\phi /2)$-expansion method is promising technique based on its simplicity and variety of solutions. The results have been observed that all traveling wave solutions of Eq. (3.1) are new behaviors. The ITEM is easier and reliable than other methods. We think that this approach plays an important role for finding traveling wave behaviors to the systems.