1 Introduction

Any phenomena in physical sciences can be modeled by the partial differential equations (PDEs). For example, in physics, the flow of temperature in a body and transmission of the wave is expressed by the PDE. The phenomena of my fingers pushing pressure on the keyboard and words being entered can be modeled by a particular class of PDEs. In the field of biology, most models related to people are expressed by partial differential equations. It is very easy to define that most of the phenomena governing electricity, quantum physics, plasma Physics, fluid dynamics, and some other models lie inside the domain of PDEs. In recent times, a new direction regarding the examination or evaluation analytically and dynamically of nonlinear evolution equations (NLEEs) or nonlinear PDEs in various areas of nonlinear sciences has been observed. NLEE has a significant and imperative impact in different areas of physical and mathematical sciences such as water waves, telecommunication, ocean engineering, fluid mechanics, plasma physics, etc Bilal et al. (2021); Habib et al. (2023); Murtaza et al. (2022); Shah et al. (2022); Khan et al. (2023); Bilal et al. (2021); Cao et al. (2023a, 2023b); Yin et al. (2023); Bai et al. (2023); Xu et al. (2015); Lou et al. (2015). Since many physical models are characterized by NLEEs, it is crucial to design analytical solutions for NLEEs. Different computationally sound approaches have been developed in order to discuss the characteristics of the various solutions for nonlinear physical models. Different powerful and effective computational techniques have been established by the mathematician and scholars to seek the anlytical solutions of NLEEs such as Backlund transformation (Zhao 2019), Kudryashov scheme (Kudryashov 2012), fractional sub-equation method (Karaagac 2019), the unified technique and its generalized version (Osman 2019), reductive perturbation scheme (Houwe 2020), expansion function approach (Yıldırım et al. 2020), the Darboux transformation technique (Amjad and Haider 2020), the generalized exponential rational function and modified Khater methods (Khater et al. 2020), the extended sinh-Gordon equation expansion approach (Sulaiman 2020), Hirota bilinear method (Li et al. 2019), extended Fan sub-equation technique (Younis et al. 2020), extended modified rational expansion approach (Iqbal et al. 2020), variational iteration method (Wang et al. 2020), amplitude ansatz approach (Seadawy 2017), modified simple and trial function techniques (Yıldırım 2019), the homogenous balance method (Kumar et al. 2010), first integral method (Eslami et al. 2014), modified sub-ODE method (Zayed and Alngar 2020), semi-inverse variational method (Xing et al. 2016), F-expansion scheme (Zhang et al. 2006), ansatz and Gaussian approaches (Bilal et al. 2021), and a plethora of others Younas et al. (2022); Bilal et al. (2021); Seadawy et al. (2021); Murtaza et al. (2023); Bilal and Ren (2022); Sulaiman (2020); Bilal et al. (2021, 2023); Khatri et al. (2019); Kumar et al. (2017); Malik et al. (2019); Dahiya et al. (2021); Kumar et al. (2021) have been developed for figuring out how nonlinear complex phenomena work by computing solitons and exact solutions.

Parts of the scientific community were particularly interested in the story of John Scott Russell’s discovery of the soliton when he was studying the waves created by the boats moving through a channel. Over time, scientists discovered that a variety of mathematical physics areas can produce these perfect waves. Numerous scientific disciplines, including fluid mechanics, nonlinear optics, quantum field theory, plasma physics, and a wide range of nonlinear physical events, including shallow water waves or ion acoustic waves, are connected by a wide variety of phenomena (Younas et al. 2022; Rezazadeh et al. 2021; Bilal et al. 2021). In fact, solitons are the result between nonlinearity (the tendency of waves to increase in slope) and dispersion (the tendency to distract attention). They range from high-peace-rate media communications and the generation of controllable soliton occur in many important areas of technology and physics.Because of Galilean symmetry, solitons are characterized by their own Broglie wavelength analogues as self-positioning wave units. On the other hand, since the solitonis an extended particle-like entity, it becomes bound at the self-induced trapping potential due to nonlinear self-interaction and has negative self-interaction energy (binding energy).It gives information about the shape and geometry of solitons. In the past few years, exact solutions to differential equations and the solitary wave have been the focus of a lot of research. NLEEs, or nonlinear partial differential equations (NLPDEs), are used to model a wide range of phenomena in many applied sciences, such as plasma physics, optics, and biomedical science (Younis et al. 2022; Raddadi et al. 2021; Younis et al. 2021; Bilal et al. 2023). We show how each solution works in terms of its actual parts, so we can copy the physical features of each one. Solitary waves with discontinuous derivatives are singular soliton solutions. Additional noteworthy physical characteristics are present in some of the given outcomes.

In this work, we study the damped Improved Boussinesq (IBq) equation. The first Bq model deduced by Bq Boussinesq (1872, 1877) which describes the propagation of long wave in shallow water. The Bq equation can be written in two basic forms follows:

$$\begin{aligned} \phi _{tt}-\phi _{xx}+\delta \phi _{xxxx}=(\phi ^{2})_{xx}, \end{aligned}$$
(1)
$$\begin{aligned} \phi _{tt}-\phi _{xx}-\phi _{xxtt}=(\phi ^{2})_{xx}. \end{aligned}$$
(2)

When \(\delta >0\), then Eq. 1 is linearly stable and governs mini nonlinear crosscut oscillations of an elastic beam, which is called the good Bq equation (Varlamov 2001). When \(\delta <0\), then it is linearly instable and referred as the bad Bq equation (Hatice et al. 2013). The Eq. 2 is called the IBq equation. The difference of the IBq equation from the Bq equation is that it contains a fourth-order space-time derivative \(\phi _{xxtt}\). In existing literature, lattice soliton dynamics of a single atomic chain under damping and external forces are investigated. The IBq model with hydrodynamic damping is considered and investigated analytically. It describes wave propagation in ion sound, nonlinear wave dynamics in weakly dispersive media, and acoustic waves on elastic rods. Therefore, it is imperative to study this model analytically and extract the solutions. The IBq equation with Hydro-dynamical damping (Fan and Zhou 2020) is read as:

$$\begin{aligned} \phi _{tt}- \phi _{xx}-\phi _{xxtt}-\rho \phi _{xxt} =(\phi ^2)_{xx},~~~~x\in [a, b], t\in [0,T]~~T>0.~~ \end{aligned}$$
(3)

Where \(\rho\) is the damping constant of internal friction or named as hydrodynamical damping term. The hydrodynamical damping term introduces a mechanism for wave damping and dissipation in the model. This means that as waves propagate through a medium, they gradually lose energy due to this damping effect. The magnitude of \(\rho\) determines the rate at which this energy loss occurs. A higher value corresponds to more significant damping and faster dissipation of wave energy. Likewise, in shallow water wave modeling, a non-zero leads to the attenuation of wave amplitudes over time and distance. As waves propagate, their heights decrease, and their shapes change due to the action of the damping term. The rate of attenuation is directly related to \(\rho\). In certain scenarios, the value of \(\rho\) can affect the resonance behavior of waves. Resonance occurs when wave frequencies match the natural frequencies of the system. Adjusting \(\rho\) can potentially influence the resonance properties of the waves and their interaction with structures or boundaries. The \(\phi =\phi (x, t)\) is wave profile with x represents spatial component and t indicates temporal component. Recently, different authors have developed its numerical algorithms using different techniques to find its numerical solutions, but no such attention has been given to constructing its exact solutions. Zoheiry had studied it numerically using the compact implicit method (El-Zoheiry 2002). Yang and Wang constructed its blow up solutions by a Garlekin technique (Yang and Wang 2003). Numerical solutions to the modified type IBq equation were also developed in Karaagac et al. (2020). Improved Boussinesq model is primarily used to study shallow water waves in coastal and marine environments, its applications in the field of plasma physics, including fusion research, space plasmas, and astrophysics. this model contribute to our understanding of physical phenomena in its respective domains and have practical implications in various scientific and engineering applications.

From literature review, we observe that the specified equation have not yet been solved by new extended direct algebraic method (NEDAM) (Mirhosseni-Alizamini et al. 2020). Thus, the main goal of this study is to enhance the accuracy of feasible soliton solutions to the IBq equation using novel techniques. The proposed method is efficient to produce a variety of soliton solutions, quicker for simulating, and flexible. The contour, 3D, and 2D plots are used to describe the graphical representations of the solutions that were found with specific values for the free parameters. As a result, in this research work, we successfully apply the proposed method to extract a sequence of solutions to IBq equations. This approach is strong, reliable, skilled in analyzing NLEEs, trustworthy with computer algebra, and offers more extended solutions.

The article’s remaining sections are organized as follows: the NEDAM m has been described in Sect. 2. Application of the given method is anticipated in Sect. 3. Section 4 provides a brief discussion. Finally, the conclusion is presented in Sect. 5.

2 Overview of the NEDAM

This section provides a brief summary of proposed method (Mirhosseni-Alizamini et al. 2020).


  • Step 1: Consider a NLPDE

    $$\begin{aligned} H(J, J_{t}, J_{x}, J_{tt}, J_{xt}, J_{xx},...)=0, \end{aligned}$$
    (4)

    where \(J=J(x,t)\) denotes an unknown function and H denotes a polynomial of J(x, t) with its arguments.


  •  Step 2: The compound variable \(\zeta\) is created by combining the real variables x and t.

    $$\begin{aligned} J(x,t)=\psi (\zeta ), \quad \quad \zeta =k x-\rho t, \end{aligned}$$
    (5)

    where \(\rho\) denotes the wave velocity and k denotes the wave number. Equation 4 becomes an ODE when the traveling wave transformation Eq. 5 is applied.

    $$\begin{aligned} \Pi (\psi , \psi ', \psi '', \psi ''', \cdots )=0, \end{aligned}$$
    (6)

    where \(\Pi\) is a polynomial of \(\psi\) with its derivatives.


  •  Step 3: We suppose that the trail solution to Eq. 6 can be written as the following polynomial \(\Omega (\zeta )\)

    $$\begin{aligned} \psi (\zeta )= & \sum _{i=0}^{N}\alpha _{i} ~\Omega ^{i}(\zeta ),\quad \alpha _{N}\ne 0, \end{aligned}$$
    (7)

    where \(\alpha _{i}\) \((0\le i \le N)\) are unknown constants and \(\Omega (\zeta )\) satisfies the auxiliary ODE,

    $$\begin{aligned} \Omega ^{\prime }(\zeta )=\ln (B)(\mu +\lambda \Omega (\zeta )+\nu \Omega ^{2}(\zeta )),\quad B \ne 0,1. \end{aligned}$$
    (8)

    where \(\mu , \lambda\), and \(\nu\) are constant. The solutions to the Eq. 8 can be expressed as follows: (1)When \(\lambda ^{2}-4\mu \nu <0\) and \(\nu \ne 0\) then,

    $$\begin{aligned} \Omega _{1}(\zeta )= & -\frac{\lambda }{2\nu }+\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2 \nu }\tan _{B}\left( \frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2}\zeta \right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (9)
    $$\begin{aligned} \Omega _{2}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2 \nu }\cot _{B}\left( \frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2}\zeta \right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (10)
    $$\begin{aligned} \Omega _{3}(\zeta )= & -\frac{\lambda }{2\nu }+\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2 \nu }\left( \tan _{B}\left( \sqrt{-(\lambda ^{2}-4\mu \nu )}~\zeta \right) \pm \sqrt{p q}\sec _{B}\left( \sqrt{-(\lambda ^{2}-4\mu \nu )}~\zeta \right) \right) , \end{aligned}$$
    (11)
    $$\begin{aligned} \Omega _{4}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2\nu }\left( \cot _{B}\left( \sqrt{-(\lambda ^{2}-4\mu \nu )}~\zeta \right) \pm \sqrt{p q}\csc _{B}\left( \sqrt{-(\lambda ^{2}-4\mu \nu )}~\zeta \right) \right) , \end{aligned}$$
    (12)
    $$\begin{aligned} \Omega _{5}(\zeta )= & -\frac{\lambda }{2\nu }+\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{4 \nu }\left( \tan _{B}\left( \frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{4}~\zeta \right) -\cot _{B}\left( \frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{4}~\zeta \right) \right) . \end{aligned}$$
    (13)

    (2) When \(\lambda ^{2}-4\mu \nu >0\) and \(\nu \ne 0\) then,

    $$\begin{aligned} \Omega _{6}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{\lambda ^{2}-4\mu \nu }}{2 \nu }\tanh _{B}\left( \frac{\sqrt{\lambda ^{2}-4\mu \nu }}{2}\zeta \right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (14)
    $$\begin{aligned} \Omega _{7}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{\lambda ^{2}-4\mu \nu }}{2 \nu }\coth _{B}\left( \frac{\sqrt{\lambda ^{2}-4\mu \nu }}{2}\zeta \right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (15)
    $$\begin{aligned} \Omega _{8}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{\lambda ^{2}-4\mu \nu }}{2 \nu }\left( \tanh _{B}\left( \sqrt{\lambda ^{2}-4\mu \nu }~\zeta \right) \pm i\sqrt{p q}~\text{ sech}_{B}\left( \sqrt{\lambda ^{2}-4\mu \nu }~\zeta \right) \right) , \end{aligned}$$
    (16)
    $$\begin{aligned} \Omega _{9}(\zeta )= & -\frac{\lambda }{2\nu }-\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{2 \nu }\left( \coth _{B}\left( \sqrt{\lambda ^{2}-4\mu \nu }~\zeta \right) \pm \sqrt{p q}~\text{ csch}_{B}\left( \sqrt{\lambda ^{2}-4\mu \nu }~\zeta \right) \right) , \end{aligned}$$
    (17)
    $$\begin{aligned} \Omega _{10}(\zeta )= & -\frac{\lambda }{2\nu }+\frac{\sqrt{-(\lambda ^{2}-4\mu \nu )}}{4\nu }\left( \tanh _{B}\left( \frac{\sqrt{\lambda ^{2}-4\mu \nu }}{4}~\zeta \right) +\coth _{B}\left( \frac{\sqrt{\lambda ^{2}-4\mu \nu }}{4}~\zeta \right) \right) . \end{aligned}$$
    (18)

    (3) When \(\mu \nu >0\) and \(\lambda =0\) then,

    $$\begin{aligned} \Omega _{11}(\zeta )= & \sqrt{\frac{\mu }{\nu }}\tan _{B}(\sqrt{\mu \nu }~\zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (19)
    $$\begin{aligned} \Omega _{12}(\zeta )= & -\sqrt{\frac{\mu }{\nu }}\cot _{B}(\sqrt{\mu \nu }~\zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (20)
    $$\begin{aligned} \Omega _{13}(\zeta )= & \sqrt{\frac{\mu }{\nu }}\left( \tan _{B}(2\sqrt{\mu \nu }~\zeta )\pm \sqrt{pq}\sec _{B}(2\sqrt{\mu \nu }~\zeta )\right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (21)
    $$\begin{aligned} \Omega _{14}(\zeta )= & -\sqrt{\frac{\mu }{\nu }}\left( \cot _{B}(2\sqrt{\mu \nu }~\zeta )\pm \sqrt{pq}\csc _{B}(2\sqrt{\mu \nu }~\zeta )\right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (22)
    $$\begin{aligned} \Omega _{15}(\zeta )= & \frac{1}{2}\sqrt{\frac{\mu }{\nu }}\left( \tan _{B}(\frac{\sqrt{\mu \nu }}{2}\zeta )-\cot _{B}(\frac{\sqrt{\mu \nu }}{2}\zeta )\right) .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (23)

    (4) When \(\mu \nu <0\) and \(\lambda =0\) then,

    $$\begin{aligned} \Omega _{16}(\zeta )= & -\sqrt{-\frac{\mu }{\nu }}\tanh _{B}(\sqrt{-\mu \nu }~\zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (24)
    $$\begin{aligned} \Omega _{17}(\zeta )= & -\sqrt{-\frac{\mu }{\nu }}\coth _{B}(\sqrt{-\mu \nu }~\zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (25)
    $$\begin{aligned} \Omega _{18}(\zeta )= & -\sqrt{-\frac{\mu }{\nu }}\left( \tanh _{B}(2\sqrt{-\mu \nu }~\zeta )\pm i \sqrt{pq}~\text{ sech}_{B}(2\sqrt{-\mu \nu }~\zeta )\right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (26)
    $$\begin{aligned} \Omega _{19}(\zeta )= & -\sqrt{-\frac{\mu }{\nu }}\left( \coth _{B}(2\sqrt{-\mu \nu }~\zeta )\pm \sqrt{pq}~\text{ csch}_{B}(2\sqrt{-\mu \nu }~\zeta )\right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (27)
    $$\begin{aligned} \Omega _{20}(\zeta )= & -\frac{1}{2}\sqrt{-\frac{\mu }{\nu }}\left( \tanh _{B}(\frac{\sqrt{-\mu \nu }}{2}\zeta )-\coth _{B}(\frac{\sqrt{-\mu \nu }}{2}\zeta )\right) .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (28)

    (5) When \(\lambda =0\) and \(\nu =\mu\) then,

    $$\begin{aligned} \Omega _{21}(\zeta )=\tan _{B}(\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (29)
    $$\begin{aligned} \Omega _{22}(\zeta )=-\cot _{B}(\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (30)
    $$\begin{aligned} \Omega _{23}(\zeta )=\tan _{B}(2\mu \zeta )\pm \sqrt{p q}\sec _{B}(2\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (31)
    $$\begin{aligned} \Omega _{24}(\zeta )=-\cot _{B}(2\mu \zeta )\pm \sqrt{p q}\csc _{B}(2\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (32)
    $$\begin{aligned} \Omega _{25}(\zeta )=\frac{1}{2}\left( \tan _{B}(\frac{\mu }{2}\zeta )-\cot _{B}(\frac{\mu }{2}\zeta )\right) .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (33)

    (6) When \(\lambda =0\) and \(\nu =-\mu\) then,

    $$\begin{aligned} \Omega _{26}(\zeta )=-\tanh _{B}(\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (34)
    $$\begin{aligned} \Omega _{27}(\zeta )=-\coth _{B}(\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (35)
    $$\begin{aligned} \Omega _{28}(\zeta )=-\tanh _{B}(2\mu \zeta )\pm i \sqrt{p q}~\text{ sech}_{B}(2\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (36)
    $$\begin{aligned} \Omega _{29}(\zeta )=-\coth _{B}(2\mu \zeta )\pm \sqrt{p q}~\text{ csch}_{B}(2\mu \zeta ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (37)
    $$\begin{aligned} \Omega _{30}(\zeta )=-\frac{1}{2}\left( \tanh _{B}(\frac{\mu }{2}\zeta )+\coth _{B}(\frac{\mu }{2}\zeta )\right) .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (38)

    (7) When \(\lambda ^{2}=4 \mu \nu\) then,

    $$\begin{aligned} \Omega _{31}(\zeta )=\frac{-2 \mu (\lambda \zeta \ln B+2)}{\lambda ^{2}\zeta \ln B}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (39)

    (8) When \(\lambda =\chi\), \(\mu =r \chi (r\ne 0)\) and \(\nu =0\) then,

    $$\begin{aligned} \Omega _{32}(\zeta )=B^{\chi \zeta }-r.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (40)

    (9) When \(\lambda =\nu =0\) then,

    $$\begin{aligned} \Omega _{33}(\zeta )=\mu \zeta \ln B.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (41)

    (10) When \(\lambda =\mu =0\) then,

    $$\begin{aligned} \Omega _{34}(\zeta )=\frac{-1}{\nu \zeta \ln B}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (42)

    (11) When \(\mu =0\) and \(\lambda \ne 0\) then,

    $$\begin{aligned} \Omega _{35}(\zeta )=-\frac{p\lambda }{\nu (\cosh _{B}(\lambda \zeta )-\sinh _{B}(\lambda \zeta )+p)},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (43)
    $$\begin{aligned} \Omega _{36}(\zeta )=-\frac{\lambda (\sinh _{B}(\lambda \zeta )+\cosh _{B}(\lambda \zeta ))}{\nu (\sinh _{B}(\lambda \zeta )+\cosh _{B}(\lambda \zeta )+q)},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (44)

    (12) When \(\lambda =\chi\), \(\nu =r\chi (r\ne 0)\) and \(\mu =0\) then,

    $$\begin{aligned} \Omega _{37}(\zeta )=\frac{p B^{\chi \zeta }}{p-r q B^{\chi \zeta }}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (45)

    The following statements describe the generalized hyperbolic and trigonometric functions according to the above solutions: for details see refrence (Mirhosseni-Alizamini et al. 2020),

    $$\begin{aligned} \sinh _{B}(\zeta )=\frac{p B^{\zeta }-qB^{-\zeta }}{2},\quad \cosh _{B}(\zeta )=\frac{p B^{\zeta }+qB^{-\zeta }}{2}, \\ \tanh _{B}(\zeta )=\frac{p B^{\zeta }-qB^{-\zeta }}{p B^{\zeta }+qB^{-\zeta }},\quad \coth _{B}(\zeta )=\frac{p B^{\zeta }+qB^{-\zeta }}{p B^{\zeta }-qB^{-\zeta }}, \\ \text{ sech}_{B}(\zeta )=\frac{2}{p B^{\zeta }+qB^{-\zeta }},\quad \text{ csch}_{B}(\zeta )=\frac{2}{p B^{\zeta }-qB^{-\zeta }}, \\ \sin _{B}(\zeta )=\frac{p B^{i\zeta }-qB^{-i\zeta }}{2},\quad \cos _{B}(\zeta )=\frac{p B^{i\zeta }+qB^{-i\zeta }}{2}, \\ \tan _{B}(\zeta )=-i\frac{p B^{i\zeta }-qB^{-i\zeta }}{p B^{i\zeta }+qB^{-i\zeta }},\quad \cot _{B}(\zeta )=i\frac{p B^{i\zeta }+qB^{-i\zeta }}{p B^{i\zeta }-qB^{-i\zeta }}, \\ \sec _{B}(\zeta )=\frac{2}{p B^{i\zeta }+qB^{-i\zeta }},\quad \csc _{B}(\zeta )=\frac{2i}{p B^{i\zeta }-qB^{-i\zeta }}, \end{aligned}$$

     where \(\zeta\) is an independent variable and \(p, q> 0\).

  •  Step 4: We use homogeneous balancing technique in Eq. 6 to determine N for Eq. 7.

  •  Step 5: The strategic equations are simply produced by placing Eq. 7 and its derivatives in Eq. 6 and equating coefficients of same power of \(\Omega (\zeta )\) to zero. We must solve the system in order to find the values of unknowns when Mathematica solves the strategic equations.

3 Exact wave solutions

The Eq. 3 may be solved using the wave transformation \(\phi (x, t)\) = \(Q(\zeta ),~\text{ where }~\zeta =x-c t\) and \(c\ne 0\). Substitute the transformation to Eq. (3), integrate once w.r.t \(\zeta\), and let the integration constant equal zero. We get the following form of ordinary differential equation,

$$\begin{aligned} (c^2-1)Q'- c^2 Q^{'''}+c \rho Q^{''}-2 Q Q' =0.~~ \end{aligned}$$
(46)

3.1 Application of NEDAM

In this section, the proposed method is employed for extracting the novel solutions to the Eq. 3. Using the homogeneous balance principle, which Eq. (46) yields, \(n=2\). So the solution to Eq. (46) is supposed to be expressed as:

$$\begin{aligned} Q(\zeta )=b_{0}+b_{1} \Omega (\zeta )+b_{2} \Omega ^2(\zeta ). \end{aligned}$$
(47)

We can easily find the strategic equations by plugging Eq. 47 and its derivatives into Eq. 46 and setting the coefficients of similar powers of \(\Omega (\zeta )\) to zero. By solving the algebraic equations system with the use of Mathematica, the constant values can be determined. Family-1.

$$\begin{aligned} {\left\{ \begin{array}{ll} b_0= -\frac{6 \lambda \sqrt{c^4 \nu ^2 \ln ^4(B) \left( \lambda ^2-4 \mu \nu \right) }+12 c^2 \mu \nu ^2 \ln ^2(B)-c^2 \nu +\nu }{2 \nu },~~b_1=-6 \left( \sqrt{c^4 \nu ^2 \ln ^4(B) \left( \lambda ^2-4 \mu \nu \right) }+c^2 \lambda \nu \ln ^2(B)\right) ,\\ b_2 = -6 c^2 \nu ^2 \ln ^2(B),~\rho =-\frac{5 \sqrt{c^4 \nu ^2 \ln ^4(B) \left( \lambda ^2-4 \mu \nu \right) }}{c \nu \ln (B)}. \end{array}\right. } \end{aligned}$$

Family-2.

$$\begin{aligned} {\left\{ \begin{array}{ll} b_0= \frac{1}{2} \left( c^2 \ln ^2(B) \left( -\left( \lambda ^2+8 \mu \nu \right) \right) +c^2-1\right) ,~b_1=-6 c^2 \lambda \nu \ln ^2(B),~ b_2 = -6 c^2 \nu ^2 \ln ^2(B),~\rho = 0. \end{array}\right. }~~~~~~~~~~~~ \end{aligned}$$

For the family 1, the solutions to Eq. 3 can be summed up as follows.

Fig. 1
figure 1

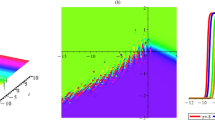
Graphical view of the Eq. 48, with the suitable parameters \(c=1.3,~ \lambda =0.7,~ \mu =0.8,~ \nu =1.1\) and \(B=e\)

Full size image

  • (1) For the cases \(\lambda ^{2}-4\mu \nu <0\) and \(\nu \ne 0\), the following couple of outcomes that we obtain in term of trigonometric and mixed-trigonometric solutions

    $$\begin{aligned} \phi _{1}(x,t) & = \frac{1}{2 \nu } \times \bigg \lbrace -6 \sqrt{4 \mu \nu -\lambda ^2} \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \text {tan}_{B }\left( \frac{1}{2} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) +3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \text {tan}^2_{B }\left( \frac{1}{2} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \bigg \rbrace . \end{aligned}$$
    (48)
    $$\begin{aligned} \phi _{2}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \text {cot}^2_{B }\left( \frac{1}{2} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \nonumber ~~~~~\\ & \quad +6 \sqrt{4 \mu \nu -\lambda ^2} \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \text {cot}_{B }\left( \frac{1}{2} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \bigg \rbrace . \end{aligned}$$
    (49)
    $$\begin{aligned} \phi _{3}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace -6 \sqrt{4 \mu \nu -\lambda ^2} \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times \left( \text {tan}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \pm \sqrt{p q} ~\text {sec}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \right) +3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times \left( \text {tan}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \pm \sqrt{p q} ~\text {sec}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \right) ^2+\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (50)
    $$\begin{aligned} \phi _{4}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 6 \sqrt{4 \mu \nu -\lambda ^2} \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times \left( \text {cot}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \pm \sqrt{p q} ~\text {csc}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \right) +3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times \left( \text {cot}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \pm \sqrt{p q} ~\text {csc}_{B }\left( \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \right) ^2+\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (51)
    $$\begin{aligned} \phi _{5}(x,t) & =\frac{1}{8\nu } \times \bigg \lbrace 4 \nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) +3 \bigg (\text {cot}_{B }\left( \frac{1}{4} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) -\text {tan}_{B }\left( \frac{1}{4} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \bigg )\nonumber \\ & \quad \times \bigg (4 \sqrt{4 \mu \nu -\lambda ^2} \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) }+c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \nonumber \\ & \quad \times \left( \text {cot}_{B }\left( \frac{1}{4} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) -\text {tan}_{B }\left( \frac{1}{4} \zeta \sqrt{4 \mu \nu -\lambda ^2}\right) \right) \bigg )\bigg \rbrace . \end{aligned}$$
    (52)

  • (2) For \(\lambda ^{2}-4\mu \nu >0\) and \(\nu \ne 0\), The following couple of outcomes are found. The solution to the kink is written as

    $$\begin{aligned} \phi _{6}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 6 \sqrt{\lambda ^2-4 \mu \nu } \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \text {tanh}_{B }\left( \frac{1}{2} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) -3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \text {tanh}^2_{B }\left( \frac{1}{2} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \bigg \rbrace . \end{aligned}$$
    (53)

    The singular solution is expressed as

    $$\begin{aligned} \phi _{7}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 6 \sqrt{\lambda ^2-4 \mu \nu } \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \text {coth}_{B }\left( \frac{1}{2} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad -3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \text {coth}^2_{B }\left( \frac{1}{2} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (54)
Fig. 2
figure 2

Graphical view of the Eq. 53, with the suitable parameters \(c=0.65,~\lambda =1.1,~\mu =-0.75,~\nu =0.70\) and \(B=e\)

Full size image

The complex kink-antikink solution is constructed as

$$\begin{aligned} ~\phi _{8}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 6 \sqrt{\lambda ^2-4 \mu \nu } \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \left( \text {tanh}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \pm i \sqrt{p q} ~\text {sech}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) \nonumber \\ & \quad -3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \left( \text {tanh}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \pm i \sqrt{p q} ~\text {sech}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) ^2\nonumber \\ & \quad +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \bigg \rbrace . \end{aligned}$$
(55)

The combined singular solution is retrieved as

$$\begin{aligned} ~~\phi _{9}(x,t)&=\frac{1}{8 \nu } \times \bigg \lbrace 6 \sqrt{\lambda ^2-4 \mu \nu } \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) } \left( \text {coth}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \pm \sqrt{p q} ~\text {csch}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) \nonumber \\ & \quad -3 c^2 \nu \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) \left( \text {coth}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \pm \sqrt{p q} ~\text {csch}_{B }\left( \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) ^2 \nonumber \\ & \quad +\nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) \bigg \rbrace . \end{aligned}$$
(56)

The kink-singular solution is gained as

$$\begin{aligned} \phi _{10}(x,t) & =\bigg \lbrace 4 \nu \left( 3 c^2 \ln ^2(B ) \left( \lambda ^2-4 \mu \nu \right) +c^2-1\right) +3 \left( \text {coth}_{B }\left( \frac{1}{4} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) +\text {tanh}_{B }\left( \frac{1}{4} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) \nonumber \\ & \quad \bigg (4 \sqrt{\lambda ^2-4 \mu \nu } \sqrt{c^4 \nu ^2 \ln ^4(B ) \left( \lambda ^2-4 \mu \nu \right) }+c^2 \nu \ln ^2(B ) \left( 4 \mu \nu -\lambda ^2\right) \nonumber \\ & \quad \left( \text {coth}_{B }\left( \frac{1}{4} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) +\text {tanh}_{B }\left( \frac{1}{4} \zeta \sqrt{\lambda ^2-4 \mu \nu }\right) \right) \bigg ) \bigg \rbrace \times \frac{1}{8 \nu }. \end{aligned}$$
(57)

  • (3) For \(\mu \nu >0\) and \(\lambda =0\), periodic solutions are shown as

    $$\begin{aligned} \phi _{11}(x,t) & =\bigg \lbrace -\frac{12 \sqrt{\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \text {tan}_{B }\left( \zeta \sqrt{\mu \nu }\right) }{\sqrt{\nu }}-6 c^2 \mu \nu \ln ^2(B ) \left( \text {tan}^2_{B }\left( \zeta \sqrt{\mu \nu }\right) +1\right) &\quad +\frac{1}{2} \left( c^2-1\right) \bigg \rbrace .~~~~~~~ \end{aligned}$$
    (58)
    $$\begin{aligned} \phi _{12}(x,t) & =\bigg \lbrace \frac{12 \sqrt{\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \text {cot}_{B }\left( \zeta \sqrt{\mu \nu }\right) }{\sqrt{\nu }}-6 c^2 \mu \nu \ln ^2(B ) \left( \text {cot}^2_{B }\left( \zeta \sqrt{\mu \nu }\right) +1\right) &\quad +\frac{1}{2} \left( c^2-1\right) \bigg \rbrace .~~~~~~~~~ \end{aligned}$$
    (59)

    The combined-trigonometric solutions are derived as

    $$\begin{aligned} \phi _{13}(x,t) & =\bigg \lbrace \frac{1}{2} \left( c^2-1\right) -\frac{12 \sqrt{\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {tan}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \pm \sqrt{p q} ~\text {sec}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \right) }{\sqrt{\nu }}\nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad -6 c^2 \mu \nu \ln ^2(B ) \left( \left( \text {tan}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \pm \sqrt{p q} ~\text {sec}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \right) ^2+1\right) \bigg \rbrace . \end{aligned}$$
    (60)
    $$\begin{aligned} \phi _{14}(x,t) & =\bigg \lbrace \frac{12 \sqrt{\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {cot}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \pm \sqrt{p q} ~\text {csc}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \right) }{\sqrt{\nu }}+\frac{1}{2} \left( c^2-1\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad -6 c^2 \mu \nu \ln ^2(B ) \left( \left( \text {cot}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \pm \sqrt{p q} ~\text {csc}_{B }\left( 2 \zeta \sqrt{\mu \nu }\right) \right) ^2+1\right) \bigg \rbrace . \end{aligned}$$
    (61)
    $$\begin{aligned} \phi _{15}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace -3 c^2 \mu \nu \ln ^2(B ) \left( \text {cot}_{B }\left( \frac{1}{2} \zeta \sqrt{\mu \nu }\right) -\text {tan}_{B }\left( \frac{1}{2} \zeta \sqrt{\mu \nu }\right) \right) ^2-12 c^2 \mu \nu \ln ^2(B )+c^2-1\nonumber ~~~~~~~~~\\ & \quad +\frac{12 \sqrt{\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {cot}_{B }\left( \frac{1}{2} \zeta \sqrt{\mu \nu }\right) -\text {tan}_{B }\left( \frac{1}{2} \zeta \sqrt{\mu \nu }\right) \right) }{\sqrt{\nu }}\bigg \rbrace . \end{aligned}$$
    (62)
Fig. 3
figure 3

Graphical view of the Eq. 57, with the suitable parameters \(c=0.4,~\lambda =0.9,~\mu =-2,~\nu =2\) and \(B=e\)

Full size image

  • (4) For \(\mu \nu <0\) and \(\lambda =0\), we recover the kink solutions as

    $$\begin{aligned} \phi _{16}(x,t)=\bigg \lbrace \frac{12 \sqrt{-\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \text {tanh}_{B }\left( \zeta \sqrt{-\mu \nu }\right) }{\sqrt{\nu }}+6 c^2 \mu \nu \ln ^2(B ) \left( \text {tanh}^2_{B }\left( \zeta \sqrt{-\mu \nu }\right) -1\right) +\frac{1}{2} \left( c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (63)

    The singular solution is obtained as

    $$\begin{aligned} \phi _{17}(x,t) & =\bigg \lbrace \frac{12 \sqrt{-\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \text {coth}_{B }\left( \zeta \sqrt{-\mu \nu }\right) }{\sqrt{\nu }}+6 c^2 \mu \nu \ln ^2(B ) \left( \text {coth}^2_{B }\left( \zeta \sqrt{-\mu \nu }\right) -1\right) & \quad +\frac{1}{2} \left( c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (64)

    The diverse kinds of complex mixed solutions are derived as

    $$\begin{aligned} \phi _{18}(x,t) & =\bigg \lbrace \frac{1}{2} \left( c^2-1\right) +\frac{12 \sqrt{-\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {tanh}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \pm i \sqrt{p q} ~\text {sech}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \right) }{\sqrt{\nu }}\nonumber ~~~~~~~~~~~~~~~~\\ & \quad +6 c^2 \mu \nu \ln ^2(B ) \left( -1+\left( \text {tanh}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \pm i \sqrt{p q} ~\text {sech}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \right) ^2\right) \bigg \rbrace . \end{aligned}$$
    (65)
    $$\begin{aligned} \phi _{19}(x,t) & =\bigg \lbrace \frac{12 \sqrt{-\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {coth}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \pm \sqrt{p q} ~\text {csch}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \right) }{\sqrt{\nu }}+\frac{1}{2} \left( c^2-1\right) \nonumber ~~~~~~~~~~~~~~~~\\ & \quad +6 c^2 \mu \nu \ln ^2(B ) \left( \left( \text {coth}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \pm \sqrt{p q} ~\text {csch}_{B }\left( 2 \zeta \sqrt{-\mu \nu }\right) \right) ^2-1\right) \bigg \rbrace . \end{aligned}$$
    (66)
    $$\begin{aligned} \phi _{20}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace \frac{12 \sqrt{-\mu } \sqrt{-c^4 \mu \nu ^3 \ln ^4(B )} \left( \text {coth}_{B }\left( \frac{1}{2} \zeta \sqrt{-\mu \nu }\right) +\text {tanh}_{B }\left( \frac{1}{2} \zeta \sqrt{-\mu \nu }\right) \right) }{\sqrt{\nu }}\nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad +3 c^2 \mu \nu \ln ^2(B ) \left( \text {coth}_{B }\left( \frac{1}{2} \zeta \sqrt{-\mu \nu }\right) +\text {tanh}_{B }\left( \frac{1}{2} \zeta \sqrt{-\mu \nu }\right) \right) ^2-12 c^2 \mu \nu \ln ^2(B )+c^2-1\bigg \rbrace . \end{aligned}$$
    (67)
Fig. 4
figure 4

Graphical view of the Eq. 63, with the suitable parameters \(c=1.5,~\mu =-1.2,~\nu =0.4\) and \(B=e\)

Full size image
Fig. 5
figure 5

Graphical view of the Eq. 65, with the suitable parameters \(c=1.5,~\mu =-0.25,~\nu =0.1,~\lambda =0.5,~p=0.6,~q=0.4\) and \(B=e\)

Full size image

  • (5) For \(\lambda =0\) and \(\nu =\mu\), the following couple of outcomes are obtain as,

    $$\begin{aligned} \phi _{21}(x,t) & =\bigg \lbrace -12 \sqrt{-c^4 \mu ^4 \ln ^4(B )} \text {tan}_{B }(\mu \zeta )-\frac{1}{2} c^2 \left( 12 \mu ^2 \ln ^2(B )+12 \mu ^2 \ln ^2(B ) \text {tan}^2_{B }(\mu \zeta )-1\right) -\frac{1}{2}\bigg \rbrace .~~~~~~~~~~~~~ \end{aligned}$$
    (68)
    $$\begin{aligned} \phi _{22}(x,t) & =\bigg \lbrace 12 \sqrt{-c^4 \mu ^4 \ln ^4(B )} \text {cot}_{B }(\mu \zeta )-\frac{1}{2} c^2 \left( 12 \mu ^2 \ln ^2(B ) \text {cot}^2_{B }(\mu \zeta )+12 \mu ^2 \ln ^2(B )-1\right) -\frac{1}{2}\bigg \rbrace .~~~~~~~~~~~~~~~~ \end{aligned}$$
    (69)
    $$\begin{aligned} \phi _{23}(x,t) & =\bigg \lbrace -12 \sqrt{-c^4 \mu ^4 \ln ^4(B )} \left( \text {tan}_{B }(2 \mu \zeta )\pm \sqrt{\text {pq}} ~\text {sec}_{B }(2 \mu \zeta )\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad -\frac{1}{2} c^2 \left( 12 \mu ^2 \ln ^2(B )+12 \mu ^2 \ln ^2(B ) \left( \text {tan}_{B }(2 \mu \zeta )\pm \sqrt{\text {pq}} ~\text {sec}_{B }(2 \mu \zeta )\right) ^2-1\right) -\frac{1}{2}\bigg \rbrace . \end{aligned}$$
    (70)
    $$\begin{aligned} \phi _{24}(x,t) & =\bigg \lbrace -12 \sqrt{-c^4 \mu ^4 \ln ^4(B )} \left( -\text {cot}_{B }(2 \mu \zeta )\pm \sqrt{\text {pq}} ~\text {csc}_{B }(2 \mu \zeta )\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad -\frac{1}{2} c^2 \left( 12 \mu ^2 \ln ^2(B ) \left( -\text {cot}_{B }(2 \mu \zeta )\pm \sqrt{\text {pq}} ~\text {csc}_{B }(2 \mu \zeta )\right) ^2+12 \mu ^2 \ln ^2(B )-1\right) -\frac{1}{2}\bigg \rbrace . \end{aligned}$$
    (71)
    $$\begin{aligned} \phi _{25}(x,t) & =\bigg \lbrace \frac{1}{2} \bigg (-12 c^2 \mu ^2 \ln ^2(B )+c^2+3 \left( \text {cot}_{B }\left( \frac{\mu \zeta }{2}\right) -\text {tan}_{B }\left( \frac{\mu \zeta }{2}\right) \right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \left( 4 \sqrt{-c^4 \mu ^4 \ln ^4(B )}+c^2 \mu ^2 \ln ^2(B ) \left( \text {tan}_{B }\left( \frac{\mu \zeta }{2}\right) -\text {cot}_{B }\left( \frac{\mu \zeta }{2}\right) \right) \right) -1\bigg )\bigg \rbrace . \end{aligned}$$
    (72)

  • (6) For \(\lambda =0\) and \(\nu =-\mu\), we secure the following exact solutions,

    $$\begin{aligned} \phi _{26}(x,t) & =\bigg \lbrace \frac{1}{2} \left( 24 \sqrt{c^4 \mu ^4 \ln ^4(B )} \text {tanh}_{B }(\mu \zeta )+12 c^2 \mu ^2 \ln ^2(B )-12 c^2 \mu ^2 \ln ^2(B ) \text {tanh}^2_{B }(\mu \zeta )+c^2-1\right) \bigg \rbrace .~~~~~~~~~~ \end{aligned}$$
    (73)
    $$\begin{aligned} \phi _{27}(x,t) & =\bigg \lbrace \frac{1}{2} \left( 24 \sqrt{c^4 \mu ^4 \ln ^4(B )} \text {coth}_{B }(\mu \zeta )-12 c^2 \mu ^2 \ln ^2(B ) \text {coth}^2_{B }(\mu \zeta )+12 c^2 \mu ^2 \ln ^2(B )+c^2-1\right) \bigg \rbrace .~~~~~~~~~~ \end{aligned}$$
    (74)
    $$\begin{aligned} \phi _{28}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace 12 c^2 \mu ^2 \ln ^2(B )+c^2-1-12 \left( -\text {tanh}_{B }(2 \mu \zeta )\pm i \sqrt{p q} ~\text {sech}_{B }(2 \mu \zeta )\right) \nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times 2 \sqrt{c^4 \mu ^4 \ln ^4(B )}+c^2 \mu ^2 \ln ^2(B ) \left( -\text {tanh}_{B }(2 \mu \zeta )\pm i \sqrt{p q} ~\text {sech}_{B }(2 \mu \zeta )\right) \bigg \rbrace . \end{aligned}$$
    (75)
    $$\begin{aligned} \phi _{{29}} (x,t) & = \frac{1}{{2\nu }} \times \{ 12c^{2} \mu ^{2} \ln ^{2} (B) + c^{2} - 1 - 12\left( { - {\text{coth}}_{B} (2\mu \zeta ) \pm \sqrt {pq} ~{\text{csch}}_{B} (2\mu \zeta )} \right) \\ & \quad \times 2\sqrt {c^{4} \mu ^{4} \ln ^{4} (B)} + c^{2} \mu ^{2} \ln ^{2} (B)\left( { - {\text{coth}}_{B} (2\mu \zeta ) \pm \sqrt {pq} ~{\text{csch}}_{B} (2\mu \zeta )} \right)\} . \\ \end{aligned}$$
    (76)
    $$\begin{aligned} \phi _{30}(x,t) & =\frac{1}{2 \nu } \times \bigg \lbrace c^2-1+12 \sqrt{c^4 \mu ^4 \ln ^4(B )}+12 c^2 \mu ^2 \ln ^2(B )\nonumber ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \times \left( \text {coth}_{B }\left( \frac{\mu \zeta }{2}\right) +\text {tanh}_{B }\left( \frac{\mu \zeta }{2}\right) \right) -3 c^2 \mu ^2 \ln ^2(B ) \left( \text {coth}_{B }\left( \frac{\mu \zeta }{2}\right) +\text {tanh}_{B }\left( \frac{\mu \zeta }{2}\right) \right) ^2\bigg \rbrace . \end{aligned}$$
    (77)

  • (7) For \(\lambda ^2=4 \mu \nu\), we obtain plane wave solutions as

    $$\begin{aligned} \phi _{31}(x,t)=\bigg \lbrace \frac{12 c^2 \lambda \mu \nu \zeta \ln (B ) \left( \lambda ^2-4 \mu \nu \right) (\lambda \zeta \ln (B )+4)+\left( c^2-1\right) \lambda ^4 \zeta ^2-192 c^2 \mu ^2 \nu ^2}{2 \lambda ^4 \zeta ^2}\bigg \rbrace .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (78)

  • (8) For \(\mu =0\) and \(\lambda \ne 0\), we attain hyperbolic function solutions as follows

    $$\begin{aligned} \phi _{32}(x,t) & =\bigg \lbrace \frac{6 c^2 \lambda ^2 p \ln ^2(B ) \left( \text {cosh}_{B }(\lambda \zeta )-\text {sinh}_{B }(\lambda \zeta )\right) }{\left( \text {cosh}_{B }(\lambda \zeta )+p-\text {sinh}_{B }(\lambda \zeta )\right) ^2} +\frac{1}{2} \left( \frac{6 \lambda \sqrt{c^4 \lambda ^2 \nu ^2 \ln ^4(B )} \left( -\text {cosh}_{B }(\lambda \zeta )+p+\text {sinh}_{B }(\lambda \zeta )\right) }{\nu \left( \text {cosh}_{B }(\lambda \zeta )+p-\text {sinh}_{B }(\lambda \zeta )\right) }+c^2-1\right) \bigg \rbrace . \end{aligned}$$
    (79)
    $$\begin{aligned} \phi _{33}(x,t) & =\bigg \lbrace \frac{1}{2} \left( -\frac{6 \lambda \sqrt{c^4 \lambda ^2 \nu ^2 \ln ^4(B )}}{\nu }+c^2-1\right) -\frac{6 c^2 \lambda ^2 \ln ^2(B ) \left( \text {cosh}_{B }(\lambda \zeta )+\text {sinh}_{B }(\lambda \zeta )\right) ^2}{\left( \text {cosh}_{B }(\lambda \zeta )+q+\text {sinh}_{B }(\lambda \zeta )\right) ^2}\nonumber ~~~~~~~~~~~~~~~~~~~~~~\\ & \quad \frac{6 \lambda \left( \sqrt{c^4 \lambda ^2 \nu ^2 \ln ^4(B )}+c^2 \lambda \nu \ln ^2(B )\right) \left( \text {cosh}_{B }(\lambda \zeta )+\text {sinh}_{B }(\lambda \zeta )\right) }{\nu \left( \text {cosh}_{B }(\lambda \zeta )+q+\text {sinh}_{B }(\lambda \zeta )\right) }\bigg \rbrace . \end{aligned}$$
    (80)
Fig. 6
figure 6

Graphical view of the Eq. 75, with the suitable parameters \(c=1.4,~\mu =0.2,~p=0.7,~q=0.5\) and \(B=e\)

Full size image
Fig. 7
figure 7

Graphical view of the Eq. 80, with the suitable parameters \(\chi =2.9,~c=1.3,~\mu =0.5,~p=0.4,~q=0.8,~r=2.5\) and \(B=e\)

Full size image

  • (9) For \(\mu =0\), \(\lambda =\chi\) and \(\nu =r \chi\), we obtain rational function solution as

    $$\begin{aligned} \phi _{34}(x,t)=\bigg \lbrace \frac{1}{2} \left( \frac{6 \sqrt{c^4 r^2 \chi ^4 \ln ^4(B )} \left( r (2 p-q) B ^{\zeta \chi }+p\right) }{r \left( q r B ^{\zeta \chi }-p\right) }+c^2-1\right) -\frac{6 c^2 p r \chi ^2 \ln ^2(B ) B ^{\zeta \chi } \left( r (p-q) B ^{\zeta \chi }+p\right) }{\left( p-q r B ^{\zeta \chi }\right) ^2}\bigg \rbrace .~~~~ \end{aligned}$$
    (81)

    For all solutions  \(\zeta =x-c t\).

  • Note: We can obtain all above solutions with similar procedure for family 2. Due to limits of length we can,t express each solutions here.

4 Results discussion and physical explanation

The attained travelling wave solutions are represented in three types of diagrams namely a three-dimensional plotline, 2-D plotline, and a plot of contour for diverse values of the arbitrary constants with the help of Mathematica. The importance of graphical representations is that they can aid in improving our comprehension of solutions and analysis of complex data. Wave propagation for the IBq model have significant role in soliton theory, applied physics, and mathematical sciences. Finding diverse exact wave structures for the IBq equation is therefore critical for mathematics and physicists. We compare our achieved results with other existing results in the literature with the other methods. The suggested equations presented above were examined by earlier researchers using a variety of methods. It is noticed that in Fan and Zhou (2020) the authors obtained three types of traveling wave exact solutions bu using \(G'/G\) method. But we have retrieved diverse exact wave solutions in this research paper related to single and combined exact wave structures and presented with different graphs. Furthermore, when comparing our results with those obtained by other approaches (Yokus 2021; Causanilles et al. 2022; Baskonus and Gao 2022; Yokus and Baskonus 2022), it becomes evident that some types of solutions already exist in the literature, but the vast majority are new, which demonstrates the novelty of our work. It is significant to note that the solutions revealed in this study are mostly new which interpret generally the one-way propagation of long waves in certain nonlinear dispersive system, plasma waves and shallow waters in coastal oceans. In this portion, we present some of the suggested model’s stated results for the physical explanations. Exact wave structures to IBq equation with with hydrodynamical damping for discussing the various kinds of analytic solutions. By utilizing the given approach, the solutions are obtained and physically depicted into different physical wave behaviors in the form of hyperbolic, trigonometric, mixed hyperbolic, rational periodic, and singular wave behaviors. These analytic solutions have different physical explanations. The achieved outcomes are examined using 3D surface plots, 2D line plots, and corresponding contour graphs to visualize and support the theoretical conclusions using appropriate parameter values. The perspective view of the trigonometric, kink, kink-singular, kink, bright, dark and exponential solutions of Eqs. 48, 53, 57, 63, 65, 75 and 80 can be seen in the 3D, 2D and contour wave profiles which reveal in Figs. 1, 2, 3, 4, 5, 6, 7, respectively. At last, the solutions generated can be utilized to describe a wide variety of enjoyable physical processes. These reported solutions have some physical significance for example, hyperbolic functions, for example, appear in a variety of areas, including special relativity computation and speed, the Langevin function for attractive polarization, the gravitational capabilitiesof a chamber and the estimation of as far as possible, and the profile of a laminar jet. There are further types of solitary waves called singular solitons that have singularities, typically infinite discontinuities. Singular solitons might be linked to solitary waves when the location of the center of the solitary wave is imaginary. Therefore, discussing the topic of singular solitons is relevant. This type of solution contains spikes and therefore may recommend a description for the development of rogue waves. Periodic wave solution describes a wave with repeating continuous pattern, which determines its wavelength and frequency, while period defines as time required to complete cycle of waveform and frequency is a number of cycles per second of time. Our results are important to understanding the nonlinear phenomena in dispersive waves, which are widely applicable in engineering and applied physics. Furthermore, the primary accomplishment of this strategy is that they allowed for the extraction of the maximum number of solutions in a single step, which distinguishes it from other procedures. As a result, we believe the findings reported in this paper will be useful in clarifying the true meaning of various nonlinear advancement conditions that arise in various domains of nonlinear sciences.

5 Conclusion

In this study, with the assistance of NEDAM, we solve the IBq equation with hydro-dynamical damping. By employing this technique, we establish different sorts of solutions, such as kink, anti-kink, singular, bright, dark and their combo forms. The periodic and rational function solutions have also been observed. The physical behavior of the attained solutions is analyzed comprehensively through 3D, 2D, and contour graphs. We notice that the retrieved solutions are fresh, and to our knowledge, the offered technique has never been used to solve the IBq equation with hydro-dynamical damping in the literature beforehand. This study demonstrates that the proposed technique is a useful, effective, and compatible mathematical tool for solving a broad range of nonlinear PDEs that arise in various domains of mathematical physics and engineering. Physicists or engineers can use the newly acquired solutions to conduct further research on various situations. This approach not only yields identical solutions, but it also has the potential to identify novel solutions that have not been reported by other researchers. The main advantage of using applied method in such a way that we can collect a wide range of novel solutions in a single step. It is among the more general methods that, in certain conditions, can lead to the derivation of other methods, such as the \((G'/G)\)-expansion method, the tanh-function method, or the direct algebraic method and the extended tanh-function method. In the future, the IBq model can be examined with various nonlinear terms that simulate non-linearity in the dynamics of soliton propagation through the plasma wave propagation in complex media especially in shallow waters or ion acrostic waves. As a result, it is beneficial to stimulate new ideas for future in ion sound, weakly dispersive media, and acoustic waves applications. The results will become apparent in due time. The technique employed in this study is highly effective in identifying exact traveling wave solutions and solitary wave solutions for a wide range of nonlinear problems.