Abstract
We present a novel numerical method for calculating optimal design in topology optimization problems for 3D linear elastic structures. The algorithm is based on necessary conditions of optimality for problem which was obtained by relaxing the original one via the homogenization method in the sense of operators (G- or H-convergence), and can be implemented for self-adjoint problems. The method relies on recently obtained explicit expressions for the lower Hashin–Shtrikman bound on complementary energy and information on the microstructure that saturates the bound. We tested the algorithm on two benchmark examples, namely the cantilever and the bridge problem. The algorithm provides the solution in a first few iterations and the true composites appear in the optimal design. We also implement a penalization procedure to obtain classical design with slight increase of the cost functional.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Shape or structural optimization consists in arranging given materials such that obtained body satisfies some optimality criteria, which is mathematically usually expressed as minimization of some (integral) functional under some (PDE) constrains. This type of problem has a long history and has been studied by many different methods (for beginning we refer to books (Allaire 2002; Bendsøe 1995; Bendsøe and Sigmund 2003; Milton 2002; Querin et al. 2017; Rozvany 1989; Save and Prager 1985) and reference therein). To be more specific, in this paper we are interested in finding the best way of mixing two elastic materials yielding the most rigid structure and under a volume constraint on the stiff material.
We shall start by setting the problem more precisely (we follow notation from Allaire’s book (Allaire 2002), and we refer to it for clarification of statements from this introductory section): the governing equation that describes underlying physics is the stationary linearized elasticity system in three space dimensions. We chose to write it in the direct tensor form, which paired with the homogeneous Dirichlet boundary condition reads

Here, an open and bounded set \(\Omega \subseteq \textbf{R}^3\) represents an elastic medium, \(\partial \Omega \) its boundary, and the displacement \(\textsf{u}:\Omega \rightarrow \textbf{R}^3\) is uniquely determined by the force density \(\textsf{f}:\Omega \rightarrow \textbf{R}^3\). The strain matrix \(e(\textsf{u})\) is connected with the displacement via so called strain–displacement equation \(e(\textsf{u})=\frac{1}{2}(\nabla \textsf{u}+\nabla \textsf{u}^\top )\), while the stress matrix \(\varvec{\sigma }\) is, by the Hooke’s constitutive law, given as  .
.
Elastic properties of a material are described by the fourth order stiffness tensor  , whose elements are indexed by four indices
, whose elements are indexed by four indices  , and satisfy symmetries: \(a_{ijkl}=a_{klij}=a_{jikl}=a_{ijlk}\), for \(i,j,k,l=1,2,3\). The space of such fourth order tensors we denote by \(\mathrm{Sym^4}\), and if we denote by \(\textrm{Sym}\) the space of all \(3\times 3\) symmetric matrices, then such fourth order tensors can be seen as symmetric linear operators acting on \(\textrm{Sym}\). Clearly, in general non-homogeneous situation the stiffness is a tensor function
, and satisfy symmetries: \(a_{ijkl}=a_{klij}=a_{jikl}=a_{ijlk}\), for \(i,j,k,l=1,2,3\). The space of such fourth order tensors we denote by \(\mathrm{Sym^4}\), and if we denote by \(\textrm{Sym}\) the space of all \(3\times 3\) symmetric matrices, then such fourth order tensors can be seen as symmetric linear operators acting on \(\textrm{Sym}\). Clearly, in general non-homogeneous situation the stiffness is a tensor function  , for which we assume that it is positive definite and coercive, i.e. that there exist \(0<\alpha <\beta \) such that for any symmetric matrix \(\varvec{\xi }\) it satisfies (almost everywhere on \(\Omega \))
, for which we assume that it is positive definite and coercive, i.e. that there exist \(0<\alpha <\beta \) such that for any symmetric matrix \(\varvec{\xi }\) it satisfies (almost everywhere on \(\Omega \))

where : stands for the matrix inner product. Note that the second inequality in (2) also implies that  is bounded by \(\beta \).
is bounded by \(\beta \).
Under such assumptions on the stiffness tensor, and if we assume that the force density \(\textsf{f}\) is square integrable, then the well-possednes of (1) follows from the classical theory for elliptic boundary-value problems.
Let us now introduce the structural optimization framework: we shall assume that the domain \(\Omega \) is filled with two well-ordered isotropic elastic phases

which satisfy inequalities (2). Here, \(\textbf{I}_4\) and \(\textbf{I}_2\) stand for identity tensor and matrix, respectively, while the assumption on well-orderedness of phases implies inequalities \(0<\mu _1\le \mu _2\) for shear moduli and \(0<\kappa _1\le \kappa _2\) for bulk moduli. Therefore, the overall stiffness tensor is given as

where \(\chi \in {\textrm{L}^\infty (\Omega ;\{0,1\})}\) is a characteristic function of the part of the domain occupied by  . Note that this function completely describes the tensor
. Note that this function completely describes the tensor  and rearrangement of given two materials, and thus we call it a (classical) design. The restriction on the amount of materials can be expressed as \(\int _\Omega \chi \,d\textbf{x}=q\), where \(q \in \left\langle 0, |\Omega |\right\rangle \) is in advance prescribed volume of the material
and rearrangement of given two materials, and thus we call it a (classical) design. The restriction on the amount of materials can be expressed as \(\int _\Omega \chi \,d\textbf{x}=q\), where \(q \in \left\langle 0, |\Omega |\right\rangle \) is in advance prescribed volume of the material  . The quality of a design is typically measured through a function of the form
. The quality of a design is typically measured through a function of the form
where \(g_1\), \(g_2\) are some function that are regular enough, and \(\textsf{u}\) is the corresponding displacement, i.e. the solution of (1).
Finally, as we seek for an optimal design, our problems read: for given  and \(g_2\) solve
and \(g_2\) solve
Unfortunately, usually there is no solution for the above minimization problem (if it exists, we call it classical), so we need an appropriate relaxation. There is a number of different approaches and methods that tackle with problem (3), but probably the most successful approach for dealing with typical ill-posedness of such optimization problem is the homogenization method. Its application in optimal design begins with works of Murat and Tartar (1978, 1985) and Tartar (1975), Cherkaev, Lurie and their collaborators (Gibianski and Cherkaev 1997; Lurie 1970; Lurie et al. 1982; Lurie and Cherkaev 1986), Raitums (1978), and Kohn and Strang (1986). Actually, early homogenization results by Tartar (1975) and Murat and Tartar (1978) were motivated by optimal design problems in conductivity (see also Burazin et al. 2018; Burazin and Crnjac 2020), but this approach can also be adapted to the elasticity setting (Francfort and Murat 1986; Tartar 1986; Zhikov et al. 1994). The method became extremely popular in its over-simplified version, called SIMP (Solid Isotropic Material with Penalisation) (Bendsøe and Sigmund 2003), which takes into account only isotropic materials and retains only the notion of material density. However, the maturing of additive manufacturing technologies, which are now able to build finely graded microstructures (sometimes called lattice materials), drastically changes the picture and one can see a resurrection of the homogenization method for such applications (Allaire et al. 2019; Groen and Sigmund 2018; Geoffroy-Donders et al. 2020). Indeed, when dealing with topology optimization problems where true composite materials with optimal (possibly non isotropic) microstructures appear, the homogenization is the right technique to be used, as anisotropy is a feature which is absent from SIMP.
To be more specific, a relaxation of the original optimal design problem by the homogenization method consists in introducing generalized designs as composite materials, achieved by mixing original materials on a fine scale. Thus, a generalized design in this method is a couple  , where \(\theta \) represents a local fraction of the first phase in a mixture, while
, where \(\theta \) represents a local fraction of the first phase in a mixture, while  is a homogenized elasticity tensor which contains information on how the materials are mixed.
is a homogenized elasticity tensor which contains information on how the materials are mixed.
After introducing a Lagrange multiplier in order to handle the volume constraint of the first phase, the relaxed problem in this method reads

where

and \(G(\theta )\) is the set of all possible homogenized elasticity tensors which can be obtained by mixing phases with the prescribed local fraction \(\theta \in [0,1]\). Under appropriate assumptions on \(g_1\) and \(g_2\) (e.g. if they are Carathéodory functions which satisfy some specific growth condition (Allaire 2002)) this is indeed a proper relaxation of the problem (3).
Remark 1
An important class of two-phase elastic composites are laminated composites (Francfort and Murat 1986; Allaire 2002), where the phases are stacked in layers orthogonal to some given direction. For the isotropic phases  and
and  , and unit vector \(\textsf{e}\in \textbf{R}^3\), the homogenized tensor
, and unit vector \(\textsf{e}\in \textbf{R}^3\), the homogenized tensor  , obtained by simple lamination of phases
, obtained by simple lamination of phases  and
and  in proportions \(\theta \) and \((1-\theta )\), and in the direction \(\textsf{e}\) (called a simple laminate), is given with
in proportions \(\theta \) and \((1-\theta )\), and in the direction \(\textsf{e}\) (called a simple laminate), is given with

where \(f_2(\textsf{e})\) is a symmetric positive semidefinite fourth order tensor defined by the quadratic form
with \(\lambda _2=\kappa _2-\displaystyle \frac{2\mu _2}{3}\) being the Lamé coefficient.
If we repeat this lamination process, with different choices for \(\theta \) and \(\textsf{e}\), we get a whole family of laminated materials from phases  and
and  . Explicit formulae for elasiticity tensor of such composites are known (Francfort and Murat 1986) for sequential laminates, where at each stage of lamination, the previous laminate is laminated again with the same pure phase. For example, if we laminate \(p\in \textbf{N}\) times with the phase
. Explicit formulae for elasiticity tensor of such composites are known (Francfort and Murat 1986) for sequential laminates, where at each stage of lamination, the previous laminate is laminated again with the same pure phase. For example, if we laminate \(p\in \textbf{N}\) times with the phase  in directions \(\textsf{e}_1,\dots , \textsf{e}_p\), the obtained composite is determined by the formula
in directions \(\textsf{e}_1,\dots , \textsf{e}_p\), the obtained composite is determined by the formula

where \(m_i\ge 0\), \(i=1,\dots ,p\) and \(\sum _{i=1}^p m_i=1\), while \(f_2\) is given by (6). We call it a rank-p sequential laminate, with core  and matrix
and matrix  , in proportions \(\theta \) and \((1-\theta )\), respectively, with the lamination directions \(\textsf{e}_i\), \(i=1,\dots ,p.\) From the lamination parameters \(m_1, \dots , m_p\) and density \(\theta \) one can get proportions \(\theta _1,\dots ,\theta _p\) of the first phase in each lamination step from the system
, in proportions \(\theta \) and \((1-\theta )\), respectively, with the lamination directions \(\textsf{e}_i\), \(i=1,\dots ,p.\) From the lamination parameters \(m_1, \dots , m_p\) and density \(\theta \) one can get proportions \(\theta _1,\dots ,\theta _p\) of the first phase in each lamination step from the system
As analytical solutions of (4) are achievable only in some specific situations (Murat and Tartar 1978; Vrdoljak 2016; Burazin and Vrdoljak 2019; Burazin 2018; Casado-Diaz 2015), such problems are usually solved numerically, and advantage of the homogenization method is that corresponding schemes find a global minimizer in most instances (see Allaire 2002 and references therein). However, the applicability of the method in the elasticity setting is restricted by the lack of knowledge of the G-closure set \(G(\theta )\) (Murat and Tartar 1978; Tartar 1985; Lurie and Cherkaev 1984) to some specific but important cases (e.g., for self-adjoint problems (Allaire et al. 1997; Allaire and Kohn 1993c; Kohn and Strang 1986; Gibianski and Cherkaev 1997; Lurie et al. 1982; Lurie and Cherkaev 1986; Burazin et al. 2021), or for eigenfrequency optimization (Allaire et al. 2001; Bendsøe and Diaz 1994; Casado-Diaz 2022)). For such problems the relaxation can be performed over sequential laminates instead of \(G(\theta )\) (Avellaneda 1987, see also Kohn and Lipton 1988; Milton and Kohn 1988) and the necessary conditions of optimality in this case are easily derived. However, even in these cases it is crucial to have Hashin-Shtrikman energy bounds explicitly calculated, as such bounds naturally appear in optimality conditions for those structural optimization problems. They are given as bounds on the elastic energy written in terms of strain (primal energy),  , or as bounds on the elastic energy written in terms of stress (complementary energy),
, or as bounds on the elastic energy written in terms of stress (complementary energy),  . For example, and to be specific, the lower Hashin-Shtrikman bound on the complementary energy is given by
. For example, and to be specific, the lower Hashin-Shtrikman bound on the complementary energy is given by

Explicit calculation of these bounds was done for 2D linearized elasticity (Allaire and Kohn 1993a, b), while in the three-dimensional case the computation was formally done only when one material is replaced by the void (Gibianski and Cherkaev 1997, 1987; Allaire and Kohn 1993c; Allaire 2002).
The recent result Burazin et al. (xxxx) on explicit calculation of Hashin-Shtrikman energy bounds for three-dimensional elastic composite made of two isotropic materials, which was an open problem for decades due to its technical complexity, paves the way for new applications of the homogenization method in optimal design problems. In this paper we shall derive a numerical method suitable for solving compliance minimization problems in 3D linearized elasticity setting (for 2D case see Burazin et al. 2021). It is based on necessary conditions of optimality, which state that optimal stiffness tensor saturates lower Hashin-Shtrikman energy bound on complementary energy, while optimal volume fraction minimizes a perturbation of this bound by a linear function in \(\theta \). Therefore, explicit information on this bound is crucial for the method. We demonstrate our method on some benchmark examples, namely the cantilever and the bridge problem. As expected, a true composite design appears to be optimal. Thus we also perform a penalization procedure which gives us (mostly) the classical design, with slight increase of the energy functional. As a mid-step we also calculate the derivative of \(f_-^c\) with respect to \(\theta \).
The rest of the paper is organized as follows: in the second section we recall the necessary conditions of optimality for compliance minimization problems in 3D linearized elasticity, and propose an algorithm for finding approximate solution based on optimality criteria method. In the third section we give explicit lower Hashin-Shtrikman bound on the complementary energy in three space dimensions together with optimal microstructure that saturates the bound Burazin et al. (xxxx) and calculate the derivative of the bound with respect to \(\theta \). In the fourth section we demonstrate our method on some benchmark examples. We finish the paper with some concluding remarks.
2 Compliance minimization
In the rest of the paper we restrict ourselves to the compliance minimization, i.e. in functional J we take \(g_1=g_2=\textsf{f}\cdot \textsf{u}\) and therefore strive to minimize the quantity \(\int _\Omega \textsf{f}\cdot \textsf{u}\, d\textbf{x}\), which represents the work done by the load. Then the functional in (4) takes the form

where \(\textsf{u}\) solves (1). By minimizing (9), one would like to find the most rigid structure made of two elastic materials in the presence of the Lagrange multiplier term. The compliance functional can itself be written as a minimization problem using the principle of minimal complementary energy, yielding the expression

where the above minimum is uniquely achieved by  . The relaxed problem (4) now can be considered as a double minimization in
. The relaxed problem (4) now can be considered as a double minimization in  and in \(\varvec{\sigma }\):
and in \(\varvec{\sigma }\):

and since the order of minimization is irrelevant, we obtain

This representation is suitable for deriving the necessary conditions of optimality (Allaire 2002, Theorem 4.1.9).
Necessary conditions of optimality. If  is a minimizer of the objective function (9), and if \(\varvec{\sigma }^*\) is the unique corresponding minimizer in (10), then
is a minimizer of the objective function (9), and if \(\varvec{\sigma }^*\) is the unique corresponding minimizer in (10), then  , where \(\textsf{u}^*\) is the state function for
, where \(\textsf{u}^*\) is the state function for  . Furthermore,
. Furthermore,  satisfies, almost everywhere in \(\Omega \),
satisfies, almost everywhere in \(\Omega \),

while \(\theta ^*\) is the unique minimizer of the convex minimization problem
\(\square \)
From above conditions of optimality we can deduce that in the case of compliance minimization, one does not need the knowledge on the entire \(G(\theta )\) in order to find an optimal pair  . Indeed, it suffices to know the lower Hashin-Shtrikman bound on the complementary energy and a microstructure that saturates this bound, i.e. a minimizer in (8). If this would be the case, then we could easily derive an algorithm for finding an approximate optimal design by using an optimality criteria method and the necessary conditions of optimality. The algorithm is stated below.
. Indeed, it suffices to know the lower Hashin-Shtrikman bound on the complementary energy and a microstructure that saturates this bound, i.e. a minimizer in (8). If this would be the case, then we could easily derive an algorithm for finding an approximate optimal design by using an optimality criteria method and the necessary conditions of optimality. The algorithm is stated below.
Algorithm 1
Take some initial \(\theta ^0\) and  . For \(k\ge 0\):
. For \(k\ge 0\):
-
(1)
Calculate \(\textsf{u}^k\), the solution of
 (14)
(14)and define
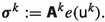
-
(2)
For \(\textbf{x}\in \Omega \), take \(\theta ^{k+1}(\textbf{x})\) as a zero of the function
$$\begin{aligned} \theta \mapsto {\displaystyle \frac{\partial f_-^c}{\partial \theta }(\theta ,\varvec{\sigma }^k(\textbf{x})) +l}, \end{aligned}$$(15)and if a zero doesn’t exist, take 0 (or 1) if the function is positive (or negative) on [0, 1]. Take
 to be a minimizer in the definition of \(f_-^c(\theta ^{k+1}(\textbf{x}),\varvec{\sigma }^k(\textbf{x}))\).
to be a minimizer in the definition of \(f_-^c(\theta ^{k+1}(\textbf{x}),\varvec{\sigma }^k(\textbf{x}))\).
Remark 2
Since the function \(f_-^c\) is \(C^1\) function with the respect to \(\theta \) (Allaire 2002), a minimizer in the convex problem (13) coincides with a zero of the function (15).
Remark 3
Algorithm 1 coincides with the alternate direction algorithm (Allaire et al. 1997), which amounts to minimizing (11) iteratively and separately in \(\varvec{\sigma }\) and  .
.
Remark 4
The above necessary conditions of optimality are also valid if we pair the governing equation with mixed boundary condition, i.e. consider the problem

instead of (1), with \(\Gamma _D\) of positive surface measure and \(\Gamma _D\cup \Gamma _N=\partial \Omega \). In this case the compliance functional is

so by adding the Lagrange term \(l\int _\Omega \theta \, d\textbf{x}\) equality (11) analogously holds, as well as the corresponding necessary conditions of optimality.
3 Hashin–Shtrikman energy bounds
In order to implement Algorithm 1 we shall need an explicit calculation of the lower Hashin–Shtrikman bound on the complementary energy (8). More precisely, we need derivative of \(f_-^c\) with respect to \(\theta \) for calculating the next iteration of local material fraction of the first phase in the mixture, and the corresponding microstructure that saturates the bound for iterations of the stiffness tensor.
We present here the lower bound on the complementary energy (Allaire and Kohn 1993a).
Lower bound on the complementary energy. For a symmetric matrix \(\varvec{\sigma }\) and \(\theta \in [0,1]\) it holds

where \(g^c(\varvec{\eta })\) is a nonlocal term given by

Furthermore, the minimum in definition (8) is achieved by a rank-3 sequential laminate with the lamination directions given by the extremal vectors in the definition of the nonlocal term \(g^c(\varvec{\eta })\). In particular, lamination directions of the optimal rank-3 sequential laminate for the lower bound are also eigendirections of \(\varvec{\sigma }\). \(\blacksquare \)
Deriving the Hashin-Shtrikman bounds in such form is a classical matter: it goes back to the original work of Hashin and Shtrikman (1962, 1963), while modern expositions may be found in Allaire and Kohn 1993a, Milton 1990, or in Gibianski and Cherkaev 1997, Gibianski and Cherkaev 1987 where the translation method is used, instead of the Hashin-Shtrikman variational principle. However, in order to derive an explicit expression for the lower complementary bound, one needs to solve the maximization problem in (18). For the two-dimensional case, this was done in (Allaire and Kohn 1993b; Burazin et al. 2021) for the mixture of two isotropic phases, while the three-dimensional case remained open for three decades, until it was recently calculated in Burazin et al. (xxxx). For similar results in shape optimization and conductivity setting see Gibianski and Cherkaev (1997), Gibianski and Cherkaev (1987), Allaire and Kohn (1993c), Allaire (1994), Allaire (2002), Bendsøe (1995), Rozvany (1989), Save and Prager (1985), Burazin et al. (2018), Vrdoljak (2010), Burazin and Crnjac (2020). In the sequel we shall present the explicit expresion for \(f_-^c\), as derived in Burazin et al. (xxxx), and here, additionally, we provide information on the derivative of \(f_-^c\) with respect to \(\theta \), which is necessary for implementation of our numerical algorithm.
Explicit lower Hashin–Shtrikman bound on the complementary energy. Let \(\theta \in [0,1]\) and let us introduce numbers \(\delta \!\mu =\mu _2-\mu _1\), \(\delta \!\kappa =\kappa _2-\kappa _1\), \(\gamma _2=3\kappa _2+4\mu _2\), \(\zeta =\mu _2-\theta \delta \!\mu \), \(\vartheta =\kappa _2-\theta \delta \!\kappa \), \(\rho = \kappa _1\mu _2-\kappa _2\mu _1,\) and linear functions
In three dimensional, well-ordered case, let \(\varvec{\sigma }\) be a symmetric matrix with eigenvalues \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) and corresponding orthonormal eigenvectors \(\textsf{e}_1\), \(\textsf{e}_2\) and \(\textsf{e}_3\). Then, the lower Hashin-Shtrikman bound on complementary energy can be expressed explicitly by exactly one of the following five cases. In each case (except the case D) one is free to take any choice \((i,j,k)\in \{(3,2,1), (2,1,3), (1,3,2)\}\).
- A.:
-
If
$$\begin{aligned} \begin{aligned} n(\sigma _i,\sigma _j,\sigma _k)p(\sigma _i,\sigma _j,\sigma _k)<&0\\ n(\sigma _j,\sigma _i,\sigma _k)p(\sigma _j,\sigma _i,\sigma _k)<&0, \end{aligned} \end{aligned}$$then

and
$$\begin{aligned} \frac{\partial {f_-^c(\theta , \varvec{\sigma })}}{\partial \theta }= & {} \frac{-\theta ^2\delta \!\mu (3\delta \!\mu \kappa _1\kappa _2+4\mu _1\mu _2\delta \!\kappa )+\mu _2^2\kappa _2 (3\kappa _1+4\mu _1)}{9\kappa _2\mu _2\zeta ^2(3\kappa _1\kappa _2\zeta +4\mu _1\mu _2\vartheta )^2}\\{} & {} \bigg ( 9\delta \!\mu \kappa _2\mu _2\zeta (\kappa _1+3(1-\theta )\delta \!\kappa ) \sigma _k^2+\zeta (3\kappa _1\kappa _2\delta \!\mu (3\kappa _2+\mu _2)\\{} & {} +\mu _1\mu _1\delta \!\kappa \gamma _2)(\sigma _i+\sigma _j+\sigma _k)^2 +9\mu _1\mu _2\kappa _2\delta \!\mu \vartheta (\sigma _j-\sigma _i)^2\\{} & {} -9\kappa _1\kappa _2\delta \!\mu \zeta \big (3\kappa _2\sigma _j\sigma _i+(3\kappa _2+2\mu _2)\sigma _k(\sigma _j+\sigma _i)\big )\bigg )\\{} & {} +\frac{\theta \delta \!\mu }{9\kappa _2\mu _2\zeta (3\kappa _1\kappa _2\zeta +4\mu _1\mu _2\vartheta )}\\{} & {} \bigg ( -9\kappa _2\mu _2(\delta \!\mu \kappa _1+3\mu _1\delta \!\kappa +6(1-\theta )\delta \!\mu \delta \!\kappa ) \sigma _k^2-(3\kappa _1\kappa _2\delta \!\mu (3\kappa _2\\{} & {} +\mu _2)+\mu _1\mu _1\delta \!\kappa \gamma _2)(\sigma _i+\sigma _j+\sigma _k)^2-9\mu _1\mu _2 \kappa _2\delta \!\kappa (\sigma _j-\sigma _i)^2\\{} & {} +9\kappa _1\kappa _2\delta \!\mu \big (3\kappa _2\sigma _j\sigma _i+(3\kappa _2+2\mu _2)\sigma _k(\sigma _j+\sigma _i)\big )\bigg ). \end{aligned}$$This bound is achieved by a simple laminate with the lamination direction \(\textsf{e}_k\).
- B.:
-
If
$$\begin{aligned} \begin{aligned}&\frac{n(\sigma _i,\sigma _j,\sigma _k)}{n(\sigma _i,\sigma _j,\sigma _k)+n(\sigma _i,\sigma _k,\sigma _j)}\ge 0\\&\frac{n(\sigma _i,\sigma _k,\sigma _j)}{n(\sigma _i,\sigma _j,\sigma _k)+n(\sigma _i,\sigma _k,\sigma _j)}\ge 0\\&o(\sigma _i,\sigma _j,\sigma _k)(q(\sigma _j,\sigma _i,\sigma _k)+q(\sigma _k,\sigma _i,\sigma _j)\\&\quad -6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2(-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k))<&0, \end{aligned} \end{aligned}$$then

while
$$\begin{aligned} \begin{aligned} \frac{\partial {f_-^c(\theta , \varvec{\sigma })}}{\partial \theta }&=\frac{\mu _2(\kappa _2(3\kappa _1+\mu _1+3\mu _2)-3\theta ^2\delta \!\kappa \delta \!\mu )}{36\kappa _2\mu _2(3\zeta (\kappa _1\kappa _2+\mu _2\vartheta )+\mu _1\mu _2\vartheta )^2} \\ {}&\quad \bigg (27(1- \theta ) \mu _2 \kappa _2\delta \kappa \delta \mu (-\sigma _i+\sigma _j+\sigma _k)^2+\gamma _2\big (\mu _2\delta \kappa (3\zeta \\&\quad +\mu _1)(\sigma _i +\sigma _j+\sigma _k)^2 +3\kappa _1\kappa _2\delta \mu (2\sigma _i-\sigma _j-\sigma _k)^2\big )\bigg )\\&\quad +\frac{\theta }{36\kappa _2\mu _2(3\zeta (\kappa _1\kappa _2+\mu _2\vartheta )+\mu _1\mu _2\vartheta )} \bigg ( -27 \mu _2 \kappa _2\delta \kappa \delta \mu (-\sigma _i\\&\quad +\sigma _j+\sigma _k)^2-3\gamma _2\mu _2\delta \kappa \delta \!\mu (\sigma _i +\sigma _j+\sigma _k)^2 \bigg ). \end{aligned} \end{aligned}$$This bound can be achieved by the rank-2 sequential laminate with the lamination directions \(\textsf{e}_j\) and \(\textsf{e}_k\), and lamination parameters
$$\begin{aligned} m_j= \frac{n(\sigma _i,\sigma _j,\sigma _k)}{n(\sigma _i,\sigma _j,\sigma _k)+n(\sigma _i,\sigma _k,\sigma _j)}\quad \text {and}\quad m_k=\frac{n(\sigma _i,\sigma _k,\sigma _j)}{n(\sigma _i,\sigma _j,\sigma _k)+n(\sigma _i,\sigma _k,\sigma _j)}. \end{aligned}$$ - C.:
-
If
$$\begin{aligned} \begin{aligned}&\frac{p(\sigma _i,\sigma _j,\sigma _k)}{\sigma _k-\sigma _j}\ge 0\\&\frac{p(\sigma _i,\sigma _k,\sigma _j)}{\sigma _j-\sigma _k}\ge 0\\&q(\sigma _i,\sigma _j,\sigma _k)q(\sigma _i,\sigma _k,\sigma _j)>0, \end{aligned} \end{aligned}$$then

and
$$\begin{aligned} \begin{aligned} \frac{\partial {f_-^c(\theta , \varvec{\sigma })}}{\partial \theta }&=\frac{\delta \!\mu \mu _2(3\kappa _2+\mu _2+3\mu _1)}{9\kappa _2\mu _2(\zeta (3\kappa _2+\mu _2)+3\mu _1\mu _2)^2}\bigg ( \big (\mu _2(\sigma _i+\sigma _j+\sigma _k)+\\&\quad +3\kappa _2(-\sigma _i+\sigma _j+\sigma _k)\big )^2 +9\kappa _2^2\big (\sigma _i(\sigma _j+\sigma _k)-3\sigma _j\sigma _k\big )\\&\quad +3\kappa _2\mu _2\big (4\sigma _i^2+\sigma _i(\sigma _j+\sigma _k)-12\sigma _j\sigma _k\big )\\&\quad + \frac{\mu _2(-4\mu _1\delta \!\kappa +\kappa _1\delta \!\mu )}{4\theta \delta \!\kappa \delta \!\mu (3\kappa _2+\mu _2)-4\kappa _2\mu _2(3\delta \!\kappa +\delta \!\mu )}\\&\quad \big (3\kappa _2(2\sigma _i-\sigma _j-\sigma _k)+2\mu _2(\sigma _i+\sigma _j+\sigma _k)\big )^2\bigg )\\&\quad -\frac{4\theta \delta \!\kappa \delta \!\mu ^2(3\kappa _2+\mu _2)(\mu _2(-4\mu _1\delta \!\kappa +\kappa _1\delta \!\mu ))}{9\kappa _2\mu _2(\zeta (3\kappa _2+\mu _2)+3\mu _1\mu _2)(4\theta \delta \!\kappa \delta \!\mu (3\kappa _2+\mu _2)-4\kappa _2\mu _2(3\delta \!\kappa +\delta \!\mu ))^2}\\&\quad \big (3\kappa _2(2\sigma _i-\sigma _j-\sigma _k)+2\mu _2(\sigma _i+\sigma _j+\sigma _k)\big )^2. \end{aligned} \end{aligned}$$This bound can be achieved by the rank-2 sequential laminate with the lamination directions \(\textsf{e}_j\) and \(\textsf{e}_k\), and lamination parameters
$$\begin{aligned} \begin{aligned}&m_j= \frac{p(\sigma _i,\sigma _j,\sigma _k)}{6(1-\theta )\delta \!\mu (3\kappa _2\delta \!\kappa \zeta +\mu _2\delta \!\mu \vartheta )(\sigma _k-\sigma _j)}\\ \quad \text {and}\quad&m_k=\frac{p(\sigma _i,\sigma _k,\sigma _j)}{6(1-\theta )\delta \!\mu (3\kappa _2\delta \!\kappa \zeta +\mu _2\delta \!\mu \vartheta )(\sigma _j-\sigma _k)}. \end{aligned} \end{aligned}$$ - D.:
-
If
$$\begin{aligned} \begin{aligned} \frac{-o(\sigma _1,\sigma _2,\sigma _3)}{\sigma _1+\sigma _2+\sigma _3}\ge&0\\ \frac{-o(\sigma _2,\sigma _1,\sigma _3)}{\sigma _1+\sigma _2+\sigma _3}\ge&0\\ \frac{-o(\sigma _3,\sigma _2,\sigma _1)}{\sigma _1+\sigma _2+\sigma _3}\ge&0, \end{aligned} \end{aligned}$$then

while
$$\begin{aligned} \begin{aligned} \frac{\partial {f_-^c(\theta , \varvec{\sigma })}}{\partial \theta }=\frac{\delta \!\kappa \gamma _2(4\mu _2\delta \!\kappa +\kappa _1\gamma _2)(\sigma _1+\sigma _2+\sigma _3)^2}{9\kappa _2(4\mu _2(1-\theta )\delta \!\kappa +\kappa _1\gamma _2)^2}. \end{aligned} \end{aligned}$$In this case, the bound can be achieved by the rank-3 sequential laminate with the lamination directions \(\textsf{e}_1\), \(\textsf{e}_2\) and \(\textsf{e}_3\), and lamination parameters
$$\begin{aligned} \begin{aligned} m_1=&\frac{-o(\sigma _1,\sigma _2,\sigma _3)}{6(1-\theta )\delta \!\kappa \mu _2(\sigma _1+\sigma _2+\sigma _3)}, \quad m_2=\frac{-o(\sigma _2,\sigma _1,\sigma _3)}{6(1-\theta )\delta \!\kappa \mu _2(\sigma _1+\sigma _2+\sigma _3)},\\ {}&\text {and}\quad m_3=\frac{-o(\sigma _3,\sigma _2,\sigma _1)}{6(1-\theta )\delta \!\kappa \mu _2(\sigma _1+\sigma _2+\sigma _3)}. \end{aligned} \end{aligned}$$ - E.:
-
If
$$\begin{aligned} \begin{aligned}&\frac{1}{9\kappa _2\sigma _i-(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)}\bigg (q(\sigma _j,\sigma _i,\sigma _k) +q(\sigma _k,\sigma _i,\sigma _j)\\&\quad -6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2\big (-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)\big )\bigg )\ge 0\\&\frac{q(\sigma _j,\sigma _i,\sigma _k)}{-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)}\ge 0\\&\frac{q(\sigma _k,\sigma _i,\sigma _j)}{-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)}\ge 0, \end{aligned} \end{aligned}$$then

and
$$\begin{aligned} \begin{aligned} \frac{\partial {f_-^c(\theta , \varvec{\sigma })}}{\partial \theta }&=\frac{\delta \!\kappa \delta \!\mu \gamma _2 \big (4\delta \!\kappa \delta \!\mu (3\kappa _2+\mu _2)^2+\gamma _2(12\kappa _2\mu _1\delta \!\kappa +\mu _2\kappa _1\delta \!\mu )\big )}{9\kappa _2\mu _2\big (4(1-\theta )\delta \!\kappa \delta \!\mu (3\kappa _2+\mu _2)^2+\gamma _2(12\kappa _2\mu _1\delta \!\kappa +\mu _2\kappa _1\delta \!\mu )\big )^2}\\&\quad \big (3\kappa _2(-2\sigma _i+\sigma _j+\sigma _k)+\mu _2(\sigma _i+ \sigma _j+\sigma _k)\big )^2. \end{aligned} \end{aligned}$$In this case, the bound can be achieved by the rank-3 sequential laminate with the lamination directions \(\textsf{e}_i\), \(\textsf{e}_j\) and \(\textsf{e}_k\), and lamination parameters
$$\begin{aligned} \begin{aligned} m_i&= \frac{1}{6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2\big (9\kappa _2\sigma _i-(3\kappa _2+\mu _2) (\sigma _i+\sigma _j+\sigma _k)\big )}\bigg ( q(\sigma _j,\sigma _i,\sigma _k)\\&\quad +q(\sigma _k,\sigma _i,\sigma _j) -6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2\big (-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)\big )\bigg ),\\ m_j&= \frac{q(\sigma _j,\sigma _i,\sigma _k)}{6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2\big (-9\kappa _2\sigma _i +(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)\big )}\\&\text {and}\quad m_k=\frac{q(\sigma _k,\sigma _i,\sigma _j)}{6(1-\theta )\delta \!\kappa \delta \!\mu \mu _2\big (-9\kappa _2\sigma _i+(3\kappa _2+\mu _2)(\sigma _i+\sigma _j+\sigma _k)\big )}. \end{aligned} \end{aligned}$$
Remark 5
Above expresions for \(f_-^c\) might look overly complicated and not very elegant, but this is mostly due to the large number of parameters. Namely, in each of the above cases \(f_-^c\) is a quadratic function with respect to \(\sigma _i\) and a rational function with respect to \(\theta \), with numerator being of the most degree 3, and denominator of the most degree 2 (case A; note that \(\zeta \) and \(\vartheta \) that appear in expressions for \(f_-^c\) depend linearly on \(\theta \)). Thus, the calculation of the derivative \(\frac{\partial f_-^c}{\partial \theta }\) is just some technical manipulation, while finding its zero in the second step of the algorithm reduces to solving quadratic or quartic equation, depending on the case.
All expressions that we derived were additionally checked by symbolic computation in Wolfram’s Mathematica. In degenerate case, when one material is void, our bounds coincide with those in Allaire (2002) (see Burazin et al. (xxxx) for more).
4 Numerical examples
In this section we shall apply the optimality criteria algorithm 1, and calculate optimal structure for some benchmark examples. The state equation is solved by the finite element method in the deal.II library (Bangerth et al. xxxx) using Lagrange elements on a mesh with a total of 262 144 cells. Moreover, a design  is discretized on a (possibly different Casado-Díaz et al. 2011) mesh, by piecewise constant elements. For numerical integration we used Gaussian quadrature of order two, and the Lagrange multiplier l is adjusted in each step in order to satisfy the volume constraint \(\int _\Omega \theta (\textbf{x})\,d\textbf{x}=q\). We present two structural optimization problems where two given materials are arranged to minimize the compliance functional. In both examples one material correspond to steel, and we take the other one to be ten times weaker, i.e. we take isotropic phases
is discretized on a (possibly different Casado-Díaz et al. 2011) mesh, by piecewise constant elements. For numerical integration we used Gaussian quadrature of order two, and the Lagrange multiplier l is adjusted in each step in order to satisfy the volume constraint \(\int _\Omega \theta (\textbf{x})\,d\textbf{x}=q\). We present two structural optimization problems where two given materials are arranged to minimize the compliance functional. In both examples one material correspond to steel, and we take the other one to be ten times weaker, i.e. we take isotropic phases  and
and  with shear moduli \(\mu _1=7.93\), \(\mu _2=79.3\), and bulk moduli \(\kappa _1=16\), \(\kappa _2=160\). We illustrate the result of the 20th iteration of the algorithm, although a similar design is reached already by its first few iterations. In addition, we provide a penalized solution, where, instead of updating density \(\theta ^k\) with the true optimal density \(\theta ^{k+1}\), we use value
with shear moduli \(\mu _1=7.93\), \(\mu _2=79.3\), and bulk moduli \(\kappa _1=16\), \(\kappa _2=160\). We illustrate the result of the 20th iteration of the algorithm, although a similar design is reached already by its first few iterations. In addition, we provide a penalized solution, where, instead of updating density \(\theta ^k\) with the true optimal density \(\theta ^{k+1}\), we use value
In this way, \(\theta ^{pen}\) is closer to 0 or 1 than \(\theta ^{k+1}\), since \(0<\theta ^{k+1}<\frac{1}{2}\) implies \(\theta ^{pen}<\theta ^{k+1}\), while \(\frac{1}{2}<\theta ^{k+1}<1\) implies \(\theta ^{pen}>\theta ^{k+1}\). Therefore, in a few more iterations of the algorithm, optimal penalized design will be very close to the classical one.
Finally, we should mention that we parallelized the numerical code and ran it on computer with multiple cores in order to reduce time of its execution. This particularly refers to the first step of the algorithm, i.e. to solving the state equation.
4.1 The cantilever problem
Let us take domain \(\Omega =[0,10]\times [0,5]\times [0,15]\) and consider the compliance minimization
where \(\textsf{u}\) is the solution of the linearized elasticity system with mixed boundary conditions,

The boundary part \(\Gamma _D\) corresponds to the left side of the domain (where \(z=0\); see Fig. 1), while \(\Gamma _N\) corresponds to the rest of the boundary. We take \(\textsf{f}=\textsf{0}\), while a unit force in the x-direction is applied at the small circle in the middle of the right side, more precisely, \(\textsf{g}=\begin{bmatrix} 1&0&0\end{bmatrix}^\top \) on the circle \(B\left( (5,2.5),\,0.2\right) \) in the plane \(z=15\), and zero elsewhere. The overall proportion of the first (weaker) phase is set to \(60\%\). For the initial design we take \(\theta ^0=0.6\) and a simple laminate  with \(\textsf{e}_1=\begin{bmatrix} 1&0&0 \end{bmatrix}^\top \) as the lamination direction.
with \(\textsf{e}_1=\begin{bmatrix} 1&0&0 \end{bmatrix}^\top \) as the lamination direction.
A numerical solution of this optimal design problem is presented in Fig. 1 (see also Fig. 3a–c). For the better representation of the solution, the part of the domain occupied with the phase \(\textbf{A}_1\) is omitted as well as the upper front half in the figure (the design is symmetrical with respect to the mid-planes \(x=5\) and \(y=2.5\)). The black part of the domain corresponds to the phase \(\textbf{A}_2\), while the gray tones correspond to composite materials. A part of the domain \(\{z=15, \,x\in [6.25,6.55],y\in [2.55,2.8]\}\) is extracted in the figure in order to take a closer look at the structure. In this particular part of the domain the design consists of the pure phase \(\textbf{A}_2\) and simple laminates in almost the same lamination directions. As can be seen, the differences in ratio \(\theta \) in those cells are more pronounced. For example, the proportion of the weaker material in the first cell is 0.25 and the lamination direction is \(\textsf{e}=[-0.22\,\, -0.13\,\, -0.97]^\top \), which is also presented at the figure.
Composite materials that constitute optimal design in this example are either simple laminates or rank-2 laminates. Positions of these composites are shown in Fig. 2. Due to symmetry of the design, simple laminates are omitted in the upper half of the domain in order to see where the rank-2 laminates appear. A lighter shade of the gray color represents simple laminates, while rank-2 laminates are represented by the darker one.
After 20 iterations of the algoritm, an additional 10 iterations were made with penalty function (20) in order to recover a classical design. In Fig. 3 we presented parts of the domain for optimal and penalized design in which the proportion of the first material is less than or equal to some \(\theta \in [0,1]\). Note that they are different for the optimal design due to usage of composites, while they are all almost the same for the penalized design (which is expected since here the proportion takes mainly the values zero and one).
The convergence history is presented in Fig. 4. As convergence criterion we used the \(L^2\) norm of the difference \(\theta ^{k+1}-\theta ^k\) volume fractions from two consecutive iteration. During the penalization process, objective function increases for approximately \(9.8\%\). Note that the bump in the convergence history in the twentieth iteration corresponds to the beginning of the penalization process.
4.2 The bridge problem
For the second example we take a cuboid \([0,2]\times [0,4]\times [0,1]\) as domain \(\Omega \), filled with phases  and
and  , and with a volume constraint of \(90\%\) for the first material. We consider the compliance minimization
, and with a volume constraint of \(90\%\) for the first material. We consider the compliance minimization

where the function \(\textsf{u}\) is the solution of the linearized elasticity system with mixed boundary conditions

The boundary part \(\Gamma _D=\{(x,y,z)\in \partial \Omega : z=0 \wedge (y\le 0.1 \vee y\ge 3.9)\}\) corresponds to the lower-left and lower-right corner of the domain where the bridge is supported, while \(\Gamma _N\) represents the rest of the boundary. We take \(\textsf{f}=\textsf{0}\), while \(\textsf{g}=\begin{bmatrix} 0&0&-1\end{bmatrix}^\top \) on the circle \(B((1,2),\,0.5)\) in the plane \(z=1\) and zero on the rest of the \(\Gamma _N\). For the initial design we take \(\theta ^0=0.9\) and a simple laminate  with \(\textsf{e}_1=\begin{bmatrix} 1&0&0 \end{bmatrix}^\top \) as the lamination direction. The numerical solution is shown in Fig. 5 (see also Fig. 7a–c). Similarly as in the previous example, the part of the domain occupied with the phase
with \(\textsf{e}_1=\begin{bmatrix} 1&0&0 \end{bmatrix}^\top \) as the lamination direction. The numerical solution is shown in Fig. 5 (see also Fig. 7a–c). Similarly as in the previous example, the part of the domain occupied with the phase  is omitted and a quarter of the domain is cutted in order to represent the interior of the domain (the design is symmetrical with respect to the mid-planes \(x=1\) and \(y=2\)). The black part of the domain corresponds to the phase
is omitted and a quarter of the domain is cutted in order to represent the interior of the domain (the design is symmetrical with respect to the mid-planes \(x=1\) and \(y=2\)). The black part of the domain corresponds to the phase  , while the gray tones correspond to composite materials. On the extracted part of the domain \(\{x=2,\,y\in [3.85, 4], z\in [0,0.05]\}\), a pure phases \(\textbf{A}_1\) and \(\textbf{A}_2\) occur, as well as simple and rank-2 laminates. For example, in the rank-2 laminate, the overall proportion of material \(\textbf{A}_1\) is 0.46, lamination parameters are \(m_1=0.85\) and \(m_2=0.15\), while directions of laminations are presented at the figure and equal \(\textsf{e}_1=[-0.15\,\, 0.8 \,\, 0.56]^\top \) and \(\textsf{e}_2=[-0.95\,\, 0.04\,\, -0.3]^\top \).
, while the gray tones correspond to composite materials. On the extracted part of the domain \(\{x=2,\,y\in [3.85, 4], z\in [0,0.05]\}\), a pure phases \(\textbf{A}_1\) and \(\textbf{A}_2\) occur, as well as simple and rank-2 laminates. For example, in the rank-2 laminate, the overall proportion of material \(\textbf{A}_1\) is 0.46, lamination parameters are \(m_1=0.85\) and \(m_2=0.15\), while directions of laminations are presented at the figure and equal \(\textsf{e}_1=[-0.15\,\, 0.8 \,\, 0.56]^\top \) and \(\textsf{e}_2=[-0.95\,\, 0.04\,\, -0.3]^\top \).
Composites that form the optimal design in this example are either simple or rank-2 laminates. Their position within the domain is shown in Fig. 6. A lighter shade of the gray color represents simple laminates, and the darker one represents rank-2 laminates. Again, simple laminates on the right side of the domain are omitted to show where rank-2 laminates are located.
In order to reveal a classical design, penalization method described in the beginning of the section was executed. An additional 10 iterations were made with penalty function (20) after 20 iterations of the algoritm. Parts of the domain for optimal and penalized design in which the proportion of the first material is less than or equal to some \(\theta \in [0,1]\) is presented in Fig. 7. Since composite materials are used to obtain the optimal design, presented parts differ from each other here, while for the penalized design they are all almost the same.
The convergence history is presented in Fig. 8. Objective function for the bridge problem increases for approximately \(2\%\) upon penalization. Again, the bump in the convergence history in the twentieth iteration corresponds to the beginning of the penalization process.
5 Concluding remarks and further perspectives
We have presented a novel numerical method for solving compliance minimization problems in 3D linearized elasticity setting, over a set of designs obtained by mixing two isotropic materials in prescribed proportions. As such problem typically has no solution we have useed a relaxation by the homogenization method which results with well-posed problem, with cost of introducing the composite materials. The necessary conditions of optimality for relaxed problem state that optimal stiffness tensor saturates the lower Hashin-Shtrikman energy bound on the complementary energy, while the optimal volume fraction minimizes a perturbation of this bound by a linear function in \(\theta \). We have exploited a recent explicit calculation of this bound in 3D elasticity setting (Burazin et al. xxxx), computed its derivative with respect to the volume fraction \(\theta \), and implemented an optimality criteria algorithm for computing approximate optimal design.
We have demonstrated our method on some benchmark examples, namely the cantilever and the bridge problem. Results look reasonable, with symmetries appearing where we anticipated them. Moreover, the convergence seems indifferent to the initial design, behaves well on mesh refinement, and the algorithm provides the solution in a first few iterations. As expected, a true composite materials appear in the optimal design, in form of either a simple or second-order laminate. This is a known feature of the problem that some well established methods like SIMP can not exhibit. However, if one is more interested in classical designs, we have performed a simple penalization procedure which derives it, with some increase in the cost functional.
Finally, the method could be adjusted for some other self-adjoint problems, like the eigenfrequency optimization. Additionally, there are interesting problems, such as when mixing structural and responsive material in order to design structural actuator (Akerson et al. 2022), when objective function can be represented as a function of compliances of different states corresponding to the various stiffnesses of responsive material. In such problems the homogenization method can be used for relaxing the problem and provide numerical solution (Akerson et al. 2022), and we expect that our approach might provide good results in this setting, as well.
References
Akerson A, Bourdin B, Bhattacharya K (2022) Optimal design of responsive structures. Struct Multidiscip Optim 65:111. https://doi.org/10.1007/s00158-022-03200-5
Allaire G (1994) Explicit lamination parameters for three-dimensional shape optimization. Control Cybern 23:309–326
Allaire G (2002) Shape optimization by the homogenization method. Springer, Berlin
Allaire G, Kohn RV (1993) Optimal bounds on the effective behavior of a mixture of two well-ordered elastic materials. Q Appl Math 51(4):643–674
Allaire G, Kohn RV (1993) Explicit optimal bounds on the elastic energy of a two-phase composite in two space dimensions. Q Appl Math 51(4):675–699
Allaire G, Kohn RV (1993) Optimal design for minimum weight and compliance in plane stress using extremal microstructures. Eur J Mech A/Solids 12(6):839–878
Allaire G, Bonnetier E, Francfort G, Jouve F (1997) Shape optimization by the homogenization method. Numer Math 76:27–68
Allaire G, Aubry S, Jouve F (2001) Eigenfrequency optimization in optimal design. Comput Methods Appl Mech Eng 190(28):3565–3579
Allaire G, Geoffroy-Donders P, Pantz O (2019) Topology optimization of modulated and oriented periodic microstructures by the homogenization method. Comput Math Appl 78:2197–2229
Avellaneda M (1987) Optimal bounds and microgeometries for elastic two-phase composites. SIAM J Appl Math 47(6):1216–1228
Bangerth W, Hartmann R, Kanschat G et al (2021) The deal.II library. http://www.dealii.org/
Bendsøe M (1995) Methods for optimization of structural topology, shape and material. Springer, Berlin
Bendsøe M, Diaz A (1994) Optimization of material properties for improved frequency response. Struct Optim 7:138–140
Bendsøe M, Sigmund O (2003) Topology optimization: theory, methods and applications, 2nd edn. Springer, Berlin
Burazin K (2018) On unique solutions of multiple-state optimal design problems on an annulus. J Optim Theory Appl 177:329–344
Burazin K, Crnjac I (2020) Convergence of the optimality criteria method for multiple state optimal design problems. Comput Math Appl 79(5):1382–1392
Burazin K, Vrdoljak M (2019) Exact solutions in optimal design problems for stationary diffusion equation. Acta Appl Math 161(1):71–88
Burazin K, Crnjac I, Vrdoljak M (2018) Variant of optimality criteria method for multiple state optimal design problems. Commun Math Sci 16(6):1597–1614
Burazin K, Crnjac I, Vrdoljak M (2021) Optimality criteria method in 2D linearized elasticity problems. Appl Numer Math 160:192–204
Burazin K, Crnjac I, Vrdoljak M (2023) Explicit Hashin-Shtrikman bounds in 3D linearized elasticity, under review
Casado-Diaz J (2015) Some smoothness results for the optimal design of a two-composite material which minimizes the energy. Calc Var Partial Differ Equ 53:649–673
Casado-Diaz J (2022) The maximization of the first eigenvalue for a two-phase material. Appl Math Optim. https://doi.org/10.1007/s00245-022-09825-8
Casado-Díaz J, Castro C, Luna-Laynez M, Zuazua E (2011) Numerical approximation of a one-dimensional elliptic optimal design problem. Multiscale Model Simul 9:1181–1216
Francfort G, Murat F (1986) Homogenization and optimal bounds in linear elasticity. Arch Rat Mech Anal 94:307–334
Geoffroy-Donders P, Allaire G, Pantz O (2020) 3-d topology optimization of modulated and oriented periodic microstructures by the homogenization method. J Comput Phys 401:108994
Gibianski L, Cherkaev A (1987) Microstructures of composites of extremal rigidity and exact bounds of the associated energy density. Ioffe Physicotechnical Institute preprint
Gibianski L, Cherkaev A (1997) Design of composite plates of extremal rigidity, Ioffe Physicotechnical Institute preprint, 1984 (english translation in: Topics in the mathematical modelling of composite materials, Ser. PNLDE, vol 31, Birkhauser, Basel, 95-137)
Groen JP, Sigmund O (2018) Homogenization based topology optimization for high resolution manufacturable microstructures. Int J Numer Methods Eng 113:1148–1163
Hashin Z, Shtrikman S (1962) A variational approach to the theory of the effective magnetic permeability of multiphase materials. J Appl Phys 33:3125–3131
Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids 11(2):127–140
Kohn RV, Lipton R (1988) Optimal bounds for the effective energy of a mixture of isotropic, incompressible, elastic materials. Arch Rat Mech Anal 102:331–350
Kohn R, Strang G (1986) Optimal design and relaxation of variational problems I–III. Commun Pure Appl Math 39:113–137, 139–182, 353–377
Lurie K (1970) On the optimal distribution of the resistivity tensor of the working substance in a magnetohydrodynamic channel. J Appl Math Mech (Prikladnaya Matematika i Mekhanika) 34(2):255–274 (in Russian)
Lurie K, Cherkaev A (1984) Exact estimates of conductivity of composites formed by two isotropically conducting media, taken in prescribed proportion. Proc R Soc Edinb 99A:71–87
Lurie K, Cherkaev A (1986) Effective characteristics of composite materials and the optimal design of structural elements. Uspekhi Mekhaniki 9:3–81
Lurie K, Cherkaev A, Fedorov A (1982) Regularization of optimal design problems for bars and plates I–II. J Optim Theory Appl 37:499–543
Milton GW (1990) On characterizing the set of possible effective tensors of composites: the variational method and the translation method. Commun Pure Appl Math 43(1):63–125
Milton GW (2002) The theory of composites. Cambridge University Press, Cambridge
Milton GW, Kohn RV (1988) Variational bounds on the effective moduli of anisotropic composites. J Mech Phys Solids 36:597–629
Murat F, Tartar L (1985) Optimality conditions and homogenization. In: Marino A et al (eds) Nonlinear variational problems. Pitman, Boston, pp 1–8
Murat F, Tartar L (1978) H-convergence. In: Séminaire d’Analyse Fonctionnelle et Numérique de l’Université d’Alger. Lecture Notes
Querin O, Victoria M, Alonso C, Loyola R, Montrull P (2017) Topology design methods for structural optimization. Elsevier, Amsterdam
Raitums U (1978) The extension of extremal problems connected with a linear elliptic equation. Sov Math 19:1342–1345
Rozvany G (1989) Structural design and optimality criteria. kluwer Academic Publishers, Alphen aan den Rijn
Save M, Prager W (1985) Structural optimization, volume 1 optimality criteria. In Warner W (ed). Plenum Press, New York
Tartar L (1975) Problèmes de contrôle des coefficients dans des équations aux dérivées partielles. In: Bensoussan A, Lions J-L (eds) Control theory, numerical methods and computer systems modelling, international symposium, Rocquencourt, June 1974. Lecture notes in economy and mathematical systems, vol 107. Springer, Berlin, pp 420–426
Tartar L (1985) Estimations fines des coefficients homogénéisés, Ennio DeGiorgi colloquium (Paris, 1983). In: Krée P (ed) Research notes in mathematics, vol 125. Pitman, London, pp 168–187
Tartar L (1986) Homogenization and effective moduli of materials and media. In: Ericsen JL et al (eds) Remarks on homogenization. Springer, Berlin, pp 228–246
Vrdoljak M (2010) On Hashin–Shtrikman bounds for mixtures of two isotropic materials. Nonlinear Anal Real World Appl 11:4597–4606
Vrdoljak M (2016) Classical optimal design in two-phase conductivity problems. SIAM J Control Optim 54(4):2020–2035
Zhikov V, Kozlov S, Oleinik O (1994) Homogenization of differential operators and integral functionals. Springer, Berlin
Acknowledgements
We would like to thank to Prof. Domagoj Matijević (School of Applied Mathematics and Computer Science, J. J. Strossmayer University of Osijek) who provided us with technical support for execution of parts of the algorithm.
Funding
This work has been supported in part by Croatian Science Foundation under the projects 8904 Homdirestroptcm.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Burazin, K., Crnjac, I. Application of explicit energy bounds in optimization of 3D elastic structures. Optim Eng 25, 1179–1202 (2024). https://doi.org/10.1007/s11081-023-09840-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-023-09840-w




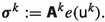
 to be a minimizer in the definition of
to be a minimizer in the definition of 











