Multimaterial Topology Optimization of Variational Inequalities

Abstract

The paper is concerned with the analysis and the numerical solution of the multimaterial topology optimization problems for bodies in unilateral contact. The contact phenomenon with Tresca friction is governed by the elliptic variational inequality. The structural optimization problem consists in finding such topology of the domain occupied by the body that the normal contact stress along the boundary of the body is minimized. The original cost functional is regularized using the multiphase volume constrained Ginzburg-Landau energy functional. The first order necessary optimality condition is formulated. The optimal topology is obtained as the steady state of the phase transition governed by the generalized Allen-Cahn equation. The optimization problem is solved numerically using the operator splitting approach combined with the projection gradient method. Numerical examples are provided and discussed.

1 Introduction

Multimaterial topology optimization aims to find the optimal distribution of several elastic materials in a given design domain to minimize a criterion describing the mechanical or the thermal properties of the structure or its cost under constraints imposed on the volume or the mass of the structure [1]. In recent years multiple phases topology optimization problems have become subject of the growing interest [1, 5, 15]. The use of multiple number of phases during design of engineering structures opens a new opportunities in the design of smart and advanced structures in material science and/or industry. In contrast to single material design the use of multiple number of materials extends the design space and may lead to better design solutions.

Analytical and numerical aspects of the multimaterial structural optimization are subject of intensive research (see references in [1, 15]). Many methods including the homogenization method [2], the Solid Isotropic Material Penalization (SIMP) method [3] or different methods based on the level set approach [8, 11, 12], successful in single material optimization, have been extended to deal with the multimaterial optimization. The extension of these methods faces several challenges. A crucial issue in the solution of the multimaterial optimization problems is the lack of physically based parametrization of the phases mixture [1, 15]. Although in the literature are proposed different material interpolation schemes, in general, they may influence the optimization path in terms of the computational efficiency and the final design. The level set methods can eliminate the need of the material interpolation schemes provided that interphase interfaces are actually tracked explicitly [1]. Among others, in [1] a multimaterial topology optimization problem for the elliptic equation has been solved using the level set method. The elasticity tensor has been smeared out using the signed distance function. In [15] similar optimization problem has been solved numerically using a generalized Allen–Cahn equation.

The paper is concerned with the structural topology optimization of systems governed by the variational inequalities. The class of such systems includes among others unilateral contact phenomenon [9] between the surfaces of the elastic bodies. This optimization problem consists in finding such topology of the domain occupied by the body that the normal contact stress along the boundary of the body is minimized. In literature [11] this problem usually is considered as two-phase material optimization problem with voids treated as one of the materials. In the paper the domain occupied by the body is assumed to consist from several elastic materials rather than two materials. Material fraction function is a variable subject to optimization. The regularization of the objective functional by the multiphase volume constrained Ginzburg-Landau energy functional is used. The derivative formula of the cost functional with respect to the material fraction function is calculated and is employed to formulate a necessary optimality condition for the topology optimization problem. The cost functional derivative is also used to formulate a gradient flow equation for this functional in the form of the generalized Allen–Cahn equation governing the evolution of the material phases. Two step operator splitting approach [15] is used to solve this gradient flow equation. The optimal topology is obtained as a steady state solution to this equation. Finite difference and finite element methods are used as the approximation methods. Numerical examples are reported and discussed.

2 Problem Formulation

Consider deformations of an elastic body occupying two–dimensional bounded domain $\varOmega$ with the smooth boundary $\varGamma$ (see Fig. 1). The body is subject to body forces $f(x)=(f_1(x),$ $f_2(x))$, $x \in \varOmega$. Moreover, the surface tractions $p(x)=(p_1(x),p_2(x))$, $x \in \varGamma$, are applied to a portion $\varGamma _1$ of the boundary $\varGamma$. The body is clamped along the portion $\varGamma _0$ of the boundary $\varGamma$ and the contact conditions are prescribed on the portion $\varGamma _2$. Parts $\varGamma _0$, $\varGamma _1$, $\varGamma _2$ of the boundary $\varGamma$ satisfy: ${\varGamma }_i \cap {\varGamma }_j = \emptyset$, $i\ne j, \; i,j = 0,1,2$, $\varGamma = \bar{\varGamma }_0 \cup \bar{\varGamma }_1 \cup \bar{\varGamma }_2$.

Fig. 1.

Elastic body occupying domain $\varOmega$ in unilateral contact with the foundation.

The domain $\varOmega$ is assumed to be occupied by $s \ge 2$ distinct isotropic elastic materials. Each material is characterized by Young modulus. The voids are considered as one of the phases, i.e., as a weak material characterized by low value of Young modulus [2]. The materials distribution is described by a phase field vector $\rho =\{ \rho _m \}_{m=1}^s$ where the local fraction field $\rho _m=\rho _m(x): \varOmega \rightarrow R$, $m=1,...,s$, corresponds to the contributing phase. The phase field approach allows for a certain mixing between different materials. This mixing is restricted only to a small interfacial region. In order to ensure that the phase field vector describes the fractions the following pointwise bound constraints called in material science the Gibbs simplex [5, 15] are imposed on every $\rho _m$

$$\begin{aligned} \alpha _m \le \rho _m \le \beta _m, \; \text{ for } \; m=1,...,s, \; \; \text{ and } \; \; \sum _{m=1}^s \rho _m = 1, \end{aligned}$$

(1)

where the constants $0 \le \alpha _m \le \beta _m \le 1$ are given and the summation operator is understood componentwise. The second condition in (1) ensures that no overlap and gap of fractions are allowed in the expected optimal domain. Moreover the total spatial amount of material fractions satisfies

$$\begin{aligned} \int _\varOmega \rho _m(x) dx = w_m \mid \varOmega \mid , \; \; 0 \le w_m \le 1, \; \text{ for } \; m=1,...,s, \; \; \text{ and } \; \; \sum _{m=1}^s w_m=1. \end{aligned}$$

(2)

The parameters $w_m$ are user defined and $\mid \varOmega \mid$ denotes the volume of the domain $\varOmega$. From the equality (1) it results that $\rho _s=1-\sum _{m=1}^{s-1} \rho _m$ and the fraction $\rho _s$ may be removed from the set of the design functions. Therefore from now on the unknown phase field vector $\rho$ is redefined as $\rho =\{ \rho _m \}_{m=1}^{s-1}$. Due to the simplicity and robustness the SIMP material interpolation model [3, 4] is used. Following this model the elastic tensor $\mathcal{A}(\rho )=\{ a_{ijkl}(\rho ) \}_{i,j,k,l=1}^2$ of the material body is assumed to be a function depending on the fraction function $\rho$:

$$\begin{aligned} \mathcal{A}(\rho ) =\sum _{m=1}^s g(\rho _m) \mathcal{A}_m = \sum _{m=1}^{s-1} g(\rho _m)\mathcal{A}_m+g(1-\sum _{m=1}^{s-1} \rho _m)\mathcal{A}_s, \end{aligned}$$

(3)

with $g(\rho _m)=\rho _m^3$. The constant stiffness tensor $\mathcal{A}_m=\{\tilde{a}_{ijkl}^m \}_{i,j,k,l=1}^2$ characterizes the m-th elastic material of the body. For detailed discussion of the interpolation of the material elasticity tensor see [1, 4, 7]. It is assumed, that elements $a_{ijkl}$ and $\tilde{a}_{ijkl}^m(x)$, $i,j,k,l=1,2$, $m=1,...,s$, of the elasticity tensors $\mathcal{A}$ and $\mathcal{A}_m$, respectively, satisfy [9] usual symmetry, boundedness and ellipticity conditions. Denote by $u=(u_1,u_2)$, $u=u(x)$, $x \in \varOmega$, the displacement of the body and by $\sigma (x) = \{ \sigma _{ij} (u(x)) \}$, $i,j = 1,2$, the stress field in the body. Consider elastic bodies obeying Hooke’s law, i.e., for $x \in \varOmega$ and $i,j,k,l=1,2$,

$$\begin{aligned} \sigma _{ij} (u(x)) = a_{ijkl}(\rho ) e_{kl}(u(x)), \; \; \; e_{kl}(u(x)) \mathop {=}\limits ^{def} \frac{1}{2}(u_{k,l}(x) + u_{l,k}(x)), \end{aligned}$$

(4)

where $u_{k,l}(x) = \frac{\partial u_k(x)}{\partial x_l}$. We use here and throughout the paper the summation convention over repeated indices [9]. The stress field $\sigma$ satisfies the system of equations in the domain $\varOmega$ [9]

$$\begin{aligned} - \sigma _{ij}(x)_{,j} = f_i(x) \; \; \; \sigma _{ij}(x)_{,j} = \frac{\partial \sigma _{ij}(x)}{\partial x_j}, \; \; \; x \in \varOmega , \; i,j =1,2. \end{aligned}$$

(5)

The following boundary conditions are imposed on the boundary $\partial \varOmega$

$$\begin{aligned} u_i(x) = 0 \; \; \text{ on } \; \; \varGamma _0, \; \; \; \sigma _{ij}(x)n_j = p_i \; \; \text{ on } \; \; \varGamma _1, \; \; i,j=1,2, \end{aligned}$$

(6)

$$\begin{aligned} (u_{N}+v) \le 0, \; \; \sigma _N \le 0, \; \; (u_{N}+v)\sigma _N = 0 \; \; \text{ on } \varGamma _2, \end{aligned}$$

(7)

$$\begin{aligned} \mid \sigma _T \mid \le 1 , \; \; \; u_{T} \sigma _T + \mid u_{T} \mid = 0 \; \text{ on } \varGamma _2 , \end{aligned}$$

(8)

where $n=(n_1,n_2)$ is the unit outward versor to the boundary $\varGamma$. Here $u_N = u_in_i$ and $\sigma _N = \sigma _{ij}n_in_j$, $i,j=1,2$, represent [9] the normal components of displacement u and stress $\sigma$, respectively. The tangential components of displacement u and stress $\sigma$ are given [9] by $(u_T )_i = u_i - u_Nn_i$ and $(\sigma _T)_i = \sigma _{ij}n_j - \sigma _Nn_i$, $i,j = 1,2$, respectively. $\mid u_T \mid$ denotes the Euclidean norm in $R^2$ of the tangent vector $u_T$. A gap between the bodies is described by a given function v.

Let us formulate contact problem (5)–(8) in the variational form. Denote by $V_{sp}=\{ z \in H^1(\varOmega ; R^2) \; : \; z_i = 0 \; \text{ on } \varGamma _0, \; i= 1,2 \}$ and $K=\{ z\in V_{sp} \; : \; z_N +v \le 0 \; \; \text{ on } \; \; \varGamma _2 \}$ the space and the set of kinematically admissible displacements and by $\varLambda =\{ \zeta \in L^2(\varGamma _2; R^2) \; : \; \mid \zeta \mid \; \le 1 \}$ the set of tangential tractions on $\varGamma _2$. Variational formulation of problem (5)–(8) has the form: for a given $(f,p,\rho ) \in$ $L^2(\varOmega ;R^2) \times L^2(\varGamma _2;R^2) \times L^\infty (\varOmega ; R^{s-1})\cap H^1(\varOmega ; R^{s-1})$ find a pair $(u,\lambda ) \in K \times \varLambda$ satisfying for $i,j,k,l=1,2$

$$\begin{aligned} \int _\varOmega a_{ijkl}(\rho )e_{ij}(u)e_{kl}(\varphi _i - u_i) dx - \int _{\varOmega } f_i (\varphi _i-u_i)dx - \nonumber \\ \int _{\varGamma _1} p_i (\varphi _i -u_i)ds + \int _{\varGamma _2} \lambda _i (\varphi _{Ti} - u_{Ti}) ds \ge 0 \; \; \forall \varphi _i \in K, \end{aligned}$$

(9)

$$\begin{aligned} \int _{\varGamma _2} (\zeta _i - \lambda _i) u_{Ti} ds \le 0 \; \; \; \forall \zeta _i \in \varLambda . \end{aligned}$$

(10)

The function $\lambda$ is interpreted as a Lagrange multiplier corresponding to the term $\mid u_T \mid$ in equality constraint in (8) [9]. This function is equal to tangent stress along the boundary $\varGamma _2$, i.e., $\lambda = -\sigma _{T_{\mid \varGamma _2}}$ and belongs to space $H^{-1/2}(\varGamma _2;R^2)$. Here following [9] function $\lambda$ is assumed to be more regular, i.e., $\lambda \in L^2(\varGamma _2;R^2)$. Recall from [9, 14] under assumptions imposed on the elasticity tensors by standard arguments for a given $(f,p,\rho ) \in$ $L^2(\varOmega ;R^2) \times L^2(\varGamma _2;R^2) \times L^\infty (\varOmega ; R^{s-1})$ there exists a unique solution $(u, \lambda ) \in K \times \varLambda$ to the system (9)–(10).

3 Phase Field Based Topology Optimization Problem

Before formulating a structural optimization problem for the system (9)–(10) let us introduce a set $U_{ad}^\rho$ of the admissible fraction functions:

$$\begin{aligned} U_{ad}^\rho = \{ \rho \in L^\infty (\varOmega ; R^{s-1}) \cap H^1(\varOmega ; R^{s-1}): 1-\beta _s \le \sum _{m=1}^{s-1} \rho _m \le 1-\alpha _s, \; \; \nonumber \\ \alpha _m \le \rho _m \le \beta _m, \; \; \int _\varOmega \rho _m dx= w_m \mid \varOmega \mid \; \; \text{ for } \; \; m=1,...,s-1 \}. \end{aligned}$$

(11)

The set $U_{ad}^\rho$ is assumed to be nonempty. The aim of the structural optimization of the bodies in contact is to reduce the normal contact stress responsible for wear, vibrations of the contacting surfaces or generated noise. The structural optimization problem with normal contact stress functional is difficult to analyze it and to solve it numerically. Therefore following [11] we shall use the cost functional $J_\eta : H^1(\varOmega ) \rightarrow R$ approximating the normal contact stress on the contact boundary $\varGamma _2$

$$\begin{aligned} J_\eta (u(\rho )) = \int _{\varGamma _2} \sigma _N(u(\rho )) \eta _{N}(x) ds, \end{aligned}$$

(12)

depending on a given auxiliary bounded function $\eta (x) \in M^{st}$. The set $M^{st}=\{ \eta =(\eta _1,\eta _2) \in H^1(\varOmega ; R^2): \eta _i \le 0 \; \; \text{ on } \varOmega , \; i=1,2, \; \; \; \parallel \eta \parallel _{H^1(\varOmega ;R^2)} \; \le \; 1 \}$. Functions $\sigma _N$ and $\eta _N$ are the normal components of the stress field $\sigma$ and the function $\eta$, respectively. The optimization problem consisting in finding such $\rho \in U_{ad}^\rho$ to minimize the functional $J_\eta (u(\rho ))$ in general has no solutions [2, 6, 7, 9, 14, 15]. In order to ensure the existence of optimal solutions let us regularize the cost functional (12) by adding to it a regularizing term $E(\rho ): U_{ad}^\rho \rightarrow R$ rather than the standard perimeter term [2, 7, 14]

$$\begin{aligned} J(\rho ,u(\rho )) = J_\eta (u(\rho )) + E(\rho ). \end{aligned}$$

(13)

The Ginzburg-Landau free energy functional $E(\rho )$ is expressed as [7, 15]

$$\begin{aligned} E(\rho ) = \sum _{m=1}^{s-1} \int _\varOmega \psi (\rho _m)d\varOmega , \; \; \; \psi (\rho _m) = \frac{\gamma \epsilon }{2} \mid \nabla \rho _m \mid ^2 + \frac{\gamma }{\epsilon } \psi _B(\rho _m), \end{aligned}$$

(14)

where $\epsilon >0$ is a real constant governing the width of the intrefaces, $\gamma >0$ is a real parameter related to the interfacial energy density. Moreover $\nabla \rho _m \cdot n=0$ on $\varGamma$ for each m. The function $\psi _B(\rho _m)=\rho _m^2(1-\rho _m)^2$ is a double-well potential [7] which characterizes the concentration of the material phases [15]. The structural optimization problem for the system (9)–(10) takes the form: find $\rho ^\star \in U_{ad}^\rho$ such that

$$\begin{aligned} J(\rho ^\star , u^\star ) = \min _{\rho \in U_{ad}^\rho } J(\rho , u(\rho )), \end{aligned}$$

(15)

where $u^\star = u(\rho ^\star )$ denotes a solution to the state system (9)–(10) depending on $\rho ^\star \in L^\infty (\varOmega ; R^{s-1}) \cap H^1(\varOmega ; R^{s-1})$ and the set $U_{ad}^\rho$ is given by (11). The existence of an optimal solution $\rho ^\star \in U_{ad}^\rho$ to the problem (15) follows by classical arguments (see [5, 6, 14]).

4 Necessary Optimality Condition

Let us apply the Lagrangian approach to compute the derivative of the cost functional (13) with respect to the function $\rho$. The Lagrangian $L(\rho )= L(\rho , u, \lambda , p^a,$ $q^a): L^\infty (\varOmega ;R^{s-1}) \cap H^1(\varOmega ;R^{s-1}) \cap U_{ad}^\rho \times H^1(\varOmega ; R^2) \times L^2(\varGamma _2; R^2) \times K_1 \times \varLambda _1$ associated to the problem (15) is expressed for $i,j,k,l=1,2$ as

$$\begin{aligned} L(\rho , u, \lambda , p^a, q^a) = J_\eta (u(\rho )) + E(\rho ) + \int _\varOmega a_{ijkl}(\rho ) e_{ij}(u) e_{kl}(p^a) dx - \nonumber \\ \int _{\varOmega } f_i p^a_i dx - \int _{\varGamma _1} p_i p^a_i ds + \int _{\varGamma _2} \lambda _i p^a_{Ti} ds + \int _{\varGamma _2} q^a_i u_{Ti} ds. \end{aligned}$$

(16)

Using the same approach as in proof of [14, Theorem 4.35, p. 219] an adjoint state $(p^a,q^a) \in K_1 \times \varLambda _1$ for $i,j,k,l=1,2$ is defined as the solution to the system

$$\begin{aligned} \int _{\varOmega } a_{ijkl}(\rho ) e_{ij}( \eta + p^{a})e_{kl}(\varphi ) dx + \int _{\varGamma _2} q^{a}_i \varphi _{Ti} ds = 0 \; \; \; \forall \varphi _i \in K_{1}, \; \end{aligned}$$

(17)

$$\begin{aligned} \int _{\varGamma _2} \zeta _i (p^{a}_{Ti } + \eta _{Ti}) ds = 0 \; \; \forall \zeta _i \in \varLambda _1. \end{aligned}$$

(18)

The sets $K_{1}$ and $\varLambda _1$ are given by $K_{1} = \{ \xi \in V_{sp} \; : \; \xi _N = 0 \; \text{ on } A^{st}{} \}$ as well as $\varLambda _1 = \{ \zeta \in \varLambda \; : \; \zeta (x) = 0 \text{ on } B_1 \cup B_2 \cup B_1^+ \cup B^+_2 \}$, while the coincidence set $A^{st} = \{ x \in \varGamma _2 \; : \; u_N +v = 0 \}$. Moreover the other sets are determined as $B_1=\{ x \in \varGamma _2 : \lambda (x)=-1\}$, $B_2=\{ x \in \varGamma _2 : \lambda (x)=+1\}$, $\tilde{B}_i=\{ x \in B_i: u_N(x)+ v =0 \}$, $i=1,2$, $B_i^+=B_i\setminus \tilde{B}_i$, $i=1,2$. From [12], [14, Theorems 4.16, 4.27] it follows the mapping $\rho \rightarrow u(\rho )$ is Gâteaux differentiable. Using (9)–(10) and (16)–(18) the derivative of the Lagrangian L with respect to $\rho$ is determined for all $\zeta \in H^1(\varOmega ;R^{s-1} )$ and $i,j,k,l=1,2$ as

$$\begin{aligned} \int _\varOmega \frac{\partial J}{\partial \rho }(\rho ,u) \zeta dx = \int _\varOmega \frac{\partial L}{\partial \rho }(\rho , u, \lambda , p^a, q^a)\zeta dx = \sum _{m=1}^{s-1} \int _\varOmega [ \gamma \epsilon \nabla \rho _m \cdot \nabla \zeta _m + \nonumber \\ \frac{\gamma }{\epsilon } \psi ^\prime _B(\rho _m) \zeta _m ]dx + \int _\varOmega [a_{ijkl}^\prime (\rho _m) e_{ij}(u) e_{kl} (p^a + \eta ) - f_i(p^a_i + \eta _i)] \zeta _m dx. \end{aligned}$$

(19)

From (1) and (3) it results the derivatives of the function $\psi _B(\rho _m)$ and the tensor element $a_{ijkl}(\rho _m)$ with respect to $\rho _m$ are equal to $\psi ^\prime _B(\rho _m)=4\rho _m^3-6\rho _m^2+2\rho _m$ and $a_{ijkl}^\prime (\rho )=3\rho _m^2\tilde{a}^m_{ijkl}-3\rho _s^2 \tilde{a}^s_{ijkl}$, respectively. Using (19) the necessary optimality condition to the optimization problem (15) takes the form [2], [13, Lemma 2.21]:

Theorem 1

Let $U_{ad}^\rho$ be a nonempty closed convex subset of $H^1(\varOmega ;R^{s-1})$ and $\rho ^\star \in U_{ad}^\rho$ be an optimal solution to the structural optimization problem (15). Then

$$\begin{aligned} \int _\varOmega \frac{\partial J}{\partial \rho }(\rho ^\star ,u^\star ) (\rho - \rho ^\star )dx \ge 0 \; \; \; \forall \rho \in U_{ad}^\rho . \end{aligned}$$

(20)

The functions $(u^\star , \lambda ^\star ) \in K \times \varLambda$ and $(p^{a\star }, q^{a\star }) \in K_1 \times \varLambda _1$ in the derivative formula (19) denote the solutions to the systems (9)–(10) and (17)–(18) for $\rho =\rho ^\star$.

Using the orthogonal projection operator $P_{U_{ad}^\rho }: L^2(\varOmega ;R^{s-1}) \rightarrow U_{ad}^\rho$ from $L^2(\varOmega ;R^{s-1})$ on the set $U_{ad}^\rho$ condition (20) can be written [15] in the form: if $\rho ^\star \in U_{ad}^\rho$ is an optimal solution to the structural optimization problem (15), then for $\mu \in R$ and $\mu >0$

$$\begin{aligned} P_{U_{ad}^\rho }[\rho ^\star - \mu \frac{\partial J(\rho ^\star , u^\star )}{\partial \rho }] - \rho ^\star =0. \end{aligned}$$

(21)

Recall [7] the structural optimization problem (15) can be considered as a phase transition setting problem consisting in such evolution of the phases to minimize the cost functional (13) with respect to the initial configuration. In order to describe the evolution of phases in time let us assume that the phase field vector $\rho$ depends not only on $x\in \varOmega$ but also on time variable $t \in [0,T]$, $T>0$ is a given constant, i.e., $\rho =\rho (x,t)=\{ \rho _m(x,t)\}_{m=1}^{s-1}$. The variable t may be interpreted as an artificial time or iteration number in the computational algorithm [7, 15]. Using the right hand side of (21) let us formulate the constrained gradient flow equation of Allen-Cahn type [5, 7, 15] for the cost functional (13): find function $\rho \in U_{ad}^\rho$ satisfying the initial boundary value problem:

$$\begin{aligned}&\frac{\partial \rho }{\partial t} = -P_{U_{ad}^\rho }[{\rho } - \mu \frac{\partial J(\rho ,u)}{\partial \rho }] + {\rho } \; \;&\text{ in } \; \; \varOmega , \; \forall t \in [0,T), \end{aligned}$$

(22)

$$\begin{aligned}&\nabla \rho \cdot n =0 \; \;&\text{ on } \; \; \partial \varOmega , \; \forall t \in [0,T), \end{aligned}$$

(23)

$$\begin{aligned}&\rho (0,x) = \rho _{0}(x) \; \;&\text{ in } \; \; \varOmega , \; t=0, \end{aligned}$$

(24)

with $\rho _0(x)= \{ \rho _{0m}(x)\}_{m=1}^{s-1}$ denoting a given $H^1(\varOmega ;R^{s-1})$ regular function. For $\rho _0 \in H^1(\varOmega ; R^{s-1})$ the system (22)–(24) possesses a solution $\rho \in L^\infty (0,T;H^1(\varOmega ))$ $\cap H^1(0,T;L^2(\varOmega ; R^{s-1}))$ (see [10]). The stationary solutions of (22)–(24) fulfill the first order necessary optimality conditions (20) or (21) for the problem (15) [5, 7]. For $\frac{\partial \rho }{\partial t}= 0$ the right hand side of the Eq. (22) vanishes and $\rho (x,t)=\rho ^\star (x,t)$ is an optimal solution to the problem (15).

For the sake of numerical calculations we reformulate the initial boundary value problem (22)–(24) using the operator splitting approach [5, 15]. Remark, the cost functional (13) may be represented as a sum of two functionals, i.e., $J(\rho , u) = J_1(\rho ,u) + J_2(\rho )$ given by $J_1(\rho ,u)=J_\eta (u(\rho )) + \sum _{m=1}^{s-1} \int _\varOmega \frac{\gamma }{\epsilon } \psi _B(\rho _m)d\varOmega$ and $J_2(\rho ) = \sum _{m=1}^{s-1}\int _\varOmega \frac{\gamma \epsilon }{2} \mid \nabla \rho _m \mid ^2 d\varOmega$. The derivatives of these functionals result from formula (19). Assume the time interval [0, T] is divided into N subintervals with stepsize $\varDelta t=t_{k+1}-t_k$, $k=1,...,N$ and $\rho _k=\rho (t_k)$ is known. The design variable $\rho _{k+1}$ at the next time step $t_{k+1}$ is calculated in two substeps. First the trial value $\tilde{\rho }$ is calculated from the gradient flow Eq. (22) for the functional $J_1$ only. Next this solution is updated to ensure its $H^1(\varOmega )$ regularity [5] by solving the gradient flow Eq. (22) for the functional $J_2$ only with the boundary condition (23), i.e.,

$$\begin{aligned} \frac{\partial \tilde{\rho }}{dt} = -P_{U_{ad}^\rho }[\tilde{\rho } - \frac{\partial J_1(\tilde{\rho },u)}{\partial \rho }] + \tilde{\rho } , \; \; \tilde{\rho }(t_k)=\rho _k, \; \; t_k < t \le t_{k+1}. \end{aligned}$$

(25)

$$\begin{aligned} \frac{\partial \rho }{dt} = - \frac{\partial J_2(\rho )}{\partial \rho }, \; \; \rho (t_k) = \tilde{\rho }_{k+1}, \; \; t_k < t \le t_{k+1}. \end{aligned}$$

(26)

5 Numerical Results

The topology optimization problem (15) has been discretized and solved numerically. Time derivatives are approximated by the forward finite difference. Piecewise constant and piecewise linear finite element method is used as discretization method in space variables. The derivative of the double well potential is linearized with respect to $\rho _m$. Primal-dual active set method has been used to solve the state and adjoint systems (5)–(8) and (17)–(18). The initial boundary value problem (22)–(24) has been solved in two steps according to scheme (25)–(26). The algorithms are programmed in Matlab environment. As an example a body occupying 2D domain

$$\begin{aligned} \varOmega = \{ (x_1,x_2) \in R^2 : 0 \le x_1 \le 8 \; \wedge \; 0 < v(x_1) \le x_2 \le 4 \}, \end{aligned}$$

(27)

is considered. The boundary $\varGamma$ of the domain $\varOmega$ is divided into three disjoint pieces $\varGamma _0 = \{(x_1,x_2) \in R^2 : x_1=0, 8 \; \wedge \; 0 < v(x_1) \le x_2 \le 4 \}$, $\varGamma _1 = \{ ( x_1 ,x_2 ) \in R^2 : 0 \le x_1 \le 8 \; \wedge \; x_2 = 4 \}$, $\varGamma _2 = \{ (x_1,x_2) \in R^2 : 0 \le x_1 \le 8 \; \wedge \; v(x_1) = x_2 \}$. The domain $\varOmega$ and the boundary $\varGamma _2$ depend on the function $v(x_1)=0.125\cdot (x_1-4)^2$. Domain $\varOmega$ is filled with $s=3$ elastic materials. The Poisson’s ratio of each material is $\nu =.3$. The Young’s moduli of materials are: $E_1=6\cdot E_0$, $E_2=3\cdot E_0$ and $E_3=E_0$, $E_0=2.1 \cdot 10^{11}$ Pa. The parameters $w_1$, $w_2$, $w_3$ are equal to .25, .5 and .25 respectively. As an initial design $\rho _0$ a feasible design with the uniform material distribution has been taken. The body is loaded by the boundary traction $p_1=0$, $p_2 = -5.6\cdot 10^6$ N along the boundary $\varGamma _1$, the body forces $f_i=0$, $i=1,2$. The auxiliary function $\eta$ is selected as a piecewise linear on $\varOmega$ and is approximated by a piecewise linear function. The domain $\varOmega$ is divided into 80 $\times$ 40 grid. The parameters $\varepsilon$ and $\gamma$ are equal to the mesh size and to 0.5, respectively. The total number of iterations $k_{max}$ in the optimization algorithm has been set to 90. It is approximately equivalent to final time $T=125$ s.

Fig. 2.

Optimal material distribution in domain $\varOmega ^\star$.

Fig. 3.

Initial and optimal normal contact stress.

Fig. 4.

Convergence of the cost functional value.

Fig. 5.

Convergence of the cost functional gradient.

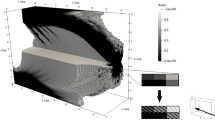
Figure 2 presents the optimal topology domain obtained by solving structural optimization problem (15) using the necessary optimality condition (22)–(24). The areas with the weak phases appear in the central part of the body and near the fixed edges. The areas with the strong phases appear close to the contact zone and along the edges. The rest of the domain is covered with the intermediate phase. The obtained normal contact stress for the optimal topology is almost constant along the contact boundary and has been significantly reduced comparing to the initial one (see Fig. 3). The convergence of the cost functional value and its gradient as a function of the number of iterations are shown on Figs. 4 and 5, respectively. The cost functional value decreases almost monotonically when the number of iterations increases. At the beginning this decrease is significant and finally the cost functional value is almost steady. The regularized functional value at first is increasing and next rapidly decreasing (see Fig. 4). Similarly, after a few initial iterations the gradient of the cost functional also almost monotonically decreases to reach the steady state (Fig. 5).

6 Conclusions

The topology optimization problem for elastic contact problem with Tresca friction has been solved numerically in the paper. Obtained numerical results indicate that the optimal topologies are qualitatively comparable to the results reported in other phase-field topology optimization methods. Since the optimization problem is non-convex it has possibly many local solutions dependent on initial estimate. Gradient flow method employed in $H^1$ space is more regular and efficient than standard Allen-Cahn approach.