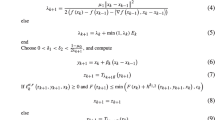Abstract
In this paper, for solving a broad class of large-scale nonconvex and nonsmooth optimization problems, we propose a stochastic two-step inertial Bregman proximal alternating linearized minimization (STiBPALM) algorithm with variance-reduced stochastic gradient estimators. And we show that SAGA and SARAH are variance-reduced gradient estimators. Under expectation conditions with the Kurdyka–Łojasiewicz property and some suitable conditions on the parameters, we obtain that the sequence generated by the proposed algorithm converges to a critical point. And the general convergence rate is also provided. Numerical experiments on sparse nonnegative matrix factorization and blind image-deblurring are presented to demonstrate the performance of the proposed algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we are interested in solving the following composite optimization problem:
where \(f:\mathbb {R}^l\rightarrow {(-\infty ,+\infty ]}\) and \(g:\mathbb {R}^m\rightarrow {(-\infty ,+\infty ]}\) are proper lower semicontinuous. \(H(x,y)=\frac{1}{n} \sum _{i=1}^{n} H_i(x,y)\) has a finite-sum structure, \(H_i:\mathbb {R}^l\times \mathbb {R}^m \rightarrow \mathbb {R}\) is continuously differentiable, and \(\nabla H_i\) is Lipschitz continuous on bounded subsets. Note that here and throughout the paper, no convexity is imposed on \(\Phi \). In practical application, numerous problems can be formulated into the form of (1.1), such as signal and image processing [1, 2], nonnegative matrix factorization [3,4,5], blind image-deblurring [5, 6], sparse principal component analysis [7, 8], and compressed sensing [9, 10]. Here, we list two applications of (1.1), which will also be used in the numerical experiments.
(1) Sparse nonnegative matrix factorization (S-NMF). The S-NMF has important applications in image processing (face recognition) and bioinformatics (clustering of gene expressions) (see [4] for details). Given a matrix \(A\in \mathbb {R} ^{ l\times m}\) and an integer \(r>0\), we want to seek a factorization \(A \approx XY\), where \(X \in \mathbb {R} ^{ l\times r}\) and \(Y \in \mathbb {R} ^{r\times m}\) are nonnegative with \(r \le \min \left\{ l,m\right\} \) and X is sparse. One way to solve this problem is by finding a solution for the nonnegative least squares model given by
where \(\eta >0\), \(X_i\) denotes the ith column of X, and \(\left\| X_i \right\| _0\) denotes the number of nonzero elements of the ith column of X. In this formulation, the sparsity on X is strictly enforced using the nonconvex \(l_ 0\) constraint. Let \(H(X,Y)=\frac{\eta }{2}\left\| A-XY \right\| _{F}^{2}=\sum _{i=1}^l\frac{\eta }{2}\left\| A_i-X_iY \right\| _{F}^{2}\), \(f(X)=\iota _{X\ge 0}(X)+\iota _{\left\| X_1\right\| _0\ge s}(X)+\cdots +\iota _{\left\| X_r \right\| _0\ge s}(X)\), \(g(Y)=\iota _{Y\ge 0}(Y)\), where \(A_i\) denotes the ith low of A, and \(\iota _C\) is the indicator function on C. Then, this model (1.2) can be converted to (1.1).
(2) Blind image deconvolution (BID). Let A be the observed blurred image, and let X be the unknown sharp image of the same size. Furthermore, let Y denote a small unknown blur kernel, and a typical variational formulation of the blind deconvolution problem is given by the following:
where \(\eta >0\), \(\odot \) is the two-dimensional convolution operator, X is the image to recover, and Y is the blur kernel to estimate. Here, \(R(\cdot )\) is an image regularization term, that imposes sparsity on the image gradient and hence favors sharp images. \(D(\cdot )\) is the differential operator, computing the horizontal and vertical gradients for each pixel. This model (1.3) can be converted to (1.1), where \(H(X,Y)=\frac{1}{2}\left\| A-X\odot Y \right\| _{F}^{2}+\eta \sum _{r=1}^{2d} R([D(X)]_r)\), \(f(X)=\iota _{0\le X\le 1}(X)\), \(g(Y)=\iota _{\left\| Y \right\| _1\le 1}(Y)+\iota _{0\le Y\le 1}(Y)\). See [6] for details.
For solving problem (1.1), a frequently applied algorithm is the following proximal alternating linearized minimization algorithm (PALM) by Bolte et al. [11] based on results in [12, 13]:
where \(\{\lambda _k\}_{k\in \mathbb {N}}\) and \(\{\mu _k\}_{k\in \mathbb {N}}\) are positive sequences. To further improve the performance of PALM, Pock and Sabach [6] introduced an inertial step to PALM and proposed the following inertial proximal alternating linearized minimization (iPALM) algorithm:
where \(\alpha _{1k},\alpha _{2k},\beta _{1k},\beta _{2k}\in \left[ 0,1 \right] \). Then, Gao et al. [14] presented a Gauss–Seidel type inertial proximal alternating linearized minimization (GiPALM) algorithm, in which the inertial step is performed whenever the x or y-subproblem is updated. In order to use the existing information as much as possible to further improve the numerical performance, Wang et al. [15] proposed a new inertial version of proximal alternating linearized minimization (NiPALM) algorithm, which inherits both advantages of iPALM and GiPALM.
The Bregman distance regularization is an effective way to improve the numerical results of the algorithm. In [16], the authors constructed the following two-step inertial Bregman alternating minimization (TiBAM) algorithm using the information of the previous three iterates:
where \(D_{\phi _i}(i=1,2)\) denotes the Bregman distance with respect to \(\phi _i(i=1,2)\). By linearizing H(x, y) in TiBAM algorithm, the authors [17] proposed the following two-step inertial Bregman proximal alternating linearized minimization (TiBPALM) algorithm:
If we take \(\phi _1(x)=\frac{1}{2\lambda }\Vert x\Vert ^2_2\) and \(\phi _2(y)=\frac{1}{2\mu }\Vert y\Vert ^2_2\) for all \(x\in \mathbb {R}^l\) and \(y\in \mathbb {R}^m\), then (1.7) becomes two-step inertial proximal alternating linearized minimization (TiPALM) algorithm. Then, based on alternating minimization algorithm, Chao et al. [18] proposed inertial alternating minimization with the Bregman distance (BIAM) algorithm. Other related work can be found in [19, 20] and their references.
It should be noted that all these works are obtained for deterministic methods, i.e., no randomness involved. But when the dimension of data is very large, the computing cost of the full gradient of the function H(x, y) is often prohibitively expensive. In order to overcome this difficulty, stochastic gradient approximations were applied (see, e.g., [21] and the references therein). A block stochastic gradient iteration combining a simple stochastic gradient descent (SGD) estimator with PALM was first proposed by Xu and Yin [22]. To weaken the assumptions on the objective function in [22] and improve the estimates on the convergence rate of a stochastic PALM algorithm, Driggs et al. [23] used more sophisticated so-called variance-reduced gradient estimators instead of the simple stochastic gradient descent estimators and proposed the following stochastic proximal alternating linearized minimization (SPRING) algorithm:
The key of SPRING algorithm is replacing the full gradient computations \(\nabla _x H(x_k,y_k)\) and \(\nabla _yH(x_{k+1},y_k)\) with stochastic estimations \(\widetilde{\nabla }_x(x_k,y_k)\) and \(\widetilde{\nabla }_y(x_{k+1},y_k)\), respectively. Then, Hertrich et al. [24] introduced the following inertial variant of a stochastic PALM algorithm with a variance-reduced gradient estimator, called SiPALM:
where \(\alpha _{1k},\alpha _{2k},\beta _{1k},\beta _{2k}\in \left[ 0,1 \right] \). Also, some variance-reduced gradient estimators are proposed to solve the nonconvex optimization problem. The classical stochastic gradient direction is modified in various ways so as to drive the variance of the gradient estimator towards zero, such as SAG [25], SVRG [26, 27], SAGA [28], and SARAH [29, 30].
In this paper, we combine the inertial technique, Bregman distance, and stochastic gradient estimators to develop a stochastic two-step inertial Bregman proximal alternating linearized minimization (STiBPALM) algorithm to solve the nonconvex optimization problem (1.1). Our contributions are listed as follows:
- (1):
-
We propose the STiBPALM algorithm with variance-reduced stochastic gradient estimators to solve the nonconvex optimization problem (1.1). And we show that SAGA and SARAH are variance-reduced gradient estimators (Definition 3.4) in the appendix.
- (2):
-
We provide theoretical analysis to show that the proposed algorithm with the variance-reduced stochastic gradient estimator has global convergence under expectation conditions. Under the expectation version of Kurdyka–Łojasiewicz (KŁ) property, the sequence generated by the proposed algorithm converges to a critical point and the general convergence rate is also obtained.
- (3):
-
We use several well-studied stochastic gradient estimators (e.g., SGD, SAGA, and SARAH) to test the performance of STiBPALM for sparse nonnegative matrix factorization and blind image-deblurring problems. And compared with some existing algorithms (e.g., PALM, iPALM, SPRING, and SiPALM) in the literature, we report some preliminary numerical results to demonstrate the effectiveness of the proposed algorithm.
This paper is organized as follows. In Sect. 2, we recall some concepts and important lemmas which will be used in the proof of main results. Section 3 introduces our STiBPALM algorithm in detail. We discuss the convergence behavior of STiBPALM in Sect. 4. In Sect. 5, we perform some numerical experiments and compare the results with other algorithms. We give the specific theoretical analysis to show that SAGA and SARAH have variance-reduced stochastic gradient estimators in the appendix.
2 Preliminaries
In this section, we summarize some useful definitions and lemmas.
Definition 2.1
Let \(F: \mathbb {R}^d \rightarrow (-\infty ,+\infty ]\) be a proper and lower semicontinuous function. For \(x\in \) domF, the Fréchet subdifferential of F at x, written \(\hat{\partial }F(x)\), is the set of vectors \(v\in \mathbb {R}^d\) which satisfy
If \(x\not \in \) domF, then \(\hat{\partial }F(x)=\emptyset \). The limiting-subdifferential, or simply the subdifferential for short, of F at \(x\in \) domF, written \(\partial F(x)\), is defined as follows:
Remark 2.1
-
(a)
The above definition implies that \(\hat{\partial }F(x)\subseteq \partial F(x)\) for each \(x\in \mathbb {R}^d\), where the first set is convex and closed while the second one is closed. (see [31]).
-
(b)
(Closedness of \(\partial F\)) Let \(\{x_k\}_{k\in \mathbb {N}}\) and \(\{v_k\}_{k\in \mathbb {N}}\) be sequences in \(\mathbb {R}^d\) such that \(v_k \in \partial F(x_k)\) for all \(k\in \mathbb {N}\). If \((x_k,v_k)\rightarrow (x,v)\) and \(F(x_k)\rightarrow F(x)\) as \(k\rightarrow \infty \), then \(v \in \partial F (x)\).
-
(c)
If \(F: \mathbb {R}^d \rightarrow (-\infty ,+\infty ]\) be a proper and lower semicontinuous and \(H: \mathbb {R}^d \rightarrow \mathbb {R}\) is a continuously differentiable function, then \(\partial (F+H)(x) = \partial F(x)+\nabla H(x)\) for all \(x \in \mathbb {R}^d\).
-
(d)
A necessary (but not sufficient) condition for \(x\in \mathbb {R}^d\) to be a minimizer of F is
$$0\in \partial F(x).$$A point satisfying \(0\in \partial F(x)\) is called limiting-critical or simply critical. The set of critical points of F is denoted by critF.
Definition 2.2
(Kurdyka–Łojasiewicz property [12]) Let \(F: \mathbb {R}^d \rightarrow (-\infty ,+\infty ]\) be a proper and lower semicontinuous function.
-
(i)
The function \(F: \mathbb {R}^d \rightarrow (-\infty ,+\infty ]\) is said to have the Kurdyka–Łojasiewicz (KŁ) property at \(x^*\in \)domF if there exist \(\eta \in (0,+\infty ]\), a neighborhood U of \(x^*\) and a continuous concave function \(\varphi :[0,\eta )\rightarrow \mathbb {R}_{+}\) such that \(\varphi (0)=0\), \(\varphi \) is \(C^1\) on \((0,\eta )\), for all \(s\in (0,\eta )\), it is \(\varphi '(s)>0\), and for all x in \(U\cap [F(x^*)<F<F(x^*)+\eta ]\), the Kurdyka–Łojasiewicz inequality holds
$$\varphi '(F(x)-F(x^*))\textrm{dist}(0,\partial F(x))\ge 1.$$ -
(ii)
Proper lower semicontinuous functions which satisfy the Kurdyka–Łojasiewicz inequality at each point of the domain of its subdifferential are called Kurdyka–Łojasiewicz (KŁ) functions.
Roughly speaking, KŁ functions become sharp up to reparameterization via \(\varphi \), a desingularizing function for F. Typical KŁ functions include the class of semialgebraic functions [32, 33]. For instance, the \(l _0\) pseudonorm and the rank function are KŁ. Semialgebraic functions admit desingularizing functions of the form \(\varphi (r)=ar^{1-\vartheta } \) for \(a > 0\), and \(\vartheta \in [0, 1)\) is known as the KŁ exponent of the function [11, 32]. For these functions, the KŁ inequality reads
for some \(C>0\).
Definition 2.3
A function F is said convex if domF is a convex set and if, for all x, \(y\in \)domF, \(\alpha \in [0,1]\),
F is said \(\theta \)-strongly convex with \(\theta > 0\) if \(F-\frac{\theta }{2}\Vert \cdot \Vert ^2\) is convex, i.e.,
for all x, \(y\in \)domF and \(\alpha \in [0,1]\).
Suppose that the function F is differentiable. Then, F is convex if and only if domF is a convex set and
holds for all x, \(y\in \)domF. Moreover, F is \(\theta \)-strongly convex with \(\theta > 0\) if and only if
for all x, \(y\in \)domF.
Definition 2.4
Let \(\phi :\mathbb {R}^d \rightarrow (-\infty ,+\infty ]\) be a convex and Gâteaux differentiable function. The function \(D_\phi :\) dom\(\phi \,\,\times \) intdom\(\phi \rightarrow [0,+\infty )\), defined by
is called the Bregman distance with respect to \(\phi \).
From the above definition, it follows that
if \(\phi \) is \(\theta \)-strongly convex.
Lemma 2.1
(Descent lemma[34]) Let \(F: \mathbb {R}^{d}\rightarrow \mathbb {R}\) be a continuously differentiable function with gradient \(\nabla F\) assumed L-Lipschitz continuous. Then,
Lemma 2.2
Let \(F:\mathbb R^{d}\rightarrow \mathbb R\) be a function with L-Lipschitz continuous gradient, \(G:\mathbb R^{d}\rightarrow \mathbb R\) a proper lower semicontinuous function, and \(z\in \arg \min _{v\in \mathbb {R}^d}\{G(v)+\langle d,v-x\rangle +D_{\phi }(v,x)+\gamma \langle v,u\rangle +\mu \langle v,w\rangle \}\), where \(D_{\phi }\) denotes the Bregman distance with respect to \(\phi \), and x, d, u, \(w\in \mathbb R^{d}\). Then, for all \(y\in \mathbb R^{d}\),
Proof
By Lemma 2.1, we have the inequalities
which implies that
Furthermore, by the definition of z, taking \(v=y\), we obtain
which implies that
Adding (2.5) and (2.6) completes the proof. \(\square \)
Lemma 2.3
(sufficient decrease property) Let F, G, and z be defined as in Lemma 2.2, where x, d, u, \(w\in \mathbb R^{d}\). Assume that \(\phi \) is \(\theta \)-strongly convex. Then, the following inequality holds, for any \(\lambda >0\),
Proof
From Lemma 2.2 with \(y=x\), we have
Using Young’s inequality \(\left\langle \nabla F(x)-d,z-x \right\rangle \le \frac{1}{2L\lambda }\left\| d-\nabla F(x) \right\| ^2 +\frac{L\lambda }{2} \left\| x-z \right\| ^2\) and (2.2), we can obtain
which can be abbreviated as the desired result. \(\square \)
3 Stochastic two-step inertial Bregman proximal alternating linearized minimization algorithm
Throughout this paper, we impose the following assumptions.
Assumption 3.1
-
(i)
The function \(\Phi \) is bounded from below, i.e., \(\Phi (x,y)\ge \underline{\Phi }.\)
-
(ii)
For any fixed y, the partial gradient \(\nabla _{x} H_i(\cdot ,y)\) is globally Lipschitz with module \(L_y\) for all \(i\in \left\{ 1,\dots ,n \right\} \), that is,
$$\left\| \nabla _{x} H_i\left( x_{1},y \right) - \nabla _{x} H_i\left( x_{2},y \right) \right\| \le L_y\left\| x_{1}-x_{2} \right\| , \ \forall x_{1},x_{2} \in \mathbb R^{l}. $$Likewise, for any fixed x, the partial gradient \(\nabla _{y} H_i(x,\cdot )\) is globally Lipschitz with module \(L_x\),
$$\left\| \nabla _{y} H_i\left( x,y_{1} \right) - \nabla _{y} H_i\left( x,y_{2} \right) \right\| \le L_x\left\| y_{1}-y_{2} \right\| , \ \forall y_{1},y_{2} \in \mathbb R^{m}. $$ -
(iii)
\(\nabla H\) is Lipschitz continuous on bounded subsets of \(\mathbb R^{l}\times \mathbb R^{m}\). In other words, for each bounded subset \(B_1\times B_2\) of \(\mathbb R^{l}\times \mathbb R^{m}\), there exists \(M_{B_1\times B_2} > 0\) such that
$$\begin{aligned} \left\| \left( \nabla _{x} H\left( x_{1} ,y_1 \right) \!-\! \nabla _{x} H\left( x_{2},y_2 \right) ,\nabla _{y} H\left( x_1,y_{1} \right) \!-\! \nabla _{y} H\left( x_2,y_{2} \right) \right) \right\| \!\le \! M_{B_1\times B_2}\left\| \left( x_{1}\!-\!x_{2},y_{1}\!-\!y_{2} \right) \right\| . \end{aligned}$$for all \(( x_{1},y_1), ( x_{2},y_2)\in B_1\times B_2\).
(iv) \(\phi _i(i=1,2)\) is \(\theta _i\)-strongly convex differentiable function. And the gradient \(\nabla \phi _i\) is \(\eta _i\)-Lipschitz continuous, i.e.,
We now introduce a stochastic version of the two-step inertial Bregman proximal alternating linearized minimization algorithm. The key of our algorithm is replacing the full gradient computations \(\nabla _x H(u_k,y_k)\) and \(\nabla _y(x_{k+1},v_k)\) with stochastic estimations \(\widetilde{\nabla }_x(u_k,y_k)\) and \(\widetilde{\nabla }_y(x_{k+1},v_k)\), respectively. We describe the resulting algorithm as follows.
Algorithm 3.1
Choose \((x_0,y_0)\in \)dom\(\Phi \) and set \((x_{-i},y_{-i})=(x_0,y_0)\), \(i=1, 2\). Take the sequences \(\{\gamma _{1k}\}\), \(\{\mu _{1k}\}\subseteq [0,\gamma _1]\), \(\{\gamma _{2k}\}\), \(\{\mu _{2k}\}\subseteq [0,\gamma _2]\), \(\{\alpha _{1k}\}\), \(\{\beta _{1k}\}\subseteq [0,\alpha _1]\) and \(\{\alpha _{2k}\}\), \(\{\beta _{2k}\}\subseteq [0,\alpha _2]\), where \(\gamma _1\ge 0\), \(\gamma _2\ge 0\), \(\alpha _1\ge 0\) and \(\alpha _2\ge 0\). For \(k\ge 0\), let
where \(D_{\phi _1}\) and \(D_{\phi _2}\) denote the Bregman distance with respect to \(\phi _1\) and \(\phi _2\), respectively.
Stochastic gradients \(\widetilde{\nabla }_x(u_k,y_k)\) and \(\widetilde{\nabla }_y(x_{k+1},v_k)\) use the gradients of only a few indices \(\nabla _xH_i(u_k,y_k)\) and \(\nabla _yH_i(x_{k+1},v_k)\) for \(i \in B_k \subset \left\{ 1,2,\dots , n \right\} \). The minibatch \(B_k\) is chosen uniformly at random from all subsets of \(\left\{ 1,2,\dots , n \right\} \) with cardinality b. The simplest one is the stochastic gradient descent (SGD) estimator [35]. While the SGD estimator is not variance-reduced, many popular gradient estimators as the SAGA [28] and SARAH [29, 30] estimators have this property. In this paper, we mainly consider SAGA (Appendix A) and SARAH (Appendix B) gradient estimators.
Definition 3.1
(SGD [35]) The SGD gradient estimator \(\widetilde{\nabla }_x^{SGD}(x_k,y_k)\) is defined as follows:
where \(B_k\) are mini-batches containing b indices.
The SGD gradient estimator uses the gradient of a randomly sampled batch to represent the full gradient.
Definition 3.2
(SAGA [28]) The SAGA gradient estimator \(\widetilde{\nabla }_x^{SAGA}(x_k,y_k)\) is defined as follows:
where \(B_k\) are mini-batches containing b indices. The variables \(\varphi _{k}^{i}\) follow the update rules \(\varphi _{k+1}^{i}=x_k\) if \(i\in B_k\) and \(\varphi _{k+1}^{i}=\varphi _{k}^{i}\) otherwise.
Definition 3.3
(SARAH [29, 30]) The SARAH gradient estimator reads for \(k = 0\) as
For \(k = 1, 2,\dots \), we define random variables \(p_k\in \left\{ 0,1 \right\} \) with \(P(p_k=0)=\frac{1}{p}\) and \(P(p_k=1)=1-\frac{1}{p}\), where \(p \in (1,\infty )\) is a fixed chosen parameter. Let \(B_k\) be a random subset uniformly drawn from \(\left\{ 1,\dots , n \right\} \) of fixed batch size b. Then, for \(k= 1, 2,\dots \), the SARAH gradient estimator reads as
In our analysis, we assume that stochastic gradient estimator used in Algorithm 3.1 is variance-reduced, which is a quite general assumption in stochastic gradient algorithms [23, 24]. The following definition is analogous to Definition 2.1 in [23].
Definition 3.4
(Variance-reduced gradient estimator) Let \(\left\{ z_k \right\} _{k\in \mathbb {N} }=\left\{ (x_k,y_k)\right\} _{k\in \mathbb {N} }\) be the sequence generated by Algorithm 3.1 with some gradient estimator \(\widetilde{\nabla }\). This gradient estimator is called variance-reduced with constants \(V_1,V_2,V_\Upsilon \ge 0\), and \(\rho \in (0,1]\) if it satisfies the following conditions:
-
(i)
(MSE bound) There exists a sequence of random variables \(\left\{ \Upsilon _k \right\} _{k\in \mathbb {N} }\) of the form \(\Upsilon _k=\sum _{i=1}^{s} (v_{k}^{i} )^2\) for some nonnegative random variables \(v_{k}^{i}\in \mathbb {R} \) such that
$$\begin{aligned}&\mathbb {E}_k\left[ \left\| \widetilde{\nabla }_x(u_k,y_k)-\nabla _xH(u_k,y_k) \right\| ^2+\left\| \widetilde{\nabla }_y(x_{k+1},v_k)-\nabla _yH(x_{k+1},v_k) \right\| ^2\right] \nonumber \\ \le&\Upsilon _k\!+\!V_1\left( \mathbb {E}_k\left\| z_{k+1}\!-\!z_{k} \right\| ^{2}\!+\!\left\| z_{k}\!-\!z_{k-1} \right\| ^{2} \!+\!\left\| z_{k-1}\!-\!z_{k-2} \right\| ^{2}\!+\!\left\| z_{k-2}\!-\!z_{k-3} \right\| ^{2}\right) , \end{aligned}$$(3.2)and, with \(\Gamma _k=\sum _{i=1}^{s} v_{k}^{i} \)
$$\begin{aligned}&\mathbb {E}_k\left[ \left\| \widetilde{\nabla }_x(u_k,y_k)-\nabla _xH(u_k,y_k) \right\| +\left\| \widetilde{\nabla }_y(x_{k+1},v_k)-\nabla _yH(x_{k+1},v_k) \right\| \right] \nonumber \\ \le&\Gamma _k+V_2\left( \mathbb {E}_k\left\| z_{k+1}-z_{k} \right\| +\left\| z_{k}-z_{k-1} \right\| +\left\| z_{k-1}-z_{k-2} \right\| +\left\| z_{k-2}-z_{k-3} \right\| \right) . \end{aligned}$$(3.3) -
(ii)
(Geometric decay) The sequence \(\left\{ \Upsilon _k \right\} _{k\in \mathbb {N} }\) decays geometrically:
$$\begin{aligned} \mathbb {E}_k\Upsilon _{k+1}\le&(1-\rho )\Upsilon _k+V_\Upsilon \left( \mathbb {E}_k\left\| z_{k+1}-z_{k} \right\| ^{2}+\left\| z_{k}-z_{k-1} \right\| ^{2}+\left\| z_{k-1}-z_{k-2} \right\| ^{2}\right. \nonumber \\&\left. +\left\| z_{k-2}-z_{k-3} \right\| ^{2}\right) . \end{aligned}$$(3.4) -
(iii)
(Convergence of estimator) If \(\left\{ z_k \right\} _{k\in \mathbb {N} }\) satisfies \(\lim _{k \rightarrow \infty } \mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^{2}=0\), then \( \mathbb {E}\Upsilon _k\rightarrow 0\) and \(\mathbb {E}\Gamma _k\rightarrow 0\).
In the following, if \(\left\{ z_k \right\} _{k\in \mathbb {N} }=\left\{ (x_k,y_k)\right\} _{k\in \mathbb {N} }\) is the bounded sequence generated by Algorithm 3.1, we assume \(\nabla H\) is M-Lipschitz continuous on \(\left\{ (x_k,y_k)\right\} _{k\in \mathbb {N} }\).
Assumption 3.2
For the sequences \(\left\{ x_k \right\} _{k\in \mathbb {N} } \) and \(\left\{ y_k \right\} _{k\in \mathbb {N} } \) generated by Algorithm 3.1, there exists \(L> 0\) such that
where \(L _{y_k}\) and \(L _{x_k}\) are the Lipschitz constants for \(\nabla _{x} H_i(\cdot ,y_k)\) and \(\nabla _{y} H_i(x_k,\cdot )\), respectively.
Proposition 3.1
Let \(\left\{ z_k \right\} _{k\in \mathbb {N} }=\left\{ (x_k,y_k)\right\} _{k\in \mathbb {N} }\) be the bounded sequence generated by Algorithm 3.1. Then, the SAGA gradient estimator is variance-reduced with parameters \(V_{1}=\frac{16N^2\gamma ^2}{b}\), \(V_{2}=\frac{4N\gamma }{\sqrt{b}}\), \(V_{\Upsilon }=\frac{408nN^2(1+2\gamma _1^2+\gamma _2^2)}{b^2}\) and \(\rho =\frac{b}{2n}\), where \(N=\max \left\{ M,L \right\} \), \(\gamma =\max \left\{ \gamma _1,\gamma _2 \right\} \). The SARAH estimator is variance-reduced with parameters \(V_{1}=6\left( 1-\frac{1}{p} \right) M^2(1+2\gamma _{1}^2+\gamma _{2}^2)\), \(V_{2}=M\sqrt{6(1-\frac{1}{p})(1 +2\gamma _{1}^2+\gamma _{2}^2) }\), \(V_{\Upsilon }=6\left( 1-\frac{1}{p} \right) M^2(1+2\gamma _{1}^2+\gamma _{2}^2)\) and \(\rho = \frac{1}{p}\).
See the detailed proof of Proposition 3.1 in Appendix A and B. And the conclusion that SVRG gradient estimator is variance-reduced can be obtained similarly.
Below, we give the supermartingale convergence theorem that will be applied to obtain almost sure convergence of sequences generated by STiBPALM (Algorithm 3.1).
Lemma 3.1
(Supermartingale convergence) Let \(\left\{ X_k \right\} _{k\in \mathbb {N} } \) and \(\left\{ Y_k \right\} _{k\in \mathbb {N} } \) be sequences of bounded nonnegative random variables such that \(X_k\) and \(Y_k\) depend only on the first k iterations of Algorithm 3.1. If
for all k, then \(\sum _{k=0}^{\infty } Y_k<+\infty \) a.s. and \(\left\{ X_k \right\} \) converges a.s.
4 Convergence analysis under the KŁ property
In this section, under Assumptions 3.1 and 3.2, we prove convergence of the sequence and extend the convergence rates of SPRING to Algorithm 3.1, for semialgebraic function \(\Phi \). Given \(k\in \mathbb {N}\), define the quantity
where \(\lambda =\sqrt{\frac{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)}{L^2}}\), \(Z=\frac{V_1+V_\Upsilon /\rho }{\sqrt{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)} }+\epsilon >0\), \(\epsilon >0\) is small enough. Our first result guarantees that \(\Psi _k\) is decreasing in expectation.
Lemma 4.1
(\( l _2\) summability) Suppose Assumptions 3.1 and 3.2 hold. Let \(\left\{ z_k \right\} _{k\in \mathbb {N} } \) be the sequence generated by Algorithm 3.1 with variance-reduced gradient estimator, and let
then the following conclusions hold.
- (i):
-
\(\Psi _k\) satisfies
$$\begin{aligned} \mathbb {E}_k\left[ \Psi _{k+1}\! +\!\kappa \left\| z_{k+1}\!-\!z_{k} \right\| ^2\!+\!\epsilon \left\| z_{k}\!-\!z_{k-1} \right\| ^2\!+\! \epsilon \left\| z_{k-1}\!-\!z_{k-2} \right\| ^2\!+\! Z \left\| z_{k-2}\!-\!z_{k-3} \right\| ^2 \right] \!\le \! \Psi _k, \end{aligned}$$(4.2)where \(\kappa =-\frac{L -\theta }{2}-\alpha _1-\alpha _2-\sqrt{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)}-3\epsilon >0\).
- (ii):
-
The expectation of the squared distance between the iterates is summable:
$$\sum _{k=0}^{\infty } \mathbb {E} [\left\| x_{k+1}-x_{k} \right\| ^2+\left\| y_{k+1}-y_{k} \right\| ^2]=\sum _{k=0}^{\infty } \mathbb {E}\left\| z_{k+1}-z_{k} \right\| ^2<\infty .$$
Proof
(i) Applying Lemma 2.3 with \(F(\cdot )=H(\cdot ,y_k)\), \(G(\cdot )=f(\cdot )\), \(z=x_{k+1}\), \(x= x_k\), \(d =\widetilde{\nabla }_x(u_k,y_k)\), \(u = x_{k-1}-x_{k}\) and \(w = x_{k-2}-x_{k-1}\), for any \(\lambda >0\), we have
Inequality (1) is the standard inequality \(\left\| a-c\right\| ^2\le 2\left\| a-b\right\| ^2+2\left\| b-c\right\| ^2\), and (2) uses Assumption 3.1 (ii) and Assumption 3.2. Analogously, for the updates in \(y_k\), we use Lemma 2.3 with \(F(\cdot )=H( x_{k+1},\cdot )\), \(G(\cdot )=g(\cdot )\), \(z=y_{k+1}\), \(x= y_k\), \(d =\widetilde{\nabla }_y(x_{k+1},v_k)\), \(u = y_{k-1}-y_{k}\) and \(w = y_{k-2}-y_{k-1}\), we have
Adding (4.3) and (4.4), we have
where \(\theta =\min \left\{ \theta _1,\theta _2 \right\} \). Applying the conditional expectation operator \(\mathbb {E} _k\), we can bound the MSE terms using (3.2). This gives
Next, we use (3.4) to say that
Combining these inequalities, we have
This is equivalent to
We have
By \(\lambda = \sqrt{\frac{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)}{L^2}}\), we have \(-\frac{L(\lambda +1) -\theta }{2}- \frac{2(V_1+V_\Upsilon /\rho ) }{L\lambda }-\alpha _1-\alpha _2-\frac{2L(\gamma _{1}^2+\gamma _{2}^2)}{\lambda }-3Z=-\frac{L -\theta }{2}-\alpha _1-\alpha _2-\sqrt{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)}-3\epsilon =\kappa \). Hence, (4.7) becomes
According to \(\theta > L+2\alpha _1+2\alpha _2+2\sqrt{10(V_1+V_\Upsilon /\rho )+4L^2(\gamma _{1}^2+\gamma _{2}^2)}+6\epsilon \), we have \(\kappa >0\). So we prove the first claim.
(ii) We apply the full expectation operator to (4.8) and sum the resulting inequality from \(k=0\) to \(k=T-1\),
Using the fact that \(\underline{\Phi } \le \Psi _T\),
Taking the limit \(T \rightarrow +\infty \), we have the sequence \(\left\{ \mathbb {E}\left\| z_{k+1}-z_{k} \right\| ^2 \right\} \) is summable. \(\square \)
The next lemma establishes a bound on the norm of the subgradients of \(\Phi (z_k)\).
Lemma 4.2
(Subgradient bound) Suppose Assumptions 3.1 and 3.2 hold. Let \(\{z_k\}_{k\in \mathbb {N}}\) be a bounded sequence, which is generated by Algorithm 3.1 with variance-reduced gradient estimator. For \(k\ge 0\), define
Then, \((A_{x}^{k},A_{y}^{k} )\in \partial \Phi (x_k,y_k)\) and
where \(p=2(2N+\eta +N\gamma _1+N\gamma _2+\alpha _{1}+\alpha _{2})+V_2\), \(N=\max \left\{ M,L \right\} \), \(\eta =\max \left\{ \eta _1,\eta _2 \right\} \).
Proof
By the definition of \(x_{k}\), we have that 0 must lie in the subdifferential at point \(x_{k}\) of the function
Since \(\phi \) are differential, we have
which implies that
Similarly, we have
Because of the structure of \(\Phi \), from (4.11) and (4.12), we have \((A_{x}^{k},A_{y}^{k} )\in \partial \Phi (x_k,y_k).\) All that remains is to bound the norms of \(A_{x}^{k}\) and \(A_{y}^{k}\). Because \(\nabla H\) is M-Lipschitz continuous on bounded sets, then from Assumption 3.1 (iii) and (iv), we have
A similar argument holds for \(A_{y}^{k}\):
Adding (4.13) and (4.14), we get
where \(N=\max \left\{ M,L \right\} \), \(\eta =\max \left\{ \eta _1,\eta _2 \right\} \). Applying the conditional expectation operator and using (3.3) to bound the MSE terms, we can obtain
where \(p=2(2N+\eta +N\gamma _1+N\gamma _2+\alpha _{1}+\alpha _{2})+V_2\). \(\square \)
Define the set of limit points of \(\left\{ z_k\right\} _{k\in \mathbb {N} }\) as
The following lemma describes properties of \(\Omega \).
Lemma 4.3
(Limit points of \(\left\{ z_k\right\} _{k\in \mathbb {N} }\)) Suppose Assumptions 3.1 and 3.2 hold. Let \(\{z_k\}_{k\in \mathbb {N}}\) be a bounded sequence, which is generated by Algorithm 3.1 with variance-reduced gradient estimator, and let
where \(\epsilon >0\) is small enough. Then,
- (1):
-
\(\sum _{k=1}^{\infty } \left\| z_{k}-z_{k-1} \right\| ^2<\infty \) a.s., and \(\left\| z_{k}-z_{k-1} \right\| \rightarrow 0\) a.s.;
- (2):
-
\(\mathbb {E} \Phi (z_k)\rightarrow \Phi ^*\), where \(\Phi ^*\in [\underline{\Phi },\infty )\);
- (3):
-
\(\mathbb {E} \textrm{dist}(0,\partial \Phi (z_k)) \rightarrow 0\);
- (4):
-
the set \(\Omega \) is nonempty, and for all \(z^*\in \Omega \), \(\mathbb {E} \textrm{dist}(0,\partial \Phi (z^*)) = 0\);
- (5):
-
\(\textrm{dist}(z_k,\Omega )\rightarrow 0\) a.s.;
- (6):
-
\(\Omega \) is a.s. compact and connected;
- (7):
-
\(\mathbb {E} \Phi (z^*)= \Phi ^*\) for all \(z^*\in \Omega \).
Proof
By Lemma 4.1, we have claim (1) holds.
According to (4.2), the supermartingale convergence theorem ensures \(\left\{ \Psi _{k}\right\} \) converges to a finite, positive random variable. Because \(\left\| z_{k}-z_{k-1} \right\| \rightarrow 0\) a.s., \(\left\| z_{k-1}-z_{k-2} \right\| \rightarrow 0\) a.s., \(\left\| z_{k-2}-z_{k-3} \right\| \rightarrow 0\) a.s. and \(\widetilde{\nabla }\) is variance-reduced so \(\mathbb {E} \Upsilon _k \rightarrow 0\), we can say
which implys claim (2).
Claim (3) holds because, by Lemma 4.2,
We have that \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| \rightarrow 0\) and \(\mathbb {E} \Gamma _{k-1} \rightarrow 0\). This ensures that \(\mathbb {E}\left\| (A_{x}^{k},A_{y}^{k} )\right\| \rightarrow 0\). Since \((A_{x}^{k},A_{y}^{k} )\) is one element of \(\partial \Phi (z_k)\), we obtain \(\mathbb {E} \textrm{dist}(0,\partial \Phi (z_k))\le \mathbb {E}\left\| (A_{x}^{k},A_{y}^{k} )\right\| \rightarrow 0\).
To prove claim (4), suppose \(z^*=(x^*,y^*)\) is a limit point of the sequence \(\left\{ z_k\right\} _{k\in \mathbb {N} }\) (a limit point must exist because we suppose the sequence \(\left\{ z_k\right\} _{k\in \mathbb {N} }\) is bounded). This means there exists a subsequence \(\left\{ z_{k_j}\right\} \) satisfying \(\lim _{j\rightarrow \infty } z_{k_j}= z^*\). Furthermore, by the variance-reduced property of \(\widetilde{\nabla }(u_{k_j-1},y_{k_j-1})\), we have \(\mathbb {E} \left\| \widetilde{\nabla }_x(u_{k_j-1},y_{k_j-1})-\nabla _x H(u_{k_j-1},y_{k_j-1}) \right\| ^2\rightarrow 0\).
Because f and g are lower semicontinuous, we have
By the update rule for \(x_{k_j}\), letting \(x=x^*\), we have
Taking the expectation and taking the limit \(j \rightarrow \infty \),
The second term on the right goes to zero because \(x_{k_j}\rightarrow x^*\) and \(\left\{ \nabla _xH(u_{k_j-1},y_{k_j-1})\right\} \) is bounded. The thrid term is zero almost surely because it is bounded above by \(\left\| x^*-x_{k_j} \right\| ^2\), and \(\widetilde{\nabla }_x(u_{k_j-1},y_{k_j-1})-\nabla _xH(u_{k_j-1},y_{k_j-1})\) \(\rightarrow 0\) a.s. Noting that \(\phi _1\) is differentiable, so \(\limsup _{j\rightarrow \infty }f(x_{k_j})\le f(x^*)\) a.s., which, together with (4.15), implies that \(\lim _{j\rightarrow \infty }f(x_{k_j})= f(x^*)\) a.s. Similarly, we have \(\lim _{j\rightarrow \infty }g(y_{k_j})= g(y^*)\) a.s., and hence
Claim (3) ensures that \(\mathbb {E} \textrm{dist}(0,\partial \Phi (z_k)) \rightarrow 0\). Combining (4.16) and the fact that the subdifferential of \(\Phi \) is closed, we have \(\mathbb {E} \textrm{dist}(0,\partial \Phi (z^*)) = 0\).
Claims (5) and (6) hold for any sequence satisfying \(\left\| z_{k}-z_{k-1} \right\| \rightarrow 0\) a.s. (this fact is used in the same context in [11, 36]).
Finally, we must show that \(\Phi \) has constant expectation over \(\Omega \). From claim (2), we have \(\mathbb {E} \Phi (z_k)\rightarrow \Phi ^*\), which implies \(\mathbb {E} \Phi (z_{k_j})\rightarrow \Phi ^*\) for every subsequence \(\left\{ z_{k_j}\right\} _{j\in \mathbb {N} }\) converging to some \(z^*\in \Omega \). In the proof of claim (4), we show that \(\Phi (z_{k_j})\rightarrow \Phi (z ^*)\) a.s., so \(\mathbb {E} \Phi (z^*)= \Phi ^*\) for all \(z^*\in \Omega \). \(\square \)
The following lemma is analogous to the uniformized Kurdyka–Łojasiewicz property [11]. It is a slight generalization of the KŁ property showing that \(z_k\) eventually enters a region of \(\tilde{z} \) for some \(\tilde{z} \) satisfying \(\Phi (\tilde{z} )= \Phi (z ^*)\), and in this region, the KŁ inequality holds.
Lemma 4.4
Assume that the conditions of Lemma 4.3 hold and that \(z_k\) is not a critical point of \(\Phi \) after a finite number of iterations. Let \(\Phi \) be a semialgebraic function with KŁ exponent \(\vartheta \). Then, there exists an index m and a desingularizing function \(\varphi \) so that the following bound holds:
where \(\Phi _k ^*\) is a nondecreasing sequence converging to \(\mathbb {E} \Phi (z^*)\) for all \(z^*\in \Omega \).
The proof is almost the same as that of Lemma 4.5 in [23]. We omit the proof here. We now show that the iterates of Algorithm 3.1 have finite length in expectation.
Theorem 4.1
(Finite length) Assume that the conditions of Lemma 4.3 hold and \(\Phi \) is a semialgebraic function with KŁ exponent \(\vartheta \in [0,1)\). Let \(\{z_k\}_{k\in \mathbb {N}}\) be a bounded sequence, which is generated by Algorithm 3.1 with variance-reduced gradient estimator.
- (i):
-
Either \(z_k\) is a critical point after a finite number of iterations or \(\left\{ z_k\right\} _{k\in \mathbb {N} }\) satisfies the finite length property in expectation:
$$\sum _{k=0}^{\infty } \mathbb {E}\left\| z_{k+1}-z_{k} \right\| <\infty , $$and there exists an integer m so that, for all \(i > m\),
$$\begin{aligned}&\sum _{k=m}^{i}\mathbb {E}\left\| z_{k+1}\!-\!z_{k} \right\| \!+\!\sum _{k=m}^{i} \mathbb {E}\left\| z_{k}\!-\!z_{k-1} \right\| \!+\! \sum _{k=m}^{i}\mathbb {E}\left\| z_{k-1}\!-\!z_{k-2} \right\| \!+\! \sum _{k=m}^{i}\mathbb {E}\left\| z_{k-2}\!-\!z_{k-3} \right\| \nonumber \\ \le&\sqrt{\mathbb {E}\left\| z_{m}-z_{m-1} \right\| ^2} +\sqrt{\mathbb {E}\left\| z_{m-1}-z_{m-2} \right\| ^2}+ \sqrt{\mathbb {E}\left\| z_{m-2}-z_{m-3} \right\| ^2}\nonumber \\&+ \sqrt{\mathbb {E}\left\| z_{m-3}-z_{m-4} \right\| ^2} +\frac{2\sqrt{s} }{K_1\rho } \sqrt{\mathbb {E}\Upsilon _{m-1}}+K_3\triangle _{m,i+1}, \end{aligned}$$(4.17)where
$$K_1=p+\frac{2\sqrt{sV_\Upsilon } }{\rho }, \ K_3=\frac{4K_1 }{K_2},\ K_2=\min \left\{ \kappa ,\epsilon ,Z \right\} , $$p is as in Lemma 4.2, and \(\triangle _{p,q}=(\mathbb {E}[\Psi _p-\Phi _{p}^{*} ]-\mathbb {E}[\Psi _q-\Phi _{q}^{*} ])\).
- (ii):
-
\(\left\{ z_k\right\} _{k\in \mathbb {N} }\) generated by Algorithm 3.1 converge to a critical point of \(\Phi \) in expectation.
Proof
(i) If \(\vartheta \in (0,\frac{1}{2})\), then \(\Phi \) satisfies the KŁ property with exponent \(\frac{1}{2}\), so we consider only the case \(\vartheta \in [ \frac{1}{2},1)\). By Lemma 4.4, there exists a function \(\varphi _0(r)=ar^{1-\vartheta }\) such that
Lemma 4.2 provides a bound on \(\mathbb {E}\textrm{dist}(0,\partial \Phi (z_k))\).
The final inequality is Jensen’s inequality. Because \(\Gamma _k=\sum _{i=1}^{s} v_{k}^{i} \) for some nonnegative random variables \(v_{k}^{i} \), we can say \(\mathbb {E}\Gamma _k=\mathbb {E}\sum _{i=1}^{s} v_{k}^{i} \le \mathbb {E}\sqrt{s\sum _{i=1}^{s} (v_{k}^{i} )^2} \le \sqrt{s\mathbb {E}\Upsilon _{k} } \). We can bound the term \(\sqrt{\mathbb {E}\Upsilon _{k} } \) using (3.4):
The final inequality uses the fact that \(\sqrt{1-\rho } =1-\frac{\rho }{2}- \frac{\rho ^2 }{8}-\cdots \). This implies that
Then, from (4.18) and (4.20), we have
where \(K_1=p+\frac{2\sqrt{sV_\Upsilon } }{\rho }\). Define \(C_k\) to be the right side of this inequality:
We then have
By the definition of \(\varphi _0\), this is equivalent to
We would like to hold the inequality above for \(\Psi _k\) rather than \(\Phi (z_k)\). Replace \(\mathbb {E} \Phi (z_k)\) with \(\mathbb {E}\Psi _k\) by introducing a term of \(\mathcal {O}\left( \left( \mathbb {E}\left[ \left\| z_{k}-z_{k-1} \right\| ^2+\left\| z_{k-1}-z_{k-2} \right\| ^2\right. \right. \right. \)\(\left. \left. \left. +\left\| z_{k-2}-z_{k-3} \right\| ^2+\Upsilon _k \right] \right) ^\vartheta \right) \) in the denominator. We show that inequality (4.22) still holds after this adjustment because these terms are small compared to \(C_k\). Indeed, the quantity
for some constant \(c_1>0\). And because \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^2 \rightarrow 0\), \(\mathbb {E} \Upsilon _k \rightarrow 0\), and \(\vartheta >\frac{1}{2} \), there exists an index m and constants \(c_2,c_3>0\) such that
The first inequality uses (3.4). Because the terms above are small compared to \(C_k\), there exists a constant d such that \(c_3<d<+\infty \) and
For \(\vartheta \in [ \frac{1}{2},1)\), using the fact that \((a+b)^\vartheta \le a^\vartheta +b^\vartheta \) for all \(a, b \ge 0\), we have
Therefore, with \(\varphi (r)=adr^{1-\vartheta }\),
By the concavity of \(\varphi \),
where the last inequality follows from the fact that \(\Phi _k ^*\) is nondecreasing. With \(\triangle _{p,q}=\varphi (\mathbb {E}[\Psi _p-\Phi _{p}^{*} ])-\varphi (\mathbb {E}[\Psi _q-\Phi _{q}^{*} ])\), we have shown
Using Lemma 4.1, we can bound \(\mathbb {E}[\Psi _k-\Psi _{k+1}]\) below by both \(\mathbb {E}\left\| z_{k+1}-z_{k} \right\| ^2\), \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^2\), \(\mathbb {E}\left\| z_{k-1}-z_{k-2} \right\| ^2\) and \(\mathbb {E}\left\| z_{k-2}-z_{k-3} \right\| ^2\). Specifically,
where \(K_2=\min \left\{ \kappa ,\epsilon ,Z \right\} >0\), \(\kappa \), \(\lambda \), \(\epsilon \) and Z are set as in Lemma 4.1. Let us use the first of these inequalities to begin. Applying Young’s inequality to (4.24) yields
Summing inequality (4.25) from \(k=m\) to \(k=i\), set
Then,
which implies that
Dropping the nonpositive term \(-\sqrt{\mathbb {E}\Upsilon _{i} }\), this shows that
where \(K_3=\frac{4K_1}{K_2}\). Applying Jensen’s inequality to the terms on the left gives
The term \(\lim _{i \rightarrow \infty } \triangle _{m,i+1}\) is bounded because \(\mathbb {E}\Psi _k\) is bounded due to Lemma 4.1. Letting \(i \rightarrow \infty \), we prove the assertion.
(ii) An immediate consequence of claim (i) is that the sequence \(\left\{ z_k\right\} _{k\in \mathbb {N} }\) converges in expectation to a critical point. This is because, for any \(p,q \in \mathbb {N}\) with \(p \ge q\), \(\mathbb {E}\left\| z_{p}-z_{q} \right\| =\mathbb {E}\left\| \sum _{k=q}^{p-1}( z_{k+1}-z_{k}) \right\| \le \sum _{k=q}^{p-1} \mathbb {E}\left\| z_{k+1}-z_{k} \right\| \), and the finite length property implies this final sum converges to zero. This proves claim (ii). \(\square \)
Theorem 4.2
Assume that the conditions of Lemma 4.3 hold and \(\Phi \) is a semialgebraic function with KŁ exponent \(\vartheta \in [0, 1)\). Let \(\{z_k\}_{k\in \mathbb {N}}\) be a bounded sequence, which is generated by Algorithm 3.1 with variance-reduced gradient estimator. The following convergence rates hold:
- (i):
-
If \(\vartheta \in (0, \frac{1}{2} ]\), then there exist \(d_1 > 0\) and \(\tau \in [1 - \rho ,1)\) such that \(\mathbb {E} \left\| z_k-z^*\right\| \le d_1\tau ^k\).
- (ii):
-
If \(\vartheta \in (\frac{1}{2},1)\), then there exists a constant \(d_2 > 0\) such that \(\mathbb {E} \left\| z_k-z^*\right\| \le d_2k ^{-\frac{1-\vartheta }{2\vartheta -1} }\).
- (iii):
-
If \(\vartheta = 0\), then there exists an \(m \in \mathbb {N}\) such that \(\mathbb {E} \Phi (z_k)=\mathbb {E} \Phi (z^*)\) for all \(k \ge m\).
Proof
As in the proof of Theorem 4.1, if \(\vartheta \in (0, \frac{1}{2} )\), then \(\Phi \) satisfies the KŁ property with exponent \(\frac{1}{2} \), so we consider only the case \(\vartheta \in [\frac{1}{2},1)\).
Let
Substituting the desingularizing function \(\varphi (r)=ar^{1-\vartheta }\) into (4.27), let \(i\rightarrow \infty \), then we have
Because \(\Psi _m=\Phi (z_m)+\mathcal {O}(\left\| z_{m}-z_{m-1} \right\| ^2+\left\| z_{m-1}-z_{m-2} \right\| ^2+\left\| z_{m-2}-z_{m-3} \right\| ^2+\Upsilon _m) \), we can rewrite the final term as \(\Phi (z_m)-\Phi _{m}^{*}\).
Inequality (1) is due to the fact that \((a+b) ^{1-\vartheta }\le a^{1-\vartheta }+b^{1-\vartheta }\). Applying the KŁ inequality (2.1),
for all \(\xi _m\in \partial \Phi (z_m)\) and we have absorbed the constant C into \(K_4\). Inequality (4.18) provides a bound on the norm of the subgradient:
Let
Therefore, it follows from (4.28) to (4.30) that
(i) If \(\vartheta = \frac{1}{2}\), then \(\left( \mathbb {E}\left\| \xi _m \right\| \right) ^{\frac{1-\vartheta }{\vartheta } }=\mathbb {E}\left\| \xi _m \right\| \). Equation (4.31) then gives
where \(K_5=\max \left\{ K_3,K_4 \right\} \). Using (4.19), we have that, for any constant \(c > 0\),
Combining this inequality with (4.32),
Defining \(A=1+aK_5\left( p+\sqrt{ \frac{V_1+V_\Upsilon /\rho }{L\lambda }+\frac{\alpha _1+\alpha _2}{2}+\frac{2L(\gamma _{1}^2+\gamma _{2}^2)}{\lambda }+3Z }+c\sqrt{V_\Upsilon }\right) \), we have shown
Then, we get
This implies
For large c, the second coefficient in the above expression approaches \(1-\frac{\rho }{2}\). So there exist \(\tau \in [1 - \rho ,1)\) such that
for some constant \(d_1\). Then, using the fact that \(\mathbb {E}\left\| z_{m}\!-\!z^{*} \right\| \!=\!\mathbb {E}\left\| \sum _{k=m+1}^{\infty } (z_{k}\!-\!z_{k-1}) \right\| \)\(\le \sum _{k=m}^{\infty }\mathbb {E}\left\| z_{k}-z_{k-1} \right\| \), we prove claim (i).
(ii) Suppose \(\vartheta \in (\frac{1}{2},1)\). Each term on the right side of (4.31) converges to zero, but at different rates. Because
and \(\vartheta \) satisfies \(\frac{1-\vartheta }{\vartheta }< 1\), the term \(\Theta _{m}^{\frac{1-\vartheta }{\vartheta } }\) dominates the first five terms on the right side of (4.31) for large m. Also, because \(\frac{1-\vartheta }{2\vartheta }< 1-\vartheta \), \(\Theta _{m}^{\frac{1-\vartheta }{\vartheta } }\) dominates the final four terms as well. Combining these facts, there exists a natural number \(M_1\) such that for all \(m \ge M_1\),
for some constant \(P>(aK_3)^{\frac{\vartheta }{1-\vartheta } }\). The bound of (4.20) implies
Therefore,
Furthermore, because \({\frac{\vartheta }{1-\vartheta } }>1\) and \(\mathbb {E}\Upsilon _m\rightarrow 0\), for large enough m, we have \(\left( \sqrt{\mathbb {E}\Upsilon _m} \right) ^{\frac{\vartheta }{1-\vartheta } } \ll \sqrt{\mathbb {E}\Upsilon _m} \). This ensures that there exists a natural number \(M_2\) such that for every \(m \ge M_2\),
The constant appearing on the left was chosen to simplify later arguments. Therefore, (4.33) implies
Here, (1) follows by convexity of the function \(x^{\frac{\vartheta }{1-\vartheta }}\) for \(\vartheta \in [1/2, 1)\) and \(x \ge 0\), (2) is (4.35), and (3) is (4.33) combined with (4.34). We absorb the constant \(\frac{2^{{\frac{\vartheta }{1-\vartheta } }}}{2}\) into P. Define
\(S_m\) is bounded for all m because \(\sum _{k=m}^{\infty } \sqrt{\mathbb {E}\left\| z_{k+1}-z_{k} \right\| ^2}\) is bounded by (4.28). Hence, we have shown
The rest of the proof is almost the same as what was mentioned in [23, 37]. We omit the proof here. (iii) When \(\vartheta = 0\), the KŁ property (2.1) implies that exactly one of the following two scenarios holds: either \(\mathbb {E} \Phi (z_k)\ne \Phi _{k}^{*}\) and
or \(\mathbb {E} \Phi (z_k)= \Phi _{k}^{*}\). We show that the above inequality can hold only for a finite number of iterations.
Using the subgradient bound (4.10), the first scenario implies
where we have used the inequality \((a_1+a_2+\cdots +a_s)^2\le s (a_1^2+a_2^2+\cdots +a_s^2)\) and Jensen’s inequality. Applying this inequality to the decrease of \(\Psi _ k\) (4.2), we obtain
for some constant \(C^2\). Because the final five terms go to zero as \(k \rightarrow \infty \), there exists an index \(M_4\) so that the sum of these five terms is bounded above by \(\frac{C^2}{2}\) for all \(k \ge M_4\). Therefore,
Because \(\Psi _k\) is bounded below for all k, this inequality can only hold for \(N < \infty \) steps. After N steps, it is no longer possible for the bound (4.37) to hold, so it must be that \(\mathbb {E} \Phi (z_k)= \Phi _{k}^{*}\). Because \(\Phi _{k}^{*}<\Phi (z^{*})\), \(\Phi _{k}^{*}<\mathbb {E} \Phi (z_k)\), and both \(\mathbb {E} \Phi (z_k)\), \(\Phi _{k}^{*}\) converge to \(\mathbb {E}\Phi (z^{*})\), we must have \(\Phi _{k}^{*}=\mathbb {E} \Phi (z_k)=\mathbb {E}\Phi (z^{*})\). \(\square \)
5 Numerical experiments
In this section, to demonstrate the advantages of STiBPALM (Algorithm 3.1), we present our numerical study on the practical performance of the proposed STiBPALM with three different stochastic gradient estimators, i.e., SGD estimator [35] (STiBPALM-SGD), SAGA gradient [28] estimator (STiBPALM-SAGA), and SARAH gradient [29] estimator (STiBPALM-SARAH), compared with PALM [11], iPALM [6], TiPALM [17], SPRING [23], and SiPALM [24] algorithms. We refer to SPRING with SGD, SAGA, and SARAH gradient estimators as SPRING-SGD, SPRING-SAGA, and SPRING-SARAH; and SiPALM using the SGD, SAGA, and SARAH gradient estimators as SiPALM-SGD, SiPALM-SAGA, and SiPALM-SARAH, respectively. Two applications are considered here for comparison: sparse nonnegative matrix factorization (S-NMF) and blind image-deblurring (BID).
Since the proposed algorithm is based on the stochastic gradient estimator, we report the average results (over 10 independent runs) of objective values for all algorithms. The initial point is also the same for all algorithms. In addition, we choose step size which is suggested in [11] for PALM and in [6] for iPALM, respectively, and the same step size based on [23] for all stochastic algorithms for simplicity.
5.1 Sparse nonnegative matrix factorization
Given a matrix A, sparse nonnegative matrix factorization (S-NMF) [38,39,40] problem can be formulated as the following model:
In dictionary learning and sparse coding, X is called the learned dictionary with coefficients Y. In this formulation, the sparsity on X is restricted \(75\%\) of the entries to be 0.
ORL face database which includes 400 normalized cropped frontal faces which we used in our S-NMF example
We use the extended Yale-B dataset and the ORL dataset, which are standard facial recognition benchmarks consisting of human face images.Footnote 1 For solving this S-NMF problem (5.1), [6, 14] gave the details on how to solve the X-subproblems and Y-subproblems. The extended Yale-B dataset contains 2414 cropped images of size \(32 \times 32\), while the ORL dataset contains 400 images sized \(64 \times 64\) (see Fig. 1). In the experiment for the Yale dataset, we extract 49 sparse basis images for the dataset. For the ORL dataset, we extract 25 sparse basis images. In each iteration of the stochastic algorithms, we randomly subsample \(5\%\) of the full batch as a minibatch. Here, for SARAH gradient estimator, we set \(p=\frac{1}{20}\).
In STiBPALM, let \(\phi _1(X)=\frac{\theta _1 }{2} \left\| X\right\| ^{2}\), \(\phi _2(Y)=\frac{\theta _2 }{2} \left\| Y \right\| ^{2}\). In a numerical experiment, we choose \(\eta =3\) and calculate \(\theta _1\) and \(\theta _2\) by computing the largest eigenvalues of \(\eta YY^T\) and \(\eta X^TX\) at k-th iteration, respectively. We choose \(\alpha _{1k}=\beta _{1k}=\gamma _{1k}=\mu _{1k}=\frac{k-1}{k+2}\), \(\alpha _{2k}=\beta _{2k}=\gamma _{2k}=\mu _{2k}=\frac{k-1}{k+2}\) in TiPALM and STiBPALM and \(\alpha _{1k}=\beta _{1k}=\gamma _{1k}=\mu _{1k}=\frac{k-1}{k+2}\) in iPALM and SiPALM. We use BTiPALM and BSTiPALM to denote TiPALM and STiBPALM with \(\phi _1(X)=\frac{\theta _1^2 }{4} \left\| X\right\| ^{4}\), \(\phi _2(Y)=\frac{\theta _2 }{2} \left\| Y \right\| ^{2}\), respectively. We refer to BSTiPALM using the SGD, SAGA, and SARAH gradient estimators as BSTiPALM-SGD, BSTiPALM-SAGA, and BSTiPALM-SARAH, respectively.
Objective decrease comparison of S-NMF with \(s = 25\%\) on Yale dataset. From the left column to the right column are the results of SGD, SAGA, and SARAH, respectively
Objective decrease comparison of S-NMF with \(s = 25\%\) on Yale dataset
In Figs. 2 and 3, we report the numerical results for Yale-B dataset. A similar result for the ORL dataset is plotted in Figs. 4 and 5. One can observe from these four figures that the STiBPALM can get slightly lower values than the other algorithms within almost the same computation time. In addition, STiBPALM can get better performance than the SPRING and SiPALM stochastic algorithms with epoch changes. The stochastic algorithms can improve the numerical results compared with the corresponding deterministic method. Furthermore, compared with the stochastic gradient algorithm without variance reduction (SGD), the variance-reduced stochastic gradient (SAGA, SARAH) algorithm can get better numerical results.
Objective decrease comparison of S-NMF with \(s = 25\%\) on ORL dataset. From the left column to the right column are the results of SGD, SAGA, and SARAH, respectively
Objective decrease comparison of S-NMF with \(s = 25\%\) on ORL dataset
The numerical results applying different Bregman distances under the Yale-B dataset and ORL dataset are reported in Figs. 6 and 7, respectively. We can observe that BSTiPALM algorithm can obtain better numerical results compared to STiBPALM algorithm, where SARAH gradient estimator can get the best performance with epoch changes.
Objective decrease comparison of S-NMF with \(s = 25\%\) on Yale dataset with different Brengman distance
Objective decrease comparison of S-NMF with \(s = 25\%\) on ORL dataset with different Brengman distance
The results for 25 basis faces using different sparsity settings. From the left column to the right column are the results of TiPALM, STiBPALM-SGD, STiBPALM-SAGA, and STiBPALM-SARAH, respectively. From top row to bottom row are the result of \(s = 25\%\) and \(s = 50\%\), respectively
We also compare STiBPALM with SGD, SAGA, and SARAH for different sparsity settings (the value of s). The results of the basis images are shown in Fig. 8. One can observe from Fig. 8 that for smaller values of s, the four algorithms lead to more compact representations. This might improve the generalization capabilities of the representation.
Objective decrease comparison (epoch counts) of blind image-deconvolution experiment on Kodim08 image using an \(11 \times 11\) motion blur kernel
Objective decrease comparison (epoch counts) of blind image-deconvolution experiment on Kodim15 image using an \(11 \times 11\) motion blur kernel
Image and kernel reconstructions from the blind image-deconvolution experiment on the Kodim08 image using an \(11 \times 11\) motion blur kernel
Image and kernel reconstructions from the blind image-deconvolution experiment on the Kodim08 image using an \(11 \times 11\) motion blur kernel
5.2 Blind image-deblurring
Let A be a blurred image, the problem of blind deconvolution is given by
In numerical experiment, we choose \(R(v)= \log (1 + \sigma v^2)\) as in [6], where \(\sigma =10^3\) and \(\eta =5\times 10^{-5}\).
We consider two images, Kodim08 and Kodim15, of size \(256 \times 256\) for testing. For each image, two blur kernels—linear motion blur and out-of-focus blur—are considered with additional additive Gaussian noise. In this numerical experiment, we mainly use SARAH gradient estimator and set \(p=\frac{1}{64}\). We take \(\alpha _{1k}=\beta _{1k}=\gamma _{1k}=\mu _{1k}=\frac{k-1}{k+2}\), \(\alpha _{2k}=\beta _{2k}=\gamma _{2k}=\mu _{2k}=\frac{k-1}{k+2}\) in TiPALM and STiBPALM and \(\alpha _{1k}=\beta _{1k}=\gamma _{1k}=\mu _{1k}=\frac{k-1}{k+2}\) in iPALM.
The convergence comparisons of the algorithms for both images with motion blur are provided in Figs. 9 and 10, from which we observe STiBPALM-SARAH is faster than the other methods. Figures 11 and 12 provide comparisons of the recovered image and blur kernel. We observe superior performance of stochastic algorithms over deterministic algorithms in these figures as well. In particular, when comparing the estimated blur kernels of the two algorithms every 20 epochs, we clearly see that STiBPALM-SARAH more quickly recovers more accurate solutions than TiPALM.
6 Conclusion
In this paper, we propose a stochastic two-step inertial Bregman proximal alternating linearized minimization (STiBPALM) algorithm with the variance-reduced gradient estimator to solve a class of nonconvex nonsmooth optimization problems. Under some mild conditions, we analyze the convergence properties of STiBPALM when using a variety of variance-reduced gradient estimators and prove specific convergence rates using the SAGA and SARAH estimators. We also implement the STiBPALM algorithm to sparse nonnegative matrix factorization and blind image-deblurring problems and perform some numerical experiments to demonstrate the effectiveness of the proposed algorithm.
Data Availability
All data generated or analyzed during this study are included in this article.
References
Chao, M.T., Han, D.R., Cai, X.J.: Convergence of the Peaceman-Rachford splitting method for a class of nonconvex programs. Numer. Math. Theory Methods Appl. 14(2), 438–460 (2021)
Fu, X., Huang, K., Sidiropoulos, N.D., Ma, W.: Nonnegative matrix factorization for signal and data analytics: identifiability, algorithms, and applications. IEEE Signal Process. Mag. 36(2), 59–80 (2019)
Paatero, P., Tapper, U.: Positive matrix factorization: a nonnegative factor model with optimal utilization of error estimates of data values. Environmetrics 5, 111–126 (1994)
Lee, D.D., Seung, H.S.: Learning the parts of objects by nonnegative matrix factorization. Nat. 401, 788–791 (1999)
Ma, Y., Hu, X., He, T., Jiang, X.: Clustering and integrating of heterogeneous microbiome data by joint symmetric nonnegative matrix factorization with Laplacian regularization. IEEE/ACM Trans. Comput. Biol. Bioinform. 17(3), 788–795 (2020)
Pock, T., Sabach, S.: Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J. Imaging Sci. 9, 1756–1787 (2017)
Aspremont, A., Ghaoui, L. E., Jordan, M. I., Lanckriet, G. R.: A direct formulation for sparse PCA using semidefinite programming. in Advances in Neural Information Processing Systems 41–48 (2005)
Zou, H., Hastie, T., Tibshirani, R.: Sparse principal component analysis. J. Comput. Graph. Statist. 15, 265–286 (2006)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Guass-Seidel methods. Math. Program. 137, 91–129 (2013)
Donoho, D.L.: Compressed sensing. IEEE Trans. Inform. Theory 4, 1289–1306 (2006)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearised minimization for nonconvex and nonsmooth problems. Math. Program. 146, 459–494 (2014)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 35, 438–457 (2010)
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. Publ. Math. Program. Soc. 116(1–2), 5–16 (2009)
Gao, X., Cai, X.J., Han, D.R.: A Gauss-Seidel type inertial proximal alternating linearized minimization for a class of nonconvex optimization problems. J. Glob. Optim. 76, 863–887 (2020)
Wang, Q.X., Han, D.R.: A generalized inertial proximal alternating linearized minimization method for nonconvex nonsmooth problems. Appl. Numer. Math. 189, 66–87 (2023)
Zhao, J., Dong, Q.L., Michael, Th.R., Wang, F.H.: Two-step inertial Bregman alternating minimization algorithm for nonconvex and nonsmooth problems. J. Glob. Optim. 84, 941–966 (2022)
Guo, C. Z., Zhao, J.: Two-step inertial Bregman proximal alternating linearized minimization algorithm for nonconvex and nonsmooth problems, (2023). arXiv:2306.07614v1
Chao, M.T., Nong, F.F., Zhao, M.Y.: An inertial alternating minimization with Bregman distance for a class of nonconvex and nonsmooth problems. J. Appl. Math. Comput. 69, 1559–1581 (2023)
Mukkamala, M.C., Ochs, P., Pock, T., Sabach, S.: Convex-concave backtracking for inertial Bregman proximal gradient algorithms in nonconvex optimization. SIAM J. Math. Data Sci. 2, 658–682 (2020)
Ahookhosh, M., Hien, L.T.K., Gillis, N., Patrinos, P.: A block inertial Bregman proximal algorithm for nonsmooth nonconvex problems with application to symmetric nonnegative matrix tri-factorization. J. Optim. Theory Appl. 190, 234–258 (2021)
Bottou, L.: In: Large-scale machine learning with stochastic gradient descent. In Proceedings of COMPSTAT’2010, 1, 177–186 (2010)
Xu, Y., Yin, W.: Block stochastic gradient iteration for convex and nonconvex optimization. SIAM J. Optim. 25(3), 1686–1716 (2015)
Driggs, D., Tang, J.Q., Liang, J.W., Davies, M., Schonlieb, C.B.: SPRING: a stochastic proximal alternating minimization for nonsmooth and nonconvex optimization. SIAM J. Imaing Sci. 4, 1932–1970 (2021)
Hertrich, J., Steidl, G.: Inertial stochastic PALM and applications in machine learning. Sampl. Theory Sign Process. Data Anal. 20, (2022). https://doi.org/10.1007/s43670-022-00021-x
Schmidt, M., Le Roux, N., Bach, F.: Minimizing finite sums with the stochastic average gradient. Math. Program. 162, 83–112 (2017)
Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. in Advances in Neural Information Processing Systems 315–323 (2013)
Konecny, J., Liu, J., Richtarik, P., Takac, M.: Mini-batch semi-stochastic gradient descent in the proximal setting. IEEE J. Sel. Top. Sign Process. 10, 242–255 (2016)
Defazio, A., Bach, F., Lacoste-Julien, S.: SAGA: a fast incremental gradient method with support for non-strongly convex composite objectives. in Advances in Neural Information Processing Systems 1646–1654 (2014)
Li, B., Ma, M., Giannakis, G. B.: On the convergence of SARAH and beyond. in International Conference on Artificial Intelligence and Statistics, PMLR 223–233 (2020)
Nguyen, L. M., Liu, J., Scheinberg, K., and Takáĉ, M.: SARAH: a novel method for machine learning problems using stochastic recursive gradient. in Proceedings of the 34th International Conference on Machine Learning, 2613–2621 (2017)
Rockafellar, R.T., Wets, R.: Variational analysis, Grundlehren der Mathematischen Wissenschaften, vol. 317. Springer, Berlin (1998)
Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17, 1205–1223 (2007)
Bolte, J., Daniilidis, A., Ley, O., Mazet, L.: Characterizations of Lojasiewicz inequalities: subgradient flows, talweg, convexity. Trans. Amer. Math. Soc. 362, 3319–3363 (2010)
Bertsekas, D.P., Tsitsiklis, J.N.: Parallel and distributed computation: numerical methods. Prentice hall, Englewood Cliffs, NJ (1989)
Robbins, H., Siegmund, D.: A convergence theorem for non-negative almost supermartingales and some applications. Optimizing Methods in Statistics, Academic Press, New York, 233–257 (1971)
Damek, D.: The asynchronous PALM algorithm for nonsmooth nonconvex problems (2016). arXiv:1604.00526
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. B 116, 5–16 (2007)
Lee, D.D., Seung, H.S.: Learning the parts of objects by non-negative matrix factorization. Nat. 788–791 (1999)
Pan, J., Gillis, N.: Generalized separable nonnegative matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 43(5), 1546–1561 (2021)
Rousset, F., Peyrin, F., Ducros, N.: A semi nonnegative matrix factorization technique for pattern generalization in single-pixel imaging. IEEE Trans. Comput. Imaging 4(2), 284–294 (2018)
Peharz, R., Pernkopf, F.: Sparse nonnegative matrix factorization with \(l_0\)-constraints. Neurocomput. 80, 38–46 (2012)
Acknowledgements
We are grateful to the editor and reviewers for their comments that improved the quality of our paper.
Funding
This work is supported by the Scientific Research Project of Tianjin Municipal Education Commission (2022ZD007).
Author information
Authors and Affiliations
Contributions
All authors contributed to the manuscript and approved the submitted version.
Corresponding author
Ethics declarations
Ethics approval
Not applicable
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A SAGA variance bound
We define the SAGA gradient estimators \(\widetilde{\nabla }_x(u_k,y_k)\) and \(\widetilde{\nabla }_y(x_{k+1},v_k)\) as follows:
where \(I_k^x\) and \(I_k^y\) are mini-batches containing b indices. The variables \(\varphi _{k}^{i}\) and \(\xi _{k}^{i}\) follow the update rules \(\varphi _{k+1}^{i}=u_k\) if \(i\in I_k^x\) and \(\varphi _{k+1}^{i}=\varphi _{k}^{i}\) otherwise, and \(\xi _{k+1}^{i}=v_k\) if \(i\in I_k^y\) and \(\xi _{k+1}^{i}=\xi _{k}^{i}\) otherwise.
To prove our variance bounds, we require the following lemma.
Lemma A.1
Suppose \(X_1,\cdots ,X_t\) are independent random variables satisfying \(\mathbb {E}_{k}X_i\)\(=0\) for \(1\le i\le t\). Then
Proof
Our hypotheses on these random variables imply \(\mathbb {E}_{k}\left\langle X_i,X_j \right\rangle =0\) for \(i\ne j\). Therefore,
\(\square \)
We are now prepared to prove that the SAGA gradient estimator is variance-reduced.
Lemma A.2
The SAGA gradient estimator satisfies
as well as
where \(N=\max \left\{ M,L \right\} \), \(\gamma =\max \left\{ \gamma _1,\gamma _2 \right\} \).
Proof
According to (A.1), we have
Inequality (1) follows from Lemma A.1. By the Jensen’s inequality, we can say that
We use an analogous argument for \(\widetilde{\nabla }_y(x_{k+1},v_k)\). Let \(\mathbb {E}_{k,x}\) denote the expectation conditional on the first k iterations and \(I_k^x\). By the same reasoning as in (A.5), applying the Lipschitz continuity of \(\nabla _yH_j\), we obtain that
where \(N=\max \left\{ M,L \right\} \), \(\gamma =\max \left\{ \gamma _1,\gamma _2 \right\} \). Also, by the same reasoning as in (A.6),
Applying the operator \(\mathbb {E}_{k}\) to (A.7) and (A.8), we get the desired result. \(\square \)
Now, define
By Lemma A.2, we have
and
This is exactly the MSE bound, where \(V_{1}=\frac{16N^2\gamma ^2}{b}\) and \(V_{2}=\frac{4N\gamma }{\sqrt{b}}\).
Lemma A.3
(Geometric decay) Let \(\Upsilon _{k}\) be defined as in (A.9), then we can establish the geometric decay property:
where \(\rho =\frac{b}{2n}\), \(V_{\Upsilon }=\frac{408nN^2(1+2\gamma _1^2+\gamma _2^2)}{b^2}\).
Proof
We show that \(\mathbb {E}_{k}\Upsilon _{k+1}\) is decreasing at a geometric rate. By applying the inequality \(\left\| a-c \right\| ^2\le (1+\varepsilon )\left\| a-b \right\| ^2+(1+\varepsilon ^{-1} )\left\| b-c \right\| ^2\) twice, it follows that
Similarly,
With
adding (A.11) and (A.12), we can obtain
where \(N=\max \left\{ M,L \right\} \). Choosing \(\varepsilon =\frac{b}{6n}\), we have \((1+\varepsilon )^3(1-\frac{b}{n} ) \le 1-\frac{b}{2n}\), producing the inequality
This completes the proof. \(\square \)
Lemma A.4
(Convergence of estimator) If \(\left\{ z_k \right\} _{k\in \mathbb {N} }\) satisfies \(\lim _{k \rightarrow \infty } \mathbb {E}\left\| z_{k}\!-\!z_{k-1} \right\| ^{2}\!=0\), then \( \mathbb {E}\Upsilon _k\rightarrow 0\) and \(\mathbb {E}\Gamma _k\rightarrow 0\) as \(k\rightarrow \infty \).
Proof
We frist show that \(\sum _{j=1}^n \mathbb {E}\left\| \nabla _xH_j(u_{k},y_{k})- \nabla _xH_j(\varphi _{k}^{j},y_{k}) \right\| ^2\rightarrow 0\) as \(k\rightarrow \infty \). Indeed,
As \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^{2}\rightarrow 0\), so \(\mathbb {E}\left\| u_{k}-u_{k-1} \right\| ^{2}\rightarrow 0\), it is clear that \(\sum _{l=1}^k(1-\frac{b}{2n})^{k-l} \mathbb {E}\left\| u_{l}\!-\!u_{l-1}\right\| ^2 \!\rightarrow \! 0\), and hence \(\sum _{j=1}^n \mathbb {E}\left\| \nabla _xH_j(u_{k},y_{k})\!-\! \nabla _xH_j(\varphi _{k}^{j},y_{k}) \right\| ^2\! \rightarrow \! 0\) as \(k\!\rightarrow \! \infty \). An analogous argument shows that \(\sum _{j=1}^n \!\mathbb {E}\!\left\| \nabla _yH_j(x_{k},v_{k})\!-\! \nabla _yH_j(x_{k},\xi _{k}^{j}) \!\right\| ^2\)\(\rightarrow 0\) as \(k\rightarrow \infty \). So \(\mathbb {E}\Upsilon _k\rightarrow 0\) as \(k\rightarrow \infty \). Similarly, we can get \(\mathbb {E}\Gamma _k\rightarrow 0\) as \(k\rightarrow \infty \). Indeed,
Because \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^{2}\rightarrow 0\), it follows that \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| \rightarrow 0\) (because Jensen’s inequality implies \(\mathbb {E}\left\| z_{k}-z_{k-1} \right\| \le \sqrt{\mathbb {E}\left\| z_{k}-z_{k-1} \right\| ^{2}}\rightarrow 0\)). So \(\mathbb {E}\left\| u_{k}-u_{k-1} \right\| \rightarrow 0\), then it follows that the bound on the right goes to zero as \(k\rightarrow \infty \), hence \(\mathbb {E}\Gamma _k\rightarrow 0\).
\(\square \)
1.2 B SARAH variance bound
As in the previous section, we use \(I_k^x\) and \(I_k^y\) to denote the mini-batches used to approximate \(\nabla _xH(u_k,y_k) \) and \(\nabla _yH(x_{k+1},v_k)\), respectively.
Lemma B.1
The SARAH gradient estimator satisfies
as well as
where \(V_{1}=6\left( 1-\frac{1}{p} \right) M^2(1+2\gamma _{1}^2+\gamma _{2}^2)\) and \(V_{2}=M\sqrt{6(1-\frac{1}{p})(1+2\gamma _{1}^2+\gamma _{2}^2) }\).
Proof
Let \(\mathbb {E}_{k,p}\) denote the expectation conditional on the first k iterations and the event that we do not compute the full gradient at iteration k. The conditional expectation of the SARAH gradient estimator in this case is
and further
By (B.1), we see that
Thus, the first two inner products in (B.2) sum to zero and the third one is equal to
This yields
We can bound the second term by computing the expectation.
The inequality is due to the convexity of the function \(x\mapsto \left\| x \right\| ^2\). This results in the recursive inequality
This bounds the MSE under the condition that the full gradient is not computed. When the full gradient is computed, the MSE is equal to zero, so taking the M-Lipschitz continuity of the gradients of the \(H_j\) into account, we get
Using \((a+b+c) ^2\le 3(a^2+b^2+c^2)\), we can estimate
Substituting the above inequality, we can obtain
By symmetric arguments, it holds
Combining (B.3) and (B.4), we can obtain
Similar bounds hold for \(\Gamma _k\) due to Jensen’s inequality:
This completes the proof. \(\square \)
Now, define
By Lemma B.1, we have
and
This is exactly the MSE bound, where \(V_{1}=6\left( 1-\frac{1}{p} \right) M^2(1+2\gamma _{1}^2+\gamma _{2}^2)\) and
\(V_{2}=M\sqrt{6(1-\frac{1}{p})(1+2\gamma _{1}^2+\gamma _{2}^2) }\).
Lemma B.2
(Geometric decay) Let \(\Upsilon _{k}\) be defined as in (B.5), then we can establish the geometric decay property:
where \(\rho = \frac{1}{p}\), \(V_{\Upsilon }=6\left( 1-\frac{1}{p} \right) M^2(1+2\gamma _{1}^2+\gamma _{2}^2)\).
Proof
This is a direct result of Lemma B.1. \(\square \)
Lemma B.3
(Convergence of estimator) If \(\left\{ z_k \right\} _{k\in \mathbb {N} }\) satisfies \(\lim _{k \rightarrow \infty } \mathbb {E}\left\| z_{k}\!-\!z_{k-1} \right\| ^{2}\!=0\), then \( \mathbb {E}\Upsilon _k\rightarrow 0\) and \(\mathbb {E}\Gamma _k\rightarrow 0\) as \(k \rightarrow \infty \).
Proof
By (B.6), we have
which implies \( \mathbb {E}\Upsilon _k\rightarrow 0\) as \(k \rightarrow \infty \). By Jensen’s inequality, we have \(\mathbb {E}\Gamma _k\rightarrow 0\) as \(k \rightarrow \infty \). \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Guo, C., Zhao, J. & Dong, QL. A stochastic two-step inertial Bregman proximal alternating linearized minimization algorithm for nonconvex and nonsmooth problems. Numer Algor 97, 51–100 (2024). https://doi.org/10.1007/s11075-023-01693-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-023-01693-9