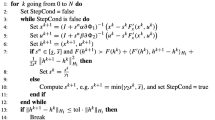Proximal linearization methods for Schatten p-quasi-norm minimization

Abstract

Schatten p-quasi-norm minimization has advantages over nuclear norm minimization in recovering low-rank matrices. However, Schatten p-quasi-norm minimization is much more difficult, especially for generic linear matrix equations. In this paper, we first extend the lower bound theory of $\ell _p$ minimization to Schatten p-quasi-norm minimization. We prove that the positive singular values of local minimizers are bounded from below by a constant. Motivated by this property, we propose a proximal linearization method, whose subproblems can be solved efficiently by the (linearized) alternating direction method of multipliers. The convergence analysis of the proposed method involves the nonsmooth analysis of singular value functions. We give a necessary and sufficient condition for a singular value function to be a Kurdyka–Łojasiewicz function. The subdifferentials of related singular value functions are computed. The global convergence of the proposed method is established under some assumptions. Experiments on matrix completion, Sylvester equation and image deblurring show the effectiveness of the algorithm.

1 Introduction

Consider the following minimization problem

$$\begin{aligned} \begin{aligned} \min _{X \in \mathbb {R}^{m \times n}}\quad&\textrm{rank}(X) \\ \mathrm { s.t. }\quad&\mathcal {A}(X)= \varvec{b}, \end{aligned} \end{aligned}$$

(1)

where $\mathcal {A}:\mathbb {R}^{m\times n}\rightarrow \mathbb {R}^d$ is a linear operator and $\varvec{b} \in \mathbb {R}^{d}$. This is called the affine rank minimization problem [41] and arises in various application areas, such as control applications [18, 19, 37], stochastic PDEs [30], matrix completion [8, 10], and image processing [22, 23]. This problem is NP-hard. Let the singular values of X be $\sigma _1(X),\ldots ,\sigma _h(X)$, where $h=\min \{m,n\}$. The nuclear norm of X is $\Vert X\Vert _* = \sum _{i=1}^{h}\sigma _i(X)$. It is proved in [19] that the nuclear norm is the convex envelope of the rank function over the unit ball under the spectral norm. Using the nuclear norm to replace the rank function is a common method [7, 8, 10, 40, 41, 50] for finding low-rank solutions, i.e.,

$$\begin{aligned} \begin{aligned} \min _{X \in \mathbb {R}^{m \times n}}\quad&\Vert X \Vert _* \\ \mathrm { s.t. }\quad&\mathcal {A}(X)= \varvec{b}. \end{aligned} \end{aligned}$$

(2)

In practice, $\varvec{b}$ is usually contaminated by noise, or we just want to gain a low-rank approximate solution. In such cases, (2) is often relaxed to the nuclear norm regularized least squares problem

$$\begin{aligned} \min _{X\in \mathbb {R}^{m \times n}}\ \Vert X\Vert _* + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2, \end{aligned}$$

(3)

where $\lambda >0$ is the regularization parameter.

For diagonal matrices, the nuclear norm is just the $\ell _1$ norm of the diagonal elements. In sparse reconstruction and image recovery, using the $\ell _1$ norm to replace the cardinality function (also called the $\ell _0$ quasi-norm) for finding sparse solutions is a well-known technique in the literature [9, 16, 43]. So, (3) can be regarded as a generalization of the $\ell _1$ minimization problem. Compared to the $\ell _1$ norm $\Vert \varvec{x}\Vert _1$, the power p of the $\ell _p$ quasi-norm $\Vert \varvec{x}\Vert _p^p:=\sum _{i} |x_i|^p,0<p<1$, makes a closer approximation to the cardinality function $\Vert \varvec{x}\Vert _0$. Therefore, the $\ell _p$ quasi-norm is widely used in sparse reconstruction [11, 15, 27] and image recovery [39, 52]. Specifically, the $\ell _p$ minimization for sparse reconstruction is

$$\begin{aligned} \min _{\varvec{x}\in \mathbb {R}^{n}}\ \Vert \varvec{x}\Vert _p^p + \frac{\lambda }{2}\Vert A\varvec{x}-\varvec{b}\Vert _2^2, \end{aligned}$$

(4)

where $A\in \mathbb {R}^{m\times n},\varvec{b} \in \mathbb {R}^{m},\lambda >0$; and the $\ell _p$ minimization is often used for applications where $\varvec{x}$ is an image:

$$\begin{aligned} \min _{\varvec{x} \in \mathbb {R}^n} \sum _{i=1}^n \Vert D_i \varvec{x} \Vert _2^p + \frac{\lambda }{2} \Vert A\varvec{x} - \varvec{b}\Vert _2^2, \end{aligned}$$

(5)

where $A\in \mathbb {R}^{m\times n},\varvec{b} \in \mathbb {R}^{m},\lambda >0$, and $D_i \varvec{x}$ is the discrete gradient of $\varvec{x}$ at pixel i. The Schatten p-quasi-norm of X is defined as

$$\begin{aligned} \Vert X\Vert _{*,p} := \left( \sum _{i=1}^{h}\sigma _i^p(X) \right) ^{\frac{1}{p}}. \end{aligned}$$

Similarly, the Schatten p-quasi-norm ($0<p<1$) is also used for finding low-rank solutions, e.g., [21, 27, 36, 38]. The corresponding Schatten p-quasi-norm regularized least squares problem is

$$\begin{aligned} \min _{X\in \mathbb {R}^{m \times n}}\ \Vert X\Vert _{*,p}^p + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2, \end{aligned}$$

(6)

where $\lambda >0$ is the regularization parameter. Recently, a sufficient condition stating when the Schatten p-quasi-norm minimization can be used for low-rank matrix recovery was established in [26].

To solve (6), most existing methods follow the framework of the iteratively reweighted least-squares algorithms (IRLS-p) [20]. These methods are motivated by the following fact

$$\begin{aligned} \textrm{tr}\left( (X^{\top }X)^{p/2} \right) = \Vert X\Vert _{*,p}^p. \end{aligned}$$

By introducing a smoothing parameter $\varepsilon >0$, (6) is converted into

$$\begin{aligned} \min _{X\in \mathbb {R}^{m \times n}}\ \textrm{tr}\left( (X^{\top }X+\varepsilon I)^{p/2} \right) + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2. \end{aligned}$$

The first-order optimality condition of the above problem reads

$$\begin{aligned} pX(X^{\top }X + \varepsilon I)^{p/2-1} + \lambda \mathcal {A}^*(\mathcal {A}(X)-\varvec{b})=0, \end{aligned}$$

where $\mathcal {A}^*$ is the adjoint operator of $\mathcal {A}$. Given $X_k$ at iteration k, $X_{k+1}$ can be solved by

$$\begin{aligned} pX W_k + \lambda \mathcal {A}^*(\mathcal {A}(X)-\varvec{b})=0, \end{aligned}$$

(7)

where $W_k:= (X_k^{\top }X_k + \varepsilon I)^{p/2-1}$. Let the vectorized result of X be $\varvec{x}:=\textrm{vec}(X) \in \mathbb {R}^{mn}$. For a generic linear operator $\mathcal {A}$, (7) is a linear system in the form of $C \varvec{x}=\varvec{d}$, where $C \in \mathbb {R}^{mn\times mn},\varvec{d} \in \mathbb {R}^{mn}$. Hence, directly solving (7) is too expensive for general cases. For example, if $\mathcal {A}(X)=\varvec{b}$ is a Sylvester equation, then (7) is a general matrix equation, which is difficult to solve. See the discussion in Sect. 5.4. In the case of X being square, Gazzola et al. [21] converts (7) into a Tikhonov-regularized problem

$$\begin{aligned} X_{k+1}\in \arg \min _{X} \frac{p}{2}\left\| (X_kX_k^{\top } + \varepsilon I)^{p/4-1/2} X\right\| _F^2 + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2, \end{aligned}$$

and uses Krylov methods to solve it.

In this paper, we first give some theoretical analysis on (6). Our motivation comes from the low bound theory of the $\ell _p$ minimization for image recovery and sparse reconstruction. Suppose $\widetilde{\varvec{x}}$ is a (local) minimizer of (5). It is proved in [39, 52] that there exists a constant $\theta >0$ such that if $D_i \widetilde{\varvec{x}}\ne 0$, then

$$\begin{aligned} \Vert D_i \widetilde{\varvec{x}}\Vert _2 \ge \theta . \end{aligned}$$

Note that $\Vert D_i \widetilde{\varvec{x}}\Vert _2$ represents the contrast between neighboring pixels. This result suggests that the image restored by (5) has neat edges. Suppose $\widetilde{\varvec{x}}$ is a (local) minimizer of (4). Similarly, it is proved in [15] that there exists a constant $\theta >0$ such that if $\widetilde{x}_i\ne 0$, then

$$\begin{aligned} |\widetilde{x}_i| \ge \theta . \end{aligned}$$

This explains the advantage of (4) for sparse reconstruction: Each nonzero $\widetilde{x}_i$ plays a significant role, and we cannot obtain a sparser solution by changing any nonzero $\widetilde{x}_i$ into zero, without affecting the approximation error greatly. We will give a similar result for (6), i.e., there is a lower bound for the nonzero singular values of (local) minimizers of (6).

In solving nonlinear optimization problem, proximal linearization is a common technique; see, e.g., [5, 35, 54,55,56]. However, this technique cannot be used directly on (6), because $\Vert X\Vert _{*,p}^p$ is non-Lipschitz when X is singular. In IRLS-p, introducing a smoothing parameter $\varepsilon >0$ is just to tackle the non-Lipschitzian of $\Vert X\Vert _{*,p}^p$. After establishing the low bound theory, we will find that the non-Lipschitzian can be overcome by adding a rank constraint. Then the objective function can be proximally linearized and the converted subproblem is a weighted nuclear norm minimization with rank constraints. The subproblem can be solved efficiently by the (linearized) alternating direction method of multipliers. Unlike the existing methods [20, 21, 27, 36, 38], we do not need to solve the complicated linear system (7).

The Kurdyka–Łojasiewicz (KL) property of objective functions has been widely used in the proof of convergence of first-order methods, but most of these methods are aimed at functions whose arguments are vectors. For this work, the objective function (6) involves a singular value function $\Vert X\Vert _{*,p}^p$. We give a necessary and sufficient condition for a singular value function to be a KL function. The subdifferentials of related singular value functions are computed. In previous works on the convergence analysis based on the KL property, e.g., [2, 3, 5], Lipschitz gradient is usually a key assumption. For this work, the function $\Vert X\Vert _{*,p}^p$ does not have Lipschitz gradient. To tackle this difficulty, we prove the lower bound property of the iterate sequence $\{X_k\}$, under the assumption that the nonzero singular values of $X_k$ are strictly decreasing. In practical applications, this assumption holds generically. See Sect. 4.3 for details. With all these preparation, we prove the global convergence of the proposed algorithm.

The rest of this paper is organized as follows. In Sect. 2, we establish the low bound theory of the Schatten p-quasi-norm minimization. The algorithm is proposed in Sect. 3 and the convergence analysis is given in Sect. 4. Experimental results are given in Sect. 5. Conclusions are presented in Sect. 6.

1.1 Notation

Scalars are denoted by lowercase letters, e.g., $a,\alpha$. Vectors are denoted by boldface lowercase letters, e.g., $\varvec{a},\varvec{\alpha }$. Matrices are denoted by capital letters, e.g., $A,\Sigma$. The n-dimensional nonnegative real vector space is denoted by $\mathbb {R}^n_+$. Given a vector $\varvec{x}\in \mathbb {R}^n$, $|\varvec{x}|=[|x_1|,\ldots ,|x_n|]^\top \in \mathbb {R}^n_+$. Given a vector $\varvec{x}\in \mathbb {R}^m$, we use $\mathop {\textrm{diag}}(\varvec{x})$ to denote a matrix whose main diagonal is $x_1,\ldots ,x_m$. Usually, we do not mention the size of $\mathop {\textrm{diag}}(\varvec{x})$, which will be clear from the context. The $\ell _2$ norm of $\varvec{x}$ is denoted by $\Vert \varvec{x}\Vert _2$. The Frobenius norm of X is denoted by $\Vert X\Vert _F$. The spectral norm of X is denoted by $\Vert X\Vert _2$. Let $X\in \mathbb {R}^{m\times n}$. The singular value vector of X is denoted by $\varvec{\sigma }(X):=\left[ \sigma _1(X),\ldots , \sigma _h(X)\right] ^\top \in \mathbb {R}^{h}$, where $h =\min \{m,n\}$ and $\sigma _1(X)\ge \cdots \ge \sigma _h(X)$ are all singular values of X. The Stiefel manifold is defined as

$$\begin{aligned} \textrm{ St }_t^m:=\{Y \in \mathbb {R}^{m\times t}: Y^\top Y = I\}. \end{aligned}$$

The set of all singular matrices of X is denoted by

$$\begin{aligned} \textrm{ Sm }(X):=\left\{ (U,V)\in \textrm{ St }^m_m \times \textrm{ St }^n_n: U\mathop {\textrm{diag}}(\varvec{\sigma }(X))V^\top =X \right\} . \end{aligned}$$

(8)

Let $\mathscr {S}$ be a subset of $\mathbb {R}^n$. The indicator function of $\mathscr {S}$ is defined as

$$\begin{aligned} \delta _{\mathscr {S}}(\varvec{x})={\left\{ \begin{array}{ll} 0, &{} \text{ if } \varvec{x}\in \mathscr {S}, \\ +\infty , &{} \text{ otherwise }.\end{array}\right. } \end{aligned}$$

2 Lower bound of singular values

Theorem 2.1

Let $\theta = \left( \frac{p(1-p)}{\lambda \Vert \mathcal {A}\Vert _2^2} \right) ^{\frac{1}{2-p}}$, where $\Vert \mathcal {A}\Vert _2$ is the spectral norm of $\mathcal {A}$. For each (local) minimizer $\widetilde{X}$ of (6), we have

$$\begin{aligned} \sigma _r(\widetilde{X}) \ge \theta \quad \mathrm{for\, all }\, r=1,\ldots ,\textrm{rank}(\widetilde{X}). \end{aligned}$$

Proof

Let $h=\min \{m,n\}$ in (6). Each $X \in \mathbb {R}^{m\times n}$ can be written as

$$\begin{aligned} X = U\Gamma V^{\top }, \end{aligned}$$

where $U=[\varvec{u}_1 \cdots \varvec{u}_h]\in \textrm{ St }_h^m,V=[\varvec{v}_1 \cdots \varvec{v}_t]\in \textrm{ St }_h^n$, and $\Gamma =\mathop {\textrm{diag}}(\gamma _1, \ldots ,\gamma _h)$. Then $|\gamma _i|,i=1,\ldots ,h$ are all singular values of X. Define $\varvec{\gamma }:=[\gamma _1, \ldots , \gamma _h]^{\top } \in \mathbb {R}^h$. Problem (6) is equivalent to

$$\begin{aligned} \min _{\varvec{\gamma } \in \mathbb {R}^h}\min _{U\in \textrm{ St }_h^m}\min _{V\in \textrm{ St }_h^n}\ \Vert \varvec{\gamma }\Vert _p^p + \frac{\lambda }{2}\Vert \mathcal {A}(U\Gamma V^{\top })- \varvec{b}\Vert _2^2. \end{aligned}$$

Suppose $(\widetilde{\varvec{\gamma }},\widetilde{U},\widetilde{V})$ is a local minimizer of the above problem. Then $\widetilde{\varvec{\gamma }}$ is a local minimizer of

$$\begin{aligned} \min _{\varvec{\gamma } \in \mathbb {R}^h}\ \Vert \varvec{\gamma }\Vert _p^p + \frac{\lambda }{2} \Vert \mathcal {A}(\widetilde{U}\Gamma \widetilde{V}^{\top })- \varvec{b}\Vert _2^2. \end{aligned}$$

(9)

Note that $\mathcal {A}$ is a linear operator. We have

$$\begin{aligned} \mathcal {A}(\widetilde{U}\Gamma \widetilde{V}^\top ) = \mathcal {A}\left( \sum _{i=1}^{h}\gamma _i \widetilde{\varvec{u}}_i\widetilde{\varvec{v}}_i^\top \right) = \sum _{i=1}^{h}\gamma _i \mathcal {A}\left( \widetilde{\varvec{u}}_i\widetilde{\varvec{v}}_i^{\top }\right) . \end{aligned}$$

Define a matrix $C=[\varvec{c}_1 \cdots \varvec{c}_h]\in \mathbb {R}^{d\times h}$ with $\varvec{c}_i = \mathcal {A}\left( \widetilde{\varvec{u}}_i\widetilde{\varvec{v}}_i^{\top }\right) \in \mathbb {R}^{d},i=1,\ldots ,h$. Then $\mathcal {A}(\widetilde{U}\Gamma \widetilde{V}^\top ) = C \varvec{\gamma }$ and (9) is converted into

$$\begin{aligned} \min _{\varvec{\gamma } \in \mathbb {R}^h}\ \Vert \varvec{\gamma }\Vert _p^p+ \frac{\lambda }{2}\Vert C\varvec{\gamma }-\varvec{b}\Vert _2^2, \end{aligned}$$

which is an $\ell _p-\ell _2$ minimization problem. Note that $\Vert \textrm{vec}(\widetilde{\varvec{u}}_i\widetilde{\varvec{v}}_i^{\top })\Vert _2 = \Vert \widetilde{\varvec{u}}_i\Vert _2 \Vert \widetilde{\varvec{v}}_i\Vert _2=1$ and $\Vert \varvec{c}_i\Vert _2 = \Vert \mathcal {A}\left( \widetilde{\varvec{u}}_i\widetilde{\varvec{v}}_i^{\top }\right) \Vert _2 \le \Vert \mathcal {A}\Vert _2$. By Chen et al. [15, Theorem 2.1], if $\widetilde{\gamma }_i \ne 0$, we have

$$\begin{aligned} |\widetilde{\gamma }_i|\ge \left( \frac{p(1-p)}{\lambda \Vert \varvec{c}_i\Vert _2^2} \right) ^{\frac{1}{2-p}} \ge \left( \frac{p(1-p)}{\lambda \Vert \mathcal {A}\Vert _2^2} \right) ^{\frac{1}{2-p}} = \theta . \end{aligned}$$

This completes the proof. $\square$

Like the lower bound theory of (4), the preceding theorem explains the advantage of (6) for low-rank matrix recovery: Each nonzero singular value plays a significant role, and we cannot obtain a lower rank solution by changing any nonzero singular value into zero, without affecting the approximation error greatly. On the other hand, if the original low-rank matrix has some singular values with very small magnitudes, using (6) cannot recover the original matrix exactly.

Let

$$\begin{aligned} \mathscr {M}_{\le r} := \{X \in \mathbb {R}^{m\times n}: \textrm{rank}(X)\le r\} \end{aligned}$$

(10)

denote the set of matrices of rank at most r. We have the following corollary.

Corollary 2.2

Let $\theta =\left( \frac{p(1-p)}{\lambda \Vert \mathcal {A}\Vert _2^2} \right) ^{\frac{1}{2-p}}$ and $\widetilde{X}$ be a local minimizer of (6). Then we have

$$\begin{aligned} \Vert X - \widetilde{X}\Vert _F \ge \theta \quad \forall X \in \mathscr {M}_{\le \textrm{rank}(\widetilde{X})-1}. \end{aligned}$$

Proof

Let $h=\min \{m,n\}$. By Horn and Johnson [24, Corollary 7.4.1.3], for any $X \in \mathscr {M}_{\le \textrm{rank}(\widetilde{X})-1}$, we have

$$\begin{aligned} \Vert X-\widetilde{X}\Vert _F^2&\ge \sum _{i=1}^{h}\left( \sigma _i(X) - \sigma _i(\widetilde{X})\right) ^2 \ge \left( \sigma _{\textrm{rank}(\widetilde{X})}(X) - \sigma _{\textrm{rank}(\widetilde{X})}(\widetilde{X})\right) ^2 \\&= \sigma _{\textrm{rank}(\widetilde{X})}^2(\widetilde{X}) \ge \theta ^2, \end{aligned}$$

which completes the proof. $\square$

With $\theta$ defined in the preceding corollary, denote the ball of radius $\theta$ around X by

$$\begin{aligned} \mathscr {B}(X,\theta ):= \{Y\in \mathbb {R}^{m\times n}: \Vert Y-X\Vert _F \le \theta \}. \end{aligned}$$

The preceding corollary is equivalent to say that any minimizer in $\mathscr {B}(X,\theta )$ has rank less than $\textrm{rank}(X)$.

3 Algorithm

Suppose we use an iterative algorithm to find a local minimizer $\widetilde{X}$ of (6) and the iterate sequence is $\{X_k\}$. By Corollary 2.2, if $\lim _{k\rightarrow \infty } X_k = \widetilde{X}$, then there is a $\widetilde{k}$ such that $\textrm{rank}(\widetilde{X}) \le r_k:=\textrm{rank}(X_k)$ for all $k\ge \widetilde{k}$. Motivated by this phenomenon, we consider solving $X_{k+1}$ by

$$\begin{aligned} \min _{\textrm{rank}(X)\le r_k}\ \mathcal {P}(X):=\Vert X\Vert _{*,p}^p + \frac{\lambda }{2} \Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2. \end{aligned}$$

(11)

Directly solving (11) is difficult. Usually, the linearization technique, i.e, the first-order Taylor approximation of some term around $X_k$, is employed to obtain an approximate objective function which is easy to solve. In (11), what we need to linearize is the term $\Vert X\Vert _{*,p}^p$. Generally, the linearization cannot be used because $\Vert X\Vert _{*,p}^p$ is non-Lipschitz when $X_k$ is singular. However, thanks to the constraint $\textrm{rank}(X)\le r_k$, we can still employ the linearization on (11). Specifically, for $X\in \mathbb {R}^{m\times n}$ with $\textrm{rank}(X)\le r_k$, we have

$$\begin{aligned} \Vert X\Vert _{*,p}^p = \sum _{j=1}^{r_k}\sigma _j^p(X)\approx \sum _{j=1}^{r_k} \left( \sigma _j^p(X_k) + p \sigma _j^{p-1}(X_k)\cdot \left( \sigma _j(X) - \sigma _j(X_k) \right) \right) . \end{aligned}$$

(12)

For convenience, we define

$$\begin{aligned}&\sigma _{k,j}=\sigma _j(X_k),&\quad \varvec{\sigma }_{k} = [\sigma _{k,1},\ldots ,\sigma _{k,r_k}]^\top \in \mathbb {R}^{r_k}, \nonumber \\&w_{k,j}=p \sigma _{k,j}^{p-1},&\quad \varvec{w}_{k} = [w_{k,1},\ldots ,w_{k,r_k}]^\top \in \mathbb {R}^{r_k}. \end{aligned}$$

(13)

Since $\sigma _1(X_k) \ge \cdots \ge \sigma _{r_k}(X_k)> 0$, we have

$$\begin{aligned} w_{k,1} \le \cdots \le w_{k,r_k}. \end{aligned}$$

(14)

In addition, since the function $z \mapsto z^p$ is concave on $[0,+\infty )$, it follows that for all $X\in \mathbb {R}^{m\times n}$ with $\textrm{rank}(X)\le r_k$,

$$\begin{aligned} \Vert X\Vert _{*,p}^p \le \sum _{j=1}^{r_k}w_{k,j}\sigma _j(X) + \sum _{j=1}^{r_k} (\sigma _{k,j}^p - w_{k,j}\sigma _{k,j}). \end{aligned}$$

(15)

Substituting (12) into (11), deleting some constants and adding a proximal term, we obtain the following proximal linearization version of (11):

$$\begin{aligned} \min _{\textrm{rank}(X)\le r_k}\ \mathcal {H}_k(X):=\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2 + \frac{\tau }{2}\Vert X - X_k\Vert _F^2. \end{aligned}$$

(16)

The proximal term $\frac{\tau }{2}\Vert X - X_k\Vert _F^2$ is to increase the robustness of the nonconvex algorithm and is helpful in the global convergence. By (15), we can set $\tau$ to be any positive scalar. Let $\delta _{\mathscr {M}_{\le r}}(X)$ be the indicator function of $\mathscr {M}_{\le r}$, where $\mathscr {M}_{\le r}$ is defined in (10). Then (16) is equivalent to

$$\begin{aligned} \min _{X\in \mathbb {R}^{m\times n}}\mathcal {G}_k(X):=\mathcal {H}_k(X)+ \delta _{\mathscr {M}_{\le r_k}}(X). \end{aligned}$$

(17)

We will use an iterative algorithm to solve (16) or (17). Precisely solving the subproblem (17) needs infinite iteration steps, which cannot be realized in real computation. Therefore, we consider solving (17) inexactly. The whole procedure of the proximal linearization method (PLM) is summarized in Algorithm 1. In general, algorithms for nonconvex problems seek only a local solution. Therefore, the initial values are important for nonconvex optimization. For Algorithm 1, $r_0$ and $\varvec{w}_{0}$ are determined by $X_0$. In addition, PLM has used the scheme of proximal linearization, which approximates the original model linearly. If the starting point $X_0$ is far from the final result, a large number of steps would be required for convergence. Therefore, the initial value $X_0$ is very crucial for PLM. We will elaborate this issue in Sect. 5.1.

Remark 3.1

The problem (17) will be solved by an iterative algorithm, whose starting point is $X_k$. Hence, the condition (18) can be satisfied easily.

Remark 3.2

The inexact optimal condition (19) originates from the algorithmic framework proposed in [3]. Similar inexact optimal conditions can be found in [35, 55, 56]. The rationality of this condition will be elaborated in Remark 4.18.

Before solving (16), we discuss how to solve a simpler problem as follows

$$\begin{aligned} \min _{\textrm{rank}(X) \le r} \sum _{i=1}^{r}w_i \sigma _i(X) + \frac{1}{2} \Vert X-Y\Vert _F^2, \end{aligned}$$

which constitutes a core step in solving (16). Let $M \in \mathbb {R}^{m\times n},h = \min \{m,n\}$, and let $\varvec{w}=[w_1, \ldots , w_r]^\top \in \mathbb {R}^r$ with $r\le h$. We define the following set

$$\begin{aligned} \mathcal {D}^r_{\varvec{w}}(M):= \bigg \{&U\Sigma ^r_{\varvec{w}}V^\top : (U,V)\in \textrm{ Sm }(M), \\&\Sigma ^r_{\varvec{w}}=\mathop {\textrm{diag}}\left( (\sigma _1(M)-w_1)_+,\ldots ,(\sigma _r(M)-w_r)_+,0, \ldots ,0 \right) \bigg \}, \end{aligned}$$

where $\textrm{ Sm }(M)$ is defined in (8) and $(a)_+ = \max \{a,0\}$. We have the following lemma.

Lemma 3.3

Let $Y \in \mathbb {R}^{m\times n},h = \min \{m,n\}$, and $\varvec{w}=[w_1, \ldots , w_r]^\top \in \mathbb {R}^r$ with $r\le h$. If $(\sigma _1(Y)-w_1)_+ \ge \cdots \ge (\sigma _r(Y)-w_r)_+$, then we have

$$\begin{aligned} \mathcal {D}^r_{\varvec{w}}(Y) = \arg \min _{\textrm{rank}(X) \le r} \sum _{i=1}^{r}w_i \sigma _i(X) + \frac{1}{2} \Vert X-Y\Vert _F^2. \end{aligned}$$

(20)

Proof

For any $X \in \mathbb {R}^{m\times n}$ with $\textrm{rank}(X) \le r$, by Horn and Johnson [24, Corollary 7.4.1.3], we have

$$\begin{aligned}&\sum _{i=1}^{r}w_i \sigma _i(X) + \frac{1}{2} \Vert X-Y\Vert _F^2 \\&\quad \ge \sum _{i=1}^{r}w_i \sigma _i(X) + \frac{1}{2}\sum _{i=1}^{r}(\sigma _i(X) - \sigma _i(Y))^2 + \frac{1}{2} \sum _{i=r+1}^{h}\sigma _i^2(Y) \\&\quad = \sum _{i=1}^{r}\left( \frac{1}{2}\sigma _i^2(X)+(w_i- \sigma _i(Y))\sigma _i(X) \right) + \frac{1}{2} \sum _{i=1}^{h}\sigma _i^2(Y), \end{aligned}$$

where the equality holds if and only if there are orthogonal matrices U and V such that $X=U \Sigma _X V^\top$ and $Y=U \Sigma _Y V^\top$ are SVD’s of X and Y, respectively. Therefore, the matrix optimization problem (20) is equivalent to the following vector optimization problem

$$\begin{aligned} \begin{aligned} \min _{\sigma _i(X),1\le i\le r}\quad&\sum _{i=1}^{r} \frac{1}{2}\sigma _i^2(X)+(w_i- \sigma _i(Y))\sigma _i(X) \\ \mathrm { s.t. }\quad&\sigma _1(X)\ge \cdots \ge \sigma _r(X)\ge 0. \end{aligned} \end{aligned}$$

(21)

This problem is a strictly convex quadratic programming and has a unique solution. If $(\sigma _1(Y)-w_1)_+ \ge \cdots \ge (\sigma _r(Y)-w_r)_+$, the minimum of (21) is achieved by $\sigma _i(X)=(\sigma _i(Y)- w_i)_+,i=1,\ldots ,r$. This completes the proof. $\square$

The result (20) can be viewed as a combination of the classic Eckart-Young theorem [17] and the singular value shrinkage [7, Theorem 2.1]. In addition, just like the low-rank approximation problem [17], (20) has a unique solution if and only if $\sigma _r(Y)>\sigma _{r+1}(Y)$.

The problem (16) is a weighted nuclear norm minimization with rank constraints, and its computation can follow that of the standard nuclear norm minimization (3). Refer to Yang and Yuan [50, Sect. 5] and references therein for a thorough review on the computation of (3). As shown in [50], in general, the alternating direction method of multipliers (ADMM) or linearized ADMM (LADMM) is more efficient than other methods for solving (3). Therefore, we also use (L)ADMM to solve (16).

3.1 Solving (16) via ADMM

By introducing an auxiliary variable $Y \in \mathbb {R}^{m\times n}$, (16) is equivalently transformed into

$$\begin{aligned} \begin{aligned} \min _{\textrm{rank}(X)\le r_k}\min _{Y\in \mathbb {R}^{m\times n}}\quad&\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\lambda }{2}\Vert \mathcal {A}(Y)-\varvec{b}\Vert _2^2 + \frac{\tau }{2}\Vert Y - X_k\Vert _F^2 \\ \mathrm { s.t. }\quad&X = Y. \end{aligned} \end{aligned}$$

The augmented Lagrangian function of the above problem reads

$$\begin{aligned} \mathcal {L}(X,Y,Z,\beta _k)&= \sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \langle Z, X- Y\rangle + \frac{\beta _k}{2}\Vert X-Y\Vert _F^2 \\&\quad + \,\frac{\lambda }{2}\Vert \mathcal {A}(Y)-\varvec{b}\Vert _2^2 + \frac{\tau }{2}\Vert Y - X_k\Vert _F^2, \end{aligned}$$

where Z is the Lagrange multiplier and $\beta _k>0$ is the penalty parameter. The iterative scheme of ADMM reads

The two subproblems in the above algorithm are calculated as follows.

• 1. The X-subproblem (22). We can simplify (22) as

  $$\begin{aligned} X_{t+1} \in \arg \min _{\textrm{rank}(X)\le r_k}\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\beta _k}{2} \left\| X - \left( Y_t-\frac{1}{\beta _k}Z_t\right) \right\| _F^2. \end{aligned}$$

  (24)

  Combining (20) and (14) gives one solution of (24):

  $$\begin{aligned} X_{t+1} \in \mathcal {D}_{\varvec{w}_k/\beta _k}^{r_k}\left( Y_t-\frac{1}{\beta _k}Z_t\right) . \end{aligned}$$

  (25)

• 2. The Y-subproblem (23). We can simplify (23) as

  $$\begin{aligned} Y_{t+1} \in \arg \min _{Y \in \mathbb {R}^{m\times n}}\left( \langle Z_t, X_t- Y\rangle + \frac{\beta _k}{2}\Vert X_t-Y\Vert _F^2 + \frac{\lambda }{2}\Vert \mathcal {A}(Y)-\varvec{b}\Vert _2^2 + \frac{\tau }{2}\Vert Y - X_k\Vert _F^2 \right) . \end{aligned}$$

  This is a least squares problem and the corresponding normal equation is

  $$\begin{aligned} \left( \mathcal {I}+ \frac{\lambda }{\beta _k+\tau }\mathcal {A}^*\mathcal {A} \right) Y= \frac{1}{\beta _k+\tau }\left( Z_t+\beta _k X_t + \lambda \mathcal {A}^*(\varvec{b}) + \tau X_k \right) , \end{aligned}$$

  (26)

  where $\mathcal {I}$ represents the identity operator.

We summarize the whole procedure of ADMM in Algorithm 2.

The computation of (25) is just a partial SVD and has a time cost $O(mnr_k)$. The efficiency of Algorithm 2 depends heavily on whether we can solve (26) efficiently and this is related to the feature of $\mathcal {A}: \mathbb {R}^{m\times n}\rightarrow \mathbb {R}^d$. For a generic linear operator $\mathcal {A}$, the time cost of (26) is as high as $O(m^3n^3)$. However, if $\mathcal {A}$ has special structures or features, (26) can be solved much faster with specifical methods. For example, if there exists $A\in \mathbb {R}^{s\times m}$ such that $\mathcal {A}(X)= \textrm{vec}(AX)$, then (26) is just a matrix equation in the form of $CY =B$, where $C \in \mathbb {R}^{m\times m}, B \in \mathbb {R}^{m \times n}$. More generally, if the matrix representation of $\mathcal {A}$ is block diagonal, (26) can be solved in a low cost. In the following, we will give two special cases where (26) can be solved efficiently.

3.1.1 The case $\mathcal {A}\mathcal {A}^*=\mathcal {I}$

In the matrix completion problem, $\mathcal {A}$ is a sampling operator collecting a fraction of entries of a matrix, and $\mathcal {A}\mathcal {A}^*=\mathcal {I}$. When $\mathcal {A}\mathcal {A}^*=\mathcal {I}$, by the Sherman-Morrison-Woodbury formula, we have

$$\begin{aligned} \left( \mathcal {I}+\frac{\lambda }{\beta _k+\tau } \mathcal {A}^*\mathcal {A}\right) ^{-1} = \mathcal {I} - \frac{\lambda }{\lambda +\beta _k+\tau } \mathcal {A}^*\mathcal {A}. \end{aligned}$$

(27)

By noting (27), (26) has a closed-form solution:

$$\begin{aligned} Y_{t+1}= \frac{1}{\beta _k+\tau }\left( \mathcal {I} - \frac{\lambda }{\lambda +\beta _k+\tau } \mathcal {A}^*\mathcal {A} \right) \left( Z_t+\beta _k X_t + \lambda \mathcal {A}^*(\varvec{b})+ \tau X_k \right) . \end{aligned}$$

3.1.2 The case where $\mathcal {A}$ is a convolution operator

In signal processing, image processing and many other engineering applications, convolution has a wide applications. If $\mathcal {A}$ is a convolution operator, then (26) is a circulant linear system and can be solved efficiently by the discrete Fourier transform (DFT). If $\mathcal {A}$ is a 2D convolution operator, then the matrix representation of $\mathcal {A}^*\mathcal {A}$ is a block circulant matrix with circulant blocks and can be diagonalized by the two-dimensional DFT.

Specifically, if $\mathcal {A}$ is a convolution operator, let $\varvec{y}:=\textrm{vec}(Y)$. Suppose the matrix representation of $\mathcal {A}$ is a circulant matrix A whose first column is $\varvec{a}_1 \in \mathbb {R}^{mn}$. Let $\varvec{e}_1$ be the first standard basis. Then (26) is transformed into

$$\begin{aligned} \left( (\beta _k+\tau )I+ \lambda A^\top A\right) \varvec{y} = \textrm{vec}\left( Z_t+\beta _k X_t + \tau X_k \right) + \lambda A^\top \varvec{b}. \end{aligned}$$

(28)

Let $\mathcal {F}$ be the DFT operator, $\bar{\varvec{c}}$ be the conjugate of $\varvec{c}$ and “$\circ$” be the Hadamard product. Applying the DFT on both sides of (28), we obtain

$$\begin{aligned}&\left( (\beta _k+\tau )\mathcal {F}(\varvec{e}_1) + \lambda \overline{\mathcal {F}(\varvec{a}_1)} \circ \mathcal {F}(\varvec{a}_1) \right) \circ \mathcal {F}(\varvec{y}) \nonumber \\&\quad = \mathcal {F}\left( \textrm{vec}\left( Z_t+\beta _k X_t + \tau X_k \right) \right) + \lambda \overline{\mathcal {F}(\varvec{a}_1)} \circ \mathcal {F}(\varvec{b}) \nonumber \\ \Rightarrow \quad&\varvec{y} = \mathcal {F}^{-1}\left( \frac{\mathcal {F}\left( \textrm{vec}\left( Z_t+\beta _k X_t +\tau X_k \right) \right) + \lambda \overline{\mathcal {F}(\varvec{a}_1)} \circ \mathcal {F}(\varvec{b})}{(\beta _k+\tau )\mathcal {F}(\varvec{e}_1)+\lambda \overline{\mathcal {F}(\varvec{a}_1)} \circ \mathcal {F}(\varvec{a}_1)}\right) . \end{aligned}$$

(29)

Note that $\mathcal {F}(\varvec{e}_1)$ is a vector of all ones and all quantities but $Z_t+\beta _k X_t + \tau X_k$ are constant. Hence, computing $\varvec{y}$ from (29) involves one DFT and one inverse DFT, once the constant quantities are computed.

The case where $\mathcal {A}$ is a 2D convolution operator is similar. Refer to [47, Sect. 2] for details.

3.2 Solving (16) via LADMM

If (26) is too expensive to solve, we consider using LADMM. By introducing an auxiliary variable $\varvec{y} \in \mathbb {R}^{d}$, (16) is equivalently transformed into

$$\begin{aligned} \begin{aligned} \min _{\textrm{rank}(X)\le r_k}\min _{\varvec{y}\in \mathbb {R}^{d}}\quad&\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\lambda }{2}\Vert \varvec{y}\Vert _2^2 + \frac{\tau }{2}\Vert X - X_k\Vert _F^2 \\ \mathrm { s.t. }\quad&\mathcal {A}(X)-\varvec{b} = \varvec{y}. \end{aligned} \end{aligned}$$

The augmented Lagrangian function of the above problem reads

$$\begin{aligned} \mathcal {L}(X,\varvec{y},\varvec{z},\beta _k) =&\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \langle \varvec{z}, \mathcal {A}(X)-\varvec{b}- \varvec{y}\rangle + \frac{\beta _k}{2} \Vert \mathcal {A}(X)-\varvec{b}- \varvec{y}\Vert _2^2 \\&+ \frac{\lambda }{2}\Vert \varvec{y}\Vert _2^2 + \frac{\tau }{2}\Vert X - X_k\Vert _F^2, \end{aligned}$$

where $\varvec{z}$ is the Lagrange multiplier and $\beta _k>0$ is the penalty parameter. The iterative scheme of ADMM reads

The $\varvec{y}$-subproblem (30) can be simplified as

$$\begin{aligned} \varvec{y}_{t+1} \in \arg \min _{\varvec{y}}\frac{\lambda }{2}\Vert \varvec{y}\Vert _2^2 + \frac{\beta }{2} \left\| \varvec{y} - \left( \mathcal {A}(X_{t})-\varvec{b}+\frac{1}{\beta _k}\varvec{z}_t\right) \right\| _2^2, \end{aligned}$$

which has a closed-form solution given by

$$\begin{aligned} \varvec{y}_{t+1} = \frac{\beta _k}{\lambda +\beta _k}\left( \mathcal {A}(X_{t})- \varvec{b}+\frac{1}{\beta _k}\varvec{z}_t\right) . \end{aligned}$$

The X-subproblem (31) can be simplified as

$$\begin{aligned} X_{t+1} \in \arg \min _{\textrm{rank}(X)\le r_k}\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\beta _k}{2}\left\| \mathcal {A}(X)- \varvec{c}_t \right\| _2^2 + \frac{\tau }{2}\Vert X - X_k\Vert _F^2, \end{aligned}$$

(32)

where $\varvec{c}_t = \varvec{b} + \varvec{y}_{t+1} - \frac{1}{\beta _k}\varvec{z}_t$. Like (12), we consider the proximal linearization:

$$\begin{aligned} \frac{1}{2}\left\| \mathcal {A}(X)- \varvec{c}_t \right\| _2^2 \approx \frac{1}{2}\left\| \mathcal {A}(X_t)- \varvec{c}_t \right\| _2^2 + \langle X - X_t, G_t \rangle + \frac{\eta }{2}\Vert X - X_t\Vert _F^2, \end{aligned}$$

(33)

where

$$\begin{aligned} G_t = \mathcal {A}^*(\mathcal {A}(X_t)- \varvec{c}_t)= \mathcal {A}^* \left( \mathcal {A}(X_t)- \varvec{b} -\varvec{y}_{t+1} + \frac{1}{\beta _k}\varvec{z}_t \right) \end{aligned}$$

(34)

is the gradient of $\frac{1}{2}\left\| \mathcal {A}(X)- \varvec{c}_t \right\| _2^2$ at $X_t$ and $\eta >0$ is the proximal parameter. We will choose

$$\begin{aligned} \eta \ge \Vert \mathcal {A}^* \mathcal {A}\Vert _2 \end{aligned}$$

(35)

to guarantee the right hand of (33) is an upper bound of $\frac{1}{2}\left\| \mathcal {A}(X)- \varvec{c}_t \right\| _2^2$ near $X_t$. Substituting (33) into (32) and deleting some constants, we obtain the following proximal linearization version of (32)

$$\begin{aligned} X_{t+1} \in \arg \min _{\textrm{rank}(X)\le r_k}\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X) + \frac{\beta _k\eta +\tau }{2}\left\| X - \frac{\beta _k\eta X_t-\beta _k G_t+\tau X_k}{\beta _k\eta + \tau }\right\| _F^2, \end{aligned}$$

whose solution is

$$\begin{aligned} X_{t+1} = \mathcal {D}_{\varvec{w}_k/(\beta _k\eta +\tau )}^{r_k} \left( \frac{\beta _k\eta X_t-\beta _k G_t +\tau X_k}{\beta _k\eta + \tau }\right) , \end{aligned}$$

(36)

where $G_t$ and $\eta$ are given in (34) and (35).

We summarize the whole procedure of LADMM in Algorithm 3.

4 Convergence analysis

We discuss the convergence properties of PLM in Algorithm 1. In Sect. 4.1, we will establish the convergence properties of $\{r_k\}$ and $\{\mathcal {P}(X_k)\}$, where $\mathcal {P}(X)$ is the objective function defined in (11). The global convergence of $\{X_k\}$ will be discussed in Sect. 4.3.

4.1 Basic convergence properties of PLM

Proposition 4.1

Let $\{X_k\}$ be generated by Algorithm 1. Then,

• 1. The objective function sequence $\{\mathcal {P}(X_k)\}$ satisfies

  $$\begin{aligned} \frac{\tau }{2}\Vert X_{k+1}-X_{k}\Vert _F^2 \le \mathcal {P}(X_k)-\mathcal {P}(X_{k+1}) \end{aligned}$$

  (37)

  and converges;

• 2. The iterate sequence $\{X_k\}$ is bounded and satisfies

  $$\begin{aligned} \lim _{k\rightarrow \infty } \Vert X_k - X_{k+1}\Vert _F = 0. \end{aligned}$$

  (38)

Proof

For $X\in \mathbb {R}^{m\times n}$ with $\textrm{rank}(X)\le r_k$, it follows from (15) that

$$\begin{aligned} \mathcal {P}(X)+\frac{\tau }{2}\Vert X- X_k\Vert _F^2 \le \mathcal {H}_k(X)+\sum _{j=1}^{r_k}(\sigma _{k,j}^p - w_{k,j}\sigma _{k,j}). \end{aligned}$$

(39)

Note that $\delta _{\mathscr {M}_{\le r_k}}(X_k)=\delta _{\mathscr {M}_{\le r_k}}(X_{k+1})=0$. We have

$$\begin{aligned} \mathcal {H}_k(X_{k+1}) = \mathcal {H}_k(X_{k+1})+\delta _{\mathscr {M}_{\le r_k}}(X_{k+1}) \overset{(18)}{\le }\ \mathcal {H}_k(X_{k})+\delta _{\mathscr {M}_{\le r_k}}(X_{k}) =\mathcal {H}_k(X_{k}).\nonumber \\ \end{aligned}$$

(40)

Combining the above results, we have

$$\begin{aligned} \mathcal {P}(X_{k+1})+\frac{\tau }{2}\Vert X_{k+1} - X_k\Vert _F^2&\overset{(39)}{\le }\ \mathcal {H}_k(X_{k+1}) + \sum _{j=1}^{r_k}(\sigma _{k,j}^p - w_{k,j}\sigma _{k,j}) \\&\overset{(40)}{\le }\ \mathcal {H}_k(X_{k}) + \sum _{j=1}^{r_k}(\sigma _{k,j}^p - w_{k,j}\sigma _{k,j})\\&\overset{(16)}{=}\ \sum _{j=1}^{r_k}\sigma _{k,j}^p + \frac{\lambda }{2}\Vert \mathcal {A}(X_{k})-\varvec{b}\Vert _2^2=\mathcal {P}(X_{k}), \end{aligned}$$

which proves (37).

Combining (37) and the fact that $\mathcal {P}(X_k)\ge 0$ yields the convergence of $\{\mathcal {P}(X_k)\}$. Since $\mathcal {P}(X)$ is coercive, it follows that $\{X_k\}$ is bounded. Let $c > 1$ be an integer. Summing (37) from $k=0$ to $c-1$ we obtain

$$\begin{aligned} \sum _{k=0}^{c-1}\Vert X_{k+1}-X_k\Vert _F^2 \le \frac{2}{\tau } \left( \mathcal {P}(X_0) - \mathcal {P}(X_c)\right) \le \frac{2}{\tau }\mathcal {P}(X_0). \end{aligned}$$

Taking the limit as $c\rightarrow \infty$ gives $\sum _{k=0}^{\infty } \Vert X_{k+1}-X_k\Vert _F^2 < +\infty$, and hence yields (38). $\square$

For the convergence of $\{r_k\}$, we have the following result.

Lemma 4.2

The sequence $\{r_k\}$ satisfies $r_{k+1}\le r_k$ and converges within finite steps.

Proof

From Algorithm 1 we know that $r_{k+1}\le r_k$. Since $r_k \in \{0,1,\ldots ,r_0\}$, it follows that $\{r_k\}$ will converge within finite steps. $\square$

The preceding lemma implies that

$$\begin{aligned} \exists \widetilde{r},\widetilde{k} \text { such that } r_k = \widetilde{r} \quad \forall k \ge \widetilde{k}. \end{aligned}$$

(41)

Let

$$\begin{aligned} \mathscr {M}_r := \{X \in \mathbb {R}^{m\times n}: \textrm{rank}(X)= r\} \end{aligned}$$

denote the manifold of fixed-rank matrices and let $\delta _{\mathscr {M}_{\widetilde{r}}}(X)$ be the indicator function of $\mathscr {M}_{\widetilde{r}}$. When $k\ge \widetilde{k}$, $\mathcal {G}_k(X)$ defined in (17) has the following form:

$$\begin{aligned} \mathcal {G}_k(X)=\sum _{j=1}^{\widetilde{r}} w_{k,j} \sigma _j(X)+ \frac{\lambda }{2} \Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2 + \frac{\tau }{2}\Vert X - X_k\Vert _F^2+ \delta _{\mathscr {M}_{\widetilde{r}}}(X). \end{aligned}$$

(42)

4.2 Singular value functions and KL functions

To prove the global convergence of $\{X_k\}$, we need some knowledge on singular value functions and KL functions.

Definition 4.3

A function $f: \mathbb {R}^n \rightarrow [-\infty ,+\infty ]$ is an absolutely symmetric function if $f(\varvec{x})=f(P|\varvec{x}|)$ for every $\varvec{x}\in \mathbb {R}^{n}$ and every permutation matrix $P \in \mathbb {R}^{n\times n}$.

Absolutely symmetric functions are extensions of symmetric gauge functions, which play a special role in unitarily invariant norms. Refer to Horn and Johnson [24, Chapter 7.4] and Lewis and Sendov [31, Sect. 5] for details.

Definition 4.4

A function $\mathcal {F}: \mathbb {R}^{m\times n} \rightarrow [-\infty ,+\infty ]$ is a singular value function if there is an absolutely symmetric function f such that $\mathcal {F}(X)=f(\varvec{\sigma }(X))$.

The subdifferential of a singular value function has the following formula.

Theorem 4.5

(See [31, Theorem 7.1]) The subdifferential of a singular value function $\mathcal {F}(X)=f(\varvec{\sigma }(X))$ is given by the formula

$$\begin{aligned} \partial \mathcal {F}(X)=\left\{ U \mathop {\textrm{diag}}(\varvec{y})V^\top : (U,V)\in \textrm{ Sm }(X), \varvec{y}\in \partial f(\varvec{\sigma }(X)) \right\} . \end{aligned}$$

(43)

The following lemma gives the subdifferential of the Schatten p-quasi-norm.

Lemma 4.6

Define $\mathcal {S}(X):\mathbb {R}^{m\times n} \rightarrow (-\infty ,+\infty )$ by $\mathcal {S}(X)=\Vert X\Vert _{*,p}^p (0<p<1)$ and let $h=\min \{m,n\}$. For a matrix $\hat{X}\in \mathbb {R}^{m\times n}$ with $\textrm{rank}(\hat{X})=r$, we have

$$\begin{aligned} \begin{aligned} \partial \mathcal {S}(\hat{X}) = \bigg \{&U\begin{bmatrix} D &{}\quad 0 \\ 0 &{}\quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix}V^\top : (U,V)\in \textrm{ Sm }(\hat{X}), \varvec{a} \in \mathbb {R}^{h-r}, \\ {}&D = \mathop {\textrm{diag}}(p\sigma _1^{p-1}(\hat{X}),\ldots , p\sigma _r^{p-1}(\hat{X})) \in \mathbb {R}^{r\times r} \bigg \}. \end{aligned} \end{aligned}$$

(44)

Proof

Define $f(\varvec{x}): \mathbb {R}^{h}\rightarrow \mathbb {R}$ by $f(\varvec{x})=\sum _{i=1}^{h}|x_i|^p$. Then f is an absolutely symmetric function and $\mathcal {S}(X)=f(\varvec{\sigma }(X))$. Note that

$$\begin{aligned} \partial |x|^p = {\left\{ \begin{array}{ll} \{p|x|^{p-1}\}, &{} \text{ if } x\ne 0 \\ (-\infty ,+\infty ), &{} \text{ otherwise }.\end{array}\right. } \end{aligned}$$

Then the subdifferential of $\mathcal {S}(X)$ at $\hat{X}$ is obtained by (43). $\square$

In (16) or (17), there is one term $\sum _{j=1}^{r_k} w_{k,j} \sigma _j(X)$. For convenience, we define $\mathcal {W}(X):\mathbb {R}^{m\times n} \rightarrow (-\infty ,+\infty )$ by

$$\begin{aligned} \mathcal {W}(X)=\sum _{i=1}^{r} b_i\sigma _i(X), \end{aligned}$$

(45)

where $r\le \min \{m,n\}$ and $b_i>0,i=1,\ldots ,r$. The function $\mathcal {W}(X)$ can be regarded as a generalization of Ky Fan r-norms; see [24, Chapter 7.4.8] for details. Generally, it is difficult to give an explicit formula of $\partial \mathcal {W}(X)$. However, when the first $r+1$ singular values of X are strictly decreasing, we have the following result.

Lemma 4.7

Let $\mathcal {W}(X)$ be defined in (45) and $h=\min \{m,n\}$. For a matrix $\hat{X}\in \mathbb {R}^{m\times n}$ with $\sigma _1(\hat{X})> \cdots> \sigma _r(\hat{X})> \sigma _{r+1}(\hat{X})$, where $\sigma _{h+1}(\hat{X}):=0$, we have

$$\begin{aligned} \partial \mathcal {W}(\hat{X}) = \bigg \{U\begin{bmatrix} D &{}\quad 0 \\ 0 &{}\quad 0 \end{bmatrix}V^\top : (U,V)\in \textrm{ Sm }(\hat{X}), D = \mathop {\textrm{diag}}(b_1,\ldots , b_r) \in \mathbb {R}^{r\times r}\bigg \}.\nonumber \\ \end{aligned}$$

(46)

Proof

Given $\varvec{x} \in \mathbb {R}^h$, we write $\underline{\varvec{x}}$ for the vector in $\mathbb {R}^h_+$ with the same entries as $|\varvec{x}|$ arranged in nonincreasing order. Define

$$\begin{aligned} f(\varvec{x})=\sum _{i=1}^{r}b_i \underline{x}_i. \end{aligned}$$

(47)

Then f is an absolutely symmetric function and $\mathcal {W}(X)=f(\varvec{\sigma }(X))$.

Given $\hat{\varvec{x}}\in \mathbb {R}^h_+$, suppose $\hat{x}_1>\cdots> \hat{x}_r> \hat{x}_d,d=r+1,\ldots ,h$, where $\hat{x}_{h+1}:=0$. Then, $f(\hat{\varvec{x}})=\sum _{i=1}^{r}b_i \hat{x}_i$. There exists $\varepsilon >0$ such that for each $\varvec{y}\in \mathbb {R}^h$ with $\Vert \varvec{y}\Vert _2<\varepsilon$, $\varvec{z}:=\hat{\varvec{x}}+\varvec{y}$ satisfies $\underline{z}_i = z_i,i=1,\ldots ,r$. Hence, $f(\varvec{z})=\sum _{i=1}^{r}b_i z_i$. It follows that f is differentiable at $\hat{\varvec{x}}$ and

$$\begin{aligned} \nabla f(\hat{\varvec{x}})=[b_1,\ldots , b_r,0,\ldots ,0]^\top . \end{aligned}$$

Then the subdifferential of $\mathcal {W}(X)$ at $\hat{X}$ follows from (43). $\square$

With the same condition of the preceding lemma, we can give an explicit formula of the subdifferential of $\mathcal {W}(X)+\delta _{\mathscr {M}_{r}}(X)$.

Lemma 4.8

Define $\mathcal {R}(X):\mathbb {R}^{m\times n} \rightarrow (-\infty ,+\infty ]$ by $\mathcal {R}(X):=\mathcal {W}(X)+\delta _{\mathscr {M}_{r}}(X)$, where $\mathcal {W}(X)$ is defined in (45) and let $h=\min \{m,n\}$. For a matrix $\hat{X}\in \mathbb {R}^{m\times n}$ with $\textrm{rank}(\hat{X})=r$ and $\sigma _1(\hat{X})> \cdots > \sigma _r(\hat{X})$, we have

$$\begin{aligned} \begin{aligned} \partial \mathcal {R}(\hat{X}) = \bigg \{&U\begin{bmatrix} D &{}\quad 0 \\ 0 &{}\quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix}V^\top : (U,V)\in \textrm{ Sm }(\hat{X}),\varvec{a} \in \mathbb {R}^{h-r} \\&D = \mathop {\textrm{diag}}(b_1,\ldots , b_r) \in \mathbb {R}^{r\times r} \bigg \}. \end{aligned} \end{aligned}$$

(48)

Proof

First, it is well know that $\mathscr {M}_{r}$ is a smooth manifold; see, e.g., [46, Proposition 2.1] and [25, Theorem 2.1] for the formulae of tangent cone and the normal cone of $\mathscr {M}_{r}$, in terms of SVD. Denote by $\mathscr {N}_{\mathscr {M}_{r}}(X)$ the normal cone of $\mathscr {M}_{r}$ at $\hat{X}$. By [42, Exercise 8.14], we have

$$\begin{aligned} \partial \delta _{\mathscr {M}_{r}}(\hat{X}) = \mathscr {N}_{\mathscr {M}_{r}}(\hat{X}) = \bigg \{U\begin{bmatrix}0_{r\times r} &{}\quad 0 \\ 0 &{}\quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix}V^\top : (U,V)\in \textrm{ Sm }(\hat{X}),\varvec{a} \in \mathbb {R}^{h-r} \bigg \}.\nonumber \\ \end{aligned}$$

(49)

Clearly, $\delta _{\mathscr {M}_{r}}(X)$ is regular at $\hat{X}$. From the proof of (46), we know that $f(\varvec{x})$ defined in (47) is differentiable at $\varvec{\sigma }(\hat{X})$ and of course regular at $\varvec{\sigma }(\hat{X})$. By Lewis and Sendov [31, Corollary 7.5], $\mathcal {W}(X)$ is regular at $\hat{X}$. Consequently, by Rockafellar and Wets [42, Corollary 10.9], $\mathcal {R}(X)$ is regular at $\hat{X}$ and

$$\begin{aligned} \partial \mathcal {R}(\hat{X}) = \partial \mathcal {W}(\hat{X})+ \partial \delta _{\mathscr {M}_{r}}(\hat{X}). \end{aligned}$$

(50)

Combining (46), (49) and (50) yields (48). $\square$

We next recall the Kurdyka–Łojasiewicz (KL) property. This property has been widely used in establishing convergence and analyzing the convergence rate of first-order methods; see, for example, [1,2,3, 5, 33, 51] First we introduce some notation and definitions. We use $\mathbb {E}$ to denote a Euclidean space and $\Vert \cdot \Vert$ to denote the Euclidean norm. For any subset $\mathscr {S} \subseteq \mathbb {E}$ and any point $u \in \mathbb {E}$, the distance from u to $\mathscr {S}$ is defined by $\text {dist} (u, \mathscr {S}):= \inf \{\Vert v-u\Vert : v \in \mathscr {S}\}$. An extended-real-valued function $f: \mathbb {E} \rightarrow (-\infty ,+\infty ]$ is said to be proper if $\{x \in \mathbb {E}: f(x) < +\infty \} \ne \emptyset$. Let $\eta \in (0,\infty ]$. We denote by $\Phi _\eta$ the class of all concave and continuous functions $\varphi :[0,\eta ) \rightarrow (0,+\infty ]$ which satisfy the following conditions

• (i) $\varphi (0)=0$;

• (ii) $\varphi$ is continuous differentiable on $(0,\eta )$;

• (iii) $\varphi ' >0$ on $(0,\eta )$.

Definition 4.9

(KL property and KL functions) A proper and lower semicontinuous function $f: \mathbb {E} \rightarrow (-\infty ,+\infty ]$ is said to have the KL property at $\hat{x} \in \text {dom } \partial f:= \{x \in \mathbb {E}: \partial f(x) \ne \emptyset \}$ if there exist $\eta \in (0,+\infty ]$, a neighborhood $\mathscr {V}$ of $\hat{x}$, and a function $\varphi \in \Phi _\eta$ such that for all $x \in \mathscr {V} \cap \{y \in \mathbb {E}: f(\hat{x})< f(y)< f(\hat{x})+ \eta \}$, the KL inequality holds:

$$\begin{aligned} \varphi '(f(x)-f(\hat{x})) \text {dist} (0,\partial f(x)) \ge 1. \end{aligned}$$

If f satisfies the KL property at each point of $\text {dom } \partial f$, f is called a KL function.

A rich class of KL functions used widely in practice belongs to a special structure called o-minimal structure. Related facts can be found in [2, 45]. The KL properties of some related functions are proved in the Appendix.

Proposition 4.10

Let $\mathcal {F}: \mathbb {R}^{m\times n} \rightarrow (-\infty ,+\infty ],h=\min \{m,n\}$ and $f: \mathbb {R}^h \rightarrow (-\infty ,+\infty ]$ be an absolutely symmetric function. Suppose $\mathcal {F}(X)=f(\varvec{\sigma }(X))$. Then $\mathcal {F}$ is a KL function if and only if f is a KL function.

Proof

First, we assume that f is a KL function. For any $\hat{X} \in \text {dom } \partial \mathcal {F}$, by the subdifferential formula (43), $\varvec{\sigma }(\hat{X}) \in \text {dom } \partial f$. Since f is a KL function, there exist $\eta \in (0,+\infty ]$, a neighborhood $\mathscr {V}$ of $\varvec{\sigma }(\hat{X})$, and a function $\varphi \in \Phi _\eta$ such that for all

$$\begin{aligned} \varvec{x} \in \mathscr {V} \cap \{\varvec{y} \in \mathbb {R}^h: \mathcal {F}(\hat{X})< f(\varvec{y}) < \mathcal {F}(\hat{X})+ \eta \}, \end{aligned}$$

the KL inequality holds:

$$\begin{aligned} \varphi '(f(\varvec{x})-\mathcal {F}(\hat{X})) \text {dist} (0,\partial f(\varvec{x})) \ge 1, \end{aligned}$$

where $\mathcal {F}(\hat{X})=f(\varvec{\sigma }(\hat{X}))$ has been used. By the continuity of singular values (see [24, Corollary 7.4.1.3]), there exists a neighborhood $\mathscr {U}$ of $\hat{X}$ such that $\varvec{\sigma }(X)\in \mathscr {V}$ for all $X \in \mathscr {U}$. Hence, for any $X\in \mathscr {U} \cap \{Y \in \mathbb {R}^{m\times n}: \mathcal {F}(\hat{X})< \mathcal {F}(Y) < \mathcal {F}(\hat{X})+ \eta \}$, we have $\varvec{\sigma }(X) \in \mathscr {V} \cap \{\varvec{y} \in \mathbb {R}^h: \mathcal {F}(\hat{X})< f(\varvec{y}) < \mathcal {F}(\hat{X})+ \eta \}$ and

$$\begin{aligned}&\varphi '(\mathcal {F}(X)-\mathcal {F}(\hat{X})) \text {dist} (0,\partial \mathcal {F}(X)) \\&\quad = \varphi '(f(\varvec{\sigma }(X)) -\mathcal {F}(\hat{X})) \text {dist}(0,\partial f(\varvec{\sigma }(X))) \ge 1, \end{aligned}$$

where $\text {dist}(0,\partial \mathcal {F}(X))=\text {dist}(0,\partial f(\varvec{\sigma }(X)))$ follows from (43). By definition, $\mathcal {F}$ is a KL function.

To show the opposite, we can fix $U\in \textrm{ St }^m_m,V \in \textrm{ St }^n_n$. Then $f(\varvec{x})=\mathcal {F}(U \mathop {\textrm{diag}}(\varvec{x})V^\top )$ for all $\varvec{x}\in \mathbb {R}^h$ and the KL property of f can be verified by definition. $\square$

By Proposition 4.10 and Examples –, $\mathcal {P}(X)$ defined in (11) and $\mathcal {G}_k(X)$ defined in (17) are both KL functions.

4.3 Global convergence of PLM and remarks on nonconvex ADMM

Now we start to prove the global convergence of $\{X_k\}$. We need the following assumption.

Assumption 4.11

The sequence $\{X_k\}$ generated by Algorithm 1 satisfies

$$\begin{aligned} \sigma _{k,1}> \cdots > \sigma _{k,\widetilde{r}} \quad \forall k \ge \widetilde{k}, \end{aligned}$$

where $\widetilde{r},\widetilde{k}$ are defined in (41).

Remark 4.12

In the convergence analysis based on the KL property for proximal linearization methods, the function that is linearized is usually assumed to have Lipschitz gradient. See, for example, [5, Assumption 2] and [55, Assumption 2.2]. In (12), the function that is linearized is $f(z)=z^p$, which does not have Lipschitz gradient on $(0,+\infty )$. Our strategy is to prove the lower bound property of the nonzero singular values of $\{X_k\}$; see Lemma 4.13. Then, f(z) also has Lipschitz gradient in the domain where the nonzero singular values lie; see (55). To prove Lemma 4.13 and obtain a subdifferential lower bound for the iterates gap (Lemma 4.14), we need the explicit formula of $\partial \mathcal {G}_k(X)$, which is ensured by Assumption 4.11.

In Theorem 2.1, we obtain a lower bound property for the original problem (6). Since $\{X_k\}$ is generated by approximately solving the proximal linearization (17), Theorem 2.1 does not hold for $\{X_k\}$. In the following, we give a similar result with respect to $\{X_k\}$ .

Lemma 4.13

Suppose that Assumption 4.11 holds. Let $\{X_k\}$ be generated by Algorithm 1 and $k \ge \widetilde{k}$. Then, there is a constant $\vartheta >0$ such that

$$\begin{aligned} \sigma _{r}(X_k) \ge \vartheta \quad \mathrm{for\, all }\, r=1,\ldots ,\widetilde{r}. \end{aligned}$$

Proof

Define $D_{k}:=\mathop {\textrm{diag}}(w_{k,1},\ldots ,w_{k,\widetilde{r}})$. By noting (42) and (48), the subdifferential of $\mathcal {G}_k(X)$ at $X_{k+1}$ is

$$\begin{aligned} \begin{aligned} \partial \mathcal {G}_k(X_{k+1}) = \bigg \{&U \begin{bmatrix}D_{k} &{}\quad 0 \\ 0 &{} \quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix} V^\top + \lambda \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b}) + \tau (X_{k+1} - X_k): \\& (U,V)\in \textrm{ Sm }(X_{k+1}),\varvec{a} \in \mathbb {R}^{h-\widetilde{r}} \bigg \}. \end{aligned} \end{aligned}$$

(51)

There exist $Y_{k+1} \in \partial \mathcal {G}_k(X_{k+1})$ and $(U,V)\in \textrm{ Sm }(X_{k+1})$ such that

$$\begin{aligned} U \begin{bmatrix}D_{k} &{}\quad 0 \\ 0 &{}\quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix} V^\top = Y_{k+1} - \lambda \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b})- \tau (X_{k+1} - X_k). \end{aligned}$$

By noting the condition (19), we have

$$\begin{aligned}&p\sigma _{\widetilde{r}}^{p-1}(X_k) = w_{k,\widetilde{r}}\le \Vert \varvec{w}_{k}\Vert _2=\Vert D_{k}\Vert _F \le \left\| \begin{bmatrix}D_{k} &{} \quad 0 \\ 0 &{}\quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix}\right\| _F \\ \le&\Vert Y_{k+1}\Vert _F + \lambda \Vert \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b})\Vert _F + \tau \Vert X_{k+1} - X_k\Vert _F \\ \le&(\rho +\tau )\Vert X_{k+1} - X_k\Vert _F + \lambda \Vert \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b})\Vert _F. \end{aligned}$$

Since $\{X_k\}$ is bounded (see Proposition 4.1), there is a constant $\alpha$ such that

$$\begin{aligned} p\sigma _{\widetilde{r}}^{p-1}(X_k) \le \alpha \Rightarrow \sigma _{\widetilde{r}}(X_k) \ge \left( \frac{p}{\alpha } \right) ^{\frac{1}{1-p}}=:\vartheta , \end{aligned}$$

which completes the proof. $\square$

Lemma 4.14

Suppose that Assumption 4.11 holds. Let $\{X_k\}$ be generated by Algorithm 1 and $k \ge \widetilde{k}$. Define $D_{k}:=\mathop {\textrm{diag}}(w_{k,1},\ldots ,w_{k,\widetilde{r}})$. Then there exist $Y_{k+1} \in \partial \mathcal {G}_k(X_{k+1}),(U,V)\in \textrm{ Sm }(X_{k+1})$ and $\mu >0$ such that

$$\begin{aligned} B_{k+1}:=Y_{k+1} + U\begin{bmatrix}D_{k+1}-D_k &{}\quad 0 \\ 0 &{}\quad 0 \end{bmatrix}V^\top + \tau (X_k - X_{k+1}) \in \partial \mathcal {P}(X_{k+1}) \end{aligned}$$

(52)

and

$$\begin{aligned} \Vert B_{k+1}\Vert _F \le \mu \Vert X_{k+1}-X_k\Vert _F. \end{aligned}$$

Proof

Note that $\textrm{rank}(X_k)=\widetilde{r}$ for all $k\ge \widetilde{k}$. By using (44), we have

$$\begin{aligned} \begin{aligned} \partial \mathcal {P}(X_{k+1})= \bigg \{&U\begin{bmatrix} D_{k+1} &{}\quad 0 \\ 0 &{} \quad \mathop {\textrm{diag}}(\varvec{a}) \end{bmatrix}V^\top + \lambda \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b}): \\&(U,V)\in \textrm{ Sm }(X_{k+1}),\varvec{a} \in \mathbb {R}^{h-\widetilde{r}} \bigg \} . \end{aligned} \end{aligned}$$

(53)

By noting (51), there exist $Y_{k+1} \in \partial \mathcal {G}_k(X_{k+1})$ and $(U,V)\in \textrm{ Sm }(X_{k+1})$ such that

$$\begin{aligned} \lambda \mathcal {A}^*(\mathcal {A}(X_{k+1})-\varvec{b}) = Y_{k+1} + \tau (X_k - X_{k+1}) - U\begin{bmatrix} D_k &{} 0 \\ 0 &{} 0 \end{bmatrix}V^\top . \end{aligned}$$

(54)

Combining (53) and (54) yields (52).

Now we estimate the norm of $B_{k+1}$. First, by the condition (19), we have

$$\begin{aligned} \Vert B_{k+1}\Vert _F \le \Vert D_{k+1}-D_k\Vert _F + (\rho +\tau ) \Vert X_{k+1}-X_k\Vert _F. \end{aligned}$$

By Lemma 4.13, $\sigma _{k,r}\ge \vartheta$ for all $k \ge \widetilde{k}$ and $r=1,\ldots ,\widetilde{r}$. Consider the function $[\vartheta ,+\infty )\rightarrow \mathbb {R}$ defined by $z\mapsto z^{p-1}$. For any $z_2 > z_1 \ge \vartheta$, by the mean value theorem, there exists $z_0 \in (z_1,z_2)$ such that

$$\begin{aligned} |z_1^{p-1} -z_2^{p-1}| = (1-p)z_0^{p-2}|z_1-z_2| \le (1-p)\vartheta ^{p-2}|z_1-z_2|. \end{aligned}$$

(55)

With this fact, we have

$$\begin{aligned} \Vert D_{k+1}-D_k\Vert _F^2&= \Vert \varvec{w}_{k+1}-\varvec{w}_{k}\Vert _2^2 = p^2 \sum _{r=1}^{\widetilde{r}}\left| \sigma _{k,r}^{p-1}-\sigma _{k+1,r}^{p-1}\right| ^2 \\ \le&p^2(1-p)^2\vartheta ^{2p-4}\sum _{r=1}^{\widetilde{r}} \left| \sigma _{k,r} -\sigma _{k+1,r} \right| ^2 \le p^2(1-p)^2\vartheta ^{2p-4} \Vert X_{k+1}-X_k\Vert _F^2, \end{aligned}$$

where the last inequality follows from Horn and Johnson [24, Corollary 7.4.1.3]. Therefore, we have

$$\begin{aligned} \Vert B_{k+1}\Vert _F&\le p(1-p)\vartheta ^{p-2} \Vert X_{k+1}-X_k\Vert _F \\&\quad +\,(\rho +\tau ) \Vert X_{k+1}-X_k\Vert _F =:\mu \Vert X_{k+1}-X_k\Vert _F, \end{aligned}$$

which completes the proof. $\square$

Now we can use the framework in [3] to establish the global convergence. To match the theme of this paper, we present the framework of Attouch et al. [3] in the form matrix functions as follows.

Lemma 4.15

(See [3, Theorem 2.9]) Suppose $\mathcal {F}(X): \mathbb {R}^{m\times n} \rightarrow (-\infty ,+\infty ]$ is a KL function. Let $\{X_k\}$ be a sequence of $\mathbb {R}^{m\times n}$. Suppose there exist $a>0,b>0$ such that

$\textbf{H}1$.:

$\mathcal {F}(X_k)-\mathcal {F}(X_{k+1})\ge a\Vert X_k-X_{k+1}\Vert ^2$ for all k.

$\textbf{H}2$.:

There exists $Y_{k+1}\in \partial \mathcal {F}(X_{k+1})$ such that

$$\begin{aligned} \Vert Y_{k+1}\Vert _F \le b \Vert X_{k}-X_{k+1}\Vert _F. \end{aligned}$$

$\textbf{H}3$.:

There exists a subsequence $\{X_{k_j}\}$ and $\widetilde{X}$ such that

$$\begin{aligned} X_{k_j}\rightarrow \widetilde{X} \quad \textrm{and }\quad \mathcal {F}(X_{k_j}) \rightarrow \mathcal {F}(\widetilde{X}), \quad \textrm{as }\, j \rightarrow \infty . \end{aligned}$$

Then $\lim _{k\rightarrow \infty }X_k= \widetilde{X}$, and $\widetilde{X}$ is a critical point of $\mathcal {F}(X)$.

Theorem 4.16

Suppose that Assumption 4.11 holds. Let $\{X_k\}$ be a sequence generated by PLM. Then $\{X_k\}$ converges to a critical point of $\mathcal {P}(X)$.

Proof

Proposition 4.1 and Lemma 4.14 show that conditions $\textbf{H}1$ and $\textbf{H}2$ are satisfied. Combining the fact that $\{X_k\}$ is bounded (see Proposition 4.1) and the fact that $\mathcal {P}(X)$ is continuous gives that $\textbf{H}3$ is satisfied. In addition, $\mathcal {P}(X)$ is a KL function. These together with Lemma 4.15 demonstrate the assertion. $\square$

The convergence analysis of nonconvex (L)ADMM can also be established by using the KL property; see [6, 32, 48]. Note that $\mathcal {G}_k(X)$ is a KL function. Algorithm 2 is in the framework of Li and Pong [32], Wang et al. [48] and Boţ and Nguyen [6], while Algorithm 3 is only in the framework of Wang et al. [48]. We summarize the results in the following proposition.

Proposition 4.17

Let $\{X_t\}$ be the sequence in Algorithm 2 or Algorithm 3. Then for any sufficiently large $\beta _k$, $\{X_t\}$ converges globally to a critical point of $\mathcal {G}_k(X)$ defined in (17).

The lower bounds of $\beta _k$ have been given in all these three references. Note that these bounds are only for sufficient conditions of convergence, and computing them is not very easy. In practice, setting $\beta _k$ empirically is more efficient.

Remark 4.18

Proposition 4.17 implies that, after a sufficiently large number of iterations of (L)ADMM, the condition (19) will be satisfied. However, checking (19) is not easy. Like [35, 55, 56], in practical computation, we adopt the relative change as stopping criterion in the inner loop; see the next section. It turns out numerically that PLM shows good convergence behaviour with this stopping criterion.

5 Experiments

We evaluate the performance of PLM in this section. All experiments are performed on MATLAB R2016a on a laptop (Intel Core i5-6300HQ CPU @ 2.30GHz, 8.00G RAM). We measure the quality of a solution X by its relative error (RErr) to the true low-rank matrix $\hat{X}$:

$$\begin{aligned} \text {RErr}:= \frac{\Vert X-\hat{X}\Vert _F}{\Vert \hat{X}\Vert _F}. \end{aligned}$$

It turns out that the performance of a low-rank matrix recovery algorithm is related to the distribution of singular values; see [28, 49]. We will test low-rank matrices with singular values in different distributions. To obtain a matrix $Z \in \mathbb {R}^{m\times n}$ with $\textrm{rank}(Z) = r_{\text {true}}$, firstly we generate $M_L \in \textrm{ St }^m_{r_{\text {true}}}$ and $M_R \in \textrm{ St }^n_{r_{\text {true}}}$. Then we generate a vector $\varvec{s} \in \mathbb {R}^{r_{\text {true}}}$ with a given distribution, which will be specified later. The yielded low-rank matrix is

$$\begin{aligned} Z = c M_L \mathop {\textrm{diag}}(\varvec{s}) M_R^\top , \end{aligned}$$

where c is a random scalar. We consider two types of distributions of singular values:

• 1. Uniform distribution in [a, b]: $\varvec{s}$ is generated by the Matlab command “$a+(b-a)*$rand($r_{\text {true}}$,1)”.

• 2. Power-law distribution with power a: $\varvec{s}$ has entries $s_i = i^{a}, i=1,\ldots ,r_{\text {true}}$.

5.1 Implementation details

As mentioned before, the initial value $X_0$ is crucial for PLM. The ideal choice would be a matrix not far from the solution of (6). Note that (3) and (6) are both approximate models of the original problem (1), meaning that the solution of (3) is not very far from that of (6). Therefore, we use the solution of the convex problem (3), which can be solved efficiently by (L)ADMM [50], as the initialization $X_0$. We call the algorithm [50] nuclear-(L)ADMM. An important advantage of nuclear-(L)ADMM is that the yielded solutions have low-rank. Because the subproblem (25) or (36) is solved by partial SVD, a smaller $r_0$ results in a lower time cost. We will use this initialization in all tests.

The magnitudes of different datasets may differ greatly, which brings difficulties in the settings of parameters. This issue can be tackled by scaling. Specifically, we set the scaling value $c=\Vert X_0\Vert _2$. The scaled model corresponding to (11) is

$$\begin{aligned} \min _{\textrm{rank}(X)\le r_k}\ \Vert X\Vert _{*,p}^p + \frac{\lambda }{2} \Vert \mathcal {A}(X)-\varvec{b}/c\Vert _2^2, \end{aligned}$$

(56)

and the scaled initialization is $X_0/c$. After obtaining the solution $\widetilde{X}$ of (56) by PLM, the solution of the original problem is $c\widetilde{X}$. Similar scaling can be used in nuclear-(L)ADMM: we set $c=\Vert \varvec{b}\Vert _2$ and the scaled model corresponding to (3) is

$$\begin{aligned} \min _{ X }\ \Vert X\Vert _* + \frac{\lambda }{2} \Vert \mathcal {A}(X)-\varvec{b}/c\Vert _2^2. \end{aligned}$$

(57)

In the remainder of this section, PLM is discussed based on the scaled model (56), and $\mathcal {P}(X)$ and $\{X_k\}$ are the scaled objective function and the scaled sequence, respectively.

In our implementation, the partial SVD is realized by the optPROPACK package¹ [34]. By our test, this package outperforms the influential PROPACK package [29].

As discussed in [27] and based our own test, $p=0.5$ performs better than other choice of p generally. For simplicity, we fix $p=0.5$ for all tests. As mentioned before, $\tau$ can be any positive scalar. To approximate the original model well, we set $\tau$ as small as $10^{-5}$. As with Yang and Yuan [50], we set $\eta = \Vert \mathcal {A}^* \mathcal {A}\Vert _2$ for LADMM. The performance of PLM depends heavily on whether the (L)ADMM in the inner loops converges well. Hence, the stopping tolerance for the inner loops cannot be too loose. In our tests, as suggested by Remark 4.18, the stopping tolerance of the inner loops is set as

$$\begin{aligned} \frac{\Vert X_{t+1}-X_t\Vert _F}{\max (\Vert X_t\Vert _F,1)} \le 10^{-6}; \end{aligned}$$

and the stopping tolerance of the outer loops is set as

$$\begin{aligned} \frac{\Vert X_{k+1}-X_k\Vert _F}{\max (\Vert X_k\Vert _F,1)} \le 10^{-5}. \end{aligned}$$

5.2 Convergence behaviour of PLM

We show the convergence behaviour of PLM on the matrix completion problem. First, we generate a low-rank matrix $Z \in \mathbb {R}^{500\times 500}$ with $\textrm{rank}(Z)=10$ and singular values in power-law distribution, where the power is set to be $-3$. Then, we select $30\%$ entries of Z randomly (i.e, the sample ratio is $30\%$) and use $\varvec{b}'$ to denote the vector formed by these entries. At last, we impose some Gaussian noise on $\varvec{b}'$ and obtain the observed vector $\varvec{b}$ by

$$\begin{aligned} \varvec{b} = \varvec{b}' + \varepsilon \frac{\Vert \varvec{b}'\Vert _2}{\Vert \varvec{n}\Vert _2}\varvec{n}, \end{aligned}$$

where the entries of $\varvec{n}$ are drawn from a standard normal distribution and $\varepsilon$ is the noise level. We set $\varepsilon =10^{-3}$ in this test. Besides using the solution of (3) as the initialization, we use two other initializations to show the convergence behaviour of PLM:

• 1. the initialization $X_0^{(1)}$ is the solution of (3) solved by nuclear-ADMM;

• 2. the initialization $X_0^{(2)}$ is a random generated matrix with $\textrm{rank}(X_0^{(2)})=10$;

• 3. the initialization $X_0^{(3)}$ is the best rank-7 approximation of $X_0^{(1)}$, obtained by the truncated SVD of $X_0^{(1)}$.

We run PLM to 8 outer loops, ignoring the stopping tolerance of outer loops, with different initializations.

Fig. 1

The values $\mathcal {P}(X_k),\textrm{rank}(X_k)$ and $\Vert X_{k+1}-X_k\Vert _F/ \Vert X_k\Vert _F$ versus the outer iteration number in PLM, where all values are with respect to the scaled model (56). The first row is with the initialization $X_0^{(1)}$, the second row is with the initialization $X_0^{(2)}$, and the third row is with the initialization $X_0^{(3)}$

As shown in Fig. 1, the sequence $\{\mathcal {P}(X_k)\}$ is monotonically decreasing. For the initializations $X_0^{(1)}$ and $X_0^{(3)}$, $\textrm{rank}(X_k)$ is unchanged for all k, and for the initialization $X_0^{(2)}$, $\textrm{rank}(X_k)$ is unchanged when $k\ge 3$. PLM converges very fast: the relative change between $X_3$ and $X_4$ is less than $10^{-5}$ for all initializations. For the initialization $X_0^{(2)}$, the change between $\mathcal {P}(X_0)$ and $\mathcal {P}(X_1)$ and the relative change between $X_0$ and $X_1$ are both very large, implying that $X_0^{(2)}$ is far from a critical point.

The iteration number of nuclear-ADMM for generating $X_0^{(1)}$ is 81, and we show the iteration numbers of inner loops of PLM in Table 1. We can find that these numbers are relatively small for $X_0^{(1)}$ and $X_0^{(3)}$, while for $X_0^{(2)}$ the iteration number of inner loops for the first step is as high as 5448. The iteration numbers are consistent with the results shown in Fig. 1.

Table 1 Iteration numbers of inner loops of each step, with different initializations

5.3 Matrix completion

In this subsection, we compare PLM with nuclear-ADMM and t-IRucLq-M [27] on the matrix completion problem. We choose these two methods to compare due to their significant superiorities to many other existing methods. See the numerical results in [13, 27, 50]. We test matrices with singular values uniformly distributed in [0.1, 1] and matrices with singular values in power-law distribution, where the power is set to be $-3$. We consider three levels of noise $\varepsilon = 10^{-3},10^{-4},10^{-5}$.

nuclear-ADMM is run based on the scaled model (57), whose parameters are relatively stable. We set $\lambda =10^3/\varepsilon$ and the stopping tolerance to be $10^{-5}$. For PLM (56), we set $\lambda =10^3/\varepsilon$ and $\beta _k=10^5$ for all k. t-IRucLq-M solves (6) by (7). Its model parameters p and $\lambda$ are set to be the same as those of PLM for the original model (6). The rank estimate of t-IRucLq-M is set to be $r_0$ and the stopping tolerance is set to be $10^{-3}$. The comparison results are shown in Tables 2 and 3, where the running time of PLM has included the time for generating the initialization. For matrices with singular values in power-law distribution, we only test $r_{\text {true}}=10$, because $\sigma _{r_{\text {true}}}/\sigma _1$ is too small for greater $r_{\text {true}}$, resulting in difficulties in recovering the original matrices. All results are averaged over 10 trials for each case.

Table 2 Comparison results of different methods on matrix completion: matrices with uniformly distributed singular values

Table 3 Comparison results of different methods on matrix completion: matrices with singular values in power-law distribution

We consider the relative error. For matrices with uniformly distributed singular values, as shown in Table 2, when the noise level is as high as $10^{-3}$, the results of different methods are close; as the noise level decreases, the advantage of Schatten p-quasi-norm minimizations becomes obvious: both t-IRucLq-M and PLM outperform nuclear-ADMM and PLM has the best performance. For matrices with singular values in power-law distribution, as shown in Table 3, nuclear-ADMM performs worse than it does on the former type of matrices; both t-IRucLq-M and PLM outperform nuclear-ADMM and PLM has the best performance.

Now, we focus on the running time. We can see that the time cost of nuclear-ADMM is very cheap, which has also been demonstrated in previous works. PLM converges very fast: the numbers of outer loops of PLM are at most 2 for all cases. The gap between the running time of nuclear-ADMM and PLM is not very big, and PLM is much faster than t-IRucLq-M.

5.4 Sylvester equation

In this subsection, we consider solving a low-rank solution of a Sylvester equation

$$\begin{aligned} AX + XB \approx C, \end{aligned}$$

where $A\in \mathbb {R}^{m\times m},B\in \mathbb {R}^{n\times n},C\in \mathbb {R}^{m\times n}$. This problem is mentioned in [44]. In this case,

$$\begin{aligned} \mathcal {A}(X) = \textrm{vec}(AX + XB)= (I_m\otimes A + B^\top \otimes I_n) \textrm{vec}(X), \end{aligned}$$

(58)

where $\otimes$ is the Kronecker product, and $I_s \in \mathbb {R}^{s\times s}$ is an identity matrix, $s=m,n$. We define $\mathcal {B}: \mathbb {R}^{m\times n}\rightarrow \mathbb {R}^{m\times n}$ by $\mathcal {B}(X) = AX + XB$. Equation (58) implies that the representing matrix of $\mathcal {B}$ is $(I_m\otimes A + B^\top \otimes I_n)$ and hence $\mathcal {B}^*(Y) = A^\top Y + YB^\top$. Therefore,

$$\begin{aligned} \mathcal {A}^*\mathcal {A}(X) =A^\top A X + A^\top XB + AXB^\top + XBB^\top , \end{aligned}$$

and (7) is a difficult linear matrix equation; see the discussion for Simoncini [44, Eq. (2)]. We compare PLM with nuclear-LADMM and the Matlab function “sylvester".

We test matrices with singular values uniformly distributed in [0.1, 1] and matrices with singular values in power-law distribution, where the power is set to be $-2$. We generate A and B by the Matlab commands “randn(m)" and “randn(n)", respectively. Then we generate a low-rank matrix X with singular values in specified distributions. After getting C by $C = AX + XB$, we impose some Gaussian noise on C. We consider three levels of noise $\varepsilon = 10^{-3},10^{-4},10^{-5}$.

For nuclear-LADMM (57), we set $\lambda =10^3/\varepsilon$ and the stopping tolerance to be $10^{-6}$. For PLM (56), we set $\lambda =10^3/\varepsilon$ and $\beta _k=10^6$ for all k. The comparison results are shown in Tables 4 and 5, where the running time of PLM has included the time for generating the initialization. All results are averaged over 10 trials for each case.

Table 4 Comparison results of different methods on solving Sylvester equations: matrices with uniformly distributed singular values

Table 5 Comparison results of different methods on solving Sylvester equations: matrices with singular values in power-law distribution

We consider the relative error. sylvester performs badly. For all cases with noise level $10^{-3}$, its RErr is greater than 1, meaning the failure in recovering X. nuclear-LADMM performs well, but its performance is affected by the distribution of singular values. Like the results for matrix completion, nuclear-LADMM performs worse on matrices with singular values in power-law distribution than it does on matrices with uniformly distributed singular values. PLM outperforms nuclear-LADMM in all cases and its performance is independent of the distribution of singular values. The advantage of PLM over nuclear-LADMM is very obvious in the cases where the noise level is lower or singular values are with power-law distributions.

Now we look at the running time. sylvester is a direct method and consumes the least running time. The running time of nuclear-LADMM depends on the size of the matrix and the distribution of singular values. PLM converges fast: only two outer loops are needed in all cases. PLM consumes much longer time than nuclear-LADMM, but less than twice the consumed time of nuclear-LADMM in almost all cases.

5.5 Image deblurring

In this subsection, we consider a grayscale image deblurring problem. The original image is the Greek flag shown in Fig. 2, whose size is $256\times 384$ and numerical rank² is 4. The original image is corrupted by a $9\times 9$ Gaussian blurring kernel with standard deviation 5 (fspecial (’gaussian’,[9,9],5)) and Gaussian noise. We consider three levels of noise $\varepsilon = 10^{-3},10^{-4},10^{-5}$.

Suppose the original image is X, the blurring kernel is $\mathcal {A}$ (a convolution operator), and the noise is N. Then the observed image is

$$\begin{aligned} B = \mathcal {A}(X)+N. \end{aligned}$$

Image deblurring is estimating X from the observed image B, where $\mathcal {A}$ is known and N is unknown. This problem is ill-conditioned. Deblurring by solving the linear system $\mathcal {A}(X)=B$ directly cannot obtain a good image restoration. To overcome this difficulty, regularization methods are required to stabilize the solution. Besides (3) and (6), we also consider the Tikhonov regularization method:

$$\begin{aligned} \min _{X\in \mathbb {R}^{m \times n}}\ \Vert X\Vert _F^2 + \frac{\lambda }{2}\Vert \mathcal {A}(X)-B\Vert _F^2. \end{aligned}$$

We compare PLM with the Tikhonov method and nuclear-ADMM, where the feature of $\mathcal {A}$ will be considered (see Sect. 3.1.2). For nuclear-ADMM (57), we set $\lambda =10^3/\varepsilon$; for PLM (56), we set $\lambda =10^4/\varepsilon$.

Table 6 Comparison results of different methods on image deblurring

Fig. 2

Restorations of different methods, where the noise level is $10^{-5}$

The comparison results are shown in Table 6, where the running time of PLM has included the time for generating the initialization. All results are averaged over 10 trials for each case. nuclear-ADMM and PLM obtain the same numerical rank as that of the original image, while the Tikhonov method yields a much higher numerical rank. This illustrates the advantage of nuclear-ADMM and PLM in recovering low-rank matrix. In terms of relative error, the Tikhonov method is the worst, nuclear-ADMM yields an acceptable result, and PLM outperforms nuclear-ADMM. In terms of the running time, the Tikhonov method is very fast; the running time of nuclear-ADMM depends on the noise level; PLM converges very fast and consumes much longer time than nuclear-ADMM; the gap between PLM time and nuclear-ADMM time becomes smaller as the noise level decreases. The visual comparison of some restorations is shown in Fig. 2.

6 Conclusion

We have proved the lower bound theory for Schatten p-quasi-norm minimization: the positive singular values of local minimizers are bounded from below by a constant. This property explains the advantage of the Schatten p-quasi-norm minimization in recovering low-rank matrices. Using this property, we have proposed a proximal linearization method to solve the Schatten p-quasi-norm minimization problem. After studying singular value functions, we proved the global convergence of the proposed algorithm by using the KL property of the objective function. In the experiments, we considered matrix completion, Sylvester equation and image deblurring. The proposed method outperforms existing methods in terms of approximation error, and has acceptable running time.

Experiments show that PLM converges very fast. The convergence rate can be analysed based on the use of the KL exponent. See [33, 51] and references therein. The convergence rate of PLM will be discussed in the future.

In many applications, the entries of X lie in a certain range: $l\le x_{ij} \le u$, where $-\infty \le l \le u \le +\infty$. For example, in imaging applications, we usually have nonnegativity constraints, i.e., $l=0,u=+\infty$. To fit this situation, we can consider the following model:

$$\begin{aligned} \min _{X\in \mathbb {R}^{m \times n}}\ \Vert X\Vert _{*,p}^p + \frac{\lambda }{2}\Vert \mathcal {A}(X)-\varvec{b}\Vert _2^2+\delta _{\mathscr {D}}(X), \end{aligned}$$

(59)

where $\mathscr {D}$ is a convex closed set. Models with similar constraints corresponding to (5) have been studied in many papers, e.g., [4, 12, 14, 53]. Theories and algorithms related to (59) will be considered in the future.

Appendix

This appendix summarizes some important results on KL theory and gives some examples. The following definition is adopted from Attouch et al. [2, Definition 4.1].

Definition 7.1

(o-minimal structure on $\mathbb {R}$) Let $\mathscr {O} = \{\mathscr {O}_n\}_{n \in \mathbb {N}}$ such that each $\mathscr {O}_n$ is a collection of subsets of $\mathbb {R}^n$. The family $\mathscr {O}$ is an o-minimal structure on $\mathbb {R}$, if it satisfies the following axioms:

• (i) Each $\mathscr {O}_n$ is a boolean algebra. Namely $\emptyset \in \mathscr {O}_n$ and for each $\mathscr {A},\mathscr {B}$ in $\mathscr {O}_n$, $\mathscr {A} \cup \mathscr {B}$, $\mathscr {A} \cap \mathscr {B}$, and $\mathbb {R}^n \setminus \mathscr {A}$ belong to $\mathscr {O}_n$.

• (ii) For all $\mathscr {A}$ in $\mathscr {O}_n$, $\mathscr {A} \times \mathbb {R}$ and $\mathbb {R} \times \mathscr {A}$ belong to $\mathscr {O}_{n+1}$.

• (iii) For all $\mathscr {A}$ in $\mathscr {O}_{n+1}$, $\{(x_1,\ldots ,x_n)\in \mathbb {R}^n: (x_1,\ldots ,x_n,x_{n+1}) \in \mathscr {A}\}$ belongs to $\mathscr {O}_{n}$.

• (iv) For all $i \ne j$ in $\{1,2,\ldots ,n\}$, $\{(x_1,\ldots ,x_n) \in \mathbb {R}^n: x_i = x_j\}$ belongs to $\mathscr {O}_n$.

• (v) The set $\{(x_1,x_2) \in \mathbb {R}^2: x_1<x_2\}$ belongs to $\mathscr {O}_2$.

• (vi) The elements of $\mathscr {O}_1$ are exactly finite unions of intervals.

Let $\mathscr {O}$ be an o-minimal structure on $\mathbb {R}$. We say that a set $\mathscr {A} \subseteq \mathbb {R}^n$ is definable (on $\mathscr {O}$) if $\mathscr {A} \in \mathscr {O}_n$. A function $f: \mathbb {R}^n \rightarrow (-\infty , +\infty ]$ is definable if its graph $\{(\varvec{x},y) \in \mathbb {R}^n \times (-\infty ,+\infty ]: y \in f(\varvec{x})\}$ is definable on $\mathscr {O}$. We list some known elementary properties of definable functions below.

Property 7.2

(See [2]) Finite sums of definable functions are definable; indicator functions of definable sets are definable; compositions of definable functions or mappings are definable.

It is known that any proper lower semicontinuous function that is definable is a KL function; see [2, Theorem 4.1].

Example 7.3

A class of o-minimal structure is the log-exp structure [45, Example 2.5]. By this structure, the following functions are all definable:

• 1. semi-algebraic functions; see Definition below.

• 2. the function $\mathbb {R} \rightarrow \mathbb {R}$ given by

  $$\begin{aligned} x \mapsto {\left\{ \begin{array}{ll} x^r, &{} x >0 \\ 0, &{} x \le 0, \end{array}\right. } \end{aligned}$$

  where $r \in \mathbb {R}$.

• 3. the exponential function: $\mathbb {R} \rightarrow \mathbb {R}$ given by $x \mapsto e^x$ and the logarithm function: $(0,\infty ) \rightarrow \mathbb {R}$ given by $x \mapsto \log (x)$.

Definition 7.4

(See [5, Definition 5]) A subset $\mathscr {S}$ of $\mathbb {R}^d$ is a real semi-algebraic set if there exists a finite number of real polynomial functions $f_{ij},g_{ij}: \mathbb {R}^d \rightarrow \mathbb {R}$ such that

$$\begin{aligned} \mathscr {S}=\bigcup _{j=1}^s\bigcap _{i=1}^t \left\{ \varvec{x}\in \mathbb {R}^{d}: f_{ij}(\varvec{x})=0 \text { and } g_{ij}(\varvec{x})<0 \right\} \end{aligned}$$

A function $f: \mathbb {R}^{d} \rightarrow (-\infty ,+\infty ]$ is called semi-algebraic if its graph

$$\begin{aligned} \left\{ (\varvec{x},y)\in \mathbb {R}^{d+1}: f(\varvec{x})=y \right\} \end{aligned}$$

is a semi-algebraic subset of $\mathbb {R}^{d+1}$.

The class of semi-algebraic sets is stable under the following operations: finite unions, finite intersections, complementation and Cartesian products.

Example 7.5

[5, Example 2] There is broad class of semi-algebraic sets and functions arising in optimization.

• 1. Real polynomial functions.

• 2. Indicator functions of semi-algebraic sets.

• 3. Finite sums and product of semi-algebraic functions.

• 4. Composition of semi-algebraic functions.

• 5. In matrix theory, all the following are semi-algebraic sets: cone of positive semidefinite matrices, Stiefel manifolds and constant rank matrices.

Example 7.6

Define $f(\varvec{x}): \mathbb {R}^{n}\rightarrow \mathbb {R}$ by $f(\varvec{x})=\sum _{i=1}^{n}|x_i|^p$. We prove that f is definable. First, consider the function $g(t)=|t|$. The graph of g(t) is

$$\begin{aligned}{} & {} \{(t,y)\in \mathbb {R}^2: y = t, t>0 \}\cup \{(t,y)\in \mathbb {R}^2: y = -t, t>0 \}\\{} & {} \quad \cup \{(t,y)\in \mathbb {R}^2: y = t, t=0 \}. \end{aligned}$$

Hence, g(t) is a semi-algebraic function. From Property and Example , we know that $f(\varvec{x})$ is definable.

Example 7.7

We prove that the function $f(\varvec{x})$ defined in (47) is a semi-algebraic function. From Example , we see that it suffices to prove that the function $f_i(\varvec{x}):=b_i \underline{x}_i,i=1,\ldots ,r$ is semi-algebraic. We only prove that $f_1(\varvec{x})=b_1 \underline{x}_1$ is semi-algebraic, and the other cases are similar. Define

$$\begin{aligned} \mathscr {T}_j:=\{\varvec{x}\in \mathbb {R}^h: x_j=\underline{x}_1\}, \quad j=1,\ldots ,h. \end{aligned}$$

By the definition of $\underline{\varvec{x}}$, we have

$$\begin{aligned} \mathscr {T}_j=\bigcap _{k=1}^{h}\{\varvec{x}\in \mathbb {R}^h: |x_j|\ge |x_k|\} \end{aligned}$$

and $\{\varvec{x}\in \mathbb {R}^h: |x_j|\ge |x_k|\}$ can be written as a union of some semi-algebraic sets. Hence, $\mathscr {T}_j$ is semi-algebraic. The graph of $f_1(\varvec{x})$ is

$$\begin{aligned} \bigcup _{j=1}^h \left( \left\{ (\varvec{x},y)\in \mathbb {R}^{h+1}:y = b_1 |x_j| \right\} \cap (\mathscr {T}_j\times \mathbb {R}) \right) , \end{aligned}$$

which is a semi-algebraic set.