Reduced-order finite element approximation based on POD for the parabolic optimal control problem

Abstract

In this paper, we construct a reduced-order finite element (ROFE) method holding seldom unknowns for the parabolic optimal control problem. We apply the proper orthogonal decomposition (POD) technique to develop two unsteady systems about state and co-state approximations, which efficiently reduces the number of unknowns and computational costs. Optimal a priori error estimates for the state, co-state and control approximations are derived. Finally, numerical examples are presented to verify that the ROFE method is accurate and efficient for solving the parabolic optimal control problem.

1 Introduction

Optimal control problems play a ubiquitous role in several applications, including shape optimizations [1, 2], fluid dynamics [3, 4], biomedical applications [5, 6] and environmental applications [7, 8]. It is very challenging to analyze theoretically and simulate numerically. In this paper, we focus our attention on the following parabolic optimal control problem.

$$\begin{aligned} \min _{u \in K}\left\{ \int _{0}^{T}(g(y)+h(u)) d t\right\} , \end{aligned}$$

(1)

subject to the state equation

$$\begin{aligned} \left\{ \begin{array}{ll} y_{t}-{\text {div}}(a_0\nabla y)=f+B u, &{} \text{ in } \Omega \times I, \\ y(x, t)=0, &{} \text{ on } \partial \Omega \times I, \\ y(x, 0)=y_{0}(x), &{} \text{ in } \Omega , \end{array}\right. \end{aligned}$$

(2)

where $I= [0, T]$ is the time interval. $\Omega$ and $\Omega _U$ are bounded open convex polygons in $R^n$ $(n\le 3)$, with Lipschitz boundaries $\partial \Omega$ and $\partial \Omega _U$. $a_0$ is a positive real number. B is a linear continuous operator. $g(\cdot )$ and $h(\cdot )$ are two convex functionals. K denotes the admissible set of the control variable u. The mathematical model can be used to describe a temperature control problem [9].

Numerical discretizations for optimal control problems usually lead to large-scale algebraic systems so that computational cost is large in real-world engineering applications. Especially, the computational cost gets larger if the optimization is constrained to time-dependent PDEs. Surely, time optimization makes the mathematical model more complete and it arises in many applications [10,11,12,13]. An available approach to reduce the computational costs is to rely on reduced-order methods, which allows us to solve the large-scale system in a low-dimensional framework. Up to now, many efficient reduced-order methods have been developed to solve PDEs, including the sparse grid method [14], the spectral element method [15], the balanced truncation method [16] and the proper orthogonal decomposition (POD) method [17]. Among them, the proper orthogonal decomposition (POD) method seems to be the most widely used and has received increasing attention. We refer the reader to [18,19,20,21,22,23,24] for more references.

The basis elements based on the POD technique are generated from the numerical solutions of the systems or from the experimental measurements, and these basis elements express characteristics of the expected solutions. This is in contrast to traditional methods, where the basis elements are uncorrelated to the physical properties of the systems. For example, specific polynomials are used in spectral methods; piecewise polynomials are used in finite element methods; grid functions are used in finite difference methods.

It is worth noting that a new POD technique was used to solve the two-dimensional Sobolev equation by Luo [25] in 2014, where the POD basis is generated from the solutions of the traditional method on the initial seldom time nodes, so that it does not have reduplicated computations. This is a development and improvement on the methods mentioned above. Since then, such reduced-order methods have been applied to solve non-stationary Navier-Stokes equation [26], viscoelastic wave equation [27], unsteady conduction-convection equation [28], non-stationary Boussinesq equation [29], nonlinear Rosenau equation [30] and so on.

It is well known [31, 32] that one-to-one correspondence between the linear optimal control problem and the optimality condition. The optimality condition contains a state, a co-state system and a variational inequality. We note that the co-state system should be calculated against the time direction, which combined with the coupling between systems lead to that the above way of generating the POD basis is not feasible. In the above way, we have to solve the full-order solutions on all-time nodes to construct the POD basis, so it’s meaningless to construct such a reduced-order model. [33] and [34] present a feasible way that the snapshots are related to a specified control input, which may not be optimal. This lead to that the POD basis obtained can not better express the physical characteristics of the system, so that the accuracy of the reduced-order solutions is affected. Building upon our studies on optimal control using ROMs [35,36,37], we propose a perfect way, where the snapshots are related to the optimal control input and we don’t have to solve full-order solutions on all-time nodes. The details will be specified later on. In a word, the proposed ROFE method can approximate the optimal control problems accurately and efficiently.

In this paper, we construct a ROFE method based on POD for the parabolic optimal control problem. For the convenience of analysis, we introduce the finite element (FE) method and some corresponding results, where piecewise linear continuous elements for the state and co-state approximation are adopted, and piecewise constant element for the control approximation is adopted. Considering that the state and co-state systems are unsteady, the POD technique is used on the two systems, which produces two low-dimensional systems and effectively reduces computational costs. And we still use piecewise constant elements to discrete variational inequality. We then present optimal a priori error estimates for the state, co-state and control approximations. Finally, some numerical examples are carried out to verify that the numerical results are in agreement with the theoretical analysis. By comparing the numerical results of the FE and ROFE methods, we came to that the ROFE method is accurate and efficient for solving the parabolic optimal control problem.

The rest of the paper is organized as follows. In Section 2, we review the FE method and the corresponding results. In Section 3, we construct the POD basis and build the ROFE method. Optimal a priori error estimates for the state, co-state and control approximations are derived in Section 4. In Section 5, numerical examples are used to verify the accuracy and efficiency of the ROFE method.

Throughout this paper, we employ the usual notion for Lebesgue and Sobolev spaces [38, 39]. In addition, we use K and $\epsilon$, with or without subscripts, to denote a generic positive constant and an arbitrarily small positive constant, respectively, which could have different values at different appearances.

2 Review the FE method

In this section, we present the finite element approximation for the parabolic optimal control problem (1)-(2), and give optimal a priori error estimates for the finite element solutions.

We take the state space $V = H_0^1(\Omega )$, the control space $U = L^2(\Omega _U)$. Let $K=\left\{ v \in U: v \ge 0 \right\}$.

We now present the weak formulation of the state equation (2): find $y(u) \in V$ such that for $t \in I$

$$\begin{aligned} \left\{ \begin{array}{ll} \left( y_{t}(u), w\right) +a(y(u), w)=(f+B u, w), &{} \forall w \in V,\\ y(u)(x, 0)=y_{0}(x), &{} x \in \Omega , \end{array}\right. \end{aligned}$$

(3)

where $a(v,w) = (a_0\nabla v, \nabla w)$. It is clear that problem (3) has a unique solution for any $u\in K$.

The parabolic optimal control problem can be restated as follows:

$$\begin{aligned} \min _{u \in K}\left\{ \int _{0}^{T} J(u) d t\right\} , \end{aligned}$$

(4)

where $J(u)=g(y(u))+h(u)$, and $y(u)\in V$, subject to

$$\begin{aligned} \left\{ \begin{array}{l} \left( y_{t}(u), w\right) +a(y(u), w)=(f+B u, w), \quad \forall w \in V, \\ y(u)(x, 0)=y_{0}(x). \end{array}\right. \end{aligned}$$

(5)

We assume that

$$ h(u)=\int _{\Omega _{U}} j(u), $$

where $j(\cdot )$ is a convex continuous differential function. It is easy to see that

$$ \left( h^{\prime }(u), v\right) _{U}=\left( j^{\prime }(u), v\right) _{U}=\int _{\Omega _{U}} j^{\prime }(u) v, $$

where $h^{\prime }(\cdot )$ and $j^{\prime }(\cdot )$ are the derivatives of $h(\cdot )$ and $j(\cdot )$, respectively, and $(\cdot , \cdot )_U$ is the $L^2$ inner product on $\Omega _U$.

From [40], the parabolic optimal control problem has a solution (y, u), and a pair (y, u) is the solution of the parabolic optimal control problem if there is a co-state $p \in V$ such that the triplet (y, p, u) satisfies the following optimality condition:

$$\begin{aligned}&\left\{ \begin{array}{l} \left( y_{t}, w\right) +a(y, w)=(f+B u, w), \quad \forall w \in V, \ y(0)=y_{0}, \end{array}\right. \end{aligned}$$

(6)

$$\begin{aligned}&\left\{ \begin{array}{l} -\left( p_{t}, q\right) +a(q, p)=\left( g^{\prime }(y), q\right) , \quad \forall q \in V, \\ p(T)=0, \end{array}\right. \end{aligned}$$

(7)

$$\begin{aligned}&\int _{0}^{T}\left( j^{\prime }(u)+B^{*} p, v-u\right) _{U} d t \ge 0, \quad \forall v \in K , \end{aligned}$$

(8)

where $B^*$ is the adjoint operator of B, $g^{\prime }(\cdot )$ is the derivative of $g(\cdot )$.

Let $\mathscr {T}^{h}$ and $\mathscr {T}_U^{h}$ be regular triangulations of $\Omega$ and $\Omega _U$, respectively, and $h=\max _{\tau \in \mathscr {T}^{h}} h_{\tau }$, $h_U=\max _{\tau _U \in \mathscr {T}_U^{h}} h_{\tau _U}$, where $h_{\tau }$ and $h_{\tau _U}$ denote the diameters of the elements $\tau$ and $\tau _U$, respectively.

Let $V^h \subset V$ consist of continuous, piecewise linear functions on $\mathscr {T}^{h}$, and $U^h \subset U$ consist of piecewise constant functions on $\mathscr {T}_U^{h}$. Let $K^h = K\cap U^h$.

Let $\Delta t=T/N_T$ be the time step and $t^i=i\Delta t,\ i=0,1,\cdots ,N_T$. We define, for $1 \le q < \infty$, the discrete time-dependent norms

$$ \Vert f\Vert _{l^{q}\left( I ; W^{m, p}(\Omega )\right) }=\left( \sum _{i=1}^{N_{T}} \Delta t\left\| f^{i}\right\| _{m, p}^{q}\right) ^{\frac{1}{q}}, $$

and the standard modification for $q =\infty$. Let

$$ l^{q}\left( I ; W^{m, p}(\Omega )\right) :=\left\{ f:\Vert f\Vert _{l^{q}\left( I ; W^{m, p}(\Omega )\right) }<\infty \right\} , \quad 1 \le q \le \infty . $$

Define

$$d_t \phi ^i=\frac{\phi ^i-\phi ^{i-1}}{\Delta t},\quad 1\le n \le N_T.$$

A fully discrete approximation scheme of the parabolic optimal control problem is to find $( y_h^i , u_h^i) \in V^h \times K^h, i = 1,2,\cdots , N_T$, such that

$$\begin{aligned} \min _{u_{h}^{i} \in K^{h}} \sum _{i=1}^{N_{T}} \Delta t J_{h}\left( u_{h}^{i}\right) , \end{aligned}$$

(9)

where $J_{h}\left( u_{h}^{i}\right) =g\left( y_{h}^{i}\right) +h\left( u_{h}^{i}\right)$, subject to

$$\begin{aligned} \left\{ \begin{array}{ll} \left( d_{t} y_{h}^{i}, w_{h}\right) +a\left( y_{h}^{i}, w_{h}\right) =\left( f\left( x, t_{i}\right) +B u_{h}^{i}, w_{h}\right) , &{} \forall w_{h} \in V^{h}, \\ y_{h}^{0}(x)=y_{0}^{h}(x), &{} x \in \Omega , \end{array}\right. \end{aligned}$$

(10)

where $y_0^h \in V^h$ is an approximation of $y_0$, which is determined by the following elliptic projection (30).

From [40], the fully discrete approximation scheme has a solution $(Y_h^i, U_h^i)$, and a pair $(Y_h^i, U_h^i) \in V^h \times K^h$ is the solution of the fully discrete approximation scheme if there is a co-state $P_h^{i-1}\in V^h$, such that the triplet $(Y_h^i, P_h^{i-1}, U_h^i) \in V^h \times V^h \times K^h$, satisfies the following optimality condition:

$$\begin{aligned}{} & {} \!\!\!\!\!\!\!\!\!\!\!\left\{ \begin{array}{l} \left( d_{t} Y_{h}^{i}, w_{h}\right) +a\left( Y_{h}^{i}, w_{h}\right) =\left( f^{i}+B U_{h}^{i}, w_{h}\right) , \quad \forall w_{h} \in V^{h}, i=1, \cdots , N_{T}, \\ Y_{h}^{0}(x)=y_{0}^{h}(x), \quad x \in \Omega , \end{array}\right. \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \!\!\!\!\!\!\!\!\!\!\left\{ \begin{array}{l} -\left( d_{t} P_{h}^{i}, q_{h}\right) +a\left( q_{h}, P_{h}^{i-1}\right) =\left( g^{\prime }\left( Y_{h}^{i}\right) , q_{h}\right) , \quad \forall q_{h} \in V^{h}, i=N_{T}, \cdots , 1, \\ P_{h}^{N_{T}}(x)=0, \quad x \in \Omega ,\end{array}\right. \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \!\!\!\!\!\!\!\!\!\!\left( j^{\prime }\left( U_{h}^{i}\right) +B^{*} P_{h}^{i-1}, v_{h}-U_{h}^{i}\right) _{U} \ge 0, \quad \forall v_{h} \in K^{h}, i=1, \cdots , N_{T} . \end{aligned}$$

(13)

The following convergence of the FE solutions can be obtained from [40].

Theorem 2.1

Assume that $u\in l^ 2(I; H^1(\Omega _U))$, $p \in l^2 (I; H^1(\Omega ))$, $y, \ p \in l^\infty (I; H_0^1(\Omega )\cap H^2(\Omega )) \cap H^1(I; H^2(\Omega )) \cap H^2(I; L^2(\Omega ))$, and $j^{\prime }(\cdot )$ and $g^{\prime }(\cdot )$ are Lipschitz continuous. Let (y, p, u) be the solutions of (6)-(8) and $(Y_h, P_h, U_h)$ be the solutions (11)-(13). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned} \begin{aligned}&\left\| y-Y_{h}\right\| _{l^{\infty }\left( I ; L^{2}(\Omega )\right) }^2+\left\| p-P_{h}\right\| _{l^{\infty }\left( I ; L^{2}(\Omega )\right) }^2+\left\| u-U_{h}\right\| _{l^{2}\left( I ; L^{2}\left( \Omega _{U}\right) \right) }^2 \\ \le&K\left( h_{U}^2+h^{4}+(\Delta t)^2\right) . \end{aligned} \end{aligned}$$

(14)

3 Build the ROFE method

In this section, we build a reduced-order finite element approximation for the parabolic optimal control problem. In order to obtain a low-dimensional model, the POD technique is used on the state and co-state systems, and we still use piecewise constant elements to discrete variational inequality.

The snapshots $\{Y_{h1}^{i}\}_{i=1}^{L}$, $\{P_{h1}^{i-1}\}_{i=N_T}^{N_{T}-L+1}$ and the reduced-order solutions $({Y}_{d}^{i}, P_{d}^{i-1},$$U_{h1}^{i})$ satisfy the following reduced-order optimality conditions:

$$\begin{aligned} i=&1, \cdots ,L,\nonumber \\&\left( d_{t} Y_{h1}^{i}, w_{h}\right) +a\left( Y_{h1}^{i}, w_{h}\right) =\left( f^{i}+B U_{h1}^{i}, w_{h}\right) , \quad \forall w_{h} \in V^{h}, \end{aligned}$$

(15)

$$\begin{aligned}&{Y}_{d}^{i}=\sum _{j=1}^{yd}\left( \nabla \varphi _{y j}, \nabla {Y}_{h1}^{i}\right) \varphi _{y j},\\ i=&L+1, \cdots ,N_{T},\nonumber \\&\left( d_{t} Y_{d}^{i}, w_{d}\right) +a\left( Y_{d}^{i}, w_{d}\right) =\left( f^{i}+B U_{h1}^{i}, w_{d}\right) , \quad \forall w_{d} \in V_1^{d}, \end{aligned}$$

(16)

$$\begin{aligned} i=&N_{T}, \cdots ,N_{T}-L+1,\nonumber \\&-\left( d_{t} P_{h1}^{i}, q_{h}\right) +a\left( q_{h}, P_{h1}^{i-1}\right) =\left( g^{\prime }\left( Y_{d}^{i}\right) , q_{h}\right) , \quad \forall q_{h} \in V^{h}, \end{aligned}$$

(17)

$$\begin{aligned}&{P}_{d}^{i-1}=\sum _{j=1}^{pd}\left( \nabla \varphi _{p j}, \nabla {P}_{h1}^{i-1}\right) \varphi _{p j},\\ i=&N_{T}-L, \cdots , 1, \nonumber \\&-\left( d_{t} P_{d}^{i}, q_{d}\right) +a\left( q_{d}, P_{d}^{i-1}\right) =\left( g^{\prime }\left( Y_{d}^{i}\right) , q_{d}\right) , \quad \forall q_{d} \in V_2^{d}, \end{aligned}$$

(18)

$$\begin{aligned} i=&1, \cdots ,N_{T},\nonumber \\&\left( j^{\prime }\left( U_{h1}^{i}\right) +B^{*} P_{d}^{i-1}, v_{h}-U_{h1}^{i}\right) _{U} \ge 0, \quad \forall v_{h} \in K^{h}, \end{aligned}$$

(19)

where $V_1^{d}$ and $V_2^{d}$ are the reduced-order spaces for the state and co-state variables. The two spaces span of the POD basis $\varphi _{y j}$ and $\varphi _{p j}$, respectively, which are constituted as follows.

Definition 1

We introduce the correlation matrix $\varvec{A_y}=\left( A_{yi j}\right) _{L \times L} \in R^{L \times L}$ and $\varvec{A_p}=\left( A_{pi j}\right) _{L \times L} \in R^{L \times L}$ via $A_{yi j}=\left( \nabla Y_{h1}^i, \nabla Y_{h1}^j\right) / L$, $A_{pi j}=\left( \nabla P_{h1}^{N_T-i}, \nabla P_{h1}^{N_T-j}\right) / L$. Related positive eigenvalues and corresponding standard orthonormal eigenvectors are $\lambda _{yj}$ and $\varvec{v}_{yj}$, $\lambda _{pj}$ and $\varvec{v}_{pj}$.

The matrices $\varvec{A_y}$ and $\varvec{A_p}$ are positive semi-definite and have rank yl and pl, and the POD basis can be determined in a similar way as [22, 23, 28]. We have the following results.

Lemma 3.1

The POD basis is constituted by

$$\begin{aligned} {\varphi _{yj}}&=\frac{1}{\sqrt{L\lambda _{yj}}} \sum _{i=1}^{L}\left( \varvec{v}_{yj}\right) _{i} Y_{h1}^i, \quad 1 \le j \le yd\le yl, \end{aligned}$$

(20)

$$\begin{aligned} {\varphi _{pj}}&=\frac{1}{\sqrt{L\lambda _{pj}}} \sum _{i=1}^{L}\left( \varvec{v}_{pj}\right) _{i} P_{h1}^{N_T-i}, \quad 1 \le j \le pd\le pl, \end{aligned}$$

(21)

where $(\varvec{v}_{yj})_i$ and $(\varvec{v}_{pj})_i \ (1\le i \le L)$ denote the ith component of the standard orthonormal eigenvectors $\varvec{v}_{yj}$ and $\varvec{v}_{pj}$, $\lambda _{y1}\ge \lambda _{y2}\ge \cdots \ge \lambda _{yl}>0$ and $\lambda _{p1}\ge \lambda _{p2}\ge \cdots \ge \lambda _{pl}>0$. Furthermore, we have the following error estimate:

$$\begin{aligned}&\frac{1}{L} \sum _{i=1}^{L}\left\| Y_{h1}^i-\sum _{j=1}^{yd}\left( Y_{h1}^i, {\varphi }_{yj}\right) _W \varphi _{yj}\right\| _{W}^{2}=\sum _{j=yd+1}^{yl} \lambda _{yj},\end{aligned}$$

(22)

$$\begin{aligned}&\frac{1}{L} \sum _{i=1}^{L}\left\| P_{h1}^{N_T-i}-\sum _{j=1}^{pd}\left( P_{h1}^{N_T-i}, {\varphi }_{pj}\right) _W \varphi _{pj}\right\| _{W}^{2}=\sum _{j=pd+1}^{pl} \lambda _{pj}, \end{aligned}$$

(23)

where $\left( Y_{h1}^{i}, {\varphi }_{yj}\right) _{W}=(\nabla Y_{h1}^{i},\nabla {\varphi }_{yj})$, $\Vert Y_{h1}^{i}\Vert _W^2=\Vert \nabla Y_{h1}^{i}\Vert ^2$.

Then the reduced-order spaces $V_1^d$ and $V_2^d$ for the state and co-state variables as follows:

$$\begin{aligned} V_1^d={\text {span}}\left\{ \varphi _{y 1}, \varphi _{y 2}, \cdots , \varphi _{y d}\right\} ,\quad V_2^d={\text {span}}\left\{ \varphi _{p 1}, \varphi _{p 2}, \ldots , \varphi _{p d}\right\} . \end{aligned}$$

(24)

It is easy to see that $V_1^d \subset V^h$ and $V_2^d \subset V^h$.

Remark 3.1

The equation (11) at each time level contains $N_h$ unknowns, where $N_h$ represents the number of unknowns of the finite element space in triangulations $\mathscr {T}^{h}$. However, the equation (17) at the same time level only has yd unknowns, where $yd\le yl\le L \ll N_T\ll N_h$. For instance, in Example 5.1, $yd=6, \ N_h=129^2$. Likewise, $pd\le pl\le L \ll N_T\ll N_h$. So the ROFE method can immensely decrease the number of unknowns.

4 Error estimates

In this section, we present the error estimates between the FE solutions and the ROFE solutions, then obtain error results between the analytical solutions and the ROFE solutions.

In the following paper, we assume the following convexity condition:

$$\begin{aligned} (j^{\prime }(t)-j^{\prime }(s))(t-s) \ge K(t-s)^2, \quad \forall s, t \in R. \end{aligned}$$

(25)

For $y_h\in V^h$ and $p_h\in V^h$ define two projections $Q^d:V^h \rightarrow V_1^d$ and $R^d:V^h \rightarrow V_2^d$ as follows:

$$\begin{aligned}&a\left( y_h-Q^d y_h, w_{d}\right) =0, \quad \forall w_{d} \in V_1^{d}, \end{aligned}$$

(26)

$$\begin{aligned}&a\left( q_{d}, p_h-R^d p_h\right) =0, \quad \forall q_{d} \in V_2^{d}. \end{aligned}$$

(27)

Then it is easily known from functional analysis principles [41] that there are two extensions $Q^h:V \rightarrow V^h$ and $R^h:V \rightarrow V^h$ of $Q^d$ and $R^d$ such that $Q^h|_{V^h}=Q^d$ and $R^h|_{V^h}=R^d$ are defined by

$$\begin{aligned}&a\left( y-Q^h y, w_{h}\right) =0, \quad \forall w_{h} \in V^{h}, \end{aligned}$$

(28)

$$\begin{aligned}&a\left( q_{h}, p-R^h p\right) =0, \quad \forall q_{h} \in V^{h}, \end{aligned}$$

(29)

where $y\in V$, $p\in V$.

Define the negative norm:

$$\Vert v\Vert _{-1}=\sup _{0 \ne \phi \in H^{1}} \frac{(v, \phi )}{\Vert \phi \Vert _{1}}.$$

From [28], the projections $Q^h$ and $R^h$ are bounded such that

$$\begin{aligned}&\Vert Q^h y\Vert \le K\Vert y\Vert , \quad \forall y \in V,\end{aligned}$$

(30)

$$\begin{aligned}&\Vert R^h p\Vert \le K\Vert p\Vert ,\quad \forall p\in V. \end{aligned}$$

(31)

And there are the following results:

$$\begin{aligned}&\Vert y-Q^h y\Vert \le Kh\Vert \nabla (y-Q^h y)\Vert ,\quad \forall y \in V,\end{aligned}$$

(32)

$$\begin{aligned}&\Vert y-Q^h y\Vert _{-1}\le Kh\Vert y-Q^h y\Vert ,\quad \forall y\in V, \end{aligned}$$

(33)

$$\begin{aligned}&\Vert p-R^h p\Vert \le Kh\Vert \nabla (p-R^h p)\Vert ,\quad \forall p\in V, \end{aligned}$$

(34)

$$\begin{aligned}&\Vert p-R^h p\Vert _{-1}\le Kh\Vert p-R^h p\Vert , \quad \forall p\in V. \end{aligned}$$

(35)

From [28], there are the following conclusions.

Lemma 4.1

For $yd \ (1\le yd \le yl), pd \ (1\le pd \le pl)$, the projections $Q^d$ and $R^d$ satisfy

$$\begin{aligned}{} & {} \!\!\!\frac{1}{L} \sum _{i=1}^{L}\left[ \left\| {Y}_{h1}^{i}-Q^{d} {Y}_{h1}^{i}\right\| ^{2}+h^{2}\left\| \nabla \left( {Y}_{h1}^{i}-Q^{d} {Y}_{h1}^{i} \right) \right\| ^{2}\right] \le K h^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}, \end{aligned}$$

(36)

$$\begin{aligned}{} & {} \!\!\!\frac{1}{L} \sum _{i=1}^{L}\left[ \left\| P_{h1}^{N_T-i}\!-\!R^{d} P_{h1}^{N_T-i}\right\| ^{2}\!+\!h^{2}\left\| \nabla \left( P_{h1}^{N_T-i}\!-\!R^{d} P_{h1}^{N_T-i}\right) \right\| ^{2}\right] \!\le \!K h^{2}\! \sum _{j=pd+1}^{pl} \lambda _ {pj}.\nonumber \\ \end{aligned}$$

(37)

where $Y_{h1}^{i}\in V^h \ (i = 1,2, \cdots , L)$, $P_{h1}^{i}\in V^h \ (i= N_T-1,N_T-2, \cdots ,N_T-L)$ are the L solutions of equations (15) and (18). Moreover, suppose that $(y^i, p^i) \in V \times V\ (i = 0,1, \cdots , N_T)$ are the solutions of the equations (6)-(8), the projections $Q^h$ and $R^h$ satisfy the following error estimates:

$$\begin{aligned}&\left\| y^i-Q^h y^i\right\| ^{2}+h^2\left\| \nabla (y^i-Q^h y^i)\right\| ^{2} \le Kh^{4},\quad i=0,1,\cdots , N_T,\end{aligned}$$

(38)

$$\begin{aligned}&\left\| p^i-R^h p^i\right\| ^{2}+h^2\left\| \nabla (p^i-R^h p^i)\right\| ^{2} \le K h^{4}, \quad i=0,1,\cdots , N_T, \end{aligned}$$

(39)

where the constant K is independent of $h_U$, h and $\Delta t$.

Lemma 4.2

Assume that all conditions of Theorem 2.1 are valid. Let $Y_h^i \in V^h\ (i = L+1, L+2, \cdots ,N_T)$, $P_h^i \in V^h \ (i = N_T-L-1, N_T-L-2, \cdots ,0)$ be the solutions of (11)-(13), then the projections $Q^d$ and $R^d$ satisfy the following error estimates:

$$\begin{aligned}{} & {} \Vert Y_{h}^{i}-Q^dY_{h}^{i}\Vert ^2\le K(h_{U}^{2}+h^{4}+(\Delta t)^2),\end{aligned}$$

(40)

$$\begin{aligned}{} & {} \Vert P_{h}^{i}-R^dP_{h}^{i}\Vert ^2\le K(h_{U}^{2}+h^{4}+(\Delta t)^2), \end{aligned}$$

(41)

where the constant K is independent of $h_U$, h and $\Delta t$.

Proof

For $i = L+1, L+2, \cdots ,N_T$, since $Q^hY_{h}^{i}=Q^dY_{h}^{i}$, using (14) and (40), we have

$$\begin{aligned} \Vert Y_{h}^{i}-Q^dY_{h}^{i}\Vert ^2\le & {} \Vert Y_{h}^{i}-y^{i}\Vert ^2+\Vert y^{i}-Q^hy^{i}\Vert ^2+\Vert Q^hy^{i}-Q^hY_{h}^{i}\Vert ^2\nonumber \\\le & {} \Vert y^{i}-Y_{h}^{i}\Vert ^2+\Vert y^{i}-Q^hy^{i}\Vert ^2 \nonumber \\\le & {} K(h_{U}^{2}+h^{4}+(\Delta t)^2). \end{aligned}$$

(42)

For $i = N_T-L-1, N_T-L-2, \cdots ,0$, since $R^hP_{h}^{i}=R^dP_{h}^{i}$, using (14) and (41), we have

$$\begin{aligned} \Vert P_{h}^{i}-R^dP_{h}^{i}\Vert ^2\le & {} \Vert P_{h}^{i}-p^{i}\Vert ^2+\Vert p^{i}-R^hp^{i}\Vert ^2+\Vert R^hp^{i}-R^hP_{h}^{i}\Vert ^2\nonumber \\\le & {} \Vert p^{i}-P_{h}^{i}\Vert ^2+\Vert p^{i}-R^hp^{i}\Vert ^2 \nonumber \\\le & {} K(h_{U}^{2}+h^{4}+(\Delta t)^2). \end{aligned}$$

(43)

Then the proof ends. $\square$

Lemma 4.3

Assume that all conditions of Theorem 2.1 are valid and $\Delta t=O(h)$. Let $Y_h^i \in V^h\ (i = 1, 2, \cdots , N_T)$ be the solutions of (11)-(13) and $Y_{h1}^i \in V^h\ (i = 1, 2, \cdots ,L)$ and $Y_{d}^{i}\in V_1^d\ (i = 1, 2, \cdots , N_T)$ be the solutions of (15)-(21). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned} \left\| Y_{h}^{L_0}\!-\!Y_{h1}^{L_0}\right\| ^{2}\!+\!2 \sum _{i=1}^{L_0} \Delta t\left\| \nabla (Y_{h}^{i}\!-\!Y_{h1}^{i})\right\| ^{2} \!\le \! K \sum _{i=1}^{L_0} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2}, \quad 1 \!\le \! {L_0} \!\le \! L. \end{aligned}$$

(44)

$$\begin{aligned} \begin{aligned} \left\| Y_{h}^{L_0}\!-\!Y_{d}^{L_0}\right\| ^{2}\!+\!2 \sum _{i=1}^{L_0} \Delta t\left\| \nabla (Y_{h}^{i}\!-\!Y_{h1}^{i})\right\| ^{2} \!\le \! K\sum _{i=1}^{L_0} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2}\!+\!KLh^{2}\! \sum _{j=yd+1}^{yl}\! \lambda _{yj},\! \!\!\!\quad 1\!\le \! {L_0} \!\le \! L. \end{aligned} \end{aligned}$$

(45)

$$\begin{aligned} \begin{aligned} \left\| Y_{h}^{L_1}-Y_{d}^{L_1}\right\| ^{2}+2\sum _{i=L+1}^{L_1} \Delta t\left\| \nabla (Q^dY_{h}^{i}-Y_{d}^{i})\right\| ^{2} \le&K(h_{U}^{2}+h^{4}+(\Delta t)^2) \! +KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj} \\ {}&+K\sum _{i=1}^{L_1} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2},\!\!\! \quad L\!+\!1 \!\le \!{L_1} \!\le \! N_T. \end{aligned} \end{aligned}$$

(46)

Proof

For $i = 1, 2, \cdots , L$, subtracting (15) from (11), we obtain

$$\begin{aligned} \left( d_{t} (Y_{h}^{i}-Y_{h1}^{i}), w_{h}\right) +a\left( Y_{h}^{i}-Y_{h1}^{i}, w_{h}\right) =\left( B\left( U_{h}^{i}-U_{h1}^{i}\right) , w_{h}\right) , \quad \forall w_{h} \in V^{h}. \end{aligned}$$

(47)

Select $w_{h}=Y_{h}^{i}-Y_{h1}^{i}$ as a test function. The inequality $a(a -b)\ge \frac{1}{2}(a^2 -b^2)$ shows that

$$\begin{aligned} \left( d_{t}(Y_{h}^{i}-Y_{h1}^{i}), Y_{h}^{i}-Y_{h1}^{i}\right) \ge \frac{1}{2\Delta t}\left( \left\| Y_{h}^{i}-Y_{h1}^{i}\right\| ^{2}-\left\| Y_{h}^{i-1}-Y_{h1}^{i-1}\right\| ^{2}\right) . \end{aligned}$$

(48)

Combing (49) and (50), multiplying both sides of (49) by $2\Delta t$ and summing over i from 1 to $L_0$ $(1 \le L_0 \le L)$, we then derive from the continuous property of B that

$$\begin{aligned} \left\| Y_{h}^{L_0}-Y_{h1}^{L_0}\right\| ^{2}+2 \sum _{i=1}^{L_0} \Delta t\left\| \nabla (Y_{h}^{i}-Y_{h1}^{i})\right\| ^{2} \le K \sum _{i=1}^{L_0} \Delta t\left\| Y_{h}^{i}-Y_{h1}^{i}\right\| ^{2}+K \sum _{i=1}^{L_0} \Delta t\left\| U_{h}^{i}-U_{h1}^{i}\right\| _{U}^{2}. \end{aligned}$$

(49)

From the discrete Gronwall’s lemma, (46) holds for sufficiently small $\Delta t$.

For $i = 1, 2, \cdots , L$, there is $Q^dY_{h1}^{i}=Y_{d}^{i}$. From (38) and (46), we can find that (47) holds.

For $i=L+1, L+2, \cdots , N_{T}$, subtracting (17) from (11), we obtain

$$\begin{aligned} \left( d_{t} (Q^dY_{h}^{i}-Y_{d}^{i}), w_{d}\right) +a\left( Q^dY_{h}^{i}-Y_{d}^{i}, w_{d}\right)= & {} -\left( d_{t} (Y_{h}^{i}-Q^dY_{h}^{i}), w_{d}\right) \\ {}{} & {} \!+\! \left( B(U_{h}^{i}\!-\!U_{h1}^{i}), w_{d}\right) , \!\!\!\quad \forall w_{d} \!\in \! V_1^{d}.\nonumber \end{aligned}$$

(50)

Let $w_{d}=Q^dY_{h}^{i}-Y_{d}^{i}$ and multiply both sides of (52) by $2\Delta t$. We denote the first right-hand side terms of (52) by $G_1$, if $\Delta t=O(h)$, since (35) and $Q^hY_h^i=Q^dY_h^i$, we have

$$\begin{aligned} |G_1|&\le K(\Delta t)^{-1}(\Vert Y_{h}^{i}-Q^dY_{h}^{i}\Vert _{-1}^2+\Vert Y_{h}^{i-1}-Q^dY_{h}^{i-1}\Vert _{-1}^2)+\epsilon \Delta t\Vert Q^dY_{h}^{i}-Y_{d}^{i}\Vert _1^2\nonumber \\&\le K(\Delta t)^{-1}h^2(\Vert Y_{h}^{i}-Q^dY_{h}^{i}\Vert ^2+\Vert Y_{h}^{i-1}-Q^dY_{h}^{i-1}\Vert ^2)+\epsilon \Delta t\Vert Q^dY_{h}^{i}-Y_{d}^{i}\Vert _1^2\nonumber \\&\le K\Delta t(\Vert Y_{h}^{i}-Q^dY_{h}^{i}\Vert ^2+\Vert Y_{h}^{i-1}-Q^dY_{h}^{i-1}\Vert ^2)+ \epsilon \Delta t\Vert Q^dY_{h}^{i}-Y_{d}^{i}\Vert _1^2.\nonumber \end{aligned}$$

(51)

Then sum over i from $L+1$ to $L_{1}$ $(L+1 \le L_1 \le N_T)$, we get

$$\begin{aligned}{} & {} \left\| Q^dY_{h}^{L_{1}}-Y_{d}^{L_{1}}\right\| ^{2}+2\sum _{i=L+1}^{L_{1}} \Delta t\left\| \nabla (Q^dY_{h}^{i}-Y_{d}^{i})\right\| ^{2} \\ \!\le & {} \! \epsilon \!\!\! \sum _{i=L+1}^{L_{1}}\!\!\! \Delta t\left\| Q^dY_{h}^{i}\!-\!Y_{d}^{i}\right\| _1^{2}\!+\!K \!\sum _{i=L}^{L_{1}}\! \Delta t\left\| Y_{h}^{i}\!-\!Q^dY_{h}^{i}\right\| ^{2} \!+\!K \!\sum _{i=L+1}^{L_{1}} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2}\!+\!K\left\| Q^dY_{h}^{L}\!-\!Y_{d}^{L}\right\| ^{2}. \nonumber \end{aligned}$$

(52)

From (42), (46) and (47), we have

$$\begin{aligned} \begin{aligned} \left\| Q^dY_{h}^{L}-Y_{d}^{L}\right\| ^{2}&\le \left\| Q^dY_{h}^{L}-Y_{h}^{L}\right\| ^{2}+\left\| Y_{h}^{L}-Y_{h1}^{L}\right\| ^{2}+\left\| Y_{h1}^{L}-Y_{d}^{L}\right\| ^{2} \\ {}&\le K(h_{U}^{2}+h^{4}+(\Delta t)^2)+KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}+K\left\| Y_{h}^{L}-Y_{h1}^{L}\right\| ^{2}. \end{aligned} \end{aligned}$$

(53)

Combing (42), (53) and (54), we get (48) from the discrete Gronwall’s lemma.    $\Box$

Lemma 4.4

Assume that all conditions of Theorem 2.1 are valid and $\Delta t=O(h)$. Let $P_h^i \in V^h\ (i = N_T-1, N_T-2, \cdots , 0)$ be the solutions of (11)-(13) and $P_{h1}^i \in V^h\ (i = N_T-1, N_T-2, \cdots ,N_T-L)$ and $P_{d}^{i}\in V_2^d\ (i = N_T-1, N_T-2, \cdots , 0)$ be the solutions of (15)-(21). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned}{} & {} \left\| P_{h}^{M_0}-P_{h1}^{M_0}\right\| ^{2}+2\sum _{i=M_0+1}^{N_{T}} \Delta t\left\| \nabla (P_{h}^{i-1}-P_{h1}^{i-1})\right\| ^{2} \end{aligned}$$

(54)

$$\begin{aligned}\le & {} K(h_{U}^{2}\!+\!h^{4}+(\Delta t)^2)\!+\!KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj} \!+\!K\sum _{i=1}^{N_{T}} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2},\!\! \quad N_T\!-\!L \!\le \! {M_0} \!\le \! N_T-1.\nonumber \\{} & {} \left\| P_{h}^{M_0}-P_{d}^{M_0}\right\| ^{2}+2\sum _{i=M_0+1}^{N_{T}} \Delta t\left\| \nabla (P_{h}^{i-1}-P_{h1}^{i-1})\right\| ^{2}\end{aligned}$$

(55)

$$\begin{aligned}\le & {} K(h_{U}^{2}\!+\!h^{4}\!+\!(\Delta t)^2)\!+\!KLh^{2}\!\!\!\! \sum _{j\!=yd\!+1}^{yl}\!\! \lambda _{yj}\!+\!KL h^{2}\!\!\! \sum _{j\!=pd\!+1}^{pl}\!\!\! \lambda _{pj} \!+\! K\sum _{i\!=1}^{N_{T}} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2},\!\!\! \quad \!\!N_T\!-\!L \!\le \! {M_0} \!\le \! N_T\!-\!1. \nonumber \\{} & {} \left\| P_{h}^{M_1}-P_{d}^{M_1}\right\| ^{2}+2\sum _{i=M_1+1}^{N_{T}-L} \Delta t\left\| \nabla (R^dP_{h}^{i-1}-P_{d}^{i-1})\right\| ^{2}\end{aligned}$$

(56)

$$\begin{aligned} \!\le & {} \! K(h_{U}^{2}\!+\!h^{4}\!+\!(\Delta t)^2)\!+\!KLh^{2}\!\!\! \sum _{j\!=yd\!+1}^{yl}\!\! \lambda _{yj}\!+\!KLh^{2}\!\!\!\! \sum _{j\!=pd\!+1}^{pl}\!\!\! \lambda _{pj} \!+\! K\sum _{i\!=1}^{N_{T}}\!\! \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _U^{2},\!\!\! \quad 0\!\le \! {M_1} \!\le \! N_T\!-\!L\!-\!1.\nonumber \end{aligned}$$

(57)

Proof

For $i=N_{T}, \cdots ,N_{T}-L+1$, subtracting (18) from (12), we obtain

$$\begin{aligned} \begin{aligned} \!-\!\left( d_{t} (P_{h}^{i}\!-\!P_{h1}^{i}), q_{h}\right) \!+\!a\left( q_{h}, P_{h}^{i-1}\!-\!P_{h1}^{i-1}\right) \!=\!\left( g^{\prime }\left( Y_{h}^{i}\right) \!-\!g^{\prime }\left( Y_{d}^{i}\right) , q_{h}\right) , \!\!\!\quad \forall q_{h}\! \in \! V^{h}. \end{aligned} \end{aligned}$$

(58)

Let $q_{h}=P_{h}^{i-1}-P_{h1}^{i-1}$ and multiply both sides of (58) by $2\Delta t$ and sum over i from $N_{T}$ to $M_0+1$ $(N_{T}-L\le M_0 \le N_{T}-1)$, we have

$$\begin{aligned} \left\| P_{h}^{M_0}\!-\!P_{h1}^{M_0}\right\| ^{2}\!+\! 2\!\!\!\sum _{i=M_0+1}^{N_{T}}\!\!\! \Delta t\left\| \nabla (P_{h}^{i-1}\!-\!P_{h1}^{i-1})\right\| ^{2}\!\! \le \!K\!\!\!\! \sum _{i=M_0+1}^{N_{T}}\!\! \Delta t\left\| P_{h}^{i\!-1}\!-\!P_{h1}^{i\!-1}\right\| ^{2}\!+\!K\!\!\!\sum _{i=M_0+1}^{N_{T}}\!\!\! \Delta t\left\| Y_{h}^{i}\!-\!Y_{d}^{i}\right\| ^{2}.\nonumber \\ \end{aligned}$$

(59)

From the discrete Gronwall’s lemma and (48), we get that (55) holds.

For $i=N_{T}-1, \cdots ,N_{T}-L$, there is $R^dP_{h1}^{i}=P_{d}^{i}$. From (39) and (55), we can find that (56) holds.

For $i=N_{T}-L, N_{T}-L-1, \cdots , 1$, subtracting (20) from (12), we obtain

$$\begin{aligned} \!-\!\left( d_{t}(R^dP_{h}^{i}\!-\!P_{d}^{i}), q_{d}\right) \!+\!a\left( q_{d}, R^dP_{h}^{i-\!1}\!-\!P_{d}^{i\!-1}\right) \!= & {} \!\left( d_{t}(P_{h}^{i}\!-\!R^dP_{h}^{i}), q_{d}\right) \\{} & {} +\!(\left. g^{\prime }\left( Y_{h}^{i}\right) \!-\!g^{\prime }\left( Y_{d}^{i}\right) , q_{d}\right) ,\!\! \quad \!\! \forall q_{d} \!\in \! V_2^{d}.\nonumber \end{aligned}$$

(60)

Similarly, let $q_{d}=R^dP_{h}^{i-1}-P_{d}^{i-1}$ and multiply both sides of (60) by $2\Delta t$ and sum over i from $N_{T}-L$ to $M_1+1$ $(0\le M_1\le N_{T}-L-1 )$, we get

$$\begin{aligned}{} & {} \left\| R^dP_{h}^{M_1}-P_{d}^{M_1}\right\| ^{2}+2\sum _{i=M_1+1}^{N_{T}-L} \Delta t\left\| \nabla (R^dP_{h}^{i-1}-P_{d}^{i-1})\right\| ^{2} \\\le & {} \epsilon \sum _{i=M_1+1}^{N_{T}-L} \Delta t\left\| R^dP_{h}^{i-1}-P_{d}^{i-1}\right\| _1^{2}+K \sum _{i=M_1}^{N_{T}-L} \Delta t\left\| P_{h}^{i}-R^dP_{h}^{i}\right\| ^{2}\nonumber \\ {}{} & {} +K\sum _{i=M_1+1}^{N_{T}-L} \Delta t\left\| Y_{h}^{i}-Y_{d}^{i}\right\| ^{2}+K\left\| R^dP_{h}^{N_{T}-L}-P_{d}^{N_{T}-L}\right\| ^{2}.\nonumber \end{aligned}$$

(61)

From (43), (55) and (56), we have

$$\begin{aligned} \begin{aligned} \left\| R^dP_{h}^{N_{T}-L}-P_{d}^{N_{T}-L}\right\| ^{2}\le&\left\| R^dP_{h}^{N_{T}-L}-P_{h}^{N_{T}-L}\right\| ^{2}+\Bigg \Vert P_{h}^{N_{T}-L}\\ {}&-P_{h1}^{N_{T}-L}\Bigg \Vert ^{2}+\left\| P_{h1}^{N_{T}-L}-P_{d}^{N_{T}-L}\right\| ^{2} \\ \le&K( h_{U}^{2}+h^{4}+(\Delta t)^2)+KLh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj}\\ {}&+K\left\| P_{h}^{N_{T}-L}-P_{h1}^{N_{T}-L}\right\| ^{2} \end{aligned} \end{aligned}$$

(62)

Combing (43), (61) and (62), we get (57) from the discrete Gronwall’s lemma. $\square$

Lemma 4.5

Assume that all conditions of Theorem 2.1 are valid. Let $U_h^i \in V^h\ (i = 1, 2, \cdots , N_T)$ be the solutions of (11)-(13) and $U_{h1}^i \in V^h\ (i = 1, 2, \cdots , N_T)$ be the solutions of (15)-(21). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned} \sum _{i=1}^{L_2} \Delta t\left\| U_{h}^{i}-U_{h1}^{i}\right\| _{U}^{2} \le K\sum _{i=1}^{L_2} \Delta t\left\| P_{d}^{i-1}-P_{h}^{i-1}\right\| ^2, \quad 1\le L_2\le N_T. \end{aligned}$$

(63)

Proof

From (27) about the uniform convexity of $j(\cdot )$, we have

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^{L_2} \Delta t\left\| U_{h}^{i}-U_{h1}^{i}\right\| _{U}^{2} \le K\sum _{i=1}^{L_2} \Delta t\left( j^{\prime }\left( U_{h}^{i}\right) -j^{\prime }\left( U_{h1}^{i}\right) , U_{h}^{i}-U_{h1}^{i}\right) _{U}\\ =&K\sum _{i=1}^{L_2} \Delta t\left( j^{\prime }\left( U_{h}^{i}\right) \!+\!B^{*} P_{h}^{i-\!1}, U_{h}^{i}\!-\!U_{h1}^{i}\right) _{U}\!+\!K\sum _{i=1}^{L_2} \Delta t\left( j^{\prime }\left( U_{h1}^{i}\right) \!+\!B^{*} P_{d}^{i-1}, U_{h1}^{i}\!-\!U_{h}^{i}\right) _{U}\\&+K\sum _{i=1}^{L_2} \Delta t\left( B^{*}( P_{d}^{i-1}-P_{h}^{i-1}),U_{h}^{i}-U_{h1}^{i}\right) _{U} \\ \le&K \sum _{i=1}^{L_2} \Delta t\left( B^{*}( P_{d}^{i-1}-P_{h}^{i-1}),U_{h}^{i}-U_{h1}^{i}\right) _{U} \\ \le&K \sum _{i=1}^{L_2} \Delta t\left\| P_{d}^{i-1}-P_{h}^{i-1}\right\| ^{2}+\epsilon \sum _{i=1}^{L_2} \Delta t\left\| U_{h}^{i}-U_{h1}^{i}\right\| ^{2}_{U}, \end{aligned} \end{aligned}$$

(64)

where (13) and (21) are used. So (63) holds. $\square$

Theorem 4.1

Assume that all conditions of Theorem 2.1 are valid and $\Delta t=O(h)$. Let $(Y_h, P_h, U_h )$ be the solutions of (11)-(13) and $(Y_{d},P_d, U_{h1} )$ be the solutions of (15)-(21). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned} \begin{aligned}&\left\| Y_{h}-Y_{d}\right\| ^2_{l^{\infty }\left( I ; L^{2}(\Omega )\right) }+\left\| P_{h}-P_{d}\right\| ^2_{l^{\infty }\left( I ; L^{2}(\Omega )\right) }+\left\| U_{h}-U_{h1}\right\| ^2_{l^{2}\left( I ; L^{2}\left( \Omega _{U}\right) \right) } \\ \le&K(h_{U}^{2}+h^{4}+(\Delta t)^2)+KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}+KLh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj}. \end{aligned} \end{aligned}$$

(65)

Proof

From (63), we get

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N_{T}} \Delta t\left\| U_{h}^{i}-U_{h1}^{i}\right\| _{U}^{2}&\le K\sum _{i=0}^{N_{T}-1} \Delta t\left\| P_{d}^i-P_{h}^i\right\| ^2. \end{aligned} \end{aligned}$$

(66)

Combing (56), (57) and (66), we obtain

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N_{T}} \Delta t\left\| U_{h}^{i}\!-\!U_{h1}^{i}\right\| _{U}^{2} \!\le \! K( h_{U}^{2}\!+\!h^{4}\!+\!(\Delta t)^2)\!+\!KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}\!+\!KLh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj}. \end{aligned} \end{aligned}$$

(67)

Combing (47), (48), (56), (57) and (67), we have

$$\begin{aligned} \left\| Y_{h}^{i}-Y_{d}^{i}\right\| ^{2}\!+\!\left\| P_{h}^{i}\!-\!P_{d}^{i}\right\| ^{2} \!\le \! K(h_{U}^{2}\!+\!h^{4}\!+\!(\Delta t)^2)\!+\!KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}+KLh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj}. \end{aligned}$$

(68)

So (65) holds. $\square$

Combing Theorem 2.1 and Theorem 4.1, we have the following theorem.

Theorem 4.2

Assume that all conditions of Theorem 2.1 are valid and $\Delta t=O(h)$. Let (y, p, u) be the solutions of (6)-(8) and $(Y_{d},P_d, U_{h1} )$ be the solutions of (15)-(21). There exists a positive constant K independent of $h_U$, h and $\Delta t$ such that

$$\begin{aligned} \begin{aligned}&\left\| y-Y_{d}\right\| ^2_{l^{\infty }\left( I ; L^{2}(\Omega )\right) }+\left\| p-P_{d}\right\| ^2_{l^{\infty }\left( I ; L^{2}(\Omega )\right) }+\left\| u-U_{h1}\right\| ^2_{l^{2}\left( I ; L^{2}\left( \Omega _{U}\right) \right) } \\ \le&K(h_{U}^{2}+h^{4}+(\Delta t)^2)+KLh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}+KLh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj}. \end{aligned} \end{aligned}$$

(69)

Remark 4.1

In the theorem, $\Delta t=O (h)$ is a assumption in the proof process. Due to the limitation of analytical technique, we cannot remove this condition at present. Ideally, we would obtain the same error results without this assumption. In order to reflect the ideal results, this assumption is not used in the statement of the main results.

In addition, the piecewise constant is used to approximate the control, which achieves the first-order optimal approximation of the control. The state variables also reach the corresponding second-order optimal approximation. According to [40], if the piecewise linear function is used for control, $h_ U^2$ will become $h_U^3$ in the error result (69). This paper focuses on the application of the POD technique in the optimal control model. Whether the piecewise linear function or piecewise constant is used for control, it will not affect our research.

5 Numerical experiments

In this section, we carry out some numerical examples to verify the accuracy and efficiency of the ROFE method for solving the parabolic optimal control problem. The accuracy and CPU time of the ROFE method are compared with that of the FE method.

In the numerical examples below, the number of snapshots L is chosen such that further increasing it will not produce better results for the ROFE method. From Theorem 4.2, we choose yd, pd to satisfy $Lh^{2} \sum _{j=yd+1}^{yl} \lambda _{yj}+Lh^{2} \sum _{j=pd+1}^{pl} \lambda _{pj} \le K(h_{U}^{2}+h^{4}+(\Delta t)^2)$, where $K=0.1$, so that the reduced order method has convergence order.

We consider the following parabolic optimal control problems:

$$\begin{aligned} \min _{u(t) \in K} \frac{1}{2} \int _{0}^{T}\left( \left\| y-y_{d}\right\| ^{2}+\left\| u-u_{d}\right\| ^{2}\right) d t, \end{aligned}$$

(70)

subject to the parabolic equation:

$$\begin{aligned} \left\{ \begin{array}{ll} y_{t}-\Delta y=f+u, &{} \text{ in } \Omega \times I, \\ y(x, 0)=y_{0}(x), &{} \text{ in } \Omega , \end{array}\right. \end{aligned}$$

(71)

and the co-state equation is

$$\begin{aligned} \left\{ \begin{array}{ll} -p_{t}-\Delta p=y-y_{d}, &{} \text{ in } \Omega \times I, \\ p(x, T)=0, &{} \text{ in } \Omega . \end{array}\right. \end{aligned}$$

(72)

Both equations (71) and (72) are combined with homogeneous Dirichlet boundary conditions.

In the first two examples, we choose the domain $\Omega = [0,1]\times [0,1]$, and in the third example, we consider the $L-shaped$ domain $\Omega = [0,1]\times [0,1] \setminus (0.5,1]\times (0.5,1]$. $T=10$. We adopt the same mesh partition for the state and control such that the mesh size $h=2^{-m}, \ m=3,4,5,6,7$, and time step $\Delta t = h$. Does E denote the $l^{\infty }\left( I ; L^{2}(\Omega )\right)$-norm for the state and co-state approximations and $l^{2}\left( I ; L^{2}(\Omega )\right)$-norm for the control approximation.

Example 5.1

We consider the analytical solutions as follows:

$$\begin{aligned} {\begin{matrix} \left\{ \begin{array}{l} \begin{aligned} &{}y=x_1x_2\sin (\pi x_1)sin(\pi x_2)\sin (\pi t),\\ &{}p=0.5x_1x_2\sin (\pi x_1)\sin (\pi x_2)\sin (\pi t),\\ &{}u_d=1-\sin (\pi x_1)-\sin (\pi x_2),\\ &{}u=max(u_d-p,0). \end{aligned} \end{array} \right. \end{matrix}} \end{aligned}$$

where the functions f and $y_d$ are determined by inserting the known functions y, p, and u into (71)-(72).

Table 1 The errors and the convergence rates of Example 5.1

Table 2 The number of POD basis and the CPU time of Example 5.1 for $h=1/128$

Fig. 1

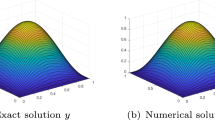
The state solutions at $t=4.5$ with $h=1/128$ of Example 5.1 ( (a): FE method and (b): ROFE method )

In this example, the number of the snapshots is taken as $L = min\{20, 2^m\}$. The errors and the convergence rates of the two methods are listed in Table 1. The number of the POD basis and the CPU time of the two methods are listed in Table 2. The profiles of the ROFE solutions at $t=4.5$ with $h=1/128$ are displayed in (b) graphs of Figs. 1, 2 and 3. Moreover, we also display the profiles of the FE solutions at $t=4.5$ with $h=1/128$ in (a) graphs of Figs. 1, 2 and 3.

Fig. 2

The co-state solutions at $t=4.5$ with $h=1/128$ of Example 5.1 ( (a): FE method and (b): ROFE method )

Fig. 3

The control solutions at $t=4.5$ with $h=1/128$ of Example 5.1 ( (a): FE method and (b): ROFE method )

Example 5.2

We consider the analytical solutions as follows:

$$\begin{aligned} {\begin{matrix} \left\{ \begin{array}{l} \begin{aligned} &{}y=exp(-t/10)tsin(2\pi x_1)sin(2\pi x_2 ),\\ &{}p=exp(-t/10)(10-t)sin(2\pi x_1)sin(2\pi x_2),\\ &{}u_d=exp(-t/10)sin(2\pi x_1)sin(2\pi x_2),\\ &{}u=max(u_d-p,0), \end{aligned} \end{array} \right. \end{matrix}} \end{aligned}$$

where the functions f and $y_d$ are determined by inserting the known functions y, p, and u into (71)-(72).

Table 3 The errors and the convergence rates of Example 5.2

Table 4 The number of POD basis and the CPU time of Example 5.2 for $h=1/128$

Fig. 4

The state solutions at $t=4.5$ with $h=1/128$ of Example 5.2 ( (a): FE method and (b): ROFE method )

Fig. 5

The co-state solutions at $t=4.5$ with $h=1/128$ of Example 5.2 ( (a): FE method and (b): ROFE method )

Fig. 6

The control solutions at $t=4.5$ with $h=1/128$ of Example 5.2 ( (a): FE method and (b): ROFE method )

Table 5 The errors and the convergence rates of Example 5.3

In this example, the number of the snapshots is taken as $L = min\{20, 2^m\}$. The errors and the convergence rates of the two methods are listed in Table 3. The number of the POD basis and the CPU time of the two methods are listed in Table 4. The profiles of the ROFE solutions at $t=4.5$ with $h=1/128$ are displayed in (b) graphs of Figs. 4, 5 and 6. Moreover, we also display the profiles of the FE solutions at $t=4.5$ with $h=1/128$ in (a) graphs of Figs. 4, 5 and 6.

Example 5.3

We consider the analytical solutions as follows:

$$\begin{aligned} {\begin{matrix} \left\{ \begin{array}{l} \begin{aligned} &{}y=sin(\pi t)exp(t)x_1(x_1-0.5)(x_1-1)x_2(x_2-0.5)(x_2-1),\\ &{}p=sin(\pi t)sin(2\pi x_1)sin(2\pi x_2),\\ &{}u_d=1-sin(2\pi x_1)-sin(2\pi x_2),\\ &{}u=max(u_d-p,0), \end{aligned} \end{array} \right. \end{matrix}} \end{aligned}$$

where the functions f and $y_d$ are determined by inserting the known functions y, p, and u into (71)-(72).

Table 6 The number of POD basis and the CPU time of Example 5.3 for $h=1/128$

Fig. 7

The state contours at $t=4.5$ with $h=1/128$ of Example 5.3 ( (a): FE method and (b): ROFE method )

In this example, the number of the snapshots is taken as $L = min\{20, 2^m\}$. The errors and the convergence rates of the two methods are listed in Table 5. The number of the POD basis and the CPU time of the two methods are listed in Table 6. The contours of the ROFE solutions at $t=4.5$ with $h=1/128$ are displayed in (b) graphs of Figs. 7, 8 and 9. Moreover, we also display the contours of the FE solutions at $t=4.5$ with $h=1/128$ in (a) graphs of Figs. 7, 8 and 9.

Fig. 8

The co-state contours at $t=4.5$ with $h=1/128$ of Example 5.3 ( (a): FE method and (b): ROFE method )

Fig. 9

The control contours at $t=4.5$ with $h=1/128$ of Example 5.3 ( (a): FE method and (b): ROFE method )

From Tables 1, 3 and 5, we see that the ROFE method has the same convergence rates as the FE method. And the numerical results are consistent with the theoretical analysis. Besides, we can see that the ROFE method and FE method have almost the same numerical accuracy. Every pair of graphs in Figs. 1-9 are basically identical. From Tables 2, 4 and 6 about CPU time, we can see that the efficiency of the ROFE method is more than 6 times that of the FE method. And the efficiency of the ROFE method for solving algebraic equations is more than 23 times that of the FE method for solving algebraic equations, which is accordant with the number of unknowns of the two methods. Specifically, in Example 5.3 with complex geometry, the accuracy and efficiency of the ROFE method have achieved the expected results, which means that our method can handle the situation with complex geometry. Therefore, the proposed ROFE method is an accurate and effective numerical method for solving parabolic optimal control problems.