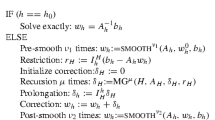Suboptimal Feedback Control of PDEs by Solving HJB Equations on Adaptive Sparse Grids

Abstract

An approach to solve finite time horizon suboptimal feedback control problems for partial differential equations is proposed by solving dynamic programming equations on adaptive sparse grids. A semi-discrete optimal control problem is introduced and the feedback control is derived from the corresponding value function. The value function can be characterized as the solution of an evolutionary Hamilton–Jacobi Bellman (HJB) equation which is defined over a state space whose dimension is equal to the dimension of the underlying semi-discrete system. Besides a low dimensional semi-discretization it is important to solve the HJB equation efficiently to address the curse of dimensionality. We propose to apply a semi-Lagrangian scheme using spatially adaptive sparse grids. Sparse grids allow the discretization of the value functions in (higher) space dimensions since the curse of dimensionality of full grid methods arises to a much smaller extent. For additional efficiency an adaptive grid refinement procedure is explored. The approach is illustrated for the wave equation and an extension to equations of Schrödinger type is indicated. We present several numerical examples studying the effect the parameters characterizing the sparse grid have on the accuracy of the value function and the optimal trajectory.

1 Introduction

In this paper we present a framework for finite horizon closed-loop suboptimal control of evolutionary partial differential equations (PDEs) based on a dynamic programming approach on adaptive sparse grids. We consider control problems for systems which arise from a semi-discretization (in space) of a PDE and solve the corresponding dynamic programming equations with adaptive semi-Lagrangian schemes on sparse grids. More precisely, we consider optimal control problems of the following type

$$\begin{aligned} \left\{ \begin{aligned}&\min _{u \in U_{\text {ad}}} J(u)= \int _0^T l(y(t),u(t)) \, \text {d}t,\\&y_t(t)=f(y(t),u(t)),\\&y(0)=y_0, \end{aligned} \right. \end{aligned}$$

(1.1)

with dynamics $f:\mathbb {R}^d\times \mathbb {R}^m \rightarrow \mathbb {R}, d,m \in \mathbb {N}$, which arise from a semi-discretization of a PDE, running cost $l:\mathbb {R}^d \times \mathbb {R}^m \rightarrow \mathbb {R}$, the initial state $y_0\in \mathbb {R}^d$, the set of admissible controls $U_{\text {ad}}$, and time horizon $0<T<\infty$. The presented approach is illustrated and numerically analyzed for the wave equation. Additionally we show how the approach can be transferred to equations of Schrödinger type and present numerical examples for a simplified bilinear setting in 2D. Although other approaches may be considered to control the solution of the corresponding semi-discrete systems—without using Hamilton–Jacobi Bellman (HJB) equations—the presented approach aims to give a general framework which is applicable on a wider class of problems. There are only few results on numerical methods for closed-loop optimal control of partial differential equations which are suitable for nonlinear problems.

To set up a feedback law we characterize the value function of problem (1.1) as the viscosity solution of an instationary HJB equation, from which we derive a control in feedback form. However, solving the HJB equation numerically is due to the curse of dimensionality very challenging in higher dimension. To reduce the computational effort there exist different possibilities. On the one hand the dimension of the dynamical system can be reduced by using model order reduction techniques for the discretization of the underlying PDE. An efficient reduction method is, e.g., proper orthogonal decomposition (POD) for certain classes of nonlinear equations, see, e.g., [32, 33]. A low-dimensional discretization based on spectral elements (taking the first d sinus-modes as a basis of the discrete state space) is used in [31]. On the other hand efficient numerical methods are crucial for solving the HJB equation. There exists a wide range of methods including (higher order) finite difference [41], semi-Lagrangian [13, 15], discontinuous Galerkin methods [28], sparse grids [10], or low rank tensor approximation for linear HJB equations [27].

In this paper we use spectral elements for the discretization of the underlying PDE following the approach in [31]. The corresponding HJB equation is solved by an adaptive semi-Lagrangian scheme on sparse grids based on [10]. While the HJB equation is defined on the full space, for the numerical approximation a finite computational domain and an artificial boundary condition has to be chosen carefully. The use of regular sparse grids implies a reduction of the degrees of freedom. For functions f from the Sobolev-space with dominating mixed derivative $H^2_{\text {mix}}$ the number of grid points on discretization level n, with one-dimensional mesh size $h_n = 2^{-n}$, reduces from $O(h_n^{-d})$ to $O(h_n^{-1}(\log h_n^{-1})^{d-1})$, whereas the asymptotic accuracy with respect to $L^2$- or $L^{\infty }$-norm decreases only from $O(h_n^2)$ to $O(h_n^2(\log h_n^{-1})^{d-1})$. Sparse grids go back to the work by Smolyak [44] and in particular Zenger [47], Griebel [23], and Griebel and Bungartz [11]. In case of nonsmoothness of the solution an adaptive sparse grid scheme may allow to improve the accuracy of the approximation, we refer to [17, 43] for references on adaptive sparse grids. Note that the interpolation on sparse grids is not monotone [10, 43], e.g., the sparse grid interpolant of a non-negative function can be negative on non-interpolation points. Therefore the scheme is in general not monotone and a convergence theorem follows not directly from Barles and Souganidis [5].

In this paper we consider control problems for the wave and the bilinear Schrödinger equation. In contrast to [10] we consider different underlying systems and allow more general controls than bang-bang controls. We study numerically the error in the approximating value function (for $d=2$) and the optimal trajectory and control ($2\le d \le 8$). Since for normal sparse grids the nodes on the boundary become dominant in the computational complexity in higher dimensions, i.e. the ratio of points on the boundary versus that in the interior grows significantly with increasing dimensions [43], it is crucial to solve the equation by using only inner nodes and to use a fast approach to determine the Hamiltonian minimizing control.

To put the results in a general context we give an overview of some related work. For results on feedback control of infinite dimensional, second-order (in time), linear oscillators, see [21]; further we refer to the review article by Morris [39] on feedback control problems of PDEs considering in particular applications in the control of noise and plate vibrations. Moreover, we mention the monograph by Lasiecka and Triggiani [34] on control theory of PDEs. Regarding feedback stabilization of (the finite- and infinite-dimensional) Schrödinger equations, see, e.g., [7, 37, 38]. For optimal feedback control problems by solving HJB equations for reduced systems using proper orthogonal decomposition we refer to [1, 2, 22, 26, 32, 33], for reduced system using spectral elements to [31]. Regarding estimates for the error between the value functions of the continuous and semi-discrete optimal control problem in case of linear dynamics we refer to [16]. For publications on sparse grids we refer, e.g., to [11, 19, 23, 25, 43, 47]. For sparse approximation of PDEs in high dimensions, see, e.g., [14] and for sparse grids methods for solving Schrödinger equations we refer to [20, 24]. Higher order semi-Lagrangian schemes on sparse grids for second order HJB equations are considered in [46]. Furthermore, in [45] several two dimensional numerical examples for semi-Lagrangian schemes on sparse grids for first order HJB equation are considered. We further mention that model order reduction in combination with sparse grids was considered in [6, 42].

The paper is organized as follows. In Sect. 3 we formulate the closed-loop optimal control problems arising from control of the wave and Schrödinger equation, in Sect. 4 we recall the basic ideas of sparse grids, in Sect. 5 we formulate the semi-Lagrangian scheme, and in Sect. 6 we present several numerical examples illustrating our approach.

2 Notation

Throughout the paper we use for given interval (resp. bounded domain) $\varOmega \subset \mathbb {K}$ with $\mathbb {K}\in \{\mathbb {R},\mathbb {C}\}$ the usual notation for the real-valued (resp. complex-valued) Lebesgue spaces $L^2(\varOmega ,\mathbb {K})$ (resp. ${\bar{L}}^2(\varOmega ,\mathbb {K})$), and analogue for Sobolev spaces $H^1_0(\varOmega )=H^1_0(\varOmega ,\mathbb {R})$ (resp. ${\bar{H}}^1_0(\varOmega ) = H^1_0(\varOmega ,\mathbb {C})$), $m\in \mathbb {N}$. We set $H=L^2(\varOmega ,\mathbb {R})$ and ${\bar{H}}=L^2(\varOmega ,\mathbb {C})$. Furthermore, we introduce for a Hilbert space W the Bochner and Hölder spaces by $L^2(0,T;W)$ and $C^k(0,T;W), k=0,1$, omitting the index for $k=0$. For the Euclidean and maximum norm in $\mathbb {R}^n, n \in \mathbb {N}$, we use the usual notation $\left||\cdot \right||_{2}$ and $\left||\cdot \right||_{\infty }$.

3 Optimal Control Problems

In this section we introduce an optimal control problem for the wave and Schrödinger equation and the corresponding semi-discrete (in space) problems.

In the following, let $T>0$ be a finite time horizon, $L>0$, and c be a positive scalar.

3.1 Optimal Control of the Wave Equation

To formulate the optimal control problem for the wave equation, we first define the set of admissible controls

$$\begin{aligned} U_{\text {ad}}^w:=L^2\left( 0,T;U^w\right) ,\quad \text {with} \quad U^w:=\left\{ u\in \mathbb {R}^m| u_a \le u \le u_b \right\} \end{aligned}$$

(3.1)

for $u_a,u_b \in \mathbb {R}^m, m\in \mathbb {N}$. For controls $u\in U_{\text {ad}}^w$ the equation is given by

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{y}}_{tt}-c\varDelta {\hat{y}}=B^w u&{}\quad \text {in }(0,T)\times \varOmega ,\\ {\hat{y}}(0)= {\hat{y}}_0,\quad {\hat{y}}_t(0)= {\hat{y}}_1&{}\quad \text {in } \varOmega , \\ {\hat{y}}=0&{}\quad \text {on }(0,T) \times \partial \varOmega \end{array} \right. \end{aligned}$$

(3.2)

for initial state and velocity ${\hat{y}}_0 \in H^1_0(\varOmega )$ and ${\hat{y}}_1\in L^2(\varOmega )$, and control operator $B^w(x):=(\sin (\pi x_1), \ldots ,\sin (m \pi x_2))$ for $x \in \varOmega$. Equation (3.2) has a unique solution

$$\begin{aligned} {\hat{y}}\in C\left( 0,T;H^1_0(\varOmega )\right) \cap C^1\left( 0,T;L^2(\varOmega )\right) , \end{aligned}$$

(3.3)

see [35, pp. 275 and 288]. Let the cost functional be given by

$$\begin{aligned} J^w\left( u, {\hat{y}}\right) := \int _0^T \left( \beta _y \left|| {\hat{y}}(t)-y_{\text {d}}\right||_{H}^2 +\beta _u |u(t)|^2 \right) \, \text {d}t, \end{aligned}$$

(3.4)

for $y_{\text {d}}\in H$ and $\beta _y>0$ and $\beta _u>0$. We denote the control-to-state operator for the wave equation by $\hat{y}_w[\cdot ]$. The optimal control problem is given by

$$\begin{aligned} \min F^w(u):=J^w\left( u, {\hat{y}}_w[u]\right) ,\quad u\in U_{\text {ad}}^w. \end{aligned}$$

(3.5)

The existence of a unique solution of the control problem (3.5) follows by classical arguments, see, e.g., [36].

Next, we introduce a semi-discrete formulation of the control problem, in particular we use the method of lines. For a given basis $b:=(\varphi _1,\ldots ,\varphi _d)$, with $\varphi _i \in H^1_0(\varOmega ), d \in \mathbb {N}$, we define

$$\begin{aligned} \begin{aligned} A&:=\left( (\nabla \varphi _i(x),\nabla \varphi _j(x))_{i,j=1,\ldots ,d}\right)&\quad \text {(stiffness matrix)}, \\ M&:=\left( (\varphi _i(x),\varphi _j(x))_{i,j=1,\ldots ,d}\right)&\quad \text {(mass matrix)}. \end{aligned} \end{aligned}$$

(3.6)

Note that for our numerical experiments in Sect. 6 we will choose

$$\begin{aligned} \varphi _i(x):=\sin (i\pi x),\quad i=1,\ldots ,d, \end{aligned}$$

(3.7)

and obtain

$$\begin{aligned} \begin{aligned} A&={\text {diag}}\left( \left( 1/2 (i\pi )^2\right) _{i=1,\ldots ,d}\right) , \quad M={\text {diag}}((1/2)_{i=1,\ldots ,d}). \end{aligned} \end{aligned}$$

(3.8)

although the following exposition holds for a general basis b.

A semi-discrete formulation of the wave equation with respect to a basis b is obtained by a first order system in time given by

$$\begin{aligned} \dot{y}_w(t)=f^w(y_w(t),u(t)),\quad t>0,\quad y(0)=y_0 \end{aligned}$$

(3.9)

with $y_w(t) \in \mathbb {R}^{2d}$ and the dynamics

$$\begin{aligned}&f^w:\mathbb {R}^{2d} \times \mathbb {R}^m \rightarrow \mathbb {R},\quad f^w(x,u):= \mathcal {A}^w x+\mathcal {B}^w u, \end{aligned}$$

(3.10)

where

$$\begin{aligned} \mathcal {A}^w:=\begin{pmatrix} 0 &{}\quad I_d \\ -cM^{-1}A &{}\quad 0 \end{pmatrix} , \quad \mathcal {B}^w:=\begin{pmatrix} 0 \\ {\text {id}} \end{pmatrix} , \quad y_0\in \mathbb {R}^{2d}. \end{aligned}$$

(3.11)

Furthermore, we define the functional

$$\begin{aligned} J^w_h(u,y)&:=\int _0^T l^w(y(t), u(t)) \, \text {d}t \end{aligned}$$

(3.12)

with running cost $l^w(x,u):=\beta _y x_1^T Mx_1 + \beta _u u^T u$ for $x=(x_1,x_2) \in \mathbb {R}^{2d}, u\in U^w$. The semi-discrete optimal control problem is given as

$$\begin{aligned} \min F^w_h(u):=J^w_h(u,y_w[u]),\quad u\in U_{\text {ad}}^w. \end{aligned}$$

(3.13)

Existence of a solution for (3.13) follows similarly as in the continuous case.

3.2 Optimal Control of the Schrödinger Equation

We define the set of admissible controls for the Schrödinger equation

$$\begin{aligned} U_{\text {ad}}^s:=L^2\left( 0,T;U^s\right) ,\quad \text {with}\;U^s:=\{u\in \mathbb {R}| u_a \le u \le u_b \} \end{aligned}$$

(3.14)

and introduce the equation for controls $u\in U_{\text {ad}}^s$ by

$$\begin{aligned} \left\{ \begin{array}{ll} i {\hat{y}}_t+c\varDelta {\hat{y}}- u B^s {\hat{y}}=0&{}\quad \text {in}\;(0,T)\times \varOmega ,\\ {\hat{y}}(0)= {\hat{y}}_0 &{}\quad \text {in}\;\varOmega , \\ {\hat{y}}=0 &{}\quad \text {on}\;(0,T) \times \partial \varOmega , \end{array} \right. \end{aligned}$$

(3.15)

with initial state ${\hat{y}}_0 \in {\bar{H}}^1_0(\varOmega )$, and scalar $B^s\in \mathbb {R}$. Equation (3.15) has a unique solution in

$$\begin{aligned} C\left( 0,T;{\bar{H}}^1_0(\varOmega )\right) \cap C^1\left( 0,T;{\bar{H}}^{-1}(\varOmega )\right) , \end{aligned}$$

(3.16)

see [35]. We define the cost functional as

$$\begin{aligned} J^s\left( u, {\hat{y}}\right) := \int _0^T \left( \beta _y \left|| {\hat{y}}(t)-y_{\text {d}}\right||_{{\bar{H}}}^2 +\beta _u |u(t)|^2 \right) \, \text {d}t \end{aligned}$$

(3.17)

with $y_{\text {d}}\in {\bar{H}}, \beta _y>0$ and $\beta _u>0$. The optimal control problem is given by

$$\begin{aligned} \min F^s(u):=J^s\left( u, {\hat{y}}_s[u]\right) ,\quad u\in U_{\text {ad}}^s \end{aligned}$$

(3.18)

where, in analogy to the wave equation, ${\hat{y}}_s[u]$ denotes the solution of (3.15) for given $u \in U_{\text {ad}}^s$. The existence of a solution of (3.18) can be shown using classical arguments, see [3, Proposition 7.5].

We introduce a semi-discretization of the Schrödinger equation as a real-valued system as

$$\begin{aligned} f^s:\mathbb {R}^{2d} \times \mathbb {R}\rightarrow \mathbb {R},\quad f^s(x,u)&:= \mathcal {A}^s x+u \mathcal {B}^s y \end{aligned}$$

(3.19)

with

$$\begin{aligned} \begin{aligned} \mathcal {A}^s&:=\begin{pmatrix} 0 &{}\quad cM^{-1}A \\ -cM^{-1}A &{}\quad 0 \end{pmatrix},&\mathcal {M}&:= \begin{pmatrix} M &{}\quad 0 \\ 0 &{}\quad M \end{pmatrix}, \quad \mathcal {B}^s:=\mathcal {M}^{-1} \hat{B},&\\ \hat{B}&:= \begin{pmatrix} 0 &{}\quad - \bar{B}\\ \bar{B} &{}\quad 0 \end{pmatrix},&\quad \bar{B}&={\text {diag}}\left( B^s,\ldots ,B^s\right) \in \mathbb {R}^{d\times d}. \end{aligned} \end{aligned}$$

(3.20)

The discrete cost functional is given by

$$\begin{aligned} J^s_h(u,y)&:=\int _0^T l^s(y(t), u(t)) \, \text {d}t \end{aligned}$$

(3.21)

with running cost

$$\begin{aligned} l^s(x,u):=\beta _y x^T \mathcal {M}x + \beta _u u^T u, \end{aligned}$$

(3.22)

where $x=(x_1,x_2) \in \mathbb {R}^{2d}, u\in U$. The semi-discrete optimal control problem is given as

$$\begin{aligned} \min F^s_h(u):=J^s_h(u,y_s[u]),\quad u\in U_{\text {ad}}^s. \end{aligned}$$

(3.23)

Again, existence of a solution of (3.23) follows similarly as in the continuous case.

3.3 Suboptimal Feedback Control

We introduce the value function for both semi-discrete problems (3.13) and (3.23):

$$\begin{aligned} v(x,t)&:= \inf _{u \in U } \int _t^T l(y(s),u(s)) \, \text {d}s,\quad \text {s.t.} \end{aligned}$$

(3.24)

$$\begin{aligned} \dot{y}(s)&= f(y(s),u(s)),\quad y(t)=x,\quad s>t, \end{aligned}$$

(3.25)

for $t\in [0,T]$ and $x \in \mathbb {R}^{2d}$ with $l=l^w, f=f^w$, and $U=U^w$ (resp. $l=l^s, f=f^s$, and $U=U^s$) for the wave (resp. Schrödinger) equation. The value function satisfies the dynamic programming principle

$$\begin{aligned} \begin{aligned} v(x,t)=\inf _{u\in U } \left( \int _t^{\tau }l(y(s),u(s))\, \text {d}s+v(y(\tau ),\tau ) \right) \quad \text {in } \mathbb {R}^{2d} \times [0,T], \end{aligned} \end{aligned}$$

(3.26)

for all $\tau \in [t,T]$ and can be characterized as the unique viscosity solution of

$$\begin{aligned} \left\{ \begin{array}{ll} -v_t(x,t)+H(x,\nabla v)=0 &{}\quad \text {in}\; \mathbb {R}^{2d} \times [0,T],\\ v(x,T)=0&{}\quad \text {in}\;\mathbb {R}^{2d}, \end{array} \right. \end{aligned}$$

(3.27)

with Hamiltonian

$$\begin{aligned} H(x,p):=\sup _{u\in U}\left( -f(x,u)^T p -l(x,u)\right) \end{aligned}$$

(3.28)

for $x \in \mathbb {R}^{2d}$ and $p \in \mathbb {R}^{2d}$, see [4, 29].

We assume that for the value function holds $v\in C^1(\mathbb {R}^{2d} \times [0,T])$. To derive a feedback control law from the value function we introduce the set-valued map (following the notation in [18, Chapter I]) given by

$$\begin{aligned} g^*(x,t):={\mathop {{\text {argmin}}}\limits _{u\in U}}\left\{ -f(x,u)^T \nabla _x v(x,t) - l(x,u)\right\} . \end{aligned}$$

(3.29)

We call $\underline{u} :\mathbb {R}^{2d} \times (t,T) \rightarrow U$ an admissible feedback control and define $u(s):=\underline{u}(y(s),s)$. Let $\underline{u}^*$ be an admissible feedback control with

$$\begin{aligned} \underline{u}^*(x,s)\in g^*(x,s) \end{aligned}$$

(3.30)

for all $(x,s) \in \mathbb {R}^{2d} \times (t,T)$ and admissible for the initial condition (x, t), then we call $\underline{u}^*$ an optimal feedback control and with the corresponding solution $y^*$ we have

$$\begin{aligned} u^*(s)=\underline{u}^*(y^*(s),s). \end{aligned}$$

(3.31)

We call the corresponding trajectory for given initial state (x, t) optimal.

Note that for f and l given as above we obtain from the feedback law in (3.29) that

$$\begin{aligned} \underline{u}^*\left( y^*(s),s\right)&=P_{U_{\text {ad}}^w}\left( -\frac{1}{\beta _u} (\mathcal {B}^w)^T \nabla _x v\left( y^*(s),s\right) \right) \end{aligned}$$

(3.32)

for the semi-discrete wave equation and

$$\begin{aligned} \underline{u}^*\left( y^*(s),s\right)&=P_{U_{\text {ad}}^s}\left( -\frac{1}{\beta _u} y^*(s)^T \left( \mathcal {B}^s\right) ^T \nabla _x v\left( y^*(s),s\right) \right) \end{aligned}$$

(3.33)

for the semi-discrete Schrödinger equation, where $P_{U_{\text {ad}}^w}$ (resp. $P_{U_{\text {ad}}^s}$) denotes the projection on the set of admissible controls.

3.4 Curse of Dimensionality

Optimal control problems of type (3.24) and (3.25) allow to derive controls in feedback form from the corresponding value function given as the unique viscosity solution of an instationary HJB equation (3.27). However, when the problem arises from a semi-discrete optimal control problem governed from a PDE, it usually leads to a high dimensional state space and, because of the curse of dimensionality, the numerical approximation becomes very challenging.

For the numerical approach, the first step is a restriction of the state space to a suitable bounded subdomain $Q \subset \mathbb {R}^{2d}$. To make the problem numerically feasible and to reduce the computational effort two different aspects are crucial. On the one hand the reduction of the dimension of the underlying system and on the other hand efficient schemes for solving the HJB equation (3.27). In this paper we focus on the latter and analyze the approximation by adaptive semi-Lagrangian schemes on sparse grids. Nevertheless, a low dimensional approximation is necessary such that the problem is numerically feasible. Here, following the approach presented in [31], we consider semi-discretizations based on spectral elements and the aim is to control the lower modes (neglecting the behaviour of the higher modes). However, the presented framework could also be applied to optimal control problems of parabolic equations for which model order reduction techniques like proper orthogonal decomposition are very efficient (cf. the cited references in the introduction).

4 Sparse Grids

For the numerical approximation of the value function we use a semi-Lagrangian scheme on adaptive sparse grids. In the following we recall the main ideas behind (adaptive) sparse grids, more details can be found in e.g., [11, 19, 43]. Let here, to simplify the exposition, $Q =[0,1]^d, d \in \mathbb {N}$. For a multiindex $\underline{l}=(l_1,\ldots ,l_d) \in \mathbb {N}^d$ we introduce a mesh $Q_{\underline{l}}$ with mesh parameters $h_{\underline{l}}=(h_{l_1},\ldots ,h_{l_d})$ which are constant $h_{l_i} := 2^{-l_i}$ in each direction but may differ with respect to the dimensions. The grid points are denoted by

$$\begin{aligned} x_{\underline{l},\underline{j}}=\left( x_{l_1,j_1},\ldots ,x_{l_d,j_d}\right) , \quad x_{l_t,j_t}= j_t \cdot h_{l_t},\quad t=1,\ldots ,d. \end{aligned}$$

(4.1)

Here, $\underline{l}$ denotes the level which characterizes the resolution of the discretization and $\underline{j}$ defines the position of the mesh point. Let

$$\begin{aligned} V_{\underline{l}}:={\text {span}}\left\{ \varphi _{\underline{l},\underline{j}}\left| j_t=0,\ldots ,2^{l_t},t=1,\ldots ,d \right. \right\} \end{aligned}$$

(4.2)

be the space of all d-dimensional piecewise d-linear hat functions. The hierarchical difference space is given by

$$\begin{aligned} W_{\underline{l}}:=V_{\underline{l}}{\setminus } \bigoplus _{t=1}^d V_{{\underline{l}}-\underline{e_t}}, \end{aligned}$$

(4.3)

where $\underline{e_t}$ denotes the tth unit vector. Therefore $W_{\underline{l}}$ consists of the functions in $V_{\underline{l}}$ which are not in any $V_{{\underline{l}}-\underline{e_t}}$ and this allows the construction of a multilevel subspace splitting. Thus we define, denoting by $\le$ a component-wise relation here and in the following,

$$\begin{aligned} V_{\underline{l}}=\bigoplus _{\underline{k}\le \underline{l}} W_{\underline{k}}, \end{aligned}$$

(4.4)

cf. Fig. 1. With $V_n:=V_{(n,\ldots ,n)}$ for $n\in \mathbb {N}$ every $f\in V_n$ can be characterized as

$$\begin{aligned} f\left( \underline{x}\right) = \sum _{|\underline{l}|_{\infty } \le n} \sum _{\underline{j}\in B_{\underline{l}}} \alpha _{\underline{l},\underline{j}} \cdot \varphi _{\underline{l},\underline{j}}\left( \underline{x}\right) , \end{aligned}$$

(4.5)

with so-called hierarchical coefficients $\alpha _{\underline{l},\underline{j}} \in \mathbb {R}$ and for

$$\begin{aligned} {{\mathcal {B}}_{\underline{l}}} := \left\{ \underline{j} \in \mathbb {N}^d \left| \begin{array}{lll} j_t = 1,\ldots ,2^{l_t}-1,&{} j_t \text{ odd }, &{} t=1,\ldots ,d,\quad \text{ if }\;l_t >1 , \\ j_t =0,1,2,&{}&{}t=1,\ldots ,d,\quad \text{ if }\; l_t=1 \end{array} \right. \right\} . \end{aligned}$$

(4.6)

In nodal (4.2) or hierarchical (4.5) basis a function $f\in V_n$ with discretization level n is characterized by $(2^n+1)^d$ points.

Fig. 1

Supports of the basis functions $\varphi _{\underline{l},\underline{j}}$ of the hierarchical subspaces $W_{\underline{l}}$ of the space $V_4 = V_{(4,4)}$, where the functions of each $W_{\underline{l}}$ have disjunct support. The regular sparse grid $V_{4}^s$ contains the upper left triangle of spaces

To proceed, we need the so-called Sobolev-space with dominating mixed derivative $H^2_{\text {mix}}$. We introduce the corresponding norm and semi-norm

$$\begin{aligned} \Vert f\Vert ^2_{H^2_{\text {mix}}(Q)} = \sum _{0\le \underline{k}\le 2} |\partial ^{|\underline{k}|_1}_{x^{k_1}_1\ldots x_d^{k_d} } f|_2^2, \quad \text {and} \quad |f|_{H^2_{\text {mix}}(Q)} = \left||\partial ^{2d}_{x^2_1\ldots x_d^2 } f \right||_{2}, \end{aligned}$$

(4.7)

respectively. One formally defines

$$\begin{aligned} H^2_{\text {mix}}(Q)= \left\{ f\in H \; \big |\; \Vert f\Vert _{ H^2_{\text {mix}}} \le C\quad \text { for}\quad C>0 \right\} \end{aligned}$$

(4.8)

which satisfies the relation $H^{2 \cdot d}(Q)\subset H^{2}_{\text {mix}}(Q)\subset H^2(Q)$, see [25]. For $f \in H^2_{\text {mix}}(Q)$ there holds, see e.g., [11],

$$\begin{aligned} \left||f_{\underline{l}}\right||_{2} \le C(d) \cdot 2^{-2 |\underline{l}|_1} |f|_{H^2_{\text {mix}}(Q)} \end{aligned}$$

(4.9)

with constant $C(d)>0$ depending on the dimension d and

$$\begin{aligned} f_{\underline{l}}:= \sum _{\underline{j}\in B_{\underline{l}}} \alpha _{\underline{l},\underline{j}} \phi _{\underline{l},\underline{j}}(x) \in W_{\underline{l}}. \end{aligned}$$

The hierarchical mesh becomes a sparse mesh when taking out those basis function which have a small contribution to the representation of the function, i.e. those with a small support due to estimate (4.9). Following Griebel [23] and Zenger [47], we replace $\left||\underline{l}\right||_{\infty } \le n$ by the rule

$$\begin{aligned} \left||\underline{l}\right||_{1} \le n+d-1. \end{aligned}$$

(4.10)

For the dimension of the sparse grid space it holds ${\text {dim}} V_n^s=\mathcal {O}(2^n \cdot n^{d-1})$, in comparison to regular grids where we have ${\text {dim}} V_n = \mathcal {O}(2^{nd})$. For functions $f\in H^2_{{\text {mix}}}(Q)$ there holds the error estimate

$$\begin{aligned} \left||f -f_n^s\right||_{2}=O\left( h_n^2\left( \log h_n^{-1}\right) ^{d-1}\right) \end{aligned}$$

(4.11)

in comparison to the approximation on regular grids, where we have

$$\begin{aligned} \left||f -f_n^s\right||_{2}=\mathcal {O}\left( h_n^2\right) . \end{aligned}$$

(4.12)

This fact leads to a strong reduction of the computational storage consumption in comparison to a full mesh approach for a similar approximation quality. If the required $H^2_{\text {mix}}$-regularity is given, the points in the sparse grid are optimal in a cost-benefit analysis [11].

4.1 Adaptive Sparse Grids

For a further reduction of the number of nodes we use an adaptive refinement strategy as in [10], where the values of the hierarchical coefficients are employed as error indicators [17, 43].

We now collect the indices $(\underline{l},\underline{j})$ of the employed adaptive sparse grid functions in an index set $\mathcal {I}$, denote the resulting discretization mesh as $Q_\mathcal {I}$ and start with some suitable initialization $\mathcal {I}= \{(\underline{l},\underline{j})|\varphi _{\underline{l},\underline{j}} \in V_n^s \}$ for a small n. In the iterative adaptive procedure to build the refined index set $\mathcal {I}$, an index $(\underline{l},\underline{j}) \in \mathcal I$ is then marked for refinement if there holds, for given parameter $\varepsilon >0$,

$$\begin{aligned} |a_{\underline{l},\underline{j}}| \left||\phi _{\underline{l},\underline{j}}\right||_{ } > \varepsilon \end{aligned}$$

(4.13)

for the hierarchical coefficient $a_{\underline{l},\underline{j}}$ in the function representation (4.5). In such a case the 2d children, left and right in each dimension, are added to $\mathcal {I}$, where for consistency one might need to add fathers in other dimensions of these newly added sparse grid points. The spatially adaptive refinement algorithm to build an adaptive sparse grid for given function F, initial $\mathcal {I}$, and $\varepsilon$ is presented in Algorithm 1 and is based on [10] and described in more detail therein.

Additionally, we also use coarsening of the spatially adaptive sparse grid, i.e. for given parameter $\eta >0$ we remove an index $(\underline{l},\underline{j})$ from $\mathcal {I}$ if

$$\begin{aligned} |a_{\underline{l},\underline{j}}| \left||\phi _{\underline{l},\underline{j}}\right||_{ } < \eta , \end{aligned}$$

(4.14)

and no children of $(\underline{l},\underline{j})$ are in $\mathcal {I}$, see Algorithm 2. This is to avoid unnecessary function evaluations on sparse grid points whose basis function only have little contribution, again see [10] for more details. A typical choice is $\eta = \varepsilon {/}10$, which we will use in our experiments in Sect. 6.

Note that several norms are possible in (4.13) and (4.14), e.g., $L^{\infty }(Q), L^2(Q), L^1(Q), H^1(Q)$ or mixtures thereof. In the numerical experiments we use $\Vert \cdot \Vert _{L^{\infty }(Q)}$ which is one for the employed basis functions.

5 The Semi-Lagrangian Scheme

To compute the value function numerically we apply a semi-Lagrangian scheme, cf., e.g., [15]. For a bounded domain $Q \subset \mathbb {R}^{2d}$ we apply for its discretization $Q_\mathcal {I}$ the procedure

$$\begin{aligned} \left\{ \begin{array}{l} v^k(\underline{x})={\mathop {\min }\limits _{u\in U}} \left( \varDelta t l(\underline{x},u) + I\left[ v^{k+1}\right] (y_{\underline{x}} (\varDelta t ))\right) ,\\ v^k(\underline{x})=0 \end{array} \right. \end{aligned}$$

(5.1)

for all $\underline{x}\in Q_{\mathcal {I}}$, time step $\varDelta t>0, k=K,\ldots ,0$, and $K=T{/}\varDelta t$, where $\mathcal {I}$ is either the index set of a regular or adaptive sparse grid. The interpolation operator I is defined on the grid points of $Q_{\mathcal {I}}$ by $I[v](\underline{x})=v(\underline{x})$ for all $\underline{x}\in Q_{\mathcal {I}}$ and $y_{\underline{x}} (\varDelta t)$ denotes the state obtained by a time discretization scheme when going from $\underline{x}$ one step forward in time.

5.1 Computational Domain and Boundary Treatment

When using sparse grids, the number of points on the boundary increases, in comparison to inner points, strongly with respect to the refinement level and the dimension, see, e.g., [43]. To avoid this behaviour we use so-called fold out ansatz functions which are defined with inner nodes only and extrapolate them to and over the boundary following ideas developed in [10, 43], see Fig. 2a, b.

Fig. 2

Normal and fold out basis functions. a Normal basis, b fold-out basis, c last basis before the boundary gets folded up and linearly extrapolated across the boundary

Besides this, we have to prescribe some boundary condition for solving the dynamic programming equation on the extended domain. We set the second derivative equal to zero, which corresponds to a linear extension of the values on inner nodes over the boundary. With the fold out basis functions we have this extrapolation outside of the domain naturally, see Fig. 2c. For the normal basis function we set the value of v for an evaluation point outside of the domain, i.e. $({\tilde{x}},y) = (x\pm h,y)$ with $(x,y) \in \partial Q_l$ and $h>0$ the distance from ${\tilde{x}}$ to $Q_l$, as

$$\begin{aligned} v\left( {\tilde{x}},y\right) = v(x\pm h,y):=2\cdot v( x,y) \mp v( x\mp h , y), \end{aligned}$$

(5.2)

taking either the backward or forward difference quotient depending on which part of the boundary we are. If the evaluation point is outside of the domain in more than one dimension we treat all affected dimensions in this way.

5.2 Computational Aspects of the Minimization in the Hamiltonian and the Feedback Law

In general the determination of the minimum in the right hand side of (5.1) over the set of admissible controls on sparse grids is a non-trivial task; already on regular grids this questions has to be addressed carefully, for a discussion of first-order and second-order algorithms see [30]. For global minimization algorithms on sparse grids see, e.g., [40]. In the following we discuss two different methods to determine the minimizing control which can be used within the SL-scheme as well as for computing optimal trajectories.

5.2.1 Feedback Law Based on Minimization by Comparison

In this approach a finite subset $U_{\sigma }\subset U$ can be chosen over which the minimizer is determined by comparison over its elements, i.e. we chose

$$\begin{aligned} \underline{u}^*(\underline{x},s) \in {\mathop {{\text {argmin}}}\limits _{u\in U}}\left( v^k(\underline{x} + \varDelta t \cdot f(\underline{x}, u),s)+\varDelta t \cdot l(\underline{x},u)\right) ,\quad \underline{x}\in Q_{\mathcal {I}}, \end{aligned}$$

(5.3)

see, e.g., [4, 15]. This approach is easy to implement and allows to consider also non-smooth cost functionals, however it is very time consuming in higher dimensions in particular if the control has several components.

5.2.2 Feedback Law Based on the Gradient of the Value Function

In case of differentiability of the value function a projection formula for the minimization using the gradient of the value function can be used, see (3.32) and (3.33). Within the semi-Lagrangian scheme, the value function of the previous time step is used to evaluate the right hand side in the feedback law. A suitable approximation of the gradient has to be chosen. A finite difference approximation using the interpolation on sparse grids can be used given by

$$\begin{aligned} u^{n}(\underline{x},s)=P_{U}\left( {-\frac{1}{\beta _u} (\mathcal {B}^w)^T} \nabla ^h v^{n+1}(\underline{x},s)\right) \end{aligned}$$

(5.4)

for the wave equation and

$$\begin{aligned} u^{n}(\underline{x},s)=P_{U}\left( {-\frac{1}{\beta _u} x^T (\mathcal {B}^s)^T} \nabla ^h v^{n+1}(\underline{x},s)\right) \end{aligned}$$

(5.5)

for the Schrödinger equation, respectively, with

$$\begin{aligned} \left( \nabla ^h v^{n+1}(\underline{x},s)\right) _i := \frac{v^{n+1}(\underline{x}+h_i,s)-v^{n+1}(\underline{x}-h_i,s)}{2h} \end{aligned}$$

(5.6)

for $h_i=(0,\ldots ,h,0,\ldots 0)\in \mathbb {R}^{2d}$ and $h>0$. However, the choice of $h>0$ in the difference quotient approximation is not naturally given on sparse grids as it is the case for regular grids.

In Sect. 6 we will compare numerically both approaches for determining the minimizing control.

5.3 Evaluation of the Right Hand Side in (5.1)

For the computation of $y_{\underline{x}}(\varDelta t)$ we use the second order Heun scheme

$$\begin{aligned} y_{\underline{x}}(\varDelta t):=\frac{1}{2} \left( \underline{x} + \tilde{\underline{x}} + \varDelta t \cdot f\left( \tilde{\underline{x}}, u\right) \right) , \end{aligned}$$

(5.7)

where $\tilde{\underline{x}}$ is computed with the Euler scheme

$$\begin{aligned} y_{\underline{x}}(\varDelta t):=\underline{x}+\varDelta t f(\underline{x},u). \end{aligned}$$

(5.8)

For the evaluation of the right hand side of (5.1) in the n-dimensional space given by

$$\begin{aligned} F_k(\underline{x})=\min _{u\in U}\left( v_k(y_{\underline{x}}(\varDelta t))+\varDelta t l(\underline{x},u)\right) , \quad k=K,\ldots ,0, \end{aligned}$$

(5.9)

we interpolate the expression on sparse grids as presented in Algorithm 3.

5.4 Computation of the Trajectory

For the computation of optimal trajectories we solve the dynamical system (3.25) with the control given by the feedback laws using comparison after (5.3) or using the gradient of the value function after (5.4) and (5.5), respectively. The dynamical system is solved by the Heun time-stepping scheme. Note that one can choose the stepsize h for computing (5.6) for the trajectory differently from the choice within the semi-Lagrangian scheme.

The computational domain is chosen (by ‘testing’ and ‘checking’) in such a way that the trajectory does not reach the boundary to avoid numerical artefacts.

6 Numerical Examples

In this section we present several numerical examples in which we study for optimal control problems of type (3.24) and (3.25) the accuracy of the discrete value function (for $d=2$) and optimal trajectories (for $2\le d \le 8$) when solving the corresponding HJB equation by the SL-SG-scheme described in Sect. 5. For the study of convergence of the SL-SG-scheme we focus on the discretization error in space while using a time resolution which is “good enough”. While on regular grids various error estimates for semi-Lagrangian schemes are known, see, e.g., [4, Appendix A] and [5], on sparse grids very little results are available in the literature, see, e.g., [46] where under a certain assumptions an estimate is derived.

Since we only have an inefficient proof-of-concept sparse grid implementation available, we abstain from giving runtimes. Using efficient sparse grid implementations [12, 43] would significantly (an order of magnitude or more) change the needed runtime.

In the following experiments with the semi Lagrangian scheme, we use for the feedback law by comparison (5.3) a discretization of the control space with 40 equidistantly spaced controls in one dimension, while for the feedback law by using the gradient after (5.4) and (5.5) we use the stepsize $h= \frac{1}{40}$.

6.1 Reference Solutions

To analyze the accuracy of our computed discrete value function we compare it with a reference solution $v_{\text {ref}}$ computed with a higher order finite difference code on a uniform mesh based on methods developed in [9, 41]. We compute a reference solution $v_{\text {ref}}$ by an ENO scheme as a variant of a Lax–Friedrichs scheme

$$\begin{aligned} v_{\text {ref}}^{k-1}(x_I)=v_{\text {ref}}^k(x_I)-\varDelta t\mathcal {H}_{LF}\left( x_I,D^+ v_{\text {ref}}^k(x_I),D^- v_{\text {ref}}^k(x_I)\right) , \end{aligned}$$

(6.1)

where $\mathcal {H}_{LF}$ is the numerical Hamiltonian, $D^{\pm } v_{\text {ref}}^k(x_I)$ are higher order approximations of the gradient in grid point $x_I, I\in \mathbb {Z}, k$ is the time step, $\varDelta t$ the temporal mesh parameter, and coupled with a Runge–Kutta time discretization scheme of second order, for details see [31]. For the numerical realization of the scheme we use the software library ROC-HJ (see [8]).

To quantify the error in the optimal trajectories for the control problem for the semi-discrete wave equation we compute reference trajectories $y_r$ in state space and $u_r$ in control space using a Riccati approach, i.e. we solve backward in time

$$\begin{aligned} \left\{ \begin{array}{l} -P_t(t)=\mathcal {A}P(t) - P(t) \mathcal {A}+ P^T(t) \mathcal {B}^T \mathcal {R}\mathcal {B}P y(t)=0,\quad t>0\\ P(T)=0 \end{array} \right. \end{aligned}$$

(6.2)

with $\mathcal {A}=\mathcal {A}^w, \mathcal {B}=\mathcal {B}^w$ and set the feedback operator as

$$\begin{aligned} \underline{u}( x,t)=-\mathcal {R}^{-1}\mathcal {B}^T P(t)x \end{aligned}$$

(6.3)

with $\mathcal {R}=\beta _u$. For computing the trajectory from our solution, we employ $h= \frac{2}{40}$ in (5.6). This is to decouple the step sizes for the semi-Lagrangian scheme and the trajectory computation.

We estimate the error in the value function by computing the vector difference to the reference solution on its discretization grid, and denote it by

$$\begin{aligned} e^v_2&:=\Vert v-v^* \Vert _{L^2(Q)} \approx \frac{\Vert v - v_r\Vert _2}{\sqrt{N_r}}, \end{aligned}$$

(6.4)

$$\begin{aligned} e^v_\infty&:=\Vert v-v^* \Vert _{L^\infty (Q)} \approx \Vert v - v_r\Vert _\infty . \end{aligned}$$

(6.5)

For the errors in the state and control we use the following notation:

$$\begin{aligned} e^y_2&:=\Vert y-y^* \Vert _{L^2\left( 0,T;\mathbb {R}^{2d}\right) }, \quad e^y_\infty :=\Vert y-y^* \Vert _{L^\infty \left( 0,T;\mathbb {R}^{2d}\right) }, \end{aligned}$$

(6.6)

$$\begin{aligned} e^u_2&:=\Vert u-u^* \Vert _{L^2\left( 0,T;\mathbb {R}^m\right) },\quad e^u_\infty :=\Vert u-u^* \Vert _{L^\infty \left( 0,T;\mathbb {R}^m\right) }, \end{aligned}$$

(6.7)

and approximate the $L^\infty$-error by $\max _{k=1, \ldots , T{/}\varDelta t} |y^k - y_r^k |$ and the $L^2$-error by

$$\begin{aligned} \frac{1}{\sqrt{T{/}\varDelta t}}\sum _{k=1}^{T{/}\varDelta t} |y^k - y_r^k|^2. \end{aligned}$$

Furthermore, we give convergence rates for the different discretization errors $e_i$ as

$$\begin{aligned} \rho _e(i)=\log _2\left( \frac{e_{i-1}}{e_{i}} \right) , \end{aligned}$$

(6.8)

where $e_i$ denotes the error on level i or the error for $\varepsilon = 0.1 \times 1{/}2^i$, respectively, and e is any one of the above errors.

6.2 Control of the Harmonic Oscillator

As a first example we consider a simplification of the semi-discrete wave equation, namely the Harmonic oscillator, i.e. we consider dynamics of type (3.10) with

$$\begin{aligned} \beta _y=2,\quad \beta _u=0.1,\quad T=1,\quad \varDelta t = 0.01,\quad \mathcal {A}^w= \begin{pmatrix} 0 &{}\quad 1 \\ -1 &{}\quad 0 \end{pmatrix}, \quad \mathcal {B}^w = \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \end{aligned}$$

(6.9)

initial data $x \in \mathbb {R}^2$, computational domain $Q=[-1,1]^2, U_w = [-3.5,3.5]$. We solve the corresponding HJB equation (3.27) and compare different variants of our semi-Lagrangian scheme on sparse grids. The reference value function is computed as described in Sect. 6.1 on the domain $[-1,1]^2$ with $\varDelta x=1{/}200 \times {\text {length}}(Q) = 1{/}200 \times 2$ and $\varDelta t=T{/}1000$.

6.2.1 Error in the Value Function

To show the overall behaviour of the four different variants of our approach (namely using normal or fold out basis functions and uniform or adaptive refinement, respectively) we present in Fig. 3 combined convergence plots for the error in the value function at the initial time in comparison to the reference solution.

Fig. 3

Harmonic oscillator (6.9) in 2D: error in the approximating value function comparing the scheme based on sparse grids using normal hat and fold out basis functions and feedback laws from 5.2.1 and 5.2.2. a Error in the value function versus level, b error in the value function versus $\varepsilon$, c nodes versus $\varepsilon$ and d error in the value function versus nodes, feedback law based on gradient approach

We also show two exemplary convergence tables with more detailed numbers. In Table 1 we give the error on regular sparse grids using the scheme presented in Algorithm 3 which includes nodes on the boundary, as well as fold out basis functions following Sect. 5.1; while in Table 2 we compare the error on the adaptive sparse grids with normal hat functions for decreasing refinement thresholds at the initial time zero by using either the gradient or comparison of all actions to realize the minimization on the sparse grid.

Table 1 Harmonic oscillator (6.9) in 2D: error in the value function with regular sparse grids using both kinds of basis functions and the gradient approach

Table 2 Harmonic oscillator (6.9) in 2D: error in the value function for adaptively refined sparse grids using compare and gradient approaches with the normal basis functions

From Table 1 and Fig. 3a we can see that the different variants show the similar convergence of the error in regard to the level. Since a regular sparse grid with the fold-out basis functions uses less points, it is the preferred choice in this setting, although for very fine resolution the convergence stagnates. Note that for a sparse grid with level 10 one has 13,313 nodes with normal hat functions and 9217 with fold out hat functions, respectively. To study the influence of the artificial boundary condition on the error, we also computed regular sparse grid solutions on the enlarged domain $[-2,2]^2$, but evaluated the error only on $Q=[-1,1]^2$. We observe overall very similar convergence behaviour for this setting and essentially identical errors for the normal and fold out basis functions, which indicates that the treatment of the boundary of the enlarged domain has little effect on the value function in Q.

From Table 2 and Fig. 3b we also see no big difference between the compare and gradient variants. We observe that the normal hat functions show slightly better performance when looking at the decrease of the error in comparison to $\varepsilon$. When taking the effort into account by counting the number of points in the adaptive sparse grids at the end of the computation, we see a stronger increase in the number of points for the fold-out basis function than for the normal ones, while for coarser $\varepsilon$ the fold-out ones use less basis functions, see Fig. 3c. When comparing the error reduction with increasing number of nodes for adaptive versus regular grids, we see in Fig. 3d, that for normal hat functions there is no real difference, while for fold out hat functions the regular approach performs better and more stable.

Table 3 Harmonic oscillator (6.9) in 2D: error in the trajectory and control with regular sparse grids using the gradient approach and fold out basis functions

6.2.2 Error in the Trajectory and Control

Next we study for given initial point $x = (0.4, -0.2)^T$ the accuracy of the corresponding trajectory and control when using regular/adaptive sparse grids, the gradient/comparison approach, and normal/fold out basis functions. Overall, the behaviour is very similar over the different measured errors, in particular when comparing the different basis functions and feedback laws on regular sparse grids. However, on adaptive sparse grids we observe for the fold out basis functions oscillating convergence behaviour.

In Table 3 we see the error in the state and control with respect to the $L^2$- and $L^{\infty }$-norm and the corresponding rates of convergence on regular sparse grids with the gradient approach and fold out basis functions. The rate of convergence shows a similar behaviour in all three variables with values from 0.5 to values around 1.

Table 4 Harmonic oscillator (6.9) in 2D: error in the trajectory and control with adaptive grids using the gradient approach and fold out basis functions

For adaptive and regular sparse grids using the gradient approach and normal basis functions we observe a similar behaviour, see Fig. 4. When using fold out hat functions in comparison to normal ones we observe a slight reduction of the convergence rate for the feedback law by comparison and the amplitude of the oscillations increases when using the feedback law based on the gradient on adaptive sparse grids, see Fig. 5 and Table 4. In Fig. 6 the behaviour on regular and adaptive sparse grids with respect to the number of nodes is shown. We again observe an oscillatory behaviour when using fold out basis functions on adaptive sparse grids. The corresponding adaptive sparse mesh at initial time with normal and fold out basis functions is shown in Fig. 7.

Since we have numerically confirmed that the compare and gradient approaches behave essentially the same, we only investigate the gradient approach for the following examples to avoid the more costly comparison approach in the higher dimensional control spaces.

Fig. 4

Harmonic oscillator (6.9) in 2D: comparing the scheme on regular sparse grids using normal hat and fold out basis functions. a Error in the trajectory versus level, b error in the control versus level

Fig. 5

Harmonic oscillator (6.9) in 2D: comparing the scheme on adaptive sparse grids using normal hat and fold out basis functions. a Error in the trajectory versus $\varepsilon$, b error in the control versus $\varepsilon$

Fig. 6

Harmonic oscillator (6.9) in 2D: comparing the scheme using the gradient approach 5.2.2 on adaptive and regular sparse grids using normal hat and fold out basis functions. a Error in the trajectory versus nodes, b error in the control versus nodes

Fig. 7

Harmonic oscillator (6.9) in 2D: adaptive sparse grid for $\varepsilon = 1.95\times 10^{-4}$. a Normal hat functions, b fold-out hat functions

6.3 Control of the Semi-discrete Wave Equation (4D)

In this example we consider the optimal control problem (3.24) and (3.25) for the semi-discrete wave equation (3.10) in dimension four, that means we discretize the state and velocity by two modes using (3.7). We choose the parameters as

$$\begin{aligned} Q = [-3,3]^4,\quad \beta _y=2,\quad \beta _u=0.1, \quad T=4,\quad \varDelta t = 0.01, \quad c=0.05. \end{aligned}$$

(6.10)

Since a full grid approach is very costly in four dimensions, we consider directly the error in the state and control along an optimal trajectory for a given initial point to study the convergence. For the initial point $x=(0.4, 0.6,0,0)^T$ we see in Tables 5 and 6 the behaviour of the error for $d=2$ and $m=2$ using fold out basis functions on regular and adaptive sparse grids. Note that when using normal basis functions on an adaptive sparse grid we observe a similar performance. In Fig. 8a we see the error on adaptive sparse grids. As before the error with respect to the threshold $\varepsilon$ behaves similarly for normal and fold out basis function, here not only in the convergence rate, but also in absolute values. In this four dimensional example the fold out basis functions use less basis functions for the same $\varepsilon$, therefore when considering the error with respect to the number of nodes we observe in Fig. 8b that the fold out basis functions perform better than the normal ones. Furthermore, when comparing adaptive against regular sparse grids, we see from the figure and Tables 5 and 6 that the adaptive scheme needs an order of magnitude less points for the same accuracy. Since the absolute value of the entries in the stiffness matrix increase in higher dimension and require a finer discretization, the behaviour of the error can therefore be interpreted in the way that the adaptive algorithm automatically leads to adaptivity with respect to the different dimensions leading to anisotropic sparse grids.

Table 5 Wave equation (6.10) in 4D: error in the trajectory and control with regular sparse grids using the gradient approach and fold out basis functions

Table 6 Wave equation (6.10) in 4D: error in the trajectory and control with adaptive grids using the gradient approach and fold out basis functions

Fig. 8

Wave equation (6.10) in 4D: error in the control comparing the scheme based on sparse grids using normal hat and fold out basis functions, regular and adaptive sparse grids. a Error in the control versus $\varepsilon$, b error in the control versus nodes

Fig. 9

Wave equation (6.10) in 4D: Components of the optimal state y and corresponding optimal control u resulting from the SL-SG approach on a sparse grid with threshold $\varepsilon =2.44\times 10^{-5}$. As a reference solution the corresponding components of a solution generated by a Riccati approach are presented. a $y_{1}$, b $y_{3}$, c $u_{1}$, d $y_{2}$, e $y_{4}$, f $u_{2}$

In Fig. 9 we confirm that the feedback control we derive from the value function leads to a trajectory which coincide (up to a small error depending on the mesh parameter) with a reference trajectory derived from a Riccati equation.

6.4 Control of the Semi-discrete Wave Equation (6D)

Next, we consider problem (3.24) and (3.25) for the semi-discrete wave equation (3.10) in six dimensions with data as given in (6.10) and initial point $x=(0.4, 0.6, 0.2, 0, 0, 0)^T$. Note that we have to decrease the size of the time step to $\varDelta t = 0.0025$ when increasing the entries in the stiffness matrix. We remark that larger entries in the stiffness matrix lead to an increase of the derivative $|H_p(x,p)|$, which requires in the context of finite difference schemes a smaller time step because of the CFL-condition. As before we use the gradient approach to derive the feedback and now employ only fold out basis function to keep the computational cost low. In Table 7 and Fig. 10 the behaviour in the state along an optimal trajectory is shown, overall similar to the 4D case, although a certain resolution needs to be there for the convergence to kick in.

Table 7 Wave equation (6.10) in 6D: error in the trajectory and control with adaptive grids using the gradient approach and fold out basis functions

Fig. 10

Wave equation (6.10) in 6D: the adaptive sparse grids scheme using fold out basis functions. a error in the trajectory versus $\varepsilon$, b error in the control versus $\varepsilon$

Table 8 Wave equation (6.10) in 8D: error in the trajectory and control with adaptive grids using the gradient approach and fold out basis functions

6.5 Control of the Semi-discrete Wave Equation (8D)

Next, we consider problem (3.24) and (3.25) for the semi-discrete wave equation (3.10) in eight dimension with data as given in (6.10) and initial point $x=(0.4, 0.6, 0.2, 0.1, 0, 0, 0, 0)^T$. Again, we needed to decrease the time step, now to $\varDelta t = 0.00125$. In Fig. 11 and Table 8 we see the errors with respect to the threshold $\varepsilon$. Again, the approach needs a certain resolution for a stable convergence behaviour, which now starts for a smaller $\varepsilon$ than in the 6D case. The number of mesh points on the finest refinement level is still moderate, however the computational cost is relatively high.

Fig. 11

Wave equation (6.10) in 8D: the adaptive sparse grids scheme using fold out basis functions. a Error in the trajectory versus $\varepsilon$, b error in the control versus $\varepsilon$

This being our example with the largest number of dimensions, we note that we needed about 2.5 GB of main memory during the computation for the finest resolution.

6.6 Control of a Bilinear System (2D)

In this last example we consider a dynamics arising from a bilinear dynamical system which is of Schrödinger type, see (3.19). Because of the nonlinear coupling of state and control the Riccati approach is here not directly applicable.

We consider two settings; while in the first one we observe numerically a smooth value function, in the second one a non-differentiability appears.

Remark 1

If the value function is not differentiable in a point (x, t), then (x, t) is not a regular point, i.e. there exists not a unique optimal trajectory $y^*(\cdot )$ starting in x at time t with $y^*(t)=x$, see [18, p. 42, Thm. 10.2].

Example 1

Let $Q = [-2,2]^2, T=1, \varDelta t = 1/200, \beta _y=2, \beta _u=0.1$,

$$\begin{aligned} \mathcal {A}^s= \begin{pmatrix} 0 &{} 0.1 \\ -0.1 &{} 0 \end{pmatrix}, \quad {\hat{B}}=\begin{pmatrix} 0 &{}\quad -0.1 \\ 0.1 &{}\quad 0 \end{pmatrix}, \quad \mathcal {M}=\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}, \end{aligned}$$

(6.11)

and control bounds inactive, i.e. we choose $U_s = [-10,10]$ big enough for the comparison approach. For computing a reference value function as described in Sect. 6.1 we choose $\varDelta x$ and $\varDelta t$ as given in Sect. 6.2. In Fig. 12 we see the error when using comparison and the gradient. Using normal/fold out basis functions and a comparison/gradient based approach lead to a similar behaviour of the error in the value function with respect to the threshold $\varepsilon$.

Fig. 12

Bilinear equation (6.11): error in the value function comparing the scheme based on sparse grids using normal and fold out basis functions, adaptive sparse grid (2D). a Error in the value function versus $\varepsilon$, b error in the value function versus nodes

Fig. 13

Bilinear equation (6.12) in 2D: error in the value function comparing the scheme based on sparse grids using normal and fold out basis functions, adaptive sparse grid. a Error in the value function versus $\varepsilon$, b error in the value function versus nodes

Example 2

Let

$$\begin{aligned} \mathcal {A}^s= \begin{pmatrix} 0 &{}\quad 0.5 \\ -0.5 &{}\quad 0 \end{pmatrix}, \quad {\hat{B}}=\begin{pmatrix} 0 &{}\quad -0.5 \\ 0.5 &{}\quad 0 \end{pmatrix}, \end{aligned}$$

(6.12)

and, besides $\varDelta t = 1/500$, the other parameters as in Example 1, and let the control space be given by $U=[-4,4]$. In Fig. 13 we see the behaviour of the error when using the comparison approach and normal and fold out basis functions, respectively. In Fig. 14 the meshes for $\varepsilon =1.95 \times 10^{-4}$ and $\varepsilon =7.78\times 10^{-4}$ are shown. We observe a strong refinement of the mesh along the non-differentiability.

Fig. 14

Bilinear equation (6.11) and (6.12) in 2D: adaptive sparse grid. a Example (6.11) with feedback (5.3), fold-out basis functions and $\varepsilon = 1.95\times 10^{-4}$, b example (6.12) with feedback (5.3), fold-out basis functions and $\varepsilon = 7.78\times 10^{-4}$

In both example we observe a similar convergence behaviour as for the wave equation. Furthermore, in this two dimensional setting again the different approaches lead to quite the same results.

7 Outlook

The presented approach allows to include further aspects to increase the accuracy and to reduce the computational costs. A higher order interpolation could be used within the semi-Lagrangian scheme (cf. also [46]). Additionally an efficient numerical algorithm to determine the minimum within the Hamiltonian in the semi-Lagrangian scheme could be developed which is also suitable for a more general class of cost functionals. Finally information on the basis function could be used to introduce a priori an adaptivity with respect to the dimensions.

Note that the computational bottleneck is the evaluation of the sparse grid function in the scheme (5.1). Our current proof-of-concept implementation is essentially unoptimized for this aspect. The more evolved and sophisticated SG++-library [43] already would most likely show a much reduced computational time. Furthermore, there are recent results for more efficient and suitable data structures for sparse grids which take machine constraints into consideration [12], which have the potential to gain a factor of two to three in serial runtime against the mature SG++, while allowing for multicore parallelism. In conclusion, although the runtime for the eight dimensional problem is in our implementation in the order of days, it is fully justified to assume it can be reduced to hours, if not less, on multicore architectures.

Besides an efficient implementation of the sparse grid function evaluation, two other aspects warrant further investigation. One is the interplay between spatial and time resolution. While in this work we concentrated on the spatial resolution, it is well known that these discretizations should be analyzed jointly. Here, the non-local nature of the sparse grid basis function pose additional difficulties in the analysis. The other is the spatial adaptivity, here we concentrated on using the hierarchical coefficients, but these refine in all dimensions, which results in the examples in overrefinement in some dimensions due to anisotropic nature of the problem. Only through the coarsening these grid points will be removed again, but of course it would be much more efficient, if the adaptive procedure only refines in some dimensions.