Weak and strong convergence theorems for solving pseudo-monotone variational inequalities with non-Lipschitz mappings

Abstract

The aim of this paper is to study a classical pseudo-monotone and non-Lipschitz continuous variational inequality problem in real Hilbert spaces. Weak and strong convergence theorems are presented under mild conditions. Our methods generalize and extend some related results in the literature and the main advantages of proposed algorithms there is no use of Lipschitz condition of the variational inequality associated mapping. Numerical illustrations in finite and infinite dimensional spaces illustrate the behaviors of the proposed schemes.

1 Introduction

The main purpose of this paper to study the classical variational inequality of Fichera [13, 14] and Stampacchia [38] (see also Kinderlehrer and Stampacchia [25]) in real Hilbert spaces. Precisely, the classical variational inequality problem (VIP) is of the form: finding a point x^∗∈ C such that

$$ \langle Ax^{*},x-x^{*}\rangle \geq 0 \ \ \forall x\in C, $$

(1)

Let us denote by VI(C, A) the solutions set of VIP (1).

This problem plays an important role as a modeling tool in diverse fields such as in economics, engineering mechanics, transportation, and many more (see for example, [2, 3, 15, 26, 28]). Recently, many iterative methods have been constructed for solving variational inequalities and their related optimization problems (see monographs [12, 28] and references therein).

One of the most popular methods for solving variational inequalities with monotone and Lipschitz continuous mappings is the method proposed by Korpelevich [30] (also independently by Antipin [1]) which is called the extragradient method in the finite dimensional Euclidean space. This method was based on a double-projection method onto the feasible set.

The extragradient method has been studied and extended in infinite-dimensional spaces by many authors (see, e.g., [6,7,8,9, 20, 22, 23, 32, 33, 39, 41,42,43,44] and the references therein). It is easy to observe that, when the mapping-associated variational inequality is not Lipschitz continuous or the Lipschitz constant of the associated variational inequality mapping is very difficult to compute, it is clear that the extragradient method is not applicable to implement because we can not determine the stepsize.

Khobotov [27] proposed the linesearch for the extragradient method and Marcotte’s paper [34] contains its implementation. The first extrapolation method using Armijo-type linesearch was proposed in [29] and the method [19] follows the same approach (see comments of Section 1.3 in [28] and and Section 12.1 in [12]).

This modification in [19, 29] allows convergence without Lipschitz continuity of the mapping-associated variational inequality in finite-dimensional Euclidean space. The algorithm is of the form

Moreover, Algorithm 1 converges under the condition the mapping-associated variational inequality is monotone and continuous on the feasible set in finite-dimensional spaces. This brings the following natural question.

Question:

Can we obtain convergence result for VIP using a new modification of the extragradient method under a much weaker condition than monotonicity of the cost function?

Our aim in this paper is to answer the above question in the affirmative. Precisely, our contributions in this paper are:

• to construct another modification of extragradient algorithm that converges under a weaker condition in an infinite-dimensional Hilbert space;

• to introduce a modification of extragradient method for solving VIP with uniformly continuous pseudo-monotone mapping in infinite-dimensional real Hilbert spaces;

• to use a different Armijo-type linesearch and obtain convergence results (weak and strong convergence results) when the mapping is pseudo-monotone in the sense of Karamardian [24]

• to compare, using numerical examples, our proposed methods with some methods in the literature. Our numerical analysis (performed both in finite- and infinite-dimensional Hilbert spaces) shows that our methods outperform certain already established methods for solving variational inequality problem with pseudo-monotone mapping in the literature.

We organize the paper as follows: In Sect. 2, we give some definitions and preliminary results to be used in our convergence analysis. In Sect. 3, we deal with analyzing the convergence of the proposed algorithms. Finally, in Sect. 4, several numerical experiments are performed to illustrate the implementation of our proposed algorithms and compare our proposed algorithms with previously known algorithms.

2 Preliminaries

Let C be a non-empty, closed, and convex subset of a real Hilbert space H, A : H → H is a single-valued mapping, and 〈⋅,⋅〉 and ∥⋅∥ are the inner product and the norm in H, respectively.

The weak convergence of $\{x_{n}\}_{n=1}^{\infty }$ to x is denoted by $x_{n}\rightharpoonup x$ as n →∞, while the strong convergence of $\{x_{n}\}_{n=1}^{\infty }$ to x is written as x_n → x as n →∞. For each x, y ∈ H and $\alpha \in \mathbb {R}$, we have

Definition 2.1

Let T : H → H be a mapping.

• 1. The mapping T is called L-Lipschitz continuous with L > 0 if

  $$ \|Tx-Ty\|\le L \|x-y\| \ \ \ \forall x,y \in H. $$

  if L = 1 then the mapping T is called non-expansive and if L ∈ (0,1), T is called contraction.

• 2. The mapping T is called monotone if

  $$ \langle Tx-Ty,x-y \rangle \geq 0 \ \ \ \forall x,y \in H. $$

• 3. The mapping T is called pseudo-monotone if

  $$ \langle Tx,y-x \rangle \geq 0 \Longrightarrow \langle Ty,y-x \rangle \geq 0 \ \ \ \forall x,y \in H. $$

• 4. The mapping T is called α-strongly monotone if there exists a constant α > 0 such that

  $$ \langle Tx-Ty,x-y\rangle\geq \alpha \|x-y\|^{2} \ \ \forall x,y\in H. $$

• 5. The mapping T is called sequentially weakly continuous if for each sequence {x_n} we have: x_n converges weakly to x implies x_n converges weakly to Tx.

It is easy to see that very monotone mapping is pseudo-monotone but the converse is not true. For example, take $Tx:=\frac {1}{1+x}, x >0$.

For every point x ∈ H, there exists a unique nearest point in C, denoted by P_Cx such that ∥x − P_Cx∥≤∥x − y∥ ∀y ∈ C. P_C is called the metric projection of H onto C.

Lemma 2.1

[16] Givenx ∈ Handz ∈ C.Thenz = P_Cx⇔〈x − z, z − y〉≥ 0 ∀y ∈ C.

Lemma 2.2

[16] Letx ∈ H.Then

• i) ∥P_Cx − P_Cy∥² ≤〈P_Cx − P_Cy, x − y〉 ∀y ∈ H;

• ii) ∥P_Cx − y∥² ≤∥x − y∥² −∥x − P_Cx∥² ∀y ∈ C;

• iii) 〈(I − P_C)x − (I − P_C)y, x − y〉≥∥(I − P_C)x − (I − P_C)y∥² ∀y ∈ H.

Lemma 2.3

[5] Givenx ∈ Handv ∈ H,v≠ 0 and letT = {z ∈ H : 〈v, z − x〉 ≤ 0}.Then, for allu ∈ H,the projectionP_T(u) is defined by

$$ P_{T}(u)=u-\max\left\{0,\frac{\left\langle v, u-x\right\rangle}{||v||^{2}}\right\}v. $$

In particular, if u∉T then

$$ P_{T}(u)=u-\frac{\left\langle v, u-x\right\rangle}{||v||^{2}}v. $$

Lemma 2.3 gives us an explicit formula to find the projection of any point onto a half-space.

For properties of the metric projection, the interested reader could be referred to Section 3 in [16] and Chapter 4 in [5].

The following Lemmas are useful for the convergence of our proposed methods.

Lemma 2.4

[11] Forx ∈ Handα ≥ β > 0 the following inequalities hold.

$$ \frac{\|x-P_{C}(x-\alpha Ax)\|}{\alpha}\le \frac{\|x-P_{C}(x-\beta Ax)\|}{\beta}, $$

$$ \|x-P_{C}(x-\beta Ax)\|\le \|x-P_{C}(x-\alpha Ax)\|. $$

Lemma 2.5

[21] LetH₁andH₂be two real Hilbert spaces. SupposeA : H₁ → H₂is uniformly continuous on bounded subsets ofH₁and M is a bounded subset ofH₁.Then,A(M) is bounded.

Lemma 2.6

[[10], Lemma 2.1] Consider the problemVI(C, A) withC being a non-empty, closed, convex subset of a real Hilbert spaceH andA : C → Hbeing pseudo-monotone and continuous. Then,x^∗is a solution ofVI(C, A) if and only if

$$ \langle Ax, x - x^{*}\rangle\geq 0 \ \ \forall x \in C. $$

Lemma 2.7

[36] LetC be a non-empty set ofH and{x_n} be asequence inH such that the following two conditions hold:

• i) for everyx ∈ C,$\lim _{n\to \infty }\|x_{n}-x\|$exists;

• ii) every sequential weak cluster point of{x_n} is in C.

Then, {x_n} converges weakly to a point inC.

The proof of the following lemma is the same with Lemma 2.3 and was given in [17]. Hence, we state the lemma and omit the proof in real Hilbert spaces.

Lemma 2.8

LetH be a real Hilbert space and h be a real-valued function onH and defineK := {x ∈ H : h(x) ≤ 0}.If K is nonempty and h is Lipschitz continuous onH with modulus𝜃 > 0,then

$$ \text{dist}(x, K) \geq \theta^{-1} \max\{h(x), 0\}\ \ \forall x \in H, $$

where dist(x, K) denotes the distance function from x to K.

Lemma 2.9

[31] Let {a_n} be a sequence of non-negative real numbers such that there exists asubsequence$\{a_{n_{j}}\}$of{a_n} such that$a_{n_{j}}<a_{n_{j}+1}$forall$j\in \mathbb {N}$.Then there exists a non-decreasing sequence{m_k} of$\mathbb {N}$suchthat$\lim _{k\to \infty }m_{k}=\infty$andthe following properties are satisfied by all (sufficiently large)number$k\in \mathbb {N}$:

$$ a_{m_{k}}\le a_{m_{k}+1} \text{ and} a_{k}\le a_{m_{k}+1}. $$

In fact, m_k is the largest number n in the set {1,2,⋯ ,k} such that a_n < a_n+ 1.

Lemma 2.10

[45] Let{a_n} be a sequence of non-negative real numbers such that:

$$ a_{n+1}\le (1-\alpha_{n})a_{n}+\alpha_{n} b_{n}, $$

where {α_n}⊂ (0,1) and {b_n} is a sequence such that

• a) ${\sum }_{n=0}^{\infty } \alpha _{n}=\infty$;

• b) $\limsup _{n\to \infty }b_{n}\le 0.$

Then ,$\lim _{n\to \infty }a_{n}=0.$

3 Main results

The following conditions are assumed for the convergence of the methods.

Condition 1

The feasible set C is a non-empty, closed, and convex subset of the real Hilbert space H.

Condition 2

The mapping A : H → H is a pseudo-monotone, uniformly continuous on H and sequentially weakly continuous on C. In finite-dimensional spaces, it suffices to assume that A : H → H is a continuous pseudo-monotone on H.

Condition 3

The solution set of the VIP (1) is non-empty, that is VI(C, A)≠∅.

3.1 Weak convergence

In this section, we introduce a new algorithm for solving VIP which is constructed based on modified projection-type methods.

Remark 3.1

We note that our Algorithm 3.1 in this paper is proposed in infinite-dimensional real Hilbert spaces while the method proposed by Solodov and Tseng in [40] was done in finite-dimensional spaces. Furthermore, our method is much more general than that of Solodov and Tseng [40] even with a more general cost function than that of Solodov and Tseng [40]. This is confirmed in our numerical examples, where we give examples of variational inequalities with pseudomonotone functions which are not monotone (as assumed in the paper of Solodov and Tseng [40]) even in finite-dimensional spaces.

We start the analysis of the algorithm’s convergence by proving the following lemmas

Lemma 3.1

Assume that Conditions 1–2 hold. The Armijo-line search rule (2) is welldefined.

Proof

If x_n ∈ VI(C, A) then x_n = P_C(x_n − γAx_n) and m_n = 0. We consider the situation x_n∉VI(C, A) and assume the contrary that for all m we have

$$ \gamma l^{m} \langle Ax_{n}{\kern-.5pt}-{\kern-.5pt}AP_{C}(x_{n}{\kern-.5pt}-{\kern-.5pt}\gamma l^{m} Ax_{n}), x_{n}{\kern-.5pt}-{\kern-.5pt}P_{C}(x_{n}{\kern-.5pt}-{\kern-.5pt}\gamma l^{m} Ax_{n})\rangle > \mu \|x_{n}-P_{C}(x_{n}{\kern-.5pt}-{\kern-.5pt}\gamma l^{m} Ax_{n})\|^{2} $$

By Cauchy-Schwartz inequality, we have

$$ \gamma l^{m}\|Ax_{n}-AP_{C}(x_{n}-\gamma l^{m} Ax_{n})\|> \mu \|x_{n}-P_{C}(x_{n}-\gamma l^{m} Ax_{n})\|. $$

(4)

This implies that

$$ \|Ax_{n}-AP_{C}(x_{n}-\gamma l^{m} Ax_{n})\|> \mu \frac{\|x_{n}-P_{C}(x_{n}-\gamma l^{m} Ax_{n})\|}{\gamma l^{m}}. $$

(5)

We consider two possibilities of x_n. First, if x_n ∈ C, then since P_C and A are continuous, we have $\lim _{m\to \infty }\|x_{n}-P_{C}(x_{n}-\gamma l^{m} Ax_{n})\|=0.$ From the uniform continuity of the mapping A on bounded subsets of C, it implies that

$$ \lim_{m\to\infty}\|Ax_{n}-AP_{C}(x_{n}-\gamma l^{m} Ax_{n})\|=0. $$

(6)

Combining (5) and (6) we get

$$ \lim_{m\to\infty}\frac{\|x_{n}-P_{C}(x_{n}-\gamma l^{m} Ax_{n})\|}{\gamma l^{m}}=0. $$

(7)

Assume that z_m = P_C(x_n − γl^mAx_n) we have

$$ \langle z_{m}-x_{n}+\gamma l^{m} Ax_{n},x-z_{m}\rangle \geq 0 \ \ \forall x\in C. $$

This implies that

$$ \langle\frac{ z_{m}-x_{n}}{\gamma l^{m}},x-z_{m}\rangle +\langle Ax_{n},x-z_{m}\rangle\geq 0 \ \ \forall x\in C. $$

(8)

Taking the limit m →∞ in (8) and using (7) we obtain

$$ \langle Ax_{n},x-x_{n}\rangle\geq 0 \ \ \forall x\in C, $$

which implies that x_n ∈ VI(C, A) is a contraction.

Now, if x_n∉C, then we have

$$ \lim_{m\to\infty} \|x_{n}-P_{C}(x_{n}-\gamma l^{m} Ax_{n})\|=\|x_{n}-P_{C}x_{n}\| >0. $$

(9)

and

$$ \lim_{m\to\infty} \gamma l^{m}\|Ax_{n}-AP_{C}(x_{n}-\gamma l^{m} Ax_{n})\|=0 $$

(10)

Combining (4), (9), and (10), we get a contradiction. □

Remark 3.2

• 1. In the proof of Lemma 3.1, we do not use the pseudo-monotonicity of A.

• 2. Now, we show that if x_n = y_n then stop and y_n is a solution of VI(C, A). Indeed, we have 0 < λ_n ≤ γ, which together with Lemma 2.4, we get

  $$ 0=\frac{\|x_{n}-y_{n}\|}{\lambda_{n}}=\frac{\|x_{n}-P_{C}(x_{n}-\lambda_{n} Ax_{n})\|}{\lambda_{n}}\geq \frac{\|x_{n}-P_{C}(x_{n}-\gamma Ax_{n})\|}{\gamma}. $$

  This implies that x_n is a solution of VI(C, A), thus y_n is a solution of VI(C, A).

• 3. Next, we show that if Ay_n = 0 then stop and y_n is a solution of VI(C, A). Indeed, since y_n ∈ C, it is easy to see that if Ay_n = 0 then y_n ∈ VI(C, A).

Lemma 3.2

Assume that Conditions 1–3 hold. Letx^∗be a solution of problem (1) and the functionh_nbe defined by (5). Thenh_n(x^∗) ≤ 0 andh_n(x_n) ≥ (1 − μ)∥x_n − y_n∥².In particular, ifx_n≠y_nthenh_n(x_n) > 0.

Proof

Since x^∗ be a solution of problem (1), using Lemma 2.6 we have

$$ \langle Ay_{n}, x^{*}-y_{n}\rangle \le 0. $$

(11)

It is implied from (11) and y_n = P_C(x_n − λ_nAx_n) that

$$ \begin{array}{@{}rcl@{}} h_{n}(x^{*})&=&\langle x_{n}-y_{n}-\lambda_{n}(Ax_{n}-Ay_{n}),x^{*}-y_{n}\rangle\\ &=&\langle x_{n}-y_{n}-\lambda_{n}Ax_{n},x^{*}-y_{n}\rangle+\lambda_{n} \langle Ay_{n},x^{*}-y_{n}\rangle\\ & \le& 0. \end{array} $$

The first claim of Lemma 3.2 is proven. Now, we prove the second claim. Using (2), we have

$$ \begin{array}{@{}rcl@{}} h_{n}(x_{n})&=&\langle x_{n}-y_{n}-\lambda_{n}(Ax_{n}-Ay_{n}),x_{n}-y_{n}\rangle\\ &=&\|x_{n}-y_{n}\|^{2}-\lambda_{n} \langle Ax_{n}-Ay_{n},x_{n}-y_{n}\rangle\\ &\geq& \|x_{n}-y_{n}\|^{2}-\mu\|x_{n}-y_{n}\|^{2}\\ &=&(1-\mu)\|x_{n}-y_{n}\|^{2}. \end{array} $$

□

Remark 3.3

Lemma 3.2 implies that x_n∉C_n. According to Lemma 2.3, then x_n+ 1 is of the form

$$ x_{n+1}=x_{n}-\frac{\langle x_{n}-y_{n}-\lambda_{n} (Ax_{n}-Ay_{n}),x_{n}-y_{n}\rangle}{\|x_{n}-y_{n}-\lambda_{n} (Ax_{n}-Ay_{n})\|^{2}}(x_{n}-y_{n}-\lambda_{n} (Ax_{n}-Ay_{n})). $$

Lemma 3.3

Assume that Conditions 1–3 hold. Let{x_n} be a sequence generated by Algorithm 3.1. If there exists asubsequence$\{x_{n_{k}}\}$of{x_n} such that$\{x_{n_{k}}\}$convergesweakly toz ∈ Hand$\lim _{k\to \infty }\|x_{n_{k}}-y_{n_{k}}\|=0$thenz ∈ VI(C, A).

Proof

From $x_{n_{k}}\rightharpoonup z, \lim _{k\to \infty }\|x_{n_{k}}-y_{n_{k}}\|=0$, and {y_n}⊂ C, we get z ∈ C. We have $y_{n_{k}}=P_{C}(x_{n_{k}}-\lambda _{n_{k}}Ax_{n_{k}})$ thus,

$$ \langle x_{n_{k}}-\lambda_{n_{k}}Ax_{n_{k}}-y_{n_{k}},x-y_{n_{k}}\rangle \le 0 \ \ \forall x\in C. $$

or equivalently

$$ \frac{1}{\lambda_{n_{k}}}\langle x_{n_{k}}-y_{n_{k}},x-y_{n_{k}}\rangle \le \langle Ax_{n_{k}},x-y_{n_{k}}\rangle \ \ \forall x\in C. $$

This implies that

$$ \frac{1}{\lambda_{n_{k}}}\langle x_{n_{k}}-y_{n_{k}},x-y_{n_{k}}\rangle +\langle Ax_{n_{k}},y_{n_{k}}-x_{n_{k}}\rangle \le \langle Ax_{n_{k}},x-x_{n_{k}}\rangle \ \ \forall x\in C. $$

(12)

Now, we show that

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}},x-x_{n_{k}}\rangle \geq 0. $$

(13)

For showing this, we consider two possible cases. Suppose first that $\liminf _{k\to \infty }\lambda _{n_{k}}>0$. We have $\{x_{n_{k}}\}$ is a bounded sequence, A is uniformly continuous on bounded subsets of H. By Lemma 2.6, we get that $\{Ax_{n_{k}}\}$ is bounded. Taking k →∞ in (12) since $\|x_{n_{k}}-y_{n_{k}}\|\to 0$, we get

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}},x-x_{n_{k}}\rangle \geq 0. $$

Now, we assume that $\liminf _{k\to \infty }\lambda _{n_{k}}=0$. Assume $z_{n_{k}}=P_{C}(x_{n_{k}}-\lambda _{n_{k}}.l^{-1}Ax_{n_{k}})$, we have $\lambda _{n_{k}}l^{-1}>\lambda _{n_{k}}$. Applying Lemma 2.4, we obtain

$$ \|x_{n_{k}}-z_{n_{k}}\|\le \frac{1}{l}\|x_{n_{k}}-y_{n_{k}}\|\to 0 \text{ as} k\to \infty. $$

Consequently, $z_{n_{k}}\rightharpoonup z\in C$, this implies that $\{z_{n_{k}}\}$ is bounded, which the uniformly continuity of the mapping A on bounded subsets of H follows that

$$ \|Ax_{n_{k}}-Az_{n_{k}}\|\to 0 \text{ as} k\to \infty. $$

(14)

By the Armijo linesearch rule (2), we must have

$$ \lambda_{n_{k}}.l^{-1} \langle Ax_{n}-AP_{C}(x_{n}-\lambda_{n_{k}}.l^{-1} Ax_{n}), x_{n}-P_{C}(x_{n}-\lambda_{n_{k}}.l^{-1} Ax_{n})\rangle \!>\! \mu \|x_{n}-P_{C}(x_{n}-\lambda_{n_{k}}.l^{-1} Ax_{n})\|^{2} $$

By Cauchy-Schwartz inequality, we have

$$ \lambda_{n_{k}}.l^{-1}\|Ax_{n_{k}}-AP_{C}(x_{n_{k}}-\lambda_{n_{k}}l^{-1} Ax_{n_{k}})\|> \mu \|x_{n_{k}}-P_{C}(x_{n_{k}}-\lambda_{n_{k}}l^{-1} Ax_{n_{k}})\|. $$

That is,

$$ \frac{1}{\mu} \|Ax_{n_{k}}-Az_{n_{k}}\|>\frac{\|x_{n_{k}}-z_{n_{k}}\|}{\lambda_{n_{k}}l^{-1}}. $$

(15)

Combining (14) and (15), we obtain

$$ \lim_{k\to\infty}\frac{\|x_{n_{k}}-z_{n_{k}}\|}{\lambda_{n_{k}}l^{-1}}=0. $$

Furthermore, we have

$$ \langle x_{n_{k}}-\lambda_{n_{k}} l^{-1}Ax_{n_{k}}-z_{n_{k}},x-z_{n_{k}}\rangle \le 0 \ \ \forall x\in C. $$

This implies that

$$ \frac{1}{\lambda_{n_{k}}l^{-1}}\langle x_{n_{k}}-z_{n_{k}},x-z_{n_{k}}\rangle +\langle Ax_{n_{k}},z_{n_{k}}-x_{n_{k}}\rangle \le \langle Ax_{n_{k}},x-x_{n_{k}}\rangle \ \ \forall x\in C. $$

(16)

Taking the limit k →∞ in (16), we get

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}},x-x_{n_{k}}\rangle \geq 0. $$

Therefore, the inequality (13) is proven.

On the other hand, we have

$$ \langle Ay_{n_{k}},x-y_{n_{k}}\rangle=\langle Ay_{n_{k}}- Ax_{n_{k}},x-x_{n_{k}}\rangle+\langle Ax_{n_{k}},x-x_{n_{k}}\rangle+\langle Ay_{n_{k}},x_{n_{k}}-y_{n_{k}}\rangle. $$

(17)

Since $\lim _{k\to \infty }\|x_{n_{k}}-y_{n_{k}}\|=0$ and the uniformly continuity of A on H, we get

$$\lim_{k\to\infty}\|Ax_{n_{k}}-Ay_{n_{k}}\|=0,$$

which, together with (13) and (17) implies that

$$ \liminf_{k\to\infty}\langle Ay_{n_{k}},x-y_{n_{k}}\rangle \geq 0. $$

(18)

Next, we show that z ∈ VI(C, A). Indeed, we choose a sequence {𝜖_k} of positive numbers decreasing and tending to 0. For each k, we denote by N_k the smallest positive integer such that

$$ \langle Ay_{n_{j}},x-y_{n_{j}}\rangle +\epsilon_{k} \geq 0 \ \ \forall j\geq N_{k}, $$

(19)

where the existence of N_k follows from (18). Since {𝜖_k} is decreasing, it is easy to see that the sequence {N_k} is increasing. Furthermore, for each k, since $\{y_{N_{k}}\}\subset C$ we have $Ay_{N_{k}}\ne 0$, and setting

$$ v_{N_{k}} = \frac{Ay_{N_{k}}}{\|Ay_{N_{k}}\|^{2}} , $$

we have $\langle Ay_{N_{k}}, v_{N_{k}}\rangle = 1$ for each k. Now, we can deduce from (19) that for each k

$$ \langle Ay_{N_{k}}, x+\epsilon_{k} v_{N_{k}}-y_{N_{k}}\rangle \geq 0. $$

Since the fact that A is pseudo-monotone, we get

$$ \langle A(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-y_{N_{k}}\rangle \geq 0. $$

This implies that

$$ \langle Ax, x-y_{N_{k}}\rangle \geq \langle Ax-A(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-y_{N_{k}} \rangle-\epsilon_{k} \langle Ax, v_{N_{k}}\rangle. $$

(20)

Now, we show that $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Indeed, since $x_{n_{k}}\rightharpoonup z$ and $\lim _{k\to \infty }\|x_{n_{k}}-y_{n_{k}}\|=0,$we obtain $y_{N_{k}}\rightharpoonup z \text { as} k \to \infty$. Since A is sequentially weakly continuous on C, $\{ Ay_{n_{k}}\}$ converges weakly to Az. We have that Az≠ 0 (otherwise, z is a solution). Since the norm mapping is sequentially weakly lower semicontinuous, we have

$$ 0 < \|Az\|\le \liminf_{k\to \infty}\|Ay_{n_{k}}\|. $$

Since $\{y_{N_{k}}\}\subset \{y_{n_{k}}\}$ and 𝜖_k → 0 as k →∞, we obtain

$$ \begin{array}{@{}rcl@{}} 0 \le \limsup_{k\to\infty} \|\epsilon_{k} v_{N_{k}} \|= \limsup_{k\to\infty} \left( \frac{\epsilon_{k}}{\|Ay_{n_{k}}\|}\right)\le \frac{\limsup_{k\to\infty}\epsilon_{k}} {\liminf_{k\to\infty}\|Ay_{n_{k}}\|}=0, \end{array} $$

which implies that $\lim _{k\to \infty } \epsilon _{k} v_{N_{k}} = 0.$

Now, letting k →∞, then the right hand side of (20) tends to zero by A is uniformly continuous, $\{x_{N_{k}}\}, \{v_{N_{k}}\}$ are bounded and $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Thus, we get

$$ \liminf_{k\to\infty}\langle Ax,x-y_{N_{k}}\rangle \geq 0. $$

Hence, for all x ∈ C we have

$$ \langle Ax, x-z\rangle=\lim_{k\to\infty} \langle Ax, x-y_{N_{k}}\rangle =\liminf_{k\to\infty} \langle Ax, x-y_{N_{k}}\rangle \geq 0. $$

By Lemma 2.6, we obtain z ∈ VI(C, A) and the proof is complete. □

Remark 3.4

When the function A is monotone, it is not necessary to impose the sequential weak continuity on A.

Theorem 3.5

Assume that Conditions 1–3 hold. Then any sequence{x_n} generated by Algorithm 3.1 converges weakly to an element ofVI(C, A).

Proof

Claim 1

{x_n} is a bounded sequence. Indeed, let p ∈ VI(C, A) we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}=\|P_{C_{n}}x_{n}-p\|^{2}&\le& \|x_{n}-p\|^{2}-\|P_{C_{n}}x_{n}-x_{n}\|^{2} \\ &=&\|x_{n}-p\|^{2}-\text{dist}^{2}(x_{n},C_{n}). \end{array} $$

(21)

This implies that

$$ \|x_{n+1}-p\|\le \|x_{n}-p\|. $$

This implies that $\lim _{n\to \infty }\|x_{n}-p\|$ exists. Thus, the sequence {x_n} is bounded and we also have {y_n} is bounded.

Claim 2

$$ \left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}\le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}, $$

for some M > 0. Indeed, since {x_n},{y_n} are bounded, thus {Ax_n},{Ay_n} are bounded, thus there exists M > 0 such that ∥x_n − y_n − λ_n(Ax_n − Ay_n)∥≤ M for all n. Using this fact, we get for all u, v ∈ H that

$$ \begin{array}{@{}rcl@{}} \|h_{n}(u)-h_{n}(v)\|&=&\|\langle x_{n}-y_{n}-\lambda_{n}(Ax_{n}-Ay_{n}), u-v\rangle\|\\ &\le& \|x_{n}-y_{n}-\lambda_{n}(Ax_{n}-Ay_{n})\|\|u-v\|\\ &\le& M \|u-v\|. \end{array} $$

This implies that h_n(⋅) is M-Lipschitz continuous on H. By Lemma 2.8, we obtain

$$ \text{dist}(x_{n}, C_{n})\geq \frac{1}{M} h_{n}(x_{n}), $$

which, together with Lemma 3.2, we get

$$ \text{dist}(x_{n}, C_{n})\geq \frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}. $$

(22)

Combining (21) and (22), we obtain

$$ \|x_{n+1}-p\|^{2}\le \|x_{n}-z\|^{2}-\left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}, $$

which implies Claim 2 is proved.

Claim 3

The sequence {x_n} converges weakly to an element of VI(C, A). Indeed, since {x_n} is a bounded sequence, there exists the subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges weakly to z ∈ H.

According to Claim 2, we find

$$ \lim_{n\to\infty}\|x_{n}-y_{n}\|=0. $$

(23)

It is implied from Lemma 3.3 and (23) that z ∈ VI(C, A).

Therefore, we proved that:

• i) For every p ∈ VI(C, A), $\lim _{n\to \infty }\|x_{n}-p\|$ exists;

• ii) Each sequential weak cluster point of the sequence {x_n} is in VI(C, A).

By Lemma 2.7 the sequence {x_n} converges weakly to an element of VI(C, A).

□

3.2 Strong convergence

In this section, we introduce an algorithm for strong convergence which is constructed based on viscosity method [35] and modified projection-type methods for solving VIs. In addition, we assume that f : C → H is a contractive mapping with a coefficient ρ ∈ [0,1), and we add the following condition

Condition 4

Let {α_n} be a real sequences in (0,1) such that

$$ \lim_{n\to\infty}\alpha_{n}=0, \sum\limits_{n=1}^{\infty}\alpha_{n}=\infty. $$

Theorem 3.6

Assume that Conditions 1–4 hold. Then any sequence{x_n} generated by Algorithm 3.2 converges strongly top ∈ VI(C, A),wherep = P_{VI(C, A)} ∘ f(p).

Proof

Claim 1

The sequence {x_n} is bounded. Indeed, let $z_{n}=P_{C_{n}}(x_{n})$, according to Claim 1 in Theorem 3.5, we get

$$ \|z_{n}-p\|^{2}\le \|x_{n}-p\|^{2}-\left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}. $$

(24)

This implies that

$$ \|z_{n}-p\|\le \|x_{n}-p\|. $$

Therefore,

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|&=&\|\alpha_{n} f(x_{n})+(1-\alpha_{n})z_{n}-p\|\\ &=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(z_{n}-p)\|\\ &\le& \alpha_{n}\|f(x_{n})-p\|+(1-\alpha_{n})\|z_{n}-p\|\\ &\le& \alpha_{n}\|f(x_{n})-f(p)\|+\alpha_{n} \|f(p)-p\|+(1-\alpha_{n})\|z_{n}-p\|\\ &\le& \alpha_{n} \rho \|x_{n}-p\|+\alpha_{n}\|f(p)-p\|+(1-\alpha_{n})\|x_{n}-p\|\\ &\le& [1-\alpha_{n}(1-\rho)]\|x_{n}-p\|+\alpha_{n}(1-\rho)\frac{\|f(p)-p\|}{1-\rho}\\ &\le& \max\{\|x_{n}-p\|,\frac{\|f(p)-p\|}{1-\rho}\}\\ &\le& ...\le \max\{\|x_{1}-p\|,\frac{\|f(p)-p\|}{1-\rho}\}. \end{array} $$

This implies that the sequence {x_n} is bounded. Consequently, {f(x_n)},{y_n}, and {z_n} are bounded.

Claim 2

$$ \|z_{n}-x_{n}\|^{2}\le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p, x_{n+1}-p\rangle. $$

Indeed, we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(z_{n}-p)\|^{2} \\ &\le&(1-\alpha_{n})\|z_{n}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle \\ &\le& \|z_{n}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. \end{array} $$

(25)

On the other hand, we have

$$ \|z_{n}-p\|^{2}=\|P_{C_{n}}x_{n}-p\|^{2}\le \|x_{n}-p\|^{2}-\|z_{n}-x_{n}\|^{2}. $$

(26)

Substitute (26) into (25), we get

$$ \|x_{n+1}-p\|^{2} \le \|x_{n}-p\|^{2}-\|z_{n}-x_{n}\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. $$

This implies that

$$ \|z_{n}-x_{n}\|^{2} \le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. $$

Claim 3

$$ (1-\alpha_{n})\left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}\le\|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+\alpha_{n}\|f(x_{n})-p\|^{2}. $$

Indeed, from the definition of the sequence {x_n} and (24) we obtain

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(z_{n}-p)\|^{2}\\ &=&\alpha_{n}\|f(x_{n})-p\|^{2}+(1-\alpha_{n})\|z_{n}-p\|^{2}-\alpha_{n}(1-\alpha_{n})\|f(x_{n})-z_{n}\|^{2}\\ &\le&\alpha_{n}\|f(x_{n})-p\|^{2}+(1-\alpha_{n})\|x_{n}-p\|^{2}-(1-\alpha_{n})\left[\frac{1}{L} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}\\ &\le&\alpha_{n}\|f(x_{n})-p\|^{2}+\|x_{n}-p\|^{2}-(1-\alpha_{n})\left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}. \end{array} $$

This implies that

$$ (1-\alpha_{n})\left[\frac{1}{M} (1-\mu)\|x_{n}-y_{n}\|^{2}\right]^{2}\le\|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+\alpha_{n}\|f(x_{n})-p\|^{2}. $$

Claim 4

$$ \|x_{n+1}-p\|^{2}\le (1-(1-\rho)\alpha_{n})\|x_{n}-p\|^{2}+(1-\rho)\alpha_{n}\frac{2}{1-\rho}\langle f(p)-p,x_{n+1}-p\rangle. $$

Indeed, we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}f(x_{n})+(1-\alpha_{n})z_{n}-p\|^{2} \\ &=&\|\alpha_{n}(f(x_{n}) - f(p))+(1 - \alpha_{n})(z_{n} - p)+\alpha_{n}(f(p) - p)\|^{2} \\ &\le& \|\alpha_{n}(f(x_{n}) - f(p)) + (1 - \alpha_{n})(z_{n} - p)\|^{2}+2\alpha_{n}\langle f(p) - p,x_{n+1} - p\rangle \\ &\le&\alpha_{n}\|f(x_{n}) - f(p)\|^{2} + (1 - \alpha_{n})\|z_{n} - p\|^{2} + 2\alpha_{n}\langle f(p) - p,x_{n+1}-p\rangle \\ &\le&\alpha_{n}\rho\|x_{n}-p\|^{2}+(1-\alpha_{n})\|x_{n}-p\|^{2}+2\alpha_{n}\langle f(p)-p,x_{n+1}-p\rangle \\ &=&(1 - (1 - \rho)\alpha_{n})\|x_{n} - p\|^{2}+(1 - \rho)\alpha_{n}\frac{2}{1-\rho}\langle f(p)-p,x_{n+1}-p\rangle.\\ \end{array} $$

(27)

Claim 5

The sequence {∥x_n − p∥²} converges to zero. We consider two possible cases on the sequence {∥x_n − p∥²}.

Case 1

There exists an $N\in {\mathbb N}$ such that ∥x_n+ 1 − p∥² ≤∥x_n − p∥² for all n ≥ N. This implies that $\lim _{n\to \infty }\| x_{n}-p\|^{2}$ exists. It is implied from Claim 2 that

$$ \lim_{n\to\infty} \|x_{n}-z_{n}\|=0. $$

Now, according to Claim 3,

$$ \lim_{n\to \infty}\|x_{n}-y_{n}\|=0. $$

(28)

Since the sequence {x_n} is bounded, it implies that there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} that weak convergence to some z ∈ C such that

$$ \limsup\limits_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle =\lim_{k\to \infty}\langle f(p)-p,x_{n_{k}}-p\rangle=\langle f(p)-p,z-p\rangle. $$

(29)

Since $x_{n_{k}}\rightharpoonup z$ and (28), it implies from Lemma 3.3 that z ∈ VI(C, A). On the other hand,

$$ \|x_{n+1}-z_{n}\|=\alpha_{n}\|f(x_{n})-z_{n}\|\to 0 \text{ as} n\to \infty. $$

Thus,

$$ \|x_{n+1}-x_{n}\|=\|x_{n+1}-z_{n}\|+\|x_{n}-z_{n}\|\to 0 \text{ as} n\to \infty. $$

Since p = P_{VI(C, A)}f(p) and $x_{n_{k}} \rightharpoonup z\in VI(C,A)$, using (29), we get

$$ \limsup_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle =\langle f(p)-p,z-p\rangle\le 0. $$

This implies that

$$ \begin{array}{@{}rcl@{}} \limsup\limits_{n\to \infty}\langle f(p)-p,x_{n+1}-p\rangle&\le& \limsup\limits_{n\to \infty}\langle f(p)-p,x_{n+1}-x_{n}\rangle\\ &&+\limsup\limits_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle\le 0, \end{array} $$

which, together with Claim 4, implies from Lemma 2.10 that

$$ x_{n}\to p \text{ as} n\to \infty. $$

Case 2

There exists a subsequence $\{\| x_{n_{j}}-p\|^{2}\}$ of {∥x_n − p∥²} such that $\| x_{n_{j}}-p\|^{2} < \| x_{n_{j}+1}-p\|^{2}$ for all $j\in \mathbb {N}$. In this case, it follows Lemma 2.9 that there exists a nondecreasing sequence {m_k} of $\mathbb {N}$ such that $\lim _{k\to \infty }m_{k}=\infty$ and the following inequalities hold for all $k\in \mathbb {N}$:

$$ \| x_{m_{k}}-p\|^{2}\le \| x_{m_{k}+1}-p\|^{2} \text{ and} \| x_{k}-p\|^{2}\le \| x_{m_{k}+1}-p\|^{2}. $$

(30)

According to Claim 2, we have

$$ \begin{array}{@{}rcl@{}} \|z_{m_{k}}-x_{m_{k}}\|^{2}&\le \|x_{m_{k}}-p\|^{2}-\|x_{{m_{k}}+1}-p\|^{2}+2\alpha_{m_{k}} \langle f(x_{m_{k}})-p, x_{{m_{k}}+1}-p\rangle.\\ &\le\alpha_{m_{k}} \langle f(x_{m_{k}})-p, x_{{m_{k}}+1}-p\rangle\\ &\le\alpha_{m_{k}}\| f(x_{m_{k}})-p\| |x_{{m_{k}}+1}-p\|\to 0 \text{ as} k \to \infty. \end{array} $$

According to Claim 3, we have

$$ \begin{array}{@{}rcl@{}} (1 - \alpha_{m_{k}})\!\left[\!\frac{1}{M} (1 - \mu)\|x_{m_{k}} - y_{m_{k}}\|^{2}\!\right]^{2}&\!\le\!\|x_{m_{k}} - p\|^{2} - \|x_{{m_{k}}+1} - p\|^{2} + \alpha_{m_{k}}\|f(x_{m_{k}}) - p\|^{2}\\ &\le \alpha_{m_{k}}\|f(x_{m_{k}})-p\|^{2} \to 0 \text{ as} k\to\infty. \end{array} $$

Using the same arguments as in the proof of Case 1, we obtain

$$ \|x_{m_{k}+1}-x_{m_{k}}\|\to 0 $$

and

$$ \limsup_{k\to \infty}\langle f(p)-p,x_{m_{k}+1}-p\rangle\le 0. $$

Since (27), we get

$$ \begin{array}{@{}rcl@{}} \|x_{m_{k}+1}-p\|^{2}&\le (1-\alpha_{m_{k}}(1- \rho))\|x_{m_{k}}-p\|^{2}+2\alpha_{m_{k}}\langle f(p)-p,x_{m_{k}+1}-p\rangle\\ &\le (1-\alpha_{m_{k}}(1- \rho))\|x_{m_{k}+1}-p\|^{2}+2\alpha_{m_{k}}\langle f(p)-p,x_{m_{k}+1}-p\rangle. \end{array} $$

which, together with (30), implies that

$$ \|x_{k}-p\|^{2}\le \|x_{m_{k}+1}-p\|^{2}\le 2\langle f(p)-p,x_{m_{k}+1}-p\rangle. $$

Therefore, $\limsup _{k\to \infty }\|x_{k}-p\|\le 0$, that is x_k → p. The proof is completed.

□

Applying Algorithm 3.2 with f(x) := x₁ for all x ∈ C, we obtain the following corollary.

Corollary 3.7

Givenγ > 0,l ∈ (0,1),μ ∈ (0,1).Letx₁ ∈ Cbe arbitrary. Compute

$$y_{n}=P_{C}(x_{n}-\lambda_{n} Ax_{n}),$$

whereλ_nis chosen to be the largestλ ∈{γ, γl, γl²,...} satisfying

$$ \lambda \langle Ax_{n}-Ay_{n}, x_{n}-y_{n}\rangle \le \mu \|x_{n}-y_{n}\|^{2}. $$

Ify_n = x_n then stop and x_nis the solution of VIP. Otherwise, compute

$$ x_{n+1}=\alpha_{n} x_{1}+ (1 -\alpha_{n}) P_{C}(x_{n}),$$

where

$$C_{n}:=\{x\in H: h_{n}(x)\le 0\}$$

and

$$ h_{n}(x)=\langle x_{n}-y_{n}-\lambda_{n} (Ax_{n}-Ay_{n}),x-y_{n}\rangle. $$

Assume that Conditions 1–4 hold. Then the sequence {x_n} converges strongly top ∈ VI(C, A), wherep = P_{VI(C, A)}x₁.

4 Numerical illustrations

Some numerical implementations of our proposed methods in this paper are provided in this section. We give the test examples both in finite-dimensional and infinite-dimensional Hilbert spaces and give numerical comparisons in all cases.

In the first two examples, we consider test examples in finite dimensional and implement our proposed Algorithm 3.1. We compare our method with Algorithm 1 of Iusem [19] (Iusem Alg. 1.1).

Example 4.1

Let us consider VIP (1) with

$$ \begin{array}{@{}rcl@{}} A(x)= \left[ \begin{array}{c} ({x_{1}^{2}}+(x_{2}-1)^{2})(1+x_{2}) \\ \\ -{x_{1}^{3}}-x_{1}(x_{2}-1)^{2} \end{array} \right] \end{array} $$

and

$$C:=\{x \in \mathbb{R}^{2}:-10 \leq x_{i} \leq 10, i=1,2\}.$$

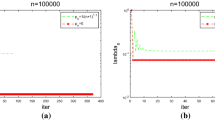
This VIP has unique solution x^∗ = (0,− 1)^T. It is easy to see that A is not a monotone map on C. However, using the Monte Carlo approach (see [18]), it can be shown that A is pseudo-monotone on C. Let x₁ be the initial point be randomly generated vector in C, l = 0.1, γ = 2. We terminate the iterations if ∥x_n − y_n∥₂ ≤ ε with ε = 10^− 3, ∥.∥₂ is the Euclidean norm on $\mathbb {R}^{2}$. The results are listed in Table 1 and Figs. 1, 2, 3, and 4 below. We consider different values of μ (Table 2).

Table 1 Example 1 comparison: proposed alg. 3.2 vs Iusem alg. 1.1

Fig. 1

Example 1 comparison with μ = 0.1

Fig. 2

Example 1 comparison with μ = 0.5

Fig. 3

Example 1 comparison with μ = 0.7

Fig. 4

Example 1 comparison with μ = 0.9

Table 2 Example 1: comparison of the inner loop to obtain λ_n

Example 4.2

Consider VIP (1) with

$$ \begin{array}{@{}rcl@{}} A(x)= \left[ \begin{array}{c} 0.5x_{1}x_{2}-2x_{2}-10^{7}\\ \\ -4x_{1}+0.1{x_{2}^{2}}-10^{7} \end{array} \right] \end{array} $$

and

$$C:=\{x \in \mathbb{R}^{2}:(x_{1}-2)^{2}+(x_{2}-2)^{2}\leq 1\}.$$

Then A is not monotone on C but pseudo-monotone (see [18]). Furthermore, the VIP (1) has a unique solution x^∗ = (2.707,2.707)^T. Take l = 0.1, γ = 3, and μ = 0.2. We terminate the iterations if ∥x_n − y_n∥₂ ≤ ε with ε = 10^− 2. The results are listed in Table 3 and Figs. 5, 6, 7, and 8 below. We consider different choices of initial point x₁ in C.

Table 3 Example 2 Comparison: proposed alg. 3.2 vs Iusem alg. 1.1

Fig. 5

Example 2 comparison with x₁ = (1.5,1.7)^T

Fig. 6

Example 2 comparison with x₁ = (2,3)^T

Fig. 7

Example 2 comparison with x₁ = (2,1)^T

Fig. 8

Example 2 comparison with x₁ = (2.7,2.6)^T

Next, we give the following two examples in infinite-dimensional spaces to illustrate our proposed Algorithm 2. Here, we compare our proposed Algorithm 2 with the method proposed by Vuong and Shehu in [46] with $\alpha _{n}=\frac {1}{n+1}$.

Example 4.3

Consider H := L²([0,1]) with inner product $\langle x,y\rangle :={{\int }_{0}^{1}} x(t)y(t)dt$ and norm $\|x\|_{2}:=({{\int }_{0}^{1}} |x(t)|^{2}dt)^{\frac {1}{2}}$. Suppose C := {x ∈ H : ∥x∥₂ ≤ 2}. Let $g: C\rightarrow \mathbb {R}$ be defined by

$$g(u):=\frac{1}{1+\|u\|_{2}^{2}}.$$

Observe that g is L_g-Lipchitz continuous with $L_{g}=\frac {16}{25}$ and $\frac {1}{5}\leq g(u)\leq 1, \forall u \in C$. Define the Volterra integral mapping F : L²([0,1]) → L²([0,1]) by

$$ F(u)(t):={{\int}_{0}^{t}} u(s)ds, \forall u \in L^{2}([0,1]), t \in [0,1]. $$

Then F is bounded linear monotone (see Exercise 20.12 of [4]). Now, define A : C → L²([0,1]) by

$$A(u)(t):=g(u)F(u)(t), \forall u \in C, t \in [0,1].$$

As given in [37], A is pseudo-monotone mapping but not monotone since

$$\langle Av-Au,v-u\rangle=-\frac{3}{10}<0$$

with v = 1 and u = 2.

Take l = 0.015, γ = 3 and μ = 0.1 (Table 4). We terminate the iterations if ∥x_n − P_C(x_n − A(x_n))∥₂ ≤ ε with ε = 10^− 2. The results are listed in Table 5 and Figs. 9, 10 ,and 11 below. We consider different choices of initial point x₁ in C (Table 6).

Table 4 Example 2: comparison of the inner loop to obtain λ_n

Table 5 Example 3 comparison: proposed alg. 3.3 vs Vuong and Shehu alg.

Fig. 9

Example 3 comparison with $x_{1}=\frac {\sin (t)}{6}$

Fig. 10

Example 3 comparison with $x_{1}=\frac {5}{29}t$

Fig. 11

Example 3 comparison with $x_{1}=\frac {\cos (t)}{7}$

Table 6 Example 3: Comparison of the inner loop to obtain λ_n

Example 4.4

Take

$$H:=L^{2}([0,1])\qquad \text{and}\qquad C:=\{x \in H:\|x\|_{2}\leq 2\}.$$

Define A : L²([0,1]) → L²([0,1]) by

$$A(u)(t):=e^{-\|u\|_{2}}{{\int}_{0}^{t}} u(s)ds, \forall u \in L^{2}([0,1]), t \in [0,1].$$

It can also be shown that A is pseudo-monotone but not monotone on H.

Take l = 0.015, γ = 4, and μ = 0.1. We terminate the iterations if ∥x_n − P_C(x_n − A(x_n))∥₂ ≤ ε with ε = 10^− 2. The results are listed in Table 7 and Figs. 12, 13, and 14 below. We consider different choices of initial point x₁ in C.

Table 7 Example 4 comparison: proposed alg. 3.3 vs Vuong and Shehu alg.

Fig. 12

Example 4 comparison with $x_{1}=\frac {\sin (t)}{6}$

Fig. 13

Example 4 comparison with $x_{1}=\frac {5}{29}t$

Fig. 14

Example 4 comparison with $x_{1}=\frac {\cos (t)}{7}$

Remark 4.5

• 1. Our proposed algorithms are efficient and easy to implement evident from many examples provided above.

• 2. We observe that the choices of initial point x₁ and μ have no significant effect on the number of iterations and the CPU time required to reach the stopping criterion. See all the examples above.

• 3. Clearly from the numerical examples presented above, our proposed algorithms outperformed Algorithm 1 proposed by Iusem both in the number of iterations and CPU time required to reach the stopping criterion. The same observation is seen when compared with the algorithm proposed by Vuong and Shehu in [46].

• 4. Furthermore, comparison of our proposed algorithms 3.2 and 3.3 are made with both algorithms proposed by Iusem and Vuong and Shehu using the inner loop to obtain λ_n, see Tables 2, 4, 6, and 8. Again, we could observe great advantages of our proposed algorithms over others.

Table 8 Example 4: comparison of the inner loop to obtain λ_n

5 Conclusions

We obtain weak and strong convergence of two projection-type methods for solving VIP under pseudo-monotonicity and non-Lipschitz continuity of the VI-associated mapping A. These two properties emphasize the applicability and advantages over several existing results in the literature. Numerical experiments performed in both finite- and infinite-dimensional spaces real Hilbert spaces show that our proposed methods outperform some already known methods for solving VIP in the literature.