Weak convergence of iterative methods for solving quasimonotone variational inequalities

Abstract

In this work, we introduce self-adaptive methods for solving variational inequalities with Lipschitz continuous and quasimonotone mapping(or Lipschitz continuous mapping without monotonicity) in real Hilbert space. Under suitable assumptions, the convergence of algorithms are established without the knowledge of the Lipschitz constant of the mapping. The results obtained in this paper extend some recent results in the literature. Some preliminary numerical experiments and comparisons are reported.

1 Introduction

Let C be a nonempty closed and convex set in a real Hilbert space H and $F: H\longrightarrow H$ is a continuous mapping, $\langle \cdot , \cdot \rangle$ and $\parallel \cdot \parallel$ denote the inner product and the induced norm in H, respectively. The variational inequality (VI(C, F)) is

$$\begin{aligned} {\text {find}} \quad x^*\in C \quad {\text {such that}} \quad \langle F(x^*),y-x^*\rangle \ge 0, \quad \forall y\in C. \end{aligned}$$

(1)

Weak converge of the sequence $\{{x_n}\}$ to a point x is denoted by $x_n\rightharpoonup x$ while $x_n\rightarrow x$ to denote the sequence $\{{x_n}\}$ converges strongly to x. Let S be the solution set of (1) and $S_D$ be the solution set of the following problem,

$$\begin{aligned} {\text {find}} \quad x^*\in C \quad {\text {such that}} \quad \langle F(y),y-x^*\rangle \geqslant 0, \quad \forall y\in C. \end{aligned}$$

(2)

It is obvious that $S_D$ is a closed convex set (possibly empty). As F is continuous and C is convex, we get

$$\begin{aligned} S_D\subseteq S. \end{aligned}$$

(3)

If F is a pseudomonotone and continuous mapping, then $S=S_D$(see Lemma 2.1 in [1]). The inclusion $S\subset S_D$ is false, if F is a quasimonotone and continuous mapping [2]. For solving quasimonotone variational inequalities, the convergence of interior proximal algorithm [3, 4] was obtained under more assumptions than $S_D\ne \emptyset$. Under the assumption of $S_D\ne \emptyset$, Ye and He [2] proposed a double projection algorithm for solving quasimonotone (or without monotonicity) variational inequalities in $R^n$. For a nonempty closed and convex set $C\subseteq H$, $P_C$ is called the projection from H onto C, that is, for every element $x\in H$ such that $\Vert x-P_C(x)\Vert =min\{{\parallel y-x \parallel \mid y\in C }\}$. It is easy to check that problem (1) is equivalent to the following fixed point problem:

$$\begin{aligned} {\text {find}} \quad x^*\in C \quad {\text {such that}} \quad x^*=P_C(x^*-\lambda F(x^*)) \end{aligned}$$

(4)

for any $\lambda >0$. Various projection algorithms have been proposed and analyzed for solving variational inequalities [2, 5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Among them, the extragradientmethod was proposed by Korpelevich [5] and Antipin [18], that is

$$\begin{aligned} y_n=P_C(x_n-\lambda F(x_n)),\quad x_{n+1}=P_C(x_n-\lambda F(y_n)), \end{aligned}$$

(5)

where $\lambda \in (0,\frac{1}{L})$ and L is the Lipschitz constant of F. Tseng [8] modified the extragradient method with the following method

$$\begin{aligned} y_n=P_C(x_n-\lambda F(x_n)), \quad x_{n+1}=y_n+\lambda ( F(x_n)-F(y_n)), \end{aligned}$$

(6)

where $\lambda \in (0,\frac{1}{L})$. Recently, Censor et al.[7] introduced the following subgradient extragradient algorithm

$$\begin{aligned} y_n=P_C(x_n-\lambda F(x_n)),\quad x_{n+1}=P_{T_{n}}(x_n-\lambda F(y_n)), \end{aligned}$$

(7)

where $T_{n}=\{x\in H|\langle x_n-\lambda F(x_n)-y_{n},x-y_{n} \rangle \le 0\}$ and $\lambda \in (0,\frac{1}{L})$. In the original papers, the methods (5), (6) and (7) were applied for solving monotone variational inequalities. It is known that these methods can be applied for solving pseudomonotone variational inequalities in infinite dimensional Hilbert spaces [22]. Very recently, Yang et al. [19,20,21] proposed modifications of gradient methods for solving monotone variational inequalities with the new step size rules. But the step sizes are non-increasing and the algorithms [19,20,21] may depend on the choice of initial step size. The natural question is whether the gradient algorithms still hold using nonmonotonic step sizes for solving quasimonotone variational inequalities (or without monotonicity). The goal of this paper is to give an answer to this question.

The paper is organized as follows. In Sect. 2 , we first give some preliminaries that will be needed in the sequel. In Sect. 3 , we present algorithms and analyze their convergence. Finally, in Sect. 4 we provides numerical examples and comparisons.

2 Preliminaries

In this section, we give some concepts and results for further use.

Definition 2.1

A mapping $F : H \longrightarrow H$ is said to be as follows:

• (a) $\gamma$-strongly monotone on H if there exists a constant $\gamma >0$ such that

  $$\begin{aligned} \langle F(x)-F(y), x-y\rangle \ge \gamma \parallel x-y \parallel ^2,\ \ \forall x, y\in H. \end{aligned}$$

  (8)

• (b) monotone on H if

  $$\begin{aligned} \langle F(x)-F(y), x-y\rangle \ge 0,\ \ \forall x, y\in H. \end{aligned}$$

  (9)

• (c) pseudomonotone on H, if

  $$\begin{aligned} \langle F(y),x-y\rangle \ge 0 \Rightarrow \langle F(x),x-y\rangle \ge 0, \quad \forall x, y\in H. \end{aligned}$$

  (10)

• (d) quasimonotone on H, if

  $$\begin{aligned} \langle F(y),x-y\rangle >0 \Rightarrow \langle F(x),x-y\rangle \ge 0, \forall x, y\in H. \end{aligned}$$

  (11)

• (e) Lipschitz-continuous on H, if there exists $L>0$ such that

  $$\begin{aligned} \parallel F(x)-F(y) \parallel \le L\parallel x-y \parallel ,\ \ \forall x, y\in H. \end{aligned}$$

  (12)

From the above definitions, we see that $(a)\Rightarrow (b)\Rightarrow (c)\Rightarrow (d)$. But the converses are not true.

In this paper, we assume that the following conditions hold

(A1):

$S_D\ne \emptyset .$

(A2):

The mapping F is Lipschitz-continuous with constant $L>0$.

(A3):

The mapping F is sequentially weakly continuous, i.e., for each sequence $\{x_n\}$: $\{x_n\}$ converges weakly to x implies $\{F(x_n)\}$ converges weakly to F(x).

(A4):

The mapping F is quasimonotone on H.

$(A4^{\prime })$:

If $x_n\rightharpoonup {\overline{x}}$ and $\limsup \nolimits _{n\rightarrow \infty }\langle F(x_n),x_n\rangle \le \langle F({\overline{x}}),{\overline{x}}\rangle$, then $\lim \limits _{n\rightarrow \infty }\langle F(x_n),x_n\rangle = \langle F({\overline{x}}),{\overline{x}}\rangle$.

(A5):

The set $A=\{z\in C: F(z)=0\}\setminus S_D$ is a finite set.

$(A5^{\prime })$:

The set $B=S\setminus S_D$ is a finite set.

Remark 2.1

• (i) If $x_n\rightharpoonup {\overline{x}}$ and the function $g(x)=\langle F(x),x\rangle$ is weak lower semicontinuous(i.e., $\liminf \limits _{n\rightarrow \infty }\langle F(x_n),x_n\rangle \ge \langle F({\overline{x}}),{\overline{x}}\rangle$ for every sequence $\{x_n\}$ converges weakly to ${\overline{x}}$), then F satisfies $(A4^{\prime })$.

• (ii) If $x_n\rightharpoonup {\overline{x}}$ and F is sequentially weakly-strongly continuous( i.e., $x_n\rightharpoonup {\overline{x}} \Rightarrow F(x_n)\rightarrow F({\overline{x}})$), then F satisfies $(A4^{\prime })$. Indeed, since $x_n\rightharpoonup {\overline{x}}$ and F is sequentially weakly-strongly continuous, we obtain $\lim \limits _{n\rightarrow \infty }\langle F({\overline{x}}), x_n\rangle =\langle F({\overline{x}}), {\overline{x}}\rangle$ and $\lim \limits _{n\rightarrow \infty }\Vert F(x_n)-F({\overline{x}}) \Vert =0$. Thus, we have

  $$\begin{aligned}&\lim \limits _{n\rightarrow \infty }(\langle F(x_n), x_{n}\rangle -\langle F({\overline{x}}), {\overline{x}}\rangle )=\lim \limits _{n\rightarrow \infty }\langle F(x_n)-F({\overline{x}}),x_{n}\rangle \\&\quad +\lim \limits _{n\rightarrow \infty }(\langle F({\overline{x}}), x_{n}\rangle -\langle F({\overline{x}}), {\overline{x}}\rangle )=0. \end{aligned}$$

  That is, $\limsup \nolimits _{n\rightarrow \infty }\langle F(x_n),x_n\rangle =\lim \limits _{n\rightarrow \infty }\langle F(x_n), x_{n}\rangle =\langle F({\overline{x}}), {\overline{x}}\rangle .$

• (iii) If $x_n\rightharpoonup {\overline{x}}$ and F is sequentially weakly continuous and monotone mapping, we get

  $$\begin{aligned} \langle F(x_n)-F({\overline{x}}), x_n-{\overline{x}}\rangle \ge 0. \end{aligned}$$

  Which means that

  $$\begin{aligned} \langle F(x_n), x_n\rangle \ge \langle F(x_n), {\overline{x}}\rangle +\langle F({\overline{x}}), x_n\rangle -\langle F({\overline{x}}), {\overline{x}}\rangle . \end{aligned}$$

  Let $n\rightarrow \infty$ in the last inequality, we have $\limsup \nolimits _{n\rightarrow \infty }\langle F(x_n),x_n\rangle \ge \langle F({\overline{x}}), {\overline{x}}\rangle .$ We have F satisfies $(A4^{\prime })$.

Remark 2.2

If $intC\ne \emptyset$, F is a continuous and quasimonotone mapping, then the condition (A5) is equivalent to $(A5^{\prime })$. It is easy to see that $(A5^{\prime })\Rightarrow (A5)$. On the other hand, from $intC\ne \emptyset$, we obtain $\{z\in C: F(z)=0\}=\{z\in C: \langle F(z), y-z\rangle =0, \forall y\in C\}$(see Theorem 2.1 in [2]). Since F is a continuous and quasimonotone mapping, we have $S\setminus \{z\in C: \langle F(z), y-z\rangle =0, \forall y\in C\}\subset S_D$ (see Lemma 2.7 in [2]). Hence $S\setminus \{z\in C: F(z)=0\}\subset S_D\subset S.$ It follow that $S\setminus S_D\subset \{z\in C: F(z)=0\}\setminus S_D.$ By (A5), we get $\{z\in C: F(z)=0\}\setminus S_D$ is a finite set. This implies that (A5′) holds.

Lemma 2.1

[2] If either

• (i) F is pseudomonotone on C and $S\ne \emptyset$;

• (ii) F is the gradient of G, where G is a differentiable quasiconvex function on anopen set $K \supset C$and attains its global minimum on C;

• (iii) F is quasimonotone on C, $F \ne 0$on C and C is bounded;

• (iv) F is quasimonotone on C, $F \ne 0$on C and there exists a positive number r such that, for every $x \in C$with $\Vert x\Vert \ge r$, there exists $y \in C$such that $\Vert y\Vert \le r$and $\langle F(x), y-x\rangle \le 0;$

• (v) F is quasimonotone on C, intC is nonempty and there exists $x^* \in S$such that $F(x^*)\ne 0$. Then $S_D$is nonempty.

Proof

See Proposition 2.1 in [2] and Proposition 1 in [28]. $\square$

Lemma 2.2

Let C be a nonempty, closed and convex set in H and $x \in H$. Then

$$\begin{aligned} \ \langle P_Cx-x, y-P_Cx\rangle \ge 0,\ \ \forall y\in C. \end{aligned}$$

Lemma 2.3

(Opial) For any sequence $\{{x_n}\}$in H such that $x_n\rightharpoonup x$, then

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\Vert x_n-x\Vert <\liminf \limits _{n\rightarrow \infty }\Vert x_n-y\Vert ,\ \ \forall y\ne x. \end{aligned}$$

(13)

3 Main results

First, we give a iterative algorithm for solving variational inequality.

Algorithm 3.1

(Step 0) Take $\lambda _0>0$, $x_0\in H,$$0<\mu <1$. Choose a nonnegative real sequence $\{p_n\}$ such that $\sum _{n=0}^\infty p_n<+\infty$.

(Step 1) Given the current iterate $x_n$, compute

$$\begin{aligned} y_{n}=P_C(x_n-\lambda _n F(x_n)). \end{aligned}$$

(14)

If $x_n = y_n$ (or $F(y_n)=0$), then stop: $y_n$ is a solution. Otherwise,

(Step 2) Compute

$$\begin{aligned} x_{n+1}=y_n+\lambda _n(F(x_n)-F(y_n)) \end{aligned}$$

(15)

and

$$\begin{aligned} \ \lambda _{n+1}= {\left\{ \begin{array}{ll} min\left\{ {\frac{\mu \Vert x_n-y_n\Vert }{\Vert F(x_n)-F(y_n)\Vert },\lambda _n+p_n }\right\} , &\quad if\quad F(x_n)-F(y_n)\ne 0, \\ \lambda _n+p_n,&\quad otherwise. \\ \end{array}\right. } \end{aligned}$$

(16)

Set $n := n + 1$ and return to step 1.

Remark 3.1

If Algorithm 3.1 stops in a finite step of iterations, then $y_n$ is a solution of the variational inequality. So in the rest of this section, we assume that the Algorithm 3.1 does not stop in any finite iterations, and hence generates an infinite sequence.

Remark 3.2

In numerical experiments, the condition A5(or $A5^{\prime }$) does not need to be considered. Indeed, if $\Vert y_n-x_n\Vert <\epsilon$, Algorithm 3.1 terminates in a finite step of iterations. In the process of proving the conclusion $\lim \limits _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0$, the condition A5(or $A5^{\prime }$) is not used (see(26) in Lemma 3.2).

Lemma 3.1

Let $\{\lambda _n\}$be the sequence generated by Algorithm 3.1. Then we get $\lim \limits _{n\rightarrow \infty }\lambda _n=\lambda$and $\lambda \in [ \min \{{\frac{\mu }{L },\lambda _0 }\},\lambda _0+P].$Where $P=\sum _{n=0}^\infty p_n.$

Proof

Since F is Lipschitz-continuous with constant $L>0$, in the case of $F(y_n)-F(x_n)\ne 0$, we get

$$\begin{aligned} \frac{\mu \Vert x_n-y_n\Vert }{\Vert F(x_n)-F(y_n)\Vert }\ge \frac{\mu \Vert x_n-y_n\Vert }{L\Vert x_n-y_n\Vert }=\frac{\mu }{L}. \end{aligned}$$

(17)

By the definition of $\lambda _{n+1}$ and mathematical induction, then the sequence $\{\lambda _n\}$ has upper bound $\lambda _0+P$ and lower bound $\min \{{\frac{\mu }{L },\lambda _0 }\}$. Let $(\lambda _{n+1}-\lambda _{n})^+= \max \{0, \lambda _{n+1}-\lambda _{n}\}$ and $(\lambda _{n+1}-\lambda _{n})^-= \max \{0, -(\lambda _{n+1}-\lambda _{n})\}$. From the definition of $\{\lambda _n\}$, we have

$$\begin{aligned} \sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^+\le \sum _{n=0}^\infty p_n<+\infty . \end{aligned}$$

(18)

That is, the series $\sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^+$ is convergence. Next we prove the convergence of the series $\sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^-$. Assume that $\sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^- =+\infty$. From the fact that

$$\begin{aligned} \lambda _{n+1}-\lambda _{n}=(\lambda _{n+1}-\lambda _{n})^+-(\lambda _{n+1}-\lambda _{n})^- , \end{aligned}$$

(19)

we get

$$\begin{aligned} \lambda _{k+1}-\lambda _{0}=\sum _{n=0}^k(\lambda _{n+1}-\lambda _{n})=\sum _{n=0}^k(\lambda _{n+1}- \lambda _{n})^+-\sum _{n=0}^k(\lambda _{n+1}-\lambda _{n})^- . \end{aligned}$$

(20)

Taking $k\rightarrow +\infty$ in (20), we have $\lambda _{k}\rightarrow -\infty (k\rightarrow \infty )$. That is a contradiction. From the convergence of the series $\sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^+$ and $\sum _{n=0}^\infty (\lambda _{n+1}-\lambda _{n})^-$, taking $k\rightarrow +\infty$ in (20), we obtain $\lim \limits _{n\rightarrow \infty }\lambda _n=\lambda .$ Since $\{\lambda _n\}$ has the lower bound $\min \{{\frac{\mu }{L },\lambda _0 }\}$ and the upper bound $\lambda _0+P$, we have $\lambda \in [ \min \{{\frac{\mu }{L },\lambda _0 }\},\lambda _0+P].$$\square$

Remark 3.3

The step size in Algorithm 3.1 is allowed to increase from iteration to iteration and so Algorithm 3.1 reduces the dependence on the initial step size $\lambda _0$. Since the sequence $\{p_n\}$ is summable, we get $\lim \limits _{n\rightarrow \infty }p_n=0.$ So the step size $\lambda _n$ may non-increasing when n is large. If $p_n\equiv 0,$ then the step size in Algorithm 3.1 is similar to the methods in [19, 21].

Lemma 3.2

Under the conditions (A1) and (A2). Then the sequence $\{x_n\}$generated by Algorithm 3.1is bounded and $\lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0$.

Proof

Let $u\in S_D,$ since $x_{n+1}=y_n+\lambda _n(F(x_n)-F(y_n))$, we obtain

$$\begin{aligned}&\Vert x_{n+1}-u\Vert ^2=\Vert y_n-\lambda _n(F(y_n)-F(x_n))-u\Vert ^2\nonumber \\&\quad =\Vert y_n-u\Vert ^2+\lambda _n^2\Vert F(y_n)-F(x_n)\Vert ^2-2\lambda _n\langle F(y_n)-F(x_n),y_n-u\rangle \nonumber \\&\quad =\Vert x_n-u\Vert ^2+\Vert y_n-x_n\Vert ^2+2\langle y_n-x_n,x_n-u\rangle \nonumber \\&\qquad +\lambda _n^2\Vert F(y_n)-F(x_n)\Vert ^2-2\lambda _n\langle F(y_n)-F(x_n),y_n-u\rangle \nonumber \\&\quad =\Vert x_n-u\Vert ^2+\Vert y_n-x_n\Vert ^2-2\langle y_n-x_n,y_n-x_n\rangle +2\langle y_n-x_n,y_n-u\rangle \nonumber \\&\qquad +\lambda _n^2\Vert F(y_n)-F(x_n)\Vert ^2-2\lambda _n\langle F(y_n)-F(x_n),y_n-u\rangle . \end{aligned}$$

(21)

Note that $y_{n}=P_C(x_n-\lambda _n F(x_n))$ and $u\in S_D\subseteq S\subseteq C$, by Lemma 2.2, we obtain $\langle y_n-x_n+\lambda _n F(x_n),y_n-u\rangle \le 0.$ It follows that

$$\begin{aligned} \langle y_n-x_n,y_n-u\rangle \le -\lambda _n \langle F(x_n),y_n-u\rangle . \end{aligned}$$

(22)

Using $y_n\in C$ and $u\in S_D,$ we get $\langle F(y_n),y_n-u\rangle \ge 0, \ \forall n\ge 0.$ From (16), (21) and (22), we have

$$\begin{aligned} \Vert x_{n+1}-u\Vert ^2\le & {} \Vert x_n-u\Vert ^2-\Vert y_n-x_n\Vert ^2-2\lambda _n \langle F(x_n),y_n-u\rangle \nonumber \\&+\lambda _n^2\Vert F(y_n)-F(x_n)\Vert ^2-2\lambda _n\langle F(y_n)-F(x_n),y_n-u\rangle \nonumber \\= & {} \Vert x_n-u\Vert ^2-\Vert y_n-x_n\Vert ^2+\lambda _n^2\Vert F(y_n)-F(x_n)\Vert ^2-2\lambda _n\langle y_n-u,F(y_n) \rangle \nonumber \\\le & {} \Vert x_n-u\Vert ^2-\Vert y_n-x_n\Vert ^2+\lambda _n^2\frac{\mu ^2}{\lambda _{n+1}^2}\Vert y_n-x_n\Vert ^2. \end{aligned}$$

(23)

Since

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left( 1-\lambda _n^2\frac{\mu ^2}{\lambda _{n+1}^2}\right) =1-\mu ^2>0, \end{aligned}$$

(24)

we obtain $\exists N\ge 0, \ \forall n\ge N,$ such that $1-\lambda _n^2\frac{\mu ^2}{\lambda _{n+1}^2}>0$.

It implies that $\forall n\ge N,$$\Vert x_{n+1}-u\Vert \le \Vert x_n-u\Vert .$ This implies that $\{x_n\}$ is bounded and $\lim \limits _{n\rightarrow \infty }\Vert x_n-u \Vert$ exists. Returning to (23), we have

$$\begin{aligned} \left( 1-\lambda _n^2\frac{\mu ^2}{\lambda _{n+1}^2}\right) \Vert y_n-x_{n}\Vert ^2 \le \Vert x_{n}-u\Vert ^2-\Vert x_{n+1}-u\Vert ^2. \end{aligned}$$

(25)

This implies that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0. \end{aligned}$$

(26)

Observe that

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert&=\Vert y_n+\lambda _n(F(x_n)-F(y_n))-x_n\Vert \\&\le \Vert y_n-x_n\Vert +(\lambda _0+P)L\Vert y_n-x_n\Vert , \end{aligned}$$

we obtain $\lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$$\square$

Remark 3.4

We note that the quasimonotonicity of the mapping is not used in the proof of the Lemma 3.2. In finite dimensional Hilbert space, under the conditions (A1) and (A2), then all the accumulation points of $\{x_n\}$ belong to S. Indeed, the existence of the accumulation points can be obtained by boundedness of the $\{x_n\}$. If $x^*$ is an accumulation point of $\{x_n\}$, then there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ that converges to some $x^*\in C.$ In view of the fact that $y_{{n_k}}=P_C(x_{n_k}-\lambda _{n_k} F(x_{n_k}))$ and the continuity of F, we get

$$\begin{aligned} x^*=\lim \limits _{k\rightarrow \infty }y_{{n_k}}=\lim \limits _{k\rightarrow \infty }P_C(x_{n_k}-\lambda _{n_k} F(x_{n_k}))=P_C(x^*-\lambda F(x^*)). \end{aligned}$$

We deduce from (4) that $x^*\in S$.

Lemma 3.3

Assume that (A1)–(A4) hold. Let $\{x_n\}$be the sequence generated by Algorithm 3.1. Then at least one of the following must hold : $x^*\in S_D$ or $F(x^*)=0$. Where x* is one of the weak cluster point of {x_n}.

Proof

By Lemma 3.2, we have the sequence $\{x_n\}$ is bounded. Moreover, there exist a subsequence $\{x_{n_k}\}$ that converges weakly to $x^*\in H$. Using (26), we obtain $y_{n_k}\rightharpoonup x^*$ and $x^*\in C.$ We divide the following proof into two cases.

Case 1 If $\limsup \nolimits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert =0$, we have $\lim \limits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert =\liminf \limits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert =0$. Since $\{y_{n_k}\}$ converges weakly to $x^*\in C$ and F is sequentially weakly continuous on C, we have $\{F(y_{n_k})\}$ converges weakly to $F(x^*)$. Since the norm mapping is sequentially weakly lower semicontinuous, we have

$$\begin{aligned} 0\le \Vert F(x^*)\Vert \le \liminf \limits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert =0. \end{aligned}$$

We obtain $F(x^*)=0$.

Case 2 If $\limsup \nolimits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert >0$, without loss of generality, we take $\lim \limits _{k\rightarrow \infty }\Vert F(y_{n_k})\Vert =M>0$(Otherwise, we take a subsequence of $\{F(y_{n_k})\})$. That is, there exists a $K\in {\mathbb {N}}$ such that $\Vert F(y_{n_k})\Vert >\frac{M}{2}$ for all $k\ge K$. Since $y_{n_k}=P_C(x_{n_k}-\lambda _{n_k} F(x_{n_k}))$ and Lemma 2.2, we have

$$\begin{aligned} \langle y_{n_k}-x_{n_k}+\lambda _{n_k}F(x_{n_k}), z-y_{n_k}\rangle \ge 0, \quad \forall z\in C. \end{aligned}$$

That is

$$\begin{aligned} \langle x_{n_k}-y_{n_k}, z-y_{n_k}\rangle \le \lambda _{n_k}\langle F(x_{n_k}), z-y_{n_k}\rangle , \quad \forall z\in C. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \frac{1}{\lambda _{n_k}}\langle x_{n_k}-y_{n_k}, z-y_{n_k}\rangle -\langle F(x_{n_k})-F(y_{n_k}), z-y_{n_k}\rangle \le \langle F(y_{n_k}), z-y_{n_k}\rangle , \quad \forall z\in C. \end{aligned}$$

(27)

Fixing $z\in C$, let $k\rightarrow \infty$, using the facts $\lim \limits _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0$, $\{y_{n_k}\}$ is bounded and $\lim \limits _{k\rightarrow \infty }\lambda _{n_k}=\lambda >0,$ we obtain

$$\begin{aligned} 0\le \liminf \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle \le \limsup \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle <+\infty . \end{aligned}$$

(28)

If $\limsup \nolimits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle >0$, there exists a subsequence $\{y_{n_{k_i}}\}$ such that $\lim \limits _{i\rightarrow \infty }\langle F(y_{n_{k_i}}), z-y_{n_{k_i}}\rangle > 0$. Then there exists an $i_0\in {\mathbb {N}}$ such that $\langle F(y_{n_{k_i}}), z-y_{n_{k_i}}\rangle > 0$ for all $i\ge i_0$. By the definition of quasidomonotone, we obtain $\forall i\ge i_0,$

$$\begin{aligned} \langle F(z),z-y_{n_{k_i}}\rangle \ge 0. \end{aligned}$$

Let $i\rightarrow \infty$, we get $x^*\in S_D.$

If $\limsup \nolimits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle =0$, we deduce from (28) that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle =\limsup \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle =\liminf \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle =0. \end{aligned}$$

Let $\varepsilon _k=|\langle F(y_{n_k}), z-y_{n_k}\rangle |+\frac{1}{k+1}$. This implies that

$$\begin{aligned} \langle F(y_{n_k}), z-y_{n_k}\rangle +\varepsilon _k>0. \end{aligned}$$

(29)

Let $z_{n_{k}}=\frac{F(y_{n_{k}})}{\Vert F(y_{n_{k}})\Vert ^2}$$(\forall k\ge K)$, we get $\langle F(y_{n_{k}}), z_{n_{k}}\rangle =1$. Moreover, from (29), we have $\forall k>K,$

$$\begin{aligned} \langle F(y_{n_{k}}), z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\rangle > 0. \end{aligned}$$

By the definition of quasidomonotone, we obtain $\forall k>K,$

$$\begin{aligned} \langle F(z+\varepsilon _kz_{n_{k}}), z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\rangle \ge 0. \end{aligned}$$

(30)

This implies that $\forall k>K,$

$$\begin{aligned} \langle F(z), z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\rangle= & {} \langle F(z)-F(z+\varepsilon _kz_{n_{k}}), z+\varepsilon _kz_{n_{k}}\nonumber \\&-y_{n_{k}}\rangle +\langle F(z+\varepsilon _kz_{n_{k}}), z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\rangle \nonumber \\\ge & {} \langle F(z)-F(z+\varepsilon _kz_{n_{k}}), z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\rangle \nonumber \\\ge & {} - \Vert F(z)-F(z+\varepsilon _kz_{n_{k}})\Vert \Vert z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\Vert \nonumber \\\ge & {} -\varepsilon _kL\Vert z_{n_{k}}\Vert \Vert z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\Vert \nonumber \\= & {} -\varepsilon _k\frac{L}{\Vert F(y_{n_{k}})\Vert }\Vert z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\Vert \nonumber \\\ge & {} -\varepsilon _k\frac{2L}{M}\Vert z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\Vert . \end{aligned}$$

(31)

Let $k\rightarrow \infty$ in (31), using the fact $\lim \limits _{k\rightarrow \infty }\varepsilon _k=0$ and boundedness of $\{\Vert z+\varepsilon _kz_{n_{k}} -y_{n_{k}}\Vert \}$ , we get

$$\begin{aligned} \langle F(z), z -x^*\rangle \ge 0. \quad \forall z\in C. \end{aligned}$$

This implies that $x^*\in S_D.$$\square$

Lemma 3.4

Assume that $(A1)-(A5)$hold. Then the sequence $\{x_n\}$generated by Algorithm 3.1has finite weak cluster points in S.

Proof

First we prove $\{x_n\}$ has at most one weak cluster point in $S_D$.

Assume that $\{x_n\}$ has at least two weak cluster points $x^*\in S_D$ and ${\bar{x}}\in S_D$ such that $x^*\ne {\bar{x}}$. Let $\{x_{n_i}\}$ be a sequence such that $x_{n_i}\rightharpoonup {\bar{x}}$ as $i\rightarrow \infty$, noting the fact that $\lim \limits _{n\rightarrow \infty }\Vert x_n-u \Vert$ exists for all $u\in S_D$, by Lemma 2.3, we obtain

$$\begin{aligned}&\lim \limits _{n\rightarrow \infty }\Vert x_n-{\bar{x}}\Vert \nonumber \\&\quad = \lim \limits _{i\rightarrow \infty }\Vert x_{n_i}-{\bar{x}}\Vert =\liminf \limits _{i\rightarrow \infty }\Vert x_{n_i}-{\bar{x}}\Vert \nonumber \\&\quad<\liminf \limits _{i\rightarrow \infty }\Vert x_{n_i}-x^*\Vert \ =\lim \limits _{n\rightarrow \infty }\Vert x_n-x^*\Vert =\lim \limits _{k\rightarrow \infty }\Vert x_{n_k}-x^*\Vert =\liminf \limits _{k\rightarrow \infty }\Vert x_{n_k}-x^*\Vert \nonumber \\&\quad <\liminf \limits _{k\rightarrow \infty }\Vert x_{n_k}-{\bar{x}}\Vert =\lim \limits _{n\rightarrow \infty }\Vert x_{n_k}-{\bar{x}}\Vert =\lim \limits _{n\rightarrow \infty }\Vert x_n-{\bar{x}}\Vert , \end{aligned}$$

(32)

which is impossible. Since $A=\{z\in C: F(z)=0\}\setminus S_D$ is a finite set, using Lemma 3.3, then $\{x_n\}$ has finite weak cluster points in S. $\square$

Lemma 3.5

Assume that (A1)–(A5) hold and $\{x_n\}$has finite weak cluster points $z^1,z^2,\ldots z^m$. Then There exists $N_1>N, \ \forall n\ge N_1,$such that $x_n\in B$. Where $B=\bigcup _{j=1}^mB^j$, $B^l=\bigcap _{j=1,j\ne l}^m\{x: \langle x, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\rangle >\epsilon _0 +\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }\}$and $\epsilon _0=min\{\frac{\Vert z^l-z^j\Vert }{4}: l,j\in \{1,2,\ldots ,m\}, l\ne j \}.$

Proof

Let $\{x_{n_i}^l\}$ be a subsequence of $\{x_n\}$ such that $x_{n_i}^l\rightharpoonup z^l$ as $\rightarrow \infty$, we get $\forall \ j\ne l$

$$\begin{aligned} \lim \limits _{i\rightarrow \infty }\langle x_{n_i}^l, z^l-z^j \rangle = \langle z^l, z^l-z^j \rangle . \end{aligned}$$

(33)

For $\ j\ne l$, one has

$$\begin{aligned} \langle z^l, z^l-z^j \rangle= & {} \Vert z^l\Vert ^2-\langle z^l, z^j \rangle =\frac{\Vert z^l-z^j\Vert ^2}{2}+\frac{\Vert z^l\Vert ^2}{2}-\frac{\Vert z^j\Vert ^2}{2}\nonumber \\> & {} \frac{\Vert z^l-z^j\Vert ^2}{4}+\frac{\Vert z^l\Vert ^2}{2}-\frac{\Vert z^j\Vert ^2}{2}. \end{aligned}$$

(34)

This implies that $\forall \ j\ne l$

$$\begin{aligned} \left\langle z^l, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\right\rangle >\frac{\Vert z^l-z^j\Vert }{4}+\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }. \end{aligned}$$

(35)

From (33) and (35), when i is sufficiently large, we have $x_{n_i}^l\in \{x: \langle x, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\rangle >\frac{\Vert z^l-z^j\Vert }{4}+\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }\}$. Therefore, when i is sufficiently large, we have

$$\begin{aligned} x_{n_i}^l\in B^l , \end{aligned}$$

where

$$\begin{aligned} B^l=\bigcap _{j=1,j\ne l}^m\left\{ x: \left\langle x, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\right\rangle >\epsilon _0 +\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }\right\} \end{aligned}$$

(36)

and $\epsilon _0=min\left\{ \frac{\Vert z^l-z^j\Vert }{4}: l,j\in \left\{ 1,2,\ldots ,m\right\} , l\ne j \right\} .$ It is obvious that

$$\begin{aligned} B^l=\bigcap _{j=1,j\ne l}^m\left\{ x: \left\langle -x, \frac{z^l-z^j }{\Vert z^j-z^l\Vert }\right\rangle <-\epsilon _0+\frac{\Vert z^j\Vert ^2-\Vert z^l\Vert ^2}{2\Vert z^l-z^j\Vert }\right\} . \end{aligned}$$

(37)

Set $B=\bigcup _{j=1}^mB^j$. Next we prove $x_n\in B$ for sufficiently large n. Assume that there exists $\left\{ x_{n_k}\right\}$ of $\left\{ x_n\right\}$ such that $x_{n_k}\not \in B$$(\forall k)$. Using the boundedness of the $\left\{ x_{n_k}\right\}$, there exists a subsequence of $x_{n_k}$ convergent weakly to ${\overline{z}}\in C$. Without loss of generality, we still denote the subsequence as $\left\{ x_{n_k}\right\}$, that is, $x_{n_k}\rightharpoonup {\overline{z}}$. Since $x_{n_k}\not \in B$, for $\forall l\in \left\{ 1,2,\ldots ,m\right\}$, we have

$$\begin{aligned} x_{n_k}\not \in B^l=\bigcap _{j=1,j\ne l}^m\left\{ x: \left\langle x, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\right\rangle >\epsilon _0+\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }\right\} . \end{aligned}$$

(38)

Using the principle of drawer, there exists subsequence $\left\{ x_{n_{k_i}}\right\}$ of $\left\{ x_{n_{k}}\right\}$ and $l_0\in \left\{ 1,2,\ldots ,m\right\} \backslash \left\{ l\right\}$ such that $\forall i\ge 0$

$$\begin{aligned} x_{n_{k_i}}\not \in \left\{ x: \left\langle x, \frac{z^l-z^{l_0} }{\Vert z^l-z^{l_0}\Vert }\right\rangle >\epsilon _0+\frac{\Vert z^l\Vert ^2-\Vert z^{l_0}\Vert ^2}{2\Vert z^l-z^{l_0}\Vert }\right\} , \ \end{aligned}$$

(39)

We have

$$\begin{aligned} {\overline{z}}\not \in \left\{ x: \left\langle x, \frac{z^l-z^{l_0} }{\Vert z^l-z^{l_0}\Vert }\right\rangle >\epsilon _0+\frac{\Vert z^l\Vert ^2-\Vert z^{l_0}\Vert ^2}{2\Vert z^l-z^{l_0}\Vert }\right\} . \end{aligned}$$

(40)

Combining (34), (40) and $\left\langle z^l, \frac{z^l-z^{l_0} }{\Vert z^l-z^{l_0}\Vert }\right\rangle >\frac{\Vert z^l-z^{l_0}\Vert }{4}+\frac{\Vert z^l\Vert ^2-\Vert z^{l_0}\Vert ^2}{2\Vert z^l-z^{l_0}\Vert } \ge \epsilon _0+\frac{\Vert z^l\Vert ^2-\Vert z^{l_0}\Vert ^2}{2\Vert z^l-z^{l_0}\Vert }$, we get ${\overline{z}}\ne z^l$. As l is arbitrary, we have ${\overline{z}}\not \in \left\{ z^1,z^2,\ldots z^m\right\}$, which is impossible. So we have $x_n\in B$ for sufficiently large n. That is, $\exists N_1>N, \ \forall n\ge N_1,$ such that $x_n\in B$. $\square$

Theorem 3.1

Assume that $(A1)-(A5)$hold. Let $\left\{ x_n\right\}$be a sequence generated by Algorithm 3.1. Then $\left\{ x_n\right\}$converges weakly to a point $x^*\in S$.

Proof

By Lemma 3.2, we have $\lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$ It follows that $\exists N_2>N_1>N, \ \forall n\ge N_2,$ such that $\Vert x_{n+1}-x_n\Vert <\epsilon _0$. Assume that $\left\{ x_n\right\}$ has more than one weak cluster point, from Lemma 3.5, then $\exists N_3\ge N_2>N_1>N,$ we have $x_{N_3} \in B^l$, $x_{{N_3}+1} \in B^j$. Where $l\ne j$, $l,j\in \left\{ 1,2,\ldots ,m\right\}$ and $m\ge 2.$ In particular, we have

$$\begin{aligned} \Vert x_{N_3+1}-x_{N_3}\Vert <\epsilon _0. \end{aligned}$$

(41)

Using (36) and (37), we get

$$\begin{aligned} x_{N_3}\in B^l=\bigcap _{j=1,j\ne l}^m\left\{ x: \left\langle x, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\right\rangle >\epsilon _0 +\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert }\right\} \end{aligned}$$

(42)

and

$$\begin{aligned} x_{{N_3}+1}\in B^j=\bigcap _{l=1,l\ne j}^m\left\{ x: \left\langle -x, \frac{z^j-z^l }{\Vert z^j-z^l\Vert }\right\rangle <-\epsilon _0+\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^j-z^l\Vert }\right\} . \end{aligned}$$

(43)

Moreover, we obtain

$$\begin{aligned} \left\langle x_{N_3}, \frac{z^l-z^j }{\Vert z^l-z^j\Vert }\right\rangle >\epsilon _0 +\frac{\Vert z^l\Vert ^2-\Vert z^j\Vert ^2}{2\Vert z^l-z^j\Vert } \end{aligned}$$

(44)

and

$$\begin{aligned} \left\langle -x_{{N_3}+1}, \frac{z^l-z^j }{\Vert z^j-z^l\Vert }\right\rangle >\epsilon _0+\frac{\Vert z^j\Vert ^2-\Vert z^l\Vert ^2}{2\Vert z^l-z^j\Vert }. \end{aligned}$$

(45)

Combining (44) and (45), we get

$$\begin{aligned} 2\epsilon _0<\left\langle x_{N_3}-x_{{N_3}+1}, \frac{z^l-z^j }{\Vert z^j-z^l\Vert }\right\rangle \le \Vert x_{N_3+1}-x_{N_3}\Vert <\epsilon _0. \end{aligned}$$

(46)

Which is impossible. This implies that $\{x_n\}$ has only a weak cluster point in S.

Hence we deduce that $x_n\rightharpoonup x^*$. $\square$

Now we prove the convergence of the Algorithm 3.1 without monotonicity.

Theorem 3.2

Assume that $(A1)-(A3)$, $(A4^{\prime })$and $(A5^{\prime })$hold. Let $\{x_n\}$be a sequence generated by Algorithm 3.1. Then $\{x_n\}$converges weakly to a point $x^*\in S$.

Proof

According to (28) and the proof in Lemma 3.3, fixing $z\in C$, we have $y_n\rightharpoonup x^*,$$x^*\in C$ and

$$\begin{aligned} \liminf \limits _{k\rightarrow \infty }\langle F(y_{n_k}), z-y_{n_k}\rangle \ge 0. \end{aligned}$$

We choose a positive sequence $\{\varepsilon _k\}$ such that $\lim \limits _{k\rightarrow \infty }\varepsilon _k=0$ and

$$\begin{aligned} \langle F(y_{n_k}), z-y_{n_k}\rangle +\varepsilon _k>0, \quad \forall k\ge 0. \end{aligned}$$

It follows that

$$\begin{aligned} \langle F(y_{n_k}), z\rangle +\varepsilon _k>\langle F(y_{n_k}), y_{n_k}\rangle , \quad \forall k\ge 0. \end{aligned}$$

(47)

In particular, set $z=x^*$ in (47), we have

$$\begin{aligned} \langle F(y_{n_k}), x^*\rangle +\varepsilon _k>\langle F(y_{n_k}), y_{n_k}\rangle , \quad \forall k\ge 0. \end{aligned}$$

Let $k\rightarrow \infty$ in the last inequality, from (A3) and $y_{n_k}\rightharpoonup x^*$, we obtain

$$\begin{aligned} \langle F(x^*), x^*\rangle \ge \limsup \limits _{k\rightarrow \infty }\langle F(y_{n_k}), y_{n_k}\rangle . \end{aligned}$$

From $(A4^{\prime })$, we get $\lim \limits _{n\rightarrow \infty }\langle F(y_{n_k}),y_{n_k}\rangle = \langle F(x^*),x^*\rangle$.

At the same time, from (47), we obtain

$$\begin{aligned} \langle F(x^*), z\rangle&=\lim \limits _{k\rightarrow \infty }(\langle F(y_{n_k}), z\rangle +\varepsilon _k)\\&\ge \liminf \limits _{k\rightarrow \infty }\langle F(y_{n_k}), y_{n_k}\rangle \\&=\lim \limits _{n\rightarrow \infty }\langle F(y_{n_k}),y_{n_k}\rangle =\langle F(x^*), x^*\rangle . \end{aligned}$$

which implies that

$$\begin{aligned} \langle F(x^*), z -x^*\rangle \ge 0. \quad \forall z\in C. \end{aligned}$$

We have $x^*\in S$. By the condition $(A5^{\prime })$, similar to the proof of Lemmas 3.4, 3.5 and Theorem 3.1, we get $\{x_n\}$ converges weakly to a point $x^*\in S$. $\square$

For the extragradient method and the subgradient extragradient, we introduce the following algorithms.

Algorithm 3.2

(Step 0) Take $\lambda _0>0$, $x_0\in H,$$\mu \in (0, 1)$. Choose a nonnegative real sequence $\{p_n\}$ such that $\sum _{n=0}^\infty p_n<+\infty$.

(Step 1) Given the current iterate $x_n$, compute

$$\begin{aligned} y_{n}=P_C(x_n-\lambda _n F(x_n)). \end{aligned}$$

If $x_n = y_n$(or $F(y_n)=0$), then stop: $y_n$ is a solution. Otherwise, go to Step 2.

(Step 2) Compute

$$\begin{aligned} x_{n+1}=P_{C}(x_n-\lambda _n F(y_n)). \end{aligned}$$

(Step 3) Compute

$$\begin{aligned} \lambda _{n+1}= {\left\{ \begin{array}{ll} min\left\{ {\frac{\mu (\Vert x_n-y_n\Vert ^2+\Vert x_{n+1}-y_n\Vert ^2)}{2\langle F(x_n)-F(y_n),x_{n+1}-y_n \rangle },\lambda _n+p_n }\right\} , &{} if\ \ \langle F(x_n)-F(y_n),x_{n+1}-y_n \rangle >0, \\ \lambda _n+p_n,&{} otherwise. \\ \end{array}\right. } \end{aligned}$$

Set $n := n + 1$ and return to step 1.

Algorithm 3.3

(Step 0) Take $\lambda _0>0$, $x_0\in H,$$\mu \in (0, 1)$. Choose a nonnegative real sequence $\{p_n\}$ such that $\sum _{n=0}^\infty p_n<+\infty$.

(Step 1) Given the current iterate $x_n$, compute

$$\begin{aligned} y_{n}=P_C(x_n-\lambda _n F(x_n)). \end{aligned}$$

If $x_n = y_n$(or $F(y_n)=0$), then stop: $y_n$ is a solution. Otherwise, go to Step 2.

(Step 2) Construct $T_{n}=\{x\in H|\langle x_n-\lambda _n F(x_n)-y_{n},x-y_{n} \rangle \le 0\}$ and compute

$$\begin{aligned} x_{n+1}=P_{T_{n}}(x_n-\lambda _n F(y_n)). \end{aligned}$$

(Step 3) Compute

$$\begin{aligned} \lambda _{n+1}= {\left\{ \begin{array}{ll} min\left\{ {\frac{\mu (\Vert x_n-y_n\Vert ^2+\Vert x_{n+1}-y_n\Vert ^2)}{2\langle F(x_n)-F(y_n),x_{n+1}-y_n \rangle },\lambda _n+p_n }\right\} , &\quad if\quad \langle F(x_n)-F(y_n),x_{n+1}-y_n \rangle >0, \\ \lambda _n+p_n,&\quad otherwise. \\ \end{array}\right. } \end{aligned}$$

Set $n := n + 1$ and return to step 1.

Remark 3.5

If $p_n\equiv 0,$ then the step sizes in Algorithms 3.2 and 3.3 are similar to the method in [20]. The conclusion in Theorems 3.1 and 3.2 still hold for Algorithms 3.2 and 3.3.

4 Numerical experiments

In this section, we compare the proposed methods with the Algorithm 2.1 in [2]. We choose $\mu =0.5$, $p_n=\frac{100}{(n+1)^{1.1}}$ and $\lambda _0=1$ for our algorithms. We choose $\gamma =0.4$ and $\sigma =0.99$ for Algorithm 2.1 in [2]. The stopping criterion are the following

• Algorithms 3.1, 3.2, 3.3    $\Vert y_n-x_n\Vert /\min \{\lambda _n,1\}\le \varepsilon$ and $\Vert F(y_n)\Vert \le \varepsilon$.    (45)

• Algorithm 2.1 in [2]   $\Vert x_n-z_n\Vert =\Vert x_n-P_C(x_n-F(x_n))\Vert \le \varepsilon$.    (46)

We do not use the criterion $\Vert x_n-P_C(x_n-F(x_n))\Vert \le \varepsilon$ and $\Vert F(y_n)\Vert \le \varepsilon$ for Algorithms 3.1, 3.2 and 3.3 because we do not want to compute $\Vert x_n-P_C(x_n-F(x_n))\Vert$ extra. If $\lambda _n<1$, we have

$$\begin{aligned} \Vert x_n-P_C(x_n-F(x_n))\Vert \le \Vert x_n-P_C(x_n-\lambda _nF(x_n))\Vert /\lambda _n=\Vert y_n-x_n\Vert /\min \{\lambda _n,1\}. \end{aligned}$$

(47)

If $\lambda _n\ge 1$, we have

$$\begin{aligned} \Vert x_n-P_C(x_n-F(x_n))\Vert \le \Vert x_n-P_C(x_n-\lambda _nF(x_n))\Vert =\Vert y_n-x_n\Vert /\min \{\lambda _n,1\}. \end{aligned}$$

(48)

Moreover, we notice that termination criteria (45) is stronger than (46). We denoted by $x_0$ the starting point of the experiment and by x the solution of the variational inequality. We also added the total number (nf) of all values F that is evaluated. For the test problems, we also have generated random samples with different choice of $x_0$ in C. For all algorithms, we take $\varepsilon =10^{-6}$.

Problem 1

Let $C=[-1,1]$ and

$$\begin{aligned}\ F(x)= {\left\{ \begin{array}{ll} 2x-1 , &\quad x>1, \\ x^2,&\quad x\in [-1,1], \\ -2x-1, &\quad x<-1. \end{array}\right. } \end{aligned}$$

Then F is a quasimonotone and Lipschitz continuous mapping. We have $S_D=\{-1\}$ and $S=\{-1,0\}$. The results are presented in Table 1. As we can see from Table 1, the number of iterations of our Algorithms is much smaller than Algorithm 2.1 in [2].

Table 1 Problem 1

Problem 2

Let $C =\{x \in R^2 : x_1^2 + x_2^2 \le 1, 0\le x_1 \}$ and $F(x_1, x_2)=(-x_1e^{x_2}, x_2)$. It is not difficulty to check that F is not a quasimonotone mapping. Indeed, take $x=(0,\frac{1}{4})$ and $y=(\frac{\sqrt{3}}{2},\frac{1}{2}),$ we have $\langle F(y), x-y \rangle =\frac{3}{4}e^{0.5}-\frac{1}{8}>0$ and $\langle F(x), x-y \rangle =-\frac{1}{16}<0.$ It’s easy to validate that $(1,0)\in S_D$. By the KKT conditions to the VI(C, F) and convexity of $S_D$, we have $S=\{(1,0),(0,0)\}$ and $(0,0)\notin S_D$. This problem is tested in Table 2. Tables 2 shows that our Algorithms work better.

Table 2 Problem 2

Problem 3

This problem was considered in [10, 29]. Let $C=[0,1]^m$ and

$$\begin{aligned} F(x)= & {} (f_1(x),f_2(x),\ldots ,f_m(x)),\\ f_i(x)= & {} x_{i-1}^2+x_{i}^2+x_{i-1}x_i+x_{i}x_{i+1}\\&-2x_{i-1}+4x_{i}+x_{i+1}-1, i=1,2,\ldots ,m, x_0=x_{m+1}=0. \end{aligned}$$

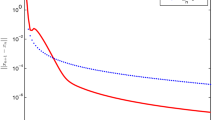
When n greater than 1000, we aborted the evaluation of Algorithm 2.1 in [2](Since it involves the calculation of quadratic programming). The results are presented in Tables 3 and 4. In this example, our Algorithms are faster than Algorithm 2.1 in [2]. In Fig. 1, we illustrate the behavior of the stepsisizes for this problem with $n=100000$.

Table 3 Problem 3

Table 4 Problem 3

Fig. 1

Comparison of different $p_n$ and $x_0=(0,0,\ldots ,0)$ with $\epsilon =10^{-6}$ for the Problem 3 with $n=100000$, (a): $\lambda _n$ for Algorithm 3.1; (b): $\lambda _n$ for Algorithm 3.2

5 Conclusions

In this paper, we consider convergence results for variational inequalities involving Lipschitz continuous quasimonotone mapping (or without monotonicity) but the Lipschitz constant is unknown. We modify the gradient methods with the new step sizes. Weak convergence theorems are proved for sequences generated by the Algorithms. Numerical experiments confirm the effectiveness of the proposed Algorithms.