1 Introduction

In the beginning, there was only Chaos, the Abyss…

Hesiod, “Theogony.”

The phenomenon of dynamical chaos and chaotic attractors was discovered by Lorenz in 1963 [1]. He was studying atmospheric convection when he made this discovery. In 1976, Hénon developed a simpler dynamical system with chaotic behavior [2]. This system is known as the Hénon map and is created by mapping explicit equations. In parallel with Hénon, Rössler was also involved in solving the problem of studying of dynamical systems with chaotic attractors. He acquired a dynamical system with a single nonlinear term in differential equations [3]. These differential equations simulate the chemical reaction processes. Further study of chaotic attractors in dynamical systems led to the discovery of Chua’s circuit [4, 5]. Chua’s circuit is typically used to study various chaotic attractors. This has been demonstrated in previous studies [6,7,8]. Sprott analyzed dynamical systems with chaotic attractors. He identified the form of differential equations in which chaotic attractors occur [9].

Generally, chaos is considered a negative and harmful aspect of system dynamics. Therefore, typical research is aimed at both the detection and prevention/elimination of chaos. Moreover, the tasks of chaos detection are considering for the type of homo-/heteroclinic chaos, using on the Melnikov method and its modifications. In the papers [10, 11], the chaotic motion of an asymmetric spacecraft under internal and external perturbations was investigated. The Melnikov method is used to predict chaotic pitch motion [12]. The effect of the spacecraft flexible panels was evaluated in [13]. In studies [14,15,16,17], perturbed dynamics problem for dual-spin and multi-spin (multi-rotor) spacecraft was examined. The Melnikov method adaptation was recently developed for cases with damped perturbations [18]. It was used to investigate of nanosatellite attitude dynamics at the presence of internal dissipation properties. The Wiggins generalization of the Melnikov method is important and useful [19]. In addition, chaotic modes in spacecraft attitude dynamics with liquid-filled cavities have been investigated [20,21,22,23]. The papers [10,11,12,13,14,15,16,17,18,19,20,21,22,23] analyzed ways to suppress homo-/heteroclinic chaos.

However, there are studies in which chaos is seen as a positive aspect. One of the first studies is presented in the paper [24]. On the basis of the numerical results, Ott et al. concluded that the desired periodic motions can be achieved using chaotic attractors. This assumption was later confirmed in the framework of the targeting problem [25]. The numerical results of [25] showed that chaotic attractors can reduce the targeting time. Later, the results obtained in [24] were extended to high-dimensional systems [26, 27]. Macau also explored the possibility of using chaos to solve targeting problems [28, 29]. He developed a chaotic targeting method [28, 29]. This method was used to solve the planar Earth–Moon transfer problem with minimum fuel cost. In addition to the above-mentioned method, the hybrid method has also been proposed as a solution to this problem [30]. The hybrid method can obtain a set of flight trajectories. These trajectories have specific fuel costs and maneuver times. It is worth noting that chaos control was applied in some space missions. Belbruno [31] used chaos theory to create low-cost trajectories. These trajectories rescued the Japanese spacecraft “Hiten,” in 1991 and the American communication satellite “HGS-1,” in 1998.

Chaos control can also be used in attitude dynamics. In [32], an adaptive backstepping sliding mode control was proposed. This control method aims to synchronize the chaotic satellite attitude. The authors obtained stable control laws using this approach. These control laws suppress any undesirable effects from unknown disturbances. A similar problem was solved in [33]. The authors designed a fixed-time adaptive synchronization controller satellite systems. The controller adapts to unknown moments of inertia and disturbance. In addition, chaos control is used in the attitude dynamics of single satellites. In the papers [34, 35], the spacecraft angular reorientation problem was solved by chaos initiation. Chaos initiation was provided by an internal rotor system. The control laws for initializing Wang-Sun and Chen-Lee chaotic attractors are derived. These laws involve rotor (reaction wheel) control. The problem of the spacecraft chaotic transition was solved [36]. This transition occurs from the initial zone to the desired zone, and, therefore, the spacecraft desired angular reorientation is possible. For example, in [36] chaotic reorientation was fulfilled by creating heteroclinic chaos. The heteroclinic chaos is occurred in areas of heteroclinic orbits in the phase space of dynamical system at the action of small perturbations.

This study develops the ideas reflected in the research [36]. In this paper, we also focus on the spacecraft angular reorientation problem. But now, we will explore the creation of chaotic attractors in the phase space to reorient the spacecraft. Moreover, using the differential evolution algorithm [37], we consider the optimal reorientation process, when the desired spatial orientation will be achieved at the minimization of the angular velocity value.

The paper is organized as follows. In Sect. 2, the basic concepts related to the mathematical model of multi-rotor spacecraft angular motion are presented. In addition, possible motion modes and reorientation with the help of chaotic attractors are described. In Sect. 3, the chaotic reorientation results obtained using five new chaotic attractors are given. The conclusions are drawn in Sect. 4.

2 Mechanical and mathematical models

2.1 Coordinate system

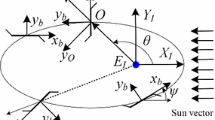
Let us consider a multi-spin spacecraft [18] with six sets of rotors placed along the principal axes (Fig. 1). The main coordinate frames are the inertial frame CXYZ and the frame Cxyz. The frame Cxyz is connected to the main body of the spacecraft.

Fig. 1
figure 1

Mechanical structure of the considered spacecraft

Full size image

2.2 Dynamic and kinematic equations

We are studying a rotor system with six identical rotors. Rotors are placed along the principal axes. The angular momentum of the multi-rotor mechanical system in frame Cxyz has the following form:

$$ K = {K_b} + {K_r}, $$
(1)
$$ {K_b} = \left[ {\begin{array}{*{20}{c}} {Ap} \\ {Bq} \\ {Cr} \end{array}} \right], $$
(2)
$$ {K_r} = I\left[ {\begin{array}{*{20}{c}} {{\sigma_1} + {\sigma_2}} \\ {{\sigma_3} + {\sigma_4}} \\ {{\sigma_5} + {\sigma_6}} \end{array}} \right]. $$
(3)

Here, K is the angular momentum vector of the complete mechanical system; Kb is the angular momentum of the main body with immovable rotors; Kr is the relative angular momentum of rotors; p, q, r are components of the angular velocity of the main body ω in projections onto connected axes Cxyz; σl is relative angular velocity of the l-th rotor relative to the main body. Parameters A, B, and C are the moments of inertia of the main body with fixed rotors:

$$ \left\{ \begin{gathered} A = \widetilde A + 4J + 2I, \hfill \\ B = \widetilde B + 4J + 2I, \hfill \\ C = \widetilde C + 4J + 2I, \hfill \\ \end{gathered} \right. $$
(4)

where \(\widetilde A\), \(\widetilde B\), \(\widetilde C\) are the general inertia moments of the main body; I and J are the longitudinal and equatorial inertia moments of the rotor, respectively.

The equation for the angular motion of the system in the connected frame Cxyz has the following form:

$$ \frac{{{\text{d}}K}}{{{\text{d}}t}} + \omega \times K = {M^e}, $$
(5)

where Me is the vector of the external torques acting on the system. The scalar form of Eq. (5) has the shape [18]:

$$\left\{ \begin{gathered} A\dot p + I\left\{ {{{\dot \sigma }_1} + {{\dot \sigma }_2}} \right\} + \left( {C - B} \right)qr + I\left[ {q\left\{ {{\sigma_5} + {\sigma_6}} \right\} - r\left\{ {{\sigma_3} + {\sigma_4}} \right\}} \right] = M_x^e, \hfill \\ B\dot q + I\left\{ {{{\dot \sigma }_3} + {{\dot \sigma }_4}} \right\} + \left( {A - C} \right)rp + I\left[ {r\left\{ {{\sigma_1} + {\sigma_2}} \right\} - p\left\{ {{\sigma_5} + {\sigma_6}} \right\}} \right] = M_y^e, \hfill \\ C\dot r + I\left\{ {{{\dot \sigma }_5} + {{\dot \sigma }_6}} \right\} + \left( {B - A} \right)pq + I\left[ {p\left\{ {{\sigma_3} + {\sigma_4}} \right\} - q\left\{ {{\sigma_1} + {\sigma_2}} \right\}} \right] = M_z^e. \hfill \\ \end{gathered} \right. $$
(6)

The equations of the relative rotations of rotors can be derived. They are based on the law of change in angular momentums:

$$ \left\{ \begin{gathered} I\left( {\dot p + {{\dot \sigma }_1}} \right) = M_1^e + M_1^i, \hfill \\ I\left( {\dot p + {{\dot \sigma }_2}} \right) = M_2^e + M_2^i, \hfill \\ I\left( {\dot q + {{\dot \sigma }_3}} \right) = M_3^e + M_3^i, \hfill \\ I\left( {\dot q + {{\dot \sigma }_4}} \right) = M_4^e + M_4^i, \hfill \\ I\left( {\dot r + {{\dot \sigma }_5}} \right) = M_5^e + M_5^i, \hfill \\ I\left( {\dot r + {{\dot \sigma }_6}} \right) = M_6^e + M_6^i. \hfill \\ \end{gathered} \right. $$
(7)

Here, \(M_l^e\) and \(M_l^i\) are external and internal torques acting on the l-th rotor, respectively. Electric motors installed in the main body create internal torque.

The kinematical equations for the Euler angles have the well-known form:

$$ \left\{ \begin{gathered} \dot \theta = p\cos \varphi - q\sin \varphi , \hfill \\ \dot \psi = {{\left( {p\sin \varphi + q\cos \varphi } \right)} \mathord{\left/ {\vphantom {{\left( {p\sin \varphi + q\cos \varphi } \right)} {\sin \theta }}} \right. \kern-0pt} {\sin \theta }}, \hfill \\ \dot \varphi = r - {{\left( {p\sin \varphi + q\cos \varphi } \right)} \mathord{\left/ {\vphantom {{\left( {p\sin \varphi + q\cos \varphi } \right)} {tg\theta }}} \right. \kern-0pt} {tg\theta }}, \hfill \\ \end{gathered} \right. $$
(8)

where θ is the nutation angle, ψ is the precession angle, and φ is the intrinsic rotation. Therefore, the multi-rotor (multi-spin) spacecraft attitude dynamics is fully described by Eqs. (6-–8).

2.3 Reorientation stages and phase space zones

As shown in [36], a spacecraft attitude can be reoriented by initiating heteroclinic chaotic modes. In this research, we use a different type of chaos. This corresponds to chaotic attractors, which can be created by the rotation of internal rotors (Fig. 1). This is based on the following algorithm:

  1. 1.

    The spacecraft realizes the initial regular mode of free angular motion.

  2. 2.

    The control system generates torques using jet-rocket and electric engines. These torques brake the main body and rotors.

  3. 3.

    The control system switches to form special control laws. These laws create and support the chaotic mode. The spacecraft moves chaotically at this stage. The control system monitors the current dynamic parameters.

  4. 4.

    The control system stops all rotor rotations and jet-rocket engine work. This occurs when the motion parameters and phase trajectory reach the target zone. The chaotic attractor in phase space immediately disappears. The spacecraft then smoothly transitions to a new regular motion as a single rigid body into the target zone.

As we already said, the spacecraft final regular motion is the free angular motion of a single rigid body. This occurs when all rotors are stopped and fixed relative to the spacecraft main body. We can observe the final zones of the spacecraft regular motion [36]. These zones are shown as the single rigid body in Fig. 2.

Fig. 2
figure 2

Zones of rigid body angular motion in phase space of angular velocity components

Full size image

The first zone or the \(\mathfrak{A}\)-zone (Fig. 2) describes the rotational motion of the longitudinal axes (Cz) of the rigid body. These axes rotate around the vector of angular momentum K with acute angles of nutation θ. The rotation of the spacecraft around the Cz-axis is positive. It also has motion with positive precession velocity and positive intrinsic rotation velocity. The second zone or the \(\mathfrak{B}\)-zone is the same as the \(\mathfrak{A}\)-zone. However, the spacecraft rotates in the opposite direction relative to the angular momentum. The angular motion has a positive precession velocity. It also has a negative intrinsic rotation velocity. In addition, the values of nutation are substantially large. The third zone or the \( \mathfrak{C}\)-zone describes the rotation preferably relative to the transversal axis Cx. The spacecraft rotates around vector K with a positive precession velocity. The intrinsic rotation periodically oscillates around φ = π/2. The motion in this zone is usually the worst. The spacecraft rotates sideways in relation to the main direction. Finally, the fourth zone or the D-zone is analogous to the \( \mathfrak{C}\)-zone. However, the spacecraft rotates periodically around the value φ = 3π/2. Similarly, the \(\mathfrak{D}\)-zone is an undesirable zone of the motion modes, similar to the \( \mathfrak{C}\)-zone.

To achieve the mentioned zones, we introduce infinitely close times. These times occur before and after rotor fixations on the border. The border is between the third and fourth steps of the reorientation algorithm:

$$ t_-^* = {t^*} - \varepsilon, $$
(9)
$$ t_+^* = {t^*} + \varepsilon , $$
(10)

where t* is the time the rotors stop during the chaotic mode; \(t_-^*\), \(t_+^*\) are times before and after the rotors stop, respectively; ε is an infinitesimal value.

The angular momentum before the rotors stop is calculated as the angular momentum of the multi-rotor system with rotating rotors:

$$ \left\{ \begin{gathered} {K_x} = Ap\left( {t_-^*} \right) + I\left[ {{\sigma_1}\left( {t_-^*} \right) + {\sigma_2}\left( {t_-^*} \right)} \right], \hfill \\ {K_y} = Bq\left( {t_-^*} \right) + I\left[ {{\sigma_3}\left( {t_-^*} \right) + {\sigma_4}\left( {t_-^*} \right)} \right], \hfill \\ {K_z} = Cr\left( {t_-^*} \right) + I\left[ {{\sigma_5}\left( {t_-^*} \right) + {\sigma_6}\left( {t_-^*} \right)} \right], \hfill \\ \end{gathered} \right. $$
(11)

where we suppose that at time t*, the rotors are stopped and, therefore, σl(t*) = 0. Thus, the components of angular velocity \(p\left( {t_+^*} \right)\), \(q\left( {t_+^*} \right)\), \(r\left( {t_+^*} \right)\) after rotors stop can be calculated from the law of angular momentum conservation, similar to the components of the angular momentum of the single rigid body:

$$ \left\{ \begin{gathered} p\left( {t_+^*} \right) = p_0^+ = \frac{{K_x}}{A}, \hfill \\ q\left( {t_+^*} \right) = q_0^+ = \frac{{K_y}}{B}, \hfill \\ r\left( {t_+^*} \right) = r_0^+ = \frac{{K_z}}{C}. \hfill \\ \end{gathered} \right. $$
(12)

Then, after the rotors stop, we have the following twice the kinetic energy and square of the angular momentum:

$$ h = 2T = A{\left( {p_0^+ } \right)^2} + B{\left( {q_0^+ } \right)^2} + C{\left( {r_0^+ } \right)^2}, $$
(13)
$$ {G^2} = {\left( {Ap_0^+ } \right)^2} + {\left( {Bq_0^+ } \right)^2} + {\left( {Cr_0^+ } \right)^2}. $$
(14)

Let us assume (without any loss of generality) that A > B > C. Thus, Eq. (13) and Eq. (14) can be rewritten as follows:

$$ Ah - {G^2} = B\left( {A - B} \right)\lambda_1^2, $$
(15)
$$ {G^2} - Ch = B\left( {B - C} \right)\lambda_2^2. $$
(16)

Therefore, we express the parameters \(\lambda_1^2\) and \(\lambda_2^2\):

$$ \lambda_1^2 = q_+^2 + \frac{{\left( {C + 2I} \right)\left( {A - C} \right)r_+^2}}{{\left( {B + 2I} \right)\left( {A - B} \right)}}, $$
(17)
$$ \lambda_2^2 = q_+^2 + \frac{{\left( {A + 2I} \right)\left( {A - C} \right)p_+^2}}{{\left( {B + 2I} \right)\left( {B - C} \right)}}, $$
(18)

Now, we can describe the following conditions for entry into the \(\mathfrak{A}\)-zone:

$$ \left| {\lambda_1} \right| > \left| {\lambda_2} \right|\,\,\,\& \,\,\,{r_+ } > 0, $$
(19)

into the \(\mathfrak{B}\)-zone:

$$ \left| {\lambda_1} \right| > \left| {\lambda_2} \right|\,\,\,\& \,\,\,{r_+ } < 0, $$
(20)

into the \( \mathfrak{C}\)-zone:

$$ \left| {\lambda_1} \right| < \left| {\lambda_2} \right|\,\,\,\& \,\,\,{p_+ } > 0, $$
(21)

and into the \( \mathfrak{D}\)-zone:

$$ \left| {\lambda_1} \right| < \left| {\lambda_2} \right|\,\,\,\& \,\,\,{p_+ } < 0. $$
(22)

It is worth noting that the cases of \( {\lambda_1} = 0\) and \( {\lambda_2} = 0\) mean the rotation around only the Cx-axis and Cz-axis, respectively. If \( {\lambda_1} = {\lambda_2}\) then the rotational motion occurs along the separatrixes (these are the black lines at Fig. 2).

Now, let us describe the control laws and stages of attitude reorientation realization. The first stage describes the natural initial regular motion of the spacecraft.

In the second stage, we need to stop the main body and all the rotors. This can be realized by the corresponding actuators (by the jet engines of the main body and by the electric engines of rotors). This process can be fulfilled with the help of the following modeling laws:

$$ \left\{ \begin{gathered} M_x^e = - \nu H\left( {t - {t_{brb}}} \right)p, \hfill \\ M_y^e = - \nu H\left( {t - {t_{brb}}} \right)q, \hfill \\ M_z^e = - \nu H\left( {t - {t_{brb}}} \right)r, \hfill \\ \end{gathered} \right. $$
(23)

where ν is the positive constant and H(t) is the Heaviside function, tbrb is the start time of the process of stopping the main body. At the same time, the complete stop of the relative rotation of all rotors is fulfilled with internal torques of the form:

$$ M_l^i = - \nu \left( {t - {t_{brr}}} \right){\sigma_l}, $$
(24)

where tbrr is the start time of the process of stopping the l-th rotor. At the action of torques (23) and (24), all bodies of our system (the main body and all rotors) will stop their angular motion relative to the inertial frame CXYZ.

The third stage forms and supports a chaotic attractor and a corresponding chaotic motion mode. The third stage starts after stopping elements of the mechanical system. After elements immobility achieving, the spin-up mode is initiated for rotors #2, 4, and 6. The goal here is to reach specific relative angular velocities [21] of these rotors: \({\sigma_2} = {\alpha_0},\,\,\,\,\,\,{\sigma_4} = {\beta_0},\,\,\,\,\,\,{\sigma_6} = {\gamma_0}\). The spin-up process is implemented using internal torques. These torques come from the electric internal rotor engines:

$$ \left\{ \begin{gathered} M_2^i = {m_{acc}}H\left( {t - {t_{acr}}} \right)\left[ {H\left( {t - {t_{acr}}} \right) - H\left( {t - {t_{acr}} - \frac{{I\left| {\alpha_0} \right|}}{{{m_{xacc}}}}} \right)} \right]sign\left( {\alpha_0} \right), \hfill \\ M_4^i = {m_{acc}}H\left( {t - {t_{acr}}} \right)\left[ {H\left( {t - {t_{acr}}} \right) - H\left( {t - {t_{acr}} - \frac{{I\left| {\beta_0} \right|}}{{{m_{yacc}}}}} \right)} \right]sign\left( {\beta_0} \right), \hfill \\ M_6^i = {m_{acc}}H\left( {t - {t_{acr}}} \right)\left[ {H\left( {t - {t_{acr}}} \right) - H\left( {t - {t_{acr}} - \frac{{I\left| {\gamma_0} \right|}}{{{m_{zacc}}}}} \right)} \right]sign\left( {\gamma_0} \right). \hfill \\ \end{gathered} \right. $$
(25)

Here, macc is the constant, tacr is the start time of rotors accelerating, α0, β0, γ0 are some predefined constant parameters.

Spin-up of the rotors occurs until the following three conditions are met:

$$ \left| {{\alpha_0} - {\sigma_2}} \right| < \xi , $$
(26)
$$\left| {{\beta_0} - {\sigma_4}} \right| < \xi , $$
(27)
$$ \left| {{\gamma_0} - {\sigma_6}} \right| < \xi , $$
(28)

where ξ is an acceptable small error. When conditions (26–28) are met, the rotors must support the chaotic mode [34, 35]. In this case, rotors should be controlled by internal electrical engines according to the following laws:

$$ \left\{ \begin{gathered} {\sigma_1}(t) = p(t)\left( {{\alpha_p} - 2I} \right)/I, \hfill \\ {\sigma_3}(t) = q(t)\left( {{\beta_q} - 2I} \right)/I, \hfill \\ {\sigma_5}(t) = r(t)\left( {{\gamma_r} - 2I} \right)/I, \hfill \\ {\sigma_2}(t) = {\alpha_0}, \hfill \\ {\sigma_4}(t) = {\beta_0}, \hfill \\ {\sigma_6}(t) = {\gamma_0}, \hfill \\ \end{gathered} \right. $$
(29)

where αp, βq, γr are some predefined constant parameters. In addition, it is necessary [34, 35] to create external torque on the main body. This torque can be formed by the jet engines. The torque should follow the control laws:

$$ \left\{ \begin{gathered} M_x^e = {m_x} + {\alpha_1}p, \hfill \\ M_y^e = {m_y} + {\beta_1}q, \hfill \\ M_z^e = {m_z} + {\gamma_1}r. \hfill \\ \end{gathered} \right. $$
(30)

Here, mx, my, mz, α1, β1, γ1 is also predefined constant parameters. Thus, the following vector of control parameters is used to create and support a chaotic mode:

$$ {\text{Control}} = {\left[ {{\alpha_0},{\alpha_1},{\alpha_p},{m_x},{\beta_0},{\beta_1},{\beta_q},{m_y},{\gamma_0},{\gamma_1},{\gamma_r},{m_z}} \right]^T} $$
(31)

Certain values of the control parameters (31) will be defined. The description will be given in Sect. 2.5. At the end of the third stage, the spacecraft will implement chaotic motion. The motion will be of a predefined type of chaotic attractor. These attractors are defined by certain values, specifically (31).

Finally, the fourth stage involves immediately disabling the control at the time-point tfinish. Together with the control disabling, all of the rotors should also be immediately stopped in their relative rotations \(\left( {\forall l:\,\,\,\,\,\,{\sigma_l} \to 0} \right)\) by the internal large friction (at the torques like (24) with an extremely large value ν). The spacecraft enters the fourth stage and transitions to a new mode. This mode is in the target zone of the phase space. The spacecraft operates as a single rigid body system.

2.4 Additional conditions for an optimal exit from the chaotic mode

As mentioned above, chaos can help achieve the desired target zone in spacecraft attitude dynamics. After entering the target zone, the spacecraft's angular velocity changes. The new values may be similar to the initial zone. In this study, we added a condition for reaching the target zone. The condition requires a minimum angular velocity:

$$ \sqrt {{p^2} + {q^2} + {r^2}} \to \min . $$
(32)

In addition, we can include another requirement for spacecraft reorientation. This involves achieving a specific position in relation to the inertial axis CZ. The mathematical shape of this condition is quite simple:

$$\left| {{\gamma_b} - \gamma } \right| \to \min , $$
(33)

where γb and γ are the target boundary and the real obtained values of the so-called “direction cosines,” respectively. The directional cosines of the CZ axis are evaluated by the following well-known differential equations:

$$ \left\{ \begin{gathered} {{\dot \gamma }_1} = r{\gamma_2} - q{\gamma_3}, \hfill \\ {{\dot \gamma }_2} = p{\gamma_3} - r{\gamma_1}, \hfill \\ {{\dot \gamma }_3} = q{\gamma_1} - p{\gamma_2}. \hfill \\ \end{gathered} \right. $$
(34)

Finally, we can introduce one more additional condition in our study. This is a requirement for the coincidence of the angular momentum vector with the CZ-axis of the inertial coordinate system:

$$ \frac{K \cdot \gamma }{{\left| K \right|}} \to 1. $$
(35)

Thus, the problem of the optimal exit from the chaotic mode is described as follows: it is necessary to reorient the spacecraft from the initial zone to the final target zone of the phase space of the attitude dynamics at the given orientation of the spacecraft relative to the inertial CZ-axis (33), at the coincidence of the angular momentum vector with the CZ-axis (35), and at the minimum of the angular velocity value (32). This can be expressed mathematically as follows:

$$ f\left( {{t_{{\text{finish}}}}} \right) = \sqrt {{p^2} + {q^2} + {r^2}} + \left| {{\gamma_b} - {\gamma_{ob}}} \right| + \left( {1 - \frac{K \cdot \gamma }{{\left| K \right|}}} \right) \to \min . $$
(36)

In our research, the search for time-point tfinish with conditions (32), (33), and (35) is carried out using the differential evolution algorithm [37]. To guarantee entry into the final target zone, we introduce the following penalty function:

$$ \begin{aligned} & {\text{if}}\,\,\,\left( {final\,\,zone \ne target\,\,zone\,} \right)\,\,\,{\text{then}} f\left( {{t_{{\text{finish}}}}} \right) = M \\ & {\text{else}} \\ & f\left( {{t_{{\text{finish}}}}} \right) = {k_{w1}}\sqrt {{p^2} + {q^2} + {r^2}} + {k_{w2}}\left| {{\gamma_b} - {\gamma_{ob}}} \right| + {k_{w3}}\left( {1 - \frac{K \cdot \gamma }{{\left| K \right|}}} \right) \to \min , \\ \end{aligned} $$
(37)

where M is the penalty value and the coefficients kwi are the weights. The parameters M and kwi are described in Sect. 3.1.

2.5 Chaotic attractors

Dynamical systems with chaotic attractors can be described by the following simple differential equations [9]:

$$ \left\{ \begin{gathered} \dot x = {a_0} + {a_1}x + {a_2}y + {a_3}z + {a_4}{x^2} + {a_5}{y^2} + {a_6}{z^2} + {a_7}xy + {a_8}xz + {a_9}yz, \hfill \\ \dot y = {b_0} + {b_1}x + {b_2}y + {b_3}z + {b_4}{x^2} + {b_5}{y^2} + {b_6}{z^2} + {b_7}xy + {b_8}xz + {b_9}yz, \hfill \\ \dot z = {c_0} + {c_1}x + {c_2}y + {c_3}z + {c_4}{x^2} + {c_5}{y^2} + {c_6}{z^2} + {c_7}xy + {c_8}xz + {c_9}yz, \hfill \\ \end{gathered} \right. $$
(38)

where ai, bi, ci are constant coefficients.

Let us establish the link between Eq. (38) and Eq. (6). First, we substitute expression (29) into Eq. (6). Taking into account Eq. (29), we can consider Eq. (6) as the complete first-order system of differential equations relatively \(p,\,\,q,\,\,r.\) After reassigning the variables \(\left( {p \leftrightarrow x,\,\,q \leftrightarrow y,\,\,r \leftrightarrow z\,} \right)\), we can write [34] the following correspondences for the system (38) coefficientsai, bi, and ci:

$$ \left\{ \begin{gathered} {a_0} = {m_x}{\left( {A + {\alpha _p}} \right)^{ - 1}},\,\,\,{b_0} = {m_y}{\left( {B + {\beta _q}} \right)^{ - 1}},\,\,\,{c_0} = {m_z}{\left( {C + {\gamma _r}} \right)^{ - 1}}, \hfill \\ {a_1} = {\alpha _1}{\left( {A + {\alpha _p}} \right)^{ - 1}},\,\,\,{b_1} = {\gamma _0}{\left( {B + {\beta _q}} \right)^{ - 1}},\,\,\,{c_1} = - {\beta _0}{\left( {C + {\gamma _r}} \right)^{ - 1}}, \hfill \\ {a_2} = - {\gamma _0}{\left( {A + {\alpha _p}} \right)^{ - 1}},\,\,\,{b_2} = {\beta _1}{\left( {B + {\beta _q}} \right)^{ - 1}},\,\,\,{c_2} = {\alpha _0}{\left( {C + {\gamma _r}} \right)^{ - 1}}, \hfill \\ {a_3} = {\beta _0}{\left( {A + {\alpha _p}} \right)^{ - 1}},\,\,\,{b_3} = - {\alpha _0}{\left( {B + {\beta _q}} \right)^{ - 1}},\,\,\,{c_3} = {\gamma _1}{\left( {C + {\gamma _r}} \right)^{ - 1}}, \hfill \\ {a_4} = {a_5} = {a_6} = {b_4} = {b_5} = {b_6} = {c_4} = {c_5} = {c_6} \equiv 0, \hfill \\ {a_7} = {b_7} \equiv 0,\,\,\,{c_7} = \left( {A - B - {\beta _q} + {\alpha _p}} \right){\left( {C + {\gamma _r}} \right)^{ - 1}}, \hfill \\ {a_8} = {c_8} \equiv 0,\,\,\,{b_8} = \left( {C - A - {\alpha _p} + {\gamma _r}} \right){\left( {B + {\beta _q}} \right)^{ - 1}}, \hfill \\ {b_9} = {c_9} \equiv 0,\,\,\,{a_9} = \left( {B - C - {\gamma _r} + {\beta _q}} \right){\left( {A + {\alpha _p}} \right)^{ - 1}}. \hfill \\ \end{gathered} \right. $$
(39)

If we know the numerical values of the coefficients ai, bi, and ci which provide the birth of the chaotic attractor in the system (38), then we can find the corresponding values of the control parameters (31) that satisfy the conditions (39).

Let us provide a concrete example of the detection of these parameters. First, we found a new set of coefficients for system (38) with a new chaotic attractor (the chaotic attractor #1):

$$ \left\{ \begin{gathered} {a_0} = 0.1247,\;\,\,{a_1} = 0.0901,\,\,\,{a_2} = 0.3172,\,\,\,{a_9} = - 0.4341,\,\, \hfill \\ {b_0} = - 0.747,\,\,\,\,{b_1} = - 0.5605,\,\,\,{b_2} = - 0.5813, \hfill \\ {c_0} = 0.3638,\,\,\,\,{c_7} = 0,434, \hfill \\ {a_{\{ 3,4,5,6,7,8\} }} = {b_{\{ 3,4,5,6,7,8,9\} }} = {c_{\{ 1,2,3,4,5,6,8,9\} }} = 0. \hfill \\ \end{gathered} \right. $$
(40)

The system (38) with coefficient values (40) has a chaotic attractor in the phase space {x, y, z} (Fig. 3a). The Lyapunov characteristic exponents (LCE) for this attractor are shown in Fig. 3. The LCE values were computed using the Benettin method [38]. The final LCE values are equal to \({\lambda_1} = 0.056;\,\,{\lambda_2} = 0;\,\,\,{\lambda_3} = - 0.548\).

Fig. 3
figure 3

a Phase portrait and b LCE of chaotic attractor #1

Full size image

The Kaplan–Yorke dimension for chaotic attractor #1 has the following value:

$$ D = 2 + \frac{0.056 + 0}{{\left| { - 0.548} \right|}} = 2.1012. $$
(41)

The fractional Kaplan–Yorke dimension indicates the fractality of the attractor. In this case, the attractor is commonly referred to as "strange attractor." The presence of a positive LCE indicates the chaotic behavior of the dynamics along the attractor; therefore, the found attractor is the “strange chaotic attractor.”

To calculate the control values (31), we need to define the moments of inertia of our spacecraft and rotors. In this study, we use the following values \(\widetilde A = 90,\,\,\,\widetilde B = 70,\,\,\,\widetilde C = 50,\,\,\,I = 1,\,\,\,J = 1\). Now, we can use optimization methods to find numerical values (31) that satisfy conditions (39). This requires knowing the chaotic attractor coefficients (40) and inertia moment values. For example, it is possible, to build an auxiliary function [34]:

$$ \begin{aligned} & \Psi \left( {{\alpha _0},{\alpha _1},{\alpha _p},{m_x},{\beta _0},{\beta _1},{\beta _q},{m_y},{\gamma _0},{\gamma _1},{\gamma _r},{m_z}} \right) \\ & = {\left( {{a_0} - \frac{{{m_x}}}{{A + {\alpha _p}}}} \right)^2} + {\left( {{b_0} - \frac{{{m_y}}}{{B + {\beta _q}}}} \right)^2} + {\left( {{c_0} - \frac{{{m_z}}}{{C + {\gamma _r}}}} \right)^2} + {\left( {{a_1} - \frac{{{\alpha _1}}}{{A + {\alpha _p}}}} \right)^2} \\ & \quad + {\left( {{b_1} - \frac{{{\gamma _0}}}{{B + {\beta _q}}}} \right)^2} + {\left( {{c_1} + \frac{{{\beta _0}}}{{C + {\gamma _r}}}} \right)^2} + {\left( {{a_2} + \frac{{{\gamma _0}}}{{A + {\alpha _p}}}} \right)^2} + {\left( {{b_2} - \frac{{{\beta _1}}}{{B + {\beta _q}}}} \right)^2} \\ & \quad + {\left( {{c_2} - \frac{{{\alpha _0}}}{{C + {\gamma _r}}}} \right)^2} + {\left( {{a_3} - \frac{{{\beta _0}}}{{A + {\alpha _p}}}} \right)^2} + {\left( {{b_3} + \frac{{{\alpha _0}}}{{B + {\beta _q}}}} \right)^2} + {\left( {{c_3} - \frac{{{\gamma _1}}}{{C + {\gamma _r}}}} \right)^2} \\ & \quad + {\left( {{{{c_7} - \left( {A - B - {\beta _q} + {\alpha _p}} \right)} \mathord{\left/ {\vphantom {{{c_7} - \left( {A - B - {\beta _q} + {\alpha _p}} \right)} {\left( {C + {\gamma _r}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {C + {\gamma _r}} \right)}}} \right)^2} + {\left( {{b_8} - {{\left( {C - A - {\alpha _p} + {\gamma _r}} \right)} \mathord{\left/ {\vphantom {{\left( {C - A - {\alpha _p} + {\gamma _r}} \right)} {\left( {B + {\beta _q}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {B + {\beta _q}} \right)}}} \right)^2} \\ & \quad + {\left( {{a_9} - {{\left( {B - C - {\gamma _r} + {\beta _q}} \right)} \mathord{\left/ {\vphantom {{\left( {B - C - {\gamma _r} + {\beta _q}} \right)} {\left( {A + {\alpha _p}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {A + {\alpha _p}} \right)}}} \right)^2} \\ \end{aligned}$$
(42)

Next, we attempt to obtain the global minimum of the function using the gradient method [34]:

$$ {\text{while}}\,\,\,\left| {\sqrt {\Psi \left( {{\text{Contro}}{{\text{l}}_i}} \right)} } \right| > \delta :\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Contro}}{{\text{l}}_{i + 1}} = {\text{Contro}}{{\text{l}}_i} - h\,\nabla \Psi \left( {{\text{Contro}}{{\text{l}}_i}} \right), $$
(43)

where \({\text{Contro}}{{\text{l}}_0}\) is the starting approximation of the vector of control parameters, δ is an accuracy of calculations, and h is the step of the parametric motion to the minimum in the parametric space of vector (31) in the direction opposite to the gradient vector:

$$ \nabla = {\left[ {\frac{\partial }{{\partial {\alpha_0}}},\frac{\partial }{{\partial {\alpha_1}}},\frac{\partial }{{\partial {\alpha_p}}},\frac{\partial }{{\partial {m_x}}},\frac{\partial }{{\partial {\beta_0}}},\frac{\partial }{{\partial {\beta_1}}},\frac{\partial }{{\partial {\beta_q}}},\frac{\partial }{{\partial {m_y}}},\frac{\partial }{{\partial {\gamma_0}}},\frac{\partial }{{\partial {\gamma_1}}},\frac{\partial }{{\partial {\gamma_r}}},\frac{\partial }{{\partial {m_z}}}} \right]^T}. $$

After iterations (43) are completed, we can obtain the clarified values of the control vector. The iteration process can lead to a local minimum of the function. In this case, we cannot find the right control parameters to form the attractor with the given coefficients. Nevertheless, in all cases of our research, these iterations were successful. As a result, we obtain quite accurate control parameter values (31), which are presented in Table 1. The calculation of the control parameter (31) can be solved using other optimization methods. One of these methods is the differential evolution algorithm [37].

Table 1 Control parameters for the initialization of chaotic attractor #1
Full size table

We discovered four new systems with chaotic attractors, in addition to the previously mentioned case of attractor #1. These systems are presented in Appendix A.

The next section of this paper describes similar modeling results for the system (38). These results provide the birth of new chaotic attractors. These results are presented in Appendix B.

3 Applied results to spacecraft attitude dynamics

Now, we can use new chaotic attractors to reorient the spacecraft. This uses the natural properties of dynamical chaos. Let us divide this section of our article into three subsections. The first subsection provides the initial conditions for θ, φ, ψ, p, q, r. It also includes boundary conditions for γ1, γ2, γ3, and the values of control constants (Eqs. 23–25). The second subsection includes the estimated spacecraft transition from the initial zone to the target zone. This estimation is performed using five new chaotic attractors. The transition from the initial zone to the target zone is performed by considering the goal function in Eq. (36). In the third subsection, the efficiency of transitioning from the initial zone to the target zone is compared. This research only focuses on the \( \mathfrak{C}\) → \(\mathfrak{A}\) transition case. A comparison is made for the angular velocity components p, q, r, the final attitude position of the spacecraft γ1, γ2, γ3, and the projection of the angular momentum vector K.

3.1 Modeling parameters

The initial conditions for modeling are presented in Table 2. All of them were used for modeling and presented in Figs. 4, 5, 6, 7, 8, and 9.

Table 2 Initial conditions
Full size table
Fig. 4
figure 4

Dependence of angular velocity components on time

Full size image
Fig. 5
figure 5

Dependence of (a) nutation, (b) p velocity component, (c) q velocity component, and (d) r velocity component on time

Full size image
Fig. 6
figure 6

Dependence of (a) nutation, (b) p velocity component, (c) q velocity component, and (d) r velocity component on time

Full size image
Fig. 7
figure 7

Dependence of (a) nutation, (b) p velocity component, (c) q velocity component, and (d) r velocity component on time

Full size image
Fig. 8
figure 8

Dependence of angular velocity magnitude on time

Full size image
Fig. 9
figure 9

Dependence of directional cosines on time

Full size image

The boundary conditions for the directional cosines are presented in Table 3. It should be noted that the presented boundary conditions are common for all considered cases.

Table 3 Boundary conditions (initial and target values)
Full size table

The numerical parameters of laws (23–25) are given in Table 4. The considered chaotic attractors obviously have different control coefficients (Eq. (31)). Therefore, the parameters mxacc, myacc, mzacc are defined by the constants α0, β0, γ0. The penalty value is M = 15,000, and the weights are kw1 = 1 and, kw2 = kw3 = 1000. These parameters are applied to all considered cases.

Table 4 Control constants
Full size table

3.2 Transitions from the initial zone to the target zone

Let us consider the transition case \( \mathfrak{C}\) → \(\mathfrak{A}\). The results of the numerical modeling are presented in Fig. 4. The red line is the initial motion of the spacecraft; the dark-blue and light-blue lines are the braking stage of the body and rotor, respectively (Eqs. (23) and (24)); the yellow line is the spinning-up stage of the rotors (Eq. (25)); the black line is the chaotic motion of the spacecraft (Eqs. 29 and 30); and the violet line is the final motion of the spacecraft.

The nutation angle began to fluctuate between 0.57 and 1.22 radians after entering the target A-zone (Fig. 5a). Figure 5b–d shows a significant decrease in angular velocity compared to the initial values. The time spent by the spacecraft in the chaotic mode of motion was 218.22 s.

Similar results were obtained for the transition \(\mathfrak{B}\) → \(\mathfrak{A}\) (Fig. 5a). However, the chaotic motion time increased from 218.22 to 986.51 s. This can be explained by the form of the chaotic attractor. During the transition, the nutation angle varied from 4.2 to 5.57 rad (Fig. 6a). The angular velocity components (Fig. 6b–d) also decreased significantly, as in the case of the transition \( \mathfrak{C}\) → \(\mathfrak{A}\).

Finally, during the transition \(\mathfrak{A}\) → \( \mathfrak{C}\), the time of the chaotic motion of the spacecraft decreased to 105.5 s due to the form of the chaotic attractor. The nutation angle in zone \( \mathfrak{C}\) has large fluctuations (Fig. 7a). In addition, the angular velocity components (Fig. 7b–d) have large amplitudes compared to previous cases. This trend is observed in all considered chaotic attractors (see Appendix B).

Thus, the concept proposed in [36] also works in chaotic attractor cases. The spacecraft's attitude transition \( \mathfrak{C}\) → \(\mathfrak{A}\) is crucial for space missions. A comparative analysis of efficiency will focus solely on this case..

3.3 Comparative analysis of efficiency

Due to the best performance obtained in terms of Eq. (32), Eq. (33), and Eq. (35), the best chaotic attractor for the case \( \mathfrak{C}\) → \(\mathfrak{A}\) should be assigned to attractor #1. The proposed approach reduced the angular velocity value by five times (Fig. 8). It also eliminated fluctuations.

In addition, the spacecraft can be reoriented to the desired position (Fig. 9). After leaving the chaos, the spacecraft also receives small nutation values. These values are shown in Fig. 10. This means that the angular momentum vector aligns with the CZ-axis. The spacecraft will mainly rotate in the CZ-direction with a small nutation angle. It is the preferred motion.

Fig. 10
figure 10

Dependence of the angular momentum vector on time

Full size image

The modeling results (Figs. 4, 5, 6, 7, 8, and 9) demonstrate that chaotic attractors enable spacecraft reorientation.

In Appendix B, we additionally present alternative cases of dynamics modeling. These cases involve other new chaotic attractors.

4 Conclusion

In this paper, the angular reorientation of the spacecraft with the help of the dynamic chaos initiation was considered. To initiate dynamic chaos, some chaotic attractors were used. Five new chaotic attractors were found. All new chaotic attractors can reorient spacecraft but have pros and cons. In conclusion, the following points can be made:

  • The idea [36] of spacecraft attitude reorientation by chaos was confirmed in the case of chaotic attractors using.

  • The spacecraft multi-rotor system can generate different chaotic attractors. These attractors can be one-scroll, two-scroll, and three-scroll types.

  • Using the optimization algorithm, we can determine the exit time from the chaotic mode. This can be performed with minimal angular velocity.

  • The exit time from the chaotic mode can be selected such that the spacecraft will have an orientation close to the desired one.