Attitude evolution of a dual-liquid-filled spacecraft with internal energy dissipation

Abstract

In this paper, the attitude evolution of a dual-liquid-filled spacecraft with internal energy dissipation is investigated. The dynamic equations of the spacecraft system are established to study various trajectories including major axis spin, period-n limit cycle, and chaotic motion. A criterion is obtained by Melnikov’s method to predict the occurrence of chaotic motion of the system. The effects of system parameters, especially liquid parameters, on the chaotic region, are discussed in detail. The comparison of analytical and numerical results shows that our criterion can accurately separate the chaotic from nonchaotic region of the system in parameter space. Therefore, this paper contributes to avoid the potentially periodic and chaotic motions of spacecraft.

1 Introduction

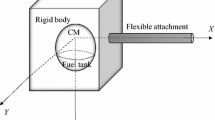
The mechanism of attitude evolution is an important problem in the field of spacecraft dynamics. Previous studies have shown that energy dissipation will drive a single-body spacecraft from minor to major axis spin (MAS) [1, 2], and a practical example is the US Explorer I [3]. However, external perturbations (e.g., gravity gradient, atmosphere drag, and geomagnetic field) and internal perturbations (e.g., liquid sloshing, vibration of flexible panels, and oscillation of spring–mass–damper) may lead to the chaotic motion of spacecraft, which is harmful to the attitude stability. Therefore, it is necessary to understand when and how chaos plays a role in the attitude dynamics of spacecraft. Since spacecraft is normally nonlinear systems, the analytical solutions for their equations of motion are fundamentally unobtainable. Nevertheless, one can obtain a lot of physical insight into the behavior of these systems by using a simpler rigid body with perturbations approximation for modeling and analyzing the spacecraft [16,17,18]. In addition, for a perturbed spacecraft system, the existence of transversal intersection of its heteroclinic (homoclinic) orbits provides a necessary condition for the onset of chaos in the sense of the Smale horseshoe [2]. Melnikov proposed an analytical technique, called Melnikov’s method, to detect the transversal intersections of the heteroclinic (homoclinic) orbits in Poincaré map of the perturbed system [4]. In this way, we studied the chaotic dynamics of a dual-liquid-filled spacecraft undergoing attitude maneuver via a rotor, in which the rotation rate of the rotor is periodic and the internal energy dissipation is caused by the viscous damping of liquids, as shown in Fig. 1.

Fig. 1

Schematic diagram of the spacecraft system

In recent decades, the chaotic dynamics and control of spacecraft, especially spacecraft of single body and dual spin, under various perturbations have been extensively studied [5,6,7,8,9,10,11,12,13,14,15,16]. Modern spacecraft often contains large quantities of liquid fuel to execute station keeping and attitude maneuvers, so that the motion of the fuel may have a great impact on that of the whole spacecraft. Therefore, the attitude dynamics of liquid-filled spacecraft has attracted more and more attention. In some work associated with liquid-filled spacecraft, Miller et al. [17] investigated the attitude dynamics of a spacecraft perturbed by the motion of small oscillating submasses, a plate of torsional vibration, and a rotor immersed in a viscous fluid. However, the fluid was not really considered but merely used to apply damping to the rotor. Yue [18] studied the chaotic dynamics of a spacecraft with a small flexible appendage and a completely liquid-filled cavity by Melnikov’s method. Nichkawde et al. [19] examined the coupled slosh-vehicle dynamics of a four-degree-of-freedom multibody system in planar motion, in which the sloshing motion of the liquid was modeled as a simple pendulum. Kuang et al. [20] investigated the attitude motions of a gyrostat with an axisymmetrical and fluid-filled cavity in the cases of no torque and small perturbation torque, respectively. Zhou et al. [21] studied the chaotic dynamics of a damped satellite with a partially liquid-filled cylindrical tank subjected to external disturbances by means of linearization analysis. To simplify the model, they assumed that the liquid is solidified and has the same angular velocity as the satellite.

The contribution of this work to the current literature is mainly in two aspects. Firstly, in the previous studies, only one liquid-filled cavity is considered in the spacecraft. However, to meet the requirements of space missions, spacecraft may need to carry multiple liquids stored in different cavities. Because of the differences in the properties, such as mass and viscosity, of these liquids, the motion of spacecraft becomes more complex and its chaotic behaviors are more difficult to predict. By contrast, we not only obtained an analytical criterion for predicting the chaotic motion of the dual-liquid-filled spacecraft but also verified the validity of the criterion by numerical simulation. Secondly, because the parameters of the rotor and liquids are uncoupled in the obtained criterion, it is easy to modify the criterion to fit the systems with multiple liquids and rotors. In addition, we also discussed the comprehensive effects of the parameters of the liquids on the chaotic region, and the results are of guiding significance for the systems with multiple liquids.

This paper is organized as follows. In Sect. 2, the dynamic equations of the spacecraft system are derived and transferred into dimensionless form. In Sect. 3, the analytical criterion is obtained by Melnikov’s method. In Sect. 4, the attitude evolution of the system is analyzed by the criterion and numerical simulation. Finally, the conclusions are illustrated in Sect. 5.

2 Dynamic equations of the system

2.1 Model description

The spacecraft under investigation is presented in Fig. 1, which consists of a main rigid body $B_1$, homogeneous liquids filled in spherical tanks $B_2$ and $B_3$, and a rotor $B_4$. The body-fixed frame $\mathcal {F}(C_s ,e_1 ,e_2 ,e_3 )$ is attached to the center of mass of the entire system $C_s$. The rotation axis of the rotor is parallel to the $e_2$ axis. The mass of the component $B_i \;(i=1, 2, 3, 4)$ is $m_i$, and its center of mass is located at $C_i$. The vector from $C_s$ to $C_i$, called the position vector of $B_i$, is denoted as ${\varvec{\rho }}_i$. In addition, the mass moment of inertia of $B_i$ about its center of mass is ${{\varvec{J}}}_i$, which can be particularly expressed as ${{\varvec{J}}}_2 =J_2 {{\varvec{E}}}_3$ and ${{\varvec{J}}}_3 =J_3 {{\varvec{E}}}_3$ for the liquids, respectively, where ${{\varvec{E}}}_3$ represents a $3\times 3$ identity matrix. The inertial angular velocity of $B_1$ in the frame $\mathcal {F}$ is $\varvec{\omega }_1$, and the relative angular velocity between $B_1$ and $B_i \;(i=2, 3, 4)$ is defined in the frame $\mathcal {F}$ as $\varvec{\omega }_i$, and thus, the inertial angular velocity of $B_i \;(i=2, 3, 4)$ can be expressed as $\varvec{\omega }_1 +\varvec{\omega }_i$. It is worth noting that the motion of each component dose not shift the position of the center of mass of the whole system.

Due to the complexity of space environment, the attitude evolution of spacecraft will be affected by many factors, such as gravity gradient, atmosphere drag, and orbital motion. To simplify our problem, some physical assumptions are made as follows:

• Assumption 1 the spacecraft is in a high orbit

• Assumption 2 the mass of the spacecraft is much less than that of the earth

• Assumption 3 the dimensions of the spacecraft relative to the high orbit around the earth are small

• Assumption 4 the spacecraft is fast spinning

• Assumption 5 the rotation rate of the rotor is periodic

Assumption 1 means that the atmosphere drag is negligible. Assumptions 2 and 3 indicate that the orbital motion is independent of the rotation of the spacecraft and the gravity gradient can be regarded as a perturbation of the attitude dynamics [22, 23]. Assumption 4 demonstrates that for a spacecraft with large rotational angular momentum, the effect of the gravity gradient on its chaotic motion can be neglected [24]. Under the above assumptions, the orbital dynamics and attitude dynamics of the spacecraft are decoupled and the center of mass of the spacecraft is always in orbit. Assumption 5 causes a periodic internal perturbation to the spacecraft [25, 26]. Hence, the external perturbations and orbital dynamics can be neglected, that is, our spacecraft is torque-free and is only subject to the internal perturbation.

2.2 Dynamic equations

The dynamic equations of the spacecraft are derived based on Hamiltonian mechanics. According to the model description, the kinetic energy of the system is

$$\begin{aligned} T= & {} \frac{1}{2}\varvec{\omega }_1^T \left( {{{\varvec{J}}}_1 -\sum _{i=1}^4 {m_i \tilde{\varvec{\rho }}_i \tilde{\varvec{\rho }}_i } } \right) \varvec{\omega }_1\nonumber \\&+\frac{1}{2}\sum _{i=2}^4 {(\varvec{\omega }_1 +\varvec{\omega }_i )^{T}{{\varvec{J}}}_i (\varvec{\omega }_1 +\varvec{\omega }_i )} \end{aligned}$$

(1)

where the symbol “$\sim$” represents the skew symmetric matrix of a vector. Under the aforementioned assumptions, the external torques such as gravity gradient and atmospheric drag are neglected so that the potential energy of the system is $V=0$. Assuming that $e_1$, $e_2$, and $e_3$ are the principle axes of inertia, the moment of inertia matrix of the system in the frame $\mathcal {F}$ can be expressed as

$$\begin{aligned} {{\varvec{J}}}_s =\sum _{i=1}^4 {{{\varvec{J}}}_i -m_i \tilde{\varvec{\rho }}_i \tilde{\varvec{\rho }}_i } =\hbox {diag}(J_{s1} ,\;J_{s2} ,\;J_{s3} ). \end{aligned}$$

(2)

Then, the Hamiltonian of the system can be written as

$$\begin{aligned} \mathcal {H}=\frac{1}{2}\varvec{\omega }_1^T {{\varvec{J}}}_s \varvec{\omega }_1 +\frac{1}{2}\sum _{i=2}^4 {\varvec{\omega }_1^T {{\varvec{J}}}_i \varvec{\omega }_i +\varvec{\omega }_i^T {{\varvec{J}}}_i (\varvec{\omega }_1 +\varvec{\omega }_i )}. \end{aligned}$$

(3)

Denoting the angular momentum vector of the system as ${{\varvec{h}}}_s =[{\begin{array}{ccc} {h_{s1} }&{} {h_{s2} }&{} {h_{s3} } \\ \end{array} }]^{T}$. Since the components of ${{\varvec{h}}}_s$ canonically conjugate those of $\varvec{\omega }_1$, one can obtain

$$\begin{aligned} {{\varvec{h}}}_s =\left( {\frac{\partial \mathcal {H}}{\partial \varvec{\omega }_1 }} \right) ^{T}={{\varvec{J}}}_s \varvec{\omega }_1 +\sum _{i=2}^4 {{{\varvec{J}}}_i \varvec{\omega }_i } \end{aligned}$$

(4)

and $\varvec{\omega }_1$ can be explicitly expressed as

$$\begin{aligned} \varvec{\omega }_1 ={{\varvec{J}}}_s^{-1} \left( {{{\varvec{h}}}_s -\sum _{i=2}^4 {{{\varvec{J}}}_i \varvec{\omega }_i } } \right) . \end{aligned}$$

(5)

Taking the derivative of ${{\varvec{h}}}_s$ with respect to time yields

$$\begin{aligned} \dot{{{\varvec{h}}}}_s +\tilde{\varvec{\omega }}_1 {{\varvec{h}}}_s ={{\varvec{M}}}_e \end{aligned}$$

(6)

where ${{\varvec{M}}}_e$ is the external torque vector (here, ${{\varvec{M}}}_e =\mathbf{0})$. Since $\tilde{\varvec{\omega }}_1 {{\varvec{h}}}_s =-\tilde{{{\varvec{h}}}}_s \varvec{\omega }_1$, Eq. (6) can be simplified to be

$$\begin{aligned} \dot{{{\varvec{h}}}}_s =\tilde{{{\varvec{h}}}}_s {{\varvec{J}}}_s^{-1} \left( {{{\varvec{h}}}_s -\sum _{i=2}^4 {{{\varvec{J}}}_i \varvec{\omega }_i } } \right) . \end{aligned}$$

(7)

The angular momentum vectors of the liquids can be written as

$$\begin{aligned} {{\varvec{h}}}_i ={{\varvec{J}}}_i (\varvec{\omega }_1 +\varvec{\omega }_i ),\quad i=2, 3, \end{aligned}$$

(8)

and the time derivative of Eq. (8) yields

$$\begin{aligned} \dot{{{\varvec{h}}}}_i ={{\varvec{J}}}_i (\dot{\varvec{\omega }}_1 +\dot{\varvec{\omega }}_i )={{\varvec{M}}}_i ,\quad i=2, 3 \end{aligned}$$

(9)

where ${{\varvec{M}}}_i =-c_i \varvec{\omega }_i$ is the damping torque acting on the liquid $B_i$, in which $c_i$ is the viscous damping coefficient; then, one can obtain

$$\begin{aligned} \dot{\varvec{\omega }}_i =- \dot{\varvec{\omega }}_1 -c_i {{\varvec{J}}}_i^{-1} \varvec{\omega }_i ,\quad i=2, 3. \end{aligned}$$

(10)

Substituting the time derivative of Eq. (5) in Eq. (10) gives

$$\begin{aligned}&\left[ {{\begin{array}{l} {\dot{\varvec{\omega }}_2 } \\ {\dot{\varvec{\omega }}_3 } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {{{\varvec{J}}}_s -{{\varvec{J}}}_2 }&{} {-{{\varvec{J}}}_3 } \\ {-{{\varvec{J}}}_2 }&{} {{{\varvec{J}}}_s -{{\varvec{J}}}_3 } \\ \end{array} }} \right] ^{-1} \times \left[ {{\begin{array}{c} {-\dot{{{\varvec{h}}}}_s +{{\varvec{J}}}_4 \dot{\varvec{\omega }}_4 -c_2 {{\varvec{J}}}_s {{\varvec{J}}}_2^{-1} \varvec{\omega }_2 } \\ {-\dot{{{\varvec{h}}}}_s +{{\varvec{J}}}_4 \dot{\varvec{\omega }}_4 -c_3 {{\varvec{J}}}_s {{\varvec{J}}}_3^{-1} \varvec{\omega }_3 } \\ \end{array} }} \right] \nonumber \\&\quad =\left[ {{\begin{array}{c} {({{\varvec{J}}}_s -{{\varvec{J}}}_2 -{{\varvec{J}}}_3 )^{-1}\left( {-\dot{{{\varvec{h}}}}_s +{{\varvec{J}}}_4 \dot{\varvec{\omega }}_4 -c_2 ({{\varvec{J}}}_s -{{\varvec{J}}}_3 ){{\varvec{J}}}_2^{-1} \varvec{\omega }_2 -c_3 \varvec{\omega }_3 } \right) } \\ {({{\varvec{J}}}_s -{{\varvec{J}}}_2 -{{\varvec{J}}}_3 )^{-1}\left( {-\dot{{{\varvec{h}}}}_s +{{\varvec{J}}}_4 \dot{\varvec{\omega }}_4 -c_2 \varvec{\omega }_2 -c_3 ({{\varvec{J}}}_s -{{\varvec{J}}}_2 ){{\varvec{J}}}_3^{-1} \varvec{\omega }_3 } \right) } \\ \end{array} }} \right] . \end{aligned}$$

(11)

The angular velocity of the rotor on account of Assumption 5 can be written as

$$\begin{aligned} \varvec{\omega }_4 =[{\begin{array}{c@{\quad }c@{\quad }c} 0&{\varpi _0 + \Lambda \hbox {sin}(\varOmega _1 t)}&0 \end{array} }]^{T} \end{aligned}$$

(12)

where $\varpi _0$ is a constant term and $\Lambda \hbox {sin}(\varOmega _1 t)$ is a time-varying term with the amplitude $\Lambda$ and frequency $\varOmega _1$. Then, the time derivative of $\varvec{\omega }_4$ is given by

$$\begin{aligned} \dot{\varvec{\omega }}_4 =[{\begin{array}{c@{\quad }c@{\quad }c} 0&{\Lambda \varOmega _1 \cos (\varOmega _1 t)}&0 \end{array} }]^{T}, \end{aligned}$$

(13)

and accordingly, the rotor torque is simple harmonic. In practice, such a torque may arise under malfunction of the control system or from an unbalanced rotor [9]; besides, the periodic torque can be generated actively and then be used to stabilize the attitude trajectory or change the evolution type of spacecraft by adjusting the amplitude and frequency [26].

Equations (7) and (11–13) are the dynamic equations governing the attitude evolution of the system.

2.3 Nondimensionalization

To analyze the dynamic behavior of the system in parameter space expediently, Eqs. (7) and (11–13) are expressed in dimensionless form. Without loss of generality, we assume that $J_{s1}<J_{s3} <J_{s2}$. Moreover, a small disturbance parameter $\varepsilon$ is required for the application of Melnikov’s method. The relative sizes of spacecraft parameters are assumed to be

$$\begin{aligned} {{\varvec{J}}}_4= & {} \mathcal {O}(\varepsilon ),\quad {{\varvec{J}}}_2 =\mathcal {O}(\sqrt{\varepsilon }),\quad {{\varvec{J}}}_3 =\mathcal {O}(\sqrt{\varepsilon }),\nonumber \\ \varvec{\omega }_2= & {} \mathcal {O}(\sqrt{\varepsilon }),\quad \varvec{\omega }_3 =\mathcal {O}(\sqrt{\varepsilon }) \end{aligned}$$

(14)

and all other quantities are $\mathcal {O}(1)$, that is, the rotor and liquids are small with respect to the entire spacecraft and the relative angular velocities of the liquids are also small. Then, we define $\tau =h t/J_{s3}$ as dimensionless time, in which h is the magnitude of ${{\varvec{h}}}_s$; hence, the derivative with respect to $\tau$ can be expressed as

$$\begin{aligned} ( \cdot )'=\frac{\hbox {d}( \cdot )}{\hbox {d}\tau }=\frac{J_{s3} }{h}\frac{\hbox {d}( \cdot )}{\hbox {d} t} \end{aligned}$$

(15)

and other dimensionless quantities are introduced as follows:

$$\begin{aligned} \begin{aligned} \varepsilon&=\frac{J_{42} }{J_{s3} },\quad \hat{{\gamma }}_1 =\frac{J_{s1} }{J_{s3} },\quad \hat{{\gamma }}_2 =\frac{J_{s2} }{J_{s3} },\\\ \hat{{\eta }}_2&=\frac{\sqrt{\varepsilon }J_2 }{J_{42} },\quad \hat{{\eta }}_3 =\frac{\sqrt{\varepsilon }J_3 }{J_{42} }, \\ \hat{{c}}_2&=\frac{c_2 }{h},\quad \hat{{c}}_3 =\frac{c_3 }{h},\quad \hat{{\varpi }}_0 =\frac{J_{s3} }{h}\varpi _0 ,\\ \hat{{\Lambda }}&=\frac{J_{s3} }{h}\Lambda ,\quad \hat{{\varOmega }}_1 =\frac{J_{s3} }{h}\varOmega _1 , \\ \hat{{{{\varvec{h}}}}}_s&=\frac{{{\varvec{h}}}_s }{h},\quad \hat{{\varvec{\omega }}}_1 =\frac{J_{s3} }{h}\varvec{\omega }_1 ,\quad \\ \hat{{\varvec{\omega }}}_2&=\frac{J_{s3} }{\sqrt{\varepsilon }h}\varvec{\omega }_2 ,\quad \hat{{\varvec{\omega }}}_3 =\frac{J_{s3} }{\sqrt{\varepsilon }h}\varvec{\omega }_3 \\ \end{aligned} \end{aligned}$$

(16)

where $J_{42}$ is the component of ${{\varvec{J}}}_4$ on the $e_2$ axis and all dimensionless quantities except $\varepsilon$ and $\tau$ are denoted with a hat. Thus, the dimensionless moment of inertia matrices of the system and liquids can be expressed as

$$\begin{aligned} \hat{{{{\varvec{J}}}}}_s= & {} \frac{{{\varvec{J}}}_s }{J_{s3} }=\hbox {diag}(\hat{{\gamma }}_1 , \hat{{\gamma }}_2 , 1),\quad \hat{{{{\varvec{J}}}}}_2 =\frac{{{\varvec{J}}}_2 }{J_{s3} }=\sqrt{\varepsilon }\hat{{\eta }}_2 {{\varvec{E}}}_3 ,\nonumber \\ \hat{{{{\varvec{J}}}}}_3= & {} \frac{{{\varvec{J}}}_3 }{J_{s3} }=\sqrt{\varepsilon }\hat{{\eta }}_3 {{\varvec{E}}}_3. \end{aligned}$$

(17)

Substituting Eq. (16) in Eqs. (7) and (11–13) yields

$$\begin{aligned} {\hat{{{{\varvec{h}}}}}'}_s ={{\varvec{D}}} \hat{{{{\varvec{h}}}}}_s -\varepsilon {{\varvec{D}}}(\hat{{\eta }}_2 \hat{{\varvec{\omega }}}_2 +\hat{{\eta }}_3 \hat{{\varvec{\omega }}}_3 +\hat{{\varvec{\omega }}}_4 ) \end{aligned}$$

(18)

where

$$\begin{aligned} {{\varvec{D}}}(\hat{{{{\varvec{h}}}}}_s )=\left[ {{\begin{array}{ccc} 0&{} {-\hat{{h}}_{s3} /\hat{{\gamma }}_2 }&{} {\hat{{h}}_{s2} } \\ {\hat{{h}}_{s3} /\hat{{\gamma }}_1 }&{} 0&{} {-\hat{{h}}_{s1} } \\ {-\hat{{h}}_{s2} /\hat{{\gamma }}_1 }&{} {\hat{{h}}_{s1} /\hat{{\gamma }}_2 }&{} 0 \\ \end{array} }} \right] \end{aligned}$$

and

$$\begin{aligned} \sqrt{\varepsilon }{\hat{{\varvec{\omega }}}'}_{2}= & {} (\hat{{{{\varvec{J}}}}}_s -\hat{{{{\varvec{J}}}}}_2 -\hat{{{{\varvec{J}}}}}_3 )^{-1}\left( -{\hat{{{{\varvec{h}}}}}'}_s +\varepsilon {\hat{{\varvec{\omega }}}'}_4 \right. \nonumber \\&\quad \left. -\sqrt{\varepsilon }\hat{{c}}_2 (\hat{{{{\varvec{J}}}}}_s -\hat{{{{\varvec{J}}}}}_3 )\hat{{{{\varvec{J}}}}}_2^{-1} \hat{{\varvec{\omega }}}_2 -\sqrt{\varepsilon }\hat{{c}}_3 \hat{{\varvec{\omega }}}_3 \right) \nonumber \\= & {} \left( {\hat{{{{\varvec{J}}}}}_s -\sqrt{\varepsilon }(\hat{{\eta }}_2 +\hat{{\eta }}_3 ){{\varvec{E}}}_3 } \right) ^{-1}\nonumber \\&\left( -{\hat{{{{\varvec{h}}}}}'}_s +\varepsilon {\hat{{\varvec{\omega }}}'}_4 -\hat{{c}}_2 (\hat{{{{\varvec{J}}}}}_s -\sqrt{\varepsilon }\hat{{\eta }}_3 {{\varvec{E}}}_3 )\hat{{\varvec{\omega }}}_2 /\hat{{\eta }}_2\right. \nonumber \\&\quad \left. -\sqrt{\varepsilon }\hat{{c}}_3 \hat{{\varvec{\omega }}}_3 \right) \end{aligned}$$

(19)

$$\begin{aligned} \sqrt{\varepsilon }{\hat{{\varvec{\omega }}}'}_{3}= & {} (\hat{{{{\varvec{J}}}}}_s -\hat{{{{\varvec{J}}}}}_2 -\hat{{{{\varvec{J}}}}}_3 )^{-1}\left( -{\hat{{{{\varvec{h}}}}}'}_s +\varepsilon {\hat{{\varvec{\omega }}}'}_4 -\sqrt{\varepsilon }\hat{{c}}_2 \hat{{\varvec{\omega }}}_2\right. \nonumber \\&\left. -\sqrt{\varepsilon }\hat{{c}}_3 (\hat{{{{\varvec{J}}}}}_s -\hat{{{{\varvec{J}}}}}_2 )\hat{{{{\varvec{J}}}}}_3^{-1} \hat{{\varvec{\omega }}}_3 \right) \nonumber \\= & {} \left( {\hat{{{{\varvec{J}}}}}_s -\sqrt{\varepsilon }(\hat{{\eta }}_2 +\hat{{\eta }}_3 ){{\varvec{E}}}_3 } \right) ^{-1}\left( -{\hat{{{{\varvec{h}}}}}'}_s +\varepsilon {\hat{{\varvec{\omega }}}'}_4\right. \nonumber \\&\left. -\sqrt{\varepsilon }\hat{{c}}_2 \hat{{\varvec{\omega }}}_2 -\hat{{c}}_3 (\hat{{{{\varvec{J}}}}}_s-\sqrt{\varepsilon }\hat{{\eta }}_2 {{\varvec{E}}}_3 )\hat{{\varvec{\omega }}}_3 /\hat{{\eta }}_3 \right) \end{aligned}$$

(20)

$$\begin{aligned} \hat{{\varvec{\omega }}}_4= & {} [{\begin{array}{ccc} 0&{} {\hat{{\varpi }}_0 +\hat{{\Lambda }}\hbox {sin}(\hat{{\varOmega }}_1 \tau )}&{} 0 \\ \end{array} }]^{T} \end{aligned}$$

(21)

$$\begin{aligned} {\hat{{\varvec{\omega }}}'}_4= & {} [{\begin{array}{ccc} 0&{} {\hat{{\Lambda }}\hat{{\varOmega }}_1 \cos (\hat{{\varOmega }}_1 \tau )}&{} 0 \\ \end{array} }]^{T} \end{aligned}$$

(22)

Now, the dynamic equations of the system have been transformed into a form suitable for the application of Melnikov’s method.

3 Application of Melnikov’s method

3.1 Solutions for the unperturbed system

Melnikov’s method is an analytical technique to obtain the criterion for predicting the chaotic motion of the perturbed system based on unperturbed space phase. To apply the method, the unperturbed space phase must have a structure that includes heteroclinic connections between pairs of saddle points or orbits homoclinic to a single saddle point [17, 18]. Let $\varepsilon =0$, our system becomes unperturbed and its dynamic equations are given by

$$\begin{aligned} {\hat{{{{\varvec{h}}}}}'}_s= & {} {{\varvec{D}}} \hat{{{{\varvec{h}}}}}_s =\left[ {{\begin{array}{l} {(\hat{{\gamma }}_2 -1)\hat{{h}}_{s2} \hat{{h}}_{s3} /\hat{{\gamma }}_2 } \\ {(1-\hat{{\gamma }}_1 )\hat{{h}}_{s1} \hat{{h}}_{s3} /\hat{{\gamma }}_1 } \\ {(\hat{{\gamma }}_1 -\hat{{\gamma }}_2 )\hat{{h}}_{s1} \hat{{h}}_{s2} /(\hat{{\gamma }}_1 \hat{{\gamma }}_2 )} \\ \end{array} }} \right] \end{aligned}$$

(23)

$$\begin{aligned} \hat{{\varvec{\omega }}}_{2}= & {} -\hat{{\eta }}_2 \hat{{{{\varvec{J}}}}}_s^{-1} {\hat{{{{\varvec{h}}}}}'}_s /\hat{{c}}_2 =\left[ {{\begin{array}{l} {-\hat{{\eta }}_2 {\hat{{h}}}'_{s1} /(\hat{{c}}_2 \hat{{\gamma }}_1 )} \\ {-\hat{{\eta }}_2 {\hat{{h}}}'_{s2} /(\hat{{c}}_2 \hat{{\gamma }}_2 )} \\ {-\hat{{\eta }}_2 {\hat{{h}}}'_{s3} /\hat{{c}}_2 } \\ \end{array} }} \right] \end{aligned}$$

(24)

$$\begin{aligned} \hat{{\varvec{\omega }}}_{3}= & {} -\hat{{\eta }}_3 \hat{{{{\varvec{J}}}}}_s^{-1} {\hat{{{{\varvec{h}}}}}'}_s /\hat{{c}}_3 =\left[ {{\begin{array}{l} {-\hat{{\eta }}_3 {\hat{{h}}}'_{s1} /(\hat{{c}}_3 \hat{{\gamma }}_1 )} \\ {-\hat{{\eta }}_3 {\hat{{h}}}'_{s2} /(\hat{{c}}_3 \hat{{\gamma }}_2 )} \\ {-\hat{{\eta }}_3 {\hat{{h}}}'_{s3} /\hat{{c}}_3 } \\ \end{array} }} \right] \end{aligned}$$

(25)

and $\hat{{\varvec{\omega }}}_4$ and ${\hat{{\varvec{\omega }}}'}_4$ are unchanged from Eqs. (21) and (22). Obviously, the phase space of the unperturbed system is determined once the solutions for $\hat{{{{\varvec{h}}}}}_s$ are obtained. Utilizing hyperbolic trigonometric functions, the solutions along the heteroclinic orbits are given by

$$\begin{aligned} \hat{{{{\varvec{h}}}}}_s =\left[ {{\begin{array}{l} {\alpha _1 Q_1 \hbox {sech}(\hat{{\varOmega }}_2 \tau )} \\ {\alpha _2 Q_2 \hbox {sech}(\hat{{\varOmega }}_2 \tau )} \\ {\alpha _3 \hbox {tanh}(\hat{{\varOmega }}_2 \tau )} \\ \end{array} }} \right] \end{aligned}$$

(26)

where

$$\begin{aligned} Q_1= & {} \sqrt{\hat{{\gamma }}_1 (\hat{{\gamma }}_2 -1)/(\hat{{\gamma }}_2 -\hat{{\gamma }}_1 )}, \\ Q_2= & {} \sqrt{\hat{{\gamma }}_2 (1-\hat{{\gamma }}_1 )/(\hat{{\gamma }}_2 -\hat{{\gamma }}_1 )}, \\ \hat{{\varOmega }}_2= & {} \sqrt{(\hat{{\gamma }}_2 -1)(1-\hat{{\gamma }}_1 )/(\hat{{\gamma }}_1 \hat{{\gamma }}_2 )} \\ \end{aligned}$$

and $\alpha _i =\pm 1$ satisfying $\prod _{i=1}^3 {\alpha _i } =-1$ [1]. These permutations describe four heteroclinic orbits that can be seen from Fig. 2.

3.2 Melnikov criterion

The general form of Melnikov’s method considers the following systems:

$$\begin{aligned} {{\varvec{x}}'}={{\varvec{f}}}({{\varvec{x}}})+\varepsilon \;{{\varvec{g}}}({{\varvec{x}}},\tau ),\quad \quad {{\varvec{x}}}=[{\begin{array}{cc} {x_1 }&{} {x_2 } \\ \end{array} }]\in \mathbb {R}^{2} \end{aligned}$$

(27)

where ${{\varvec{f}}}({{\varvec{x}}})$ is a Hamiltonian vector field and $\varepsilon \;{{\varvec{g}}}({{\varvec{x}}},\tau )$ is a small periodic perturbation which is not necessarily Hamiltonian. Apparently, it is only suitable for systems whose Poincaré map is planar rather than our three-dimensional system about $\hat{{{{\varvec{h}}}}}_s$. However, the references [17, 18, 27] introduce an extension of Melnikov’s method, and the Melnikov integral is given by

$$\begin{aligned} \mathcal {M}_\pm (\tau _0 )= & {} \int _{-\infty }^{+\infty } \nabla \hat{{\mathcal {H}}}_0 [{{\varvec{y}}}_0 (\tau )]\cdot \{{{\varvec{f}}}[{{\varvec{y}}}_0 (\tau )]\nonumber \\&+ {{\varvec{g}}}[{{\varvec{y}}}_0 (\tau ),\tau +\tau _0 ]\}\hbox {d}\tau \end{aligned}$$

(28)

where $\hat{{\mathcal {H}}}_0 =\frac{1}{2}\hat{{{{\varvec{h}}}}}_s^T {{\varvec{J}}}_s^{-1} \hat{{{{\varvec{h}}}}}_s$ is the dimensionless Hamiltonian of the unperturbed system, $\nabla =\partial /\partial \hat{{{{\varvec{h}}}}}_s$ is a gradient operator, ${{\varvec{y}}}_0 (\tau )$ is the solution for the heteroclinic orbits of the unperturbed system, and ${{\varvec{f}}}[{{\varvec{y}}}_0 (\tau )]={{\varvec{D}}} \hat{{{{\varvec{h}}}}}_s$ and ${{\varvec{g}}}[{{\varvec{y}}}_0 (\tau ),\tau +\tau _0 ]=-{{\varvec{D}}}(\hat{{\eta }}_2 \hat{{\varvec{\omega }}}_2 +\hat{{\eta }}_3 \hat{{\varvec{\omega }}}_3 +\hat{{\varvec{\omega }}}_4 )$ are the unperturbed and perturbed parts of the system [see Eq. (18)], respectively. Note that

$$\begin{aligned} \begin{aligned}&\nabla \hat{{\mathcal {H}}}_0 \cdot {{\varvec{f}}}=\hat{{{{\varvec{h}}}}}_s^T {{\varvec{J}}}_s^{-1} {{\varvec{D}}} \hat{{{{\varvec{h}}}}}_s =[{\begin{array}{ccc} {\hat{{h}}_{s1} /\hat{{\gamma }}_1 }&{} {\hat{{h}}_{s2} /\hat{{\gamma }}_2 }&{} 1 \\ \end{array} }]\\&\quad \times \left[ {{\begin{array}{l} {(\hat{{\gamma }}_2 -1)\hat{{h}}_{s2} \hat{{h}}_{s3} /\hat{{\gamma }}_2 } \\ {(1-\hat{{\gamma }}_1 )\hat{{h}}_{s1} \hat{{h}}_{s3} /\hat{{\gamma }}_1 } \\ {(\hat{{\gamma }}_1 -\hat{{\gamma }}_2 )\hat{{h}}_{s1} \hat{{h}}_{s2} /(\hat{{\gamma }}_1 \hat{{\gamma }}_2 )} \\ \end{array} }} \right] =0; \\ \end{aligned} \end{aligned}$$

(29)

thus, the Melnikov integral can be simplified to

$$\begin{aligned} \begin{aligned} \mathcal {M}_\pm (\tau _0 )&=\int _{-\infty }^{+\infty } {\nabla \hat{{\mathcal {H}}}_0 [{{\varvec{y}}}_0 (\tau )]\cdot {{\varvec{g}}}[{{\varvec{y}}}_0 (\tau ),\tau +\tau _0 ]\hbox {d}\tau } \\&=-\int _{-\infty }^{+\infty } {\hat{{{{\varvec{h}}}}}_s^T {{\varvec{J}}}_s^{-1} {{\varvec{D}}}(\hat{{\eta }}_2 \hat{{\varvec{\omega }}}_2 +\hat{{\eta }}_3 \hat{{\varvec{\omega }}}_3 +\hat{{\varvec{\omega }}}_4 )\hbox {d}\tau }. \\ \end{aligned} \end{aligned}$$

(30)

Next, we also need to replace $\tau$ that appears explicitly by $\tau +\tau _0$ in terms of Melnikov’s method, and $\hat{{\varvec{\omega }}}_4 (\tau )$ can be rewritten as

$$\begin{aligned} \hat{{\varvec{\omega }}}_4 (\tau +\tau _0 )= & {} [ 0\; \hat{{\varpi }}_0 +\hat{{\Lambda }}\hbox {sin}(\hat{{\varOmega }}_1 \tau )\hbox {cos}(\hat{{\varOmega }}_1 \tau _0 )\nonumber \\&+\hat{{\Lambda }}\cos (\hat{{\varOmega }}_1 \tau )\sin (\hat{{\varOmega }}_1 \tau _0 )\; 0 ]^{T}. \end{aligned}$$

(31)

Substituting Eqs. (23–26) and (31) in Eq. (30), the Melnikov integral becomes

$$\begin{aligned} \mathcal {M}_\pm (\tau _0 )=\mathcal {M}_1 (\tau _0 )+\mathcal {M}_2 (\tau _0 )+\mathcal {M}_3 (\tau _0 ) \end{aligned}$$

(32)

where

$$\begin{aligned} \mathcal {M}_1 (\tau _0 )= & {} -\frac{Q_1^2 (\hat{{\gamma }}_2 -\hat{{\gamma }}_1 )^{2}}{\hat{{\gamma }}_1^2 \hat{{\gamma }}_2^2 }\left( {\frac{\hat{{\eta }}_2^2 }{\hat{{c}}_2 }+\frac{\hat{{\eta }}_3^2 }{\hat{{c}}_3 }} \right) \\&\times \int _{-\infty }^{+\infty } {\hbox {sech}^{{4}}(\hat{{\varOmega }}_2 \tau )\hbox {d}\tau } \\ \mathcal {M}_2 (\tau _0 )= & {} -\frac{Q_1^2 (1-\hat{{\gamma }}_1 )^{2}+Q_2^2 (\hat{{\gamma }}_2 -1)^{2}}{\hat{{\gamma }}_1^2 \hat{{\gamma }}_2^2 }\left( {\frac{\hat{{\eta }}_2^2 }{\hat{{c}}_2 }+\frac{\hat{{\eta }}_3^2 }{\hat{{c}}_3 }} \right) \\&\times \int _{-\infty }^{+\infty } {\hbox {sech}^{{2}}(\hat{{\varOmega }}_2 \tau )\hbox {tanh}^{\hbox {2}}(\hat{{\varOmega }}_2 \tau )\hbox {d}\tau } \\ \mathcal {M}_3 (\tau _0 )= & {} \frac{\alpha _1 \alpha _3 Q_1 \hat{{\Lambda }}(1-\hat{{\gamma }}_1 )\cos (\hat{{\varOmega }}_1 \tau _0 )}{\hat{{\gamma }}_1 \hat{{\gamma }}_2 } \\&\times \int _{-\infty }^{+\infty } {\hbox {sech}(\hat{{\varOmega }}_2 \tau )\hbox {tanh}(\hat{{\varOmega }}_2 \tau )\hbox {sin}(\hat{{\varOmega }}_1 \tau )\hbox {d}\tau } \\ \end{aligned}$$

The integrals in Eq. (32) can be evaluated symbolically by Mathematica. After integrating, the Melnikov function of our system is given by

$$\begin{aligned} \mathcal {M}_\pm (\tau _0 )= & {} \frac{\hbox {2}}{3\hat{{\varOmega }}_2 \hat{{\gamma }}_1^2 \hat{{\gamma }}_2^2 }\left[ \frac{3\alpha _1 \alpha _3 \pi (1-\hat{{\gamma }}_1 )\hat{{\gamma }}_1 \hat{{\gamma }}_2 Q_1 \hat{{\varOmega }}_1 \hat{{\Lambda }}}{2\hat{{\varOmega }}_2}\right. \nonumber \\&\left. \hbox {sech}\left( {\frac{\pi \hat{{\varOmega }}_1 }{2\hat{{\varOmega }}_2 }} \right) \cos (\hat{{\varOmega }}_1 \tau _0 )-\Delta _c \right] \end{aligned}$$

(33)

where

$$\begin{aligned} \Delta _c= & {} (\hat{{\eta }}_2^2 /\hat{{c}}_2 +\hat{{\eta }}_3^2 /\hat{{c}}_3 )[2(\hat{{\gamma }}_2 -\hat{{\gamma }}_1 )^{2}Q_1^2 Q_2^2 \\&+(1-\hat{{\gamma }}_1 )^{2}Q_1^2 +(\hat{{\gamma }}_2 -1)^{2}Q_2^2 ]. \end{aligned}$$

The transversal zeros of the Melnikov function indicate the existence of Smale horseshoes and chaos according to the Smale–Birkhoff theorem introduced in [2]. Since the cosinoidal term varies with $\tau _0$ and the constant term $\Delta _c >0$, zeros will occur whenever the amplitude of the cosinoidal term is greater than $\Delta _c$; namely, the Melnikov criterion for predicting the onset of chaos of the system in parameter space is

$$\begin{aligned} \frac{3\pi (1-\hat{{\gamma }}_1 )\hat{{\gamma }}_1 \hat{{\gamma }}_2 \;Q_1 \hat{{\varOmega }}_1 \hat{{\Lambda }}}{2\hat{{\varOmega }}_2 }\hbox {sech}\left( {\frac{\pi \hat{{\varOmega }}_1 }{2\hat{{\varOmega }}_2 }} \right) >\Delta _c. \end{aligned}$$

(34)

Fig. 2

Typical trajectories of the system

Table 1 Dimensionless system parameters used in Figs. 2 and 3

4 Analysis of the Melnikov criterion and numerical simulations

4.1 Classes of trajectories of the system

The trajectory of the spacecraft is generated by Eqs. (18–22), and its type is governed by the dimensionless system parameters $(\varepsilon ,\;\hat{{\gamma }}_1 ,\;\hat{{\gamma }}_2 ,\;\hat{{c}}_2 ,\;\hat{{c}}_3 ,\;\hat{{\eta }}_2 ,\;\hat{{\eta }}_3 ,\;\hat{{\varpi }}_0 ,\hat{{\Lambda }},\;\hat{{\varOmega }}_1 )$. The function ode45 of MATLAB that implements a Runge–Kutta method with a variable time step is used to solve these dynamic equations. The absolute and relative tolerances are set to $10^{-9}$ in all simulations. Considering that the magnitude of $\hat{{{{\varvec{h}}}}}_s$ is equal to 1 and the $e_2$ axis is the major axis of the spacecraft, the initial conditions of the system are set to

$$\begin{aligned} \begin{aligned} \hat{{{{\varvec{h}}}}}_s&=[{\cos (\pi /60)}\; 0\; {\sin (\pi /60)}]^\mathrm{T},\\ \hat{{\varvec{\omega }}}_2&=[{- 0.02}\; 0\; 0 ]^\mathrm{T}, \\ \hat{{\varvec{\omega }}}_3&=[ 0\; 0\; {-0.01} ]^\mathrm{T},\quad \hat{{\varvec{\omega }}}_4 =[0\; {0.10}\; 0 ]^\mathrm{T} \end{aligned} \end{aligned}$$

(35)

Figure 2 shows three types of trajectories of the system whose corresponding system parameters are listed in Table 1. In each subplot, the red dot represents the initial position of $\hat{{{{\varvec{h}}}}}_s$, the two red circles passing through the $\hat{{h}}_{s3}$ axis are the heteroclinic orbits given by Eq. (26), and the blue curve describes the trajectory of $\hat{{{{\varvec{h}}}}}_s$ on the surface of momentum sphere.

The first type of trajectory that decays to the positive or negative major axis spin (PMAS or NMAS) is shown in Fig. 2a, b, where the trajectory spirals outward from the start point of $\hat{{{{\varvec{h}}}}}_s$, crosses the heteroclinic orbits, and eventually reaches the stable center on the $\hat{{h}}_{s2}$ axis corresponding to the major axis $e_2$. The second type of trajectory that ends up in a period-1, period-2, or period-3 limit cycle around the $\hat{{h}}_{s2}$ axis is shown in Fig. 2c–e, where the blue band is the limit cycle. Note that we only show the steady-state structure of the period-3 limit cycle without previous unstable part. The third type of trajectory that is chaotic is shown in Fig. 2f, where the curve dose not settle down into a regular pattern like the others. In fact, a chaotic trajectory contains an infinite number of unstable periodic orbits.

The time history of $\hat{{{{\varvec{h}}}}}_{{\varvec{s}}}$ corresponding to the above trajectories is shown in Fig. 3. A large number of simulations illustrate that the first type of trajectory can reach PMAS or NMAS in a relatively short time and that for the second type of trajectory, it takes longer and longer for the trajectory to stabilize to a period-n limit cycle as n increases. As for the chaotic trajectory, even if the simulation time is very long, it will not stabilize to any regular structure and will eventually fill almost surface of the momentum sphere.

Fig. 3

Time history of the components of $\hat{{{{\varvec{h}}}}}_{{\varvec{s}}}$ corresponding to the trajectories of Fig. 2

4.2 Analysis of the Melnikov criterion in parameter subspaces

The dimensionless parameters $(\hat{{\gamma }}_1 ,\;\hat{{\gamma }}_2 ,\;\hat{{\eta }}_2 ,\;\hat{{\eta }}_3 ,\;\hat{{c}}_2 ,\;\hat{{c}}_3 ,\hat{{\Lambda }},\;\hat{{\varOmega }}_1 )$ that appear in the Melnikov criterion determine the hypersurface separating chaotic from nonchaotic region of the system. When the criterion and the restriction on the moment of inertia $(0<\hat{{\gamma }}_1<1<\hat{{\gamma }}_2 <1+\hat{{\gamma }}_1 )$ are satisfied, the system may exhibit chaotic behavior. By fixing some of these parameters, the surface generated by the rest is studied in a series of parameter subspaces, as shown in Figs. 4, 5, 6 and  7. The region surrounded by the surface in each subplot is chaotic. The values of the fixed system parameters in each case are listed in Table 2. Note that the ranges of $\hat{{\gamma }}_1$ and $\hat{{\gamma }}_2$ are $(\hat{{\gamma }}_2 -1,\;1)$ and $(1,\;1+\hat{{\gamma }}_1 )$, respectively, when they are treated as variables.

Fig. 4

Surface separating chaotic from nonchaotic region in $\hat{{\gamma }}_1 -\hat{{\Lambda }}-\hat{{\varOmega }}_1$ parameter space

Fig. 5

Surface separating chaotic from nonchaotic region in $\hat{{\gamma }}_2 -\hat{{\Lambda }}-\hat{{\varOmega }}_1$ parameter space

In Fig. 4, one can see that the chaotic region in each case shrinks and eventually disappears with the increase in $\hat{{\varOmega }}_1$ or $\hat{{\gamma }}_1$ but enlarges with the increase in $\hat{{\Lambda }}$. In addition, for a determined value of $\hat{{\Lambda }}$, the maximum of $\hat{{\varOmega }}_1$ which can lead to the chaotic motion of the spacecraft is larger in the case of $\hat{{\gamma }}_2 =1.05$. Figure 5 shows that the chaotic region in each case will decrease to zero as $\hat{{\varOmega }}_1$ increases or $\hat{{\gamma }}_2$ decreases. Moreover, for the same value of $\hat{{\gamma }}_2$, the chaotic region in the case of $\hat{{\gamma }}_1 =0.60$ is significantly greater than that in the case of $\hat{{\gamma }}_1 =0.90$. From Figs. 4 and 5, we can conclude that reducing the amplitude $\Lambda$ and increasing the frequency $\varOmega _1$ of periodic rotation of the rotor can effectively avoid the onset of chaotic motion. Figures 4 and 5 also demonstrate that the when the spacecraft becomes nearly symmetric, the chaotic motion is almost impossible to occur. It can be explained by the parameter $\hat{{\varOmega }}_2$ of heteroclinic orbits given in Eq. (26). Since $\hat{{\varOmega }}_2$ tends to zero as $\hat{{\gamma }}_1 \rightarrow 1$ or $\hat{{\gamma }}_2 \rightarrow 1$, the heteroclinic orbits will disappear, which in turn implies a nonchaotic behavior.

Fig. 6

Surface separating chaotic from nonchaotic region in $\hat{{c}}_2 -{\hat{{\Lambda }}}-\hat{{\varOmega }}_1$ parameter space

It can be observed from Fig. 6 that the chaotic region in each case enlarges rapidly when $\hat{{c}}_2$ is less than about 0.05 and then expands slowly; namely, the chaotic region is sensitive to the liquid with small damping coefficient. The surface vertically descents at $\hat{{c}}_2 =0.5$ because we impose $\hat{{c}}_i <0.5\;(i=2, 3)$. Comparing the two cases, we can see that the chaotic region of a nearly symmetric spacecraft, i.e., the case b), is significantly less than that of the case a).

Fig. 7

Surface separating chaotic from nonchaotic region in $\hat{{\eta }}_2 -{\hat{{\Lambda }}}-\hat{{\varOmega }}_1$ parameter space

As shown in Fig. 7, the chaotic region in each case monotonously shrinks on the axis of $\hat{{\eta }}_2$, but on the axis of $\hat{{\varOmega }}_1$, it first rises to a critical value and then gradually declines to zero. Since ${{\varvec{J}}}_2 =\sqrt{\varepsilon }\hat{{\eta }}_2 {{\varvec{J}}}_s$ [see Eq. (16)], the above result demonstrates that increasing the moment of inertia of the liquid is useful to avoid the chaotic motion of the spacecraft. The comparison of the two cases indicates that the maximum of $\hat{{\varOmega }}_1$ resulting in the chaotic motion in the case a) is much greater than that in the case b), while $\hat{{\eta }}_2$ has the opposite result. There are similar results for the $\hat{{c}}_3$ and $\hat{{\eta }}_3$.

Table 2 Dimensionless system parameters used in Figs. 4, 5, 6, 7

These above results indicate that the weight of each system parameter to the occurrence of chaotic motion of spacecraft may significantly alter in different cases. Therefore, determining the key parameters in the required conditions by an analytical criterion will contribute to the design and control of spacecraft, which is difficult to achieve by numerical simulation.

Fig. 8

Effect of the equivalent dimensionless liquid parameters a$\hat{{\eta }}_{\mathrm{eq}}$, and b$\hat{{c}}_{\mathrm{eq}}$ on the chaotic region

After analyzing each parameter of the liquids separately, the comprehensive effect of these parameters on the chaotic region is considered. Inspection of Eq. (34) reveals that the term associated with the liquids is $\hat{{\eta }}_2^2 /\hat{{c}}_2 +\hat{{\eta }}_3^2 /\hat{{c}}_3$, and thus, we define

$$\begin{aligned} \begin{aligned} \hat{{\eta }}_{\mathrm{eq}}&=\sqrt{\hat{{\eta }}_2^2 +\hat{{\eta }}_3^2 }, \\ \frac{1}{\hat{{c}}_{\mathrm{eq}} }&=\frac{1}{\hat{{c}}_2 }+\frac{1}{\hat{{c}}_3 } \\ \end{aligned} \end{aligned}$$

(36)

as the dimensionless equivalent moment of inertia and dimensionless equivalent viscous damping coefficient of the liquids $B_2$ and $B_3$, respectively. Figure 8a shows the Melnikov curve in $\hat{{\eta }}_{\mathrm{eq}} -\hat{{\Lambda }}-\hat{{\varOmega }}_1$ parameter space whose color shades from blue to red with the increase in $\hat{{\eta }}_{\mathrm{eq}}$. Note that $\hat{{\eta }}_2$ and $\hat{{\eta }}_3$ both change within the interval [0,1.4] with the step size of 0.05. Figure 8b shows the Melnikov curve in $\hat{{c}}_{\mathrm{eq}} -\hat{{\Lambda }}-\hat{{\varOmega }}_1$ parameter space whose color shades from blue to red with the increase in $\hat{{c}}_{\mathrm{eq}}$. Note that $\hat{{c}}_2$ and $\hat{{c}}_3$ both change within the interval [0.001,0.5] with the step size of 0.02. From Fig. 8, one can see that the chaotic region tends to zero with the increase in $\hat{{\eta }}_{\mathrm{eq}}$ and rapidly enlarges with $\hat{{c}}_{\mathrm{eq}} \in [0.001, 0.01]$, which is coincided with the results in Figs. 6 and 7. These results illuminate that the probability of chaotic motion of the spacecraft can be reduced availably by increasing the sum of squares of the moments of inertia $J_2^2 +J_3^2$ or reducing the sum of reciprocals of the viscous damping coefficient $1/c_2 +1/c_3$ of the liquids.

Fig. 9

Comparison of analytical and numerical results

Since the parameters of the rotor and liquids in Eq. (34) are uncoupled, it is easy to modify the criterion to fit the system with multiple liquids and rotors. For a spacecraft containing multiple liquids and rotors, its analytical criterion will have a similar form to Eq. (34), in which the term associated with the liquids $B_k \;(k=1, 2,\ldots ,l)$ will be $\sum _{k=1}^l {\hat{{\eta }}_k^2 /\hat{{c}}_k }$. In this case, the dimensionless equivalent parameters of the liquids are given by

$$\begin{aligned} \begin{aligned} \hat{{\eta }}_{\mathrm{eq}}&=\left( {\sum _{k=1}^l {\hat{{\eta }}_k^2 } } \right) ^{1/2}, \\ \frac{1}{\hat{{c}}_{\mathrm{eq}} }&=\sum _{k=1}^l {1/\hat{{c}}_k } \\ \end{aligned} \end{aligned}$$

(37)

and the chaotic region will still have the same relationship with $\hat{{\eta }}_{\mathrm{eq}}$ and $\hat{{c}}_{\mathrm{eq}}$. Therefore, the conclusions on the dimensionless equivalent parameters of liquids have wide applicability.

4.3 Comparison of the Melnikov criterion with numerical simulations

Numerical simulations are performed to verify the validity of the Melnikov criterion. The trajectories of the system need to be classified in terms of their steady-state structures. To avoid the extensive time consumption of enumerated procedure and the artificial error in the classification of trajectories, the largest Lyapunov exponent (LLE) is used to determine the types of trajectories. The trajectory of our system will decay to MAS if $\hbox {LLE}<0$, end up in a period-n limit cycle if $\hbox {LLE}=0$, and be chaotic if $\hbox {LLE}>0$ [2].

We used a method proposed in [28] for estimating LLE from small datasets, which directly follows from the definition of LLE and is fast, easy to implement, and robust to changes in quantities. The method is implemented by MATLAB, and the initial conditions are the same as Eq. (35). In addition, the default values of the system parameters used in each subplot are given in Eq. (38), which means that if a parameter is not treated as a variable or is not declared separately in a subplot, its value equals to that in Eq. (38). Finally, we used $1.2\times 10^{5}$ time steps with the step size of 0.1 and intercepted the last 2000 steps to reconstruct the phase space of system.

$$\begin{aligned} \hat{{\gamma }}_1= & {} 0.90,\quad \hat{{\gamma }}_2 =1.05,\quad \hat{{\eta }}_2 =0.20,\quad \hat{{\eta }}_3 =0.16,\nonumber \\ \hat{{c}}_2= & {} 0.10,\quad \hat{{c}}_3 =0.12 \end{aligned}$$

(38)

Figure 9 shows the comparison of analytical and numerical results. In each subplot, the red U-shaped curve represents the Melnikov criterion, the dark dots ($\bullet$) are trajectories that decay to PMAS, the green dots ( ) are trajectories that end in NMAS, the blue circles ( ) are limit-cycle trajectories, and the red crosses ( ) are chaotic trajectories. It can be seen that the Melnikov criterion can provide a good estimate of not only the chaotic but also periodic regions, which is helpful to avoid such two types of motion of the spacecraft.

5 Conclusions

The attitude evolution of a dual-liquid-filled spacecraft with energy dissipation subjected to internal periodic perturbations is studied, and an analytical criterion for predicting the occurrence of its chaotic motions is obtained, of which validity is verified by numerical simulation. The individual and comprehensive effects of system parameters on the chaotic region are investigated by using the criterion, which yields many valuable results: (1) the chaotic motion of spacecraft is almost impossible to occur if the components of moment of inertia approach each other, (2) the chaotic region is very sensitive to the liquid with small damping coefficient, (3) the chaotic region monotonically varies with the dimensionless equivalent liquid parameters $\hat{{\eta }}_{\mathrm{eq}}$ and $\hat{{c}}_{\mathrm{eq}}$, and (4) the criterion can provide a good estimate of not only the chaotic but also periodic regions. These results can be easily applied to the system containing multiple liquids and rotors with wide applicability. Therefore, our work provides a useful tool to analyze and predict the chaotic behavior of liquid-filled spacecraft for avoiding the potentially problematic chaotic motion.