Nonlinear vibrations of graphene-reinforced porous rotating conical shell with arbitrary boundary conditions using traveling wave vibration analysis

Abstract

In this paper, the nonlinear traveling wave vibrations are investigated for the graphene-reinforced porous aluminum-based sandwich rotating conical (GRPA-SRC) shell with the arbitrary boundary conditions. The material of the rotating conical shell is the sandwich structure composed of the graphene-reinforced porous aluminum-based (GRPA) material. Two surfaces of the rotating conical are made of the metallic aluminum and central core layer is the GRPA. There are three graphene distribution types and three porosity distributions applied to the nonlinear vibration analysis. We consider the comprehensive effect of combining the transverse harmonic excitation and in-plane load on the nonlinear traveling wave vibrations of the rotating conical shells. The first-order shear deformation theory (FSDT) and von Kármán nonlinear strain–displacement relations are employed in the structural modeling. The effects of Coriolis forces and initial hoop tensions are considered to obtain the kinetic energy, potential energy and external force work. Since the vibration form of the rotating conical shell is the traveling wave vibration, the trigonometric functions are used to represent the mode in the circumferential direction. Chebyshev polynomials are used to solve the axial direction. Further utilizing energy principle, the nonlinear ordinary differential equations are obtained for the GRPA-SRC shell with two degrees of freedom. The amplitude–frequency response curves, force–amplitude response curves, bifurcation diagrams, maximum Lyapunov exponent, waveforms, phase portraits and Poincare map of the GRPA-SRC shell are calculated by using Runge–Kutta method. Adding the springs at both ends of the GRPA-SRC shell can simulate the arbitrary boundary conditions. During the solution process, the circumferential direction of the GRPA-SRC shell is represented by the trigonometric function, and direction of the generatrix is denoted by using Chebyshev polynomials. The arbitrary boundary conditions are obtained for changing the spring potential energy. This work is expected to provide the practical value for the nonlinear vibrations of the graphene-reinforced porous metal rotating shell with the arbitrary boundary conditions.

1 Introduction

The GRPA materials retain the excellent properties of the graphene-reinforced composites, including two-dimensional open large surface, high conductivity and high thermal conductivity. Additionally, research has demonstrated that the graphene-reinforced porous materials can exhibit unique properties including the open band gap, large specific surface area and high mechanical strength [1,2,3]. The rotating conical shells are widely used in the aerospace, missile nose cones, gas turbines, high-speed centrifugal separators, high-power jet engines, motors and rotor systems. The top of the missile, namely the missile nose cone, is the conical shell structure with the cantilever boundary condition. In the design process, starting from the requirements of the lightweight structure, the metal porous materials are widely used in this structure. Adding a small amount of the graphene materials will cause the changes of the significant structural parameters. In order to meet the requirements of the structural performance, the material selected in this article is the GRPA material. This article conducts the theoretical research on the nonlinear vibrations of the GRPA-SRC shell and provides the practical references for the engineering fields. The GRPA-SRC shells are influenced by Coriolis force and initial ring tensor, making the nonlinear vibrations of the GRPA-SRC shells more complex and requiring investigation through the traveling wave vibrations [4,5,6]. At present, a significant amount of researches have been conducted on the conical shells with the classical boundary conditions, such as the simply supported, clamped supported and free boundary conditions. However, some structures cannot be described by the classical boundary conditions. The novelty of this paper is the adding the springs at both ends of the GRPA-SRC shell to simulate the arbitrary boundary conditions. The circumferential direction of the GRPA-SRC shell is represented by the trigonometric function, and the direction of the generatrix is solved by using Chebyshev polynomials during the solution process. The arbitrary boundary conditions are achieved by changing the spring potential energy. This paper provides the valuable ideas for studying of the nonlinear vibrations in other rotating shells with the arbitrary boundary conditions.

The graphene-reinforced composites can significantly impact the mechanical properties of various composite structures, and a majority of researches have been conducted as referenced in [7,8,9,10,11]. The vibration researches of the graphene-reinforced metal porous (GRMP) focus on the beam, plate and shell structures. Kitipornchai et al. [12] examined the vibration characteristics of the GRMP beams based on the Timoshenko beam theory and found that the smaller the number of pores on the upper and lower surfaces of the beam, the larger the vibration frequency. Yas and Rahimi [13] investigated the thermal vibration of the functionally graded porous nanocomposite beams reinforced by the graphene platelets. Pan et al. [14] employed the differential quadrature method to solve the natural vibration problem of the GRMP plates. Using the FSDT and Chebyshev polynomials, Yang et al. [15] conducted research on the free vibration and buckling of the GRMP nanocomposite plates. Through the improved Donnell shell theory and Hamilton’s principle, the control equations of the GRMP cylindrical shells are obtained. The nonlinear frequencies of the GRMP cylindrical shells are determined by using the multi-scale method, as described in reference [16]. Dong et al. [17] explored the dimensionless natural frequency and critical velocity of the GRMP rotating cylindrical shells.

There are amounts of literatures interested in the free vibration and buckling of the rotating shell structures and other’s structures with the linear strain–displacement relations. Civalek et al. [18, 19] conducted the free vibration and buckling analysis on the carbon nanotube-reinforced composite material rectangular and non-rectangular plates by using the discrete singular convolution method. Sobhani et al. [20, 21] studied the vibration characteristics of the cowl shell-like structures and hemispherical–cyclical–conical shell structures. Yang et al. [22, 23] conducted studies on the free vibration and buckling analysis of the eccentric rotating cylindrical shells, utilizing carbon fiber-reinforced composites and graphene-reinforced composites as materials, respectively. Ghasemi and Meskini [24] explored the free vibration of the porous laminated composite rotating cylindrical shells under the simply supported boundary conditions. Song et al. [25] employed a combination of the orthogonal polynomials with Rayleigh–Ritz method to investigate the free vibration of the rotating cylindrical shells. Alujević et al. [26] analyzed the natural vibrations and mode shapes of the rotating cylindrical shells with the free boundary condition, assuming that the modes are represented by the trigonometric functions in the circumferential direction and the axis direction is represented by the sum of eight weighted exponential functions. Dey and Karmakar [27] utilized the finite element method to analyze the free vibration of the delaminated twisted graphite–epoxy cross-ply composite rotating conical shells. Under various classical boundary conditions, Hossein et al. [28, 29] examined the forward and backward wave frequencies of the thick rotating conical shells using the graphene nanoplatelet-reinforced materials and functionally graded agglomerated carbon nanotubes materials. Shakouri et al. [30], based on the generalized differential quadrature method and Donnel shell theory, considered the thermal condition and rotational speed to solve the natural vibration characteristics of the functionally graded material truncated conical shells.

There have been extensive researches on the nonlinear vibrations of the non-rotating cylindrical shells, conical shells and shells with interesting shapes. Among them, references [31,32,33,34] utilized various deformation theories and methodologies, exploring various boundary conditions in their investigation of the nonlinear vibrations of these shells. Pinho et al. [35] used Sanders-Koiter's nonlinear strain–displacement relationship to obtain the nonlinear dynamic governing equation of motion for the hyperbolic shell on the nonlinear free vibration. Dastjerdi et al. [36] studied the nonlinear dynamics of the functionally graded materials toroidal shape and cylindrical shell structures and took into account the combined effects of the temperature and humidity. Due to the fact that the rotating cylindrical and conical shell belongs to the traveling wave vibration, it is crucial to study the nonlinear large amplitude vibration. Based on the Lagrange equation and Chebyshev polynomials, Chai et al. [37, 38] investigated the nonlinear frequencies and frequency responses of the rotating cylindrical shells with the arbitrary elastic supports boundary conditions. In the study of the frequency responses, the boundary conditions are discontinuous. Sun et al. [39,40,41] explored the nonlinear traveling wave vibrations of the rotating thin-walled cylindrical shells with the multiple internal resonances, considering the influence of carbon nanotube-reinforced composite materials. Song et al. [42] conducted theoretical and experimental research on the nonlinear vibration of rotating cylindrical shells under the action of tip friction. Zhang et al. [43] studied the nonlinear forced vibration of the rotating thin-walled cylindrical shells under the harmonic excitations. Abdollahi et al. [44] investigated the nonlinear vibrations of the annular cylinders coupled with the fluid medium to identify the effective parameters on the stability margins at different rotation speeds. Aris and Ahmadi et al. [45] proposed the semi-analytical method to analyze the nonlinear vibration responses of the functionally graded material rotating conical shells.

One can observe that a large amount of researches are dedicated to the free vibration of the rotating cylindrical shells and conical shells, as well as the nonlinear vibration of cylindrical shells with the classical boundary conditions. It is a significant problem to study the nonlinear vibrations of the rotating conical shells with the general boundary conditions, for which the arbitrary boundary conditions are obtained by introducing the artificial springs. Li et al. [46] conducted the nonlinear vibration control of the cylindrical shell with the discontinuous piezoelectric plate on the elastic boundary conditions. Li et al. [47] used the artificial springs on all four sides of the cylindrical curved plate to simulate actual boundary conditions and analyzed the free vibration and modal shapes using the differential quadrature method. Regarding the arbitrary boundary conditions, references [48,49,50,51] analyzed the free vibration analysis of the cylindrical shells, conical shells, joined cylindrical–conical shells and other coupled shell structures. Ye et al. [52] established the unified solution to solve the free vibration problems for different types of open shell structures, including the cylindrical, conical and spheres shells with the spring boundary conditions.

In this paper, the nonlinear traveling wave vibrations are investigated for the GRPA-SRC shell. Five evenly distributed springs are added to both ends of the GRPA-SRC shells to obtain the arbitrary boundary conditions. The material of the rotating conical shell with the arbitrary boundary conditions is the graphene-reinforced metal porous materials. There are three graphene distribution types and three porosity distributions applied to the nonlinear vibration analysis. We consider the comprehensive effect of combining the transverse harmonic excitation and in-plane load on the nonlinear traveling wave vibrations of the rotating conical shells. The kinetic energy, potential energy and external force work of the rotating conical shell are obtained by using the FSDT and von Kármán nonlinear strain–displacement relations. Since the vibration form of the rotating conical shell is the traveling wave vibration, the trigonometric functions are used to represent the mode in the circumferential direction. Chebyshev polynomials are used to solve the axial direction. Further utilizing energy principle, the nonlinear ordinary differential equations are obtained for the GRPA-SRC shell with two degrees of freedom. The amplitude–frequency response curves, force–amplitude response curves, bifurcation diagram, maximum Lyapunov exponent, waveforms, phase portraits and Poincare map of the GRPA-SRC shell are calculated by using Runge–Kutta method. The approach in this paper provides a valuable idea for the study of the nonlinear vibrations in the rotational shell structures with the arbitrary boundary conditions.

2 Dynamic modeling of vibration

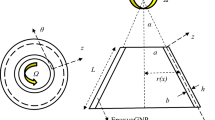
Figure 1a depicts the rotating conical shell model, where the length of the generatrix, semi-vertex angle, large radius and small radius are L, β, R_b and R_a, respectively. The orthogonal curvilinear coordinate system (x, θ, z) is fixed on the middle surfaces of the rotating conical shell. The conical shell rotates around the central axis at speed Ω; two torsion springs ($k_{\phi x} ,k_{\phi \theta }$) and three linear springs ($k_{u} ,k_{v} ,k_{w}$) are evenly distributed at both ends of the GRPA-SRC shell. The units for linear springs and rotational springs are N/m² and N/rad, respectively. The arbitrary elastic support boundary conditions are achieved by changing the elastic stiffness of the springs. The arbitrary position radius of the rotating conical shell is expressed as $R = R_{a} + x \cdot \sin \beta$.

Fig. 1

Dynamic model of the GRPA-SRC shell is given, a the rotating conical shell model, b the material distribution diagram of sandwich conical shell

Figure 1b demonstrates the material distribution types of the sandwich rotating conical shell, where the material on both sides with the thickness h_b is the metallic aluminum. The material of the central core layer with the thickness h is the GRPA material. There are three pore distribution types of the GRPA-SRC shells. According to the distribution forms of the pores along thickness of the conical shell, they are divided into the Type-1, Type-2 and Type-3, as shown in Fig. 2. The porosity distribution of the Type-1 is characterized by more pores in the middle. The Type-2 porosity distribution indicates that there are fewer pores in the middle. The Type-3 porosity distribution means that the pores are evenly distributed along the core layer thickness. Their material properties are presented as [15]

Fig. 2

Sketch maps are given for different porosity distribution types, a Type-1, b Type-2, c Type-3

Type-1:

$$ E_{{{\text{T1}}}} \left( z \right) = E_{G}^{ * } \left( {1 - N_{{\text{c}}} \cos \left( {\frac{\pi z}{h}} \right)} \right),\,\rho_{{{\text{T1}}}} \left( z \right) = \rho_{G}^{ * } \left( {1 - \rho_{{\text{c}}} \cos \left( {\frac{\pi z}{h}} \right)} \right),\,\rho_{{{\text{T1}}}} \left( z \right) = \rho_{G}^{ * } \left( {1 - \rho_{{\text{c}}} \cos \left( {\frac{\pi z}{h}} \right)} \right) $$

(1a)

Type-2:

$$ E_{{{\text{T2}}}} \left( z \right) = E_{G}^{ * } \left( {1 - N_{{\text{c}}}^{ * } \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right)} \right),\,\rho_{{{\text{T2}}}} \left( z \right) = \rho_{G}^{ * } \left( {1 - \rho_{{\text{c}}}^{ * } \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right)} \right) $$

(1b)

Type-3:

$$ E_{{{\text{T3}}}} \left( z \right) = E_{G}^{ * } \alpha ,\,\rho_{{{\text{T3}}}} \left( z \right) = \rho_{G}^{ * } \alpha^{ * } $$

(1c)

where $E_{G}^{ * }$ and $\rho_{G}^{ * }$ are the effective elastic modulus and density without the porosity, $N_{{\text{c}}}$, $N_{{\text{c}}}^{ * }$ and $\alpha$ correspond to the porosity coefficient of three distributions, respectively, $\rho$, $\rho_{c}^{ * }$ and $\alpha^{ * }$ are the mass density coefficients of three distributions, respectively.

Based on the improved Halpin–Tsai micromechanical model [15], the effective Young’s modulus of the graphene-reinforced composite materials is given as:

$$ E_{G}^{ * } = \frac{{3\left( {1 + \xi_{L} \eta_{L} V_{{{\text{GPL}}}} } \right)}}{{8\left( {1 - \eta_{L} V_{{{\text{GPL}}}} } \right)}}\,E_{{\text{m}}} + \frac{{5\left( {1 + \xi_{W} \eta_{W} V_{{{\text{GPL}}}} } \right)}}{{8\left( {1 - \eta_{W} V_{{{\text{GPL}}}} } \right)}}E_{{\text{m}}} $$

(2)

where

$$ \eta_{L}^{{}} = \frac{{E_{{{\text{GPL}}}} - E_{{\text{m}}} }}{{E_{{{\text{GPL}}}} + \xi_{L} E_{{\text{m}}} }},\,\eta_{W} = \frac{{E_{{{\text{GPL}}}} - E_{{\text{m}}} }}{{E_{{{\text{GPL}}}} + \xi_{W} E_{{\text{m}}} }},\,\xi_{L}^{{}} = \frac{{2l_{{{\text{GPL}}}} }}{{h_{{{\text{GPL}}}} }},\,\xi_{W}^{{}} = \frac{{2w_{{{\text{GPL}}}} }}{{h_{{{\text{GPL}}}} }} $$

(3)

where $l_{{{\text{GPL}}}}$, $w_{{{\text{GPL}}}}$ and $h_{{{\text{GPL}}}}$ are the length, width and thicknesses of the graphene platelets, respectively, $E_{{\text{m}}}$ and $E_{{{\text{GPL}}}}$ represent the Young’s modulus of the metal matrix and graphene materials, respectively, $V_{{{\text{GPL}}}}$ means volume content of the graphene.

According to the extended rule of the mixture, the density and Poisson’s ratio of the porous graphene-reinforced functionally gradient materials are obtained as follows [53]:

$$ \rho_{G}^{ * } = \rho_{{{\text{GPL}}}}^{{}} V_{{{\text{GPL}}}} + \rho_{{\text{m}}} \left( {1 - V_{{{\text{GPL}}}} } \right),\,v_{G}^{ * } = v_{{{\text{GPL}}}}^{{}} V_{{{\text{GPL}}}} + v_{{\text{m}}} \left( {1 - V_{{{\text{GPL}}}} } \right) $$

(4)

where $\rho_{{{\text{GPL}}}}^{{}}$ and $v_{{{\text{GPL}}}}^{{}}$ are the mass density and Poisson’s ratio of the graphene material, and ρ_m and v_m denote the parameters of the metal matrix. Poisson’s ratio for the open metal foam conical shell is fixed.

The typical mechanical property of the open-cell metal foams, Young’s modulus and density of the porous and non-porous materials are related to [53]

$$ \frac{{E_{T} \left( z \right)}}{{E_{G}^{ * } }} = \left( {\frac{{\rho_{T} \left( z \right)}}{{\rho_{G}^{ * } }}} \right)^{2} $$

(5)

The relationship between the porosity and mass density coefficients of three porosity distributions is further obtained as follows

$$ 1 - \rho_{{\text{c}}} \cos \left( {\frac{\pi z}{h}} \right) = \sqrt {1 - N_{{\text{c}}} \cos \left( {\frac{\pi z}{h}} \right)} ,\,\alpha^{ * } = \sqrt \alpha $$

(6a)

$$ 1 - \rho_{{\text{c}}}^{ * } \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right) = \sqrt {1 - N_{{\text{c}}}^{ * } \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right)} $$

(6b)

Assuming that the mass is equal for the graphene nanocomposite plates with different pores, it is deduced that the relationship between the porosities of the Type-1 distribution and other two distributions is given as follows

$$ \int_{0}^{{{\text{h}}/2}} {\sqrt {1 - N_{{\text{c}}}^{ * } \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right)} {\text{d}}z} = \int_{0}^{{{\text{h}}/2}} {\sqrt {1 - N_{{\text{c}}}^{{}} \cos \left( {\frac{\pi z}{h}} \right)} {\text{d}}z} $$

(7a)

$$ \int_{0}^{{{\text{h}}/2}} {\sqrt \alpha {\text{d}}z} = \int_{0}^{{{\text{h}}/2}} {\sqrt {1 - N_{{\text{c}}}^{{}} \cos \left( {\frac{\pi z}{h}} \right)} {\text{d}}z} $$

(7b)

Figure 3 demonstrates the distribution patterns of three graphene nanocomposite plates. In the figure, the blue color indicates a high graphene content, while the yellow color indicates a low graphene content. The GPL-X pattern denotes a low amount of the graphene in the middle and a high amount of the graphene on both sides. The GPL-O pattern means a high content of the graphene in the middle and less on both sides. The GPL-U pattern represents a uniform distribution of the graphene in the thickness direction. We assume that the content of the graphene nanocomposite plates in each pattern is equal, but the volume composition of the graphene varies differently along the plate thickness; the mathematical expressions for graphene volume fraction are as follows [15]

Fig. 3

Sketch maps are obtained for different distribution types of the graphene-reinforced types, a GPL-X, b GPL-O, c GPL-U

GPL-X

$$ V_{{{\text{GPL}}}} \left( z \right) = V_{i1} \left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right) $$

(8a)

GPL-O

$$ V_{{{\text{GPL}}}} \left( z \right) = V_{i2} \cos \left( {\frac{\pi z}{h}} \right) $$

(8b)

GPL-U

$$ V_{{{\text{GPL}}}} \left( z \right) = V_{i3} $$

(8c)

where $V_{i1}$, $V_{i2}$ and $V_{i3}$ denote the maximum volume components of three graphene distributions in the thickness direction, respectively, and subscripts i = 1, 2 and 3 correspond to the pore distributions of the Type-1, Type-2 and Type-3, respectively.

The total volume component $V_{{{\text{GPL}}}}^{ * }$ of the graphene is expressed by the total content $\Lambda_{{{\text{GPL}}}}^{{}}$ of the graphene nanocomposite plates [16]

$$ V_{{{\text{GPL}}}}^{ * } = \frac{{\Lambda_{{{\text{GPL}}}} \rho_{{\text{m}}} }}{{\Lambda_{{{\text{GPL}}}} \rho_{{\text{m}}} + \rho_{{{\text{GPL}}}} - \Lambda_{{{\text{GPL}}}} \rho_{{{\text{GPL}}}} }} $$

(9)

where the maximum volume components $V_{i1}$, $V_{i2}$ and $V_{i3}$ are calculated by the following formula.

GPL-X

$$ V_{{{\text{GPL}}}}^{ * } \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z = V_{i1} \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\left( {1 - \cos \left( {\frac{\pi z}{h}} \right)} \right)\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z $$

(10a)

GPL-O

$$ V_{{{\text{GPL}}}}^{ * } \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z = V_{i2} \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\left( {\cos \left( {\frac{\pi z}{h}} \right)} \right)\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z $$

(10b)

GPL-U

$$ V_{{{\text{GPL}}}}^{ * } \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z = V_{i3} \int_{{ - {\text{h}}/2}}^{{{\text{h}}/2}} {\frac{{\rho_{{\text{T}}} \left( z \right)}}{{\rho_{G}^{ * } \left( z \right)}}} {\text{d}}z $$

(10c)

According to reference [15], there is no special explanation for the material properties of the GRPA-SRC shell listed as follows

$$ \begin{gathered} E_{{{\text{GPL}}}} = {1}.0{1}\,{\text{TPa}},\; \, \rho_{{{\text{GPL}}}} = {1}0{62}.{5}\,{\text{kg}}/{\text{m}}^{{3}} ,\,v_{{{\text{GPL}}}} = 0.{186},\;l_{{{\text{GPL}}}} = {2}.{5}\,\mu {\text{m}}, \hfill \\ w_{{{\text{GPL}}}} = {1}.{5}\,\mu {\text{m}},\;h_{{{\text{GPL}}}} = {1}.{5}\,{\text{nm}},\;E_{{\text{m}}} = {7}0{\text{GPa}},\,\rho_{{\text{m}}} = {27}0{7}\,{\text{kg}}/{\text{m}}^{{3}} ,\;v_{{\text{m}}} = 0.{3}. \hfill \\ \end{gathered} $$

The displacement fields for the GRPA-SRC shell in the framework of the FSDT are written as:

$$ \hat{u} = u_{0} + z\phi_{x} ,\,\hat{v} = v_{0} + z\phi_{\theta } ,\,\hat{w} = w_{0} $$

(11)

where u₀, v₀ and w₀ are the mid-plane displacements and $\phi_{x}$ and $\phi_{\theta }$ represent the angular displacements about θ and x, respectively.

As a consequence, the following the nonlinear strain–displacement relationships are obtained as:

$$ \begin{gathered} \varepsilon_{x} = \varepsilon_{x}^{0} + z\varepsilon_{x}^{1} ,\,\varepsilon_{\theta } = \varepsilon_{\theta }^{0} + {\text{z}}\varepsilon_{\theta }^{1} ,\,\gamma_{x\theta } = \gamma_{x\theta }^{0} + z\gamma_{x\theta }^{1} \hfill \\ \gamma_{xz} = \phi_{x} + \frac{{\partial w_{0} }}{\partial x},\,\gamma_{\theta z} = \frac{1}{R}\left( {\frac{{\partial w_{0} }}{\partial \theta } - v_{0} \cos \beta } \right) + \phi_{\theta } \hfill \\ \end{gathered} $$

(12)

where $\varepsilon_{j}^{i}$ and $\gamma_{x\theta }^{i}$$\left( {i = 0,1;j = x,\theta ,x\theta } \right)$ are the expressions for the strain components, as shown in Appendix A.

In addition, the linear elastic constitutive relation of the GRPA-SRC shell is given as:

$$ \left\{ {\left. {\begin{array}{*{20}c} {\hat{\sigma }_{x} } \\ {\hat{\sigma }_{\theta } } \\ {\hat{\sigma }_{\theta z} } \\ {\hat{\sigma }_{xz} } \\ {\hat{\sigma }_{x\theta } } \\ \end{array} } \right\} = } \right.\left[ {\begin{array}{*{20}c} {\hat{Q}_{11} } & {\hat{Q}_{21} } & {} & {} & {} \\ {\hat{Q}_{12} } & {\hat{Q}_{22} } & {} & {} & {} \\ {} & {} & {K\hat{Q}_{44} } & {} & {} \\ {} & {} & {} & {K\hat{Q}_{55} } & {} \\ {} & {} & {} & {} & {\hat{Q}_{66} } \\ \end{array} } \right]\left. {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{\theta z} } \\ {\gamma_{xz} } \\ {\gamma_{x\theta } } \\ \end{array} } \right.} \right\} $$

(13)

where K = 5/6 is the shear correction coefficient, as shown in reference [15] and $\hat{Q}_{ij}$ are the stiffness coefficients are obtained as:

$$ \hat{Q}_{11} = \hat{Q}_{22} = \frac{{E_{{{\text{Ti}}}} \left( z \right)}}{{1 - \left( {v_{G}^{ * } } \right)^{2} }},\,\hat{Q}_{12} = \hat{Q}_{21} = \frac{{v_{G}^{ * } E_{{{\text{Ti}}}} \left( z \right)}}{{1 - \left( {v_{G}^{ * } } \right)^{2} }},\,\hat{Q}_{44} = \hat{Q}_{55} = \hat{Q}_{66} = \frac{{E_{Ti} \left( z \right)}}{{2\left( {1 + v_{G}^{ * } } \right)}} $$

(14)

The strain energy is expressed as:

$$ U = U_{{\text{c}}} + U_{{\text{h}}} + V_{{\text{s}}} $$

(15)

where U_c is the strain energy of the static conical shell, U_h is the strain energy caused by initial ring tensor and V_s is the spring potential energy.

The expressions are obtained as follows

$$ \begin{aligned} U_{{\text{c}}} = & \frac{1}{2}\iiint\limits_{V} {\left( {\varepsilon_{x} \hat{\sigma }_{x} + \varepsilon_{\theta } \hat{\sigma }_{\theta } + \gamma_{\theta z} \hat{\sigma }_{\theta z} + \gamma_{xz} \hat{\sigma }_{xz} + \gamma_{x\theta } \hat{\sigma }_{x\theta } } \right)R{\text{d}}V} \\ & = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{{\text{L}}} {(N_{xx} \varepsilon_{x}^{0} + M_{xx} \varepsilon_{x}^{1} + N_{\theta \theta } \varepsilon_{\theta }^{0} + M_{\theta \theta } \varepsilon_{\theta }^{1} + Q_{\theta z} \gamma_{\theta z} + N_{x\theta } \gamma_{x\theta }^{0} } } + M_{x\theta } \gamma_{x\theta }^{1} + Q_{xz} \gamma_{xz} )R{\text{d}}x{\text{d}}\uptheta \\ \end{aligned} $$

(16a)

$$ \left. {U_{{2}} = \frac{1}{2}\iiint\limits_{V} {\frac{{N_{\theta }^{\theta } }}{{R^{2} }}\left( {\left( {\hat{v}\cos \beta - \frac{{\partial \hat{w}}}{\partial \theta }} \right)^{2} + \left( {\hat{v}\sin \beta - \frac{{\partial \hat{u}}}{\partial \theta }} \right)^{2} } \right.} + \left( {\frac{{\partial \hat{v}}}{\partial \theta } + \hat{u}\sin \beta + \hat{w}\cos \beta } \right)^{2} } \right)R{\text{d}}V $$

(16a)

$$ \begin{aligned} V_{{\text{s}}} = & \frac{1}{2}\int_{0}^{2\pi } {\left[ {k_{u0} u_{0} + k_{v0} v_{0} + k_{w0} w_{0} + k_{\phi x0} \phi_{x} + k_{\phi \theta 0} \phi_{\theta } } \right]}_{x = 0} R_{a} {d\theta } \\ & + \frac{1}{2}\int_{0}^{2\pi } {\left[ {k_{uL} u_{0} + k_{vL} v_{0} + k_{wL} w_{0} + k_{\phi xL} \phi_{x} + k_{\phi \theta L} \phi_{\theta } } \right]}_{x = L} R_{b} {d\theta } \\ \end{aligned} $$

(16c)

where the internal forces and moments of the GRPA-SRC shell are obtained in Appendix B and the initial hoop tension of the GRPA-SRC shell $N_{\theta }^{\theta }$ is obtained by $N_{\theta }^{\theta } = \rho_{T} h\Omega^{2} R^{2}$.

The kinetic energy is represented as

$$ \begin{aligned} K = & \frac{1}{2}\iiint\limits_{V} {\rho \left( {2\Omega \sin \beta \left( {\dot{\hat{v}}\hat{u} - \hat{v}\dot{\hat{u}}} \right) + 2\Omega \cos \beta \left( {\dot{\hat{v}}\hat{w} - \dot{\hat{w}}\hat{v}} \right)} \right.} \\ & + \left. {\left( {\dot{\hat{u}}^{2} + \dot{\hat{v}}^{2} + \dot{\hat{w}}^{2} } \right) + \Omega^{2} \hat{v}^{2} + \Omega^{2} \left( {\hat{u}\sin \beta + \hat{w}\cos \beta } \right)^{2} } \right)R{\text{d}}V \\ \end{aligned} $$

(17)

The work done by the in-plane load and transverse harmonic excitation in terms of the transverse displacement is written as:

$$ W = \frac{1}{2}\int_{0}^{{2\pi }} {\int_{0}^{L} P } \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} R{\text{d}}x{\text{d}}\theta + \frac{1}{2}\int_{0}^{{2\pi }} {\int_{0}^{L} F } wR{\text{d}}x{\text{d}}\theta - \frac{1}{2}\int_{0}^{{2\pi }} {\int_{0}^{L} {\mu w\dot{w}R} } {\text{d}}x{\text{d}}\theta $$

(18)

where the in-plane load $P = P_{0} + P_{a} \cos (\varpi t)$, P₀ and P_a are the amplitudes of the static and dynamic parts of the in-plane load P, respectively, $F = F_{{\text{a}}} \cos (\varpi t)\left( {{\text{sin}}\left( {n\theta } \right) + \cos \left( {n\theta } \right)} \right)$ is the transverse harmonic excitation, F_a is the amplitude of F, μ is the damping coefficient and $\varpi$ represents the external excitation frequency.

3 Solution method

The vibration problem of the GRPA-SRC shell needs to investigate from the perspective of traveling wave vibration [24,25,26,27]. Therefore, the circumferential direction θ is represented by the trigonometric functions. The mode function along the x-direction is solved by Chebyshev polynomials [46].

The five displacement components in the middle plane are expressed as

$$ u_{0} = \sum\limits_{m = 1}^{M} {U_{m} T_{m}^{u0} \left( \xi \right)} \cdot \cos \left( {n\theta + \omega t} \right),\,v_{0} = \sum\limits_{m = 1}^{M} {V_{m} T_{m}^{v0} \left( \xi \right) \cdot \sin \left( {n\theta + \omega t} \right)} $$

(19a)

$$ w_{0} = \sum\limits_{m = 1}^{M} {W_{m} T_{m}^{w0} \left( \xi \right) \cdot \cos \left( {n\theta + \omega t} \right)} ,\,\phi_{x} = \sum\limits_{m = 1}^{M} {\Phi_{xm} T_{m}^{\phi x} \left( \xi \right) \cdot \cos \left( {n\theta + \omega t} \right)} $$

(19b)

$$ \phi_{\theta } = \sum\limits_{m = 1}^{M} {\Phi_{\theta m} T_{m}^{\phi \theta } \left( \xi \right) \cdot \sin \left( {n\theta + \omega t} \right)} $$

(19c)

where ξ = (2x/L − 1) are coordinate transformations from x to ξ. The reason for Chebyshev polynomials is orthogonal within the range of (− 1, 1). Letter n is the circumferential wave number. $U_{m}$, $V_{m}$, $W_{m}$, $\Phi_{xm}$ and $\Phi_{\theta m}$ are the unknown coefficients; $T_{m}^{a} \left( \xi \right)$ (a = u0, v0, w0, $\phi x$, $\phi \theta$) are Chebyshev polynomials and are obtained as follows [27, 46]

$$ T_{1}^{a} \left( \xi \right) = 1,\,T_{2}^{a} \left( \xi \right) = \xi ,\,T_{m}^{a} \left( \xi \right) = 2\xi T_{m - 1}^{a} \left( \xi \right) - T_{m - 2}^{a} \left( \xi \right),\,(m\, \ge \,{3}) $$

(20)

The algebraic equations are obtained by substituting Eqs. (19)–(20) into Eqs. (15)-(17) according to the Rayleigh–Ritz method.

$$ \begin{gathered} \frac{{\partial \left( {U_{\max } - T_{\max } } \right)}}{{U_{mn} }} = 0,\,\frac{{\partial \left( {U_{\max } - T_{\max } } \right)}}{{V_{mn} }} = 0,\,\frac{{\partial \left( {U_{\max } - T_{\max } } \right)}}{{W_{mn} }} = 0,\,\frac{{\partial \left( {U_{\max } - T_{\max } } \right)}}{{\Phi_{xmn} }} = 0 \hfill \\ \frac{{\partial \left( {U_{\max } - T_{\max } } \right)}}{{\Phi_{\theta mn} }} = 0,\,\left( {m = 1,2,3,...,M - 1,M.\,n = 1,2,3,...,N - 1,N.} \right) \hfill \\ \end{gathered} $$

(21)

In order to obtain the modes and frequencies of the GRPA-SRC shell, homogeneous linear algebra equations are solved by ignoring the nonlinear terms in Eq. (21). We further gain the characteristic equation matrix.

$$ \left( {{\mathbf{K}}_{{\mathbf{1}}} + \omega {\mathbf{K}}_{{\mathbf{2}}} + \omega^{2} {\mathbf{M}}} \right){\mathbf{X}} = 0 $$

(22)

where ${\mathbf{X}} = \left[ {U_{{1}} ,U_{{2}} ,...,U_{M} ,V_{{1}} ,V_{{2}} ,...,V_{M} ,W_{{1}} ,W_{{2}} ,...,W_{M} ,\Phi_{{x{1}}} ,\Phi_{x2} ,...,\Phi_{xM} ,\Phi_{{\theta {1}}} ,\Phi_{{\theta {2}}} ,...,\Phi_{\theta M} } \right]^{T}$ represents displacement vector, K₁ and M are the stiffness matrix and mass matrix, respectively, and K₂ represents the gyroscopic effect in spinning state.

The influence of Coriolis acceleration reflected in the K₂ matrix will cause the traveling wave vibrations of the GRPA-SRC shell, producing different forward ($\omega_{f}$) and backward ($\omega_{b}$) traveling wave frequencies under the same mode. Conducting research on the nonlinear vibrations of the traveling wave for the GRPA-SRC shell, we use the single-mode vibration corresponding to the fundamental frequency and reconsider the modal function expressions [33,34,35]

$$ u_{0} = T_{1}^{u0} \left( \xi \right)\left( {u_{1} \left( t \right)\cos \left( {n\theta } \right) + u_{2} \left( t \right)\sin \left( {n\theta } \right)} \right),\,v_{0} = T_{1}^{v0} \left( \xi \right)\left( {v_{1} \left( t \right)\sin \left( {n\theta } \right) + v_{2} \left( t \right)\cos \left( {n\theta } \right)} \right) $$

(23a)

$$ w_{0} = T_{1}^{{w0}} \left( \xi \right)\left( {w_{1} \left( t \right)\cos \left( {n\theta } \right) + w_{2} \left( t \right)\sin \left( {n\theta } \right)} \right),{\mkern 1mu} \phi _{x} = T_{1}^{{\phi x}} \left( \xi \right)\left( {\phi _{{x_{1} }} \left( t \right)\cos \left( {n\theta } \right) + \phi _{{x_{2} }} \left( t \right)\sin \left( {n\theta } \right)} \right) $$

(23b)

$$ \phi _{\theta } = T_{1}^{{\phi \theta }} \left( \xi \right)\left( {\phi _{{\theta _{1} }} \left( t \right)\sin \left( {n\theta } \right) + \phi _{{\theta _{2} }} \left( t \right)\cos \left( {n\theta } \right)} \right) $$

(23c)

where $u_{{\text{s}}}$, $v_{{\text{s}}}$, $w_{{\text{s}}}$, $\phi_{xs}$ and $\phi_{\theta s}$(s = 1, 2) represent the displacement of time t.

The subscript 1 or 2 is added to the generalized coordinate to indicate if it is associated with the cos or sin functions in θ except for v₀ and $\phi_{\theta }$, for which the two functions are exchanged (this subscript is not used for axisymmetric terms, since they have no dependence on θ). $\xi$ is the same as that in Eq. (18), and $T_{1}^{a}$ (a = u0, v0, w0 φx, φθ) are the first mode shape functions corresponding to the circumferential wave number n of the GRPA-SRC shell.

According to the Lagrange equation L = T − U, the nonlinear dynamic equations of the GRPA-SRC shell are given as

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{r} }}} \right) - \frac{\partial L}{{\partial q_{r} }} - \frac{\partial W}{{\partial q_{r} }} = 0 $$

(24)

where $q_{r} = \left[ {u_{1} ,u_{2} ,v_{1} ,v_{2} ,w_{1} ,w_{2} ,\phi_{x1} ,\phi_{x2} ,\phi_{\theta 1} ,\phi_{\theta 2} } \right]^{T}$.

The in-plane displacement ($u_{{\text{s}}}$,$v_{{\text{s}}}$) and rotational displacement $\left( {\phi_{xs} ,\phi_{{\theta {\text{s}}}} } \right)$ are represented by the transverse displacement (w_s) according to ignore their inertial terms (s = 1, 2) [29]. Further, the form of the nonlinear dynamic equations coupled with w₁ and w₂ of the GRPA-SRC shell is obtained as:

$$ \begin{aligned} \ddot{w}_{1} = & \mu_{11} \dot{w}_{1}^{{}} + \left( {\xi_{11} + \xi_{12} P_{a} } \right)w_{1}^{{}} + \left( {\xi_{13} + \xi_{14} P_{a} } \right)w_{2}^{{}} + \xi_{15} w_{1}^{2} + \xi_{16} w_{2}^{2} + \xi_{17} w_{1}^{2} w_{2}^{{}} + \xi_{18} w_{1}^{{}} w_{2}^{2} \\ & + \xi_{19} w_{1}^{3} + \xi_{110} w_{2}^{3} + \xi_{111} w_{1}^{{}} \dot{w}_{1}^{{}} + \xi_{112} \dot{w}_{1}^{{}} w_{2}^{{}} + + \xi_{113} w_{1}^{{}} \dot{w}_{2}^{{}} + \xi_{114} w_{2}^{{}} \dot{w}_{2}^{{}} + \xi_{115} w_{2}^{{}} + \xi_{116} F_{a} \\ \end{aligned} $$

(25a)

$$ \begin{aligned} \ddot{w}_{2} = & \mu_{12} \dot{w}_{2}^{{}} + \left( {\xi_{21} + \xi_{22} P_{a} } \right)w_{1}^{{}} + \left( {\xi_{23} + \xi_{24} P_{a} } \right)w_{2}^{{}} + \xi_{25} w_{1}^{2} + \xi_{26} w_{2}^{2} + \xi_{27} w_{1}^{2} w_{2}^{{}} + \xi_{28} w_{1}^{{}} w_{2}^{2} \\ & + \xi_{29} w_{1}^{3} + \xi_{210} w_{2}^{3} + \xi_{211} w_{1}^{{}} \dot{w}_{1}^{{}} + \xi_{212} \dot{w}_{1}^{{}} w_{2}^{{}} + + \xi_{213} w_{1}^{{}} \dot{w}_{2}^{{}} + \xi_{214} w_{2}^{{}} \dot{w}_{2}^{{}} + \xi_{215} w_{1}^{{}} + \xi_{216} F_{a} \\ \end{aligned} $$

(25b)

where μ_ij and $\xi_{ij}$ are coefficients.

In the following analyses, the nonlinear dynamic behaviors are investigated of the GRPA-SRC shell under the in-plane and transverse excitations by using Runge–Kutta method in Eq. (25). We obtain the amplitude–frequency response curves, force–amplitude response curves, bifurcation diagrams, maximum Lyapunov exponent, phase portraits, waveforms and Poincaré map, the detailed research of the GRPA-SRC shell with the arbitrary boundary conditions.

The arbitrary spring-supported boundary conditions of the GRPA-SRC shell are obtained by varying the spring stiffness. Table 1 shows the boundary conditions corresponding to spring stiffness values, with C, S and F corresponding to the clamed support, simple support and free support, respectively. E1, E2 and E3 are the elastic support boundary conditions.

Table 1 Values of the spring stiffness and its boundary conditions

3.1 Convergence and comparison

The material properties, geometric parameters and dimensionless frequency expressions are selected as follows:

$\beta = 30^\circ$, n = 1, h/R_a = 0.01, L/R_a = 6,$\upsilon = 0.3$, $\left( {\overline{\omega }_{b}^{ * } ,\overline{\omega }_{f}^{ * } } \right) = \left( {\omega_{b} ,\omega_{f} } \right)R_{b} \sqrt {\left( {1 - \upsilon^{2} } \right)\rho /E}$.

Table 2 verifies the convergence of Chebyshev polynomials. The frequency results are compared with Han and Chu [54] and Dai et al. [55]. The errors in Table 2 are given the between the existing literature with the results M = 7. It is seen that the frequency obtained in this paper is very consistent with the results of the existing literature. In other words, when M = 7, the results of this paper converge. Therefore, M = 7 is considered in the subsequent research.

Table 2 Verification of the convergence of Chebyshev polynomials

3.1.1 Comparison 1

The material properties and geometric dimensions are given as follows:

$E = 70\,{Gpa}$, $\rho = 2707{\text{kg}}/{\text{m}}^{3}$, $\upsilon = 0.3$, $\beta = 30^\circ$, $R_{a} = 0.5\,{m}$, $L = 1\,{m}$.

Table 3 demonstrates the results of frequencies and mode shapes of the homogeneous material non-rotating conical shell are compared with ANSYS software to verify the reliability. Brackets (n, m) represent the m-th-order frequency corresponding to the circumferential wave number n. It is seen that the comparison results are very perfect.

Table 3 Comparison of the frequencies (Hz) and mode shapes for conical shell under the F–C

3.1.2 Comparison 2

Table 4 lists that comparison on the dimensionless frequency parameters of the rotating conical shell with the C–C boundary condition. $\hat{\Omega } = \Omega R\sqrt {\left( {1 - \upsilon^{2} } \right)\rho /E}$ and $\left( {\omega_{b}^{ * } ,\omega_{f}^{ * } } \right) = \left( {\omega_{b} ,\omega_{f} } \right)R\sqrt {\left( {1 - \upsilon^{2} } \right)\rho /E}$ are expressed for the dimensionless frequencies and dimensionless rotating speeds. The results indicate that there is high consistency between the present work and existing researches [6, 37, 56].

Table 4 Comparison of the dimensionless fundamental frequency parameters for the rotating conical shell under the C–C

4 Amplitude–frequency and force–amplitude response curves

It is noticed that unless otherwise specified, the physical dimensions of the GRPA-SRC shell are given as follows:

$\beta = 30^\circ$, $R_{a} = 0.5\,\,{m}$, $L = 2\,\,{m}$, $h = 0.005\,{m}$, $h_{b} = 0.001\,{m}$, $N_{{\text{c}}} = 0.2$, $\Lambda_{{{\text{GPL}}}}^{{}} = 1.0\%$, $\Omega = 200\,{\text{rad}}/{\text{s}}$,$P_{0} = 1000\,{\text{N}}$, $P_{0} = 6000\,{\text{N}}$, $F_{{\text{t}}} = 300\,{\text{N}}$.

Figure 4 illustrates the influence of the dimensionless frequency of the GRPA-SRC shell with the circumferential wave number n. In Fig. 4a, the representation is for the stationary conical shell at $\Omega = 0$, and Fig. 4b denotes the rotating conical shell. The results indicate that when the conical shell is stationary, a circumferential wave number n corresponds to a frequency. At this time, the GRPA conical shell is subjected to the standing wave vibrations. The influence of Coriolis force and initial ring tensor, the rotating conical shells exhibit two different frequencies corresponding to a circumferential wave number n, namely the forward traveling wave frequency and backward traveling wave frequency, as shown in Fig. 4b. Therefore, the rotating conical shells are the traveling wave vibrations. During the vibration of the GRPA-SRC shell, the main vibration is low-order mode vibration. Therefore, the first-order mode is taken in subsequent investigates. Figure 5 shows the first-order modal diagrams are obtained with $\Omega = 0$ (n = 4) and $\Omega = 200\,{\text{rad}}/{\text{s}}$ (n = 2).

Fig. 4

Variation in the dimensionless frequency of the GRPA-SRC shell with the n in the Type-1 and GPL-X under the C-F boundary condition, a $\tilde{\Omega } = 0$, b $\tilde{\Omega } = 0.1$

Fig. 5

Modal diagrams are given of the GRPA-SRC shell with the C-F boundary condition, a n = 2, b n = 4

Figure 6 reveals the amplitude–frequency response curves of the non-rotating GRPA sandwich conical shell under the C-F boundary condition. It is easy to observe that the amplitude–frequency response curves exhibit the jumping phenomenon and hard spring characteristic, which are the typical nonlinear characteristic. The amplitude difference between the forward sweep and backward sweep is not significant. Figures 7, 8, 9 and 10 present the amplitude–frequency response curves of the GRPA-SRC shell. There is no obvious jumping phenomenon and the amplitudes of the forward and backward sweeps are the same, indicating that the rotating conical shells exhibit weak nonlinear characteristics. It is also shown that the nonlinear vibrations of the GRPA-SRC shells are more difficult to excite than the static vibration. There are two resonance peaks in the amplitude–frequency response curves, corresponding to the forward and backward traveling wave frequencies, respectively. Additionally, the external excitation frequencies of resonance are greater than the frequencies of the stationary conical shell.

Fig. 6

Amplitude–frequency response curves are obtained of the non-rotating GRPA conical shell in the Type-1 and GPL-X, a amplitude frequency response curve of w₁, b amplitude frequency response curve of w₂

Fig. 7

Amplitude–frequency response curves are obtained of the GRPA-SRC shell under different graphene distributions and porosity distributions, a–b amplitude–frequency response curves of the Type-1 with three different graphene distributions, c–d amplitude–frequency response curves of the GPL-X pattern with three different porosity distributions

Fig. 8

Amplitude–frequency response curves are obtained of the GRPA-SRC shell under different V_GPL and N_c, a–b amplitude–frequency response curves of the Type-1 and GPL-X with different V_GPL, c–d amplitude–frequency response curves of the Type-1 and GPL-X pattern with different porosity N_c

Fig. 9

Amplitude–frequency response curves are obtained of the GRPA-SRC shell under different rotation speeds, a amplitude frequency response curve of w₁, b amplitude frequency response curve of w₂

Fig. 10

Amplitude–frequency response curves are obtained of the GRPA-SRC shell under different boundary condition, a amplitude frequency response curve of w₁, b amplitude frequency response curve of w₂

The amplitude–frequency response curves of the GRPA-SRC shell under different graphene distributions of the Type-1 are investigated, as shown in Fig. 7a, b. The amplitude–frequency response curves of the GPL-X pattern with different porosity distributions are shown in Fig. 7c, d. For w₁ and w₂, the GPL-O pattern has a higher jump phenomenon, indicating a larger resonance region. The amplitude of w₁ is higher than that of w₂. Figure 7c, d gives that the amplitudes of the three porosity distributions are almost the same. The Type-2 has higher amplitudes than the other two distributions, which means the Type-1 and Type-3 stiffness are larger.

Figure 8a, b describes that the amplitude–frequency response curves of the GRPA-SRC shell under different V_GPL with the Type-1 and GPL-X. As shown in this figure, the greater the frequency ratio ($\varpi /\omega_{i}$) when reaching the first and second resonance peaks and increased resonance area with reduce of the V_GPL for w₁ and w₂. Figure 8c, d indicates the amplitude–frequency response curves of the GRPA-SRC shell under different N_c with the Type-1 and GPL-X. It is illustrated that increasing the porosity of the GRPA-SRC shell, the lower the stiffness of the system, the higher the amplitude of reaching the resonance peaks, increasing the resonance area and the greater the resonance frequency ratio ($\varpi /\omega_{i}$).

As shown in Fig. 9, there are the amplitude–frequency response curves of the GRPA-SRC shell under different rotation speeds. The results are shown that as the dimensionless rotational speeds $\tilde{\Omega }$ increase, the frequency ratio increases when the resonance peak reached. For the w₁, the amplitude of the GRPA-SRC shell gradually decreases with increasing speeds, while for the w₂, the amplitude of the GRPA-SRC shell remains almost unchanged with the change of speeds; only the external excitation frequency that reaches the resonance peak changes.

The amplitude–frequency response curves of the GRPA-SRC shell with the Type-1 and GPL-X under different boundary conditions are shown in Fig. 10. The values of spring stiffness corresponding to the boundary conditions are obtained and presented in Table 1. The primary focus of the research is on small end the clamed support, large end the free support and elastic support of the rotating conical shells. The results indicate that the resonance peak and resonance region at the C–F boundary are the largest, followed by the C–E3, C–E1, C–C and C–E2. It is worth mentioning that the frequency ratio of the first resonance peak at the C–E3 boundary is less than 1. At the C–E1, C-E2 and C–C boundary conditions, there is only one resonance peak for w₁.

The effects of different graphene distributions on the force–amplitude response curves of the GRPA-SRC shell are provided, as shown in Fig. 11. It is found that the amplitudes among three different graphene distributions increase in the GRPA-SRC shell with increasing for the transverse excitations F_a and vibration amplitudes have a small difference for the w₁. With the increase in external excitation F_a, the amplitude difference of the three porosity distributions gradually increases. There is a small difference between the forward and backward sweep amplitudes for the porosity distribution of the Type-1. For the w₁, the amplitudes of three graphene distributions from large to small are the GPL-X, GPL-O and GPL-U, respectively. For the w₂, the amplitudes of three graphene distributions from large to small are the GPL-U, GPL-O and GPL-X, respectively.

Fig. 11

Force–amplitude response curves are obtained of the GRPA-SRC shell under different graphene distributions, a force–amplitude response curve of w₁, b force–amplitude response curve of w₂

Figure 12 demonstrates that the force–frequency response curves of the GRPA-SRC shell under different porosity distributions. From Fig. 12, it reveals that for three different porosity distributions, the amplitudes of the GRPA-SRC shell monotonically increase with the increase in the transverse excitations F_a. For the w₁, when F_a < 0.35 × 10⁵ N, the amplitudes of three different porosity distributions from large to small are the Type-2, Type-3 and Type-1, respectively. The amplitude of the final the Type-1 porosity distribution is the larger, while the Type-3 porosity distribution is the smallest. For the w₂, the amplitudes of three different porosity distributions from large to small are the Type-2, Type-3 and Type-1, respectively. The amplitude difference between the Type-2 and Type-3 porosity distributions of the GRPA-SRC is very small.

Fig. 12

Force–amplitude response curves are obtained of the GRPA-SRC shell under different porosity distributions, a force–amplitude response curve of w₁, b force–amplitude response curve of w₂

Figure 13 exhibits the force–amplitude response curves of the GRPA-SRC shell under different volume fraction of graphene V_GPL. It is demonstrated that the amplitude of graphene with different volume fraction monotonically increases with the increase in transverse force F_a, and the amplitude difference also gradually increases. This means that the more the graphene content, the smaller the amplitude of the GRPA-SRC shells. This also indicates that increasing the content of the graphene will increase the stiffness of the GRPA-SRC shell. There is a special phenomenon for the Type-2 when F_a > 0.34 × 10⁵N, the amplitude of GRPA-SRC shell V_GPL = 5% is greater than V_GPL = 1%.

Fig. 13

Force–amplitude response curves are obtained of the GRPA-SRC shell under different V_GPL, a force–amplitude response curve of w₁, b force–amplitude response curve of w₂

The force–amplitude response curves of the GRPA-SRC shell under different boundary conditions are presented, as shown in Fig. 14. It is observed that the amplitude of different boundary conditions increases with the increase in transverse force F_a. For w_1, it is seen that when F_a < 0.35 × 10⁵ N, the amplitude of the GRPA-SRC shell corresponding to the C–F and C–E3 boundary conditions is the highest, while the amplitude of the C–E2 boundary condition is the least. When F_a > 0.35 × 10⁵N, the C–F boundary condition has the largest amplitude and the C–C and C–E1 boundary conditions have the least amplitude. For w_2, it is seen that when F_a < 0.1 × 10⁵ N, the amplitude of the GRPA-SRC shell corresponding to the C–F boundary condition is the highest. When F_a > 0.1 × 10⁵ N, the C–E3 boundary condition of the GRPA-SRC shell has the largest amplitude and the C–C boundary condition has the least amplitude.

Fig. 14

Force–amplitude response curves are obtained of the GRPA-SRC shell under different boundary conditions, a force–amplitude response curve of w₁, b force–amplitude response curve of w₂

5 Effect of transverse excitation on nonlinear vibrations

In this section, the effect of the transverse external excitations F_a on the nonlinear dynamic characteristics of the GRPA-SRC shell is studied under three different porosity distributions of the GPL-O. The material properties and geometric dimensions are the same as the previous study on the amplitude–frequency response curves. The external excitation frequencies of the bifurcation diagrams are obtained the frequency at which the amplitude–frequency response curves reach the first resonance peak. The initial conditions are chosen as $w_{1} = - {0}{\text{.0001}}$,$\dot{w}_{1} = 0$,$w_{2} = - {0}{\text{.000025}}$, $\dot{w}_{2} = 0$, and $t = 0$.

Figures 15, 16 and 17 describe the bifurcation diagrams and maximum Lyapunov exponent of the GRPA-SRC shell with three types of porosity distributions under the GPL-O when the transverse excitations F_a increase from 0.45 × 10⁷ to 0.9 × 10⁷ N. Figure (a) depicts the bifurcation diagram of the relationship between w₁ and F_a. Figure (b) illustrates the bifurcation diagram of the relationship between w₂ and F_a. Figure (c) shows the relation on the maximum Lyapunov exponent versus F_a. It is observed that the vibration laws of the GRPA-SRC shell are demonstrated as follows: the periodic vibrations → chaotic vibrations → periodic vibrations (including the chaotic vibrations window) → chaotic vibrations, as shown in Figs. 15, 16 and 17. In Figs. 15 and 17, the GRPA-SRC shells of Type-1 and Type-3 exhibit the inverse-period doubling bifurcation, while Type-2 shows no the bifurcation behavior.

Fig. 15

Bifurcation diagrams and the maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the transverse excitations with the Type-1, a the bifurcation diagram of w₁, b bifurcation diagram of w₂, c maximum Lyapunov exponent

Fig. 16

Bifurcations diagrams and the maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the transverse excitations with the Type-2, a bifurcation diagram of w₁, b bifurcation diagram of w₂, c the maximum Lyapunov exponent

Fig. 17

Bifurcation diagrams and the maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the transverse excitations with the Type-3, a the bifurcation diagram of w₁, b bifurcation diagram of w₂, c maximum Lyapunov exponent

It is seen from Fig. 15 that the periodic vibration occurs for the GRPA-SRC shell with the GPL-O and Type-1 when the transverse excitations are

$$ F_{a} \epsilon \, \left( {0.{45} \times {1}0^{{7}} {\text{N}} - 0.{51} \times {1}0^{{7}} {\text{N}}} \right) \, \,{\text{and}}\,F_{a} \epsilon \left( {0.{6847} \times {1}0^{{7}} {\text{N}} - 0.{7385} \times {1}0^{{7}} {\text{N}}} \right). $$

When the transverse excitations F_a are 0.4877 × 10⁷N, the GRPA-SRC shell undergoes bifurcation behavior. When F_a = 0.7 × 10⁷N, there exists a chaotic vibration window within the periodical vibrations. When the transverse excitation is F_a = 0.7385 × 10⁷N, the chaotic vibrations occur in the GRPA-SRC shell.

Figure 16 exhibits that the periodic vibrations occur for the GPL-O and Type-2 of the GRPA-SRC shell when the transverse excitations are

$F_{a} \epsilon \, \left( {0.{45} \times {1}0^{{7}} {\text{N}} - 0.{5}0{67} \times {1}0^{{7}} {\text{N}}} \right)\,{\text{and}}\,F_{a} \epsilon \, \left( {0.{6371} \times {1}0^{{7}} {\text{N}} - 0.{7152} \times {1}0^{{7}} {\text{N}}} \right).$ When the transverse excitations are between 0.5068 × 10⁷ and 0.5182 × 10⁷N, the GRPA-SRC shell undergoes the almost periodic vibrations, including the chaos vibrations windows in here. When the transverse excitations are between 0.5183 × 10⁷N and 0.637 × 10⁷N, there are the multi periodic vibration windows in the chaotic vibrations. When the transverse excitation is F_a = 0.7153 × 10⁷N, the chaotic vibrations occur in the GRPA-SRC shell.

Figure 17 demonstrates that the periodic vibrations occur for the GPL-O and Type-3 of the GRPA-SRC shell when the transverse excitations are given as

$$ F_{a} \epsilon\, \left( {0.{45} \times {1}0^{{7}} {\text{N}} - 0.{517} \times {1}0^{{7}} {\text{N}}} \right)\,{\text{and}}\,F_{a} \epsilon \, \left( {0.{6492} \times {1}0^{{7}} {\text{N}} - 0.{734} \times {1}0^{{7}} {\text{N}}} \right). $$

When the transverse excitations F_a are 0.49 × 10⁷N, the GRPA-SRC shell undergoes bifurcation behaviors. When the transverse excitations are between 0.517 × 10⁷N and 0.53 × 10⁷N, the GRPA-SRC shell undergoes the almost periodic vibrations. In the transverse excitations F_a ϵ (0.6492 × 10⁷–0.8 × 10⁷N), both the chaotic and periodic vibrations occur. According to the above analysis, under the same graphene distribution pattern, the stiffness of the GRPA-SRC shell with three different porosity distributions has little difference and Type-2 shows no bifurcation behavior, as shown in Figs. 15, 16 and 17.

Figures 18, 19 and 20 depict the waveforms, phase portraits and Poincare maps of the GRPA-SRC shell with the GPL-O and Type-2 under different transverse excitations. (a) and (c) are the waveforms of w₁ and w₂, respectively. (b) and (d) are the phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$, and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$. (e) and (f) are the Poincare maps of w₁ and w₂, respectively. Figure 18 demonstrates the periodic vibrations of the GRPA-SRC shell with the GPL-O and Type-2 when the transverse excitation F_a = 0.5 × 10⁷N. Figure 19 denotes the almost periodic vibrations of the GRPA-SRC shell with the GPL-O and Type-2 when the transverse excitation F_a = 0.51 × 10⁷N. Figure 20 illustrates the chaotic vibrations of the GRPA-SRC shell with the GPL-O and Type-2 when the transverse excitation F_a = 0.8 × 10⁷N.

Fig. 18

Periodic vibrations of the GPL-O and Type-2 are obtained when the transverse excitation is F_a = 0.5 × 10⁷ N, a and c waveforms of w₁ and w₂, b and d phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$ and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$

Fig. 19

Almost periodic vibrations of the GPL-O and Type-2 are obtained when the transverse excitation is F_a = 0.51 × 10⁷ N, a and c waveforms of w₁ and w₂, b and d phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$ and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$

Fig. 20

Chaotic vibrations of the GPL-O and Type-2 are obtained when the transverse excitation is F_a = 0.8 × 10⁷ N, a and c waveforms of w₁ and w₂, b and d phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$ and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$

6 Effect of in-plane load on nonlinear vibrations

This section investigates the nonlinear vibrations of the GRPA-SRC shells with the GPL-O under the in-plane loading and different porosity distribution when the in-plane load P_a increases from 0 to 3.5 × 10⁷N. Other material properties and geometric parameters are the same as before. The initial conditions are chosen as $w_{1} = - {0}{\text{.0001}}$, $\dot{w}_{1} = 0$, $w_{2} = - 0.000025$, $\dot{w}_{2} = 0$, and $t = 0$. Figure (a) represents the bifurcation diagram of w₁. Figure (b) shows the bifurcation diagram of w₂. Figure (c) indicates the maximum Lyapunov exponent. Figures 21, 22 and 23 depict bifurcation diagrams of the in-plane load variation P_a within the GRPA-SRC shells for Type-1, Type-2 and Type-3, respectively.

Fig. 21

Bifurcation diagrams and maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the in-plane loads with the Type-1, a bifurcation diagram of w₁, b bifurcation diagram of w₂, c maximum Lyapunov exponent

Fig. 22

Bifurcation diagrams and maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the in-plane loads with the Type-2, a bifurcation diagram of w₁, b bifurcation diagram of w₂, c maximum Lyapunov exponent

Fig. 23

Bifurcation diagrams and maximum Lyapunov exponent are obtained of the GRPA-SRC shell under the in-plane loads with the Type-3, a bifurcation diagram of w₁, b bifurcation diagram of w₂, c maximum Lyapunov exponent

Figure 21 shows the bifurcation diagram of the GRPA-SRC shell with the Type-1 porosity distribution as the in-plane load P_a. The vibration pattern follows: the periodic vibrations → chaotic vibrations → periodic vibrations (with a brief chaotic vibrations window) → chaotic vibrations. There is the chaotic vibration window near the in-plane load P_a = 1.3562 × 10⁷N.

Figure 22 illustrates the bifurcation diagram of the GRPA-SRC shell with Type-2 porosity distribution as the in-plane load (P_a) varies. The vibration pattern follows: the periodic vibrations → quasi-periodic vibrations → periodic vibrations → quasi-periodic vibrations → chaotic vibrations → periodic vibrations → chaotic vibrations. When the in-plane loads P_a are between 1.47 × 10⁷ and 2.0225 × 10⁷ N the quasi-periodic vibrations, there exists the periodic vibration window near 1.89 × 10⁷N.

Figure 23 depicts the bifurcation diagram of the GRPA-SRC shell with Type-3 porosity distribution as the in-plane load (P_a) varies. The vibration pattern: the periodic vibrations → quasi-periodic vibrations → periodic vibrations → chaotic vibrations (with a simultaneous presence of the periodic vibrations window) → periodic vibrations.

Figures 24 and 25 depict the waveforms, phase portraits and Poincare maps of the GRPA-SRC shell with the GPL-O and Type-1 under different in-plane loadings. (a) and (c) are the waveforms of w₁ and w₂, respectively. (b) and (d) are the phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$, and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$. (e) and (f) are the Poincare maps of w₁ and w₂, respectively. Figure 24 illustrates the almost periodic vibrations of the GRPA-SRC shell with the GPL-O and Type-2 when the in-plane load is P_a = 0.8 × 10⁷N. Figure 25 demonstrates the chaotic vibrations of the GRPA-SRC shell with the GPL-O and Type-2 when the in-plane load is P_a = 2.5 × 10⁷N.

Fig. 24

Almost periodic vibrations of the GPL-O and Type-2 are obtained when the in-plane load is P_a = 0.8 × 10⁷N, a and c waveforms of w₁ and w₂, b and d phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$ and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$, e and f Poincare map of w₁ and w₂

Fig. 25

Chaotic vibrations of the GPL-O and Type-2 are obtained when the in-plane load is P_a = 2.5 × 10⁷N, a and c are waveforms of w₁ and w₂, b and d phase portraits on planes $\left( {w_{1} ,\dot{w}_{1} } \right)$ and $\left( {w_{{2}} ,\dot{w}_{{2}} } \right)$, e and f Poincare maps of w₁ and w₂

7 Conclusions

This paper investigates that the nonlinear traveling wave vibrations of the GRPA-SRC shell with the arbitrary boundary conditions. Five evenly distributed springs are added to both ends of the GRPA-SRC shells to obtain the arbitrary boundary conditions. The elastic potential energy of the GRPA-SRC shell is altered by changing the elastic stiffness of the springs. Therefore, we obtain the arbitrary elastic support boundary conditions. In the study of the vibration process for the rotating conical shells, it is necessary for us to analyze these boundary conditions through using the traveling wave vibrations. The circumferential direction of the GRPA-SRC shell is represented by using the trigonometric functions and solution of the generatrix direction is denoted by using Chebyshev polynomials. The nonlinear ordinary differential equations of the GRPA-SRC shell with two degrees of freedom are obtained through the energy principle. Runge–Kutta method is used to solve the amplitude–frequency response curves, force–amplitude response curves, bifurcation diagram, maximum Lyapunov exponent, waveforms, phase portraits and Poincare map of the GRPA-SRC shell. This paper provides a valuable approach for the vibration analysis of the rotating shell structures with the arbitrary boundary conditions. Numerical simulations and theoretical analysis are depicted and the conclusions are drawn as follows.

• 1. In the comparison with the shell structures [16, 20, 21, 34], it is observed that a mode shape of the rotating conical shell corresponds to two different frequencies, which are referred to as the forward traveling wave frequency and backward traveling wave frequency. Due to the presence of this unique property, the vibration analysis of the GRPA-SRC shells must be conducted by using the traveling wave vibrations. The nonlinear characteristics of the stationary conical shell are relatively obvious with a jumping phenomenon in the amplitude–frequency response curves. The amplitude–frequency response curves of the rotating conical shell exhibit weak nonlinear characteristics, but there are two resonance peaks for the GRPA-SRC shell.

• 2. The influence of the graphene distribution types and porosity distribution types on the amplitude–frequency response curves of the GRPA-SRC shells illustrates that there is a relatively small difference in the vibration amplitude. Reducing the graphene content and increasing the porosity content lead to the decrease in the stiffness for the GRPA-SRC shell. Consequently, this causes an increase in the amplitude of the GRPA-SRC shell and expands the resonant regions.

• 3. For the impact of the rotation speed on the amplitude–frequency response curves for the GRPA-SRC shell, the results are indicated that as the dimensionless rotational speeds $\tilde{\Omega }$ increase, the frequency ratio increases when the resonant peaks are reached. The effect of the boundary conditions on the amplitude–frequency response curves for the GRPA-SRC shells is more complex. The resonant peak and resonant region of the C-F boundary condition are larger.

• 4. The force–amplitude response curves of the GRPA-SRC shell monotonically increase with the increase in the transverse external excitation F_a. The impact of different porosity distributions and graphene distribution types on the structure is relatively small. The higher graphene content results in the lower amplitude corresponding to the force–amplitude response curve of the GRPA-SRC shell, which indicates that adding graphene to the porous metal conical shell will increase the structural stiffness.

• 5. When the transverse excitations F_aincrease from 0.45 × 10⁷ to 0.9 × 10⁷N, bifurcation behaviors of the Type-1 and Type-3 occur. The GRPA-SRC shells with the Type-2 and Type-3 porosity distributions change from the periodic vibrations to the quasi-periodic vibrations and then enter the chaotic vibrations. In contrast, the GRPA-SRC shell with the Type-1 porosity distribution does not exhibit the quasi-periodic vibrations.

Appendices

Appendix A

The expressions for the strain components are obtained as follows

$$ \varepsilon_{x}^{0} = \frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} ,\,\varepsilon_{\theta }^{0} = \frac{1}{R}\left( {u_{0} \sin \beta + w_{0} \cos \beta + \frac{{\partial v_{0} }}{\partial \theta }} \right) + \frac{1}{{2R^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} $$

(A1)

$$ \gamma_{x\theta }^{0} = \frac{1}{R}\left( {\frac{{\partial u_{0} }}{\partial \theta } - v_{0} \sin \beta + \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x}} \right) + \frac{{\partial v_{0} }}{\partial x},\,\varepsilon_{x}^{1} = \frac{{\partial \phi_{x} }}{\partial x},\,\varepsilon_{\theta }^{1} = \frac{1}{R}\left( {\phi_{x} \sin \beta + \frac{{\partial \phi_{\theta } }}{\partial \theta }} \right) $$

(A2)

$$ \gamma_{x\theta }^{1} = \frac{1}{R}\left( {\frac{{\partial \phi_{x} }}{\partial \theta } - \phi_{\theta } \sin \beta + R\frac{{\partial \phi_{\theta } }}{\partial x}} \right) $$

(A3)

Appendix B

The expressions for the stress resultants of the GRPA-SRC are given as follows

$$ N_{xx} = A_{11} \varepsilon_{x}^{0} + A_{12} \varepsilon_{\theta }^{0} + B_{11} \varepsilon_{x}^{1} + B_{12} \varepsilon_{\theta }^{1} ,\,N_{\theta \theta } = A_{12} \varepsilon_{x}^{0} + A_{22} \varepsilon_{\theta }^{0} + B_{12} \varepsilon_{x}^{1} + B_{22} \varepsilon_{\theta }^{1} $$

(B1)

$$ M_{xx} = B_{11} \varepsilon_{x}^{0} + B_{12} \varepsilon_{\theta }^{0} + D_{11} \varepsilon_{x}^{1} + D_{12} \varepsilon_{\theta }^{1} ,\,M_{\theta \theta } = B_{12} \varepsilon_{x}^{0} + B_{22} \varepsilon_{\theta }^{0} + D_{12} \varepsilon_{x}^{1} + D_{22} \varepsilon_{\theta }^{1} $$

(B2)

$$ N_{x\theta } = A_{66} \gamma_{x\theta }^{0} + B_{66} \gamma_{x\theta }^{1} ,\,M_{x\theta } = B_{66} \gamma_{x\theta }^{0} + D_{66} \gamma_{x\theta }^{1} ,\,Q_{\theta z} = A_{44} \gamma_{\theta z}^{{}} ,\,Q_{xz} = A_{55} \gamma_{xz}^{{}} $$

(B3)

where A_ij, B_ij, and D_ij represent the tensile stiffnesses, tensile-bending coupled stiffnesses and bending stiffnesses, respectively, expressed as follows

$$ \begin{gathered} \left( {A_{{ij}} ,B_{{ij}} ,D_{{ij}} } \right) = \int_{{{\text{ - h/2}}}}^{{{\text{h/2}}}} {\hat{Q}_{{ij}} \left( {1,z,z^{2} } \right){\text{d}}z} \hfill \\ \quad \quad \quad \quad \quad \quad + \int_{{{\text{ - h/2 - h}}_{{\text{b}}} }}^{{{\text{ - h/2}}}} {\hat{Q}_{{ij}} \left( {1,z,z^{2} } \right){\text{d}}z} \hfill \\ \quad \quad \quad \quad \quad \quad + \int_{{{\text{h/2}}}}^{{{\text{h/2}} + {\text{h}}_{{\text{b}}} }} {\hat{Q}_{{ij}} \left( {1,z,z^{2} } \right){\text{d}}z} \left( {i,j = 1,2,6} \right),{\mkern 1mu} \hfill \\ \quad \quad \quad \quad A_{{ij}} = \int_{{{\text{ - h/2}}}}^{{{\text{h/2}}}} {\hat{Q}_{{ij}} {\text{d}}z + \int_{{{\text{ - h/2 - h}}_{{\text{b}}} }}^{{{\text{ - h/2}}}} {\hat{Q}_{{ij}} {\text{d}}z} + \int_{{{\text{h/2}}}}^{{{\text{h/2}} + {\text{h}}_{{\text{b}}} }} {\hat{Q}_{{ij}} {\text{d}}z} } .\left( {i,j = 4,5} \right) \hfill \\ \end{gathered} $$

(B4)