Periodic transmission and vaccination effects in epidemic dynamics: a study using the SIVIS model

Abstract

This work explores the dynamics of an epidemic considering an SIVIS (susceptible-infected-vaccinated-infected-susceptible) epidemiological model, accounting for heterogeneous susceptibility, governmental interventions, social behavioral dynamics and public reactions in both of autonomous and nonautonomous aspects. The study frames the system as an optimal control problem, considering time-dependent control strategies for strength of social behavior of public and pharmaceutical treatments. The emergence of a coexistence steady state is analyzed based on the basic reproduction number. The impact of model parameters on disease propagation is assessed through sensitivity analysis. Transcritical bifurcation-induced stability alteration is explored, and numerical simulations illustrate theoretical findings. The proposed system investigates the dynamical behavior in case of periodic transmission rate. It vividly highlights the profound impact of factors such as vaccination rates, frequency and amplitude of transmission on the enduring and evolving dynamic patterns exhibited by the disease.

1 Introduction

An epidemic disease model is a mathematical framework employed to analyze the transmission and dynamics of infectious diseases among a population. The primary purpose of these models is to aid researchers and public health officials in comprehending the patterns of disease propagation, predicting their potential impact and formulating effective strategies to manage and reduce their spread. Understanding the behavior of infectious diseases is essential for devising effective prevention and control measures. By applying the knowledge gained from epidemic disease models, public health officials can assess the potential impact of interventions such as vaccination campaigns, social distancing measures and quarantine protocols. Mathematical modeling of epidemiological phenomena has a considerably long history, dating back to the eighteenth century when Bernoulli conducted early studies [1, 2]. These models aim to provide a mathematical framework for understanding the significance of historical observations and the dynamics of infectious diseases. The foundations of many current studies are rooted in the work of Kermack and McKendrick [3, 4] from the 1930s. These compartment models form the basis for most contemporary investigations in epidemiology. These models comprise a set of nonlinear ordinary differential equations, where state variables represent the size of the population in various stages of the infectious disease spread. These mathematical models serve as valuable tools for explaining real-world disease dynamics within a quantitative framework. They facilitate the exploration of different scenarios, the evaluation of potential interventions and prediction of disease outcomes. By integrating historical data and scientific knowledge, these models contribute significantly to our understanding of epidemiological processes and guide public health strategies for disease control. Significant progress has been made in the examination of models for infectious diseases [5, 6]. According to Zhan et al. [5] an epidemic with high prevalence will result in a slow information decay which will prevent the epidemic from spreading. Finally, additional theoretical study shows that the coupling dynamics have an impact on the emergence of multi-outbreak event. This research may help in better understanding how the dynamics of disease propagation and information diffusion interact. In [6], the study focuses on network-based epidemic models designed to simulate the spread of influenza-like diseases. These models specifically account for the potential infectiousness of individuals during their incubation or asymptomatic stages. Numerous renowned contemporary textbooks cover basic concepts in the mathematics of epidemiology [7,8,9].

The government plays a crucial role in safeguarding public health and well-being by preventing epidemics. Implementing proactive measures and strategies to curb the spread of infectious diseases are essential. To achieve this, governments must establish robust disease surveillance systems to monitor the occurrence and transmission of contagious diseases [10, 11]. Early detection enables timely responses, containment and prevention of outbreaks. Clear, accurate and timely information should be provided to the public during an epidemic, highlighting potential risks, preventive measures and necessary actions. Effective communication fosters awareness and encourages a sense of collective responsibility [12]. Vaccination programs are crucial, and governments play a pivotal role in facilitating access to vaccines and promoting vaccination campaigns to protect populations from vaccine-preventable diseases. In times of epidemics, governments may need to implement quarantine and isolation protocols to contain disease spread and prevent further transmission. Travel restrictions and border control measures can limit the importation and exportation of infectious diseases. Overall, the government’s active involvement in epidemic prevention is most important, as it ensures the health and safety of its citizens and contributes to global public health efforts. As a result, the conventional SIRS model can be enhanced by integrating two crucial aspects: the impact of governmental intervention and public response [11, 13, 14]. Governmental intervention involves quarantine, travel restrictions and mass vaccination campaigns implemented by authorities to control disease spread. On the other hand, public response refers to how individuals and communities react to the outbreak, such as adopting preventive behaviors, seeking medical attention or complying with government directives [12]. By incorporating these factors into the model, researchers can gain a better understanding of how social dynamics and human behavior impact disease transmission. This enhanced model can lead to more accurate predictions and insights into the effectiveness of various intervention strategies. Recently, Saha et al. [13] have studied the dynamical behavior of SIRS model incorporating government action and public response in presence of deterministic and fluctuating environments. They have shown that governmental action plays a crucial role to control an epidemic situation, and the system turns out to be disease-free sooner if the government takes action at an early stage during a disease outbreak. Considering a system of fractional-order differential equations, Das et al. [14] have also studied an epidemic model on COVID-19 using governmental measures and public response where they have observed that the government measures are more helpful than only public responses to the eradication of the COVID-19 pandemic.

Several authors have studied epidemic models taking heterogeneity; it may be in the form of immunity of the susceptible or the information about the disease to the susceptible. In this context Zhang et al. [15] have reviewed as well as discussed a recent model on epidemic that considered heterogeneity in the susceptible and infected class about information of disease. However, there are very few research works related to the heterogeneity about immunity of the susceptible class. Heterogeneous susceptibility refers to the variation in immune responses among individuals in a population due to differences in their immune systems, previous exposures to pathogens or vaccination histories. This heterogeneity can significantly influence the dynamics of infectious diseases within a population. Some individuals may have strong immune responses to certain pathogens, making them less susceptible to infection or experiencing milder symptoms when exposed to the pathogen. Genetic factors and previous exposure to related pathogens can influence this natural immunity. Immunity can also be acquired through previous infections or vaccinations. Some individuals may have received vaccines or encountered the pathogen before, resulting in a higher level of immunity against the disease. In a study conducted by Pagliara et al. [16], researchers have identified a bistable phenomenon within a SIRI (susceptible-infected-recovered-infected) system. This phenomenon indicates that once an individual has been infected with an ailment for the first time, it becomes challenging for them to become susceptible to the same disease again. With age, immune responses can change. For instance, the immune systems of young infants and the elderly are frequently weakened, causing them to be more susceptible to certain infections. There are a few referrals concerning heterogeneous susceptibility [17,18,19,20], to the best of our knowledge. Miller [17] has investigated how heterogeneity influences the likelihood that an epidemic would arise by using a generating function technique. He has demonstrated that an epidemic is most likely when infectivity is homogeneous and least likely when infectivity variance is extensive. Similar to this, the attack rate is highest when susceptibility is homogeneous and lowest when the variance is maximal. There is currently no analysis investigating the affect of heterogeneous susceptibility including partial immunity, government action, social interaction and public response.

Vaccination is very important in preventing epidemics and controlling the spread of infectious diseases. It is produced to provide immunity against specific diseases. By administering vaccines, individuals develop immunity without experiencing the actual illness. This immunity helps to prevent the occurrence and transmission of the disease, thereby curbing epidemics [21, 22]. For instance, vaccines have led to the near-elimination of diseases like smallpox and have significantly reduced the prevalence of diseases like polio and measles. Vaccination benefits people of all age groups, from infants to older people. Vaccination offers a high level of immunity against infectious diseases, but it does not guarantee ultimate or lifelong immunity for every individual [23, 24]. The efficacy of vaccines can vary based on factors like the vaccine type, the specific disease being targeted and an individual’s immune response. Most vaccines are designed to trigger a robust immune response that provides significant protection against the targeted disease. As a result, vaccinated individuals are less likely to become infected with the disease or experience severe symptoms when exposed to the pathogen. In many cases, vaccines can provide long-lasting immunity, offering protection for several years or even a lifetime [24,25,26]. For example, vaccines against diseases like measles, mumps and rubella (MMR) are known to confer enduring immunity for the majority of vaccinated individuals. However, there are instances where immunity from vaccination may diminish over time. Some diseases may require booster shots or additional vaccine doses to sustain protective immunity. An example of this is the tetanus vaccine, which necessitates periodic booster shots to maintain protection. Turkyilmazoglu [27] has studied an extended epidemic model with vaccination and shown that when the vaccination rate is substantial, countries are not expected to be significantly affected by low levels of weak immunity. Conversely, a lack of immunity leads to the prolonged persistence of the contagious disease, characterized by the emergence of multiple secondary peaks within the epidemic compartments, particularly in situations with relatively small vaccination rates. Zaman et al. [28] have studied an SIR epidemic model assuming that a portion of the susceptible population is vaccinated. It is demonstrated that an optimal control solution exists for the control problem. There are numerous works on epidemic emphasizing the importance on vaccination [21,22,23,24,25,26, 29].

Nonautonomous epidemic models are essential for understanding and predicting the dynamics of infectious diseases in real-world scenarios where factors such as seasonal variations, interventions and changes in population behavior play a significant role. The period of survival of the virus in bird secretions, feces and aerosols depends on a number of factors, including ambient temperature and humidity which fluctuate with seasons [30]. The role of wild migratory birds in the global spread of H5N1 has been controversial and is still being investigated [31]. It appears that some wild migratory birds can be asymptomatic to HP H5N1 and can carry the virus over long distances [32]. These models differ from autonomous models, which assume constant parameters and do not account for external influences. Nonautonomous models can better capture the complexity and variability of real-world epidemic dynamics. They allow for time-varying parameters, reflecting changes in disease transmission rates, contact patterns or intervention strategies over time. This flexibility enhances the model’s accuracy in predicting the spread of diseases under different conditions. Many infectious diseases exhibit seasonal patterns due to various factors, such as weather conditions, human behavior and immunity variations. Nonautonomous models can incorporate seasonal effects, which are crucial for understanding disease transmission and designing targeted intervention strategies. During an epidemic, human behavior can change in response to public health messages or fear of infection. Nonautonomous models can incorporate these changes, providing insights into the impact of behavioral adaptations on disease spread. Researcher focuses on the mathematical abstraction of seasonality by considering time-dependent model parameters. A compartmental model with time-varying birth and death rates is one of the recent examples in this regard [33]. For further exploration, we suggest [34], which is a recent review that surveys the literature on seasonal dynamics. Recently, Kambali et al. [35] have discussed a nonlinear epidemic model incorporating the effects of vaccination and dynamic transmission on COVID-19. There are various compartmental models with different transmission formulations studied in [36, 37].

This manuscript investigates an SIVIS epidemiological system with heterogeneous susceptibility, examining the impact of governmental interventions, social behavioral dynamics and public responses on disease progression. The study transforms this system into an optimal control problem by considering time-dependent controls for social behavior dynamics as (D) and pharmaceutical treatment denoted as $(\gamma )$. In Sect. 2, an SIVIS epidemiological model is formulated, incorporating biological and sociological factors that govern ailment spread. Section 3 delves into the investigation of positivity, boundedness to underscore the biological validity of the system. The emergence of a coexistence steady state based on the basic reproduction number is explored in Sect. 4. Analyzing the influence of model parameters on disease propagation is followed in Sect. 5. Section 6 examines the alteration of the stability of the infection-free steady state through transcritical bifurcation. In Sect. 7, the proposed system is studied taking periodic disease transmission rate. Optimal control problem is formulated in Sect. 8 to mitigate disease burden. Also, the impact of optimal control measures on the model’s behavior is visually depicted in numerical figures. Finally, the discussion of this work in Sect. 9 offers a concise summary and outlines the potential avenues for future research.

Table 1 Descriptions of system parameters from a biological perspective

2 Model formulation

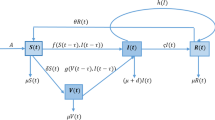
The article is dealt with a compartmental SIVIS model, where two different susceptible states are considered based on the immunity power. The total population N(t) is divided into four sub-classes, named as, susceptible population with lower immunity $(S_{1}(t))$, susceptible population with higher immunity $(S_{2}(t))$, infected population (I(t)) and vaccinated population (V(t)). The mode of transmission follows mass action law in this model. Now, when people recover from a disease, either they achieve permanent recovery, or the recovery is temporary leaving a chance of reinfection and so moving to susceptible class due to the waning effect of medicines or vaccines. The immunity power is not same for all people. Some get infected very soon due to lower immunity power, whereas for others the virus takes some time to affect the immune system. Here, we have presumed that rate of propagation of infection for $S_{1}$ class $(\theta _{1})$ is higher than $S_{2}$ class $(\theta _{2})$. It means the people in $S_{2}$ class have the higher resistance power against a disease, and people in $S_{1}$ class can easily become infected while coming in contact with an infected person $(\theta _{2}<\theta _{1})$. We have considered that the infection here does not confer any long-lasting immunity. So, the disease does not give permanent immunity upon recovery from infection, and individuals become infected again. Indeed, individuals are more susceptible to infection if the efficiency of vaccination declines. In such circumstances, if an individual from the infectious compartment encounters these individuals, there exists a possibility of reinfection and they move to I class direct from vaccinated class with rate $\varepsilon$. So, it is considered that $\varepsilon$ will not be as high as the disease transmission rate among people with weak immune system $(\varepsilon <\theta _{1})$. During an epidemic, there are different social platforms that disseminate important informations about disease symptoms, appropriate precautions and medications via various media, such as TV, radio, or even via educational campaigns. People are encouraged to keep adequate protection for safety, and the government imposes various limitations based on the severity. Therefore, successfully executed governmental regulations and social behavior of individuals are crucial in preventing the spread of infection. The societal component $\alpha$ here indicates the effectiveness of governmental intervention; meanwhile, D and k stand for, respectively, the effectiveness of social behavioral dynamics and public reaction. It is considered that $0\le \alpha< 1,\ 0\le D< 1$. So, people from both susceptible classes move to infected class after coming in contact with an infected person with the disease transmission rate $(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$. After taking into account all the details, the following model has been suggested:

$$\begin{aligned} \frac{dS_{1}(t)}{dt}= & {} q\Pi -(1-\alpha )(1-D)^{k}\theta _{1}S_{1}(t)I(t)\nonumber \\{} & {} -v _1S_1(t)+\beta _1\gamma I(t)-\mu S_{1}(t),~~ S_1(0)>0 \nonumber \\ \frac{dS_{2}(t)}{dt}= & {} (1-q)\Pi -(1-\alpha )(1-D)^{k}\theta _{2}S_{2}(t)I(t)\nonumber \\{} & {} -v _2S_2(t)+\beta _2\gamma I(t)-\mu S_{2}(t),~~ S_2(0)>0 \nonumber \\ \frac{dI(t)}{dt}= & {} (1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)\nonumber \\{} & {} -\gamma I(t)+\varepsilon I(t)V(t)- (\mu +m)I(t), ~~ I(0)\ge 0 \nonumber \\ \frac{dV(t)}{dt}= & {} (v _1S_1(t)+v _2S_2(t))+(1-\beta _1-\beta _2)\gamma I(t)\nonumber \\{} & {} - \varepsilon I(t)V(t)-\mu V(t), \quad V(0)\ge 0. \end{aligned}$$

(2.1)

The description of the model parameters and variables are presented in Table 1, and the schematic diagram associated to system (2.1) is depicted in Fig. 1.

Note (Description of incidence rate $(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$): Here, in this expression $\theta _{1}$ and $\theta _{2}$ are the rates at which an infected person can transmit infection to the individuals of susceptible classes $S_{1}$ and $S_{2}$, respectively. Therefore, the incidence rate between susceptible classes and infected class appeared as $(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$. Now, if we assume that government implements some regulations to prevent disease propagation, then this transmission rate will depend on strength of governmental intervention ($\alpha$), effectiveness of sociological behavioral dynamics (D) and strength of public reaction (k). Now, growing intensity of governmental action ($\alpha$) will diminish disease transmission and this effect can be incorporated by multiplying a factor $(1-\alpha )$ to disease transmission rate. Thus, the individuals will now leave the susceptible class $S_{1}$ and $S_{2}$ at rate $(1-\alpha )\theta _{1}S_{1}(t)I(t)$ and $(1-\alpha )\theta _{2}S_{2}(t)I(t)$, respectively. If the people are motivated by the measures of government action to prevent transmission of disease, effectiveness of sociological behavioral dynamics (D) and strength of public reaction (k) will increase and ultimately reduce the spreading of ailment.

In the proposed system, it is assumed that $0\le \alpha \le 1,\ 0\le D \le 1$. Now, the scenario $\alpha = 0$ and $D=0$ signifies that there is an absence of governmental intervention and a lack of social behavioral dynamics, respectively. As these sociological parameters approach to the value 1, the factor $(1-\alpha )(1-D)$ reduces. The dynamics of social behavior and the reactions of the public are intricately linked to each other. Now, taking the parameter public reaction (k) as an exponent applied to $(1-D)$, it accelerates the reduction of the term $(1-D)^{k}$. Consequently, the overall factor $(1-\alpha )(1-D)^{k}$ becomes a notably smaller quantity. Thus, when we multiply this factor with the transmission rate $(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$, the rate at which individuals (from the susceptible classes) move to the infected class can be expressed as $(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$. Considering the transmission rate as $(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)$ signifies that as the amplitude of $\alpha$, D and k raises, the infection rate from susceptible to infected class reduces, which is more realistic.

Fig. 1

Schematic representation of system (2.1)

3 Preliminary findings

To establish the existence and uniqueness of the solution for model (2.1), following lemma is required.

Lemma 3.1

[38] Consider the system:

$$\begin{aligned} y'(t)=f(t,y),\quad t_{0}>0 \end{aligned}$$

(3.1)

with initial condition $y(t_{0})=y_{t_{0}}$, $f:[t_{0},\infty )\times {\mathcal {T}}\longrightarrow {\mathbb {R}}^{n}$, ${\mathcal {T}}\in {\mathbb {R}}^{n}$, if f(t, y) satisfies the local Lipschitz condition with respect to y, then there exists a unique solution of (2.1) on $[t_{0},\infty )\times {\mathcal {T}}$.

Each of the right-hand side (RHS) functions of system (2.1) is polynomial function of $(S_1,S_2,I,V)$. Thus, the RHS functions are continuous as there is no discontinuity.

To study the existence and uniqueness of the solution of system (2.1), consider the region ${\mathcal {T}} \times \left[ 0, T\right]$ where

$$\begin{aligned} {\mathcal {T}}= & {} \Big \{\left( S_1(t),S_2(t),I(t),V(t)\right) \in {\mathbb {R}}^{4}\\{} & {} :\max {\{|S_1(t)|,|S_2(t)|, |I(t)|,|V(t)|}\}\le M\Big \} \end{aligned}$$

and $T<\infty$. Let us denote $X\!=\left( S_1(t),\!S_2(t),\!I(t),\!V(t)\right)$ and $\overline{X}=\left( \overline{S_1}(t),\overline{S_2}(t),\overline{I}(t),\overline{V}(t)\right)$. Consider a mapping

$$\begin{aligned} L(X)=\left( L_{1}(X),L_{2}(X),L_{3}(X),L_{4}(X)\right) \end{aligned}$$

where

$$\begin{aligned} L_{1}(X)&=q\Pi -(1-\alpha )(1-D)^{k}\theta _{1}S_{1}(t)I(t)\\&\quad -v _1S_1(t)+\beta _1\gamma I(t)-\mu S_{1}(t) \\ L_{2}(X)&=(1-q)\Pi -(1-\alpha )(1-D)^{k}\theta _{2}S_{2}(t)I(t)\\&\quad -v _2S_2(t)+\beta _2\gamma I(t)-\mu S_{2}(t) \\ L_{3}(X)&=(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)\\&\quad -\gamma I(t)+\varepsilon I(t)V(t)- (\mu +m)I(t)\\ L_{4}(X)&=(v _1S_1(t)+v _2S_2(t))+(1-\beta _1-\beta _2)\\&\quad \gamma I(t)-\varepsilon I(t)V(t)-\mu V(t). \end{aligned}$$

Now,

$$\begin{aligned} \displaystyle \Vert L(X)-L(\overline{X})\Vert&= |L_{1}(X)-L_{1}(\overline{X})|+|L_{2}(X)\\&\quad -L_{2}(\overline{X})|+|L_{3}(X)-L_{3}(\overline{X}) |+|L_{4}(X)-L_{4}(\overline{X})|\\&\quad \le | -\theta _1(1-\alpha ) (1-D)^k (S_1 I -\overline{S_1}\overline{I}) -v_1 (S_1- \overline{S_1})\\&\quad +\beta _1 \gamma (I-\overline{I}) -\mu (S_1- \overline{S_1}) | \\&\quad + |-\theta _2(1-\alpha ) (1-D)^k (S_2 I -\overline{S_2}\overline{I})\\&\quad -v_2 (S_2- \overline{S_2}) +\beta _2 \gamma (I-\overline{I}) -\mu (S_2- \overline{S_2})| \\&\quad + | (1-\alpha ) (1-D)^k \{\theta _1 (S_1 I -\overline{S_1}\overline{I})+ \theta _2 (S_2 I -\overline{S_2}\overline{I})\}\\&\quad -\gamma (I-\overline{I}) +\varepsilon (IV - \overline{I}\overline{V})\\&\quad -(\mu +m)(I-\overline{I}) | + | v_1(S_1- \overline{S_1})+ v_2 (S_2- \overline{S_2}) \\&\quad +(1-\beta _1-\beta _2)\gamma (I-\overline{I})\\&\quad -\varepsilon (IV - \overline{I}\overline{V}) -\mu (V-\overline{V}) |\\&\quad \le [ 2M\theta _1 (1-\alpha ) (1-D)^k+2v_1+\mu ]|S_1-\overline{S_1}| \\&\quad +[ 2M\theta _2 (1-\alpha ) (1-D)^k+2v_2\\&\quad +\mu ]|S_2-\overline{S_2}|\\&\quad +[2M\theta _1 (1-\alpha ) (1-D)^k+2M\theta _2 (1-\alpha ) (1-D)^k\\&\quad +2M \varepsilon +\mu + m+2\gamma ]|I-\overline{I}|\\&\quad +[2M \varepsilon +\mu ]|V-\overline{V}|. \end{aligned}$$

Let

$$\begin{aligned} E= & {} \max \bigg \{ \left[ 2M\theta _1 (1-\alpha ) (1-D)^k+2v_1+\mu \right] ,\\{} & {} \quad \left[ 2M\theta _2 (1-\alpha ) (1-D)^k+2v_2+\mu \right] , \\{} & {} \quad \Bigg [2M\theta _1 (1-\alpha ) (1-D)^k \\ {}{} & {} \quad +2M\theta _2 (1-\alpha ) (1-D)^k \\{} & {} \quad +2M \varepsilon +\mu + m+2\gamma \Bigg ],\\{} & {} \quad \left[ 2M \varepsilon +\mu \right] \bigg \} \\{} & {} \quad \therefore \Vert L(X)-L(\overline{X})\Vert \le E \Vert X-\overline{X}\Vert . \end{aligned}$$

Thus, L(X) satisfies the Lipschitz’s condition with respect to X; it follows from Lemma 3.1 that there exists a unique solution X(t) of system (2.1) with initial condition $X(0)=(S_1(0),S_2(0),I(0),V(0))$.

Proposed system (2.1) is biologically relevant since the system variables are positive and bounded, and this is shown in the following two theorems.

Theorem 3.2

All solutions of model (2.1) in ${\mathbb {R}}_{+}^{4}$ are positive for all $t>0$.

Proof

Let $\phi (S_{1},S_{2},I,V)=(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}+\theta _{2}S_{2})- (\mu +m+\gamma ) +\varepsilon V$. From the third equation of (2.1) we have,

$$\begin{aligned} I(t)= & {} I(0)\exp \left[ \int ^t_0 \phi (S_{1}(u),S_{2}(u),I(u),V(u))\,du\right] \\\ge & {} 0, \quad \text {as} \quad I(0)\ge 0. \end{aligned}$$

Now, we want to show, $S_{1}(t)>0,\ S_{2}(t)>0 \ \forall \, t\in [0,\eta ),\, 0< \eta \le +\infty$. If the assumptions are not true, then $\exists \ t_{1},\ t_{2} \in (0,\eta )$ so that $S_{1}(t_{1})=0,\ {\dot{S}}_{1}(t_{1})\le 0,\ S_{1}(t)>0, \ \forall \, t\in [0,t_{1})$ and $S_{2}(t_{2})=0,\ {\dot{S}}_{2}(t_{2})\le 0,\ S_{2}(t)>0, \ \forall \, t\in [0,t_{2})$. From the first equation we get

$$\begin{aligned} \frac{dS_{1}}{dt}\bigg |_{t=t_{1}}= q\Pi +\beta _1\gamma I(t_1)> 0 \end{aligned}$$

which is a contradiction to ${\dot{S}}_{1}(t_{1})\le 0.$ And, the second equation gives

$$\begin{aligned} \frac{dS_{2}}{dt}\bigg |_{t=t_{2}}= (1-q)\Pi +\beta _2\gamma I(t_2)> 0 \end{aligned}$$

which contradicts ${\dot{S}}_{2}(t_{2})\le 0.$ So we get, $S_{1}(t)> 0$ and $S_{2}(t)> 0, \ \forall \, t\in [0,\eta )$, where $0<\eta \le +\infty$. Next, our claim is $V(t)\ge 0,\ \forall \, t\in [0,\eta ).$ If it does not hold, then $\exists \ t_{3} \in (0,\eta )$ such that $V(t_{3})=0,\ {\dot{V}}(t_{3})\le 0$ and $V(t)> 0, \ \forall \, t\in [0,t_{3})$. From the last equation we get

$$\begin{aligned} \frac{dV}{dt}\bigg |_{t=t_{3}}= & {} (v _1S_1(t_3)+v _2S_2(t_3))\\{} & {} +(1-\beta _1-\beta _2)\gamma I(t_3)> 0 \end{aligned}$$

which contradicts the assumption ${\dot{V}}(t_{3})\le 0.$ So, $V(t)\ge 0, \ \forall \, t\in [0,\eta )$ for $0<\eta \le +\infty .$ $\square$

Theorem 3.3

All solutions of model (2.1), starting from ${\mathbb {R}}_{+}^{4}$, are bounded for all $t>0$.

Proof

We have considered the total population as $N(t)=S_{1}(t)+S_{2}(t)+I(t)+V(t)$. Then,

$$\begin{aligned} \frac{dN}{dt}&=\Pi -\mu S_{1}-\mu S_{2}-(\mu +m)I-\mu V \le \Pi -\mu N \\&\Rightarrow 0<N(t)\le \frac{\Pi }{\mu }+\left( N(0)-\frac{\Pi }{\mu }\right) e^{-\mu t} \end{aligned}$$

where $N(0)=S_{1}(0)+S_{2}(0)+I(0)+V(0)$. Then, $\displaystyle 0<\lim _{t\rightarrow \infty }N(t)\le \frac{\Pi }{\mu } +\epsilon$, for any $\epsilon >0$. Hence, the solutions of model (2.1) are confined in the region: $\bar{\Delta }=\left\{ (S_{1},S_{2},I,V)\in {\mathbb {R}}_{+}^{4}: 0< N(t)\le \frac{\Pi }{\mu }+\epsilon \right.$, $\left. \mathrm{for ~ any ~} \epsilon \right. \left. > 0 \right\}$. $\square$

4 Equilibrium state analysis of model (2.1)

System (2.1) possesses a disease-free equilibrium (DFE) point $\displaystyle E_{0}(S_{10},S_{20},0,V_0)$ with $\displaystyle S_{10}=\frac{q\Pi }{v_1+\mu }$, $\displaystyle S_{20}=\frac{(1-q)\Pi }{v_2+\mu }$ and $\displaystyle V_0=\frac{v _1S_{10}+v _2S_{20}}{\mu }$. Basic reproduction number $(R_{0})$ indicates the size of newly contaminated persons from a single infected person in a susceptible community, and it is determined by the procedure recommended by van den Driessche and Watmough [39]. Now, $R_{0}$ is the reproduction number and is denoted by:

$$\begin{aligned} R_{0}&=\frac{(1-\alpha )(1-D)^{k}\theta _{1}S_{10}}{(\mu +m+\gamma -\varepsilon V_0)}\nonumber \\&\quad +\frac{(1-\alpha )(1-D)^{k}\theta _{2}S_{20}}{(\mu +m+\gamma -\varepsilon V_0)} \end{aligned}$$

(4.1)

provided $\mu +m+\gamma >\varepsilon V_0$. The first part is due to weak susceptible compartment, and second part is due to strong susceptible compartment. The detailed calculation process of basic reproduction number (4.1) is provided in Appendix A.

4.1 Endemic equilibrium point

The endemic equilibrium point $E^{*}(S_{1}^{*},S_{2}^{*}, I^{*}, V^{*})$ of system (2.1) can be obtained by solving the following equations:

$$\begin{aligned}&q\Pi -(1-\alpha )(1-D)^{k}\theta _{1}S_{1}I\\&\quad -v _1S_1+\beta _1\gamma I-\mu S_{1}=0 \\&\quad (1-q)\Pi -(1-\alpha )(1-D)^{k}\theta _{2}S_{2}I\\&\quad -v _2S_2+\beta _2\gamma I-\mu S_{2}=0 \\&\quad (1-\alpha )(1-D)^{k}(\theta _{1}S_{1}+\theta _{2}S_{2})I\\&\quad -\gamma I+\varepsilon IV- (\mu +m)I =0 \\&\quad (v _1S_1+v _2S_2)+(1-\beta _1-\beta _2)\\&\quad \gamma I-\varepsilon IV-\mu V=0 \end{aligned}$$

where $p_{1}=\mu +m+\gamma$. Solving, we get $V^{*}=\frac{v_1 S_1^*+v _2S_2^*+(1-\beta _1-\beta _2)\gamma I^*}{\varepsilon I^{*}+\mu }$, $S_{1}^{*}=\frac{q\Pi +\beta _1\gamma I^{*}}{\mu +v_1+(1-\alpha )(1-D)^{k}\theta _{1}I^{*}}$, $S_{2}^{*}=\frac{(1-q)\Pi +\beta _2\gamma I^{*}}{\mu +v_2+(1-\alpha )(1-D)^{k}\theta _{2}I^{*}},$ and $I^{*}$ is the positive root of the following equation:

$$\begin{aligned} f(I)\equiv A_{11}I^{3}+A_{12}I^{2}+A_{13}I+A_{14}=0 \end{aligned}$$

here $k_{1}=(1-\alpha )(1-D)^{k}\theta _1$, $k_{2}=(1-\alpha )(1-D)^{k}\theta _2$

$$\begin{aligned} A_{11}&=-\varepsilon k_1 k_2 (\mu +m)<0\\ A_{12}&= \varepsilon k_1 k_2 \Pi q + \mu \varepsilon \gamma k_1 \beta _1 + \mu \gamma k_1 k_2 \beta _1 \\&\quad + \varepsilon \gamma k_2 v_1 \beta _1 + \varepsilon \gamma k_1 v_2 \beta _1+ \varepsilon k_1 k_2 \Pi - \varepsilon k_1 k_2 \Pi q \\&\quad + \mu \varepsilon \gamma k_2 \beta _2 + \mu \gamma k_1 k_2 \beta _2\\&\quad + \varepsilon \gamma k_2 v_1 \beta _2 + \varepsilon \gamma k_1 v_2 \beta _2\\&\quad - \mu \varepsilon k_1 p_1 - \mu \varepsilon k_2 p_1 - \mu k_1 k_2 p_1 - \varepsilon k_2 v_1 p_1 \\&\quad - \varepsilon k_1 v_2 p_1+ \mu \varepsilon \gamma k_1 + \mu \varepsilon \gamma k_2 + \varepsilon \gamma k_2 v_1\\&\quad + \varepsilon \gamma k_1 v_2 - \mu \varepsilon \gamma k_1 \beta _1 - \mu \varepsilon \gamma k_2 \beta _1 \\&\quad - \varepsilon \gamma k_2 v_1 \beta _1- \varepsilon \gamma k_1 v_2 \beta _1 - \mu \varepsilon \gamma k_1 \beta _2 \\&\quad - \mu \varepsilon \gamma k_2 \beta _2 - \varepsilon \gamma k_2 v_1 \beta _2- \varepsilon \gamma k_1 v_2 \beta _2\\ A_{13}&=\mu ^2 \varepsilon \gamma + \mu \varepsilon \gamma v_1+ \mu \varepsilon \gamma v_2+ \varepsilon \gamma v_1 v_2\\&\quad - \mu ^2 \varepsilon \gamma \beta _1- \mu \varepsilon \gamma v_1 \beta _1- \mu \varepsilon \gamma v_2 \beta _1\\&\quad - \varepsilon \gamma v_1 v_2 \beta _1- \mu ^2 \varepsilon \gamma \beta _2- \mu \varepsilon \gamma v_1 \beta _2\\&\quad -\mu \varepsilon \gamma v_2 \beta _2- \varepsilon \gamma v_1 v_2 \beta _2-\mu ^2 \varepsilon p_1\\&\quad -\mu ^2 k_1 p_1-\mu ^2 k_2 p_1-\mu \varepsilon v_1 p_1\\&\quad -\mu k_2 v_1 p_1-\mu \varepsilon v_2 p_1-\mu k_1 v_2 p_1\\&\quad -\varepsilon v_1 v_2 p_1+\mu \varepsilon k_2 \Pi + \mu k_1 k_2 \Pi \\&\quad + \varepsilon k_2 \Pi v_1+ \varepsilon k_1 \Pi v_2 \\&\quad - \mu \varepsilon k_2 \Pi q - \mu k_1 k_2 \Pi q - \varepsilon k_2 \Pi v_1 q - \varepsilon k_1 \Pi v_2 q \\&\quad + \mu ^2 \gamma k_2 \beta _2 + \mu \gamma k_2 v_1 \beta _2 + \mu \varepsilon \gamma v_2 \beta _2\\&\quad + \varepsilon \gamma v_1 v_2 \beta _2+ \mu \varepsilon k_1 \Pi q + \mu k_1 k_2 \Pi q \\&\quad + \varepsilon k_2 \Pi v_1 q+ \varepsilon k_1 \Pi v_2 q + \mu ^2 \gamma k_1 \beta _1 \\&\quad + \mu \varepsilon \gamma v_1 \beta _1 + \mu \gamma k_1 v_2 \beta _1 + \varepsilon \gamma v_1 v_2 \beta _1 \\ A_{14}&= \mu (p_1-\varepsilon V_0)(v _1+\mu )(v _2+\mu )[R_0-1]. \end{aligned}$$

Now, $f(0)=A_{14}>0$ when $R_{0}>1$, and $f(\infty )=-\infty$. So, there will be at least one positive root of the equation for $R_{0}>1$. It means system (2.1) contains at least one endemic equilibrium point $E^{*}(S_{1}^{*}, S_{2}^{*}, I^{*}, V^{*})$ when basic reproduction number exceeds unity.

5 Sensitivity analysis

The formulation of basic reproduction number ($R_0$) reveals that $R_0$ is influenced by governmental actions ($\alpha$), sociological behavioral dynamics (D) and public reaction (k), rate of transmission of disease ($\theta _1, \theta _2$), vaccination rate ($v_1, v_2$), recovery rate ($\gamma$) and reinfection rate due to reduction of efficacy of vaccination ($\varepsilon$). This section examines the implications of the aforementioned parameters on spread of ailment. The basic reproduction number of model (2.1) is obtained as $R_{0}=\frac{(1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})}{(p_1-\varepsilon V_0)}$, where $p_{1}=\mu +m+\gamma$, $S_{10}=\frac{q\Pi }{v_1+\mu }$, $S_{20}=\frac{(1-q)\Pi }{v_2+\mu }$ and $V_0=\frac{v _1S_{10}+v _2S_{20}}{\mu }$. Then, we get:

$$\begin{aligned}&\frac{\partial R_0}{\partial \alpha }=-\frac{(1-D)^{k}}{(p_1-\varepsilon V_0)}\left( \theta _{1}S_{10}+\theta _{2}S_{20}\right)<0,\\&\frac{\partial R_0}{\partial D}=-\frac{k(1-\alpha )(1-D)^{k-1}}{(p_1-\varepsilon V_0)}\\&\quad \left( \theta _{1}S_{10}+\theta _{2}S_{20}\right)<0 \\&\frac{\partial R_0}{\partial k}= \frac{(1-\alpha )(1-D)^{k}\ln (1-D)}{(p_1-\varepsilon V_0)}\\&\quad \left( \theta _{1}S_{10}+\theta _{2}S_{20}\right)<0,\\&\quad (\text {as}\ 0<D<1 \Rightarrow \ln (1-D)<0)\\&\frac{\partial R_0}{\partial \theta _1}= \frac{(1-\alpha )(1-D)^{k} S_{10}}{(p_1-\varepsilon V_0)}>0, \\&\frac{\partial R_0}{\partial \theta _2}= \frac{(1-\alpha )(1-D)^{k} S_{20}}{(p_1-\varepsilon V_0)}>0\\&\frac{\partial R_0}{\partial \gamma }= -\frac{(1-\alpha )(1-D)^{k}}{(p_1-\varepsilon V_0)^2}\\&\quad \left( \theta _{1}S_{10}+\theta _{2}S_{20}\right) <0, \\&\frac{\partial R_0}{\partial \varepsilon }=\frac{V_0(1-\alpha )(1-D)^{k}}{(p_1-\varepsilon V_0)^2}\\&\quad \left( \theta _{1}S_{10}+\theta _{2}S_{20}\right) >0. \end{aligned}$$

Considering each of those parameters, the associated normalized forward sensitivity index is provided as [40]:

$$\begin{aligned}&\Theta _{\alpha }=\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial \alpha }{\alpha }}\right] =\left[ \frac{\alpha }{R_0}\frac{\partial R_0}{\partial \alpha }\right] =-\left( \frac{\alpha }{1-\alpha }\right) ,\\&\Theta _{D} =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial D}{D}}\right] =\left[ \frac{D}{R_0}\frac{\partial R_0}{\partial D}\right] =-k\left( \frac{D}{1-D}\right) \\&\Theta _{k} =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial k}{k}}\right] =\left[ \frac{k}{R_0}\frac{\partial R_0}{\partial k}\right] =k\ln (1-D), \\&\Theta _{\theta _1 } =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial \theta _1}{\theta _1}}\right] =\left[ \frac{\theta _1}{R_0}\frac{\partial R_0}{\partial \theta _1}\right] =\frac{\theta _1 S_{10}}{(\theta _{1}S_{10}+\theta _{2}S_{20})}\\&\Theta _{\theta _2 } =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial \theta _2}{\theta _2}}\right] =\left[ \frac{\theta _2}{R_0}\frac{\partial R_0}{\partial \theta _2}\right] =\frac{\theta _2 S_{20}}{(\theta _{1}S_{10}+\theta _{2}S_{20})}\\&\Theta _{\gamma } =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial \gamma }{\gamma }}\right] =\left[ \frac{\gamma }{R_0}\frac{\partial R_0}{\partial \gamma }\right] =-\frac{\gamma }{(p_1-\varepsilon V_0)}, \\&\Theta _{\varepsilon } =\left[ \frac{\frac{\partial R_0}{R_0}}{\frac{\partial \varepsilon }{\varepsilon }}\right] =\left[ \frac{\varepsilon }{R_0}\frac{\partial R_0}{\partial \varepsilon }\right] =\frac{\varepsilon V_0}{(p_1-\varepsilon V_0)}. \end{aligned}$$

The effective implementation of governmental actions, coupled with strict adherence to regulations, can play a pivotal role in controlling an epidemic situation over time. Additionally, the public’s willingness to adopt necessary behavioral changes during a disease outbreak is crucial in interrupting continuous transmission. Conversely, if the disease spreads rapidly among the population, the infection can escalate at a faster rate, posing a greater challenge to the control measures in place. Public response is another significant factor in managing the epidemic situation. Increased public awareness and education have been observed to impede the transmission of the disease, as people become more informed about preventive measures and take necessary precautions. Furthermore, the recovery of individuals from the disease, whether through natural immunity or clinical treatment, can contribute in reducing the overall disease prevalence. Recovered individuals are less likely to contribute to further transmission, thereby lowering the overall burden on the healthcare system. Increasing the vaccination rate against the infection can lead to a reduction in the reproduction number, which signifies a decrease in the transmission of the disease due to a less quantity of infected individuals. The effectiveness of the vaccine, particularly when it provides a high level of protection for humans, plays a crucial role in effectively controlling the spread of the infection. In Fig. 2, a multifaceted approach involving governmental actions, public cooperation and awareness, combined with efforts to improve recovery rates and vaccination efficiency, is essential for effectively controlling and mitigating the impact of an epidemic. The sensitivity indices of system parameters are displayed by the tornado plot in Fig. 3, with their values as: $\Theta _{\alpha }=-0.25, \Theta _{D}=-0.8571,\ \Theta _{k}=-0.7133,\ \Theta _{\theta _1}=0.5882, \Theta _{\theta _2}=0.4118, \Theta _{\gamma }=-0.3218$ and $\Theta _{\varepsilon }= 0.4483$. Therefore, the sensitivity indices provide a justification for the depicted scenario in Fig. 2. This illustration visually represents the manner in which these parameters exert an influence on the propagation of disease.

Fig. 2

Changes of $R_0$ when the model parameters $\alpha , D, k, \theta _1, \theta _2, \gamma$ and $\varepsilon$ are varied. Parameter values are taken as $q = 0.4, \Pi = 10, \alpha = 0.2, D = 0.3, k = 2, \theta _1 = 0.2, v_1= 0.3, \beta _1 = 0.3, \gamma = 0.2, \mu = 0.4, \theta _2 = 0.08, v_2 = 0.2, \beta _2 = 0.4, m = 0.3, \varepsilon = 0.03$

Fig. 3

The visual representation of sensitivity index for $\alpha , D, k, \theta _1, \theta _2, \gamma$ and $\varepsilon$ of model (2.1)

Figure 4 depicts how the reproduction number varies with the change of any of the parameters $v_1$ and $v_2$. The reproduction number is a critical indicator of disease transmission, and its behavior is investigated concerning vaccination rates for different population groups. It is observed that the reproduction number reduces with the increase of the vaccination rate for weaker community. This implies that higher vaccination coverage in the vulnerable population leads to a reduced potential for disease transmission. In contrary to this, if the vaccination rate for weaker class remains constant with a increase rate of vaccination for higher immunity population, then the reproduction number increases. The cause behind this is less immunity class $(S_1)$ can generally be infected due to ailment propagation; however, $S_2$ susceptible individuals have the higher immunity from becoming infected. To effectively control the disease prevalence, it is necessary to increase the vaccination rate $(v_1)$ for the weaker section $(S_1)$ over time while keeping the vaccination rate $(v_2)$ for the higher immunity population $(S_2)$ constant. Moreover, Fig. 4c highlights how the simultaneous interaction of $v_1$ and $v_2$ influences the propagation of the disease in the dynamical system. Understanding these interactions is essential for devising effective vaccination strategies that take into account the varying susceptibility levels within the population and ultimately contribute to disease control and prevention.

Fig. 4

Changes of $R_0$ with the parameters $v_1$ and $v_2$. Parameter values are taken as in Fig. 2

5.1 Dynamics of model (2.1)

According to Routh–Hurwitz criterion, a particular steady-state point of a system is considered to be locally asymptotically stable (LAS) whether all the eigenvalues of the variational matrix that corresponds to it contain negative real parts. Let $\displaystyle p_{1}=\mu +m+\gamma$. The variational matrix of model (2.1) is:

$$\begin{aligned} \ {\overline{J}}=\begin{pmatrix} a_{11} &{} 0 &{} a_{13} &{} 0 \\ 0 &{} a_{22} &{} a_{23} &{} 0 \\ a_{31} &{} a_{32} &{} a_{33} &{} a_{34} \\ a_{41} &{} a_{42} &{} a_{43} &{} a_{44} \end{pmatrix} \end{aligned}$$

(5.1)

where $\displaystyle a_{11}=-\mu -v _1-(1-\alpha )(1-D)^{k}\theta _{1}I, \ a_{12}=0,\ a_{13}=-(1-\alpha )(1-D)^{k}\theta _{1}S_{1}+\beta _1\gamma ,\ a_{14}=0, \ a_{21}=0, \ a_{22}=-\mu -v _2-(1-\alpha )(1-D)^{k}\theta _{2}I,\ a_{23}=-(1-\alpha )(1-D)^{k}\theta _{2}S_{2}+\beta _2\gamma ,\ a_{24}=0,\ a_{31}=(1-\alpha )(1-D)^{k}\theta _{1}I,\ a_{32}=(1-\alpha )(1-D)^{k}\theta _{2}I, a_{33}=(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}+\theta _{2}S_{2})-p_{1}+\varepsilon V,\ a_{34}=\varepsilon I,\ a_{41}=v _1, \ a_{42}=v _2, \ a_{43}=(1-\beta _1-\beta _2)\gamma -\varepsilon V,\ a_{44}=-(\varepsilon I+\mu )$.

Theorem 5.1

The disease-free steady state $(E_{0})$ is LAS if $R_{0}<1$.

Proof

At DFE $\displaystyle E_{0} \equiv (S_{10},S_{20},0,V_0)$ with $\displaystyle S_{10}=\frac{q\Pi }{v _1+\mu }$, $\displaystyle S_{20}=\frac{(1-q)\Pi }{v _2+\mu }$ and $\displaystyle V_0=\frac{v _1S_{10}+v _2S_{20}}{\mu }$, the Jacobian matrix is:

$$\begin{aligned}\ {\overline{J}}\big |_{E_{0}}= \begin{pmatrix} -\mu -v_1 &{} 0 &{} -(1-\alpha )(1-D)^{k}\theta _{1}S_{10}+\beta _1\gamma &{} 0 \\ 0 &{} -\mu -v _2 &{} -(1-\alpha )(1-D)^{k}\theta _{2}S_{20}+\beta _2\gamma &{} 0 \\ 0 &{} 0 &{} (1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})-p_{1}+\varepsilon V_{0} &{} 0 \\ v _1 &{} v _2 &{} (1-\beta _1-\beta _2)\gamma -\varepsilon V_{0} &{} -\mu \end{pmatrix}. \end{aligned}$$

The eigenvalues of ${\overline{J}}\big |_{E_{0}}$ are $\lambda _{1}=-\mu , \lambda _{2}=-\mu -v _1, \lambda _{3}=-\mu -v _2$ and $\lambda _{4}=(p_{1}-\varepsilon V_{0})(R_{0}-1)$. So, $\lambda _{i}<0$, for $i=1,2,3$, and $\lambda _{4}<0$ when $R_{0}<1$. $\square$

It is therefore possible to verify that the condition specified in Theorem 5.1 is fulfilled, having taken the parameter values as stated in Fig. 2 with $\alpha = 0.3, D = 0.4$ and we have established that basic reproduction number $R_0 = 0.7879 <1$. The corresponding eigenvalues of ${\overline{J}}\big |_{E_{0}}$ are obtained as $-0.4,-0.7,-0.6,-0.1318$. From Fig. 5a, it can be noticed that the trajectory converges to disease-free steady state, $E_0=(S_{10},S_{20},0,V_0)=(5.71,10,0,9.29)$ when $\alpha = 0.3, D = 0.4$. Hence, infection-free system might be achieved.

Theorem 5.2

The interior equilibrium $(E^{*})$ is locally asymptotically stable under the conditions stated in the proof.

Proof

At $E^{*}$, the variational matrix is represented as follows:

$$\begin{aligned} {\overline{J}}\big |_{E^{*}}=\begin{pmatrix} a^{'}_{11} &{} 0 &{} a^{'}_{13} &{} 0 \\ 0 &{} a^{'}_{22} &{} a^{'}_{23} &{} 0 \\ a^{'}_{31} &{} a^{'}_{32} &{} a^{'}_{33} &{} a^{'}_{34} \\ a^{'}_{41} &{} a^{'}_{42} &{} a^{'}_{43} &{} a^{'}_{44} \end{pmatrix} \end{aligned}$$

where $\displaystyle a^{'}_{11}=-\mu -v _1-(1-\alpha )(1-D)^{k}\theta _{1}I^*,\ a^{'}_{13}=-(1-\alpha )(1-D)^{k}\theta _{1}S_{1}^*+\beta _1\gamma , \ a^{'}_{22}=-\mu -v _2-(1-\alpha )(1-D)^{k}\theta _{2}I^*,\ a^{'}_{23}=-(1-\alpha )(1-D)^{k}\theta _{2}S_{2}^*+\beta _2\gamma ,\ a^{'}_{31}=(1-\alpha )(1-D)^{k}\theta _{1}I^*,\ a^{'}_{32}=(1-\alpha )(1-D)^{k}\theta _{2}I^*, a^{'}_{33}=(1-\alpha )(1-D)^{k}(\theta _{1}S_{1}^*+\theta _{2}S_{2}^*)-p_{1}+\varepsilon V^*,\ a^{'}_{34}=\varepsilon I^*,\ a^{'}_{41}=v _1, \ a^{'}_{42}=v _2, \ a^{'}_{43}=(1-\beta _1-\beta _2)\gamma -\varepsilon V^*,\ a^{'}_{44}=-(\varepsilon I^*+\mu )$.

Characteristic equation corresponding to ${\overline{J}}\big |_{E^{*}}$ is $\lambda ^{4}+A_{1}\lambda ^{3}+A_{2}\lambda ^{2}+A_{3}\lambda +A_{4}=0,$ where

$$\begin{aligned}&A_{1}=-(a'_{11}+a'_{22}+a'_{33}+a'_{44})>0 \\&A_{2}=a'_{11}a'_{22}-a'_{13}a'_{31}-a'_{23}a'_{32}+a'_{11}a'_{33}\\&\quad +a'_{22}a'_{33} -a'_{34}a'_{43}+a'_{11}a'_{44}+a'_{22}a'_{44}+a'_{33}a'_{44}\\&A_{3}=a'_{13}a'_{22}a'_{31}+a'_{11}a'_{23}a'_{32}-a'_{11}a'_{22}a'_{33}-a'_{13}a'_{34}a'_{41}\\&\quad -a'_{23}a'_{34}a'_{42}+a'_{11}a'_{34}a'_{43}+a'_{22}a'_{34}a'_{43}-a'_{11}a'_{22}a'_{44}\\&\quad +a'_{13}a'_{31}a'_{44}+a'_{23}a'_{32}a'_{44}-a'_{11}a'_{33}a'_{44}-a'_{22}a'_{33}a'_{44}\\&A_{4}=a'_{13}a'_{22}a'_{34}a'_{41}+a'_{11}a'_{23}a'_{34}a'_{42}-a'_{11}a'_{22}a'_{34}a'_{43}\\&\quad -a'_{13}a'_{22}a'_{31}a'_{44}-a'_{13}a'_{23}a'_{32}a'_{44}+a'_{11}a'_{22}a'_{33}a'_{44}. \end{aligned}$$

The equation has roots with negative real parts only when Routh–Hurwitz criterion is satisfied. Hence, the endemic state $E^{*}$ is LAS if $A_{1}>0,\ A_{4}>0,\ A_{1}A_{2}>A_{3}$ and $A_{3}(A_{1}A_{2}-A_{3})>A_{1}^{2}A_{4}$. $\square$

Furthermore, when selecting smaller values for both $\alpha$ and D, a noteworthy observation emerges. In the context of the values of parameter depicted in Fig. 2, the eigenvalues associated to ${\overline{J}}\big |_{E^{*}}$ are obtained as $-0.1747,-0.3186,-0.8099,-0.6574$.

Thus, a trajectory starting from (18, 20, 12, 8) ultimately leads to the coexistence state $E^{*}(S_{1}^{*},S_{2}^{*}, I^{*}, V^{*})\!=\!(4.86,9.34,1.86,7.54)$ and $R_0$ becomes 1.2256 (see Fig. 5b ). Hence, the occurrence of an infection takes place when value of the basic reproduction number $R_0$ surpasses the threshold of unity.

Fig. 5

Nature of model (2.1) around a infection-free state $(E_0)$ and b coexistence state $(E^*)$

6 Bifurcation analysis

This section illustrates the occurrence of transcritical bifurcation around DFE ($E_0$), using the framework of central manifold theory, as elucidated by [41]. Suppose, $S_1=x_{1},\ S_2=x_{2},\ I=x_{3}$ and $V=x_{4}$, then system (2.1) is written as:

$$\begin{aligned} \frac{dx_1}{dt}&=q\Pi -(1-\alpha )(1-D)^{k}\theta _{1}x_1x_3\nonumber \\&\quad -v _1x_1+\beta _1\gamma x_3-\mu x_1 \equiv f_{1} \nonumber \\ \frac{dx_2}{dt}&=(1-q)\Pi -(1-\alpha )(1-D)^{k}\theta _{2}x_2x_3\nonumber \\&\quad -v _2x_2+\beta _2\gamma x_3-\mu x_2 \equiv f_{2} \nonumber \\ \frac{dx_3}{dt}&=(1-\alpha )(1-D)^{k}(\theta _{1}x_1+\theta _{2}x_2)x_3\nonumber \\&\quad -\gamma x_3+\varepsilon x_3x_4- (\mu +m)x_3 \equiv f_{3} \nonumber \\ \frac{dx_4}{dt}&=(v _1x_1+v _2x_2)\nonumber \\&\quad +(1-\beta _1-\beta _2)\gamma x_3-\varepsilon x_3x_4-\mu x_4 \equiv f_{4}. \end{aligned}$$

(6.1)

Theorem 6.1

A transcritical (forward or backward) bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ in which $\theta _1$ functions as a bifurcating parameter.

Proof

Choosing, $\theta _1$ as bifurcating parameter and at $R_{0} \!= 1$, $\displaystyle \theta _1\!=\theta _{1[TB]}{=}\frac{1}{S_{10}}\left[ \frac{(p_1-\varepsilon V_0)}{(1-\alpha )(1-D)^{k}} - \theta _2S_{20}\right]$, where $\displaystyle S_{10}=\frac{q\Pi }{v _1+\mu }$, $\displaystyle S_{20}=\frac{(1-q)\Pi }{v _2+\mu }$ and $\displaystyle V_0=\frac{v _1S_{10}+v _2S_{20}}{\mu }$. The linearized matrix of system (2.1) in accordance with $\displaystyle E_{0}\left( S_{10},S_{20},0,V_0\right)$ is calculated as

$$\begin{aligned}\ {\overline{J}}\big |_{E_{0}}= \begin{pmatrix} -\mu -v_1 &{} 0 &{} -(1-\alpha )(1-D)^{k}\theta _{1}S_{10}+\beta _1\gamma &{} 0 \\ 0 &{} -\mu -v _2 &{} -(1-\alpha )(1-D)^{k}\theta _{2}S_{20}+\beta _2\gamma &{} 0 \\ 0 &{} 0 &{} (1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})-p_{1}+\varepsilon V_{0} &{} 0 \\ v _1 &{} v _2 &{} (1-\beta _1-\beta _2)\gamma -\varepsilon V_{0} &{} -\mu \end{pmatrix}. \end{aligned}$$

The eigenvalues are $\lambda _{1}=-\mu , \lambda _{2}=-\mu -v _1, \lambda _{3}=-\mu -v _2$ and $\lambda _{4}=(p_{1}-\varepsilon V_{0})(R_{0}-1)$ which show that an eigenvalue ${\overline{J}}|_{E_{0}}(\theta _{1[TB]})$ will be zero if $R_{0}=1$. The zero eigenvalue has right eigenvector, which is denoted by $w= (w_{1},w_{2},w_{3},w_{4})^{T}$ where

$$\begin{aligned}&w_{1}= \mu (\mu +v_2) \left[ \beta _1\gamma -(1-\alpha )(1-D)^{k}\theta _{1}S_{10} \right] ,\\&w_{2}= \mu (\mu +v_1) \left[ \beta _2\gamma -(1-\alpha )(1-D)^{k}\theta _{2}S_{20} \right] ,\\&w_3 = \mu (\mu +v_1)(\mu +v_2),\\&w_4 = (\mu +v_1)(\mu +v_2)\left\{ (1-\beta _1-\beta _2)\gamma -\varepsilon V_{0} \right\} \\&\quad +v_1(\mu +v_2)\left[ \beta _1\gamma -(1-\alpha )(1-D)^{k}\theta _{1}S_{10} \right] \\&\quad +v_2(\mu +v_1)\left[ \beta _2\gamma -(1-\alpha )(1-D)^{k}\theta _{2}S_{20} \right] . \end{aligned}$$

The left eigenvector is $u= (u_{1},u_{2},u_{3},u_{4})^{T}=(0,0,1,0)^{T}$. Henceforth,

$$\begin{aligned} {\overline{a}}&= \sum _{k,i,j=1}^{n}u_{k}w_{i}w_{j}\frac{\partial ^{2}f_{k}}{\partial x_{i}\partial x_{j}}(E_{0})\nonumber \\&= 2w_3\left[ (1-\alpha )(1-D)^{k}(w_1\theta _1+w_2\theta _2)+w_4\varepsilon \right] \end{aligned}$$

(6.2)

$$\begin{aligned} {\overline{b}}&= \sum _{k,i=1}^{n}u_{k}w_{i}\frac{\partial ^{2}f_{k}}{\partial x_{i}\partial \theta _1}(E_{0})\nonumber \\&=w_3(1-\alpha )(1-D)^{k}S_{10}>0 \end{aligned}$$

(6.3)

The central manifold theory [41] states that the local dynamical behavior of a system around DFE can be obtained with the help of signs of ${\overline{a}}$ and ${\overline{b}}$, and from the theory there will be an occurrence of forward bifurcation around DFE for ${\overline{a}}<0,\ {\overline{b}}>0$, and backward bifurcation for ${\overline{a}}>0,\ {\overline{b}}>0$. We have already got that ${\overline{b}}>0$. So, from the result it can be stated that the DFE $(E_{0})$ changes its stability from stable to unstable through forward or backward bifurcation according to ${\overline{a}}<0$ or ${\overline{a}}>0$. And, there could be a chance of a negative unstable coexistence steady state turns into positive and locally asymptotic stable endemic state for $R_{0}>1$. $\square$

Several additional parameters within the system, namely $\theta _2, \alpha , D, k, \gamma$ and $\varepsilon$, play the key roles in controlling the behavior of system.

Theorem 6.2

A transcritical (forward or backward) bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle \theta _2=\theta _{2[TB]}=\frac{1}{S_{20}}\left[ \frac{(p_1-\varepsilon V_0)}{(1-\alpha )(1-D)^{k}} - \theta _1S_{10}\right]$ in which $\theta _2$ functions as a bifurcating parameter.

Theorem 6.3

A transcritical bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle \alpha =\alpha _{[TB]}=1-\frac{p_1-\varepsilon V_0}{(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})}$ in which $\alpha$ functions as a bifurcating parameter.

Theorem 6.4

A transcritical bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle D=D_{[TB]}=1-\left[ \frac{p_1-\varepsilon V_0}{(1-\alpha )(\theta _{1}S_{10}+\theta _{2}S_{20})}\right] ^{1/k}$ in which D functions as a bifurcating parameter.

Theorem 6.5

A transcritical bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle k=k_{[TB]}=\frac{\ln (p_1-\varepsilon V_0)-\ln ((1-\alpha )(\theta _{1}S_{10}+\theta _{2}S_{20}))}{\ln (1-D)}$ in which k functions as a bifurcating parameter.

Theorem 6.6

A transcritical bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle \gamma =\gamma _{[TB]}=(1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})-(\mu +m-\varepsilon V_0)$ in which $\gamma$ functions as a bifurcating parameter.

Theorem 6.7

A transcritical bifurcation occurs around $E_{0}$ of system (2.1) at $R_{0}=1$ for $\displaystyle \varepsilon =\varepsilon _{[TB]}=\frac{1}{V_0}\left[ (\mu +m+\gamma ){-}(1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})\right]$ in which $\varepsilon$ functions as a bifurcating parameter.

The disease propagation rates or infection propagation rates for weak and strong susceptible individuals $(\theta _1, \theta _2)$ act as a controlling parameters as a stable endemic situation has been occurred when $\theta _1, \theta _2$ exceeded their threshold values via transcritical bifurcations and DFE alters its stable configuration to unstable. Figure 6a and b depict that model (2.1) undergoes transcritical bifurcations at $\theta _{1[TB]}=0.137$ and $\theta _{2[TB]}=0.044$. Similarly, the sociological parameters $(\alpha , D)$, public reaction (k), recovery rate $(\gamma )$ and reinfection rate due to the reduction of efficacy of vaccination $(\varepsilon )$ may additionally serve as bifurcating parameters to regulate the dynamics of the system. The system generates transcritical bifurcations about $E_0$ which can be observed in Fig. 6c–f at $\alpha _{[TB]}=0.347$, $D_{[TB]}=0.3677$, $k_{[TB]}=2.57$, $\gamma _{[TB]}=0.34$ and $\varepsilon _{[TB]}=0.015$, respectively. Within each of the graphs in Fig. 6c–e, it is revealed that DFE attains stability when the parameters are crossed their respective transcritical thresholds. Conversely, a stable branch of an endemic state emerges whenever parameter values fall below the critical value. Moreover, an opposite phenomenon can be achieved in Fig. 6f, in which $\varepsilon$ is considered as bifurcating parameter.

Fig. 6

Change of the level of state variable assuming a $\theta _1$, b $\theta _2$, c $\alpha$, d D, e k, f $\gamma$ and g $\varepsilon$ as bifurcating parameters. Remaining parameters are considered as in Fig. 2

Figure 7 portrays the feasible regions of the endemic equilibrium of model (2.1) across multiple parameter planes. Specifically, $\alpha k$-plane is illustrated in Fig. 7a, $\alpha D$-plane in Fig. 7b and $\gamma \varepsilon$-plane in Fig. 7c. This visualization offers a profound insight into the intricate interplay between these sociological parameters and their consequential effects on the transmission dynamics of infection. Figure 7a includes transcritical bifurcation curve (dot–dot) of black-colored which partitions the whole $\alpha k$-parametric plane into two sub-regions which are labeled as $R_1$ (light-red-colored) and $R_2$ (light-green-colored). The analysis reveals that as both $\alpha$ and k are elevated to higher values, a discernible outcome becomes evident, namely, the progression toward a disease-free state. Even if the government is implementing interventions at an accelerated pace, the continuation of the infection within the system is dependent on the moderation of public response strength. Conversely, when governmental actions are intensified and societal dynamics to such behaviors increase, there is going to be no infectiousness within the system (see Fig. 7b). In Fig. 7c, we have plotted the stability regions of two different steady states emerging from system (2.1) in $\gamma \varepsilon$-parametric plane. We summarize the characteristics of the regions related to the steady states in Table 2. The graph clearly illustrates that the speed at which people recover from the contagious ailment has a direct impact on how quickly the infection will be eradicated. However, the overall outcome also relies on the effectiveness of vaccination. Whether individuals recover from the disease through vaccination or natural means, if the efficacy of the vaccination is insufficient to adequately protect human health, there is a risk of the infection persisting within the population. Therefore, a successful containment of the ailment requires a combination of rapid recovery rates and highly effective vaccination strategies to ensure the infection does not spread through the system.

Table 2 Nature of the regions formed in two parametric bifurcation

Fig. 7

Stability region of coexistence steady state of model (2.1) in a $\alpha k$-plane, b $\alpha D$-plane, and c $\gamma \varepsilon$-plane. All of the parameters are considered as in Fig. 2

7 Impacts of periodic transmission rates

While the precise factors governing the intricate dynamics of an endemic disease may not be fully elucidated, some rational speculations can be indulged. Several plausible factors contribute to this complex dynamic such as the presence of imperfect vaccines, influence of environmental variables, emergence of novel virus variants characterized by distinct infection rates, as well as the interplay of societal and biological elements, like, population density, implementation of social distancing policies and efficacy of governmental interventions. A study of Martcheva [42] suggests that autonomous models inherently manifest intricate dynamic behavior characterized by oscillations with a constant value of infection propagation rate. In real-world scenarios, the nuanced dynamics of a disease using a static transmission rate proves to be a challenging endeavor. Current research programs indicate that the behavior of disease can be more effectively interpreted by considering a periodic transmission rate [43]. Hence, in order to encompass and integrate the evolving dynamics of the disease, transmission rates $\theta _1, \theta _2$ are defined as

$$\begin{aligned} \theta _1 (t)= & {} a+b\cos \left( \frac{2\pi }{T} t+c\right) ; \nonumber \\ \theta _2(t)= & {} a_1+b_1\cos \left( \frac{2\pi }{T} t+c\right) \end{aligned}$$

(7.1)

This forms assume T-day periodicity and have amplitudes b (for transmission rate $\theta _1$) and $b_1$ (for transmission rate $\theta _2$), vertical shifts a (for transmission rate $\theta _1$) and $a_1$ (for transmission rate $\theta _2$) with phase difference c. The selection of this simple sinusoidal function is motivated by two primary factors: (1) its inherent simplicity and computational convenience offer distinct advantages; (2) in certain instances, this sinusoidal function can effectively depict a linear transformation of a weather covariate. Let us suppose that $a\ge b, a_1 \ge b_1$ so that $\theta _1, \theta _2 \ge 0$ for all time.

Within this study, our focus is primarily directed toward establishing the criteria that facilitate the eventual eradication of ailment. The widely acknowledged pivotal threshold for disease extinction in epidemic models is commonly referred to as basic reproduction number. For autonomous scenarios, this number can be quantified through approaches like the next-generation matrix method or through linearization around a disease-free equilibrium. However, when dealing with nonautonomous models, a uniform procedure for determining the basic reproduction number is not universally established. Specifically, we demonstrate that basic reproduction number associated with these models can be derived from the equivalent autonomous model through the utilization of time average of coefficients. Ma and Ma [44] and Greenhalgh and Moneim [45] have contributed significant insights in nonautonomous SIR-type epidemic models characterized by periodic transmission rates and constant population size. These researchers have demonstrated that the basic reproduction number associated with nonautonomous epidemic model aligns with that of the autonomous SIR epidemic model, where the periodic coefficients are substituted with their corresponding averages. As a consequence, the basic reproduction number can be defined as

$$\begin{aligned} R_{N}= & {} \frac{(1-\alpha )(1-D)^{k}}{(\mu +m+\gamma -\varepsilon V_0)} \nonumber \\{} & {} \left( \frac{S_{10}}{T}\int _0^T \theta _1(t) dt +\frac{S_{20}}{T}\int _0^T \theta _2(t) dt\right) . \end{aligned}$$

(7.2)

If $\varepsilon =0$, i.e., vaccination is very capable of preventing disease, then

$$\begin{aligned} R_{N(\varepsilon =0)}= & {} \frac{(1-\alpha )(1-D)^{k}}{(\mu +m+\gamma )}\nonumber \\{} & {} \left( \frac{S_{10}}{T}\int _0^T \theta _1(t) dt +\frac{S_{20}}{T}\int _0^T \theta _2(t) dt\right) \nonumber \\\le & {} R_{N} \end{aligned}$$

(7.3)

Figure 8a and b illustrate three different situations for $\varepsilon \ne 0$; (i): $\varepsilon = 0.03$, (ii): $\varepsilon = 0.04$, (iii): $\varepsilon = 0.05$ and remaining parameters are considered as $q = 0.4, \Pi = 10, \alpha = 0.2, D = 0.3, k = 2, \theta _1 = 0.2, v_1= 0.3, \beta _1 = 0.3, \gamma = 0.2, \mu = 0.4, \theta _2 = 0.08, v_2 = 0.2, \beta _2 = 0.4, m = 0.3, a = 0.2, b = 0.036, a_1 = 0.08, b_1 = 0.006, c = 0.8, T = 180$. Consequently, the reproduction numbers are obtained in each case as, (i): $R_{N} = 1.2256$, (ii): $R_{N} = 1.4409$, (iii): $R_{N} = 1.7479$. It can be noticed from Fig. 8a and b that growing values of the reinfection rate due to reduction of vaccination efficiency ($\varepsilon$) that means the reduction in vaccination effectiveness allow the disease to persist within the ecosystem. Through observation, a notable trend has been identified as we increase the parameter $\varepsilon$ from 0.03 to 0.04 and further to 0.05. Specifically, during this progression, there is a significant rise in the population of infected class, indicating an increase in the number of individuals affected by disease. In contrast, simultaneously, the size of vaccinated compartment experiences a decline. This suggests that as the value of $\varepsilon$ increases, the effectiveness of vaccination appears to decrease, leading to a reduced proportion of individuals receiving protection from ailment. Consequently, a larger portion of population remains susceptible to infection, resulting in a notable surge in the number of infected individuals. When the effectiveness of vaccination is insufficient, the process of eradicating a disease becomes considerably challenging, as the endemic state of the infection will persist for an extended period. In particular, when $\varepsilon =0.03$, it is found that the size of both infected and vaccinated community tends to stabilize and converge to 1.86 and 7.54, respectively (see Fig. 5b) in context of nonperiodic transmission rate. In contrast, considering a scenario with periodic transmission rate, a different phenomenon is noticed. Here, the level of both infected and vaccinated individuals exhibit oscillations around 1.86 and 7.54, respectively (see light green curves in Fig. 8a and b). It is evident that a population cannot remain constant in a real-world scenario; it will fluctuate; sometime, it may increase and sometime diminish. A similar trend is reflected in Fig. 8a and b due to consideration of periodic transmission rate. Equivalent to this, an oscillation behavior can also be seen if we would draw the population profiles of $S_{1}$ and $S_{2}$ taking periodic transmission rate. Thus, this brings the considered model to a quite realistic situation when periodic transmission rate is taken into account. Figure 8c portrays that how the extent of diseased population is influenced by the pace of vaccination among those who are susceptible to the contagious ailment. In this context, it becomes evident that administering vaccinations within less resilient communities yields a higher degree of effectiveness in diminishing infections.

Fig. 8

a, b Nature of vaccinated class (V) and infected class (I) when reinfection rate due to the reduction of efficacy of vaccination decreased. c Change of the size of infected compartment due to various rate of vaccination in both susceptible community

In Fig. 9a and b, we are presented with a visual representation that offers valuable insights into the intricate connection between disease transmission frequency and the duration for which the disease remains prevalent. The graph presents us with two distinct scenarios, each associated with a different time period (T) for disease persistence. The first scenario involves $T = 180$, corresponding to a calculated value of $\Omega =\frac{2\pi }{T}= 0.0349$. Subsequently, the second scenario is characterized by $T = 90$, resulting in $\Omega =\frac{2\pi }{T} = 0.0698$. These temporal variations serve as key variables in our analysis. In scenario one $(T = 180)$, where the disease transmission frequency is relatively higher, a distinctive pattern becomes apparent: the bandwidth of the infection peaks noticeably expands. Conversely, as we transition to scenario two $(T = 90)$, where the transmission frequency is reduced, an intriguing shift occurs: the bandwidth of the infection peaks narrows. The width of the bandwidth serves as a valuable indicator of the disease’s ability to persist over a specific time frame; a broader bandwidth corresponds to an extended duration of disease presence. In conclusion, the comprehensive analysis describes the intricate interrelationship between disease transmission frequency, disease persistence and the resulting patterns of infection prevalence. Furthermore, an interesting observation emerges as the time period of infection transmission rises: the peak of infected class demonstrates a noticeable increment (see Fig. 9c, d). This phenomenon occurs because when a population is exposed to a contagious disease on multiple times, the human body naturally develops immunity that enables it to resist the spread of infection. Thus, by taking into account the periodic transmission rate, we gain a new understanding that if disease transmission occurs more frequently or occurs over a shorter period of time, the population’s oscillatory nature that is, its size will fluctuate quickly as well as level of infected population will decrease.

Fig. 9

Change of population biomass for different values of time period

The amplitude of the transmission rate plays a very important role in the spread of the pandemic. Figure 10a shows three situations for (a): $b=0.036, b_1 = 0.006$, (b): $b=0.03, b_1 = 0.00576$, (c): $b=0.04, b_1 = 0.0064$. Figure 10b exhibits multiple curves, each illustrating distinct scenarios in the context of infection transmission. The solid green curve portrays a specific scenario characterized by parameter values: $a=0.2, b=0.036, a_1 =0.08, b_1=0.006$, yielding a calculated reproduction number $R_N = 1.2256$. Moving on, the dot–dot violet curve captures a different setting, where the parameters are adjusted as follows: $a=0.22, b=0.044, a_1 =0.1, b_1=0.009$, leading to an increased reproduction number $R_N = 1.4238$. This alteration in parameter values leads to a notable shift in the curve, indicating a higher peak in the infected population. This observation is crucial as it demonstrates the direct correlation between the amplitude of the transmission rate and the magnitude of the infection peak. Moreover, a subsequent exploration involves a slight reduction in the values of parameters b and $b_1$, specifically to $b=0.0396, b_1=0.0075$. This modification results in a distinct curve, depicted in solid yellow. Notably, the peak of the infected class is mitigated, as visually depicted in the graph. This adjustment in parameters contributes to a nuanced understanding of the infection dynamics and how they respond to changes in transmission rates. By analyzing Fig. 10 in its entirety, we can deduce a significant trend: as the amplitude of the transmission rate increases, the peak of the infected population also experiences a corresponding rise. Furthermore, it is important to highlight the parallel increase in the reproduction number as the transmission rate amplifies. The reproduction number serves as a critical indicator of the disease’s potential to spread within a population. Thus, this observation reinforces the interconnectedness between the transmission rate, infection peaks and the overall transmissibility of the disease.

Fig. 10

Response of the nonautonomous system when amplitude of the both transmission rates varies

8 Optimal control modeling in accordance with system (2.1)

There introduces an SIVIS model in Eq. (2.1), where system parameters remain constant. In this section, an associated optimal control problem is presented incorporating impactful measures to curtail disease transmission. The dynamics of social behavior are influenced by prevailing disease conditions. Consequently, modifications in individual behavioral patterns within the population emerge as a potent strategy for mitigating heightened disease transmission rates. Additionally, the clinical treatment has been addressed as a pharmaceutical intervention capable of reducing the disease burden. In this context, our analysis explores how these time-dependent control strategies affect disease transmission patterns. Our primary objective is to optimize the expenses associated with executing the strategies.

8.1 Strengthening susceptible individuals through social behavioral Enhancement

Alterations in the nature of susceptible individuals are primarily triggered by an understanding of the seriousness of a disease outbreak. This alteration in behavior develops gradually as a response to changes in disease prevalence over time, offering a potential means to disrupt ongoing disease transmission. In the system defined by Eq. (2.1), we denote the potency of this social behavior as D, constrained within the range $0 \le D < 1$. In this context, 0 signifies no behavioral changes, while 1 indicates a complete shift toward modified behavior. In this context, the socialized behavior D(t) is treated as a control parameter to reinforce individual responsiveness to disease symptoms and precautions. Our objective is to assessed the optimal level of social behavioral strength within the susceptible community, aiming to diminish the overall impact of ailment. Since changes in behavior correspond to the severity of the circumstances, D(t) is regarded as a single control measure.

8.2 Enhancement of clinical treatment for contaminated individuals

Administering medical treatment to those who are infectious plays a vital role in diminishing disease prevalence and impeding its progression. This strategy involves providing clinical treatment to diagnosed individuals, involving steps like symptom detection and medical care. Importantly, these aspects undergo modifications and improvements over time. To account for this dynamic, the treatment rate is introduced as time-dependent function indicated as $\gamma (t)$ in the model. In this scenario, costs associated with medication, diagnosis, hospitalization and other related factors are taken into account. The treatment intensity, represented by $\gamma (t)$, functions as an additional control parameter within certain boundaries, where $0 \le \gamma < 1$. Here, values of 0 and 1 correspond, respectively, to no response and full adherence to the prescribed treatment.

Our objective involves finding the most effective social behavior strength and treatment strategy, while keeping costs to a minimum. To do this, we must establish a valid range of choices for the control actions D(t) and $\gamma (t)$. This permissible range for these interventions can be defined as:

$$\begin{aligned}{} & {} \Xi =\left\{ \left( D(t),\gamma (t)\right) |\left( D(t),\gamma (t)\right) \right. \\{} & {} \quad \left. \in [0,1]\times [0,1],t\in [0,T_{f}]\right\} , \end{aligned}$$

in which $T_{f}$ denotes concluding time until the control strategies remain in effect. Additionally, the functions D(t) and $\gamma (t)$, representing social behavior and treatment intensity respectively, are assumed to be measurable and constrained within certain limits.

8.3 Evaluating of total expenses

8.3.1 Cost incurred in preserving sociological behavioral dynamics

The overall expenditure related to enhancing societal behavior is calculated as $\int _{0}^{T_{f}} \left[ g_{2}D^{k}(t)\right] dt$. This cost encompasses the essential actions required to promote early precautionary measures among the people. Some existing research [46] employs a second-order nonlinear term to represent costs linked to mitigation strategies like self-protective measures, etc. It is important to note that costs associated with spreading awareness tend to be higher, especially when targeting individuals already exhibiting a heightened level of response. This leads to a rapid cost escalation with increased response intensity. Consequently, we account for this phenomenon by incorporating a nonlinear term of order k.

8.3.2 Cost due to infectiousness and pharmaceutical therapy

The overall expense stemming from ailment impact and medical policies is expressed as $\int _{0}^{T_{f}} \left[ g_{1}I(t){+}g_{3}\gamma ^{2}(t)\right] dt$. Here, $g_{1}I(t)$ accounts for the expenses incurred due to a reduced workforce resulting from infectivity, which could also encompass the productivity decline due to illness. On the other hand, the term $g_{3}\gamma ^{2}(t)$ corresponds to the expenses linked to treatment policies, covering elements like diagnostic fees, medication costs and hospitalization expenditures. Incorporating a nonlinear component in the treatment strategy, $\gamma (t)$, up to the second order is justifiable based on its applicability as documented in prior research [46, 47].

Table 3 Value of parameters utilized for numerical validation of model(8.2)

In light of the preceding facts, the ensuing control is framed alongside the cost function denoted as Z.

$$\begin{aligned}{} & {} Z[D(t),\gamma (t)]\nonumber \\{} & {} \quad =\int _{0}^{T_{f}} \left[ g_{1}I(t)+g_{2}D^{k}(t)+g_{3}\gamma ^{2}(t)\right] dt \end{aligned}$$

(8.1)

subject to the model system:

$$\begin{aligned} \frac{dS_{1}(t)}{dt}&=q\Pi -(1-\alpha )(1-D(t))^{k}\theta _{1}S_{1}(t)I(t)\nonumber \\&\quad -v _1S_1(t)+\beta _1\gamma (t) I(t)\nonumber \\ {}&\quad -\mu S_{1}(t),~~ S_1(0)>0 \nonumber \\ \frac{dS_{2}(t)}{dt}&=(1-q)\Pi -(1-\alpha )(1-D(t))^{k}\theta _{2}S_{2}(t)I(t)\nonumber \\&\quad -v _2S_2(t)+\beta _2\gamma (t) I(t)\nonumber \\ {}&\quad -\mu S_{2}(t),~~ S_2(0)>0 \nonumber \\ \frac{dI(t)}{dt}&=(1-\alpha )(1-D(t))^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t)\nonumber \\&\quad -\gamma (t) I(t)+\varepsilon I(t)V(t)- (\mu +m)I(t),\nonumber \\ {}&\quad ~~ I(0)\ge 0 \nonumber \\ \frac{dV(t)}{dt}&=(v _1S_1(t)+v _2S_2(t))\nonumber \\&\quad +(1-\beta _1-\beta _2)\gamma (t) I(t)-\varepsilon I(t)V(t)\nonumber \\ {}&\quad -\mu V(t),\nonumber \\&\quad V(0)\ge 0. \end{aligned}$$

(8.2)

the functional Z denotes the overall cost as well as the integrand is as follows:

$$\begin{aligned}{} & {} L_1(S_1,S_2,I,V,D(t),\gamma (t))\\{} & {} \quad =g_{1}I(t)+g_{2}D^{k}(t)+g_{3}\gamma ^{2}(t) \end{aligned}$$

which represents the cost at time t. $g_{1}$, $g_{2}$ and $g_{3}$ are weight constants which have chosen to ensure appropriate unit balance within the integrand, as discussed in existing references [46, 47]. Our aim is to identify optimal control strategies, denoted as $D^{*}$ and $\gamma ^{*}$, within the set $\Xi$, which collectively optimize the cost function Z.

Theorem 8.1

The optimal control interventions $(D^{*},\ \gamma ^{*})$ of system (8.1)–(8.2) exist in $\Xi$ s.t. $Z(D^{*},\gamma ^{*})=\min [Z(D,\gamma )]$.

Proof

The proof is found in Appendix B. $\square$

Theorem 8.2

For optimal controls $D^{*},\ \gamma ^{*}$ and associating optimal states $(S_{1}^{*},S_{2}^{*}, I^{*}, V^{*})$, $\exists$ adjoint variables $l=\left( l_{1},l_{2},l_{3},l_{4}\right) \in {\mathbb {R}}^{4}$ satisfying the canonical equations:

$$\begin{aligned} \frac{dl_1}{dt}&= l_1\left[ (1-\alpha )(1-D)^{k}\theta _{1}I +v_1+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{1}I \right] - l_4\Big [v_1 \Big ]\nonumber \\ \frac{dl_2}{dt}&= l_2\left[ (1-\alpha )(1-D)^{k}\theta _{2}I +v_2+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{2}I \right] - l_4\Big [v_2 \Big ]\nonumber \\ \frac{dl_3}{dt}&= -g_1 + l_1 \left[ (1-\alpha )(1-D)^{k}\theta _{1}S_1 - \beta _1 \gamma \right] \nonumber \\&\quad + l_2 \left[ (1-\alpha )(1-D)^{k}\theta _{2}S_2 - \beta _2 \gamma \right] \nonumber \\&\quad - l_3 \left[ (1-\alpha )(1-D)^{k} (\theta _{1}S_1+\theta _{2}S_2) \right. \nonumber \\&\quad \left. - (\mu +m+\gamma ) +\varepsilon V \right] \nonumber \\&\quad - l_4\Big [ (1-\beta _1 - \beta _2) \gamma - \varepsilon V \Big ]\nonumber \\ \frac{dl_4}{dt}&= -l_3\Big [\varepsilon I \Big ] - l_4\Big [-\varepsilon I -\mu \Big ] \end{aligned}$$

(8.3)

with the transversality conditions $l_{i}(T_{f})=0$, $i=1,2,3,4$. The optimal controls $D^{*}$ and $\gamma ^{*}$ that minimize $Z(D,\gamma )$ within $\Xi$ are provided as:

$$\begin{aligned}&D^{*} \nonumber \\ {}&= \min \left\{ \max \left\{ 0, \left( \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}\right) \right\} ,1\right\} , \\ \gamma ^{*}&= \min \left\{ \max \left\{ 0, \left( \frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2-\left( l_{4}-l_{3}\right) \right\} \right) \right\} ,1\right\} . \nonumber \end{aligned}$$

(8.4)

Proof

The proof is contained in Appendix B. $\square$

In the optimal control problem, we explore how the socialized behavioral strength of susceptible individuals (D) and the pharmaceutical therapy level for diseased individuals $(\gamma )$ evolves with time based on disease prevalence. These factors have been used as controls to lessen contaminated ailment impact. Using the forward–backward sweep method [48], numerical simulations are employed to demonstrate how control measures influence system dynamics. We analyze various scenarios of applying these controls individually or together to minimize costs. The parameter values are slightly varied as outlined in Table 3, including positive weight constants. Additionally, it can be presumed that continuous implementation of these control strategies is applied over a span of 100 days.

Figure 11 portrays the model dynamics of (8.2) in absence of time-dependent control strategies. The population level becomes $(1467.5454, 756.1982, 1.2927, 252.931)$ at $T_f=100$ in this case.

Fig. 11

Graphs depicting population dynamics in absence of control policies

Now, let us explore a scenario where social behavior of the susceptible group varies over time, while a consistent rate of clinical treatment is maintained for infectious individuals. Figure 12 illustrates the profiles of population when $D=D^{*}$ and $\gamma = 0.0001$. By the time $T_f$ reaches 100, the population distribution becomes (1468.1511, 756.2750, 0.6346, 253.0044). In this case, both the counts of susceptible and vaccinated individuals increase as more people adjust their behavior to limit disease spread. Additionally, the count of the infected population decreases. The graph of the optimal control intervention $(D^{*})$ is represented by the violet curve in Fig. 12. This curve demonstrates that the control measure becomes more intense immediately after being applied and gradually decreases its intensity during the final days of implementation.

Fig. 12

Graphs depicting population dynamics under the influence of optimal control $D^*$ alone

Moving forward, we explore a scenario where only the treatment given to infected individuals varies based on the severity of their condition. In Fig. 13, we present the population profiles for $\gamma =\gamma ^*$ and $D=0.05$. By the time $T_f=100$, the population distribution becomes (1468.2648, 756.2897, 0.0747, 253.6767). The effectiveness of optimal treatment, especially through vaccination, substantially increases the count of vaccinated individuals compared to situations without control measures. Additionally, due to the temporary impact of vaccination, the count of susceptible individuals also rises. The graph illustrating the optimal control strategy $\gamma ^*$ is presented as the brown curve in Fig. 13.

Fig. 13

Graphs depicting population dynamics under the influence of optimal control $\gamma ^*$ alone

A more effective control of disease burden is achievable when both control measures are employed simultaneously. Hence, a scenario has been investigated where the sociological behavioral dynamics of individuals and the medical treatment for diseased individuals are adjusted based on disease severity, aiming to curb higher disease transmission. The population trajectories are depicted in Fig. 14 at $T_f=100$ and the population distribution becomes $(1404.1673, 790.846, 0.05663, 283.235)$. Notably, the infected population experiences the greatest reduction in this scenario. Moreover, a higher level of susceptible classes is observed for the combined effect of control strategies. The count of vaccinated individuals is also higher compared to previous cases. The final two curves in Fig. 14 illustrate the optimal profiles for both control measures. The intensity of $D^*$ rises initially and subsequently decreases during the final days, whereas the strength of $\gamma ^*$ begins to decline after execution.

Fig. 14

Graphs depicting population dynamics under the implementation of both optimal control strategies $D^*$ as well as $\gamma ^*$

The effectiveness of the implemented control measures is determined by their cost-effectiveness. In Fig. 15, we observe the impact of implemented control interventions $(D^*, \gamma ^*)$ over the cost function (Z) and the number of the infectious individuals (I). When no control strategies are employed, the cost stems from the productivity loss caused by the diseased class. Since the number of contaminated community is highest without control measures, it leads to greater opportunity loss, resulting in a heavier economic burden. The optimal cost notably decreases when both control strategies are enforced, as the number of infected individuals is lower in this case. Moreover, the cost levels are consistently higher when only one control strategy is implemented compared to the scenario where both strategies are executed. Thus, it is concluded that utilizing both policies simultaneously is economically advantageous.

Fig. 15

a Variation in costs associated with different time-dependent control strategies. b Graphs of infected population under different time-dependent control strategies

9 Discussion

Epidemiological studies offer insight into the complex dynamics of disease outbreaks and identify factors influencing these dynamics. While researchers have long focused on SIRS-type epidemic models, recent attention has shifted toward exploring ways to control these outbreaks. As part of these efforts, a nonlinear SIVIS epidemiological model is proposed and examined in this study. This model delves into disease dynamics considering government actions, public response and social reactions. Certain diseases exhibit partial recovery upon infection and the possibility of reinfection after a period. Examples like Influenza, Hepatitis B, Hepatitis Delta, dengue, malaria, tuberculosis, encephalitis and COVID-19 fit the SIVIS model due to their reinfection characteristics. During outbreaks, governments play a pivotal role in implementing regulations to manage panic. Various National Health Programs have been established over the years for disease prevention and control [49]. Nonperiodic behaviors of compartmental models that trend toward an endemic equilibrium point have been analyzed, often reflecting actions such as the opening and closing of public places, seasonal changes, social behavior shifts and new variants. These are often modeled using forced oscillation concepts. Seasonality in epidemic models mirrors natural population and disease dynamics, offering biological realism for understanding disease outbreaks in human and wildlife systems. Contact rate periodicity, influenced by social and weather factors, is a rich area of mathematical and computational epidemiology. In this work, we adapt and expand a SIVIS model that incorporates vaccination and harmonic transmission rates.

The incorporation of sociological factors leads to a decrease in the disease transmission rate. Proposed model (2.1) maintains biological validity as each population category remains positive and bounded over time. The derived reproduction number ($R_0$) determines disease infectiousness; $R_0$ greater than one indicates ongoing infection in the deterministic system. Numerical illustrations reveal that parameters such as government actions $(\alpha )$, infection propagation rates $(\theta _1, \theta _2)$, social behavior (D), public response (k), recovery rate $(\gamma )$ and reinfection rate due to the reduction of efficacy of vaccination $(\varepsilon )$ possess the capacity to influence and manage the system dynamics.

The sensitivity study also indicates that the system’s ability to manage infection level is most sensitive to the rate at which the disease spreads from the people with lower immunity power. Figure 4 reveals that in order to efficiently manage the occurrence of the disease, it is imperative to progressively enhance the vaccination rate $(v_1)$ within weaker susceptible population $(S_1)$, while simultaneously maintaining a constant vaccination rate $(v_2)$ among individuals in the higher immunity category $(S_2)$. Throughout this work, rate of transmission of disease ($\theta _1, \theta _2$), sociological parameters ($\alpha , D$), public response (k), recovery rate ($\gamma$) and reinfection rate due to the reduction of efficacy of vaccination ($\varepsilon$) have performed a significant role. As a result, we have examined the fundamental changes in the behavior of the system by exploring variations in the parameters $\theta _1, \theta _2, \alpha , D, k, \gamma$ and $\varepsilon$. We have also established the conditions for transcritical bifurcation in model (2.1), using $\theta _1, \theta _2, \alpha , D, k, \gamma$ and $\varepsilon$ as the parameters causing the bifurcation.

The study also highlights how the frequency and amplitude of the transmission rate play a significant role in shaping the disease’s dynamics. The model indicates that, even with varying transmission rates over time, rapid vaccination of the susceptible population with weaker immunity leads to a faster decline in the peak of infected individuals. The frequency of the transmission rate measures the disease’s persistence, whereas the amplitude of the transmission rate measures the peak of the infected population. These insights underline that the dynamic nature of endemic diseases like COVID-19 is influenced by factors such as vaccination effectiveness, environmental conditions and virus variants. Additionally, social and biological factors such as population density, social distancing measures and governmental actions contribute to the intricate dynamics of the disease.

Moreover, as regulations and recovery rates (via clinical treatment or natural recovery) for infected individuals evolve over time, an associated optimal control modeling is suggested to measure their influence on the dynamics of the system. Numerical simulations consistently demonstrate that implementing both control interventions significantly reduce the size of infected individuals. This reduction not only curbs disease prevalence but also lessens the economical burden. Thus, these time-dependent control measures prove effective in reducing infection rates during epidemic outbreaks.

This study has illuminated various potential dynamic behaviors that an epidemiological system could exhibit within a deterministic setting and under periodic transmission rates. Based on these insights, a range of possibilities awaits exploration in the upcoming years. It is important to note that the strategies employed here can be applied to investigate other intriguing models, such as the SEIR model, SIQR model, and these models may be useful for future and unexpected epidemics. Future research could also explore the impact of white noise and color noise on these models. A follow-up study is required to comprehend the more intricate dynamics of realistic yet complex systems, which might incorporate several response functions and time delays in different communities.

Appendices

Appendix A

1.1 A.1 Reproduction number

Suppose that, $x\equiv (I,V)$. Then we have:

$$\begin{aligned}{} & {} \frac{dx}{dt}={\mathfrak {F}}(x)-\nu (x),\ \text {where}\\{} & {} {\mathfrak {F}}(x)=\begin{pmatrix} (1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t) \\ 0 \end{pmatrix}\\{} & {} \quad \text {and}\ \nu (x)=\begin{pmatrix} \left( \mu +m+\gamma \right) I-\varepsilon I V \\ -(v _1S_1+v _2S_2)-(1-\beta _1-\beta _2)\gamma I+\varepsilon IV+\mu V \end{pmatrix}. \end{aligned}$$

Here, ${\mathfrak {F}}(x)$ consists of the compartment in which infection is introduced first and $\nu (x)$ contains rest of the terms. Then, at $\displaystyle E_{0}(S_{10},S_{20},0,V_0)$, we have

$$\begin{aligned}{} & {} \displaystyle F=\left( D{\mathfrak {F}}(x)\right) _{E_{0}} \\{} & {} \quad =\begin{pmatrix} (1-\alpha )(1-D)^{k}(\theta _{1}S_{10}(t)+\theta _{2}S_{20}(t)) &{} 0 \\ 0 &{} 0 \end{pmatrix} \\{} & {} \quad \text {and}\quad \displaystyle V=\left( D\nu (x)\right) _{E_{0}}=\begin{pmatrix} \left( \mu +m+\gamma \right) -\varepsilon V_0 &{} 0\\ (1-\beta _1-\beta _2)\gamma +\varepsilon V_0 &{} \mu \end{pmatrix}. \end{aligned}$$

Reproduction number is the spectral radius of next-generation matrix. Now, $FV^{-1}$ is the next-generation matrix whose spectral radius is denoted as:

$$\begin{aligned} R_{0}=\frac{(1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})}{(\mu +m+\gamma -\varepsilon V_0)}. \end{aligned}$$

Appendix B

1.1 B.1 Existence of optimal control functions

Here, we describe the existence of optimal control measures with a minimized cost function in a finite time interval.

Proof of Theorem 8.1

Model (8.2) assumes $N=S_1+S_2+I+V$ be the total population. So,

$$\begin{aligned} \frac{dN}{dt}&=\Pi -\mu S_{1}-\mu S_{2}-(\mu +m)I-\mu V \\&\le \Pi -\mu N\Rightarrow 0<N(t)\\&\le \frac{\Pi }{\mu }+\left( N(0)-\frac{\Pi }{\mu }\right) e^{-\mu t} \end{aligned}$$

where N(0) represents the overall population at initial state. As $\displaystyle t\rightarrow \infty ,\ 0<N(t)\le \frac{\Pi }{\mu }+\epsilon , ~ \mathrm{for ~ any ~} \epsilon > 0.$

Thus, when control factors are present, the solution of model (8.2) remains bounded, and the functions on the right side of system (8.2) are Lipschitz continuous within $\Xi$. Thus, according to the Picard–Lindelöf theorem, optimal control model system (8.2) exhibits nontrivial solutions within $\Xi$ [50]. Moreover, the control elements are confined within a closed and convex set $\Xi$. Each equation system (8.2) can be expressed linearly using D and $\gamma$, with coefficients dependent on time and state variables. Moreover, the control variables are of second order, leading to the integrand $L(S_1,S_2,I,V,D,\gamma )$ being a convex function on the solution set $\Xi$.

$$\begin{aligned}{} & {} \text {Again,}\ L_1(S_1,S_2,I,V,D,\gamma )= g_{1}I(t)+g_{2}D^{k}(t)\\{} & {} \quad +g_{3}\gamma ^{2}(t) \ge g_{2}D^{k}+g_{3}\gamma ^{2}. \end{aligned}$$

Let us take, ${\overline{g}} = \min (g_{2},g_{3})>0$ and $h(D,\gamma )={\overline{g}}(D^{k}+\gamma ^{2})$. Hence, $h(D,\gamma )$ is a continuous function, and $L(S_1,S_2,I,V,D,\gamma )\ge h(D,\gamma )$. Furthermore, $||(D,\gamma )||^{-1}h(D,\gamma )\rightarrow \infty$ for $||(D,\gamma )||\rightarrow \infty .$ Therefore, using the outcomes of [47, 51], it can be stated that optimal control interventions $D^{*}$ and $\gamma ^{*}$ exist such that $Z(D^{*},\gamma ^{*})=\min [Z(D,\gamma )]$. $\square$

1.2 B.2 Characterization of control interventions

The optimal control strategies are derived through the utilization of Pontryagin’s principle [51, 52]. Now, the Hamiltonian function is given by:

$$\begin{aligned}&H\left( S_1,S_2,I,V,D,\gamma ,l\right) =L_1(S_1,S_2,I,V,D,\gamma )\nonumber \\&\quad +l_{1} \frac{dS_1}{dt}+l_{2}\frac{dS_2}{dt}+l_{3}\frac{dI}{dt}+l_{4}\frac{dV}{dt}.\nonumber \\&H = g_{1}I(t)+g_{2}D^{k}(t)+g_{3}\gamma ^{2}(t) \nonumber \\&\qquad \quad + l_1\left[ q\Pi -(1-\alpha )(1-D(t))^{k}\theta _{1}S_{1}I\right. \nonumber \\&\qquad \quad \left. -v _1S_1+\beta _1\gamma I-\mu S_{1} \right] \nonumber \\&\qquad \quad + l_2 \left[ (1-q)\Pi -(1-\alpha )(1-D(t))^{k}\theta _{2}S_{2}I\right. \nonumber \\&\qquad \quad \left. -v _2S_2+\beta _2\gamma I-\mu S_{2} \right] \nonumber \\&\qquad \quad + l_3\Big [(1-\alpha )(1-D(t))^{k}(\theta _{1}S_{1}+\theta _{2}S_{2})I\nonumber \\&\qquad \quad - (\mu +m)I-\gamma I+\varepsilon IV \Big ] + l_4 \nonumber \\&\quad \Big [(v _1S_1+v _2S_2)+(1-\beta _1-\beta _2)\gamma I-\varepsilon IV-\mu V \Big ] \end{aligned}$$

(B.1)

Here $l=\left( l_{1},l_{2},l_{3},l_4\right)$ indicates adjoint variables. Our primary concern is to minimize Hamiltonian H by utilizing Pontryagin’s principle so that a minimal cost function is obtained.

Proof of Theorem 8.2

Consider $D^{*}$ and $\gamma ^{*}$ be the applied optimal control along with the corresponding optimal state variables are $S_1^{*}, S_2^*, I^{*}$ and $V^{*}$ of (8.2) which minimize the cost functional Z defined in (8.1). Therefore, we have adjoint variables $l_{i}$ for $i=1,2,3,4$, satisfying the canonical equations:

$$\begin{aligned}{} & {} \frac{dl_{1}}{dt}=-\frac{\partial H}{\partial S_1}, \qquad \frac{dl_{2}}{dt}=-\frac{\partial H}{\partial S_2}, \\{} & {} \frac{dl_{3}}{dt}=-\frac{\partial H}{\partial I}, \qquad \frac{dl_{4}}{dt}=-\frac{\partial H}{\partial V}. \end{aligned}$$

So, we have

$$\begin{aligned}&\frac{dl_1}{dt}= l_1\left[ (1-\alpha )(1-D)^{k}\theta _{1}I +v_1+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{1}I \right] - l_4\Big [v_1 \Big ]\nonumber \\&\frac{dl_2}{dt}= l_2\left[ (1-\alpha )(1-D)^{k}\theta _{2}I +v_2+\mu \right] \nonumber \\&\qquad \quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{2}I \right] - l_4\Big [v_2 \Big ]\nonumber \\&\frac{dl_3}{dt}= -g_1 + l_1 \left[ (1-\alpha )(1-D)^{k}\theta _{1}S_1 - \beta _1 \gamma \right] \nonumber \\&\qquad \quad + l_2 \left[ (1-\alpha )(1-D)^{k}\theta _{2}S_2 - \beta _2 \gamma \right] \nonumber \\&\qquad \quad - l_3 \left[ (1-\alpha )(1-D)^{k} (\theta _{1}S_1+\theta _{2}S_2) \right. \nonumber \\&\qquad \quad \left. - (\mu +m+\gamma ) +\varepsilon V \right] \nonumber \\&\qquad \quad - l_4\Big [ (1-\beta _1 - \beta _2) \gamma - \varepsilon V \Big ]\nonumber \\&\frac{dl_4}{dt}= -l_3\Big [\varepsilon I \Big ] - l_4\Big [-\varepsilon I -\mu \Big ] \end{aligned}$$

with the transversality conditions $l_{i}(T_{f})=0$, for $i=1,2,3,4$.

$$\begin{aligned}{} & {} \text {From optimality conditions}: ~~~ \frac{\partial H}{\partial D}\bigg |_{D=D^{*}}=0, \\ {}{} & {} \text {and} \ \frac{\partial H}{\partial \gamma }\bigg |_{\gamma =\gamma ^{*}}=0. \end{aligned}$$

So, $\displaystyle D^{*}{=} \frac{\left[ \frac{(1{-}\alpha )I^*}{g_{2}}\left\{ (l_{3}{-}l_{1})\theta _1 S_1^* {+} (l_{3}{-}l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1{+}\left[ \frac{(1{-}\alpha )I^*}{g_{2}}\left\{ (l_{3}{-}l_{1})\theta _1 S_1^* {+} (l_{3}{-}l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}$

and $\displaystyle \gamma ^{*}{=}\frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\}$.

In $\Xi ,$ we have

$$\begin{aligned}{} & {} \begin{aligned} D^{*}&= {\left\{ \begin{array}{ll} 0, &{} \text {if}\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}< 0 \\ \\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}, &{} \text {if}\ 0\le \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}\le 1 \\ \\ 1, &{} \text {if}\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}> 1 \end{array}\right. } \end{aligned} \\{} & {} \begin{aligned} \gamma ^{*}&= {\left\{ \begin{array}{ll} 0, &{} \text {if}\quad \frac{ I^{*}}{2g_{3}}\{(l_{4}-l_{1})\beta _1+(l_{4}-l_{2})\beta _2 -(l_{4}-l_{3})\}<0 \\ \frac{I^{*}}{2g_{3}}\{(l_{4}-l_{1})\beta _1&{}\\ +(l_{4}-l_{2})\beta _2 -(l_{4}-l_{3})\}, &{} \text {if}\quad 0\le \frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\} \le 1 \\ 1, &{} \text {if}\quad \frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\} > 1 \end{array}\right. } \end{aligned} \end{aligned}$$

which is equivalent as (8.4). $\square$

1.3 B.3 Optimal system

The optimal system which includes the optimal control measures $D^{*}$ and $\gamma ^{*}$ and minimizing the Hamiltonian $H^{*}$ at $(S_1^{*},S_2^{*}, I^{*}, V^{*}, l_{1}, l_{2}, l_{3},l_4)$ is

$$\begin{aligned} \frac{dS_{1}^*}{dt}&=q\Pi -(1-\alpha )(1-D^*)^{k}\theta _{1}S_{1}^*I^*\nonumber \\&\quad -v _1S_1^*+\beta _1\gamma ^* I^*-\mu S_{1}^* \nonumber \\ \frac{dS_{2}^*}{dt}&=(1-q)\Pi -(1-\alpha )(1-D^*)^{k}\theta _{2}S_{2}^*I^*\nonumber \\&\quad -v _2S_2^*+\beta _2\gamma ^* I^*-\mu S_{2}^*\nonumber \\ \frac{dI^*}{dt}&=(1-\alpha )(1-D^*)^{k}(\theta _{1}S_{1}^*\nonumber \\&\quad +\theta _{2}S_{2}^*)I^*-\gamma ^* I^*+\varepsilon I^*V^*- (\mu +m)I^*\nonumber \\ \frac{dV^*}{dt}&=(v _1S_1^*+v _2S_2^*)\nonumber \\&\quad +(1-\beta _1-\beta _2)\gamma ^* I^*-\varepsilon I^*V^*-\mu V^*\ge 0. \end{aligned}$$

(B.2)

with non-negative initial conditions $S_1^{*}(0)>0,\ S_2^{*}(0)>0, \ I^{*}(0)\ge 0,\ V^{*}(0) \ge 0$, and the corresponding adjoint system is:

$$\begin{aligned} \frac{dl_1}{dt}&= l_1\left[ (1-\alpha )(1-D^*)^{k}\theta _{1}I^* +v_1+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D^*)^{k}\theta _{1}I^* \right] - l_4\Big [v_1 \Big ]\nonumber \\ \frac{dl_2}{dt}&= l_2\left[ (1-\alpha )(1-D^*)^{k}\theta _{2}I^* +v_2+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D^*)^{k}\theta _{2}I^* \right] - l_4\Big [v_2 \Big ]\nonumber \\ \frac{dl_3}{dt}&= -g_1 + l_1 \left[ (1-\alpha )(1-D^*)^{k}\theta _{1}S_1^* - \beta _1 \gamma ^* \right] \nonumber \\&\quad + l_2 \left[ (1-\alpha )(1-D^*)^{k}\theta _{2}S_2^* - \beta _2 \gamma ^* \right] \nonumber \\&\quad - l_3 \left[ (1-\alpha )(1-D^*)^{k} (\theta _{1}S_1^*+\theta _{2}S_2^*) \right. \nonumber \\&\quad \left. - (\mu +m+\gamma ^*) +\varepsilon V^* \right] \nonumber \\&\quad - l_4\Big [ (1-\beta _1 - \beta _2) \gamma ^* - \varepsilon V^* \Big ]\nonumber \\ \frac{dl_4}{dt}&= -l_3\Big [\varepsilon I^* \Big ] - l_4\Big [-\varepsilon I^* -\mu \Big ] \end{aligned}$$

(B.3)

with transversality conditions $l_{i}(T_{f})=0$, for $i=1,2,3,4$ and the control interventions $D^{*},\ \gamma ^{*}$ are the same as in (8.4).