1 Introduction

Epidemiology is often called the core science of public health, considering the appropriation and determinants of infection risk in human populations. Mathematical epidemic models help to understand the transmission and spread of infectious diseases, recognize the characteristics controlling the transmission process to identify successful control techniques, and evaluate the effectiveness of surveillance strategies and intervention measures. Deterministic models for communicable diseases have been introduced systematically by Kermack and McKendrick [1, 2]. In their model, three epidemiological classes are considered as the basic elements describing infectious diseases: the susceptible class (S(t)), i.e., those individuals who are capable of contracting the disease and becoming infective, the infective class (I(t)), i.e., those capable of transmitting the disease to others, and the removed class (R(t)), i.e., those individuals who have recovered from the infection. Based on the theory of Kermark and Mckendrick [1, 2], the dynamics of infectious diseases can usually be described mathematically based on compartmental models such as SIR or SIRS models, with each letter referring to a “compartment” in which an individual can reside. Thus, to understand the mechanism of infectious disease transmission, several authors have studied various kinds of epidemic models by considering different compartment models such as SI [3], SIS [4], SIR [5,6,7,8,9,10,11], SIRS [12], SEIR [13, 14], SVEIR [15], and many more.

Controlling infectious diseases has become an increasingly complex issue in recent years. One methodology to control infectious diseases is vaccination. Vaccination plays an important role among the health interventions aimed at reducing the spread of infectious diseases thanks to its safety and cost-effectiveness. Indeed, high immunization take-up levels have brought about radical decreases in numerous vaccine-preventable infectious diseases or even their eradication, as in the very notable instance of smallpox [16]. Nevertheless, a critical aspect of vaccination is its level of safety as far as viability in preventing the illness as well as the duration of the induced immunity. Some vaccines are highly effective, e.g., measles [17], while others are not, as is the case of varicella [18]. The effectiveness of and levels of protection provided by a vaccine may naturally decrease over time because of medical conditions (medications, aging, or when the immune system may work less well) and the alteration and evolution of infectious diseases; For example, the flu virus [19] can change very rapidly, meaning that last year’s flu vaccine is unlikely to protect individuals from virus strains circulating this year. In contrast, the measles virus [17] prevented by the measles–mumps–rubella (MMR) vaccine hardly changes from year to year, indicating that it is as likely to protect individuals today as it was 10 years ago. Some vaccines minimize the infection risk but do not prevent a vaccinated individual from catching and transmitting the infection. These imperfect vaccines may not completely prevent infection but rather could decrease the likelihood of becoming infected or reduce its consequences, thereby lessening the infectious disease burden. In mathematical epidemiology literature, many studies have dealt with epidemic models including imperfect vaccination (see, just to specify a couple of studies, [20,21,22,23,24,25]). With imperfect vaccination, the outcome of an epidemic model may lead to the occurrence of backward bifurcation under particular conditions because vaccinated individuals may return to the susceptible pool or become directly infected by transmission. Backward bifurcation thus plays a relevant role in disease control and eradication. Indeed, it is well known that, in classical disease transmission models, a necessary condition for disease eradication is that the basic reproductive number\(R_0\) [26] be less than unity. This type of bifurcation is known as forward bifurcation, where for \(R_0 < 1\) the disease-free equilibrium (DFE) is the only equilibrium and is asymptotically stable, while for \(R_0 > 1\) the DFE is unstable and only one asymptotically stable, endemic equilibrium exists. However, via the occurrence of backward bifurcation, an endemic equilibrium may also exist even when the basic reproduction number \(R_0\) is less than unity. From the public viewpoint, the occurrence of backward bifurcation may have significant health implications regarding disease elimination. In literature, many epidemic models including backward bifurcation have been studied, for both generic and specific diseases [27, 28]. Analysis of such forward and backward bifurcation is based on the center manifold theory [27].

To determine the dynamics of epidemic models, the incidence rate (the rate of new infections) plays a major role in the modeling of infectious diseases. Kermack and Mckendrick introduced the incidence rate in the form kSI (called the standard mass action form) in 1927 [1]. In this incidence rate, the interaction term is a linearly increasing function of the number of infectives, which is not suitable for a large population. Therefore, Capasso and Serio [29] introduced the nonlinear incidence rate in the form g(I)S with \(g'(I)<0\), which allows the introduction of some “psychological” effects. Capasso and Serio motivated their formulation with behavioral changes: in epochs of high prevalence, the perceived risk of infection might become very large, yielding dramatic changes in individuals’ behavior and therefore also reducing the actual risk of getting the disease (as widely discussed in [30]). Numerous authors have focused on the significance of considering nonlinear incidence rates in the study of the transmission

dynamics of infectious diseases (see, for example, Capasso et al. [29, 31, 32], Anderson and May [33],

Wei and Chen [34], Zhang et al. [35], Li et al. [36], Kumar and Nilam [37,38,39], Goel and Nilam [8, 40]). Li et al. [36] proposed a SIR model with a nonlinear incidence rate given by

$$\begin{aligned} f(S,I)=\frac{\beta S I}{1+\gamma I}. \end{aligned}$$

In this incidence rate, the number of effective contacts between infective and susceptible individuals may saturate at high infective levels due to overcrowding of infective individuals. The delay differential equation plays a significant role in the estimation of both past and ongoing epidemics and the structure of future-focused control interventions. It can be said with a high level of conviction that, when a disease emerges, there will be an initial delay in recognizing it. Such a delay in the recognition of an infectious disease will lead to a delay in applying appropriate protection measures. Infected individuals will be able to transmit the infection because healthcare workers, family members, and infected individuals will not know how to protect themselves. In mathematical epidemiology literature, many studies have dealt with the time delay (called the latent or incubation period) (see, e.g., [4, 37,38,39,40,41,42]) and studied its impact on their models. Motivated by the work of Capasso and Serio [29], d’Onofrio and Manfredi [30], and Li et al. [36], a saturated nonlinear incidence rate, reflecting the psychological or inhibition effect, with the inclusion of a time delay \(\tau \) as the latent period, is considered herein.

The loss of quality of life and economic productivity due to severe illness further increase the societal cost. Therefore, it is very important to prevent and reduce the spread of infectious diseases among people. Treatment is the key to fight many infectious diseases. Wang and Ruan [43] considered an SIR epidemic model with a constant treatment rate as given below:

$$\begin{aligned} h (I) = \left\{ \begin{array}{cc} r, &{} \quad I>0, \\ 0, &{} \quad I=0, \end{array} \right. \end{aligned}$$

where r is a positive constant and I is the number of infected individuals. They carried out stability analysis and showed that the model exhibits various bifurcations. Furthermore, in 2012, Zhou and Fan [44] modified the treatment rate to a Holling type II functional, as given below:

$$\begin{aligned} h (I)&= \frac{\beta I}{1+\alpha I}, \quad I \ge 0, \quad \beta \ge 0, \quad \alpha \ge 0. \end{aligned}$$

They showed that, with varying amounts of medical resources and their supply efficiency, the target model admits both backward and Hopf bifurcation. Motivated by the work of Zhou and Fan [44], a Holling type II treatment rate is considered herein, and its effect on the present epidemic model is studied.

The purpose of the present work is to study the effect of saturated incidence, an imperfect vaccine, and saturated treatment to achieve substantial progress in implementing measures to prevent and control infectious diseases among people. For this, a compartmental susceptible–vaccinated–infected–recovered–susceptible (SVIRS) epidemic model with a saturated incidence rate and including a time delay (representing the latent period) and saturated treatment rate is considered. Qualitative analysis is performed through the stability and bifurcation theory approach using center manifold theory, revealing the existence of backward, forward, and Hopf bifurcations under certain conditions, which enrich the dynamics of infectious diseases among humans.

The remainder of this manuscript is organized as follows: in Sect. 2, the model is introduced, and some of its basic properties are presented. Section 3 is devoted to the existence and stability analysis of disease-free and endemic equilibria. In this section, the distribution of roots of the characteristic equation is analyzed, revealing the existence of stability switches. The conditions for backward and forward bifurcation are also obtained. Furthermore, by regarding the delay \(\tau \) as a bifurcation parameter, the existence of Hopf bifurcation when the delay is varied is shown. Numerical simulations are performed to provide a complete representation of the model dynamics in Sect. 4. Finally, a discussion is given in Sect. 5.

2 The model and its basic properties

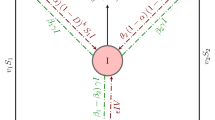
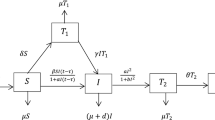
Assume that the epidemiological status of the total population N(t) of individuals can be identified, dividing them into susceptibles S(t), vaccinated V(t), infectives I(t), and recovered R(t). Individuals can move from one state to another as their status concerning the disease evolves. A is the recruitment rate of susceptibles and hence of those entering the susceptible state. Susceptible individuals are vaccinated at a rate of \(\delta \) and enter the state V(t). The term \(f(S(t-\tau ),I(t-\tau ))=(\beta S(t-\tau ) I(t-\tau ))/(1+\alpha I(t-\tau ))\) is the Holling type II functional response representing the incidence of infection among susceptibles, where \(\beta \) is the force of infection, \(\alpha \) describes the inhibition measures taken by the infected, and the time delay parameter \(\tau \) represents the latent period. The protection provided by an imperfect vaccine is only partial, so some individuals can catch the disease when they come into contact with infected individuals. Therefore, it is assumed that \(\gamma \) is the rate at which vaccinated individuals become infected when coming into contact with infected individuals. This occurs due to the imperfect nature of the vaccine, which leaves a percentage of the susceptibles unprotected even if vaccinated. Assume that \(\beta > \gamma \), as it is expected that the vaccine will be at least partly effective in preventing infection, yielding a reduction in the force of infection. The term \(g(V(t-\tau ),I(t-\tau ))=(\gamma V(t-\tau )I(t-\tau ))/(1+\alpha I(t-\tau ))\) represents the incidence of infection among vaccinated individuals who move from state V(t) to state I(t). The term \((aI)/(1+bI)\), where a is the treatment (cure) rate and b is a rate of limitation in medical resources, describes the treated individuals who recover and thus move from state I(t) to R(t). Also, it is assumed that recovered individuals become susceptible again, thus the term \(\theta R\) describes recovered individuals who reenter the class of susceptible individuals. The parameters \(\mu \) and d are the natural and disease-induced mortality rates, respectively. The parameter \(\varsigma \) denotes the recovery rate, hence \(\varsigma I\) individuals move from the infected to recovered class.

Thus, the proposed SVIRS epidemic model consists of the following system of delay differential equations:

$$\begin{aligned} \begin{aligned} \frac{\mathop {}\!\mathrm {d}S}{\mathop {}\!\mathrm {d}t}&= A - \delta S- \frac{\beta S(t-\tau ) I(t-\tau )}{1+\alpha I(t- \tau )}-\mu S+\theta R,\\ \frac{\mathop {}\!\mathrm {d}V}{\mathop {}\!\mathrm {d}t}&= \delta S -\frac{ \gamma V(t-\tau ) I(t-\tau )}{1+\alpha I(t- \tau )}-\mu V,\\ \frac{\mathop {}\!\mathrm {d}I}{\mathop {}\!\mathrm {d}t}&= \frac{\beta S(t-\tau ) I(t-\tau )}{1+\alpha I(t- \tau )} + \frac{ \gamma V(t-\tau ) I(t-\tau )}{1+\alpha I(t- \tau )}-(\mu +d+ \varsigma )I-\frac{aI}{1+b I},\\ \frac{\mathop {}\!\mathrm {d}R}{\mathop {}\!\mathrm {d}t}&= \varsigma I + \frac{aI}{1+b I} -\theta R-\mu R. \end{aligned} \end{aligned}$$
(1)

For biological reasons, the initial conditions are nonnegative continuous functions

$$\begin{aligned} S(\Theta ) = \phi _1(\Theta ), V(\Theta ) = \phi _2(\Theta ), I(\Theta ) = \phi _3(\Theta ), R(\Theta ) = \phi _4(\Theta ), \end{aligned}$$

where \(\phi (\Theta ) = (\phi _1, \phi _2, \phi _3, \phi _4)^T\) are functions such that \(\phi _i(\Theta ) \ge 0, (-\tau \le \Theta \ge 0, i = 1,2,3,4)\). C denotes the Banach space \(C\left( [-\tau ,0], {\mathbb {R}}_+^4 \right) \) of continuous functions mapping the interval \([-\tau ,0]\) into \({\mathbb {R}}_+^4\) with supremum norm

$$\begin{aligned} \left\| \phi \right\| = \sup _{\Theta \in [-\tau , 0]} |\phi (\Theta ) |, \end{aligned}$$

where \(|.|\) is any norm in \({\mathbb {R}}^4_+\).

The transition diagram of the model (1) is shown in Fig. 1.

Fig. 1
figure 1

Transition diagram of the model (1)

Full size image

The model (1) monitors populations. Using Proposition 2.3 in Yang et al. [45] and Proposition 2.1 given in Hattaf et al. [7], it can be checked that all state variables of the model (1) are nonnegative, i.e., \((S,V,I,R) \in {R^4_+}\). For ecological reasons, it is assumed that all the parameters are positive; i.e., \(A,~ \delta ,~ \beta ,~\alpha ,~\mu ,~\theta ,~\gamma ,~d,~ \varsigma ,~a,~\text {and}~b \) are positive.

Lemma 1

The compact set

$$\begin{aligned} \Omega =\left\{ (S(t),V(t),I(t),R(t)) \in {\mathbb {R}}_+^4 : N(t)=S(t)+V(t)+I(t)+R(t) \le \frac{A}{\mu } \right\} \end{aligned}$$

is invariant for the solutions of the model (1).

Proof

The well-posedness of the model is ensured by the continuity of the terms on the right-hand side of the model (1) and its derivatives.

Addition of the equations of the model (1) yields

$$\begin{aligned} \begin{aligned} \frac{\mathop {}\!\mathrm {d}N}{\mathop {}\!\mathrm {d}t }&=A-\mu N-dI \le A-\mu N. \end{aligned} \end{aligned}$$
(2)

Thus, the invariant region for the existence of the solutions is given as

$$\begin{aligned} 0< \liminf \limits _{t\rightarrow \infty } N(t) \le \limsup \limits _{t\rightarrow \infty } N(t) \le \frac{A}{\mu }. \end{aligned}$$
(3)

Hence, the solutions of the model (1) are closed and bounded. \(\square \)

3 Equilibria and stability analysis

In this section, the existence of equilibria of the model (1) is confirmed. The model has two equilibria, namely:

  1. 1.

    The disease-free equilibrium \(E_0\), in which infected individuals are permanently absent from the population, i.e., \( I\equiv 0 ~\text {for all}~ t > 0\)), discussed in Sect. 3.1

  2. 2.

    The endemic equilibrium \(E_\mathrm{e}\), in which an infected population persists above a certain positive level, discussed in Sect. 3.2

3.1 The disease-free equilibrium and its stability

Here it is established that the model (1) has a disease-free equilibrium of the form \(E_0 = \left( \frac{A}{\mu +\delta }, \frac{\delta A}{\mu (\mu +\delta )}, 0, 0 \right) \).

At \(E_0\), the characteristic equation of the linearized model (1) is obtained as follows:

$$\begin{aligned} \left( \lambda +\mu \right) \left( \lambda +\mu +\delta \right) \left( \lambda +\mu +\theta \right) \left( \lambda +(d+\mu +\varsigma +a)-\frac{A (\beta \mu +\gamma \delta )\mathrm {e}^{ -\lambda \tau }}{\mu (\delta +\mu )}\right) =0. \end{aligned}$$
(4)

Equation (4) has real negative roots \(\lambda _1 = -\mu , ~ \lambda _2 = -\mu -\delta , ~ \lambda _3 = -\mu -\theta \), and other roots are the solution of

$$\begin{aligned} \lambda +(d+\mu +\varsigma +a)-\frac{A (\beta \mu +\gamma \delta )\mathrm {e}^{ -\lambda \tau }}{\mu (\delta +\mu )}=0. \end{aligned}$$
(5)

The term \((A(\mu \beta +\gamma \delta )\mathrm {e}^{-\lambda \tau })/(\mu (\mu +\delta )(d+\mu +\varsigma +a))\) at \(\tau =0\) is defined as the basic reproduction number \(R_0\) of the model (1). The basic reproduction number \(R_0\) is defined as the average number of secondary infections caused by a single infected agent, during his/her entire infectious period, in a completely susceptible population [26]. Therefore, \(R_0\) for the model (1) is given as

$$\begin{aligned} R_0= \frac{A (\mu \beta +\gamma \delta )}{\mu (\mu +\delta ) (d+\mu +\varsigma +a)}. \end{aligned}$$

The stability of \(E_0\) is shown as follows:

Theorem 1

The disease-free equilibrium \(E_0 = \left( \frac{A}{\mu +\delta }, \frac{\delta A}{\mu (\mu +\delta )}, 0, 0 \right) \) of the model (1) is

  1. 1.

    Unstable if \(R_0 > 1\)

  2. 2.

    Linearly neutrally stable if \(R_0=1\)

  3. 3.

    Asymptotically stable if \(R_0<1\)

Proof

As mentioned above, Eq. (4) has real negative roots \(\lambda _1 = -\mu , ~ \lambda _2 = -\mu -\delta , ~ \lambda _3 = -\mu -\theta \), and other roots are the solution of

$$\begin{aligned} f(\lambda ):=\lambda +(d+\mu +\varsigma +a)-\frac{A (\beta \mu +\gamma \delta )\mathrm {e}^{ -\lambda \tau }}{\mu (\delta +\mu )}=0. \end{aligned}$$
(6)
  1. 1.

    Assuming that \(R_0>1\), then

    $$\begin{aligned} f(0)&=d+\mu +\varsigma +a-\frac{A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}\\&=(d+\mu +\varsigma +a)\left( 1-\frac{A(\beta \mu +\gamma \delta )}{\mu (\mu +\delta ) (d+\mu +\varsigma +a)}\right) \\&= (d+\mu +\varsigma +a)(1-R_0)\\&<0. \end{aligned}$$

    i.e., when \(R_0>1\) then \(f(0)<0\). Also, \(f'(\lambda )= 1+\frac{\tau A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}\mathrm {e}^{-\lambda \tau }~>0\)   so, \(\mathop {\lim }_{\lambda \rightarrow \infty } f(\lambda ) = +\infty \).

    Hence, \(f(\lambda )=0\) and \(f'(\lambda )>0\) imply that there exists a unique positive root of Eq. (6) when \(R_0>1\).

  2. 2.

    If \(R_0=1\), then \(\lambda =0\) is a simple characteristic root of Eq. (6). Let \(\lambda =\alpha +\mathrm {i} \omega \) be any of the other solutions of Eq. (6), then Eq. (6) turns into

    $$\begin{aligned} \alpha +\mathrm {i} \omega +(d+\mu +\varsigma +a)-\frac{A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}\mathrm {e}^{-\alpha \tau }(\cos {\omega \tau }-\mathrm {i} \sin {\omega \tau })=0. \end{aligned}$$
    (7)

    Using Euler’s formula and separating real and imaginary parts yields

    $$\begin{aligned}&\alpha +d+\mu +\varsigma +a =\frac{A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}\mathrm {e}^{-\alpha \tau }\cos {\omega \tau }, \end{aligned}$$
    (8)
    $$\begin{aligned}&\omega =-\frac{A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}\mathrm {e}^{-\alpha \tau }\sin {\omega \tau }. \end{aligned}$$
    (9)

    Note that \(R_0=1\) implies that \((A (\beta \mu +\gamma \delta ))/(\mu (\mu +\delta ))=(d+\mu +\varsigma +a)\). In addition, if there exists a root satisfying both Eqs. (8) and (9), then this root also satisfies the equation obtained by squaring and adding Eqs. (8) and (9), thus

    $$\begin{aligned} \begin{aligned} \left( \alpha +d+\mu +\varsigma +a\right) ^2+\omega ^2&=\left( d+\mu +\varsigma +a\right) ^2 \mathrm {e}^{-2\alpha \tau }. \end{aligned} \end{aligned}$$
    (10)

    For Eq. (10) to be verified, \(\alpha \le 0\) must apply. Therefore, \(E_0\) is linearly neutrally stable.

  3. 3.

    Let \(R_0<1\). The goal is to prove that, for any values of the parameters, the roots of the characteristic equation cannot reach the imaginary axis, which means that, for any values of the parameters and all delays \(\tau \), then \({\text {Re}}(\lambda )<0\).

    Note that

    $$\begin{aligned} {\text {Re}}(\lambda )= \frac{A (\beta \mu +\gamma \delta ) \mathrm {e}^{ -{\text {Re}}(\lambda ) \tau }\cos (\mathrm{Im}(\lambda ) )\tau }{\mu (\delta +\mu )}-(d+\mu +\varsigma +a)<\frac{A (\beta \mu +\gamma \delta )}{\mu (\delta +\mu )}-(d+\mu +\varsigma +a)<0. \end{aligned}$$

    Therefore, all the roots of Eq. (6) must have a negative real part. Thus, \(E_0\) is asymptotically stable.

\(\square \)

3.1.1 Bifurcation analysis

In this section, a qualitative analysis of the model (1) is performed without delay, i.e., with \(\tau = 0\). The stability properties of the model (1) without delay are investigated near criticality (i.e., at \(E_0\) and \(R_0 = 1\)). To this aim, the bifurcation theory approach developed in [27], which is based on the center manifold theory [46], is applied. For this, redefine \(S= x_1\), \(V=x_2\), \(I=x_3\), and \(R=x_4\) so that the model (1) reduces to

$$\begin{aligned} \begin{aligned} \frac{\mathop {}\!\mathrm {d}x_1}{\mathop {}\!\mathrm {d}t}&= A - \delta x_1- \frac{\beta x_1 x_3}{1+\alpha x_3}-\mu x_1+\theta x_4,\\ \frac{\mathop {}\!\mathrm {d}x_2}{\mathop {}\!\mathrm {d}t}&= \delta x_1 - \frac{\gamma x_2 x_3}{1+\alpha x_3}-\mu x_2,\\ \frac{\mathop {}\!\mathrm {d}x_3}{\mathop {}\!\mathrm {d}t}&= \frac{\beta x_1 x_3}{1+\alpha x_3} + \frac{\gamma x_2 x_3}{1+\alpha x_3}-(\mu +d+ \varsigma )x_3-\frac{ax_3}{1+b x_3},\\ \frac{\mathop {}\!\mathrm {d}x_4}{\mathop {}\!\mathrm {d}t}&= \varsigma x_3 + \frac{ax_3}{1+b x_3} -\theta x_4-\mu x_4, \end{aligned} \end{aligned}$$
(11)

observing that

$$\begin{aligned} R_0=1 \;\iff \;\gamma =\gamma ^* = \frac{\mu \left( \mu +\delta \right) \left( \mu +d+\varsigma +a\right) -A \mu \beta }{\delta A}. \end{aligned}$$

The Jacobian matrix \(J\left( E_0, \gamma ^*\right) \) of the system (11) at the disease-free equilibrium \(E_0\) is given by

$$\begin{aligned} J\left( E_0, \gamma ^*\right) = \begin{pmatrix} -\delta -\mu &{} 0 &{} -\frac{A \beta }{\delta +\mu } &{} \theta \\ \delta &{} -\mu &{} -\frac{A \delta \gamma ^*}{\mu \left( \delta +\mu \right) } &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} a+\varsigma &{}-\theta -\mu \end{pmatrix} \end{aligned}$$
(12)

so that the eigenvalues of the Jacobian matrix \(J\left( E_0, \gamma ^*\right) \) are given by \(\lambda _1 = 0, \lambda _2 = -\mu , \lambda _3 = -\delta -\mu \) and \( \lambda _4 = -\theta -\mu \).

Thus, \(\lambda _1 = 0\) is a simple zero eigenvalue, and other eigenvalues are real and negative.

Hence, when \(\gamma = \gamma ^*\) (or equivalently when \(R_0 = 1\)), the disease-free equilibrium \(E_0\) is a nonhyperbolic equilibrium.

The right eigenvector \( {\varvec{u}} = \left( u_1, u_2, u_3, u_4\right) ^T\) of (12) associated with \(\lambda _1 = 0\) is given by \(J\left( E_0, \gamma ^*\right) \cdot {\varvec{u}} =0\), thus

$$\begin{aligned} u_1&=\frac{\theta (a+\varsigma ) (\delta +\mu )-A \beta (\theta +\mu )}{(a+\varsigma ) (\delta +\mu )^2},\\ u_2&= \frac{\delta \theta }{\mu (\delta +\mu )}-\frac{(\theta +\mu ) \left( (\delta +\mu )^2 (a+d+\mu +\varsigma )-A \beta \mu \right) }{\mu (a+\varsigma ) (\delta +\mu )^2},\\ u_3&= \frac{\theta +\mu }{a+\varsigma },\\ u_4&= 1. \end{aligned}$$

The left eigenvector \( {\varvec{w}} = \left( w_1, w_2, w_3, w_4\right) \) of (12) associated with \(\lambda _1 = 0\) is given by \( {\varvec{w}} \cdot J\left( E_0, \gamma ^*\right) =0\), thus

$$\begin{aligned} {\varvec{w}}= \left( 0, 0, 1, 0\right) . \end{aligned}$$

Let \(f_k\)’s denote the right-hand side of the model system (11). The coefficients \(a_1\) and \(b_1\) defined in Theorem 4.1 of Castillo-Chavez and Song [27] are given by

$$\begin{aligned} a_1&= \sum \limits _{k,i,j = 1}^4 {w_k u_i u_j \left( \frac{\partial ^2f_k}{\partial x_i \partial x_j}\right) _{E_0}},\\ b_1&= \sum \limits _{k,i=1}^4 {w_k u_i \left( \frac{\partial ^2 f_k}{\partial x_i \partial \beta ^*}\right) _{E_0}}. \end{aligned}$$

Consideration of only the nonzero partial derivative associated with the functions \(f_k\)’s evaluated at \(E_0\) gives

$$\begin{aligned} \left( \frac{\partial ^2 f_3}{\partial x_1 \partial x_3}\right) _{E_0} = \beta , \quad \left( \frac{\partial ^2 f_3}{\partial x_2 \partial x_3}\right) _{E_0} = \gamma ^*, \left( \frac{\partial ^2 f_3}{\partial x_3 \partial x_1}\right) _{E_0} = \beta , \quad \left( \frac{\partial ^2 f_3}{\partial x_3 \partial x_2}\right) _{E_0} = \gamma ^*, \left( \frac{\partial ^2 f_3}{\partial x_3^2}\right) = 2ab-\frac{2\alpha \beta A}{\mu +\delta }. \end{aligned}$$

Thus, the bifurcation coefficients \(a_1\) and \(b_1\) can be computed as

$$\begin{aligned} a_1&=-\frac{2 (\theta +\mu )}{A \delta (a+\varsigma )^2 (\delta +\mu )} (-A (\theta +\mu ) (a (\delta (b-\alpha ) (\delta +\mu )+\beta (\delta +2 \mu ))+(d+\mu +\varsigma ) (\beta (\delta +2 \mu )\\&\quad -\alpha \delta (\delta +\mu )))+(\delta +\mu ) (a+d+\mu +\varsigma ) (\mu (a (\delta +\theta +\mu )+\delta (\theta +\mu +\varsigma )+(\theta +\mu ) (\mu +\varsigma ))\\&\quad +d (\delta +\mu ) (\theta +\mu ))+A^2 \beta ^2 (\theta +\mu )),\\&=-\frac{2 (\theta +\mu )}{A \delta (a+\varsigma )^2 (\delta +\mu )} \eta (\beta ),\\ b_1&= \frac{A\left( \mu +\theta \right) }{\left( a+\varsigma \right) \left( \mu +\delta \right) }, \end{aligned}$$

where

$$\begin{aligned} \eta (\beta )&= A^2 \beta ^2 (\theta +\mu )+\beta (-a A (\delta +2 \mu ) (\theta +\mu )-A (\delta +2 \mu ) (\theta +\mu ) (d+\mu +\varsigma ))\\&\quad -a A \delta (b-\alpha ) (\delta +\mu ) (\theta +\mu )+(\delta +\mu ) (a+d+\mu +\varsigma ) (\mu (a (\delta +\theta +\mu )+\delta (\theta +\mu +\varsigma )\\&\quad +(\theta +\mu ) (\mu +\varsigma ))+d (\delta +\mu ) (\theta +\mu ))+\alpha A \delta (\delta +\mu ) (\theta +\mu ) (d+\mu +\varsigma ). \end{aligned}$$

\(\eta (\beta )\) can be written as

$$\begin{aligned} \eta (\beta )= A_1 \beta ^{2}+A_2 \beta +A_3, \end{aligned}$$
(13)

where

$$\begin{aligned} A_1&=A^2 (\theta +\mu ),\\ A_2&=-A (\delta +2 \mu ) (\theta +\mu ) (a+d+\mu +\varsigma ),\\ A_3&=(\delta +\mu ) (a A \delta (\alpha -b) (\theta +\mu )+(a+d+\mu +\varsigma ) (\mu (a (\delta +\theta +\mu )+\varsigma (\delta +\theta +\mu )+(\delta +\mu ) (\theta +\mu ))\\&\qquad +d (\delta +\mu ) (\theta +\mu ))+\alpha A \delta (\theta +\mu ) (d+\mu +\varsigma )). \end{aligned}$$

Note that \(b_1\) is always positive. According to Theorem 4.1 of Castillo-Chavez and Song [27], the sign of \(a_1\), and hence the sign of \(\eta (\beta )\), determines the local dynamics around the disease-free equilibrium.

Note that \(A_1>0 ~\text {and}~ A_2<0\). The discriminant D of (13) is obtained as

$$\begin{aligned} \begin{aligned} D&=A_2^2-4A_1A_3\\&=A^2 \delta (\theta +\mu ) (a^2 (\delta (\theta -3 \mu )-4 \mu ^2)+2 a (2 A (b-\alpha ) (\delta +\mu ) (\theta +\mu )-(d+\mu ) (\delta (\theta +3 \mu )+2 \mu (\theta +2 \mu ))\\&\quad +\varsigma (\delta (\theta -3 \mu )-4 \mu ^2))-(d+\mu +\varsigma ) ((\theta +\mu ) (4 \alpha A (\delta +\mu )+d (3 \delta +4 \mu )+\mu (3 \delta +4 \mu ))\\&\quad +\varsigma (-\delta \theta +3 \delta \mu +4 \mu ^2))). \end{aligned} \end{aligned}$$
(14)

Let \(\beta _1\) and \(\beta _2\) be the two real positive roots of the equation \(A_1\beta ^2+A_2\beta +A_3=0\), given by

$$\begin{aligned} \beta _1=\frac{-A_2-\sqrt{D}}{2A_1} \quad \text {and} \quad \beta _2=\frac{-A_2+\sqrt{D}}{2A_1}. \end{aligned}$$

By applying Theorem 4.1 [27], the occurrence of forward and backward bifurcations is discussed separately below:

Backward bifurcation The model (11) exhibits a backward bifurcation if \(\eta ({\beta })<0\). Hence, the following conditions allow the existence of backward bifurcation around \(E_0\):

$$\begin{aligned} \left\{ \begin{aligned} D&>0,\\ \beta _1&<\beta <\beta _2. \end{aligned}\right. \end{aligned}$$
(15)

Forward bifurcation The forward bifurcation occurs if \(\eta (\beta )>0\). Thus, the conditions for the existence of forward bifurcation are as follows:

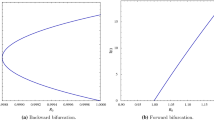
$$\begin{aligned} \left\{ \begin{aligned} D&>0,\\ \beta&<\beta _1\; \text {or}\;\beta >\beta _2. \end{aligned}\right. \end{aligned}$$
(16)

The forward and backward bifurcations are illustrated numerically in Fig. 2:

Fig. 2
figure 2

Graphs depicting the forward and backward bifurcation for the parameter values \(A = 5,~ \alpha = 0.01,~ \mu = 0.01,~ \theta = 0.04,~ d = 0.01,~ \varsigma = 0.01,~ a = 2,~ b = 0.1,~ \delta = 0.01\)

Full size image

For the above set of parameter values, the discriminant D, obtained in Eq. (14), is evaluated as \(D=0.0000278476~>~0\). According to the theoretical results, stated in inequalities (15), the backward bifurcation occurs for \(D>0\), and \(\beta _1=0.00397917<\beta <\beta _2=0.00820083\). Setting \(\beta =0.007\), the model (11) exhibits a backward bifurcation, as shown in Fig. 2b. This figure shows that the reduction of the value of \(R_0\) below unity does not guarantee the elimination of the infection. This implies a range that exhibits a region of coexistence of the disease-free equilibrium and two endemic equilibria: a smaller endemic equilibrium, i.e., with a small number of infected individuals, which is unstable, and a larger one, i.e., with a larger number of infected individuals, which is stable. According to the inequalities given in (16), the forward bifurcation occurs when \(D>0\) and if \(\beta \) is sufficiently small or sufficiently large, i.e., if either \(\beta <\beta _1\) or \(\beta >\beta _2\) holds. Figure 2a is plotted for \(\beta =0.003 <\beta _1=0.00397917\), and Fig. 2c for \(\beta =0.009>\beta _2\), revealing that, when \(R_0<1\), the disease-free equilibrium is stable, while if \(R_0\) crosses unity, the model admits a stable unique endemic equilibrium.

3.2 Endemic equilibrium

Stability analysis of the endemic equilibrium \(E_\mathrm{e}\) for the model (1) is now carried out. First, equate the right-hand terms of the model (1) to zero, to establish the existence of endemic equilibrium, as given below:

$$\begin{aligned}&A - \delta S^*- \frac{\beta S^* I^*}{1+\alpha I^*}-\mu S^*+\theta R^* =0, \end{aligned}$$
(17)
$$\begin{aligned}&\delta S^* - \frac{\gamma V^* I^*}{{1+\alpha I^*}}-\mu V^* =0, \end{aligned}$$
(18)
$$\begin{aligned}&\frac{\beta S^* I^*}{1+\alpha I^*} + \frac{\gamma V^* I^*}{{1+\alpha I^*}}-(\mu +d+ \varsigma )I^*-\frac{aI^*}{1+b I^*} =0,\end{aligned}$$
(19)
$$\begin{aligned}&\varsigma I^* + \frac{aI^*}{1+b I^*} -\theta R^*-\mu R^* =0 . \end{aligned}$$
(20)

Solution of these algebraic equations yields the endemic equilibrium \(E_\mathrm{e}=(S^*, V^*, I^*, R^*)\) as

$$\begin{aligned} S^*&= \frac{(\alpha I^*+1) (\theta I^* (a+b I^* \varsigma +\varsigma )+A (b I^*+1) (\theta +\mu ))}{(b I^*+1) (\theta +\mu ) (\delta +\mu +I^* (\alpha (\delta +\mu )+\beta ))},\\ V^*&= \frac{\delta (\alpha I^*+1)^2 (\theta I^* (a+b I^* \varsigma +\varsigma )+A (b I^*+1) (\theta +\mu ))}{(b I^*+1) (\theta +\mu ) (\mu +I^* (\alpha \mu +\gamma )) (\delta +\mu +I^* (\alpha (\delta +\mu )+\beta ))},\\ R^*&= \frac{I^* (a+b I^* \varsigma +\varsigma )}{(b I^* +1) (\theta +\mu )}, \end{aligned}$$

where \(I^*\) is given by the real positive solutions of the equation

$$\begin{aligned} A_3 I^{*3}+A_2 I^{*2}+A_1 I^{*}+A_0=0, \end{aligned}$$
(21)

with the coefficients \(A_3\), \(A_2\), \(A_1\), and \(A_0\) given as

$$\begin{aligned} A_3&=-b (\mu (\beta (\alpha \mu +\gamma ) (\theta +\mu +\varsigma )+\alpha (\alpha (\delta +\mu ) (\theta +\mu ) (\mu +\varsigma )+\gamma \varsigma (\delta +\theta +\mu )\\&\qquad +\gamma (\delta +\mu ) (\theta +\mu )))+d (\theta +\mu ) (\alpha \mu +\gamma ) (\alpha (\delta +\mu )+\beta )),\\ A_2&= -\mu (a (\beta (\alpha \mu +\gamma )+\alpha (\alpha (\delta +\mu ) (\theta +\mu )+\gamma (\delta +\theta +\mu )))+\varsigma (\alpha (\alpha (\delta +\mu ) (\theta +\mu )\\&\qquad + \gamma (\delta +\theta +\mu ))+\beta (\mu (\alpha +b)+\gamma )+b (2 \alpha (\delta +\mu ) (\theta +\mu )+\gamma (\delta +\theta +\mu ))) \\&\qquad + (\theta +\mu ) (\beta (\mu (\alpha +b)+\gamma )+(\delta +\mu ) (\gamma (\alpha +b)+\alpha \mu (\alpha +2 b))))+A b (\theta +\mu ) (\beta (\alpha \mu +\gamma )+\alpha \gamma \delta ) \\&\qquad -d (\theta +\mu ) (\beta (\mu (\alpha +b)+\gamma )+(\delta +\mu ) (\gamma (\alpha +b)+\alpha \mu (\alpha +2 b))),\\ A_1&= -\mu (a (2 \alpha (\delta +\mu ) (\theta +\mu )+\beta \mu +\gamma (\delta +\theta +\mu ))+\varsigma ((2 \alpha +b) (\delta +\mu ) (\theta +\mu )+\beta \mu +\gamma (\delta +\theta +\mu ))\\&\qquad +(\theta +\mu ) ((\delta +\mu ) (\mu (2 \alpha +b)+\gamma )+\beta \mu ))+A (\theta +\mu ) (\beta (\mu (\alpha +b)+\gamma )+\gamma \delta (\alpha +b))\\&\qquad - d (\theta +\mu ) ((\delta +\mu ) (\mu (2 \alpha +b)+\gamma )+\beta \mu ),\\ A_0&= \mu (\delta +\mu ) (\theta +\mu ) (a+d+\mu +\varsigma )\left( R_0-1\right) . \end{aligned}$$

Theorem 2

If \(R_0>1\), then there is either one unique or three positive endemic equilibria, if all equilibria are simple roots.

Proof

Suppose \(R_0>1\). Equation (21) gives a third-degree polynomial in \(I^*\):

$$\begin{aligned} F(I^*)=A_3 I^{*3}+A_2 I^{*2}+A_1 I^{*}+A_0. \end{aligned}$$

The leading coefficient of \(I^*\) is \(A_3\), which is negative. Hence

$$\begin{aligned} \lim _{I^* \rightarrow \infty }F(I^*)=-\infty . \end{aligned}$$

Also, \(F(0)=A_0\) and \(A_0>0\) if \(R_0>1\). \(F(I^*)\) is a continuous function of \(I^*\), and using the fundamental theorem of algebra, this polynomial can have at most three real roots. \(\square \)

The case of a unique endemic equilibrium only is considered herein. (H1): Suppose that \(R_0>1\). It is noted that \(A_3\) is negative and \(A_0\) is positive. For the existence of a unique endemic equilibrium, the following possibilities for the signs of \(A_1\) and \(A_2\) exist:

$$\begin{aligned} \begin{aligned} \mathrm{(i)}~&A_1>0,~ \text {and}~ A_2>0,\\ \mathrm{(ii)} ~&A_1>0, ~\text {and}~ A_2<0,\\ \mathrm{(iii)} ~&A_1<0,~\text {and}~ A_2<0. \end{aligned} \end{aligned}$$
(22)

Now, the local stability of the endemic equilibrium for the model (1) is discussed.

The characteristic equation of the model (1) at \({E_\mathrm{e}}\) is a fourth-degree transcendental equation:

$$\begin{aligned} \lambda ^4+(p_0 \lambda ^3+q_0 \lambda ^2+r_0 \lambda +s_0)+(p_1 \lambda ^3+q_1 \lambda ^2+r_1 \lambda +s_1) \mathrm {e}^{-\lambda \tau }+(q_2 \lambda ^2+r_2 \lambda +s_2) \mathrm {e}^{-2\lambda \tau }=0, \end{aligned}$$
(23)

where

$$\begin{aligned} s_0&=\frac{\mu (\delta +\mu ) (\theta +\mu ) \left( a+(bI^*+1)^2 (d+\mu +\varsigma )\right) }{(bI^*+1)^2},\\ s_1&=\frac{1}{(bI^*+1)^2 (\alpha I^*+1)^2} (a I^* (\alpha I^*+1) (\beta \mu (2 \theta +\mu )+\gamma (\delta (2 \theta +\mu )+\mu (\theta +\mu )))\\&\quad + (bI^*+1)^2 (d I^* (\theta +\mu ) (\alpha I^*+1) (\beta \mu +\gamma (\delta +\mu ))+\beta \mu (-S^*) (\delta +\mu ) (\theta +\mu )-\mu (\theta +\mu ) (\gamma V^* (\delta +\mu )\\&\quad -I^* (\alpha I^*+1) (\mu (\beta +\gamma )+\gamma \delta ))+I^* \varsigma (\alpha I^*+1) (\beta \mu (2 \theta +\mu )+\gamma (\mu (\delta +\theta )+2 \delta \theta +\mu ^2)))),\\ s_2&=\frac{1}{(bI^*+1)^2 (\alpha I^*+1)^3}((\beta \gamma I^* (a I^* (2 \theta +\mu ) (\alpha I^*+1)+(bI^*+1)^2 ((\theta +\mu ) (I^* (d+\mu ) (\alpha I^*+1)\\&\quad +\mu (-S^*-V^*))+I^* \varsigma (2 \theta +\mu ) (\alpha I^*+1))))),\\ r_0&=\frac{1}{{(bI^*+1)^2}}(a (2 \mu (\delta +\theta )+\delta \theta +3 \mu ^2)+(bI^*+1)^2 (d (2 \mu (\delta +\theta )+\delta \theta +3 \mu ^2)+\varsigma (2 \mu (\delta +\theta )\\&\quad + \delta \theta +3 \mu ^2)+\mu (3 \mu (\delta +\theta )+2 \delta \theta +4 \mu ^2))), \\ r_1&=\frac{1}{(bI^*+1)^2 (\alpha I^*+1)^2}(a I^* (\alpha I^*+1) (2 \beta (\theta +\mu )+\gamma (\delta +\theta +2 \mu ))+(bI^*+1)^2 (d I^* (\alpha I^*+1) (\beta (\theta +2 \mu )\\&\quad + \gamma (\delta +\theta +2 \mu ))-\beta S^* (2 \mu (\delta +\theta )+\delta \theta +3 \mu ^2)-\gamma \delta \theta V^*-2 \gamma \delta \mu V^*-2 \gamma \theta \mu V^*-3 \gamma \mu ^2 V^* +2 \alpha \beta \theta \mu I^{*2}\\&\quad + 3 \alpha \beta \mu ^2 I^{*2}+\alpha \gamma \delta \theta I^{*2}+2 \alpha \gamma \delta \mu I^{*2}+2 \alpha \gamma \theta \mu I^{*2}+3 \alpha \gamma \mu ^2I^{*2}+I^* \varsigma (\alpha I^*+1) (2 \beta (\theta +\mu )\\&\quad +\gamma (\delta +\theta +2 \mu ))+ 2 \beta \theta \mu I^*+3 \beta \mu ^2 I^*+\gamma \delta \theta I^*+2 \gamma \delta \mu I^*+2 \gamma \theta \mu I^*+3 \gamma \mu ^2 I^*)),\\ r_2&=\frac{\beta \gamma I^* \left( a I^* (\alpha Y+1)+(bI^*+1)^2 (I^* (\alpha I^*+1) (d+\theta +2 \mu +\varsigma )+(\theta +2 \mu ) (-S^*-V^*))\right) }{(bI^*+1)^2 (\alpha I^*+1)^3},\\ q_0&=\frac{a (\delta +\theta +3 \mu )+(bI^*+1)^2 (d (\delta +\theta +3 \mu )+\delta (\theta +3 \mu +\varsigma )+\varsigma (\theta +3 \mu )+3 \mu (\theta +2 \mu ))}{(bI^*+1)^2},\\ q_1&=\frac{1}{(bI^*+1)^2 (\alpha I^*+1)^2}(a I^* (\beta +\gamma ) (\alpha I^*+1)+(bI^*+1)^2 (d I^* (\beta +\gamma ) (\alpha I^*+1)-\beta S^* (\delta +\theta +3 \mu )\\&\quad -\gamma \delta V^*- \gamma \theta V^*-3 \gamma \mu V^*+\alpha \beta \theta I^{*2}+3 \alpha \beta \mu I^{*2}+\alpha \gamma \delta I^{*2}+\alpha \gamma \theta I^{*2}+3 \alpha \gamma \mu I^{*2}+I^* \varsigma (\beta +\gamma ) (\alpha I^*+1)\\&\quad +\beta \theta I^*+ 3 \beta \mu I^*+\gamma \delta I^*+\gamma \theta I^*+3 \gamma \mu I^*)),\\ q_2&=\frac{\beta \gamma I^* \left( -S^*-V^*+\alpha I^{*2}+I^*\right) }{(\alpha I^*+1)^3},\\ p_0&=\frac{a+(bI^*+1)^2 (d+\delta +\theta +4 \mu +\varsigma )}{(bI^*+1)^2},\\ p_1&=\frac{\beta (-S^*)-\gamma V^*+I^* (\beta +\gamma ) (\alpha I^*+1)}{(\alpha I^*+1)^2}. \end{aligned}$$

Theorem 3

At \(\tau =0\), the endemic equilibrium \(E_\mathrm{e}\) is locally asymptotically stable if the real parts of all the roots of (23) are negative.

Proof

Equation (23) reveals that the characteristic equation at \(\tau =0\) near \(E_\mathrm{e}\) is given by

$$\begin{aligned} \lambda ^4+(p_0+p_1) \lambda ^3+(q_0+q_1+q_2) \lambda ^2+(r_0+r_1+r_2 )\lambda +(s_0+s_1+s_2)=0. \end{aligned}$$
(24)

The proof of this theorem is based on the conditions proposed by the Routh–Hurwitz criterion. Using this criterion, all roots of Eq. (24) have negative real parts if and only if

(H2):\(p_0+p_1>0\), \(r_0+r_1+r_2>0\), \(s_0+s_1+s_2>0\) and, \((p_0+p_1)(q_0+q_1+q_2)(r_0+r_1+r_2)>(p_0+p_1)^2(s_0+s_1+s_2)+(r_0+r_1+r_2)^2.\)\(\square \)

Equation (23) yields

$$\begin{aligned} p_1 \lambda ^3+q_1 \lambda ^2+r_1 \lambda +s_1+(\lambda ^4+p_0 \lambda ^3+q_0 \lambda ^2+r_0 \lambda +s_0) \mathrm {e}^{\lambda \tau }+(q_2 \lambda ^2+r_2 \lambda +s_2) \mathrm {e}^{-\lambda \tau }=0. \end{aligned}$$
(25)

Let \(\mathrm {i} \omega \) (\(\omega >0\)) be a root of Eq. (25), then

$$\begin{aligned} -\mathrm {i} p_1 \omega ^3-q_1 \omega ^2+\mathrm {i} r_1\omega +s_1+\left( \omega ^4-\mathrm {i} p_0\omega ^3-q_0\omega ^2+\mathrm {i} r_0\omega +s_0\right) \mathrm {e}^{\mathrm {i} \omega \tau }+\left( -q_0\omega ^2+\mathrm {i} r_2\omega +s_2\right) \mathrm {e}^{-\mathrm {i}\omega \tau }=0.\nonumber \\ \end{aligned}$$
(26)

Equation (26) implies that

$$\begin{aligned}&\left( \left( p_0 \omega ^3-r_0 \omega +r_2 \omega \right) \sin (\tau \omega )+\left( -q_0 \omega ^2-q_2 \omega ^2+s_0+s_2+\omega ^4\right) \cos (\tau \omega )-q_1 \omega ^2+s_1\right) \nonumber \\&\quad +\mathrm {i}\left( \left( -p_0 \omega ^3+r_0 \omega +r_2 \omega \right) \cos (\tau \omega )-p_1 \omega ^3+\left( -q_0 \omega ^2+q_2 \omega ^2+s_0-s_2+\omega ^4\right) \sin (\tau \omega )+r_1 \omega \right) =0. \end{aligned}$$
(27)

Separation of real and imaginary parts gives

$$\begin{aligned}&q_1 \omega ^2-s_1 =\left( p_0 \omega ^3-r_0 \omega +r_2 \omega \right) \sin (\tau \omega )+\left( -q_0 \omega ^2-q_2 \omega ^2+s_0+s_2+\omega ^4\right) \cos (\tau \omega ), \end{aligned}$$
(28)
$$\begin{aligned}&p_1 \omega ^3-r_1 \omega =\left( -p_0 \omega ^3+r_0 \omega +r_2 \omega \right) \cos (\tau \omega )+\left( -q_0 \omega ^2+q_2 \omega ^2+s_0-s_2+\omega ^4\right) \sin (\tau \omega ); \end{aligned}$$
(29)

That is,

$$\begin{aligned} h_1(\omega ) \cos {\omega \tau }-h_2(\omega ) \sin {\omega \tau }&=h_3(\omega ), \end{aligned}$$
(30)
$$\begin{aligned} h_4(\omega ) \sin {\omega \tau }+h_5(\omega ) \cos {\omega \tau }&=h_6(\omega ), \end{aligned}$$
(31)

where

$$\begin{aligned} h_1(\omega )&=\omega ^4-\left( q_0+q_2\right) \omega ^2+s_0+s_2,\\ h_2(\omega )&=\left( r_0-r_2\right) \omega -p_0 \omega ^3,\\ h_3(\omega )&=q_1 \omega ^2-s_1,\\ h_4(\omega )&=\omega ^4-\left( q_0-q_2\right) \omega ^2+s_0-s_2,\\ h_5(\omega )&=\left( r_0+r_2\right) \omega -p_0 \omega ^3,\\ h_6(\omega )&=p_1 \omega ^3-r_1 \omega . \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \cos {\omega \tau }&=\frac{P_{01}(\omega )}{P_{00}(\omega )},\\ \sin {\omega \tau }&=\frac{P_{02}(\omega )}{P_{00}(\omega )}, \end{aligned} \end{aligned}$$
(32)

with

$$\begin{aligned} \begin{aligned} P_{00}(\omega )&= \omega ^4 \left( -2 p_0 r_0+q_0^2-q_2^2+2 s_0\right) +\omega ^6 \left( p_0^2-2 q_0\right) +\omega ^2 \left( -2 q_0 s_0+2 q_2 s_2+r_0^2-r_2^2\right) \\&\quad +s_0^2-s_2^2+\omega ^8,\\ P_{01}(\omega )&=\omega ^4 \left( p_0 r_1+p_1 \left( r_0-r_2\right) +q_1 \left( q_2-q_0\right) -s_1\right) +\omega ^6 \left( q_1-p_0 p_1\right) \\&\quad +\omega ^2 \left( \left( q_0-q_2\right) s_1+q_1 \left( s_0-s_2\right) +r_1 \left( r_2-r_0\right) \right) -s_0 s_1+s_1 s_2,\\ P_{02}(\omega )&=p_1 \omega ^7+\omega ^5 \left( p_0 q_1-p_1 \left( q_0+q_2\right) -r_1\right) + \omega ^3 \left( -p_0 s_1+p_1 \left( s_0+s_2\right) +\left( q_0+q_2\right) r_1-q_1 \left( r_0+r_2\right) \right) \\&\quad +\omega \left( \left( r_0+r_2\right) s_1-r_1 \left( s_0+s_2\right) \right) . \end{aligned} \end{aligned}$$
(33)

Equation (32) gives

$$\begin{aligned} P_{01}^2(\omega )+P_{02}^2(\omega )=P_{00}^2(\omega ). \end{aligned}$$
(34)

Now, assume that, (H3): Eq. (34) has at least one positive root \(\omega _0\).

Then, Eq. (25) has a pair of purely imaginary roots \(\pm \mathrm {i} \omega _0\). For \(\omega _0\), the corresponding critical value of the time delay is obtained as

$$\begin{aligned} \tau _0 =\frac{1}{\omega _0}\arccos {\frac{P_{01}(\omega _0)}{P_{00}(\omega _0)}+\frac{2 \pi j}{\omega _0}}, \quad j=0,1,2,\ldots \end{aligned}$$
(35)

To establish the Hopf bifurcation at \(\tau =\tau _0\), it must be shown that

$$\begin{aligned} {\text {Re}}\left( \frac{\text {d} \lambda }{\text {d} \tau }\right) \ne 0. \end{aligned}$$

Differentiating Eq. (23) with respect to \(\tau \) gives

$$\begin{aligned} \begin{aligned} \frac{\mathop {}\!\mathrm {d}\lambda }{\mathop {}\!\mathrm {d}\tau }&=\frac{-\lambda \mathrm {e}^{\lambda \tau } \left( \lambda ^4+P_0 \lambda ^3+q_0 \lambda ^2+r_0 \lambda +s_0\right) +\lambda \left( q_2 \lambda ^2+r_2 \lambda +s_2\right) \mathrm {e}^{-\lambda \tau }}{L}, \end{aligned} \end{aligned}$$
(36)

where

$$\begin{aligned} L&=3 P_1 \lambda ^2+2 q_1 \lambda +r_1+\left( 4 \lambda ^3+3 P_0 \lambda ^2+2 q_0 \lambda +r_0\right) \mathrm {e}^{\lambda \tau }+\tau \left( \lambda ^4+P_0\lambda ^3+q_0\lambda ^2+r_0 \lambda +s_0\right) \mathrm {e}^{\lambda \tau }\\&\quad +\left( 2q_2 \lambda +r_2\right) \mathrm {e}^{-\lambda \tau }-\tau \mathrm {e}^{-\lambda \tau }\left( q_2 \lambda ^2+r_2 \lambda +s_2\right) . \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned} \left( \frac{\mathop {}\!\mathrm {d}\lambda }{\mathop {}\!\mathrm {d}\tau }\right) ^{-1}&=-\frac{Y_1(\lambda )}{Y_2(\lambda )}-\frac{\tau }{\lambda }, \end{aligned} \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{aligned} Y_1(\lambda )&=\left( 3 P_1 \lambda ^2+2 q_1 \lambda +r_1\right) +\left( 4 \lambda ^3+3 P_0 \lambda ^2+2 q_0 \lambda +r_0\right) \mathrm {e}^{\lambda \tau }+\left( 2 q_2 \lambda +r_2\right) \mathrm {e}^{-\lambda \tau },\\ Y_2(\lambda )&=\lambda \mathrm {e}^{\lambda \tau }\left( \lambda ^4+P_0 \lambda ^3+q_0 \lambda ^2+r_0 \lambda +s_0\right) -\left( q_2 \lambda ^2+r_2 \lambda +s_2\right) \mathrm {e}^{-\lambda \tau }. \end{aligned} \end{aligned}$$
(38)

Application of \(\lambda =\mathrm {i} w_0\) yields

$$\begin{aligned} \left( \frac{\mathop {}\!\mathrm {d}\lambda }{\mathop {}\!\mathrm {d}\tau }\right) ^{-1}\Big |_{\lambda =\mathrm {i} \omega _0}&=\frac{-3 P_1 \omega _0 ^2+2 \mathrm {i} q_1 \omega _0 +r_1+ \mathrm {e}^{\mathrm {i} \tau \omega } \left( -4 \mathrm {i} \omega _0 ^3-3 P_0 \omega _0 ^2+2 \mathrm {i} q_0 \omega _0 +r_0\right) + \mathrm {e}^{-\mathrm {i} \tau \omega } \left( 2 \mathrm {i} q_2 \omega _0 +r_2\right) }{\mathrm {i} \omega _0 ~\mathrm {e}^{\mathrm {i} \tau \omega _0 } \left( \omega _0 ^4-\mathrm {i} P_0 \omega _0 ^3+\mathrm {i} r_0 \omega _0 -q_0 \omega _0 ^2+s_0\right) - \mathrm {e}^{-\mathrm {i} \tau \omega _0 } \left( \mathrm {i} r_2 \omega _0 -q_2 \omega _0 ^2+s_2\right) }\\&\qquad +\mathrm {i}\frac{\tau }{\omega _0}. \\ {{\text {Re}}}\left( \frac{\mathop {}\!\mathrm {d}\lambda }{\mathop {}\!\mathrm {d}\tau }\right) ^{-1}\Big |_{\lambda =\mathrm {i} \omega _0}&= \frac{V_1 V_2 + V_3 V_4}{V_2^2 + V_4^2}. \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_1&=4 \omega _0 ^3 \sin (\tau \omega _0 )-3 P_0 \omega _0 ^2 \cos (\tau \omega _0 )-3 P_1 \omega _0 ^2-2 q_0 \omega _0 \sin (\tau \omega _0 )+2 q_2 \omega _0 \sin (\tau \omega _0 )+r_0 \cos (\tau \omega _0 )\\&\qquad +r_2 \cos (\tau \omega _0 )+r_1,\\ V_2&=P_0 \omega _0 ^4 \sin (\tau \omega _0 )+q_0 \omega _0 ^3 \sin (\tau \omega _0 )+q_2 \omega _0 ^2 \cos (\tau \omega _0 )-r_0 \omega _0 ^2 \cos (\tau \omega _0 )-r_2 \omega _0 \sin (\tau \omega _0 )-s_0 \omega _0 \sin (\tau \omega _0 )\\&\qquad -s_2 \cos (\tau \omega _0 )+\omega _0 ^5 (-\sin (\tau \omega _0 )),\\ V_3&=3 P_0 \omega _0 ^2 \sin (\tau \omega _0 )-2 q_0 \omega _0 \cos (\tau \omega _0 )-2 q_2 \omega _0 \cos (\tau \omega _0 )-2 q_1 \omega _0 -r_0 \sin (\tau \omega _0 )+r_2 \sin (\tau \omega _0 )\\&\qquad +4 \omega _0 ^3 \cos (\tau \omega _0 ),\\ V_4&=-P_0 \omega _0 ^4 \cos (\tau \omega _0 )-q_0 \omega _0 ^3 \cos (\tau \omega _0 )-q_2 \omega _0 ^2 \sin (\tau \omega _0 )-r_0 \omega _0 ^2 \sin (\tau \omega _0 )-r_2 \omega _0 \cos (\tau \omega _0 )+s_2 \sin (\tau \omega _0 )\\&\qquad +s_0 \omega _0 \cos (\tau \omega _0 )+\omega _0 ^5 \cos (\tau \omega _0 ). \end{aligned} \end{aligned}$$

If (H4): \(V_1 V_2 + V_3 V_4\ne 0\) holds, then \( {\text {Re}}\left( \frac{\mathop {}\!\mathrm {d}\lambda }{\mathop {}\!\mathrm {d}\tau }\right) ^{-1}\Big |_{\lambda =\mathrm {i} \omega _0} \ne 0\). Thus, the following theorem can be stated:

Theorem 4

For the model (1), if conditions (H1–H4) hold, then the endemic equilibrium \(E_\mathrm{e}=(S^*, V^*, I^*, R^*)\) is locally asymptotically stable when \(\tau \in [0, \tau _0)\); the model (1) undergoes a Hopf bifurcation at \(E_\mathrm{e}=(S^*, V^*, I^*, R^*)\) when \(\tau =\tau _0\), and a family of periodic solutions bifurcate from \(E_\mathrm{e}=(S^*, V^*, I^*, R^*)\).

4 Numerical simulations

In this section, numerical simulations are carried out to illustrate the effectiveness of the obtained results.

The case of endemic equilibrium is illustrated for the following numerical data: \(A=12\), \(\beta =0.05\), \(\alpha =0.15\), \(\mu =0.1\), \(d=0.01\), \(\theta =0.1\), \(\delta =0.1\), \(a=2\), \(b=10\), \(\varsigma =0.1\), and \(\gamma =0.001\). It is estimated that, with these parameter values, the basic reproduction number of the model (1) is \(R_0 = 1.38462\) and the endemic equilibrium is \(E_\mathrm{e}(S,V,I,R)=(28.9926, 27.4302, 39.1123,20.5536)\).

Fig. 3
figure 3

Impact of time delay on population

Full size image

Figure 3a shows the behavior of the susceptible, vaccinated, infected, and recovered populations at \(\tau =1\). It can be seen that, as time increases, the susceptible population decreases while the vaccinated, infected, and recovered population increase, and finally, all the subpopulations settle down to the endemic equilibrium \(E_\mathrm{e}\). Figure 3b shows the impact of time delay on the infected population, clearly revealing that infection increases among society with an increase in the time delay \(\tau \).

Fig. 4
figure 4

Infected population with and without saturated treatment rate for \(\tau =1\)

Full size image
Fig. 5
figure 5

Impact of vaccination on infected population

Full size image

Figure 4 reveals the impact of saturated treatment on the infected population for a time delay of \(\tau =1\). When treatment is given to infected individuals, the infection spreads at a lower level compared with the case without treatment, revealing that medical resources and their supply efficiency have a great influence on the spread and control of an epidemic. Thus, it can be seen that the saturated treatment rate helps to lessen the transmission and to control the spread of the infection. Therefore, it is very important to make treatment facilities available quickly to infectives to diminish the infection among society.

Fig. 6
figure 6

Hopf bifurcation for various values of time delay \(\tau \) with parameter values of \(A=12, ~ \beta = 0.05, ~ \alpha =0.15, ~ \delta = 0.01,~ \mu =0.1, ~ \theta =0.1,~ \gamma = 0.001,~d=0.01, ~\varsigma =0.1,~a=5, ~b=10\)

Full size image

Figure 5 shows the impact of vaccination on infected individuals. Figure 5a shows the infected population with and without vaccination, revealing that, even though the vaccine is imperfect, it helps to reduce the spread of the infection. Meanwhile, Fig. 5b shows the variation in the infected population for different values of the vaccination rate, where the infected population is plotted for \(\delta = 0.1,~0.2,~ \text {or}~0.3\). It can be seen that, when the vaccination rate is high, the infected population diminishes at a higher rate. Thus, immunization by vaccination is a counteractive tool that can lessen the transmission of an infection and control its spread. Therefore, public health agencies need to ensure effective vaccination by increasing the time until loss of immunity and immunizing the maximum number of individuals.

Figure 6 shows the relation between the susceptible and infected populations for different values of the time delay, confirming the occurrence of Hopf bifurcation. The red dot on the curves indicates the endemic equilibrium \(E_\mathrm{e}\) whose components are \((S,I)=(36.4105,48.5345)\), and at this value the results give \((S,V,I,R)=(36.4105,3.43944,48.5345,26.7621)\). These figures show how the fraction of infectives oscillates for higher values of the time delay, finally approaching the endemic equilibrium \(E_\mathrm{e}\). Figure 6c, d indicates that increasing the time delay \(\tau \) results in a longer period of periodic oscillations around the endemic equilibrium \(E_\mathrm{e}\).

5 Discussion

An SVIRS epidemic model with a Holling type II functional incidence rate, time delay, imperfect vaccine, and saturated treatment rate is studied herein. The analysis of the model shows that it exhibits two equilibria: a disease-free equilibrium (DFE) and an endemic equilibrium (EE). The basic reproduction number \(R_0\) is obtained, and the dynamics of the model for disease transmission is characterized by \(R_0\), both with and without time delay. For \(\tau >0\), it is shown that the DFE is locally asymptotically stable when \(R_0\) is less than unity, unstable when \(R_0\) is greater than unity, and linearly neutrally stable at \(R_0\) equal to unity. However, use of center manifold theory reveals that the model undergoes backward or forward bifurcation at \(R_0=1\) when there is no time delay. This analysis is of interest in itself, as it provides some information on the stability of the DFE and EE. The model exhibits forward or backward bifurcation under particular conditions obtained by inequalities (15), and (16). The phenomenon where the disease-free equilibrium loses its stability and a stable endemic equilibrium appears as \(R_0\) increases through unity is the case of forward bifurcation, whereas the phenomenon where a stable endemic equilibrium coexists with a stable DFE when \(R_0 < 1\) is the case of backward bifurcation. The epidemiological implication of backward bifurcation is that the condition \(R_0<1\) is necessary but not sufficient for eradication of the infectious disease. Schematic diagrams of forward and backward bifurcation are depicted in Fig. 2. Furthermore, stability analysis of the endemic equilibrium is performed, and the local stability of the endemic equilibrium is shown in Theorems 3 and 4. Regarding time delay as a bifurcation parameter and analyzing the corresponding characteristic equation, the occurrence of Hopf bifurcation near the endemic equilibrium is shown, illustrating the presence of oscillatory and periodic solutions. Numerical simulations are performed to demonstrate the effectiveness of the theoretical findings. The graphical representation elucidates the impact of time delay on infected individuals, revealing that, when the time delay is high, there is a large number of infected individuals. The impact of a saturated treatment rate is also shown graphically, revealing that the considered treatment is imperative to control the spread of the infection, as it lessens transmission and reduces the number of infectives. The occurrence of the oscillatory and periodic solution is also illustrated, confirming the existence of Hopf bifurcation. The present study demonstrates that an imperfect vaccine and saturated treatment rate may lead to backward bifurcation, but at the same time it should be emphasize that these measures reduce the size of the infected population. High vaccine take-up levels result in radical decreases of infectious disease, as shown in Fig. 5. If a vaccine which is completely effective can be made, this plausibility does not emerge, while a program which reduces the contact rate can further control infection without inciting backward bifurcation.