Rational and semi-rational solutions to the Davey–Stewartson III equation

Abstract

In this paper, based on the combination of Hirota’s bilinear method and long wave limit technique, we investigate rational and semi-rational solutions to the third-type Davey–Stewartson (DS III) equation and its nonlocal version. Rational solutions to the DS III equation demonstrate to be kinks, lumps and line rogue waves, while semi-rational solutions display hybrids of solitons, lumps and line rogue waves. As to the nonlocal DS III equation, we derive (semi-)rational solutions and breather solutions. Semi-rational solutions show lumps on the periodic line backgrounds, hybrids of breathers and lumps, line rogue waves and line breathers on the periodic line background.

1 Introduction

Rogue waves are widely concerned in nonlinear sciences and they are found in many fields, such as ultra-broadband supercontinuum generation, optical fibers, ocean technology and so on. Rogue waves are also adapted in many fields of science including Bose–Einstein condensate [1, 2], nonlocal media [3], superfluids [4], plasma [5, 6] and optical systems [7, 8]. Rogue waves appear in the ocean without traces, attain a huge amplitude and then suddenly merge into the background [9,10,11]. In mathematics, rogue waves are firstly reported in the nonlinear Schrödinger equation (NLS) by Peregrine [12], and thus called Peregrine solitons. Three typical features are concerned as the definition of $(1+1)$-dimensional first-order rogue waves. Firstly, they are rational or quasi-rational in expressions. Secondly, they are spatial and temporal localized. Thirdly, they share a maximum amplitude usually more than three times of the background. Higher-order rogue waves are also concerned in many integrable systems, such as Hirota equation [13], Sasa–Satsuma equation [14, 15], three wave interaction system [16] and so on. Many methods are used to build higher-order rogue wave solutions including Darboux transformation method and Hirota’s bilinear method [17, 18]. In addition to rogue wave solutions, many integrable equations admit lump solutions [19, 20]. Lump patterns of the Kadomtsev–Petviashvili (KP) equation are analytically studied [21, 22].

In the pioneer works of Bender and Boettcher, studies on non-Hermitian physical systems have been on the rise [23]. They prove that as long as a non-Hermitian Hamiltonian satisfies the PT symmetry condition, it can possess an entirely real spectra. In general, if the complex potential satisfies the condition $V(x)=V^{*}(-x)$, one can define the non-Hermitian PT symmetric Hamiltonian $H=\hat{p}^{2}/2+V(x)$, where V(x) is a complex potential, $\hat{p}$ is the momentum operator and asterisk denotes complex conjugate [24,25,26,27,28,29]. A lot of non-Hermitian Hamiltonian systems have been investigated in the past three decades [30,31,32,33,34]. Studies in optics and photonics provide the test bed for the experimental observations of phenomena associated with the PT symmetry [35,36,37]. Many works reveal that a complex-valued potential which only shares a parity symmetry may also be applied in optics, photonics and many other related areas [30,31,32,33,34,35,36,37]. To understand a PT symmetry system better, it is worthwhile to find out its associated integrable model. Ablowitz and Musslimani proposed a nonlocal NLS equation with a PT symmetric potential [38]. Stimulated by this work, many (1+1)-dimensional nonlocal systems are investigated. Recently, the (2+1)-dimension nonlocal NLS was proposed [39].

Hirota’s bilinear method has shown its effectiveness in constructing explicit solutions of integrable equations [40]. Based on Hirota’s bilinear method, the long wave limit approach [19] was introduced by Ablowitz and Satsuma to construct rational solutions of the KP equation and two-dimensional NLS equation. They proposed the algorithm and the general form of rational solutions starting from soliton solutions. This method has been successfully applied to (2+1)-dimensional nonlocal NLS and Fokas system [41, 42]. Moreover, the long wave limit method combined with the KP hierarchy reduction has been developed. Many interesting patterns of rational and semi-rational solutions are found, such as W-shaped rogue waves, kink-type rogue waves, lumps, rogue waves on periodic line wave backgrounds and so on.

In this paper, we investigate the third-type Davey–Stewartson (DS III) equation

$$\begin{aligned}&\textrm{i}q_{t}-q_{xx}+q_{yy}-2\gamma q\left[ \left( \int ^{x}_{-\infty }|q|^{2}_{y}dx'+u_{1}(y,t)\right) \nonumber \right. \nonumber \\&\left. -\left( \int ^{y}_{-\infty }|q|^{2}_{x}dy'+u_{2}(x,t)\right) \right] =0,\quad \gamma =\pm 1, \end{aligned}$$

(1)

where q(x, y, t) is a complex function and $u_{1}(y,t), \,u_{2}(x,t)$ are real. By the transformation

$$\begin{aligned}&V=\int ^{x}_{-\infty }(|q|^{2})_{y}dx'+u_{1}(y,t), \end{aligned}$$

(2)

$$\begin{aligned}&U=\int ^{y}_{-\infty }(|q|^{2})_{x}dy'+u_{2}(x,t), \end{aligned}$$

(3)

the DS III Equation (1) is transformed into the form

$$\begin{aligned} \begin{aligned}&\textrm{i}q_{t}-q_{x}+q_{yy}-2\gamma q(V-U)=0,\\&V_{x}=(|q|^{2})_{y},\\&U_{y}=(|q|^{2})_{x}, \end{aligned} \end{aligned}$$

(4)

where U and V are two real functions. Schulman [43], Santani and Fokas [44, 45] derived the DS III equation via symmetry method. Afterward, Boiti [46] found this equation again by the direct linearization method [47]. Recently, much attention has been paid to the DS III equation in many aspects. General dark solitons, mixed solutions of dark solitons and breathers, semi-rational solutions consisting of rogue waves, breathers and solitons for the DS III equation were generated by employing the bilinear method [48]. The residual symmetry and exact solutions were considered by using function expansion method in [49]. By means of the multilinear variable separation approach, the variable separation solution for the DS III equation was obtained in [50].

In addition to the local DS III equation, based on the fully and partially parity-time (PT) symmetry, two kinds of nonlocal DS III equation are proposed. The first one [51] is nonlocal both in x and y direction

$$\begin{aligned} \begin{aligned}&\textrm{i}q_{t}-q_{x}+q_{yy}-2\gamma q(V-U)=0,\\&V_{x}=\Big (q q^*(-x,-y,t)\Big )_{y},\\&U_{y}=\Big (q q^*(-x,-y,t)\Big )_{x}, \end{aligned} \end{aligned}$$

(5)

and the second one [52] is reverse time with

$$\begin{aligned} \begin{aligned}&\textrm{i}q_{t}-q_{x}+q_{yy}-2\gamma q(V-U)=0,\\&V_{x}=\Big (q q(x,y,-t)\Big )_{y},\\&U_{y}=\Big (q q(x,y,-t)\Big )_{x}. \end{aligned} \end{aligned}$$

(6)

For the fully PT symmetric nonlocal DS III Equation (5) and the reverse-time nonlocal DS III Equation (6), Gram-type determinant soliton solutions were derived via the KP hierarchy reduction method and Hirota’s bilinear approach [51, 52].

Recently, (semi-)rational solutions of many integrable systems were investigated, such as Boussinesq–Burgers system [53], Mel’nikov system [54], Kadomtsev–Petviashvili-based system [55], (2+1)-dimensional NLS system [56], Hirota–Maccari system [57] and so on. As to the DS III (4), (semi-)rational have been derived from KP hierarchy reduction approach. To the best of our knowledge, (semi-)rational solutions for the DS III have not been reported by taking the long wave limit method. Besides, (semi-)rational solutions for the nonlocal DS III Equation (5) have never been obtained. These motivate us to consider study rational and semi-rational solutions to local and nonlocal DS III equation based on the combination of Hirota’s bilinear method and the long wave limit technique. We aim to derive various types of solutions such as kink-shaped rogue wave, lumps, line rogue waves, breathers, line breathers, solitons to the local and nonlocal DS III equation. Furthermore, we will depict these obtained solutions both in (x, y) and (x, t)-plane and explore their dynamics.

The paper is organized as follows. In Sect. 2, several kinds of rational and semi-rational solutions to the DS III equations are derived using the combination of Hirota’s bilinear method and the long wave limit approach. These solutions contain solitons, line breathers, lumps and line rogue waves and hybrid solutions. Furthermore, dynamics of the derived solutions are analyzed with plots. In Sect. 3, solitons and semi-rational solutions to the nonlocal DS III equation are deduced. These solutions demonstrate to be breathers, lumps and line rogue waves, respectively. The mixed solutions composed of breathers, lumps and line rogue waves on the background of line breathers are also derived. Finally, the conclusion and discussion are given.

2 Solutions of the DS III equation

In this section, we focus on solutions of the DS III equation via Hirota’s bilinear method and long wave limit technique. The DS III system (4) is transformed into the bilinear form

$$\begin{aligned} \left\{ \begin{aligned}&(\textrm{i}D_{t}-D^{2}_{x}+D^{2}_{y})g\cdot f=0, \\&(\gamma D_{x}D_{y}-2)f\cdot f=-2|g|^{2}, \\ \end{aligned} \right. \end{aligned}$$

(7)

through the dependent variable transformation

$$\begin{aligned} q=\frac{g}{f},\quad U=-\gamma (\ln f)_{xx},\quad V=-\gamma (\ln f)_{yy}, \end{aligned}$$

(8)

where $\gamma =\pm 1$, f is real and g is complex with respect to variables x, y, t. Hirota’s bilinear operator D is defined as [40]

$$\begin{aligned} D^{m}_{x}D^{k}_{t}a \cdot b&=\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{m}\left( \frac{\partial }{\partial t}\right. \\&\quad \left. -\frac{\partial }{\partial t'}\right) ^{k}a(x,t)b(x',t')\Big |_{x'=x,t'=t}. \end{aligned}$$

In the following, we first present soliton solutions of the DS III Equation (4) by Hirota’s bilinear method and then generate rational and semi-rational solutions by using the long wave limit technique.

2.1 Soliton solutions to the DS III equation

Although the Gram-type solution to the DS III equation was derived by the KP-Toda hierarchy reduction method in Ref. [48], we give general N-soliton solution by making the perturbation expansion from the bilinear form. We obtain the N-soliton solution to the DS III Equation (4) with

$$\begin{aligned}&f=\sum _{\mu =0,1}\exp \left( {\sum _{j<k}^{(N)}\mu _{j}\mu _{k}A_{jk}+\sum _{j<k}^{N}\mu _{j}\eta _{j}}\right) , \end{aligned}$$

(9)

$$\begin{aligned}&g=\sum _{\mu =0,1}\exp \left( {\sum _{j<k}^{(N)}\mu _{j}\mu _{k}A_{jk}+\sum _{j<k}^{N}\mu _{j}(\eta _{j}+\textrm{i}\Phi _{j}})\right) , \end{aligned}$$

(10)

where

$$\begin{aligned} \begin{aligned}&\eta _{j}=P_{j}x+Q_{j}y+\Omega _{j}t+\eta ^{0}_{j},\\&\quad \Omega _{j}=-\frac{\delta _{j}\sqrt{-\gamma ^{2}P^{2}_{j}Q^{2}_{j} +4\gamma P_{j}Q_{j}}(P^{2}_{j}-Q^{2}_{j})}{\gamma P_{j}Q_{j}}, \\&\quad \cos (\Phi _{j})=\frac{-\gamma P_{j}Q_{j}+2}{2}, \\&\quad \sin (\Phi _{j})=\delta _{j}\frac{\sqrt{-\gamma ^{2}P^{2}_{j}Q^{2}_{j}+4\gamma P_{j}Q_{j}}}{2},\\&\quad \delta _{j}=\pm 1,\\&\quad e^{A_{jk}}=-\frac{2\cos (\Phi _{j}-\Phi _{k})+\gamma (P_{j}-P_{k})(Q_{j}-Q_{k})-2}{2\cos (\Phi _{j}+\Phi _{k}) +\gamma (P_{j}+P_{k})(Q_{j}+Q_{k})-2}. \end{aligned} \end{aligned}$$

(11)

Here, j, k, N are arbitrary positive integers, $P_{j},Q_{j}$ are arbitrary real parameters, and $\eta ^{0}_{j}$ is a complex constant. The notation $\sum _{\mu =0,1}$ indicates summation over all possible combinations of $\mu _{1}=0,1,\mu _{2}=0,1,\cdot \cdot \cdot ,\mu _{N}=0,1,$ and $\sum _{j<k}^{(N)}$ summation is over all possible combinations of the N elements with the suitable parametric condition $j<k$.

2.2 Rational solutions of the DS III equation

In Ref. [48], rational solutions were constructed by applying differential operators to the parameters of Gram determinant solutions. Here, to construct rational solutions of the DS III Equation (4) from the obtained N-soliton solutions (9), (10), we take long wave limits on f and g. To this end, we set parameter constrains

$$\begin{aligned} Q_{j}=\lambda _{j}P_{j},\qquad \eta ^{0}_{j}=\textrm{i}\pi \quad (1\le j\le N), \end{aligned}$$

with $\lambda _j \in \mathbb {R}$ and take the limits $P_{j}\rightarrow 0$. Under the circumstance, f and g tend to polynomials that lead to rational solutions of the DS III equation.

Theorem 1

The DS III Equation (4) admits the Nth-order rational solutions

$$\begin{aligned} q=\frac{g_{N}}{f_{N}},\quad U=-\gamma (\ln f_{N})_{xx},\quad V=-\gamma (\ln f_{N})_{yy}, \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} f_{N}=&\prod _{j=1}^{N}\theta _{j}+\frac{1}{2}\sum _{j,k}^{(N)}a_{jk}\prod _{l\ne j,k}^{N}\theta _{l}+\cdot \cdot \cdot \\&+\frac{1}{M!2^{M}}\sum _{j,k,\cdots ,m,n}^{(N)}\overbrace{a_{jk}a_{sl} \cdot \cdot \cdot a_{mn}}^{M}\\&\prod _{p\ne j,k,\cdot \cdot \cdot ,m,n}^{N}\theta _{p}+\cdot \cdot \cdot ,\\ g_{N}=&\prod _{j=1}^{N}(\theta _{j}+b_{j})+\frac{1}{2}\sum _{j,k}^{(N)}a_{jk}\prod _{l\ne j,k}^{N}(\theta _{l}+b_{l})+\cdot \cdot \cdot \\&+\frac{1}{M!2^{M}}\sum _{j,k,\cdots ,m,n}^{(N)}\overbrace{a_{jk}a_{sl}\cdot \cdot \cdot a_{mn}}^{M}\\&\prod _{p\ne j,k,\cdots ,m,n}^{N}(\theta _{p}+b_{p})+\cdots , \end{aligned} \end{aligned}$$

(13)

and

$$\begin{aligned} \begin{aligned}&\theta _{j}=x+\lambda _{j}y+\frac{2\delta _{j}(-\lambda ^{2}_{j}+1)}{\sqrt{\gamma \lambda _{j}}}t,\\&b_{j}=-\textrm{i}\delta _{j}\sqrt{\gamma \lambda _{j}},\\&a_{jk}=\frac{-\lambda _{j}\lambda _{k}}{2\delta _{j}\sqrt{\lambda _{j}}\sqrt{\lambda _{k}} +(\lambda _{j}+\lambda _{k})}, \quad \delta _{j}=\pm 1. \end{aligned} \end{aligned}$$

(14)

Here $\sum _{j,k,\cdots ,m,n}^{(N)}$ stands for the summation over all the possible combinations of j, k, ..., m, n that are taken from 1, 2, ..., N and all different. The first four sets of functions f and g in (13) are expressed as

$$\begin{aligned} \begin{aligned} f_{1}=\,&\theta _{1},\\ f_{2}=\,&\theta _{1}\theta _{2}+a_{12},\\ f_{3}=\,&\theta _{1}\theta _{2}\theta _{3}+a_{12}\theta _{3}+a_{13}\theta _{2}+a_{23}\theta _{1},\\ f_{4}=\,&\theta _{1}\theta _{2}\theta _{3}\theta _{4}+a_{12}\theta _{3}\theta _{4}+a_{13}\theta _{2}\theta _{4}\\&+a_{14}\theta _{2}\theta _{3}+a_{23}\theta _{1}\theta _{4}+a_{24}\theta _{1}\theta _{3}\\&+a_{34}\theta _{1}\theta _{2}+a_{12}a_{34}+a_{13}a_{24}+a_{14}a_{23},\\ g_{1}=\,&\theta _{1}+b_{1},\\ g_{2}=\,&(\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12},\\ g_{3}=\,&(\theta _{1}+b_{1})(\theta _{2}+b_{2})(\theta _{3}+b_{3})\\&+a_{12}(\theta _{3}+b_{3})+a_{13}(\theta _{2}+b_{2})+a_{23}(\theta _{1}+b_{1}),\\ g_{4}=\,&(\theta _{1}+b_{1})(\theta _{2}+b_{2})(\theta _{3}+b_{3})(\theta _{4}+b_{4})\\&+a_{12}(\theta _{3}+b_{3})(\theta _{4}+b_{4})+a_{13}(\theta _{2}+b_{2})(\theta _{4}\\&+b_{4})+a_{14}(\theta _{2}+b_{2})(\theta _{3}+b_{3})\\&+a_{23}(\theta _{1}+b_{1})(\theta _{4}\\&+b_{4})+a_{24}(\theta _{1}+b_{1})(\theta _{3}+b_{3})\\&+a_{34}(\theta _{1}+b_{1})(\theta _{2}+b_{2}) \\&+a_{12}a_{34}+a_{13}a_{24}+a_{14}a_{23}. \end{aligned} \end{aligned}$$

(15)

Similar results have been given in Ref. [19] and one can refer to it therein for the detailed proof.

Remark 1

We can obtain lump solutions of the DS III equation with parameters

$$\begin{aligned}&N=2n,\quad \lambda _{n+j}=\lambda _{j},\nonumber \\&\quad \sin (\Phi _{n+j})=-\sin (\Phi _{j}),\quad j=1,2,\cdot \cdot \cdot ,n. \end{aligned}$$

(16)

In the following, based on the expressions of f and g in the above theorem, we construct explicit rational solutions of the DS III equation. Without loss of generality, we put $\gamma =1$ in the following discussion. The explicit expressions of solutions with some different N values are given in Appendix.

2.2.1 $N=1$ case

Firstly, we consider the simple case $N=1$. The rational solution is expressed as

$$\begin{aligned} q&=\frac{x+\lambda _1 y+\frac{2(-\lambda ^{2}_1+1)t}{\sqrt{\lambda _1}}-\textrm{i} \sqrt{\lambda _1}}{x+\lambda _1 y+\frac{2(-\lambda ^{2}_1+1)t}{\sqrt{\lambda _1}}}, \end{aligned}$$

(17)

$$\begin{aligned} U&=-\frac{1}{\Big (x+\lambda _1 y+\frac{2(-\lambda ^{2}_1+1)t}{\sqrt{\lambda _1}}\Big )^{2}}, \end{aligned}$$

(18)

$$\begin{aligned} V&=-\frac{\lambda ^{2}_1}{\Big (x+\lambda _1 y-\frac{2(-\lambda ^{2}_1+1)t}{\sqrt{\lambda _1}}\Big )^{2}}. \end{aligned}$$

(19)

We find that these rational solutions are singular along the line $x+\lambda _1 y=0$ at $t=0$. Furthermore, for $t\ne 0$, we take $\lambda _1=-\alpha _1$. In this case, q has two critical lines,

$$\begin{aligned}&L_{1}: x=\alpha _1 y+\frac{\alpha ^{2}_1-\Delta }{2\alpha ^{\frac{3}{2}}_1}, \end{aligned}$$

(20)

$$\begin{aligned}&L_{2}: x=\alpha _1 y+\frac{\alpha ^{2}_1+\Delta }{2\alpha ^{\frac{3}{2}}_1}, \end{aligned}$$

(21)

and the maximum and minimum amplitude of |q| are given by

$$\begin{aligned}{} & {} |q|_\mathrm{{max}}=|q|_{L_{1}}\nonumber \\{} & {} \quad =\left| {\frac{(-\textrm{i}\alpha ^{2}_1+4\alpha ^{3}_1t-4\alpha _1 t+\textrm{i}\Delta )(-\textrm{i}\alpha ^{2}_1-4\alpha ^{3}_1t+4\alpha _1t+\textrm{i}\Delta )}{(4\alpha ^{3}_1t+\textrm{i}\alpha ^{2}_1-4\alpha _1 t+\textrm{i}\Delta )(-4\alpha ^{3}_1t+\textrm{i}\alpha ^{2}_1+4\alpha _1 t+\textrm{i}\Delta )}}\right| ,\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}{} & {} |q|_\mathrm{{min}}=|q|_{L_{2}}=\frac{1}{|q|_\mathrm{{max}}}. \end{aligned}$$

(23)

Besides, the distance d between two lines $L_{1}$ and $L_{2}$ is

$$\begin{aligned} d=\frac{\Delta }{\alpha _1^{\frac{3}{2}}\sqrt{1+\alpha ^{2}_1}}, \end{aligned}$$

(24)

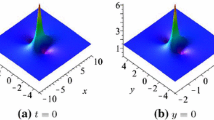
with $\Delta =\sqrt{16\alpha ^{6}_1t^{2}-32\alpha ^{4}_1t^{2}+\alpha ^{4}_1+16\alpha ^{2}_1t^{2}}$. When $\alpha _1=2$, the corresponding profiles of $|q|_\mathrm{{max}}$, $|q|_\mathrm{{min}}$ and d along t are shown in Fig. 1. As seen in the above analysis, $|q|_\mathrm{{max}}\rightarrow |q|_\mathrm{{min}}$ and $d\rightarrow \infty$ as $t\rightarrow \infty$, which means the solution approaches a constant when the time goes to infinity. Thus, it is proper to call the kink-shaped line wave a rogue wave. Although this wave blows up when $t=0$, we still regard it to be a rogue wave. This kink-shaped rogue wave has been discovered firstly in [58]. It is a rare phenomenon that does not exist even in many usual (2+1)-dimensional systems such as local DSI and KPI. It might be a special phenomenon in the nonlocal DS III equation.

With the corresponding profile as kink-shaped line rogue, see Fig. 2. It is also of great significance to make a comparison between the kink-shaped line rogue wave and the W-shaped line rogue wave. Firstly, though that the kink-shaped line rogue wave arises from a constant background, the height of the two sides of the main amplitude is different while the W-shaped line rogue wave only has one asymptotic plane. Secondly, the W-shaped line rogue wave means it possesses one maximum amplitude and two minimal ones. However, the kinked-shaped soliton only has two critical lines, a maximum amplitude and a minimal one. Finally, the kink-shaped line rogue wave blows up at finite time when $t=0$ while the amplitude of the W-shaped line rogue wave always keeps finite.

Fig. 1

a $|q|_{max}$ (blue line) and $|q|_{min}$ (red line) along t. b L . (Color figure online)

Fig. 2

The time evolution of the kink-shaped line rogue q given by (17) in the (x, y)-plane

2.2.2 $N=2$ case

To demonstrate the typical dynamics of these rational solutions, we consider the first-order lump solution associated with $N=2$. We set parametric conditions

$$\begin{aligned}&N=2,\quad Q_{1}=\lambda _{1}P_{1}, \nonumber \\&Q_{2}=\lambda _{2}P_{2},\ \lambda _{2}=\lambda _{1}=\lambda \ne 0, \end{aligned}$$

(25)

and take the limits $P_{j}\rightarrow 0,(j=1,2)$. In this case, we have $\sin \Phi _1=-\sin \Phi _2, \Omega _1=-\Omega _2$ and

$$\begin{aligned}&\theta _{1}=x+\lambda y+\frac{2(-\lambda ^{2}+1)}{\sqrt{\lambda }}t,\nonumber \\&\theta _{2}=x+\lambda y-\frac{2(-\lambda ^{2}+1)}{\sqrt{\lambda }}t, \end{aligned}$$

(26)

$$\begin{aligned}&b_{1}=-\textrm{i}\sqrt{\lambda },\quad b_{2}=\textrm{i}\sqrt{\lambda },\quad a_{12}=-\frac{\lambda }{4}. \end{aligned}$$

(27)

The explicit first-order lump solution is expressed by

$$\begin{aligned}&q=\frac{g_{2}}{f_{2}}\nonumber \\&\quad =\frac{(x+\lambda y)^{2}-\Big (\frac{2(-\lambda ^{2}+1)t}{\sqrt{\lambda }} +\textrm{i}\sqrt{\lambda }\Big )^{2}-\frac{1}{4}\lambda }{(x+\lambda y)^{2}-\Big (\frac{2(-\lambda ^{2}+1)t}{\sqrt{\lambda }}\Big )^{2}-\frac{1}{4}\lambda }, \end{aligned}$$

(28)

$$\begin{aligned}&U =-(\ln f_{2})_{xx}\nonumber \\&\quad =\frac{2(x+\lambda y)^{2}-2\Big (\frac{2(-\lambda ^{2}+1)t}{\sqrt{\lambda }}\Big )^{2}+\frac{\lambda }{2}}{\left( (x+\lambda y)^{2}-\Big (\frac{2(-\lambda ^{2}+1)t}{\sqrt{\lambda }}\Big )^{2}-\frac{1}{4}\lambda \right) ^{2}}, \end{aligned}$$

(29)

$$\begin{aligned}&V=-(\ln f_{2})_{yy} \nonumber \\&\quad =\frac{2\lambda ^{2}(x+\lambda y)^{2}-2\lambda ^{2}\Big (\frac{(-\lambda ^{2}+1)t}{\sqrt{\lambda }}\Big )^{2} +\frac{\lambda ^{3}}{2}}{\left( (x+\lambda y)^{2}-\Big (\frac{2(-\lambda ^{2}+1)t}{\sqrt{\lambda }}\Big )^{2}-\frac{1}{4}\lambda \right) ^{2}}. \end{aligned}$$

(30)

One can verify that the rational solution (28) is nonsingular when $\lambda <0$. In particular, we take $\lambda =-2$. At $y=0$, the corresponding profile of |q| and its density plot are depicted in (x, t)-plane (see Fig. 3) that demonstrates to be a fundamental lump.

Fig. 3

One-lump solution q of the DS III equation defined by (28) in the (x, t)-plane with $N=2, \lambda =-2$

Fig. 4

The line rogue wave solution q of the DS III equation given by (28) in the (x, y)-plane with parameters $N=2, \lambda =-2$

With the same parameters as those for Fig. 3, the rational solution (28) demonstrates to be a line rogue wave in (x, y)-plane. The profile of the line rogue wave is displayed in Fig. 4. When $t\rightarrow \pm \infty$, the line rogue wave q uniformly degenerates to a constant background in (x, y)-plane. The amplitude of the line rogue wave varies, and attains the maximum value along the line $x+\lambda y=0$ at $t=0$.

2.2.3 $N=4$ case

Furthermore, we consider higher-order rational solutions. We choose parameters

$$\begin{aligned} N=4,\quad Q_{j}=\lambda _{j}P_{j},\quad \lambda _{j}\ne 0,\quad (j=1,2,3), \end{aligned}$$

(31)

and take the limit of $P_{j}\rightarrow 0,(j=1,2)$. The higher-order rational solution of the DS III equation is given by

Fig. 5

Higher-order lump solution q of the DS III equation defined by (32) in the (x, t)-plane with $N=4, \lambda _{1}=\lambda _{3}=-\frac{2}{3},\lambda _{2}=\lambda _{4}=-2$

$$\begin{aligned}&q=\frac{g_{4}}{f_{4}},\quad U=-(\ln f_{4})_{xx},\quad V=-(\ln f_{4})_{yy}, \end{aligned}$$

(32)

where $f_{4}$ and $g_{4}$ are presented in (15) with

$$\begin{aligned}{} & {} \theta _{1}=x+\lambda _{1}y+\frac{2(-\lambda ^{2}_{1}+1)}{\sqrt{\lambda _{1}}}t,\\{} & {} \theta _{2}=x+\lambda _{2}y+\frac{2(-\lambda ^{2}_{2}+1)}{\sqrt{\lambda _{2}}}t,\\{} & {} \theta _{3}=x+\lambda _{3}y-\frac{2(-\lambda ^{2}_{3}+1)}{\sqrt{\lambda _{3}}}t,\\{} & {} \theta _{4}=x+\lambda _{4}y-\frac{2(-\lambda ^{2}_{4}+1)}{\sqrt{\lambda _{4}}}t,\\{} & {} a_{12}=\frac{\lambda _{1}\lambda _{2}}{2\sqrt{\lambda _{1}}\sqrt{\lambda _{2}}-(\lambda _{1}+\lambda _{2})},\\{} & {} a_{13}=\frac{-\lambda _{1}\lambda _{3}}{2\sqrt{\lambda _{1}}\sqrt{\lambda _{3}}+(\lambda _{1}+\lambda _{3})},\\{} & {} a_{14}=\frac{-\lambda _{1}\lambda _{4}}{2\sqrt{\lambda _{1}}\sqrt{\lambda _{4}}+(\lambda _{1}+\lambda _{4})},\\{} & {} a_{23}=\frac{-\lambda _{2}\lambda _{3}}{2\sqrt{\lambda _{2}}\sqrt{\lambda _{3}}+(\lambda _{2}+\lambda _{3})},\\{} & {} a_{24}=\frac{-\lambda _{2}\lambda _{4}}{2\sqrt{\lambda _{2}}\sqrt{\lambda _{4}}+(\lambda _{2}+\lambda _{4})},\\{} & {} a_{34}=\frac{\lambda _{3}\lambda _{4}}{2\sqrt{\lambda _{3}}\sqrt{\lambda _{4}}-(\lambda _{3}+\lambda _{4})},\\{} & {} b_{1}=-\textrm{i}\sqrt{\lambda _{1}},\quad b_{2}=-\textrm{i}\sqrt{\lambda _{2}},\\{} & {} b_{3}=\textrm{i}\sqrt{\lambda _{3}},\quad b_{4}=\textrm{i}\sqrt{\lambda _{4}}. \end{aligned}$$

Under the constrain $\lambda _{1}=\lambda _{3}$ and $\lambda _{2}=\lambda _{4}$ the rational solution (32) describes the interaction between two lumps in (x, t)-plane. In particular, when $\lambda _{1}=-\frac{2}{3},\lambda _{2}=-2$, the evolution of q with different y values is displayed in Fig. 5. It displays the interaction between two fundamental lumps. Apparently, the lump with higher amplitude travels faster than the lower one. The higher lump catches the lower one and they inosculate as a whole. The superposition amplitude of these two lumps is lower than each original one. After the collision, the two lumps separate from each other and move on.

With the same parameters as in Fig. 5, the corresponding solution q describes the second-order line rogue wave in (x, y)-plane. The profiles of the line rogue wave at different t values are shown in Fig. 6. One can find that the line rogue wave appears from the plane background and disappears into the constant background. When $t=0$, the profile displays the elastic collision of two solitons. As t grows, the line wave attains higher amplitudes and finally disappears into a constant background as $t\rightarrow \infty$.

Fig. 6

Higher-order rational solution q of the DS III equation defined by (32) in the (x, y)-plane with $N=4, \lambda _{1}=\lambda _{3}=-\frac{2}{3},\lambda _{2}=\lambda _{4}=-2$

2.3 Semi-rational solutions of the DS III equation

In this part, we consider several types of the semi-rational solutions to the DS III equation. To this end, we take long wave limits in a part of exponential functions f, g in (9), (10) and other exponential functions keep no change. In this case, we find the hybrid of rational and exponential function solutions, which describes interactions between the lump, soliton and line rogue wave.

2.3.1 $N=3$ case

Firstly, we construct semi-rational solutions based on the third-order soliton. We choose parameters

$$\begin{aligned} N=3,\quad Q_{1}=\lambda _{1}P_{1},\quad Q_{2}=\lambda _{2}P_{2},\quad \eta ^{0}_{1}=\eta ^{0}_{2}=\textrm{i}\pi , \end{aligned}$$

(33)

and take the limit of $P_{j}\rightarrow 0,(j=1,2)$. The semi-rational solution of the DS III equation is given by

$$\begin{aligned}&q=\frac{g}{f},\quad U=-(\ln f)_{xx},\quad V=-(\ln f)_{yy}, \end{aligned}$$

(34)

where f and g are presented as

$$\begin{aligned} f=\,&(\theta _{1}\theta _{2}+a_{12})\nonumber \\&\quad +\Big (\theta _{1}\theta _{2}+a_{12}\nonumber \\&+a_{13}\theta _{2}+a_{23}\theta _{1}+a_{13}a_{23}\Big )e^{\eta _{3}}, \end{aligned}$$

(35)

$$\begin{aligned} g=\,&\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}\Big )\nonumber \\&\quad +\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}+a_{13}(\theta _{2}+b_{2}) \nonumber \\&\quad +a_{23}(\theta _{1}+b_{1})+a_{13}a_{23}\Big )e^{\eta _{3}+\textrm{i}\Phi _{3}}, \end{aligned}$$

(36)

where

$$\begin{aligned} a_{13}=\frac{-P_{3}Q_{3}\lambda }{\sqrt{\lambda }\sqrt{-P^{2}_{3}Q^{2}_{3}+4P_{3}Q_{3}}+(\lambda P_{3}+Q_{3})},\\ a_{23}=\frac{P_{3}Q_{3}\lambda }{\sqrt{\lambda }\sqrt{-P^{2}_{3}Q^{2}_{3}+4P_{3}Q_{3}}-(\lambda P_{3}+Q_{3})}, \end{aligned}$$

and $a_{12},b_{1},b_2,\theta _1,\theta _2, \Phi _{3},\eta _{3}$ are given by (11) and (14). Furthermore, we take $P_{3}=1,Q_{3}=2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=-2\pi$. With these parameters, we get the semi-rational solution composed of a dark soliton and a lump and the plot is shown in (x, t)-plane (see Fig. 7). From the plot, we find that the lump travels from one side of the dark soliton to the other side and they immerse into each other when $y=3$. One can find that the amplitude of the lump becomes lower during the interaction.

We take the same parameters as Fig. 7 and consider dynamics of the semi-rational |q| in (x, y)-plane. We find that a line rogue wave is generated on the dark-soliton background (see Fig. 8). The line wave grows from the dark-soliton background and finally decays into the same background. We note that the amplitudes of the line wave in both sides of the dark soliton are different.

Fig. 7

Rational solutions q of the DS III equation given by (34) in the (x, t)-plane with parameters $N=3, P_{3}=1,Q_{3}=2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=-2\pi$

Fig. 8

Rational solutions q of the DS III equation given by (34) in the (x, y)-plane with parameters $N=3, P_{3}=1,Q_{3}=2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=-2\pi$

2.3.2 $N=4$ case

To derive higher-order semi-rational solutions, we set

$$\begin{aligned}&N=4,\quad Q_{1}=\lambda _{1}P_{1},\quad Q_{2}=\lambda _{2}P_{2},\nonumber \\&\eta ^{0}_{1}=\eta ^{0}_{2}=\textrm{i}\pi ,\quad \eta ^{0}_{3}=\eta ^{0}_{4}. \end{aligned}$$

(37)

Taking the limits $P_{j}\rightarrow 0, (j=1,2)$ leads to the higher-order semi-rational solution of the DS III equation

$$\begin{aligned}&q=\frac{g}{f},\quad U=-(\ln f)_{xx},\quad V=-(\ln f)_{yy}, \end{aligned}$$

(38)

where f and g are presented as

$$\begin{aligned} f=\,&(\theta _{1}\theta _{2}+a_{12})+\nonumber \\&\Big (\theta _{1}\theta _{2}+a_{12}+a_{13}\theta _{2}+a_{23}\theta _{1}+a_{13}a_{23}\Big )e^{\eta _{3}}\nonumber \\&+\Big (\theta _{1}\theta _{2}+a_{12}+a_{14}\theta _{2}+a_{24}\theta _{1}+a_{14}a_{24}\Big )e^{\eta _{4}}\nonumber \\&+\Big (\theta _{1}\theta _{2}+a_{12}+a_{13}\theta _{2}+a_{23}\theta _{1} \nonumber \\&+a_{14}\theta _{2}+a_{24}\theta _{1}+a_{13}a_{23}+a_{13}a_{24} \nonumber \\&+a_{14}a_{23}+a_{14}a_{24}\Big )e^{\eta _{3}+\eta _{4}}e^{A_{34}}, \end{aligned}$$

(39)

$$\begin{aligned} g=\,&\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}\Big )\nonumber \\&+\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}\nonumber \\&+a_{13}(\theta _{2}+b_{2})+a_{23}(\theta _{1}+b_{1})+a_{13}a_{23}\Big )e^{\eta _{3}+\textrm{i}\Phi _{3}}\nonumber \\&+\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}+a_{14}(\theta _{2}+b_{2})\nonumber \\&+a_{24}(\theta _{1}+b_{1})+a_{14}a_{24}\Big )e^{\eta _{4}+\textrm{i}\Phi _{4}}\nonumber \\&+\Big ((\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}+a_{13}(\theta _{2}+b_{2})\nonumber \\&+a_{23}(\theta _{1}+b_{1})+a_{14}(\theta _{2}+b_{2})+a_{24}(\theta _{1}+b_{1})\nonumber \\&+a_{13}a_{23}+a_{13}a_{24}+a_{14}a_{23}\nonumber \\&+a_{14}a_{24}\Big )e^{\eta _{3}+\textrm{i}\Phi _{3}+\eta _{4}+\textrm{i}\Phi _{4}}e^{A_{34}}, \end{aligned}$$

(40)

where $a_{jk}=\frac{\delta _{j}P_{k}Q_{k}\lambda }{\sqrt{\lambda }\sqrt{-P^{2}_{k}Q^{2}_{k}+4P_{k}Q_{k}}+(\lambda P_{k}+Q_{k})}$, and $\theta _{j},a_{12},b_{j},\Phi _{j},\eta _{j},A_{34}$ are given by (11) and (14). We put $P_{3}=-P_{4}=1,Q_{3}=-Q_{4}=2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=\eta ^{0}_{4}=-\frac{\pi }{2}$. The solution describes the evolution of one lump on the background of a dark two-soliton in (x, t)-plane, (see Fig. 9). When $y=0$, the soliton and lump collide with each other and the amplitude of the lump becomes lower. The lump and soliton recover their origin amplitudes after the collision.

The interactions between the line rogue wave and dark two-soliton in (x, y)-plane are displayed in Fig. 10 with the same parameters in Fig. 9. The line rogue wave appears from the two parallel solitons background. It is interesting to find that the amplitude of the line rogue wave grows first to the maximum value. Then, the line rogue wave decays and finally disappears without a trace.

Fig. 9

Semi-rational solutions q of the DS III equation defined by (38) in the (x, t)-plane with parameters $N=4, P_{3}=1,P_{4}=-1,Q_{3}=2,Q_{4}=-2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=\eta ^{0}_{4}=-\frac{\pi }{2}$

Fig. 10

Semi-rational solutions q of the DS III equation defined by (38) in the (x, y)-plane with parameters $N=4, P_{3}=1,P_{4}=-1,Q_{3}=2,Q_{4}=-2,\lambda =-\frac{1}{2},\eta ^{0}_{3}=\eta ^{0}_{4}=-\frac{\pi }{2}$

3 Solutions of the nonlocal DS III equation

In this part, we consider solutions of the nonlocal DS III Equation (5) and their dynamic behaviors. By the variable transformation

$$\begin{aligned} q=\frac{\tilde{g}}{\tilde{f}},\quad U=-\gamma (\ln \tilde{f})_{xx},\quad V=-\gamma (\ln \tilde{f})_{yy}, \end{aligned}$$

(41)

the nonlocal DS III Equation (5) is transformed into the bilinear equation

$$\begin{aligned} \left\{ \begin{aligned}&(\textrm{i}D_{t}-D^{2}_{x}+D^{2}_{y})\tilde{g}\cdot \tilde{f}=0, \\&(\gamma D_{x}D_{y}-2)\tilde{f}\cdot \tilde{f}=-2\tilde{g}\tilde{g}^{*}(-x,-y,t),\\ \end{aligned} \right. \end{aligned}$$

(42)

where $\gamma =\pm 1$, $\tilde{f}$ is real and $\tilde{g}$ is complex with respect to x, y, t. It is required that the function $\tilde{g}$ satisfies the condition

$$\begin{aligned}{}[\tilde{g}(-x,-y,t)]^{*}=\tilde{g}(x,y,t). \end{aligned}$$

Similar to the local case, in the following, we investigate soliton solutions, rational and semi-rational solutions of the nonlocal DS III Equation (5) by taking the long wave limit technique. The explicit expressions of solutions for the nonlocal DS III Equation (5) with different N values are given in Appendix.

3.1 Soliton, breather solutions of the nonlocal DS III equation

Using the Hirota’s bilinear method, we can obtain the Nth-order soliton solution of the nonlocal DS III equation, and $\tilde{f}$ and $\tilde{g}$ admit the expression

$$\begin{aligned}&\tilde{f}=\sum _{\mu =0,1}\exp \Big (\sum _{j<k}^{(N)}\mu _{j}\mu _{k}\tilde{A}_{jk}+\sum _{j<k}^{N}\mu _{j}\tilde{\eta }_{j}\Big ), \end{aligned}$$

(43)

$$\begin{aligned}&\tilde{g}=\sum _{\mu =0,1}\exp \Big (\sum _{j<k}^{(N)}\mu _{j}\mu _{k}\tilde{A}_{jk}+\sum _{j<k}^{N} \mu _{j}(\tilde{\eta }_{j}+\textrm{i}\tilde{\Phi }_{j})\Big ), \end{aligned}$$

(44)

where

$$\begin{aligned} \begin{aligned}&\tilde{\Omega }_{j}=-\frac{\delta _{j}\sqrt{-\gamma ^{2}P^{2}_{j}Q^{2}_{j}-4\gamma P_{j}Q_{j}}(P^{2}_{j}-Q^{2}_{j})}{\gamma P_{j}Q_{j}},\\&\tilde{\eta }_{j}=\textrm{i}P_{j}x+\textrm{i}Q_{j}y+\tilde{\Omega }_{j}t+\eta ^{0}_{j},\\&\cos (\tilde{\Phi }_{j})=\frac{\gamma P_{j}Q_{j}+2}{2}, \\&\sin (\tilde{\Phi }_{j})=\delta _{j}\frac{\sqrt{-\gamma ^{2}P^{2}_{j}Q^{2}_{j}-4\gamma P_{j}Q_{j}}}{2},\\&e^{\tilde{A}_{jk}}=-\frac{2\cos (\tilde{\Phi }_{j}-\tilde{\Phi }_{k})-\gamma (P_{j}-P_{k})(Q_{j}-Q_{k})-2}{2\cos (\tilde{\Phi }_{j}+\tilde{\Phi }_{k})-\gamma (P_{j}+P_{k})(Q_{j}+Q_{k})-2}, \\&\gamma =\pm 1. \end{aligned} \end{aligned}$$

(45)

Here j, k, N are arbitrary positive integers, $P_{j},Q_{j}$ are arbitrary real parameters, and $\eta ^{0}_{j}$ is a complex constant. In the following, we suppose $\gamma =1$ without loss of generality. In order to guarantee that $\tilde{\Omega }_{j}$ is real, the parameters constraint $-P^{2}_{j}Q^{2}_{j}-4P_{j}Q_{j}>0$ must be hold. So we suppose $-4<P_{j}Q_{j}<0$.

Since $\tilde{\eta }_{j}$ is complex, we can build breather solutions from soliton solutions under proper constraints on parameters. We choose parameters in the Nth-order soliton solution (43), (44) as

$$\begin{aligned} N&=2n,\quad P_{n+j}=-P_{j}, \quad Q_{n+j}=-Q_{j},\nonumber \\&\quad \eta ^{0}_{n+j}=\eta ^{0}_{j}, \end{aligned}$$

(46)

to generate Nth-order breather solutions. With $N=2$ and parameters

$$\begin{aligned}&N=2,\quad P_{2}=-P_{1}=P, \quad Q_{2}=-Q_{1}=Q,\nonumber \\&\eta ^{0}_{2}=\eta ^{0}_{1}=\eta ^{0}, \end{aligned}$$

(47)

we get first-order breather solution

$$\begin{aligned} q=\frac{g}{f},\quad U=-(\ln f)_{xx},\quad V=-(\ln f)_{yy}, \end{aligned}$$

(48)

where

$$\begin{aligned} f&=\sqrt{M}\cosh \Theta +\cos (Px+Qy), \end{aligned}$$

(49)

$$\begin{aligned} g&=\sqrt{M}\Big (\cos ^{2}\phi \cosh \Theta +\sin ^{2}\phi \sinh \Theta \nonumber \\&\quad +\textrm{i}\cosh \sin (\cosh \Theta -\sinh \Theta )\Big )\nonumber \\&\quad +\cos (Px+Qy)(\cos \phi +\textrm{i}\sin \phi ), \end{aligned}$$

(50)

and

$$\begin{aligned}&M=1-\frac{PQ}{PQ+4},\quad e^{\eta _{0}}=\sqrt{M}e^{\eta ^{0}},\end{aligned}$$

(51)

$$\begin{aligned}&e^{\textrm{i}\phi }=\frac{PQ+1}{2}+\textrm{i}\frac{\sqrt{-P^{2}Q^{2}-4PQ}}{2},\end{aligned}$$

(52)

$$\begin{aligned}&\Theta =-(\tilde{\Omega } t+\eta _{0}),\quad \tilde{\Omega }=-\frac{\sqrt{-P^{2}Q^{2}-4PQ}(P^{2}-Q^{2})}{PQ}. \end{aligned}$$

(53)

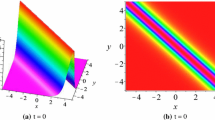
In particular, we take $P=\frac{2}{3},Q=-1,\eta ^{0}=0$ and obtain a typical first-order breather solution in (x, t)-plane. The breather and its density are shown in Fig. 11. The period of the breather |q| is $\frac{2\pi }{P}$ along the x direction on (x, t)-plane.

If we fix t, we get one line breather solution in (x, y)-plane. As shown in Fig. 12, the periodic line waves appear from a flat background and finally disappear into the background. The line rogue wave solution admits a set of parallel propagation with varying heights.

Fig. 11

First-order breather solution q of the nonlocal DS III equation defined by (48) in the (x, t)-plane with parameters $N=2, P_{1}=-P_{2}=\frac{2}{3},Q_{1}=Q_{2}=-1$

Fig. 12

Line breather solutions q of the nonlocal DS III equation defined by (48) in the (x, y)-plane with parameters $N=2, P_{1}=-P_{2}=\frac{2}{3},Q_{1}=Q_{2}=-1$

3.2 Rational solutions of the nonlocal DS III equation

In this subsection, we use a long wave limits method on exponential form solutions $\tilde{f}$ and $\tilde{g}$ to generate rational solutions of the nonlocal DS III equation. By setting

$$\begin{aligned} Q_{j}=\lambda _{j}P_{j},\quad \eta ^{0}_{j}=\textrm{i}\pi ,(1\le j\le N), \end{aligned}$$

and taking the limit $P_{j}\rightarrow 0$, we transform $\tilde{f}$ and $\tilde{g}$ into rational functions.

Theorem 2

The nonlocal DS III Equation (5) admits Nth-order rational solutions

$$\begin{aligned} q&=\frac{\tilde{g}_{N}}{\tilde{f}_{N}},\quad U=-\gamma (\ln \tilde{f}_{N})_{xx},\nonumber \\&\quad V=-\gamma (\ln \tilde{f}_{N})_{yy}, \end{aligned}$$

(54)

where

$$\begin{aligned} \begin{aligned}&\tilde{f}_{N}=\prod _{j=1}^{N}\tilde{\theta }_{j}+\frac{1}{2}\sum _{j,k}^{(N)}\tilde{a}_{jk}\\&\quad \prod _{l\ne j,k}^{N}\tilde{\theta }_{l}+\cdot \cdot \cdot +\frac{1}{M!2^{M}}\\&\quad \sum _{j,k\cdot \cdot \cdot ,m,n}^{(N)}\overbrace{\tilde{a}_{jk}\tilde{a}_{sl}\cdot \cdot \cdot \tilde{a}_{mn}}^{M}\prod _{p\ne j,k,\cdot \cdot \cdot ,m,n}^{N}\tilde{\theta }_{p}+\cdot \cdot \cdot ,\\&\tilde{g}_{N}=\prod _{j=1}^{N}(\tilde{\theta }_{j}+\tilde{b}_{j})\\&\quad +\frac{1}{2}\sum _{j,k}^{(N)}\tilde{a}_{jk}\prod _{l\ne j,k}^{N}(\tilde{\theta }_{l}+\tilde{b}_{l})+\cdot \cdot \cdot +\frac{1}{M!2^{M}}\\&\quad \sum _{j,k\cdot \cdot \cdot ,m,n}^{(N)}\overbrace{\tilde{a}_{jk}\tilde{a}_{sl}\cdot \cdot \cdot \tilde{a}_{mn}}^{M}\prod _{p\ne j,k,\cdot \cdot \cdot ,m,n}^{N}(\tilde{\theta }_{p}+\tilde{b}_{p})+\cdot \cdot \cdot , \end{aligned} \end{aligned}$$

(55)

with

$$\begin{aligned} \begin{aligned} \tilde{\theta }_{j}=&\textrm{i}x+\textrm{i}\lambda _{j}y\\&+\frac{\delta _{j}(-\lambda ^{2}+1)\sqrt{-4\lambda _{j}}}{\lambda _{j}}t,\\ \tilde{b}_{j}=&\frac{-\delta _{j}\lambda _{j}}{\textrm{i}\sqrt{-\lambda _{j}}},\\ \tilde{a}_{jk}=&\frac{\lambda _{j}\lambda _{k}}{-2\delta _{j}\sqrt{-\lambda _{j}}\sqrt{-\lambda _{k}}+(\lambda _{j}+\lambda _{k})},\quad \delta _{j}=\pm 1. \end{aligned} \end{aligned}$$

(56)

Remark 2

Here, the constraint $-4\lambda _{j}>0$ must be hold to make $\sqrt{-4\lambda _{j}}$ real. In order to guarantee solutions to be nonsingular, we take the parametric conditions $\lambda _j<0$ and define $\lambda _j=-\alpha _j,\alpha _j>0$. In the following, we focus on nonsingular rational solutions under these constraints.

Remark 3

When we apply the long wave limit technique to generate lump solutions from even order N, we obtain the same solution of the nonlocal DS III Equation (5) as that of the local DS III Equation (4) by choosing appropriate $\delta _j$ such that

$$\begin{aligned} \tilde{\theta }_j&=\textrm{i}(x+\lambda _jy)-\frac{2\textrm{i}(1-\lambda ^{2}_{j})}{\sqrt{\lambda _{j}}}t,\\ \theta _j&=x+\lambda _jy+\frac{2(1-\lambda ^{2}_{j})}{\sqrt{\lambda _{j}}}t,\\ \tilde{b}_j&=-\textrm{i}b_j,\quad \tilde{a}_{jk}=-a_{jk}. \end{aligned}$$

For $N=1$, we can derive the kink-shaped rogue wave solution (17)–(19) for the nonlocal DS III.

3.3 Semi-rational solutions of the nonlocal DS III equation

In this section, to clearly understand the dynamic behaviors of the nonlocal DS III equation, we consider several types of semi-rational solutions. Similarly, we take a long wave limit only in parts of exponential functions in $\tilde{f}$ and $\tilde{g}$ in (43), (44), and the other parts still keep the exponential form. In this case, we can generate lumps, breathers, solitons and the hybrid solutions. We find that the semi-rational solutions of the nonlocal DS III equation are different from those of the local DS III equation in the exponential parts. In particular, we will construct solutions on the periodic line wave background based on the imaginary exponential parts in the expression.

3.3.1 $N=3$ case

To construct semi-rational solutions from third-order soliton, we set parameters as the following, namely

$$\begin{aligned}&N=3,\quad Q_{1}=\lambda _{1}P_{1},\quad Q_{2}=\lambda _{2}P_{2},\nonumber \\&\quad \lambda _{1}=\lambda _{2}=\lambda \ne 0,\quad \eta ^{0}_{1}=\eta ^{0}_{2}=\textrm{i}\pi , \quad \Omega _{3}=0, \end{aligned}$$

(57)

and take the limit of $P_{j}\rightarrow 0,(j=1,2)$. The semi-rational solution of the nonlocal DS III equation is given by

$$\begin{aligned}&q=\frac{\tilde{g}}{\tilde{f}},\quad U=-(\ln \tilde{f})_{xx},\quad V=-(\ln \tilde{f})_{yy}, \end{aligned}$$

(58)

where $\tilde{f}$ and $\tilde{g}$ are presented as

$$\begin{aligned}&\tilde{f}=(\tilde{\theta }_{1}\tilde{\theta }_{2}+\tilde{a}_{12})\nonumber \\&\quad +(\tilde{\theta }_{1}\tilde{\theta }_{2}+\tilde{a}_{12}+\tilde{a}_{13}\tilde{\theta }_{2}+\tilde{a}_{23}\tilde{\theta }_{1}+\tilde{a}_{13}\tilde{a}_{23})e^{\eta _{3}}, \end{aligned}$$

(59)

$$\begin{aligned}&\tilde{g}=\Big ((\tilde{\theta }_{1}+\tilde{b}_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{12}\Big )\nonumber \\&\quad +\Big ((\tilde{\theta }_{1}+\tilde{b}_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{12}+\tilde{a}_{13}(\tilde{\theta }_{2}+\tilde{b}_{2})\nonumber \\&\quad +\tilde{a}_{23}(\tilde{\theta }_{1}+\tilde{b}_{1})+\tilde{a}_{13}\tilde{a}_{23}\Big )e^{\eta _{3}+\textrm{i}\tilde{\Phi }_{3}}. \end{aligned}$$

(60)

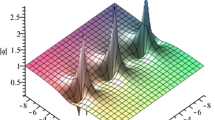
where $a_{13}=\frac{P_{3}Q_{3}\lambda }{-\sqrt{-\lambda }\sqrt{-P^{2}_{3}Q^{2}_{3}-4P_{3}Q_{3}}+(\lambda P_{3}+Q_{3})},a_{23}=\frac{P_{3}Q_{3}\lambda }{\sqrt{-\lambda }\sqrt{-P^{2}_{3}Q^{2}_{3}-4P_{3}Q_{3}}+(\lambda P_{3}+Q_{3})}$, and $a_{12}, b_{j}, \phi _{j},\eta _{3}$ are given in (45) and (56). Further, taking the parameters $P_{3}=-Q_{3}=\frac{1}{2},\lambda =-\frac{1}{2},\eta ^{0}_{3}=-\frac{\pi }{2}$, the corresponding semi-rational solution composed of a lump and periodic line waves are generated. In the (x, t)-plane, a lump on the background of the periodic line waves with period $\frac{2\pi }{P_3}$ is depicted in Fig. 13. Besides, the amplitude of the lump is larger than the fundamental lump, that is, it’s value is more than 3. In this case, the interaction between periodic and the lump can generate higher peaks.

With the corresponding semi-rational solution is a line rogue wave on the background of the periodic line wave in the (x, y)-plane, see Fig. 14. The line rogue wave grows from the periodic line background and decays into the periodic line background. Around $t=0$, the interaction between the line wave and the periodic line background generates a much higher line rogue wave, which can attain the maximum amplitude 8 (i.e., 8 times the background amplitude). Finally, the line wave disappears into the background consisted of the periodic line wave at $t\rightarrow \pm \infty$.

Fig. 13

Semi-rational solutions q of the nonlocal DS III equation given by (58) in the (x, t)-plane with parameters $N=3, P_{3}=-Q_{3}=\frac{1}{2},\lambda _{1}=-\frac{1}{2},\eta ^{0}_{3}=-\frac{\pi }{2}$

Fig. 14

Semi-rational solutions q of the nonlocal DS III equation given by (58) in the (x, y)-plane with parameters $N=3, P_{3}=-Q_{3}=\frac{1}{2},\lambda _{1}=-\frac{1}{2},\eta ^{0}_{3}=-\frac{\pi }{2}$

3.3.2 $N=4$ case

Higher-order semi-rational solutions consisting of one breather and one lump can also be obtained in the same way, taking

$$\begin{aligned}&N=4,\quad Q_{1}=\lambda _{1}P_{1},\quad Q_{2}=\lambda _{2}P_{2},\quad \eta ^{0}_{1}=\eta ^{0}_{2}=\textrm{i}\pi ,\nonumber \\&\quad \eta ^{0}_{3}=\eta ^{0}_{4}, \end{aligned}$$

(61)

and take the limit of $P_{j}\rightarrow 0(j=1,2)$, we obtain the higer-order semi-rational solutions of the nonlocal DS III

$$\begin{aligned}&q=\frac{\tilde{g}}{\tilde{f}},\quad U=-(\ln \tilde{f})_{xx},\quad V=-(\ln \tilde{f})_{yy}, \end{aligned}$$

(62)

where $\tilde{f}$ and $\tilde{g}$ are presented as

$$\begin{aligned} \tilde{f}&=(\tilde{\theta }_{1}\tilde{\theta }_{2}+\tilde{a}_{12})+(\tilde{\theta }_{1}\tilde{\theta }_{2}\nonumber \\&\quad +\tilde{a}_{12}+\tilde{a}_{13}\tilde{\theta }_{2}+\tilde{a}_{23}\tilde{\theta }_{1}\nonumber \\&\quad +\tilde{a}_{13}\tilde{a}_{23})e^{\eta _{3}}+(\tilde{\theta }_{1}\tilde{\theta }_{2}+\tilde{a}_{12}+\tilde{a}_{14}\tilde{\theta }_{2}\nonumber \\&\quad +\tilde{a}_{24}\tilde{\theta }_{1}+\tilde{a}_{14}\tilde{a}_{24})e^{\eta _{4}}\nonumber \\&\quad +\Big (\tilde{\theta }_{1}\tilde{\theta }_{2}+\tilde{a}_{12}+\tilde{a}_{13}\tilde{\theta }_{2} +\tilde{a}_{23}\tilde{\theta }_{1}+\tilde{a}_{14}\tilde{\theta }_{2}\nonumber \\&\quad +\tilde{a}_{24}\tilde{\theta }_{1} +\tilde{a}_{13}\tilde{a}_{23}\nonumber \\&\quad +\tilde{a}_{13}\tilde{a}_{24} +\tilde{a}_{14}\tilde{a}_{23}+\tilde{a}_{14}\tilde{a}_{24}\Big )e^{\eta _{3}+\eta _{4}}e^{\tilde{A}_{34}}, \end{aligned}$$

(63)

$$\begin{aligned} \tilde{g}&=\Big ((\tilde{\theta }_{1}+\tilde{b}_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{12}\Big )\nonumber \\&\quad +\Big ((\tilde{\theta }_{1}+b_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})\nonumber \\&\quad +\tilde{a}_{12}+\tilde{a}_{13}(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{23}(\tilde{\theta }_{1}\nonumber \\&\quad +\tilde{b}_{1})+\tilde{a}_{13}\tilde{a}_{23}\Big )e^{\eta _{3}+\textrm{i}\tilde{\Phi }_{3}}\nonumber \\&\quad +\Big ((\tilde{\theta }_{1}+\tilde{b}_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{12}\nonumber \\&\quad +\tilde{a}_{14}(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{24}(\tilde{\theta }_{1}+\tilde{b}_{1})+\tilde{a}_{14}\tilde{a}_{24}\Big )e^{\eta _{4}+\textrm{i}\Phi _{4}}\nonumber \\&\quad +\Big ((\tilde{\theta }{1}+\tilde{b}_{1})(\tilde{\theta }_{2}+\tilde{b}_{2})\nonumber \\&\quad +\tilde{a}_{12}+\tilde{a}_{13}(\tilde{\theta }_{2}+\tilde{b}_{2})\nonumber \\&\quad +\tilde{a}_{23}(\tilde{\theta }_{1}+\tilde{b}_{1})+\tilde{a}_{14}(\tilde{\theta }_{2}+\tilde{b}_{2})+\tilde{a}_{24}(\tilde{\theta }_{1}+\tilde{b}_{1})\nonumber \\&\quad +\tilde{a}_{13}\tilde{a}_{23}+\tilde{a}_{13}\tilde{a}_{24}+\tilde{a}_{14}\tilde{a}_{23}\nonumber \\&\quad +\tilde{a}_{14}\tilde{a}_{24}\Big )e^{\eta _{3}+\textrm{i}\tilde{\Phi }_{3}+\eta _{4}+\textrm{i}\tilde{\Phi }_{4}}e^{\tilde{A}_{34}}, \end{aligned}$$

(64)

where $a_{jk}=\frac{\delta _{j}P_{k}Q_{k}\lambda }{\sqrt{\lambda }\sqrt{-P^{2}_{k}Q^{2}_{k}-4P_{k}Q_{k}}+(\lambda P_{k}+Q_{k})}$, and $a_{12}, b_{j}, \phi _{j},\eta _{j},e^{A_{34}}$ are given by (45) and (56). In particular, taking the parameters $P_{3}=-P_{4}=\frac{2}{3},Q_{3}=-Q_{4}=-1,\lambda =-\frac{1}{2}$, the corresponding semi-rational solution of the nonlocal DS III equation is hybrid solution of breather and lump in the (x, t)-plane. Further, we take $\eta ^{0}_{3}=\eta ^{0}_{4}=\eta$, and find that the distance between breather and lump alters with $|\eta |$. As can be seen in Fig. 15, when $|\eta |\rightarrow 0$, the distance between the breather and the lump turn to zero.

With the same parameters, the corresponding semi-rational solution composed of the line rogue wave and the line breather in the (x, y)-plane. As can be seen in Fig. 16, the line rogue wave arises from the background of the line breather and decay into the line breather background. The amplitude of the line rogue wave reaches the maximum value 3 (i.e., 3 times the background amplitude) around $t=0$. When $t\rightarrow \pm \infty$, the background transform from the line breather into the flat background.

Fig. 15

Semi-rational solutions q of the nonlocal DS III equation defined by (62) in the (x, t)-plane with parameters $N=4,y=0,P_{3}=-P_{4}=\frac{2}{3},Q_{3}=-Q_{4}=-1,\lambda =-\frac{1}{2}$

Fig. 16

Semi-rational solutions q of the nonlocal DS III equation defined by (62) in the (x, y)-plane with parameters $N=4,P_{3}=-P_{4}=\frac{2}{3},Q_{3}=-Q_{4}=-1,\lambda =-\frac{1}{2},\eta ^{0}_{3}=\eta ^{0}_{4}=-\frac{\pi }{2}$

4 Summary

In this paper, by the Hirota’s bilinear method, we have derived N-soliton solutions for the DS III Equation (4) and the nonlocal DS III Equation (5), respectively. By taking long wave limit in the N-soliton solutions of the DS III equation, we can obtain the corresponding rational solutions, including kink-shaped rogue wave solutions, lump solutions and the line rogue wave solutions. Besides, taking a long wave limit in part of the parameters in N-soliton solutions of the DS III, the semi-rational solutions composed of lumps, line rogue waves and solitons are generated. Similarly, by taking long wave limit in soliton solutions of the nonlocal DS III equation, (semi-)rational solutions are given. For the semi-rational solutions, lumps on the periodic line wave background, hybrids of the breathers and the lumps, line rogue waves on the periodic line/breather background are generated and demonstrated.

Furthermore, we compare the key results of the DS III equation with the nonlocal version in detail, the main results can be summarized in following items:

–Breather solutions. The nonlocal DS III equation has breathers in (x, t)-plane (see Fig. 11), which are periodic in x direction. Moreover, the nonlocal DS III equation also admits line breathers in (x, y)-plane (see Fig. 12), which are periodic in both x and y direction. However, we do not find breather solutions for the local DS III equation.

–Nonsingular rational solutions. The fundamental rational solutions of the DS III equation and the nonlocal DS III equation have the same types, including lumps in the (x, t)-plane (see Figs. 3 and 5), and line rogue wave in the (x, y)-plane (see Figs. 4 and 6).

–Semi-rational solutions. The simplest semi-rational solutions of the DS III equation are hybrids of the lumps and the solitons in (x, t)-plane (see Figs. 7 and 9), hybrids of the line rogue waves and the solitons in (x, y)-plane (see Figs. 8 and 10). However, for the nonlocal DS III equation, the semi-rational solutions display two types in (x, t)-plane: lumps in the periodic line wave background (see Fig. 13), hybrids of the breathers and the lumps (see Fig. 15). Besides, in (x, y)-plane, the solutions demonstrate the line rogue waves in the periodic line background (see Fig. 14) and the line rogue waves in the breather background (see Fig. 16).

The aforementioned results provide useful models to enrich the diversity of dynamic structures produced by the local and nonlocal DS III equation, including kink-shaped rogue waves, breathers, lumps, line rogue waves, W-shaped line rogue waves and their hybrids. We expect other systems with PT symmetric to be considered and explored more.

Appendix

Rational solution for the DS III with $N=4$ is expressed in the following

$$\begin{aligned} q&=\Big (108 x^4-576 x^3 y+(-1056 \textrm{i} t\\&\quad +2144 t^2+1056 y^2+648) x^2\\&\quad +768y(\textrm{i} t-\frac{53}{12} t^2-y^2-\frac{39}{16}) x+192 y^4\\&\quad +(384 \textrm{i} t+1664 t^2+864) y^2+1920 \textrm{i} t^3+3600 t^4\\&\quad +1440\textrm{i} t +5928 t^2+2457\Big ) \Big /\Big (108 x^4-576 x^3 y\\&\quad +(2144 t^2+1056 y^2+936)x^2\\&\quad +(-3392 t^2 y-768 y^3-2448 y) x+192 y^4\\&\quad +(1664 t^2+1248) y^2+3600 t^4+4744 t^2+1521\Big ). \end{aligned}$$

Semi-rational solution for the DS III with $N=3$ admits the explicit form

$$\begin{aligned} q&=\Big ((136 \textrm{i} x^2+(-136 \textrm{i} y+96 \textrm{i}) x+34 \textrm{i}y^2\\&\quad -48 \textrm{i} y-64-19 \textrm{i}+612 \textrm{i}t^2+(-408\\&\quad +192 \textrm{i}) t) e^{x+2 y+3 t-2 \pi }+408 \textrm{i} t+612 t^2+136 x^2\\&\quad -136 x y+34 y^2-51\Big )\Big /\Big ((136 x^2+(-136 y+96)x\\&\quad +612 t^2+34 y^2+192 t-48 y+49) e^{x+2 y+3 t-2 \pi }\\&\quad +612 t^2+136 x^2-136 x y+34 y^2+17\Big ). \end{aligned}$$

Semi-rational solution for DS III with $N=4$ is written as

$$\begin{aligned} q&=\Big ((2312 \textrm{i} x^2+(-2312 \textrm{i} y-1632 \textrm{i} )x+578\textrm{i} y^2\\&\quad +816 \textrm{i} y-1088-323\textrm{i}+10404 \textrm{i} t^2 \\&\quad +(-6936+3264 \textrm{i}) t) e^{-x-2 y+3 t-\frac{1}{2} x}\\&\quad +(2312 \textrm{i} x^2+(-2312 \textrm{i} y+1632 \textrm{i}) x\\&\quad +578\textrm{i} y^2-816 \textrm{i} y-1088-323 \textrm{i}+10404\textrm{i} t^2 \\&\quad +(-6936+3264 \textrm{i}) t) e^{x+2 y+3 t-\frac{1}{2} \pi }+(-4624 x^2\\&\quad +4624 x y-1156 y^2-314-4352\textrm{i}\\&\quad -20808 t^2+(-13056-13872 \textrm{i}) t)e^{6 t-\pi }\\&\quad +6936 \textrm{i}t+10404 t^2+2312 x^2\\&\quad -2312 x y+578 y^2-867\Big )\Big /\Big ((2312 x^2\\&\quad +(-2312 y-1632)x+10404 t^2\\&\quad +578 y^2+3264 t+816 y\\&\quad +833)e^{-x-2 y+3 t-\frac{1}{2} \pi }\\&\quad +(2312 x^2+(-2312 y+1632)x\\&\quad +10404 t^2+578 y^2+3264t\\&\quad -816 y+833) e^{x+2 y+3 t-\frac{1}{2} \pi }\\&\quad +(20808 t^2+4624 x^2-4624 x y\\&\quad +1156 y^2+13056 t+2626) e^{6t-\pi }+10404 t^2\\&\quad +2312 x^2-2312 x y+578y^2+289\Big ). \end{aligned}$$

Semi-rational solution for the nonlocal DS III with $N=3$ has the expression

$$\begin{aligned} q&=\Big (((24\textrm{i}x^2+(-24\textrm{i}y-48)x+108\textrm{i}t^2\\&\quad +6\textrm{i}y^2-69\textrm{i}-240t+24y)\sqrt{15}\\&\quad +168x^2+(336\textrm{i}-168y)x+144\textrm{i}t-168\textrm{i}y\\&\quad +756t^2+42y^2+29)e^{\frac{1}{2}\textrm{i}x-\frac{1}{2}\textrm{i}y-\frac{1}{2}\pi }+576\textrm{i}t\\&\quad +864t^2+192x^2-192xy+48y^2\\&\quad -72\Big )\Big /\Big ((-192\sqrt{15}t+192x^2\\&\quad +(384\textrm{i}-192y)x-192\textrm{i}y+864t^2+48y^2-8)\\&\quad e^{\frac{1}{2}\textrm{i}x-\frac{1}{2}\textrm{i}y-\frac{1}{2}\pi }+864t^2+192x^2-192xy+48y^2+24\Big ). \end{aligned}$$

Semi-rational solution for the nonlocal DS III with $N=4$ owns the form

$$\begin{aligned} q&=\Big (((-1620\textrm{i} t^2-36\textrm{i} x^2+435\textrm{i}+1800 t-480 x)\sqrt{5}\\&\quad -360\textrm{i}t+960\textrm{i}x-3240 t^2-720 x^2\\&\quad -210)e^{-\frac{2}{3} \textrm{i} x-\frac{9}{9} \sqrt{5} t+\eta }+((435 \textrm{i}-360 \textrm{i} x^2\\&\quad -1620 \textrm{i} t^2+1800 t+480 x) \sqrt{5}-360\textrm{i}t\\&\quad -960\textrm{i}x-3240 t^2-720 x^2-210)e^{\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }\\&\quad +((-2592 \textrm{i} t^2-576 \textrm{i} x^2-520 \textrm{i}+1440 t) \sqrt{5}+6192 \textrm{i} t\\&\quad +648 t^2+144 x^2-1814)e^{-\frac{10}{9} \sqrt{5} t+2 \eta }-3240\textrm{i} t \\&\quad -4860 t^2-1080 x^2+405\Big ) \Big /\Big ((1440 \textrm{i} x\\&\quad +1080 \sqrt{5} t-4860 t^2-1080 x^2+45)e^{-\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }\\&\quad +(-1440 \textrm{i} x-4860 t^2+1080 \sqrt{5} t-1080 x^2\\&\quad +45)e^{\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }+(-5832 t^2+2592 \sqrt{5} t-1296 x^2\\&\quad -1602)e^{-\frac{10}{9} \sqrt{5} t+2 \eta }-4860 t^2-1080 x^2-135\Big ). \end{aligned}$$