1 Introduction

Non-Hermitian physical systems have been on the rise since the pioneering work of Bender and Boettcher [1], which proved that a wide class of non-Hermitian Hamiltonians can possess entirely real spectra as long as these Hamiltonians obey the conditions of parity and time (PT) symmetry. Since then, a lot of PT-symmetric non-Hermitian Hamiltonian systems and their physical implementations have attracted a lot of attention during the past three decades [2,3,4,5,6,7,8,9,10]; for a recent review on this topic, see Ref. [11].

It is worth mentioning that the very active research field of optics and photonics has provided a test bed for the experimental observation of the unique phenomena related to PT symmetry, e.g., in specially designed optical waveguide structures and optical lattices [12,13,14,15,16,17]. Moreover, a series of works [18,19,20,21,22,23] have proved that if the complex-valued potential is not fully PT symmetric but is partially PT symmetric, it may also have new and interesting applications in optics and photonics and in other related areas. In a seminal work, Yang [18] introduced multidimensional complex optical potentials with partial PT symmetry. It is well known that the standard PT symmetry demands that the complex-valued external potential must be invariant under the complex conjugation of the corresponding physical field and the simultaneous reflection in all spatial coordinates. By using both analytical and numerical techniques, Yang [18] has demonstrated that if the external potential is only partially PT symmetric, i.e., it is invariant under complex conjugation and reflection in only a spatial coordinate, then it can also possess all real eigenvalues and continuous families of soliton solutions. Thus, further investigations in the area of partially PT-symmetric physical systems are both worthwhile and necessary.

In order to get a better understanding of a PT-symmetric physical system, it is necessary to find out the associated integrable model for it. We recall that a nonlocal nonlinear Schrödinger (NLS) equation with a PT-symmetric potential was proposed in a seminal work by Ablowitz and Musslimani [24]. This work immediately stimulated extensive studies on the nonlocal (1 + 1)-dimensional integrable equations including the obtaining of various types of exact solutions and the construction of other nonlocal integrable equations [25,26,27,28,29,30,31,32,33,34,35,36]. Later, Fokas extended the nonlocal NLS equation to (2 + 1)-dimensional space and introduced two new integrable nonlocal Davey–Stewartson (DS) equations [37]. Recently, a new nonlocal Davey–Stewartson II (DS II) equation was introduced by Ablowitz and Musslimani [38] in the form of

$$\begin{aligned}&iA_{t}=A_{xx}-A_{yy}+(\epsilon V-2Q)A,\nonumber \\&Q_{xx}+Q_{yy}=(\epsilon V)_{xx}, \end{aligned}$$
(1)

where

$$\begin{aligned} V= & {} A(x,y,t)\,[A(x,-y,t)]^{*}, \end{aligned}$$
(2)

the asterisk denotes complex conjugate, A is a complex-valued function of spatial variable x and y, and temporal variable t, and Q is a function of \(x\,,y\), and t. Here V is a PT-symmetric potential with respect to the y-direction, and thus, Eq. (1) is called the y-nonlocal DSII equation from now on. Obviously, the y-nonlocal DS II equation can be reduced to the usual DS II equation [39, 40] by setting \(V=A(x,y,t)\,[A(x,y,t)]^{*}\).

Note that rogue waves of the usual DS II equation have been derived by Ohta and Yang [40]. It is worth mentioning that rogue waves (or freak waves), a term coined to provide the adequate description of the high-amplitude ocean waves [41], have recently attracted much attention in the study of their complex dynamics in different physical systems [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. The most recent theoretical and experimental results in this fast developing area were summarized in Refs. [66,67,68,69].

In recent works [70, 71], the (2 + 1)-dimensional breather, rational, and semirational exact solutions of partially PT-symmetric nonlocal DS equations (of type I and type II) with respect to the spatial variable x (the so-called x-nonlocal DS equations of type I and type II) have been reported. Thus, it is natural to seek various exact solutions of the partially PT-symmetric nonlocal DS II equation with respect to the spatial variable y (the so-called y-nonlocal DS II equation) by using the Hirota bilinear method and then show the key features of the evolution Eq. (1), characterized by a partially PT-symmetric complex-valued potential V.

This paper is organized as follows. In Sect. 2, the main theorem on the rational solutions is provided. In Sect. 2.1, the fundamental rational solutions are derived and their dynamics is studied. The unique dynamics of higher-order rational solutions is discussed in Sect. 2.2. Our results are summarized in Sect. 3.

2 Rational solutions of the y-nonlocal DS II equation

In this section, we derive rational solutions of the y-nonlocal DS II equation, which can be transformed into the bilinear form as follows:

$$\begin{aligned}&\left( D_{x}^{2}-D_{y}^{2}-iD_{t}\right) g \cdot f =0,\nonumber \\&\left( D_{x}^{2}+D_{y}^{2}\right) f \cdot f =2\epsilon \left( f^{2}-gh\right) , \end{aligned}$$
(3)

and with the variable transformation

$$\begin{aligned} A=\sqrt{2}\frac{g}{f},\quad Q=\epsilon -2( \mathrm{log} f)_{xx}, \end{aligned}$$
(4)

the function g and f satisfy the following conditions:

$$\begin{aligned}{}[f(x,-y,t)]^{*}= & {} f(x,y,t)\,,[g(x,-y,t)]^{*}\nonumber \\= & {} h(x,y,t)\, . \end{aligned}$$
(5)

Here the operator D is the Hirota’s bilinear differential operator[72] defined by

$$\begin{aligned}&P(D_{x},D_{y},D_{t},\ldots )F(x,y,t,\ldots )\cdot G(x,y,t,\ldots )\\&\quad =P(\partial _{x}\!-\!\partial _{x^{'}},\partial _{y}\!-\!\partial _{y^{'}}, \partial _{t}-\partial _{t^{'}},\ldots )F(x,y,t,\ldots )\\&\qquad \times G(x^{'},y^{'},t^{'}, \ldots )|_{x^{'}=x,\quad y^{'}=y,\quad t^{'}=t,} \end{aligned}$$

where P is a polynomial of \(D_{x}\), \(D_{y}\), \(D_{t}, \ldots \).

With the bilinear transform method [72], the Nth-order periodic solution of the nonlocal DS II equation can be derived. It can be written in the following form:

$$\begin{aligned} f= & {} \sum _{\mu =0,1}\exp \left( \sum _{j<k}^{(N)}\mu _{j}\mu _{k}A_{jk}+\sum _{j=1}^{N}\mu _{j}\eta _{j}\right) ,\nonumber \\ g= & {} \sum _{\mu =0,1}\exp \left( \sum _{j<k}^{(N)}\mu _{j}\mu _{k}A_{jk}\!+\!\sum _{j=1}^{N}\mu _{j}(\eta _{j}\!+\,i\phi _{j})\right) ,\nonumber \\ \end{aligned}$$
(6)

where

$$\begin{aligned}&\eta _{j}=P_{j}\,x+iQ_{j}\,y+\Omega _{j}t+\eta _{j}^{0}\,,\nonumber \\&\Omega _{j}=\left( P_{j}^{2}+Q_{j}^{2}\right) \sqrt{-1+\frac{4\epsilon }{P_{j}^{2}-Q_{j}^{2}}}\,,\nonumber \\&\exp (A_{jk})\!=\!-\,\frac{2\epsilon \cos (\phi _{j}-\phi _{k})+(P_{j}-P_{k})^{2}-(Q_{j}-Q_{k})^{2}-2\epsilon }{2\epsilon \cos (\phi _{j}\!+\!\phi _{k})\!+\!(P_{j}\!+\!P_{k})^{2}-(Q_{j}+Q_{k})^{2}\!-\!2\epsilon }\,,\nonumber \\&\cos (\phi _{j})=1-\frac{P_{j}^{2}-Q_{j}^{2}}{2\epsilon }\,,\sin (\phi _{j})\nonumber \\&\quad \quad =-\,\,\frac{\left( P_{j}^{2}-Q_{j}^{2}\right) \sqrt{-1+\frac{4\epsilon }{P_{j}^{2}-Q_{j}^{2}}}}{2\epsilon }, \end{aligned}$$
(7)

and \(j\,,k\,,N\) are arbitrary positive integers, \(P_{j}\) and \(Q_{j}\) are real constants, and \(\eta _{j}^{0}\) is an arbitrary complex constant. The notation \(\sum _{\mu =0}\) indicates summation over all possible combinations of \(\mu _{1}=0,1\,,\mu _{2}=0,1\,,\ldots ,\mu _{N}=0,1\), and the \(\sum _{j<k}^{(N)}\) summation is over all possible combinations of the N elements with the specific condition \(j<k\).

In order to derive line rogue waves of the y-nonlocal DS II equation (1), we use long wave limits on the f and g functions. Putting

$$\begin{aligned} N=2n,\quad Q_{j}=\lambda _{j}P_{j},\quad \eta _{j}^{0}=i\pi \end{aligned}$$
(8)

in Eq. (6), then using the limit \(P_{j}\rightarrow 0\), the functions A and Q are translated from exponential functions to pure rational functions.

By the gauge freedom of f and g functions, the rational solutions of the y-nonlocal DS II equation can be presented in the following Theorem.

Theorem

The Nth-order rational solutions A and Q of the y-nonlocal DS II equation can be generated by Eq. (4) with the help of the following

$$\begin{aligned} f= & {} \prod _{j=1}^{N}\theta _{j}+\frac{1}{2}\sum _{j,k}^{(N)}\alpha _{jk}\prod _{l\ne j,k}^{N}\theta _{l}+\cdots \nonumber \\&\quad +\,\frac{1}{M!2^{M}}\sum _{j,k,\ldots ,m,n}^{(N)}\overbrace{\alpha _{jk}\cdots \alpha _{mn}}^{M}\nonumber \\&\quad \prod _{p\ne j,k,\ldots ,m,n}^{N}\theta _{p} +\cdots ,\nonumber \\ g= & {} \prod _{j=1}^{N}(\theta _{j}+b_{j})+\frac{1}{2}\sum _{j,k}^{(N)}\alpha _{jk}\prod _{l\ne j,k}^{N}\left( \theta _{l}+\,b_{l}\right) +\cdots \nonumber \\&\quad +\,\frac{1}{M!2^{M}}\sum _{j,k,\ldots ,m,n}^{(N)}\overbrace{\alpha _{jk}\cdots \alpha _{mn}}^{M}\nonumber \\&\quad \prod _{p\ne j,k,\ldots ,m,n}^{N}\left( \theta _{p}+\,b_{p}\right) +\cdots ,\nonumber \\ \end{aligned}$$
(9)

with

$$\begin{aligned} \theta _{k}= & {} \lambda _{k}\,x+i\,y+2\gamma _{k}\sqrt{\frac{\epsilon }{\lambda _{k}^{2}-1}}\left( 1+\lambda _{k}^{2}\right) t\,,\nonumber \\ b_{k}= & {} -\frac{i\gamma _{k}\sqrt{\epsilon \left( \lambda ^{2}_{k}-1\right) }}{\epsilon }\,,\nonumber \\ a_{jk}= & {} \frac{\left( \lambda _{j}^{2}-1\right) \left( \lambda _{k}^{2}-1\right) }{2\gamma _{j}\gamma _{k}\sqrt{\frac{1}{\left( \lambda _{j}^{2}-1\right) \left( \lambda _{k}^{2}-1\right) }}\left( \lambda ^{2}_{j}\lambda ^{2}_{k}\!-\!\lambda ^{2}_{j}\!-\!\lambda ^{2}_{k}+1\right) -\lambda _{j}\lambda _{k}+\epsilon },\nonumber \\ \end{aligned}$$
(10)

where the two positive integers j and k are not larger than N, \(\lambda _{j}\) are arbitrary complex constants, and \(\gamma _{j}=\pm 1\).

Remark

By using the above Theorem, we can obtain the rational solutions of the nonlocal DS II equation, which are different from rational solutions of the classical DS II equation [73]. In addition, if we set \(\epsilon =-1, \lambda _{j}=-\lambda _{j+n}\ne 0, |\lambda _{j}|<1, \gamma _{j}\gamma _{j+n}=-1\) in Eq. (10), we can obtain lump solutions. These solutions are non-singular; this property has been proved in [73, 74], and thus, we omit the proof in the present paper.

2.1 Dynamics of fundamental rational solutions

The first-order lump solutions of the y-nonlocal DS II equation can be derived if we choose the parameters

$$\begin{aligned}&N=2,\quad \gamma _{1}=-\gamma _{2}=-1,\quad \nonumber \\&\quad \lambda _{1}=-\lambda _{2}=\frac{1}{2},\quad \epsilon =-1 \end{aligned}$$
(11)

in the rational solutions (9). According to the above Theorem, this exact solution has the form

$$\begin{aligned}&A(x,y,t)=\sqrt{2}\frac{(\theta _{1}+b_{1})(\theta _{2}+b_{2})+a_{12}}{\theta _{1}\theta _{2}+a_{12}}\nonumber \\&\quad =\frac{\sqrt{2}\left( 48x^{2}+(96i\sqrt{3}-320\sqrt{3}t)x-960it+1600t^{2}+192y^{2}-117\right) }{(4\sqrt{3}x-40t)^{2}+192y^{2}+27},\nonumber \\&\qquad Q(x,y,t)=\epsilon -2( \mathrm{log} (\theta _{1}\theta _{2}+a_{12}))_{xx}\nonumber \\&\quad =\frac{1}{((4\sqrt{3}x-40t)^{2}+192y^{2}+27)^{2}} \left( -\,2304x^{4}+30720\sqrt{3}tx^{3}\right. \nonumber \\&\qquad +\,(-460800t^{2}-18432y^{2}\!+\!6624)x^{2}\nonumber \\&\qquad +(1024000\sqrt{3}t^{3}+122880\sqrt{3}ty^{2}-44160\sqrt{3}t)x-36864y^{4}\nonumber \\&\qquad \left. +(-614400t^{2}-47232)y^{2}-2560000t^{4}+220800t^{2}-5913\right) .\nonumber \\ \end{aligned}$$
(12)
Fig. 1
figure 1

The lump solutions |A| in (12) of the y-nonlocal DS II equation in the (x, y)-plane (a) and the (y, t)-plane (b). The parameters are given by (11)

Full size image
Fig. 2
figure 2

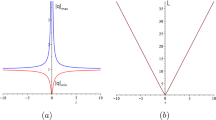
The line rogue wave solution |A| given by (12) of the y-nonlocal DS II equation. The line waves are plotted in the (x, t)-plane for different values of the spatial variable y

Full size image

As shown in Fig. 1, these rational solutions look as permanent lumps moving on the constant background in either the (x, y)-plane or the (y, t)-plane. From a careful analysis of the rational solution |A| given in (12), it must be a bright lump in either the (x, y)-plane or the (y, t)-plane.

Interestingly, in the (x, t)-plane, as shown in Fig. 2, the exact solution A given by Eq. (12) is a typical line wave solution. When \(|y|\rightarrow \infty \), these line waves disappear to the constant background. When \(|y|\rightarrow 0\), the amplitudes of these line waves increase, and for \(|y|=0\) the amplitude of the line wave reaches the highest value. Moreover, these line waves are not always bright-type waves (see the panels fot \(y=\pm \,1, \pm \,2, 3\) in Fig. 2). Thus, they feature remarkably different profiles when comparing the variety of line rogue wave profiles plotted in Fig. 2 to the corresponding ones for the standard DS II equation [40, 75].

Fig. 3
figure 3

A Peregrine-type solution |A(y, t)| of the nonlocal NLS Eq. (13), obtained by a reduction from a two-spatially dimensional W-shaped rogue wave A(x, y, t) defined in (4), (9), and (10), with parameters \(N=2, \gamma _{1}=-\gamma _{2}=-1, \lambda _{1}=\lambda _{2}=0, \epsilon =-1\). The right panel is a density plot of the left panel

Full size image
Fig. 4
figure 4

The time evolution in the (x, y) plane of the two lump solution |A|, which is given by Eq. (4), of the nonlocal DS II Eq. (1). The parameters are given in Eq. (16)

Full size image

It is also interesting to note that the nonlocal DS II equation can be reduced to the nonlocal NLS equation [24], i.e.,

$$\begin{aligned} iA_{t}=-A_{yy}+[2-A(y,t)A^{*}(-y,t)]A, \end{aligned}$$
(13)

by setting A to be independent of x and \(Q=\epsilon =-1\). This equation is a special reduction in the third-order nonlocal Schrödinger equation; see Ref. [27] for a detailed study of this issue. Further, setting \(N=2, \gamma _{1}=-\,\gamma _{2}=-\,1, \lambda _{1}=\lambda _{2}=0, \epsilon =-\,1\) in the rational solutions (4), (9), and (10), the fundamental (Peregrine) rogue wave of the nonlocal NLS Eq. (13) can be given in an analytical form and is plotted in Fig. 3; see also the recent work [27].

2.2 Dynamics of high-order rational solutions

In this subsection, we construct the high-order rational solutions according to Theorem. Setting \(\epsilon =-1\) and \(N=2n\) (\(n>1\)), where n is an integer number, and taking the following set of parameters in Theorem,

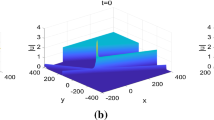
$$\begin{aligned}&\lambda _{j}=-\,\lambda _{j+n}, |\lambda _{j}|<1, \gamma _{j}\gamma _{j+n}=-1,\nonumber \\&\quad j=1,2,\ldots ,n, \end{aligned}$$
(14)

then the nth-order rational solutions of the y-nonlocal DS II Eq. (1) can be derived. If \(\lambda _{j}\ne 0\), we can derive higher-order lump solutions in the (x, y)-plane; see Fig. 4 for the evolution of two lump solutions in the (x, y)-plane. In the (x, t)-plane, the second-order solutions can describe the interaction of two line waves, namely the growing-and-decaying process of line wave amplitudes; see Fig. 5. If \(\lambda _{j}=0, \lambda _{k}\ne 0\), where \(j\ne k\), then we can derive hybrid solutions composed of lumps and line rogue waves in the (x, y)-plane; see Fig. 6.

Fig. 5
figure 5

The second-order line rogue wave solution A of the y-nonlocal DS II equation, plotted in the (x, t)-plane. The parameters are given in Eq. (16)

Full size image

For instance, we set \(n=2\) (i.e., \(N=4\)) in Theorem, then the functions f and g can be derived as follows:

$$\begin{aligned} f= & {} \theta _{1}\theta _{2}\theta _{3}\theta _{4}+\alpha _{12}\theta _{3}\theta _{4}+\alpha _{13}\theta _{2}\theta _{4}+\alpha _{14}\theta _{2}\theta _{3}\nonumber \\&\quad +\,\alpha _{23}\theta _{1}\theta _{4}+\alpha _{24}\theta _{1}\theta _{3}+\alpha _{34}\theta _{1}\theta _{2}\nonumber \\&\quad +\,\alpha _{12}\alpha _{34}+\alpha _{13}\alpha _{24}+\alpha _{14}\alpha _{23},\nonumber \\ g= & {} (\theta _{1}+b_{1})(\theta _{2}+b_{2})(\theta _{3}+b_{3})(\theta _{4}+b_{4})\nonumber \\&\quad +\,\alpha _{12}(\theta _{3}+b_{3})(\theta _{4}+b_{4})\nonumber \\&\quad +\,\alpha _{13}(\theta _{2}+b_{2})(\theta _{4}+b_{4})\nonumber \\&\quad +\,\alpha _{14}(\theta _{2}+b_{2})(\theta _{3}+b_{3})\nonumber \\&\quad +\,\alpha _{23}(\theta _{1}+b_{1})(\theta _{4}+b_{4})\nonumber \\&\quad +\,\alpha _{24}(\theta _{1}+b_{1})(\theta _{3}+b_{3})\nonumber \\&\quad +\,\alpha _{34}(\theta _{1}+b_{1})(\theta _{2}+b_{2})\nonumber \\&\quad +\,\alpha _{12}\alpha _{34}+\alpha _{13}\alpha _{24}+\alpha _{14}\alpha _{23}, \end{aligned}$$
(15)

where the parameters \(\theta _{j}, \alpha _{jk}, b_{j}\) are given by Eq. (10). As we discussed above, if \(\lambda _{j}\ne 0\), the functions f and g given by Eq. (15) generate the second-order lumps in the (x, y)-plane or the (y, t)-plane. For example, as shown in Fig. 4, we can obtain the solutions describing the interaction of two first-order lumps in the (x, y)-plane, if we consider the parameter conditions

$$\begin{aligned} \lambda _{1}= & {} -\lambda _{3}=\frac{1}{2},\quad \lambda _{2}=-\lambda _{4}=-\,\frac{1}{2},\nonumber \\ \gamma _{1}= & {} -\gamma _{3}=1,\quad \gamma _{2}=-\gamma _{4}=1, \end{aligned}$$
(16)

in Eq. (10). There are two first-order lumps interacting with each other in Fig. 4. Interestingly, when \(t=0\) (see Fig. 4), these two lumps merge into a single one, but the amplitude of the emerging lump is much lower than the corresponding amplitudes of the two separate interacting lumps.

Fig. 6
figure 6

The interaction of a lump with a line rogue wave solution in the (x, y)-plane. The parameters are given in Eq. (17)

Full size image

Then, we consider this solution in the (x, t)-plane. Similar to the case of \(N=2\) (see Fig. 2), there are two line waves in Fig. 5 that arise from the constant background and disappear into the constant background again. Depending on the special values of the spatial coordinate y, these line waves can be either bright waves or dark ones.

Moreover, we consider the hybrid solutions of lumps and line rogue waves according to Theorem. We set

$$\begin{aligned} \lambda _{1}= & {} -\lambda _{3}=0,\quad \lambda _{2}=-\lambda _{4}=-\,\frac{1}{2},\nonumber \\ \gamma _{1}= & {} -\gamma _{3}=1,\quad \gamma _{2}=-\gamma _{4}=1 \end{aligned}$$
(17)

in Eq. (10) of Theorem. The corresponding rational solutions generated by Theorem are shown in Fig. 6. For \( -3<t\), we see a lump moving on the constant background (the height of the background is \(\sqrt{2}\)). At the intermediate time, a line rogue wave arises (see the panel corresponding to \(t=-\,1\) in Fig. 6) and then interacts with the lump (see the panel corresponding to \(t=0\) in Fig. 6). Finally, the line rogue wave disappears into the constant background, and the moving lump is preserved eventually. Interestingly, the interaction of these two very different types of waves implies a slight downward deformation of the line rogue wave (see the panel corresponding to \(t=0\) in Fig. 6).

Fig. 7
figure 7

The time evolution in the (x, y)-plane of a third-order lump A of the y-nonlocal DSII equation. The parameters are given in Eq. (18)

Full size image
Fig. 8
figure 8

The interaction dynamics in the (x, y)-plane of a second-order lump and a line rogue wave of the y-nonlocal DS II equation. The parameters are given in Eq. (19)

Full size image

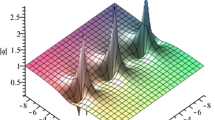
For larger values of N, the dynamics of these higher-order rational solutions is qualitatively similar. We can also obtain two types of rational solutions. One of them is the nth-lump solution, the second one is a hybrid (compound) solution composed of lumps and line rogue waves. If we set \(N=6\) and

$$\begin{aligned} \lambda _{1}= & {} -\lambda _{4}=\frac{1}{2},\quad \lambda _{2}=-\lambda _{5}=-\,\frac{1}{2},\quad \lambda _{3}=-\lambda _{6}=\frac{1}{3}, \nonumber \\ \gamma _{1}= & {} -\gamma _{4}=1,\quad \gamma _{2}=-\gamma _{5}=1, \quad \gamma _{3}=-\gamma _{6}=1\nonumber \\ \end{aligned}$$
(18)

in Eq. (10), then Theorem generates a third-order lump solution. As shown in Fig. 7, there are three lumps moving on the constant background. The paired lumps are moving together from the right-hand side to the left-hand side, while the third lump is moving from the left-hand side to the right-hand side. The two soliton complexes will collide at a certain time. The collision of lumps implies the fusion and fission of them. At \(t=-1\), the third lump merges into the left one of the paired lumps, and then at \(t=0\) it is moving further into the middle of paired lumps. Next, at \(t=1\), the third lump merges the right one of the paired lumps, and then at \(t=2\) the third lump is split from the right one of the paired lumps. Finally, at \(t>4\), the third lump is passed through the paired lumps. In order to get the hybrid solutions of lumps and line rogue waves in Theorem, we set

$$\begin{aligned} \lambda _{1}= & {} -\lambda _{4}=\frac{1}{2},\quad \lambda _{2}=-\lambda _{5}=-\frac{1}{2},\quad \lambda _{3}=\lambda _{6}=0, \nonumber \\ \gamma _{1}= & {} -\gamma _{4}=1,\quad \gamma _{2}=-\gamma _{5}=1,\quad \gamma _{3}=-\gamma _{6}=1\nonumber \\ \end{aligned}$$
(19)

in Eq. (10). The associated solution is plotted in Fig. 8, and for \(t\ll -3\) we see two moving lumps sitting on the constant background. In the intermediate time range, a line rogue wave arises (see the panel corresponding to \(t=-1\) in Fig. 8), and then, this line wave interacts with the two lumps. At \(t=0\), the two lumps merge into a single one and a high-amplitude line rogue wave arise. As we can see in the panel corresponding to \(t=0\), the line rogue wave reaches the highest amplitude as a result of its interaction with the two lumps. After interaction, the line rogue wave disappears into the constant background again, while the single lump is divided into two lumps (see the panels corresponding to \(t=\frac{3}{2}\) and \(t=\frac{7}{2}\) in Fig. 8).

3 Summary and discussion

In this paper, a general formula for the nth-order rational solutions of the y-nonlocal DS II equation is derived by using the Hirota bilinear method, which yields two types of rational solutions. The first type of rational solutions is the lump solution that has permanent peaks moving on the constant background in either the (x, y)-plane or the (y, t)-plane. In the (x, t)-plane, we found line wave solutions that arise from a constant background and then disappear into the same background again. For the nth-order solutions, there are n lumps moving in either the (x, y)-plane or the (y, t)-plane and n line waves growing and decaying in the (x, t)-plane. The second type of rational solution is a hybrid solution composed of both lumps and line rogue waves.

In addition, if we compare the key features of the families of rational solutions of the y-nonlocal DS II equation, which are reported in this paper, with the families of rational solutions of the fully PT-symmetric DS II equation and with the corresponding solutions of the x-nonlocal DS II equation [70], we see the following essential differences:

  • In the (x, y)-plane, the rational solution of the fully PT- symmetric DS II equation behaves as a line rogue wave, but the rational solution of the y-nonlocal DSI II equation is a lump (see Fig. 1). In the (x, t)-plane, the former solution is a localized lump-shaped wave, while the latter solution is a growing- and-decaying line wave (see Fig. 2).

  • In the (x, t)-plane, the rational solution of the x-nonlocal DS II equation is a localized lump-shaped wave, but the rational solution of the y-nonlocal DS II equation is a growing- and-decaying line wave (see Fig. 2). In the (y, t)-plane, the former solution is a growing-and-decaying line wave, while the latter solution is a localized lump-shaped wave (see Fig. 1). What is more, the solutions of the x-nonlocal DS II equation [70] cannot simply transform into the solutions of the y-nonlocal DS II equation by interchanging of the spatial variables x and y.

  • The unique patterns shown in Figs. 4, 5, 6, 7 and 8 are typical for the families of rational solutions of the y-nonlocal DS II equation, and they have not been found in the study of rational solutions of the fully PT-symmetric DS II equation and of the corresponding solutions of the x-nonlocal DS II equation; see [70].

Thus, the above-listed differences between the essential features of families of rational solutions of the fully PT-symmetric DS II equation, the partially symmetric x-nonlocal DS II equation, and the partially symmetric y-nonlocal DSII equation suggest us that these nonlinear evolution equations deserve to be further studied. We expect new results in this area helping us to understand the unique properties of PT-symmetric nonlinear systems in the multidimensional space.