1 Introduction

Stochastic resonance (SR) is an important discovery in stochastic dynamics. It was first used to explain the glacial problems in Quaternary, which described the influence of the periodic action of the sun on the earth on the alternation of the glacial and warm epochs in paleo meteorology [1]. Meanwhile, it is the phenomenon that the output of the nonlinear system is enhanced by the synergy of periodic signal and random noise [2]. It is widely used in the field of physics [3, 4], chemistry [5], biology [6], communication [7, 8], signal processing [9,10,11], etc.

In stochastic dynamics, coupled oscillators have been widely studied by scholars because of its interesting nonlinear dynamic phenomena and application of signal enhancement [12]. Array coupled is a kind of coupled SR array obtained by coupling several oscillators. There are many kinds of connection modes, such as chain array [13], ring array [14], and global coupling array [15], etc., among which chain array connection mode is cascading SR array which is a simple connection mode. It can enhance the weak characteristic signal step by step and improve the output signal-to-noise ratio (SNR), so it has been widely used [16, 17]. The basic idea of cascaded SR is to cascade the SR system in multiple layers, that is, the output signal of the upper-level system is input into the lower-level system as the input signal, so that the weak periodic signal is enhanced step by step. Cascaded SR has made many advances and received considerable attention. He et al. [18] addressed the nonlinear filter characteristic of cascaded bistable SR system, which is well applied in rolling bearing diagnosis. Li et al. [13] studied a new adaptive cascaded SR method and applied it to gear fault diagnosis, which realized the step-by-step enhancement of weak gear pulse signal. Shi et al. [19] proposed a signal enhancement method based on cascaded multi-stable SR and empirical mode decomposition, which used empirical mode decomposition to filter interference noise and cascaded SR to enhance the weak fault signal.

In the study of SR, the bistable system is a classical nonlinear system [20], which has been widely studied because of the typical nonlinear effect of noise and wide application in physics, chemistry, and other fields, whereas its output exists saturation phenomenon, which limits the enhanced efficacy in signal processing. To solve this problem, many scholars have studied the SR behavior of different systems and found that different types of piecewise systems can overcome this saturation characteristic [21, 22]. By transforming the continuous potential function into the piecewise potential function, the output of the system will increase with the increase of the input potential energy. Compared with the bistable system, the SR in a piecewise system achieves the higher output SNR and the more obvious signal enhancement effect when the width and depth of the potential well are consistent.

Some previous studies have focused on the stochastic dynamics under a stationary and periodic excitation [23,24,25]. In fact, non-stationary excitation occupies a major portion in external excitations, so it is of great engineering value to study the stochastic dynamic response under a non-stationary excitation. Yang et al. [26] proposed a time–frequency analysis method based on SR for the non-stationary signal, which can effectively enhance the non-stationary signal and apply it to bearing fault diagnosis. Wu et al. [27] used SR in a fractional-order system to identify the unknown non-stationary signal under strong noise background and effectively enhance it. Yang et al. [28] used SR based on EMD to enhance the non-stationary signal. It shows that the stochastic dynamics method of non-stationary signals has strong potential in signal processing.

In the field of signal processing, one of the greatest concerns is signal de-noising. Signals can effectively characterize the laws of some things and are widely present in the actual environment. In terms of the mechanical equipment fault diagnosis, vibration signal is often used to characterize the operation state of mechanical equipment and can effectively identify the abnormalities and faults in the operation of the equipment. In fact, most of the equipment works under variable speed condition, and its vibration signal is non-stationary. For example, during the hoisting process of a mine hoist, the hoist frequently experiences acceleration, steady speed, and deceleration conditions, which causing relatively large impact on bearings and other parts [29]. Industrial robots are widely used in manufacturing assembly, welding and other fields because of their high efficiency and repeatability. Its operation condition is also a complex variable speed condition, which has a great impact on robot joints, so the bearing is also prone to damage [30]. Therefore, the research on bearing fault diagnosis under variable speed condition has more practical significance. For the fault diagnosis under variable speed condition, there are two kinds of methods: the order analysis (OA) method and the time–frequency analysis method. The methods based on time–frequency analysis mainly include the Wigner-Ville time–frequency distribution [31], the short-time Fourier transform [32], the wavelet time–frequency analysis [33], and the generalized S transform [34], etc. The basic principle of the method based on time–frequency analysis is to arrange a vibration signal in its time series and frequency by calculation. From the time–frequency figure, the rotation frequency curve, its frequency multiplication curve, and fault characteristic frequency curve can be obtained directly. However, the time–frequency analysis method needs a large amount of calculation, and the calculation is complicated. Compared with the time–frequency analysis method, the OA method [35] is convenient, accurate, and fast in calculation, so it is widely used in fault diagnosis. The basic idea of OA is to collect the rotational speed information synchronously while collecting the vibration signal. By interpolation and resampling methods, the non-stationary signal in the time domain is transformed into the stationary signal in the angle domain for analysis. Finally, the fault diagnosis problem under variable working condition is transformed into the fault diagnosis problem under constant speed working condition. OA is mainly divided into Hardware Order Analysis (HOA) [36], Computed Order Analysis (COA) [37] and Tachometer-less Order Analysis (TOA) [38]. HOA is to sample the pulse signal of the tachometer through the hardware circuit. Due to the limitation of the hardware circuit, it is difficult to extract the fault characteristic information when speed changes rapidly, and the cost is high. TOA is to extract instantaneous frequency components from the vibration signal and estimate rotation speed information to realize the conversion of signal in the angle domain. The advantages are that there is no need to arrange the phase detector and the cost is low. However, this method has poor resistance to noise. In a word, COA gets rid of the limitation and complexity of HOA. Compared with TOA, it has stronger ability to resist environmental noise and can extract fault feature information under speed fluctuation effectively. Variational mode decomposition (VMD) was proposed by Dragomiretskiy et al. [39] in 2014. Because VMD can solve the problems of endpoint effect and modal aliasing compared with empirical mode decomposition, so it is widely used in signal processing of mechanical equipment [40,41,42,43]. This method is mainly used to decompose complex signals to realize the analysis and judgment of signal components.

In terms of fault diagnosis, bearing fault signal is essentially a series of weak pulse signals, which is difficult to find the relevant characteristics of the bearing fault signal submerged by strong noise. Maximum correlation kurtosis deconvolution (MCKD) can extract the weak periodic pulses to highlight the periodic fault components of a signal. This method was proposed by McDonald et al. [44] in 2011, which effectively realized the extraction of gear fault features by setting a series of filter parameters and iteration periods. Following this, this method is widely applied to the fault diagnosis of bearing and other parts under constant speed conditions. Lyu et al. [45] used the quantum genetic algorithm to optimize the relevant parameters of MCKD, which realized the adaptive parameters selection and verified the effectiveness by bearing and gear fault signals. Wang et al. [46] proposed a time–frequency method based on MCKD, which effectively extracted the bearing fault characteristic information under variable speed condition. This method has strong ability to extract periodic fault characteristic information and resist noise interference.

Most of the above researches belong to weak signal enhancement research under constant speed condition. However, in engineering, the background noise is strong and the strong rotation speed fluctuation of the mechanical equipment leads to obvious non-stationary characteristic of the signal, which means the fault characteristic signal cannot be obtained by classical signal processing methods. Based on this, we focus on the problem of the signal feature extraction based on the dynamics method under strong noise background and variable speed condition. The content of this paper is arranged as follows. In Sect. 2, related theories are mainly introduced. In Sect. 3, numerical simulation is carried out to verify the validity of the theory in Sect. 2. In Sect. 4, the experiment is set up to verify the effectiveness of above method. Finally, the main conclusions of this article are provided in the last section.

2 Theoretical formulations

The core of non-stationary signal processing in strong noise background is the signal extraction method based on adaptive SR. Because SR is difficult to be used to process non-stationary signals directly, it is necessary to realize the conversion from non-stationary signals to stationary signals at first. The following systematically introduces the adaptive cascade SR method, the signal conversion from non-stationary characteristic to stationary characteristic based on COA, and the specific process of fault feature extraction method.

2.1 Adaptive cascade SR

SR phenomenon occurs by the synergy by the periodic force, random noise and nonlinear system. The dynamic equation of a system is expressed as Eq. (1)

$$ \left\{ \begin{gathered} \frac{{{\text{d}}x_{0} (t)}}{{{\text{d}}t}} = - \frac{{\partial U_{0} (x_{0} )}}{{\partial x_{0} }} + N_{0} (t) + s_{0} (t) \hfill \\ s_{0} (t) = A_{0} \cos (2\pi f_{0} t) \hfill \\ \end{gathered} \right. $$
(1)

where x0(t), U0 (x0) and s0(t) are the output response of the system, the potential function of the system, and the low-frequency periodic input of the system, respectively. \(N_{0} (t) = \sqrt {2D_{0} } \xi (t)\) is the Gaussian white noise, where ξ(t) and D0 are the standard Gaussian white noise with the mean of 0 and the variance of 1 and the noise intensity, respectively. N0(t) satisfies the following statistical characteristics, as shown in Eq. (2)

$$ \langle N_{0} (t)\rangle = 0,\;\langle N_{0} (t),N_{0} (0)\rangle = 2D_{0} \delta (t) $$
(2)

where δ(t) represents the Dirac function.

A kind of piecewise linear system is selected as the system model. To facilitate comparison with the bistable system, the potential function is given as follows:

$$ U_{1} (x) = \left\{ \begin{gathered} - \frac{{a_{1}^{2} }}{{4b_{1} }}(\frac{{x + c_{1} }}{{c_{1} - \sqrt {a_{1} /b_{1} } }}),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x < - \sqrt {a_{1} /b_{1} } \hfill \\ \frac{{\sqrt {a_{1}^{3} /b_{1} } }}{4}x{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sqrt {a_{1} /b_{1} } \le x < 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ - \frac{{\sqrt {a_{1}^{3} /b_{1} } }}{4}x,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le x < \sqrt {a_{1} /b_{1} } \hfill \\ \frac{{a_{1}^{2} }}{{4b_{1} }}(\frac{{x - c_{1} }}{{c_{1} - \sqrt {a_{1} /b_{1} } }}),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \ge \sqrt {a_{1} /b_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right. $$
(3)

where a1 and b1 (a1 > 0, b1 > 0) are the system parameters, and \(c_{1} = \sqrt {2a_{1} /b_{1} }\).

The potential function of the bistable system is

$$ U_{2} (x) = - \frac{1}{2}a_{2} x^{2} + \frac{1}{4}b_{2} x^{4} $$
(4)

where a2 and b2 (a2 > 0, b2 > 0) are the system parameters.

The potential functions of two systems are shown in Fig. 1a when the system parameters are set as a1 = b1 = a2 = b2 = 1, where the blue solid line represents the potential function curve of the piecewise linear system, and the red dotted line represents the potential function curve of the bistable system. As shown in Fig. 1a, these two systems have two identical stable equilibrium points \(X_{ \pm }^{*}\) and one identical unstable equilibrium point \(X_{0}^{*}\). Also, the depth and width of the potential well are identical, which can be adjusted by the system parameters a1, b1 and a2, b2.

Fig. 1
figure 1

Comparison of the two systems: a the potential functions of the piecewise linear system and the bistable system, b the SNRs of the output versus noise intensity D

Full size image

Corresponding to the systems in Fig. 1b, take the input signal s(t) = Acos(2πft) as an example, where f = 0.01, A = 0.5. Figure 1b shows the output SNR curves of these two system responses versus to noise intensity D, in which the optimal output SNRs of the piecewise linear system and the bistable system are obtained as 0.76 and 0.06 when D = 0.12, respectively. The results indicate that the optimal output SNR of the piecewise linear system is larger than that of the bistable system and has better performance in signal enhancement.

Therefore, the piecewise linear system is taken as the potential function. Equation (1) represents the dynamic equation driven by a system, a periodic driving force and noise. If the potential function U0(x0) in Eq. (1) is replaced with U1(x), it is called the piecewise linear SR dynamic equation. Equation (1) satisfies the small parameter conditions of classical SR, that is, the signal frequency f0 and amplitude A0 should be far less than 1. In practical engineering, the signal frequency is generally high which cannot satisfy the conditions for SR.

The high-frequency signal s(t) is used to simulate the real signal, and the piecewise linear system under its excitation is expressed as:

$$ \frac{{{\text{d}}x(t)}}{{{\text{d}}t}} = C(a_{1} ,b_{1} ) + s(t) + \sqrt {2D} \xi (t) $$
(5)

where \(C(a_{1} ,b_{1} ) = \left\{ \begin{gathered} - \frac{{\sqrt {a_{1}^{3} } }}{{4(\sqrt 2 - 1)\sqrt {b_{1} } }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x < - \sqrt {a_{1} /b_{1} } \hfill \\ \frac{{\sqrt {a_{1}^{3} /b_{1} } }}{4}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sqrt {a_{1} /b_{1} } \le {\kern 1pt} x < 0 \hfill \\ - \frac{{\sqrt {a_{1}^{3} /b_{1} } }}{4}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\kern 1pt} x < \sqrt {a_{1} /b_{1} } \hfill \\ \frac{{\sqrt {a_{1}^{3} } }}{{4(\sqrt 2 - 1)\sqrt {b_{1} } }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \ge \sqrt {a_{1} /b_{1} } \hfill \\ \end{gathered} \right.\) and s(t) = Acos(2πft).

Here we introduce variable substitution x(t) = z(τ), τ = mt, Eq. (5) is expressed as:

$$ \frac{{{\text{d}}z(\tau )}}{{{\text{d}}\tau }} = \frac{1}{m}C(a_{1} ,b_{1} ) + \frac{A}{m}\cos (\frac{2\pi f\tau }{m}) + \sqrt {2D} \xi (\frac{\tau }{m}) $$
(6)

Let \(a_{3} = \frac{{a_{1} }}{m}\), \(b_{3} = \frac{{b_{1} }}{m}\), \(f_{3} = \frac{f}{m}\), Eq. (6) is written as:

$$ \frac{{{\text{d}}z(\tau )}}{{{\text{d}}\tau }} = C(a_{3} ,b_{3} ) + \frac{A}{m}\cos (2\pi f_{3} \tau ) + \sqrt{\frac{2D}{m}} \xi (\tau ) $$
(7)

where m is the scale coefficient. Compared with Eq. (5), the signal amplitude A/m and noise intensity D/m are reduced to 1/m of the original ones, the system parameters a3, b3 and signal frequency f3 satisfy the small parameter conditions in time scale τ. To match to the classical small parameter SR conditions [see Eq. (1)], the signal amplitude A/m and noise intensity D/m are recovered to the original amplitudes. Therefore, the signal amplitude A/m and noise intensity D/m in Eq. (7) are amplified by m times, there is

$$ \frac{{{\text{d}}z(\tau )}}{{{\text{d}}\tau }} = C(a_{3} ,b_{3} ) + A\cos (2\pi f_{3} \tau ) + \sqrt {2D} \xi (\tau ) $$
(8)

Mathematically, it is equivalent to amplifying the signal by m times and the noise by \(\sqrt m\) times to obtain Eq. (8), which satisfies the small parameter conditions of classical SR and is equivalent to Eq. (1), in which SR will occur.

It is known from the statistical characteristics of a Gaussian white noise:

$$ \left\{ \begin{gathered} \left\langle {\xi (mt),\xi (0)} \right\rangle = \frac{1}{m}\delta (t) \hfill \\ \left\langle {\xi (t)} \right\rangle = 0,\left\langle {\xi (t),\xi (0)} \right\rangle = \delta (t) \hfill \\ \end{gathered} \right. $$
(9)

So, there is

$$ \xi (mt) = \sqrt {1/m} \xi (t) $$
(10)

Changing the time scale τ to the original time scale t, one gets

$$ \frac{{{\text{d}}x(t)}}{{{\text{d}}t}} = C(a_{1} ,b_{1} ) + mA\cos (2\pi ft) + \sqrt {2Dm} \xi (t) $$
(11)

Equation (11) is a large-parameter SR dynamic equation, which has the same dynamic features as Eq. (8), and it can detect and enhance the actual signal of any high frequency. As the large-parameter SR model in Eq. (11), the width and depth of the potential well in the system become larger. In order to ensure that the energy of Brownian particles can satisfy the transition energy in the model, it is necessary to amplify the amplitude and noise intensity of the input signal in equal proportion, as given in Eq. (11).

Quantum particle swarm optimization (QPSO) algorithm [47] is an intelligent optimization algorithm, which can optimize multiple parameters at the same time in parameter optimization. It can overcome the dependence of PSO algorithm on the parameters and the shortcomings of easy to fall into the local optimal solution, so it is widely used in parameter optimization. Here, SNR is selected as the fitness function in QPSO algorithm. QPSO algorithm takes the maximum SNR as the optimization objective to realize the optimal SR response, which can achieve the optimal enhancement of the characteristic signal. Since the signal processed by COA transforms to the signal in the angle domain, SNR in the angle domain is defined, which is similar to the SNR in the time domain, as follows:

$$ \left\{ \begin{gathered} {\text{SNR}} = 10\log \frac{{S(O_{{\text{c}}} )}}{{A(O_{{\text{c}}} )}} \hfill \\ S(O_{{\text{c}}} ) = \left| {X(g)} \right|^{2} \hfill \\ A(O_{{\text{c}}} ) = 1/2N\sum\limits_{p = 1}^{N} {(\left| {X(g - p)} \right|^{2} + \left| {X(g + p)} \right|^{2} )} \hfill \\ \end{gathered} \right. $$
(12)

where Oc, S(Oc), and A(Oc) are the characteristic order, the energy at Oc and the average energy within a certain range at Oc, respectively. g and X(g) are the position of the point where the characteristic order is located and the amplitude at g-th point of the signal in the order spectrum, respectively. N is the number of data points with left–right symmetry of the characteristic order Oc. SNR is the ratio of the energy of the characteristic signal to the average energy of the surrounding noise, reflecting the strength of the characteristic signal.

The classical adaptive cascaded SR is described as follows. Firstly, the weak signal submerged by noise is input to the nonlinear system for adaptive SR processing. Then, the output of the upper level system is input into the next level system for adaptive SR processing. The above steps are repeated to realize the adaptive cascade SR until the output meets the requirement. By cascading the system, the energy of the high-frequency noise in the original signal is transferred to the low characteristic frequency, so the weak characteristic signal is enhanced step by step. If the signal needed to be enhanced has complex frequency and the noise interference is strong, the classical adaptive cascade SR may perform poor in the signal enhancement and need more levels.

To overcome the problem above, VMD is introduced in cascaded SR. VMD adopts a non-recursive processing strategy, constructs and solves the constrained variational problem to decompose the signal into several amplitude-modulation-frequency-modulation (AM-FM) signals with different center frequencies. These AM-FM signals are called intrinsic mode functions (IMFs). By selecting characteristic IMF, we can realize the judgment and extraction of bearing fault characteristic signal under noise background. VMD has better decomposition accuracy of complex data and anti-noise performance than empirical mode decomposition. Therefore, we introduce VMD to decompose the signal components containing the characteristic information in the cascading process and select the characteristic IMF to put into the next level SR system, so as to simplify the cascading process and effectively enhance the weak characteristic signal.

2.2 The main idea of non-stationary signal processing

The main idea of non-stationary signal processing is shown in Fig. 2.

Fig. 2
figure 2

The main processing idea

Full size image

Firstly, the signal collected under variable speed condition of a faulty bearing is a non-stationary signal, that is, a non-periodic signal, which is difficult to be analyzed by Fourier transform method. Secondly, the non-stationary signal in the time domain is transformed into the stationary signal in the angle domain through signal resampling by COA technology. In this process, the aperiodic signal is effectively transformed into periodic signal for analysis. Then, in order to solve the problem of serious noise interference in the spectrum, MCKD is used as the signal preprocessing method to extract the unknown characteristic signal. Finally, the adaptive cascaded SR is used to process the fault characteristic signal of the previous step to realize the adaptive signal enhancement.

Herein, COA is a non-stationary signal analysis method in fault diagnosis [48]. The acceleration sensor and eddy current sensor synchronously collect the vibration signal and speed signal of the reference shaft. The two kinds of signals are processed through some signal preprocessing methods, respectively. The pulse time of equal angle sampling is determined by the signal resampling algorithm of the speed pulses, and the signal resampling in the angle time is realized by the interpolation algorithm. The non-stationary signal is effectively transformed to the stationary signal. The stationary signal processing method can be used to process. It is widely used in mechanical equipment fault diagnosis because of its convenience, low cost and good reliability. In analysis processing, a certain shaft is selected as the reference shaft, and its rotating frequency is used as the reference. The multiple frequency relative to the rotating frequency is called the order, which is defined as follows:

$$ O_{c} = \frac{{f_{c} }}{{f_{r} }}{ = }\frac{{f_{c} }}{{n_{r} /60}} $$
(13)

where Oc and fc represent the characteristic order and the characteristic frequency, respectively. fr and nr represent the rotating frequency of the reference shaft and the rotating speed of the reference shaft, respectively. The characteristic order represents the vibration characteristics which is independent of the rotating frequency.

The order is defined as the number of vibrations in per revolution of the reference shaft. The equations of the order of different types of a faulty bearing are shown in Eq. (14)

$$ \left\{ \begin{gathered} O_{i} = \frac{{f_{i} }}{{f_{r} }} = \frac{1}{2}(1 + \frac{{D_{b} }}{{D_{c} }}\cos \beta )z \hfill \\ O_{o} = \frac{{f_{o} }}{{f_{r} }} = \frac{1}{2}(1 - \frac{{D_{b} }}{{D_{c} }}\cos \beta )z \hfill \\ O_{b} = \frac{{f_{b} }}{{f_{r} }} = \frac{1}{2}\frac{{D_{c} }}{{D_{b} }}(1 - \frac{{D_{b}^{2} }}{{D_{c}^{2} }}\cos^{2} \beta ) \hfill \\ \end{gathered} \right. $$
(14)

where Oi, Oo and Ob represent the theoretical fault characteristic order of the inner raceway, outer raceway, and rolling element of rolling bearing, respectively; Db and Dc represent the diameter of the rolling element and the pitch diameter of the bearing, respectively. β and z represent the contact angle and the number of rolling elements, respectively; fi, fo and fb represent the bearing fault frequency of the inner raceway, outer raceway, and rolling element, respectively. In Eq. (14), different types of fault characteristic orders are irrelevant to the speed working conditions of the shaft, but only with the inherent parameters of the bearing. Therefore, this method is widely used in bearing fault diagnosis under variable speed condition.

MCKD is the maximum correlation kurtosis deconvolution, which is a technology developed on the basis of the minimum entropy deconvolution method. It is an effective method to extract periodic pulses by deconvolution to highlight continuous pulses submerged by strong noise background. In this paper, MCKD is used as a preprocessing method for the weak characteristic signal. SNR is a commonly evaluation index for signals, which can only be used for the measurement of known signals but cannot measure unknown signals. Due to the interference of strong noise, the fault characteristics are always unknown. Therefore, MCKD is used as the signal preprocessing algorithm to extract the unknown fault characteristics. Proper shifts and pulse signal period are chosen to achieve good noise reduction and highlight weak characteristic signals.

2.3 The detail process for the method

The overall technical route is shown in Fig. 3, which is mainly divided into the following steps:

Fig. 3
figure 3

The flow chart of the proposed method

Full size image

  • Step 1: Collect the vibration signal of the faulty bearing and the speed pulse signal of the reference shaft synchronously by the acceleration sensor and the eddy current sensor.

  • Step 2: Preprocess the vibration signal and speed pulse signal, respectively. Determine the resampling time of equal angle through the correlation calculation of speed pulse signal, select the proper resampling frequency, resample the vibration signal through interpolation algorithm to obtain a stationary signal in the angle domain, where the non-stationary vibration signal in the time domain is transformed into a stationary signal in the angle domain.

  • Step 3: MCKD is used to deconvolute the stationary signal in the angle domain. The proper pulse shift and period are selected to highlight the fault characteristic order. Identify the fault characteristic order in the output order spectrum.

  • Step 4: The piecewise linear system is used as the SR model, and the stationary signal in the angle domain processed in step 3 is input into the SR model. Herein, SNR is chosen as the fitness function, and QPSO algorithm is used to adaptively adjust the system parameters to achieve the optimal resonance output.

  • Step 5: The cascade mechanism is adopted to connect multiple SR models in series, and VMD is applied to filter out the interference signal. Process the output of the upper level SR system by VMD, select the component containing fault characteristics, then input the component into the next level SR system to enhance the fault characteristics step by step.

3 Numerical simulation analysis of bearing fault diagnosis under variable speed condition

According to the simulated signal equation of bearing outer raceway fault under variable speed condition proposed by Feng et al. [49], we propose the simulated signal of bearing outer raceway fault under linear rising-stable-linear declining condition, as follows:

$$ \left\{ \begin{gathered} w(t) = \sum\limits_{{m_{1} = 1}}^{{M_{1} }} {A_{{m_{1} }} \exp \{ - 2{\uppi }\beta f_{{\text{n}}} [t - v_{{m_{1} }} (t)]\} \sin \{ 2{\uppi }f_{{\text{n}}} [t - v_{{m_{1} }} (t)]} {\kern 1pt} + \phi \} u[t - v_{{m_{1} }} (t)] \hfill \\ v_{{m_{1} }} = \sum\limits_{j = 1}^{{m_{1} }} {T_{j} } \hfill \\ \end{gathered} \right. $$
(15)

where Am1 and fn are the amplitude of the m1-th fault pulse and the natural frequency of the bearing, respectively; β and u(t) are the damping coefficient and unit step function, respectively; Tj, w(t) and vm1 are the repetition period of the j-th pulse at the moment of occurrence, the simulated fault characteristic signal and pulse time. The simulation parameters are set as fs = 10,240 Hz, β = 12,000, fn = 2000 Hz, Am1 = 0.02 fr, \(\phi\) = 0.

The simulated rotational frequency is set as \(f_{r} = \left\{ \begin{gathered} 15t{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 < t \le 1) \hfill \\ 15{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 < t \le 3) \hfill \\ 60 - 15t{\kern 1pt} {\kern 1pt} (3 < t \le 4) \hfill \\ \end{gathered} \right.\), which satisfies the following equation:

$$ \int_{0}^{{v_{{m_{1}}} }} {2{\uppi }f_{r}} {\text{d}} t = 2{\uppi }i $$
(16)

where i represents the number of revolutions of the bearing, and the fault characteristic order is assumed to be 5 × . Considering the amplitude modulation phenomenon, Am1 is assumed as 0.02fr. In the simulated process, in order to facilitate the analysis, the signal amplitude and the amplitude by Fourier transform are all set as dimensionless numbers, which are uniformly expressed by “Amplitude.”

The simulated fault signal is shown in Fig. 4, where Fig. 4a and c are the time-domain waveform and spectrum of the raw simulated fault signal, respectively. Figure 4(b) is corresponding speed curve. Gaussian white noise with a noise intensity of 0.25 is added to the simulated fault signal to simulate the strong noise background. Figure 4d and f are the time domain waveform and spectrum of the simulated fault signal submerged by noise, respectively. Figure 4e represents the key-phase signal.

Fig. 4
figure 4

The simulated signal of bearing outer raceway fault: a the time domain waveform (without noise), b the speed signal, c the spectrum (without noise), d the time domain waveform (with noise), e the key-phase signal, f the spectrum (with noise)

Full size image

Due to the influence of speed fluctuations and strong noise, we cannot obtain the relevant information about the fault characteristics. Therefore, the simulated signal submerged by noise is analyzed and processed in Fig. 5. The non-stationary signal in the time domain is transformed into a stationary signal in the angle domain, as shown in Fig. 5a and b. The fault characteristic order [5 ×] is completely submerged by noise and cannot be observed in Fig. 5b. Then, the angle domain signal is processed by resonance demodulation, as shown in Figs. 5c and d. The low-frequency components are removed by high-pass filtering, where the results are shown in Figs. 5e and f. Due to the interference of strong background noise, it is impossible to obtain information about the fault characteristics through resonance demodulation. Therefore, an effective filtering method that highlights periodic features-MCKD is used to process the angle domain signal to highlight the periodic fault characteristic components in the noisy signal. The results of the processing are shown in Fig. 5g and h. In this case, the length of filter is 500, the deconvolution period is 5, and the offset is 1. The fault characteristic order [5 ×] is obviously highlighted, but there is still a lot of interference near the high order band in the order spectrum. Hence, the signal is processed by low-pass filtering, and the results are shown in Figs. 5i and j.

Fig. 5
figure 5

Signal preprocessing: a the angle domain waveform, b the order spectrum, c the angle domain waveform after demodulation, d the order spectrum after demodulation, e the angle domain waveform after filtered, f the order spectrum after filtered, g the angle domain waveform after MCKD processed, h the order spectrum after MCKD processed, i the angle domain waveform after filtered, j the order spectrum after filtered

Full size image

In order to enhance and highlight the fault characteristic order, adaptive SR is used to process the angular signal in Fig. 5i. Figure 6 shows the system output response by SR. It can be found that the fault characteristic order [5 ×] is significantly enhanced and the amplitude in the order spectrum is enhanced to 0.0077. Meanwhile, the optimized system parameters are a3 = 0.001, b3 = 0.0438, the scale coefficient m is 64.4479, and the output SNR is 13.6545.

Fig. 6
figure 6

The first-level SR processing results: a the angle domain waveform, b the order spectrum

Full size image

Then, the signal is decomposed by VMD. The decomposed result is shown in Fig. 7. From top to bottom, there are different IMFs, which are represented as IMF1 ~ IMF9 and residual signal in turn. In Fig. 7, the left side and the right side represent the angle domain waveform and the order spectrum of different IMFs. The fault characteristic order [5 ×] is observed in the order spectrum of IMF8, so the angle domain waveform of IMF8 is extracted as the input of the next level piecewise linear system for adaptive SR processing.

Fig. 7
figure 7

The angle domain waveforms (left) and the order spectrums (right) of IMFs by VMD processing

Full size image

According to the signal processing method in the detail process [see Sect. 2.3], the responses of the second-level SR and the third-level SR are shown in Fig. 8. Figure 8a shows that the amplitude of the fault characteristic order [5 ×] in the order spectrum is enhanced to 0.0658 by second-level SR processing. The system parameters are a3 = 0.0063, b3 = 0.4789, the scale coefficient m is 272.7031, and the output SNR is 14.7272. By VMD, the angle domain waveform of IMF8 is extracted and input into the third-level system for adaptive SR processing. In Fig. 8b, the amplitude of the fault characteristic order [5 ×] in the order spectrum is enhanced to 0.3382 by third-level SR processing. The system parameters are a3 = 0.001, b3 = 0.7234, the scale coefficient m is 163.1320, and the output SNR is 15.4451.

Fig. 8
figure 8

Comparison of the results of SR processing: a the second level, b the third level

Full size image

Comparing the output results of the three-level cascade SR, it can be found that with the gradual increase of coupled level, the amplitude and SNR of the fault characteristic signal in the order spectrum increase step by step. Through the three-level cascade SR processing, the fault characteristic signal has been significantly enhanced and noise interference are filtered out.

4 Experimental verifications

The effectiveness of the above method is verified by two groups of measured bearing fault data. The experimental setup is shown in Fig. 9. The experimental platform is mainly composed of a 198 BGL series spindle servo motor, a 5E103-type eddy current sensor, a 1A206-type acceleration sensor, a laptop, two N306E-type fault bearings, a NI9234-type signal acquisition card, a frequency converter, etc. For the acceleration sensor and eddy current sensor, the collected vibration signal and the speed signal are displayed in the form of voltage, and the unit is “mv”. This paper mainly focuses on spectrum analysis, which does not affect the analysis results. So the amplitude is represented by “Amplitude” in the following figures. The frequency converter is used to control motor speed. It controls the motor to transfer force and torque to the faulty bearing through the coupling. We analyze the running state of the bearing by collecting the vibration signal and the speed pulse signal of the reference shaft synchronously. The sampling frequency is set as 10,240 Hz. As shown in Fig. 9, the types of bearing faults are bearing outer raceway scratch (dimension: 1.5 × 1 mm (width × depth)) and rolling element scratch (dimension: 1.5 × 1 mm (width × depth)), respectively.

Fig. 9
figure 9

The experiment settings and bearing fault types

Full size image

Table 1 shows the structural parameters of N306E bearing. According to Eq. (14), the theoretical fault characteristic orders of the bearing outer raceway fault, inner raceway fault and rolling element fault are calculated as 4.44 × , 6.56 × , 5.01 × , respectively.

Table 1 The structural parameters of the bearing
Full size table

The experiment selects fault characteristic signals of the bearing outer raceway and rolling element to verify the above-mentioned method. The experimental steps are as follows:

  • Step 1: As shown in Fig. 9, install the faulty bearing, and perform debug on the sensor, signal acquisition card and laptop.

  • Step 2: The frequency converter is used to control the three-phase motor to produce the speed characteristics of linear rising–steady–linear falling (the speed of the test outer raceway fault is 1420–1500 r/min, and the speed of the test rolling element fault is 1350–1500 r/min). The eddy current sensor is placed in front of the reference shaft with a fixed frame to collect the key-phase signal generated by the rotation speed of the reference shaft. The acceleration sensor is placed directly above the bearing pedestal to collect the vibration signal generated by the rotation of the bearing.

  • Step 3: Collect and save the measured vibration signal data and key-phase signal data through the laptop, and analyze the collected signals by MATLAB and LabVIEW.

4.1 The experimental signal of bearing outer raceway fault

For the experimental signal of bearing outer raceway fault, Gaussian white noise with intensity of 1 is added into the experimental signal to simulate external interference noise, as shown in Fig. 10. Figure 10a and c are the time domain waveform and spectrum of the experimental signal, respectively. Figure 10b and d are the key-phase signal collected by the eddy current sensor and the calculated speed signal, respectively. It is obvious that the fault signal is generated by the speed regulation in the range of 1420–1500 r/min to simulate the bearing operating condition under variable speed condition in Fig. 10d.

Fig. 10
figure 10

The experimental signal of bearing outer raceway fault: a the time domain waveform (with noise), b the key-phase signal, c the spectrum (with noise), d the speed curve

Full size image

As shown in Fig. 11, the vibration signal is preprocessed. First, the non-stationary vibration signal in the time domain is transformed into a stationary signal in the angle domain by COA in Fig. 11a and b, and it is found that the fault characteristic order [4.44 ×] is completely submerged by noise. After resonance demodulation processing in Fig. 11c and d, the fault features still cannot be observed, and high-pass filtering processing in Fig. 11d and e is performed. The filtered signal is preprocessed by MCKD in Figs. 11g and h. Meanwhile, the length of the filter is 620, the deconvolution period is 5 and the offset is 1. The high-frequency interference component is filtered by low-pass filtering in Figs. 11i and j.

Fig. 11
figure 11

Signal preprocessing: a the angle domain waveform, b the order spectrum, c the angle domain waveform after demodulation, d the order spectrum after demodulation, e the angle domain waveform after filtered, f the order spectrum after filtered, g the angle domain waveform after MCKD processed, h the order spectrum after MCKD processed, i the angle domain waveform after filtered, j the order spectrum after filtered

Full size image

The process of adaptive cascaded SR to enhance the experimental signal is consistent with the method in Sect. 3. The angular signal in Fig. 11i is input into the next system for adaptive SR processing. To make the overall content concise and clear, we only give the output order spectrum of the first-level, second-level and third-level SR in the subsequent processing. Figure 12a shows the result of the first-level SR processing, where the amplitude of the fault characteristic order [4.44 ×] increases to 0.0019. The system parameters are a3 = 0.0001, b3 = 0.3459, the scale coefficient m is 58.3713, and the output SNR is 13.5686. Figure 12b shows the result of the second-level SR processing. The amplitude of the fault characteristic order [4.44 ×] increases to 0.1168. The system parameters are a3 = 0.0033, b3 = 0.5780, the scale coefficient m is 756.7491 and the output SNR is 14.5981. Figure 12c shows the result of the third-level SR processing. The amplitude of the fault characteristic order [4.44 ×] increases to 0.8259. The system parameters are a3 = 0.8555, b3 = 0.0086, the scale coefficient m is 872.8246, and the output SNR is 14.6151.

Fig. 12
figure 12

Comparison of the results of three-level SR processing: a the first level, b the second level, c the third level

Full size image

The results are consistent with the results of the simulated fault signal. Comparing the output results of three-level cascade SR, it is found that with the gradual increase of coupled levels, the amplitude and SNR of the fault characteristic order [4.44 ×] gradually increase. Through three-level cascade SR processing, the fault characteristic signal has been significantly enhanced.

4.2 The experimental signal of bearing rolling element fault

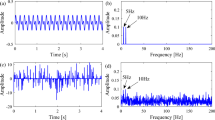
Similarly, the experimental signal of rolling element scratch fault is collected to verify. The vibration signal of bearing running is collected by setting the speed of 1350 r/min–1500 r/min. Then, Gaussian white noise with noise intensity of 1.5 is added into the experimental signal to simulate the strong interference noise. Figure 13 shows the experimental signal of bearing rolling element fault. From the speed curve in Fig. 13d, it is found that the vibration signal is non-stationary, from which the useful characteristic information is unable to obtained.

Fig. 13
figure 13

The experimental signal of bearing rolling element fault: a the time domain waveform (with noise), b the key-phase signal, c the spectrum (with noise), d the speed curve

Full size image

The enhancement results on the fault characteristic signal of bearing rolling element are shown in Fig. 14, which are the output order spectrums of the first-level, the second-level and the third-level SR processing, respectively. Figure 14a shows the result of the first-level SR processing, where the amplitude of the fault characteristic order [5.01 ×] increases to 0.0018. The system parameters are a3 = 0.001, b3 = 0.2776, the scale coefficient m is 117.6515, and the output SNR is 13.6233. Figure 14b shows the result of the second-level SR processing, where the amplitude of the fault characteristic order [5.01 ×] increases to 0.0529. The system parameters are a3 = 0.0033, b3 = 0.5780, the scale coefficient m is 756.7491, and the output SNR is 14.5981. Figure 14c shows the result of the third-level SR processing, where the amplitude of the fault characteristic order [5.01 ×] increases to 0.7850. The system parameters are a3 = 0.3888, b3 = 5, the scale coefficient m is 1654.36, and the output SNR is 16.6719.

Fig. 14
figure 14

Comparison of the results of three-level SR processing: a the first level, b the second level, c the third level

Full size image

Comparing the output results of three-level cascaded SR, it is found that with the gradual increase of coupled levels, the amplitude and SNR of fault characteristic order [5.01 ×] gradually increase. Through three-level cascaded SR processing, the fault characteristic signal has been significantly enhanced.

5 Conclusions

In this paper, extracting the non-stationary bearing fault characteristic information by the stochastic response of coupled oscillators is studied, where an adaptive cascade SR method is proposed to extract weak fault characteristic information step by step. The effectiveness of this fault diagnosis method is verified by numerical simulation and experimental verification. The main conclusions are as follows:

  1. (1)

    Using COA to transform the non-stationary signal reflecting bearing fault characteristics under variable speed condition in the time domain into a stationary signal in the angle domain, which can effectively reduce the difficulty of feature extraction.

  2. (2)

    The advanced signal processing method, i.e. MCKD, is applied to extract the non-stationary unknown bearing fault characteristic information under strong noise background. By MCKD, the fault characteristic information in the angle domain is effectively extracted and whether a fault exists and the type of bearing fault under variable speed condition is accurately judged.

  3. (3)

    A cascade SR mechanism is proposed to enhance fault characteristic information, which is to introduce VMD into adaptive SR in the cascade piecewise linear system. By VMD, the interference signal of the signal is gradually filtered out. Through the cascade mechanism, the weak bearing fault characteristic signals are effectively enhanced step by step.

It is worth noting that VMD is used to process the enhanced signal at each level. For different IMFs, we only need to focus on extracting the IMF containing the fault feature information, which effectively represents the state of the bearing. Then, by the signal enhancement mechanism of adaptive SR, the high-order noise energy is transferred to the characteristic order and the fault characteristic information is effectively enhanced. The method can not only be used in the bearing fault diagnosis but also other rotary parts of the equipment.