1 Introduction

Weak fault characteristic extraction, as a challenge in mechanical fault detection, has attracted sustaining attention. Up to now, adopting effective signal processing methods to extract weak fault characteristics embedded in signals has become a widely used strategy in mechanical fault detection [1, 2]. To do this, lots of the advanced signal processing methods have been proposed by the scholars in the field of signal processing and mechanical fault diagnosis, such as singular value decomposition [3], wavelet denoising [4], kurtogram [5] and maximum correlated kurtosis deconvolution [6]. However, most of them aim to cancel or suppress rather than utilize the noise imbedded in a signal for extracting weak fault characteristics. Thus, there are two drawbacks for them: (1) weak fault characteristics would be inevitably damaged more or less in the denoising process due to the intrinsic properties of noise cancellation or suppression-based signal processing methods; (2) strong background noise may reduce the reliability and robustness of noise cancellation or suppression-based signal processing methods in weak fault characteristic extraction.

Different from noise cancellation or suppression-based signal processing methods, stochastic resonance (SR) [7, 8] is able to harvest the energy of noise for enhancing weak fault characteristics embedded in signals [9,10,11,12]. Therefore, it has been extensively investigated and widely applied to mechanical fault detection [13,14,15], and some significant achievements have been achieved [16,17,18]. To date, the methodologies applied SR to mechanical fault detection almost can be categorized into integer-order SR methods including first-order and second-order ones.

Among them, since the second-order SR characterizes nonlinear band-pass filtering property instead of the low-pass one of first-order SR [19], it can utilize the multiscale noise located at the different frequency bands to enhance weak fault characteristics and is superior to first-order SR in mechanical fault detection. For example, Li et al. [20] proposed a noise-controlled second-order SR method for wind turbine drivetrain fault diagnosis. Qin et al. [21] used second-order SR with different frequency-scale ratios to separate different components embedded in a vibration signal for extracting rotor fault characteristics. Rebolledo-Herrera and Espinosa FV [22] developed a second-order tuning SR method to enhance weak characteristics embedded in signals. Lei et al. [23] proposed a second-order SR method with stable-state matching to diagnose incipient faults of train wheel bearings. López et al. [24] developed a second-order SR method with a FitzHugh–Nagumo potential to detect rolling element bearing defects. Elhattab et al. [25] employed frequency-independent second-order SR method with pinning potentials for drive-by-bridge inspection under operational roadway speeds. However, the second-order SR and even integer-order SR neglect high dependence among the values of a mechanical state variable and are unable to utilize such a dependence to enhance weak fault characteristics embedded in a signal that records the values of a mechanical state variable as time varies.

As we all know, mechanical degradation process is continuous where mechanical current value of a state variable, e.g., vibration, is highly dependent on its previous values. Assuming that SR is able to utilize the dependence among the values of the mechanical state variable to enhance weak fault characteristics, the potential of SR in mechanical fault detection would be further improved to outperform integer-order SR. Inspired by fractional-order derivative that characterizes memory-dependent property and reflects the high dependence between current and previous values of the state variable of a system [26, 27], the fractional-order derivative [28] would be incorporated into a second-order SR model to improve the capability of SR for weak fault characteristic extraction. Numerical simulation and experimental results demonstrate that the proposed method outperforms the integer-order SR methods, even kurtogram and maximum correlated kurtosis deconvolution in extracting weak fault characteristics of machinery overwhelmed by strong background noise.

The remainder of this paper is organized as follows: Section 2 builds an improved second-order SR model induced by fractional-order derivative and further proposes a second-order SR method enhanced by fractional-order derivative to extract weak fault characteristics embedded in signals for mechanical fault detection. In Sect. 3, numerical simulations are performed to illustrate the superiority of both the improved second-order SR model and the proposed method. In Sect. 4, two experiments including a bearing with slight flaking on the outer race and a gear with scuffing from wind turbine drivetrain are performed to validate the effectiveness of the proposed method. Conclusions are drawn in Sect. 5.

2 A second-order SR method enhanced by fractional-order derivative

First, an improved second-order SR model is built by incorporating fractional-order derivative into a second-order bistable SR model. Moreover, the numerical solution method for the improved second-order SR model is given. Second, based on the improved second-order SR model, a second-order SR method enhanced by fractional-order derivative is proposed for mechanical fault detection, and its detailed procedures and flowchart are provided.

2.1 An improved second-order SR model

As a widely used SR model, the second-order SR model with the classical bistable potential can be described as:

$$ {{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = - \gamma {{{\text{d}}x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}x\left( t \right)} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} - {{\partial U\left( x \right)} \mathord{\left/ {\vphantom {{\partial U\left( x \right)} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} + A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right), $$
(1)

where \(\gamma\) denotes the damping ratio and \(\gamma > 0\), \(\xi \left( t \right)\) is the stochastic noise with zero mean and variance \(D\) and \(U\left( x \right)\) is the classical bistable potential

$$ U\left( x \right) = - {{ax^{2} } \mathord{\left/ {\vphantom {{ax^{2} } 2}} \right. \kern-\nulldelimiterspace} 2} + {{bx^{4} } \mathord{\left/ {\vphantom {{bx^{4} } 4}} \right. \kern-\nulldelimiterspace} 4}, $$
(2)

where \(a > 0\) and \(b > 0\) are the potential parameters.

In the absence of the weak characteristic \(A\cos \left( {\Omega t + \varphi } \right)\) with amplitude \(A\), characteristic frequency \(\Omega\) and phase \(\varphi\), the noise-induced particle hopping rate between double potential wells can be quantified as [13]

$$ r_{K} \left( {\Delta U, \, x_{m} , \, D, \, \gamma } \right) = {{2\sqrt 2 \Delta U\exp \left( { - {{\Delta U} \mathord{\left/ {\vphantom {{\Delta U} D}} \right. \kern-\nulldelimiterspace} D}} \right)} \mathord{\left/ {\vphantom {{2\sqrt 2 \Delta U\exp \left( { - {{\Delta U} \mathord{\left/ {\vphantom {{\Delta U} D}} \right. \kern-\nulldelimiterspace} D}} \right)} {\left( {{\uppi }\gamma x_{m}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\uppi }\gamma x_{m}^{2} } \right)}}, $$
(3)

where \(\Delta U{ = }{{a^{2} } \mathord{\left/ {\vphantom {{a^{2} } {\left( {4b} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4b} \right)}}\) is the barrier height of classical bistable potential and \(x_{m} = \pm \sqrt {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b}}\) are the bottoms of potential wells that determine the potential-well width, i.e., \(2x_{m}\). In parameter-induced second-order SR, therefore, the potential-well width \(x_{m}\) and barrier height \(\Delta U\) in classical bistable potential jointly decide the time-scale matching condition to trigger SR for amplifying the weak characteristic embedded in a noisy signal

$$ T_{\Omega } = {{2{\uppi }} \mathord{\left/ {\vphantom {{2{\uppi }} \Omega }} \right. \kern-\nulldelimiterspace} \Omega } = 2T_{K} = {2 \mathord{\left/ {\vphantom {2 {r_{K} }}} \right. \kern-\nulldelimiterspace} {r_{K} }}. $$
(4)

Considering the effect of potential-well width \(x_{m}\) and barrier height \(\Delta U\) on the time-scale matching condition in Eq. (4), the classical bistable potential in Eq. (2) is rewritten as:

$$ U\left( x \right) = - \Delta U\left[ {2\left( {{x \mathord{\left/ {\vphantom {x {x_{m} }}} \right. \kern-\nulldelimiterspace} {x_{m} }}} \right)^{2} - \left( {{x \mathord{\left/ {\vphantom {x {x_{m} }}} \right. \kern-\nulldelimiterspace} {x_{m} }}} \right)^{4} } \right]. $$
(5)

Hence, Eq. (1) can be transformed into the following equivalent equation

$$ {{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = - \gamma {{{\text{d}}x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}x\left( t \right)} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} + 4\Delta U\left[ {{{x\left( t \right)} \mathord{\left/ {\vphantom {{x\left( t \right)} {x_{m}^{2} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{2} }} - {{x^{3} \left( t \right)} \mathord{\left/ {\vphantom {{x^{3} \left( t \right)} {x_{m}^{4} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{4} }}} \right] + A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right). $$
(6)

According to Eq. (6), one can adjust the potential-well width \(x_{m}\) and barrier height \(\Delta U\) to trigger SR for enhancing the weak characteristic \(A\cos \left( {\Omega t + \varphi } \right)\) embedded in the noisy signal \(A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right)\). Although second-order SR is able to utilize the multiscale noise located at different frequency bands to amplify the weak characteristic, it neglects the dependence among the values of the mechanical state variable and is unable to utilize the dependence to enhance the weak characteristic.

Inspired by fractional-order derivative that characterizes memory-dependent property and reflects the high dependence between current and previous values of the state variable of a system [29, 30], an improved second-order SR model is established by incorporating the fractional-order derivative into the second-order bistable SR model in Eq. (6)

$$ {{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = - \gamma {{{\text{d}}^{\alpha } x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{\alpha } x\left( t \right)} {{\text{d}}t^{\alpha } }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{\alpha } }} + 4\Delta U\left[ {{{x\left( t \right)} \mathord{\left/ {\vphantom {{x\left( t \right)} {x_{m}^{2} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{2} }} - {{x^{3} \left( t \right)} \mathord{\left/ {\vphantom {{x^{3} \left( t \right)} {x_{m}^{4} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{4} }}} \right] + A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right), $$
(7)

where \(\alpha\) denotes the fractional order and \(\alpha \in \left( {0, \, 2} \right]\). To discretize the above equation for numerical solution, Eq. (7) can be rewritten as the following equivalent equation

$$ \left\{ {\begin{array}{*{20}l} {{{{\text{d}}^{\alpha } x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{\alpha } x\left( t \right)} {{\text{d}}t^{\alpha } }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{\alpha } }} = y\left( t \right).} \hfill \\ {{{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = {{{\text{d}}^{\beta } y\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{\beta } y\left( t \right)} {{\text{d}}t^{\beta } }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{\beta } }}, \, \beta { = 2 - }\alpha .} \hfill \\ {{{{\text{d}}^{\beta } y\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{\beta } y\left( t \right)} {{\text{d}}t^{\beta } }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{\beta } }} = - \gamma y\left( t \right) + 4\Delta U\left[ {{{x\left( t \right)} \mathord{\left/ {\vphantom {{x\left( t \right)} {x_{m}^{2} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{2} }} - {{x^{3} \left( t \right)} \mathord{\left/ {\vphantom {{x^{3} \left( t \right)} {x_{m}^{4} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{4} }}} \right] + A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right).} \hfill \\ \end{array} } \right. $$
(8)

Among many definitions of fractional-order derivatives including Riemann–Liouville definition, Grünwald–Letnikov definition and Caputo definition, the widely used Grünwald–Letnikov definition is employed to discretize Eq.(8) for solving it numerically. The Grünwald–Letnikov fractional-order derivative of \(x\left( t \right)\) is defined as [31]:

$$ \frac{{{\text{d}}^{\alpha } x\left( t \right)}}{{{\text{d}}t^{\alpha } }}\left| {_{t = kh} } \right. = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)x\left( {kh - jh} \right)} , $$
(9)

where \(h\) stands for the time step and \(\left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\) is a binomial coefficient and can be written as:

$$ \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right) = \frac{{\Gamma \left( {\alpha + 1} \right)}}{{\Gamma \left( {j + 1} \right)\Gamma \left( {\alpha - j + 1} \right)}}, $$
(10)

where \( \Gamma \left( \right)\) denotes the Gamma function. Here, if \(\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\) is notated as \(\omega_{j}^{\alpha }\), Eq. (8) can be obtained

$$ \omega_{0}^{\alpha } { = }1,\,\,\omega_{k}^{\alpha } = \left[ {1 - {{\left( {\alpha + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\alpha + 1} \right)} k}} \right. \kern-\nulldelimiterspace} k}} \right]\omega_{k - 1}^{\alpha } ,\,\,k = 1, \, 2, \, \ldots , \, n. $$
(11)

where \(n\) is the length of the noisy signal \(A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right)\). Substituting Eq. (11) into Eq. (9), one can obtain

$$ \frac{{{\text{d}}^{\alpha } x\left( t \right)}}{{{\text{d}}t^{\alpha } }}\left| {_{t = kh} } \right. = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\alpha } }}\left[ {x\left( {kh} \right) + \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\alpha } x\left( {kh - jh} \right)} } \right]. $$
(12)

According to Euler formula, substituting Eq. (12) into Eq. (8), under zero initial conditions one can obtain

$$ \left\{ {\begin{array}{*{20}l} {\mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\alpha } }}\left[ {x\left( k \right) + \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\alpha } x\left( {k - j} \right)} } \right] = y\left( {k - 1} \right),} \hfill \\ {\mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\beta } }}\left[ {y\left( k \right) + \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\beta } y\left( {k - j} \right)} } \right] = - \gamma y\left( {k - 1} \right) + 4\Delta U\left[ {\frac{{x\left( {k - 1} \right)}}{{x_{m}^{2} }} - \frac{{x^{3} \left( {k - 1} \right)}}{{x_{m}^{4} }}} \right] + F\left( {k - 1} \right),} \hfill \\ \end{array} } \right. $$
(13)

where \(F\left( t \right) = A\cos \left( {\Omega t + \varphi } \right) + \xi \left( t \right)\). For a small time step \(h\), the limitation operator of Eq. (13) can be reduced and Eq. (13) can be rewritten as:

$$ \left\{ {\begin{array}{*{20}l} {x\left( k \right) = - \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\alpha } x\left( {k - j} \right) + } h^{\alpha } y\left( {k - 1} \right).} \hfill \\ {y\left( k \right) = - \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\beta } y\left( {k - j} \right)} + h^{\beta } \left[ { - \gamma y\left( {k - 1} \right) + 4\Delta U\left( {\frac{{x\left( {k - 1} \right)}}{{x_{m}^{2} }} - \frac{{x^{3} \left( {k - 1} \right)}}{{x_{m}^{4} }}} \right) + F\left( {k - 1} \right)} \right].} \hfill \\ \end{array} } \right. $$
(14)

Here, \(x\left( k \right)\), \(y\left( k \right)\) and \(F\left( k \right)\) are the corresponding discrete signals to continuous signal \(x\left( t \right)\), \(y\left( t \right)\) and \(F\left( t \right)\). Therefore, one can use Eq. (14) to numerically solve the response \(x\left( k \right)\) of the improved second-order SR model in Eq. (7). It can be seen from Eq. (14) that the response of the improved second-order SR model closely depends on the fractional order \(\alpha\), barrier height \(\Delta U\), potential-well width \(x_{m}\) and damping ratio \(\gamma\). The optimal combination of these parameters would make the improved second-order SR model produce the optimal response where the weak characteristic embedded in the noisy signal can be enhanced optimally and the noise embedded in the signal can be eliminated largely.

2.2 The proposed method

Based on the improved model in Sect. 2.1, a second-order bistable SR method enhanced by fractional-order derivative is proposed to enhance weak characteristic extraction for mechanical fault detection, where quantum genetic algorithms (QGAs) are employed to optimize its parameters because QGAs are derived from the fusion of both genetic algorithms and quantum computation and are superior to genetic algorithms [32, 33]. Even other scholars would attempt to employ the better intelligent algorithm to optimize these parameters in the future, e.g., deep learning. The flowchart of the proposed method is shown in Fig. 1, and its detailed procedures are described as follows.

Fig. 1
figure 1

The flowchart of a second-order SR method enhanced by fractional-order derivative for fault detection

Full size image

2.2.1 Parameter initialization

As we all know, when the time-scale matching condition between the weak fault characteristic embedded in the noisy signal \(F\left( t \right)\) with both the length \(K\) and the sampling frequency \(f_{{\text{s}}}\) and the noise-induced particle hopping rate \(r_{K}\) is satisfied, SR would be triggered to harvest the energy of noise for amplifying the weak fault characteristic. However, potential-well width \(x_{m}\), barrier height \(\Delta U\), damping ratio \(\gamma\) and fractional order \(\alpha\) jointly decide the magnitude of the noise-induced particle hopping rate \(r_{K}\). Therefore, QGAs are employed to optimize these parameters (\(\alpha , \, \gamma , \, \Delta U, \, x_{m}\)) for obtaining the optimal time-scale matching between the weak fault characteristic and the noise-induced particle hopping rate \(r_{K}\), amplifying the weak fault characteristic embedded in the signal \(F\left( t \right)\). Here, the population size \(N\), the length of each binary variable \(L\) and the terminal or maximal generation size \(G_{\max }\) of QGAs are initialized as 40, 20 and 50, respectively [23], where the objective function is the output SNR [13]. Potential-well width \(x_{m}\), barrier height \(\Delta U\), damping ratio \(\gamma\) and fractional order \(\alpha\) of the improved second-order SR model are initialized as \(x_{m} \in \left( {0, \, 100} \right]\), \(\Delta U \in \left( {0, \, 10} \right]\), \(\gamma \in \left( {0, \, 10} \right]\) and \(\alpha \in \left( {0, \, 2} \right]\) , respectively [22], to obtain as optimal as possible detection result.

2.2.2 Discretization and numerical solution

The acquired signal \(F\left( t \right)\) is fed into the improved second-order SR model

$$ {{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = - \gamma {{{\text{d}}^{\alpha } x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{\alpha } x\left( t \right)} {{\text{d}}t^{\alpha } }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{\alpha } }} + 4\Delta U\left[ {{{x\left( t \right)} \mathord{\left/ {\vphantom {{x\left( t \right)} {x_{m}^{2} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{2} }} - {{x^{3} \left( t \right)} \mathord{\left/ {\vphantom {{x^{3} \left( t \right)} {x_{m}^{4} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{4} }}} \right] + F\left( t \right). $$
(15)

Then, Eq. (15) can be discretized and solved numerically by using Eq. (16) under zero initial conditions

$$ \left\{ {\begin{array}{*{20}l} {x\left( k \right) = - \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\alpha } x\left( {k - j} \right) + } h^{\alpha } y\left( {k - 1} \right),} \hfill \\ {y\left( k \right) = - \sum\limits_{j = 1}^{k - 1} {\omega_{j}^{\beta } y\left( {k - j} \right)} + h^{\beta } \left[ { - \gamma y\left( {k - 1} \right) + 4\Delta U\left( {{{x\left( {k - 1} \right)} \mathord{\left/ {\vphantom {{x\left( {k - 1} \right)} {x_{m}^{2} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{2} }} - {{x^{3} \left( {k - 1} \right)} \mathord{\left/ {\vphantom {{x^{3} \left( {k - 1} \right)} {x_{m}^{4} }}} \right. \kern-\nulldelimiterspace} {x_{m}^{4} }}} \right) + F\left( {k - 1} \right)} \right],} \hfill \\ \end{array} } \right. $$
(16)

where \(h = {R \mathord{\left/ {\vphantom {R {f_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {f_{{\text{s}}} }}\) with the scaling factor \(R\) and \(k = 2,{ 3,} \ldots , \, K\). When \(k = 1\), \(x\left( k \right)\) and \(y\left( k \right)\) are initialized as zero. The scaling factor \(R\) should be slightly larger than the fault characteristic frequency to be detected for rescaling it into a small frequency that satisfies the detection range of SR, but it would make the response \(x\left( k \right)\) of the improved second-order SR model divergent if \(R\) is too large. Therefore, a moderate \(R\) should be given artificially according to the magnitude of fault characteristic frequency to be detected and generally satisfies the condition \(0 < R < f_{{\text{s}}}\).

2.2.3 Response quantification

The SNR of the response \(x\left( k \right)\) of the improved second-order SR model is calculated as the objective function of QGAs for guiding to optimize the parameters (\(\alpha , \, \gamma , \, \Delta U, \, x_{m}\)). The expression of SNR is written as [13]:

$$ {\text{SNR}} = 10\log_{10} \left[ {{{A_{{\text{d}}} } \mathord{\left/ {\vphantom {{A_{{\text{d}}} } {\left( {\sum\limits_{i = 1}^{{{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-\nulldelimiterspace} 2}}} {A_{i} } - A_{{\text{d}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sum\limits_{i = 1}^{{{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-\nulldelimiterspace} 2}}} {A_{i} } - A_{{\text{d}}} } \right)}}} \right], $$
(17)

where \(A_{{\text{d}}}\) is the amplitude at the fault characteristic frequency in the power spectrum of the response \(x\left( k \right)\), and \(\sum\nolimits_{i = 1}^{{{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-\nulldelimiterspace} 2}}} {A_{i} } - A_{{\text{d}}}\) denotes the sum of noise power at each spectrum line in the power spectrum of the response \(x\left( k \right)\). A higher SNR indicates a better enhancement result.

2.2.4 Terminal condition judgment

If the generation size \(G\) satisfies the condition \(G < G_{\max }\), then update the parameters (\(\alpha , \, \gamma , \, \Delta U, \, x_{m}\)) in their initialization ranges and go back to the step (3) in sect. 2.2.3, else output the maximum of SNR and the optimal parameters (\(\alpha_{{{\text{opt}}}} , \, \gamma_{{{\text{opt}}}} , \, \Delta U_{{{\text{opt}}}} , \, x_{m}^{{{\text{opt}}}}\)).

2.2.5 Fault characteristic extraction and fault recognition

The optimal parameters (\(\alpha_{{{\text{opt}}}} , \, \gamma_{{{\text{opt}}}} , \, \Delta U_{{{\text{opt}}}} , \, x_{m}^{{{\text{opt}}}}\)) are used to set the improved second-order SR model in Eq. (15) for obtaining the optimal improved second-order SR model. Then, Eq. (16) is employed to discretize the optimal improved second-order SR model in Eq. (15) and numerically solve its response \(x\left( k \right)\). Finally, the spectrum analysis is performed on the response \(x\left( k \right)\) to extract weak fault characteristics for recognizing fault locations.

3 Numerical simulations

In this section, two simulations are conducted to illustrate the superiority of the improved second-order SR model and to demonstrate the effectiveness of the proposed method based on the improved model, respectively.

3.1 Numerical illustration of improved second-order SR model

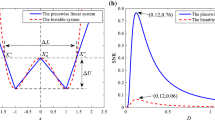
A sinusoidal signal with both the characteristic frequency \(f_{{\text{d}}} = 0.1{\text{ Hz}}\) and the amplitude \(A = 1\) plus stochastic noise with intensity \(D = 1\) is fed into the improved second-order SR model in Eq. (15). The sampling frequency is \(f_{{\text{s}}} = 10{\text{ Hz}}\) and the sampling time is \(t = 200{\text{ s}}\). The response of the improved second-order SR model can be obtained by using Eq. (16) where the time step is \(h = 0.1\). Its output SNR as a function of fractional order \(\alpha\) is shown in Fig. 2 where \(\Delta U = 0.5\) and \(x_{m} = 10\). It is seen from Fig. 2 that when \(\gamma { = }1.2\) and \(\gamma { = }0.5\) , respectively, output SNR starts to increase and then decreases as fractional order \(\alpha\) increases gradually, which is a typical feature of SR induced by fractional-order derivative. Such a behavior is first observed in a second-order bistable system induced by fractional-order derivative. Moreover, the maximum of output SNR is obtained at non-integer of \(\alpha\), suggesting that the fractional-order derivative is able to improve the potential of SR for weak characteristic extraction. Compared Fig. 2a with Fig. 2b, it is found that the SR induced by different damping ratios has a different capability to enhance the weak characteristic, e.g., two different maxima of output SNR in Fig. 2, indicating that there is an optimal damping ratio to maximize output SNR of the response of the improved second-order SR model for a given signal.

Fig. 2
figure 2

Output SNR versus fractional order \(\alpha\) of the improved second-order SR model with different damping ratios \(\gamma\): (a) \(\gamma = 1.2\) and (b) \(\gamma = {0}{\text{.5}}\)

Full size image

To observe the response of the improved second-order SR model induced by the pure sinusoidal signal plus stochastic noise, Fig. 3 shows the input signal and the corresponding responses of the improved second-order SR model to the maxima of output SNR in Fig. 2a, b, respectively. One can see from Fig. 3b, c that the noise embedded in the raw signal of Fig. 3a has been harvested by SR to enhance the periodic sinusoidal signal, where its amplitude is much larger than that of original pure sinusoidal signal. Moreover, the SR induced by different damping ratios would produce different detection results, e.g., Figure 3b where \(\gamma { = }1.2\) and Fig. 3c where \(\gamma { = }0.5\). Therefore, a suitable damping ratio is vital to extract the weak characteristic from the raw noisy signal.

Fig. 3
figure 3

a A noisy signal, b the corresponding response of improved second-order SR model to the maximum of SNR in Fig. 2a, c the corresponding response of the improved second-order SR model to the maximum of SNR in Fig. 2b

Full size image

In addition, Fig. 4 illustrates the frequency response properties of the improved second-order SR model induced by the stochastic noise with intensity \(D{ = }1\), where the sampling frequency is 10 kHz and the sampling time is 2 s. One can see from Fig. 4b that the spectrum lines of stochastic noise completely cover the whole frequency band in the range of \(\left[ {0,{{ \, f_{{\text{s}}} } \mathord{\left/ {\vphantom {{ \, f_{{\text{s}}} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right]\). However, when the stochastic noise is input into the improved second-order SR model, the main energy of its response is aggregated into a narrow frequency band, as shown in Fig. 4c. Moreover, the narrow frequency band is shifted from low-frequency band to high-frequency band as the scaling factor \(R\) amplifies. Such a behavior indicates that the improved second-order SR model inherits the advantage of second-order SR that characterizes the nonlinear band-pass filtering property. Therefore, the improved second-order SR model is able to not only suppress the multiscale noise but also use the fractional-order derivative to enhance second-order SR for extracting weak characteristics embedded in the signal. Even weak characteristics located at different frequency bands can be enhanced and extracted by tuning the scaling factor.

Fig. 4
figure 4

a A stochastic noise, b its frequency spectrum and c the frequency spectrum of the response of the improved second-order SR model solely induced by the stochastic noise under different scaling factors \(R\)

Full size image

3.2 Simulation demonstration of proposed method

Here, a series of transients is generated according to the following simulation model

$$ F\left( t \right) = B\left( t \right)\sum\limits_{q} {\chi \left( {t - {q \mathord{\left/ {\vphantom {q {f_{0} }}} \right. \kern-\nulldelimiterspace} {f_{0} }}} \right)} + \xi_{{{\text{band}}}} \left( t \right) + \xi \left( t \right), $$
(18)

where B(t) is the amplitude of the repetitive transients and \(B\left( t \right) = 1\), q stands for the number of the transients, f0 is the fault characteristic frequency and f0 = 56 Hz, \(\xi_{{{\text{band}}}} \left( t \right)\) is the band-limited noise for overwhelming the resonant frequency band of transients, \(\xi \left( t \right)\) is the stochastic noise for polluting the whole frequency band of transients, and \(\chi (t)\) is the periodic impulse response function given by

$$ \chi \left( t \right) = \left\{ {\begin{array}{*{20}l} {\exp \left( { - \beta_{w} t} \right)\sin \left( {2{\uppi }f_{re} t} \right), \, t > 0,} \hfill \\ {0, \, \,\,\,t \le 0,} \hfill \\ \end{array} } \right. $$
(19)

where \(\beta_{w}\) is the structural damping ratio and \(\beta_{w} = 666.67{\text{ Hz}}\), and \(f_{re}\) is the resonance frequency and \(f_{re} = 1683.4{\text{ Hz}}\). In this simulated case, the sampling frequency \(f_{{\text{s}}} = 12{\text{ kHz}}\) and the sampling time is 1 s.

The simulated repetitive transients are shown in Fig. 5a and its impulsive interval is equal to the reciprocal of fault characteristic frequency. The stochastic noise and band-limited noise are added into the pure repetitive transients, and then, the transients with noise are obtained, as shown in Fig. 5b. Moreover, the corresponding frequency spectrum and zoomed envelope spectrum are depicted in Fig. 5c, d, respectively. It can be seen from Fig. 5c that the resonant frequency band excited by transients is polluted by noise, especially band-limited noise, and the whole frequency band contains lots of interferences from noise. In the zoomed envelope spectrum of Fig. 5d, one can observe weak fault characteristic frequency and its obvious third harmonic.

Fig. 5
figure 5

Simulated signals: a a series of transients, b transients with noise, c the frequency spectrum and d zoomed envelope spectrum of transients with noise

Full size image

Since the weak fault characteristics of rolling element bearings are generally modulated into the resonant frequency band, the Hilbert demodulation technique is initially used to obtain the envelope of the corresponding transients with noise. Then, the proposed method is used to process the envelope, and the detected results are shown in Fig. 6, where \(\gamma = 0.1508\), \(R{ = }1000\), \(\alpha { = }0.05664\), \(\Delta U{ = }9.3231\) and \(x_{m} = 49.8072\). One can clearly see from Fig. 6b that the fault characteristic frequency 56 Hz is dominant in the whole frequency spectrum, which keeps consistent with the value of the simulated fault characteristic frequency, demonstrating the effectiveness of the proposed method for mechanical fault detection. Moreover, the optimal fractional order is \(\alpha { = }0.05664\), suggesting that the benefits of noise to mechanical fault detection are able to be enhanced by the fractional-order derivative and the SR induced by the fractional-order derivative outperforms that induced by integer-order derivative for weak characteristic extraction.

Fig. 6
figure 6

The detected results for a simulated signal using the proposed method: a time-domain waveform and b its zoomed frequency spectrum

Full size image

Kurtogram and maximum correlated kurtosis deconvolution are two advanced signal processing methods and have been widely applied to mechanical fault detection. For comparison, Figs. 7 and 8 show the detected results for a simulated signal using kurtogram and maximum correlated kurtosis deconvolution, respectively. One cannot observe the obvious spectral peaks at the fault characteristic frequency and its harmonics from the zoomed envelope spectrum in Fig. 7c and kurtogram fails to detect weak fault characteristics because it is difficult to exactly locate the resonant frequency band for removing the strong background noise. Meanwhile, it can be seen from Fig. 8 that weak fault characteristics are overwhelmed by strong background noise and the spectral peaks at the fault characteristic frequency and its harmonics cannot be identified from the zoomed envelope spectrum in Fig. 8c. That is because filter-based methods including kurtogram and maximum correlated kurtosis deconvolution may fail to design the exact filter for extracting weak fault characteristics due to strong background noise, especially when noise and weak fault characteristics are located at the same frequency band.

Fig. 7
figure 7

The detected results for a simulated signal using kurtogram: a kurtogram, b the filtered signal and its envelope spectrum

Full size image
Fig. 8
figure 8

The detected results for a simulated signal using maximum correlated kurtosis deconvolution: a the filtered signal, b its frequency spectrum and c zoomed envelope spectrum

Full size image

4 Experimental validation of proposed method in bearing and gear fault detection

In this section, two experiments including a bearing with slight flaking on its outer race and a gear with scuffing from wind turbine drivetrain are used to validate the effectiveness of the proposed method, respectively.

4.1 Fault detection of rolling element bearings

The bearing experimental setup consists of a motor, a support bearing, a coupling, a tested bearing whose type is LDK UER204 and a hydraulic cylinder, as shown in Fig. 9a. This bearing tested setup is designed to conduct the accelerated degradation tests of rolling element bearings. In the process of the accelerated degradation tests, a tested rolling element bearing has occurred a slight flaking on its outer race, as shown in Fig. 9b. The corresponding vibration signals are acquired by using two PCB 352C33 accelerometers, which are placed on the housing of the tested bearings. In the experiment, the rotating frequency of motor is 30 Hz, the sampling frequency is 25.6 kHz and the sampling time is 1.28 s. In addition, the structural parameters and fault characteristic frequencies of the tested bearing are shown in Table 1, respectively.

Fig. 9
figure 9

a A bearing experimental setup and b the tested bearing with slight flaking on its outer race

Full size image
Table 1 Experimental parameters of the tested rolling element bearing
Full size table

The raw vibration signal of the tested bearing with slight flaking on its outer race is shown in Fig. 10. There are obvious impulsive components with the interval of 30 Hz excited by the rotating shaft in the time-domain waveform, and meanwhile, one can see the rotating frequency 30 Hz and its harmonics from its zoomed envelope spectrum, as well. However, it is difficult for us to observe the clear spectral peaks at the outer race fault characteristic frequency 92.49 Hz and its harmonics from the frequency and zoomed envelope spectrum of raw vibration signal. By checking the experimental setup, it is found that there is a shaft-bending defect to occur at the experimental setup, which excites obvious rotating frequency and its harmonics. This shows that the outer race fault characteristics of the tested bearing are overwhelmed completely by the shaft-bending fault characteristics and strong background noise.

Fig. 10
figure 10

A raw bearing vibration signal: a time-domain waveform, b its frequency spectrum and c zoomed envelope spectrum

Full size image

First, two widely used fault detection tool, i.e., maximum correlated kurtosis deconvolution and kurtogram, are employed to process the raw bearing vibration signal for extracting the outer race fault characteristics of the tested bearing. The detected results are shown in Figs. 11 and 12, respectively. It can be seen from Fig. 11c that the rotating frequency 30 Hz and its harmonics are dominant in the whole envelope spectrum of the filtered signal. One can hardly observe the eye-catching spectral peaks at the outer race fault characteristic frequency and its harmonics. In this bearing case, therefore, maximum correlated kurtosis deconvolution fails to extract the outer race fault characteristics of the tested bearing. Similarly, Fig. 12 shows that kurtogram cannot extract weak outer race fault characteristics of the tested bearing yet because it fails to determine the optimal filtering frequency band.

Fig. 11
figure 11

The detected results for the tested bearing using maximum correlated kurtosis deconvolution: a the filtered signal, b its zoomed frequency spectrum and c envelope spectrum

Full size image
Fig. 12
figure 12

The detected results for the tested bearing using kurtogram: a kurtogram, b the filtered signal and c its envelope spectrum

Full size image

Thus, the proposed method is used to enhance weak fault characteristics of the tested bearing embedded in the envelope of the raw vibration signal. The detected results are depicted in Fig. 13, where the optimal parameters are written as below: \(\alpha_{{{\text{opt}}}} = 0.05485\), \(R{ = }1000\), \(\Delta U_{{{\text{opt}}}} = 8.85726\), \(x_{m}^{{{\text{opt}}}} = 71.7072\) and \(\gamma_{{{\text{opt}}}} = 0.3629\). It can be noticed that the periodic component excited by the slight flaking on the outer race of the tested bearing is amplified by the proposed SR method, and the interferences from both background noise and the components excited by healthy parts are eliminated. In the zoomed frequency spectrum as shown in Fig. 13b, one can clearly see that the spectral peak at the outer race fault characteristic frequency of the tested bearing is eye-catching, which indicates a slight defect occurs on the outer race of the tested bearing. The diagnostic result is consistent with the fact that the slight flaking occurs on the outer race of the tested bearing. Moreover, the optimal fractional order \(\alpha_{{{\text{opt}}}} = 0.05485\) suggests that the fractional-order derivative in the proposed method is able to enhance the benefits of noise to bearing fault detection.

Fig. 13
figure 13

The detected results for the tested bearing using the proposed method: a time-domain waveform and b its zoomed frequency spectrum

Full size image

4.2 Fault detection of gears

In this section, the vibration signal from wind turbine drivetrain is used to validate the effectiveness of the proposed method, where a scuffing occurs on the pinion of high-speed stage fixed-axis gearset due to two loss-of-oil events [34,35,36,37], as shown in Fig. 14b. The internal configuration of wind turbine drivetrain is shown in Fig. 14a. The experimental parameters of high-speed stage fixed-axis gearset are shown as below: the gear tooth number is 88, the pinion tooth number is 22, the high-speed shaft rotating frequency is 30 Hz, the sampling frequency is 40 kHz and the sampling time is 2 s.

Fig. 14
figure 14

Wind turbine drivetrain: a internal configuration and b high-speed stage pinion with scuffing

Full size image

The raw vibration signal from the pinion of high-speed stage fixed-axis gearset and its frequency spectrum is plotted in Fig. 15a, b, respectively. To observe weak fault characteristics excited by the defect on the pinion of high-speed stage fixed-axis gearset, the frequency spectrum centered by meshing frequency of high-speed stage fixed-axis gearset is zoomed as the subfigure of Fig. 15b. It can be seen from the zoomed frequency spectrum that the spectral peak at the meshing frequency of high-speed stage fixed-axis gearset is dominant, while the amplitudes at the sidebands spaced by the meshing frequency of high-speed stage fixed-axis gearset are somewhat weak to identify them.

Fig. 15
figure 15

The raw vibration signal from the pinion of high-speed stage fixed-axis gearset: a time-domain waveform and b its frequency spectrum

Full size image

The weak fault characteristics of gearboxes are organized by the meshing frequency and its sidebands. Generally, one can observe more abundant fault characteristics from the frequency spectrum of the raw vibration signal instead of its envelope spectrum, which is beneficial to identify the fault location of multiple-stage gearboxes. Therefore, the raw vibration signal of gearboxes is fed into the proposed method. The detected results are shown in Fig. 16, where the optimal parameters are written as below: \(\alpha_{{{\text{opt}}}} = 0.01134\), \(\Delta U_{{{\text{opt}}}} = 5.1282\), \(x_{m}^{{{\text{opt}}}} = 15.6134\) and \(\gamma_{{{\text{opt}}}} = 0.9916\). There are obvious impulsive components in the time-domain waveform of Fig. 16a compared with the raw gear vibration signal. Moreover, one can see from the zoomed frequency spectrum of Fig. 16b that the amplitudes at the sidebands spaced by the meshing frequency 660 Hz of high-speed stage fixed-axis gearset are noticeable and their interval 30 Hz equals the rotating frequency of the pinion of high-speed stage fixed-axis gearset, demonstrating that a defect occurs on the opinion of high-speed stage fixed-axis gearset. The diagnostic result is consistent with the fact that a defect has occurred on the pinion of high-speed stage fixed-axis gearset. When the scaling factor is tuned to \(R{ = }5000\), the detected results under the same parameters are plotted in Fig. 17. Compared with the detected results in Fig. 16, it is found that the spectral peaks at the right sidebands in Fig. 17 become more evident. Such a behavior is because the improved second-order SR model characterizes nonlinear band-pass filtering property, and moreover, the narrow pass-band can be shifted by adjusting the scaling factor, as shown in Fig. 4c. Therefore, the proposed method with the scaling factor \(R{ = }3900\) enhances the left sidebands, whereas that with the scaling factor \(R{ = }5000\) amplifies the right sidebands. In addition, when the fractional order is \(\alpha_{{{\text{opt}}}} = 0.01134\) the optimal detected results are obtained, suggesting that the fractional-order derivative is able to enhance the performance of SR for gear fault detection.

Fig. 16
figure 16

The detected results for the pinion of high-speed stage fixed-axis gearset using the proposed method with \(R{ = }3900\): a time-domain waveform and b its frequency spectrum

Full size image
Fig. 17
figure 17

The detected results for the pinion of high-speed stage fixed-axis gearset using the proposed method with \(R{ = }5000\): a time-domain waveform and b its frequency spectrum

Full size image

Besides the proposed method, maximum correlated kurtosis deconvolution and kurtogram are also used to process the raw gear vibration signal and the detected results are depicted in Figs. 18 and 19, respectively. It can be seen from Fig. 18 that the spectral peaks at the meshing frequency and sidebands of high-speed stage fixed-axis gearbox are very weak in the zoomed frequency spectrum. Unfortunately, Fig. 19 shows that the optimal filtering frequency band range cannot cover the meshing frequency and its sidebands of high-speed stage fixed-axis gearbox, indicating that kurtogram fails to extracting weak gear fault characteristics. Compared the detected results in Figs. 16 and 18, the spectral peaks at the meshing frequency and sidebands in the detected results using the proposed method characterize higher amplitudes and are easier to identify. That is, the proposed method is able to harvest the energy of noise to enhance weak gear fault characteristics embedded in the raw vibration signal, whereas maximum correlated kurtosis deconvolution and kurtogram are to eliminate the noise embedded in the raw vibration signal for detecting gear fault characteristics.

Fig. 18
figure 18

The detected results for the pinion of high-speed stage fixed-axis gearset using maximum correlated kurtosis deconvolution: a the time-domain waveform of filtered signal and b its frequency spectrum

Full size image
Fig. 19
figure 19

The kurtogram for the pinion of high-speed stage fixed-axis gearset

Full size image

5 Conclusions

The fractional-order derivative characterizes memory-dependent property and reflects high dependence between current and previous values of the state variable of a system. Such a behavior is able to reflect the continuous mechanical degradation process where the current value of the mechanical state variable, e.g., vibration, is highly dependent on its previous values. Meanwhile, the second-order bistable SR model characterizes nonlinear band-pass filtering property and is able to suppress the multiscale noise located at different frequency bands. Therefore, an improved second-order SR model is established by incorporating the fractional-order derivative into the second-order bistable SR model. The improved second-order SR model is able to not only suppress the multiscale noise embedded in signals but also characterize better performance than integer-order SR models in weak characteristic enhancement. Afterward, based on the improved model a second-order SR method enhanced by the fractional-order derivative is proposed for mechanical fault detection. Experiments including a bearing with slight flaking and a gear with scuffing from wind turbine drivetrain are performed to validate the effectiveness of the proposed method. The results show that the proposed method is able to extract weak fault characteristics embedded in signals and the benefits of noise in the proposed method to weak fault characteristic extraction are able to be enhanced by the fractional-order derivative. Compared with maximum correlated kurtosis deconvolution and kurtogram, the proposed method is a good alternative for mechanical fault detection. In this article, we just use QGAs to optimize the parameters of the second-order SR enhanced by Grünwald–Letnikov fractional-order derivatives for mechanical fault detection. In future work, we would investigate deep learning-based multi-objective fusion algorithms to optimize the parameters of the second-order SR enhanced by Grünwald–Letnikov fractional-order derivative. Even, we would explore the application of SR induced by other types of fractional-order derivative to mechanical fault detection for developing the architecture of SR induced by fractional-order derivative and the benefits of noise in neural networks for mechanical fault detection [38].