Tuning methods for tuned inerter dampers coupled to nonlinear primary systems

Abstract

This study develops displacement- and kinetic energy-based tuning methods for the design of the tuned inerter dampers (TIDs) coupled to both linear and nonlinear primary systems. For the linear primary system, the design of the TID is obtained analytically. The steady-state frequency–response relationship of the nonlinear primary system with a softening or hardening stiffness nonlinearity is obtained using the harmonic balance (HB) method. Analytical and numerical tuning approaches based on HB results are proposed for optimal designs of the TID to achieve equal peaks in the response curves of the displacement and the kinetic energy of the primary system. Via the developed approaches, the optimal stiffness of the TID can be obtained according to the stiffness nonlinearity of the primary system and the inertance of the absorber. Unlike the linear primary oscillator case, for a nonlinear primary oscillator the shape of its resonant peaks is mainly affected by the damping ratio of the TID, while the peak values depend more on the stiffness ratio. The proposed designs are shown to be effective in a wide range of stiffness nonlinearities and inertances. This study demonstrates the benefits of using inerters in vibration suppression devices, and the adopted methods are directly applicable for nonlinear systems with different types of nonlinearities.

1 Introduction

Tuned mass dampers (TMDs) or dynamic vibration absorbers are widely used for suppressing the vibrations of engineering structures subjected to external loads. To reduce the peak dynamic response of a primary vibrating system, a classical TMD comprising a mass, spring and damper can be attached to the system to achieve the desired frequency–response behaviour of the integrated system. The response curve of a harmonically excited single-degree-of-freedom (DOF) primary system with a TMD was shown to pass through two fixed points [1]. Thus, the equal-peak method can be used to find approximate optimal values of the stiffness and damping of an absorber with a given mass. Recently, the exact closed-form solutions of the optimal stiffness and damping of a TMD were found [2, 3].

While vibration absorbers have been widely used for linear structures [4,5,6,7], high-performance vibration suppression devices are required for nonlinear primary systems. Some studies have included nonlinear passive elements in TMDs to achieve enhanced performance. Silveira et al. [8] proposed the use of nonlinear asymmetrical shock absorber to improve the passenger comfort in vehicles. Casalotti et al. [9] studied the vibration absorption capability and dynamic response behaviour of a metamaterial beam with the embedded array of nonlinear spring–mass absorbers. Potential use of nonlinear vibration absorbers in rotor and propulsion systems has also been investigated for vibration attenuation purpose [10, 11]. Viguie and Kerschen [12, 13] proposed a qualitative tuning method to suppress vibrations using a nonlinear dynamic absorber. They used a frequency–energy plot based on the energy conservation law and obtained the parameter values of the absorber by computational iterations. Batou and Adhikari [14] investigated the dynamic performance of a vibration absorber with viscoelastic properties. Yang et al. [15] examined the power flow characteristics of a nonlinear vibration absorber coupled to a nonlinear primary system with stiffness and damping nonlinearity. They found that a softening stiffness absorber could effectively improve the power absorption efficiency for the case of a hardening stiffness primary system.

In addition to the inclusion of stiffness and damping nonlinearities, the recently proposed inerter can be used to improve the performance of dynamic vibration absorbers. The inerter is a passive mechanical element with two terminals whose relative acceleration is proportional to the force applied [16]. This device can be built using a flywheel-based (e.g. [16]) or fluid-based (e.g. [17, 18]) mechanisms. The introduction of inerter has fundamentally enlarged vibration absorbers’ performance that can be achieved passively, with significant benefits identified for trains [19], building structures [20,21,22], cables [23, 24] and aircraft landing gear [25]. Another benefit of inerter in a vibration suppression device is that it reduces the total physical weight compared to the traditional TMD, while maintaining similar performance. Based on these benefits, a specific network connection of the inerter, damper and spring elements, namely the tuned inerter damper (TID), has attracted a lot of interest [26, 27]. Pietrosanti et al. [28] used a tuned mass damper inerter (TMDI) to reduce dynamic vibrations excited by a white noise. The corresponding optimisation was carried out by minimising displacement and acceleration and maximising of the ratio of the dissipated energy to total input energy. Marian and Giaralis [29] proposed a closed-form analytical expression for the design of a linear TMDI attached to a linear system so as to achieve vibration control and energy harvesting. Brzeski et al. [30] examined a pendulum-based absorber with an inerter attached to a nonlinear Duffing oscillator and showed that it could eliminate the unwanted bifurcations and the instabilities of the primary system.

It is noted that many previous studies on vibration suppression systems have been focused on the use of individual displacement responses in quantifying the vibration level. The power flow and energy transfer information have been usually ignored. The power flow analysis (PFA) is a widely accepted tool for dynamic analysis and performance evaluation of linear and nonlinear dynamical systems, including inerter-based suppression systems [31]. Yang et al. [32] explored the vibration power flow and energy transmission behaviour of a proposed inerter-based nonlinear vibration isolator. Zhu et al. [33] studied the vibration suppression performance and energy transfer path of laminated composite plates with different inerter-based suppression devices. Zhuang et al. [34] examined the vibration energy transmission behaviour for performance analysis of coupled systems with a nonlinear inerter-based joint. There has been much recent research interest in developing nonlinear energy sink (NES) acting essentially as passive vibration absorbers without the linear restoring force term [35]. Compared with conventional vibration absorbers, NES has been shown to have a wide effective frequency range. With an NES attached to a primary vibrating system, targeted energy transfer (TET) occurs from the vibrating source to a nonlinear attachment in a one-way and irreversible manner, which was also referred to as energy pumping [36, 37]. Zhang et al. [38] proposed a type of NES that replaced the conventional mass in an attachment by an inerter. The inerter-based NES was shown to have a better vibration suppression performance compared with the conventional NES. Javidialesaadi and Wierschem [39] studied the optimal design of a novel structure with NES and inerter. The use of inerter-based NES devices in a number of vibration control applications including fluid pipe [40], suspension system [41] and elastic beam [42] has been investigated. Ding and Chen [43] presented a comprehensive review on the recent development of NES in design, analysis and engineering applications.

While there has been work reported on TID and its applications, its optimum parameter tuning when connected with a nonlinear primary system has not yet been discussed. Some work has been reported to present an explicit formula of the optimal nonlinear stiffness of a TMD attached to a primary system [44, 45]. In this study, a displacement- and kinetic energy-based tuning method is developed for a TID attached to linear and nonlinear primary systems. The main novelties of this work are: (1) the closed-form expressions of optimal stiffness and damping ratios of tuned inerter dampers for nonlinear primary systems are obtained; (2) optimal equal peaks of the response amplitude or the kinetic energy of the nonlinear primary system mass are achieved; and (3) systematic tuning methods based on analytical and numerical (semi-analytical) approaches are proposed. For the linear primary system, the optimal stiffness and damping ratios of the TID for achieving equal peaks of the displacement response amplitude and kinetic energy curves are obtained using the fixed-point theory. For the nonlinear primary system with possible softening or hardening stiffness nonlinearity, the frequency–response relationship is obtained by using the harmonic balance (HB) method. Expressions for the optimal stiffness and damping ratios of the TID are obtained analytically and numerically based on iterations and regression fitting. It has been shown that both methods can identify the optimum TID parameters with minor discrepancies and work for a large range of nonlinearities and inertance values.

The rest of this paper is organised as follows. Section 2 presents the displacement- and kinetic energy-based equal-peak design of the TID for a linear primary system. Section 3 derives the analytical frequency–response relationship of the system with a TID attached to a nonlinear primary system using the HB method. In Sect. 4, the analytical and numerical tuning methods are developed for the design of the TID to achieve equal peaks in the displacement and in the kinetic energy curves of the nonlinear primary mass. The conclusions are presented in the final section of the paper.

2 TID coupled to a linear primary system

2.1 Displacement-based equal-peak method

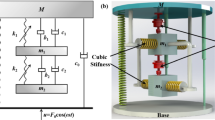
Figure 1a shows a dynamical system comprising a harmonically forced linear single-DOF primary system with mass $m_{1}$, spring constant $k_{1}$ and damping factor $c_{1}$. A TMD with mass m₂, linear spring constant $k_{2}$ and viscous damping factor $c_{2}$ is attached to a single-DOF primary system, to reduce its response amplitude at the original resonance. The displacements of the primary system and absorber are denoted by $x_{1} {\text{and}} x_{2}$, respectively.

Fig. 1

Application of the a TMD and b TID to a linear primary system

Den Hartog [1] pointed out that, for a given absorber mass, the steady-state response of the harmonically excited primary system passes through two fixed points, independently of the absorber damping. Based on this property, the equal-peak method was proposed to achieve the equal response peaks of the primary system, by setting the optimal stiffness and optimal damping of the TMD as

$$ \gamma_{opt} = \frac{{\omega_{2} }}{{\omega_{1} }} = \sqrt {\frac{{k_{2} m_{1} }}{{k_{1} m_{2} }}} \approx \frac{1}{{1 + \lambda_{m} }},$$

(1a)

$$ \zeta_{opt} = \frac{{c_{2} }}{{2\sqrt {k_{2} m_{2} } }} \approx \sqrt {\frac{{3\lambda_{m} }}{{8\left( {1 + \lambda_{m} } \right)}}} $$

(1b)

respectively, where $\omega_{1} = \sqrt {k_{1} /m_{1} }\,\, {\text{and}} \,\, \omega_{2} = \sqrt {k_{2} /m_{2} }$ are the undamped natural frequencies for the primary system and the TMD, respectively, and $\lambda_{m} = m_{2} /m_{1}$ is the mass ratio, the maximum value of which is often constrained in practical designs. If the values of $m_{2}$ and $\lambda_{m}$ are set, the optimal spring stiffness of the TMD can be obtained using Eq. (1a), and its damping can then be determined using Eq. (1b). Note that Eq. (1) only provides approximate solutions of the TMD parameter values for the realisation of the equal response peaks.

Figure 1b shows the application of the TID consisting of an inerter with inertance b, spring constant $k_{2}$ and damping factor $c_{2}$ to the same harmonically excited primary system. Many studies have been reported using inerter-based devices with one terminal grounded as a vibration absorber [26, 46,47,48], in particular for vibration reduction of civil engineering structures subject to base excitation [49]. The displacements of the inerter terminals are denoted by $x_{1}$ and $x_{2}$. The equations of motion of the system are

$$ m_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} - b\left( {\ddot{x}_{2} - \ddot{x}_{1} } \right) = f_{e} \cos \omega t, $$

(2a)

$$ b\left( {\ddot{x}_{2} - \ddot{x}_{1} } \right) + k_{2} x_{2} + c_{2} \dot{x}_{2} = 0. $$

(2b)

To facilitate the later derivation process, the following parameters are introduced:

$$ \begin{gathered} \omega_{1} = \sqrt {\frac{{k_{1} }}{m}} , \omega_{20} = \sqrt {\frac{{k_{2} }}{b}} , \gamma = \frac{{\omega_{20} }}{{\omega_{1} }}, l_{0} = \frac{{m_{1} g}}{{k_{1} }},\lambda = \frac{b}{{m_{1} }},\zeta_{1} = \frac{{c_{1} }}{{2m_{1} \omega_{1} }}, \hfill \\ \zeta_{2} = \frac{{c_{2} }}{{2b\omega_{20} }},X_{1} = \frac{{x_{1} }}{{l_{0} }}, X_{2} = \frac{{x_{2} }}{{l_{0} }},F_{e} = \frac{{f_{e} }}{{k_{1} l_{0} }}, \Omega = \frac{\omega }{{\omega_{1} }}, \tau = \omega_{1} t \hfill \\ \end{gathered} $$

where $\omega_{1}$ and $\omega_{20}$ are the natural frequencies of the primary system and the TID, respectively; $\gamma$ is the ratio of these two frequencies; $l_{0}$ is a characteristic length used for later non-dimensionalisation; $\lambda$ is the inertance-to-mass ratio; $\zeta_{1}$ and $\zeta_{2}$ are the damping ratios of the primary system and the TID, respectively; X₁ and X₂ are the dimensionless displacements of the two terminals of the inerter; $F_{e}$ and ${\Omega }$ are the dimensionless external force amplitude and frequency, respectively; and $\tau$ is the non-dimensional time. Then, Eq. (2) can be transformed into a dimensionless matrix form as follows:

$$ \left[ {\begin{array}{*{20}l} {1 + \lambda } \hfill & { - \lambda } \hfill \\ { - \lambda } \hfill & \lambda \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{1}^{\prime \prime } } \\ {X_{2}^{\prime \prime } } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {2\zeta_{1} } \hfill & 0 \hfill \\ 0 \hfill & {2\zeta_{2} \lambda \gamma } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{1}^{\prime } } \\ {X_{2}^{\prime } } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill \\ 0 \hfill & {\lambda \gamma^{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {F_{\text{e}} \text{e}^{\text{i}\Omega \tau } } \hfill \\ 0 \hfill \\ \end{array} } \right\}, $$

(3)

where the primes denote the differentiation operations with respect to $\tau$. The steady-state solutions of Eq. (3) can be written as

$$ X_{1} = R_{1} {\text{e}}^{\text{i}\Omega \tau } , X_{2} = R_{2} \text{e}^{\text{i}\Omega \tau } , $$

(4a,b)

where R₁ and R₂ are the response amplitudes of the primary mass and the absorber, respectively. By inserting Eq. (4) and its first- and second-order derivatives into Eq. (3), we obtain

$$ \left[ {\begin{array}{*{20}l} { - \Omega^{2} \left( {1 + \lambda } \right) + 2\Omega \zeta_{1} \text{i} + 1} \hfill & {\Omega^{2} \lambda } \hfill \\ {\Omega^{2} \lambda } \hfill & { - \Omega^{2} \lambda + 2\Omega \zeta_{2} \lambda \gamma \text{i} + \lambda \gamma^{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{e} } \\ 0 \\ \end{array} } \right\}. $$

(5)

Equation (5) can be further transformed into

$$ \left\{ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} { - \Omega^{2} \left( {1 + \lambda } \right) + 2\Omega \zeta_{1} \text{i} + 1} \hfill & {\Omega^{2} \lambda } \hfill \\ {\Omega^{2} \lambda } \hfill & { - \Omega^{2} \lambda + 2\Omega \zeta_{2} \lambda \gamma \text{i} + \lambda \gamma^{2} } \hfill \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {F_{e} } \\ 0 \\ \end{array} } \right\}, $$

(6)

where $\left[ \right]^{ - 1}$ denotes the operation of taking the inverse matrix. Therefore, the nonlinear receptance function of the primary mass is

$$\frac{{R_{1} }}{{F_{e} }} = \frac{{ - \Omega^{2} \lambda + \lambda \gamma^{2} + 2\Omega \zeta_{2} \lambda \gamma \text{i}}}{{\left( {\left( { - \Omega^{2} \left( {1 + \lambda } \right) + 1} \right)\left( { - \Omega^{2} \lambda + \lambda \gamma^{2} } \right) - 4\Omega^{2} \zeta_{1} \zeta_{2} \lambda \gamma - \Omega^{4} \lambda^{2} } \right) + \left( { - \Omega^{2} \lambda \zeta_{1} + \lambda \gamma^{2} \zeta_{1} + \zeta_{2} \lambda \gamma - \Omega^{2} \zeta_{2} \lambda \gamma - \Omega^{2} \zeta_{2} \lambda^{2} \gamma } \right)2\Omega \text{i}}}$$

(7)

For an undamped primary system with $\zeta_{1} = 0$, the square of $R_{1} /F_{e}$ can be expressed as

$$ \left( {\frac{{R_{1} }}{{F_{e} }}} \right)^{2} = \frac{{\left( {\gamma^{2} - \Omega^{2} } \right)^{2} + 4\zeta_{2}^{2} \Omega^{2} \gamma^{2} }}{{\left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)^{2} + 4\zeta_{2}^{2} \Omega^{2} \gamma^{2} \left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)^{2} }} $$

(8)

For the TID, the displacement-based equal-peak approach can also be applied to find the approximate optimal stiffness and damping parameters [29], which should be set as

$$ \gamma_{opt} \approx \frac{1}{1 + \lambda },\,\zeta_{opt} \approx \sqrt {\frac{3\lambda }{{8\left( {1 + \lambda } \right)}}}\, , $$

(9a, 9b)

where $\gamma_{{{\text{opt}}}}$ and $\zeta_{{{\text{opt}}}}$ are the optimal stiffness and damping ratios required for the TID system to achieve equal resonant peaks of the response amplitude. The optimal stiffness and damping ratios of the TMD and TID (shown by Eqs. (9) and (1), respectively) share the same expression just by changing $\lambda_{m}$ to $\lambda$. If the inertance-to-mass ratio $\lambda$ of the TID is set equal to the mass ratio $\lambda_{m}$ of the TMD, their optimal stiffness and damping coefficients will also be the same.

Figure 2a, b shows the application of the displacement-based equal-peak approach to the TID with an inertance-to-mass ratio $\lambda$ of 0.02 and 0.05, respectively. The parameters are set as $\zeta_{1} = 0.001$ and $F_{e} = 0.05.$ The optimal stiffness ratio is $\gamma_{{{\text{opt}}}} = 0.9804$ and the optimal damping of the TID is $\zeta_{{{\text{opt}}}} = 0.0857$ when $\lambda$ equals 0.02, according to Eq. (9). When the damping coefficient takes the other values of 0.1 or 0.05, the two peaks in each curve of the displacement response have different heights. Nevertheless, the frequency–response curves of all three cases pass through the two invariant points P and Q, see in Fig. 2a. When the inertance-to-mass ratio increases from 0.02 to 0.05, two equal-height peaks of displacement still can be obtained with the optimal parameters $\gamma_{opt} = 0.9524$ and $\zeta_{opt} = 0.1336$ based on Eq. (9). It is also noted that the optimal equal peaks cam be further reduced as the increase of inertance-to-mass ratio.

Fig. 2

Displacement-based equal-peak approach for the TID coupled to a linear primary system with a $\lambda = 0.02$ and b $\lambda = 0.05$. The parameters are set as ${ }\zeta_{1} = 0.001$ and $F_{e} = 0.05$

2.2 Kinetic energy-based equal-peak method

In some applications, the kinetic energy of the primary system is important for vibration suppression. Therefore, it is useful to develop the equal-peak method based on the kinetic energy. The dimensionless kinetic energy $K_{{\text{p}}}$ of the primary mass is defined as

$$ K_{p} \left( \Omega \right) = \frac{1}{2}\left( {\left| {X_{1}^{\prime } } \right|_{\max } } \right)^{2} = \frac{1}{2}R_{1}^{2} \Omega^{2} , $$

(10)

where $\left| {X_{1}^{\prime } } \right|_{\max }$ represents the maximum dimensionless velocity of the primary system. Figure 2 suggests that, with set spring stiffness and mass ratios of the TID, the kinetic energy curves of the primary system maintain the invariant points at $P|_{{\Omega = \Omega_{1} }}$ and $Q|_{{\Omega = \Omega_{2} }}$ regardless of the changes in the damping of the absorber. Therefore, for the absorber with zero or infinite damping,

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \frac{1}{2}R_{1}^{2} \Omega^{2} = \mathop {\lim }\limits_{{\zeta_{2} \to 0}} \frac{1}{2}R_{1}^{2} \Omega^{2} , $$

(11)

have to be satisfied at $\Omega = \Omega_{1}$ and $\Omega = \Omega_{2}$. By using Eq. (8) to replace $R_{1}$ in Eq. (10), and further simplifying the resultant equation, we have

$$ \Omega^{4} \left( {2 + \lambda } \right) - 2\left( {\lambda \gamma^{2} + \gamma^{2} + 1} \right)\Omega^{2} + 2\gamma^{2} = 0, $$

(12)

which is a quadratic equation of $\Omega^{2}$; the solutions are $\Omega_{1}^{2}$ and $\Omega_{2}^{2}$, providing the corresponding frequencies of the invariant points. Based on the property of the quadratic equations, we have

$$ \Omega_{1} \Omega_{2} = \gamma \sqrt {\frac{2}{{\left( {2 + \lambda } \right)}}} . $$

(13)

To achieve two equal peaks in the kinetic energy curve, two conditions have to be established. The first one is that the two peaks in the kinetic energy curve are of the same height at the frequencies associated with the two fixed points. When the absorber damping tends to infinity, the kinetic energy of the primary system at the corresponding frequencies $\Omega_{1}$ and $\Omega_{2}$ should remain the same:

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \frac{1}{2}\Omega_{1}^{2} \left( {R_{1} \left. \right|_{{\Omega = \Omega_{1} }} } \right)^{2} = \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \frac{1}{2}\Omega_{2}^{2} \left( {R_{1} \left. \right|_{{\Omega = \Omega_{2} }} } \right)^{2} . $$

(14)

By inserting Eq. (8) into Eq. (14), we have.

$$ \Omega_{1} \Omega_{2} = \frac{1}{\lambda + 1}. $$

(15)

Based on Eqs. (13) and (15), the optimal stiffness ratio of the TID is found to be

$$ \gamma_{opt} = \frac{{\sqrt {2 + \lambda } }}{{\left( {\lambda + 1} \right)\sqrt 2 }}. $$

(16)

The other condition for achieving equal peaks of the kinetic energy is that the gradient of the kinetic energy $K_{{\text{p}}}$ at the frequencies of the invariant points is zero [2, 29], i.e.

$$ \left. {\frac{{\text{d}\left( {\frac{1}{2} R_{1}^{2} \Omega^{2} } \right)}}{\text{d}\Omega }} \right|_{{\Omega = \Omega_{1} }} = \left. {\frac{{\text{d}\left( {\frac{1}{2} R_{1}^{2} \Omega^{2} } \right)}}{\text{d}\Omega }} \right|_{{\Omega = \Omega_{2} }} = \frac{{\text{d}\left( {\frac{{G^{2} + 4\zeta_{2}^{2} H^{2} }}{{P^{2} + 4\zeta_{2}^{2} Q^{2} }}} \right)}}{\text{d}\Omega } = 0, $$

(17)

where $G = \left( {\gamma^{2} - \Omega^{2} } \right)\Omega , H = \gamma \Omega^{2} , P = \Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2}$ and $Q = \Omega \gamma \left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)$. Equation (17) is equivalent to

$$ \left( {G^{2} + 4\zeta_{2}^{2} H^{2} } \right)^{\prime } \left( {P^{2} + 4\zeta_{2}^{2} Q^{2} } \right) - \left( {G^{2} + 4\zeta_{2}^{2} H^{2} } \right)\left( {P^{2} + 4\zeta_{2}^{2} Q^{2} } \right)^{\prime } = 0, $$

(18)

where the primes denote the first-order derivatives of the function with respect to Ω, and

$$ \left( {G^{2} + 4\zeta_{2}^{2} H^{2} } \right)^{\prime } = \left( {2\Omega \left( {\gamma^{2} - \Omega^{2} } \right)\left( {\gamma^{2} - 3\Omega^{2} } \right) + 16\zeta_{2}^{2} \gamma^{2} \Omega^{3} } \right), $$

(19)

$$ \begin{aligned} \left( {P^{2} + 4\zeta_{2}^{2} Q^{2} } \right)^{\prime } = & 4\Omega \left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)\left( {2\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) \\ & + 8\Omega \zeta_{2}^{2} \gamma^{2} \left( {1 - 3\Omega^{2} - 3\Omega^{2} \lambda } \right)\left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right). \\ \end{aligned} $$

(20)

By substituting Eqs. (19) and (20) into Eq. (18), it follows that

$$ \begin{gathered} \left( {2\Omega \left( {\gamma^{2} - \Omega^{2} } \right)\left( {\gamma^{2} - 3\Omega^{2} } \right) + 16\zeta_{2}^{2} \gamma^{2} \Omega^{3} } \right)\left( {\left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)^{2} + 4\zeta_{2}^{2} \Omega^{2} \gamma^{2} \left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)^{2} } \right) \hfill \\ - \left( {\Omega^{2} \left( {\gamma^{2} - \Omega^{2} } \right)^{2} + 4\zeta_{2}^{2} \gamma^{2} \Omega^{4} } \right)\left( {4\Omega \left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)\left( {2\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right)} \right. \hfill \\ \left. { + 8\Omega \zeta_{2}^{2} \gamma^{2} \left( {1 - 3\Omega^{2} - 3\Omega^{2} \lambda } \right)\left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)} \right) = 0. \hfill \\ \end{gathered} $$

(21)

Equation (21) could be further simplified into

$$ \begin{gathered} \left( {A + 16\zeta_{2}^{2} \gamma^{2} \Omega^{3} } \right)\left( {B + 4\zeta_{2}^{2} \Omega^{2} \gamma^{2} \left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)^{2} } \right) - \left( {C + 4\zeta_{2}^{2} \gamma^{2} \Omega^{4} } \right) \hfill \\ \left( {D + 8\Omega \zeta_{2}^{2} \gamma^{2} \left( {1 - 3\Omega^{2} - 3\Omega^{2} \lambda } \right)\left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)} \right) = 0, \hfill \\ \end{gathered} $$

(22)

where

$$ A = 2\Omega \left( {\gamma^{2} - \Omega^{2} } \right)\left( {\gamma^{2} - 3\Omega^{2} } \right), $$

(23a)

$$ B = \left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)^{2} , $$

(23b)

$$ C = \Omega^{2} \left( {\gamma^{2} - \Omega^{2} } \right)^{2} , $$

(23c)

$$ D = 4\Omega \left( {\Omega^{2} \left( {\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right) + \gamma^{2} } \right)\left( {2\Omega^{2} - 1 - \gamma^{2} - \lambda \gamma^{2} } \right). $$

(23d)

Using the notations in Eq. (23), Eq. (22) becomes

$$ \begin{gathered} \left( {32\gamma^{4} \Omega^{5} \left( {1 - \Omega^{4} \left( {1 + \lambda } \right)^{2} } \right)} \right)\zeta_{2}^{4} + \left( {4\Omega^{2} \gamma^{2} \left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)^{2} A + 16\gamma^{2} \Omega^{3} B - 8\Omega \gamma^{2} } \right. \hfill \\ \left. {\left( {1 - 3\Omega^{2} - 3\Omega^{2} \lambda } \right)\left( {1 - \Omega^{2} - \Omega^{2} \lambda } \right)C - 4\gamma^{2} \Omega^{4} D} \right)\zeta_{2}^{2} + AB - CD = 0 \hfill \\ \end{gathered} $$

(24)

which is a quadratic equation of $\zeta_{2}^{2}$, and its solutions are denoted as $\zeta_{{2,\Omega_{1} }}^{2}$ and $\zeta_{{2,\Omega_{2} }}^{2}$, the squares of the damping values at two invariant points. This single algebraic equation can be solved either analytically or numerically. The approximate mean of the two values of the damping ratio can be used as the optimal damping [2]:

$$ \zeta_{opt} \approx \frac{1}{{4\left( {2 + \lambda } \right)}}\sqrt {\frac{{\lambda \left( {24 + 24\lambda + 5\lambda^{2} } \right)}}{1 + \lambda }} . $$

(25)

Equations (16) and (25) present the optimal stiffness and damping ratios of the TID required to achieve equal peaks of the kinetic energy curve for the primary mass.

Figure 3a, b shows the use of the kinetic energy-based equal-peak approach for the TID with an inertance-to-mass ratio $\lambda$ of 0.02 and 0.05, respectively,$\zeta_{1} = 0.001,$ and $F_{e} = 0.05.$ Based on Eqs. (16) and (25), the values of the optimal stiffness and optimal damping coefficients of the TID in Fig. 3a are calculated to be 0.9853 and 0.0857, respectively. The kinetic energy curves associated with a lower damping $\zeta_{2} = 0.05$ of the TID and a higher damping $\zeta_{2} = 0.1$ are also included for comparison. Figure 3a shows that when the optimal parameter values of the TID are used, equal peaks in the kinetic energy are achieved. It is interesting to note that when the TID damping is set as $\zeta_{2} = 0.05$, the peak values of $K_{{\text{p}}}$ become much larger, compared with the optimal case. However, for the same case with $\zeta_{2} = 0.05$, the local minimum value of $K_{{\text{p}}}$ at the anti-peak near $\Omega \approx 0.99$ is much smaller than the other two cases. Figure 3b shows that when a larger inertance-to-mass ratio of $\lambda = 0.05$ is used for the TID, equal peaks in the curve of kinetic energy can be achieved by setting $\gamma = 0.9642$ and $\zeta_{2} = 0.1336$. A comparison of Fig. 3a, b shows that the peaks of $K_{{\text{p}}}$ for the optimal design cases become lower when the inertance-to-mass ratio $\lambda$ of the TID increases, suggesting the potential benefits of having a larger inertance in the absorber.

Fig. 3

Kinetic energy-based equal-peak method for the TID with an inertance-to-mass ratio $\lambda$ of a 0.02 and b 0.05. Parameters are set as $\zeta_{1} = 0.001,$ and $F_{e} = 0.05$

3 TID coupled to a nonlinear primary system

3.1 Mathematical modelling

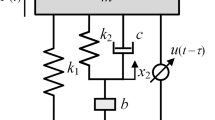
In certain applications, the primary structure, the vibration response of which needs to be suppressed, may behave nonlinearly. In this section, a nonlinear primary system is considered; the TID is attached to the system to obtain equal peaks in the displacement and kinetic energy curves. As shown in Fig. 4, the nonlinearity of the primary system is modelled with a nonlinear spring with restoring force $g\left( {x_{1} } \right) = k_{n} x_{1}^{3}$. The excitation force and other system parameters are defined as shown in Fig. 1b.

Fig. 4

Schematic of a nonlinear primary system with an attached TID

The equations of motion of the integrated system can be written as

$$ m_{1} \ddot{x}_{1} + c\dot{x}_{1} + k_{1} x_{1} + k_{n} x_{1}^{3} - b\left( {\ddot{x}_{2} - \ddot{x}_{1} } \right) = f_{e} \cos \omega t, $$

(26a)

$$ b\left( {\ddot{x}_{2} - \ddot{x}_{1} } \right) + k_{2} x_{2} + c_{2} \dot{x}_{2} = 0. $$

(26b)

By using parameters $\omega_{1} ,\omega_{20} , \gamma , l_{0} ,\lambda ,\zeta_{1} , \zeta_{2} ,X_{1} , X_{2} ,$ $F_{e} , {\Omega }$ and $\tau$ defined in Sect. 2.1 and introducing a nonlinear stiffness ratio $\varepsilon = k_{n} l_{0}^{2} /k_{1}$ for the nonlinear spring of the primary system, Eq. (26) is rewritten into a dimensionless form as

$$ X_{1}^{\prime \prime } + 2\zeta_{1} X_{1}^{\prime } + X_{1} + \varepsilon X_{1}^{3} - \lambda \left( {X_{2}^{\prime \prime } - X_{1}^{\prime \prime } } \right) = F_{e} \cos \Omega \tau , $$

(27a)

$$ \lambda \left( {X_{2}^{\prime \prime } - X_{1}^{\prime \prime } } \right) + \lambda \gamma^{2} X_{2} + 2\zeta_{2} \lambda \gamma X_{2}^{\prime } = 0. $$

(27b)

These two differential equations can be transformed into a set of first-order differential equations, which may be solved using a time-marching method. Analytical approximations based on the HB method are made to find the steady-state response of the system and to determine the optimal parameters of the TID based on the application of the equal-peak method.

3.2 Frequency–response relationship

Here, a first-order approximation of the steady-state frequency–response relationship of the system is derived using the HB method. The steady-state dimensionless displacements, velocities and accelerations for the periodic response of the system are approximated as

$$ X_{1} = R_{1} \cos \left( {\Omega \tau + \phi } \right),$$

(28a)

$$X_{1}^{\prime } = - R_{1} \Omega \sin \left( {\Omega \tau + \phi } \right),$$

(28b)

$$X_{1}^{\prime \prime } = - R_{1} \Omega^{2} \cos \left( {\Omega \tau + \phi } \right), $$

(28c)

$$ X_{2} = R_{2} \cos \left( {\Omega \tau + \theta } \right),$$

(28d)

$$X_{2}^{\prime } = - R_{2} \Omega \sin \left( {\Omega \tau + \theta } \right),$$

(28e)

$$X_{2}^{\prime \prime } = - R_{2} \Omega^{2} \cos \left( {\Omega \tau + \theta } \right), $$

(28f)

where R₁ and R₂ represent the non-dimensional displacement amplitudes of X₁ and X₂, respectively, and $\phi$ and θ are the corresponding phase angles. By inserting Eq. (28) into Eq. (27) and neglecting high-order terms, we have

$$ R_{1} \left( {1 - \Omega^{2} + \frac{3}{4}\varepsilon R_{1}^{2} - \lambda \Omega^{2} } \right)\cos \left( {\Omega \tau + \phi } \right) - 2\zeta_{1} R_{1} \Omega \sin \left( {\Omega \tau + \phi } \right) + \lambda \Omega^{2} R_{2} \cos \left( {\Omega \tau + \theta } \right) = F_{e} \cos \Omega \tau , $$

(29a)

$$ \lambda \Omega^{2} R_{1} \cos \left( {\Omega \tau + \phi } \right) + \lambda R_{2} \left( {\gamma^{2} - \Omega^{2} } \right)\cos \left( {\Omega \tau + \theta } \right) - 2\zeta_{2} \lambda \gamma R_{2} \Omega \sin \left( {\Omega \tau + \theta } \right) = 0. $$

(29b)

By balancing the coefficients of the harmonic term $\cos \left( {{\Omega }\tau + \phi } \right)$ in Eq. (29a), we have

$$ R_{1} \left( {1 - \Omega^{2} + \frac{3}{4}\varepsilon R_{1}^{2} - \lambda \Omega^{2} } \right) + \lambda R_{2} \Omega^{2} \cos \left( {\theta - \phi } \right) = F_{e} \cos \phi , $$

(30)

where terms $\cos \left( {\Omega \tau + \theta } \right)$ and $\cos {\Omega }\tau$ in Eq. (29a) can be rewritten as $\cos \left( {\Omega \tau + \phi + \theta - \phi } \right)$ and $\cos \left( {\Omega \tau + \phi - \phi } \right)$ for using the trigonometric identities $\cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ retaining the terms with $\cos \left( {\Omega \tau + \phi } \right)$ and $\sin \left( {\Omega \tau + \phi } \right)$. Similarly, by equating the coefficients of the harmonic term $\sin \left( {\Omega \tau + \phi } \right)$ in Eq. (29a), we obtain

$$ - 2\zeta_{1} R_{1} \Omega - \lambda R_{2} \Omega^{2} \sin \left( {\theta - \phi } \right) = F_{e} \sin \phi . $$

(31)

The term $\cos \left( {\Omega \tau + \phi } \right)$ in Eq. (29b) is equivalent to $\cos \left( {\Omega \tau + \theta + \phi - \theta } \right)$ for using the trigonometric identities $\cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ retaining the terms with $\cos \left( {\Omega \tau + \theta } \right)$ and $\sin \left( {\Omega \tau + \theta } \right)$. By balancing the coefficients of the harmonic term $\cos \left( {\Omega \tau + \theta } \right)$ in Eq. (29b), it follows that

$$ \lambda R_{2} \left( {\gamma^{2} - \Omega^{2} } \right) + \lambda R_{1} \Omega^{2} \cos \left( {\theta - \phi } \right) = 0. $$

(32)

Equating the coefficients of the harmonic term $\sin \left( {\Omega \tau + \theta } \right)$ in Eq. (29b), we have

$$ - 2\zeta_{2} \lambda \gamma R_{2} \Omega + \lambda R_{1} \Omega^{2} \sin \left( {\theta - \phi } \right) = 0. $$

(33)

By using Eqs. (32) and (33), the trigonometric terms $\cos \left( {\theta - \phi } \right)$ and $\sin \left( {\theta - \phi } \right)$ are expressed as

$$ \cos \left( {\theta - \phi } \right) = - \frac{{R_{2} \left( {\gamma^{2} - \Omega^{2} } \right)}}{{R_{1} \Omega^{2} }}, $$

(34a)

$$ \sin \left( {\theta - \phi } \right) = \frac{{2\zeta_{2} \gamma R_{2} \Omega }}{{R_{1} \Omega^{2} }}. $$

(34b)

The sum of the squares of Eqs. (34a) and Eq. (34b) to remove the terms with $\cos \left( {\theta - \phi } \right)$ and $\sin \left( {\theta - \phi } \right)$, we have

$$ R_{2}^{2} \left( {\gamma^{2} - \Omega^{2} } \right)^{2} + R_{2}^{2} \left( {2\zeta_{2} \gamma \Omega } \right)^{2} = R_{1}^{2} \Omega^{4} . $$

(35)

A replacement of the trigonometric term $\cos \left( {\theta - \phi } \right)$ in Eq. (30) with Eq. (34a) leads to

$$ R_{1} \left( {1 - \Omega^{2} + \frac{3}{4}\varepsilon R_{1}^{2} - \lambda \Omega^{2} } \right) - \frac{{\lambda R_{2}^{2} \left( {\gamma^{2} - \Omega^{2} } \right)}}{{R_{1} }} = F_{e} \cos \phi . $$

(36)

Similarly, the term $\sin \left( {\theta - \phi } \right)$ in Eq. (31) can be replaced by using Eq. (34b). In this way, Eq. (31) becomes

$$ - 2\zeta_{1} R_{1} \Omega - \frac{{2\zeta_{2} \gamma \lambda \Omega R_{2}^{2} }}{{R_{1} }} = F_{e} \sin \phi . $$

(37)

Based on Eqs. (36) and (37), the trigonometric terms $\cos \phi$ and $\sin \phi$ can be cancelled out, and we have

$$ \left( {\left( {1 - \Omega^{2} + \frac{3}{4}\varepsilon R_{1}^{2} - \lambda \Omega^{2} } \right)R_{1}^{2} - \lambda \left( {\gamma^{2} - \Omega^{2} } \right)R_{2}^{2} } \right)^{2} + \left( {2\zeta_{1} R_{1}^{2} \Omega + 2\zeta_{2} \lambda \gamma \Omega R_{2}^{2} } \right)^{2} = R_{1}^{2} F_{e}^{2} . $$

(38)

Note that Eqs. (35) and (38) are nonlinear algebraic equations providing the frequency–response relationship of the system. When the system and the excitation parameter values are known, the displacement variable $R_{1}$ can be expressed as a function of $R_{2}$, using Eq. (35). By inserting the resultant expression of $R_{1}$ into Eq. (38), we obtain a single nonlinear algebraic equation of dimensionless displacement amplitude $R_{2}$, which can be subsequently solved by using a standard bisection method [50]. Then, all the responses of the system in terms of amplitudes $R_{1}$ and $R_{2}$ and phase angles can be obtained. Alternatively, Eqs. (35) and (38) can be solved using the Newton–Raphson algorithm to find the steady-state response. It is then possible to apply the equal-peak method to the analysis and design of the TID for a nonlinear primary system. For the validation of the frequency–response relationship obtained by using the HB method, the displacement and kinetic energy curves obtained based on the solutions of FRFs and Eq. (27) using HB and the fourth-order Runge–Kutta method are plotted in Fig. 5a, b, respectively. Both the hardening stiffness nonlinearity with a nonlinear stiffness ratio of $\varepsilon = 1$ and the softening stiffness nonlinearity with $\varepsilon = - 0.05$ are considered. The other parameters are set as $F_{e} = 0.05,\zeta_{1} = \zeta_{2} = 0.001,\lambda = 0.1,$ and $\gamma = 1$. The figure shows a good agreement between the analytical approximations and the numerical integration results. Therefore, Eqs. (35) and (38) are used in the subsequent section for determining the optimal parameter values for the TID required to achieve equal peaks in the displacement response and kinetic energy curves.

Fig. 5

Frequency–response relationship of the a displacement amplitude and b kinetic energy ($\zeta_{1} = \zeta_{2} = 0.001,\gamma = 1,\lambda = 0.1,F_{e} = 0.05$). Solid lines and squares for $\varepsilon = 1$; dashed lines and circles for $\varepsilon = - 0.05$. Lines: HB results; Symbols: Runge–Kutta results

4 Tuning approaches for TID coupled to nonlinear systems

4.1 Displacement-based equal-peak method

4.1.1 Analytical tuning approach

Based on the frequency–response relationship in Eqs. (35) and (38), Fig. 6a, b shows the effects of the damping and stiffness of the attached TID on the displacement response of the nonlinear primary system, respectively. The parameters of the primary system are set as $\varepsilon = 0.08$ and $\zeta_{1} = 0.001$, indicating the presence of a hardening stiffness nonlinearity and a light damping, respectively. The excitation magnitude is $F_{e} = 0.05$. For the TID, the inertance-to-mass ratio is set as $\lambda = 0.02$. By using Eq. (9), the optimal stiffness and damping of the TID designed for a corresponding linear primary system are calculated to be ${ }\gamma = 0.9804$ and $\zeta_{2} = 0.0857$, respectively, and the corresponding response curves are shown by the dashed lines. Figure 6 shows that the use of linear optimal values does not lead to equal peaks of the displacement amplitude $R_{1}$. Therefore, Eq. (9) cannot be directly used for the design of TIDs when the primary system is nonlinear. In Fig. 6a, the damping coefficient $\zeta_{2}$ of the TID reduces from 0.11 to 0.07 at intervals of 0.01 while fixing $\gamma = 0.9804$, and the results are represented by solid lines. The curve for the correspondingly linear primary system attached with an optimal TID based on Eq. (9) is shown by the dash dotted line. The figure reveals that, regardless of the variations of $\zeta_{2}$, the response curve of the nonlinear primary system passes through two invariant points of different heights. When the absorber damping is $\zeta_{2} = 0.11$, there is only one peak in the curve of $R_{1}$. With the reduction in $\zeta_{2}$ from 0.11 to 0.07, firstly the peak value reduces, and then two peaks appear. In Fig. 6b, the stiffness ratio $\gamma$ of the TID decreases from 0.99 to 0.97 at intervals of 0.01, while the damping is fixed at $\zeta_{2} = 0.0857$. The corresponding results are denoted by solid lines. It can be seen that the variations in $\gamma$ can effectively modify the peak values of the displacement. It is also observed that the left resonant peak is higher than the right with $\gamma = 0.99$, while the right peak is higher than the left one with $\gamma = 0.97$. As a result, there must exist an optimal stiffness value between 0.97 and 0.99 to achieve equal resonant peaks. The optimal value could be determined manually with the relative difference of the two peaks height meets the tolerance requirement of 0.1%. Furthermore, the equal resonant peaks of $R_{1}$ may be achieved by setting $\gamma_{opt} = 0.9560$, as shown by the dotted line. It also shows that the nonlinear optimal results match well with those obtained from the numerical RK method, which are denoted by the square symbols.

Fig. 6

Effects of different a damping ratio $\zeta_{2}$ with $\gamma = 0.9804$ and b stiffness ratio $\gamma$ with $\zeta_{2} = 0.0857$ of the TID on the displacement response of the primary mass ($\varepsilon = 0.08, \zeta_{1} = 0.001, F_{e} = 0.05,$ and $\lambda = 0.02$)

Figure 6 shows that the damping ratio $\zeta_{2}$ of the TID mainly affects the shape of the resonant peaks, while its stiffness ratio $\gamma$ considerably affects the peak values. Therefore, to achieve equal peaks of $R_{1}$, the value of the stiffness ratio $\gamma$ can be determined while setting the damping ratio $\zeta_{2}$ at its linear optimal value obtained by Eq. (9b). The frequency–response relationship in Eqs. (35) and (38) can be used to find the optimal parameter values of the TID for the nonlinear primary system. In Fig. 6b, the average peak value $R_{NP}$ of the dotted line associated with the nonlinear primary system with an optimally designed TID, is 0.4877. In comparison, in Fig. 6a, the average peak value $R_{LP}$ of the dash dotted line, i.e. for the corresponding linear primary system with an optimally designed TID is 0.4942. It shows that these two peak values are similar, i.e. $R_{NP} \approx R_{LP}$. The reason may be that the nonlinear and the corresponding linear primary systems are attached with optimally designed TIDs, their vibrations of the primary systems are suppressed with low peak response amplitudes. Correspondingly, the nonlinear term in the governing equation arising from the stiffness nonlinearity will be small, such that the optimal peak values for the two cases will be approximately the same. This property will be used to develop an analytical tuning approach of the TID coupled to nonlinear primary system. Figure 6a shows that the frequency–response curves corresponding to different values of the damping ratio $\zeta_{2}$ in the TID pass through two fixed points. This behaviour indicates that an analytical tuning approach can be proposed and developed for the design of TID coupled to a nonlinear primary oscillator. Note that Eq. (35) can be further transformed into

$$ R_{2}^{2} = \frac{{R_{1}^{2} \Omega^{4} }}{A}, $$

(39)

where $A = \left( {\gamma^{2} - \Omega^{2} } \right)^{2} + \left( {2\zeta_{2} \gamma \Omega } \right)^{2} .$ By substituting the Eq. (39) into Eq. (38), we have

$$ \left( {\frac{{R_{1} }}{{F_{e} }}} \right)^{2} = 1/\left( {\left( {1 - \Omega^{2} + \frac{3}{4}\varepsilon R_{1}^{2} - \lambda \Omega^{2} - \lambda \left( {\gamma^{2} - \Omega^{2} } \right)\frac{{\Omega^{4} }}{A}} \right)^{2} + \left( {2\zeta_{1} \Omega + 2\zeta_{2} \lambda \gamma \frac{{\Omega^{5} }}{A}} \right)^{2} } \right). $$

(40)

Here, to facilitate design of the TID, the value of $R_{1}$ on the right-hand side of Eq. (40) may be approximated by using ${R}_{LP}$, the peak value of the corresponding linear primary system attached with an optimal TID. When the response amplitudes associated with the two fixed points do not change with damping ratio $\zeta_{2}$ of the TID, we have

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \left( {\frac{{R_{1} }}{{F_{e} }}} \right)^{2} = \mathop {\lim }\limits_{{\zeta_{2} \to 0}} \left( {\frac{{R_{1} }}{{F_{e} }}} \right)^{2} . $$

(41)

Equation (41) is equivalent to

$$ \Omega^{4} \left( {2 + \lambda } \right) - \left( {2 + \frac{3}{2}\varepsilon R_{LP}^{2} + 2\gamma^{2} + 2\lambda \gamma^{2} } \right)\Omega^{2} + \left( {2 + \frac{3}{2}\varepsilon R_{LP}^{2} } \right)\gamma^{2} = 0, $$

(42)

which is a quadratic equation of $\Omega^{2}$. Here the two solutions to Eq. (42) are denoted as $\Omega_{1}^{2}$ and $\Omega_{2}^{2}$, the sum of which should be

$$ \Omega_{1}^{2} + \Omega_{2}^{2} = \frac{{4 + 3\varepsilon R_{LP}^{2} + 4\gamma^{2} + 4\lambda \gamma^{2} }}{{2\left( {2 + \lambda } \right)}}. $$

(43)

To achieve equal peaks in the curve of the steady-state displacement response for the nonlinear primary system at the two excitation frequencies $\Omega_{1}$ and $\Omega_{2}$, we also need

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \left( {\frac{{R_{1} \left. \right|_{{\Omega = \Omega_{1} }} }}{{F_{e} }}} \right)^{2} = \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \left( {\frac{{R_{1} \left. \right|_{{\Omega = \Omega_{2} }} }}{{F_{e} }}} \right)^{2} . $$

(44)

Equation (44) can be further transformed into

$$ \Omega_{1}^{2} + \Omega_{2}^{2} = \frac{{4 + 3\varepsilon R_{LP}^{2} }}{{2\left( {\lambda + 1} \right)}}. $$

(45)

By combining Eqs. (43) and (45), we obtain

$$ \gamma_{DA} = \frac{{\sqrt {4 + 3\varepsilon R_{LP}^{2} } }}{{2\left( {1 + \lambda } \right)}}, $$

(46)

where $\gamma_{{{\text{DA}}}}$ is the optimal stiffness ratio for TID to achieve equal peaks in the displacement response curve based on the analytical tuning approach, $\varepsilon$ is the nonlinear stiffness ratio of the primary system and $\lambda$ is the inertance-to-mass ratio of the TID. When $\varepsilon = 0$, i.e. when the primary oscillator is linear, Eq. (46) becomes equivalent to Eq. (9a).

It is noted that to obtain more accurate results of the optimal stiffness of the TID, the whole derivation process can be iterative. The idea is that in the first iteration, the linear optimal resonant peak value $R_{LP}$ is used in Eq. (46) to obtain the stiffness of the absorber. With the first set of parameter values of the TID, the averaged peak values of $R_{1}$ can be obtained using Eqs. (35) and (38), and used to replace $R_{LP}$ in Eq. (46) to obtain the updated stiffness ratio $\gamma_{{{\text{DA}}}}$. By following this iterative process, the optimal stiffness of the TID can be obtained with sufficient accuracy.

4.1.2 Numerical (semi-analytical) tuning approach

Apart from analytical tuning approach to obtain the optimal design of the TID coupled to nonlinear primary systems, numerical tuning is also carried out as follows. It should be pointed out that the numerical method in this paper refers to the numerical solution to the frequency–response equations derived by the HB method, not the direction numerical integration of the system equations of motion. Therefore, it can also be called as a semi-analytical approach. As Fig. 6 confirms that equal peaks in the response curve of a nonlinear primary system can be achieved by designing the stiffness ratio $\gamma$ of the TID while setting the damping to the linear optimal value. Following this procedure, the required optimal stiffness ratio $\gamma$ required for the TID to achieve equal peaks in the displacement response is plotted in Fig. 7 as a function of the nonlinear stiffness ratio $\varepsilon$ of the primary system; the system parameters are $\zeta_{1} = 0.001$ and $F_{e} = 0.05$. At set values of $\varepsilon$ and $\lambda$, the damping coefficient $\zeta_{2}$ of the TID is obtained using Eq. (9b), and the frequency–response relationship in Eqs. (35) and (38) is used to obtain the optimal stiffness ratio $\gamma$. The results are firstly shown in Fig. 7 and are then curve-fitted to obtain the curves corresponding to specific values of the inertance-to-mass ratio $\lambda$ from 0.01 to 0.1 at intervals of 0.01. Figure 7 shows that at a fixed value of the nonlinear stiffness ratio $\varepsilon$, the optimal stiffness ratio $\gamma_{DN}$ generally decreases as the inertance-to-mass ratio $\lambda$ increases. It also shows that at a set value of $\lambda$, $\gamma_{DN}$ of the TID has an approximately linear relationship with $\varepsilon$ between $- 0.1$ and 0.1. This mathematical relationship can be expressed as

$$ \gamma_{DN} = f_{1} \left( \lambda \right)\varepsilon + f_{2} \left( \lambda \right), $$

(47)

where $\gamma_{{{\text{DN}}}}$ denotes the optimal stiffness ratio to achieve equal peak in displacement obtained based on the numerical tuning, while $f_{1} \left( \lambda \right)$ and $f_{2} \left( \lambda \right)$ are functions of the inertance-to-mass ratio $\lambda$; the function values are denoted by the solid dots in Fig. 8. By curve fitting the results, the following expressions are obtained:

$$ f_{1} \left( \lambda \right) \approx 0.0017\lambda^{ - 1.01},$$

(48a)

$$f_{2} \left( \lambda \right) \approx - 0.8986\lambda + 0.9976. $$

(48b)

Fig. 7

Variations in the optimal stiffness ratio $\gamma_{{{\text{DN}}}}$ of the TID with respect to the nonlinear stiffness ratio $\varepsilon$ and the inertance-to-mass ratio $\lambda$ for equal peaks in the displacement response amplitude ($F_{e} = 0.05,$ and $\zeta_{1} = 0.001$)

Fig. 8

Curve fitting of functions $f_{1} \left( \lambda \right)$ and $f_{2} \left( \lambda \right)$ of the TID for a nonlinear primary system using the displacement-based equal-peak method based on numerical optimisation ($F_{e} = 0.05,$ and $\zeta_{1} = 0.001$)

Therefore, $f_{1} \left( \lambda \right)$ has an approximately negative power relationship with the inertance-to-mass ratio $\lambda$, and $f_{2} \left( \lambda \right)$ has an approximately linear relationship with $\lambda$. By inserting Eq. (48) into Eq. (47), the optimal stiffness ratio of the TID can be expressed as a function of $\varepsilon$ and $\lambda$:

$$ \gamma_{DN} \approx 0.0017\lambda^{ - 1.01} \varepsilon - 0.8986\lambda + 0.9976. $$

(49)

This ratio can be used when the primary system exhibits either hardening stiffness (i.e. $\varepsilon > 0$) or softening stiffness (i.e. $\varepsilon < 0$) nonlinearities. According to Eq. (49), for a fixed value of $\lambda$, the value of $\gamma_{{{\text{DN}}}}$ increases with the nonlinear stiffness ratio $\varepsilon$, in accordance with the results shown in Fig. 7.

To validate the effectiveness Eq. (49) in the design of the TID attached to a nonlinear primary system, Fig. 9 shows the change in the relative differences between the peak values of the displacement response with respect to the nonlinear stiffness ratio $\varepsilon$ and the inertance-to-mass ratio $\lambda$ when $F_{e} = 0.05$. The relative difference is defined as $\Delta \% = \left( {H_{1} - H_{2} } \right)/H_{1}$, where $H_{1}$ and $H_{2}$ ($H_{1} \ge H_{2}$) are the peak values. Figure 9 shows that for a relatively large range of parameter values for nonlinear stiffness $\varepsilon$ and the inertance $\lambda$ of the TID, the difference between the two peaks is lower than 1% and therefore negligible. Therefore, the proposed numerical tuning approach, i.e. the use of Eqs. (9b) and (49) to design the damping and stiffness of TIDs, can achieve the design target of creating approximately equal peaks in the displacement response of the nonlinear primary mass.

Fig. 9

Validation of the proposed design of the TID for a nonlinear system following the displacement-based equal-peak method using numerical optimisation. a 3-D and b 2-D contour plots of the relative percentage difference

Figure 10a, b shows the vibration suppression of a nonlinear hardening stiffness primary system with $\varepsilon = 0.1$ and a softening stiffness primary system with $\varepsilon = - 0.1$ using the proposed displacement-based equal-peak method design of the TID, respectively. The solid lines present the displacement amplitudes of the primary mass by setting the damping value of the TID to be non-optimal at $\zeta_{2} = 0.001$. The dashed lines represent the cases in which the proposed optimal parameters of the TID are used. Based on Eq. (49), the values of the optimal stiffness ratio $\gamma_{{{\text{DN}}}}$ are set as $1.0064$ and 0.9708, and the results are shown in Fig. 10a, b, respectively. Figure 10a reveals that, for the non-optimal cases, there are two peaks of $R_{1}$, both twisting to the right due to the hardening stiffness nonlinearity, while the proposed design of the TID leads to two equal peaks of the displacement amplitude. Figure 10b shows that for a softening stiffness primary system, the displacement response curves of the non-optimal cases extend towards the low-frequency range. In comparison, the use of the proposed optimal TID design can achieve equal peaks in the displacement response $R_{1}$. At the same time, multiple solution branches are eliminated, which is beneficial for vibration suppression. Figure 10c, d shows the time histories of the dimensionless displacement of the primary system for the non-optimal, the optimal and the without TID cases. Figure 10c shows the responses associated with point M with the excitation frequency $\Omega = 0.976$ and while Fig. 10(d) is for point N with $\Omega = 1.009$, as marked in Fig. 10a, b. Figure 10c, d considers the presence of hardening and softening stiffness nonlinearities with the nonlinear stiffness ratio $\varepsilon$ being $0.1$ and $- 0.1$, respectively. The steady-state dynamic responses are obtained by using the fourth-order Runge–Kutta method and shown from 1000 T for a time span of 3 T, where $T = 2\pi /\Omega$ is the excitation period. The time step size is set as T/1024. Figure 10c, d shows that the nonlinear optimal designs of the TID can yield the lowest peaks in the displacement amplitude of the primary systems among the three cases. In contrast, Fig. 10c shows that the use of the TID with the non-optimal parameters can lead to even larger amplitude in the displacement of the primary system, compared to the without TID case, i.e. for the primary system without attaching TID. The behaviour demonstrates the importance of properly setting the parameters of TID to achieve effective vibration suppression.

Fig. 10

Comparison between nonlinear optimal, without TID and non-optimal TID cases for: a, c hardening stiffness; b and d softening stiffness nonlinear primary system. a, b Displacement response amplitudes; c, d time histories of the dimensionless displacement at $\Omega = 0.976$ and $\Omega = 1.009$, respectively. The parameters are set as $\lambda = 0.01,\zeta_{1} = 0.001,$ and $F_{e} = 0.05$

Figure 11 presents the response curves of the nonlinear primary mass attached to an optimal TID designed based on Eqs. (49) and (9b). In Fig. 11a, the nonlinear stiffness ratio $\varepsilon$ changes from 0.01 to 0.05 and then to 0.1 at the prescribed value $\lambda = 0.03$; in Fig. 11b, the inertance-to-mass ratio $\lambda$ varies from 0.05 to 007 and then to 0.1 with a fixed nonlinear stiffness parameter $\varepsilon = 0.1$ of the primary system. The other parameters are set as $F_{e} = 0.05$ and $\zeta_{1} = 0.001.$ Fig. 11a shows that with the increase in $\varepsilon$, the peaks of the displacement response amplitude reduce slightly. The widths of the frequency band between the two peak frequencies in the three cases considered are almost the same. Figure 11b shows the influence of the inertance-to-mass ratio $\lambda$ of the TID on the displacement response amplitude $R_{1}$. As shown in the figure, when $\lambda$ increases from 0.05 to 0.07 and then to 0.1, the peaks of the response amplitude reduce. As $\lambda$ increases, the first peak shifts to the left (lower frequencies) because the increase in inertance of the system leads to smaller natural frequencies. In comparison, the second peak frequency does not change significantly with different $\lambda$. The figure shows a larger value of the inertance-to-mass ratio of the TID leads to improved vibration suppression of the nonlinear primary system.

Fig. 11

Effects of a nonlinear stiffness ratio $\varepsilon$ and b inertance-to-mass ratio $\lambda$ on the displacement response of the primary mass with an attached optimal TID. The parameters are set as $F_{e} = 0.05$ and $\zeta_{1} = 0.001$

Table 1 shows the comparison between the values of the optimal stiffness ratio of the TID obtained using Eqs. (46) and (49), based on the analytical and numerical (or semi-analytical) tuning approaches, respectively. The system parameters are set as $\zeta_{1} = 0.001, F_{e} = 0.05, \varepsilon = 0.05$ and the inertance-to-mass ratio $\lambda$ increases from 0.02 to 0.1. In the table, $R_{NP\_A}$ and $R_{NP\_N}$ denote the averaged resonant peak values of $R_{1}$ obtained using analytical tuning with one iteration and numerical tuning, respectively. The table shows that the optimal stiffness ratios $\gamma_{{{\text{DA}}}}$ and $\gamma_{{{\text{DN}}}}$ obtained to achieve equal peak in the displacement response amplitudes are very close. The largest relative difference $\left| {\gamma_{DA} - \gamma_{DN} } \right|/\gamma_{DN}$ is approximately 0.15% when the inertance-to-mass ratio is 0.1. The table shows that the response peak values $R_{NP\_A}$ and $R_{NP\_N}$ obtained using the two tuning approaches are similar with their relative difference $\left| {R_{NP\_A} - R_{NP\_N} } \right|/R_{NP\_N}$ being close to zero when $\lambda$ increases from 0.04 to 0.08. The table shows that the value of $R_{LP}$ used to obtain the 1^st iteration of $\gamma_{DA}$ using Eq. (46) is generally close to $R_{NP\_A}$. If not, the current value of $R_{NP\_A}$ can be used to replace $R_{LP}$ in Eq. (46) to find the next design iteration to achieve improved designs. The table again shows that the response amplitude peak value will reduce when $\lambda$ increases. It also shows that the optimal stiffness ratio decreases with the increase of the inertance-to-mass ratio $\lambda$.

Table 1 Comparison of the optimal stiffness ratio ($\gamma_{DA} ,\gamma_{DN}$) and the averaged response peak values ($R_{NP\_A} ,R_{NP\_N}$) based on the analytical and numerical tuning approaches

4.2 Kinetic energy-based equal-peak method

4.2.1 Analytical tuning approach

Here, we analyse the design of a TID for a nonlinear primary system using the kinetic energy-based equal-peak tuning approach. Figure 12a, b shows the effects of the damping ratio $\zeta_{2}$ and the stiffness ratio $\gamma$ of the TID on the non-dimensional kinetic energy $K_{{\text{p}}}$, respectively. The curves of $K_{{\text{p}}}$ for the primary mass are obtained from Eqs. (10), (35) and (38). The other parameters are set as $\varepsilon = 0.1, \zeta_{1} = 0.001,F_{e} = 0.05,$ and $\lambda = 0.05$. In Fig. 12a, the solid lines represent the results of the TID with $\zeta_{2}$ decreasing from 0.18 to 0.13 at intervals of 0.01. Using Eqs. (16) and (25), the optimal parameters of the TID designed for the corresponding linear primary system $(\varepsilon = 0)$ are $\gamma_{{{\text{opt}}}} = 0.9642$ and $\zeta_{2} = 0.1336$, and the curves are represented by dashed lines; the stiffness ratio $\gamma$ is obtained by Eq. (16) and thus is the same as that in Fig. 12a. The figure reveals two invariant points of different heights in each curve of $K_{{\text{p}}}$. This demonstrates that the equations for the kinetic energy-based design approach of the TID developed in Sect. 2.2 for a linear primary system are not directly applicable when there is stiffness nonlinearity. It also shows that the heights of the two invariant points are not sensitive to the changes in the damping level of the TID. In Fig. 12b, the stiffness ratio $\gamma$ of the TID changes from 0.99 to 0.96 at intervals of 0.01, while its damping ratio $\zeta_{2}$ is fixed at 0.1336, as determined using Eq. (25). After several iterations, equal peaks of the kinetic energy curve of the primary system can be achieved by setting $\gamma_{{{\text{opt}}}} = 0.9681$, as shown by the dotted lines. This suggests that the TID can be designed by tailoring its spring stiffness while setting its damping to the linear optimal value.

Fig. 12

Effects of the a damping ratio $\zeta_{2}$ and b stiffness ratio $\gamma$ of the TID on the kinetic energy of the nonlinear primary system ($\varepsilon = 0.1, \zeta_{1} = 0.001,F_{e} = 0.05,$ and $\lambda = 0.05$)

Figure 12a shows that the kinetic energy curves for the different cases with various values of the damping ratio $\zeta_{2}$ all pass through two fixed points. Therefore, analytical tuning approach can be developed to obtain the optimal stiffness ratio of the TID to achieve equal peaks in the kinetic energy curves of the nonlinear primary system. When the magnitude of the kinetic energy $K_{{\text{p}}}$ does not change with the damping ratio $\zeta_{2}$ of the TID, we have

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \left( {\frac{1}{2}R_{1}^{2} \Omega^{2} } \right) = \mathop {\lim }\limits_{{\zeta_{2} \to 0}} \left( {\frac{1}{2}R_{1}^{2} \Omega^{2} } \right), $$

(50)

where the expression of the dimensionless kinetic energy $K_{p} = \Omega^{2} R_{1}^{2} /2$ has been recalled. A conversion of Eq. (50) leads to the same quadratic equation of ${\Omega }^{2}$ as Eq. (42), the two solutions of which are again denoted as $\Omega_{1}^{2}$ and $\Omega_{2}^{2} .$ Based on the property of quadratic equations, we have

$$ \Omega_{1} \Omega_{2} = \gamma \sqrt {\frac{{4 + 3\varepsilon R_{LP}^{2} }}{{2\left( {2 + \lambda } \right)}}} , $$

(51)

where $R_{LP}$ has been used to as a first approximation of the peak value of $R_{1}$ when the nonlinear primary system is attached with an optimally designed TID. To have equal peaks in the curve of $K_{{\text{p}}}$ at $\Omega = \Omega_{1}$ and $\Omega = \Omega_{2}$, we need

$$ \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \frac{1}{2}\Omega_{1}^{2} \left( {R_{1} \left. \right|_{{\Omega = \Omega_{1} }} } \right)^{2} = \mathop {\lim }\limits_{{\zeta_{2} \to \infty }} \frac{1}{2}\Omega_{2}^{2} \left( {R_{1} \left. \right|_{{\Omega = \Omega_{2} }} } \right)^{2} . $$

(52)

Equation (52) can be further transformed into

$$ \Omega_{1} \Omega_{2} = \frac{{4 + 3\varepsilon R_{LP}^{2} }}{{4\left( {1 + \lambda } \right)}}, $$

(53)

where again the approximation $R_{1} \approx R_{LP}$ has been used. By equating the right-hand sides of Eqs. (51) and (53), the optimal stiffness ratio $\gamma_{KA}$ achieving equal resonant peaks of kinetic energy is obtained as

$$ \gamma_{KA} = \frac{{4 + 3\varepsilon R_{LP}^{2} }}{4 + 4\lambda }\sqrt {\frac{{2\left( {2 + \lambda } \right)}}{{4 + 3\varepsilon R_{LP}^{2} }}} . $$

(54)

It is noted that the design can be made iterative by using the current value of $\gamma_{KA}$ to find the peak response amplitude $R_{1}$, the value of which is then assigned to $R_{LP}$ in Eq. (54) for the next iteration of improved design of the stiffness ratio for the TID.

4.2.2 Numerical (semi-analytical) tuning approach

It is noted that Eqs. (54) and (16) are the same when nonlinear stiffness ratio $\varepsilon = 0$, i.e. TID attached to a linear primary oscillator. Again, it is reiterated that the numerical tuning approach refers to the numerical solution of the frequency–response relationship derived from the HB method, not the direction numerical integration of the system governing equations. Figure 12 shows the results with set values of the inertance-to-mass ratio $\lambda$ of the TID and the nonlinear stiffness ratio $\varepsilon$ of the primary system. For other sets of values of $\lambda$ and $\varepsilon$, the optimal stiffness ratio of the TID required to achieve equal peaks in the kinetic energy $K_{{\text{p}}}$ curve can be obtained by following the same analysis procedure. Figure 13 shows plots of the optimal stiffness $\gamma_{KN}$ against the stiffness nonlinearity $\varepsilon$ at different values of inertance for the TID. The optimal values are denoted by symbols and are curve-fitted based on linear regression. The other parameters are set as $F_{e} = 0.05$ and $\zeta_{1} = 0.001.$ The figure shows a range of values for $\varepsilon$ from − 0.1 to 0.1, considering both softening and hardening stiffness nonlinearities. The figure shows that for a given value of $\lambda$, the optimal stiffness ratio $\gamma_{{{\text{KN}}}}$ of the TID has an approximately linear relationship with the nonlinear stiffness coefficient $\varepsilon$ of the primary syste

$$ \gamma_{KN} = f_{3} \left( \lambda \right)\varepsilon + f_{4} \left( \lambda \right), $$

(55)

where $\gamma_{KN}$ represents the optimal stiffness ratio of the TID designed to achieve equal peaks in the kinetic energy curve using numerical integrations; and ${ }f_{3} \left( \lambda \right)$ and $f_{4} \left( \lambda \right)$ are functions of $\lambda$, the values of which shown by solid dots in Fig. 14 for different values of $\lambda$. Figure 14a shows that the value of $f_{3} \left( \lambda \right)$ generally decreases with $\lambda$ following a power function, while $f_{4} \left( \lambda \right)$ has an approximately linear relationship with $\lambda$. By using a power function fitting for $f_{3} \left( \lambda \right)$ and a linear regression curve fitting for $f_{4} \left( \lambda \right)$, we have

$$ f_{3} \left( \lambda \right) \approx 0.002\lambda^{ - 0.973} ,$$

(56a)

$$f_{4} \left( \lambda \right) \approx - 0.6716\lambda + 0.9981. $$

(56b)

Fig. 13

Variations in the optimal stiffness ratio $\gamma_{{{\text{KN}}}}$ of the TID with respect to the nonlinear stiffness ratio $\varepsilon$ and the inertance-to-mass ratio $\lambda$ for equal peaks in the kinetic energy curve ($F_{e} = 0.05$ and $\zeta_{1} = 0.001$)

Fig. 14

Curve fittings of a $f_{3} \left( \lambda \right)$ and b $f_{4} \left( \lambda \right)$ for the kinetic energy-based optimal design of the TID

Therefore, the optimal stiffness ratio $\gamma_{{{\text{KN}}}}$ for achieving equal peaks of the kinetic energy curve for the nonlinear primary system can be approximated as

$$ \gamma_{KN} \approx 0.002\lambda^{ - 0.973} \varepsilon - 0.6716\lambda + 0.9981. $$

(57)

It is useful to investigate the accuracy of Eq. (57) for the design of the optimal stiffness ratio of the TID with the design target of achieving equal peaks in the kinetic energy curve. In Fig. 15, the system parameters are set as $F_{e} = 0.05$ and $\zeta_{1} = 0.001$ while the damping of the TID is set at the linear optimal value expressed as Eq. (25). Both the nonlinear stiffness ratio $\varepsilon$ of the primary system and the inertance-to-mass ratio $\lambda$ of the TID change from 0.01 to 0.1. The first and second peak values of the kinetic energy of the primary system are denoted by $H_{3}$ and $H_{4}$, respectively. Figure 15a shows a plot of the relative difference ${\Delta }_{2} = \left| {H_{3} - H_{4} } \right|/H_{3}$ against $\varepsilon$ and $\lambda$ in terms of percentage. From the figure, it can be seen that over a large range of parameter values of $\lambda$ and $\varepsilon$, the relative difference between the peak heights is small. Figure 15b shows that by setting the inertance-to-mass ratio $\lambda$ of the TID to more than 0.03, the relative difference between the peaks of the kinetic energy curves can be less than 1% for a large range for stiffness nonlinearities $\varepsilon$ in the primary system. It can also be seen that for a set stiffness nonlinearity $\varepsilon$, the difference between the peaks decreases with the increase in the inertance $\lambda$. When $\lambda = 0.07$, the relative difference $\Delta_{2}$ can be lower than 0.75%. Figure 15 confirms that Eq. (57) can be used to achieve peaks with equal heights in the kinetic energy curves for the primary mass.

Fig. 15

Validation of the optimal designs of the TID for a nonlinear system. a 3D surface plot and b 2D contour of the relative difference between the kinetic energy peaks

Figure 16a, b shows the significant mitigation of the maximum kinetic energy of the nonlinear primary system with a hardening $\varepsilon = 0.1$ and a softening $\varepsilon = - 0.08$ stiffness nonlinearity, respectively. The solid lines represent the non-optimal cases by setting the damping ratio of the TID with a small value $\zeta_{2} = 0.001$. The nonlinear optimal cases are shown by the dashed lines, and the corresponding optimal stiffness ratios using the numerical tuning approach in Eq. (57) are calculated to be $\gamma_{KN} = 1.0090$ and 0.9773 in Fig. 16a, b, respectively. It shows that the maximum kinetic energy of the nonlinear primary oscillator with hardening or softening stiffness nonlinearity can be modified by adding the TID to achieve equal peaks, and its values can be reduced around the resonance region. The addition of the optimal TID can eliminate multiple solution at a single frequency and undesirable nonlinear behaviour such as the jump phenomenon. Therefore, the proposed tuning approach is effective for attenuation of vibration of nonlinear systems. Figure 16c, d further shows the time history information of points ${\text{M}}^{\prime }$ and ${\text{N}}^{\prime }$ at ${\Omega } = 0.976$ and ${\Omega } =$ 1.009, respectively. The dimensionless instantaneous kinetic energy of the nonlinear primary oscillator is shown for the optimal, non-optimal and without TID cases, represented by the dashed, solid and dotted lines, respectively. The results show that the use of the developed numerical tuning approach leads to the smallest value of the maximum kinetic energy by using the optimal TID.

Fig. 16

Comparisons of the kinetic energy of the primary nonlinear system between nonlinear optimal, without TID and non-optimal TID cases. Primary systems with a and c hardening stiffness; b and d softening stiffness. a and b Maximum kinetic energies; c and d time histories of the dimensionless kinetic energy at ${\Omega } = 0.976$ and ${\Omega } = 1.009$, respectively. Other parameters are set as $\lambda = 0.01,\zeta_{1} = 0.001,$ and $F_{e} = 0.05$

Figure 17 examines the effects of the nonlinear stiffness ratio $\varepsilon$ and the inertance-to-mass ratio $\lambda$ on the kinetic energy of the primary system when using optimal design of the TID based on Eqs. (25) and (57). In Fig. 17a, three cases are considered with $\varepsilon$ changing from 0.01, to 0.05 and then to 0.1 with $\lambda$ fixed as 0.03. The other parameters are set as ${ }F_{e} = 0.05$ and $\zeta_{1} = 0.001$. The figure shows that as $\varepsilon$ increases, the stiffness nonlinearity of the primary system becomes stronger, and there are slight reductions in the peak values of the kinetic energy $K_{{\text{p}}}$. It also shows that the variations of the nonlinear stiffness ratio $\varepsilon$ has only small effects on the bandwidth between the peak frequencies of the kinetic energy. In Fig. 17b, the inertance-to-mass ratio $\lambda$ of the TID varies from 0.05, to 0.07 and then to 0.1 with a fixed nonlinear stiffness ratio of $\varepsilon = 0.1$. The figure shows equal peaks of the kinetic energy curves can be achieved by the proposed design of the TID. It also shows that the increase of inertance in the TID can lead to substantial reductions in the peak values in the kinetic energy $K_{{\text{p}}}$ of the nonlinear primary system. There are also a wider frequency band between the two peak frequencies of $K_{{\text{p}}}$. These characteristics show that a larger value of the inertance $\lambda$ for the TID provides benefits to vibration suppression of the primary system.

Fig. 17

Effects of a the nonlinear coefficient $\varepsilon$ ($\lambda = 0.03)$ and b the inertance-to-mass ratio $\lambda$ ($\varepsilon = 0.1)$ on the kinetic energy of the primary mass attached with optimal TIDs

Table 2 presents the optimal stiffness ratio $\gamma$ of the TID to achieve equal peaks in the kinetic energy curve, using Eqs. (54) and (57) based on the analytical and numerical (semi-analytical) tuning approaches, respectively. The parameters are set as $\zeta_{1} = 0.001$, $F_{e} = 0.05,\varepsilon = 0.05$ while $\lambda$ increases from 0.02 to 0.1. The value of $\gamma_{KA}$ is obtained only after the 1^st design iteration. The variables $K_{NP\_A}$ and $K_{NP\_N}$ represent averaged peak values of the kinetic energy $K_{p}$ of the primary system based on the 1^st iteration of the analytical tuning and numerical tuning approaches, respectively. The table shows that for a set value of $\lambda$, the values of the optimal stiffness $\gamma_{KA}$ and $\gamma_{KN}$ of the TID obtained using the two tuning approaches agree very well. The largest relative difference $\left| {\gamma_{KA} - \gamma_{KN} } \right|/\gamma_{KN}$ is approximately 0.07% when the inertance-to-mass ratio $\lambda = 0.02$. As the value of $\lambda$ increases, the peak value of the kinetic energy reduces. The optimal stiffness ratios $\gamma_{KN}$ and $\gamma_{KA}$ generally decrease with the increase in the inertance $\lambda$ of the TID. The figure also shows that for all the considered cases, $K_{NP\_A} \approx K_{NP\_N}$ with the largest relative difference $\left| {K_{NP\_A} - K_{NP\_N} } \right|/K_{NP\_N}$ being 0.294% when $\lambda = 0.07$. The table demonstrates that both analytical and numerical tuning approaches can be used to find the optimal designs of the TID to achieve equal peaks in the curve of kinetic energy $K_{P} .$

Table 2 Comparison of the optimal stiffness ratios ($\gamma_{KA}$,$\gamma_{KN}$) and the averaged kinetic energy peak values ($K_{NP\_A} ,K_{NP\_N}$) based on the analytical and numerical tuning approaches

5 Conclusions

This study presented displacement- and kinetic energy-based equal-peak methods for the design of the tuned inerter dampers (TIDs) coupled to linear and nonlinear primary systems. For the linear primary system, the analytical expressions of the optimal damping and stiffness ratios of the TID achieving equal resonant peaks of the response amplitude and kinetic energy curves were obtained using the fixed-point theory. For the application of the TID attached to a nonlinear primary system with a cubic stiffness nonlinearity, analytical and numerical tuning methods based on the HB frequency–response relationship were carried out to achieve equal peaks in the displacement and kinetic energy responses. Unlike the linear primary oscillator case, for a nonlinear primary oscillator the shape of its resonant peaks is mainly affected by the damping ratio of the TID, while the peak values depend more on the stiffness ratio. Analytical and numerical tuning approaches have been developed to obtain the optimal stiffness and damping ratios of the TID. It was shown that the use of the two approaches can achieve equal peaks in the displacement and kinetic energy curves with good accuracy. It has also been demonstrated that the proposed tunings are valid for a wide range of stiffness nonlinearities and inertance values. The tuning approaches have been developed considering nonlinear cubic stiffness in the primary system; however, they are also directly applicable and can be extended for other types of nonlinearities.