Stochastic model analysis of cancer oncolytic virus therapy: estimation of the extinction mean times and their probabilities

Abstract

In this paper, we propose a mathematical model on the oncolytic virotherapy incorporating virus-specific cytotoxic T lymphocyte (CTL) response, which contribute to killing infected tumor cells. In order to improve the understanding of the dynamic interactions between tumor cells and virus-specific CTLs, stochastic differential equation models are constructed. We obtain sufficient conditions for existence, persistence and extinction of the stochastic system. In relation to the therapy control, we also analyze the stochasticity role of equilibrium point stabilities. The Monte Carlo algorithm is used to estimate the mean extinction time and the extinction probability of cancer cells or viruses-specific CTLs. Our simulations highlighted the switch of the system leaving the attractor basin of the three species co-existence equilibrium toward that of cancer cell extinction or that of virus-specific CTLs depletion. This allowed us to characterize the spaces of cancer control parameters. Finally, we determine the model solution robustness by analyzing the sensitivity of the model characteristic parameters. Our results demonstrate the high dependence of the virotherapy success or failure on the combination of stochastic diffusion parameters with the maximum per capita growth rate of uninfected tumor cells, the transmission rate, the viral cytotoxicity and the strength of the CTL response.

1 Introduction

The search for new effective treatments with fewer side effects has led oncology to develop a targeted strategy based on oncolytic virotherapy. In fact, oncolytic viruses (OVs) represent a promising immunotherapeutic approach for the treatment of cancer due to their ability to create a microenvironment favorable to the action of the immune system against unique determinants of cancer cells [20, 43]. However, the antiviral immunity elicited against the viral antigens of the resulting infection is considered to be detrimental to OVs as activation of the immune system against the virus itself is expected to restrict viral replication and spread, leading to decreased therapeutic efficacy [31, 36]. It is important for cancer control to find a balance between anti-tumor and anti-viral immunity. So much effort has been devoted to mathematical studies on oncolytic virotherapy [4, 7, 12, 24, 43].

Mathematical models formulated in terms of ordinary differential equations (ODEs) have been proposed by Wodarz [44, 45] to understand spreading dynamics of oncolytic viruses through tumors by including an immune response to the virus. Komarova and Wodarz [24] formulated a general computational framework depending on types of virus spread slow and fast spread. To understand how immune system reacts to the emergence of tumors and their growth, Khajanchi et al. [21] investigated a tumor–immune interaction model that consists of three nonlinear differential equations with a single time-delayed interaction.

In [7], Camara et al. extended the work of Zurakowski et al. [47] to study the consequences for the spatial structure of the tumor by analyzing a mathematical model that describes interaction between two types of tumor cells: the cells that are infected by the virus and the cells that are not infected but are susceptible to the virus.

But the process of the onset and then development of cancer is well known to be complex and stochastic [3, 5, 38]. Indeed, the acquisition of mutation somatic properties and metastatic capacity by cells involve stochastic events [32, 35]. Moreover, in real-life situations, cell population systems are always affected by various sources of noise in which the functional roles in biological processes can vary greatly [14, 39]. Thus, various mathematical models have been developed to integrate this stochastic dimension of the appearance and development of cancer cells [11, 17, 22, 25, 26]. Recently, Phan and Tian [33] proposed a stochastic model to represent interaction among tumor cells, infected tumor cells and oncolytic viruses. But in [33] the infection term does not satisfy the assumption of the fast virus spreading given in [24].

Therefore, there is a considerable need to understand the cancer cell extinction dynamics induced by oncolytic virus.

In the present article, we propose to examine the effects of the stochastic process solution of the mathematical model investigated by Choudhury and Nasipuri [8]. In their paper [8], they presented an ordinary differential equation to study the efficacy of cancer therapy using oncolytic viruses in the presence of immune response. The immune response triggered by the infection is a complex set of pathways consisting of the innate and the adaptive immune response. In our case, only do we focus on the clearing of infected cells by cytotoxic T lymphocytes (CTLs).

To provide a quantitative study of the relapse or failure of cancer control, we analyze the persistence or extinction conditions of the stochastic oncolytic virus and cancer cell system. The stability analysis of our stochastic model equilibria is also treated in terms of the first- and second-order moments. The cancer cell extinction or virus-specific CTL disappearance will be studied by estimating the First Passage Time (FPT) [9, 16, 37]. Therefore, we will use the Monte Carlo algorithm to determine the mean extinction time and the associate extinction probabilities in cases of oncolytic therapy success or failure. Finally, we will determine the model solution robustness by analyzing the sensitivity of the model characteristic parameters. We have also characterized the spaces of the cancer control parameters taking into account the system stochasticity. The sensitivity analysis results will allow us to correlate the effects of the control parameter variations on the values of the mean extinction times or the extinction probabilities.

2 Mathematical model

2.1 Formulation of models

In this paper, a stochastic term is added to the ODE model introduced by Choudhury and Nasipuri [8] in the context of fast-spreading virus [24]. The deterministic part of which the stability study and the modeling assumptions have been declined in [8] is described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t} = r x \left( 1-\frac{x+y}{k}\right) -\beta \frac{xy}{x+y+\alpha }\\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t} = \beta \frac{xy}{x+y+\alpha } -\delta y - pyz, \\ \displaystyle \frac{\mathrm{d}z}{\mathrm{d}t} = \gamma yz -qz \end{array}\right. } \end{aligned}$$

(1)

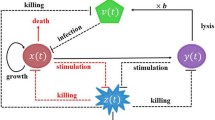
where $x = x(t)$ stands for the uninfected tumor cell population, $y = y(t)$ represents the infected tumor cell population and $z = z(t)$ is the population of the virus-specific CTLs, with initial populations $x(0) \ge 0$, $y(0) \ge 0$ and $z(0) \ge 0$.

All parameters involved with model (1) are fixed positive constants, and their interpretations are presented in Table 1.

Table 1 Parameter values used in the model simulations

The tumor cells are assumed to grow logistically with intrinsic growth rate r. The maximum size of space which the tumor is allowed to occupy is given by its carrying capacity k. The viruses spread to tumor cells at a rate $\beta$. The deaths of virus infected cells occur at a rate $\delta y$, $\delta$ is called the viral cytotoxicity. Infected cells are destroyed by the CTL response at a rate pyz, corresponding to lytic effector mechanisms of CTL response, where the coefficient p represents the strength of the lytic component. In the absence of antigenic stimulation [2], virus-specific CTLs decay at rate q. $\gamma y z$ describes the rate of immune response due to virus activation, where $\gamma$ stands for the strength of the CTL response.

In [8], the authors mainly focused on the total tumor load by analyzing each equilibrium of model (1). In the absence of the virus-specific CTL response, they found

• A trivial equilibrium state $E_1 = (0,0,0)$,

• An equilibrium state corresponding to only healthy tumor cells $E_2 = (k,0,0)$,

• A coexistence equilibrium with both infected and uninfected tumor cells $E_3:= (E_{3_1}, E_{3_2}, 0)$, with

  $$\begin{aligned}&E_{3_1} = \frac{(k+ \alpha ) \delta r - (\beta - \delta ) \delta k + \delta \sqrt{M} }{2 \beta r}, \end{aligned}$$
  $$\begin{aligned}&E_{3_2} = \frac{(\beta {-} \delta ) (k r {+} \delta k {-} \beta k ){-} (\beta {+} \delta ) \alpha r {+} (\beta {-} \delta ) \sqrt{M} }{2 \beta r},\\&M = \Big ( (k+ \alpha ) r - (\beta - \delta ) k \Big )^2 +4 \alpha \beta k r . \end{aligned}$$

In the presence of the virus-specific CTL response, they found a coexistence equilibrium with both infected and uninfected cells $E_4:= (E_{4_1}, E_{4_2}, E_{4_3})$,

$$\begin{aligned}&E_{4_1} = \frac{(k - \alpha ) \gamma - 2q + \gamma \sqrt{(k - \alpha )^2 - 4k (\frac{\beta q}{r \gamma } - \alpha )} }{2 \gamma },\\&E_{4_2} = \frac{q}{\gamma }, \\&E_{4_3}= \frac{2(\beta - \delta ) k q - r( q + \alpha \gamma ) (k+ \alpha ) +r (q + \alpha \gamma ) \sqrt{(k - \alpha )^2 - 4k \left( \frac{\beta q}{r \gamma } - \alpha \right) }}{2 k p q}. \end{aligned}$$

To take into account the influence of environmental fluctuations, the deterministic model system (1) can be extended to a stochastic model system by introducing multiplicative noise terms into the intrinsic growth rate parameters for three populations. In this study, we have chosen an Itô formulation of the stochastic model (2). Thus, the resulting stochastic process has the very practical mathematical property of martingale. This mathematical property of martingale is very useful when computing the conditional expectation of an Itô process, or in general, for analyzing and proving theorems on the Itô integral, [6].

The resulting stochastic model is as follows:

$$\begin{aligned}&\mathrm{d}x(t) \nonumber \\&= \Big [ r x(t) \displaystyle \left( 1\!-\!\frac{x(t)\!+\! y(t)}{k} \Big )\! -\!\beta \displaystyle \frac{x(t) y(t)}{x(t)+ y(t)\!+\! \alpha }\right] \mathrm{d}t \nonumber \\&\quad + \sigma _1 x(t) \, \mathrm{d}B_1(t),\nonumber \\&\mathrm{d}y(t) =\Big [ \beta \displaystyle \frac{x(t) y(t)}{x(t)+y(t)+\alpha } - \delta y(t) -p y(t) z(t) \Big ] \mathrm{d}t \nonumber \\&\, \, \quad \qquad + \sigma _2 y(t) \, \mathrm{d}B_2(t), \nonumber \\&\mathrm{d}z(t) = \Big [ \gamma y(t) z(t) -q z(t) \Big ] \mathrm{d}t + \sigma _3 z(t) \, \mathrm{d}B_3(t),\nonumber \\ \end{aligned}$$

(2)

where $\sigma _i > 0, \, (i = 1,2,3)$ are the intensities of environmental driving forces, and $B_i(t), \, (i = 1,2,3)$ are three standard one-dimensional independent Wiener processes defined over the complete probability space $(\Omega , \mathcal {F}_t, P)$ having a filtration $\mathcal {F}_0$ which satisfy the usual condition (i.e., it is right continuous and $\mathcal {F}_0$ contains all P-null sets) [29]. The solution of (2) subjected to the positive initial condition is an Ito process.

2.2 Preliminaries

In this section, we introduce the following definitions and lemmas as in [28, 40], which will be used in the following sections.

Definition 2.1

The system is said to be strongly persistent in the mean if $\langle x(t) \rangle _{*} > 0$, where $\langle x(t) \rangle _{*}:= \varliminf _{t \rightarrow +\infty } \frac{1}{t} \int _{0}^{t}x(s)\mathrm{d}s$ and $\langle x(t) \rangle ^{*}$ is defined by $\langle x(t) \rangle ^{*}:= \varlimsup _{t \rightarrow +\infty } \frac{1}{t} \int _{0}^{t}x(s)\mathrm{d}s$.

In aforementioned definition, $\langle x(t) \rangle$ stands for the time average of x(t) and is defined by $\langle x(t) \rangle _{*}:= \frac{1}{t} \int _{0}^{t}x(s)\mathrm{d}s$

To prove the persistence of populations, we need the following Lemma (2.1).

Lemma 2.1

Suppose that $x(t) \in \mathcal {C}[\Omega \times \mathbb {R}_{+}, \mathbb {R}_{+}^{0}]$, where $\mathbb {R}_{+}^{0} = \{ a | a > 0, \;\; a \in \mathbb {R} \}$.

• (i) If there exist positive constants $\mu , T, \text{ and } \lambda \ge 0$ such that

  $$\begin{aligned} \ln x(t) \le \lambda t - \mu \int _{0}^{t}x(s)\mathrm{d}s + \sum _{i=1}^{n}\beta _{i}B_{i}(t) \end{aligned}$$

  for $t \ge T$, where $\beta _{i}$’s are constants, $1 \le i \le n$, then $\langle x(t) \rangle ^{*} \le \frac{\lambda }{\mu }$, a.s.

• (ii) If there exist positive constants $\mu , T, \text{ and } \lambda \ge 0$ such that

  $$\begin{aligned} \ln x(t) \ge \lambda t - \mu \int _{0}^{t}x(s)\mathrm{d}s + \sum _{i=1}^{n}\beta _{i}B_{i}(t) \end{aligned}$$

  for $t \ge T$, where $\beta _{i}$’s are constants, $1 \le i \le n$, then $\langle x(t) \rangle _{*} \ge \frac{\lambda }{\mu }$, a.s.

The following lemma will be used to demonstrate the solution existence.

Lemma 2.2

Consider one-dimensional stochastic differential equation

$$\begin{aligned} \mathrm{d}X(t)=X(t)\left[ (\alpha - \beta X(t))\mathrm{d}t +\sigma \mathrm{d}B(t) \right] \end{aligned}$$

(3)

where parameters $\alpha$, $\beta$ and $\sigma$ are positive, B(t) is a standard Brownian motion.

Suppose $\alpha > \frac{\sigma ^2}{2}$, and X(t) is the solution of equation (3) with any initial value $X_0>0$, then we have:

$$\begin{aligned} \lim \limits _{t\longmapsto +\infty } \frac{\ln X(t)}{t}=0 \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{t\longmapsto +\infty }\frac{1}{t} \int _{0}^{t} X(s)\mathrm{d}s= \frac{\alpha - \frac{\sigma ^2}{2}}{\beta } \end{aligned}$$

almost surely (a.s.).

Consider the following stochastic differential equation.

$$\begin{aligned} \mathrm{d}X(t)=\mu (X(t),t)\mathrm{d}t +\sigma (X(t),t) \mathrm{d}B(t) \end{aligned}$$

(4)

Then, we have:

Lemma 2.3

Let $S(u)=\int _{0}^{t} e^{-\int _{0}^{s}\frac{2\mu (v)}{\sigma ^2(v)}dv}\mathrm{d}t$ and assume that X(t) is the solution of (4). If $S(-\infty ) > - \infty$ and $S(+\infty ) = + \infty$, then

$$\begin{aligned} \lim \limits _{t\longmapsto + \infty } X(t)=-\infty . \end{aligned}$$

Lemma 2.4

Consider the system of stochastic differential equations (2). Given an arbitrarily large but finite time T, there exists a constant C dependent only on T and the initial data, such that the following estimates hold uniformly for $t \le T$

$$\begin{aligned} \int _{0}^{t} \mathbb {E}[u_i^2(s)]\mathrm{d}s < + \infty \end{aligned}$$

(5)

Lemma 2.5

Let $\left( B_{t}\right) _{t\ge o}$ a Brownian motion, then we have:

$$\begin{aligned} \lim _{t\rightarrow +\infty }\dfrac{B_{t}}{t} = 0 \ as. \end{aligned}$$

3 Main results

3.1 Existence and uniqueness of positive global solution

As the coefficient of equations (2) does not satisfy the local Lipschitz condition and linear growth condition, the solution of the system (2) may explode at finite time. So, we prove first the local existence of the positive solution of system (2), and then global solution by using the comparison theorem of stochastic equations.

Theorem 3.1

Given positive initial value $(x_0, y_0, z_0)$, system (2) has a unique positive global solution (x(t), y(t), z(t)) on $t\ge 0$.

Proof

Let us introduce new variables $u(t) = \ln (x(t))$, $v(t) = \ln (y(t))$ and $w(t) = \ln (z(t))$ in the system (2). By applying the Itô’s formula [1], we obtain the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{d}u(t) = \Big [ r \displaystyle \Big ( 1-\frac{e^{u(t)}+e^{v(t)}}{k} \Big )\mathrm{d}t\\ \quad \,\,\,\, \qquad - \beta \frac{e^{v(t)}}{e^{u(t)}+e^{v(t)}+\alpha } - \frac{\sigma ^{2}_1}{2} \Big ]\mathrm{d}t + \sigma _1 \mathrm{d}B_1(t),\\ \mathrm{d}v(t)=\Big [ \displaystyle \beta \frac{e^{u(t)}}{e^{u(t)}+e^{v(t)}+ \alpha } -\delta - p e^{w(t)} - \frac{\sigma ^{2}_2}{2} \Big ] \mathrm{d}t \\ \qquad \quad \, \, \,\, + \sigma _2 \mathrm{d}B_2(t), \\ \mathrm{d}w(t) = \Big [ \gamma e^{v(t)} -q - \displaystyle \frac{\sigma ^{2}_3}{2} \Big ] \mathrm{d}t + \sigma _3 \mathrm{d}B_3(t), \end{array}\right. } \end{aligned}$$

(6)

It is obvious that the coefficients of system (6) satisfy the local Lipschitz condition, then there is a unique local solution (u(t), v(t), w(t)) on $t \in [0, \tau ), \, \tau \in \mathbb {R}^0_+$, with initial value $u_0=\ln x(0)$, $v_0= \ln y(0)$ and $w_0=\ln z(0)$ [28, 46]. Thus, we conclude that $(x(t) = e^{u(t)}, y(t) = e^{v(t)}, z(t) = e^{w(t)})$ is the unique positive local solution of system (6) with positive initial conditions.

Now, in order to show that the unique positive solution is not only local solutions but also global solution, we need to prove that $\tau = \infty$.

Consider the following set of equations of stochastic system

$$\begin{aligned} \mathrm{d}X_2(t)&= r X_2(t) \Big ( 1 - \displaystyle \frac{X_2(t)}{k} \Big )\mathrm{d}t + \sigma _1 X_2(t) \mathrm{d}B_1(t), \end{aligned}$$

(7a)

$$\begin{aligned} \mathrm{d}Y_2(t)&\!=\! Y_2(t) \left( \beta {-}\delta {-} \displaystyle \frac{\beta Y_2(t)}{k {+} \alpha }\right) \mathrm{d}t {+} \sigma _2 Y_2(t) \mathrm{d}B_2(t), \end{aligned}$$

(7b)

$$\begin{aligned} \mathrm{d}Z_2(t)&= Z_2(t) \Big ( \gamma Y_2(t) -q \Big ) \mathrm{d}t + \sigma _3 Z_2(t) \mathrm{d}B_3(t), \end{aligned}$$

(7c)

with positive initial conditions $X_2(0)= x_0, \, Y_2(0)=y_0, \, Z_2(0)=z_0$.

As x(t) and y(t) are always positive, we can write from the first equation of model (6):

$$\begin{aligned} \mathrm{d}x(t) \le r x(t) \left( 1 - \frac{x(t)}{k} \right) \mathrm{d}t + \sigma _1 x(t) \mathrm{d}B_1(t) \end{aligned}$$

(8)

By applying the comparison theorem of stochastic differential equations, we obtain $x(t) \le X_2(t), \, \forall t \in [0, \tau )$, with

$$\begin{aligned} X_2(t)=\displaystyle \frac{e^{\left[ (r - \frac{\sigma _1^{2}}{2})t+ \sigma _1 B_1(t)\right] }}{\frac{1}{x_0}+\frac{r}{k}\int _{0}^{t} e^{\left[ (r - \frac{\sigma _1^{2}}{2})s+ \sigma _1 B_1(s)\right] } \mathrm{d}s }. \end{aligned}$$

Let $X_1 (t)$ be the solution of the following equation

$$\begin{aligned}&\mathrm{d}X_1(t) = X_1(t) \left( r - \beta -\frac{r}{k} X_1(t) -\frac{r}{k} X_2(t)\right) \mathrm{d}t \nonumber \\&\quad + \sigma _1 X_1(t) \mathrm{d}B_1(t), \, X_1(0)=x_0. \end{aligned}$$

(9)

As $\displaystyle \frac{\beta y(t) }{x(t)+ y(t)+\alpha }\le \beta$, we can write from the first equation of model (6):

$$\begin{aligned}&\mathrm{d}x(t) \ge x(t) \left[ r-\beta -\frac{r x(t)}{k} -\frac{r}{k}Y_2(t) \right] \mathrm{d}t \\&\quad + \sigma _1 x(t) \mathrm{d}B_1(t) \end{aligned}$$

Therefore, we have $x(t) \ge X_1(t), \, \forall t \in [0, \tau )$, where

$$\begin{aligned} X_1(t)= \displaystyle \frac{e^{\left[ (r - \beta - \frac{\sigma _1^{2}}{2})t -\displaystyle \frac{r}{k}\int _{0}^{t}X_2(s)\mathrm{d}s + \sigma _1 B_1(t)\right] }}{\displaystyle \frac{1}{x_0}+ \displaystyle \frac{r}{k}\int _{0}^{t} e^{\left[ (r - \beta - \displaystyle \frac{\sigma _1^{2}}{2})s-\frac{r}{k}\int _{0}^{s}X_2(m)\mathrm{d}m + \sigma _1 B_1(s)\right] } \mathrm{d}s }. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} X_1(t)\le x(t)\le X_2(t), \, \forall t \in [0, \tau ). \end{aligned}$$

(10)

We are going now to construct an upper bound of the dynamics of infected cancer cells y(t).

We have

$$\begin{aligned} \mathrm{d}y&= \left[ \beta y\left( 1-\frac{\alpha }{x+y+\alpha }-\frac{y}{x+y+ \alpha }\right) \right. \nonumber \\&\quad \left. -\,\delta y -pyz\right] \mathrm{d}t + \sigma _2 y \mathrm{d}B_2(t) \nonumber \\ \mathrm{d}y(t)&\le \Big [ y (t) \left( \beta -\delta - \frac{\beta y(t)}{k+\alpha }\right) \Big ] \mathrm{d}t \nonumber \\ {}&\quad + \sigma _2 y(t) \mathrm{d}B_2(t). \end{aligned}$$

(11)

By applying the comparison theorem of stochastic differential equations, we obtain $y(t) \le Y_2(t), \, \forall t \in [0, \tau )$, with

$$\begin{aligned} Y_2(t)= \displaystyle \frac{e^{\left[ \Big (\beta -\delta - \frac{\sigma _2^{2}}{2} \Big ) t+ \sigma _2 B_2(t) \right] }}{ \displaystyle \frac{1}{y_0}+\frac{\beta }{k+\alpha }\int _{0}^{t} e^{\left[ \Big (\beta -\delta - \frac{\sigma _2^{2}}{2} \Big )s+ \sigma _2 B_2(s)\right] } \mathrm{d}s }. \end{aligned}$$

As $y(t)\le Y_2(t)$, we can deduce that

$$\begin{aligned} \mathrm{d}z(t) \le z(t)\left[ \gamma Y_2(t) -q \right] \mathrm{d}t + \sigma _3 z(t) \mathrm{d}B_3(t). \end{aligned}$$

(12)

So, by applying again the comparison theorem of stochastic differential equations, we obtain $z(t) \le Z_2(t), \, \forall t \in [0, \tau )$, with

$$\begin{aligned} Z_2(t)= z_0 e^{\left[ \gamma \displaystyle \int _{0}^{t}Y_2(s)\mathrm{d}s {-} \left( q {+} \displaystyle \frac{\sigma _3^{2}}{2}\right) t{+} \sigma _3 B_3(t)\right] }. \end{aligned}$$

(13)

We are going now to construct a lower bound of the infected cancer cell dynamics y(t). We have

$$\begin{aligned} \mathrm{d}y(t) =&\left[ \beta y(t) \left( 1-\frac{\alpha }{x(t)+y(t)+\alpha }\right. \right. \nonumber \\&\quad \left. - \delta y(t) - p y(t) z(t) \right] \mathrm{d}t + \sigma _2 y(t) \mathrm{d}B_2(t) \nonumber \\&\ge y(t) \left[ \beta -\frac{\alpha \beta }{x(t)+\alpha } \frac{\beta y(t)}{x(t)+\alpha } -\delta -p Z_2(t)\right] \mathrm{d}t \nonumber \\&\quad +\, \sigma _2 y(t) \mathrm{d}B_2(t). \end{aligned}$$

(14)

From the inequality (11) and using Lemma 2.1, we get $\displaystyle \langle y(t) \rangle ^{*} \le \frac{\beta -\delta - \frac{\sigma _2^2}{2}}{\beta } (k+\alpha )$.

On the other hand, we have,

$$\begin{aligned} \mathrm{d}x&\ge \left[ r x \left( 1-\frac{x}{k}\right) -\frac{r}{k}xy -\beta x \right] \mathrm{d}t + \sigma _1 x \mathrm{d}B_1(t)&\\ \mathrm{d}x&\ge \left[ r x \left( 1{-}\frac{x}{k}\right) {-}\frac{r\left( \beta {-} \delta {-} \frac{\sigma _2^2}{2} \right) }{k\beta } (k{+}\alpha ) x {-}\beta x \right] \mathrm{d}t \\&\quad + \sigma _1 x \mathrm{d}B_1(t)\\&\ge x \left[ r-\beta -\frac{r\left( \beta -\delta - \frac{\sigma _2^2}{2} \right) }{k\beta } (k+\alpha )-\frac{r x}{k} \right] \mathrm{d}t \\&\quad + \sigma _1 x \mathrm{d}B_1(t)&\end{aligned}$$

By Lemma 2.1, from the previous inequality we deduce this estimate of x(t)

$$\begin{aligned}&\langle x(t) \rangle _{*}\ge x_{inf}, \ \text{ where } \ x_{inf}=\left[ r-\beta -\frac{\sigma _1^2}{2}\right. \nonumber \\&\quad \left. -\frac{r\left( \beta -\delta - \frac{\sigma _2^2}{2} \right) }{k\beta } (k+\alpha )\right] \frac{k}{r} \end{aligned}$$

(15)

Using the inequality (15) below in inequality (14), we obtain:

$$\begin{aligned} \mathrm{d}y\ge & {} y \left[ \beta -\delta -\frac{\alpha \beta }{x_{inf}+ \alpha } -\frac{\beta y}{x_{inf}+\alpha } -pZ_2(t)\right] \mathrm{d}t\\&+ \sigma _2 y \mathrm{d}B_2(t) \end{aligned}$$

Denote by $Y_1 (t)$ the solution of the equation below, with $Y_1 (0) = y_0$,

$$\begin{aligned}&\mathrm{d}Y_1 = Y_1 \left[ \beta -\delta -\frac{\alpha \beta }{x_{inf}+ \alpha }\right. \\&\quad \left. -\frac{\beta Y_1}{x_{inf}+\alpha } -pZ_2(t)\right] \mathrm{d}t + \sigma _2 Y_1 \mathrm{d}B_2(t) \end{aligned}$$

So, by applying again the comparison theorem of stochastic differential equations, we get $y(t)\ge Y_1(t), \forall t \in [0, \tau )$, with

$$\begin{aligned} Y_1(t)= \frac{e^{\left[ \left( \beta -\delta -\displaystyle \frac{\alpha \beta }{x_{inf}+\alpha } - \displaystyle \frac{\sigma _2^{2}}{2}\right) t - p \int _{0}^{t}Z_2(s)\mathrm{d}s + \sigma _2 B_1(t)\right] }}{\displaystyle \frac{1}{y_0}+\frac{\beta }{x_{inf}+\alpha }\int _{0}^{t} e^{\left[ \left( \beta -\delta - \displaystyle \frac{\alpha \beta }{x_{inf}+\alpha } - \displaystyle \frac{\sigma _2^{2}}{2}\right) s-p\int _{0}^{s}Z_2(m)\mathrm{d}m + \sigma _2 B_2(s) \right] }\mathrm{d}s }. \end{aligned}$$

(16)

Thus, we obtain

$$\begin{aligned} Y_1(t)\le y(t)\le Y_2(t), \, \forall t \in [0, \tau ). \end{aligned}$$

(17)

Let $Z_1(t)$ be the solution of stochastic differential equation

$$\begin{aligned}&\mathrm{d}Z_1(t) = Z_1(t)\left[ \gamma Y_1(t) -q \right] \mathrm{d}t \\&\qquad \qquad \quad \,\, + \sigma _3 Z_1(t) \mathrm{d}B_3(t),\, Z_1(0)=z_0. \end{aligned}$$

Using similar arguments as earlier, we obtain $z(t) \ge Z_1(t), \, \forall t \in [0, \tau ),$ with

$$\begin{aligned} Z_1(t)= z_0 e^{\left[ \gamma \int _{0}^{t}Y_1(s)\mathrm{d}s - \left( q + \displaystyle \frac{\sigma _3^{2}}{2}\right) t+ \sigma _3 B_3(t)\right] }. \end{aligned}$$

(18)

Thus, we obtain

$$\begin{aligned} Z_1(t)\le z(t)\le Z_2(t), \, \forall t \in [0, \tau ). \end{aligned}$$

(19)

As the functions $X_1$, $X_2$, $Y_1$, $Y_2$, $Z_1$ and $Z_2$ are well defined for all $t \in [0, \tau )$, for an arbitrarily large magnitude of $\tau$, this implies that $\tau = \infty$. $\square$

3.2 Persistence and extinction

In this section, we will establish the persistent conditions for system (2) under certain parametric restrictions. Later, we will investigate the conditions for which system (2) goes to be extinct.

Theorem 3.2

• 1. 1. If

  $$\begin{aligned} \beta <\frac{-\left( r\alpha +\frac{\sigma _1^2}{2}k \right) +\sqrt{\left( r\alpha +\frac{\sigma _1^2}{2}k\right) ^2+4r k \left( k+\alpha \right) \left( \delta +\frac{\sigma _2^2}{2}\right) }}{2k}, \end{aligned}$$

  then x(t) is strongly persistent in mean.

• 2. If

  $$\begin{aligned} \beta > \frac{-\left( k\left( r-q-\frac{\sigma _3^2}{2} \right) +\alpha r \right) +\sqrt{\left( k\left( r-q-\frac{\sigma _3^2}{2}\right) +\alpha r \right) ^2+4rk\left( \delta +\frac{\sigma _2^2}{2} \right) }}{2k} \end{aligned}$$

  and $\gamma < \displaystyle \frac{r}{k}+\frac{2\beta }{\alpha },$ then y(t) is strongly persistent in mean.

• 3. If

  $$\begin{aligned} \beta > \frac{ k\left( \delta +\frac{\sigma _2^2}{2} \right) + \sqrt{\left( k\left( \delta +\frac{\sigma _2^2}{2}\right) \right) ^2+4rk \left( \delta +\frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) }}{2k} \end{aligned}$$

  and

  $$\begin{aligned} \frac{\left( q+\frac{\sigma _3^2}{2} \right) \left( \frac{r}{k}+\frac{2\beta }{\alpha } \right) }{rk(k+\alpha )}< \gamma < \frac{r}{k}+\frac{2\beta }{\alpha } \end{aligned}$$

  and $q <r\left( r+\alpha \right) - \frac{\sigma _3^2}{2},$ then z(t) is strongly persistent in mean.

Proof

By using the previous equation (15),

$$\begin{aligned}&\langle x(t) \rangle _{*}\ge x_{inf}, \ \text{ where } \ x_{inf}\\&\quad =\left[ r-\beta -\frac{\sigma _1^2}{2} -\frac{r\left( \beta -\delta - \frac{\sigma _2^2}{2} \right) }{k\beta } (k+\alpha )\right] \frac{k}{r} \end{aligned}$$

and by reformulating $x_{inf}$, we have

$$\begin{aligned} x_{inf}=&\left[ k\beta -\frac{k}{r}\beta ^2 -\frac{k}{r}\beta \frac{\sigma _1^2}{2} -\left( \beta -\delta - \frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) \right] \frac{1}{\beta }\\ =&\left[ -\frac{k}{r}\beta ^2 + \beta \left( k -\frac{k \sigma _1^2}{2r} - k - \alpha \right) \right. \\&\quad \left. + \left( \delta + \frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) \right] \frac{1}{\beta }\\ =&\left[ -\frac{k}{r}\beta ^2 - \beta \left( \frac{k \sigma _1^2}{2r} + \alpha \right) + \left( \delta + \frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) \right] \frac{1}{\beta }. \end{aligned}$$

So $x_{inf}$ is a quadratic equation in $\beta$. Thus, $x_{inf}>0$ whenever $\beta$ satisfy

$$\begin{aligned} 0 \!<\! \beta \!<\!\frac{-\left( \! r\alpha \!+\!\frac{\sigma _1^2}{2}k\!\right) \!+\! \sqrt{\left( \! r\alpha \!+\!\frac{\sigma _1^2}{2}k\!\right) ^2\!\!+\!4r k\left( k\!+\! \alpha \right) \left( \! \delta \!+\!\frac{\sigma _2^2}{2}\!\right) }}{2k} \end{aligned}$$

(20)

As $\displaystyle \langle x(t) \rangle _{*}\ge x_{inf}>0$, then x(t) is strongly persistent in mean.

Applying Itô’s formula and integrating both sides from 0 to t on the following expression

$$\begin{aligned}&\ln \left( \frac{x(t)}{x_0}\right) +\ln \left( \frac{y(t)}{y_0}\right) + \ln \left( \frac{z(t)}{z_0}\right) \\&\quad =\int _{0}^{t}\left[ r-\frac{r}{k} (x(s)+y(s))-\beta \frac{y(s)}{x(s)+y(s)+\alpha }-\frac{\sigma ^{2}_{1}}{2}\right] \mathrm{d}s \\&\qquad +\sigma _{1}B_1(t) + \int _{0}^{t}\left[ \beta \frac{x(s)}{x(s)+y(s)+\alpha }\mathrm{d}s\right. \\&\quad \left. - \left( \delta +\frac{\sigma ^{2}_{2}}{2}\right) -pz(s)\right] \mathrm{d}s +\sigma _{2}B_{2}(t)\\&\qquad +\int _{0}^{t}\left[ \gamma y(s)-q-\frac{\sigma _3^2}{2}\right] \mathrm{d}s+ \sigma _{3}B_{3}(t). \end{aligned}$$

Using the following equality,

$$\begin{aligned}&\displaystyle \frac{x(s)}{x(s)+y(s)+\alpha } =1-\frac{\alpha }{x(s) +y(s)+\alpha }\\&\quad -\frac{y(s)}{x(s)+y(s)+\alpha }, \end{aligned}$$

we get

$$\begin{aligned}&\ln \left( \frac{x(t)}{x_0}\right) +\ln \left( \frac{y(t)}{y_0}\right) + \ln \left( \frac{z(t)}{z_0}\right) \nonumber \\&\quad =\left( r +\beta -\delta -q -\frac{\sigma ^{2}_{1}}{2} - \frac{\sigma ^{2}_{2}}{2}-\frac{\sigma _3^2}{2}\right) t \nonumber \\&\qquad -\left[ \frac{r}{k}\int _{0}^{t}x(s)\mathrm{d}s +\left( \frac{r}{k}-\gamma \right) \int _{0}^{t}y(s)\mathrm{d}s +p\int _{0}^{t}z(s)\mathrm{d}s\right] \nonumber \\&\qquad -\left[ \int _{0}^{t}\frac{2\beta y(s)}{x(s)+y(s)+\alpha }\mathrm{d}s + \int _{0}^{t} \frac{\alpha \beta }{x(s)+y(s)+\alpha }\mathrm{d}s\right] \nonumber \\&\qquad +\sigma _{1}B_1(t) + \sigma _{2}B_{2}(t) +\sigma _{3}B_{3}(t) \nonumber \\&\quad \ge \left( r +\beta -\delta -q -\frac{\sigma ^{2}_{1}}{2} \frac{\sigma ^{2}_{2}}{2}-\frac{\sigma _3^2}{2}\right) t\nonumber \\&\qquad -\left[ \frac{r}{k}\int _{0}^{t}x(s)\mathrm{d}s+\left( \frac{r}{k}-\gamma \right) \int _{0}^{t}y(s)\mathrm{d}s+p\int _{0}^{t}z(s)\mathrm{d}s\right] \nonumber \\&\qquad -\left[ \int _{0}^{t}\frac{2\beta y(s)}{\alpha }\mathrm{d}s+ \int _{0}^{t} \frac{\alpha \beta }{x_{inf}+\alpha }\mathrm{d}s\right] \nonumber \\&\qquad +\sigma _{1}B_1(t) + \sigma _{2}B_{2}(t) +\sigma _{3}B_{3}(t) \nonumber \\&\ln \left( \frac{x(t)}{x_0}\right) +\ln \left( \frac{y(t)}{y_0}\right) + \ln \left( \frac{z(t)}{z_0}\right) \nonumber \\&\quad \ge \left( r +\beta -\delta - \frac{\alpha \beta }{x_{inf}+\alpha } -q -\frac{\sigma ^{2}_{1}}{2} - \frac{\sigma ^{2}_{2}}{2}-\frac{\sigma _3^2}{2}\right) t \nonumber \\&\qquad -\left[ \frac{r}{k}\int _{0}^{t}x(s)\mathrm{d}s+\left( \frac{r}{k}+ \frac{2\beta }{\alpha } -\gamma \right) \int _{0}^{t}y(s)\mathrm{d}s\right. \nonumber \\&\qquad \left. +p\int _{0} ^{t}z(s)\mathrm{d}s\right] +\sigma _{1}B_1(t) + \sigma _{2}B_{2}(t) +\sigma _{3}B_{3}(t) \end{aligned}$$

(21)

According to Lemma 2.5, we obtain

$$\begin{aligned} \lim _{t\rightarrow +\infty }\dfrac{B_1(t)}{t}=0, \ \lim _{t\rightarrow +\infty } \dfrac{B_2(t)}{t}=0, \ \lim _{t\rightarrow +\infty }\dfrac{B_3(t)}{t}=0.\nonumber \\ \end{aligned}$$

(22)

According to Lemma 2.2 and equations (8), (11) and (12), we have

$$\begin{aligned}&\lim _{t\rightarrow \infty }\frac{1}{t}\ln \left( \dfrac{ x(t)}{x_0} \right) =\lim _{t\rightarrow \infty }\frac{1}{t}\ln \left( \dfrac{ y(t)}{y_0} \right) \nonumber \\&\quad =\lim _{t\rightarrow \infty }\frac{1}{t}\ln \left( \dfrac{ z(t)}{z_0} \right) =0 \end{aligned}$$

(23)

By using Itô’s formula to $\mathrm{d}y$ in system (2), we get

$$\begin{aligned}&\ln \left( \dfrac{ y(t)}{y_0} \right) = -\left( \delta +\frac{\sigma ^{2}_{2}}{2}\right) t\nonumber \\&\qquad +\sigma _{2}B_2(t)-p\int _{0}^{t}z_{s}\mathrm{d}s+\beta \int _{0}^{t}\frac{x_{s}}{x_{s}+y_{s}+\alpha }\mathrm{d}s \nonumber \\&\quad =-\left( \delta +\frac{\sigma ^{2}_{2}}{2}\right) t +\sigma _{2}B_2(t)-p\int _{0}^{t}z_{s}\mathrm{d}s\nonumber \\&\qquad +\beta \int _{0}^{t}\left[ 1-\frac{\alpha }{x_{s}+y_{s}+\alpha } -\frac{y_{s}}{x_{s}+y_{s}+\alpha }\right] \mathrm{d}s\nonumber \\&\quad \le \left( \beta - \delta -\frac{\beta \alpha }{x_{inf}+\alpha } -\frac{\sigma ^{2}_{2}}{2}\right) t\nonumber \\&\qquad +\sigma _{2}B_2(t)-\frac{\beta }{\alpha } \int _{0}^{t}y(s)\mathrm{d}s -p\int _{0}^{t}z_{s}\mathrm{d}s \end{aligned}$$

(24)

From equation (21), we have

$$\begin{aligned}&-p\int _{0}^{t}z_{s}\mathrm{d}s \le \ln \left( \frac{x(t)}{x_0}\right) +\ln \left( \frac{y(t)}{y_0}\right) +\ln \left( \frac{z(t)}{z_0}\right) \nonumber \\&\qquad - \left( r +\beta -\delta -\frac{\alpha \beta }{x_{inf}+\alpha } -q -\frac{\sigma ^{2}_{1}}{2} -\frac{\sigma ^{2}_{2}}{2}-\frac{\sigma _3^2}{2}\right) t \nonumber \\&\qquad +\left[ \frac{r}{k}\int _{0}^{t}x(s)\mathrm{d}s+\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) \int _{0}^{t}y(s)\mathrm{d}s \right] \nonumber \\&\qquad -\sigma _{1}B_1(t) + \sigma _{2}B_{2}(t) +\sigma _{3}B_{3}(t) \end{aligned}$$

(25)

Using the inequalities (21) and (26) with the properties (22) and (23), we obtain

$$\begin{aligned}&\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) \langle y(t) \rangle _{*}\nonumber \\&\quad \ge \left( r+\beta -q -\frac{\alpha \beta }{x_{inf}+ \alpha } -\frac{\sigma _1^2}{2}-\frac{\sigma _3^2}{2}\right) -\frac{r}{k} \langle x(t) \rangle _{*} \nonumber \\&\quad \ge \left( r+\beta -q -\frac{\alpha \beta }{x_{inf}+\alpha } - \frac{\sigma _1^2}{2}-\frac{\sigma _3^2}{2}\right) \nonumber \\&\qquad - \left( r-\beta -\frac{\sigma _1^2}{2} -\frac{r\left( \beta - \delta - \frac{\sigma _2^2}{2} \right) }{k\beta } (k+\alpha )\right) \nonumber \\&\quad \ge 2\beta + \frac{r\left( \beta -\delta - \frac{\sigma _2^2}{2} \right) }{k\beta } (k+\alpha )\nonumber \\&\quad -q -\frac{\alpha \beta }{x_{inf}+\alpha }-* \frac{\sigma _3^2}{2}\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) \langle y(t) \rangle _{*}\nonumber \\&\quad \ge \frac{k\beta ^2 + \left[ k\left( r-q-\frac{\sigma _3^2}{2}\right) +\alpha r \right] - r\left( \delta +\frac{\sigma _2^2}{2}\right) }{k\beta } \end{aligned}$$

(26)

Thus, y(t) is strongly persistent in mean if

$$\begin{aligned} \gamma <&\frac{r}{k}+\frac{2\beta }{\alpha } \, \, \text{ and } \nonumber \\ \beta >&\frac{-\left( k\left( r-q-\frac{\sigma _3^2}{2}\right) + \alpha r \right) +\sqrt{\left( k\left( r-q-\frac{\sigma _3^2}{2}\right) +\alpha r \right) ^2+4rk\left( \delta +\frac{\sigma _2^2}{2} \right) }}{2k}. \end{aligned}$$

(27)

We deduce from the equation (21) that

$$\begin{aligned}&\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) \int _{0}^{t}y(s)\mathrm{d}s\nonumber \\&\quad \ge -\left[ \ln \left( \frac{x(t)}{x_0}\right) +\ln \left( \frac{y(t)}{y_0}\right) +\ln \left( \frac{z(t)}{z_0}\right) \right] \nonumber \\&\qquad + \left( r +\beta -\delta -\frac{\alpha \beta }{x_{inf}+\alpha } -q - \frac{\sigma ^{2}_{1}}{2} -\frac{\sigma ^{2}_{2}}{2}-\frac{\sigma _3^2}{2}\right) t \nonumber \\&\qquad -\left[ \frac{r}{k}\int _{0}^{t}x(s)\mathrm{d}s +p\int _{0}^{t}z(s)\mathrm{d}s\right] \nonumber \\&\qquad +\sigma _{1}B_1(t) + \sigma _{2}B_{2}(t) +\sigma _{3}B_{3}(t)&\end{aligned}$$

(28)

and by applying Itô’s formula to $\mathrm{d}z$ in system (2), we have

$$\begin{aligned}&\ln \left( \frac{z(t)}{z_0}\right) \nonumber \\&\quad =\int _{0}^{t}\left[ \gamma y(s)-q- \frac{\sigma _{3}^2}{2}\right] \mathrm{d}s+\sigma _{3}B_{3}(t) \nonumber \\&\quad = \displaystyle \frac{\gamma }{\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) }\int _{0}^{t}\left[ \left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) y(s)\right. \nonumber \\&\qquad \left. -\left( q+\frac{\sigma _{3}^2}{2}\right) \displaystyle \frac{\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) }{\gamma } \right] \mathrm{d}s \nonumber \\&\qquad + \displaystyle \frac{\left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) }{\gamma }\sigma _{3}B_{3}(t) \end{aligned}$$

(29)

Let us use the inequality (28) in equation (29), then multiply the resulting inequality by $\frac{1}{t}$ and let us tend t toward $+ \infty$, then we get:

$$\begin{aligned}&p \langle z(t) \rangle _{*} \ge 2 \beta -\delta \nonumber \\&\qquad -\frac{\alpha \beta }{x_{inf}+\alpha }-q +\frac{r\left( \beta -\delta -\frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) }{k\beta }\nonumber \\&\qquad -\frac{\left( q+\frac{\sigma _3^2}{2} \right) \left( \frac{r}{k}+\frac{2\beta }{\alpha } -\gamma \right) }{\gamma } -\frac{\sigma _2^2}{2}-\frac{\sigma _3^2}{2} \nonumber \\&\quad \ge \beta -\delta +\frac{r\left( k+\alpha \right) }{k} -\frac{r\left( \delta +\frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) }{k\beta } \nonumber \\&\qquad -\frac{\left( q+\frac{\sigma _3^2}{2} \right) \left( \frac{r}{k}+\frac{2\beta }{\alpha } \right) }{\gamma } -\frac{\sigma _2^2}{2} \nonumber \\&\quad \ge \frac{k\beta ^2 -\left( \delta +\frac{\sigma _2^2}{2} \right) k\beta -r\left( \delta +\frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) }{k\beta } \nonumber \\&\qquad +\frac{r\left( k+\alpha \right) }{k} -\frac{\left( q+\frac{\sigma _3^2}{2} \right) \left( \frac{r}{k}+ \frac{2\beta }{\alpha } \right) }{\gamma } \end{aligned}$$

(30)

Therefore, z(t) is strongly persistent in mean if

$$\begin{aligned}&\displaystyle \frac{\left( q+\frac{\sigma _3^2}{2} \right) \left( \frac{r}{k}+ \displaystyle \frac{2\beta }{\alpha } \right) }{rk(k+\alpha )}<\gamma< \displaystyle \frac{r}{k}+\frac{2\beta }{\alpha } \, \, \text{ and } \nonumber \\&q < r\left( r+\alpha \right) - \frac{\sigma _3^2}{2} \, \, \text{ and } \nonumber \\&\beta > \displaystyle \frac{ k\left( \delta +\frac{\sigma _2^2}{2} \right) + \sqrt{\left( k\left( \delta +\frac{\sigma _2^2}{2}\right) \right) ^2+4rk \left( \delta +\frac{\sigma _2^2}{2} \right) \left( k+\alpha \right) }}{2k} \end{aligned}$$

(31)

$\square$

Theorem 3.3

If $r-\frac{\sigma ^{2}_{1}}{2} < 0$ and $\beta -\delta -\frac{\sigma ^{2}_{2}}{2} <0$ and $\gamma \frac{\left( k+\alpha \right) \left( \beta -\delta - \frac{\sigma ^{2}_{2}}{2} \right) }{\beta }-q-\frac{\sigma ^{2}_{3}}{2} < 0$ Then, for any initial condition $(x_{0}, y_{0},\, z_{0}) \ge 0$, the stochastic model system (2) goes to extinction exponentially with probability one.

Proof

From Itô’s formula, it follows that

$$\begin{aligned} \ln (x(t)) \le \ln (x_{0})+\left( r-\frac{\sigma ^{2}_{1}}{2}\right) t+ \sigma _{1}B^{1}_{t}, \end{aligned}$$

and

$$\begin{aligned} \ln (y(t))\le & {} \ln \left( y_{0}\right) +\left( \beta - \delta - \frac{\sigma ^{2}_{2}}{2}\right) t+\sigma _{2}B^{2}_{t}\\ \ln (z(t))\le & {} \ln (z_{0})+\left( \gamma \frac{\left( k+\alpha \right) \left( \beta -\delta -\frac{\sigma ^{2}_{2}}{2} \right) }{\beta } -q- \frac{\sigma ^{2}_{3}}{2}\right) t\\&+\,\sigma _{3}B^{3}_{t} \end{aligned}$$

According to Lemmas 2.2 and 2.5, we note that

$$\begin{aligned}&\lim _{t\rightarrow +\infty }\left[ \frac{\sigma _{i}B^{i}_{t}}{t}+\frac{\ln \left( H_{0}\right) }{t}\right] =0, \,\, \text{ for } \,\,\\&H_{0}=x_{0},y_{0},z_{0}, \,\, i= 1,2,3. \end{aligned}$$

According to Lemma 2.3, we have

$$\begin{aligned}&\limsup _{t\rightarrow +\infty }\frac{x(t)}{t}\le \left( r-\frac{\sigma ^{2}_{1}}{2}\right)< 0 \ \text {a.s.,}\\&\limsup _{t\rightarrow +\infty }\frac{y(t)}{t}\le \left( \beta - \delta - \frac{\sigma ^{2}_{2}}{2}\right)< 0 \ \text {a.s.,}\\&\limsup _{t\rightarrow +\infty }\frac{z(t)}{t}\le \left( \!\gamma \frac{\left( k\!+\! \alpha \right) \left( \beta \!-\!\delta \!-\!\frac{\sigma ^{2}_{2}}{2} \right) }{\beta }-q-\frac{\sigma ^{2}_{3}}{2}\right) \\&\quad < 0 \ \text {a.s.} \end{aligned}$$

Therefore, the stochastic model system goes to extinction exponentially. $\square$

3.3 Stochastic effects on model equilibrium stability

In this section, we will establish the condition of local asymptotic stability of the equilibria $E_1 = (0,0,0)$, $E_2 =(k,0,0)$, $E_3= (E_{3_1}, E_{3_2}, 0)$ and $E_4 = (E_{4_1}, E_{4_2}, E_{4_3})$, for stochastic system (2). We note that in [8], the authors provide the local stability of equilibria mentioned above:

• $E_1$ is always unstable for system (1),

• $E_2$ is locally asymptotically stable for system (1) if $\displaystyle \frac{\beta k}{\delta \left( k+ \alpha \right) }<1$,

• $E_3$ is locally asymptotically unstable for system (1) if

  $$\begin{aligned} \displaystyle \gamma \left( \frac{k\left( \beta -\delta \right) \left( r +\delta -\beta \right) -\left( \beta +\delta \right) \alpha r+\left( \beta - \delta \right) MM}{2\beta r } \right) >q, \end{aligned}$$

  where $MM\!=\! \sqrt{\left( r\left( k+\alpha \right) \!-\!\left( \beta \!-\!\delta \right) k \right) ^2+4\alpha \beta k r },$

• $E_4$ is locally asymptotically stable for system (1) if

  $$\begin{aligned} \displaystyle r\gamma \left( k+\alpha \sqrt{\left( k+\alpha \right) ^2 - \frac{4\beta q}{r\gamma }} \right) ^2 > 4 \beta k q. \end{aligned}$$

Therefore, we will highlight the consequence of introducing multiplicative noise in a loss of regularity in the cancer cells population and virus-specific CTL dynamics. We will show how a stable equilibrium for system (1) becomes unstable for system (2). We introduce small perturbations in the vicinity of these equilibria; then, we study the dynamic stability of the first- and second-order moments which result from them.

Let $(x_*,y_*,z_*)$ denote the equilibrium point of the deterministic system (1) whose components are given explicitly in earlier section. The change of variables consists of setting:

$$\begin{aligned} x(t)= & {} x_{*}+x_{1}(t)\\ y(t)= & {} y_{*}+y_{1}(t)\\ z(t)= & {} z_{*}+z_{1}(t) \end{aligned}$$

where $|x_{1}(t)|,|y_{1}(t)|,|z_{1}(t)| \ll 1$.

Substituting this transformation in the stochastic model (2), we obtain the following linearized version by neglecting the second- and higher order terms of small quantities:

$$\begin{aligned} \mathrm{d}x_{1}(t)= & {} \left( a_{11}x_{1}+a_{12}y_{1} \right) \mathrm{d}t+ \sigma _{1} (x_* + x_1(t)) \mathrm{d}B^{1}_{t} \nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} \mathrm{d}y_{1}(t)= & {} \left( a_{21}x_{1}+a_{22}y_{1}+a_{23}z_{1}\right) \mathrm{d}t\nonumber \\&+ \sigma _{2} (y_* + y_1(t)) \mathrm{d}B^{2}_{t} \end{aligned}$$

(33)

$$\begin{aligned} \mathrm{d}z_{1}(t)= & {} \left( a_{32}y_{1}+a_{33}z_{1}\right) \mathrm{d}t+ \sigma _{3} (z_* + z_1(t)) \mathrm{d}B^{3}_{t}, \nonumber \\ \end{aligned}$$

(34)

where $a_{ij} = \displaystyle \left. \frac{\partial F_i}{\partial X_j} \right| _{(x_*,y_*,z_*)}$,  $i,j=1,2,3$ and $F(X)=(F_1(X),F_2(X), F_3(X))$, $X =(x_1,x_2,x_3)$. The expressions of $a_{ij}$ and $F_i$ are given in the “Appendix A”.

By integrating both sides of the equations (32) to (34) from 0 to t, and by using the mean zero property of Ito’s integral [1, 28], we can write the system of ordinary differential equations for first-order moments as follows:

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[x_{1}(t)]}{\mathrm{d}t}= & {} a_{11}\mathbb {E}[x_{1}(t)]+a_{12} \mathbb {E}[y_{1}(t)] \end{aligned}$$

(35)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[y_{1}(t)]}{\mathrm{d}t}= & {} a_{21}\mathbb {E}[x_{1}(t)]+a_{22} \mathbb {E}[y_{1}(t)]+a_{23}\mathbb {E}[z_{1}(t)] \nonumber \\\end{aligned}$$

(36)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[z_{1}(t)]}{\mathrm{d}t}= & {} a_{32}\mathbb {E}[y_{1}(t)]+a_{33} \mathbb {E}[z_{1}(t)] \end{aligned}$$

(37)

Once we have the equations of the first-order moments, we use Ito’s formula to obtain:

$$\begin{aligned}&\mathrm{d}x_{1}^{2}(t) = [(2a_{11}+\sigma _{1}^{2})x_{1}^{2}+2a_{12}x_{1}y_{1} + 2\sigma _{1}^{2}x_{1}x_{*}\nonumber \\&\quad +\,\sigma _{1}^{2}x_{*}^{2}]\mathrm{d}t+ 2\sigma _{1} x_{1}x \mathrm{d}B^{1}_{t} \end{aligned}$$

(38)

$$\begin{aligned}&\mathrm{d}y_{1}^{2}(t) = [2a_{21}x_{1}y_{1}+(2a_{22}+\sigma _{2}^{2}) y_1^{2}+2a_{23}y_{1}z_{1}\nonumber \\&\quad +\,2\sigma _{2}^{2}y_{1}y_{*}+\sigma _{2}^{2} y_{*}^{2}]\mathrm{d}t+ 2\sigma _{2}y_{1}y \mathrm{d}B^{2}_{t} \end{aligned}$$

(39)

$$\begin{aligned}&\mathrm{d}z_{1}^{2}(t) = [2a_{32}y_{1}z_{1}+(2a_{33}+\sigma _{3}^{2})z_{1}^2 + 2\sigma _{3}^{2}z_{1}z_{*}\nonumber \\&\quad +\,\sigma _{3}^{2}z_{*}^{2}]\mathrm{d}t+ 2\sigma _{3} z_{1}z \mathrm{d}B^{3}_{t} \end{aligned}$$

(40)

$$\begin{aligned}&\mathrm{d}x_{1}(t)y_{1}(t) = [(a_{11}+a_{22})x_{1}y_{1}+a_{12}y_{1}^{2} +a_{21}x_{1}^{2}\nonumber \\&\quad +\,a_{23}x_{1}z_{1}]\mathrm{d}t+ \sigma _{1}y_{1}x \mathrm{d}B^{1}_{t}+ \sigma _{2}x_{1}y \mathrm{d}B^{2}_{t} \end{aligned}$$

(41)

$$\begin{aligned}&\mathrm{d}y_{1}(t)z_{1}(t) = [a_{21}x_{1}z_{1}+(a_{22}+a_{33})y_{1}z_{1} +a_{23}z_{1}^{2}\nonumber \\&\quad +\,a_{32}y_{1}^{2}]\mathrm{d}t+ \sigma _{2}z_{1}y \mathrm{d}B^{2}_{t}+ \sigma _{3}y_{1}z \mathrm{d}B^{3}_{t} \end{aligned}$$

(42)

$$\begin{aligned}&\mathrm{d}x_{1}(t)z_{1}(t) = [(a_{11}+a_{33})x_{1}z_{1}+a_{12}y_{1}z_{1} \nonumber \\&\quad +\,a_{32}x_{1}y_{1}]\mathrm{d}t+ \sigma _{1}z_{1}x \mathrm{d}B^{1}_{t}\nonumber \\&\quad + \sigma _{3}x_{1}z \mathrm{d}B^{3}_{t} \end{aligned}$$

(43)

Integrating the aforementioned equations from 0 to t, then taking mathematical expectation of both sides with the help of Fubini’s theorem as explained in [19, 23, 28, 41], and finally differentiating with respect to t, we obtain the system of differential equations for second-order moments as follows:

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[x_{1}^{2}(t)]}{\mathrm{d}t}= & {} (2a_{11}+\sigma _{1}^{2}) \mathbb {E}[x_{1}^{2}]+2a_{12}\mathbb {E}[x_{1}y_{1}]\nonumber \\&+\,2\sigma _{1}^{2} x_{*}\mathbb {E}[x_{1}]+\sigma _{1}^{2}x_{*}^{2} \end{aligned}$$

(44)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[y_{1}^{2}(t)]}{\mathrm{d}t}= & {} 2a_{21}\mathbb {E}[x_{1}y_{1}]+(2a_{22}+\sigma _{2}^{2})\mathbb {E}[y_{1}^{2}] \nonumber \\&+\,2a_{23}\mathbb {E}[y_{1} z_1]\nonumber \\&+\,2\sigma _{2}^{2}y_{*}\mathbb {E}[y_{1}]+\sigma _{2}^{2}y_{*}^{2} \end{aligned}$$

(45)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[z_{1}^{2}(t)]}{\mathrm{d}t}= & {} 2a_{32}\mathbb {E}[y_{1}z_{1}] +(2a_{33}+\sigma _{3}^{2})\mathbb {E}[z_{1}^{2}]\nonumber \\&+ 2\sigma _{3}^{2}z_{*} \mathbb {E}[z_{1}]+\sigma _{3}^{2}z_{*}^{2} \end{aligned}$$

(46)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[x_{1}(t)y_{1}(t)]}{\mathrm{d}t}= & {} (a_{11}+a_{22})\mathbb {E} [x_{1}y_{1}]+a_{12}\mathbb {E}[y_{1}^{2}]\nonumber \\&+\,a_{21}\mathbb {E}[x_{1}^{2}] + a_{23}\mathbb {E}[x_{1}z_{1}] \end{aligned}$$

(47)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[y_{1}(t)z_{1}(t)]}{\mathrm{d}t}= & {} a_{21}\mathbb {E}[x_{1} z_{1}]+(a_{22}+a_{33})\mathbb {E}[y_{1}z_{1}]\nonumber \\&+a_{23}\mathbb {E}[z_1^2] + a_{32}\mathbb {E}[y_{1}^{2}] \end{aligned}$$

(48)

$$\begin{aligned} \frac{\mathrm{d}\mathbb {E}[x_{1}(t)z_{1}(t)]}{\mathrm{d}t}= & {} (a_{11}+a_{33})\mathbb {E} [x_1 z_1] \nonumber \\&+\,a_{12}\mathbb {E}[y_1 z_1] + a_{32}\mathbb {E}[x_1 y_1]. \end{aligned}$$

(49)

Steady-states of the first- and second-order moments are obtained by solving following system of equations:

$$\begin{aligned}&a_{11}\mathbb {E}[x_{1}]+a_{12}\mathbb {E}[y_{1}] = 0 \end{aligned}$$

(50)

$$\begin{aligned}&a_{21}\mathbb {E}[x_{1}]+a_{22}\mathbb {E}[y_{1}]+a_{23}\mathbb {E}[z_1] = 0 \end{aligned}$$

(51)

$$\begin{aligned}&a_{32}\mathbb {E}[y_{1}]+a_{33}\mathbb {E}[z_{1}] = 0 \end{aligned}$$

(52)

$$\begin{aligned}&(2a_{11}+\sigma _{1}^{2})\mathbb {E}[x_{1}^{2}]+2a_{12}\mathbb {E}[x_{1} y_1]\nonumber \\&\quad +\,2\sigma _{1}^{2}x_{*}\mathbb {E}[x_{1}] = -\sigma _{1}^{2}x_*^{2} \end{aligned}$$

(53)

$$\begin{aligned}&2a_{21}\mathbb {E}[x_{1}y_{1}]+(2a_{22}+\sigma _{2}^{2})\mathbb {E} [y_1^{2}]\nonumber \\&\quad +\,2a_{23}\mathbb {E}[y_{1}z_{1}]+ 2\sigma _{2}^{2}y_{*} \mathbb {E}[y_1] = -\sigma _{2}^{2}y_{*}^{2} \end{aligned}$$

(54)

$$\begin{aligned}&2a_{32}\mathbb {E}[y_{1}z_{1}]+(2a_{33}+\sigma _3^{2})\mathbb {E}[ z_1^{2}] +2\sigma _{3}^{2}z_{*}\mathbb {E}[z_{1}] \nonumber \\&\quad = -\sigma _{3}^{2} z_{*}^{2} \end{aligned}$$

(55)

$$\begin{aligned}&(a_{11}+a_{22})\mathbb {E}[x_{1}y_{1}]+a_{12}\mathbb {E}[y_{1}^{2}] \nonumber \\&\quad +\,a_{21}\mathbb {E}[x_{1}^{2}]+a_{23}\mathbb {E}[x_{1}z_{1}] = 0 \end{aligned}$$

(56)

$$\begin{aligned}&a_{21}\mathbb {E}[x_{1}z_{1}]+(a_{22}+a_{33})\mathbb {E}[y_{1}z_{1}] \nonumber \\&\quad +\,a_{23}\mathbb {E}[z_{1}^{2}]+a_{32}\mathbb {E}[y_{1}^{2}] = 0 \end{aligned}$$

(57)

$$\begin{aligned}&(a_{11}+a_{33})\mathbb {E}[x_{1}z_{1}]+a_{12}\mathbb {E}[y_{1}z_{1}] +a_{32}\mathbb {E}[x_{1}y_{1}] = 0, \nonumber \\ \end{aligned}$$

(58)

For notational convenience, we assume that the steady-state for the first- and second-order moments is denoted by $\mathbb {E}[x_{1}]_{*}$, $\mathbb {E}[y_{1}]_{*}$, $\mathbb {E}[z_{1}]_{*}$, $\mathbb {E}[x_{1}^{2}]_{*}$, $\mathbb {E}[y_{1}^{2}]_{*}$, $\mathbb {E} [z_{1}^{2}]_{*}$, $\mathbb {E}[x_{1}y_{1}]_{*}$, $\mathbb {E}[y_{1} z_{1}]_{*}$, $\mathbb {E}[x_{1}z_{1}]_{*}$.

Thus, the stability of these steady states depends upon the sign of real parts of the eigenvalues of the matrix M defined by

$$\begin{aligned} M = \left[ \begin{array}{ccccccccc} a_{11} &{} a_{12} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ a_{21} &{} a_{22} &{} a_{23} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} a_{32} &{} a_{33} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 2\sigma _{1}^{2}x_{*} &{} 0 &{} 0 &{} (2a_{11}+\sigma _{1}^{2}) &{} 0 &{} 0 &{} 2a_{12} &{} 0 &{} 0 \\ 0 &{} 2\sigma _{2}^{2}y_{*} &{} 0 &{} 0 &{} (2a_{22}+\sigma _{2}^{2}) &{} 0 &{} 2a_{21} &{} 2a_{23} &{} 0 \\ 0 &{} 0 &{} 2\sigma _{3}^{2}z_{*} &{} 0 &{} 0 &{} (2a_{33}+\sigma _{3}^{2}) &{} 0 &{} 2a_{32} &{} 0 \\ 0 &{} 0 &{} 0 &{} a_{21} &{} a_{12} &{} 0 &{} (a_{11}+a_{22}) &{} 0 &{} a_{23} \\ 0 &{} 0 &{} 0 &{} 0 &{} a_{32} &{} a_{23} &{} 0 &{} (a_{22}+a_{33}) &{} a_{21} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} a_{32} &{} a_{12} &{} (a_{11}+a_{33}) \end{array}\right] \end{aligned}$$

Applying the Routh–Hurwitz criteria, one can find the conditions for the negative real parts of all eigenvalues of the matrix M, but the obtained conditions cannot be put into explicit conditions. So all details of stochastical stability analysis are given in “Appendix (A1)–(A2A3A4A5A6)”.

Theorem 3.4

• 1. The trivial equilibrium $E_1\!=\!(0,0,0)$ is unstable in terms of first- and second-order moments.

• 2. The first- and second-order moments associated with the cancer infected cells dynamics around zero are stable if $\delta \ge \frac{\sigma _2^2}{2}$.

• 3. The first- and second-order moments associated with the virus-specific CTL dynamics around zero are stable if $q \ge \frac{\sigma _3^2}{2}$ and $q \ge r$.

Proof

Around the trivial equilibrium point $E_1=(0,0,0)$, the eigenvalues of the matrix M associated with the first- and second-order moments are given as follows

$$\begin{aligned} \begin{array}{ccc} \lambda _{1}= r, &{} \lambda _{2}= -\delta &{} \lambda _{3}= -q, \\ \lambda _{4}= 2r+ \sigma _1^2, &{} \lambda _{5}= -2\delta +\sigma _2^2, &{} \lambda _{6}= -2q + \sigma _3^2, \\ \lambda _{7}= r - \delta , &{} \lambda _{8}= -(\delta +q) &{} \lambda _{9}= r-q. \end{array} \end{aligned}$$

• 1. Note that the first-order moment $\lambda _{1}= r$ and the second-order moment $\lambda _{4}= 2r+ \sigma _1^2$ are always positive. Thus, the cancer uninfected cells dynamics around 0 are unstable and therefore, $E_1$ is also unstable.

• 2. In the vicinity of 0, the cancer infected cells dynamics are stable if the first-order moment $\lambda _2= -\delta$ and the second-order moments $\lambda _{5}= -2\delta +\sigma _2^2$ and $\lambda _8= - (\delta +q)$) are negative.

• 3. In the vicinity of 0, the dynamics of virus-specific CTLs are stable if the first-order moment $\lambda _3= -q$ and the second-order moments $\lambda _{6}= -2q + \sigma _3^2$ and $\lambda _9= r-q$ are negative.$\square$

Theorem 3.5

Under the Assumption 1, the stochastic model around the interior equilibrium point $E_3$ is stable in terms of second-order moments.

Proof

According to the calculations made in the “Appendix (A1)–(A2A3A4A5A6)” on miners using the Routh–Hurwitz theorem, we have from (A10):

$$\begin{aligned} \Delta _1 = a_1 = \tau _6 = - (m_1 + m_4), \,\,\, \Delta _2 = a_2 \Delta _1,\\ \Delta _3 = a_3 \Delta _2, \,\,\, \Delta _4 = a_4 \Delta _3 \\ \Delta _5 = a_5 \Delta _4, \,\,\, \Delta _6 = a_6 \Delta _5 \end{aligned}$$

Assumption 1: All terms $(\Delta _{i})_{i=1, \ldots , 6}$ must be positive. $\square$

Theorem 3.6

Under Assumption 3, the stochastic model around the interior equilibrium point $E_4$ is unstable in terms of first- and second-order moments.

Proof

According to the calculations made in the “Appendix (A1)–(A2A3A4A5A6)”, it is shown from (A9) that

$$\begin{aligned}&\Delta _{1}= a_{1}=\rho _{6}=-(m_{1}+m_{4})\\&= - \left( 4(a_{11} + a_{22} + a_{33}) +\,\sigma _{1}^{2} + \sigma _{2}^{2}+ \sigma _{3}^{2}\right) \end{aligned}$$

So two possible cases arise:

Assumption 2: $\Delta _{1}<0$ if $a_{11} + a_{22} + a_{33} \ge 0$.

Assumption 3: $\Delta _{1}>0$ if $\Big ( a_{11} + a_{22} + a_{33}<0 \,\, \text{ and } \,\, 4(a_{11} + a_{22} + a_{33}) \le \sigma _{1}^{2} + \sigma _{2}^{2}+ \sigma _{3}^{2} \Big ).$ $\square$

3.4 Numerical simulations of population dynamics, probabilities of extinction and mean extinction time

This section will thus illustrate the mathematical results obtained in the previous section. We use Milstein’s Higher Order Method to obtain the system (59) which is a discretization transformation of system (2). Milstein’s numerical scheme is a first-order method which can be weakly or strongly convergent [18]. Due to the Lipschitzian characteristics of the deterministic and stochastic parts of our model, we have here a strong convergence of the Milstein scheme [27]. The convergence of this numerical method has been validated in for many models having an explicit expression of their exact solution, [15, 18, 34].

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{j+1} &{}\!\!= x_j+\left[ r x_j \left( 1-\dfrac{x_j+y_j}{k}\right) \right. \\ &{}\quad \left. -\beta \dfrac{x_jy_j}{x_j +y_j+\alpha }\right] \Delta t + \sigma _1x_j B_{1, j}\sqrt{ \Delta t} \\ &{}\quad + \frac{\sigma _1^2x_j \left( B_{1, j}^2-1\right) }{2}\Delta t,\\ y_{j+1}&{}\!\!=y_j+\left[ \beta \dfrac{x_jy_j}{x_j+y_j+\alpha } -\delta y_j - p y_j z_j\right] \Delta t \\ &{}\quad + \sigma _2 y_j B_{2, j}\sqrt{ \Delta t} + \frac{\sigma _2^2y_j \left( B_{2, j}^2-1\right) }{2}\Delta t, \\ z_{j+1} &{}\!\!=z_j+ \left[ \gamma y_jz_j -qz_j\right] \Delta t \\ &{}\quad + \sigma _3z_j B_{3, j}\sqrt{ \Delta t}+ \frac{\sigma _3^2z_j \left( B_{3,j} ^2-1\right) }{2}\Delta t, \end{array}\right. }\nonumber \\ \end{aligned}$$

(59)

where the time increment $\Delta t > 0$. For a fixed observation period $\left[ 0, \ T\right]$, n is estimated as follows $n=1+round \left( \frac{T}{\Delta t}\right)$ and the time discretization is $t_j =j \Delta t, \,\, \text{ for } \,\, j = 1, \ldots , n.$ $\sigma _i > 0, \,\, \text{ for } \,\, i=1, 2, 3,$ are the noise intensities. $B_{1, j}$, $B_{1, j}$ and $B_{3, j}$ denote independent Gaussian random variables which follow the normal distribution N(0, 1) for $j = 1, \dots , n$.

We also use the Monte Carlo algorithm to estimate the extinction probabilities ($P_{x,j}$, $P_{y,j}$, $P_{z,j}$) as well as the mean extinction times ($E_{x,j}$, $E_{y,j}$, $E_{z,j}$) associated with the extinction of each of the populations. This algorithm works as follows: for each discretization interval ($t_j, t_{j+1}$), we perform RN simulation runs whose outcome is to increment by one unit the counting variable ($L_{x,j}$, $L_{y,j}$, $L_{z,j}$), when $x_{j+1}\le 0$ or $y_{j+1}\le 0$ or $z_{j+1}\le 0$. The extinction probabilities ($P_{x,j}$, $P_{y,j}$, $P_{z,j}$) are approximated by the relative frequencies $\left( \frac{ L_{x,j}}{RN} \, \ \frac{ L_{y,j}}{RN} \, \ \frac{ L_{z,j}}{RN}\right)$. The complexity and convergence of this estimation algorithm for extinction probabilities and mean extinction times have been studied in [13]. The detailed code of this algorithm is presented in “Appendix B”.

Numerical simulations will be able to show how the combination of the effects of the parameters of the deterministic model (1) with the stochastic diffusion parameters affects the stochastic population dynamics of cancer cells and viruses given by system (2). For example, we will show how a stable equilibrium for system (1) becomes unstable for system (2), thus leading to the extinction of one or all of the populations. Finally, with this first passage estimation algorithm, we analyzed the parameter variation effects of model (2) on the mean first passage time, in the case of species extinction.

Fig. 1

Noise intensity effects of the cancer cells and virus-specific CTL dynamics, when the initial population densities are close to the equilibrium $E_4$. A Represents weak persistence of the three populations for the system (2) for parameters given in (60a). B Represents extinction of the three populations for the system (2) after 100 days for parameters given in (60b). C Represents weak persistence of the three populations for the system (2) for parameters given in (60c). D Represents the virus-specific CTL depletion induced by the increase in the noise intensity $\sigma _3$ for parameters given in (60d)

Fig. 2

Distribution of frequencies of first extinction time using Monte Carlo simulation. The parameters of models are fixed as: in (60b) for the three populations extinction (A); in (60d) for virus-specific depletion (B)

Fig. 3

Effects of the variation of the viral replication rate, $\beta$, and the viral cytotoxicity, $\delta$, on mean extinction time and extinction probability for cancer cells and virus-specific CTLs. Red zone corresponds to higher values of extinction probabilities or mean extinction times, while blue zone is for their low values

Fig. 4

Effects of the variation of the strength of CTL responses, $\gamma$, and the maximum per capita growth rate of uninfected tumor cells, r, on mean extinction time and extinction probability for virus-specific CTLs. Red zone corresponds to higher values of extinction probabilities or mean extinction times, while blue zone is for their low values

3.4.1 Simulations of cancer cells and virus-specific CTLs stochastic dynamics

This section is devoted to demonstrating our main analytical results in previous subsections. During the numerical resolution of stochastic system (2), the initial density of the populations of cancer cells and virus-specific CTLs is close to the equilibrium $E_4$ of coexistence of the three populations:

$$\begin{aligned} x_0= & {} E_{4_1}-0.01,\ \ y_0=E_{4_2}-0.001,\\ z_0= & {} E_{4_3}-0.001 \end{aligned}$$

To investigate the dynamical behavior of cancer cells and virus-specific CTLs, we choose a set of parameter values:

$$\begin{aligned}&r=0.15,\ k=12.0,\ \alpha =0.001,\ \beta =0.35,\nonumber \\&\gamma =0.1,\ \delta =0.12,\ p=0.3,\ q=0.1\nonumber \\&\sigma _1=0.08,\ \sigma _2=0.1,\ \sigma _3=0.105 \end{aligned}$$

(60a)

$$\begin{aligned}&r=0.15,\ k=12.0,\ \alpha =0.001,\ \beta =0.35,\nonumber \\&\gamma =0.1,\ \delta =0.12,\ p=0.3,\ q=0.1\nonumber \\&\sigma _1=0.21,\ \sigma _2=0.1,\ \sigma _3=0.105 \end{aligned}$$

(60b)

$$\begin{aligned}&r=0.27,\ k=12.0,\ \alpha =0.001,\ \beta =0.35,\nonumber \\&\gamma =0.1,\ \delta =0.12,\ p=0.3,\ q=0.1\nonumber \\&\sigma _1=0.02,\ \sigma _2=0.02,\ \sigma _3=0.22 \end{aligned}$$

(60c)

$$\begin{aligned}&r=0.27,\ k=12.0,\ \alpha =0.001,\ \beta =0.35,\nonumber \\&\gamma =0.1,\ \delta =0.12,\ p=0.3,\ q=0.1\nonumber \\&\sigma _1=0.02,\ \sigma _2=0.02,\ \sigma _3=0.5 \end{aligned}$$

(60d)

Figure 1A corresponds to the parameter values of stochastic system (2) given in equation (60a), while Fig. 1B results from the parameter values set in equation (60b), where the intensity of stochastic noise was increased for the three populations. Notice that in equations (60a) and (60b), the parameters ($r,\ k,\ \alpha ,\ \beta ,\ \gamma ,\ \delta ,\ p,\ q$) have been fixed so that for deterministic system (1), the equilibrium $E_4$ is locally stable and the equilibrium $E_1$ is unstable. The population of cancer cells and virus-specific CTLs gradually decrease and fluctuating in the neighborhood of $E_4$ in Fig. 1A, it indicates weak persistence. Thus, the diffusion and mutation of cancer cells can be controlled by varying the strength of noise. Further, Fig. 1B indicates that fluctuation of the same population tends to zero after 100 days. This implies that the increase in noise intensity leads the stochastic system (2) from population coexistence dynamics to an extinction of the three populations. Figure 1C and D corresponds to the outputs of stochastic system (2) with the parameter values, respectively, given in equations (60c) and (60d). Note that in (60d), the stochastic noise intensity is greater than that in (60c), for only the virus-specific CTLs and the parameters ($r,\ k,\ \alpha ,\ \beta ,\ \gamma ,\ \delta ,\ p,\ q$) have been fixed so that the equilibrium $E_4$ is locally stable and the equilibrium $E_3$ is unstable for system (2). Figure 1C shows weak persistence of the three populations in the neighborhood of $E_4$. However, we show in Fig. 1D the virus-specific CTL depletion induced by the increase in the noise intensity $\sigma _3$. The stochastic system is therefore switched from endemic equilibrium $E_4$ to the equilibrium $E_3$. It is an evidence that the parameter value combination and the intensity of environmental noise play pivotal role in determining the success of virotherapy.

3.4.2 Estimation of species extinction probabilities and mean extinction time

In our numerical resolutions based on the Monte Carlo algorithm, we set the increment time at $\Delta t = 0.001$ and the repetition number RN of the simulations at $RN = 6000$, with the fixed parameter values in (60b) and (60d). The graphs in Fig. 2 represent the distribution of all first pass times over $RN = 6000$ simulations. Figure 2A corresponds to the extinction time frequencies for the three populations, whereas Fig. 2B corresponds to the extinction time frequencies for only virus population. This algorithm estimates the frequencies and the mean time of extinctions. It also computes the associate probability of extinction of the three species in the case of therapy success (extinction of cancer cells and viruses-specific CTLs) as well as in the case of failure (depletion of the virus-specific CTLs only). In the event of successful virotherapy, the extinction probabilities are $\frac{lx}{RN}=0.891$ for extinction of uninfected cells, $\frac{ly}{RN}=0.797$ for extinction of infected cells and $\frac{lz}{RN}=0.876$ for virus-specific CTLs. In this success therapy situation, the mean extinction times are 171.5032, 207.2255 and 195.8487 days for, respectively, uninfected cells, infected cells and virus specific CTLs (see Fig. 2A). However, under the conditions of failure (given parameter values in 60d), the probability of extinction and the mean extinction time for the virus-specific CTLs were estimated to $\frac{lz}{RN}=0.897$ and 142.9962 days, respectively (see Fig. 2B).

3.4.3 Model parameter sensibility on extinction probabilities and mean extinction time

In this part of the analysis, we went further to determine the effects of parameter variations on the model outputs. Therefore, we determined the spaces of parameter values leading to the success or failure of the virotherapy. We also determined the associated mean extinction times and probabilities of extinction.

To determine the parameter sensitivities and the robustness of the therapy success characterized by the extinction of cancer cells and the disappearance of virus-specific CTLs, we vary the parameters $\beta$ ($\beta \in \left[ 0.14\, \ 0.45\right]$) and $\delta$ ($\delta \in \left[ 0.01\, \ 0.35 \right]$). For the rest of the stochastic model parameters, the values are fixed as in equation (60b). The estimation robustness of the mean extinction times and extinction probabilities as well as the parameter sensitivities of the stochastic model are presented in Fig. 3. For cancer cells as well as for virus-specific CTLs, the high extinction probabilities correspond to the low mean extinction times. Due to the model nonlinearity, the extinction estimation, when $\beta$ and $\delta$ vary, show the existence of a portion of a parabolic curve separating two zones. Above this portion of the parabolic curve, the uninfected cancer cells persist (Fig. 3A, B). However, below this portion of the parabolic curve, there is an extinction of uninfected cancer cells. In this situation, the extinction probabilities (Fig. 3B) of uninfected cancer cells increase with the simultaneous variations of $\beta$ and $\delta$ (increase in $\beta$ and decrease in $\delta$). The extinction of infected cancer cells is observed for the parameter values on either side of this nonlinear separation (Fig. 3C, D). The highest probabilities of extinctions are observed for high values of $\delta$ with $\delta > 0.2$ (Fig. 3D), part above the separation or for high values of $\beta$ with $\beta > 0.4$ (Fig. 3D), part below the separation. The mean disappearance times of virus-specific CTLs are also separated into two parts by a portion of a parabolic curve (Fig. 3E). Above this curve, the mean disappearance time is lower than above it. Conversely, the probabilities of disappearance of virus-specific CTLs are higher above this portion of curve than below (Fig. 3F). Under the depletion condition of virus-specific CTLs without extinction of the cancer cells, the sensitivity analysis was carried out by varying the parameters $r \in \left[ 0.264\, \ 0.2934\right]$ and $\gamma \in \left[ 0.087\, \ 0.133\right]$. The rest of the other model parameters are fixed as in (60d). The simulations in Fig. 4 show that the low $\gamma$ values ($\gamma <0.1$) lead to a high extinction probability, greater than 0.9 (Fig. 4B) with low mean extinction times, less than 120 days (Fig. 4A). If $\gamma$ is in $\left[ 0.10\, \ 0.12\right]$, the disappearance probability of virus specific CTLs will decrease around 0.7 and 0.8, while the mean disappearance time of virus-specific CTLs increases to be around 130 and 140 days. Then, for large values of r ($r> 0.275$) and $\gamma$ ($\gamma > 0.12$), the disappearance probability of virus-specific CTLs decreases below 0.6.

4 Conclusion

In this paper, a stochastic mathematical model is analyzed in order to improve the cancer oncolytic virotherapy incorporating virus-specific CTL responses. We established the conditions of the model solution existence, persistence and extinction. In relation to the success or failure of the therapy, we investigated the equilibrium point stabilities by calculating the first- and second-order moments of the associated linearized system. Using Monte Carlo algorithm, we estimated the mean first extinction time and the probability of extinction, under the conditions of success of therapy (corresponding to the extinction of cancer cells and viruses) or failure of therapy (depletion of the virus-specific CTLs without cancer cell extinction). Furthermore, by using this algorithm, we were able to establish the robustness of estimations and also the sensibility effects or our parameter variations on the extinction probabilities or the mean extinction times. This analytical process allows to estimate, on the one hand, the probability of the therapy success and the necessary remission duration necessary. Our results also allow to determine the therapy failure probability and so to adjust the control parameters before the disappearance period of the virus-specific CTLs. Our numerical simulations allow us to characterize the spaces of the

cancer control parameters in this stochastic dynamical system. In both success or failure therapy, the population fluctuated for a long period around the attractor of the co-existence equilibrium $E_4$ before switching to the attractor of the equilibrium $E_1$ (success) or $E_3$ (failure). Finally, our simulations highlighted the decisive effects of the combination of the stochastic diffusion parameters with the viral replication rate, $\beta$, the viral cytotoxicity, $\delta$, the strength of CTL responses, $\gamma$ and the maximum per capita growth rate of uninfected tumors cells, r, on the success or failure of virotherapy.

Appendices

Appendix A: Stability conditions analysis

1.1 1. Stability analysis around $E_4$

To find the eigenvalues of the matrix M, it is necessary to solve the auxiliary equation $\text{ det }(M' - \lambda I ) = 0$, where $M'$ is the square matrix defined by retaining only the second-order moments. Let

$$\begin{aligned} \beta _1= & {} (2a_{11}+\sigma _{1}^{2} -\lambda ) \end{aligned}$$

(A1)

$$\begin{aligned} \beta _2= & {} (2a_{22}+\sigma _{2}^{2}-\lambda ) \end{aligned}$$

(A2)

$$\begin{aligned} \beta _3= & {} (2a_{33}+\sigma _{3}^{2}-\lambda ) \end{aligned}$$

(A3)

$$\begin{aligned} \beta _4= & {} (a_{11}+a_{22}-\lambda ) \end{aligned}$$

(A4)

$$\begin{aligned} \beta _5= & {} (a_{22}+a_{33}-\lambda ) \end{aligned}$$

(A5)

$$\begin{aligned} \beta _6= & {} (a_{11}+a_{33}-\lambda ). \end{aligned}$$

(A6)

Since,

$$\begin{aligned} M' - \lambda I = \left[ \begin{array}{cccccc} (2a_{11}+\sigma _{1}^{2} -\lambda ) &{} 0 &{} 0 &{} 2a_{12} &{} 0 &{} 0 \\ 0 &{} (2a_{22}+\sigma _{2}^{2}-\lambda ) &{} 0 &{} 2a_{21} &{} 2a_{23} &{} 0 \\ 0 &{} 0 &{} (2a_{33}+\sigma _{3}^{2}-\lambda ) &{} 0 &{} 2a_{32} &{} 0 \\ a_{21} &{} a_{12} &{} 0 &{} (a_{11}+a_{22}-\lambda ) &{} 0 &{} a_{23} \\ 0 &{} a_{32} &{} a_{23} &{} 0 &{} (a_{22}+a_{33}-\lambda ) &{} a_{21} \\ 0 &{} 0 &{} 0 &{} a_{32} &{} a_{12} &{} (a_{11}+a_{33}-\lambda ) \end{array}\right] \end{aligned}$$

then,

$$\begin{aligned}&\text{ det }(M' - \lambda I ) = \beta _1 \left| \begin{array}{ccccc} \beta _2 &{} 0 &{} 2a_{21} &{} 2a_{23} &{} 0 \\ 0 &{} \beta _3 &{} 0 &{} 2a_{32} &{} 0 \\ a_{12} &{} 0 &{} \beta _4 &{} 0 &{} a_{23} \\ a_{32} &{} a_{23} &{} 0 &{} \beta _5 &{} a_{21} \\ 0 &{} 0 &{} a_{32} &{} a_{12} &{} \beta _6 \end{array}\right| \\&\quad -2 a_{12} \left| \begin{array}{ccccc} 0 &{} \beta _2 &{} 0 &{} 2a_{23} &{} 0 \\ 0 &{} 0 &{} \beta _3 &{} 2a_{32} &{} 0 \\ a_{21} &{} a_{12} &{} 0 &{} 0 &{} a_{23} \\ 0 &{} a_{32} &{} a_{23} &{} \beta _5 &{} a_{21} \\ 0 &{} 0 &{} 0 &{} a_{12} &{} \beta _6 \end{array}\right| \\&\quad =\beta _1 D_1 -2 a_{12}D_2, \end{aligned}$$

with

$$\begin{aligned} D_1= & {} \beta _3 \left| \begin{array}{cccc} \beta _2 &{} 2a_{21} &{} 2a_{23} &{} 0 \\ a_{12} &{} \beta _4 &{} 0 &{} a_{23} \\ a_{32} &{} 0 &{} \beta _5 &{} a_{21} \\ 0 &{} a_{32} &{} a_{12} &{} \beta _6 \end{array}\right| + 2 a_{32} \left| \begin{array}{cccc} \beta _2 &{} 0 &{} 2a_{21} &{} 0 \\ a_{12} &{} 0 &{} \beta _4 &{} a_{23} \\ a_{32} &{} a_{23} &{} 0 &{} a_{21} \\ 0 &{} 0 &{} a_{32} &{} \beta _6 \end{array}\right| ,\nonumber \\ \end{aligned}$$

(A7)

$$\begin{aligned}&D_2 = a_{21}\left| \begin{array}{cccc} \beta _{2} &{} 0 &{} 2a_{23} &{} 0 \\ 0 &{} \beta _{3} &{} 0 &{} a_{23} \\ a_{32} &{} a_{23} &{} \beta _{5} &{} a_{21} \\ 0 &{} 0 &{} a_{12} &{} \beta _{6} \end{array}\right| = a_{21}\beta _{2}\left| \begin{array}{ccc} \beta _{3} &{} 0 &{} a_{23} \\ a_{23} &{} \beta _{5} &{} a_{21} \\ 0 &{} a_{12} &{} \beta _{6} \end{array}\right| \nonumber \\&\qquad \quad + a_{21}a_{32}\left| \begin{array}{ccc} 0 &{} 2a_{23} &{} 0 \\ \beta _{3} &{} 0 &{} a_{23} \\ 0 &{} a_{12} &{} \beta _{6} \end{array}\right| \end{aligned}$$

(A8)

In order to calculate $D_1,$ let $F_1= \beta _2 \left| \begin{array}{ccc} \beta _4 &{} 0 &{} a_{23} \\ 0 &{} \beta _5 &{} a_{21} \\ a_{32} &{} a_{12} &{} \beta _6 \end{array}\right| - 2a_{21} \left| \begin{array}{ccc} a_{12} &{} 0 &{} a_{23} \\ a_{32} &{} \beta _5 &{} a_{21} \\ 0 &{} a_{12} &{} \beta _6 \end{array}\right| + 2 a_{23} \left| \begin{array}{ccc} a_{12} &{} \beta _4 &{} a_{23} \\ a_{32} &{} 0 &{} a_{21} \\ 0 &{} a_{32} &{} \beta _6 \end{array}\right|$,

and $F_2 = \beta _2 \left| \begin{array}{ccc} 0 &{} \beta _4 &{} a_{23} \\ a_{23} &{} 0 &{} a_{21} \\ 0 &{} a_{32} &{} \beta _6 \end{array}\right| + 2 a_{21} \left| \begin{array}{ccc} a_{12} &{} 0 &{} a_{23} \\ a_{32} &{} a_{23} &{} a_{21} \\ 0 &{} 0 &{} \beta _6 \end{array}\right|$

So,

$$\begin{aligned} F_1&= \beta _2 (\beta _4 \beta _5\beta _6 -a_{32}\beta _5 a_{23}-\beta _4 a_{12} a_{21}) \\&\quad - 2 a_{21}(a_{12}\beta _5\beta _6 -a_{23}a_{32} a_{12}-a_{12}^2 a_{21}) \\&\quad + 2 a_{23}(a_{23}a_{32}^2 - \beta _4 a_{32} \beta _6 - a_{12}a_{32}a_{21}),\\ F_2&= \beta _2 (a_{23}^2 a_{32} - \beta _6 \beta _4 a_{23}) + 2 a_{12}a_{21} a_{23}\beta _6. \end{aligned}$$

Then,

$$\begin{aligned}&D_1 = \beta _{3}F_{1}+2a_{32}F_{2}= \beta _{2}\beta _{3}\beta _{4}\beta _{5} \beta _{6}\\&\quad -\,a_{32}a_{23}\beta _{2}\beta _{3}\beta _{5}-2a_{21}a_{12}\beta _{3} \beta _{5}\beta _{6}\\&\quad -2a_{21}a_{12}a_{23}a_{32}\beta _{3}\\&\quad -\,2a^{2}_{21}a^{2}_{12}\beta _{3}+2a^{2}_{23}a^{2}_{32}\beta _{3}\\&\quad -\,2a_{23}a_{32} \beta _{3}\beta _{4}\beta _{6}-2a_{23}a_{12}a_{32}a_{21}\beta _{3}\\&\quad -\,a_{12}a_{21}\beta _{2}\beta _{3}\beta _{4}+2a^{2}_{32}a^{2}_{23} \beta _{2}\\&\quad -\,2a_{32}a_{23}\beta _{2}\beta _{4}\beta _{6}+4a_{32}a_{21}a_{12}a_{23} \beta _{6}\\&\beta _{1}D_{1}=\underbrace{\beta _{1}\beta _{2}\beta _{3}\beta _{4}\beta _{5} \beta _{6}}_{M_{1}}-\underbrace{a_{32}a_{23}\beta _{1}\beta _{2}\beta _{3} \beta _{5}}_{M_{2}}\\&\quad -\,\underbrace{2a_{12}a_{21}\beta _{1}\beta _{3}\beta _{5} \beta _{6}}_{M_{3}}-\underbrace{2a_{21}a_{23}a_{32}a_{12}\beta _{1}\beta _{3}} _{M_{4}}\\&\quad -\,\underbrace{2a^{2}_{12}a^{2}_{21}\beta _{1}\beta _{3}}_{M_{5}}+ \underbrace{2a^{2}_{32}a^{2}_{23}\beta _{1}\beta _{3}}_{M_{6}}\\&\quad -\, \underbrace{2a_{32}a_{23}\beta _{1}\beta _{3}\beta _{4}\beta _{6}}_{M_{7}}- \underbrace{2a_{32}a_{23}a_{12}a_{21}\beta _{1}\beta _{3}}_{M_{8}}\\&\quad -\,\underbrace{a_{12}a_{21}\beta _{1}\beta _{2}\beta _{3}\beta _{4}}_{M_{9}}+ \underbrace{a^{2}_{32}a^{2}_{23}\beta _{1}\beta _{2}}_{M_{10}}\\&\quad -\, \underbrace{2a_{32}a_{23}\beta _{1}\beta _{2}\beta _{4}\beta _{6}}_{M_{11}}+ \underbrace{4a_{12}a_{21}a_{32}a_{23}\beta _{1}\beta _{6}}_{M_{12}} \end{aligned}$$

We set

$$\begin{aligned} M_{1} =&\,\beta _{1}\beta _{2}\beta _{3}\beta _{4}\beta _{5}\beta _{6}\\ =&\left( \!\underbrace{2a_{11}+\sigma ^{2}_{1}}_{N_{1}}-\lambda \!\right) \left( \!\underbrace{2a_{22}+\sigma ^{2}_{2}}_{N_{2}}-\lambda \!\right) \left( \!\underbrace{2a_{33}+\sigma ^{2}_{3}}_{N_{3}}-\lambda \!\right) \\&\quad \left( \!\underbrace{a_{22}+a_{11}}_{N_{4}}-\lambda \!\right) \left( \!\underbrace{a_{22}+a_{33}}_{N_{5}}-\lambda \!\right) \left( \!\underbrace{a_{33}+a_{11}}_{N_{6}}-\lambda \!\right) \\ =&\left[ \lambda ^{3}-\left( \underbrace{N_{1}+N_{2}+N_{3}}_{m_{1}}\right) \lambda ^{2}\right. \\&\quad \left. +\left( \underbrace{N_{1}N_{2}+N_{1}N_{3}+N_{2}N_{3}}_{m_{2}} \right) \lambda -\underbrace{N_{1}N_{2}N_{3}}_{m_{3}}\right] \\&\quad \times \left[ \lambda ^{3}-\left( \underbrace{N_{4}+N_{5}+N_{6}}_{m_{4}}\right) \lambda ^{2}\right. \\&\quad \left. +\left( \underbrace{N_{4}N_{5}+N_{4}N_{6}+N_{5}N_{6}}_{m_{5}}\right) \lambda -\underbrace{N_{4}N_{5}N_{6}}_{m_{6}}\right] \\&\quad = \lambda ^{6}-\left( m_{1}+m_{4}\right) \lambda ^{5}+\left( \underbrace{m_{2}+ m_{5}+m_{1}m_{4}}_{\mu _{1}}\right) \lambda ^{4}\\&\quad -\left( \underbrace{m_{3}+m_{6} +m_{1}m_{5}+m_{2}m_{4}}_{\mu _{2}}\right) \lambda ^{3}\\&\quad +\left( \underbrace{m_{1}m_{6}+m_{5}m_{2}+m_{3}m_{4}}_{\mu _{3}}\right) \lambda ^{2}\\&\qquad -\left( \underbrace{m_{2}m_{6}+m_{3}m_{5}}_{\mu _{4}}\right) \lambda + m_{3}m_{6} \end{aligned}$$

$$\begin{aligned}&M_{2}=\left( N_{1}-\lambda \right) \left( N_{2}-\lambda \right) \left( N_{3}- \lambda \right) \left( N_{5}-\lambda \right) a_{32}a_{23}\\&\quad = \left( \lambda ^{3}-m_{1}\lambda ^{2}+m_{2}\lambda -m_{3}\right) \left( N_{5}-\lambda \right) a_{32}a_{23}\\&\quad = \displaystyle \underbrace{a_{23}a_{32}}_{\mu _{5}}\lambda ^{4}- \underbrace{a_{23}a_{32}\left( m_{1}+N_{5}\right) }_{\mu _{6}}\lambda ^{3} + \underbrace{a_{23}a_{32}\left( m_{2}+m_{1}N_{5}\right) }_{\mu _{7}}\lambda ^{2} \\&\qquad -\, \underbrace{a_{23}a_{32}\left( m_{3}+m_{2}N_{5}\right) }_{\mu _{8}}\lambda + a_{32}a_{23}m_{3}N_{5}\\&M_{3}= 2a_{12}a_{21}\beta _{1}\beta _{3}\beta _{5}\beta _{6} \\&\quad = 2a_{12}a_{21} \left( N_{1}-\lambda \right) \left( N_{3}-\lambda \right) \left( N_{5}-\lambda \right) \left( N_{6}-\lambda \right) \\&\quad = \underbrace{a_{12}a_{21}}_{\mu _{9}}\lambda ^{4}-\underbrace{2a_{12}a_{21} \left( N_{6}+N_{5}+N_{3}+N_{1}\right) }_{\mu _{10}}\lambda ^{3} \\&\quad +\, \underbrace{2a_{12}a_{21}\left( N_{1}N_{6}\!+\!N_{3}N_{6}\!+\!N_{5}N_{6}\!+\!N_{3}N_{1}\!+\! N_{1}N_{5}\!+\!N_{3}N_{5}\right) }_{\mu _{11}}\lambda ^{2} \\&\qquad -\,\underbrace{2a_{12}a_{21}\left( N_{1}N_{3}N_{6}+N_{1}N_{5}N_{6}+N_{1}N_{3} N_{5} +N_{5}N_{3}N_{6}\right) }_{\mu _{12}}\lambda \\&\qquad +2a_{12}a_{21}N_{5}N_{1}N_{3} N_{6}\\&M_{4}= 2a_{21}a_{12}a_{32}a_{23}\beta _{1}\beta _{3}=2a_{21}a_{12}a_{32}a_{23} \left( N_{1}-\lambda \right) \left( N_{3}-\lambda \right) \\&\quad = 2 \underbrace{a_{21}a_{12}a_{32}a_{23}}_{\mu _{25}}\lambda ^{2}- 2\underbrace{a_{21}a_{12}a_{32}a_{23}\left( N_{1}+N_{3}\right) }_{\mu _{26}} \lambda \\&\qquad +2a_{21}a_{12}a_{32}a_{23}N_{1}N_{3}\\&M_{5}= 2a^{2}_{21}a^{2}_{12}\beta _{1}\beta _{3}\\&\quad =2a^{2}_{21}a^{2}_{12} \left( N_{1}-\lambda \right) \left( N_{3}-\lambda \right) \\&\quad = 2 \underbrace{a^{2}_{21}a^{2}_{12}}_{\mu _{27}} \lambda ^{2} -2\underbrace{a^{2}_{21}a^{2}_{12}\left( N_{1}+N_{3}\right) } _{\mu _{28}}\lambda +2a^{2}_{21}a^{2}_{12}N_{1}N_{3} \end{aligned}$$

$$\begin{aligned}&M_{6} = 2a^{2}_{32}a^{2}_{23}\beta _{1}\beta _{3}=2a^{2}_{32}a^{2}_{23} \left( N_{1}-\lambda \right) \left( N_{3}-\lambda \right) \\&\quad = 2 \underbrace{a^{2}_{32}a^{2}_{23}}_{\mu _{29}} \lambda ^{2}-2\underbrace{a^{2}_{32}a^{2}_{23}\left( N_{1}+N_{3}\right) } _{\mu _{30}}\lambda +2a^{2}_{32}a^{2}_{23}N_{1}N_{3}\\&M_{7} = 2a_{32}a_{23}\beta _{1}\beta _{3}\beta _{4}\beta _{6}\\&\quad =2a_{32}a_{23} \left( N_{1}-\lambda \right) \left( N_{3}-\lambda \right) \left( N_{4}-\lambda \right) \left( N_{6}-\lambda \right) \\&\quad = 2\underbrace{a_{32}a_{23}}_{\mu _{13}}\lambda ^{4} -2\underbrace{a_{32}a_{23} \left( N_{1}+N_{3}+N_{4}+N_{6}\right) }_{\mu _{14}}\lambda ^{3} \\&\qquad +\, 2\underbrace{a_{32}a_{23}\left( N_{1}N_{3}\!+\!N_{1}N_{4}\!+\!N_{1}N_{6}\!+\!N_{3}N_{4} \!+\!N_{3}N_{6}\!+\!N_{4}N_{6}\right) }_{\mu _{15}}\lambda ^{2}\\&\qquad -\, 2\underbrace{a_{32}a_{23}\left( N_{1}N_{3}N_{4}+N_{1}N_{3}N_{6}+N_{1}N_{6} N_{4}+N_{6}N_{3}N_{4}\right) }_{\mu _{16}}\lambda \\&\qquad +\,2a_{32}a_{23}N_{1}N_{3}N_{4} N_{6} \end{aligned}$$

$$\begin{aligned} M_8&= 2 a_{12}a_{32}a_{21}a_{23}\beta _{1}\beta _{3}\\&=2a_{12}a_{32}a_{21}a_{23} (N_{1}-\lambda )(N_{3}-\lambda )\\&= 2a_{12}a_{32}a_{21}a_{23}\lambda ^{2} - 2a_{12}a_{32}a_{21}a_{23}(N_{1}+ N_{3})\lambda \\&\quad + 2a_{12}a_{32}a_{21}a_{23}N_{1}N_{3} \end{aligned}$$

$$\begin{aligned} \begin{aligned} M_{9}&= a_{12}a_{21}\beta _{1}\beta _{2}\beta _{3}\beta _{4}\\&=a_{12}a_{21} \left( N_{1}-\lambda \right) \left( N_{2}-\lambda \right) \left( N_{3}-\lambda \right) \left( N_{4}-\lambda \right) \\&= \underbrace{a_{12}a_{21}}_{\mu _{17}}\lambda ^{4}-\underbrace{a_{12}a_{21} \left( m_{1}+N_{4}\right) }_{\mu _{18}}\lambda ^{3}\\&\qquad +\underbrace{a_{12}a_{21} \left( m_{2}+m_{1}N_{4}\right) }_{\mu _{19}}\lambda ^{2}\\&\qquad -\underbrace{a_{12}a_{21}\left( m_{3}+m_{2}N_{4}\right) }_{\mu _{20}}\lambda + a_{12}a_{21}m_{3}N_{4} \end{aligned} \end{aligned}$$

$$\begin{aligned} M_{10}&= a_{32}^{2}a_{23}^{2}\beta _{1}\beta _{2}=a_{32}^{2}a_{23}^{2}(N_{1}- \lambda )(N_{2}-\lambda )\\&= a_{32}^{2}a_{23}^{2}\lambda ^{2} - a_{32}^{2}a_{23}^{2}(N_{1}+N_{2})\lambda \\&\qquad +\, a_{32}^{2}a_{23}^{2}N_{1}N_{2} \end{aligned}$$

$$\begin{aligned} M_{11}= & {} 2a_{32}a_{23}\beta _{1}\beta _{2}\beta _{4}\beta _{6}\\= & {} 2a_{32}a_{23} \left( N_{1}-\lambda \right) \left( N_{2}-\lambda \right) \left( N_{4}-\lambda \right) \left( N_{6}-\lambda \right) \\= & {} 2 \underbrace{a_{32}a_{23}}_{\mu _{21}}\lambda ^{4}-2\underbrace{a_{32} a_{23} \left( N_{1}+N_{2}+N_{4}+N_{6}\right) }_{\mu _{22}}\lambda ^{3} \\&+\, 2\underbrace{a_{32}a_{23}\left( N_{1}N_{2}\!+\!N_{1}N_{4}\!+\!N_{1}N_{6}\!+\!N_{2}N_{4} \!+\! N_{2}N_{6}\!+\!N_{4}N_{6}\right) }_{\mu _{23}}\lambda ^{2} \\&-2\underbrace{a_{32}a_{23}\left( N_{1}N_{3}N_{4}+N_{1}N_{3}N_{6}+N_{1}N_{6} N_{4}+N_{6}N_{3}N_{4}\right) }_{\mu _{24}}\lambda \\&+2a_{32}a_{23}N_{1}N_{2}N_{4} N_{6} \end{aligned}$$

$$\begin{aligned} M_{12}&=4a_{12}a_{32}a_{21}a_{23}\beta _{1}\beta _{6}\\&=4a_{12}a_{32}a_{21}a_{23} (N_{1}-\lambda )(N_{6}-\lambda )\\&= \underbrace{4 a_{12}a_{32}a_{21}a_{23}}_{2 \mu _{31}}\lambda ^{2} \!-\! \underbrace{4a_{12} a_{32}a_{21}a_{23}(N_{1}\!+\!N_{6})}_{2 \mu _{32}} \lambda \\&\quad + 4a_{12}a_{32}a_{21}a_{23}N_{1}N_{6}. \end{aligned}$$

From (A7), we have

$$\begin{aligned}&D_2 = a_{21}\beta _{2}(\beta _{3}\beta _{5}\beta _{6}+a_{23}^{2}a_{12}-\beta _{3}a_{12}a_{21})\\&\quad - a_{12}a_{32}a_{23}\beta _{3}\beta _{6} \end{aligned}$$

Then,

$$\begin{aligned}&-2a_{12}D_2=-2a_{12}a_{21}\beta _{2}\beta _{3}\beta _{5}\beta _{6}-2a_{12}^{2} a_{23}^{2}a_{21}\beta _{2}\\&\quad +2 a_{12}^{2}a_{21}^{2}\beta _{2}\beta _{3}+ 4a_{12} a_{21}a_{23}a_{32}\beta _{3}\beta _{6}. \end{aligned}$$

We set

$$\begin{aligned} M_{13}&= 2a_{12}a_{21}\beta _{2}\beta _{3}\beta _{5}\beta _{6}\\&= 2a_{12}a_{21}\lambda ^{4} - 2a_{12}a_{21}(N_{3}+N_{2}+N_{5}+N_{6}) \lambda ^{3}\\&\quad +2a_{12}a_{21}(N_{3}N_{2}+N_{2}N_{5}+N_{6}N_{2}\\&\quad + N_{6}N_{3}+ N_{3}N_{5}+ N_{5}N_{6}) \lambda ^{2} \\&\quad - 2a_{12}a_{21}(N_{2}N_{3}N_{5}+N_{2}N_{3}N_{6}+N_{2}N_{5}N_{6}\\&\quad +N_{3}N_{5} N_{6})\lambda + 2a_{12}a_{21}N_{2}N_{3}N_{5}N_{6},\\ M_{14}&= 2a_{12}^{2}a_{23}^{2}a_{21}\beta _{2} = 2a_{12}^{2}a_{23}^{2}a_{21}(N_{2}-\lambda ) \\ M_{15}&= 2 a_{12}^{2}a_{21}^{2}\beta _{2}\beta _{3}= 2 a_{12}^{2}a_{21}^{2} \lambda ^{2} \\&\quad - 2 a_{12}^{2}a_{21}^{2}(N_{2}+ N_{3})\lambda + 2 a_{12}^{2}a_{21}^{2}N_{2}N_{3},\\ M_{16}&= 4a_{12}a_{21}a_{23}a_{32}\beta _{3}\beta _{6}= 4a_{12}a_{21}a_{23} a_{32}\lambda ^{2} \\&\quad - 4a_{12}a_{21}a_{23}a_{32}(N_{3}+ N_{6})\lambda \\&\quad +4a_{12} a_{21}a_{23}a_{32}N_{3}N_{6}. \end{aligned}$$

So,

with,

$$\begin{aligned}&\rho _{1}=-2a_{12}a_{21},\\&\rho _{2}=2a_{12}a_{21}(N_{3}+N_{2}+N_{5}+N_{6}),\\&\rho _{3}=4a_{12}a_{21}a_{23}a_{32}+2 a_{12}^{2}a_{21}^{2}-2 a_{12}a_{21} (N_{3}N_{2}\\&\quad \qquad +N_{2}N_{5}+N_{6}N_{2}+N_{6}N_{3}+ N_{3}N_{5}+ N_{5}N_{6}),\\&\rho _{4}=2a_{12}a_{21}(N_{2}N_{3}N_{5}+N_{2}N_{3}N_{6}\\&\quad \qquad +N_{2}N_{5}N_{6}+N_{3} N_{5}N_{6})\\&\quad \qquad +2a_{12}^{2}a_{23}^{2}a_{21} - 4a_{12}a_{21}a_{23}a_{32}(N_{3}+ N_{6})\\&\quad \qquad -2 a_{12}^{2}a_{21}^{2}(N_{2}+N_{3}),\\&\rho _{5}=4a_{12}a_{21}a_{23}a_{32}N_{3}N_{6}+ 2 a_{12}^{2}a_{21}^{2}N_{2} N_{3}\\&\quad \qquad -2a_{12}a_{21}N_{2}N_{3}N_{5}N_{6} - 2a_{12}^{2}a_{23}^{2}a_{21}N_{2}. \end{aligned}$$

We will have

$$\begin{aligned}&\text{ det }(M'-\lambda I) =\lambda ^{6}+\rho _{6}\lambda ^{5}\\&\quad +(\rho _{1}+\rho _{7}) \lambda ^{4}+(\rho _{2}+\rho _{8})\lambda ^{3}\\&\quad +(\rho _{3}+\rho _{9})\lambda ^{2} + (\rho _{4}+\rho _{10})\lambda +\rho _{5}+\rho _{11}, \end{aligned}$$

where

$$\begin{aligned}&\rho _{6}=m_{1}+m_{4},\\&\rho _{7}=\mu _{1}-\mu _{5}-\mu _{9}-\mu _{13}-\mu _{17}-\mu _{21},\\&\rho _{8}=\mu _{3}+\mu _{6}+\mu _{10}+\mu _{14}+\mu _{18}+\mu _{22},\\&\rho _{9}=\mu _{3}-\mu _{7}-\mu _{11}-\mu _{15}-\mu _{19}-\mu _{23}\\&\quad -\mu _{25}- \mu _{27}+\mu _{29}-\mu _{31}+\mu _{33}+\mu _{35},\\&\rho _{10}=\mu _{12}-\mu _{4}+\mu _{16}+\mu _{20}+\mu _{24}+\mu _{26}\\&\quad +\mu _{28}- \mu _{30}+\mu _{32}-\mu _{34}-\mu _{36}, \end{aligned}$$

$$\begin{aligned} \rho _{11}&= m_{3}m_{6}-2a_{12}a_{21}N_{1}N_{3}N_{5}N_{6}\\&\quad -2a_{32}a_{23}N_{1} N_{3}N_{4}N_{6} \\&\quad -2a_{32}a_{23}N_{1}N_{2}N_{4}N_{6} \\&\quad - 4a_{12}a_{21}a_{23}a_{32} N_{1}N_{3} -2 a_{23}^{2}a_{32}^{2}N_{1}N_{3} \\&\quad - 2 a_{12}^{2}a_{21}^{2}N_{1} N_{3} + a_{23}^{2}a_{32}^{2}N_{1}N_{2} \\&\quad + 4a_{12}a_{21}a_{23}a_{32}N_{1}N_{6}, \end{aligned}$$

with

$$\begin{aligned}&a_{0}=1, \,\, a_{1}=\rho _{6},\,\, a_{2}=\rho _{1}+\rho _{7},\\&a_{3}=\rho _{2}+\rho _{8},\,\, a_{4}=\rho _{3}+\rho _{9}, \,\, a_{5}=\rho _{4}+ \rho _{10},\\&a_{6}=\rho _{5}+\rho _{11}. \end{aligned}$$

$$\begin{aligned} R = \left[ \begin{array}{cccccc} a_{1} &{} a_{0} &{} 0 &{} 0 &{} 0 &{} 0 \\ a_{3} &{} a_{2} &{} a_{1} &{} a_{0} &{} 0 &{} 0 \\ a_{5} &{} a_{4} &{} a_{3} &{} a_{2} &{} a_{1} &{} a_{0} \\ 0 &{} 0 &{} 0 &{} a_{4} &{} a_{3} &{} a_{2} \\ 0 &{} 0 &{} 0 &{} 0 &{} a_{5} &{}a_{4} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}a_{6} \end{array}\right] \end{aligned}$$

Sign of $\Delta _1=a_1$:

$\Delta _{1}=a_{1}=\rho _{6}=-(m_{1}+m_{4})$, with $m_1=N_{1}+N_{2}+N_{3}, \,\, m_4=N_{4}+N_{5}+N_{6},$

$$\begin{aligned}&N_{1}=2a_{11}+\sigma _{1}^{2}, \,\, N_{4}=a_{11}+a_{22}\\&N_{2}=2a_{22}+\sigma _{2}^{2}, \,\, N_{5}=a_{22}+a_{33}\\&N_{3}=2a_{33}+\sigma _{3}^{2}, \,\, N_{6}=a_{11}+a_{33} \end{aligned}$$

Then,

$$\begin{aligned}&\Delta _{1} = a_{1}=\rho _{6}=-(m_{1}+m_{4})\nonumber \\&\quad = -\left( 4(a_{11}+a_{22}+a_{33})+ \sigma _{1}^{2} + \sigma _{2}^{2}+ \sigma _{3}^{2}\right) \nonumber \\&\quad = - \left( 4Tr(J)+ \sigma _{1}^{2} + \sigma _{2}^{2}+ \sigma _{3}^{2}\right) . \end{aligned}$$

(A9)

Therefore, two possible case arise:

• $\Delta _{1}<0$ if $Tr(J)>0$,

• $\Delta _{1}<0$ if $Tr(J)<0$ and $4Tr(J) < \sigma _{1}^{2} + \sigma _{2}^{2}+ \sigma _{3}^{2}$.

1.2 2. Stability analysis around $E_3$

The characteristic polynomial of a matrix $M'$ evaluated at the equilibrium point $E_3$ is written as

$$\begin{aligned}&P(\lambda )= \lambda ^6 + \tau _6 \lambda ^5 + (\tau _1+\tau _7) \lambda ^4 + (\tau _2+\tau _8) \lambda ^3 \\&\quad + (\tau _3+\tau _9) \lambda ^2 + (\tau _4+\tau _{10}) \lambda + (\tau _5+\tau _{11}), \end{aligned}$$

where

$\tau _1 = - 2 a_{12}a_{21}$,

$\tau _2 = 2 a_{12}a_{21} (N_2 + N_3 + N_5 + N_6)$,

,

$\tau _4 = 2 a_{12}a_{21} (N_2N_3N_5 + N_2N_3N_6 + N_2N_5N_6 + N_3N_5N_6) + 2 a_{12}^2 a_{23}^2 a_{21} - 2 a_{12}^2 a_{21}^2 (N_2 + N_3)$    ,

$\quad - 2 a_{12}a_{21} N_2 N_3 N_5 N_6 - 2 a_{12}^2 a_{23}^2 a_{21} N_2$,

$\tau _6 = - (m_1 + m_4)$,

,

,

,

,

$\tau _{11} = m_3 m_6 - 2 a_{12}a_{21} N_1 N_3 N_5 N_6 - 2 a_{12}^2 a_{21}^2 N_1 N_3$.

The minor of matrix is written as follows:

$$\begin{aligned}&\Delta _1 = a_1 = \tau _6 = - (m_1 + m_4), \,\, \Delta _2 = a_2 \Delta _1,\nonumber \\ {}&\Delta _3 = a_3 \Delta _2, \Delta _4 = a_4 \Delta _3,\nonumber \\ {}&\Delta _5 = a_5 \Delta _4, \,\, \Delta _6 = a_6 \Delta _5. \end{aligned}$$

(A10)

Sign of $\Delta _2=a_2 \Delta _1$:

$a_2 = - 5 a_{12} a_{21} + m_5 + m_1 m_4 + m_2$

$a_2 = 3 Tr(J)^2 - 2( \sigma _1^2 + \sigma _2^2 + \sigma _3^2) Tr(J) + K$,

with $K = a_{11}a_{22} + a_{11}a_{33} + a_{22}a_{33} - 5 a_{12}a_{21} + (a_{11}+ \sigma _1^2)(a_{22}+\sigma _2^2)$.

The discriminant of $3 Tr(J)^2 - 2( \sigma _1^2 + \sigma _2^2 + \sigma _3^2) Tr(J) + K = 0$ is given by $\Delta ' = ( \sigma _1^2 + \sigma _2^2 + \sigma _3^2)^2 - 3 K$.

If $\Delta '=0$, then $Tr(J)^*=\frac{1}{3}( \sigma _1^2 + \sigma _2^2 + \sigma _3^2)$. So,

If $\Delta '>0$, then $(Tr(J))_1=\frac{1}{3}( \sigma _1^2 + \sigma _2^2 + \sigma _3^2 -\sqrt{\Delta '})$ and $(Tr(J))_2=\frac{1}{3}(\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sqrt{\Delta '})$.

Therefore,

Sign of $\Delta _3=a_3 \Delta _2$:

We have $a_{3}= \tau _{2}+\tau _{8}$, with

$\tau _{2}= 2a_{12}a_{21}(N_{2}+N_{3}+N_{5}+N_{6})$ and $\tau _{8}= \mu _{3}+ \mu _{10}+\mu _{18}$,

$\mu _{3}= m_{1}m_{6}+ m_{2}m_{5}+ m_{3}m_{4}$,

$\mu _{10}=2a_{12}a_{21}(N_{1}+N_{3}+N_{5}+N_{6})$,

$\mu _{18}=a_{12}a_{21}(N_{4}+m_{1})$,

$m_1=N_{1}+N_{2}+N_{3}$,     $m_4=N_{4}+N_{5}+N_{6}$,

$m_2=N_{1}N_{2}+N_{1}N_{3}+N_{2}N_{3}$,     $m_5=N_{4}N_{5}+N_{4}N_{6}+N_{5} N_{6}$,

$m_3=N_{1}N_{2}N_{3}$,     $m_6=N_{4}N_{5}N_{6}$,

$m_1m_6= N_1N_4N_5N_6 + N_2N_4N_5N_6 + N_3N_4N_5N_6$,

$m_2m_5= N_1N_2N_4N_5 + N_1N_2N_4N_6 + N_1N_2N_5N_6 + N_1N_3N_4N_5 + N_1N_3N_4N_6 + N_1N_3N_5N_6 \quad + N_2N_3N_4N_5+ N_2N_3N_4N_6 + N_2N_3N_5N_6$,

$m_3m_4= N_1N_2N_3N_4 + N_1N_2N_3N_4 + N_1N_2N_3N_6$,

$N_1N_4N_5N_6 = a_{33}N_1 Tr^2(J)+(a_{11}a_{22}N_1-a_{33}^2N_1)Tr(J)-a_{11} a_{22}a_{33}N_1$,

$N_2N_4N_5N_6 = a_{33}N_2 Tr^2(J)+(a_{11}a_{22}N_2-a_{33}^2N_2)Tr(J)-a_{11} a_{22}a_{33}N_2$,

$N_3N_4N_5N_6 = a_{33}N_3 Tr^2(J)+(a_{11}a_{22}N_3-a_{33}^2N_3)Tr(J)-a_{11} a_{22}a_{33}N_3$,

$N_1N_2N_4N_5 = N_1N_2 (a_{22}Tr(J)+ a_{11}a_{33})$,

$N_1N_2N_4N_6 = N_1N_2 (a_{11}Tr(J)+ a_{22}a_{33})$,

$N_1N_2N_5N_6 = N_1N_2 (a_{33}Tr(J)+ a_{11}a_{22})$,

$N_1N_3N_4N_5 = N_1N_3 (a_{22}Tr(J)+ a_{11}a_{33})$,

$N_1N_3N_4N_6 = N_1N_3 (a_{11}Tr(J)+ a_{22}a_{33})$,

$N_1N_3N_5N_6 = N_1N_3 (a_{33}Tr(J)+ a_{11}a_{22})$,

$N_2N_3N_4N_5 = N_2N_3 (a_{22}Tr(J)+ a_{11}a_{33})$,

$N_2N_3N_4N_6 = N_2N_3 (a_{11}Tr(J)+ a_{22}a_{33})$,

$N_2N_3N_5N_6 = N_2N_3 (a_{33}Tr(J)+ a_{11}a_{22})$,

$N_1N_2N_3N_4 = N_1N_2N_3(Tr(J)-a_{33})$,

$N_1N_2N_3N_5 = N_1N_2N_3(Tr(J)-a_{11})$,

$N_1N_2N_3N_6 = N_1N_2N_3(Tr(J)-a_{22})$. So

$$\begin{aligned}&a_{3} = \tau _{2}+\tau _{8} \\&\quad = 9a_{12}a_{21} Tr(J)+a_{12}a_{21}(2a_{11}+2a_{22}\\&\qquad +9a_{33}+3\sigma _1^2+3\sigma _2^2+5\sigma _3^2)+ m_1m_6\\&\qquad +m_2m_5+m_3m_4\\&\quad = (N_1+N_2+N_3)a_{33}Tr^2(J) + \Big (9a_{12}a_{21} \\&\qquad + a_{11}a_{22}N_1-a_{33}^2N_1 + a_{11}a_{22}N_2 - a_{33}^2N_2 \\&\qquad + a_{11}a_{22}N_3-a_{33}^2N_3 + N_1N_2 a_{22} + N_1N_2 a_{11} \\&\qquad + N_1N_2 a_{33} + N_1N_3 a_{22} + N_1N_3 a_{11}\\&\qquad + N_1N_3 a_{33} + N_2N_3 a_{22} + N_2N_3 a_{11} \\&\qquad + N_2N_3 a_{33} + 3N_1N_2N_3 \Big )Tr(J)\\&\qquad + a_{12}a_{21}(2a_{11}+2a_{22}+9a_{33}+3\sigma _1^2\\&\qquad +3\sigma _2^2+5\sigma _3^2)- a_{11}a_{22}a_{33}(N_1+N_2+N_3) \\&\qquad + N_1N_2(a_{11}a_{33}+a_{22}a_{33}+a_{11}a_{22}) \\&\qquad + N_1N_3 (a_{11}a_{33}+a_{22}a_{33}+a_{11}a_{22}) \\&\qquad + N_2N_3 (a_{11}a_{33}+a_{22}a_{33}+a_{11}a_{22}) \end{aligned}$$

We pose $A=(N_1+N_2+N_3)a_{33}$,

$B= \Big (9a_{12}a_{21} + a_{11}a_{22}N_1-a_{33}^2N_1 + a_{11}a_{22}N_2-a_{33}^2N_2 + a_{11}a_{22}N_3-a_{33}^2N_3 + N_1N_2 a_{22} + N_1N_2 a_{11} + N_1N_2 a_{33} + N_1N_3 a_{22} + N_1N_3 a_{11} + N_1N_3 a_{33} + N_2N_3 a_{22} + N_2N_3 a_{11} + N_2N_3 a_{33} + 3N_1N_2N_3 \Big )$,

and $C= a_{12}a_{21} (2a_{11}+2a_{22}+9a_{33}+3\sigma _1^2+3\sigma _2^2+5\sigma _3^2)- a_{11}a_{22} a_{33}(N_1+N_2+N_3) + N_1N_2(a_{11}a_{33}+a_{22}a_{33}+a_{11}a_{22}) + N_1N_3 (a_{11}a_{33}+a_{22}a_{33}+a_{11}a_{22}) + N_2N_3 (a_{11}a_{33} +a_{22}a_{33}+a_{11}a_{22})$.

So we can rewrite $a_3$ as $a_3 = A Tr(J)^{2}+BTr(J)+C$.

The discriminant of the equation $a_3 = 0$ is $\Delta =B^{2}-4AC$.

If $\Delta =0$, then $Tr(J)^*=-\frac{B}{2A}$. Therefore,

If $\Delta >0$, then $Tr_1(J)=(\frac{-B -\sqrt{\Delta }}{2A}) \text{ and } Tr_2(J)=(\frac{-B +\sqrt{\Delta }}{2A})$. So

Sign of $\Delta _4=a_4 \Delta _3$:

We have $a_4 = \tau _3+\tau _9$, with

$\tau _3 = 2 a_{12}^2a_{21}^2 - 2a_{12}a_{21} (N_2N_3+N_2N_5+N_2N_6+N_3N_5+N_3N_6+N_5N_6)$,

,

$\mu _3 = m_1m_6+m_2m_5+m_3m_4$,

$\mu _{11} = 2a_{12}a_{21}(N_1N_6+N_3N_6+N_5N_6+N_1N_3+N_1N_5+N_3N_5)$,

$\mu _{19} = a_{12}a_{21}(m_2+m_1N_4)$,

$\mu _{27} = 2a_{12}^2 a_{21}^2$

So we can rewrite $a_3$ as

$$\begin{aligned} a_4= & {} \tau _3+ \tau _9 \\= & {} - a_{12}a_{21} \Big [2 N_2N_3 + 2 N_2N_5 + 2 N_2N_6 \\&+\,4 (N_3N_5+N_5N_6+N_3N_6)\\&+\,2 N_1N_6 + 2 N_1N_3 +2 N_1N_5 + m_2 + m_1N_4 \Big ] \\&+\, m_1m_6 + m_2m_5 + m_3m_4, \end{aligned}$$

with

$N_1 N_4 = N_1(Tr(J)-a_{33})$; $N_1N_5=N_1(Tr(J)-a_{11})$; $N_1N_6=N_1(Tr(J)- a_{22})$, $N_2N_4=N_2(Tr(J)-a_{33})$; $N_2N_5=N_2(Tr(J)-a_{11})$; $N_2N_6=N_2(Tr(J)- a_{22})$, $N_3N_4=N_3(Tr(J)-a_{33})$, $N_3N_5=N_3(Tr(J)-a_{11})$; $N_3N_6=N_3(Tr(J)-a_{22})$; $N_5N_6= a_{33}Tr(J) + a_{11}a_{22}$; $m_1m_6= N_1N_4N_5N_6 + N_2N_4N_5N_6 + N_3N_4N_5N_6$

$m_2m_5= N_1N_2N_4N_5 + N_1N_2N_4N_6 + N_1N_2N_5N_6 + N_1N_3N_4N_5 + N_1N_3N_4N_6 + N_1N_3N_5N_6 + N_2N_3N_4N_5+ N_2N_3N_4N_6 + N_2N_3N_5N_6$

$m_3m_4= N_1N_2N_3N_4 + N_1N_2N_3N_4 + N_1N_2N_3N_6$

$N_1N_4N_5N_6 = a_{33}N_1 Tr^2(J)+(a_{11}a_{22}N_1-a_{33}^2N_1)Tr(J)-a_{11} a_{22}a_{33}N_1$

$N_2N_4N_5N_6 = a_{33}N_2 Tr^2(J)+(a_{11}a_{22}N_2-a_{33}^2N_2)Tr(J)-a_{11} a_{22}a_{33}N_2$

$N_3N_4N_5N_6 = a_{33}N_3 Tr^2(J)+(a_{11}a_{22}N_3-a_{33}^2N_3)Tr(J)-a_{11} a_{22}a_{33}N_3$

$N_1N_2N_4N_5 = N_1N_2 (a_{22}Tr(J)+ a_{11}a_{33})$

$N_1N_2N_4N_6 = N_1N_2 (a_{11}Tr(J)+ a_{22}a_{33})$

$N_1N_2N_5N_6 = N_1N_2 (a_{33}Tr(J)+ a_{11}a_{22})$

$N_1N_3N_4N_5 = N_1N_3 (a_{22}Tr(J)+ a_{11}a_{33})$

$N_1N_3N_4N_6 = N_1N_3 (a_{11}Tr(J)+ a_{22}a_{33})$

$N_1N_3N_5N_6 = N_1N_3 (a_{33}Tr(J)+ a_{11}a_{22})$

$N_2N_3N_4N_5 = N_2N_3 (a_{22}Tr(J)+ a_{11}a_{33})$

$N_2N_3N_4N_6 = N_2N_3 (a_{11}Tr(J)+ a_{22}a_{33})$

$N_2N_3N_5N_6 = N_2N_3 (a_{33}Tr(J)+ a_{11}a_{22})$

$N_1N_2N_3N_4 = N_1N_2N_3(Tr(J)-a_{33})$

$N_1N_2N_3N_5 = N_1N_2N_3(Tr(J)-a_{11})$

$N_1N_2N_3N_6 = N_1N_2N_3(Tr(J)-a_{22})$ From where, we have:

$a_4 = - a_{12}a_{21} \Big [2 N_2N_3 + 2 (N_2(Tr(J)-a_{11})) + 2 (N_2(Tr(J)- a_{22}))$ $+ 4 (N_3(Tr(J)-a_{11})+a_{33}Tr(J)+a_{11}a_{22}+N_3(Tr(J)-a_{22}))$ $+2 N_1(Tr(J)-a_{22}) + 2 N_1N_3 + 2 N_1(Tr(J)-a_{11}) + m_2 + m_1N_4 \Big ] + m_1m_6 + m_2m_5 + m_3m_4$,

$a_4 = (N_1+N_2+N_3)a_{33}Tr^2(J)+ (3N_1N_2N_3 +a_{11}N_1N_2+a_{22} N_1N_2$ $+a_{33}N_1N_2+a_{22}N_1N_3+a_{11}N_1N_3$ $+a_{33}N_1N_3+a_{22} N_2N_3+a_{11} N_2N_3+a_{33}N_2N_3 - 5a_{12}a_{21}N_2 -$ $9a_{12}a_{21}N_3 - 5a_{12}a_{21}N_1 - 4a_{12}a_{21}a_{33} + a_{11}a_{22}N_1-a_{33}^2N_1+$ $a_{11}a_{22}N_2-a_{33}^2N_2+$ $a_{11}a_{22} N_3 - a_{33}^2N_3) Tr(J) +a_{11}a_{33}N_1N_2 + a_{22}a_{33}N_1N_2 +a_{11} a_{22}$ $N_1N_2+a_{11}a_{33}N_1N_3 + a_{22}a_{33}N_1N_3 +a_{11}a_{22}N_1 N_3 + a_{11}a_{33}N_2N_3 + a_{22}a_{33}N_2N_3$ $+a_{11}a_{22}N_2N_3 - a_{11}a_{22} a_{33}(N_1+N_2+N_3)-(a_{11}+a_{22}+a_{33})N_1N_2N_3$ $- a_{12}a_{21} (2N_2N_3-2a_{11}N_2-2a_{22}N_2-4a_{11}N_3+4a_{11}a_{22}-4a_{22}N_3-2a_{22} N_1+$ $2N_1N_3-2a_{11}N_1+N_1N_2+N_1N_3+N_2N_3-a_{33}N_1-a_{33}N_2-a_{33}N_3)$.

By setting new changes to variables, we have:

$A= (N_1+N_2+N_3)a_{33}$,

$B=(3N_1N_2N_3 +a_{11}N_1N_2+a_{22}N_1N_2+a_{33}N_1N_2+a_{22}N_1N_3$ $+a_{11} N_1N_3+a_{33}N_1N_3$ $+a_{22}N_2N_3+a_{11}N_2N_3+a_{33}N_2N_3 - 5a_{12}a_{21}N_2 - 9a_{12}a_{21}N_3$ $- 5a_{12}a_{21}N_1 - 4a_{12}a_{21}a_{33} +a_{11}a_{22}N_1-a_{33}^2N_1+a_{11}a_{22}N_2$ $-a_{33}^2N_2+a_{11}a_{22}N_3- a_{33}^2N_3)$,

$C = a_{11}a_{33}N_1N_2 + a_{22}a_{33}N_1N_2 +a_{11}a_{22}N_1N_2+a_{11}a_{33} N_1N_3 + a_{22}a_{33}N_1N_3$ $+a_{11}a_{22}N_1N_3 + a_{11}a_{33}N_2N_3 + a_{22}a_{33}N_2N_3$ $+a_{11}a_{22}N_2N_3 - a_{11}a_{22} a_{33}(N_1+N_2+N_3)-(a_{11}+a_{22}+a_{33})N_1N_2N_3$ $- a_{12}a_{21} (2N_2N_3-2a_{11}N_2-2a_{22}N_2-4a_{11}N_3+4a_{11}a_{22}$ $- 4a_{22}N_3-2a_{22}N_1+2N_1N_3-2a_{11}N_1+N_1N_2+N_1N_3+N_2N_3-a_{33}N_1- a_{33}N_2-a_{33}N_3)$.

As $a_4 = A Tr^2(J) + B Tr(J) + C$, the associate discriminant is given by $\Delta = B^2 - 4 A \times C$. So,

If $\Delta =0$, then $Tr(J)^*=-\frac{B}{2A}$. Therefore,

If $\Delta \!>\!0$, then $(Tr(J))_1=(\frac{-B -\sqrt{\Delta }}{2A}) \,\, \text{ and } \,\, (Tr(J))_2 =(\frac{-B +\sqrt{\Delta }}{2A})$. Therefore,

Sign of $\Delta _5=a_5 \Delta _4$:

We will now study the sign of the coefficient $a_{5}$. To do this, we transform $a_{5}$ in the form of a quadratic equation. We have $a_{5}=\tau _{10}+\tau _{4}$, with

$$\begin{aligned}&\tau _{4} = 2a_{12}a_{21}\left( N_{2}N_{3}N_{5}+N_{2}N_{3}N_{6}\right. \\&\quad \left. +N_{2}N_{6} N_{5}+N_{6}N_{3}N_{5}\right) \\&\quad + 2a^{2}_{12}a^{2}_{23}a_{21} - 2a^{2}_{12}a^{2}_{21}\left( N_{2}+N_{3}\right) ,\\&\tau _{10} = \mu _{12}-\mu _{4}+\mu _{20}+\mu _{28}, \\&\mu _{12} = N_{1}N_{3}N_{6}+N_{1}N_{6}N_{5}+N_{1}N_{3}N_{5}+N_{6}N_{3}N_{5}, \\&\mu _{20} = -a_{12}a_{21}\left( m_{3}+m_{2}N_{4}\right) , \\&\mu _{28} = -2a^{2}_{12}a^{2}_{21}\left( N_{1}+N_{3}\right) , \\&\mu _{4}= -\left( m_{2}m_{6}+m_{3}m_{5}\right) ,\\&m_{2} = N_{1}N_{2}+N_{1}N_{3}+N_{3}N_{2}, \\&m_{5} = N_{4}N_{5}+N_{4}N_{6}+N_{5}N_{6}, \\&m_{3} = N_{1}N_{2}N_{3}, \\&m_{6} = -N_{4}N_{5}N_{6}.\\&N_{2}N_{6}N_{5}+N_{6}N_{3}N_{5} =N_{6}N_{5}\left( N_{2}+N_{3}\right) \\&\quad =\left( N_{2}+N_{3}\right) \left( a_{22}+a_{33}+a_{11}-a_{11}\right) \\&\quad \left( a_{11}+a_{33}+a_{22}-a_{22}\right) \\&\quad =\left( N_{2}+N_{3}\right) \left( Tr(J)-a_{11}\right) \left( Tr(J)-a_{22}\right) \\&\quad =\left( N_{2}+N_{3}\right) a_{33}Tr(J)+\left( N_{2}+N_{3}\right) a_{11}a_{22}, \\&N_{2}N_{3}N_{5}+N_{2}N_{3}N_{6}= N_{2}N_{3}\left( N_{5}+N_{6}\right) \\&\quad = N_{2}N_{3}\left( a_{22}+a_{33}+a_{11}+a_{33}\right) \\&\quad = N_{2}N_{3}\left( Tr(J)+a_{33}\right) \\&\quad = N_{2}N_{3}Tr(J)+N_{2}N_{3}a_{33}, \\&N_{2}+N_{3} = N_{1}+N_{2}+N_{3}-N_{1}\\&\quad =2a_{11}+2a_{22}+2a_{33}-2a_{11}- \sigma ^{2}_{1}\\&\qquad +\,\sigma ^{2}_{1}+\sigma ^{2}_{2}+\sigma ^{2}_{3}\\&\quad = 2Tr(J)+\underbrace{\sigma ^{2}_{2}+\sigma ^{2}_{3}-2a_{11}}_{\wedge }. \end{aligned}$$

Therefore, we have

$$\begin{aligned}&N_{2}N_{6}N_{5}+N_{6}N_{3}N_{5}=\left( N_{2}+N_{3}\right) a_{33}Tr(J)\nonumber \\&\quad + \left( N_{2}+N_{3}\right) a_{11}a_{22}. \end{aligned}$$

(A11)

After using (A11), we have

$$\begin{aligned}&N_{2}N_{6}N_{5}+N_{6}N_{3}N_{5}= 2a_{33}Tr(J)^{2}\\&\quad +\left( 2a_{11}a_{22}+a_{33} \wedge \right) Tr(J) \end{aligned}$$

Finally, we get

$$\begin{aligned}&\tau _{4} = \underbrace{4a_{12}a_{21}a_{33}}_{H_{1}}Tr(J)^{2}\\&\quad + \left( \underbrace{2a_{12}a_{21}N_{2}N_{3}\!+\!4a_{12}a_{21}a_{11}a_{22}\!+\!2\wedge a_{12}a_{21}a_{33}\!-\!4a^{2}_{12}a^{2}_{21}}_{H_{2}}\!\right) \\&\qquad Tr(J) + \underbrace{2a^{2}_{12}a_{21}a^{2}_{23}+2a_{12}a_{21}a_{33}N_{2}N_{3}} _{H_{3}}\\&\qquad = H_{1}Tr(J)^{2}+H_{2}Tr(J)+H_{3}. \end{aligned}$$

We transformed $\mu _{12}$ as follows

$$\begin{aligned} \begin{aligned} N_{1}N_{3}N_{6}+N_{1}N_{3}N_{5}&= N_{1}N_{3}\left( N_{5}+N_{6}\right)&\\&= N_{1}N_{3}\left( a_{22}+a_{33}+a_{11}+a_{33}\right)&\\&= N_{2}N_{3}\left( Tr(J)+a_{33}\right)&\\&= N_{1}N_{3}Tr(J)+N_{1}N_{3}a_{33},&\end{aligned} \end{aligned}$$

$$\begin{aligned}&N_{1}N_{6}N_{5}+N_{6}N_{3}N_{5} = \left( N_{1}+N_{3}\right) N_{5}N_{6} \nonumber \\&\quad = \left( N_{1}+N_{3}\right) \nonumber \\&\quad \quad \left( a_{22}+a_{33}+a_{11}-a_{11}\right) \left( a_{11}+a_{33}+a_{22}-a_{22}\right) \nonumber \\&\quad = \left( N_{1}+N_{3}\right) \left( Tr(J)-a_{11}\right) \left( Tr(J)-a_{22}\right) \nonumber \\&\quad = \left( N_{1}+N_{3}\right) a_{33}Tr(J)+\left( N_{1}+N_{3}\right) a_{11}a_{22}, \end{aligned}$$

(A12)

$$\begin{aligned}&N_{1}+N_{3} = 2a_{11}+2a_{22}+2a_{33}-2a_{22}+\sigma ^{2}_{1}+\sigma ^{2}_{3} \nonumber \\&\quad = 2Tr(J)+\underbrace{\sigma ^{2}_{1}+\sigma ^{2}_{3}-2a_{22}}_{\wedge _{1}}. \end{aligned}$$

(A13)

Taking into account (A13) and (A12), we have

$$\begin{aligned}&\mu _{12} = 2a_{33}Tr(J)^{2}+\left( \underbrace{a_{33}\wedge _{1}+N_{1} N_{3}+2a_{11}a_{22}}_{H_{4}}\right) Tr(J)\nonumber \\&\quad +\underbrace{a_{11}a_{22}\wedge _{1} +N_{1}N_{3}a_{33}}_{H_{5}}. \end{aligned}$$

(A14)

$$\begin{aligned} \begin{aligned} N_{4}m_{2}&= N_{1}\left( N_{2}+N_{3}\right) N_{4}+N_{1}N_{2}N_{4}&\\&= N_{1}\left( 2Tr(J)+\wedge \right) \left( Tr(J)-a_{33}\right) \\&\qquad +N_{2}N_{3} \left( Tr(J)-a_{33}\right) \\&=2N_{1}Tr(J)^{2}+\left( N_{1}\wedge +N_{2}N_{3}-a_{33}N_{1}\right) \\&\qquad Tr(J)- a_{33}(\wedge +N_{2}N_{3}). \end{aligned} \end{aligned}$$

$$\begin{aligned}&\mu _{20} = \underbrace{-2N_{1}a_{12}a_{21}}_{H_{6}}Tr(J)^{2}\nonumber \\&\quad + \underbrace{a_{12}a_{21}\left( a_{33}N_{1}-N_{1}\wedge +N_{2}N_{3}\right) } _{H_{7}}Tr(J)\nonumber \\&\quad +\underbrace{a_{12}a_{21}\left( a_{33}(\wedge -N_{2}N_{3}\right) } _{H_{8}}. \end{aligned}$$

(A15)

$$\begin{aligned}&\begin{aligned} m_{5}&= N_{4}N_{5}+N_{4}N_{6}+N_{6}N_{5}\\&= N_{4}\left( N_{5}+N_{6}\right) +N_{6}N_{5}\\&= Tr(J)^{2}+a_{33}Tr(J)+ a_{11}a_{22}-a^{2}_{33}, \end{aligned}\\&\begin{aligned} m_{6}&= -N_{4}N_{5}N_{6}\\&= -a_{33}Tr(J)^{2}+\left( a^{2}_{33}-a_{11}a_{22}\right) Tr(J)\\&\quad +a_{33}a_{11} a_{22}, \end{aligned}\\&\begin{aligned} m_{2}&= N_{1}N_{2}+N_{1}N_{3}+N_{2}N_{3}\\&= N_{1}N_{2}+N_{3}\left( N_{1}+N_{2}\right) \\&= N_{1}N_{2}+N_{3}\left( 2Tr(J)+\underbrace{\sigma ^{2}_{1}+ \sigma ^{2}_{2}-2a_{33}}_{\wedge _{2}}\right) \\&= 2N_{3}Tr(J)+N_{1}N_{2}+N_{3}\wedge _{2}. \end{aligned} \end{aligned}$$

$$\begin{aligned}&m_{2}m_{6}=-a_{33}m_{2}Tr(J)^{2} +m_{2}\left( a^{2}_{33}-a_{11}a_{22} \right) Tr(J)\nonumber \\&\quad +m_{2}a_{33}a_{11}a_{22}, \end{aligned}$$

(A16)

$$\begin{aligned}&m_{3}m_{5}=m_{3}Tr(J)^{2} +m_{3}a_{33}Tr(J)+m_{3}a_{33}a_{11}a_{22}.\nonumber \\ \end{aligned}$$

(A17)

From (A16) and (A17), we have

$$\begin{aligned} \mu _{4}&= \left( \underbrace{a_{33}m_{2}-m_{3}}_{H_{9}}\right) Tr(J)^{2}\nonumber \\&\quad + \left( \underbrace{m_{2}(a_{11}a_{22}-a^{2}_{33})-a_{33}m_{3}}_{H_{10}} \right) Tr(J) \nonumber \\&+ \underbrace{a^{2}_{33}-m_{3}a_{11}a_{22}-m_{2}a_{33}a_{11}a_{22}}_{H_{11}}, \end{aligned}$$

(A18)

$$\begin{aligned} \mu _{28}&= -2a^{2}_{12}a^{2}_{21}\left( N_{1}+N_{2}\right) \nonumber \\&=\underbrace{-4a^{2}_{12}a^{2}_{21}}_{H_{12}}Tr(J)+\underbrace{2a^{2}_{12} a^{2}_{21}\left( 2a_{22}-\sigma ^{2}_{1}+\sigma ^{2}_{3}\right) }_{H_{13}}. \end{aligned}$$

(A19)

Finaly we get from (A19), (A18), (A15) and (A14),

$$\begin{aligned} a_{5}&= \underbrace{\left( H_{1}+2a_{33}-H_{9}+H_{6}\right) }_{A}Tr(J)^{2}\nonumber \\&+ \left( \underbrace{H_{2}+H_{4}-H_{10}+H_{7}+H_{12}}_{B}\right) Tr(J) \nonumber \\&+ \underbrace{H_{3}+H_{5}+H_{11}+H_{13}+H_{8}}_{C} \nonumber \\ a_{5}&= A Tr(J)^{2} + B Tr(J) + C. \end{aligned}$$

(A20)

The associate discriminant is given by $\Delta =B^{2}-4AC$. So,

If $\Delta =0$, then $Tr(J)^*=-\frac{B}{2A}$. Thus,

If $\Delta \!>\!0$, then $(Tr(J))_1=(\frac{-B -\sqrt{\Delta }}{2A}) \,\, \text{ and } \,\, (Tr(J))_2 = (\frac{-B +\sqrt{\Delta }}{2A})$. Thus,

Sign of $\Delta _6=a_6 \Delta _5$:

We have $a_{6}= \tau _{5}+\tau _{11}$, with

$$\begin{aligned} \tau _{5}&= 2a_{12}^{2}a_{21}^{2}N_{2}N_{3}-2a_{12}a_{21}N_{2}N_{3}N_{5} N_{6}\\ {}&\quad -2a_{12}^{2}a_{23}^{2}a_{21}N_{2}, \\ \tau _{11}&= m_{3}m_{6}-2a_{12}a_{21}N_{1}N_{3}N_{5}N_{6}-2a_{12}^{2} a_{21}^{2}N_{1}N_{3}, \end{aligned}$$

On other hand, we have $m_3= N_{1}N_{2}N_{3}$ and $m_6=N_{4}N_{5}N_{6}$. So, $N_{2}N_{3}N_{5}N_{6} = N_{2}N_{3}(a_{33}Tr(J)+a_{11}a_{22})$

$m_6 = N_{4}N_{5}N_{6} = (a_{11}+a_{22})(a_{22}+a_{33})(a_{11}+a_{33})=a_{22} Tr(J)^{2}+(a_{11}a_{33}-a_{22}^{2})Tr(J)-a_{11}a_{22}a_{33}$ So,

$$\begin{aligned} \tau _{11}= & {} a_{22}m_3Tr(J)^{2}+(a_{11}a_{33}m_3\\&-\,a_{22}^{2}m_3-2a_{11}a_{21} a_{33}N_{1}N_{3})Tr(J)\\&-\, a_{11}a_{22}a_{33}m_3 -2a_{12}a_{21}a_{11}a_{22}N_{1}N_{3}\\&-\,2a_{12}^{2}a_{21}^{2}N_{1}N_{3} \end{aligned}$$

or $m_{3}m_{6} = a_{22}m_{3}Tr(J)^{2}+(a_{11}a_{33}- a_{22}^{2})m_{3}Tr(J) - a_{11}a_{22}a_{33}m_{3}$,

$$\begin{aligned}&\tau _{5} = -2a_{12}a_{21}a_{33}N_{2}N_{3}Tr(J)+ 2a_{12}^{2}a_{21}^{2}N_{2} N_{3}\\&\quad -\,2a_{12}^{2}a_{23}^{2}N_{2}-2a_{11}a_{12}a_{22}a_{21}N_{2}N_{2}N_{3} \end{aligned}$$

Moreover,

$$\begin{aligned} a_6= & {} a_{22}m_3Tr(J)^{2} +\left( a_{11}a_{33}m_3-a_{22}^{2}m_3\right. \\&\left. -2a_{11}a_{21} a_{33}N_{1}N_{3}-2a_{12}a_{21}a_{33}N_{2}N_{3} \right) Tr(J) \\&- a_{11}a_{22}a_{33}m_3 -2a_{12}a_{21}a_{11}a_{22}N_{1}N_{3} \\&-2a_{12}^{2} a_{21}^{2}N_{1}N_{3}+2a_{12}^{2}a_{21}^{2}N_{2}N_{3}-2a_{12}^{2}a_{23}^{2} N_{2}\\&- 2a_{11}a_{12}a_{22}a_{21}N_{2}N_{2}N_{3} \end{aligned}$$

We pose $A = a_{22}m_3$, $B = a_{11}a_{33}m_3-a_{22}^{2}m_3-2a_{11}a_{21} a_{33}N_{1}N_{3}-2a_{12}a_{21}a_{33}N_{2}N_{3}$, and $C = - a_{11}a_{22}a_{33}m_3 - 2a_{12}a_{21}a_{11}a_{22}N_{1}N_{3} -2a_{12}^{2}a_{21}^{2}N_{1}N_{3}+2a_{12}^{2}a_{21}^{2}N_{2}N_{3}-2a_{12}^{2} a_{23}^{2}N_{2}-2a_{11}a_{12}a_{22}a_{21}N_{2}N_{2}N_{3}$.

So, $a_6 = A Tr(J)^{2}+BTr(J)+C$. Then, the associate discriminant $\Delta = B^{2}-4AC$.

If $\Delta =0$, then $Tr(J)^*=-\frac{B}{2A}$. So,

If $\Delta >0$, then $(Tr(J))_1 =(\frac{-B -\sqrt{\Delta }}{2A})$ and $(Tr(J))_2=(\frac{-B +\sqrt{\Delta }}{2A})$. Thus,

Appendix B: Algorithm for estimation of extinction probabilities and mean extinction times