A reaction–diffusion model for oncolytic M1 virotherapy with distributed delays

Abstract

Oncolytic virotherapy (OVT) is a promising treatment for cancer which can replace or support the traditional treatments like chemotherapy and radiotherapy. Mathematical models have been considered as a powerful tool to develop oncolytic viral treatments and predict the possible outcomes. We study a spatial model for OVT with cytotoxic T lymphocyte immune response and distributed delays. This model is an extended version of the model studied by Wang et al. (Math Biosci 276:19–27, 2016). We study the basic properties of the model including the existence, nonnegativity, and boundedness of solutions. We carefully analyze all equilibrium points and determine the conditions for their existence. We show the global stability of each one of these points by constructing suitable Lyapunov functionals. We use the characteristic equations to confirm the corresponding instability conditions. We carry out some numerical simulations to support the theoretical results and draw some important conclusions. The results show that the distributed delay can have a large impact on the efficacy and amount of OVT. When the immune response is present, the concentration of oncolytic viruses is decreased and the efficiency of treatment is reduced. Changing the diffusion coefficients does not affect the long-time behavior of solutions.

1 Introduction

Despite the great advances in medicine, finding a crucial cure for cancer that has no side effects is still under investigation. The traditional cancer treatments like chemotherapy and radiotherapy may damage healthy cells besides cancer cells. This may cause many side effects such as hair loss, nausea, fatigue, and mouth sores [1]. Oncolytic virotherapy (OVT) is an experimental cancer treatment which uses oncolytic viruses to destroy tumor. The oncolytic viruses can selectively infect and replicate in cancer cells without targeting healthy cells. When the infected cancer cell is lysed, many oncolytic viruses are released and continue to infect other tumor cells [2, 3]. If the treatment works successfully, it can reduce the size of tumor and eventually eradicate it [3]. Thus, OVT can be an ideal treatment for some types of tumor which show resistance to standard treatments [4, 5]. A variety of oncolytic viruses have been tested in clinical trials including vesicular stomatitis virus (VSV), herpes simplex virus (HSV), adenovirus, reovirus [6,7,8], and M1 virus [9]. Nevertheless, talimogene laherparepvec (T-VEC) is the only oncolytic virus which was approved by the US Food and Drug Administration (FDA) to treat melanoma. T-VEC is a genetically modified HSV which means that it does not cause herpes, but it selectively targets tumor cells [10]. Actually, the approval of T-VEC has increased the motivation to develop oncolytic viruses to treat other types of cancer like lung cancer, pancreatic cancer, glioblastoma, and prostate cancer [11, 12].

Although promising results have been reported by clinical studies, the complete potential of oncolytic viruses to remove the tumor has not been achieved yet [13, 14]. The initiation of different immune responses against tumor cells during the treatment is one of the major obstacles in OVT. The immune system may attack and destroy the infected tumor cells before the release of new oncolytic viruses. Also, macrophages of the innate immune system can attack oncolytic viruses. These attacks can limit the replication of oncolytic viruses and decrease the efficacy of OVT [3, 6, 15]. However, there is an evidence that the success of oncolytic viral treatment depends on the induction of strong immune responses against tumor cells [6]. Hence, the immune system is a double-edged sword in OVT, and understanding its complicated role is an active area of research. Another challenge in OVT is the ability of oncolytic viruses to spread through the tumor and infect more cells [14]. The current research efforts aim to resolve the different challenges and design effective oncolytic virotherapies with maximum safety and minimum cost [10, 12]. Thus, these efforts work on enhancing the tumor selectivity of oncolytic viruses and determining the significant amount of dosage needed to cure tumor [4, 10].

Mathematical modeling has been considered as a powerful tool to develop oncolytic viral treatments and predict the possible outcomes. Also, it helps to understand the complex virus–tumor–immune response interactions. Oncolytic modeling uses approaches that are similar to those used in virus dynamics models (see for example, [16,17,18,19,20,21,22,23]). Oncolytic virotherapy models have been formulated using different types of differential equations. Many of these models are based on the use of ordinary differential equations (ODEs). For example, a basic model for OVT was proposed by Tian [24]. The model consists of three ODEs which reflect the interactions between uninfected tumor cells, infected tumor cells and free virus population. Moreover, Komarova and Wodarz [25] performed a mathematical analysis of a general ODE model to shed light on some conditions needed for the success of OVT. Okamoto et al. [26] developed a mathematical model in which viruses are allowed to infect normal cells besides tumor cells. They argued that reducing the specificity of oncolytic viruses can lead to faster tumor elimination before the presence of an adaptive immune response. Ratajczyk et al. [27] formulated an ODE model to study the effect of combining virotherapy with TNF-$\alpha$ inhibitor. TNF-$\alpha$ is a protein produced by macrophages to destroy tumor cells. Ratajczyk and his colleagues proved that the inhibition of TNF-$\alpha$ can give a chance for oncolytic viruses to replicate, and thus it increases the effectiveness of OVT. Then, the same model was analyzed in [3] as an optimal control problem with two controls, one for the amount of OVT and the other for the amount of TNF-$\alpha$. Jenner et al. [7] performed a local stability and bifurcation analysis of a system of three ODEs which capture the interaction between oncolytic viruses, uninfected and infected tumor cells populations. Malinzi et al. [28] developed a mathematical model to determine the optimal dosage of chemovirotherapy that is needed to eliminate a tumor. They showed that, under certain conditions, virotherapy can be used to enhance chemotherapy in treating cancer patients.

As mentioned above, the spatial spread of oncolytic viruses plays a vital role in the success of OVT. This has motivated to use partial differential equations (PDEs) to take into account the spatial variations in the distribution of oncolytic viruses and cells during the treatment [29]. For example, Tao and Guo [5] investigated a spherical-symmetric oncolytic virotherapy PDE model with immune response. They found that the immune response can have a negative impact on the effectiveness of treatment. Malinzi et al. [1] got analytical traveling wave solutions of a PDE model that studies the interaction dynamics between oncolytic viruses, cytotoxic T lymphocytes (CTLs), and tumor cells. Alzahrani et al. [29] introduced a new multiscale modeling approach based on systems of reaction–diffusion equations both at macroscale and microscale. This approach addresses the complex interactions between tumor and oncolytic viruses, where the two scales are connected through a double feedback loop.

It has been shown that time delay is a pivotal element that should be carefully controlled to guarantee the success of oncolytic virotherapy in experimental and clinical trials [30, 31]. This has raised the need to extend ODEs to delay differential equations (DDEs) where the effect of time delay of some biological processes is included. Many mathematical models with DDEs have been rigorously analyzed. For instance, Wang et al. [32] determined critical values for the time delay $\tau$ at which Hopf bifurcation occurs in OVT model. Wang et al. [30] showed by means of DDEs that the time delay associated with the viral lytic cycle and the number of viruses released from the infected cancer cells are two important factors in OVT. Ashyani et al. [31] showed that the CTL immune response against infected cancer cells causes the fail of virotherapy in the second injection except for a short delay interval $[0,\tau _{0}^{+})$. Kim et al. [33] proved the existence of Hopf bifurcation and formulated an optimal control problem with two controls for DDE model with CTLs. They studied the effect of a time delay on the amount of OVT. Wang et al. [8] proposed a model with intracellular delay and CTL immune response. They suggested many strategies to enhance the effect of oncolytic viruses based on the results of their model.

Due to the sensitive role of time delay in virus dynamics models, PDEs have been extended to delay partial differential equations (DPDEs) to account for both spatial diffusion and time delay effects [34,35,36,37]. As an example, Zhao and Tian [14] formulated a delay reaction–diffusion model for OVT. They highlighted many medical implications of their results which cannot be obtained from ODE models. Wang et al. [38] determined the optimal dosage needed for complete tumor eradication in different cases depending on different gene mutations. The models in [14, 38] incorporate discrete time delays. A discrete time delay means that each individual within a population is subject to the same delay during a certain biological process [39]. On the other hand, a distributed time delay assumes that the delay is continuously distributed by a continuous distribution function. Hence, the distributed time delay is considered more general and realistic [22, 39, 40]. In this paper, we deal with PDEs with distributed delays.

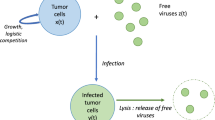
In 2014, Lin et al. [9] identified a naturally occurring alphavirus M1 as a selective oncolytic virus that targets cancer cells with Zinc-finger antiviral protein (ZAP) deficiency. More recently, Zhang et al. [41] have found that tumor cells may impair the removal of oncolytic M1 virus by tumor-associated macrophages. This impairment may enhance the tumor selectivity of M1 virus and improve its efficacy. In [42], Wang et al. formulated an ODE model to show the effect of M1 virus on the growth of normal cells and tumor cells. Their model takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\hbox {d}H(t)}{\hbox {d}t}=\kappa -dH(t)-\beta _{1}H(t)N(t)-\beta _{2}H(t)Y(t),\\ \frac{\hbox {d}N(t)}{\hbox {d}t}=\alpha _{1}\beta _{1}H(t)N(t)-(d+\eta _{1})N(t),\\ \frac{\hbox {d}Y(t)}{\hbox {d}t}=\alpha _{2}\beta _{2}H(t)Y(t)-\beta _{3}Y(t)V(t)-(d+\eta _{2})Y(t),\\ \frac{\hbox {d}V(t)}{\hbox {d}t}=\mu +\alpha _{3}\beta _{3}Y(t)V(t)-(d+\eta _{3})V(t), \end{array}\right. } \end{aligned}$$

(1)

where H(t), N(t), Y(t) and V(t) denote the concentrations of nutrient, normal cells, tumor cells, and free M1 virus particles, respectively. The model is considered in the chemostat, where the normal and tumor cells compete on a limited nutrient source. Therefore, there is a prey–predator relationship between nutrient and the normal or tumor cells. Also, there is a competition relationship between the normal cells and tumor cells. In model (1), the parameter $\kappa$ represents the recruitment rate of nutrient, and $\mu$ represents the M1 virotherapy dosage. The parameter d is the washout rate constant of nutrient and bacteria. The parameters $\eta _{1}$, $\eta _{2}$, and $\eta _{3}$ are the natural death rate constants of normal cells, tumor cells, and M1 virus, respectively. The nutrient is consumed by the normal cells and tumor cells at rates $\beta _{1}HN$ and $\beta _{2}HY$, respectively. The contribution rates of nutrient to biomass of normal cells and tumor cells are given by $\alpha _{1}\beta _{1}HN$ and $\alpha _{2}\beta _{2}HY$, respectively. The M1 virus kills tumor cells at rate $\beta _{3}YV$ and grows at rate $\alpha _{3}\beta _{3}YV$.

To the best of our knowledge, none of the previous works of OVT combine the effects of distributed delay and CTL immune response in their models. In order to design better oncolytic treatments, we need to understand the different factors that may affect the efficacy of these treatments including delays, immune responses, and spatial diffusion. Since M1 has shown high tumor selectivity and efficacy [41], forming a model to study its role might be quite beneficial to the oncolytic studies. The authors in [42] focused on one equilibrium point of model (1) corresponding to tumor elimination, and they determined the minimum effective dosage of M1 required to remove the tumor. They neglected the other equilibrium points of system (1), the effect of delays, immune responses, and diffusion. Thus, our purpose in this paper is (i) to extend model (1) to include distributed delay in the dynamics of normal and tumor cells; (ii) to study the effect of CTLs on the efficiency of OVT in the presence of delay; (iii) to include the diffusivity of all model’s components; (iv) to study the basic properties of the extended model; (v) to study the global properties of the model; (vi) to study the spatiotemporal behavior of solutions; (vii) to discuss the minimum effective dosage of M1 required to eradicate the tumor in the presence of delay. The effect of innate immune response is not included in the model due to the impairment effect exerted by tumor cells as mentioned above. The paper is organized as follows. In Sect. 2, a detailed description of the model is given. In Sect. 3, the nonnegativity and boundedness of solutions are discussed. In addition, all possible equilibrium points and their existence conditions are investigated. In Sect. 4, the global stability and local instability of these equilibrium points are proved. In Sect. 5, some numerical simulations that verify the theoretical results are provided. In Sect. 6, the results of our work are highlighted.

2 A delayed reaction–diffusion oncolytic M1 virotherapy model

In this section, we take model (1) to further destination by studying the effect of adaptive immunity, particularly CTLs, on the efficacy of OVT. We achieve this goal by considering the following reaction–diffusion model with distributed delays

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial H(x,t)}{\partial t}=D_{H}\Delta H(x,t)+\kappa -dH(x,t)-\beta _{1}H(x,t)N(x,t)-\beta _{2}H(x,t)Y(x,t),\\ \frac{\partial N(x,t)}{\partial t}=D_{N}\Delta N(x,t)+\alpha _{1}\beta _{1}\displaystyle \int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma ) \; \mathrm {d}\varsigma \\ \quad -(d+\eta _{1})N(x,t),\\ \frac{\partial Y(x,t)}{\partial t}=D_{Y}\Delta Y(x,t)+\alpha _{2}\beta _{2}\displaystyle \int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma \\ \quad -\beta _{3}Y(x,t)V(x,t)\\ -\beta _{4}Y(x,t)Z(x,t)-(d+\eta _{2})Y(x,t),\\ \frac{\partial V(x,t)}{\partial t}=D_{V}\Delta V(x,t)+\mu +\alpha _{3}\beta _{3}Y(x,t)V(x,t)-(d+\eta _{3})V(x,t),\\ \frac{\partial Z(x,t)}{\partial t}=D_{Z}\Delta Z(x,t)+\alpha _{4}\beta _{4}Y(x,t)Z(x,t)-(d+\eta _{4})Z(x,t), \end{array}\right. } \end{aligned}$$

(2)

for $t>0$ and $x\in \Omega$, where Z(x, t) denotes the concentration of CTLs at position x and time t. All components of the model are assumed to diffuse in a continuous and bounded domain $\Omega$ with a smooth boundary $\partial \Omega$. The diffusion term of any component $\nu$ of the model is given by $D_{\nu }\Delta \nu (x,t)$, where $D_{\nu }$ is the diffusion coefficient and $\Delta$ is the Laplacian operator. CTLs kill tumor cells at rate $\beta _{4}YZ$ and proliferate at rate $\alpha _{4}\beta _{4}YZ$. We assume that the normal and tumor cells consume nutrient at time $t-\varsigma$ and benefit from it at time t, where the delay $\varsigma$ is a random variable taken from a continuous probability distribution function $g_{i}(\varsigma )$ for $i=1,2$. The factor $\mathrm {e}^{-a_{1}\varsigma }$ accounts for the probability of survival of normal cells during the delay period with death rate $a_{1}$. The factor $\mathrm {e}^{-a_{2}\varsigma }$ accounts for the probability of survival of tumor cells during the delay period with death rate $a_{2}$. Thus, the term $\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma ) \; \mathrm {d}\varsigma$ gives the contribution of nutrient to biomass of normal cells at time t. Similarly, the term $\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma ) \; \mathrm {d}\varsigma$ gives the contribution of nutrient to biomass of tumor cells at time t. The probability distribution functions $g_{1}(\varsigma )$ and $g_{2}(\varsigma )$ are assumed to satisfy

$$\begin{aligned} g_{i}(\varsigma )> 0,\quad \int \limits _{0}^{\infty } g_{i}(\varsigma ) \; \mathrm {d}\varsigma =1, \quad 0<\int \limits _{0}^{\infty } g_{i}(\varsigma )\mathrm {e}^{-a_{i}\varsigma } \; \mathrm {d}\varsigma \le 1, \quad \text {for} \ i=1,2. \end{aligned}$$

The initial conditions of model (2) are given by

$$\begin{aligned} H(x,\theta )= & {} \omega _{1}(x,\theta ),\quad N(x,\theta )=\omega _{2}(x,\theta ),\quad Y(x,\theta )=\omega _{3}(x,\theta ),\nonumber \\ V(x,\theta )= & {} \omega _{4}(x,\theta ),\quad Z(x,\theta )=\omega _{5}(x,\theta ), \quad \text {for} \ (x,\theta )\in \bar{\Omega }\times (-\infty ,0], \end{aligned}$$

(3)

where $\omega _{i}(x,\theta ) (i=1,\ldots ,5)$ are nonnegative and continuous functions in $\bar{\Omega }\times (-\infty ,0]$. Also, we consider the homogeneous Neumann boundary conditions (NBCs)

$$\begin{aligned} \frac{\partial H}{\partial \vec {n}}=\frac{\partial N}{\partial \vec {n}}=\frac{\partial Y}{\partial \vec {n}}=\frac{\partial V}{\partial \vec {n} }=\frac{\partial Z}{\partial \vec {n}}=0, \quad \text {for} \ (x,t)\in \partial \Omega \times (0,+\infty ), \end{aligned}$$

(4)

where $\dfrac{\partial }{\partial \vec {n} }$ is the outward normal derivative on the boundary $\partial \Omega$. The NBCs indicate that the cells and viruses are confined within the boundary and do not cross it.

Remark 1

A model with discrete delays can be obtained from model (2) by considering special forms of $g_{1}(\varsigma )$ and $g_{2}(\varsigma )$ as

$$\begin{aligned} g_{i}(\varsigma )=\delta (\varsigma -\varsigma _{i}), \quad \text {for}\ i=1,2, \end{aligned}$$

where $\delta (.)$ is the Dirac delta function and $\varsigma _{i}$ are finite time delays. Then, the delay terms in the second and third equations of model (2) are given by $\alpha _{1}\beta _{1}\mathrm {e}^{-a_{1}\varsigma _{1}}H(x,t-\varsigma _{1})N(x,t-\varsigma _{1})$ and $\alpha _{2}\beta _{2}\mathrm {e}^{-a_{2}\varsigma _{2}}H(x,t-\varsigma _{2})Y(x,t-\varsigma _{2})$, respectively.

3 Basic properties

In this section, we show the well-posedness of model (2)–(4). Also, we identify all possible equilibrium points and establish their existence conditions.

Let $\mathbb {X}=C\left( \bar{\Omega },\mathbb {R}^{5}\right)$ be the Banach space of continuous functions from $\bar{\Omega }$ to $\mathbb {R}^{5}$. Define the Banach space of fading memory type [43] $\mathbb {C}_{\alpha }=\lbrace \psi \in C\left( (-\infty ,0] ,\mathbb {X}\right) : \psi (\theta )\mathrm {e}^{\alpha \theta } \text { is uniformly continuous for} \ \theta \in (-\infty ,0]\ \text {and} \ \sup \nolimits _{\theta \le 0}|\psi (\theta )| \mathrm {e}^{\alpha \theta }< \infty \rbrace$, where $\Vert \psi \Vert =\sup \nolimits _{\theta \le 0}|\psi (\theta )| \mathrm {e}^{\alpha \theta }$ and $\alpha$ is a positive constant. Then, we identify an element $\omega \in \mathbb {C}_{\alpha }$ as a function from $\bar{\Omega }\times (-\infty ,0]$ into $\mathbb {R}^{5}$ defined by $\omega (x,\theta )=\omega (\theta )(x)$. For any continuous function $A:(-\infty ,\overline{\varrho })\rightarrow \mathbb {X}$, we define $A_{t}\in \mathbb {C}_{\alpha }$ by $A_{t}(\theta )=A(t+\theta )$, for $\overline{\varrho }>0$ and $\theta \le 0$. It is not hard to see that $t \rightarrow A_{t}$ is a continuous function from $[0,\overline{\varrho })$ to $\mathbb {C}_{\alpha }$.

Theorem 1

Suppose that $D_{H}=D_{N}=D_{Y}=D_{V}=D_{Z}$. Then, there exists a unique nonnegative and bounded solution defined on $\bar{\Omega }\times [0,+\infty )$ for any given initial data satisfying (3).

Proof

For any $\omega =(\omega _{1},\omega _{2},\omega _{3},\omega _{4},\omega _{5})^{T}\in \mathbb {C}_{\alpha }$ and $x \in \bar{\Omega }$, we define $F=(F_{1},F_{2},F_{3},F_{4},F_{5}):\mathbb {C}_{\alpha }\rightarrow \mathbb {X}$ by

$$\begin{aligned} {\left\{ \begin{array}{ll} F_{1}(\omega )(x)=\kappa -d\omega _{1}(x,0)-\beta _{1}\omega _{1}(x,0)\omega _{2}(x,0)-\beta _{2}\omega _{1}(x,0)\omega _{3}(x,0),\\ F_{2}(\omega )(x)=\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\omega _{1}(x,-\varsigma )\omega _{2}(x,-\varsigma ) \; \mathrm {d}\varsigma -(d+\eta _{1})\omega _{2}(x,0),\\ F_{3}(\omega )(x)=\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\omega _{1}(x,-\varsigma )\omega _{3}(x,-\varsigma )\; \mathrm {d}\varsigma -\beta _{3}\omega _{3}(x,0)\omega _{4}(x,0)\\ \quad \quad \quad -\beta _{4}\omega _{3}(x,0)\omega _{5}(x,0)-(d+\eta _{2})\omega _{3}(x,0),\\ F_{4}(\omega )(x)=\mu +\alpha _{3}\beta _{3}\omega _{3}(x,0)\omega _{4}(x,0)-(d+\eta _{3})\omega _{4}(x,0),\\ F_{5}(\omega )(x)=\alpha _{4}\beta _{4}\omega _{3}(x,0)\omega _{5}(x,0)-(d+\eta _{4})\omega _{5}(x,0). \end{array}\right. } \end{aligned}$$

Then, we can rewrite problem (2)–(4) as the following abstract ordinary differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\hbox {d}A}{\hbox {d}t}=MA+F(A_{t}), \ t>0,\\ A(0)=\omega \in \mathbb {C}_{\alpha }, \end{array}\right. } \end{aligned}$$

where $A=(H,N,Y,V,Z)^{T}$ and $MA=\left( D_{H}\Delta H,D_{N}\Delta N,D_{Y}\Delta Y,D_{V}\Delta V,D_{Z}\Delta Z\right) ^{T}$. It is clear that F is locally Lipschitz in $\mathbb {C}_{\alpha }$. According to [44,45,46,47], we conclude that problem (2)–(4) has a unique local solution on its maximal existence time interval $[0,T_{\text {max}})$. Also, we have $H(x,t)\ge 0$, $N(x,t)\ge 0$, $Y(x,t)\ge 0$, $V(x,t)\ge 0$ and $Z(x,t)\ge 0$ since $\mathbf {0}=(0,0,0,0,0)$ is a lower solution of problem (2)–(4).

The next step is to show the boundedness of solutions. From the first equation of (2), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial H(x,t)}{\partial t}-D_{H} \Delta H(x,t)\le \kappa -d H(x,t),\\ \frac{\partial H}{\partial \vec {n}}=0,\\ H(x,0)=\omega _{1}(x,0)\ge 0. \end{array}\right. } \end{aligned}$$

Let $\widetilde{H}(t)$ be a solution to the following ODE system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\hbox {d}\widetilde{H}(t)}{\hbox {d}t}=\kappa -d\widetilde{H}(t),\\ \widetilde{H}(0)=\underset{ x\in \bar{\Omega }}{\max }\ \omega _{1}(x,0). \end{array}\right. } \end{aligned}$$

This implies that $\widetilde{H}(t)\le \max \left\{ \dfrac{\kappa }{d},\underset{ x\in \bar{\Omega }}{\max }\ \omega _{1}(x,0) \right\}$. From the comparison principle [48], we have $H(x,t)\le \widetilde{H}(t)$. Hence, we get

$$\begin{aligned} H(x,t)\le \max \left\{ \dfrac{\kappa }{d},\underset{ x\in \bar{\Omega }}{\max }\ \omega _{1}(x,0) \right\} ,\quad \text {for}\ (x,t)\in \bar{\Omega }\times [0,T_{\text {max}}) . \end{aligned}$$

This implies that H(x, t) is bounded. Let

$$\begin{aligned} G_{i}=\int \limits _{0}^{\infty } g_{i}(\varsigma )\mathrm {e}^{-a_{i}\varsigma } \; \mathrm {d}\varsigma , \quad \text {for}\ i=1,2. \end{aligned}$$

(5)

Then, we define

$$\begin{aligned} \Gamma (x,t)= & {} \int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma ) \; \mathrm {d}\varsigma +\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma ) \; \mathrm {d}\varsigma \\&+\frac{1}{\alpha _{1}}N(x,t)+\frac{1}{\alpha _{2}} Y(x,t)+\frac{1}{\alpha _{2}\alpha _{3}}V(x,t)+\frac{1}{\alpha _{2}\alpha _{4} }Z(x,t). \end{aligned}$$

When $D_{H}=D_{N}=D_{Y}=D_{V}=D_{Z}$, we get

$$\begin{aligned} \begin{aligned}&\frac{\partial \Gamma (x,t)}{\partial t}-D_{H} \Delta \Gamma (x,t)\\&\quad \le \frac{\mu }{\alpha _{2}\alpha _{3}}+\kappa \int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \; \mathrm {d}\varsigma +\kappa \int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \; \mathrm {d}\varsigma -d\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma ) \; \mathrm {d}\varsigma \\&\qquad -d \int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma ) \; \mathrm {d}\varsigma \\&\qquad -\frac{(d+\eta _{1})}{\alpha _{1}}N(x,t)-\frac{(d+\eta _{2})}{\alpha _{2}}Y(x,t)-\frac{(d+\eta _{3})}{\alpha _{2}\alpha _{3}}V(x,t)\\&\qquad -\frac{(d+\eta _{4})}{\alpha _{2}\alpha _{4}}Z(x,t)\\&\quad \le \frac{\mu }{\alpha _{2}\alpha _{3}}+\kappa (G_{1}+G_{2})-d\Gamma (x,t)\\&\quad \le \frac{\mu }{\alpha _{2}\alpha _{3}}+2\kappa -d\Gamma (x,t). \end{aligned} \end{aligned}$$

Thus, $\Gamma (x,t)$ satisfies the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \Gamma (x,t)}{\partial t}-D_{H} \Delta \Gamma (x,t)\le \frac{\mu }{\alpha _{2}\alpha _{3}}+2\kappa -d\Gamma (x,t),\\ \frac{\partial \Gamma }{\partial \vec {n}}=0,\\ \Gamma (x,0)=\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\omega _{1}(x,-\varsigma ) \; \mathrm {d}\varsigma +\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\omega _{1}(x,-\varsigma )\; \mathrm {d}\varsigma +\frac{1}{\alpha _{1}}\omega _{2}(x,0)\\ +\frac{1}{\alpha _{2}}\omega _{3}(x,0)+\frac{1}{\alpha _{2}\alpha _{3}}\omega _{4}(x,0)\\ +\frac{1}{\alpha _{2}\alpha _{4}}\omega _{5}(x,0)\ge 0. \end{array}\right. } \end{aligned}$$

Hence, we can deduce from the comparison principle [48] that

$$\begin{aligned} \Gamma (x,t)\le \max \left\{ \frac{\mu }{\alpha _{2} \alpha _{3}d}+\frac{2\kappa }{d},\underset{ x\in \bar{\Omega }}{\max } \ \Gamma (x,0) \right\} , \quad \text {for}\ (x,t)\in \bar{\Omega }\times [0,T_{\text {max}}). \end{aligned}$$

This implies that N(x, t), Y(x, t), V(x, t) and Z(x, t) are bounded on $\bar{\Omega }\times [0,T_{\text {max}})$. Thus, all solutions are bounded on $\bar{\Omega }\times [0,T_{\text {max}})$. Then, the boundedness of the solutions on $\bar{\Omega }\times [0,+\infty )$ are deduced from the standard theory for semi-linear parabolic systems [49]. $\square$

For the sake of simplicity, we let

$$\begin{aligned}&d_{1}=(d+\eta _{1}),\quad d_{2}=(d+\eta _{2}),\quad d_{3}=(d+\eta _{3}),\quad d_{4}=(d+\eta _{4}), \\&\nu =\nu (x,t) \ \text {for} \ \nu \in \lbrace H,N,Y,V,Z\rbrace . \end{aligned}$$

Theorem 2

There exist positive parameters $\mathcal {R}_{0}$, $\mathcal {R}_{1}$, $\mathcal {R}_{l}$, $\mathcal {R}_{m}$, $\mathcal {R}_{n}$, $\xi _{1}$, $\xi _{2}$ and $\rho$ such that model (2) has six possible equilibrium points whenever the following conditions are hold:

• (a) The competition-free equilibrium $E_{0}=(H_{0},0,0,V_{0},0)$ always exists;

• (b) The treatment failure immune-free equilibrium $E_{1} =(H_{1},0,Y_{1},V_{1},0)$ exists if $\mathcal {R}_{0}>\mathcal {R}_{l}$;

• (c) The tumor-free equilibrium $E_{2}=(H_{2},N_{2},0,V_{2},0)$ exists if $\mathcal {R}_{1}>1$;

• (d) The treatment failure equilibrium $E_{3}=(H_{3} ,0,Y_{3},V_{3},Z_{3})$ exists if $\rho >1$ and $\mathcal {R}_{0}>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$;

• (e) The partial success immune-free equilibrium $E_{4} =(H_{4},N_{4},Y_{4},V_{4},0)$ exists if $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$;

• (f) The coexistence equilibrium $E_{5}=(H_{5},N_{5},Y_{5} ,V_{5},Z_{5})$ exists if $\rho >1$, $\mathcal {R}_{1}>\mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$.

Proof

Any equilibrium point $E=(H,N,Y,V,Z)$ of model (2) satisfies the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \kappa -dH-\beta _{1}HN-\beta _{2}HY=0 ,\\ \alpha _{1}\beta _{1}G_{1}HN-d_{1}N=0,\\ \alpha _{2}\beta _{2}G_{2}HY-\beta _{3}YV-\beta _{4}YZ-d_{2}Y =0,\\ \mu +\alpha _{3}\beta _{3}YV-d_{3}V=0,\\ \alpha _{4}\beta _{4}YZ-d_{4}Z=0 . \end{array}\right. } \end{aligned}$$

(6)

By solving system (6) algebraically, we get the following equilibrium points:

• (a) The competition-free equilibrium $E_{0}=\left( H_{0},0,0,V_{0},0\right)$ with

  $$\begin{aligned} H_{0}=\frac{\kappa }{d}, \quad V_{0}=\frac{\mu }{d_{3}}. \end{aligned}$$

  The equilibrium point is biologically admissible if all of its components are nonnegative. Hence, $E_{0}$ always exists since $H_{0}>0$ and $V_{0}>0$.

• (b) Define $\xi _{1}=\beta _{2}d_{3}+\alpha _{3}\beta _{3}d$, $\mathcal {R}_{0}=\dfrac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}$ and $\mathcal {R}_{l}=1+\dfrac{\mu \beta _{3}}{d_{2}d_{3}}$.

  The treatment failure immune-free equilibrium is given by $E_{1}=(H_{1},0,Y_{1},V_{1},0)$, where

  $$\begin{aligned} \begin{aligned} H_{1}&= \frac{\beta _{2}\beta _{3}\left( \mu +\kappa \alpha _{2}G_{2}\alpha _{3} \right) +d_{2}\xi _{1}+\sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] } }{2\alpha _{2}\beta _{2}G_{2}\xi _{1}},\\ Y_{1}&=\frac{\kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}+\beta _{2}(\mu \beta _{3}+2d_{2}d_{3})-\sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] }}{2\beta _{2}\alpha _{3}\beta _{3}d_{2}}, \\ V_{1}&=\frac{\kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}+\mu \beta _{2}\beta _{3}+\sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] } }{2\beta _{3}\xi _{1}}. \end{aligned} \end{aligned}$$

  It is easy to note that $H_{1}>0$ and $V_{1}>0$. Thus, the existence condition of $E_{1}$ is determined by $Y_{1}>0$. We find

  $$\begin{aligned} \begin{aligned} Y_{1}>0&\Longleftrightarrow \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}+\beta _{2}(\mu \beta _{3}+2d_{2}d_{3})\\&\qquad \,>\sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] }\\&\Longleftrightarrow 2 \beta _{2}\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) \left( \mu \beta _{3} +2d_{2}d_{3}\right) +\beta _{2}^{2}\left( \mu \beta _{3}+2d_{2}d_{3} \right) ^{2}\\&\qquad \,>\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1}\right] \\&\Longleftrightarrow \dfrac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}>1+\dfrac{\mu \beta _{3}}{d_{2}d_{3}}\\&\Longleftrightarrow \mathcal {R}_{0}> \mathcal {R}_{l}. \end{aligned} \end{aligned}$$

  Hence, $E_{1}$ exists if $\mathcal {R}_{0}> \mathcal {R}_{l}$.

• (c) Take $\mathcal {R}_{1}=\dfrac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}$. The tumor-free equilibrium is given by $E_{2}=(H_{2} ,N_{2},0,V_{2},0)$, where

  $$\begin{aligned} H_{2}=\frac{d_{1}}{\alpha _{1}\beta _{1}G_{1}},\quad N_{2}=\frac{d}{\beta _{1} }(\mathcal {R}_{1}-1),\quad V_{2}=\frac{\mu }{d_{3}}. \end{aligned}$$

  It is clear that $H_{2}>0$, $N_{2}>0$ if $\mathcal {R}_{1}>1$, and $V_{2}>0$. Hence, the existence condition of $E_{2}$ is $\mathcal {R}_{1}>1$.

• (d) Define $\xi _{2}=\beta _{2}d_{4}+\alpha _{4}\beta _{4}d$, $\rho =\dfrac{\alpha _{4}\beta _{4}d_{3}}{\alpha _{3}\beta _{3}d_{4}}$ and $\mathcal {R}_{m}=1+\dfrac{\beta _{2}d_{4}}{\alpha _{4} \beta _{4}d}$. The treatment failure equilibrium is given by $E_{3}=(H_{3},0,Y_{3},V_{3},Z_{3})$, where

  $$\begin{aligned} H_{3}= & {} \frac{\kappa \alpha _{4}\beta _{4}}{\xi _{2}}, \quad Y_{3}=\frac{d_{4}}{\alpha _{4}\beta _{4}}, \quad V_{3}=\frac{\mu \alpha _{4}\beta _{4}}{\alpha _{3}\beta _{3}d_{4}(\rho -1)}, \\ Z_{3}= & {} \frac{\kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\alpha _{4}\beta _{4}d_{4}(\rho -1)-\xi _{2}\left[ \mu \alpha _{4}\beta _{4}+\alpha _{3}d_{2}d_{4}(\rho -1)\right] }{\alpha _{3}\beta _{4}d_{4}\xi _{2}(\rho -1)}. \end{aligned}$$

  Clearly, $H_{3}>0$, $Y_{3}>0$, and $V_{3}>0$ if $\rho >1$. Now, we need to find the condition for which $Z_{3}>0$. Indeed,

  $$\begin{aligned} \begin{aligned} Z_{3}>0&\Longleftrightarrow \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\alpha _{4}\beta _{4}d_{4}(\rho -1)>\xi _{2}\left[ \mu \alpha _{4}\beta _{4}+\alpha _{3}d_{2}d_{4}(\rho -1)\right] \\&\Longleftrightarrow \dfrac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}>1+\dfrac{\beta _{2}d_{4}}{\alpha _{4} \beta _{4}d}+\frac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}\\&\Longleftrightarrow \mathcal {R}_{0}>\mathcal {R}_{m}+\frac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}. \end{aligned} \end{aligned}$$

  Hence, the existence conditions of $E_{3}$ are $\rho >1$ and $\mathcal {R}_{0}>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$.

• (e) Take $\mathcal {R}_{n}=1+\dfrac{\beta _{2}d_{3}}{\alpha _{3}\beta _{3} d}$. The partial success immune-free equilibrium is given by $E_{4}=(H_{4},N_{4},Y_{4},V_{4},0)$, where

  $$\begin{aligned} \begin{aligned} H_{4}=&\dfrac{d_{1}}{\alpha _{1}\beta _{1}G_{1}},\quad N_{4}=\frac{\beta _{3}\left[ \kappa \alpha _{1}\beta _{1}G_{1}\alpha _{3}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)+\mu \beta _{2}d_{1}\right] -d_{1}d_{2}\xi _{1}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}{\beta _{1}\alpha _{3}\beta _{3}d_{1}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)},\\ Y_{4}=&\frac{d_{2}d_{3}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)-\mu \beta _{3}}{\alpha _{3}\beta _{3}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}, \quad V_{4}=\dfrac{d_{2}}{\beta _{3}}(\mathcal {R}_{0}/\mathcal {R}_{1}-1). \end{aligned} \end{aligned}$$

  As we can see, $H_{4}>0$, and $V_{4}>0$ if $\mathcal {R}_{0}/\mathcal {R}_{1}>1$. Next, we need to determine the conditions for which $N_{4}>0$ and $Y_{4}>0$. We have

  $$\begin{aligned} \begin{aligned} N_{4}>0&\Longleftrightarrow \beta _{3}\left[ \kappa \alpha _{1}\beta _{1}G_{1}\alpha _{3}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)+\mu \beta _{2}d_{1}\right]>d_{1}d_{2}\xi _{1}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)\\&\Longleftrightarrow \frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}+ \frac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}>1+\dfrac{\beta _{2}d_{3}}{\alpha _{3}\beta _{3} d}\\&\Longleftrightarrow \mathcal {R}_{1}+\frac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}>\mathcal {R}_{n}. \end{aligned} \end{aligned}$$

  Also, we get

  $$\begin{aligned} \begin{aligned} Y_{4}>0&\Longleftrightarrow d_{2}d_{3}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)>\mu \beta _{3} \\&\Longleftrightarrow \frac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}>\frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}+\frac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}\\&\Longleftrightarrow \mathcal {R}_{0}>\mathcal {R}_{1}+\frac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}. \end{aligned} \end{aligned}$$

  Hence, the existence conditions of $E_{4}$ are $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$.

• (f) The coexistence equilibrium is given by $E_{5}=(H_{5},N_{5},Y_{5},V_{5},Z_{5})$, where

  $$\begin{aligned} \begin{aligned} H_{5}=&\frac{d_{1}}{\alpha _{1}\beta _{1}G_{1}},\quad N_{5}=\frac{\kappa \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}-d_{1}\xi _{2}}{\beta _{1}\alpha _{4}\beta _{4}d_{1}},\quad Y_{5}=\frac{d_{4}}{\alpha _{4}\beta _{4}}, \quad V_{5}=\dfrac{\mu \alpha _{4}\beta _{4}}{\alpha _{3}\beta _{3}d_{4}(\rho -1)},\\ Z_{5}=&\frac{ \alpha _{1}\beta _{1}G_{1} \alpha _{3}d_{2}d_{4}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)(\rho -1)-\mu \alpha _{1}\beta _{1}G_{1} \alpha _{4}\beta _{4} }{\alpha _{1}\beta _{1}G_{1}\alpha _{3}\beta _{4}d_{4}(\rho -1)}. \end{aligned} \end{aligned}$$

  It is clear that $H_{5}>0$, $Y_{5}>0$, and $V_{5}>0$ if $\rho >1$. Then, we need to investigate the existence conditions corresponding to $N_{5}>0$ and $Z_{5}>0$. We get

  $$\begin{aligned} \begin{aligned} N_{5}>0&\Longleftrightarrow \kappa \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}>d_{1}\xi _{2} \\&\Longleftrightarrow \frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}>1+\dfrac{\beta _{2}d_{4}}{\alpha _{4}\beta _{4}d}\\&\Longleftrightarrow \mathcal {R}_{1}> \mathcal {R}_{m}. \end{aligned} \end{aligned}$$

  On the other hand, we have

  $$\begin{aligned} \begin{aligned} Z_{5}>0&\Longleftrightarrow \alpha _{1}\beta _{1}G_{1} \alpha _{3}d_{2}d_{4}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)(\rho -1)>\mu \alpha _{1}\beta _{1}G_{1} \alpha _{4}\beta _{4}\\&\Longleftrightarrow \frac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}>\frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}\\&\Longleftrightarrow \mathcal {R}_{0}>\mathcal {R}_{1}+\frac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}. \end{aligned} \end{aligned}$$

Hence, the existence conditions of $E_{5}$ are $\rho >1$, $\mathcal {R}_{1}> \mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. $\square$

4 Global properties

In this section, we show the global stability of all equilibrium points computed in Theorem 2. In addition, we check the local instability conditions of these points.

Define a function $\Phi :(0,+\infty )\rightarrow [0,+\infty )$ by $\Phi (\nu )=\nu -1-\ln \nu$. Clearly, $\Phi (\nu )=0$ if and only if $\nu =1$.

Theorem 3

• (a) The competition-free equilibrium $E_{0}$ is globally asymptotically stable if $\mathcal {R}_{1}\le 1$ and $\mathcal {R}_{0}\le \mathcal {R}_{l}$.

• (b) The equilibrium $E_{0}$ is unstable if $\mathcal {R}_{1}> 1$ or $\mathcal {R}_{0}> \mathcal {R}_{l}$.

Proof

• (a) We define the following Lyapunov functional

  $$\begin{aligned} \begin{aligned} \mathcal {U}_{0}(t)=&\int _{\Omega } \bigg \lbrace H_{0}\Phi \left( \frac{H}{H_{0}}\right) +\frac{1}{\alpha _{1}G_{1}}N+\frac{1}{\alpha _{2}G_{2}}Y+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{0}\Phi \left( \frac{V}{V_{0}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z\\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }H(x,t-\theta )N(x,t-\theta ) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }H(x,t-\theta )Y(x,t-\theta ) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  By taking the time derivative of $\mathcal {U}_{0}(t)$ along the solutions of (2), we get

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{0}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{0}}{H}\right) \left[ D_{H}\Delta H+\kappa -dH-\beta _{1}HN-\beta _{2}HY\right] \\&+\frac{1}{\alpha _{1}G_{1}}\left[ D_{N}\Delta N+\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma )\; \mathrm {d}\varsigma -d_{1}N\right] \\&+\frac{1}{\alpha _{2}G_{2}}\left[ D_{Y}\Delta Y+\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma \right. \\&\left. -\beta _{3}YV-\beta _{4}YZ-d_{2}Y\right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{0}}{V}\right) \left[ D_{V}\Delta V+\mu +\alpha _{3}\beta _{3}YV-d_{3}V \right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}\left[ D_{Z}\Delta Z+\alpha _{4}\beta _{4}YZ-d_{4}Z\right] \\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ HN- H(x,t-\varsigma )N(x,t-\varsigma ) \right] \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ HY- H(x,t-\varsigma )Y(x,t-\varsigma ) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\ =&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{0}}{H}\right) D_{H}\Delta H -\frac{d\left( H-H_{0}\right) ^{2}}{H}+\left( \beta _{1}H_{0}-\frac{d_{1}}{\alpha _{1}G_{1}} \right) N\\&+\left( \beta _{2}H_{0}- \frac{d_{2}}{\alpha _{2}G_{2}}-\frac{\beta _{3}V_{0}}{\alpha _{2}G_{2}} \right) Y \\&+\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\left( 2-\frac{V_{0}}{V}-\frac{V}{V_{0}}\right) -\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}}Z+\frac{1}{\alpha _{1}G_{1}}D_{N}\Delta N+\frac{1}{\alpha _{2}G_{2}}D_{Y}\Delta Y\\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{0}}{V}\right) D_{V}\Delta V+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}D_{Z}\Delta Z \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  (7)

  By using the divergence theorem and NBCs (4), we have

  $$\begin{aligned} \begin{aligned} 0=&\int _{\partial \Omega }\nabla \nu \cdot \vec {n} \; \mathrm {d}x=\int _{ \Omega } \text {div}(\nabla \nu ) \; \mathrm {d}x=\int _{ \Omega } \Delta \nu \; \mathrm {d}x,\\ 0=&\int _{\partial \Omega }\frac{1}{\nu }\nabla \nu \cdot \vec {n} \; \mathrm {d}x=\int _{ \Omega } \text {div}(\frac{1}{\nu }\nabla \nu ) \; \mathrm {d}x=\int _{ \Omega } \left[ \frac{\Delta \nu }{\nu }-\frac{\Vert \triangledown \nu \Vert ^{2}}{\nu ^{2}}\right] \; \mathrm {d}x, \\&\quad \quad \text {for} \ \nu \in \lbrace H,N,Y,V,Z\rbrace . \end{aligned} \end{aligned}$$

  Thus, we obtain

  $$\begin{aligned} \begin{aligned}&\int _{ \Omega } \Delta \nu \; \mathrm {d}x=0,\\&\int _{ \Omega } \frac{\Delta \nu }{\nu }\; \mathrm {d}x=\int _{\Omega }\frac{\Vert \triangledown \nu \Vert ^{2}}{\nu ^{2}}\; \mathrm {d}x, \quad \text {for} \ \nu \in \lbrace H,N,Y,V,Z\rbrace . \end{aligned} \end{aligned}$$

  (8)

  Therefore, Eq. (7) is reduced to

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{0}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{0}\right) ^{2}}{H}+\frac{d_{1}}{\alpha _{1}G_{1}}\left( \mathcal {R}_{1} -1 \right) N+\frac{d_{2}}{\alpha _{2}G_{2}}\left( \mathcal {R}_{0}-\mathcal {R}_{l}\right) Y \\&-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{0})^{2}}{VV_{0}}-\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}}Z\bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{0}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{V}V_{0}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x . \end{aligned} \end{aligned}$$

  We conclude that $\dfrac{\hbox {d} \mathcal {U}_{0}}{\hbox {d} t} \le 0$ if $\mathcal {R}_{1}\le 1$ and $\mathcal {R}_{0}\le \mathcal {R}_{l}$. Moreover, $\dfrac{\hbox {d} \mathcal {U}_{0}}{\hbox {d} t}=0$ when $H=H_{0}$, $N=0$, $Y=0$, $V=V_{0}$ and $Z=0$. Thus, the largest invariant set $\Psi _{0}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{0}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{0}\rbrace$. By LaSalle’s invariance principle [50, 51, Theorem 5.3], ${E_{0}}$ is globally asymptotically stable when $\mathcal {R}_{1}\le 1$ and $\mathcal {R}_{0}\le \mathcal {R}_{l}$.

• (b) To prove the local instability of $E_{0}$, we need to find the characteristic equation. Let $0=\zeta _{1}<\zeta _{2}<\cdots<\zeta _{k}< \cdots$ be the eigenvalues of the Laplace operator $-\Delta$ with the homogeneous NBCs. Let $\mathcal {E}(\zeta _{i})$ be the eigenfunction space corresponding to the eigenvalues $\zeta _{i}$$(i=1,2,\ldots )$. Let $\lbrace \rho _{ij}:j=1,2,\ldots ,\text {dim}\ \mathcal {E}(\zeta _{i})\rbrace$ be an orthonormal basis of $\mathcal {E}(\zeta _{i})$, where $\text {dim} \ \mathcal {E}(\zeta _{i})$ is the dimension of the space $\mathcal {E}(\zeta _{i})$. Define

  $$\begin{aligned} \begin{aligned}&\mathbb {S}=\lbrace (H,N,Y,V,Z)\in \left[ C^{1}(\bar{\Omega })\right] ^{5}:\frac{\partial H}{\partial \vec {n}}=\frac{\partial N}{\partial \vec {n}}=\frac{\partial Y}{\partial \vec {n}}=\frac{\partial V}{\partial \vec {n}}=\frac{\partial Z}{\partial \vec {n}}=0 \ on \ \partial \Omega \rbrace ,\\&\mathbb {S}_{ij}=\lbrace a\rho _{ij} \ | \ a \in \mathbb {R}^{5} \rbrace . \end{aligned} \end{aligned}$$

  Then, we have

  $$\begin{aligned} \mathbb {S}_{i}= \mathop {\bigoplus }_{j=1}^{\text {dim} \ \mathcal {E}(\xi _{i})} \mathbb {S}_{ij} \quad \text {and} \quad \mathbb {S}= \mathop {\bigoplus }_{i=1} ^{\infty } \mathbb {S}_{i} . \end{aligned}$$

  Let $E_{e}=(H_{e},N_{e},Y_{e},V_{e},Z_{e})$ be an arbitrary equilibrium point of system (2)–(4). Then, the linearization of system (2) at $E_{e}$ is given by

  $$\begin{aligned} \frac{\partial W}{\partial t}=\mathcal {D}\Delta W+\mathcal {J}_{1}W(x,t)+\mathcal {J}_{2}W(x,t-\varsigma ), \end{aligned}$$

  where $W=(H,N,Y,V,Z)^{T}$, $\mathcal {D}=diag(D_{H},D_{N},D_{Y},D_{V},D_{Z})$,

  $$\begin{aligned} { \mathcal {J}_{1}= \begin{bmatrix} -d-\beta _{1}N_{e}-\beta _{2}Y_{e} &{} -\beta _{1}H_{e} &{} -\beta _{2}H_{e} &{} 0 &{} 0\\ 0 &{} -d_{1} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -\beta _{3}V_{e} -\beta _{4}Z_{e}-d_{2} &{} -\beta _{3}Y_{e} &{} -\beta _{4}Y_{e}\\ 0 &{} 0 &{} \alpha _{3}\beta _{3}V_{e} &{} \alpha _{3}\beta _{3}Y_{e}-d_{3} &{} 0\\ 0 &{} 0 &{} \alpha _{4}\beta _{4}Z_{e} &{} 0 &{} \alpha _{4}\beta _{4}Y_{e}-d_{4} \end{bmatrix}, } \end{aligned}$$

  and

  $$\begin{aligned} { \mathcal {J}_{2}= \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \alpha _{1}\beta _{1}G_{1}N_{e} &{} \alpha _{1}\beta _{1}G_{1}H_{e} &{} 0 &{} 0 &{} 0\\ \alpha _{2}\beta _{2}G_{2}Y_{e} &{} 0 &{} \alpha _{2}\beta _{2}G_{2}H_{e} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix}.} \end{aligned}$$

  Define $\mathcal {L}W=\mathcal {D}\Delta W+\mathcal {J}_{1}W(x,t)+\mathcal {J}_{2}W(x,t-\varsigma )$. For each $i\ge 1$, $\mathbb {S}_{i}$ is invariant under the operator $\mathcal {L}$. In addition, $\lambda$ is an eigenvalue of $\mathcal {L}$ if and only if it is a root of the characteristic equation

  $$\begin{aligned} det(\lambda I+\mathcal {D}\zeta _{i}-\mathcal {J}_{1}-\mathcal {J}_{2}\mathrm {e}^{-\lambda \varsigma })=0, \end{aligned}$$

  (9)

  for some $i\ge 1$, for which there is an eigenvector in $\mathbb {S}_{i}$. Here, I is the identity matrix. To prove the instability of any equilibrium point, it is enough to find i such that the characteristic equation (9) has a positive root. Let

  $$\begin{aligned} \overline{G}_{i}=\int \limits _{0}^{\infty } g_{i}(\varsigma )\mathrm {e}^{-(a_{i}+\lambda )\varsigma } \; \mathrm {d}\varsigma , \quad \text {for}\ i=1,2. \end{aligned}$$

  Now, the characteristic equation at $E_{0}$ is given by

  $$\begin{aligned} f_{0,1}(\lambda ) f_{0,2}(\lambda )\left( \lambda +d+ D_{H}\zeta _{i}\right) \left( \lambda +d_{3}+D_{V}\zeta _{i} \right) \left( \lambda +d_{4}+D_{Z}\zeta _{i}\right) =0, \end{aligned}$$

  (10)

  where

  $$\begin{aligned} \begin{aligned} f_{0,1}(\lambda )=&\lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{0}+d_{1}+D_{N}\zeta _{i} ,\\ f_{0,2}(\lambda )=&\lambda -\alpha _{2}\beta _{2}\overline{G}_{2}H_{0}+d_{2}+\beta _{3}V_{0}+D_{Y}\zeta _{i}. \end{aligned} \end{aligned}$$

  From Eq. (10), two roots of the characteristic equation are given by $f_{0,1}(\lambda )=0$ and $f_{0,2}(\lambda )=0$. We can see that

  $$\begin{aligned} \lim \limits _{\lambda \rightarrow +\infty } f_{0,1}(\lambda )=+\infty , \quad \lim \limits _{\lambda \rightarrow +\infty } f_{0,2}(\lambda )=+\infty . \end{aligned}$$

  In addition, we have

  $$\begin{aligned} \begin{aligned} f_{0,1}(0)|_{i=1}=&-\alpha _{1}\beta _{1}G_{1}H_{0}+d_{1}=-d_{1}\left( \mathcal {R}_{1}-1\right)<0 \quad \text {if} \ \mathcal {R}_{1}>1,\\ f_{0,2}(0)|_{i=1}=&-\alpha _{2}\beta _{2}G_{2}H_{0}+d_{2}+\beta _{3}V_{0}=-d_{2}\left( \mathcal {R}_{0} -\mathcal {R}_{l}\right) <0 \quad \text {if} \ \mathcal {R}_{0} >\mathcal {R}_{l}. \end{aligned} \end{aligned}$$

Hence, the characteristic equation (10) has positive roots if $\mathcal {R}_{1}> 1$ or $\mathcal {R}_{0}> \mathcal {R}_{l}$. Thus, the equilibrium $E_{0}$ is unstable if $\mathcal {R}_{1}> 1$ or $\mathcal {R}_{0}> \mathcal {R}_{l}$.

In the next theorems, we will need the following quantities

$$\begin{aligned} \begin{aligned} \ln \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{HN}=&\ln \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{i}N}+\ln \frac{H_{i}}{H}, \quad \text {for} \ i= 2,4,5 ,\\ \ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{HY}=&\ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{j}Y}+\ln \frac{H_{j}}{H}, \quad \text {for} \ j= 1,3,4,5. \end{aligned} \end{aligned}$$

(11)

Theorem 4

Assume that $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$ and $\mathcal {R}_{0}>\mathcal {R}_{l}$. Then, we have the following two situations:

• (a) The treatment failure immune-free equilibrium $E_{1}$ is globally asymptotically stable if $\mathcal {R}_{n}\ge \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}\le \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$.

• (b) The equilibrium $E_{1}$ is unstable if $\mathcal {R}_{n}< \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ or $\mathcal {R}_{0}> \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$.

Proof

• (a) We take the following Lyapunov functional

  $$\begin{aligned} \begin{aligned} \mathcal {U}_{1}(t)=&\int _{\Omega } \bigg \lbrace H_{1}\Phi \left( \frac{H}{H_{1}}\right) +\frac{1}{\alpha _{1}G_{1}}N+\frac{1}{\alpha _{2}G_{2}}Y_{1}\Phi \left( \frac{Y}{Y_{1}}\right) \\&+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{1}\Phi \left( \frac{V}{V_{1}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z\\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }H(x,t-\theta )N(x,t-\theta ) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{1}Y_{1}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )Y(x,t-\theta )}{H_{1}Y_{1}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

By taking the time derivative of $\mathcal {U}_{1}(t)$ along the solutions of (2), we obtain

$$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{1}}{H}\right) \left[ D_{H}\Delta H+\kappa -dH-\beta _{1}HN-\beta _{2}HY\right] \\&+\frac{1}{\alpha _{1}G_{1}}\left[ D_{N}\Delta N+\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma )\; \mathrm {d}\varsigma -d_{1}N\right] \\&+\frac{1}{\alpha _{2}G_{2}}\left( 1-\frac{Y_{1}}{Y}\right) \left[ D_{Y}\Delta Y+\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma \right. \\&\left. -\beta _{3}YV-\beta _{4}YZ-d_{2}Y\right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{1}}{V}\right) \left[ D_{V}\Delta V+\mu +\alpha _{3}\beta _{3}YV-d_{3}V \right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}\left[ D_{Z}\Delta Z+\alpha _{4}\beta _{4}YZ-d_{4}Z\right] \\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ HN- H(x,t-\varsigma )N(x,t-\varsigma ) \right] \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{1}Y_{1}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \frac{HY}{H_{1}Y_{1}} - \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{1}Y_{1}}\right. \\&\left. +\ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{HY} \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x.\\ \end{aligned} \end{aligned}$$

From (6), we can see that $E_{1}$ satisfies the following equilibrium conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \kappa =dH_{1}+\beta _{2}H_{1}Y_{1},\\ \frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{1}V_{1}=\frac{d_{3}}{\alpha _{2}G_{2}\alpha _{3}}V_{1}-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}},\\ \beta _{2}H_{1}Y_{1}=\frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{1}V_{1}+\frac{d_{2}}{\alpha _{2}G_{2}}Y_{1}. \end{array}\right. } \end{aligned}$$

(12)

By using (12), the time derivative of $\mathcal {U}_{1}(t)$ is simplified to

$$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{1}}{H}\right) \left( dH_{1}-dH \right) +\left( \beta _{1}H_{1}-\frac{d_{1}}{\alpha _{1}G_{1}} \right) N \\&+ \frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\left( 2-\frac{V_{1}}{V}-\frac{V}{V_{1}}\right) +\left( \frac{\beta _{4}}{\alpha _{2}G_{2}}Y_{1}-\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}} \right) Z\\&+ \beta _{2}H_{1}Y_{1}\left( 2-\frac{H_{1}}{H}-\frac{1}{G_{2}} \int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{1}Y}\; \mathrm {d}\varsigma \right) \\&+ \frac{\beta _{2}}{G_{2}}H_{1}Y_{1} \int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{HY}\; \mathrm {d}\varsigma \\&+\left( 1-\frac{H_{1}}{H}\right) D_{H}\Delta H +\frac{1}{\alpha _{1}G_{1}}D_{N}\Delta N+\frac{1}{\alpha _{2}G_{2}}\left( 1-\frac{Y_{1}}{Y}\right) D_{Y}\Delta Y\\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{1}}{V}\right) D_{V}\Delta V\\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}D_{Z}\Delta Z \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

(13)

After using (8) and (11), the time derivative in (13) is transformed to

$$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{1}\right) ^{2}}{H}+\beta _{1}\left( H_{1}-H_{4}\right) N \\&-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{1})^{2}}{VV_{1}}+\frac{\beta _{4}}{\alpha _{2}G_{2}}\left( Y_{1}-Y_{3}\right) Z\\&- \frac{\beta _{2}}{G_{2}}H_{1}Y_{1}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \Phi \left( \frac{H_{1}}{H}\right) \right. \\&\left. +\Phi \left( \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{1}Y}\right) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{1}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{Y}Y_{1}}{\alpha _{2}G_{2}}\int _{\Omega }\frac{\Vert \triangledown Y \Vert ^{2}}{Y^{2}}\; \mathrm {d}x\\&-\frac{D_{V}V_{1}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x . \end{aligned} \end{aligned}$$

We can see that $\dfrac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t}\le 0$ if $\left( H_{1}-H_{4}\right) \le 0$ and $\left( Y_{1}-Y_{3}\right) \le 0$. From the equilibrium points, we have

$$\begin{aligned} H_{1}-H_{4}\le 0&\Longleftrightarrow \frac{\beta _{2}\beta _{3}\left( \mu +\kappa \alpha _{2}G_{2}\alpha _{3} \right) +d_{2}\xi _{1}+\sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] } }{2\alpha _{2}\beta _{2}G_{2}\xi _{1}}\\&\le \frac{d_{1}}{\alpha _{1}\beta _{1}G_{1}}\\&\Longleftrightarrow \sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] } \\&\le \frac{2\alpha _{2}\beta _{2}G_{2}d_{1}\xi _{1}}{\alpha _{1}\beta _{1}G_{1}}-\left[ \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}+2d_{2}\xi _{1}+\mu \beta _{2}\beta _{3}\right] \\&\Longleftrightarrow \kappa \alpha _{1}\beta _{1}G_{1}\alpha _{3}\beta _{3}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)+\mu \beta _{2}\beta _{3}d_{1}\\&\le \left( \beta _{2}d_{1}d_{2}d_{3}+\alpha _{3}\beta _{3}dd_{1}d_{2}\right) (\mathcal {R}_{0}/\mathcal {R}_{1}-1)\\&\Longleftrightarrow \frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}+ \frac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\le 1+\dfrac{\beta _{2}d_{3}}{\alpha _{3}\beta _{3} d}\\&\Longleftrightarrow \mathcal {R}_{1}+\frac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\le \mathcal {R}_{n}. \end{aligned}$$

Also, we have

$$\begin{aligned} \begin{aligned} Y_{1}-Y_{3}\le 0&\Longleftrightarrow \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}+\mu \beta _{2}\beta _{3}+2\beta _{2}d_{2}d_{3} -\frac{2\beta _{2}\alpha _{3}\beta _{3}d_{2}d_{4}}{\alpha _{4}\beta _{4}}\\&\le \sqrt{\left( \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\beta _{3}-d_{2}\xi _{1}\right) ^{2}+\mu \beta _{2}\beta _{3} \left[ \beta _{2}\beta _{3}\left( \mu +2\kappa \alpha _{2}G_{2}\alpha _{3}\right) +2d_{2}\xi _{1} \right] }\\&\Longleftrightarrow \kappa \alpha _{2}\beta _{2}G_{2}\alpha _{3}\alpha _{4}\beta _{4}d_{4}(\rho -1)\\&\le \alpha _{3}d_{2}d_{4}\left( \beta _{2}d_{4}+\alpha _{4}\beta _{4}d\right) (\rho -1)+\mu \alpha _{4}\beta _{4}\xi _{2}\\&\Longleftrightarrow \frac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}\le 1+\frac{\beta _{2}d_{4}}{\alpha _{4}\beta _{4} d}+\frac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}\\&\Longleftrightarrow \mathcal {R}_{0}\le \mathcal {R}_{m}+\frac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}. \end{aligned} \end{aligned}$$

Hence, $\dfrac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t} \le 0$ if $\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\le \mathcal {R}_{n}$ and $\mathcal {R}_{0}\le \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$. Also, one can show that $\dfrac{\hbox {d} \mathcal {U}_{1}}{\hbox {d} t} = 0$ when $H=H_{1}$, $N=0$, $Y=Y_{1}$, $V=V_{1}$ and $Z=0$. Thus, the largest invariant set $\Psi _{1}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{1}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{1}\rbrace$. When $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$ and $\mathcal {R}_{0}>\mathcal {R}_{l}$, LaSalle’s invariance principle [50, 51] ensures that the equilibrium ${E_{1}}$ is globally asymptotically stable for $\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\le \mathcal {R}_{n}$ and $\mathcal {R}_{0}\le \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$.

• (b) From (9), the characteristic equation at $E_{1}$ is given by

  $$\begin{aligned} \begin{aligned}&f_{1}(\lambda )\left( \lambda -\alpha _{4}\beta _{4}Y_{1}+d_{4}+D_{Z} \zeta _{i} \right) \bigg ( \alpha _{3}\beta _{3}^{2}Y_{1}V_{1}\left( \lambda +\beta _{2}Y_{1}+d+ D_{H}\zeta _{i}\right) \\&\quad +\left( \lambda -\alpha _{3}\beta _{3}Y_{1}+d_{3}+D_{V}\zeta _{i}\right) \\&\quad \times \left[ \alpha _{2}\beta _{2}^{2}\overline{G}_{2}H_{1}Y_{1}+\left( \lambda +\beta _{2}Y_{1}+ d+D_{H}\zeta _{i} \right) \right. \\&\quad \quad \left. \left( \lambda -\alpha _{2}\beta _{2}\overline{G}_{2}H_{1}+\beta _{3}V_{1}+d_{2}+D_{Y}\zeta _{i}\right) \right] \bigg )=0, \end{aligned} \end{aligned}$$

  (14)

  where

  $$\begin{aligned} f_{1}(\lambda )= \lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{1}+d_{1}+D_{N}\zeta _{i}. \end{aligned}$$

  Two roots of the characteristic equation (14) are given by $f_{1}(\lambda )=0$ and $( \lambda -\alpha _{4}\beta _{4}Y_{1}+d_{4}+D_{Z}\zeta _{i} )=0$. We have

  $$\begin{aligned} \begin{aligned}&\lim \limits _{\lambda \rightarrow +\infty } f_{1}(\lambda )=+\infty ,\\&f_{1}(0)|_{i=1}=-\alpha _{1}\beta _{1}G_{1}H_{1}+d_{1}=-\alpha _{1}\beta _{1}G_{1}\left( H_{1}-H_{4}\right) . \end{aligned} \end{aligned}$$

  From the proof of part (a), we can see that $f_{1}(0)|_{i=1}<0$ if $\mathcal {R}_{n}< \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$. The other root at $i=1$ is given by

  $$\begin{aligned} \lambda |_{i=1}=\alpha _{4}\beta _{4}Y_{1}-d_{4}=\alpha _{4}\beta _{4}\left( Y_{1}-Y_{3}\right)>0 \quad \text {if} \ \mathcal {R}_{0}> \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}. \end{aligned}$$

Thus, the characteristic equation has positive roots if $\mathcal {R}_{n}< \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ or $\mathcal {R}_{0}> \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$. In this situation, the equilibrium $E_{1}$ is unstable. $\square$

Theorem 5

Assume that $\mathcal {R}_{1}>1$. Then, we have the following two situations:

• (a) The tumor-free equilibrium $E_{2}$ is globally asymptotically stable if $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$.

• (b) The equilibrium $E_{2}$ is unstable if $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$.

Proof

• (a) We consider the following Lyapunov functional

  $$\begin{aligned} \begin{aligned} \mathcal {U}_{2}(t)=&\int _{\Omega } \bigg \lbrace H_{2}\Phi \left( \frac{H}{H_{2}}\right) +\frac{1}{\alpha _{1}G_{1}}N_{2}\Phi \left( \frac{N}{N_{2}}\right) +\frac{1}{\alpha _{2}G_{2}}Y\\&+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{2}\Phi \left( \frac{V}{V_{2}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z\\&+\frac{\beta _{1}}{G_{1}}H_{2}N_{2}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )N(x,t-\theta )}{H_{2}N_{2}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }H(x,t-\theta )Y(x,t-\theta ) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  By computing the time derivative of $\mathcal {U}_{2}(t)$ along the solutions of (2), we have

  $$\begin{aligned}&\frac{\hbox {d} \mathcal {U}_{2}}{\hbox {d} t}= \int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{2}}{H}\right) \left[ D_{H}\Delta H+\kappa -dH-\beta _{1}HN-\beta _{2}HY\right] \\&\quad +\frac{1}{\alpha _{1}G_{1}}\left( 1-\frac{N_{2}}{N}\right) \left[ D_{N}\Delta N +\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma )\; \mathrm {d}\varsigma -d_{1}N\right] \\&\quad +\frac{1}{\alpha _{2}G_{2}}\left[ D_{Y}\Delta Y +\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma -\beta _{3}YV-\beta _{4}YZ-d_{2}Y\right] \\&\quad +\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{2}}{V}\right) \left[ D_{V}\Delta V+\mu +\alpha _{3}\beta _{3}YV-d_{3}V \right] \\&\quad +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}\left[ D_{Z}\Delta Z+\alpha _{4}\beta _{4}YZ-d_{4}Z\right] \\&\quad +\frac{\beta _{1}}{G_{1}}H_{2}N_{2}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ \frac{HN}{H_{2}N_{2}} - \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{2}N_{2}}\right. \\&\quad \left. +\ln \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{HN} \right] \; \mathrm {d}\varsigma \\&\quad +\frac{\beta _{2}}{G_{2}}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ HY- H(x,t-\varsigma )Y(x,t-\varsigma ) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned}$$

  From (6), we can see that $E_{2}$ satisfies the following conditions

  $$\begin{aligned} {\left\{ \begin{array}{ll} \kappa =dH_{2}+\beta _{1}H_{2}N_{2},\\ \beta _{1}H_{2}N_{2}=\frac{d_{1}}{\alpha _{1}G_{1}}N_{2},\\ \frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}=\frac{d_{3}}{\alpha _{2}G_{2}\alpha _{3}}V_{2}. \end{array}\right. } \end{aligned}$$

  (15)

  By using (15), the time derivative of $\mathcal {U}_{2}(t)$ can be simplified to

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{2}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{2}}{H}\right) \left( dH_{2}-dH \right) +\left( \beta _{2}H_{2}-\frac{d_{2}}{\alpha _{2}G_{2}}-\frac{\beta _{3}}{\alpha _{2}G_{2}}V_{2} \right) Y \\&+ \frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\left( 2-\frac{V_{2}}{V}-\frac{V}{V_{2}}\right) \\&-\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}}Z+ \beta _{1}H_{2}N_{2}\left( 2-\frac{H_{2}}{H}\right. \\&\left. -\frac{1}{G_{1}} \int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{2}N}\; \mathrm {d}\varsigma \right) \\&+ \frac{\beta _{1}}{G_{1}} H_{2}N_{2}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\ln \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{HN}\; \mathrm {d}\varsigma \\&+\left( 1-\frac{H_{2}}{H}\right) D_{H}\Delta H +\frac{1}{\alpha _{1}G_{1}}\left( 1-\frac{N_{2}}{N}\right) D_{N}\Delta N\\&+\frac{1}{\alpha _{2}G_{2}}D_{Y}\Delta Y+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{2}}{V}\right) D_{V}\Delta V\\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}D_{Z}\Delta Z \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  (16)

  After using (8) and (11), the time derivative in (16) is transformed to

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{2}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{2}\right) ^{2}}{H}+\frac{dd_{1}d_{2}}{\kappa \alpha _{1}\beta _{1}G_{1}\alpha _{2}G_{2} }\left( \mathcal {R}_{0}-\mathcal {R}_{1}-\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}\right) Y \\&-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{2})^{2}}{VV_{2}}-\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}} Z\\&- \frac{\beta _{1}}{G_{1}}H_{2}N_{2}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ \Phi \left( \frac{H_{2}}{H}\right) +\Phi \left( \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{2}N}\right) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{2}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{N}N_{2}}{\alpha _{1}G_{1}}\int _{\Omega }\frac{\Vert \triangledown N \Vert ^{2}}{N^{2}}\; \mathrm {d}x -\frac{D_{V}V_{2}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x . \end{aligned} \end{aligned}$$

  We note that $\dfrac{\hbox {d} \mathcal {U}_{2}}{\hbox {d} t}\le 0$ if $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. In addition, It can be easily shown that $\dfrac{\hbox {d} \mathcal {U}_{2}}{\hbox {d} t}= 0$ if $H=H_{2}$, $N=N_{2}$, $Y=0$, $V=V_{2}$ and $Z=0$. Thus, the largest invariant set $\Psi _{2}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{2}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{2}\rbrace$. Accordingly, LaSalle’s invariance principle [50, 51] guarantees the global asymptotic stability of $E_{2}$ when $\mathcal {R}_{1}>1$ and $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$.

• (b) From (9), the characteristic equation at $E_{2}$ is given by

  $$\begin{aligned} \begin{aligned}&f_{2}(\lambda )\left( \lambda +d_{3}+D_{V}\zeta _{i}\right) \left( \lambda +d_{4}+D_{Z}\zeta _{i}\right) \\&\times \left[ \alpha _{1}\beta _{1}^{2}\overline{G}_{2}H_{2}N_{2}+\left( \lambda +\beta _{1}N_{2}+d+D_{H}\zeta _{i} \right) \left( \lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{2}+d_{1}+D_{N}\zeta _{i} \right) \right] =0, \end{aligned} \end{aligned}$$

  (17)

  where

  $$\begin{aligned} f_{2}(\lambda )=\lambda -\alpha _{2}\beta _{2}\overline{G}_{2}H_{2}+d_{2}+\beta _{3}V_{2}+D_{Y}\zeta _{i}. \end{aligned}$$

  One root of the characteristic equation (17) is given by $f_{2}(\lambda )=0$, where we have

  $$\begin{aligned} \begin{aligned}&\lim \limits _{\lambda \rightarrow +\infty } f_{2}(\lambda )=+\infty ,\\&f_{2}(0)|_{i=1}=-\alpha _{2}\beta _{2}G_{2}H_{2}+d_{2}+\beta _{3}V_{2}=-\frac{dd_{1}d_{2}}{\kappa \alpha _{1}\beta _{1}G_{1}}\left( \mathcal {R}_{0}-\mathcal {R}_{1}-\frac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}\right) . \end{aligned} \end{aligned}$$

We note that $f_{2}(0)|_{i=1}<0$ if $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$, and the characteristic equation (17) has a positive root in this case. Hence, the equilibrium $E_{2}$ is unstable if $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. $\square$

Theorem 6

Suppose that $\rho >1$ and $\mathcal {R}_{0}>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$. Then, we have the following two situations:

• (a) The treatment failure equilibrium $E_{3}$ is globally asymptotically stable if $\mathcal {R}_{1}\le \mathcal {R}_{m}$.

• (b) The equilibrium $E_{3}$ is unstable if $\mathcal {R}_{1}>\mathcal {R}_{m}$.

Proof

• (a) We consider the following Lyapunov functional

  $$\begin{aligned} \begin{aligned} \mathcal {U}_{3}(t)=&\int _{\Omega } \bigg \lbrace H_{3}\Phi \left( \frac{H}{H_{3}}\right) +\frac{1}{\alpha _{1}G_{1}}N+\frac{1}{\alpha _{2}G_{2}}Y_{3}\Phi \left( \frac{Y}{Y_{3}}\right) \\&+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{3}\Phi \left( \frac{V}{V_{3}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z_{3}\Phi \left( \frac{Z}{Z_{3}}\right) \\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }H(x,t-\theta )N(x,t-\theta ) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{3}Y_{3}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )Y(x,t-\theta )}{H_{3}Y_{3}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  By taking the time derivative of $\mathcal {U}_{3}(t)$ along the solutions of (2), we obtain

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{3}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{3}}{H}\right) \left[ D_{H}\Delta H+\kappa -dH-\beta _{1}HN-\beta _{2}HY\right] \\&+\frac{1}{\alpha _{1}G_{1}}\left[ D_{N}\Delta N+\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )N(x,t-\varsigma )\; \mathrm {d}\varsigma -d_{1}N\right] \\&+\frac{1}{\alpha _{2}G_{2}}\left( 1-\frac{Y_{3}}{Y}\right) \left[ D_{Y}\Delta Y + \alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma \right. \\&\left. -\beta _{3}YV-\beta _{4}YZ-d_{2}Y\right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{3}}{V}\right) \left[ D_{V}\Delta V+\mu +\alpha _{3}\beta _{3}YV-d_{3}V \right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}\left( 1-\frac{Z_{3}}{Z}\right) \left[ D_{Z}\Delta Z+\alpha _{4}\beta _{4}YZ-d_{4}Z\right] \\&+\frac{\beta _{1}}{G_{1}}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ HN- H(x,t-\varsigma )N(x,t-\varsigma ) \right] \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{3}Y_{3}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \frac{HY}{H_{3}Y_{3}} - \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{3}Y_{3}}\right. \\&\left. +\ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{HY} \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x.\\ \end{aligned} \end{aligned}$$

  (18)

  From (6), we can see that $E_{3}$ satisfies the following equilibrium conditions

  $$\begin{aligned} {\left\{ \begin{array}{ll} \kappa =dH_{3}+\beta _{2}H_{3}Y_{3},\\ \frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{3}V_{3}=\frac{d_{3}}{\alpha _{2}G_{2}\alpha _{3}}V_{3}-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}},\\ \frac{\beta _{4}}{\alpha _{2}G_{2}}Y_{3}Z_{3}=\frac{d_{4}}{\alpha _{2}G_{2}\alpha _{4}}Z_{3},\\ \beta _{2}H_{3}Y_{3}=\frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{3}V_{3}+\frac{\beta _{4}}{\alpha _{2}G_{2}}Y_{3}Z_{3}+\frac{d_{2}}{\alpha _{2}G_{2}}Y_{3}. \end{array}\right. } \end{aligned}$$

  (19)

  By using (19), (8) and (11), the time derivative in (18) is transformed to

  $$\begin{aligned} \frac{\hbox {d} \mathcal {U}_{3}}{\hbox {d} t}= & {} \int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{3}\right) ^{2}}{H}+\frac{\alpha _{4}\beta _{4}dd_{1}}{\alpha _{1}G_{1}\xi _{2}}\left( \mathcal {R}_{1}- \mathcal {R}_{m} \right) N-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{3})^{2}}{VV_{3}}\\&- \frac{\beta _{2}}{G_{2}}H_{3}Y_{3}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \Phi \left( \frac{H_{3}}{H}\right) \right. \\&\left. +\Phi \left( \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{3}Y}\right) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{3}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{Y}Y_{3}}{\alpha _{2}G_{2}}\int _{\Omega }\frac{\Vert \triangledown Y \Vert ^{2}}{Y^{2}}\; \mathrm {d}x \\&-\frac{D_{V}V_{3}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x-\frac{D_{Z}Z_{3}}{\alpha _{2}G_{2}\alpha _{4}}\int _{\Omega }\frac{\Vert \triangledown Z \Vert ^{2}}{Z^{2}}\; \mathrm {d}x . \end{aligned}$$

  This implies that $\dfrac{\hbox {d} \mathcal {U}_{3}}{\hbox {d} t}\le 0$ if $\mathcal {R}_{1}\le \mathcal {R}_{m}$. Moreover, $\dfrac{\hbox {d} \mathcal {U}_{3}}{\hbox {d} t}=0$ when $H=H_{3}$, $N=0$, $Y=Y_{3}$, $V=V_{3}$ and $Z=Z_{3}$. Thus, the largest invariant set $\Psi _{3}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{3}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{3}\rbrace$. By LaSalle’s invariance principle [50, 51], the equilibrium $E_{3}$ is globally asymptotically stable if $\mathcal {R}_{1}\le \mathcal {R}_{m}$ given that the point exists for $\rho >1$ and $\mathcal {R}_{0}>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$.

• (b) From (9), the characteristic equation at $E_{3}$ is given by

  $$\begin{aligned} \begin{aligned}&f_{3}(\lambda )\bigg (\left( \lambda +\beta _{2}Y_{3}+d+D_{H}\zeta _{i} \right) \left[ \alpha _{4}\beta _{4}^{2}Y_{3}Z_{3}\left( \lambda - \alpha _{3}\beta _{3}Y_{3}+d_{3}+D_{V}\zeta _{i}\right) \right. \\&\quad \left. + \alpha _{3}\beta _{3}^{2}Y_{3}V_{3}\left( \lambda -\alpha _{4}\beta _{4}Y_{3}+d_{4}+D_{Z}\zeta _{i} \right) \right] \\&\quad +\left( \lambda -\alpha _{4}\beta _{4}Y_{3}+d_{4}+D_{Z}\zeta _{i} \right) \left( \lambda - \alpha _{3}\beta _{3}Y_{3}+d_{3}+D_{V}\zeta _{i}\right) \\&\quad \times \left[ \alpha _{2}\beta _{2}^{2}\overline{G}_{2}H_{3}Y_{3}+\left( \lambda +\beta _{2}Y_{3}+d+D_{H}\zeta _{i} \right) \right. \\&\quad \left. \left( \lambda -\alpha _{2}\beta _{2}\overline{G}_{2}H_{3}+\beta _{3}V_{3}+\beta _{4}Z_{3}+d_{2}+D_{Y}\zeta _{i}\right) \right] \bigg ) =0, \end{aligned} \end{aligned}$$

  (20)

  where

  $$\begin{aligned} f_{3}(\lambda )=\lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{3}+d_{1}+D_{N}\zeta _{i}. \end{aligned}$$

  One root of the characteristic Eq. (20) is determined by $f_{3}(\lambda )=0$, where

  $$\begin{aligned} \begin{aligned}&\lim \limits _{\lambda \rightarrow +\infty } f_{3}(\lambda )=+\infty ,\\&f_{3}(0)|_{i=1}=-\alpha _{1}\beta _{1}G_{1}H_{3}+d_{1}=-\frac{\alpha _{4}\beta _{4}dd_{1}}{\xi _{2}}\left( \mathcal {R}_{1}- \mathcal {R}_{m}\right) . \end{aligned} \end{aligned}$$

When $\mathcal {R}_{1}> \mathcal {R}_{m}$, we can see that $f_{3}(0)|_{i=1}<0$ and the characteristic equation (20) has a positive root in this situation. Hence, the equilibrium $E_{3}$ is unstable if $\mathcal {R}_{1}> \mathcal {R}_{m}$. $\square$

Theorem 7

Assume that $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. Then, we have the following two situations:

• (a) The partial success immune-free equilibrium $E_{4}$ is globally asymptotically stable if $\mathcal {R}_{0}\le \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$.

• (b) The equilibrium $E_{4}$ is unstable if $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$.

Proof

• (a) We take the following Lyapunov functional

  $$\begin{aligned} \begin{aligned} \mathcal {U}_{4}(t)=&\int _{\Omega } \bigg \lbrace H_{4}\Phi \left( \frac{H}{H_{4}}\right) +\frac{1}{\alpha _{1}G_{1}}N_{4}\Phi \left( \frac{N}{N_{4}}\right) +\frac{1}{\alpha _{2}G_{2}}Y_{4}\Phi \left( \frac{Y}{Y_{4}}\right) \\&+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{4}\Phi \left( \frac{V}{V_{4}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z\\&+\frac{\beta _{1}}{G_{1}}H_{4}N_{4}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )N(x,t-\theta )}{H_{4}N_{4}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{4}Y_{4}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )Y(x,t-\theta )}{H_{4}Y_{4}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  By computing the time derivative of $\mathcal {U}_{4}(t)$ along the solutions of (2), we obtain

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{4}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace \left( 1-\frac{H_{4}}{H}\right) \left[ D_{H}\Delta H+\kappa -dH-\beta _{1}HN-\beta _{2}HY\right] \\&+\frac{1}{\alpha _{1}G_{1}}\left( 1-\frac{N_{4}}{N}\right) \left[ D_{N}\Delta N +\alpha _{1}\beta _{1}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }H(x,t-\varsigma )\right. \\&\left. \times N(x,t-\varsigma )\; \mathrm {d}\varsigma -d_{1}N \right] \\&+\frac{1}{\alpha _{2}G_{2}}\left( 1-\frac{Y_{4}}{Y}\right) \left[ D_{Y}\Delta Y +\alpha _{2}\beta _{2}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma \right. \\&\left. -\beta _{3}YV-\beta _{4}YZ-d_{2}Y\right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{3}}\left( 1-\frac{V_{4}}{V}\right) \left[ D_{V}\Delta V \right. \\&\left. +\mu +\alpha _{3}\beta _{3}YV-d_{3}V \right] \\&+\frac{1}{\alpha _{2}G_{2}\alpha _{4}}\left[ D_{Z}\Delta Z+\alpha _{4}\beta _{4}YZ-d_{4}Z\right] \\&+\frac{\beta _{1}}{G_{1}}H_{4}N_{4}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ \frac{HN}{H_{4}N_{4}} - \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{4}N_{4}}\right. \\&\left. +\ln \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{HN} \right] \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{4}Y_{4}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \frac{HY}{H_{4}Y_{4}} - \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{4}Y_{4}}\right. \\&\left. +\ln \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{HY} \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

  (21)

  From (6), we can see that $E_{4}$ satisfies the following equilibrium conditions

  $$\begin{aligned} {\left\{ \begin{array}{ll} \kappa =dH_{4}+\beta _{1}H_{4}N_{4}+\beta _{2}H_{4}Y_{4},\\ \beta _{1}H_{4}N_{4}=\frac{d_{1}}{\alpha _{1}G_{1}}N_{4},\\ \frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{4}V_{4}=\frac{d_{3}}{\alpha _{2}G_{2}\alpha _{3}}V_{4}-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}},\\ \beta _{2}H_{4}Y_{4}=\frac{\beta _{3}}{\alpha _{2}G_{2}}Y_{4}V_{4}+\frac{d_{2}}{\alpha _{2}G_{2}}Y_{4}. \end{array}\right. } \end{aligned}$$

  (22)

  By using (22), (8) and (11), the time derivative in (21) is transformed to

  $$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{4}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{4}\right) ^{2}}{H}+\frac{\beta _{4}}{\alpha _{2}G_{2}}\left( Y_{4}- Y_{5}\right) Z-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{4})^{2}}{VV_{4}}\\&-\frac{\beta _{1}}{G_{1}}H_{4}N_{4}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ \Phi \left( \frac{H_{4}}{H}\right) +\Phi \left( \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{4}N}\right) \right] \; \mathrm {d}\varsigma \\&- \frac{\beta _{2}}{G_{2}}H_{4}Y_{4}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \Phi \left( \frac{H_{4}}{H}\right) +\Phi \left( \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{4}Y}\right) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{4}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{N}N_{4}}{\alpha _{1}G_{1}}\int _{\Omega }\frac{\Vert \triangledown N \Vert ^{2}}{N^{2}}\; \mathrm {d}x\\&-\frac{D_{Y}Y_{4}}{\alpha _{2}G_{2}}\int _{\Omega }\frac{\Vert \triangledown Y \Vert ^{2}}{Y^{2}}\; \mathrm {d}x -\frac{D_{V}V_{4}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x. \end{aligned} \end{aligned}$$

  The sign of $\dfrac{\hbox {d} \mathcal {U}_{4}}{\hbox {d} t}$ is determined by the sign of $\left( Y_{4}- Y_{5}\right)$ since all other terms are negative. From the equilibrium points $E_{4}$ and $E_{5}$, we find

  $$\begin{aligned} \begin{aligned} Y_{4}-Y_{5}=&\frac{d_{2}d_{3}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)-\mu \beta _{3}}{\alpha _{3}\beta _{3}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}-\frac{d_{4}}{\alpha _{4}\beta _{4}}\\ =&\frac{\alpha _{3}d_{4}\left( \alpha _{2}\beta _{2}G_{2}d_{1}-\alpha _{1}\beta _{1}G_{1}d_{2} \right) (\rho -1)-\mu \alpha _{1}\beta _{1} G_{1}\alpha _{4}\beta _{4}}{\alpha _{1}\beta _{1}G_{1}\alpha _{3}\alpha _{4}\beta _{4}d_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\\ =&\frac{dd_{1}d_{4}(\rho -1)}{\kappa \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}\left[ \frac{\kappa \alpha _{2}\beta _{2}G_{2}}{dd_{2}}-\frac{\kappa \alpha _{1}\beta _{1}G_{1}}{dd_{1}}-\frac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3}dd_{1}d_{2}d_{4}(\rho -1)}}\right] \\ =&\frac{dd_{1}d_{4}(\rho -1)}{\kappa \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}(\mathcal {R}_{0}/\mathcal {R}_1)}\left[ \mathcal {R}_{0}- \mathcal {R}_{1} -\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}\right] . \end{aligned} \end{aligned}$$

  As a result, we find that $\dfrac{\hbox {d} \mathcal {U}_{4}}{\hbox {d} t}\le 0$ if $\mathcal {R}_{0}\le \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. Also, we can show that $\dfrac{\hbox {d} \mathcal {U}_{4}}{\hbox {d} t}= 0$ when $H=H_{4}$, $N=N_{4}$, $Y=Y_{4}$, $V=V_{4}$ and $Z=0$. Thus, the largest invariant set $\Psi _{4}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{4}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{4}\rbrace$. According to LaSalle’s invariance principle [50, 51], the equilibrium $E_{4}$ is globally asymptotically stable if $\mathcal {R}_{0}\le \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$ provided that the point is defined for $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$.

• (b) From (9), the characteristic equation at $E_{4}$ is given by

  $$\begin{aligned} \begin{aligned}&f_{4}(\lambda )\bigg (\left[ \alpha _{1}\beta _{1}^{2}\overline{G}_{1}H_{4}N_{4}+\left( \lambda +\beta _{1}N_{4}+\beta _{2}Y_{4}+d+D_{H}\zeta _{i} \right) \right. \\&\quad \left. \left( \lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{4}+d_{1}+D_{N}\zeta _{i}\right) \right] \\&\quad \times \left[ \alpha _{3}\beta _{3}^{2}Y_{4}V_{4}+\left( \lambda -\alpha _{2}\beta _{2}\overline{G}_{1}H_{4}+\beta _{3}V_{4}+d_{2}+D_{Y}\zeta _{i} \right) \right. \\&\quad \left. \left( \lambda - \alpha _{3}\beta _{3}Y_{4}+d_{3}+D_{V}\zeta _{i}\right) \right] \\&\quad +\alpha _{2}\beta _{2}^{2}\overline{G}_{2}H_{4}Y_{4}\left( \lambda -\alpha _{1}\beta _{1}\overline{G}_{1}H_{4}+d_{1}+D_{N}\zeta _{i}\right) \\&\quad \left( \lambda - \alpha _{3}\beta _{3}Y_{4}+d_{3}+D_{V}\zeta _{i}\right) \bigg ) =0, \end{aligned} \end{aligned}$$

  (23)

  where

  $$\begin{aligned} f_{4}(\lambda )= \lambda -\alpha _{4}\beta _{4}Y_{4}+d_{4}+D_{Z}\zeta _{i}. \end{aligned}$$

  One root of the characteristic equation (23) is given by $f_{4}(\lambda )=0$. In other words, we have the eigenvalue

  $$\begin{aligned} \lambda |_{i=1}=\alpha _{4}\beta _{4}Y_{4}-d_{4}=\alpha _{4}\beta _{4}\left( Y_{4}-Y_{5} \right) . \end{aligned}$$

From the proof of part (a), we can see that $\left( Y_{4}-Y_{5} \right) >0$ if $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. In this situation, the characteristic equation has a positive root, and the equilibrium $E_{4}$ is unstable. $\square$

Theorem 8

The coexistence equilibrium $E_{5}$ is globally asymptotically stable if $\rho >1$, $\mathcal {R}_{1}>\mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$.

Proof

We take the following Lyapunov functional

$$\begin{aligned} \begin{aligned} \mathcal {U}_{5}(t)=&\int _{\Omega } \bigg \lbrace H_{5}\Phi \left( \frac{H}{H_{5}}\right) +\frac{1}{\alpha _{1}G_{1}}N_{5}\Phi \left( \frac{N}{N_{5}}\right) +\frac{1}{\alpha _{2}G_{2}}Y_{5}\Phi \left( \frac{Y}{Y_{5}}\right) \\&+ \frac{1}{\alpha _{2}G_{2}\alpha _{3}}V_{5}\Phi \left( \frac{V}{V_{5}}\right) +\frac{1}{\alpha _{2}G_{2}\alpha _{4}}Z_{5}\left( \frac{Z}{Z_{5}}\right) \\&+\frac{\beta _{1}}{G_{1}}H_{5}N_{5}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )N(x,t-\theta )}{H_{5}N_{5}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \\&+\frac{\beta _{2}}{G_{2}}H_{5}Y_{5}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma } \int \limits _{0}^{\varsigma }\Phi \left( \frac{H(x,t-\theta )Y(x,t-\theta )}{H_{5}Y_{5}}\right) \;\mathrm {d}\theta \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x. \end{aligned} \end{aligned}$$

After using the equilibrium conditions at $E_{5}$, (8) and (11), the time derivative of $\mathcal {U}_{5}(t)$ is given by

$$\begin{aligned} \begin{aligned} \frac{\hbox {d} \mathcal {U}_{5}}{\hbox {d} t}=&\int _{\Omega } \bigg \lbrace -\frac{d\left( H-H_{5}\right) ^{2}}{H}-\frac{\mu }{\alpha _{2}G_{2}\alpha _{3}}\frac{(V-V_{5})^{2}}{VV_{5}}\\&-\frac{\beta _{1}}{G_{1}}H_{5}N_{5}\int \limits _{0}^{\infty } g_{1}(\varsigma )\mathrm {e}^{-a_{1}\varsigma }\left[ \Phi \left( \frac{H_{5}}{H}\right) +\Phi \left( \frac{H(x,t-\varsigma )N(x,t-\varsigma )}{H_{5}N}\right) \right] \; \mathrm {d}\varsigma \\&- \frac{\beta _{2}}{G_{2}}H_{5}Y_{5}\int \limits _{0}^{\infty } g_{2}(\varsigma )\mathrm {e}^{-a_{2}\varsigma }\left[ \Phi \left( \frac{H_{5}}{H}\right) +\Phi \left( \frac{H(x,t-\varsigma )Y(x,t-\varsigma )}{H_{5}Y}\right) \right] \; \mathrm {d}\varsigma \bigg \rbrace \; \mathrm {d}x\\&-D_{H}H_{5}\int _{\Omega }\frac{\Vert \triangledown H \Vert ^{2}}{H^{2}}\; \mathrm {d}x-\frac{D_{N}N_{5}}{\alpha _{1}G_{1}}\int _{\Omega }\frac{\Vert \triangledown N \Vert ^{2}}{N^{2}}\; \mathrm {d}x \\&-\frac{D_{Y}Y_{5}}{\alpha _{2}G_{2}}\int _{\Omega }\frac{\Vert \triangledown Y \Vert ^{2}}{Y^{2}}\; \mathrm {d}x -\frac{D_{V}V_{5}}{\alpha _{2}G_{2}\alpha _{3}}\int _{\Omega }\frac{\Vert \triangledown V \Vert ^{2}}{V^{2}}\; \mathrm {d}x\\&-\frac{D_{Z}Z_{5}}{\alpha _{2}G_{2}\alpha _{4}}\int _{\Omega }\frac{\Vert \triangledown Z \Vert ^{2}}{Z^{2}}\; \mathrm {d}x. \end{aligned} \end{aligned}$$

This implies that $\dfrac{\hbox {d} \mathcal {U}_{5}}{\hbox {d} t}\le 0$. Also, one can show that $\dfrac{\hbox {d} \mathcal {U}_{5}}{\hbox {d} t}=0$ when $H=H_{5}$, $N=N_{5}$, $Y=Y_{5}$, $V=V_{5}$ and $Z=Z_{5}$. Thus, the largest invariant set $\Psi _{5}\subseteq \Psi =\lbrace (H,N,Y,V,Z)\ | \ \frac{\hbox {d}\mathcal {U}_{5}}{\hbox {d}t} =0\rbrace$ is the singleton $\lbrace E_{5}\rbrace$. According to LaSalle’s invariance principle [50, 51], the equilibrium $E_{5}$ is globally asymptotically stable if $\rho >1$, $\mathcal {R}_{1}>\mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. $\square$

Remark 2

It follows from Theorem 5 that the tumor cells will be removed from the body when $\mathcal {R}_{1}>1$ and

$$\begin{aligned} \begin{aligned}&\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}\\ \Longleftrightarrow \,&\mathcal {R}_{0}-\mathcal {R}_{1}\le \dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}} \\ \Longleftrightarrow \,&\frac{dd_{1}d_{2}d_{3} \left( \mathcal {R}_{0}-\mathcal {R}_{1} \right) }{\kappa \alpha _{1}\beta _{1}G_{1}\beta _{3}}\le \mu \\ \Longleftrightarrow \,&\mu _{0}\le \mu , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \mu _{0}=\frac{dd_{1}d_{2}d_{3} \left( \mathcal {R}_{0}-\mathcal {R}_{1} \right) }{\kappa \alpha _{1}\beta _{1}G_{1}\beta _{3}}. \end{aligned}$$

(24)

Hence, $\mu _{0}$ is the minimum effective dosage of M1 virus required to eliminate the tumor. When $\mu < \mu _{0}$, we see from Theorem 7 that the tumor cells will persist as $t \longrightarrow \infty$.

5 Numerical simulations

In this section, we pursue some numerical simulations in order to verify the results of Theorems 3–8. For this purpose, we choose $g_{i}(\varsigma )$ in model (2) as

$$\begin{aligned} g_{i}(\varsigma )=b_{i}\mathrm {e}^{-b_{i}\varsigma }, \quad \text {for}\ i=1,2. \end{aligned}$$

Clearly, $g_{i}(\varsigma )> 0$ and $\int \nolimits _{0}^{\infty } g_{i}(\varsigma ) \; \mathrm {d}\varsigma =\int \nolimits _{0}^{\infty }b_{i}\mathrm {e}^{-b_{i}\varsigma } \; \mathrm {d}\varsigma =1$. This form of $g_{i}(\varsigma )$ was taken in [22]. Consequently, the values of $G_{1}$ and $G_{2}$ defined in Eq. (5) are given by

$$\begin{aligned} G_{i}=b_{i}\int \limits _{0}^{\infty } \mathrm {e}^{-(a_{i}+b_{i})\varsigma } \; \mathrm {d}\varsigma =\frac{b_{i}}{a_{i}+b_{i}}, \quad \text {for}\ i=1,2. \end{aligned}$$

The values of $\mathcal {R}_{0}$ and $\mathcal {R}_{1}$ are given by

$$\begin{aligned} \mathcal {R}_{0}=\frac{\kappa \alpha _{2}\beta _{2}b_{2}}{dd_{2}\left( a_{2}+b_{2} \right) }, \quad \mathcal {R}_{1}=\frac{\kappa \alpha _{1}\beta _{1}b_{1}}{dd_{1}\left( a_{1}+b_{1} \right) }. \end{aligned}$$

(25)

In order to transform system (2) to PDE system, we introduce the following new variables

$$\begin{aligned} \begin{aligned} A(x,t)=&\int \limits _{0}^{\infty }\mathrm {e}^{-(a_{1}+b_{1})\varsigma }H(x,t-\varsigma )N(x,t-\varsigma ) \; \mathrm {d}\varsigma ,\\ B(x,t)=&\int \limits _{0}^{\infty } \mathrm {e}^{-(a_{2}+b_{2})\varsigma }H(x,t-\varsigma )Y(x,t-\varsigma )\; \mathrm {d}\varsigma . \end{aligned} \end{aligned}$$

(26)

Thus, system (2) is transformed to the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial H(x,t)}{\partial t}=D_{H}\Delta H(x,t)+\kappa -dH(x,t)-\beta _{1}H(x,t)N(x,t)-\beta _{2}H(x,t)Y(x,t),\\ \frac{\partial A(x,t)}{\partial t}=H(x,t)N(x,t)-(a_{1}+b_{1})A(x,t),\\ \frac{\partial N(x,t)}{\partial t}=D_{N}\Delta N(x,t)+\alpha _{1}\beta _{1}b_{1}A(x,t) -d_{1}N(x,t),\\ \frac{\partial B(x,t)}{\partial t}=H(x,t)Y(x,t)-(a_{2}+b_{2})B(x,t),\\ \frac{\partial Y(x,t)}{\partial t}=D_{Y}\Delta Y(x,t)+\alpha _{2}\beta _{2}b_{2}B(x,t) -\beta _{3}Y(x,t)V(x,t)-\beta _{4}Y(x,t)Z(x,t)\\ \quad -d_{2}Y(x,t),\\ \frac{\partial V(x,t)}{\partial t}=D_{V}\Delta V(x,t)+\mu +\alpha _{3}\beta _{3}Y(x,t)V(x,t)-d_{3}V(x,t),\\ \frac{\partial Z(x,t)}{\partial t}=D_{Z}\Delta Z(x,t)+\alpha _{4}\beta _{4}Y(x,t)Z(x,t)-d_{4}Z(x,t). \end{array}\right. } \end{aligned}$$

(27)

For system (27), we consider the following initial conditions

$$\begin{aligned} \begin{aligned}&H(x,0)=0.3\left( 1+0.2\cos ^{2}(\pi x) \right) ,\quad N(x,0)=0.2\left( 1+0.2\cos ^{2}(\pi x) \right) ,\\&Y(x,0)=0.2\left( 1+0.2\cos ^{2}(\pi x) \right) ,\\&V(x,0)=0.3\left( 1+0.2\cos ^{2}(\pi x) \right) , \quad Z(x,0)=0.02\left( 1+0.2\cos ^{2}(\pi x) \right) . \end{aligned} \end{aligned}$$

The initial conditions for the new variables A(x, t) and B(x, t) can be computed from (26). We take the spatial domain as $\Omega =[0,2]$ with a step size $\Delta x=0.02$. We perform the simulations on a time interval [0, 400] with a step size $\Delta t=0.1$. The values of $\alpha _{2}$, $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, $\beta _{4}$, $\eta _{1}$, $\eta _{2}$, $\eta _{3}$ and $\eta _{4}$ are taken as free parameters while the other remaining parameters are listed in Table 1. Some parameter values are taken from [42], while others are taken as an assumption. The results of the numerical simulations are classified into six categories:

Table 1 List of parameters of model (2)

Fig. 1

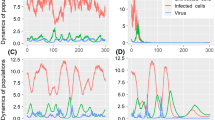
The numerical simulations of system (2) when $\mathcal {R}_{1}\le 1$ and $\mathcal {R}_{0}\le \mathcal {R}_{l}$. The competition-free equilibrium $E_{0}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

Fig. 2

The numerical simulations of system (2) when $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}\ge \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}\le \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$. The treatment failure immune-free equilibrium $E_{1}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

• (a) We consider $\alpha _{2}=0.8$, $\beta _{1}=0.03$, $\beta _{2}=0.03$, $\beta _{3}=0.1$, $\beta _{4}=0.03$, $\eta _{1}=0.04$, $\eta _{2}=0.01$, $\eta _{3}=0.008$ and $\eta _{4}=0.01$. These values give $\mathcal {R}_{1}=0.3636<1$ and $\mathcal {R}_{0}=0.7273<\mathcal {R}_{l}=2.1905$. In this situation, the competition-free equilibrium $E_{0}=(1,0,0,0.3571,0)$ is globally asymptotically stable as shown in Fig. 1. This result coincides with Theorem 3. At this point, both populations of normal and tumor cells are extinct. This extinction might be a result of a severe competition between the normal and tumor cells on a limited nutrient source. Hence, the effect of oncolytic virotherapy on tumor growth cannot be examined in this situation.

• (b) We consider $\alpha _{2}=0.8$, $\beta _{1}=0.03$, $\beta _{2}=0.1$, $\beta _{3}=0.1$, $\beta _{4}=0.2$, $\eta _{1}=0.04$, $\eta _{2}=0.008$, $\eta _{3}=0.008$ and $\eta _{4}=0.01$. This set of parameters gives $\rho =2.9867>1$, $\mathcal {R}_{0}/\mathcal {R}_{1}=7.1429>1$, $\mathcal {R}_{0}=2.5974>\mathcal {R}_{l}=2.2755$, $\mathcal {R}_{n}=3.8>\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}=0.945$ and $\mathcal {R}_{0}<\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}=5.6527$. As reported in Theorem 4, the treatment failure immune-free equilibrium $E_{1}=(0.908,0,0.0214,0.3707,0)$ is globally asymptotically stable as shown in Fig. 2. The severe competition between the normal and tumor cells led to the extinction of normal cells, where the OVT failed in demolishing the tumor and saving the normal cells. At this stage, the life of cancer’s patient can be at a real risk or he/she may die.

• (c) We consider $\alpha _{2}=0.8$, $\beta _{1}=0.1$, $\beta _{2}=0.03$, $\beta _{3}=0.1$, $\beta _{4}=0.03$, $\eta _{1}=0.008$, $\eta _{2}=0.01$, $\eta _{3}=0.006$ and $\eta _{4}=0.01$. For this combination of parameter values, we obtain $\mathcal {R}_{1}=2.5974>1$ and $\mathcal {R}_{0}=0.7273<\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}=5.9274$. In agreement with Theorem 5, the solutions of system (2) globally converge to the tumor-free equilibrium $E_{2}=(0.385,0.3195,0,0.3846,0)$ as shown in Fig. 3. This case reflects the success of OVT in reducing tumor load to zero before the initiation of CTL immune response. Thus, the parameters and global stability conditions of this point can help design oncolytic viruses with better efficacy.

• (d) We consider $\alpha _{2}=0.9$, $\beta _{1}=0.04$, $\beta _{2}=0.5$, $\beta _{3}=0.1$, $\beta _{4}=0.6$, $\eta _{1}=0.05$, $\eta _{2}=0.008$, $\eta _{3}=0.005$ and $\eta _{4}=0.02$. These values give $\rho =6>1$, $\mathcal {R}_{0}=14.6104>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}=8.369$ and $\mathcal {R}_{1}=0.4156 < \mathcal {R}_{m}= 3.0833$. As a result, the treatment failure equilibrium $E_{3}=(0.3247,0,0.0834,0.4799,0.0943)$ is globally asymptotically stable as shown in Fig. 4. This result supports Theorem 6. This case reflects the oncolytic virotherapy failure which results in normal cells extinction. At this point, the tumor is controlled by CTL immune response, which may limit the replication of oncolytic M1 virus and lead to therapy failure.

• (e) We consider $\alpha _{2}=0.9$, $\beta _{1}=0.16$, $\beta _{2}=0.35$, $\beta _{3}=0.1$, $\beta _{4}=0.1$, $\eta _{1}=0.009$, $\eta _{2}=0.008$, $\eta _{3}=0.008$ and $\eta _{4}=0.01$. Then, we get the values of the threshold parameters as $\rho =1.4933>1$, $\mathcal {R}_{0}/\mathcal {R}_{1}=2.5488>1$, $\mathcal {R}_{n}=10.8<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}=12.0832$, $\mathcal {R}_{0}=10.2273>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}=9.1306$ and $\mathcal {R}_{0}< \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}=19.505$. In this case, the partial success immune-free equilibrium $E_{4}=(0.2493,0.1593,0.0992,0.4341,0)$ is globally asymptotically stable. This result supports Theorem 7 and is shown in Fig. 5. At this point and with no immune response, the viral therapy partially succeeds in saving the normal cells, but it does not have the full ability to demolish the tumor.

• (f) We consider $\alpha _{2}=0.9$, $\beta _{1}=0.19$, $\beta _{2}=0.5$, $\beta _{3}=0.05$, $\beta _{4}=0.8$, $\eta _{1}=0.008$, $\eta _{2}=0.008$, $\eta _{3}=0.005$ and $\eta _{4}=0.03$. With this choice of parameters, we get $\rho =12.8>1$, $\mathcal {R}_{1}=4.9351>\mathcal {R}_{m}=2.9531$ and $\mathcal {R}_{0}=14.6104>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}=8.7588$. In agreement with Theorem 8, the coexistence equilibrium $E_{5}=(0.2027,0.2085,0.0781,0.4339,0.0415)$ is globally asymptotically stable in this case as shown in Fig. 6. The tumor is controlled by immune cells and the OVT loses its ability to control the tumor. Thus, the presence of CTL immune response renders the OVT ineffective.

Fig. 3

The numerical simulations of system (2) when $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. The tumor-free equilibrium $E_{2}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

To see the contribution of the distributed delay to the efficacy of OVT, we increase the value of $a_{2}$ in model (2). Increasing $a_{2}$ means decreasing the survival probability of tumor cells during the delay period. Accordingly, we consider the same parameter values given in (e) except for $a_{2}$, where we take it as $a_{2}=0.8$. The solutions in this case tend to the point with $H=0.2495$, $N=0.3758$, $Y=0$, $V=0.3574$ and $Z=0$. The associated threshold parameters are $\mathcal {R}_{1}=4.0125>1$ and $\mathcal {R}_{0}=6.25<\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}=9.1306$. This means that increasing $a_{2}$ switches the system from the partial success equilibrium $E_{4}$ to the tumor-free equilibrium $E_{2}$. The resulting figure is quite similar to Fig. 3.

Fig. 4

The numerical simulations of system (2) when $\mathcal {R}_{1}\le \mathcal {R}_{m}$. The treatment failure equilibrium $E_{3}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

Fig. 5

The numerical simulations of system (2) when $\rho >1$ and $\mathcal {R}_{0}\le \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. The partial success immune-free equilibrium $E_{4}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

Fig. 6

The numerical simulations of system (2) when $\rho >1$, $\mathcal {R}_{1}>\mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. The coexistence equilibrium $E_{5}$ is globally asymptotically stable. The sub-figures show the spatiotemporal distributions of a nutrient, b normal cells, c tumor cells, d free M1 virus, and e immune response

Fig. 7

The effect of varying $a_{1}$ and $a_{2}$ on the minimum effective dosage $\mu _{0}$ for the tumor-free equilibrium $E_{2}$

Fig. 8

The effect of varying CTL stimulation rate constant $\alpha _{4}$ on the concentration of M1 virus for the coexistence equilibrium $E_{5}$

Fig. 9

The effect of changing the diffusion coefficient on the concentration of normal cells. All parameters are identical to those used in Fig. 6 except for the diffusion coefficient $D_{N}$

In order to examine the effect of the distributed delay on the minimum effective dosage $\mu _{0}$ required to remove the tumor, we first vary $a_{1}$ in Eq. (24) while the conditions $\mathcal {R}_{1}>1$ and $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$ are hold. We fix all other parameters in Eq. (24) to the same values considered in case (e) with $a_{2}=0.8$, where the solutions approach the tumor-free equilibrium $E_{2}$. The values of $\mathcal {R}_{0}$ and $\mathcal {R}_{1}$ are computed from Eq. (25). We see from Fig. 7a that increasing $a_{1}$, which means decreasing the survival probability of normal cells during the delay period, increases the minimum amount of dose required to eliminate the tumor. The next step is to vary $a_{2}$ in Eq. (24) and fix the values of all other parameters. We observe from Fig. 7b that increasing $a_{2}$, which means decreasing the survival probability of tumor cells during the delay period, decreases the minimum effective dosage $\mu _{0}$. Thus, the delay terms can have a strong impact on the minimum amount of OVT needed to eradicate the tumor.

The effect of CTL immune response on the concentration of M1 virus can be seen by varying $\alpha _{4}$ and fixing all other parameters to the same values considered in case (f). The result is shown in Fig. 8. Increasing CTL stimulation rate constant $\alpha _{4}$ in model (2) decreases the concentration of oncolytic M1 virus. This supports the result of case (f) that CTLs reduce the efficiency of OVT.

To see the effect of changing diffusion coefficients on global stability, it is sufficient to consider the impact on normal cells. For this purpose, we change the diffusion coefficient of normal cells in case (f) to $D_{N}=0.002$ and $D_{N}=0.0002$. We note from Fig. 9 that changing the diffusion coefficient does not affect the global stability of the equilibrium, but it only affects the earlier local behavior of solution.

6 Conclusion

Oncolytic virotherapy is a promising cancer treatment depends on attacking cancer cells by viruses. Research efforts have focused on solving the different issues of OVT in order to increase its efficacy. Mathematical models have been used to shorten the path toward the adoption of this treatment. In this paper, we studied a system of five PDEs with distributed delays. The model has six equilibrium points which reflect different possible outcomes of oncolytic virotherapy. These points are

• (a) The competition-free equilibrium $E_{0}$ which always exists and it is globally asymptotically stable if $\mathcal {R}_{1}\le 1$ and $\mathcal {R}_{0}\le \mathcal {R}_{l}$. At this point, the normal and tumor cells populations are extinct and the efficacy of oncolytic virotherapy cannot be measured.

• (b) The treatment failure immune-free equilibrium $E_{1}$ which exists if $\mathcal {R}_{0}>\mathcal {R}_{l}$. It is globally asymptotically stable when the conditions $\rho >1$, $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}\ge \mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}\le \mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$ are satisfied. The extinction of normal cells at this point indicates to the fail of oncolytic virotherapy and to the death of patient.

• (c) The tumor-free equilibrium $E_{2}$ exists when $\mathcal {R}_{1}>1$ and it is globally asymptotically stable if $\mathcal {R}_{0}\le \mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. The extinction of tumor cells at this point reflects the success of oncolytic viral therapy. Hence, reaching this point is the goal of viral therapies.

• (d) The treatment failure equilibrium $E_{3}$ which exists if $\rho >1$ and $\mathcal {R}_{0}>\mathcal {R}_{m}+\dfrac{\mu \xi _{2}}{\alpha _{3}dd_{2}d_{4}(\rho -1)}$. It is globally asymptotically stable if $\mathcal {R}_{1}\le \mathcal {R}_{m}$. This point reflects the fail of oncolytic virotherapy in the presence of CTL immune response.

• (e) The partial success immune-free equilibrium $E_{4}$ exists if $\mathcal {R}_{0}/\mathcal {R}_{1}>1$, $\mathcal {R}_{n}<\mathcal {R}_{1}+\dfrac{\mu \beta _{2}}{\alpha _{3}dd_{2}(\mathcal {R}_{0}/\mathcal {R}_{1}-1)}$ and $\mathcal {R}_{0}>\mathcal {R}_{1}+\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\beta _{3}}{dd_{1}d_{2}d_{3}}$. It is globally asymptotically stable when the conditions $\rho >1$ and $\mathcal {R}_{0}\le \mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$ are met. At this point, the oncolytic virotherapy does not have the full efficacy to remove the tumor cells.

• (f) The coexistence equilibrium $E_{5}$ is defined and globally asymptotically stable if $\rho >1$, $\mathcal {R}_{1}>\mathcal {R}_{m}$ and $\mathcal {R}_{0}>\mathcal {R}_{1} +\dfrac{\kappa \mu \alpha _{1}\beta _{1}G_{1}\alpha _{4}\beta _{4}}{{\alpha _{3} dd_{1}d_{2}d_{4}(\rho -1)}}$. At this point, the immune response controls the tumor and prevents the oncolytic M1 virus from completing its role.

We found that the global stability of the equilibrium points of model (2) is ensured for any diffusion coefficients as long as the conditions given in (a)-(f) are hold. Additionally, some parameters in the distributed delay terms have a critical impact on the efficacy of oncolytic virotherapy. These parameters can change the fate of OVT or change the minimum amount of the therapy required to remove the tumor (Fig. 7). Hence, the values of these parameters should be carefully chosen and controlled. Moreover, the immune response against tumor cells decreases the concentration of oncolytic M1 virus (Fig. 8) and reduces the efficiency of cancer viral therapy. Thus, our results support the studies which suggest using some drugs with the oncolytic virotherapy to inhibit the immune response against tumor cells [5, 8, 13]. This usage of inhibition drugs is equivalent to decreasing the stimulation rate $\alpha _{4}\beta _{4}YZ$ in model (2) or increasing the death rate $(d+\eta _{4})Z$. Comparing with the existing models of OVT, the model in this paper is the first model addresses with a complete mathematical analysis the interaction between oncolytic M1 virotherapy and CTLs in the presence of distributed delay. M1 virus has shown great selectivity and efficacy in treating tumor [41]. Thus, our results can be subjected to further investigation in order to be used in the development of M1 virotherapy. The results can be used to determine the minimum effective dosage required to eliminate the tumor in the presence of CTLs and infinite delays (see Remark 2). Our results can help to estimate the parameters and compute the thresholds needed for full eradication of tumor. Further, the model can be extended to study the effect of combining oncolytic M1 virotherapy with chemotherapy. Applying the multiscale modeling approach discussed in [29] may help to better understand the dynamics of oncolytic virotherapy and its role in tumor elimination. Besides, considering model (2) with cross-diffusion may give a deeper insight into some nonlinear features associated with diffusion [52, 53]. Performing a linear stability analysis and investigating the occurrence of bifurcation is another possibility to understand the role of oncolytic virotherapy in model (2). These points are left as possible future works.