Abstract
In this paper, we study the Turing–Hopf bifurcation in the predator–prey model with cross-diffusion considering the individual behaviour and herd behaviour transition of prey population subject to homogeneous Neumann boundary condition. Firstly, we study the non-negativity and boundedness of solutions corresponding to the temporal model, spatiotemporal model and the existence and priori boundedness of solutions corresponding to the spatiotemporal model without cross-diffusion. Then by analysing the eigenvalues of characteristic equation associated with the linearized system at the positive constant equilibrium point, we investigate the stability and instability of the corresponding spatiotemporal model. Moreover, by calculating and analysing the normal form on the centre manifold associated with the Turing–Hopf bifurcation, we investigate the dynamical classification near the Turing–Hopf bifurcation point in detail. At last, some numerical simulations results are given to support our analytic results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Since the groundbreaking works of Lotka [1] and Volterra [2], the predator–prey model is used to describe the dynamical interaction between two species and has been widely researched by many scholars in the fields of biology and mathematics [3, 4]. It is well known that there are many functional response functions which are used to describe the interactional effect between the prey and predator species. For instance, the Holling I–III types [5, 6], ratio-dependent type [7, 8], Beddington–DeAngelis type [9], the different types with Allee effect [10,11,12] and so on.
Notice the fact that in natural ecosystem, many species may gather together and form herds to search for food resources or to defend the predators, which means that all members of a group do not interact at a time. This behaviour is often called as the herd behaviour. Recently, the authors in [13] have proposed a more realistic predator–prey model to describe this behaviour which can be written as
where u(t) and v(t) stand for the prey and predator densities at time t, respectively. Furthermore, \({\widetilde{\beta }} {\widetilde{\gamma }}\) is the death rate of the predator in the absence of prey, and \({\widetilde{\gamma }}\) is the conversion or consumption rate of prey to predator. The basic idea is that the prey population often gather together in huge herds with the strongest individuals on the border and the weakest will stay in the middle region of the enclosed region. Therefore, the prey which gathers together in the boundary region will be hunted by the predator. That is to say that, the prey population that occupies the outermost positions in the herds will be hunted by the predator.
In recent years, many predator–prey models with herd behaviour without diffusion term have been studied. Saha et al. [14] have studied a predator–prey model with herd behaviour and disease in prey incorporating prey refuge, which is an eco-epidemiological model of an infected predator–prey system. They assume that the susceptible prey shows the herd behaviour. The conditions for which the equilibrium point changes their stability and also the conditions for occurring Hopf bifurcation have been analysed. Manna et al. [15] have studied the dynamics of a predator–prey model with Allee effect and herd behaviour, where both predator and prey show herd behaviour. Here, the authors used the linear functional response function. A steady-state analysis has been performed, and some conditions for Hopf bifurcation are derived. Maiti et al. [16] have studied the dynamical behaviours of a predator–prey system with herd behaviour and the Holling type II functional response function, where both the predator and prey show herd behaviours. The positivity, boundedness and stability of equilibrium point are discussed.
From [17,18,19,20], we see that various reaction–diffusion predator–prey models have been extensively studied in the last decades. By considering the fact that in real natural environment, apart from the natural dispersive force of movement of an individual which is usually referred as the self-diffusion, there exists a mutual interference between individuals and is usually referred as the cross-diffusion, see [21,22,23] for details. Recently, cross-diffusion term has appeared in different fields, such as the population dynamics and ecology [24,25,26,27] and chemical reactions [28,29,30,31]. Furthermore, cross-diffusion is taken into consideration in predator–prey model which is used to measure the situation that the prey keeps away from the predator and conversely. Notice also that in recent years, many researchers have shifted from the study of the formation of stationary spatial patterns induced by Turing instability to the study of the formation of spatiotemporal patterns. For example, by combining with the model (1) and considering the self-diffusion and cross-diffusion, Tang et al. [32] have proposed a predator–prey model with herd behaviour and cross-diffusion, and they study the spatiotemporal dynamics near Turing–Hopf bifurcation point of the proposed model. Faria [33] computed the normal forms on centre manifolds (or other invariant manifolds) for partial functional differential equations (PFDEs) near the positive constant equilibrium point. Especially, when a Hopf bifurcation occurs, Faria [33] used the obtained normal forms to study the qualitative behaviours of solutions on those manifolds. In [34], Song et al. have proposed a rigorous procedure for calculating the normal form for the codimension-two Turing–Hopf bifurcation in the general reaction–diffusion system and to investigate the dynamical classification near the Turing–Hopf bifurcation point in detail.
Notice the fact that if the herd is too small, it may not be possible for the herd to form an appropriate group defence. In other words, if the herd is too small, the boundary of the herd may consist of the total number of the population. Thus, De Assis et al. [35] have proposed a modified predator–prey model with herd behaviour by considering large prey populations which display herd behaviour, and small prey populations which display individual behaviour. From a mathematical point of view, the interaction term \(a_{1}u v\) can be used to describe a small number of prey populations, and \(a_{2} \sqrt{u} v\) can be used to describe a large prey populations. Thus, the response function of their model is described by a piecewise function
where \(h_{1}\) represents a critical threshold of group size for effective defence. By considering that in real life, a smooth transition between ineffective and effective group defence is expected, at least for some species, and the function \(g^{\prime }(u)\) is discontinuous, the authors in [35] have proposed the following response function
where a and \(h_{2}\) are parameters for which the biological interpretation will be explained after some calculations. When \(u \rightarrow 0\) and \(u \rightarrow \infty \), the authors in [35] have created a smooth transition function f(u) that approximates g(u) by letting g(u)/f(u) goes to one. Through simple calculations, the authors in [35] obtained that \(a=a_{2}\) and \(h_{2}=\left( a_{2}/a_{1}\right) ^{2}\). Furthermore, it follows that \(h_{1}=\left( a_{2}/a_{1}\right) ^{2}\) from the continuity of g(u), i.e. the critical threshold \(h_{1}\) of group size for effective defence and the threshold \(h_{2}\) is consistent. Thus, f(u) can be seen as an approximation of g(u) with a smooth transition for the individual behaviour \(a_{1} u\) and the group defence \(a_{2} \sqrt{u}\). For convenience, the authors in [35] let \(h_{1}=h_{2}={\widetilde{h}}\). Then, the functional response function of their proposed model can be written as
Here, by setting \(a_{1}=1\) and \(a_{2}=\sqrt{20}\), then \(h_{1}=h_{2}={\widetilde{h}}=20\), we plot the graphs of f(u) and g(u) in Fig. 1. The coordinate of point P is (20, 20).
Thus, based on the above facts, the authors in [35] have proposed a modified predator–prey model with herd behaviour described by the following ordinary differential equations
where r is the intrinsic growth rates of the prey, K is the carrying capacity of the prey, a is the maximum value of prey consumed by per predator per unit time, \({\widetilde{h}}\) is a threshold for the transition between herd grouping and solitary behaviour, m is the death rate of the predator in the absence of prey, and e is the conversion or consumption rate of prey to predator.
To the best of our knowledge, there are no results on spatiotemporal dynamics near Turing–Hopf bifurcation point of the model (2). Therefore, by assuming that the prey and predator populations are in an isolate patch and neglecting the impact of migration, including immigration and emigration, and introducing the spatial diffusion into the model (2), we consider the following modified predator–prey model with herd behaviour and cross-diffusion subject to homogeneous Neumann boundary condition for \(x \in \varOmega :=(0, \ell \pi )\) with \(\ell \in \mathbb {R}^{+}\). That is
where u(x, t) and v(x, t) describe the prey and predator densities at the spatial location x and at time t, respectively, the nonnegative constants \(d_{11}\) and \(d_{22}\) are the self-diffusion coefficients of the prey and the predator, respectively, and the nonnegative constants \(d_{12}, d_{21}\) are the cross-diffusion coefficients, which describe the respective population fluxes of preys and predators resulting from the presence of the other species, respectively, \(\varDelta u=\partial ^{2}u/\partial x^{2}\), \(\varDelta v=\partial ^{2}v/\partial x^{2}\), and \({\mathbf {n}}\) is the outward unit normal vector at the smooth boundary \(\partial \varOmega \). Moreover, \(\phi (x)\) and \(\psi (x)\) are the initial functions. Furthermore, it is necessary to assume that \(d_{11} d_{22}>d_{12} d_{21}\), which indicates that the flux of the respective densities in the spatial domain depends more strongly on their own density than on the other [36]. Especially, we point out that the condition \(d_{11} d_{22}>d_{12} d_{21}\) can also be obtained in Sect. 3 which is one of the necessary conditions for the occurrence of Turing instability for model (4).
In this paper, by calculating the normal form for the codimension-two Turing–Hopf bifurcation in the model (4), we investigate the dynamical classification near the Turing–Hopf bifurcation point. It is necessary to point out the fact that, although we use the method of computing normal form which presented in [34], since we choose \(d_{11}\) as the bifurcation parameter and the existence of cross-diffusion, the procedure of computing \(B_{11}\) and \(B_{13}\) needs to be deduced again, see “Appendix” for details.
The remaining part of this article is organized as follows. In Sect. 2, we show the non-negativity and boundedness of solutions corresponding to the temporal model and the spatiotemporal model, respectively. Furthermore, the existence and priori boundedness of solutions corresponding to the spatiotemporal model without cross-diffusion are also researched. Section 3 is devoted to the stability analysis of the proposed spatiotemporal model, including the stability analysis for the case without self-diffusion and cross-diffusion and the stability analysis for the case with self-diffusion and cross-diffusion. Furthermore, we plot the bifurcation diagram for model (4) in \(d_{11}-\delta \) plane which can be found in Sect. 3. In Sect. 4, we compute the normal form on the centre manifold for Turing–Hopf bifurcation corresponding to the model (4) by using the method in [34]. Some numerical simulations are given to support the theoretical results in Sect. 5. Finally, we conclude this paper in Sect. 6.
2 Non-negativity and boundedness of solutions corresponding to the temporal model
With a non-dimensionalized change of variables
and let
then model (3) becomes the following non-dimensiona lized model
where \(h={\widetilde{h}}/K\) represents the critical threshold of group size for effective defence in non-dimensional scaling. Since we assumed that there is an observable group defence effect, it is reasonable to take \(0<{\widetilde{h}}<K\), and hence \(0<h<1\).
The temporal model associated with the model (4) is
For the temporal model (5), we have the following results.
Theorem 1
Suppose that \(\gamma>0,~\beta >0,~0<h<1\) and consider the system given by (5) and its trajectories u(t), v(t); if the initial value \(u(0) \ge 0,~v(0) \ge 0\), then the solutions u(t) and v(t) are always non-negative. Furthermore, for any solution (u(t), v(t)) of system (5), we have
Proof
In fact, the system (5) is composed of the following three subsystems
and
Since it is easy to verify that the solution of (7) will approach the origin (0, 0) along the v-axis as \(t \rightarrow \infty \) and the solution of (refh8) will tend to (1, 0) along the u-axis as \(t \rightarrow \infty \), we only need to consider the solutions of (6). Assume \(X(t)=(u(t), v(t))\) is a solution of system (6). If it does not remain in the first quadrant, then the solution either hits the u-axis or the v-axis in finite time. Thus, by combining with the analysis results of the subsystems (7) and (refh8), we can obtain that any solution (u(t), v(t)) of system (6) with non-negative initial value (u(0), v(0)) will remain positive for all \(t>0\), or will approach either the original or (1, 0) along the axes.
Next, the boundedness of solutions is confirmed. Let \({\widetilde{w}}(t)=u(t)+v(t)\), then by adding
to
we have
resulting in
Furthermore, notice that \({\widetilde{w}}(t)=u(t)+v(t)\), then we have
This concludes the proof. \(\square \)
2.1 Non-negativity and boundedness of solutions corresponding to the spatiotemporal model
Theorem 2
Suppose that \(\gamma>0,~\beta >0,~0<h<1\) and \(\varOmega \subset \mathbb {R}\) is a bounded domain with smooth boundary. Then for any solution (u(x, t), v(x, t)) of model (4), we have
where \(|\varOmega |\) is the length of the bounded domain \(\varOmega \).
Proof
Denote
then by integrating on both sides of each equation on the region \(\varOmega \) in system (4), we have
Let \(M(t)=M_{1}(t)+M_{2}(t)\), then by combining with Eq. (9) and noticing the homogeneous Neumann boundary defined in system (4), we can obtain
from which we obtain that
Furthermore, notice that \(M(t)=M_{1}(t)+M_{2}(t)\), then we have
This proof is completed. \(\square \)
2.2 The existence and priori boundedness of solutions corresponding to the spatiotemporal model without cross-diffusion
In this section, we give out a sufficient condition for the existence of a positive solution of system (4) without cross-diffusion. Meanwhile, we derive a priori boundedness of the solution. When \(d_{12}=d_{21}=0\), system (4) becomes
Theorem 3
Suppose that \(\gamma>0,~\beta >0,~0<h<1\) and \(\varOmega \subset \mathbb {R}\) is a bounded domain with smooth boundary. Then we have the following results:
-
(i)
For \(\phi (x) \ge 0,~\psi (x) \ge 0\) and \(\phi (x)\not \equiv 0, \psi (x) \not \equiv 0\), system (10) has a unique solution \((u(x, t), v(x, t))\) satisfying \(0<u(x, t) \le u^{*}(t),~0<v(x, t) \le v^{*}(t)\) for \(t>0\) and \(x \in \varOmega \), where \(\left( u^{*}(t), v^{*}(t)\right) \) is the unique solution of
$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d} u}{\mathrm {d} t}=\gamma u(1-u), \qquad \qquad t> 0, \\&\frac{\mathrm {d} v}{\mathrm {d} t}=-v+\frac{\beta u v}{\sqrt{u+h}}, \qquad \quad t > 0, \\&u(0)=\phi ^{*}=\sup _{x \in {\overline{\varOmega }}} \phi (x),~v(0)=\psi ^{*}=\sup _{x \in {\overline{\varOmega }}} \psi (x), \end{aligned}\right. \end{aligned}$$and \({\overline{\varOmega }}\) represents the closure of \(\varOmega \);
-
(ii)
For any solution (u(x, t), v(x, t)) of system (10), we have
$$\begin{aligned} \lim _{t \rightarrow \infty } \mathrm{{sup}}~u(x, t)&\le 1, \quad \lim _{t \rightarrow \infty } \mathrm{{sup}}~\int _{\varOmega } v(x, t) \mathrm {d} x\\&\le (\gamma +1) |\varOmega |. \end{aligned}$$
Proof
Denote
then we have \(f_{v} \le 0\) and \(g_{u} \ge 0\) for \((u, v) \in \mathbb {R}_{+}^{2}=\{(u, v) \mid u \ge 0, v \ge 0\}\). Thus, the system (10) is a mixed quasi-monotone system.
Furthermore, if we assume that \(\left( u_{1}(x, t), v_{1}(x, t)\right) =(0,0)\) and \(\left( u_{2}(x, t), v_{2}(x, t)\right) =\left( u^{*}(t), v^{*}(t)\right) \), then we can obtain
and \(0 \le \phi (x) \le \phi ^{*}\), \(0 \le \psi (x) \le \psi ^{*}\), so \(\left( u_{1}(x, t), v_{1}(x, t)\right) \) and \(\left( u_{2}(x, t), v_{2}(x, t)\right) \) are the lower and upper solutions of system (10), respectively.
According to Theorem 3.3 in Section 8.3 of Chapter 8 in [37], we know that (10) has a unique globally defined solution (u(x, t), v(x, t)) which satisfies
The strong maximum principle implies that \(u(x, t)>0, v(x, t)>0\) when \(t>0\), for \(x \in \varOmega \). This completes the proof of conclusion (i).
From the above discussion, we can obtain that \(0<u(x, t) \le u^{*}(t),~0<v(x, t) \le v^{*}(t)\) for all \(t>0\), and \(u^{*}(t)\) is the unique solution of
One can see that \(u^{*}(t) \rightarrow 1\) as \(t \rightarrow \infty \). Thus, for any \(\varepsilon >0\), there exists \(t_{0}>0\) such that \(u(x, t) \le 1+\varepsilon \) for \(t>t_{0}\) and \(x \in {\overline{\varOmega }}\), which implies that \(\underset{t_{0} \rightarrow \infty }{\lim }\sup _{t>t_{0}}~u(x, t) \le 1\).
Furthermore, if let
then
By using the homogeneous Neumann boundary condition, we can obtain
From \(\lim _{t_{0} \rightarrow \infty } \sup _{t>t_{0}}~u(x, t) \le 1\), we can obtain that \(\lim _{t_{0} \rightarrow \infty }\sup _{t>t_{0}}~N_{1}(t) \le |\varOmega |\). Thus for small \(\varepsilon >0\), there exists \(t_{1} \ge 0\) such that
It is well known that the solution N(t) of
satisfies
In terms of comparison principle and using (11) we obtain that, for \(t_{2}>t_{1}\)
which implies that
This completes the proof of conclusion (ii). \(\square \)
3 Stability analysis of the corresponding spatiotemporal model
The system (4) has two boundary equilibrium points (0, 0) and (1, 0). Moreover, when \(0<\delta <(1/\sqrt{h+1})\), the system (4) has a unique positive constant equilibrium point \(E_{*}\left( u_{*}, v_{*}\right) \) with
where \(\delta =1/\beta \) with \(\beta >0\), and \(0<h<1\), \(\gamma >0\).
Defining a real-valued Hilbert space
with the inner product defined by
for \(U_{1}=\left( u_{1}, v_{1}\right) ^{T} \in {\mathscr {X}}\) and \(U_{2}=\left( u_{2}, v_{2}\right) ^{T} \in {\mathscr {X}}\). The linearization of system (4) at positive constant equilibrium point \(E_{*}\left( u_{*}, v_{*}\right) \) is
with
It is well known that the eigenvalue problem
has eigenvalues \({\widetilde{\lambda }}_{k}=-k^{2}/\ell ^{2}\) with corresponding normalized eigenfunctions
where \(k \in \mathbb {N}_{0}=\mathbb {N}\cup \left\{ 0\right\} \) is often called wave number, and \(\mathbb {N}_{0}=\mathbb {N}\cup \left\{ 0\right\} \) is the set of all non-negative integers, \(\mathbb {N}=\left\{ 1,2,...\right\} \) represents the set of all positive integers. Thus, the eigenfunctions of \(d \varDelta \) on \({\mathscr {X}}\) corresponding to its eigenvalues have the form
where \(a_{k}, b_{k} \in \mathbb {R}\) and \(\gamma _{k}(x)\) is defined by Eq. (14).
Let
be an eigenfunction of \(\mathrm {d} \varDelta +A\) corresponding to an eigenvalue \(\lambda \), that is
Then, we have
where
which follows that the eigenvalues of \(\mathrm {d} \varDelta +A\) are given by the eigenvalues of \({\mathcal {L}}_{k}\) with \(k \in \mathbb {N}_{0}=\mathbb {N}\cup \left\{ 0\right\} \). Notice that the solutions of Eq. (12) can be obtained by using the eigenvalues and eigenvectors of the matrix \(d\varDelta +A\). Then by the Fourier expansion
which can be seen as a nontrivial solutions of Eq. (12), where
and by substituting (15) into (12), we can obtain the following sequence of characteristic equations \(\varDelta _{k}\), i.e.
where
By combining with Eqs. (16) and (17), and noticing that the necessary condition for the occurrence of Turing instability is \(d_{11} d_{22}-d_{12} d_{21}>0\) and
then in the \(d_{11}-\delta \) plane, we can define a curve \({\mathbf {L}}\) by
According to [32], we know that if there exist a nonnegative integer \(k_{1}\) and a positive integer \(k_{2} \ne k_{1}\) such that \(\varDelta _{k_{1}}=0\) has a pair of purely imaginary roots and \(\varDelta _{k_{2}}=0\) has a simple zero root, and no other roots of (16) has a zero real part, and the corresponding transversality conditions hold, then we call the bifurcation in this case as a Turing–Hopf bifurcation.
3.1 Stability analysis for the case without self-diffusion and cross-diffusion
In the case of without self-diffusion or cross-diffusion \(\left( d_{11}=d_{12}=d_{21}=d_{22}=0\right) \), the original system (4) becomes the following ordinary differential equation
Clearly, the original system (4) and (19) have the same positive constant equilibrium point \(E_{*}(u_{*}, v_{*})\). By a simple linear analysis, we can obtain the following result.
Theorem 4
For the positive constant equilibrium point \(E_{*}(u_{*},v_{*})\) of system (19) with \(\gamma>0,~\beta >0,~0<h<1\), we have the following results on its stability.
-
(i)
When \(1/2<h<1\), the positive constant equilibrium point \(E_{*}\left( u_{*}, v_{*}\right) \) is always asymptotically stable;
-
(ii)
When \(0<h \le 1/2\), the positive constant equilibrium point \(E_{*}\left( u_{*}, v_{*}\right) \) is asymptotically stable for
$$\begin{aligned} \max \left\{ 0, \delta ^{*}\right\}<\delta <\frac{1}{\sqrt{h+1}}, \quad \delta ^{*}=\frac{1-2 h}{\sqrt{3(1+h)}}, \end{aligned}$$and unstable for \(0<\delta <\delta ^{*}\).
Moreover, \(\varDelta _{0}=0\) has a pair of purely imaginary roots \(\pm i \sqrt{D_{0}}\) iff \(\delta =\delta ^{*}\), which implies that system (19) undergoes a Hopf bifurcation at \(\delta =\delta ^{*}\) near the positive constant equilibrium point \(E_{*}\left( u_{*}, v_{*}\right) \), and the Hopf bifurcation curve is defined by
Proof
By combining with Eqs. (16), (17) and \(0<\delta <1/\sqrt{h+1}\), we have
Indeed, if \(0<\delta <1/\sqrt{h+1}\), follows that \(D_{0}=a_{21}>0\), then for the stability analysis of \(E_{*}(u_{*}, v_{*})\), it is sufficient to study the sign of
Let \(P(\delta ):=-3 u_{*}+1-2h\), then by combining with
we can obtain
Notice that for \(1/2<h<1\), \(P(\delta )\) is always negative. For \(0 < h \le 1/2\), notice that \(P(\delta )\) is decreasing with respect to \(\delta \), so the sign of \(P(\delta )\) is determined by its root \(\delta ^{*}\). Thus, \(T_{0}=a_{11}\) is positive for \(\delta <\delta ^{*}\) and negative conversely. Notice also that when \(\delta =\delta ^{*}\), we can obtain \(T_{0}=a_{11}=0\). Thus, when \(\delta =\delta ^{*}\), by combining with \(\lambda ^{2}-T_{0} \lambda +D_{0}=0\), we have \(\lambda =\pm i \sqrt{D_{0}}\) iff \(\delta =\delta ^{*}\).
This completes the proof. \(\square \)
3.2 Stability analysis for the case with self-diffusion and cross-diffusion
In this section, we investigate the effect of cross-diffusion on the positive constant equilibrium point \(E_{*}(u_{*}, v_{*})\) of the original system (4). We have the following Theorem 5.
Theorem 5
Assume that \(\gamma>0,~\beta >0,~0<h<1\), \(\mathbf{{H_{0}}}\) is defined by \(\delta =\delta ^{*}=(1-2h)/\sqrt{3(1+h)}\) and \(\mathbf{{L_{k}}}\) is defined by
Then
\((\mathrm {I})\) if \(0<d_{21}<(\ell ^{2} \gamma (4h+1))/3\), then original system (4) is always stable over the Hopf bifurcation curve \(\mathbf{{H_{0}}}\), that is, system (4) doesn’t undergo Turing–Hopf bifurcation;
\((\mathrm {II})\) if \((\ell ^{2} \gamma (4h+1))/3<d_{21}<(d_{11}d_{22})/d_{12}\), then
-
(i)
The Hopf bifurcation curve \(\mathbf{{{H}_{0}}}\) intersects with the Turing bifurcation curve \(\mathbf{{L_{k}}}\), and a codimension-2 Turing–Hopf bifurcation occurs at the intersect point \(\left( d_{11}^{*}, \delta ^{*}\right) \), where
$$\begin{aligned}\begin{aligned}&d_{11}^{*}=\frac{d_{12}d_{21}\frac{k_{*}^{4}}{\ell ^{4}}+(d_{21}-d_{12}\frac{\gamma (4h+1)}{3})\frac{k_{*}^{2}}{\ell ^{2}}-\frac{\gamma (4h+1)}{3}}{d_{22}\frac{k_{*}^{4}}{\ell ^{4}}}, \\&\delta ^{*}=\frac{1-2h}{\sqrt{3(1+h)}}; \end{aligned}\end{aligned}$$ -
(ii)
For \(\left( d_{11}, \delta \right) =\left( d_{11}^{*}, \delta ^{*}\right) \), the equation \(\varDelta _{0}=0\) has a pair of purely imaginary roots \(\pm i \omega _{c}\) and \(\varDelta _{k_{*}}=0\) has a simple zero root, and for the system (4), there are no other roots with zero real parts, where
$$\begin{aligned} \omega _{c}=\sqrt{a_{21}(\delta ^{*})}=\sqrt{\frac{\gamma (4 h+1)}{3}}. \end{aligned}$$
Proof
The Turing bifurcation curve \(\mathbf {L_{k}}\) defined by (21) is followed from \(D_{k}=0\), i.e.
By combining with Eqs. (16) and (17), we can see that \(T_{k}<0\) provided that \(a_{11}<0\), and that \(D_{k}>0\) is equivalent to
Notice that \(a_{11}(\delta ^{*})=0\), \(a_{21}(\delta ^{*})=\gamma (4h+1)/3\), and when
i.e. \(0<d_{21}<(\ell ^{2} \gamma (4h+1))/3\), the Turing bifurcation curve \(\mathbf{{L_{k}}}\) doesn’t interact with the Hopf bifurcation curve \(\mathbf{{H_{0}}}\). Here, \(a_{11}(\delta ^{*})\), \(a_{21}(\delta ^{*})\) indicating \(a_{11}\) and \(a_{21}\) are dependent on \(\delta ^{*}\), respectively. That is, system (4) is always asymptotically stable over the Hopf bifurcation curve \(\mathbf{{H_{0}}}\). Thus, the conclusion \((\mathrm {I})\) is confirmed.
When \(d_{11} d_{22}-d_{12} d_{21}>0\) and
i.e. \((\ell ^{2} \gamma (4h+1))/3<d_{21}<(d_{11}d_{22})/d_{12}\), the Turing bifurcation curve \(\mathbf{{L_{k}}}\) interact with the Hopf bifurcation curve \(\mathbf{{H_{0}}}\), then by substituting \(\delta =\delta ^{*}\) into \(D_{k}=0\) and solving \(D_{k}=0\) for \(d_{11}\), we have that
where \(k^{*}\) is defined by Eq. (22). Furthermore, the symbol \([~\cdot ~]\) in Eq. (22) stands for the integer part function.
Let
we can obtain that
Therefore, if \((d_{12}\gamma (4h+1))/3-d_{21}<0\), we have \(f^{\prime }(x) \ge 0\) for \(x \le x^{*}\), and \(f^{\prime }(x)<0\) for \(x>x^{*}\), where
By setting
then there exists a \(k_{*}>k^{*}\) such that \(d_{11}^{*}=d_{11}\left( k_{*}\right) =\max _{k>k^{*}} d_{11}(k)\).
Furthermore, if \((d_{12}\gamma (4h+1)/3)-d_{21}>0\), we have \(f^{\prime }(x) \le 0\) for \(x \le x^{*}\), and \(f^{\prime }(x)>0\) for \(x>x^{*}\). By setting
then there exists a \(k_{*}>k^{*}\) such that \(d_{11}^{*}=d_{11}\left( k_{*}\right) =\min _{k>k^{*}} d_{11}(k)\).
Thus, the Hopf bifurcation curve \({\mathbf {H_{0}}}\) intersects with the Turing bifurcation curve \({\mathbf {L_{k}}}\) at
which is called as the Turing–Hopf bifurcation point.
Next, we continue to verify the transversality condition. Taking \(d_{11}\) as a bifurcation parameter and letting \(\lambda (d_{11})\) be the root of Eq. (16) near \(d_{11}=d^{*}_{11}\) satisfying \(\lambda \left( d^{*}_{11}\right) =0\). Differentiating the two sides of the characteristic equation (16) with respect to \(d_{11}\), we obtain
By combining with Eq. (17), we can obtain
Moreover, when \(\delta >\delta ^{*}\), from the discussion in Sect. 3.1, we know that \(a_{11}<0\). Thus, when \(\delta >\delta ^{*}\), we can obtain that
By combining with Eqs. (24) and (25), we have
where the symbol \(\text {Re}(\vartheta )\) represents the real part of \(\vartheta \). This, together with the fact that
we have
where the symbol sign represents the sign function.
Moreover, if taking \(\delta \) as a bifurcation parameter, letting \(\lambda (\delta )=\alpha (\delta )\pm i \beta (\delta )\) be the pair of roots of Eq. (16) near \(\delta =\delta ^{*}\) satisfying \(\alpha \left( \delta ^{*}\right) =0\) and \(\beta \left( \delta ^{*}\right) =\omega _{c}\), we have the following transversality condition. Differentiating the two sides of Eq. (16) with respect to \(\delta \), we obtain
By combining with Eqs. (17) and (26), we have
Furthermore, by Eqs. (17) and (27) as well as \(T_{0}(\delta ^{*})=a_{11}(\delta ^{*})=0\) and
we have
This, together with the fact that
we have
Thus, the proof of conclusion \((\mathrm {II})\) is completed. \(\square \)
3.3 Bifurcation diagram for system (4) in \(d_{11}-\delta \) plane
Taking \(\ell =1, \gamma =3, h=0.1, d_{12}=1, d_{21}=10, d_{22}=15\), and by combining with Eqs. (13), (18), (20), (21), (22) and (23), we can conclude that \(k^{*}=0\), \(k_{*}=1\) and
Numerical calculation confirms that when \(k_{*}=1\), the Turing bifurcation curves \(\mathbf {L_{1}}\) are tangent to the curve \({\mathbf {L}}\) at \(P_{1}(-0.0131,0.8717)\) and \(P_{2}(0.5583,0.7399)\), see Fig. 2a for details. Moreover, the Hopf bifurcation curve \({\mathbf {H_{0}}}\) intersects with Turing bifurcation curve \({\mathbf {L_{1}}}\) at the point \(\left( d_{11}^{*},\delta ^{*}\right) =\left( 1.1467, 0.4404\right) \) and system (4) undergoes Turing–Hopf bifurcation near the positive constant equilibrium point \(E_{*}\left( 0.2667, 0.5867\right) \), see Fig. 2b for details.
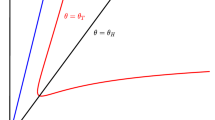
Bifurcation diagram for system (4) in \(d_{11}-\delta \) plane with \(k_{*}=1\). \(\mathbf {H_{0}}\) denotes the Hopf bifurcation curve, \(\mathbf {L_{1}}\) denotes the Turing bifurcation curve and \({\mathbf {L}}\) is the curve defined by (18). The region \(R_{1}\) is the stability region of the positive constant equilibrium point \(E_{*}\), \(R_{2}\) represents the region of Turing instability, and \(R_{3}\) and \(R_{4}\) are the instability region of the positive constant equilibrium point \(E_{*}\)
4 Normal form for Turing–Hopf bifurcation in the reaction–diffusion system (4)
Notice that the method of computing normal form of general reaction–diffusion system which presented in [34] can be used to obtain the third-order truncated normal form of system (4) by a slight modification. Denote the Turing–Hopf bifurcation point as \(\left( d_{11}^{*}, \delta ^{*}\right) \). Introduce the perturbation parameters \(\mu _{1}\) and \(\mu _{2}\) by setting \(d_{11}=d_{11}^{*}+\mu _{1}\) and \(\delta =\delta ^{*}+\mu _{2}\) such that \(\left( \mu _{1}, \mu _{2}\right) =(0,0)\) is the Turing–Hopf bifurcation point in the perturbation plane of \(\mu _{1}\) and \(\mu _{2}\). Then the system (4) becomes
The positive constant equilibrium point of system (28) becomes
with \(0<\delta ^{*}+\mu _{2}<1/\sqrt{h+1}\). Making the change of variables by the translation \({\overline{u}}=u-u_{*}\) and \({\overline{v}}=v-v_{*}\), and dropping the bars, then the system (28) is transformed into
For the system (29), when \(\mu _{1}=\mu _{2}=0\), \(\varDelta _{0}(\lambda )=0\) has a pair of purely imaginary roots \(\pm i \omega _{c}\), \(\varDelta _{k_{*}}(\lambda )=0\) has a simple zero root \(\lambda =0\) and a negative real root \(\lambda =-T_{k_{*}}\), and if \(k \ne 0, k_{*}\), all roots of \(\varDelta _{k}(\lambda )=0\) have negative real parts.
By the real-valued Hilbert space \({\mathscr {X}}\) which is defined in Sect. 3, the system (29) can be written as the following abstract ordinary differential equation (ODE), that is
where \(U=(u, v)^{T},~\mu =\left( \mu _{1}, \mu _{2}\right) ,~{\widetilde{F}}(U, \mu )=L(\mu )(U)-L_{0}(U)+{\widetilde{d}}\varDelta u+F(U, \mu )\),
Here, \(a_{11}(\delta ^{*}+\mu _{2})\), \(a_{21}(\delta ^{*}+\mu _{2})\) indicating \(a_{11}\) and \(a_{21}\) are dependent on \(\delta ^{*}+\mu _{2}\), respectively. Moreover, we have
with
For the formal Taylor expansions of L
and by Eq. (31), we can obtain
where
Let
where \(I_{2}\) is a \(2 \times 2\) identity matrix, then by a straightforward calculation, we can obtain that \(\xi _{0} \in \mathbb {C}^{2}\) and \(\xi _{k_{*}} \in \mathbb {R}^{2}\) are the eigenvectors associated with the eigenvalues \(i \omega _{c}\) and 0, respectively, and \(\eta _{0} \in \mathbb {C}^{2}\) and \(\eta _{k_{*}} \in \mathbb {R}^{2}\) are the corresponding adjoint eigenvectors, where
such that
where
Here, \(\text {col}(.)\) represents the column vector. Furthermore, for vectors \({\widehat{\varphi }}, {\widehat{\psi }} \in \mathbb {R}^{2}\), we define their scalar product as \(\left\langle {\widehat{\psi }}^{T}, {\widehat{\varphi }}\right\rangle ={\widehat{\psi }}^{T} {\widehat{\varphi }}\).
Notice that the phase space \({\mathscr {X}}\) can be decomposed as
where \({\text {dim}} {\mathcal {P}}=3\) and \(\pi : {\mathscr {X}} \mapsto {\mathcal {P}}\) is the projection defined by
According to (33), \(U \in {\mathscr {X}}\) can be decomposed as
where \(w=\text {col}\left( w_{1}, w_{2}\right) \) and
By letting
Equation (34) can be rewritten as
For the simplicity of notation, we denote
and if let \({\mathscr {L}}U:=d \varDelta U+L_{0}(U)\) and denote by \({\mathscr {L}}_{1}\) the restriction of \({\mathscr {L}}\) to \({\mathcal {Q}}\), then system (30) is equivalent to a system of abstract ordinary differential equations (ODEs) in \(\mathbb {R}^{3} \times {\mathcal {Q}}\), with finite- and infinite-dimensional variables also separated in the linear term. That is,
where
and
According to [34], by a recursive transformation, the authors obtain that the normal form for Turing–Hopf bifurcation in system (30) reads as
The normal form (35) can be written in real coordinates \({\widetilde{v}}\) through the change of variables \(z_{1}={\widetilde{v}}_{1}-i {\widetilde{v}}_{2}, z_{2}={\widetilde{v}}_{1}+i {\widetilde{v}}_{2}, z_{3}={\widetilde{v}}_{3}\), and then changing to cylindrical coordinates by \({\widetilde{v}}_{1}=\rho \cos \varTheta , {\widetilde{v}}_{2}=\rho \sin \varTheta , {\widetilde{v}}_{3}=\varsigma \), we obtain, truncating at third-order terms and removing the azimuthal term
where
According to Section 8.6 in [38], we know that the third-order truncated normal form (36) is exactly the same to the third-order truncated normal form of the four-dimensional smooth system depending on two parameters with Hopf–Hopf bifurcation. For the so-called simple case [38], i.e. \(\kappa _{11} \kappa _{22}>0\), the dynamics of system (4) near the bifurcation value is topologically equivalent to that of normal form (36). However, for the “difficult” cases, the original system (4) is never topologically equivalent to the truncated normal form (36). In general, for the “difficult” cases, in order to obtain the whole dynamics of the original (4), five-order or higher-order normal form needs to be calculated.
With the help of MATLAB software, the explicit values of the coefficients \(B_{11}\), \(B_{21}\), \(B_{13}\), \(B_{23}\), \(B_{210}\), \(B_{102}\), \(B_{111}\) and \(B_{003}\) can be obtained for the fixed parameters. Notice that the formulas which are used to calculate the above coefficients are rather complicated and we leave them in “Appendix”.
5 Numerical simulations
In this section, the third-order truncated normal form is obtained under the given parameters and some numerical simulations are made to support the results of our theoretical analysis. More precisely, some numerical simulations about the temporal patterns, spatial patterns and spatiotemporal patterns are given.
Let \(\varOmega =(0, \pi )\) and \(\gamma =3, h=0.1, d_{12}=1, d_{21}=10, d_{22}=15\), then the system (4) at least undergoes Turing–Hopf bifurcation at the point (1.1467, 0.4404). By using the above-given parameters, the normal form truncated to the third-order terms is
where \(\mu _{1}\) and \(\mu _{2}\) are perturbation parameters for the Turing–Hopf bifurcation point (1.1467, 0.4404). Notice that \(\rho >0\) and \(\varsigma \) is arbitrary real number. System (37) has a zero equilibrium point \(A_{0}(0,0)\) for any \(\mu _{1}, \mu _{2} \in \mathbb {R}\), three boundary equilibrium points
for \(0.9290\mu _{1}-2.5716\mu _{2}>0\), and two interior equilibrium points
for \(1.3134\mu _{1}+0.1605\mu _{2}>0\) and \(-0.9663\mu _{1}-2.5867\mu _{2}>0\).
Define the critical bifurcation lines are as follows:
These four lines divide the \(\mu _{1}-\mu _{2}\) parameter plane into six regions marked as \(D_{j},~j=1,2, \ldots , 6\).
Based on Section 7.5 in [39], by the different signs of \(d, b, c, d-b c\) in Table 1, the system (36) has twelve distinct types of unfoldings, which are twelve essentially distinct types of phase portraits and bifurcation diagrams. More precisely, for the system (37), we have \(d=+1,~b=1.3593>0,~c=1.3860>0,~d-bc=-0.8840<0\). That is, the unfolding of the planner system (37) corresponding to the Case \(\mathrm {I}b\) in Table 1. Thus, the phase portraits and bifurcation diagrams corresponding to Case \(\mathrm {I}b\) can be given out, see Fig. 7.5.2 in Section 7.5 in [39] for details.
The dynamics of the original reaction–diffusion system (4) can be determined by the third-order truncated normal form (37) near the neighbourhood of the Turing–Hopf bifurcation point. According to [34], the corresponding relationships between the equilibrium points of plane system (37) and the solutions of original system (4) are shown in Table 2.
Bifurcation diagram of the system (4) near the Turing–Hopf bifurcation point (1.1467, 0.4404)
Furthermore, by the defined critical bifurcation lines, the bifurcation diagram in the \(\mu _{1}-\mu _{2}\) parameter plane is shown in Fig. 3. The linearized equation of the system (37) at each equilibrium point is
where
with \(i=1,2,3,4\) and
More precisely, the coefficient matrices of linearized equation (38) at equilibrium points \(A_{0}, A_{1}, A_{2}^{\pm }, A_{3}^{\pm }\) are
respectively, where
By combining with the bifurcation diagram in Fig. 3 and the linear stability theory, we can analyse the sign of the eigenvalues corresponding to the characteristic equations; thus, the stability and instability of each equilibrium point in regions \(D_{1}\)-\(D_{6}\) can be obtained.
In region \(D_{1}\), the third-order truncated normal form (37) has only one equilibrium point \(A_{0}\) and it is asymptotically stable. This implies that the positive constant steady state \(E_{*}\) of the original system (4) is asymptotically stable, as shown in Fig. 4 for \(\left( \mu _{1}, \mu _{2}\right) =(0.60, 0.25)\) and the initial value \(u(x,0)=0.5615-0.25 \cos (x),~v(x,0)=0.7386+0.25 \cos x\).
In region \(D_{2}\), the third-order truncated normal form (37) has two equilibrium points: \(A_{0}\) and \(A_{1}\). The equilibrium point \(A_{0}\) is unstable and the equilibrium point \(A_{1}\) is asymptotically stable. This means that the system (4) has a stable spatially homogeneous periodic solution. For \(\left( \mu _{1}, \mu _{2}\right) =(-0.28, -0.1)\) and initial value \(u(x, 0)=0.1802+0.01 \cos (x), v(x, 0)=0.4431+0.01 \cos x\), Fig. 5 illustrates this result.
When \(\left( \mu _{1}, \mu _{2}\right) =(-0.28, -0.1)\) lies in region \(D_{2}\) and let \(d_{11}=1.1467, \delta =0.4404\), the positive constant steady state \(E_{*}(0.1802, 0.4431)\) is unstable and there is a stable spatially homogeneous periodic solution. The initial value is \(u(x, 0)=0.1802+0.01 \cos (x), v(x, 0)=0.4431+0.01 \cos x\)
When \(\left( \mu _{1}, \mu _{2}\right) =(-0.16, -0.08)\) lies in region \(D_{3}\) and let \(d_{11}=1.1400, \delta =0.4404\), the positive constant steady state \(E_{*}(0.1961, 0.4729)\) is unstable and there is a heteroclinic orbit connecting the unstable spatially inhomogeneous steady state to stable spatially homogeneous periodic solution. The initial value is \(u(x,0)=0.1961+0.2 \cos x,~v(x,0)=0.4729+0.2 \cos x\)
In region \(D_{3}\), the third-order truncated normal form (37) has four equilibrium points: \(A_{0}, A_{1}, A_{2}^{+}\) and \(A_{2}^{-}\). The equilibrium points \(A_{0}\), \(A_{2}^{+}\) and \(A_{2}^{-}\) are unstable and the equilibrium point \(A_{1}\) is asymptotically stable. Thus, the original system (4) has an unstable positive constant steady state, two unstable spatially inhomogeneous steady states like \(\cos x\)-shape in space, and a stable spatially homogeneous periodic solution. By choosing \(\left( \mu _{1}, \mu _{2}\right) =(-0.16, -0.08)\) and the initial value \(u(x,0)=0.1961+0.2 \cos x,~v(x,0)=0.4729+0.2 \cos x\), the dynamics of the original system (4) evolves from the spatially inhomogeneous steady states to the spatially homogeneous periodic solution, as shown in Fig. 6.
When \(\left( \mu _{1}, \mu _{2}\right) =(0.005,-0.002)\) lies in region \(D_{4}\) and let \(d_{11}=1.1467, \delta =0.4364\), the positive constant steady state \(E_{*}(0.2648, 0.5840)\) is unstable and there is a heteroclinic orbit connecting the spatially inhomogeneous periodic solution to stable spatially homogeneous periodic solution. The initial value is \(u(x,0)=0.2648-0.1 \cos x,~v(x,0)=0.5840-0.15 \cos x\). a and b are transient behaviours for u and v, respectively; c and d are middle-term behaviours for u and v, respectively; e and f are long-term behaviours for u and v, respectively
When \(\left( \mu _{1}, \mu _{2}\right) =(0.23, -0.09)\) lies in region \(D_{4}\) and let \(d_{11}=1.1467, \delta =0.4364\), the positive constant steady state \(E_{*}(0.1881, 0.4581)\) is unstable and there is stable spatially homogeneous periodic solution. The initial value is \(u(x,0)=0.1881-0.02 \cos x,~v(x,0)=0.4581-0.02 \cos x\)
When \(\left( \mu _{1}, \mu _{2}\right) =(0.17, -0.03)\) lies in region \(D_{5}\) and let \(d_{11}=1.1467, \delta =0.3\), the positive constant steady state \(E_{*}(0.2389,0.5455)\) is unstable and there is a heteroclinic orbit connecting the unstable positive constant steady state to stable spatially homogeneous periodic solution. The initial value is \(u(x,0)=0.2389-0.15 \cos x,~v(x,0)=0.5455-0.15 \cos x\). When \(\left( \mu _{1}, \mu _{2}\right) =(0.31,-0.05)\) lies in region \(D_{5}\) and let \(d_{11}=0.9, \delta =0.4004\), the positive constant steady state \(E_{*}(0.2213,0.5169)\) is unstable and there is a heteroclinic orbit connecting the unstable positive constant steady state to stable spatially inhomogeneous steady states. The initial value is \(u(x,0)=0.2213-0.2 \cos x,~v(x,0)=0.5169+0.2 \cos x\)
When \(\left( \mu _{1}, \mu _{2}\right) =(0.75, 0.1675)\) lies in region \(D_{6}\) and let \(d_{11}=0.9, \delta =0.5004\), the positive constant steady state \(E_{*}(0.4514,0.7429)\) is unstable and there are two stable spatially inhomogeneous steady states like \(\cos x\) in space. a and b: the initial value is \(u(x,0)=0.4514-0.15 \cos x,~v(x,0)=0.7429+0.15 \cos x\); c and d: the initial value is \(u(x,0)=0.4514+0.15 \cos x,~v(x,0)=0.7429-0.15 \cos x\)
In region \(D_{4}\), the third-order truncated normal form (37) has six equilibrium points: \(A_{0}, A_{1}, A_{2}^{\pm }\) and \(A_{3}^{\pm }\). The equilibrium point \(A_{0}\) is unstable, the equilibrium points \(A_{1}\), \(A_{2}^{\pm }\) and \(A_{3}^{\pm }\) are asymptotically stable. This implies that the original system (4) has an unstable positive constant steady state, a stable spatially homogeneous periodic solution, two stable spatially inhomogeneous steady states like \(\cos x\)-shape in space and two stable spatially inhomogeneous periodic solution like \(\cos x\)-shape in space. Taking the parameter \(\left( \mu _{1}, \mu _{2}\right) =(0.005,-0.002)\) and the initial value \(u(x,0)=0.2648-0.1 \cos x,~v(x,0)=0.5840-0.15 \cos x\) close to the unstable positive constant steady state, the dynamics of the original system (4) evolves from unstable spatially inhomogeneous steady states, spatially inhomogeneous periodic solution to stable spatially homogeneous periodic solution, as shown in Fig. 7. Furthermore, by taking the parameter \(\left( \mu _{1}, \mu _{2}\right) =(0.23, -0.09)\) and the initial value \(u(x,0)=0.1881-0.02 \cos x,~v(x,0)=0.4581-0.02 \cos x\) close to the unstable positive constant steady state, the dynamics of the original system (4) evolves from unstable spatially inhomogeneous steady states to stable spatially homogeneous periodic solution, as shown in Fig. 8.
In region \(D_{5}\), the third-order truncated normal form has four equilibrium points: \(A_{0}, A_{1}, A_{2}^{+}\) and \(A_{2}^{-}\). The equilibrium point \(A_{0}\) is unstable and the equilibrium points \(A_{1}\), \(A_{2}^{+}\) and \(A_{2}^{-}\) are asymptotically stable. Thus, the original system (4) has an unstable positive constant steady state, a stable spatially homogeneous periodic solution and two stable spatially inhomogeneous steady states like \(\cos x\)-shape in space. Taking the parameter \(\left( \mu _{1}, \mu _{2}\right) =(0.17, -0.03)\) and the initial value \(u(x,0)=0.2389-0.15 \cos x,~v(x,0)=0.5455-0.15 \cos x\) close to the unstable positive constant steady state, the dynamics of the original system (4) evolves from unstable positive constant steady state to stable spatially homogeneous periodic solution, as shown in Fig. 9a and b. Taking the parameter \(\left( \mu _{1}, \mu _{2}\right) =(0.31,-0.05)\) and the initial value \(u(x,0)=0.2213-0.2 \cos x,~v(x,0)=0.5169+0.2 \cos x\) close to the unstable positive constant steady state, the dynamics of the original system (4) evolves from unstable positive constant steady state to stable spatially inhomogeneous steady states, as shown in Fig. 9c and d.
In region \(D_{6}\), the third-order truncated normal form (37) has three equilibrium points: \(A_{0}, A_{2}^{+}\) and \(A_{2}^{-}\). The equilibrium point \(A_{0}\) is unstable and the equilibrium points \(A_{2}^{+}\) and \(A_{2}^{-}\) are asymptotically stable. Thus, the original system (4) has an unstable positive constant steady state and two stable non-constant steady states like \(\cos x\)-shape in space. For the fixed parameter \(\left( \mu _{1}, \mu _{2}\right) =(0.75, 0.1675)\) and choosing different initial values, the original system (4) can converge to one of these two stable non-constant steady states, as shown in Fig. 10a and b for the initial value \(u(x,0)=0.4514-0.15 \cos x,~v(x,0)=0.7429+0.15 \cos x\) and Fig. 10c and d for the initial value \(u(x,0)=0.4514+0.15 \cos x,~v(x,0)=0.7429-0.15 \cos x\).
6 Conclusion and discussion
In this paper, a predator–prey model with cross-diffusion considering the prey individual behaviour and herd behaviour transition with homogeneous Neumann boundary condition is investigated. We first show that the non-negativity and boundedness of solutions corresponding to the model without self-diffusion and cross-diffusion and the model with self-diffusion and cross-diffusion. Then we show the existence and priori boundedness of solutions corresponding to the spatiotemporal model without cross-diffusion. In order to classify the possible dynamical classification near the Turing–Hopf bifurcation point, by using the method of computing the normal form presented in [34], the third-order truncated normal form (37) is given. By the obtained third-order truncated normal form (37), we obtain a zero equilibrium point corresponding to the positive constant steady state of the original system (4), three boundary equilibrium points \(A_{1}\) and \(A_{2}^{\pm }\) in which \(A_{1}\) corresponding to the spatially homogeneous periodic solution of the original system (4) and \(A_{2}^{\pm }\) corresponding to the two spatially inhomogeneous steady states with \(\cos x\)-like shape in space of the original system (4). Furthermore, two interior equilibrium points \(A_{3}^{\pm }\) is also obtained corresponding to the two spatially inhomogeneous periodic solutions with \(\cos x\)-like shape in space of the original system (4). Moreover, we obtain four inequality which is used to ensure the existence of these different types of equilibrium points. Notice that the four inequality can be seen as the four critical bifurcation lines; thus, by the defined critical bifurcation lines, the bifurcation diagram in the \(\mu _{1}\)-\(\mu _{2}\) parameters plane which includes six different regions is shown in Fig. 3.
By the numerical simulations, the rich dynamics such as the positive constant steady state, the spatially homogeneous periodic solution, spatially inhomogeneous steady states and spatially inhomogeneous periodic solutions have been found, which can be seen in Figs. 4, 5, 6, 7, 8, 9 and 10. Especially, we would like to mention that the interaction between the Turing bifurcation curve and the Hopf bifurcation curve may leads to the emergence of the spatially inhomogeneous periodic solutions, see Fig. 7a and b for details.
We have to point out the fact that the method of computing normal form developing in this paper can also be used to the case without cross-diffusion by a slight modification. Furthermore, in order to the simplicity of notation for further normal form computation and for the convenience of carrying out the numerical simulations, we let \(\varOmega :=(0, \pi )\). However, the spatial \(\varOmega \) can also be taken \((0, \ell \pi )\) with \(\ell \in \mathbb {R}^{+}\). Notice also that the general open interval \(({\widetilde{a}},{\widetilde{b}})\) can be transformed to \((0, \pi )\) by a translation and rescaling.
Data Availability Statement
This research didn’t involve the private data, and the involving data and material are all available.
Code availability
The numerical simulations in this paper are carried by using the MATLAB software.
References
Lotka, A.J.: Relation between birth rates and death rates. Science 26(653), 21–26 (1907)
Volterra, V.: Variazione e fluttuazini del numero \(\text{ d}^{\prime }\)individui in specie animali conviventi. Memorie della R. Acc. deiLincei. 2(6), 31–113 (1926)
Freedman, H.I.: Deterministic Mathematical Models in Population Ecology. Marcel Dekker, New York (1980)
Murray, J.D.: Mathematical Biology I: An Introduction, 3rd edn. Springer-Verlag, New York (2002)
Holling, C.S.: The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91(5), 293–320 (1959)
Aziz-alaoui, M.A., Okiye, M.D.: Boundedness and global stability for a predator–prey model with modified Leslie–Gower and Holling-type II type schemes. Appl. Math. Lett. 16(7), 1069–1075 (2003)
Arditi, R., Ginzburg, L.R.: Coupling in predator–prey dynamics: ratio-dependence. J. Theor. Biol. 139(3), 311–326 (1989)
Song, Y.L., Zou, X.F.: Spatiotemporal dynamics in a diffusive ratio-dependent predator–prey model near a Hopf–Turing bifurcation point. Comput. Math. Appl. 67(10), 1978–1997 (2014)
Tripathi, J.P., Abbas, S., Thakur, M.: Dynamical analysis of a prey–predator model with Beddington–DeAngelis type function response incorporating a prey refuge. Nonlinear Dyn. 80(1–2), 177–196 (2015)
Petrovskii, S., Morozov, A., Li, B.L.: Regimes of biological invasion in a predator–prey system with the Allee effect. Bull. Math. Biol. 67(3), 637–661 (2005)
Wang, J.F., Shi, J.P., Wei, J.J.: Dynamics and pattern formation in a diffusive predator–prey system with strong Allee effect in prey. J. Differ. Equ. 251(4–5), 1276–1304 (2011)
Peng, Y.A., Zhang, T.B.: Turing instability and pattern induced by cross-diffusion in a predator–prey system with Allee effect. Appl. Math. Comput. 275, 1–12 (2016)
Ajraldi, V., Pittavino, M., Venturino, E.: Modeling herd behavior in population systems. Nonlinear Anal. Real World Appl. 12(4), 2319–2338 (2011)
Saha, S., Samanta, G.P.: Analysis of a predator–prey model with herd behavior and disease in prey incorporating prey refuge. Int. J. Biomath. 12(1), 1950007 (2019)
Manna, D., Maiti, A., Samanta, G.P.: Deterministic and stochastic analysis of a predator–prey model with Allee effect and herd behaviour. Simulation 95(4), 339–349 (2019)
Maiti, A., Sen, P., Samanta, G.P.: Deterministic and stochastic analysis of a prey–predator model with herd behaviour in both. Syst. Sci. Control Eng. 4(1), 259–269 (2016)
Murray, J.D.: Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd edn. Springer-Verlag, Heidelberg (2003)
Du, Y.H., Shi, J.P.: A diffusive predator–prey model with a protection zone. J. Differ. Equ. 229(1), 63–91 (2006)
Yi, F.Q., Wei, J.J., Shi, J.P.: Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator–prey system. J. Differ. Equ. 246(5), 1944–1977 (2009)
Cui, R.H., Shi, J.P., Wu, B.Y.: Strong Allee effect in a diffusive predator–prey system with a protection zone. J. Differ. Equ. 256(1), 108–129 (2014)
Kerner, E.H.: A statistical mechanics of interacting biological species. Bull. Math. Biol. 19(2), 121–146 (1957)
Shigesada, N., Kawasaki, K., Teramoto, E.: Spatial segregation of interacting species. J. Theor. Biol. 79(1), 83–99 (1979)
Shukla, J.B., Verma, S.: Effects of convective and dispersive interactions on the stability of two species. Bull. Math. Biol. 43(5), 593–610 (1981)
Tian, C.R., Lin, Z.G., Pedersen, M.: Instability induced by cross diffusion in reaction-diffusion systems. Nonlinear Anal. Real World Appl. 11(2), 1036–1045 (2010)
Sun, G.Q., Jin, Z., Li, L., et al.: Spatial patterns of a predator–prey model with cross diffusion. Nonlinear Dyn. 69(4), 1631–1638 (2012)
Guin, L.N.: Existence of spatial patterns in a predator–prey model with self- and cross-diffusion. Appl. Math. Comput. 226(1), 320–335 (2014)
Zhang, J.Y., Yan, G.W.: Lattice Boltzmann simulation of pattern formation under cross-diffusion. Comput. Math. Appl. 69(3), 157–169 (2015)
Gambino, G., Lombardo, M.C., Sammartino, M., et al.: Turing pattern formation in the Brusselator system with nonlinear diffusion. Phys. Rev. E 88(4), 042925 (2013)
Berenstein, I., Beta, C.: Cross-diffusion in the two-variable Oregonator model. Chaos Interdiscip. J. Nonlinear Sci. 23(3), 033119 (2013)
Fanelli, D., Cianci, C., Patti, F.D.: Turing instabilities in reaction–diffusion systems with cross diffusion. Eur. Phys. J. B 86(4), 1–8 (2013)
Gambino, G., Lombardo, M.C., Sammartino, M.: Turing instability and pattern formation for the Lengyel–Epstein system with nonlinear diffusion. Acta Applicandae Mathematicae 132(1), 283–294 (2014)
Tang, X.S., Song, Y.L., Zhang, T.H.: Turing–Hopf bifurcation analysis of a predator–prey model with herd behavior and cross-diffusion. Nonlinear Dyn. 86(1), 1–17 (2016)
Faria, T.: Normal forms and Hopf bifurcation for partial differential equations with delay. Trans. Am. Math. Soc. 352(5), 2217–2238 (2000)
Song, Y.L., Zhang, T.H., Peng, Y.H.: Turing–Hopf bifurcation in the reaction–diffusion equations and its applications. Commun. Nonlinear Sci. Numer. Simul. 33, 229–258 (2016)
De Assis, R.A., Pazim, R., Malavazi, M.C., et al.: A mathematical model to describe the herd behaviour considering group defense. Appl. Math. Nonlinear Sci. 5(1), 11–24 (2020)
Vitagliano, V.: Some phenomenological and thermodynamic aspects of diffusion in multicomponent systems. Pure Appl. Chem. 63(10), 1441–1448 (1991)
Pao, C.V.: Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York (1992)
Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, 3rd edn. Springer-Verlag, New York (2004)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag, New York (1983)
Acknowledgements
The authors are grateful to the anonymous referees for their useful suggestions which improve the contents of this article.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Contributions
This research did not involve human participants and animals. This manuscript is investigated and written by YL.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest, whether financial or non-financial.
Ethical approval
The author agrees to submit this manuscript to Nonlinear Dynamics. Once the submitted manuscript is accepted, the author agrees to publish it in Nonlinear Dynamics.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In Sect. 1, we have pointed out that the procedure of computing \(B_{11}\) and \(B_{13}\) needs to be deduced again. In the following, the detailed derivation process of \(B_{11}\) and \(B_{13}\) is given. Following Section 3.1.1 in [34], by considering the formal Taylor expansion
where \(F_{j}(\varPhi z_{x}+w, \mu ),~j \ge 2\) is the j-th Fr\(\acute{e}\)chet derivative of \(F(\varPhi z_{x}+w, \mu )\). For simplicity, we set
Furthermore, we have
where \({\widetilde{L}}_{1}(\mu )=\mu _{1} L_{1}^{(1,0)}+\mu _{2} L_{1}^{(0,1)}+{\widetilde{d}}\varDelta \), and \({\widetilde{d}}\) is defined by Eq. (31). Since \(F(0, \mu )=0\) and \(D F(0, \mu )=0\), \(F_{2}\left( \varPhi z_{x}+w, \mu \right) \) can be written as follows
where \(q_{1}, q_{2}, q_{3} \in \mathbb {N}_{0}\), \({\mathcal {S}}_{2}\left( \varPhi z_{x}, w\right) \) is the product term of \(\varPhi z_{x}\) and w, and
Here, \(A_{q_{1} q_{2} q_{3}}={\overline{A}}_{q_{2} q_{1} q_{3}}\), and \({\overline{A}}_{q_{2} q_{1} q_{3}}\) represents the conjugation of \(A_{q_{2} q_{1} q_{3}}\).
Noticing the fact that
then we can obtain that
where
with \(i=1,2\). Moreover,
with
Next, by a slight modification of the calculation procedures in [34], we give the detail calculation procedures of \(B_{11}, B_{21}, B_{13}, B_{23}, B_{210}, B_{102}, B_{111}, B_{003}\) steps by steps.
Step 1:
Step 2:
with
Step 3:
Here
with
More precisely, for the system (29), by combining with Eq.(32), we have
Furthermore, we have
Rights and permissions
About this article
Cite this article
Lv, Y. Turing–Hopf bifurcation in the predator–prey model with cross-diffusion considering two different prey behaviours’ transition. Nonlinear Dyn 107, 1357–1381 (2022). https://doi.org/10.1007/s11071-021-07058-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-07058-y
Keywords
- Turing–Hopf bifurcation
- Predator–prey model
- Self-diffusion
- Cross-diffusion
- Individual behaviour
- Herd behaviour
- Spatially inhomogeneous periodic solution