Bogdanov–Takens bifurcation for a diffusive predator–prey system with nonlocal effect and prey refuge

Abstract

In this paper, a diffusive predator–prey system with nonlocal effect and prey refuge subjects to the homogeneous Neumann boundary condition is studied. Firstly, the conditions for the occurrence of Turing, Hopf, Turing–Turing and Bogdanov–Takens bifurcations are established. Then, in order to meticulously describe the spatiotemporal dynamics resulting from the Bogdanov–Takens bifurcation, we derive an algorithm for calculating the third-order truncated normal form of Bogdanov–Takens bifurcation of this system by using the center manifold theory and normal form method, which can be applied to general diffusive predator–prey system with nonlocal effect. With the aid of the derived third-order truncated normal form, the complex spatiotemporal dynamics are theoretically predicted. At last, we carry out some numerical simulations to support the theory analysis, and the stable positive constant steady state and a pair of stable spatially inhomogeneous steady states are found.

1 Introduction

In order to model the predator–prey mite outbreak interaction on fruit trees, Wollkind et al. [1] have proposed the following ordinary differential equation (ODE) system

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\textrm{d}u(t)}{\textrm{d}t}=au(t)\left( 1-\frac{u(t)}{K}\right) -\frac{bu(t)v(t)}{u(t)+m}, \\&\frac{\textrm{d}v(t)}{\textrm{d}t}=cv(t)\left( 1-\frac{ev(t)}{u(t)}\right) , \end{aligned}\right. \end{aligned}$$

(1.1)

where u(t) and v(t) represent the prey and predator densities, respectively, a and c are the intrinsic growth rates of the prey and predator populations, respectively, K represents the carrying capacity of the prey population, b and e measure the interaction strength between the predator and prey populations, and m measures the ability for the prey population to evade attack. The saturating predator functional response $(bu(t))/(u(t)+m)$ is of Holling type II or Michaelis–Menten type in enzyme-substrate kinetics [2, 3], where m is usually called the half-saturation constant. The form of the predator equation in system (1.1) was first introduced by Leslie [4]. The function v(t)/u(t) is called the Leslie–Gower term [5]. The Leslie predator–prey model with Holling type II functional response is also called the Holling–Tanner model in the literature [3, 6].

In nature, the different predator populations may compete with each other for common prey population, and thus there is no real justification for assuming that the interaction between the prey and predator populations is local. Recently, the predator–prey systems involving nonlocal effect as well as the competition systems involving nonlocal effect have been extensively investigated by many scholars [7,8,9,10,11,12,13]. As shown in [14], the most direct method to introduce the nonlocal effect is to replace $u(t)(1-u(t)/K)$ by $u(t)(1-\widehat{u}/K)$ with

$$\begin{aligned} \widehat{u}:=\int \limits _{\Omega }K(x,y)u(y,t)\textrm{d}y, \end{aligned}$$

where K(x, y) is a general kernel function, which determines the probability of interactions among individuals at different locations, and $\Omega$ is the spatial domain. By introducing the diffusion terms and the nonlocal prey competition into the classical diffusive Holling–Tanner predator–prey system (1.1), Merchant et al. [7] have proposed the following system

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u(x,t)}{\partial t}=d_{1}\Delta u(x,t)+au(x,t)\left( 1-\frac{1}{K}\int \limits _{\Omega }K(x,y)u(y,t)\textrm{d}y\right) -\frac{bu(x,t)v(x,t)}{u(x,t)+m},~x \in \Omega ,~t>0, \\&\frac{\partial v(x,t)}{\partial t}=d_{2}\Delta v(x,t)+cv(x,t)\left( 1-\frac{ev(x,t)}{u(x,t)}\right) ,~x \in \Omega ,~t>0, \end{aligned} \right. \end{aligned}$$

(1.2)

where u(x, t) and v(x, t) stand for the densities of the prey and predator populations at location x and time t, respectively, $d_{1}$ and $d_{2}$ are the diffusion rates of the prey and predator populations, respectively. For more biological meanings of the system (1.2), see [7] for detail. Furthermore, the different diffusive Holling–Tanner predator–prey systems without the nonlocal effect have been studied by many scholars [15,16,17,18]. For $\Omega =\mathbb {R}$, Merchant et al. [7] have found that the nonlocal competition could induce complex spatiotemporal dynamics.

By noticing that in the ecological system, in order to reduce the prey population by the predator population over predation, a certain percentage or number of prey population may be protected. If the prey population with proportion $\kappa$ is protected, then the prey population of the rest proportion $1-\kappa$ is available to the predator population, where $\kappa \in (0,1)$ is a positive constant which measures the level of the prey refuge. The stability analysis of a predator–prey model without diffusion terms and with a prey refuge [19], the qualitative analysis of a diffusive predator–prey model with Holling type II functional response function incorporating a prey refuge [20], the stability analysis of a prey-predator model without diffusion terms and with Holling type III response function as well as a prey refuge [21], the dynamical analysis of a predator–prey model without diffusion terms and with Beddington-DeAngelis type functional response function as well as a prey refuge [22], a Leslie–Gower predator–prey model without diffusion terms and with disease in prey as well as a prey refuge [23], the Hopf bifurcation of a prey-predator model without diffusion terms and with prey refuge as well as fear effect [24], the dynamical analysis of a fractional-order predator–prey model with a prey refuge [25] and the stability analysis of a competitive predator–prey model without diffusion terms and with a prey refuge [26] have been studied. We can see that many scholars mainly focus on the predator–prey systems with prey refuge but without the diffusion terms, there are few studies on the diffusive predator–prey system with a prey refuge, even the diffusive predator–prey system with a prey refuge and nonlocal effect. Thus, by introducing the prey refuge to the system (1.2), and by choosing $\Omega =(0,\ell \pi )$ with $\ell \in \mathbb {R}^{+}$ and $K(x,y)=1/(\ell \pi )$, we study the following diffusive predator–prey system with nonlocal effect and prey refuge subjects to the homogeneous Neumann boundary condition

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u(x,t)}{\partial t}\!=\!d_{1}u_{xx}(x,t)+au(x,t)\left( 1-\frac{1}{K\ell \pi }\int \limits _{0}^{\ell \pi }u(y,t)\textrm{d}y\right) \!-\!\frac{b(1-\kappa )u(x,t)v(x,t)}{m+(1-\kappa )u(x,t)},~x \in (0,\ell \pi ),~t\!>\!0, \\&\frac{\partial v(x,t)}{\partial t}=d_{2}v_{xx}(x,t)+cv(x,t)\left( 1-\frac{ev(x,t)}{(1-\kappa )u(x,t)}\right) ,~x \in (0,\ell \pi ),~t>0, \\&u_{x}(0,t)=u_{x}(\ell \pi ,t)=v_{x}(0,t)=v_{x}(\ell \pi ,t)=0,~t>0, \\&u(x,0)=u_{0}(x) \ge 0,~v(x,0)=v_{0}(x) \ge 0,~x \in (0,\ell \pi ), \end{aligned}\right. \end{aligned}$$

(1.3)

where $u_{xx}(x,t)=\partial ^{2}u(x,t)/\partial x^{2}$, $v_{xx}(x,t)=\partial ^{2}v(x,t)/\partial x^{2}$, $u_{0}(x)$ and $v_{0}(x)$ are the initial functions. For the system (1.3), by applying scalings

$$\begin{aligned} \widetilde{t}=at,~\widetilde{u}=\frac{u}{m},~\widetilde{v}=\frac{ev}{m}, \end{aligned}$$

and by denoting

$$\begin{aligned} \widetilde{\beta }=\frac{m}{K},~\widetilde{b}=\frac{b}{ae},~\widetilde{c}=\frac{c}{a},~\widetilde{d}_{1}=\frac{d_{1}}{a},~\widetilde{d}_{2}=\frac{d_{2}}{a}, \end{aligned}$$

then by dropping the tildes, the system (1.3) becomes

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u(x,t)}{\partial t}=d_{1}u_{xx}(x,t)+u(x,t)\left( 1-\frac{\beta }{\ell \pi }\int \limits _{0}^{\ell \pi }u(y,t)\textrm{d}y\right) -\frac{b(1-\kappa )u(x,t)v(x,t)}{1+(1-\kappa )u(x,t)},~x \in (0,\ell \pi ),~t>0, \\&\frac{\partial v(x,t)}{\partial t}=d_{2}v_{xx}(x,t)+cv(x,t)\left( 1-\frac{v(x,t)}{(1-\kappa )u(x,t)}\right) ,~x \in (0,\ell \pi ),~t>0, \\&u_{x}(0,t)=u_{x}(\ell \pi ,t)=v_{x}(0,t)=v_{x}(\ell \pi ,t)=0,~t>0, \\&u(x,0)=u_{0}(x) \ge 0,~v(x,0)=v_{0}(x) \ge 0,~x \in (0,\ell \pi ), \end{aligned}\right. \end{aligned}$$

(1.4)

where parameters $d_{1}, d_{2}, \beta , \ell , b, \kappa , c$ are all positive constants. For simplicity, in what follows, we denote

$$\begin{aligned} \widehat{u}:=\frac{1}{\ell \pi }\int \limits _{0}^{\ell \pi }u(y,t)\textrm{d}y. \end{aligned}$$

By rigorous bifurcation analysis, we find that under some proper conditions, the system (1.4) undergoes Turing bifurcation, Hopf bifurcation, Turing–Turing bifurcation as well as Bogdanov–Takens bifurcation. Especially, the Bogdanov–Takens bifurcation usually means that by choosing proper parameters such that the characteristic equation of the original system has a double zero root with the remaining roots having negative real parts. In other words, one usually means a vector field whose linear part (in Jordan canonical form) is given by $\left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array}\right)$. However, the linear part $\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \end{array}\right)$ has also a double zero root. But, the second case is codimension 4 and is consequently more difficult to analyze, see [27] for detail. In this paper, we mainly investigate the first case. Moreover, as is well known, the Bogdanov–Takens bifurcation is one of the codimension two bifurcations in the nonlinear dynamics, which can provide some valuable information about periodic behaviors and global dynamics. For the different functional differential equation systems, the Bogdanov–Takens bifurcation of these systems has been extensively investigated [28,29,30]. However, there are only a few related researches on Bogdanov–Takens bifurcation of partial differential equation or partial functional differential equation.

On the one hand, few studies have been done on the Bogdanov–Takens bifurcation for the diffusive predator–prey system with nonlocal effect, and even the diffusive predator–prey system with nonlocal effect and prey refuge. On the other hand, the algorithms for calculating the normal form of Bogdanov–Takens bifurcation for the diffusive predator–prey system with nonlocal effect and even the diffusive predator–prey system with nonlocal effect and prey refuge need to be developed, since it can meticulously describe the spatiotemporal dynamics resulting from the Bogdanov–Takens bifurcation. Furthermore, by noticing that the Bogdanov–Takens bifurcation could help to reveal some complex spatiotemporal dynamics, thus based on the above discussion, it is worthwhile to study the Bogdanov–Takens bifurcation for the system (1.4).

This paper is organized as follows. In Sect. 2, by using the linear stability theory, the conditions for the occurrence of Turing bifurcation, Hopf bifurcation, Turing–Turing bifurcation and Bogdanov–Takens bifurcation are obtained. In Sect. 3, by using the center manifold theory and normal form method, we derive an algorithm for calculating the third-order truncated normal form of Bogdanov–Takens bifurcation for the system (1.4). In Sect. 4, by choosing proper parameters, and with the help of computer, we obtain the third-order truncated normal form of Bogdanov–Takens bifurcation for the system (1.4) by using the derived algorithm in Sect. 2. Then, by analyzing the obtained third-order truncated normal form, the spatiotemporal dynamics near the Bogdanov–Takens bifurcation point of the system (1.4) are explored. At last, the conclusion and discussion are given in Sect. 5.

2 Stability and Bogdanov–Takens bifurcation analysis for the system (1.4)

Define the real-valued Sobolev space

$$\begin{aligned} X:=\left\{ (u,v)^{T} \in \left( W^{2,2}(0,\ell \pi )\right) ^{2}:\frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=0 \text{ at } x=0,\ell \pi \right\} \end{aligned}$$

with the inner product defined by

$$\begin{aligned} \left[ U_{1},U_{2}\right] =\int \limits _{0}^{\ell \pi } U_{1}^{T}U_{2} \textrm{d}x \text{ for } U_{1}=\left( u_{1},v_{1}\right) ^{T} \in X \text { and } U_{2}=\left( u_{2},v_{2}\right) ^{T} \in X, \end{aligned}$$

where the symbol T represents the transpose of vector. It is well known that the eigenvalue problem

$$\begin{aligned} \left\{ \begin{aligned}&\widetilde{\varphi }^{\prime \prime }(x)=\widetilde{\lambda }\widetilde{\varphi }(x),~x \in (0,\ell \pi ), \\&\widetilde{\varphi }^{\prime }(0)=\widetilde{\varphi }^{\prime }(\ell \pi )=0 \end{aligned}\right. \end{aligned}$$

has eigenvalues $\widetilde{\lambda }_{n}=-n^{2}/\ell ^{2}$ with corresponding normalized eigenfunctions

$$\begin{aligned} \beta _{n}^{(j)}=\gamma _{n}(x)e_{j},~\gamma _{n}(x)=\frac{\cos (nx/\ell )}{\left\| \cos (nx/\ell )\right\| _{L^{2}}}=\left\{ \begin{aligned}&\frac{1}{\sqrt{\ell \pi }},&n=0, \\&\frac{\sqrt{2}}{\sqrt{\ell \pi }}\cos \left( \frac{nx}{\ell }\right) ,&n \ge 1, \end{aligned}\right. \end{aligned}$$

(2.1)

where $e_{j},~j=1,2$ are the unit coordinate vector of $\mathbb {R}^{2}$, and $n \in \mathbb {N}_{0}=\mathbb {N}\cup \left\{ 0\right\}$ is often called wave number, $\mathbb {N}_{0}$ is the set of all non-negative integers, $\mathbb {N}$ represents the set of all positive integers.

The system (1.4) has positive constant steady state $E_{*}=(u_{*},v_{*})$ with $u_{*} \in (0,1/\beta )$ satisfying $(1-\beta u_{*})(1+(1-\kappa )u_{*})=b(1-\kappa )^{2}u_{*}$, and $v_{*}=(1-\kappa )u_{*}$. Then, the linearized system of the system (1.4) at the positive constant steady state $E_{*}$ is

$$\begin{aligned} \left( \begin{array}{c} \frac{\partial u(x,t)}{\partial t} \\ \frac{\partial v(x,t)}{\partial t} \end{array}\right) =D\left( \begin{array}{c} u_{xx}(x,t) \\ v_{xx}(x,t) \end{array}\right) +A_{1}\left( \begin{array}{c} u(x,t) \\ v(x,t) \end{array}\right) +A_{2}\left( \begin{array}{c} \widehat{u} \\ \widehat{v} \end{array}\right) , \end{aligned}$$

(2.2)

where

$$\begin{aligned} D=\left( \begin{array}{cc} d_{1} &{} 0 \\ 0 &{} d_{2} \end{array}\right) ,~A_{1}=\left( \begin{array}{cc} \frac{u_{*}(1-\kappa )(1-\beta u_{*})}{1+(1-\kappa )u_{*}} &{} -\frac{(1-\beta u_{*})}{1-\kappa } \\ c(1-\kappa ) &{} -c \end{array}\right) ,~A_{2}=\left( \begin{array}{cc} -\beta u_{*} &{} 0 \\ 0 &{} 0 \end{array}\right) . \end{aligned}$$

(2.3)

Thus, the characteristic equation of (2.2) is

$$\begin{aligned} \prod _{n \in \mathbb {N}_{0}}\Gamma _{n}(\lambda )=0, \end{aligned}$$

(2.4)

where $\Gamma _{n}(\lambda )={\text {det}}(\mathcal {M}_{n}(\lambda ))$ with

$$\begin{aligned} \mathcal {M}_{n}(\lambda )=\left\{ \begin{aligned}&\lambda I_{2}-A_{1}-A_{2},&n=0, \\&\lambda I_{2}+D\frac{n^{2}}{\ell ^{2}}-A_{1},&n\in \mathbb {N} \end{aligned}\right. \end{aligned}$$

(2.5)

and $I_{2}$ is the identity matrix of size 2. More precisely, by combining with (2.3), (2.4) and (2.5), we have

$$\begin{aligned} \Gamma _{n}(\lambda )={\text {det}}(\mathcal {M}_{n}(\lambda ))=\left\{ \begin{aligned}&\lambda ^{2}-T_{0}\lambda +D_{0}=0,~n=0, \\&\lambda ^{2}-T_{n}\lambda +D_{n}=0,~n\in \mathbb {N}, \end{aligned}\right. \end{aligned}$$

(2.6)

where ${\text {det}}(\mathcal {M}_{n}(\lambda ))$ represents the determinant of $\mathcal {M}_{n}(\lambda )$, and

$$\begin{aligned} T_{0}=-c+u_{*}(\xi -\beta ),~D_{0}=u_{*}\beta c+\frac{c\xi }{1-\kappa }>0 \end{aligned}$$

(2.7)

with

$$\begin{aligned} \xi \triangleq \frac{(1-\kappa )(1-\beta u_{*})}{1+(1-\kappa )u_{*}}>0, \end{aligned}$$

(2.8)

and for $n \in \mathbb {N}$,

$$\begin{aligned} T_{n}=-c+u_{*}\xi -\frac{(d_{1}+d_{2})n^{2}}{\ell ^{2}},~D_{n} =\frac{c\xi }{1-\kappa }+(d_{1}c-d_{2}u_{*}\xi )\frac{n^{2}}{\ell ^{2}}+\frac{d_{1}d_{2}n^{4}}{\ell ^{4}}. \end{aligned}$$

(2.9)

Remark 2.1

We can let $u(x,t)=a_{n}\textrm{e}^{\lambda t}\cos (nx/\ell )$ and $v(x,t)=b_{n}\textrm{e}^{\lambda t}\cos (nx/\ell )$ be the solution of (2.2). By noticing that

$$\begin{aligned} \frac{1}{\ell \pi }\int \limits _{0}^{\ell \pi }\cos \frac{nx}{\ell }\textrm{d}x=\left\{ \begin{array}{cc} 1, &{} n=0, \\ 0, &{} n \ne 0, \end{array}\right. \end{aligned}$$

where $a_{n}$ and $b_{n}$ are two positive constants, and then we can obtain the characteristic equation (2.6).

For the convenience of presentation, in what follows, we first denote

$$\begin{aligned} \begin{aligned}&c=\widetilde{c}_{n}(d_{1}) \triangleq \frac{d_{2}u_{*}\xi \frac{n^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{n^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}}, \\&c=\overline{c}_{0}(d_{1}) \triangleq u_{*}(\xi -\beta ), \\&c=\overline{c}_{n}(d_{1}) \triangleq u_{*}\xi -\frac{(d_{1}+d_{2})n^{2}}{\ell ^{2}}. \end{aligned} \end{aligned}$$

(2.10)

After some analysis, we have conclusions about the occurrence of Hopf bifurcation and Turing bifurcation for the system (1.4).

Theorem 2.2

• (1) When

  $$\begin{aligned} c=\widetilde{c}_{n}(d_{1}) \triangleq \frac{d_{2}u_{*}\xi \frac{n^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{n^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}} \end{aligned}$$

  with $0<d_{1}<\widetilde{d}_{n} \triangleq (u_{*}\xi \ell ^{2})/n^{2},~n \in \mathbb {N}$ and $-c+u_{*}\xi <0$, the n-mode Turing bifurcation occurs for the system (1.4).

• (2) The system (1.4) undergoes the 0-mode Hopf bifurcation when $c=\overline{c}_{0}(d_{1}) \triangleq u_{*}(\xi -\beta )$ provided $\xi >\beta$, and the n-mode Hopf bifurcation when

  $$\begin{aligned} c=\overline{c}_{n}(d_{1}) \triangleq u_{*}\xi -\frac{(d_{1}+d_{2})n^{2}}{\ell ^{2}} \end{aligned}$$

  with $0<d_{1}<\overline{d}_{n} \triangleq (u_{*}\xi \ell ^{2})/n^{2}-d_{2},~1 \le n<\sqrt{(u_{*}\xi \ell ^{2})/d_{2}},~n \in \mathbb {N}$ and $c>\widetilde{c}_{n}(d_{1})$. Furthermore, from $1 \le n<\sqrt{(u_{*}\xi \ell ^{2})/d_{2}}$, we can deduce that $\ell >\sqrt{d_{2}/(u_{*}\xi )}$.

Proof

By regarding the conditions of the occurrence of Turing bifurcation and Hopf bifurcation as bifurcation curves in $d_{1}-c$ parameter plane, we present the argument from a geometric point of view.

(i) From (2.9), by letting $D_{n}=0$ with $n \in \mathbb {N}$, we have

$$\begin{aligned} c=\widetilde{c}_{n}(d_{1}) \triangleq \frac{d_{2}u_{*}\xi \frac{n^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{n^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}}, \end{aligned}$$

with $d_{2}u_{*}\xi (n^{2}/\ell ^{2})-d_{1}d_{2}(n^{4}/\ell ^{4})>0$, i.e., $0<d_{1}<\widetilde{d}_{n}=(u_{*}\xi \ell ^{2})/n^{2},~n \in \mathbb {N}$. Furthermore, from $-c+u_{*}\xi <0$, we can deduce that $T_{n}<0$. Moreover, if we assume that the characteristic equation (2.6) has a complex root $\lambda (c)=\alpha _{1}(c)+\textrm{i}\beta _{1}(c)$ with $\alpha _{1}(\widetilde{c}_{n}(d_{1}))=0$, $\beta _{1}(\widetilde{c}_{n}(d_{1}))=0$, then when $T_{n} \ne 0,~n \in \mathbb {N}$, the transversality condition

$$\begin{aligned} \left. \frac{\textrm{d}\lambda }{\textrm{d}c}\right| _{c=\widetilde{c}_{n}(d_{1})}=\frac{1}{T_{n}}\frac{\partial D_{n}}{\partial c}=\frac{\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}}{T_{n}} \ne 0 \end{aligned}$$

holds. Thus, when $c=\widetilde{c}_{n}(d_{1})$ with $0<d_{1}<\widetilde{d}_{n} \triangleq (u_{*}\xi \ell ^{2})/n^{2},~n \in \mathbb {N}$, the system (1.4) undergoes Turing bifurcation. Therefore, the conclusion (1) is verified.

(ii) From (2.7), by considering that $D_{0}>0$ and $\xi >\beta$, then the characteristic equation (2.6) has a pair of pure imaginary roots when $c=\overline{c}_{0}(d_{1}) \triangleq u_{*}(\xi -\beta )$ by solving $T_{0}=0$. Furthermore, if we assume that the characteristic equation (2.6) has a pair of complex roots $\lambda =\alpha _{2}(c) \pm \textrm{i}\beta _{2}(c)$ satisfying that $\alpha _{2}(\overline{c}_{0}(d_{1}))=0$ and $\beta _{2}(\overline{c}_{0}(d_{1}))>0$, then by a direct calculation, we have

$$\begin{aligned} \left. \frac{\textrm{d}\alpha _{2}(c)}{\textrm{d}c}\right| _{c=\overline{c}_{0}(d_{1})}=\frac{1}{2}\frac{\partial T_{0}}{\partial c}=-\frac{1}{2}<0, \end{aligned}$$

which indicates that the transversality condition holds. Thus, if $\xi >\beta$, the 0-mode Hopf bifurcation occurs when $c=\overline{c}_{0}(d_{1}) \triangleq u_{*}(\xi -\beta )$.

Analogously, by $T_{n}=0$, the characteristic equation (2.6) has a pair of pure imaginary roots when $c=\overline{c}_{n}(d_{1}) \triangleq u_{*}\xi -((d_{1}+d_{2})n^{2})/\ell ^{2}$ with $0<d_{1}<\overline{d}_{n} \triangleq (u_{*}\xi \ell ^{2})/n^{2}-d_{2}$ provided that $1 \le n<\sqrt{(u_{*}\xi \ell ^{2})/d_{2}}$. Furthermore, from $c>\widetilde{c}_{n}(d_{1})$, we can deduce that $D_{n}>0$. Furthermore, for $\lambda =\alpha _{2}(c) \pm \textrm{i}\beta _{2}(c)$ satisfying $\alpha _{2}(\overline{c}_{n}(d_{1}))=0$ and $\beta _{2}(\overline{c}_{n}(d_{1}))>0$, the transversality condition

$$\begin{aligned} \left. \frac{\textrm{d}\alpha _{2}(c)}{\textrm{d}c}\right| _{c=\overline{c}_{n}(d_{1})}=\frac{1}{2}\frac{\partial T_{n}}{\partial c}=-\frac{1}{2}<0 \end{aligned}$$

holds. Therefore, the conclusion (2) is verified. $\square$

In what follows, from the geometric point of view, we will discuss the conditions of occurrence of the Turing–Turing bifurcation and Bogdanov–Takens bifurcation, respectively.

Theorem 2.3

When $(d_{1},c)=(\widetilde{d}_{i,j}^{*},\widetilde{c}_{i,j}^{*})$, the (i, j)-mode Turing–Turing bifurcation occurs for the system (1.4), where

$$\begin{aligned} \begin{aligned}&\widetilde{d}_{i,j}^{*}=\frac{\left( -\frac{(i^{2}+j^{2})}{1-\kappa }+\sqrt{\frac{4i^{2}j^{2}u_{*}}{1-\kappa }+\frac{(i^{2}+j^{2})^{2}}{(1-\kappa )^{2}}}\right) \xi \ell ^{2}}{2i^{2}j^{2}}>0, \\&\widetilde{c}_{i,j}^{*}=\frac{d_{2}u_{*}\xi \frac{j^{2}}{\ell ^{2}}-\widetilde{d}_{i,j}^{*}d_{2}\frac{j^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+\widetilde{d}_{i,j}^{*}\frac{j^{2}}{\ell ^{2}}}>0,~i, j \in \mathbb {N}. \end{aligned}\end{aligned}$$

(2.11)

Proof

By noticing that

$$\begin{aligned} c=\widetilde{c}_{n}(d_{1}) \triangleq \frac{d_{2}u_{*}\xi \frac{n^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{n^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}} \end{aligned}$$

with $0<d_{1}<\widetilde{d}_{n}=(u_{*}\xi \ell ^{2})/n^{2},~n \in \mathbb {N}$, then by solving

$$\begin{aligned} \frac{d_{2}u_{*}\xi \frac{i^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{i^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{i^{2}}{\ell ^{2}}}=\frac{d_{2}u_{*}\xi \frac{j^{2}}{\ell ^{2}}-d_{1}d_{2}\frac{j^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+d_{1}\frac{j^{2}}{\ell ^{2}}}, \end{aligned}$$

(2.12)

we obtain that

$$\begin{aligned} \frac{i^{2}j^{2}}{\ell ^{4}}d_{1}^{2}+\frac{\xi (i^{2}+j^{2})}{\ell ^{2}(1-\kappa )}d_{1}-\frac{u_{*}\xi ^{2}}{1-\kappa }=0. \end{aligned}$$

(2.13)

Thus, from (2.13) and by a direct calculation, we obtain that

$$\begin{aligned} \widetilde{d}_{i,j}^{*}=\frac{\left( -\frac{(i^{2}+j^{2})}{1-\kappa }+\sqrt{\frac{4i^{2}j^{2}u_{*}}{1-\kappa }+\frac{(i^{2}+j^{2})^{2}}{(1-\kappa )^{2}}}\right) \xi \ell ^{2}}{2i^{2}j^{2}}>0. \end{aligned}$$

Moreover, from (2.12), we obtain that

$$\begin{aligned} \widetilde{c}_{i,j}^{*}=\frac{d_{2}u_{*}\xi \frac{j^{2}}{\ell ^{2}}-\widetilde{d}_{i,j}^{*}d_{2}\frac{j^{4}}{\ell ^{4}}}{\frac{\xi }{1-\kappa }+\widetilde{d}_{i,j}^{*}\frac{j^{2}}{\ell ^{2}}}>0,~i, j \in \mathbb {N}. \end{aligned}$$

$\square$

Therefore, in $d_{1}-c$ plane, by combining with (2.10) and Theorem 2.2, we can define the Hopf bifurcation curves and Turing bifurcation curves, i.e.,

$$\begin{aligned} \begin{aligned}&\mathcal {H}_{0}: c=\overline{c}_{0}(d_{1}),~0<d_{1}, \\&\mathcal {H}_{n}: c=\overline{c}_{n}(d_{1}),~0<d_{1}<\overline{d}_{n},~n \in \mathbb {N}, \\&\mathcal {T}_{n}: c=\widetilde{c}_{n}(d_{1}),~0<d_{1}<\widetilde{d}_{n},~n \in \mathbb {N}, \end{aligned}\end{aligned}$$

(2.14)

and the piecewise smooth curve

$$\begin{aligned} \mathcal {T}: c=\widetilde{c}(d_{1}) \triangleq \widetilde{c}_{n}(d_{1}),~\widetilde{d}_{n,n+1}^{*} \le d_{1}<\widetilde{d}_{n-1,n}^{*},~n \in \mathbb {N} \end{aligned}$$

(2.15)

with $\widetilde{d}_{0,1}^{*} \triangleq \widetilde{d}_{1}=u_{*}\xi \ell ^{2}$. Here, $\mathcal {T}$ is called the first Turing bifurcation curve, since when $(d_{1},c)$ crosses $\mathcal {T}$ from top to bottom, the system (1.4) undergoes Turing bifurcation for the first time.

Theorem 2.4

When $(d_{1},c)$ crosses $\mathcal {T}$ which is defined by (2.15) from top to bottom in $d_{1}-c$ plane, the system (1.4) undergoes Turing bifurcation for the first time.

Proof

According to Theorem 2.3, the Turing bifurcation curves $\mathcal {T}_{i}$ and $\mathcal {T}_{j}$ intersect uniquely at $(\widetilde{d}_{i,j}^{*},\widetilde{c}_{i,j}^{*})$ in the first quadrant. Moreover, by considering that

$$\begin{aligned} \widetilde{d}_{i,j}^{*}=\frac{\left( -\frac{(i^{2}+j^{2})}{1-\kappa } +\sqrt{\frac{4i^{2}j^{2}u_{*}}{1-\kappa }+\frac{(i^{2}+j^{2})^{2}}{(1-\kappa )^{2}}}\right) \xi \ell ^{2}}{2i^{2}j^{2}}>0, \end{aligned}$$

and by a direct calculation, we have

$$\begin{aligned} \frac{\partial \widetilde{d}_{i,j}^{*}}{\partial i}<0,~\frac{\partial \widetilde{d}_{i,j}^{*}}{\partial j}<0, \end{aligned}$$

which indicates that $\widetilde{d}_{i,j}^{*}$ decreases with i, j, respectively. Furthermore, by noticing that $\widetilde{c}(d_{1})$ decreases with $d_{1}$,

$$\begin{aligned} \begin{aligned}&\frac{\partial \widetilde{c}(d_{1})}{\partial d_{1}}=\frac{\partial \widetilde{c}_{n}(d_{1})}{\partial d_{1}}=-\frac{\xi (u_{*}+\frac{1}{1-\kappa })d_{2}\frac{n^{4}}{\ell ^{4}}}{(\frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}})^{2}}<0, \\&\frac{\partial ^{2}\widetilde{c}(d_{1})}{\partial d_{1}^{2}}=\frac{\partial ^{2}\widetilde{c}_{n}(d_{1})}{\partial d_{1}^{2}}=\frac{2\xi (u_{*}+\frac{1}{1-\kappa })d_{2}\frac{n^{6}}{\ell ^{6}}}{\left( \frac{\xi }{1-\kappa }+d_{1}\frac{n^{2}}{\ell ^{2}}\right) ^{3}}>0,~\widetilde{d}_{n,n+1}^{*} \le d_{1}<\widetilde{d}_{n-1,n}^{*},~n \in \mathbb {N}, \end{aligned} \end{aligned}$$

and $\widetilde{c}_{i,j}^{*}$ increases with i, j, respectively. Therefore, we have $\widetilde{d}_{n,n+1}^{*}<\widetilde{d}_{n-1,n+1}^{*}<\widetilde{d}_{n-1,n}^{*}$ and $\widetilde{c}_{n,n+1}^{*}>\widetilde{c}_{n-1,n+1}^{*}>\widetilde{c}_{n-1,n}^{*}$ for $n \ge 2$. Thus, for $d_{1} \in (\widetilde{d}_{n,n+1}^{*},\widetilde{d}_{n-1,n}^{*})$, the Turing bifurcation curves $\mathcal {T}_{n-1}$ and $\mathcal {T}_{n+1}$, together with the $(n-1,n+1)$-mode Turing–Turing bifurcation point $(\widetilde{d}_{n-1,n+1}^{*},\widetilde{c}_{n-1,n+1}^{*})$, are below $\mathcal {T}_{n}$. By considering that $n \ge 2$ is arbitrary, thus $\mathcal {T}$ is above Turing bifurcation curve $\mathcal {T}_{n}$ in $d_{1}-c$ plane with $\mathcal {T}$ and $\mathcal {T}_{n}$ coinciding on $(\widetilde{d}_{n,n+1}^{*},\widetilde{d}_{n-1,n}^{*})$. Furthermore, for $n=1$, $\mathcal {T}$ is also above $\mathcal {T}_{1}$ in $d_{1}-c$ plane with $\mathcal {T}$ and $\mathcal {T}_{1}$ coinciding on $(\widetilde{d}_{1,2}^{*},\widetilde{d}_{0,1}^{*})$. Therefore, $\mathcal {T}$ is above the Turing bifurcation curve $\mathcal {T}_{n}$ with $n \in \mathbb {N}$ in $d_{1}-c$ plane with $\mathcal {T}$ and $\mathcal {T}_{n}$ coinciding on $(\widetilde{d}_{n,n+1}^{*},\widetilde{d}_{n-1,n}^{*})$. That is, when $(d_{1},c)$ goes from top to bottom in $d_{1}-c$ plane, it will meet with $\mathcal {T}$ firstly. Thus, the conclusion is obtained. $\square$

Moreover, based on the above discussion, we have the following conclusions about the n-mode Bogdanov–Takens bifurcation, that is, the n-mode bifurcation from a double zero eigenvalue, where $n \in \mathbb {N}_{0}$. Here, we regard a n-mode Bogdanov–Takens bifurcation point as the intersection of n-mode steady-state bifurcation curve and n-mode Hopf bifurcation curve. Notice that when $n \in \mathbb {N}$, the n-mode steady-state bifurcation curve is actually the n-mode Turing bifurcation curve.

Theorem 2.5

If $\xi <\beta$, $0<d_{1}<\overline{d}_{1}$ and $\ell \in (\widetilde{l}_{1}^{*},\infty )$, then when $(d_{1},c)=(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})$, the 1-mode Bogdanov–Takens bifurcation occurs for the system (1.4), which satisfies the characteristic equation (2.6) has a double zero root with the remaining roots having negative real parts, where

$$\begin{aligned} \begin{aligned} \widetilde{l}_{1}^{*}&=\sqrt{\frac{d_{2}(1-\kappa )\left( \sqrt{(16u_{*}(1-\kappa )+25) (1+4u_{*}(1-\kappa ))^{2}}+(5-4u_{*}(1-\kappa ))\right) }{8u_{*}\xi (u_{*}(1-\kappa )^{2}+1-\kappa )}},\\ \widetilde{d}_{1}^{*}&=\frac{\xi \ell ^{2}(u_{*}(1-\kappa )-1)}{2(1-\kappa )} +\frac{\sqrt{\xi \ell ^{2}(u_{*}(1-\kappa )+1)(\xi \ell ^{2}(u_{*}(1-\kappa )+1)-4d_{2}(1-\kappa ))}}{2(1-\kappa )}, \\ \overline{c}_{1}^{*}&=u_{*}\xi -\frac{\widetilde{d}_{1}^{*}+d_{2}}{\ell ^{2}}. \end{aligned} \end{aligned}$$

(2.16)

Proof

Define the function $\delta (d_{1})=\widetilde{c}(d_{1})-\overline{c}_{1}(d_{1})$ for $0<d_{1}<\overline{d}_{1}=u_{*}\xi \ell ^{2}-d_{2}$, since $\widetilde{c}_{n}(d_{1})$ decreases with $d_{1}$, $\overline{c}_{1}(\overline{d}_{1})=0$ and $\widetilde{c}_{1}(\overline{d}_{1})>0$, then $\lim _{d_{1} \rightarrow \overline{d}_{1}}\delta (d_{1})=\delta (\overline{d}_{1})=\widetilde{c}(\overline{d}_{1}) -\overline{c}_{1}(\overline{d}_{1})=\widetilde{c}(\overline{d}_{1}) \ge \widetilde{c}_{1}(\overline{d}_{1})>0$. Moreover, from (2.11), we have

$$\begin{aligned} \widetilde{d}_{1,2}^{*}=\frac{\left( -\frac{5}{1-\kappa }+\sqrt{\frac{16\lambda }{1-\kappa } +\frac{25}{(1-\kappa )^{2}}}\right) \xi \ell ^{2}}{8}=\frac{\left( -5+\sqrt{16\lambda (1-\kappa )+25}\right) \xi \ell ^{2}}{8(1-\kappa )}, \end{aligned}$$

and by a direct calculation, we obtain that $\delta (\widetilde{d}_{1,2}^{*})<0$ if and only if

$$\begin{aligned} \begin{aligned}&\left( 16\lambda \xi (1-\kappa )+10\xi -2\xi \sqrt{16\lambda (1-\kappa )+25}\right) \ell ^{2} \\&>16d_{2}(1-\kappa )-40d_{2}(1-\kappa )+8d_{2}(1-\kappa )\sqrt{16\lambda (1-\kappa )+25}. \end{aligned} \end{aligned}$$

(2.17)

Hence, from (2.17), and by a direct calculation, we obtain that

$$\begin{aligned} \ell >\widetilde{l}_{1}^{*}:=\sqrt{\frac{d_{2}(1-\kappa )\left( \sqrt{(16u_{*}(1-\kappa )+25) (1+4u_{*}(1-\kappa ))^{2}}+(5-4u_{*}(1-\kappa ))\right) }{8u_{*}\xi (u_{*}(1-\kappa )^{2}+1-\kappa )}}. \end{aligned}$$

Therefore, a direct calculation yields that $\delta (\widetilde{d}_{1,2}^{*})<0$ when $\ell \in (\widetilde{l}_{1}^{*},\infty )$, which means $\overline{c}_{1}(\widetilde{d}_{1,2}^{*})>\widetilde{c}(\widetilde{d}_{1,2}^{*})=\widetilde{c}_{1}(\widetilde{d}_{1,2}^{*})>0$. By considering that $\overline{c}_{1}(d_{1})$ decreases with $d_{1}$, and thus we have $\widetilde{d}_{1,2}^{*}<\overline{d}_{1}$. Therefore, by the Intermediate Value Theorem, there exists a $\widetilde{d}^{*} \in (\widetilde{d}_{1,2}^{*},\overline{d}_{1})$ such that $\delta (\widetilde{d}^{*})=0$. Actually, $\widetilde{d}^{*}$ is the unique point satisfying $\delta (d_{1})=0$ in $(\widetilde{d}_{1,2}^{*},\overline{d}_{1})$. Otherwise, if we assume that there exist at least two point $\widetilde{d}_{j}^{*} \in (\widetilde{d}_{1,2}^{*},\overline{d}_{1}),~j=1,2,3, \cdots$ satisfying $\delta (\widetilde{d}_{j}^{*})=0$. Then, there exist at least two point $\widetilde{d}_{1}^{**}, \widetilde{d}_{2}^{**} \in (\widetilde{d}_{1,2}^{*},\overline{d}_{1})$ such that $\widetilde{c}^{\prime }(\widetilde{d}_{1}^{**})=\widetilde{c}^{\prime }(\widetilde{d}_{2}^{**}) =\widetilde{c}_{1}^{\prime }(\widetilde{d}_{1}^{**})=\widetilde{c}_{1}^{\prime }(\widetilde{d}_{2}^{**}) =\overline{c}_{1}^{\prime }(\widetilde{d}_{1}^{**})=\overline{c}_{1}^{\prime }(\widetilde{d}_{2}^{**})=-1/\ell ^{2}$, which is contradictory with $\partial ^{2}\widetilde{c}_{1}(d_{1})/\partial d_{1}^{2}>0$. Thus, by solving $\widetilde{c}_{1}(d_{1})=\overline{c}_{1}(d_{1})$, we obtain that $\widetilde{d}_{1}^{*}$ and $\overline{c}_{1}^{*}$. Then, the 1-mode Bogdanov–Takens bifurcation occurs. Also, we have $\overline{c}_{1}(d_{1})>\overline{c}_{n}(d_{1})$ with $0<d_{1}<\overline{d}_{1}$ and $n \ge 2$, which means that system (1.4) undergoes Hopf bifurcation for the first time when $(d_{1},c)$ goes from top to bottom in $d_{1}-c$ plane. Furthermore, from $\overline{c}_{1}(d_{1})>\overline{c}_{n}(d_{1})$, we can deduce that $T_{n}<0$. Therefore, except a double zero root, the remaining roots of characteristic equation (2.6) has negative real parts. Therefore, the conclusion is obtained. $\square$

By combining with the Theorem 2.5, we have the following theorem.

Theorem 2.6

If $\xi >\beta$, $0<d_{1}<\overline{d}_{n}$ and $\ell \in (\widetilde{l}_{1}^{*},\widetilde{l}^{*})$, then the 1-mode Bogdanov–Takens bifurcation occurs for the system (1.4) when $(d_{1},c)=(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})$, satisfying that characteristic equation (2.6) has a double zero root with the remaining roots having negative real parts, where

$$\begin{aligned}\begin{aligned} \widetilde{l}_{1}^{*}&=\sqrt{\frac{d_{2}(1-\kappa )\left( \sqrt{256u_{*}^{3}(1-\kappa )^{3}+528u_{*}^{2}(1-\kappa )^{2}+216u_{*}(1-\kappa )+25}+(5-4u_{*}(1-\kappa ))\right) }{8u_{*}\xi (u_{*}(1-\kappa )^{2}+1-\kappa )}}, \\ \widetilde{l}^{*}&=\sqrt{\frac{d_{2}\left( u_{*}(1-\kappa )(\beta -\xi )+\sqrt{u_{*}\xi (1-\kappa )(\xi -\beta )(u_{*}(1-\kappa )+1)}\right) }{u_{*}(\beta -\xi )(\xi +u_{*}\beta (1-\kappa ))}}, \\ \widetilde{d}_{1}^{*}&=\frac{\xi \ell ^{2}(u_{*}(1-\kappa )-1)}{2(1-\kappa )}+\frac{\sqrt{\xi \ell ^{2}(u_{*}(1-\kappa )+1)(\xi \ell ^{2}(u_{*}(1-\kappa )+1)-4d_{2}(1-\kappa ))}}{2(1-\kappa )}, \\ \overline{c}_{1}^{*}&=u_{*}\xi -\frac{\widetilde{d}_{1}^{*}+d_{2}}{\ell ^{2}}. \end{aligned}\end{aligned}$$

Proof

Since $\xi >\beta$, thus the curves $\widetilde{c}(d_{1})$ and $\overline{c}_{0}(d_{1})$ may intersect. By defining the function $\delta (d_{1})=\widetilde{c}(d_{1})-\overline{c}_{0}(d_{1})$ for $0<d_{1}<\widetilde{d}_{1}=u_{*}\xi \ell ^{2}$, since $\widetilde{c}_{1}(\widetilde{d}_{1})=0$ and $\overline{c}_{0}(\widetilde{d}_{1})>0$, then $\lim _{d_{1} \rightarrow \widetilde{d}_{1}}\delta (d_{1})=\delta (\widetilde{d}_{1})=\widetilde{c}(\widetilde{d}_{1}) -\overline{c}_{0}(\widetilde{d}_{1})=-\overline{c}_{0}(\widetilde{d}_{1})<0$. Moreover, since $\xi >\beta$, thus we can choose $\widetilde{d}_{1,2}^{*}=\lambda \beta \ell ^{2}-d_{2}$, we can see that $\widetilde{d}_{1,2}^{*}=\lambda \beta \ell ^{2}-d_{2}<\overline{d}_{1} =\lambda \xi \ell ^{2}-d_{2}<\widetilde{d}_{1}=\lambda \xi \ell ^{2}$. Therefore, by a direct calculation, we obtain that $\delta (\widetilde{d}_{1,2}^{*})>0$ if and only if

$$\begin{aligned} \lambda (\beta -\xi )(\xi +\lambda \beta (1-\kappa ))\ell ^{4} +2d_{2}\lambda (1-\kappa )(\xi -\beta )\ell ^{2}+d_{2}^{2}(1-\kappa )>0. \end{aligned}$$

(2.18)

By noticing that $\xi >\beta$, thus from (2.18), and by a direct calculation, we obtain that

$$\begin{aligned} \ell <\widetilde{l}^{*}:=\sqrt{\frac{d_{2}\left( u_{*}(1-\kappa )(\beta -\xi ) +\sqrt{u_{*}\xi (1-\kappa )(\xi -\beta )(u_{*}(1-\kappa )+1)}\right) }{u_{*}(\beta -\xi )(\xi +u_{*}\beta (1-\kappa ))}}. \end{aligned}$$

Furthermore, by noticing that $\widetilde{d}_{1,2}^{*}<\widetilde{d}_{1}$, $\delta (\widetilde{d}_{1,2}^{*})>0$ and $\delta (\widetilde{d}_{1})<0$, thus by the Intermediate Value Theorem, there exists a $\widetilde{d}^{*} \in (\widetilde{d}_{1,2}^{*},\widetilde{d}_{1})$ such that $\delta (\widetilde{d}^{*})=0$. Furthermore, when $\xi >\beta$, by combining with Theorem 2.5, we can obtain the condition of the occurrence of the 1-mode Bogdanov–Takens bifurcation for the system (1.4). Therefore, the conclusion is obtained. $\square$

3 Normal form for Bogdanov–Takens bifurcation in diffusive predator–prey system with nonlocal effect and prey refuge

3.1 Basic assumption and equation transformation

Assumption 3.1

When $(d_{1},c)=(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})$, there exists $n=n_{1} \in \mathbb {N}$ such that the characteristic equation $\Gamma _{n_{1}}(\lambda )=0$ has a double zero root with the remaining roots having negative real parts. Meanwhile, the corresponding transversality condition holds.

In what follows, we set $d_{1}=\widetilde{d}_{1}^{*}+\mu _{1}$ and $c=\overline{c}_{1}^{*}+\mu _{2}$ such that $\mu :=(\mu _{1},\mu _{2})=(0,0)$ corresponds to the Bogdanov–Takens bifurcation point of the system (1.4). Moreover, we shift the positive constant steady state $E_{*}=(u_{*},v_{*})$ to the origin by setting

$$\begin{aligned} \begin{aligned}&U(x,t)=(U_{1}(x,t),U_{2}(x,t))^{T}=(u(x,t),v(x,t))^{T}-(u_{*},v_{*})^{T}, \\&\widehat{U}=(\widehat{U}_{1},\widehat{U}_{2})^{T}=(\widehat{u},\widehat{v})^{T}-(u_{*},v_{*})^{T}. \end{aligned} \end{aligned}$$

Furthermore, we rewrite U(t) for U(x, t). Then, the system (1.4) can be written as

$$\begin{aligned} \frac{\textrm{d}U}{\textrm{d}t}=d(\mu )\Delta U+L(\mu )U+\widehat{L}(0)\widehat{U}+F(U,\widehat{U},\mu ), \end{aligned}$$

(3.1)

where

$$\begin{aligned} \begin{aligned}&d(\mu )\Delta U=(D^{c}+D_{\mu }^{c})\Delta U=(D^{c}+D_{\mu }^{c})U_{xx}, \\&L(\mu )U=A_{1}(\mu )U,~\widehat{L}(0)\widehat{U}=A_{2}\widehat{U} \end{aligned}\end{aligned}$$

(3.2)

and

$$\begin{aligned} \begin{aligned} F(U,\widehat{U},\mu )&=\left( \begin{array}{cc} (U(x,t)+u_{*})(1-\beta (\widehat{U}+u_{*}))-\frac{b(1-\kappa )(U(x,t)+u_{*})(V(x,t)+v_{*})}{1+(1-\kappa )(U(x,t)+u_{*})} \\ (\overline{c}_{1}^{*}+\mu _{2})(V(x,t)+v_{*})\left( 1-\frac{V(x,t)+v_{*}}{(1-\kappa )(U(x,t)+u_{*})}\right) \end{array}\right) \\&\quad -L(\mu )U-\widehat{L}(0)\widehat{U} \end{aligned} \end{aligned}$$

(3.3)

with

$$\begin{aligned} \begin{aligned}&A_{1}(\mu )=\left( \begin{array}{cc} \frac{u_{*}(1-\kappa )(1-\beta u_{*})}{1+(1-\kappa )u_{*}} &{} -\frac{(1-\beta u_{*})}{1-\kappa } \\ (1-\kappa )(\overline{c}_{1}^{*}+\mu _{2}) &{} -(\overline{c}_{1}^{*}+\mu _{2}) \end{array}\right) ,~A_{2}=\left( \begin{array}{cc} -\beta u_{*} &{} 0 \\ 0 &{} 0 \end{array}\right) , \\&D^{c}=\left( \begin{array}{cc} \widetilde{d}_{1}^{*} &{} 0 \\ 0 &{} d_{2} \end{array}\right) ,~D_{\mu }^{c}=\left( \begin{array}{cc} \mu _{1} &{} 0 \\ 0 &{} 0 \end{array}\right) . \end{aligned} \end{aligned}$$

(3.4)

In what follows, we assume that $F(U,\widehat{U},\mu )$ is $C^{k}(k \ge 3)$, smooth with respect to U, $\widehat{U}$ and $\mu$. Moreover, by combining with (3.1), (3.2), (3.3) and (3.4), and by denoting $d_{0}:=d(0)$, $L_{0}:=L(0)$ and $\widehat{L}_{0}:=\widehat{L}(0)$, we rewrite (3.1) as

$$\begin{aligned} \frac{\textrm{d}U}{\textrm{d}t}=d_{0}\Delta U+L_{0}U+\widehat{L}_{0}\widehat{U}+\widetilde{F}(U,\widehat{U},\mu ) \end{aligned}$$

(3.5)

by separating the linear terms from the nonlinear terms, where

$$\begin{aligned} \widetilde{F}(U,\widehat{U},\mu )=D_{\mu }^{c}\Delta U+A_{\mu }^{c}U+F(U,\widehat{U},\mu ) \end{aligned}$$

(3.6)

with

$$\begin{aligned} A_{\mu }^{c}=\left( \begin{array}{cc} 0 &{} 0 \\ (1-\kappa )\mu _{2} &{} -\mu _{2} \end{array}\right) . \end{aligned}$$

Then, the characteristic equation for the linearized system of (3.5)

$$\begin{aligned} \frac{\textrm{d}U}{\textrm{d}t}=d_{0}\Delta U+L_{0}U+\widehat{L}_{0}\widehat{U} \end{aligned}$$

(3.7)

is

$$\begin{aligned} \prod _{n \in \mathbb {N}_{0}} \widetilde{\Gamma }_{n}(\lambda )=0, \end{aligned}$$

(3.8)

where $\widetilde{\Gamma }_{n}(\lambda )={\text {det}}(\widetilde{\mathcal {M}}_{n}(\lambda ))$ with

$$\begin{aligned} \widetilde{\mathcal {M}}_{n}(\lambda )=\left\{ \begin{aligned}&\lambda I_{2}-A_{1}(0)-A_{2},&n=0, \\&\lambda I_{2}+\frac{n^{2}}{\ell ^{2}}D^{c}-A_{1}(0),&n\in \mathbb {N}. \end{aligned}\right. \end{aligned}$$

(3.9)

By comparing (3.9) with (2.5), and from the Assumption 3.1, we know that (3.8) has a double zero root with the remaining roots having negative real parts. Furthermore, by choosing

$$\begin{aligned} \Phi _{n_{1}}=(\xi _{1},\xi _{2}),~\Psi _{n_{1}}=(\eta _{1},\eta _{2})^{T}, \end{aligned}$$

(3.10)

where $\xi _{1}={\text {col}}(\xi _{11},\xi _{12}) \in \mathbb {R}^{2}$ and $\xi _{2}={\text {col}}(\xi _{21},\xi _{22}) \in \mathbb {R}^{2}$ are the eigenvectors of the system (3.7) associated with the double zero eigenvalue, $\eta _{1}={\text {col}}(\eta _{11},\eta _{12}) \in \mathbb {R}^{2}$ and $\eta _{2}={\text {col}}(\eta _{21},\eta _{22}) \in \mathbb {R}^{2}$ are the corresponding adjoint eigenvectors such that

$$\begin{aligned} \left\langle \Psi _{n_{1}},\Phi _{n_{1}}\right\rangle _{n_{1}}=I_{2}, \end{aligned}$$

where $\left\langle \Psi _{n_{1}},\Phi _{n_{1}}\right\rangle _{n_{1}}=\Psi _{n_{1}}\Phi _{n_{1}}$, and the symbol ${\text {col}}(.)$ represents the column vector.

According to [31], the phase space X can be decomposed as

$$\begin{aligned} X=\mathcal {P} \oplus \mathcal {Q},~\mathcal {P}={\text {Im}}\pi ,~\mathcal {Q}={\text {Ker}}\pi , \end{aligned}$$

(3.11)

where for $\phi \in X$, the projection $\pi : X \rightarrow \mathcal {P}$ is defined by

$$\begin{aligned} \pi (\phi )=\Phi _{n_{1}}\left\langle \Psi _{n_{1}},\left( \begin{aligned}&\left[ \phi ,\beta _{n_{1}}^{(1)}\right] \\&\left[ \phi ,\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \right\rangle _{n_{1}}\gamma _{n_{1}}(x). \end{aligned}$$

(3.12)

By combining with (3.4) and (3.9), when $n=0$, we have

$$\begin{aligned} A_{1}(0)+A_{2}=\left( \begin{array}{cc} \frac{u_{*}(1-\kappa )(1-\beta u_{*})}{1+(1-\kappa )u_{*}}-\beta u_{*} &{} -\frac{(1-\beta u_{*})}{1-\kappa } \\ (1-\kappa )\overline{c}_{1}^{*} &{} -\overline{c}_{1}^{*} \end{array}\right) , \end{aligned}$$

and when $n\in \mathbb {N}$, we have

$$\begin{aligned} D^{c}=\left( \begin{array}{cc} \widetilde{d}_{1}^{*} &{} 0 \\ 0 &{} d_{2} \end{array}\right) ,~A_{1}(0)=\left( \begin{array}{cc} \frac{u_{*}(1-\kappa )(1-\beta u_{*})}{1+(1-\kappa )u_{*}} &{} -\frac{(1-\beta u_{*})}{1-\kappa } \\ (1-\kappa )\overline{c}_{1}^{*} &{} -\overline{c}_{1}^{*} \end{array}\right) . \end{aligned}$$

Then, by a direct calculation, we have

$$\begin{aligned}\begin{aligned} \xi _{1}&=\left( 1,\frac{(1-\kappa )\overline{c}_{1}^{*}}{d_{2}\frac{n_{1}^{2}}{\ell ^{2}}+\overline{c}_{1}^{*}}\right) ^{T},~\xi _{2}=\left( 0,-\frac{(1-\kappa )\overline{c}_{1}^{*}}{\left( d_{2}\frac{n_{1}^{2}}{\ell ^{2}}+\overline{c}_{1}^{*}\right) ^{2}}\right) ^{T}, \\ \eta _{1}&=\left( 1,0\right) ^{T},~\eta _{2}=\left( d_{2}\frac{n_{1}^{2}}{\ell ^{2}}+\overline{c}_{1}^{*},-\frac{\left( d_{2}\frac{n_{1}^{2}}{\ell ^{2}}+\overline{c}_{1}^{*}\right) ^{2}}{(1-\kappa )\overline{c}_{1}^{*}}\right) ^{T}, \end{aligned}\end{aligned}$$

which satisfies

$$\begin{aligned}\begin{aligned}&\left( 0I_{2}+\frac{n_{1}^{2}}{\ell ^{2}}D^{c}-A_{1}(0)\right) \xi _{1}=(0,0)^{T},~\left\langle \eta _{1},\xi _{1}\right\rangle _{n_{1}}=1, \\&\left( 0I_{2}+\frac{n_{1}^{2}}{\ell ^{2}}D^{c}-A_{1}(0)\right) \xi _{2}+\xi _{1}=(0,0)^{T},~\left\langle \eta _{1},\xi _{2}\right\rangle _{n_{1}}=0, \\&\left\langle \eta _{2},\xi _{2}\right\rangle _{n_{1}}=1,~\left\langle \eta _{2},\xi _{1}\right\rangle _{n_{1}}=0. \end{aligned}\end{aligned}$$

By combining with (3.10), (3.11) and (3.12), U can be decomposed as

$$\begin{aligned} \begin{aligned} U&=\Phi _{n_{1}}\left( \begin{array}{c} z_{1} \\ z_{2} \end{array}\right) \gamma _{n_{1}}(x)+w=\left( z_{1}\xi _{1}+z_{2}\xi _{2}\right) \gamma _{n_{1}}(x)+w \\&=\Phi _{n_{1}}\left( \begin{array}{c} z_{1}\gamma _{n_{1}}(x) \\ z_{2}\gamma _{n_{1}}(x) \end{array}\right) +\left( \begin{array}{c} w_{1} \\ w_{2} \end{array}\right) , \end{aligned}\end{aligned}$$

(3.13)

where $w={\text {col}}(w_{1},w_{2})\in \mathcal {Q}$ and

$$\begin{aligned} \left( \begin{array}{cc} z_{1} \\ z_{2} \end{array}\right) =\left\langle \Psi _{n_{1}},\left( \begin{aligned}&\left[ U,\beta _{n_{1}}^{(1)}\right] \\&\left[ U,\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \right\rangle _{n_{1}}. \end{aligned}$$

Let

$$\begin{aligned} \Phi =\Phi _{n_{1}},~z_{x}=(z_{1}\gamma _{n_{1}}(x),z_{2}\gamma _{n_{1}}(x))^{T}, \end{aligned}$$

(3.14)

then (3.13) can be written as $U=\Phi z_{x}+w$. Therefore, the system (3.5) is decomposed as a system of abstract ODE on $\mathbb {R}^{2} \times {\text {Ker}}\pi$, with finite and infinite dimensional variables are separated in the linear term. That is

$$\begin{aligned} \left\{ \begin{aligned}&\dot{z}=Bz+\Psi \left( \begin{aligned}&\left[ \widetilde{F}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ \widetilde{F}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) , \\&\dot{w}=\mathcal {L}_{n}(w,\widehat{w})+(I_{2}-\pi )\widetilde{F}\left( \Phi z_{x}+w,\widehat{w},\mu \right) , \end{aligned}\right. \end{aligned}$$

(3.15)

where $z=(z_{1},z_{2})^{T}$, $\Psi =\Psi _{n_{1}}^{T}$, $\mathcal {L}_{n}(w,\widehat{w})$ is defined by

$$\begin{aligned} \mathcal {L}_{n}(w,\widehat{w})=D^{c}\Delta w+L(0)w+\widehat{L}(0)\widehat{w}, \end{aligned}$$

and

$$\begin{aligned} B=\left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array}\right) . \end{aligned}$$

From (3.6), and by considering the formal Taylor expansions

$$\begin{aligned}\begin{aligned}&\widetilde{F}(U,\widehat{U},\mu )=\sum _{j \ge 2}\frac{1}{j!}\widetilde{F}_{j}(U,\widehat{U},\mu ),~F(U,\widehat{U},\mu )=\sum _{j \ge 2}\frac{1}{j!}F_{j}(U,\widehat{U},\mu ), \end{aligned}\end{aligned}$$

then the system (3.15) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}&=Bz+\sum _{j \ge 2}\frac{1}{j!}f_{j}^{1}(z,w,\widehat{w},\mu ), \\ \dot{w}&=\mathcal {L}_{n}(w,\widehat{w})+\sum _{j \ge 2}\frac{1}{j!}f_{j}^{2}(z,w,\widehat{w},\mu ), \end{aligned}\right. \end{aligned}$$

(3.16)

where $f_{j}:=(f_{j}^{1},f_{j}^{2}),~j \ge 2$ are defined by

$$\begin{aligned} \begin{aligned} f_{2}^{1}(z,w,\widehat{w},\mu )&=\Psi \left( \begin{aligned}&\left[ \widetilde{F}_{2}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ \widetilde{F}_{2}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( \begin{aligned}&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x}+w)+2A_{\mu }^{c}(\Phi z_{x}+w)+F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(1)}\right] \\&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x}+w)+2A_{\mu }^{c}(\Phi z_{x}+w)+F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) , \\ f_{j}^{1}(z,w,\widehat{w},\mu )&=\Psi \left( \begin{aligned}&\left[ \widetilde{F}_{j}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ \widetilde{F}_{j}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) =\Psi \left( \begin{aligned}&\left[ F_{j}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{j}(\Phi z_{x}+w,\widehat{w},\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) ,~j\ge 3, \\ f_{2}^{2}(z,w,\widehat{w},\mu )&=(I_{2}-\pi )\left( 2D_{\mu }^{c}\Delta (\Phi z_{x}+w)+2A_{\mu }^{c}(\Phi z_{x}+w)+F_{2}(\Phi z_{x}+w,\widehat{w},0)\right) , \\ f_{j}^{2}(z,w,\widehat{w},\mu )&=(I_{2}-\pi )F_{j}(\Phi z_{x}+w,\widehat{w},\mu ),~j\ge 3. \end{aligned}\end{aligned}$$

(3.17)

Then, by a recursive transformation of variables

$$\begin{aligned} (z,w)=(\widetilde{z},\widetilde{w})+\frac{1}{j!}\left( U_{j}^{1}(\widetilde{z},\mu ),U_{j}^{2}(\widetilde{z},\mu )\right) ,~j \ge 2, \end{aligned}$$

(3.18)

where $z, \widetilde{z} \in \mathbb {R}^{2}$, $w, \widetilde{w} \in \mathcal {Q}$, $U_{j}^{1}(\widetilde{z},\mu )$ and $U_{j}^{2}(\widetilde{z},\mu )$ are homogeneous polynomials of degree j in $\widetilde{z}$ and $\mu$. From (3.18) and by dropping the tilde for simplicity of notation, the system (3.16) is transformed into the normal form

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}&=Bz+\sum _{j \ge 2}\frac{1}{j!}g_{j}^{1}(z,w,\widehat{w},\mu ), \\ \dot{w}&=\mathcal {L}_{n}(w,\widehat{w})+\sum _{j \ge 2}\frac{1}{j!}g_{j}^{2}(z,w,\widehat{w},\mu ), \end{aligned}\right. \end{aligned}$$

(3.19)

where $g_{j}^{1}$ and $g_{j}^{2}$ are given by

$$\begin{aligned} g_{j}^{1}=\widetilde{f}_{j}^{1}-M_{j}^{1}U_{j}^{1},~g_{j}^{2}=\widetilde{f}_{j}^{2}-M_{j}^{2}U_{j}^{2} \end{aligned}$$

(3.20)

with $\widetilde{f}_{j}^{1}$ and $\widetilde{f}_{j}^{2}$ are the terms of order j obtained after the changes of variables in previous step, and

$$\begin{aligned} M_{j}^{1}U_{j}^{1}=D_{z}U_{j}^{1}(z,\mu )Bz-BU_{j}^{1}(z,\mu ),~M_{j}^{2}U_{j}^{2}=D_{z}U_{j}^{2}(z,\mu )Bz-\mathcal {L}_{n}U_{j}^{2}(z,\mu ). \end{aligned}$$

(3.21)

Furthermore, by referring to [31], a locally center manifold for (3.19) satisfies $w=0$, and the flow on it is given by the two-dimensional ODE

$$\begin{aligned} \dot{z}=Bz+\sum _{j \ge 2}\frac{1}{j!}g_{j}^{1}(z,0,0,\mu ), \end{aligned}$$

(3.22)

which is the normal form as in the usual sense for ODE. Furthermore, from (3.20), we have

$$\begin{aligned} g_{2}^{1}(z,0,0,\mu )={\text {Proj}}_{{\text {Im}}(M_{2}^{1})^{c}}f_{2}^{1}(z,0,0,\mu ) \end{aligned}$$

(3.23)

and

$$\begin{aligned} \begin{aligned} g_{3}^{1}(z,0,0,\mu )&={\text {Proj}}_{{\text {Im}}(M_{3}^{1})^{c}}\widetilde{f}_{3}^{1}(z,0,0,\mu ) \\&={\text {Proj}}_{S_{1}}\widetilde{f}_{3}^{1}(z,0,0,0) +{\text {Proj}}_{S_{2}}\widetilde{f}_{3}^{1}(z,0,0,\mu )+O(|z||\mu |^{2}), \end{aligned} \end{aligned}$$

(3.24)

where ${\text {Proj}}_{p}(q)$ represents the projection of q on p, and $\widetilde{f}_{3}^{1}(z,0,0,\mu )$ is vector and its element is the cubic polynomial of $(z,\mu )$ after the variable transformation of (3.18), and it can be determined by (3.33). Furthermore, by referring to [29], we have

$$\begin{aligned} \begin{aligned} {\text {Im}}(M_{2}^{1})^{c}&={\text {span}}\left\{ \left( \begin{array}{c} 0 \\ z_{1}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}^{2} \end{array}\right) ,\right. \\&\left. \left( \begin{array}{c} 0 \\ \mu _{2}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}\mu _{2} \end{array}\right) \right\} , \\ {\text {Im}}(M_{3}^{1})^{c}&={\text {span}}\left\{ \left( \begin{array}{c} 0 \\ z_{1}^{3} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2}z_{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}\mu _{1}^{2} \end{array}\right) ,\right. \\&\left. \left( \begin{array}{c} 0 \\ z_{1}\mu _{2}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{1}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{2}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}\mu _{1}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{1}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}^{3} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{2}^{3} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}^{2}\mu _{2} \end{array}\right) ,\right. \\&\left. \left( \begin{array}{c} 0 \\ \mu _{1}\mu _{2}^{2} \end{array}\right) \right\} , \\ {\text {Im}}(M_{2}^{1})&={\text {span}}\left\{ \left( \begin{array}{c} z_{1}z_{2} \\ 0 \end{array}\right) ,\left( \begin{array}{c} z_{2}^{2} \\ 0 \end{array}\right) ,\left( \begin{array}{c} z_{2}\mu _{i} \\ 0 \end{array}\right) ,\left( \begin{array}{c} -z_{1}^{2} \\ 2z_{1}z_{2} \end{array}\right) ,\left( \begin{array}{c} -z_{1}z_{2} \\ z_{2}^{2} \end{array}\right) ,\left( \begin{array}{c} -z_{1}\mu _{i} \\ z_{2}\mu _{i} \end{array}\right) ,\left( \begin{array}{c} \mu _{i}^{2} \\ 0 \end{array}\right) \right. , \\&\left. \left( \begin{array}{c} \mu _{1}\mu _{2} \\ 0 \end{array}\right) \right\} , \\ {\text {Ker}}(M_{2}^{1})^{c}&={\text {span}}\left\{ \left( \begin{array}{c} z_{1}^{2} \\ 0 \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{2}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}\mu _{1} \end{array}\right) ,\right. \\&\left. \left( \begin{array}{c} 0 \\ z_{1}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{2}^{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ \mu _{1}\mu _{2} \end{array}\right) \right\} , \end{aligned}\end{aligned}$$

(3.25)

and thus we have

$$\begin{aligned} \begin{aligned}&S_{1}={\text {span}}\left\{ \left( \begin{array}{c} 0 \\ z_{1}^{3} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2}z_{2} \end{array}\right) \right\} , \\&S_{2}={\text {span}}\left\{ \left( \begin{array}{c} 0 \\ z_{1}^{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}^{2}\mu _{2} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2}\mu _{1} \end{array}\right) ,\left( \begin{array}{c} 0 \\ z_{1}z_{2}\mu _{2} \end{array}\right) \right\} . \end{aligned}\end{aligned}$$

(3.26)

In what follows, by combining with (3.23), (3.24), (3.25) and (3.26), we will calculate $g_{j}^{1}(z,0,0,\mu ),~j=2,3$ step by step.

3.2 Derivation of the normal form for Bogdanov–Takens bifurcation of the system (1.4)

3.2.1 Calculation of $g_{2}^{1}(z,0,0,\mu )$

From (3.17), we have

$$\begin{aligned} f_{2}^{1}(z,0,0,\mu )=\Psi \left( \begin{aligned}&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x})+2A_{\mu }^{c}\Phi z_{x}+F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(1)}\right] \\&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x})+2A_{\mu }^{c}\Phi z_{x}+F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) , \end{aligned}$$

(3.27)

where $D_{\mu }^{c}$ and $A_{\mu }^{c}$ are rewritten as

$$\begin{aligned} \begin{aligned}&D_{\mu }^{c}=\left( \begin{array}{cc} \mu _{1} &{} 0 \\ 0 &{} 0 \end{array}\right) =\mu _{1}\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array}\right) :=\mu _{1}I_{d}^{1}, \\&A_{\mu }^{c}=\left( \begin{array}{cc} 0 &{} 0 \\ (1-\kappa )\mu _{2} &{} -\mu _{2} \end{array}\right) =\mu _{2}\left( \begin{array}{cc} 0 &{} 0 \\ 1-\kappa &{} 0 \end{array}\right) -\mu _{2}\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 1 \end{array}\right) :=\mu _{2}(I_{d}^{2}-I_{d}^{3}). \end{aligned}\end{aligned}$$

(3.28)

From (3.3), we can write $F_{2}(\Phi z_{x}+w,\widehat{w},0)$ as

$$\begin{aligned} \begin{aligned} F_{2}(\Phi z_{x}+w,\widehat{w},0)&=\sum _{q_{1}+q_{2}=2}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x)+S_{2}(\Phi z_{x},w)+\widehat{S}_{2}(\Phi z_{x},\widehat{w})+O\left( |(w,\widehat{w})|^{2}\right) \\&=A_{20}z_{1}^{2}\gamma _{n_{1}}^{2}(x)+A_{02}z_{2}^{2}\gamma _{n_{1}}^{2}(x)+A_{11}z_{1}z_{2}\gamma _{n_{1}}^{2}(x) \\&+S_{2}(\Phi z_{x},w)+\widehat{S}_{2}(\Phi z_{x},\widehat{w})+O\left( |(w,\widehat{w})|^{2}\right) , \end{aligned}\end{aligned}$$

(3.29)

where $S_{2}(\Phi z_{x},w)$ is the product term of $\Phi z_{x}$ and w, $\widehat{S}_{2}(\Phi z_{x},\widehat{w})$ is the product term of $\Phi z_{x}$ and $\widehat{w}$, $q_{1}, q_{2} \in \mathbb {N}_{0}$, and

$$\begin{aligned} A_{q_{1}q_{2}}=\left( A_{q_{1}q_{2}}^{(1)},A_{q_{1}q_{2}}^{(2)}\right) ^{T}. \end{aligned}$$

Moreover, from (3.14), we have

$$\begin{aligned} \Phi z_{x}=\xi _{1}z_{1}\gamma _{n_{1}}(x)+\xi _{2}z_{2}\gamma _{n_{1}}(x). \end{aligned}$$

(3.30)

Then, by combining with (3.25), (3.27), (3.28), (3.29) and (3.30), and by noticing that

$$\begin{aligned} \int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{3}(x)\textrm{d}x=0,~\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{2}(x)\textrm{d}x=1, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \frac{1}{2!}g_{2}^{1}(z,0,0,\mu )&=\frac{1}{2!}{\text {Proj}}_{{\text {Im}}(M_{2}^{1})^{c}}f_{2}^{1}(z,0,0,\mu ) \\&=\left( \begin{array}{c} 0 \\ B_{2000}z_{1}^{2}+B_{1100}z_{1}z_{2}+B_{1010}z_{1}\mu _{1}+B_{1001}z_{1}\mu _{2}+B_{0110}z_{2}\mu _{1}+B_{0101}z_{2}\mu _{2} \end{array}\right) , \end{aligned} \end{aligned}$$

(3.31)

where

$$\begin{aligned} \left\{ \begin{aligned}&B_{2000}=0,~B_{1100}=0, \\&B_{1010}=(-\frac{n_{1}^{2}}{\ell ^{2}})\eta _{2}^{T}I_{d}^{1}\xi _{1},~B_{1001}=\eta _{2}^{T}(I_{d}^{2}-I_{d}^{3})\xi _{1}, \\&B_{0110}=(-\frac{n_{1}^{2}}{\ell ^{2}})\eta _{2}^{T}I_{d}^{1}\xi _{2},~B_{0101}=\eta _{2}^{T}(I_{d}^{2}-I_{d}^{3})\xi _{2}. \end{aligned}\right. \end{aligned}$$

(3.32)

3.2.2 Calculation of $g_{3}^{1}(z,0,0,\mu )$

In this subsection, we calculate the third-order term $g_{3}^{1}(z,0,0,\mu )$ in terms of (3.24). By noticing that $\widetilde{f}_{3}^{1}(z,0,0,\mu )$ is the term of order 3 obtained after the changes of variables in previous step, which is determined by

$$\begin{aligned} \begin{aligned} \widetilde{f}_{3}^{1}(z,0,0,\mu )&=f_{3}^{1}(z,0,0,\mu )+\frac{3}{2}\left( (D_{z}f_{2}^{1}(z,0,0,\mu ))U_{2}^{1}(z,\mu )+(D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,\mu ))\widetilde{U}_{2}^{2}(z,\mu )\right. \\&\left. -(D_{z}U_{2}^{1}(z,\mu ))g_{2}^{1}(z,0,0,\mu )\right) \end{aligned}\end{aligned}$$

(3.33)

with

$$\begin{aligned} \begin{aligned}&U_{2}^{1}(z,\mu )=(M_{2}^{1})^{-1}{\text {Proj}}_{{\text {Im}}(M_{2}^{1})}f_{2}^{1}(z,0,0,\mu ),~U_{2}^{2}(z,\mu )=(M_{2}^{2})^{-1}f_{2}^{2}(z,0,0,\mu ), \\&\widetilde{U}_{2}^{2}(z,\mu )={\text {col}}(U_{2}^{2}(z,\mu ),\widehat{U}_{2}^{2}(z,\mu ),U_{2,xx}^{2}(z,\mu )),~U_{2}^{2}(z,\mu )\triangleq h(z,\mu )=\sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x), \end{aligned}\end{aligned}$$

(3.34)

where $h_{n}(z,\mu )=\sum _{q_{1}+q_{2}+q_{3}+q_{4}=2}h_{n,q_{1}q_{2}q_{3}q_{4}}z_{1}^{q_{1}}z_{2}^{q_{2}}\mu _{1}^{q_{3}}\mu _{2}^{q_{4}}$ with $h_{n,q_{1}q_{2}q_{3}q_{4}}=\left( h_{n,q_{1}q_{2}q_{3}q_{4}}^{(1)},h_{n,q_{1}q_{2}q_{3}q_{4}}^{(2)}\right) ^{T}$.

By combining with (3.31) and (3.32), we have $g_{2}^{1}(z,0,0,0)=(0,0)^{T}$, then from (3.33), we have

$$\begin{aligned} \begin{aligned} \widetilde{f}_{3}^{1}(z,0,0,0)&=f_{3}^{1}(z,0,0,0)+\frac{3}{2}\left( (D_{z}f_{2}^{1}(z,0,0,0))U_{2}^{1}(z,0)+(D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,0))\widetilde{U}_{2}^{2}(z,0)\right) , \end{aligned}\end{aligned}$$

(3.35)

which implies that it is sufficient for obtaining $g_{3}^{1}(z,0,0,0)$ to compute

$$\begin{aligned} {\text {Proj}}_{S_{1}}f_{3}^{1}(z,0,0,0),~{\text {Proj}}_{S_{1}}((D_{z}f_{2}^{1}(z,0,0,0))U_{2}^{1}(z,0)),~{\text {Proj}}_{S_{1}}((D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,0))\widetilde{U}_{2}^{2}(z,0)). \end{aligned}$$

In what follows, from (3.35), we first calculate ${\text {Proj}}_{S_{1}}\widetilde{f}_{3}^{1}(z,0,0,0)$ step by step.

Step 1   The calculation of ${\text {Proj}}_{S_{1}}f_{3}^{1}(z,0,0,0)$

From (3.17), we have

$$\begin{aligned} f_{3}^{1}(z,0,0,\mu )=\Psi \left( \begin{aligned}&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) , \end{aligned}$$

(3.36)

and similar to (3.29), we can write $F_{3}(\Phi z_{x},0,0)$ as

$$\begin{aligned} F_{3}(\Phi z_{x},0,0)=\sum _{q_{1}+q_{2}=3}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x). \end{aligned}$$

(3.37)

Then, by combining with (3.36) and (3.37), we have

$$\begin{aligned} \begin{aligned} f_{3}^{1}(z,0,0,0)&=\Psi \left( \begin{aligned}&\left[ F_{3}(\Phi z_{x},0,0),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{3}(\Phi z_{x},0,0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( \sum _{q_{1}+q_{2}=3}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{q_{1}+q_{2}+1}(x)\textrm{d}x\right) . \end{aligned} \end{aligned}$$

(3.38)

Therefore, by combining with (3.26), (3.38) and

$$\begin{aligned} \int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{4}(x)\textrm{d}x=\frac{3}{2\ell \pi }, \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{3!}{\text {Proj}}_{S_{1}}f_{3}^{1}(z,0,0,0)=\left( \begin{array}{c} 0 \\ C_{3000}z_{1}^{3}+C_{2100}z_{1}^{2}z_{2} \end{array}\right) , \end{aligned}$$

(3.39)

where

$$\begin{aligned} C_{3000}=\frac{1}{4\ell \pi }\eta _{2}^{T}A_{30},~C_{2100}=\frac{1}{4\ell \pi }\eta _{2}^{T}A_{21}. \end{aligned}$$

Step 2   The calculation of ${\text {Proj}}_{S_{1}}((D_{z}f_{2}^{1}(z,0,0,0))U_{2}^{1}(z,0))$

By a direct calculation, we have

$$\begin{aligned}&b_{n_{1},n,\nu }=\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}(x)\gamma _{n}(x)\gamma _{\nu }(x)\textrm{d}x={\left\{ \begin{array}{ll} \frac{1}{\sqrt{\ell \pi }}, &{}{} { \text{ for } } n=0, \nu =n_{1}, \\ \frac{1}{\sqrt{2\ell \pi }}, &{}{} { \text{ for } } n=2n_{1}, \nu =n_{1}, \\ 0, &{}{}{ \text{ otherwise, } } \end{array}\right. } \end{aligned}$$

(3.40)

Then, by combining with (3.17), (3.29) and (3.40), we have

$$\begin{aligned} \begin{aligned} f_{2}^{1}(z,0,0,0)&=\Psi \left( \begin{aligned}&\left[ F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( \sum _{q_{1}+q_{2}=2}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{q_{1}+q_{2}+1}(x)\textrm{d}x\right) \\&=\left( \begin{array}{c} 0 \\ 0 \end{array}\right) . \end{aligned}\end{aligned}$$

(3.41)

Moreover, by combining with (3.25), (3.41) and

$$\begin{aligned} M_{j}^{1}(z^{q}\mu ^{l})=D_{z}(z^{q}\mu ^{l})Bz-B(z^{q}\mu ^{l})=\left( \begin{array}{c} q_{1}z_{1}^{q_{1}-1}z_{2}^{q_{2}+1}\mu ^{l}-z_{1}^{q_{1}}z_{2}^{q_{2}}\mu ^{l} \\ q_{1}z_{1}^{q_{1}-1}z_{2}^{q_{2}+1}\mu ^{l} \end{array}\right) \end{aligned}$$

(3.42)

with $j=2,3,~q=q_{1}+q_{2}=2,3,~l=l_{1}+l_{2}=2$, and by a direct calculation, we have

$$\begin{aligned} \begin{aligned} U_{2}^{1}(z,0)&=(M_{2}^{1})^{-1}{\text {Proj}}_{{\text {Im}}(M_{2}^{1})}f_{2}^{1}(z,0,0,0) \\&=\left( \begin{array}{c} 0 \\ 0 \end{array}\right) . \end{aligned} \end{aligned}$$

(3.43)

Therefore, by combining with (3.26), (3.41) and (3.43), we have

$$\begin{aligned} \frac{1}{3!}{\text {Proj}}_{S_{1}}\left( D_{z}f_{2}^{1}(z,0,0,0)U_{2}^{1}(z,0)\right) =\left( \begin{array}{c} 0 \\ D_{3000}z_{1}^{3}+D_{2100}z_{1}^{2}z_{2} \end{array}\right) , \end{aligned}$$

(3.44)

where

$$\begin{aligned} D_{3000}=0,~D_{2100}=0. \end{aligned}$$

Step 3   The calculation of ${\text {Proj}}_{S_{1}}((D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,0))\widetilde{U}_{2}^{2}(z,0))$

From (3.34), we have

$$\begin{aligned} U_{2}^{2}(z,0)\triangleq h(z)=\sum _{n \in \mathbb {N}_{0}}h_{n}(z)\gamma _{n}(x), \end{aligned}$$

(3.45)

where $h_{n}(z)=\sum _{q_{1}+q_{2}=2}h_{n,q_{1}q_{2}00}z_{1}^{q_{1}}z_{2}^{q_{2}}$ with $h_{n,q_{1}q_{2}00}=\left( h_{n,q_{1}q_{2}00}^{(1)},h_{n,q_{1}q_{2}00}^{(2)}\right) ^{T}$.

Then, by combining with (2.1) and (3.45), we have

$$\begin{aligned} \widehat{U}_{2}^{2}(z,0)=\frac{1}{\sqrt{\ell \pi }}h_{0}(z),~U_{2,xx}^{2}(z,0)=h_{xx}(z)=-\sum _{n \in \mathbb {N}_{0}}(n/\ell )^{2}h_{n}(z)\gamma _{n}(x). \end{aligned}$$

(3.46)

Furthermore, from (3.17), we have

$$\begin{aligned} f_{2}^{1}(z,w,\widehat{w},0)=\Psi \left( \begin{aligned}&\left[ F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) . \end{aligned}$$

(3.47)

By a direct calculation, we have

$$\begin{aligned} \begin{aligned}&b_{n_{1},n,\nu }=\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}(x)\gamma _{n}(x)\gamma _{\nu }(x)\textrm{d}x={\left\{ \begin{array}{ll} \frac{1}{\sqrt{\ell \pi }}, &{} {\text { for }} n=0,\,\, \nu =n_{1}, \\ \frac{1}{\sqrt{2\ell \pi }}, &{} {\text { for }} n=2n_{1},\,\, \nu =n_{1}, \\ 0,&{} {\text { otherwise, }} \end{array}\right. } \end{aligned}\end{aligned}$$

(3.48)

and

$$\begin{aligned} b_{n,\nu }=\int \limits _{0}^{\ell \pi }\gamma _{n}(x)\gamma _{\nu }(x)\textrm{d}x={\left\{ \begin{array}{ll} 1, &{} {\text { for }} n=\nu , \\ 0, &{} {\text { otherwise }}. \end{array}\right. } \end{aligned}$$

(3.49)

Therefore, by combining with (3.29), (3.34), (3.45), (3.46), (3.47), (3.48) and (3.49), we have

$$\begin{aligned}\begin{aligned}&(D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,0))\widetilde{U}_{2}^{2}(z,0) \\&=\Psi \left( \begin{aligned}&\left[ D_{w,\widehat{w}}F_{2}(\Phi z_{x}+w,\widehat{w},0)\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z)\gamma _{n}(x),\frac{1}{\sqrt{\ell \pi }}h_{0}(z)\right) ,\beta _{n_{1}}^{(1)}\right] \\&\left[ D_{w,\widehat{w}}F_{2}(\Phi z_{x}+w,\widehat{w},0)\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z)\gamma _{n}(x),\frac{1}{\sqrt{\ell \pi }}h_{0}(z)\right) ,\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( \begin{array}{cc} b_{n_{1},0,n_{1}}\left( S_{2}(\xi _{1}z_{1},h_{0}(z))+S_{2}(\xi _{2}z_{2},h_{0}(z))\right) \\ +b_{n_{1},2n_{1},n_{1}}\left( S_{2}(\xi _{1}z_{1},h_{2n_{1}}(z))+S_{2}(\xi _{2}z_{2},h_{2n_{1}}(z))\right) \\ +b_{n_{1},n_{1}}\left( \widehat{S}_{2}(\xi _{1}z_{1},\frac{1}{\sqrt{\ell \pi }}h_{0}(z))+\widehat{S}_{2}(\xi _{2}z_{2},\frac{1}{\sqrt{\ell \pi }}h_{0}(z))\right) \end{array}\right) , \end{aligned}\end{aligned}$$

which together with (3.26), yields to

$$\begin{aligned} \frac{1}{3!}{\text {Proj}}_{S_{1}}\left( (D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,0))\widetilde{U}_{2}^{2}(z,0)\right) =\left( \begin{array}{c} 0 \\ E_{3000}z_{1}^{3}+E_{2100}z_{1}^{2}z_{2} \end{array}\right) , \end{aligned}$$

(3.50)

where

$$\begin{aligned} \left\{ \begin{aligned} E_{3000}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}S_{2}(\xi _{1},h_{0,2000})+\frac{1}{6\sqrt{2\ell \pi }}S_{2}(\xi _{1},h_{2n_{1},2000})+\frac{1}{6\sqrt{\ell \pi }}\widehat{S}_{2}(\xi _{1},h_{0,2000})\right) , \\ E_{2100}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(S_{2}(\xi _{1},h_{0,1100})+S_{2}(\xi _{2},h_{0,2000}))\right) \\&+\eta _{2}^{T}\left( \frac{1}{6\sqrt{2\ell \pi }}(S_{2}(\xi _{1},h_{2n_{1},1100})+S_{2}(\xi _{2},h_{2n_{1},2000}))\right) \\&+\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(\widehat{S}_{2}(\xi _{1},h_{0,1100})+\widehat{S}_{2}(\xi _{2},h_{0,2000}))\right) . \end{aligned}\right. \end{aligned}$$

(3.51)

Next, we will calculate ${\text {Proj}}_{S_{2}}\widetilde{f}_{3}^{1}(z,0,0,\mu )$ step by step. From (3.33), we can see that it is sufficient to calculate

$$\begin{aligned}\begin{aligned}&{\text {Proj}}_{S_{2}}f_{3}^{1}(z,0,0,\mu ),~{\text {Proj}}_{S_{2}}((D_{z}f_{2}^{1}(z,0,0,\mu ))U_{2}^{1}(z,\mu )),~{\text {Proj}}_{S_{2}}((D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,\mu ))\widetilde{U}_{2}^{2}(z,\mu )), \\&{\text {Proj}}_{S_{2}}((D_{z}U_{2}^{1}(z,\mu ))g_{2}^{1}(z,0,0,\mu )). \end{aligned}\end{aligned}$$

Step 1   The calculation of ${\text {Proj}}_{S_{2}}f_{3}^{1}(z,0,0,\mu )$

From (3.17), we can see that

$$\begin{aligned}\begin{aligned} f_{3}^{1}(z,0,0,\mu )&=\Psi \left( \begin{aligned}&\left[ \widetilde{F}_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ \widetilde{F}_{j}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) =\Psi \left( \begin{aligned}&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) . \end{aligned}\end{aligned}$$

From (3.3), we can deduce that $F_{3}(\Phi z_{x},0,\mu )$ is independent of $\mu _{1}$, then by combining with (3.17), (3.26), (3.38) and (3.48), we can write $F_{3}(\Phi z_{x},0,\mu )$ as follows

$$\begin{aligned}\begin{aligned} F_{3}(\Phi z_{x},0,\mu )&=\sum _{q_{1}+q_{2}=3}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x) \\&+\sum _{q_{1}+q_{2}=2}\widehat{A}_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x)\mu _{2}+O(|z||\mu |^{2}), \end{aligned}\end{aligned}$$

then we have

$$\begin{aligned}\begin{aligned} f_{3}^{1}(z,0,0,\mu )&=\Psi \left( \begin{aligned}&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ F_{3}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( \begin{array}{c} \sum _{q_{1}+q_{2}=3}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{q_{1}+q_{2}+1}(x)\textrm{d}x \\ +\sum _{q_{1}+q_{2}=2}\widehat{A}_{q_{1}q_{2}}\mu _{2}z_{1}^{q_{1}}z_{2}^{q_{2}}\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{q_{1}+q_{2}+1}(x)\textrm{d}x \end{array}\right) , \end{aligned}\end{aligned}$$

which, together with the fact that

$$\begin{aligned} \int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{4}(x)\textrm{d}x=\frac{3}{2\ell \pi },~\int \limits _{0}^{\ell \pi }\gamma _{n_{1}}^{3}(x)\textrm{d}x=0, \end{aligned}$$

yields

$$\begin{aligned} \frac{1}{3!}{\text {Proj}}_{S_{2}}f_{3}^{1}(z,0,0,\mu )=\left( \begin{array}{c} 0 \\ G_{2010}z_{1}^{2}\mu _{1}+G_{2001}z_{1}^{2}\mu _{2}+G_{1110}z_{1}z_{2}\mu _{1}+G_{1101}z_{1}z_{2}\mu _{2} \end{array}\right) , \end{aligned}$$

(3.52)

where

$$\begin{aligned}\left\{ \begin{aligned}&G_{2010}=0,~G_{2001}=0, \\&G_{1110}=0,~G_{1101}=0. \end{aligned}\right. \end{aligned}$$

Step 2   The calculation of ${\text {Proj}}_{S_{2}}\left( (D_{z}f_{2}^{1}(z,0,0,\mu ))U_{2}^{1}(z,\mu )\right)$

By combining with (3.27), (3.28), (3.29), (3.30), (3.48) and (3.49), we have

$$\begin{aligned} \begin{aligned} f_{2}^{1}(z,0,0,\mu )&=\Psi \left( \begin{aligned}&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x})+2A_{\mu }^{c}\Phi z_{x}+F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(1)}\right] \\&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x})+2A_{\mu }^{c}\Phi z_{x}+F_{2}(\Phi z_{x},0,0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \\&=\Psi \left( (2\mu _{1}I_{d}^{1}\left( -\frac{n_{1}^{2}}{\ell ^{2}}\right) +2\mu _{2}(I_{d}^{2}-I_{d}^{3}))(\xi _{1}z_{1}+\xi _{2}z_{2}) \right) . \end{aligned}\end{aligned}$$

(3.53)

Furthermore, from (3.25), (3.42), (3.53), and by noticing that $U_{2}^{1}(z,\mu ) \in {\text {Ker}}(M_{2}^{1})^{c}$, then by a direct calculation, we have

$$\begin{aligned} \begin{aligned} U_{2}^{1}(z,\mu )&=(M_{2}^{1})^{-1}{\text {Proj}}_{{\text {Im}}(M_{2}^{1})}f_{2}^{1}(z,0,0,\mu ) \\&=(M_{2}^{1})^{-1}\left( \begin{array}{c} \eta _{1}^{T}\left( 2\mu _{1}I_{d}^{1}(-\frac{n_{1}^{2}}{\ell ^{2}})+2\mu _{2}(I_{d}^{2}-I_{d}^{3})\right) \xi _{2}z_{2} \\ 0 \end{array}\right) \\&+(M_{2}^{1})^{-1}\left( \begin{array}{c} \eta _{1}^{T}\left( -2\mu _{1}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}-2\mu _{2}(I_{d}^{3}-I_{d}^{2})\right) \xi _{1}z_{1} \\ \eta _{2}^{T}\left( 2\mu _{1}I_{d}^{1}(-\frac{n_{1}^{2}}{\ell ^{2}})+2\mu _{2}(I_{d}^{2}-I_{d}^{3})\right) \xi _{2}z_{2} \end{array}\right) \\&=\left( \begin{array}{c} 0 \\ \eta _{1}^{T}\left( 2\mu _{1}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}-2\mu _{2}(I_{d}^{2}-I_{d}^{3})\right) \xi _{2}z_{2} \end{array}\right) +\left( \begin{array}{c} 0 \\ \eta _{1}^{T}\left( 2\mu _{1}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}+2\mu _{2}(I_{d}^{3}-I_{d}^{2})\right) \xi _{1}z_{1} \end{array}\right) . \end{aligned}\end{aligned}$$

(3.54)

Therefore, by combining with (3.26), (3.53) and (3.54), we have

$$\begin{aligned} \begin{aligned}&\frac{1}{3!}{\text {Proj}}_{S_{2}}\left( (D_{z}f_{2}^{1}(z,0,0,\mu ))U_{2}^{1}(z,\mu )\right) \\&=\left( \begin{array}{c} 0 \\ H_{2010}z_{1}^{2}\mu _{1}+H_{2001}z_{1}^{2}\mu _{2}+H_{1110}z_{1}z_{2}\mu _{1}+H_{1101}z_{1}z_{2}\mu _{2} \end{array}\right) , \end{aligned}\end{aligned}$$

(3.55)

where

$$\begin{aligned}\left\{ \begin{aligned}&H_{2010}=0,~H_{2001}=0, \\&H_{1110}=0,~H_{1101}=0. \end{aligned}\right. \end{aligned}$$

Step 3   The calculation of ${\text {Proj}}_{S_{2}}((D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,\mu ))\widetilde{U}_{2}^{2}(z,\mu ))$

From (3.34), we have

$$\begin{aligned} U_{2}^{2}(z,\mu )\triangleq h(z,\mu )=\sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x), \end{aligned}$$

(3.56)

and then by combining with (2.1), we have

$$\begin{aligned} \widehat{U}_{2}^{2}(z,\mu )=\frac{1}{\sqrt{\ell \pi }}h_{0}(z,\mu ),~U_{2,xx}^{2}(z,\mu )=h_{xx}(z,\mu )=-\sum _{n \in \mathbb {N}_{0}}(n/\ell )^{2}h_{n}(z,\mu )\gamma _{n}(x). \end{aligned}$$

Furthermore, from (3.17), we have

$$\begin{aligned} f_{2}^{1}(z,w,\widehat{w},\mu )=\Psi \left( \begin{aligned}&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x}+w)+2A_{\mu }^{c}(\Phi z_{x}+w)+F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(1)}\right] \\&\left[ 2D_{\mu }^{c}\Delta (\Phi z_{x}+w)+2A_{\mu }^{c}(\Phi z_{x}+w)+F_{2}(\Phi z_{x}+w,\widehat{w},0),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) . \end{aligned}$$

Therefore, by combining with (3.28), (3.29), (3.30), (3.34) and (3.56), and by a direct calculation, we have

$$\begin{aligned}\begin{aligned}&(D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,\mu ))\widetilde{U}_{2}^{2}(z,\mu ) \\&=\Psi \left( \begin{array}{cc} b_{n_{1},0,n_{1}}\left( S_{2}(\xi _{1}z_{1},h_{0}(z,\mu ))+S_{2}(\xi _{2}z_{2},h_{0}(z,\mu ))\right) \\ +b_{n_{1},2n_{1},n_{1}}\left( S_{2}(\xi _{1}z_{1},h_{2n_{1}}(z,\mu ))+S_{2}(\xi _{2}z_{2},h_{2n_{1}}(z,\mu ))\right) \\ +b_{n_{1},n_{1}}\left( \widehat{S}_{2}(\xi _{1}z_{1},\frac{1}{\sqrt{\ell \pi }}h_{0}(z,\mu ))+\widehat{S}_{2}(\xi _{2}z_{2},\frac{1}{\sqrt{\ell \pi }}h_{0}(z,\mu ))\right) \\ +b_{n_{1},n_{1}}\left( -2(n_{1}/\ell )^{2}\mu _{1}I_{d}^{1}h_{n_{1}}(z,\mu )\right) \\ +b_{n_{1},n_{1}}\left( 2\mu _{2}(I_{d}^{2}-I_{d}^{3})h_{n_{1}}(z,\mu )\right) \end{array}\right) , \end{aligned}\end{aligned}$$

which together with (3.26), yields to

$$\begin{aligned} \begin{aligned}&\frac{1}{3!}{\text {Proj}}_{S_{2}}((D_{w,\widehat{w},w_{xx}}f_{2}^{1}(z,0,0,\mu ))\widetilde{U}_{2}^{2}(z,\mu )) \\&=\left( \begin{array}{c} 0 \\ I_{2010}z_{1}^{2}\mu _{1}+I_{2001}z_{1}^{2}\mu _{2}+I_{1110}z_{1}z_{2}\mu _{1}+I_{1101}z_{1}z_{2}\mu _{2} \end{array}\right) , \end{aligned}\end{aligned}$$

(3.57)

where

$$\begin{aligned}\left\{ \begin{aligned} I_{2010}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}S_{2}(\xi _{1},h_{0,1010})+\frac{1}{6\sqrt{2\ell \pi }}S_{2}(\xi _{1},h_{2n_{1},1010})+\frac{1}{6\sqrt{\ell \pi }}\widehat{S}_{2}(\xi _{1},h_{0,1010})-\frac{n_{1}^{2}}{3\ell ^{2}}I_{d}^{1}h_{n_{1},2000}\right) , \\ I_{2001}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}S_{2}(\xi _{1},h_{0,1001})+\frac{1}{6\sqrt{2\ell \pi }}S_{2}(\xi _{1},h_{2n_{1},1001})+\frac{1}{6\sqrt{\ell \pi }}\widehat{S}_{2}(\xi _{1},h_{0,1001})+\frac{1}{3}(I_{d}^{2}-I_{d}^{3})h_{n_{1},2000}\right) , \\ I_{1110}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(S_{2}(\xi _{1},h_{0,0110})+S_{2}(\xi _{2},h_{0,1010}))\right) +\eta _{2}^{T}\left( \frac{1}{6\sqrt{2\ell \pi }}(S_{2}(\xi _{1},h_{2n_{1},0110})+S_{2}(\xi _{2},h_{2n_{1},1010}))\right) \\&+\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(\widehat{S}_{2}(\xi _{1},h_{0,0110})+\widehat{S}_{2}(\xi _{2},h_{0,1010}))\right) -\eta _{2}^{T}\left( \frac{n_{1}^{2}}{3\ell ^{2}}I_{d}^{1}h_{n_{1},1100}\right) , \\ I_{1101}&=\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(S_{2}(\xi _{1},h_{0,0101})+S_{2}(\xi _{2},h_{0,1001}))\right) +\eta _{2}^{T}\left( \frac{1}{6\sqrt{2\ell \pi }}(S_{2}(\xi _{1},h_{2n_{1},0101})+S_{2}(\xi _{2},h_{2n_{1},1001}))\right) \\&+\eta _{2}^{T}\left( \frac{1}{6\sqrt{\ell \pi }}(\widehat{S}_{2}(\xi _{1},h_{0,0101})+\widehat{S}_{2}(\xi _{2},h_{0,1001}))\right) +\frac{1}{3}\eta _{2}^{T}(I_{d}^{2}-I_{d}^{3})h_{n_{1},1100}. \end{aligned}\right. \end{aligned}$$

Step 4   The calculation of ${\text {Proj}}_{S_{2}}((D_{z}U_{2}^{1}(z,\mu ))g_{2}^{1}(z,0,0,\mu ))$

From (3.54) and by a direct calculation, we obtain that

$$\begin{aligned}\begin{aligned}&D_{z}U_{2}^{1}(z,\mu )=\left( \begin{array}{cc} 0 &{} 0 \\ \eta _{1}^{T}\left( 2\mu _{1}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}+2\mu _{2}(I_{d}^{3}-I_{d}^{2})\right) \xi _{1} &{} \eta _{1}^{T}\left( 2\mu _{1}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}-2\mu _{2}(I_{d}^{2}-I_{d}^{3})\right) \xi _{2} \end{array}\right) , \end{aligned}\end{aligned}$$

which together with (3.26) and (3.31), yields to

$$\begin{aligned} \begin{aligned}&\frac{1}{3!}{\text {Proj}}_{S_{2}}((D_{z}U_{2}^{1}(z,\mu ))g_{2}^{1}(z,0,0,\mu )) \\&=\left( \begin{array}{c} 0 \\ J_{2010}z_{1}^{2}\mu _{1}+J_{2001}z_{1}^{2}\mu _{2}+J_{1110}z_{1}z_{2}\mu _{1}+J_{1101}z_{1}z_{2}\mu _{2} \end{array}\right) , \end{aligned}\end{aligned}$$

(3.58)

where

$$\begin{aligned}\left\{ \begin{aligned}&J_{2010}=\frac{2}{3}\eta _{1}^{T}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}\xi _{2}B_{2000},~J_{2001}=-\frac{2}{3}\eta _{1}^{T}(I_{d}^{2}-I_{d}^{3})\xi _{2}B_{2000}, \\&J_{1110}=\frac{2}{3}\eta _{1}^{T}I_{d}^{1}\frac{n_{1}^{2}}{\ell ^{2}}\xi _{2}B_{1100},~J_{1101}=-\frac{2}{3}\eta _{1}^{T}(I_{d}^{2}-I_{d}^{3})\xi _{2}B_{1100}. \end{aligned}\right. \end{aligned}$$

3.3 The normal form for Bogdanov–Takens bifurcation of the system (1.4)

By combining with (3.22), (3.23), (3.24), (3.31), (3.39), (3.44), (3.50), (3.52), (3.55), (3.57) and (3.58), the third-order normal form of Bogdanov–Takens bifurcation for the system (1.4) can be written as

$$\begin{aligned} \begin{aligned} \dot{z}&=Bz+\left( \begin{array}{c} 0 \\ B_{2000}z_{1}^{2}+B_{1100}z_{1}z_{2}+B_{1010}z_{1}\mu _{1}+B_{1001}z_{1}\mu _{2}+B_{0110}z_{2}\mu _{1}+B_{0101}z_{2}\mu _{2} \end{array}\right) \\&+\left( \begin{array}{c} 0 \\ B_{3000}z_{1}^{3}+B_{2100}z_{1}^{2}z_{2}+F_{2010}z_{1}^{2}\mu _{1}+F_{2001}z_{1}^{2}\mu _{2}+F_{1110}z_{1}z_{2}\mu _{1}+F_{1101}z_{1}z_{2}\mu _{2} \end{array}\right) \\&+O\left( |z||\mu |^{2}\right) , \end{aligned}\end{aligned}$$

(3.59)

where

$$\begin{aligned} \left\{ \begin{aligned} B_{3000}&=C_{3000}+\frac{3}{2}\left( D_{3000}+E_{3000}\right) , \\ B_{2100}&=C_{2100}+\frac{3}{2}\left( D_{2100}+E_{2100}\right) , \\ F_{2010}&=G_{2010}+\frac{3}{2}\left( H_{2010}+I_{2010}-J_{2010}\right) , \\ F_{2001}&=G_{2001}+\frac{3}{2}\left( H_{2001}+I_{2001}-J_{2001}\right) , \\ F_{1110}&=G_{1110}+\frac{3}{2}\left( H_{1110}+I_{1110}-J_{1110}\right) , \\ F_{1101}&=G_{1101}+\frac{3}{2}\left( H_{1101}+I_{1101}-J_{1101}\right) . \end{aligned}\right. \end{aligned}$$

(3.60)

By noticing that the higher-order terms of perturbation parameter $O\left( |z||\mu |^{2}\right)$ and the higher-order terms $O\left( |z|^{2}|\mu |\right)$ have few effects on bifurcation set of normal form [32]. Therefore, by omitting these higher-order terms of (3.59), the third-order truncated normal form for Bogdanov–Takens bifurcation of the system (1.4) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{z}&=Bz+\left( \begin{array}{c} 0 \\ B_{2000}z_{1}^{2}+B_{1100}z_{1}z_{2}+B_{1010}z_{1}\mu _{1}+B_{1001}z_{1}\mu _{2}+B_{0110}z_{2}\mu _{1}+B_{0101}z_{2}\mu _{2} \end{array}\right) \\&+\left( \begin{array}{c} 0 \\ B_{3000}z_{1}^{3}+B_{2100}z_{1}^{2}z_{2} \end{array}\right) +O\left( |z|^{2}|\mu |\right) +O\left( |z||\mu |^{2}\right) , \end{aligned}\end{aligned}$$

(3.61)

where $B_{2000}, B_{1100}, B_{1010}, B_{1001}, B_{0110}, B_{0101}, B_{3000}$ and $B_{2100}$ are also given by (3.32) and (3.60).

Remark 3.2

It follows from the results of [33] that when $B_{3000}B_{2100} \ne 0$, the spatiotemporal dynamics of system (1.4) in the small neighborhood of Bogdanov–Takens bifurcation point can be determined by the third-order truncated normal form (3.61). If $B_{3000}B_{2100}=0$, we have to calculate the higher-order normal formal for determining the spatiotemporal dynamics of system (1.4) near the Bogdanov–Takens bifurcation point.

4 Numerical simulations

By choosing $d_{2}=1, \beta =1, b=1, \kappa =1/6, \ell =4$, we numerically calculate the third-order truncated normal form (3.61), and investigate the spatiotemporal dynamics of system (1.4) by analyzing the normal form (3.61). Thus, we obtain that $E_{*}=(0.6945,0.5788)$. Furthermore, from (2.8), we obtain that $\xi =0.1613>0$, which also satisfies $\xi <\beta =1$. Moreover, it is easy to verify that the conditions in Theorem 2.5 are satisfied, thus according to (2.16), we obtain that $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})=(0.3895,0.0251)$. Then, from (2.10) and (2.14), and according to Theorem 2.2, the 1-mode Hopf bifurcation curve and the Turing bifurcation curves are

$$\begin{aligned}\begin{aligned}&\mathcal {H}_{1}: c=\overline{c}_{1}(d_{1})=0.0495-0.0625d_{1},~0<d_{1}<\overline{d}_{1}=u_{*}\xi \ell ^{2}-d_{2}=0.7918, \\&\mathcal {T}_{n}: c=\widetilde{c}_{n}(d_{1})=\frac{0.0070n^{2}-0.0039d_{1}n^{4}}{0.1935+0.0625d_{1}n^{2}},~0<d_{1}<\widetilde{d}_{n}=\frac{u_{*}\xi \ell ^{2}}{n^{2}}=\frac{1.7918}{n^{2}},~n \in \mathbb {N}, \end{aligned}\end{aligned}$$

which are shown in Fig. 1a.

Fig. 1

a 1-mode Hopf bifurcation curve $\mathcal {H}_{1}$ and Turing bifurcation curves $\mathcal {T}_{n}(n=1,2,3)$ in $d_{1}-c$ plane. b 1-mode Hopf bifurcation curve $\mathcal {H}_{1}$, Turing bifurcation curves $\mathcal {T}_{n}(n=1,2,3)$ and critical bifurcation curve $\mathcal{C}\mathcal{B}_{2}$ in $d_{1}-c$ plane. BT represents the Bogdanov–Takens bifurcation point, $T_{1,2}$ represents the (1, 2)-mode Turing–Turing bifurcation point, $T_{1,3}$ represents the (1, 3)-mode Turing–Turing bifurcation point and $T_{2,3}$ represents the (2, 3)-mode Turing–Turing bifurcation point

Given that $n_{1}=1$, and under the above parameter settings, by combining with (3.32) and (3.60), we have $B_{2000}=0, B_{1100}=0, B_{1010}=-0.0055, B_{1001}=-0.2181, B_{0110}=0, B_{0101}=-1, B_{3000}=0.0021, B_{2100}=-0.3357$, thus the third-order truncated normal form (3.61) is

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}_{1}&=z_{2}, \\ \dot{z}_{2}&=-0.0055z_{1}\mu _{1}-0.2181z_{1}\mu _{2}-z_{2}\mu _{2}+0.0021z_{1}^{3}-0.3357z_{1}^{2}z_{2}. \end{aligned}\right. \end{aligned}$$

(4.1)

Furthermore, by referring to section 7.3 in [32], for the following two-parameter family

$$\begin{aligned} \left\{ \begin{aligned}&\dot{z}_{1}=z_{2}, \\&\dot{z}_{2}=\beta _{1}z_{1}+\beta _{2}z_{2}+a_{1}z_{1}^{3}+b_{1}z_{1}^{2}z_{2}, \end{aligned}\right. \end{aligned}$$

(4.2)

we have the following two propositions.

Proposition 4.1

For (4.2), when $a_{1}=1>0$ and $b_{1}=-1<0$, the critical bifurcation curves are

$$\begin{aligned}\begin{aligned}&\mathcal{C}\mathcal{B}_{1}: \beta _{2}=0,~\beta _{1}<0, \\&\mathcal{C}\mathcal{B}_{2}: \beta _{1}=0, \\&\mathcal{C}\mathcal{B}_{3}: \beta _{2}=-\frac{\beta _{1}}{5},~\beta _{1}<0. \end{aligned}\end{aligned}$$

Proposition 4.2

For (4.2), when $a_{1}=-1<0$ and $b_{1}=-1<0$, the critical bifurcation curves are

$$\begin{aligned}\begin{aligned}&\mathcal {CBC}_{1}: \beta _{2}=0,~\beta _{1}>0, \\&\mathcal {CBC}_{2}: \beta _{1}=0, \\&\mathcal {CBC}_{3}: \beta _{2}=\beta _{1},~\beta _{1}>0, \\&\mathcal {CBC}_{4}: \beta _{2}=\frac{4\beta _{1}}{5},~\beta _{1}>0, \\&\mathcal {CBC}_{5}: \beta _{2}=c_{1}\beta _{1},~c_{1} \approx 0.752,~\beta _{1}>0. \end{aligned}\end{aligned}$$

In what follows, we first transform (4.1) into the form of (4.2), and then according to Proposition 4.1 or Proposition 4.2 to determine critical bifurcation curves. If we denote

$$\begin{aligned} a_{2}:=0.0021,~b_{2}:=-0.3357,~\lambda _{1}:=-(0.0055\mu _{1}+0.2181\mu _{2}),~\lambda _{2}:=-\mu _{2}, \end{aligned}$$

then the normal form (4.1) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\dot{z}_{1}=z_{2}, \\&\dot{z}_{2}=\lambda _{1}z_{1}+\lambda _{2}z_{2}+a_{2}z_{1}^{3}+b_{2}z_{1}^{2}z_{2}. \end{aligned}\right. \end{aligned}$$

(4.3)

Moreover, after time re-scaling and coordinate transformation given by

$$\begin{aligned} t=\frac{\left| b_{2}\right| }{\left| a_{2}\right| }\widetilde{t},~z_{1}=\frac{\sqrt{\left| a_{2}\right| }}{\left| b_{2}\right| }\widetilde{z}_{1},~z_{2}=\frac{\sqrt{\left| a_{2}\right| ^{3}}}{b_{2}^{2}}\widetilde{z}_{2}, \end{aligned}$$

and by dropping the tilde for simplicity of notation, the system (4.3) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\dot{z}_{1}=z_{2}, \\&\dot{z}_{2}=\frac{b_{2}^{2}}{a_{2}^{2}}\lambda _{1}z_{1}+\frac{\left| b_{2}\right| }{\left| a_{2}\right| }\lambda _{2}z_{2}+\frac{a_{2}}{\left| a_{2}\right| }z_{1}^{3}+\frac{b_{2}}{\left| b_{2}\right| }z_{1}^{2}z_{2}, \end{aligned}\right. \end{aligned}$$

(4.4)

where

$$\begin{aligned}\begin{aligned}&\frac{b_{2}^{2}}{a_{2}^{2}}=2.5554\times 10^{4},~\frac{\left| b_{2}\right| }{\left| a_{2}\right| }=159.8571, \\&\frac{b_{2}^{2}}{a_{2}^{2}}\lambda _{1}=-140.5487\mu _{1}-5.5734\times 10^{3}\mu _{2},~\frac{\left| b_{2}\right| }{\left| a_{2}\right| }\lambda _{2}=-159.8571\mu _{2}, \\&\frac{a_{2}}{\left| a_{2}\right| }=1,~\frac{b_{2}}{\left| b_{2}\right| }=-1. \end{aligned}\end{aligned}$$

By comparing (4.4) with (4.2), we can see that $a_{1}=1>0$ and $b_{1}=-1<0$, then according to Proposition 4.1, we can define the critical bifurcation curves in $\mu _{1}-\mu _{2}$ plane as

$$\begin{aligned}\begin{aligned}&\mathcal{C}\mathcal{B}_{1}: \mu _{2}=0,~\mu _{1}>0, \\&\mathcal{C}\mathcal{B}_{2}: \mu _{2}=-0.0252\mu _{1}, \\&\mathcal{C}\mathcal{B}_{3}: \mu _{2}=-0.0221\mu _{1},~\mu _{1}>0. \end{aligned}\end{aligned}$$

Remark 4.3

By noticing that $d_{1}=\widetilde{d}_{1}^{*}+\mu _{1}$ and $c=\overline{c}_{1}^{*}+\mu _{2}$, thus we obtain that $\mu _{2}=c-\overline{c}_{1}^{*}$ and $\mu _{1}=d_{1}-\widetilde{d}_{1}^{*}$. Therefore, for $\mathcal{C}\mathcal{B}_{2}: \mu _{2}=-0.0252\mu _{1}$, we have $c-\overline{c}_{1}^{*}=-0.0252(d_{1}-\widetilde{d}_{1}^{*})$, and by combining with $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})=(0.3895,0.0251)$, we obtain that

$$\begin{aligned} c=-0.0252d_{1}+0.0252\widetilde{d}_{1}^{*}+\overline{c}_{1}^{*}=0.0349-0.0252d_{1}. \end{aligned}$$

(4.5)

Thus, from (4.5), and by a direct calculation or a geometric point of view, we can see that the critical bifurcation curve $\mathcal{C}\mathcal{B}_{2}$ is actually the 1-mode Turing bifurcation curve

$$\begin{aligned} \mathcal {T}_{1}: c=\widetilde{c}_{1}(d_{1})=\frac{0.0070-0.0039d_{1}}{0.1935+0.0625d_{1}},~0<d_{1}<\widetilde{d}_{1}=u_{*}\xi \ell ^{2}=1.7918, \end{aligned}$$

see Fig. 1b for detail. Furthermore, neither the critical bifurcation curve $\mathcal{C}\mathcal{B}_{1}$ nor the critical bifurcation curve $\mathcal{C}\mathcal{B}_{3}$ corresponds to the 1-mode Hopf bifurcation curve $\mathcal {H}_{1}$. Therefore, the system (1.4) has only the stable/unstable positive constant steady state, the stable/unstable spatially inhomogeneous steady states, and it has no stable/unstable spatially inhomogeneous periodic solutions.

Notice that by using the critical bifurcation curves $\mathcal{C}\mathcal{B}_{1}$, $\mathcal{C}\mathcal{B}_{2}$ and $\mathcal{C}\mathcal{B}_{3}$, the $\mu _{1}-\mu _{2}$ parameter plane is divided into four different regions $R_{i}(i=1,2,3,4)$ near the 1-mode Bogdanov–Takens bifurcation point $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})$, see Fig. 2a for detail. Therefore, by combining with Remark 4.3, when $(\mu _{1},\mu _{2})$ is chosen in these four different regions, the dynamics of the third-order truncated normal form (4.1) can be described by the corresponding phase portraits, respectively, see Fig. 2b for detail. Furthermore, based on the center manifold theory, the dynamics of the system (1.4) near the Bogdanov–Takens bifurcation point is locally topologically equivalent to the dynamics of the third-order truncated normal form (4.1). Thus, when the parameters are chosen in these four different regions, respectively, we could reveal the dynamical behaviors of the system (1.4). For the given parameters $d_{2}=1, \beta =1, b=1, \kappa =1/6, \ell =4$, when the point $(d_{1},c)$ is chosen near the 1-mode Bogdanov–Takens bifurcation point $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})=(0.3895,0.0251)$, the system (1.4) has complex spatiotemporal dynamics.

Fig. 2

a Local bifurcation sets of the system (1.4) near the 1-mode Bogdanov–Takens bifurcation point $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})=(0.3895,0.0251)$ in $\mu _{1}-\mu _{2}$ plane. b The corresponding phase portraits

Fig. 3

For $(\mu _{1},\mu _{2})=(0.5,0.01) \in R_{1}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is locally asymptotically stable. The initial functions are $u(x,0)=0.6945-0.1\cos (x/4)$ and $v(x,0)=0.5788+0.1\cos (x/4)$

Fig. 4

For $(\mu _{1},\mu _{2})=(-0.1,0.0024) \in R_{2}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and a pair of spatially inhomogeneous steady states with the shape of $-\cos (x/4)$-like are stable. The initial functions are $u(x,0)=0.6945-0.1\cos (x/4)$ and $v(x,0)=0.5788+0.1\cos (x/4)$

Fig. 5

For $(\mu _{1},\mu _{2})=(-0.1,0.0024) \in R_{2}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and a pair of spatially inhomogeneous steady states with the shape of $\cos (x/4)$-like are stable. The initial functions are $u(x,0)=0.6945+0.05\cos (x/4)$ and $v(x,0)=0.5788$

Fig. 6

For $(\mu _{1},\mu _{2})=(0.1,-0.0023) \in R_{3}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and there are a pair of stable spatially inhomogeneous steady states with the shape of $-\cos (x/4)$-like. The initial functions are $u(x,0)=0.6945-0.2\cos (x/4)$ and $v(x,0)=0.5788+0.2\cos (x/4)$

Fig. 7

For $(\mu _{1},\mu _{2})=(0.1,-0.0023) \in R_{3}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and there are a pair of stable spatially inhomogeneous steady states with the shape of $\cos (x/4)$-like. The initial functions are $u(x,0)=0.6945+0.02\cos (x/4)$ and $v(x,0)=0.5788$

Fig. 8

For $(\mu _{1},\mu _{2})=(0.05,-0.0008) \in R_{4}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and there exist also a pair of stable spatially inhomogeneous steady states with the shape of $-\cos (x/4)$-like. The initial functions are $u(x,0)=0.6945-0.1\cos (x/4)$ and $v(x,0)=0.5788+0.1\cos (x/4)$

Fig. 9

For $(\mu _{1},\mu _{2})=(0.05,-0.0008) \in R_{4}$, the positive constant steady state $E_{*}=(0.6945,0.5788)$ of system (1.4) is unstable, and there exist also a pair of stable spatially inhomogeneous steady states with the shape of $\cos (x/4)$-like. The initial functions are $u(x,0)=0.6945+0.1\cos (x/4)$ and $v(x,0)=0.5788$

Proposition 4.4

For fixed $d_{2}=1, \beta =1, b=1, \kappa =1/6, \ell =4$, when the parameter point $(d_{1},c)$ is chosen near the 1-mode Bogdanov–Takens bifurcation point $(\widetilde{d}_{1}^{*},\overline{c}_{1}^{*})=(0.3895,0.0251)$, the system (1.4) can show complex spatiotemporal dynamics. More precisely, the complete spatiotemporal dynamics are described as follows:

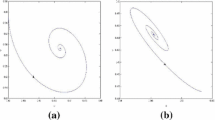
(i) when $(\mu _{1},\mu _{2})=(0.5,0.01) \in R_{1}$, i.e., $(d_{1},c)=(0.8895,0.0351)$, the positive constant steady state $E_{*}$ of the system (1.4) is locally asymptotically stable. Otherwise, the positive constant steady state $E_{*}$ of the system (1.4) is unstable while $(\mu _{1},\mu _{2})\notin R_{1}$. The whole evolutionary processes for the density of the prey population u(x, t) and the density of the predator population v(x, t) are shown in Fig. 3a and b, respectively, and the corresponding phase portrait is given in Fig. 3c;

(ii) when $(\mu _{1},\mu _{2})$ crosses $R_{1}$ into $R_{2}$, resulting in that the positive constant steady state $E_{*}$ of the system (1.4) becomes unstable and a pair of stable spatially inhomogeneous steady states with the shapes of $-\cos (x/4)$-like and $\cos (x/4)$-like emerge through the 1-mode Turing bifurcation. By choosing $(\mu _{1},\mu _{2})=(-0.1,0.0024) \in R_{2}$, i.e., $(d_{1},c)=(0.2895,0.0275)$, the whole evolutionary processes for the density of the prey population u(x, t) and the density of the predator population v(x, t) are shown in Figs. 4a and b, 5a and b, which correspond to different initial functions. Furthermore, the corresponding phase portraits are given in Figs. 4c and 5c, respectively;

(iii) when $(\mu _{1},\mu _{2})$ crosses $R_{2}$ into $R_{3}$, the pair of spatially inhomogeneous steady states with the shapes of $-\cos (x/4)$-like and $\cos (x/4)$-like still have its stability. By choosing $(\mu _{1},\mu _{2})=(0.1,-0.0023) \in R_{3}$, i.e., $(d_{1},c)=(0.4895,0.0228)$, the whole evolutionary processes for the density of the prey population u(x, t) and the density of the predator population v(x, t) are shown in Fig. 6a and b, Fig. 7a and b, which correspond to different initial functions. Furthermore, the corresponding phase portraits are given in Fig.6(c) and Fig. 7c, respectively;

(iv) when $(\mu _{1},\mu _{2})$ crosses $R_{3}$ into $R_{4}$, the pair of spatially inhomogeneous steady states with the shapes of $-\cos (x/4)$-like and $\cos (x/4)$-like are left, and they are stable. By choosing $(\mu _{1},\mu _{2})=(0.05,-0.0008) \in R_{4}$, i.e., $(d_{1},c)=(0.4395,0.0243)$, the whole evolutionary processes for the density of the prey population u(x, t) and the density of the predator population v(x, t) are shown in Figs. 8a and b, 9a and b, which correspond to different initial functions. Furthermore, the corresponding phase portraits are given in Figs. 8c and 9c, respectively.

5 Conclusion and discussion

We investigate the spatiotemporal dynamics near the Bogdanov–Takens bifurcation point for a diffusive predator–prey system with nonlocal effect and prey refuge. By linear stability analysis, we obtain the conditions for the occurrence of Turing bifurcation, Hopf bifurcation and Turing–Turing bifurcation. Furthermore, apart from these conditions, the occurrence of Bogdanov–Takens bifurcation is also obtained. Moreover, in order to investigate the spatiotemporal dynamics of the system (1.4) utilizing the normal form theory, some concise formulas for calculating the third-order truncated normal form of Bogdanov–Takens bifurcation are provided. It is worth noting that the procedures of calculating the third-order truncated normal form of Bogdanov–Takens bifurcation utilizing the obtained concise formulas could be implemented by computer program, which indicates that we could get rid of complicated manual calculations when calculating the third-order truncated normal form of Bogdanov–Takens bifurcation. Moreover, our developed algorithm for calculating the third-order truncated normal form of Bogdanov–Takens bifurcation for a diffusive predator–prey system with nonlocal effect and prey refuge could be applied to the general diffusive predator–prey system with nonlocal effect.

By noticing that the complex spatiotemporal dynamical classifications near the Bogdanov–Takens bifurcation point can be determined by calculating the corresponding normal form, and by analyzing the third-order truncated normal form of Bogdanov–Takens bifurcation for the system (1.4), we divide the $\mu _{1}-\mu _{2}$ plane into four regions and illustrate the solutions of the system (1.4) in different regions. It is necessary to point out that the Bogdanov–Takens bifurcation of the system (1.4) with the discrete time delay or the nonlocal time delay or the spatiotemporal time delay is worthwhile to study, and the corresponding algorithm for calculating the normal form of Bogdanov–Takens for the delayed system (1.4) is also worthwhile to study in the future.

Appendices

Appendix A: Calculation of $h_{n,q_{1}q_{2}q_{3}00}$

By combining with (3.21) and (3.55), we have

$$\begin{aligned} M_{2}^{2}\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x)\right) =D_{z}\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x)\right) Bz-\mathcal {L}_{n}\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x)\right) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\left( \begin{aligned}&\left[ M_{2}^{2}\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x)\right) ,\beta _{n}^{(1)}\right] \\&\left[ M_{2}^{2}\left( \sum _{n \in \mathbb {N}_{0}}h_{n}(z,\mu )\gamma _{n}(x)\right) ,\beta _{n}^{(2)}\right] \end{aligned}\right) \\&=\sum _{n \in \mathbb {N}_{0}}\left( 2h_{n,2000}z_{1}z_{2}+h_{n,1100}z_{2}^{2}+h_{n,1010}z_{2}\mu _{1}+h_{n,1001}z_{2}\mu _{2}-\mathcal {L}_{n}(h_{n}(z,\mu ))\right) , \end{aligned}\end{aligned}$$

(A.1)

where $\mathcal {L}_{n}(.)$ is defined by

$$\begin{aligned} \mathcal {L}_{n}(h_{n}(z,\mu ))=L_{n}^{d}(h_{n}(z,\mu ))+L_{0}^{n}(h_{n}(z,\mu )) \end{aligned}$$

with

$$\begin{aligned} L_{n}^{d}(h_{n}(z,\mu ))=-\frac{n^{2}}{\ell ^{2}}D^{c}h_{n}(z,\mu ),~L_{0}^{n}(h_{n}(z,\mu ))={\left\{ \begin{array}{ll} A_{1}(0)h_{n}(z,\mu )+A_{2}h_{n}(z,\mu ), &{} n=0, \\ A_{1}(0)h_{n}(z,\mu ), &{} n \in \mathbb {N}. \end{array}\right. } \end{aligned}$$

Furthermore, by combining with (3.12) and (3.17), we have

$$\begin{aligned} \begin{aligned} f_{2}^{2}(z,0,0,\mu )&=(I_{2}-\pi )\widetilde{F}_{2}(\Phi z_{x},0,\mu )=\widetilde{F}_{2}(\Phi z_{x},0,\mu )-\pi (\widetilde{F}_{2}(\Phi z_{x},0,\mu )) \\&=\widetilde{F}_{2}(\Phi z_{x},0,\mu )-\Phi _{n_{1}}\Psi _{n_{1}}\left( \begin{aligned}&\left[ \widetilde{F}_{2}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(1)}\right] \\&\left[ \widetilde{F}_{2}(\Phi z_{x},0,\mu ),\beta _{n_{1}}^{(2)}\right] \end{aligned}\right) \gamma _{n_{1}}(x). \end{aligned}\end{aligned}$$

(A.2)

By combining with (3.17), (3.28), (3.29), (3.30), (3.48), (3.49) and (A.2), we have

$$\begin{aligned} \begin{aligned}&\left( \begin{aligned}&\left[ f_{2}^{2}(z,0,0,\mu ),\beta _{n}^{(1)}\right] \\&\left[ f_{2}^{2}(z,0,0,\mu ),\beta _{n}^{(2)}\right] \end{aligned}\right) =\left\{ \begin{aligned}&\frac{1}{\sqrt{\ell \pi }}(A_{20}z_{1}^{2}+A_{02}z_{2}^{2}+A_{11}z_{1}z_{2}),~n=0, \\&-\frac{2n_{1}^{2}}{\ell ^{2}}\mu _{1}I_{d}^{1}\xi _{1}z_{1}-\frac{2n_{1}^{2}}{\ell ^{2}}\mu _{1}I_{d}^{1}\xi _{2}z_{2}+2\mu _{2}(I_{d}^{2}-I_{d}^{3})\xi _{1}z_{1}+2\mu _{2}(I_{d}^{2}-I_{d}^{3})\xi _{2}z_{2} \\&-\Phi _{n_{1}}\Psi _{n_{1}}\left( (2\mu _{1}I_{d}^{1}\left( -\frac{n_{1}^{2}}{\ell ^{2}}\right) +2\mu _{2}(I_{d}^{2}-I_{d}^{3}))(\xi _{1}z_{1}+\xi _{2}z_{2})\right) ,~n=n_{1}, \\&\frac{1}{\sqrt{2\ell \pi }}(A_{20}z_{1}^{2}+A_{02}z_{2}^{2}+A_{11}z_{1}z_{2}),~n=2n_{1}. \end{aligned}\right. \end{aligned}\end{aligned}$$

(A.3)

Thus, by combining with (A.1), (A.3) and

$$\begin{aligned} \left( \begin{aligned}&\left[ M_{2}^{2}\left( h_{n}(z,\mu )\gamma _{n}(x)\right) ,\beta _{n}^{(1)}\right] \\&\left[ M_{2}^{2}\left( h_{n}(z,\mu )\gamma _{n}(x)\right) ,\beta _{n}^{(2)}\right] \end{aligned}\right) =\left( \begin{aligned}&\left[ f_{2}^{2}(z,0,0,\mu ),\beta _{n}^{(1)}\right] \\&\left[ f_{2}^{2}(z,0,0,\mu ),\beta _{n}^{(2)}\right] \end{aligned}\right) , \end{aligned}$$

we have

$$\begin{aligned} \left\{ \begin{aligned}&n=0~\left\{ \begin{aligned}&z_{1}^{2}:~\mathcal {L}_{n}(h_{n,2000})=-\frac{1}{\sqrt{\ell \pi }}A_{20}, \\&z_{1}z_{2}:~2h_{n,2000}-\mathcal {L}_{n}(h_{n,1100})=\frac{1}{\sqrt{\ell \pi }}A_{11}, \end{aligned}\right. \\&n=2n_{1}~\left\{ \begin{aligned}&z_{1}^{2}:~\mathcal {L}_{n}(h_{n,2000})=-\frac{1}{\sqrt{2\ell \pi }}A_{20}, \\&z_{1}z_{2}:~2h_{n,2000}-\mathcal {L}_{n}(h_{n,1100})=\frac{1}{\sqrt{2\ell \pi }}A_{11}. \end{aligned}\right. \end{aligned}\right. \end{aligned}$$

(A.4)

More precisely, from (A.4), and by a direct calculation, we have

$$\begin{aligned}\left\{ \begin{aligned}&h_{0,2000}=-\frac{1}{\sqrt{\ell \pi }}(A_{1}(0)+A_{2})^{-1}A_{20}, \\&h_{0,1100}=(A_{1}(0)+A_{2})^{-1}\left( -\frac{2}{\sqrt{\ell \pi }}(A_{1}(0)+A_{2})^{-1}A_{20}-\frac{1}{\sqrt{\ell \pi }}A_{11}\right) , \\&h_{2n_{1},2000}=-\frac{1}{\sqrt{2\ell \pi }}\left( -\frac{(2n_{1})^{2}}{\ell ^{2}}D^{c}+A_{1}(0)\right) ^{-1}A_{20}, \\&h_{2n_{1},1100}=\left( -\frac{(2n_{1})^{2}}{\ell ^{2}}D^{c}+A_{1}(0)\right) ^{-1}\left( -\frac{2}{\sqrt{2\ell \pi }}\left( -\frac{(2n_{1})^{2}}{\ell ^{2}}D^{c}+A_{1}(0)\right) ^{-1}A_{20}-\frac{1}{\sqrt{2\ell \pi }}A_{11}\right) . \end{aligned}\right. \end{aligned}$$

Appendix B: Calculations of $f_{l_{1}l_{2}l_{3}l_{4}}$, $A_{q_{1}q_{2}}$, $S_{2}(\Phi z_{x},w)$ and $\widehat{S}_{2}(\Phi z_{x},\widehat{w})$

For the system (1.4), by letting $F(\varphi ,\widehat{\varphi },\mu )={\text {col}}(F^{(1)}(\varphi ,\widehat{\varphi },\mu ),F^{(2)}(\varphi ,\widehat{\varphi },\mu ))$ for any $\varphi ={\text {col}}(\varphi _{1},\varphi _{2}) \in X$ and $\widehat{\varphi }={\text {col}}(\widehat{\varphi }_{1},\widehat{\varphi }_{2}) \in X$, and writing the $\widetilde{m}$-th Fr$\acute{e}$chet derivative $F_{\widetilde{m}}(\varphi ,\widehat{\varphi },\mu ),~\widetilde{m} \ge 2$ as

$$\begin{aligned} \frac{1}{\widetilde{m}!}F_{\widetilde{m}}(\varphi ,\widehat{\varphi },\mu )=\sum _{l_{1}+l_{2}+l_{3}+l_{4}=\widetilde{m}}\frac{1}{l_{1}!l_{2}!l_{3}!l_{4}!}f_{l_{1}l_{2}l_{3}l_{4}}\varphi _{1}^{l_{1}}\varphi _{2}^{l_{2}}\widehat{\varphi }_{1}^{l_{3}}\mu _{2}^{l_{4}}, \end{aligned}$$

where $f_{l_{1}l_{2}l_{3}l_{4}}={\text {col}}(f_{l_{1}l_{2}l_{3}l_{4}}^{(1)},f_{l_{1}l_{2}l_{3}l_{4}}^{(2)})$ with

$$\begin{aligned} f_{l_{1}l_{2}l_{3}l_{4}}^{(1)}=\frac{\partial ^{l_{1}+l_{2}+l_{3}+l_{4}}F^{(1)}(0,0,0,0)}{\partial \varphi _{1}^{l_{1}}\partial \varphi _{2}^{l_{2}}\partial \widehat{\varphi }_{1}^{l_{3}}\partial \mu _{2}^{l_{4}}},~f_{l_{1}l_{2}l_{3}l_{4}}^{(2)}=\frac{\partial ^{l_{1}+l_{2}+l_{3}+l_{4}}F^{(2)}(0,0,0,0)}{\partial \varphi _{1}^{l_{1}}\partial \varphi _{2}^{l_{2}}\partial \widehat{\varphi }_{1}^{l_{3}}\partial \mu _{2}^{l_{4}}}, \end{aligned}$$

(B.1)

and $F(\varphi ,\widehat{\varphi },\mu )$ is defined by

$$\begin{aligned} \begin{aligned} F(\varphi ,\widehat{\varphi },\mu )&=\left( \begin{array}{cc} (\varphi _{1}+u_{*})(1-\beta (\widehat{\varphi }_{1}+u_{*}))-\frac{b(1-\kappa )(\varphi _{1}+u_{*})(\varphi _{2}+v_{*})}{1+(1-\kappa )(\varphi _{1}+u_{*})} \\ (\overline{c}_{1}^{*}+\mu _{2})(\varphi _{2}+v_{*})\left( 1-\frac{\varphi _{2}+v_{*}}{(1-\kappa )(\varphi _{1}+u_{*})}\right) \end{array}\right) \\&-L(\mu )\varphi -\widehat{L}(0)\widehat{\varphi }. \end{aligned}\end{aligned}$$

(B.2)

It follows from (B.1) and (B.2), we can see that $f_{l_{1}l_{2}l_{3}l_{4}}^{(1)}=0$ for either $l_{2}\ge 2$, or $l_{3}\ge 2$, and $f_{l_{1}l_{2}l_{3}l_{4}}^{(2)}=0$ for either $l_{2}\ge 3$, or $l_{3}\ge 1$. Moreover, we can verify that $f_{0110}^{(1)}=0$, $f_{1110}^{(1)}=0$ and $f_{2010}^{(1)}=0$, then we have

$$\begin{aligned} \begin{aligned}&F_{2}^{(1)}(\varphi ,\widehat{\varphi },\mu )=F_{2}^{(1)}(\varphi ,\widehat{\varphi },0)=2f_{1010}^{(1)}\varphi _{1}\widehat{\varphi }_{1}+2f_{1100}^{(1)}\varphi _{1}\varphi _{2}+f_{2000}^{(1)}\varphi _{1}^{2}, \\&F_{2}^{(2)}(\varphi ,\widehat{\varphi },\mu )=F_{2}^{(2)}(\varphi ,\widehat{\varphi },0)=f_{0200}^{(2)}\varphi _{2}^{2}+2f_{1100}^{(2)}\varphi _{1}\varphi _{2}+f_{2000}^{(2)}\varphi _{1}^{2} \end{aligned}\end{aligned}$$

(B.3)

and

$$\begin{aligned} \begin{aligned} F_{3}^{(1)}(\varphi ,\widehat{\varphi },0)&=3f_{2100}^{(1)}\varphi _{1}^{2}\varphi _{2}+f_{3000}^{(1)}\varphi _{1}^{3}, \\ F_{3}^{(2)}(\varphi ,\widehat{\varphi },0)&=3f_{1200}^{(2)}\varphi _{1}\varphi _{2}^{2}+3f_{2100}^{(2)}\varphi _{1}^{2}\varphi _{2}+f_{3000}^{(2)}\varphi _{1}^{3}. \end{aligned}\end{aligned}$$

(B.4)

By combining with (B.1), (B.2), (B.3) and (B.4), we have

$$\begin{aligned}\begin{aligned} f_{1010}^{(1)}&=-\beta , \\ f_{1100}^{(1)}&=-b(1-\kappa )(1+(1-\kappa )u_{*})^{-1}+b(1-\kappa )^{2}u_{*}(1+(1-\kappa )u_{*})^{-2}, \\ f_{2000}^{(1)}&=2b(1-\kappa )^{2}v_{*}(1+(1-\kappa )u_{*})^{-2}-2b(1-\kappa )^{3}u_{*}v_{*}(1+(1-\kappa )u_{*})^{-3}, \\ f_{0200}^{(2)}&=-2\overline{c}_{1}^{*}(1-\kappa )^{-1}u_{*}^{-1}, \\ f_{1100}^{(2)}&=2\overline{c}_{1}^{*}v_{*}(1-\kappa )^{-1}u_{*}^{-2}, \\ f_{2000}^{(2)}&=-2\overline{c}_{1}^{*}v_{*}^{2}(1-\kappa )^{-1}u_{*}^{-3}, \\ f_{2100}^{(1)}&=2b(1-\kappa )^{2}(1+(1-\kappa )u_{*})^{-2}-2b(1-\kappa )^{3}u_{*}(1+(1-\kappa )u_{*})^{-3}, \\ f_{3000}^{(1)}&=-6b(1-\kappa )^{3}v_{*}(1+(1-\kappa )u_{*})^{-3}+6b(1-\kappa )^{4}u_{*}v_{*}(1+(1-\kappa )u_{*})^{-4}, \\ f_{1200}^{(2)}&=2\overline{c}_{1}^{*}(1-\kappa )^{-1}u_{*}^{-2},~f_{2100}^{(2)}=-4\overline{c}_{1}^{*}v_{*}(1-\kappa )^{-1}u_{*}^{-3},~f_{3000}^{(2)}=6\overline{c}_{1}^{*}v_{*}^{2}(1-\kappa )^{-1}u_{*}^{-4}. \end{aligned}\end{aligned}$$

Furthermore, by noticing that $\varphi =\Phi z_{x}+w$ and $\widehat{\varphi }=\widehat{w}$. More precisely, we have

$$\begin{aligned} \begin{aligned} \varphi&=\Phi z_{x}+w=\left( \begin{aligned}&\xi _{11}z_{1}\gamma _{n_{1}}(x)+\xi _{21}z_{2}\gamma _{n_{1}}(x)+w_{1} \\&\xi _{12}z_{1}\gamma _{n_{1}}(x)+\xi _{22}z_{2}\gamma _{n_{1}}(x)+w_{2} \end{aligned}\right) , \\ \widehat{\varphi }&=\widehat{w}=\left( \begin{aligned}&\widehat{w}_{1} \\&\widehat{w}_{2} \end{aligned}\right) . \end{aligned}\end{aligned}$$

(B.5)

From (B.5) and by noticing that

$$\begin{aligned} \begin{aligned} F_{2}(\Phi z_{x},0,0)&=\sum _{q_{1}+q_{2}=2}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x) \\&=A_{20}z_{1}^{2}\gamma _{n_{1}}^{2}(x)+A_{02}z_{2}^{2}\gamma _{n_{1}}^{2}(x)+A_{11}z_{1}z_{2}\gamma _{n_{1}}^{2}(x) \end{aligned}\end{aligned}$$

(B.6)

and

$$\begin{aligned} \begin{aligned} F_{3}(\Phi z_{x},0,0)&=\sum _{q_{1}+q_{2}=3}A_{q_{1}q_{2}}z_{1}^{q_{1}}z_{2}^{q_{2}}\gamma _{n_{1}}^{q_{1}+q_{2}}(x) \\&=A_{30}z_{1}^{3}\gamma _{n_{1}}^{3}(x)+A_{03}z_{2}^{3}\gamma _{n_{1}}^{3}(x)+A_{21}z_{1}^{2}z_{2}\gamma _{n_{1}}^{3}(x)+A_{12}z_{1}z_{2}^{2}\gamma _{n_{1}}^{3}(x), \end{aligned} \end{aligned}$$

(B.7)

then by comparing the corresponding coefficients of (B.3) and (B.6) as well as (B.4) and (B.7), respectively, we have

$$\begin{aligned}\begin{aligned} A_{20}&=\left( \begin{array}{c} f_{2000}^{(1)}\xi _{11}^{2}+2f_{1100}^{(1)}\xi _{11}\xi _{12} \\ f_{2000}^{(2)}\xi _{11}^{2}+f_{0200}^{(2)}\xi _{12}^{2}+2f_{1100}^{(2)}\xi _{11}\xi _{12} \end{array}\right) , \\ A_{02}&=\left( \begin{array}{c} f_{2000}^{(1)}\xi _{21}^{2}+2f_{1100}^{(1)}\xi _{21}\xi _{22} \\ f_{2000}^{(2)}\xi _{21}^{2}+f_{0200}^{(2)}\xi _{22}^{2}+2f_{1100}^{(2)}\xi _{21}\xi _{22} \end{array}\right) , \\ A_{11}&=\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{11}\xi _{21}+2f_{1100}^{(1)}(\xi _{11}\xi _{22}+\xi _{21}\xi _{12}) \\ 2f_{2000}^{(2)}\xi _{11}\xi _{21}+2f_{0200}^{(2)}\xi _{12}\xi _{22}+2f_{1100}^{(2)}(\xi _{11}\xi _{22}+\xi _{21}\xi _{12}) \end{array}\right) \end{aligned}\end{aligned}$$

and

$$\begin{aligned}\begin{aligned} A_{30}&=\left( \begin{array}{c} f_{3000}^{(1)}\xi _{11}^{3}+3f_{2100}^{(1)}\xi _{11}^{2}\xi _{12} \\ f_{3000}^{(2)}\xi _{11}^{3}+3f_{2100}^{(2)}\xi _{11}^{2}\xi _{12}+3f_{1200}^{(2)}\xi _{11}\xi _{12}^{2} \end{array}\right) , \\ A_{03}&=\left( \begin{array}{c} f_{3000}^{(1)}\xi _{21}^{3}+3f_{2100}^{(1)}\xi _{21}^{2}\xi _{22} \\ f_{3000}^{(2)}\xi _{21}^{3}+3f_{2100}^{(2)}\xi _{21}^{2}\xi _{22}+3f_{1200}^{(2)}\xi _{21}\xi _{22}^{2} \end{array}\right) , \\ A_{21}&=\left( \begin{array}{c} 3f_{3000}^{(1)}\xi _{11}^{2}\xi _{21}+3f_{2100}^{(1)}(2\xi _{11}\xi _{21}\xi _{12}+\xi _{11}^{2}\xi _{22}) \\ 3f_{3000}^{(2)}\xi _{11}^{2}\xi _{21}+3f_{2100}^{(2)}(2\xi _{11}\xi _{21}\xi _{12}+\xi _{11}^{2}\xi _{22})+3f_{1200}^{(2)}(2\xi _{11}\xi _{12}\xi _{22}+\xi _{21}\xi _{12}^{2}) \end{array}\right) , \\ A_{12}&=\left( \begin{array}{c} 3f_{3000}^{(1)}\xi _{11}\xi _{21}^{2}+3f_{2100}^{(1)}(\xi _{21}^{2}\xi _{12}+2\xi _{11}\xi _{21}\xi _{22}) \\ 3f_{3000}^{(2)}\xi _{11}\xi _{21}^{2}+3f_{2100}^{(2)}(\xi _{21}^{2}\xi _{12}+2\xi _{11}\xi _{21}\xi _{22})+3f_{1200}^{(2)}(\xi _{11}\xi _{22}^{2}+2\xi _{21}\xi _{12}\xi _{22}) \end{array}\right) . \end{aligned}\end{aligned}$$

Moreover, if we denote

$$\begin{aligned}\begin{aligned}&\breve{\varphi }_{1}=\xi _{11}z_{1}\gamma _{n_{1}}(x)+\xi _{21}z_{2}\gamma _{n_{1}}(x), \\&\breve{\varphi }_{2}=\xi _{12}z_{1}\gamma _{n_{1}}(x)+\xi _{22}z_{2}\gamma _{n_{1}}(x), \end{aligned}\end{aligned}$$

then by combining with (3.29), (B.3) and (B.5), we have

$$\begin{aligned} \begin{aligned}&S_{2}(\Phi z_{x},w)=\left( \begin{array}{cc} 2f_{2000}^{(1)}\breve{\varphi }_{1}w_{1}+2f_{1100}^{(1)}(\breve{\varphi }_{1}w_{2}+\breve{\varphi }_{2}w_{1}) \\ 2f_{2000}^{(2)}\breve{\varphi }_{1}w_{1}+2f_{0200}^{(2)}\breve{\varphi }_{2}w_{2}+2f_{1100}^{(2)}(\breve{\varphi }_{1}w_{2}+\breve{\varphi }_{2}w_{1}) \end{array}\right) \end{aligned}\end{aligned}$$

(B.8)

and

$$\begin{aligned} \widehat{S}_{2}(\Phi z_{x},\widehat{w})=\left( \begin{array}{cc} 2f_{1010}^{(1)}\breve{\varphi }_{1}\widehat{w}_{1} \\ 0 \end{array}\right) . \end{aligned}$$

(B.9)

More precisely, by combining with (3.51), (B.8) and (B.9), we have

$$\begin{aligned}{} & {} S_{2}(\xi _{1},h_{0,2000}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{11}h_{0,2000}^{(1)}+2f_{1100}^{(1)}(\xi _{11}h_{0,2000}^{(2)}+\xi _{12}h_{0,2000}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{11}h_{0,2000}^{(1)}+2f_{0200}^{(2)}\xi _{12}h_{0,2000}^{(2)}+2f_{1100}^{(2)}(\xi _{11}h_{0,2000}^{(2)}+\xi _{12}h_{0,2000}^{(1)}) \end{array}\right) , \\{} & {} S_{2}(\xi _{1},h_{2n_{1},2000}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{11}h_{2n_{1},2000}^{(1)}+2f_{1100}^{(1)}(\xi _{11}h_{2n_{1},2000}^{(2)}+\xi _{12}h_{2n_{1},2000}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{11}h_{2n_{1},2000}^{(1)}+2f_{0200}^{(2)}\xi _{12}h_{2n_{1},2000}^{(2)}+2f_{1100}^{(2)}(\xi _{11}h_{2n_{1},2000}^{(2)}+\xi _{12}h_{2n_{1},2000}^{(1)}) \end{array}\right) , \\{} & {} S_{2}(\xi _{1},h_{0,1100}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{11}h_{0,1100}^{(1)}+2f_{1100}^{(1)}(\xi _{11}h_{0,1100}^{(2)}+\xi _{12}h_{0,1100}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{11}h_{0,1100}^{(1)}+2f_{0200}^{(2)}\xi _{12}h_{0,1100}^{(2)}+2f_{1100}^{(2)}(\xi _{11}h_{0,1100}^{(2)}+\xi _{12}h_{0,1100}^{(1)}) \end{array}\right) , \\{} & {} S_{2}(\xi _{2},h_{0,2000}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{21}h_{0,2000}^{(1)}+2f_{1100}^{(1)}(\xi _{21}h_{0,2000}^{(2)}+\xi _{22}h_{0,2000}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{21}h_{0,2000}^{(1)}+2f_{0200}^{(2)}\xi _{22}h_{0,2000}^{(2)}+2f_{1100}^{(2)}(\xi _{21}h_{0,2000}^{(2)}+\xi _{22}h_{0,2000}^{(1)}) \end{array}\right) , \\{} & {} S_{2}(\xi _{1},h_{2n_{1},1100}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{11}h_{2n_{1},1100}^{(1)}+2f_{1100}^{(1)}(\xi _{11}h_{2n_{1},1100}^{(2)}+\xi _{12}h_{2n_{1},1100}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{11}h_{2n_{1},1100}^{(1)}+2f_{0200}^{(2)}\xi _{12}h_{2n_{1},1100}^{(2)}+2f_{1100}^{(2)}(\xi _{11}h_{2n_{1},1100}^{(2)}+\xi _{12}h_{2n_{1},1100}^{(1)}) \end{array}\right) , \\{} & {} S_{2}(\xi _{2},h_{2n_{1},2000}) \\{} & {} =\left( \begin{array}{c} 2f_{2000}^{(1)}\xi _{21}h_{2n_{1},2000}^{(1)}+2f_{1100}^{(1)}(\xi _{21}h_{2n_{1},2000}^{(2)}+\xi _{22}h_{2n_{1},2000}^{(1)}) \\ 2f_{2000}^{(2)}\xi _{21}h_{2n_{1},2000}^{(1)}+2f_{0200}^{(2)}\xi _{22}h_{2n_{1},2000}^{(2)}+2f_{1100}^{(2)}(\xi _{21}h_{2n_{1},2000}^{(2)}+\xi _{22}h_{2n_{1},2000}^{(1)}) \end{array}\right) \end{aligned}$$

and

$$\begin{aligned}\begin{aligned}&\widehat{S}_{2}(\xi _{1},h_{0,2000})=\left( \begin{array}{c} 2f_{1010}^{(1)}\xi _{11}h_{0,2000}^{(1)} \\ 0 \end{array}\right) , \\&\widehat{S}_{2}(\xi _{1},h_{0,1100})=\left( \begin{array}{c} 2f_{1010}^{(1)}\xi _{11}h_{0,1100}^{(1)} \\ 0 \end{array}\right) , \\&\widehat{S}_{2}(\xi _{2},h_{0,2000})=\left( \begin{array}{c} 2f_{1010}^{(1)}\xi _{21}h_{0,2000}^{(1)} \\ 0 \end{array}\right) . \end{aligned} \end{aligned}$$