1 Introduction

Trajectory tracking control of unmanned surface vehicle (USV) is one of the important research fields in ship engineering. At present, it is the most concerned research direction in the field of ship control. This growing interest stems from the need for stability, robustness and execution efficiency of USV controller systems [1, 2]. The USV can be used in practical applications, including maritime surveillance [3], water rescue [4], independent exploration [5] and water quality sampling [6]. In fact, the control of vector propulsion USV is more challenging than that of fully actuated vessel, which is due to the highly coupled characteristics of vector propulsion inputs between various degrees of freedom [7, 8]. Although this characteristic enhances the maneuverability of USV, the design difficulty of controller increases correspondingly. In addition, environmental disturbances, model uncertainty, and input saturation also bring great challenges to the control system. These factors lead to the complexity of motion control of USV.

In recent years, with the rapid development of ship engineering technology, the development of USV has attracted more and more attention and obtained certain research results [9]. At first, the trajectory tracking control of fully actuated USV was studied [10]. However, most of the USVs are small ships, which are not suitable for carrying side thruster transposition. Therefore, the research direction has turned to underactuated USV [11]. Li et al. used the barrier Lyapunov method to solve the full state constraint problem in trajectory tracking control of underactuated USV [12]. In the literature [13], a model free guidance and control integrated framework is proposed to solve the continuous waypoint tracking problem under completely unknown dynamics and environmental factors. Khooban et al. extended the standard T-S fuzzy model and linear matrix inequality, which made the controller effective in reducing the tracking time and improving the robustness of the controller [14]. On the basis of the research on the trajectory tracking control of single USV, literatures [15, 16] extend it to the multi-USVs formation tracking problem.

At present, scholars have studied the trajectory tracking control for USV from different aspects and achieved some results. Due to the USV sailing in complex marine environment, the external disturbances and model uncertainty will affect the trajectory tracking control performance, so it is necessary to study the trajectory tracking control with external disturbances and model uncertainty. In [17,18,19], to enhance the disturbance rejection and tracking accuracy of the controller, the disturbance observer, homogeneous disturbance observer, and extended state observer are used to estimate the model uncertainty and external disturbance, respectively, so as to realize the exact trajectory tracking control of the USV. Huang et al. [20] adopt reducing order extended state observer to estimate internal and external disturbances. In [21], the nonsingular sliding mode manifold is developed by the bi-limit homogeneous theory with strong robustness against lumped uncertainties. The adaptive online construction fuzzy tracking control method is used to estimate the uncertainties without exact information of dynamic model and external environment disturbances in [22]. Then, [23] solves the influence of initial error by prescribed performance function and enhance the robustness of sliding mode controller by error transformation technique. In [24], the neural network is used to approximate the unknown external disturbance and uncertainty and ensures the robustness of tracking performance through error transformation function. And the radial basis function neural network and disturbance observer are used to estimate and compensate the influence of disturbances in [25]. The above method only considers the external disturbances and model uncertainty, but does not consider the influence of actuator error.

In addition, the range of any actuator is limited, so it is necessary to consider the problem of input saturation. In the integral sliding mode trajectory tracking controller designed by [18], a smooth function is employed to adaptively approximate the input saturation nonlinearity. In [26], the trajectory tracking control problem of state constraint is addressed by a tan-type Barrier Lyapunov function to avoid the constraint state reaching the boundary value. Park [27] does not use adaptive or intelligent technique, but uses auxiliary variables to deal with the problem of input saturation. These methods are to solve the nonlinear problem of input saturation. However, one of the main reasons for input saturation is the overshoot of control input caused by excessive tracking error. Therefore, avoiding excessive tracking error is also an effective way to solve the problem of input saturation. In addition, for dealing with the input saturation problem, the anti-windup compensator adjusts the controller to achieve better control performance when the control input has been saturated. The anti-windup compensator can be directly modified on the existing controller to improve the performance of whole closed-loop system under input saturation [28]. The design of anti-windup compensator has been fully discussed in [28,29,30]. In recent years, some scholars began to discuss the problem of fault-tolerant control in trajectory tracking of USV. In [31], the adaptive technique combined with the backstepping method is adopted to enable the actuator fault-tolerant controller to address the fault effects and the system is guaranteed to be uniformly bounded under certain actuator failure. In [32], an online fault estimator is devised to detect, isolate, and accommodate unknown faults and disturbances without using a priori knowledge, so as to achieve accurate tracking with passive fault tolerance.

Although a lot of research work has been done in terms of the trajectory tracking control of USV, their control inputs are in the form of force and torque, without considering the influence of actuator in USV system, including actuator input saturation and actuator error. In addition, the current underactuated control inputs are independent of each other. However, in the actual ship control, especially in the form of vector propulsion, the control inputs have strong coupling relationship. Motivated by the above problems, this paper designs an adaptive trajectory tracking controller with actuator error, input saturation and input coupling.

In this paper, the virtual control point method with the zero-dynamics stability analysis is used to solve the strong coupling of control input. On this basis, the guidance trajectory is designed to enhance the ability to suppress input saturation. Considering the problem of actuator stabilization and other disturbance factors, the neural network-minimum learning parameter method is used to approximate the actuator error, external disturbance and model uncertainty. Then, the bound value of approximation error is estimated by parameter self-adaptive correction method. Finally, an adaptive sliding mode trajectory tracking controller for vector propulsion USV is designed, and the effectiveness of proposed method is verified by simulation experiment. The main contributions of the proposed trajectory tracking controller can be summarized as follows:

  1. (1)

    In this paper, the coupling problem of control input is considered in the design of trajectory tracking controller, and the virtual control point method is used to solve this problem. The stability condition for control input coupling is determined by zero-dynamics stability analysis.

  2. (2)

    Considering that the excessive tracking error will cause the overshoot of control input and lead to the saturation of control input, this paper designs a guidance trajectory between the desired trajectory and the vessel to avoid the excessive tracking error and ensure that the guidance trajectory can eventually converge to the desired trajectory, so as to realize the tracking of the desired trajectory and suppress the problem of input saturation.

  3. (3)

    In the design of trajectory tracking controller, considering the actuator error and other disturbance factors, the neural network-minimum learning parameter method is used to approximate the actuator error, external disturbance and model uncertainty. And the bound value of approximation error is estimated by parameter self-adaptive correction method. In addition, for the problem of oscillation convergence of sliding mode controller caused by the discontinuity of signum function, this paper introduces a continuously differentiable approximate saturation function instead of signum function to improve the performance of controller.

The rest of this paper is organized as follows: Sect. 2 presents the mathematical model and control structure of vector propulsion USV. The adaptive trajectory tracking controller and stability analysis are provided in Sect. 3 and Sect. 4. The actuator controller is designed in Sect. 5. Simulations are carried out in Sect. 6, and conclusion is finally stated in Sect. 7.

2 Problem formulation

2.1 Mathematical model of vector propulsion USV

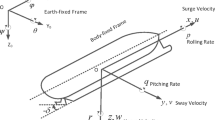
To study the USV motions, the Earth-fixed \(o_a-x_ay_a\) and the Body-fixed \(o_b-x_by_b\) reference frames are defined in Fig. 1 [33, 34].

Fig. 1
figure 1

The description of earth-fixed and body-fixed reference frames

Full size image

The kinematics and dynamics equations of USV model are as follows [35, 36]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = u\cos \psi - v\sin \psi \\ \dot{y} = u\sin \psi + v\cos \psi \\ {\dot{\psi }} = r\\ \dot{u} = {f_u} + {\varDelta _u} + \frac{1}{{{m_{11}}}}({T _u} + {b_u})\\ \dot{v} = {f_v} + {\varDelta _v} + \frac{1}{{{m_{22}}}}({T _v} + {b_v})\\ \dot{r} = {f_r} + {\varDelta _r} + \frac{1}{{{m_{33}}}}({F _r} + {b_r}) \end{array} \right. , \end{aligned}$$
(1)
Fig. 2
figure 2

Control structure for vector propulsion USV

Full size image

with

$$\begin{aligned} {f_u}&= \frac{{{m_{22}}}}{{{m_{11}}}}vr - \frac{{{d_{11}}}}{{{m_{11}}}}u\\ {f_v}&= - \frac{{{m_{11}}}}{{{m_{22}}}}ur - \frac{{{d_{22}}}}{{{m_{22}}}}v\\ {f_r}&= \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}uv - \frac{{{d_{33}}}}{{{m_{33}}}}r \end{aligned}$$

Here, \((x, y, \psi )\) are the vessel position and yaw angle in the earth-fixed frame, u and v are the longitudinal and transverse linear velocities in surge (body-fixed \(x_b\)) and sway (body-fixed \(y_b\)) directions, respectively, and r is the angular velocity in yaw axes in the body-fixed frame (see Fig. 1). \(({T _u},{T _v},{F _r})\) are the thrust (moment) component of the surge, sway, and yaw axes. \(m_{11}\), \(m_{22}\), \(m_{33}\) are the vessel inertia including added mass effects, and \(d_{11}\), \(d_{22}\), \(d_{33}\) are the hydrodynamic damping coefficients. \((\varDelta _u, \varDelta _v, \varDelta _r)\) and \((b_u, b_v, b_r)\) are the unmodeled dynamics and external disturbances induced by wind, waves, and ocean currents acting on surge, sway, and yaw directions.

For vector propulsion system, the thrust transformation equation showing the relationship between \(({T _u},\) \({T _v}, {F _r})\) and (vector propulsion angle \(\delta \), thruster speed n )is [37, 38]

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} {T _u} = T\cos (\delta )\\ {T _v} = -T\sin (\delta )\\ {F _r} = T\sin (\delta )L/2 \end{array} \right. \\ T = \left( {1 - {t_p}} \right) \rho {n^2}D_p^4{K_T} \end{aligned}, \end{aligned}$$
(2)

where T is the thrust of propulsion system, and L is the length of vessel hull. By solving the (2) in reverse, the actuator transformation equation [39, 40] can be obtained as follows can be obtained by actuator transformation equation as

$$\begin{aligned} \left\{ \begin{array}{l} \delta = \arctan \left( {\frac{{2{F _r}}}{{{T _u}L}}} \right) \\ n = \sqrt{\frac{{{T _u}}}{{\left( {1 - {t_p}} \right) \rho D_p^4{K_T}\cos (\delta )}}} \end{array} \right. . \end{aligned}$$
(3)

As an actuator, the propulsion angle \(\delta \) and thruster speed n of propulsion system need a certain response time during execution, so their response model [41, 42] is

$$\begin{aligned} \left\{ \begin{array}{l} {T_q}\dot{n}_r + n_r = {K_q}{n_a}\\ \ddot{\delta }_r + 2\zeta {\omega _n}{\dot{\delta }}_r + \omega _n^2\delta _r = {K_\delta }\omega _n^2{\delta _a} \end{array} \right. , \end{aligned}$$
(4)

where \((n_a, \delta _a)\) and \((n_r, \delta _r)\) are the control inputs and actual outputs of actuator, respectively; \(T_q\) and \(K_q\) denote the time constant, gain of n; \(\omega _n\), \(\zeta \), and \(K_\delta \) refer to the natural frequency, damping ratio, and proportionality coefficient of \(\delta \). The \(n \in [0,{n_{m}}]\) and \(\delta \in [ - {\delta _m},{\delta _m}]\) are the executable ranges of actuator.

2.2 Control structure

Aiming at the vector propulsion USV with the influence of input saturation, input coupling, actuator error, model uncertainty, and external disturbances in the marine environment, an adaptive trajectory tracking control with full state feedback is proposed for vector propulsion USV.

Figure 2 shows the structure of proposed controller. The controller structure diagram is divided into four blocks, including guidance trajectory block (pink), trajectory tracking control block (cyan), actuator control block (yellow), and USV model block (green). The guidance law converts the desired trajectory \(P_d\) into the guidance trajectory \(P_g\). Control input saturation is mainly caused by large disturbances and initial state error [43, 44]. To avoid the problem of control input saturation, guidance law is adopted to avoid input saturation. In the design of control structure, considering the influence of actuator error, the actuator control is also designed, and the thrust (moment) components \(({T _u},{T _v},{F _r})\) and (thruster speed n, propulsion angle \(\delta \)) are transformed by Eqs. (2) and (3). Considering the input coupling problem, the trajectory tracking controller is designed on the basis of virtual control point, and the disturbance effects such as actuator error, model uncertainty and unknown environment disturbances are reduced by neural network-minimum learning parameter and parameter adaptive correction method. In addition, a continuously differentiable approximate saturation function is used to avoid the oscillation caused by the signum function in controller design.

3 Trajectory tracking control

3.1 Preliminaries

In the stabilization and tracking process of the actuator, there are tracking errors between the actual control inputs \(\mathbf {u_r}\) \(={\left[ {T _{ur},F _{rr} } \right] ^T}\) and command control inputs \(\mathbf {u_c}\) \(={\left[ {T _{uc},F _{rc} } \right] ^T}\), so the actuator errors \(\mathbf {u_e}\) \(={\left[ {T _{e},F _{e} } \right] ^T}\) for thrust and torque are \(T _{e}=T _{ur}-T _{uc}\) and \(F _{e}=F _{rr}-F _{rc}\).

According to (2), the dynamics equation of vessel model (1) will be modified to be

$$\begin{aligned} \left\{ \begin{array}{l} \dot{u} = {f_u} + \frac{1}{{{m_{11}}}}{T _{ur}} + {d_u}\\ \dot{v} = {f_v} - \frac{2}{{{m_{22}}L}}{F _{rr}} + {d_v}\\ \dot{r} = {f_r} + \frac{1}{{{m_{33}}}}{F _{rr}} + {d_r} \end{array} \right. , \end{aligned}$$
(5)

where the disturbances terms are \({d_u} = {\varDelta _u} + \frac{1}{{{m_{11}}}}{b_u}, {d_v} = {\varDelta _v} + \frac{1}{{{m_{22}}}}{b_r}, {d_r} = {\varDelta _r} + \frac{1}{{{m_{33}}}}{b_r}\).

Assumption 1

The disturbances term d and actuator errors \((T_e, F_e)\) are bounded. In other words, there exists the positive constants \(\bar{d}_i\) , \({\bar{d}}_T\) and \({\bar{d}}_F\), such as \(\left| {{d_i}} \right| \le {{\bar{d}}_i}\), \(i = u,v,r\), \(\left| {{T_e}} \right| \le {\bar{d}_T}\) and \(\left| {{F_e}} \right| \le {{\bar{d}}_F}\).

The vector propulsion mode causes the coupling problem of control inputs with (5), which makes the internal dynamics of system unstable [38, 45]. Therefore, the virtual control point method is introduced to transform it into a dynamic system with internal stability. The virtual control point P is located on the longitudinal symmetrical axis of vessel with positive distance l from the geometric center as shown in Fig. 3.

Fig. 3
figure 3

The virtual control point P

Full size image

The position P is given by

$$\begin{aligned} P = \left[ {\begin{array}{*{20}{c}} {{x_p(t)}}\\ {{y_p(t)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} x(t)\\ y(t) \end{array}} \right] + l\left[ {\begin{array}{*{20}{c}} {\cos \psi (t) }\\ {\sin \psi (t) } \end{array}} \right] ,l > 0. \end{aligned}$$
(6)

where \(l > 0\), the reference trajectory \(\gamma \) of vessel tracking is represented by the desired output \({P_d} = \left[ {{x_{d}}(t)}, {{y_{d}}(t)} \right] ^T\), which is generated by a virtual reference vessel with the same dynamics parameters, but without the effect of modeling uncertainties and external disturbances.

Assumption 2

The reference trajectory \(\gamma \) is sufficient smooth with the \({x_{d}}\), \({\dot{x}_{d}}\), \({\ddot{x}_{d}}\), \({y_{d}}\), \({\dot{y}_{d}}\), \({\ddot{y}_{d}}\) bounded.

Due to the excellent performance and global approximation ability of radial basis function neural network (RBFNN), it is used to approximate the unknown nonlinear disturbance term in the system.

For an arbitrary continuous function N(X), the radial basis function neural network (RBFNN) can approximate it by \(N(X)~=~{W^T}h(X) + \varepsilon \) with ideal weight W, input variable X, Gauss basis function h, and approximation error \(\varepsilon \) [46]. To avoid increasing the computational complexity for the on-line estimation of W, the minimal-learning parameter method is used to design the adaptive law of parameter estimation \(\phi ~=~{\left\| W \right\| ^2}\), \(\phi >0\) instead of the weight W adjustment, with the estimated value \({\hat{\phi }}\) and estimation error \({\tilde{\phi }} ~=~{\hat{\phi }} - \phi \).

The control objective is to design an adaptive tracking controller, which can ensure the uniformly ultimately bounded for the vector propulsion USV under Assumptions 1 and 2.

3.2 Guidance trajectory

Define the along and cross tracking errors between the virtual point and the desired position:

$$\begin{aligned} \left[ \begin{array}{l} {x_{e}}\\ {y_{e}} \end{array} \right] = J^T{\left( {{\phi _d}} \right) }\left[ \begin{array}{l} {x_p} - {x_d}\\ {y_p} - {y_d} \end{array} \right] , \end{aligned}$$
(7)

with

$$\begin{aligned} J\left( {{\phi _d}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\phi _d}}&{}{ - \sin {\phi _d}}\\ {\sin {\phi _d}}&{}{\cos {\phi _d}} \end{array}} \right] , \end{aligned}$$

where \({\phi _d} = \mathrm{{atan}}2\left( {{{\dot{y}}_d},{{\dot{x}}_d}} \right) \).

The time derivation of \(x_e\) is

$$\begin{aligned} \begin{aligned} {{\dot{x}}_e} =&\left( {\dot{x} - {{\dot{x}}_d}} \right) \cos {\phi _d} - \left( {x - {x_d}} \right) {{{\dot{\phi }} }_d}\sin {\phi _d}\\&\quad + \left( {\dot{y} - {{\dot{y}}_d}} \right) \sin {\phi _d}+ \left( {y - {y_d}} \right) {{{\dot{\phi }} }_d}\cos {\phi _d}\\&- l\left( {r - {{{\dot{\phi }} }_d}} \right) \sin \left( {\psi - {\phi _d}} \right) \\ =&\quad \dot{x}\cos {\phi _d} + \dot{y}\sin {\phi _d} - {U_d} + {{{\dot{\phi }} }_d}{y_e}\\&- lr\sin \left( {\psi - {\phi _d}} \right) \end{aligned} \end{aligned}$$
(8)

where \({U_d} = {\dot{x}_d}\cos {\psi _d} + {\dot{y}_d}\sin {\psi _d} = \sqrt{{{\dot{x}}_d}^2 + {{\dot{y}}_d}^2} \).

According to (1), (8) can be written as

$$\begin{aligned} {{\dot{x}}_{e}}&= u\cos \left( {\psi - {\phi _d}} \right) - \left( {v + lr} \right) \sin \left( {\psi - {\phi _d}} \right) \nonumber \\&\quad \ - {U_d} + {{{\dot{\phi }} }_d}{y_{e}}\nonumber \\&= {U_p}\cos \left( {\psi - {\phi _d} + \chi } \right) - {U_d} + {{{\dot{\phi }} }_d}{y_{e}} \end{aligned}$$
(9)

where \({U_p} = \sqrt{{u^2} + {{\left( {v + lr} \right) }^2}}\) and \(\chi = \mathrm{{atan}}2( v + lr,u )\).

Next, the time derivation of \(y_e\) along (1) is

$$\begin{aligned} \begin{aligned} {{\dot{y}}_{e}}&= u\sin \left( {\psi - {\phi _d}} \right) + \left( {v + lr} \right) \cos \left( {\psi - {\phi _d}} \right) - {x_{e}}{{{\dot{\phi }} }_d}\\&= {U_p}\sin \left( {\psi - {\phi _d} + \chi } \right) - {x_{e}}{{{\dot{\phi }} }_d}\nonumber \end{aligned}\\ \end{aligned}$$
(10)

The yaw angle and speed of designed guidance trajectory are:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} {\psi _g} = {\phi _d} + \arctan \left( { - \frac{{{y_e}}}{\varDelta }} \right) - \chi \\ {U_g} = \frac{{\left( {{U_d} - k{x_e}} \right) \sqrt{y_e^2 + {\varDelta ^2}} }}{\varDelta } \end{array} \right. \end{aligned} \end{aligned}$$
(11)

with \(k>0\), \(\varDelta >0\). And the surge and sway velocities of designed guidance trajectory are such that

$$\begin{aligned} \left\{ \begin{array}{l} {u_g} = \sqrt{{U_g}^2 - {v_g}^2} \\ {v_g} = v + lr \end{array} \right. \end{aligned}$$
(12)

So the time derivation of designed guidance trajectory \(P_g\) can be described as

$$\begin{aligned} {\dot{P}_g} = \left[ \begin{array}{l} {\dot{x}_g}\\ {\dot{y}_g} \end{array} \right] = J\left( {{\psi _g}} \right) \left[ \begin{array}{l} {u_g}\\ {v_g} \end{array} \right] \end{aligned}$$
(13)

When the following error

$$\begin{aligned} \left\{ \begin{array}{l} {e_u} = u - {u_g}\\ {e_\psi } = \psi - {\psi _g} \end{array} \right. \end{aligned}$$
(14)

converges to zero, the tracking error \(x_e\) and \(y_e\) can be guaranteed to converge to zero gradually. The proof is as follows:

The following Lyapunov function \(V_1\) are constructed:

$$\begin{aligned} {V_1} = \frac{1}{2}x_{e}^2 + \frac{1}{2}y_{e}^2 \end{aligned}$$
(15)

Differentiating (15) along (9) and (10) gives

$$\begin{aligned} \begin{aligned} {{\dot{V}}_1} =&\; x_{e}^{}\dot{x}_{e}^{} + y_{e}^{}\dot{y}_{e}^{}\\ =&\quad x_{e}^{}\left( {{U_g}\cos \left( {{\psi _g} - {\phi _d} + \chi } \right) - {U_d} + {{{\dot{\phi }} }_d}{y_{e}}} \right) \\&+ y_{e}^{}\left( {{U_g}\sin \left( {{\psi _g} - {\phi _d} + \chi } \right) - {x_{e}}{{{\dot{\phi }} }_d}} \right) \\ =&- kx_{e}^2 - {U_g}\frac{{{y_{e}}^2}}{{\sqrt{{\varDelta ^2} + {y_{e}}^2} }} \end{aligned} \end{aligned}$$
(16)

It can be obtained from (16) that \({\dot{V}}_1<0\), so the tracking error \(x_e\) and \(y_e\) are converge to zero.

3.3 Controller design

In this section, we present a constructive design technique to solve the trajectory tracking control with control input coupling problem that steers vessel systems (1) along the guidance trajectory \({P_g}\). The trajectory tracking control with virtual control point method is developed to construct feedback control input \(\mathbf{{u_c}}=[T_{uc}, F_{rc}]^T\). We set \(\chi (\psi ) = {\left[ {\cos \psi ,sin\psi } \right] ^T}\), \(o(\psi ) =[ - sin\psi ,\)

\(\cos \psi ]^T\), \(R(\psi ) = \left[ {\chi (\psi ),o(\psi )} \right] \). For any \(x = {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right] ^T}\), \(y = {\left[ {{y_1},{y_2}, \cdots ,{y_n}} \right] ^T} \in \mathbb {R}{^n}( n \ge 1 )\), we have \(\left\langle {x,y} \right\rangle = {\sum \nolimits _{i = 1}^n {{x_i}y} _i}\), \(\left\| x \right\| = \sqrt{\left\langle {x,x} \right\rangle } \).

Firstly, according to Eqs. (1) and (5), the second derivative of virtual control point (6) is obtained by

$$\begin{aligned} \begin{aligned} {\ddot{P}} =&\left[ {\begin{array}{*{20}{c}} {{{\ddot{x}}_p}}\\ {{{\ddot{y}}_p}} \end{array}} \right] \\ =&\quad o(\psi )ur + \chi (\psi )\left( {{f_u} + \frac{1}{{{m_{11}}}}{T _{ur}} + {d_u}} \right) \\&+ o(\psi )\left( {{f_v} - \frac{2 }{{{m_{22}L}}}{F _{rr}} + {d_v}} \right) - \chi (\psi )vr\\&+ o(\psi )l\left( {{f_r} + \frac{1}{{{m_{33}}}}{F _{rr}} + {d_r}} \right) - \chi (\psi )l{r^2} \end{aligned}. \end{aligned}$$
(17)

Next, Eq. (17), written in a compact form, will be modified to be

$$\begin{aligned} {{\ddot{P}}} = {{F}} + {{B}\mathbf {u_r}} + {{N_0}}, \end{aligned}$$
(18)

with

$$\begin{aligned} {{F}}= & {} R(\psi )\left[ {\begin{array}{*{20}{c}} {{f_u} - vr - l{r^2}}\\ {{f_v} + ur + {f_r}l} \end{array}} \right] ,\\ {B}= & {} \left[ {\frac{{\chi (\psi )}}{{{m_{11}}}}, - o(\psi )\left( {\frac{2 }{{{m_{22}L}}} - \frac{l}{{{m_{33}}}}} \right) } \right] ,\\ \mathbf{{u_r}}= & {} \mathbf{{u_c}}+\mathbf{{u_e}}= {\left[ {{T _{ur}},{F _{rr}}} \right] ^T}, {{N_0}} = R(\psi )\left[ {\begin{array}{*{20}{c}} {{d_u}}\\ {{d_v} + {d_r}l} \end{array}} \right] . \end{aligned}$$

The control input \(\mathbf {u_c}\) is designed so that the redefined output P can converge to the guidance trajectory \(P_g\).

To this end, the target is to stabilize the \(P_{eg}=P-P_g\), an adaptive sliding mode control has been proposed. To stabilize the \(P_{eg}\), the sliding mode manifold S is defined with the form

$$\begin{aligned} S = {\dot{P}_{eg}} + \lambda {P_{eg}} + \sigma \int _0^t {{P_{eg}}(\tau )} d\tau , \end{aligned}$$
(19)

where \(S = {\left[ {{S_1},{S_2}} \right] ^T}\), \(\lambda = diag\left( {{\lambda _1},{\lambda _2}} \right) \), \({\lambda _i} > 0\), \(\sigma = diag\left( {{\sigma _1},{\sigma _2}} \right) \), \({\sigma _i} > 0\), \(i = 1,2\).

With the design of Eq. (18), the time derivative of S can be written as

$$\begin{aligned} \dot{S}&= F + B\mathbf{{u_r}} + N_0 - {\ddot{P}_g} + \lambda {\dot{P}_{eg}} + \sigma {P_{eg}}\nonumber \\&= F + B\mathbf{{u_c}}+ N - {\ddot{P}_g} + \lambda {\dot{P}_{eg}} + \sigma {P_{eg}}. \end{aligned}$$
(20)

where \(N=B\mathbf{{u_e}} + N_0\).

Then, the control law can be chosen as

$$\begin{aligned} \mathbf{{u_c}} = {B^{ - 1}}\left( {{{\ddot{P}}_g} - \lambda {{{\dot{P}}_{eg}}} - \sigma { P_{eg}} - F - N} \right) . \end{aligned}$$
(21)

Based on Subsection 3.1, the disturbance term N can be approached by RBFNN with the form

$$\begin{aligned} N~=~{W^T}h(X) + \varepsilon . \end{aligned}$$
(22)

where the ideal weight is \(W = diag(W_1, W_2)\). And according to Assumption 1, \(\varepsilon \) is bounded, so \(\left| {{\varepsilon }} \right| \le {\varpi }\), \(\varpi >0\). Define \(\phi _i ~=~{\left\| W_i \right\| ^2}\), \(i = 1, 2\), and update the control law

$$\begin{aligned} \begin{aligned} \mathbf{{u_c}} =&{B^{ - 1}}\left( {{{\ddot{P}}_g} - \lambda {{{\dot{P}}_{eg}}} - \sigma {{P_{eg}}} - F} \right) \\&- \frac{1}{2}{B^{ - 1}}{\hat{\phi }} S {h^T}h, \end{aligned} \end{aligned}$$
(23)

with the designed adaptive law

$$\begin{aligned} {\dot{\hat{{\phi }_i}}} = \frac{\gamma _i }{2}{S_i^2}{h^T}h - \kappa _i \gamma _i {\hat{\phi }}_i. \end{aligned}$$
(24)

Here, \({\gamma _i} > 0\), \({\kappa _i} > 0\), i = 1, 2.

To ensure the convergence of sliding manifold [47], the corresponding control law with a continuously derivable approximate saturation function can be written as

$$\begin{aligned} \begin{aligned} \mathbf{{u_c}}=&{B^{ - 1}}\left( { - \frac{1}{2}{\hat{\phi }} S {h^T}h + {{\ddot{P}}_g} - \lambda {\dot{P}_{eg}} - \sigma {P_{eg}}} \right) \\&+ {B^{ - 1}}\left( { - F - \mu S - \aleph {{\hat{\varpi }} } } \right) \end{aligned}, \end{aligned}$$
(25)

where \(\mu = diag\left( {{\mu _1},{\mu _2}} \right) \), \({\mu _i} > 0\);

$$\begin{aligned}&\aleph =diag\left\{ \mathrm{{sat}}(S_1/\vartheta _1 ),\mathrm{{sat}}(S_2/\vartheta _2 )\right\} ,\\&\quad \mathrm{{sat}}(S_i/\vartheta _i ) = \left\{ {\begin{array}{*{20}{c}} {{\mathrm{sgn}} (S_i),\left| {S_i} \right| > {\frac{{{\vartheta _i}}}{{{\rho _i} - 1}}}}\\ {{\frac{{{\rho _i}{S_i}}}{{\left| {{S_i}} \right| + {\vartheta _i}}}} ,\left| {S} \right| \le {\frac{{{\vartheta _i}}}{{{\rho _i} - 1}}}} \end{array}} \right. , \end{aligned}$$

and \(\rho _i > 1\), \(\vartheta _i > 0\), \(i = 1,2\); sgn(\( \cdot \)) denotes signum function.

The update law for \({{\hat{\varpi }} }\) is designed as

$$\begin{aligned} \dot{{\hat{\varpi }}} \mathrm{{ = }}\eta \left[ {\aleph S - \varLambda \left( {{\hat{\varpi }} - {\varpi ^0}} \right) } \right] , \end{aligned}$$
(26)

where \(\eta = diag\left( {{\eta _1},{\eta _2}} \right) \) and \(\varLambda = diag\left( {{\varLambda _1},{\varLambda _2}} \right) \) are all the positive design parameter diagonal matrices. \({\hat{\varpi }}\) is the estimation vector of \(\varpi \); \(\varpi ^0\in {\mathbf{{R}}^2}\) is prior estimate of \(\varpi \).

4 Stability analysis

4.1 Stability analysis for controller

Consider the following candidate Lyapunov function as

$$\begin{aligned} V_2 = \frac{1}{2}\left( {S^TS} + \frac{1}{{{\gamma _i}}}\sum \limits _{i = 1}^2 {{{{\tilde{\phi }}_i }^2}}+ {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\tilde{\varpi }\right) , \end{aligned}$$
(27)

where \(\tilde{\phi }_i\) is the approximation error for \(\phi _i\) such that \(\tilde{\phi }_i = {\hat{\phi }}_i-\phi _i\), \(i = 1,2\); \(\tilde{\varpi }\) is the estimation error for \(\varpi \) such as \(\tilde{\varpi }= {\hat{\varpi }}-\varpi \).

The time derivative of \(V_2\) can be obtained as

$$\begin{aligned} {{\dot{V}}_2}=&S^T\dot{S} + \frac{1}{{{\gamma _i}}}\sum \limits _{i = 1}^2 {{\tilde{\phi }_i \dot{\hat{\phi _i}}}}+ {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\dot{{\hat{\varpi }}}. \end{aligned}$$
(28)

According to (20) and (22), we can get

$$\begin{aligned} S^T\dot{S}&= S^T\left( {F + B\mathbf{{u_r}} + N_0 - {{\ddot{P}}_g} + \lambda {{\dot{P}}_{eg}} + \sigma {P_{eg}}} \right) \nonumber \\&= S^T\left( {F + B\mathbf{{u_c}} + \varepsilon - {{\ddot{P}}_g} + \lambda {{\dot{P}}_{eg}} + \sigma {P_{eg}}} \right) \nonumber \\&\quad + S^T{W^T}h. \end{aligned}$$
(29)

With \(\phi _i ~=~{\left\| W_i \right\| ^2}\),

$$\begin{aligned} \begin{aligned} {S_i^2}\phi _i {h^T}h + 1&= {S_i^2}{\left\| W_i \right\| ^2}{\left\| h \right\| ^2} + 1\\&= {S_i^2}{\left\| {{W_i^T}h} \right\| ^2} + 1 \ge 2S_i{W_i^T}h. \end{aligned} \end{aligned}$$
(30)

Thus,

$$\begin{aligned} S^T\dot{S}\le&S^T\left( {F + B\mathbf{{u_c}} + \varepsilon - {{\ddot{P}}_g} + \lambda {{\dot{P}}_{eg}} + \sigma {P_{eg}}} \right) \nonumber \\&+ \frac{1}{2}{S^T}\phi S {h^T}h+ \frac{1}{2} . \end{aligned}$$
(31)

Substituting the control law (25) into (31), which can be rewritten as

$$\begin{aligned} S^T\dot{S}\le&- {S^T\mu S} + S^T\varpi - S^T\aleph {{\hat{\varpi }} }\nonumber \\&- \frac{1}{2}{S^T\tilde{\phi }S} {h^T}h + \frac{1}{2} . \end{aligned}$$
(32)

Consider the adaptive law (24), we have

$$\begin{aligned} \frac{1}{{{\gamma _i}}}{{\tilde{\phi }}_i}\dot{\hat{\phi _i}}= {{\tilde{\phi }}_i}\left( {\frac{1}{2}S_i^2{h^T}h - {\kappa _i}{{\hat{\phi }}_i}} \right) . \end{aligned}$$
(33)

Because \((\tilde{\phi }_i + \phi _i )^2 \ge 0\), then \(\tilde{\phi }_i ^2 + 2\tilde{\phi }_i ({\hat{\phi }}_i - \tilde{\phi }_i ) + {\phi _i ^2} \ge 0\), i.e., \(2\tilde{\phi }_i {\hat{\phi }}_i \ge {\tilde{\phi }_i^2} - {\phi _i ^2}\), so the (33) is

$$\begin{aligned} \frac{1}{{{\gamma _i}}}{{\tilde{\phi }}_i}\dot{\hat{\phi _i}} \le \frac{1}{2}S_i^2{{\tilde{\phi }}_i}{h^T}h - \frac{1}{2}{\kappa _i}\tilde{\phi }_i^2 + \frac{1}{2}{\kappa _i}\phi _i^2. \end{aligned}$$
(34)

In light of update law (26), we can get

$$\begin{aligned} \begin{aligned} {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\dot{{\hat{\varpi }}}=&{{\tilde{\varpi }}^T}{\eta ^{ - 1}}\eta \left[ {\aleph S - \varLambda \left( {{\hat{\varpi }} - {\varpi ^0}} \right) } \right] \\ =&{{\tilde{\varpi }}^T}\aleph S - {\left( {{\hat{\varpi }} - \varpi } \right) ^T}\varLambda \left( {{\hat{\varpi }} - {\varpi ^0}} \right) \end{aligned}. \end{aligned}$$
(35)

According to the following inequalities,

$$\begin{aligned} \begin{aligned}&- {\left( {{\hat{\varpi }} - \varpi } \right) ^T}\varLambda \left( {{\hat{\varpi }} - {\varpi ^0}} \right) \\&\quad = - \frac{1}{2}{\left( {{\hat{\varpi }} - \varpi } \right) ^T}\varLambda \left( {{\hat{\varpi }} - \varpi } \right) \\&\quad - \frac{1}{2}{\left( {{\hat{\varpi }} - {\varpi ^0}} \right) ^T}\varLambda \left( {{\hat{\varpi }} - {\varpi ^0}} \right) \\&\qquad + \frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \\&\quad \le - \frac{1}{2}{\left( {{\hat{\varpi }} - \varpi } \right) ^T}\varLambda \left( {{\hat{\varpi }} - \varpi } \right) \\&\quad + \frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \end{aligned}. \end{aligned}$$
(36)

We obtain

$$\begin{aligned} \begin{aligned} {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\dot{{\hat{\varpi }}} \le&{{\tilde{\varpi }}^T}\aleph S - \frac{1}{2}{\left( {{\hat{\varpi }} - \varpi } \right) ^T}\varLambda \left( {{\hat{\varpi }} - \varpi } \right) \\&+ \frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \\ \le&{{\tilde{\varpi }}^T}\aleph S - \frac{1}{2}{\lambda _{\min }}\left( {\varLambda \eta } \right) {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\tilde{\varpi }\\&+ \frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \end{aligned}. \end{aligned}$$
(37)

where \({\lambda _{\min }}\left( \bullet \right) \) represents the minimum eigenvalue of the matrix.

According to (32), (34) and (37), (28) can be written as

$$\begin{aligned} \begin{aligned} \dot{V}_2 \le&- {S^T\mu S} +S^T\varpi - S^T\aleph { \varpi } - \frac{1}{2}\sum \limits _{i = 1}^2 {\kappa _i}{{\tilde{\phi }}_i^2}\\&+\frac{1}{2}\sum \limits _{i = 1}^2{\kappa _i}{{{\hat{\phi }} }_i^2}+ \frac{1}{2}- \frac{1}{2}{\lambda _{\min }}\left( {\varLambda \eta } \right) {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\tilde{\varpi }\\&+\frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \end{aligned}. \end{aligned}$$
(38)

For \({S_i}{\aleph _i}{{ \varpi }_i} = {S_i}{{ \varpi }_i}\mathrm{{sat}}({S_i}/{\vartheta _i})\), when \(\left| {{S_i}} \right| > \frac{{{\vartheta _i}}}{{{\rho _i} - 1}}\), \({S_i}{\aleph _i}{{ \varpi }_i} \le \left| {{S_i}} \right| {{ \varpi }_i}\); when \(\left| {{S_i}} \right| \le \frac{{{\vartheta _i}}}{{{\rho _i} - 1}}\), that is \(\frac{{{{S_i}^2}}}{{\left| S_i \right| + \vartheta _i }} \le \frac{1}{{{\rho _i}}}\left| S_i \right| \), so \({S_i}{\aleph _i}{{ \varpi }_i} \le \frac{\varpi _i\rho _i S_i^2}{{\left| S_i \right| + \vartheta _i }} \le \left| {{S_i}} \right| {{ \varpi }_i}\). It can be concluded that according to the continuously differentiable approximate saturation function, \({S_i}{\aleph _i}{{ \varpi }_i} \le \left| {{S_i}} \right| {{ \varpi }_i}\), so

$$\begin{aligned} \begin{aligned} \dot{V}_2 \le&- {S^T\mu S} - \frac{1}{2}\sum \limits _{i = 1}^2 {\kappa _i}{{\tilde{\phi }}_i^2} +\frac{1}{2}\sum \limits _{i = 1}^2{\kappa _i}{{{\hat{\phi }} }_i^2}+ \frac{1}{2}\\&- \frac{1}{2}{\lambda _{\min }}\left( {\varLambda \eta } \right) {{\tilde{\varpi }}^T}{\eta ^{ - 1}}\tilde{\varpi }\\&+\frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \end{aligned}. \end{aligned}$$
(39)

When \({q_1} = \mu \), \({q_2} = \frac{1}{2}{\lambda _{\min }}\left( {\varLambda \eta } \right) \), \(\nabla = \frac{1}{2} + \frac{1}{2}\sum \nolimits _{i = 1}^2{\kappa _i}{{{\hat{\phi }} }_i^2} + \frac{1}{2}{\left( {\varpi - {\varpi ^0}} \right) ^T}\varLambda \left( {\varpi - {\varpi ^0}} \right) \), then (39) becomes

$$\begin{aligned}&\dot{V}_2 \le -{S^T{q_1}S} -\frac{1}{2\gamma _i}\sum \nolimits _{i = 1}^2 \gamma _i{\kappa _i}{{\tilde{\phi }}_i^2} \nonumber - {q_2}{{\tilde{\varpi }}^T}{\eta ^{ - 1}}\tilde{\varpi }\\+\nabla . \end{aligned}$$
(40)

Therefore, it is obvious that the derivative of \(V_2\) with respect to time can be rewritten as

$$\begin{aligned} \dot{V}_2 \le - 2qV_2 + \nabla , \end{aligned}$$
(41)

where

$$\begin{aligned} q = \min \left\{ {{q_1},{q_2},{\frac{1}{2}\gamma _1\kappa _1},{\frac{1}{2}\gamma _2\kappa _2}} \right\} >0. \end{aligned}$$
(42)

Theorem 1

Consider the kinematics equation of (1) and dynamics equation (5) with Assumptions 1 and 2, the adaptive law is designed according to (24) to approach the disturbance term N, and the parameters updating law is designed according to (26) to estimate the bound value of approximation error. Finally, the control law (25) is designed. By properly adjusting the control parameters \(\lambda ,\sigma ,\mu ,\eta ,\gamma ,\kappa ,{\vartheta _1},{\vartheta _2},{\rho _1},{\rho _2}\) to satisfy the condition of (42), the uniform ultimately bounded stable of all variables in the closed-loop system can be guaranteed .

Proof

By solving inequality (41), the following result can be obtained.

$$\begin{aligned} 0 \le {V_2}\left( t \right) \le \frac{\nabla }{{2q}} + \left( {{V_2}\left( 0 \right) - \frac{\nabla }{{2q}}} \right) {e^{ - 2qt}} \end{aligned}$$
(43)

Therefore, \({V_2}\left( t \right) \) is uniformly ultimately bounded. According to (27), the variables S,\({\tilde{\phi }_i}\), \(\tilde{\varpi }\) in the system are uniformly ultimately bounded, and then \({P_{eg}}\) and \({\dot{P}_{eg}}\) are bounded. According to (13)-(16), the tracking errors \({x_e}\) and \({y_e}\) are bounded. The boundedness of \({{\hat{\phi }} _i}\) is obtained from the boundedness of \({\tilde{\phi }_i}\) and \({\phi _i}\), the boundedness of \({\hat{\varpi }} \) is from the boundedness of \(\tilde{\varpi }\) and \(\varpi \), so that all variables in the closed-loop system of tracking control can be guaranteed to uniformly ultimately bounded. \(\square \)

4.2 Zero-dynamics stability analysis

For the virtual control point method, the sway force caused by control input coupling will cause the instability of the control system due to the position selection of virtual control point P. In Fig. 3, the difference \(\beta \) between the yaw angle \(\psi \) of vessel and the reference velocity \({\dot{\gamma }}\) can express the state of zero dynamics. It is assumed that the virtual control point has tracked the desired trajectory, so the velocity u, v of vessel can be rewritten

$$\begin{aligned} u = U\cos (\beta ), v = - l r - U\sin (\beta ), \end{aligned}$$
(44)

where reference speed is \(U = \left\| {{\dot{\gamma }} } \right\| \). By (1) and (6), we can obtain

$$\begin{aligned} \begin{array}{l} u = \left\langle {{\dot{\gamma }} ,\chi (\psi )} \right\rangle ,v = - l r + \left\langle {{\dot{\gamma }} ,o (\psi )} \right\rangle , \\ \dot{u} = \left\langle {\ddot{\gamma },\chi (\psi )} \right\rangle + vr,\dot{v} = - l \dot{r} + \left\langle {\ddot{\gamma },o (\psi )} \right\rangle - ur. \end{array} \end{aligned}$$
(45)

Assume the disturbances terms \(d_v = 0\), based on Eqs. (44) and (45), the second equation of (5) by linearizing it about \(\beta = 0\) yields, we can give

$$\begin{aligned}&l\ddot{\beta }+ \left( \frac{{{d_{22}}l + \left( {m_{22}} - {m_{11}}\right) U}}{{{m_{22}}}}\right) {\dot{\beta }} + \frac{{{d_{22}}}}{{{m_{22}}}}U\beta \nonumber \\&\quad = \frac{\partial }{{{m_{22}}}}{\tau _r} + \left\langle {\ddot{\gamma },o (\psi )} \right\rangle , \end{aligned}$$
(46)

and its characteristic equation is given by

$$\begin{aligned} {p^2} + \left( \frac{{{d_{22}}l + \left( {m_{22}} - {m_{11}}\right) U}}{{{m_{22}}l}}\right) p + \frac{{{d_{22}}}}{{{m_{22}}l}}U = 0. \end{aligned}$$
(47)

The roots of (47) can be calculated by

$$\begin{aligned} {r_{1,2}} = \frac{{ - (\frac{{{d_{22}}l + ({m_{22}} - {m_{11}})U}}{{{m_{22}}l}}) \pm \sqrt{\frac{{4U{d_{22}}}}{{{m_{22}}l}}} \sqrt{\xi - 1} }}{2}, \end{aligned}$$
(48)

where \(\xi = {\frac{{\left( {{d_{22}}l + ({m_{22}} - {m_{11}})U} \right) }}{{4U{d_{22}}{m_{22}}l}}^2}\).

When \(\xi = 1\), the zero dynamics of system is critical damping with a compact form as

$$\begin{aligned} a{\varsigma ^2} - c\varsigma + b = 0, \end{aligned}$$
(49)

where \(\varsigma = \frac{U}{l}\), \(a = {({m_{22}} - {m_{11}})^2}\), \(b = d_{22}^2\), \(c = 2({m_{11}} + {m_{22}}){d_{22}}\). Therefore, its roots are

$$\begin{aligned} {\varsigma _1} = \frac{{c - \sqrt{{c^2} - 4ab} }}{{2a}},{\varsigma _2} = \frac{{c + \sqrt{{c^2} - 4ab} }}{{2a}}. \end{aligned}$$
(50)

To ensure sufficient stability of the system, the position of virtual control point is \(l=U/\varsigma _1+ o\) with a small positive constant o. At this time, the system enter the edge of over-damped state with \(0< U < {\varsigma _1}l\) to avoid excessive under damping effect.

5 Design of actuator controller

The backstepping method enables the actuator to track the command input variables \((\delta _c,n _c)\) quickly and stably, which can be obtained by the output variables \((T _{uc},F _{rc})\) of trajectory tracking controller with Eq. (3).

5.1 Propulsion angle control

Define the state variables \({x_1} = {\delta _r}\) and \({x_2} = {{\dot{\delta }}_r}\), the response model of propulsion angle in (4) is transformed into state space equation

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {x_2}\\ {{\dot{x}}_2} = - 2\xi {\omega _n}{x_2} - {\omega _n}^2{x_1}\mathrm{{ + }}K_\delta {\omega _n}^2\delta _a \end{array} \right. . \end{aligned}$$
(51)

Step 1: Define the propulsion angle surface

$$\begin{aligned} {z_{\delta 1} } = {x _1} - {\delta _c}. \end{aligned}$$
(52)

According to (51), we obtain

$$\begin{aligned} {{\dot{z}}_{\delta 1}} = {x_2} - {{{\dot{\delta }} }_c}. \end{aligned}$$
(53)

Step 2: Define the velocity error surface

$$\begin{aligned} {z_{\delta 2}} = {x_2} - \alpha \left( {{z_{\delta 1}}} \right) , \end{aligned}$$
(54)

then (53) becomes

$$\begin{aligned} {{\dot{z}}_{\delta 1}} = {z_{\delta 2}} + \alpha \left( {{z_{\delta 1}}} \right) - {{{\dot{\delta }} }_c}. \end{aligned}$$
(55)

To stabilize (51), the virtual control \(\alpha \left( {{z_{\delta 1}}} \right) \) is chosen as

$$\begin{aligned} \alpha \left( {{z_{\delta 1}}} \right) = - {k_1}{z_{\delta 1}} + {{{\dot{\delta }} }_c}, \end{aligned}$$
(56)

where \(k_1\) is a positive design parameter. And

$$\begin{aligned} {\dot{\alpha }} \left( {{z_{\delta 1}}} \right) = - {k_1}\left( {{z_{\delta 2}} - {k_1}{z_{\delta 1}}} \right) + {{\ddot{\delta }}_c}. \end{aligned}$$
(57)

Consider the Lyapunov function candidate \(V_{\delta 1}\) as

$$\begin{aligned} {V_{\delta 1}} = \frac{1}{2}{z_{\delta 1}}^2. \end{aligned}$$
(58)

The time derivative of \(V_{\delta 1}\) is

$$\begin{aligned} \begin{aligned} {{\dot{V}}_{\delta 1}}&= {z_{\delta 1}}\left( {{z_{\delta 2}} + \alpha \left( {{z_{\delta 1}}} \right) - {{{\dot{\delta }} }_c}} \right) \\&= - {k_1}{z_{\delta 1}}^2 + {z_{\delta 1}}{z_{\delta 2}}. \end{aligned} \end{aligned}$$
(59)

From (51) and (54), we obtain

$$\begin{aligned} \begin{aligned} {{\dot{z}}_{\delta 2}}&= - 2\xi {\omega _n}{x_2} - {\omega _n}^2{x_1} + K_\delta {\omega _n}^2\delta _a - {\dot{\alpha }} \left( {{z_{\delta 1}}} \right) \\&= f\left( {{x_1},{x_2}} \right) + K_\delta {\omega _n}^2\delta _a - {\dot{\alpha }} \left( {{z_{\delta 1}}} \right) \end{aligned}, \end{aligned}$$
(60)

where \(f\left( {{x_1},{x_2}} \right) = - 2\xi {\omega _n}{x_2} - {\omega _n}^2{x_1}\).

Consider the Lyapunov function candidate \(V_{\delta 2}\) as

$$\begin{aligned} {V_{\delta 2}} = {V_{\delta 1}} + \frac{1}{2}z_{\delta 2}^2. \end{aligned}$$
(61)

The time derivative of \(V_{\delta 2}\) is

$$\begin{aligned} {{\dot{V}}_{\delta 2}}= & {} - {k_1}{z_{\delta 1}}^2 + {z_{\delta 1}}{z_{\delta 2}} + {{\dot{z}}_{\delta 2}}{z_{\delta 2}}\nonumber \\= & {} {z_{\delta 2}}\left( {f\left( {{x_1},{x_2}} \right) + K_\delta {\omega _n}^2\delta _a - {\dot{\alpha }} \left( {{z_{\delta 1}}} \right) + {z_{\delta 1}}} \right) \nonumber \\&- {k_1}{z_{\delta 1}}^2. \end{aligned}$$
(62)

Next, we design the following nonlinear propulsion angle tracking control law

$$\begin{aligned} \begin{aligned} \delta _a =&\frac{1}{{K_\delta {\omega _n}^2}}\left( { - {k_2}{z_{\delta 2}} - {z_{\delta 1}} - f\left( {{x_1},{x_2}} \right) } \right) \\&+ \frac{1}{{K_\delta {\omega _n}^2}}{ {\dot{\alpha }} \left( {{z_{\delta 1}}} \right) } \end{aligned}. \end{aligned}$$
(63)

Then, (62) can be written as

$$\begin{aligned} {{\dot{V}}_{\delta 2}} = - {k_1}{z_{\delta 1}}^2 \le 0. \end{aligned}$$
(64)

Thus, the actual propulsion angle \(\delta _r\) of USV can track the command propulsion angle \(\delta _c\) by the control input \(\delta _a\) of propulsion angle with globally uniformly asymptotically stable.

5.2 Thruster speed control

Define the state variables \({x_3} = {n _r}\) and \({x_4} = {{\dot{n} }_r}\), the response model of thruster speed in (4) is transformed into state space equation

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_3} = {x_4}\\ {{\dot{x}}_4} = \frac{{K_qn_a - {n_r}}}{{{T_q}}} \end{array} \right. . \end{aligned}$$
(65)

Define the thruster speed surface

$$\begin{aligned} {z_{n} } = {x _3} - {n _c}. \end{aligned}$$
(66)

According to (65), we obtain

$$\begin{aligned} {{\dot{z}}_{n}} = {x_4} - {{\dot{n} }_d}=\frac{{K_qn_a - {n_r}}}{{{T_q}}} - {{\dot{n} }_c}. \end{aligned}$$
(67)

We design the following nonlinear thruster speed tracking control law

$$\begin{aligned} n_a = {T_q}{{\dot{n}}_c}/K_q + {n_r} - {T_q}{k_2}{z_n}, \end{aligned}$$
(68)

where \(k_2\) is a positive design parameter.

Consider the Lyapunov function candidate \(V_n\) as

$$\begin{aligned} {V_n} = \frac{1}{2}z_n^2. \end{aligned}$$
(69)

The time derivative of \(V_n\) is

$$\begin{aligned} \begin{aligned} {{\dot{V}}_n} = {{\dot{z}}_n}{z_n} = - {T_q}{k_2}z_n^2 \le 0. \end{aligned} \end{aligned}$$
(70)

Thus, the actual thruster speed \(n_r\) of USV can track the command thruster speed \(n_c\) by the control input \(n_a\) of thruster speed with globally uniformly asymptotically stable.

6 Simulation study

To verify the effectiveness of vector propulsion trajectory tracking controller designed in this paper, a vector propulsion USV in [42] is used for simulation. The vessel length is 7.02 m, other parameters are \(m_{11}=2652.25\), \(m_{22}=2825.29\), \(m_{33}=4201.26\), \(d_{11}=848.05\), \(d_{22}=2825.29\), \(d_{33}=22719.39\). And for response models of thruster speed and propulsion angle, their parameters are set as \({T_q} = 3\), \({K_q} = 1\), \(\omega _n = 2.84\), \( \zeta = 1.53\), and \(K_\delta = 1.02\). Moreover, the proposed method (PM) is compared with the standard sliding mode control method (SM) [48, 49] with the same parameters to highlight the advantages of proposed method. For the standard sliding mode control method, the control law (25) is replaced by

$$\begin{aligned} \begin{aligned} \mathbf{{u_c}}=&{B^{ - 1}}\left( { {{\ddot{P}}_g} - \lambda {\dot{P}_{eg}} - \sigma {P_{eg}} - F} \right) \\&+ {B^{ - 1}}\left( { - \mu S - \eta {\mathrm{sgn}} (S_i)} \right) \end{aligned}. \end{aligned}$$

In the simulation, the model uncertainties and external disturbances are added at 30 s. The uncertainty part of system is taken as \({\varDelta _i} = 0.2{f_i}, i=u, v, r\). The disturbing force and moment [50, 51] produced by external wind, wave and current are taken as

$$\begin{aligned} \begin{aligned} {b_u}&= 1000\left[ {1 + 0.5\sin (0.2t) + 0.3\cos (0.5t)} \right] ,\\ {b_v}&= 1000[ {1 + 0.5\sin (0.2t) + 0.3\cos (0.4t)} ],\\ {b_r}&= 1000\left[ {1 + 0.2\sin (0.1t) + 0.2\cos (0.2t)} \right] . \end{aligned} \end{aligned}$$

The magnitudes of actuated control variables are specified in the ranges given by \({n} \in [0 \quad 2670](r/min)\), \({\delta } \in [-5 \quad 5](^\circ )\).

The reference trajectory \(P_d\) is generated by the reference vessel with reference control variables, and the model parameters of reference vessel are consistent with the USV. For reference vessel, the initial state is (\(x_d\), \(y_d\), \(\psi _d\), \(u_d\), \(v_d\), \(r_d\)) (0) = 0. The reference control variables are

$$\begin{aligned} {n_d} = 2500 \text{ r/min }, {\delta _d} = \left\{ \begin{array}{l} 0^\circ ,\mathrm{{ t}} \le {\text{20 } \text{ s }}\\ 5^\circ ,\mathrm{{ t}} > {\text{20 } \text{ s }} \end{array} \right. . \end{aligned}$$

The initial state of USV is \(\left( {x,y,\psi ,u,v,r} \right) (0) = \{-10,-10,0,0,0,0\}\). The control point P is at the bow position with \(l=U_g/\varsigma _1+o, o = 0.7\). The control parameters are \({\lambda } = diag[0.3,0.003]\), \(\sigma = diag[0.0001,0.0001]\), \(\mu = diag[0.01,0.1]\), \(\eta = diag[0.1,1.0]\), \(\gamma = diag[10,10]\), \(\kappa = diag[0.0005,0.0005]\), \(\vartheta _1=\vartheta _2=0.02\), \(\rho _1 = \rho _2 = 2\), \(\alpha = 0.001\) and \(\varDelta = 100\).

Fig. 4
figure 4

Trajectory tracking result

Full size image
Fig. 5
figure 5

Velocities of surge, sway and yaw

Full size image
Fig. 6
figure 6

Velocity tracking errors of surge, sway and yaw

Full size image
Fig. 7
figure 7

Control inputs

Full size image
Fig. 8
figure 8

Sliding mode manifold

Full size image
Fig. 9
figure 9

The magnitude of tracking error

Full size image
Fig. 10
figure 10

The approximation curve of NN-MLP

Full size image
Fig. 11
figure 11

The approximation error estimation boundary

Full size image

The simulation results of the standard method (SM) and proposed method (PM) are shown in Figs. 4 - 11. Fig. 4 shows the reference trajectory \(P_d\) curve, the guide trajectory \(P_g\) curve and the actual motion trajectory P curve. It can be seen from the curve in Fig. 4 that the guidance trajectory can guide the controller to smoothly and gradually track the reference trajectory under the condition of large error, thus avoiding the problem of excessive control input in the initial stage. Fig. 5 shows the curves of the velocity of surge, sway and the yaw rate vary with time. It can be seen that the proposed method can achieve accurate tracking of the desired speed, while the standard method cannot achieve accurate tracking due to the disturbance. To explain the tracking effect more clearly, according to the curves of velocity tracking error \(u_e=u-u_d\), \(v_e=v-v_d\), \(r_e=r-r_d\) shown in Fig. 6, the velocity tracking error of the proposed method has better convergence than the standard method. Fig. 7 describes the control inputs n and \(\delta \), and the black dotted line represents the input saturation value. Under the constraint of input saturation, due to the influence of disturbance factors, the control input of standard method fluctuates obviously, while the control input curve of proposed method is smoother. And it can be seen that the actual control input (\(n_r\), \(\delta _r\)) can also achieve better tracking results when tracking the command control input (\(n_c\), \(\delta _c\)) from trajectory tracking controller. Figs. 8 and 9 show sliding mode manifold (\(S_1\),\(S_2\)) and the magnitude of tracking error \(E = \left| {P - {P_d}} \right| \) in the two methods. Because the parameters of the proposed method and standard method are completely consistent, it can be seen that the convergence curves of the two method are very similar in Figs. 8 and 9 before the model uncertainties and external disturbances are added at 30 s. However, after 30 s, the standard method is difficult to track accurately only relying on its own robustness. Although the convergence curves of the proposed method fluctuate at 30 s, they converge quickly afterward with a high precision. On the other hand, although the standard method cannot achieve accurate tracking due to model uncertainties and external disturbances, the standard method can still achieve tracking with certain errors under the guidance trajectory even if there is input saturation. Figs. 10 and 11 are the approximation of model uncertainty and environmental disturbance. It can be seen that NN-MLP can approach it well in Fig. 10, and its approximation error is estimated by \(\varpi \) in Fig. 11. Consequently, the simulation results demonstrate that the proposed controller is capable of attaining satisfactory tracking performance with the influence of input saturation, input coupling, actuator error, model uncertainty, and external disturbances.

7 Conclusions

In this paper, an adaptive trajectory tracking control method is proposed for vector propulsion USV. The control strategy aims to improve the robustness of system under the influence of input saturation, input coupling, actuator error, model uncertainty and external disturbances. Comparing with the previous research, the effects associated with the actuator, including input saturation, input coupling and actuator error, are considered in the development of the trajectory tracking controller, which is more in accordance with the engineering requirements. For the input coupling problem caused by vector propulsion, the virtual control point method is used to solve, and the stability condition is obtained by zero-dynamic stability analysis. To solve the problem of input saturation, a guidance trajectory is designed between the desired trajectory and the vessel to avoid overshoot of control input due to large error. Aiming at actuator error, model uncertainty and unknown environment disturbances in vessel motion control, a neural network estimation and upper bound estimation method are proposed. In addition, in the design of controller, to reduce the oscillation of controller caused by signum function, a continuously differentiable approximate saturation function is introduced instead of the signum function. In comparison with the standard sliding mode control method, the proposed control method can not only reduce the chattering of the error variable of E, but also make the E have a better performance and a small error, thus being more effective to be applied in the practical ship motion control for vector propulsion USV.

Note, this work naturally cannot attend to every detail of the motion controller design for vector propulsion USV, e.g., introducing anti-windup compensator to improve the performance of controller under input saturation, and fault-tolerant control for trajectory tracking with actuator failure. And considering that the selection of controller parameters will also affect the performance of the controller, to avoid adjusting too many control parameters, how to further simplify the number of controller parameters is also a very interesting problem to be discussed on the premise of ensuring that the controller has the same control performance.