A S-type bistable locally active memristor model and its analog implementation in an oscillator circuit

Abstract

In this paper, a S-type memristor with tangent nonlinearity is proposed. The introduced memristor can generate two kinds of stable pinched hysteresis loops with initial conditions from two flanks of the initial critical point. The power-off plot verifies that the memristor is nonvolatile, and the DC V-I plot shows that the memristor is locally active with the locally active region symmetrical about the origin. The equivalent circuit of the memristor, derived by small-signal analysis method, is used to study the dynamics near the operating point in the locally active region. Owing to the bistable and locally active properties and S-type DC V-I curve, this memristor is called S-type BLAM for short. Then, a new Wien-bridge oscillator circuit is designed by substituting one of its resistances with S-type BLAM. It finds that the circuit system can produce chaotic oscillation and complex dynamic behavior, which is further confirmed by analog circuit experiment.

1 Introduction

In 1971, Chua proposed the fourth basic circuit component called memristor in view of the symmetric logical relation of circuit theory [1], and the physical fabrication by Hewlett-Packard laboratory made the theoretical assumption of memristor come true [2]. Due to the special properties of nanometer size, low power consumption, inherent nonlinearity and nonvolatile, memristor possesses the great potentials of inducing new dynamical mode of electronic oscillation, enhancing the security of chaotic communication, increasing the reliability of chaotic encryption and improving the efficiency of neural network in searching optimal solution [3,4,5,6,7,8,9]. And it can be predicted that memristor will play a key role in the development of next-generation memory system with ultra-low energy consumption and high density memory [10]. Nevertheless, the characteristics of memristor need to be further explored and revealed.

The memristor with multistable characteristics can produce different types of pinched hysteresis loops under different initial conditions. In 2016, Ascoli proposed a bistable memristor endowed with a stable pinched hysteresis loop-pair, stimulated by DC as well as AC periodic signal [11]. Mannan found the coexisting pinched hysteresis loops in Chua corsage memristor [12]. In Ref [3], Chang proposed a bistable memristor model containing cubic term and found that its dynamics was governed by cubic term. Wang reported a three stable pinched hysteresis loops memristor by adding a polynomial characteristic function into the original Chua corsage memristor [13]. Wang also reported a multi-stable memristor by introducing periodic function and multiple equilibria [14]. It's inevitable that a multistable device would give rise to the multistability and complexity in a dynamical system. Therefore, it is of great significance to study the multistability of memristor.

Locally active memristor (LAM) is the memristor with negative memristance under a certain voltage crossed or the memristor with negative memductance under a certain current crossed [15,16,17]. It is uncovered that local activity is essential for nonlinear system to keep oscillation and amplify weak fluctuation signal. Therefore, local activity is considered to be the origin of all complexities in dynamical system [18,19,20]. In general, locally active memristor can be divided into two categories: the first one is not passive for which all points in the DC V-I plot lie in each quadrant, the second one is passive but locally active whose points in the DC V-I plot only lie in the first and third quadrant with VI ≥ 0. For example, Chua proposed a passive but locally active memristor based on piecewise linear function [21], and it was connected with an inductor and a battery to generate oscillating behavior with particular initial conditions and DC bias [12]. In addition, it has been found that some particular memristors, such as vanadium dioxide (VO2) and niobium oxide (NbOx) devices, are passive but locally active memristors [22, 23]. Pickett revealed that the NbOx devices have current-controlled negative differential resistance [24]. And the mathematical model for NbOx LAM was presented based on the Chua’s unfolding theorem and parameter optimization method [25]. Unlike nonvolatile memristor, most of the nanoscale LAMs have the characteristics of volatile resistance switching. Recently, a new type of nanoscale devices of locally active memristor, called S-Type LAM, was proposed [26,27,28]. And a S-Type LAM model with volatile resistance was then proposed [29]. S-Type LAM is a nonlinear local active device, which is simpler in concept than the passive memristor with negative resistance; thus it can form an oscillation circuit without pure negative resistor. However, the S-Type LAMs are difficult to commercially access due to the technology and cost of manufacturing nano-scale electronic component [30]. Therefore, in order to enrich the theoretical knowledge of S-Type LAM and explore its practical application in various fields, it is necessary to further study the emulator and simulation model in the area of negative differential resistance (NDR).

Memristor has been widely used in chaotic oscillator for the unique characteristics of storage and inherent nonlinear. For example, Sah proposed an oscillator made with only a memristor and a battery, which is distinct from the traditional electronic oscillator including at least two energy-storage elements and a locally active nonlinearity [31]. Wang modeled the neural network by utilizing flux-controlled memristor to describe the influence of electromagnetic radiation on neuron, and found that the simple neural network can induce infinite number of coexisting hidden attractors [32]. Zeng introduced an inductor-free two-memristor-based chaotic circuit, which is developed from a current feedback op amp-based sinusoidal oscillator. The proposed circuit has three line equilibria and can perform the dynamics of extreme multistability, amplitude death and transient transition behavior [7]. As a nonlinear locally active device, S-type LAM is conceptually simple for building oscillating circuit without pure negative resistor, and the local active region renders the oscillating system capable to amplify extremely small fluctuation in energy. Therefore, S-type LAM is preferred over other memristor in the design of chaotic oscillator [33,34,35]. In Ref [29], Wang designed a S-type LAM-based chaotic oscillator by using a resistor, a capacitor and an inductor. However, it is not clear whether S-type LAM could be used to other oscillating circuits such as Wien-bridge circuit. Therefore, it would be interesting and potentially valuable if S-type LAM could be successfully applied.

In this paper, we introduce a S-type bistable locally active memristor with tangent nonlinearity and study its associated memristor oscillator circuit. The main contribution of this work is summarized as follows: (1) The memristor can generate two kinds of stable pinched hysteresis loops induced from two flanks of the initial critical point of the initial condition. (2) The memristor is locally active and the locally active region is symmetrical about the origin. (3) The memristor has a S-type DC V-I plot and a nonvolatile power-off plot, which is different to the nanoscale LAMs and the S-type LAM in Ref [29] with volatile resistance. The rest of this paper is organized as below: In Sect. 2, the mathematical model of S-type bistable locally active memristor is presented and the voltage-current characteristics are analyzed by coexisting pinched hysteresis loops, power-off plot and DC V-I plot. In Sect. 3, the small-signal analysis method is used to study the equivalent circuit near the operating point in the locally active region and the frequency response of the impedance function is also revealed. Then, in Sect. 4, we design a new Wien-bridge oscillator circuit by using the proposed S-type BLAM and investigate its complex dynamics. In Sect. 5, an analog circuit is designed to experimentally confirm the proposed oscillator circuit. Finally, a brief conclusion including some concluding remarks is drawn in Sect. 6.

2 Memristor model and voltage-current characteristics

2.1 Model of S-type BLAM

Memristor can be categorized into ideal memristor, generic memristor and extended memristor, according to the mathematical definition [21]. The ideal memristor is the simplest model and the extended memristor is developed on the ideal one. The generic memristor is mathematically defined as

$$\left\{ \begin{gathered} y(t) = f(x,u,t)u(t) \hfill \\ \frac{{{\text{d}}x}}{{{\text{d}}t}} = g(x,u,t) \hfill \\ \end{gathered} \right. $$

(1)

where u(t), y(t) and x(t) are the input, output and internal state variable of the memristor; f(·) and g(·) are the functions that can be customized and related to the internal state variable x(t). The memristor is the voltage-controlled when the input is voltage and the output is current, while the memristor is the current-controlled if the input is current and the output is voltage. Now, a current-controlled generic memristor model is proposed, as below

$$ \left\{ {\begin{array}{*{20}c} {v = f(x,i) = (a_{0} + a_{1} x + a_{2} \tanh (x))i} \\ {\frac{{{\text{d}}x}}{{{\text{d}}t}} = g(x,i) = b_{1} x + b_{2} \tanh (x) - ci^{2} } \\ \end{array} } \right. $$

(2)

where i and v are the input current and output voltage; a₀, a₁, a₂, b₁, b₂ and c are the model parameters, which are set to a₀ = − 1, a₁ = − 1, a₂ = 3, b₁ = − 1, b₂ = 3, c = 0.5.

Next, we analyze the voltage–current characteristics of the memristor on the basis of coexisting pinched hysteresis loops, power-off plot and DC V-I plot, and consequently prove that it is bistable, nonvolatile and locally active.

2.2 Coexisting pinched hysteresis loops

When driven by a zero-mean input source with a certain amplitude and frequency, the input–output curve of memristor will pass through the origin in the voltage–current plane and exhibit a pinched hysteresis loop. A memristor with two coexisting pinched hysteresis loops is called bistable memristor [15, 33]. When two unequal initial values are located on both sides of the critical initial value X_C, the dynamic behavior of the bistable memristor appears to be two distinctly different and stable pinched hysteresis loops; when two unequal initial values are located on one side of the critical initial value, the dynamic behavior of the bistable memristor displays one monostable pinched hysteresis loop.

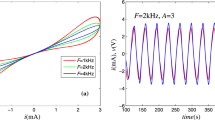
The sinusoidal current source i(t) = Asin(2πFt) with the amplitude A = 2 and frequency F = 0.1 is chosen as the driving source. When the initial values of X₀ = 0.526 and X₀ = 0.527 are located on both sides of the critical initial value X_C = 0.52677, two completely different stable pinched hysteresis loops are drawn in Fig. 1a, where the red curve stands for X₀ = 0.526 and blue curve stands for X₀ = 0.527. However, when the two initial values X₀ = 0.527 and X₀ = 0.528 are both greater than the critical initial value, the two pinched hysteresis loops are completely coincident, as shown in Fig. 1b. And when the two initial values X₀ = 0.525 and X₀ = 0.526 are both smaller than the critical initial value, the two pinched hysteresis loops are also completely identical, as shown in Fig. 1c.

Fig. 1

Coexisting pinched hysteresis loops with: different initial values of a x(0) = 0.526 and x(0) = 0.527, b x(0) = 0.527 and x(0) = 0.528; c x(0) = 0.525 and x(0) = 0.526; different amplitudes of d A = 1, e A = 1.9, f A = 2.1; different frequencies of g F = 0.08, h F = 0.0826, i F = 0.15

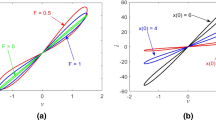
The coexisting pinched hysteresis loops depend not only on the initial value of memristor but also on the amplitude and frequency of the driving signal. When the initial values and frequency of the sinusoidal current source are fixed as X₀ =  − 1, X₀ = 1 and F = 0.1, the lower and upper limits of the critical amplitude are determined as A_C1 = 1.305 and A_C2 = 2.049227. Figure 1d shows two completely coincident pinched hysteresis loops with amplitude A = 1 (A < A_C1). While Fig. 1e displays the coexisting hysteresis loop with amplitude A = 1.9 (A_C1 < A < A_C2). When the amplitude increases to greater than the upper limit A_C2, such as A = 2.1, the two hysteresis loops coincide again, as shown in Fig. 1f.

The critical frequency value F_C is approximately equal to 0.0826 when X₀ = − 1, X₀ = 1 and A = 2. Figure 1g–i shows the evolution of pinched hysteresis loops as the frequency F monotonously increases. It’s found that the two pinched hysteresis loops with X₀ = − 1, X₀ = 1 and A = 2 evolve from stable superposition of low frequency with F < F_C, to coexistence of bistable state with F > F_C. And it’s found that the enclosed area of the pinched hysteresis loop shrinks monotonously with the increase of the excitation frequency.

It is worth noting that in the process of hardware circuit implementation, the different initial conditions can be realized by randomly switching the power supply. And in the process of PSIM circuit simulation, the different initial conditions can be realized by setting the initial voltage value of the capacitor. But in the process of DSP or FPGA implementation, the desired initial values can be expediently assigned [36].

2.3 Power-off plot and nonvolatility

When signal source is turned off, the non-volatile memristor can remember its most recent state. According to Chua’s memristor theorem [18, 21, 33], the memristor is non-volatile if the power-off plot (POP) intersects the ${{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} = 0$ axis at least twice with a negative slope. Therefore, the POP technology can not only judge the nonvolatility of memristor, but also reveal the changing process of the scalar state variable.

The POP of S-type BLAM can be obtained by setting i = 0 in g(·) of Eq. (2), as below

$$ \left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{i = 0} = b_{1} x + b_{2} \tanh (x) $$

(3)

It’s known from the POP in Fig. 2 that there are three intersections (equilibrium points) Q_-1, Q₀ and Q₁ with the ${{dx} \mathord{\left/ {\vphantom {{dx} {dt}}} \right. \kern-\nulldelimiterspace} {dt}} = 0$ axis. The scalar state variables corresponding to the three equilibrium points are x = − 2.9847, x = 0 and x = 2.9847, respectively. As we know that the two intersections Q_-1 and Q₁ with the ${{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} = 0$ axis have negative slopes, thus the designed S-type BLAM is nonvolatile. The state variable x in the upper half plane of POP will move to the right as time increases, and the state variable x in the lower half plane of POP will move to the left as time goes on. Accordingly, the equilibrium point is asymptotically stable when the state variables on both half planes converge toward it. On the contrary, the equilibrium point is unstable. Thus, we know from Fig. 2 that equilibrium points Q_-1 and Q₁ are asymptotically stable, while Q₀ is unstable. Therefore, for different initial states x₀, the memristor exhibits one of two asymptotically stable equilibrium states, i.e.

$$ x = \left\{ \begin{gathered} x({Q_{ - 1}}) = - 2.9847,\;{\text{if}}\;{x_0} \leqslant 0 \hfill \\ x({Q_1}) = 2.9847,\;{\text{if}}\;{x_0} > 0 \hfill \\ \end{gathered} \right. $$

(4)

Fig. 2

POP of S-type BLAM

2.4 DC V-I plot and local activity

As a powerful visualization tool to understand the intrinsic property of memristor, the DC V-I plot is a smooth curve composed of enough test points. A group of DC voltage v = V_k (k = 1,2,3,…,n) can be obtained by adding a group of continuous DC current i = I_k (k = 1,2,3,…,n) to S-type BLAM. Then, the state variable x = X_k (k = 1,2,3,…,n) is an equilibrium state satisfying $\frac{{{\text{d}}x}}{{{\text{d}}t}}\left| {_{{i = I_{k} }} } \right. = 0$, i.e.

$$ cI^{2} = b_{1} X + b_{2} \tanh (X) $$

(5)

It’s derived the functional relationship between the applied DC current I² and the equilibrium state X, expressed as

$$ I^{2} = \frac{{b_{1} X + b_{2} \tanh (X)}}{c} = \tilde{I}^{2} (X) $$

(6)

And the function between I and X can be deduced as

$$ I = \tilde{I}(X) $$

(7)

We obtain the DC voltage V when $a_{1} = b_{1} ,a_{2} = b_{2}$

$$ V = (a_{0} + a_{1} X + a_{2} \tanh (X))I = (a_{0} + cI^{2} )I $$

(8)

It’s further deduced the functional relationship between the output DC voltage V and the equilibrium state X by substituting Eq. (7) into Eq. (8), as denoted by

$$ V = V(I) = V(\tilde{I}(X)) = \tilde{V}(X) $$

(9)

The curves of DC V-I and equilibrium state are plotted in Fig. 3 with − 2 ≤ I ≤ 2. It can be seen from the X-I equilibrium state curve that the three equilibrium states X = 0 and X =  ± 2.9847 are consistent with the result in the POP curve. Moreover, the red curve (− 5 ≤ X ≤  − 2.9847) in the X-I diagram has a blood relationship with the red curve in the POP diagram. Similarly, the green and blue curve segments in the X-I diagram are related to the green and blue curve segments in the POP diagram, respectively. On the one hand, the slopes of the red and blue curve segments in the X-I diagram are both negative since they are caused by the stable equilibrium state, so the entire X-I curve is locally active. On the other hand, the curve segment in the lower half plane of X-I² diagram causes the discontinuity of the X-I and the X-V diagram. Moreover, each color segment in the X-V diagram has the same source with the corresponding color segment in the X-I diagram.

Fig. 3

a DC V-I plot of S-type BLAM and equilibrium state curve on b X-I² plane, c X-I plane and d X-V plane

It can be seen that the DC V-I plot has a continuous S-shaped behavior. And the slope of the green curve segment is negative, indicating that the introduced memristor is locally active. The ranges of DC current I and DC voltage V of the NDR are [− 0.8165, 0.8165] and [− 0.54433, 0.54433], shown in the cyan region. An impressive feature of the memristor is that the NDR region is symmetrical about the origin.

3 Small-signal analysis

3.1 Small-signal impedance function

There are several options for the electronic implementation of the memristor, such as high-frequency grounded memristor emulator circuit[37], memristive diode bridge [38] and floating memristor emulator circuit [39]. In this section, we will analyze the system response in NDR region by applying a small signal to the DC operating point of the nonlinear dynamical system. Also we can derive the small-signal equivalent circuit of the memristor by using the small-signal analysis method. Thus, a small-signal input current ∆i is applied to the DC operating point (V, I) of the memristor, and it gives rise to the responses v and x

$$\left\{ \begin{gathered} v = V + \Delta v \hfill \\ i = I + \Delta i \hfill \\ x = X + \Delta x \hfill \\ \end{gathered} \right. $$

(10)

Equation (2) can be expanded at equilibrium point Q(X, I) by Taylor expansion. Because the input signal working at the Q point is small enough, the higher-order term can be ignored. Accordingly, the resulting equations are given below

$$ \left\{ \begin{gathered} v = V + \Delta v = f(X,I) + {a_{11}}\Delta x + {a_{12}}\Delta i \hfill \\ \frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{{{\text{d}}(X + \Delta x)}}{{{\text{d}}t}} = g(X,I) + {a_{21}}\Delta x + {a_{22}}\Delta i \hfill \\ \end{gathered} \right. $$

(11)

where g(X, I) = 0 and

$$ \begin{aligned} {a_{11}} & = {\left. {\frac{{\partial f}}{{\partial x}}} \right|_Q} = I({a_1} + {a_2}{\operatorname{sech} ^2}(X)) \\ {a_{12}} & = {\left. {\frac{{\partial f}}{{\partial i}}} \right|_Q} = {a_0} + {a_1}X + {a_2}\tanh (X) \\ {a_{21}} & = {\left. {\frac{{\partial g}}{{\partial x}}} \right|_Q} = {b_1} + {b_2}{\operatorname{sech} ^2}(X) \\ {a_{22}} & = {\left. {\frac{{\partial g}}{{\partial i}}} \right|_Q} = - 2cI \\ \end{aligned} $$

The increments of voltage and state variable derivative can be expressed as

$$ \left\{ {\begin{array}{*{20}c} {\Delta v = a_{11} \Delta x + a_{12} \Delta i} \\ {\Delta \dot{x} = a_{21} \Delta x + a_{22} \Delta i} \\ \end{array} } \right. $$

(12)

And we obtain from (12)

$$ \left\{ {\begin{array}{*{20}c} {V(S) = a_{11} X(S) + a_{12} I(S)} \\ {SX(S) = a_{21} X(S) + a_{22} I(S)} \\ \end{array} } \right. $$

(13)

where V(S), X(S), I(S) are the Laplace transforms of ∆v, ∆x, ∆i, respectively. The small-signal impedance function of S-type BLAM at operating point Q is represented as

$$ Z\left( {S,Q} \right) = \frac{V(S)}{{I(S)}} = \frac{{a_{11} a_{22} }}{{S - a_{21} }} + a_{12} = \frac{{a_{12} S + \left| A \right|}}{{S - a_{21} }} $$

(14)

where $A = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } \\ {a_{21} } & {a_{22} } \\ \end{array} } \right]$. By setting S = jω, the frequency response Z(jω,Q) is given by

$$ Z(j\omega ,Q) = \frac{{a_{12} \omega^{2} - a_{21} \left| A \right| - ja_{11} a_{22} \omega }}{{a_{21}^{2} + \omega^{2} }} $$

(15)

The real part and imaginary part of Z(jω,Q) are obtained as

$$\left\{ \begin{gathered} \operatorname{Re} Z(j\omega ,Q) = \frac{{{a_{12}}{\omega ^2} - {a_{21}}\left| A \right|}}{{a_{21}^2 + {\omega ^2}}} \hfill \\ \operatorname{Im} Z(j\omega ,Q) = - \frac{{{a_{11}}{a_{22}}\omega }}{{a_{21}^2 + {\omega ^2}}} \hfill \\ \end{gathered} \right. $$

(16)

3.2 Small-signal equivalent circuit

The frequency responses of S-type BLAM with I = 0.8 and − 100 ≤ ω ≤ 100 are drawn in Fig. 4. It can be found that the real part ReZ(jω,Q) always remains a negative value in the entire frequency range. And the imaginary part ImZ(jω,Q) is negative when ω < 0 while it remains positive for ω > 0. What’s more, the imaginary part ImZ(jω,Q) first increases and then decreases as the frequency increases from ω = 0.

Fig. 4

Frequency responses of S-type BLAM with I = 0.8

The frequency response ImZ(jω,Q) with ω belonging to [− 100, 100] is depicted in Fig. 5a under some positive DC currents I within the local active area (I = 0, 0.2, 0.4, 0.6, 0.7 and 0.8165). It finds that the imaginary parts of the impedance functions for all the operating points are located in the first and third quadrants. When ω ≥ 0, the value of ImZ(jω,Q) is within the range of [0,0.4) and decreases with the decrease of the DC input current I. When the opposite DC input current I is selected as 0, − 0.2, −  0.4, −  0.6, −  0.7 and − 0.8165, the frequency response ImZ(jω,Q) is completely consistent with that of positive DC current I. This is probably induced by the symmetry of the local active region relative to the origin.

Fig. 5

a Frequency responses of ${\text{Im}} Z(j\omega ,Q)$ about different DC currents; b Frequency responses of ${\text{Re}} Z(j\omega ,Q)$ about different DC currents

Let ω vary in the range of [− 100, 100], the frequency response ReZ(jω,Q) with some positive DC currents I in the local active area is shown in Fig. 5b. It’s observed from Fig. 5b that the value of ReZ(jω,Q) is negative with the symmetry about ω = 0. And for the same frequency, the value of ReZ(jω,Q) increases with the increase of DC input current I. Furthermore, the frequency response ReZ(jω,Q) of the small signal impedance function is consistent with that of positive DC current I when the opposite negative current I is applied to S-type BLAM.

Based on the above analysis, the small-signal equivalent circuit of S-type BLAM at the operating point Q is depicted in Fig. 6, which can be regarded as the series connection of a negative resistance and an inductance

$$ Z(j\omega ,Q) = R(\omega ) + j\omega L(\omega ) $$

(17)

Fig. 6

Small-signal equivalent circuit of the proposed memristor

And the equivalent resistance R(ω) and inductance L(ω) are given by

$$ \left\{ \begin{gathered} R(\omega ) = \frac{{a_{12} \omega^{2} - a_{21} \left| A \right|}}{{a_{21}^{2} + \omega^{2} }} \hfill \\ L(\omega ) = - \frac{{a_{11} a_{22} }}{{a_{21}^{2} + \omega^{2} }} \hfill \\ \end{gathered} \right. $$

(18)

4 S-type BLAM-based oscillator circuit

4.1 Circuit model

Wien-bridge circuit has the advantages of stable oscillation, high-quality waveform and adjustable oscillation frequency [40, 41]. Thus, an active oscillator circuit, manipulated by substituting one resistance of Wien-bridge circuit with S-type BLAM, is built in Fig. 7.

Fig. 7

S-type BLAM-based Wien-bridge oscillator circuit

When taking the internal variable x of memristor, voltage V_C1 of capacitor C₁, voltage V_C2 of capacitor C₂ and current i_L of inductor L as the state variables, the mathematical expression of S-type BLAM-based Wien-bridge oscillator circuit is described by

$$ \left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}t}} = {b_1}x + {b_2}\tanh (x) - ci_L^2 \hfill \\ {C_1}\frac{{{\text{d}}{V_{C1}}}}{{{\text{d}}t}} = \frac{1}{{{R_3}}}\left( {\frac{{{R_5}}}{{{R_4}}}{V_{C1}} + {V_{C2}}} \right) - {i_L} - \frac{{{V_{C1}}}}{{{R_1}}} \hfill \\ {C_2}\frac{{{\text{d}}{V_{C2}}}}{{{\text{d}}t}} = - \frac{1}{{{R_3}}}\left( {\frac{{{R_5}}}{{{R_4}}}{V_{C1}} + {V_{C2}}} \right) \hfill \\ L\frac{{{\text{d}}{i_L}}}{{{\text{d}}t}} = {V_{C1}} - {R_2}{i_L} - ({a_0} + {a_1}x + {a_2}\tanh (x)){i_L} \hfill \\ \end{gathered} \right. $$

(19)

For the convenience of analysis, we introduce the following dimensionless variables and normalized circuit parameters

$$ \begin{gathered} x = x,\;\;V_{C1} = y,\;\;V_{C2} = z,\;\;i_{L} = w \\ \frac{1}{{R_{1} C_{1} }} = \frac{1}{{R_{3} C_{1} }} = \frac{1}{{R_{3} C_{2} }} = 1,\;\;\frac{{R_{5} }}{{R_{4} }} = d,\;\;\frac{1}{{C_{1} }} = e,\;\;\frac{1}{L} = f,\;\;\frac{{R_{2} }}{L} = g \\ \end{gathered} $$

Thus, the corresponding dimensionless circuit equation is deduced to be

$$\left\{ \begin{aligned} \dot x & = {b_1}x + {b_2}\tanh (x) - c{w^2} \\ \dot y & = (d - 1)y + z - ew \\ \dot z & = - (dy + z) \\ \dot w & = f(y - ({a_0} + {a_1}x + {a_2}\tanh (x))w) - gw \\ \end{aligned} \right. $$

(20)

For system (20), d, e, f, g are the control parameters; a₀, a₁, a₂, b₁, b₂, c are the internal parameters of memristor. Therefore, only some of the control parameters will be considered for the bifurcation analysis of system (20). As an inherent property of nonlinear dynamical system, symmetry may help to explain the appearance of symmetrical attractors with different shapes. We can easily notice that system (20) is invariant under the coordinate transformation (x, y, z, w) → (x, −  y, − z, −  w), which indicates the symmetry about x-coordinate axis.

4.2 Equilibrium point and its stability

When considering the parameter set P = {d = 0.5, e = 0.5, f = 1.78, g = 0.1, a₀ =− 1, a₁ =− 1, a₂ = 3, b₁ =− 1, b₂ = 3, c = 0.5}, we can obtain three equilibrium points of system (20), expressed as P₁ = (0, 0, 0, 0), P₂ = (0.22769,− 0.47107, 0.23554, 0.94215) and P₃ = (0.22769, 0.47107, −  0.23554, − 0.94215). The Jacobian matrix of system (20) can be calculated as

$$ J = \left[ {\begin{array}{*{20}c} {\frac{3}{{\cosh^{2} (x)}} - 1} & 0 & 0 & { - w} \\ 0 & {d - 1} & 1 & { - e} \\ 0 & { - d} & { - 1} & 0 \\ { - fw(\frac{3}{{\cosh^{2} (x)}} - 1)} & f & 0 & {f(1 + x - 3\tanh (x)) - g} \\ \end{array} } \right] $$

(21)

And the characteristic equation is

$$\begin{gathered} \left( {{{\left( {\lambda + 1} \right)}^{\text{2}}} - {\text{d}}\lambda } \right)\left( {\left( {\lambda - {h_2}} \right)\left( {\lambda + g - f{h_1}} \right) - f{w^2}{h_2}} \right) \hfill \\ + fe\left( {\lambda + 1} \right)\left( {\lambda - {h_2}} \right) = 0 \hfill \\ \end{gathered} $$

(22)

where $h_{1} = 1 + x - 3\tanh (x),h_{2} = \frac{3}{{\cosh^{2} (x)}} - 1$. By solving Eq. (22), the characteristic value for equilibrium point P₁ is: λ_1,2 = − 0.5216 ± 0.6114i, λ₃ = 1.2231, λ₄ = 2. Therefore, P₁ is an unstable saddle-focus of index-2. Similarly, for the equilibrium points P₂ and P₃, the eigenvalues are obtained as λ_1,2 = − 0.5367 ± 0.9942i, λ₃ = 3.061, λ₄ = − 0.7479. It shows that equilibrium points P₂ and P₃ are unstable saddle-focus of index-1.

4.3 Dissipation and existence of attractor

It is well known that chaotic flow can be divided into either conservative or dissipative one [42, 43]. For the conservative chaotic system, the phase space trajectory occupies an unchanged volume and there is no state space attribute; thus its divergence is zero. However, the phase orbit of dissipative system will shrink to a bounded subset with a zero-measured volume, which leads to the emergence of strange attractor and negative divergence [44, 45]. Accordingly, we can obtain the preliminary information related to the existence of attractive sets in the introduced S-type BLAM by calculating the volume shrinkage ∆v.

$$\Delta v = \frac{{\partial \dot x}}{{\partial x}} + \frac{{\partial \dot y}}{{\partial y}} + \frac{{\partial \dot z}}{{\partial z}} + \frac{{\partial \dot w}}{{\partial w}} = fx + \frac{{3(1 - f\sinh (x)\cosh (x))}}{{{{\cosh }^2}(x)}} + d + f - g - 3$$

(23)

The divergence curve on the system orbit x is drawn in Fig. 8. It finds that the time period for ∆v > 0 is sufficiently small before the point M(0.49, 0). And it can be considered that the divergence is always negative. Therefore, the system orbit in the phase space will converge to a subset of measure zero volume with an exponential rate, and there exists chaotic attractor in the introduced S-type BLAM.

Fig. 8

The plot of $\Delta v$ on the x system orbit

When taking the parameter set P and the initial value (x₀, y₀, z₀, w₀) = (0.1, 0.1, 0.1, 0.1), the chaotic attractors of system (20) are shown in Fig. 9. In addition, the Lapunov exponent can be calculated as LE₁ = 0.0463, LE₂ = − 0.0022, LE₃ = − 0.67338, LE₄ = − 0.6827, and the Kaplan–Yorke dimension is D_KY = 3 + (0.0463 − 0.0022 − 0.67338)/0.6827 = 2.0782. Therefore, it can be further explained that system (20) is indeed chaotic.

Fig. 9

The phase diagram of system (20) in a x-w plane; b y-w plane. c z-w plane

4.4 Dynamics evolution with control parameter

The dynamics evolution influenced by the control parameters is intuitively studied, as a rule, executed with the detecting technologies of bifurcation diagram and Lyapunov exponent.

First, the system dynamics versus control parameter d is considered, under the condition of parameter set P and initial state (0.1, 0.1, 0.1, 0.1). It can be seen from Fig. 10 that the dynamics switches between period and chaos when parameter d varies in the range of [0.01, 1.2]. The detailed dynamics is analyzed by slicing parameter ranges. In the interval of d ∈ [0.01, 0.4), the system origins from period-1 at d = 0.01, and enters into chaos through chaos crisis at d = 0.225, then exits from chaos through tangent bifurcation and enters into period-2 behavior. After a short period-2 state, it enters into chaotic state again through the chaos crisis at d = 0.26. After passing through a short chaotic region, it enters into period-3 state at d = 0.28 through tangent bifurcation. The forward period doubling bifurcation begins at d = 0.32 and it enters into chaotic state at d = 0.325. And at d = 0.365, it enters into the period-4 state through the tangent bifurcation. In the interval of d ∈ [0.4, 0.6), the system evolves from the period-4 state to the period-5 state and produces four chaos branches. After a long period-4 state, it generates four remerging primary bubbles through forward and reverse period-doubling bifurcations at d = 0.415. When d = 0.428, it exits from the period-4 state and enters into period-8 state via the forward period bifurcation again. Then it immediately enter into chaotic state. At d = 0.565, it enters into period-5 state via the tangent bifurcation. In the interval of d ∈ [0.6, 1.2], the system undergoes similar dynamics evolution of the interval d ∈ [0.01, 0.4).

Fig. 10

a Bifurcation diagram and b Lyapunov exponent spectrum versus parameter d

Then, the dynamics evolution influenced by the control parameter f is considered. As depicted in Fig. 11, the system switches between period and chaos when parameter f varies in the range of [1.74, 1.92]. In addition, it can be seen that the system enters into or exits from chaos via forward and reverse period-doubling bifurcation, tangent bifurcation and chaos crisis. In the interval of f ∈ [1.74, 1.752), the system origins from forward period-doubling bifurcation to chaos. In the interval of f ∈ [1.752, 1.88), the system enters into period-5 state through tangent bifurcation at f = 1.768. Then it enters into a short-term chaos through chaos crisis at f = 1.772. Next, the first reverse period-doubling bifurcation occurs at f = 1.782, and the system exits from chaotic state and enters into period-4 state. Then, the system has a similar evolution in the range of [1.772, 1.782). In the interval of f ∈ [1.88, 1.92], the system is mainly chaotic, accompanied by abundant short period windows.

Fig. 11

a Bifurcation diagram and b Lyapunov exponent spectrum versus parameter f

4.5 Local basins of attraction and multistability

The attraction basin can intuitively provide detailed information of multistable dynamics by measuring the size of attractor. For the typical parameter set P of S-type BLAM-based Wien-bridge system (20), the local basin of attraction in the y₀-w₀ initial plane under x₀ = 0.1 and z₀ = 0.1 and that in the x₀-z₀ initial plane under y₀ = 0.1 and w₀ = 0.1 are depicted in Fig. 12. The attraction regions marked with different colors in Fig. 12 represent the initial condition regions showing completely different oscillation patterns, i.e., different types of coexisting attractors.

Fig. 12

Local basins of attraction in a y₀-w₀ plane with x₀ = 0.1 and z₀ = 0.1; b x₀-z₀ plane with y₀ = 0.1 and w₀ = 0.1

The phase diagrams of coexisting oscillation patterns corresponding to different attraction regions are numerically drawn in Fig. 13. Specifically, the phase diagrams under the initial conditions (0.1, 0, 0.1, 0), (0.1, 0, 0.1, 1) and (0.1, 0.5, 0.1, −  1) in Fig. 13a correspond to the red, yellow and blue regions in Fig. 12a, and the phase diagrams under the initial conditions (0.2, 0.1, 0, 0.1), (− 0.2, 0.1, 0, 0.1) and (− 0.4, 0.1,−  0.2, 0.1) in Fig. 13b correspond to the red, yellow and blue regions in Fig. 12b. It is obvious that the red region corresponds to the double-scroll chaotic attractor, the yellow region corresponds to stable point attractor, and the blue region corresponds to the single-scroll chaotic attractor. The numerical results show that the disconnected coexisting attractors emerge in the S-type BLAM-based Wien-bridge system. Therefore, the dynamical behavior not only depends on the memristor initial condition x₀ but also on the other initial conditions z₀, y₀ and w₀.

Fig. 13

Different types of coexisting attractors in a different attraction regions of Fig. 12 (a); b different attraction regions of Fig. 12 (b)

4.6 Transient dynamics

The transient dynamics will emerge when there is a non-attracting chaotic saddle in the phase space, for which the orbit is always characterized by chaotic behavior before another motion mode appears. When the parameters d = 1.03, e = 0.497, f = 1.7514, g = 0.058, a₀ = − 1, a₁ = − 1, a₂ = 3, b₁ = − 1, b₂ = 3, c = 0.5 and initial conditions (x₀, y₀, z₀, w₀) = (0.1, 0.1, 0.1, 0.1) are selected, the time-domain waveform and phase diagrams of the system (20) are drawn in Fig. 14. It’s shown that it displays a double scroll chaotic attractor when t < 200 s. However, when t is in the range of [200,600], it displays the period-1 motion mode. Therefore, the transient dynamics results in the generation of two attractors with different topological structures.

Fig. 14

a Time-domain diagram of x in the region of [0 s, 600 s]; phase portrait for the time intervals [0 s, 200 s] and [200 s, 600 s] in b y-w plane and c z-w plane

5 Implementation of S-type BLAM-based circuit

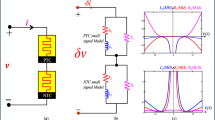
Circuit implementation is of great significance for the practical application of chaotic system. In addition, the results of theoretical analysis and numerical simulation also need to be further verified by circuit observation. In this section, an analog electronic circuit, for physically realizing system (20) in different cases, is constructed based on the improved module-based technique [46,47,48]. The circuit schematic diagram of the S-type BLAM-based Wien-bridge system is designed as Fig. 15. The hyperbolic tangent functions tanh(·) and − tanh(·) are implemented by a differential pair [6], as shown in Fig. 16. In fact, the tangent function can also be handily implemented by embedded system [49]. It's noted that the proportional compression is not performed in the circuit implementation since the variable of amplitude works in the desired ranges of the operational amplifier [50] and that it is important to ensure an appropriate DC operating point [51]. The chip model of multiplication, operational amplifier and bipolar junction transistor are selected as AD633JN, TL082 and 2N1711 to achieve low-cost execution. In addition, different resistors and ceramic capacitors are used. The main circuit in Fig. 15 consists of four integrators, three inverters, one tanh module and one inverting tanh module. And in Fig. 15, A and B are the input and output ports of the hyperbolic tangent function module, C and D are the input and output ports of the inverting hyperbolic tangent function module.

Fig. 15

Circuit diagram of memristor-based Wien-bridge circuit

Fig. 16

Circuit diagrams of a function tanh(·) and b function − tanh(·)

Based on the topology of Fig. 15 and circuit theory, we establish the circuit state equation

$$ \left\{ \begin{aligned} R{C_1}\frac{{{\text{d}}x}}{{{\text{d}}t}} & = - \frac{R}{{{R_1}}}x + \frac{R}{{{R_2}}}\tanh (x) - \frac{R}{{{R_3}}}{w^2} \\ R{C_2}\frac{{{\text{d}}y}}{{{\text{d}}t}} & = - \frac{R}{{{R_4}}}y + \frac{R}{{{R_5}}}z - \frac{R}{{{R_6}}}w \\ R{C_3}\frac{{{\text{d}}z}}{{{\text{d}}t}} & = - \frac{R}{{{R_9}}}y - \frac{R}{{{R_{10}}}}z \\ R{C_4}\frac{{{\text{d}}w}}{{{\text{d}}t}} & = \frac{R}{{{R_{11}}}}y + \frac{R}{{{R_{12}}}}w + \frac{R}{{{R_{13}}}}xw - \frac{R}{{{R_{14}}}}\tanh (x)w \\ \end{aligned} \right. $$

(24)

When the time constant is considered as RC_i = 1 ms with R = 10kΩ and C_i = 100nF (i = 1, 2, 3, 4), the other circuit parameters of Fig. 15 are determined by

$$ \begin{gathered} R_{1} = R_{5} = R_{7} = R_{8} = R_{10} = R_{15} = R_{16} = R_{17} = R_{18} = R = 10k\Omega \hfill \\ R_{2} = \frac{R}{3} = 3.333k\Omega ,\;\;R_{3} = R_{4} = R_{6} = R_{9} = \frac{R}{0.5} = 20k\Omega \hfill \\ R_{11} = R_{13} = \frac{R}{1.78} = 5.618k\Omega ,\;\;R_{12} = \frac{R}{1.68} = 5.952k\Omega ,\;\;R_{14} = \frac{R}{5.34} = 1.873k\Omega \hfill \\ \end{gathered} $$

The circuit parameters for hyperbolic tangent function and inverting hyperbolic tangent function are fixed as

$$ \begin{gathered} R_{r2} = R_{r5} = R_{r6} = R_{r7} = R_{r8} = R_{r10} = R_{r13} = R_{r14} = R_{r15} = R_{r16} = 10k\Omega \hfill \\ R_{r1} = R_{r9} = 0.52k\Omega ,\;\;R_{r3} = R_{r4} = R_{r11} = R_{r12} = 1k\Omega ,\;\;I_{1} = I_{2} = 1.1mA \hfill \\ \end{gathered} $$

For comparative analysis, the parameter condition P mentioned above is considered excepting for f = 1.75, 1.753, 1.78 to obtain period-2 attractor, single scroll chaotic attractor and double scroll chaotic attractor, as shown by the numerical results in the left part of Fig. 17. When f equals to 1.75, 1.753 and 1.78, the resistances R₁₁ and R₁₃ are calculated to be 5.7143kΩ, 5.7045kΩ and 5.618kΩ, the resistance R₁₂ is calculated to be 6.0606kΩ, 6.0496kΩ, and 5.952kΩ, and the resistance R₁₄ is calculated to be 1.9048kΩ, 1.9015kΩ, and 1.873kΩ. The corresponding phase diagrams are experimentally observed in the right part of Fig. 17, which agree well with the numerical simulation.

Fig. 17

Numerical and experimental results for (a₁-a₂) period-2 attractor; (b₁-b₂) single scroll chaotic attractor and (c₁-c₂) double scroll chaotic attractor

6 Conclusion

This paper presented a S-type locally active memristor and explored its application in oscillator circuit. The introduced S-type memristor possesses a symmetric locally active domain and two different bistable pinched hysteresis loops. Especially, the bistable pinched hysteresis loops are not only affected by the initial value, but also by the amplitude and frequency of the applied sinusoidal signal. The DC V-I plot and POP plot have been carried out to verify the locally active and nonvolatile characteristics of the memristor. Compared with the reported S-Type memristor, the obvious feature of S-type BLAM is the nonvolatility and the origin symmetry of the local active region. Moreover, a new Wien-bridge oscillator circuit is designed based on S-type BLAM. It finds that the circuit system can produce chaotic oscillation and complex dynamic behavior, which is further confirmed by analog circuit experiment. The proposed locally active memristor is compared with the one in Ref [29] from the basis of locally active range, non-volatility, bi-stability, etc., as given in Table 1.

Table 1 Comparison of S-type locally active memristor